Preference learning and multiple criteria decision aiding: differences, commonalities, and synergies—part II

Abstract

This article elaborates on the connection between multiple criteria decision aiding (MCDA) and preference learning (PL), two research fields with different roots and developed in different communities. It complements the first part of the paper, in which we started with a review of MCDA. In this part, a similar review will be given for PL, followed by a systematic comparison of both methodologies, as well as an overview of existing work on combining PL and MCDA. Our main goal is to stimulate further research at the junction of these two methodologies.

1 Introduction

Continuing the first part of this paper, in which we provided a brief survey of the state of the art in multiple criteria decision aiding (MCDA), this article begins with a similar survey of preference learning (PL). In Sect. 3, both methodologies are then compared with each other, and their differences but also commonalities are presented and discussed in a systematic way. Finally, Sect. 4 elaborates on existing work on combining PL and MCDA, prior to concluding the paper in Sect. 5.

2 Preference learning

Broadly speaking, preference learning is machine learning with preference data, that is, data in the form of preferences represented in a qualitative (e.g., order relations) or quantitative (e.g., utility degrees) way. Preference information plays a key role in automated decision-making and appears in various guises in artificial intelligence (AI) research. In particular, the formal modeling of preferences can be considered an essential aspect of autonomous agent design. Yet, in spite of the existence of formalisms for representing preferences in a compact way, such as CP-networks (Boutilier et al. 2004), modeling preferences by hand is a difficult task. This is an important motivation for preference learning, which is meant to support and partly automate the design of preference models.

Computerized methods for revealing the preferences of individuals (users) are useful not only in AI but also in many other fields showing a tendency for personalization of products and services, such as computational advertising, e-commerce, and information retrieval, where such techniques are also known as “learning to rank” (cf. Sect. 2.2). Correspondingly, a number of methods and tools have been proposed with the goal of leveraging the manifold information that users provide about their preferences, either explicitly via ratings, written reviews, etc., or implicitly via their behavior (shopping decisions, websites visited, and so on). Typical examples include recommender systems and collaborative filtering, which can be viewed as special cases of preference learning.

By way of background, we subsequently recall some basics of machine learning, which helps to better understand the preference learning methods discussed in the remainder of this section.

2.1 Background on machine learning

The field of machine learning has grown quickly over the last decades, and a wide repertoire of learning tasks and ML methodologies have been proposed. An ML setting is typically specified by a precise description of the learning task and performance metrics to be optimized, as well as assumptions on what type of data is observed by the learner, how this data has been generated, etc. Such assumptions constitute an important prerequisite for analyzing formal properties of learning algorithms solving the task. Examples of specific settings include active learning (Bachman et al. 2017), imitation learning (Hussein et al. 2017), transfer learning (Yang et al. 2020), interactive learning (Ware et al. 2001), adversarial learning (Lowd and Meek 2005), and online learning (Shalev-Shwartz 2011), amongst others. In terms of methodology, a basic distinction (according to the type of supervision) is often made between the paradigms of supervised, unsupervised, and reinforcement learning (Sutton and Barto 2018).

2.1.1 Supervised learning and predictive modeling

In supervised learning, the goal is to learn a predictive model that captures the (stochastic) dependence between instances X and associated outcomes Y. In the standard setting, training data consists of a set $\mathcal {D} = \{ (x_i, y_i) \}_{i=1}^N$ of N examples in the form of tuples $(x_i, y_i) \in \mathcal {X} \times \mathcal {Y}$, with $\mathcal {X}$ being the instance space and $\mathcal {Y}$ the set of possible outcomes. Typically, these examples are assumed to be independent and identically distributed (i.i.d.) according to some unknown probability measure $P$ on $\mathcal {X} \times \mathcal {Y}$ (with mass or density function $p$). The measure $P$ characterizes the data-generating process and is the target of generative learning. While the latter is interested in the joint occurrence of data (X, Y), discriminative learning focuses on the conditional dependence of Y on X. It proceeds from a hypothesis space $\mathcal {H} \subset \mathcal {Y}^\mathcal {X}$, where each hypothesis is a map (predictor) $\mathcal {X}\longrightarrow \mathcal {Y}$. The learner then seeks the “best predictor”, viz. the expected loss minimizer (Bayes predictor)

$$\begin{aligned} h^* \in \mathop {\textrm{argmin}}\limits _{h \in \mathcal {H}} \mathcal {R}(h) \end{aligned}$$

(1)

minimizing the risk (expected loss)

$$\begin{aligned} \mathcal {R}(h) = {\mathbb {E}}_{(X,Y) \sim P} \, \ell (Y, h(X)) = \int _{\mathcal {X}\times \mathcal {Y}} \ell ( h(x), y) \, d \, P\,, \end{aligned}$$

(2)

where $\ell$ is a loss function $\mathcal {Y} \times \mathcal {Y} \longrightarrow {\mathbb {R}}$ penalizing predictions deviating from the true outcome. To produce an approximation h of the Bayes predictor, the empirical risk

$$\begin{aligned} \mathcal {R}_{emp}(h) = \frac{1}{N} \sum _{i=1}^N \ell ( h(x_i), y_i ) \end{aligned}$$

(3)

will typically serve as an indicator of the true risk.

As can be seen, supervised learning is essentially a problem of inductive inference and generalization: How to make sure that a hypothesis h does not only perform well on the training data in the sense of having a low empirical risk (3), but also generalizes well beyond this data and yields accurate predictions ${\hat{y}}_{q} = h(x_q)$ for new query instances $x_{q} \in \mathcal {X}$ (randomly sampled according to $P_X$)? In this regard, a key insight is that a strong performance on the training data does normally not imply a strong performance on new data. Otherwise, learning could simply be accomplished through a sufficiently flexible hypothesis space $\mathcal {H}$, which allows the learner to reduce the loss on the training data close to 0. This, however, will normally result in “over-fitting” the data, a phenomenon suggesting that the data—possibly including noisy examples, outliers, etc.— is fit more than warranted. Therefore, in practice, the main challenge is to choose a hypothesis space of the right complexity, which is well adapted to the complexity of the sought relationship between X and Y as well as the amount of training data $\mathcal {D}$ available.

2.1.2 From predictive to prescriptive modeling

Recent applications of machine learning reveal a noticeable shift from its use for predictive modeling in the sense of a data-driven construction of models mainly used for the purpose of prediction (of ground-truth facts) to its use for prescriptive modeling, namely, the task of learning a model that stipulates appropriate decisions about the right course of action in real-world scenarios: Which medical therapy should be applied? Should this person be hired for the job? As argued by Hüllermeier (2021), prescriptive modeling comes with new technical conditions for learning and new demands regarding reliability, responsibility, and the ethics of decision-making.

A basic assumption in the standard setting of supervised learning is that Y does (or will) exist independently of the prediction. In other words, for every concrete instance X, there is a “ground truth” Y, and hence a ground-truth (albeit non-deterministic) dependence between instances and outcomes (specified by the map $X \mapsto p(Y \, | \,X)$). For example, if the prediction is a weather forecast for tomorrow, based on weather conditions in the last days (X), the “ground-truth weather” Y does (or will) indeed exist, independently of the prediction, just like a disease exists independently of the diagnosis or a handwritten digit independently of its image-based prediction.

This view of outcomes Y or, more generally, a dependence between instances and outcomes, as “ontic” entities that ought to be “discovered”, and hence of ML as an analytic task, is arguably less appropriate in the context of algorithmic decision making (ADM), where Y is a decision made by the learner in a situation X. Here, the problem of constructing a decision model is essentially of synthetic nature. Imagine, for example, that Y is not a diagnosis but a drug or a therapy. In this case, Y is not an ontic entity and should be perceived as a prescription rather than a prediction. As a consequence, a real ground truth may not exist in prescriptive ML, and hence not be available for training. At best, a decision is accompanied by some hint at how effective it was (Beygelzimer and Langford 2009; Bottou et al. 2013; Swaminathan and Joachims 2015a, b; Kallus 2017). Also, the training data will often be affected by various sorts of bias (Atan et al. 2018; Fernandez and Provost 2019), for example, the subjective bias of the human decision-maker acting as a teacher, or caused by dependencies between decisions (e.g., the same candidate cannot be assigned to multiple jobs in parallel), thereby violating assumptions on the data-generating process as common in the predictive modeling setup (such as independent and identically distributed data).

Switching the focus from prediction to prescription may also have an influence on the learning objectives and performance measures. For example, the optimization of average or expected performance (2) might be considered inappropriate in the context of social decision-making, as it may suggest sacrificing performance on an ethnic minority for the benefit of a bigger subpopulation (Slowik and Bottou 2021).

2.1.3 Unsupervised and weakly supervised learning

Unsupervised learning is neither of a predictive nor a prescriptive nature but rather of a descriptive nature. It is essentially concerned with summarizing the data, which consists of data objects X without label information Y, representing it in a convenient way, and extracting interesting and meaningful patterns from the data. Unsupervised learning is closely related to what is often called exploratory data analysis (Tukey 1977) or data mining (Fayyad et al. 1996). Examples include the learning of generative models (i.e., probabilistic models of the data-generating process), dimensionality reduction techniques such as principal components analysis, cluster analysis, outlier detection, association analysis (i.e., the extraction of well-supported patterns in the form of IF—THEN rules).

Weakly supervised learning (Zhou 2018) is an umbrella term for ML settings in between supervised and unsupervised learning, in which supervision in the form of label information attached to training instances is present but weaker than in the standard setting of supervised learning. In fact, supervision can be imperfect or weak in various ways, as the previous discussion about prescriptive ML has shown. However, many other scenarios are conceivable. For example, the data can be incomplete in the sense that not the entire training data is labeled but only a subset thereof, like in semi-supervised learning (van Engelen and Hoos 2020). In multi-instance learning, for example, labels are not attached to individual instances but only to sets or bags of instances (for example, a bag is labeled positive if it is known to contain at least one positive instance) (Dietterich et al. 1997; Foulds and Frank 2010). Similarly, in learning from aggregate outputs, labels are given in the form of an aggregation over a certain set of instances (e.g., an average) (Musicant et al. 2007; Bhowmik et al. 2016, 2019). Also interesting is the characterization of the outcome (response) associated with a training instance in terms of a subset (or, more generally, a graded subset (Hüllermeier 2014) or a generalized uncertainty distribution (Denoeux and Zouhal 2001; Denoeux 1995)) of possible candidates (Liu and Dietterich 2012)—imagine, for example, a situation in which some decisions can definitely be excluded as a good choice, but several candidates still remain. The problem of learning from such data, which is related to what is called coarse data in statistics (Heitjan and Rubin 1991; Gill et al. 1997), has received increasing attention in recent years (Grandvalet 2002; Jin and Ghahramani 2002; Nguyen and Caruana 2008; Cour et al. 2011).

2.1.4 Reinforcement learning

Conventional reinforcement learning (RL) considers a scenario in which an agent seeks to learn a policy prescribing appropriate state-dependent actions, so as to maximize its long-term performance in a dynamic environment (Sutton and Barto 2018): In each step of the sequential decision process, the agent observes the current state of the environment and selects an action, which in turn changes the state according to the dynamics of the environment. Occasionally, the agent receives feedback about its actions in the form of a (possibly delayed) reward signal. The goal of the agent is to choose actions so as to maximize its (expected) long-term reward.

Thus, RL may also be considered to be half-way between unsupervised learning (where the agent does not receive any form of feedback) and supervised learning (where it would be told the correct action in certain states). A typical RL problem can be formalized as a Markov Decision Process (MDP), consisting of a set of states S in which the agent operates, a set of actions A the agent can perform, a Markovian state transition function $\delta :\, S \times A \longrightarrow {\mathbb {P}}(S)$, where ${\mathbb {P}}(S)$ denotes the set of probability distributions over S (thus, $T(s,{a},s') = \delta ({s},{a})({s'})$ is the probability that action ${a} \in A$ in state ${s} \in S$ leads the agent to successor state ${s'}$), a reward function $r:\, S \times A \longrightarrow {\mathbb {R}}$, where r(s, a) is the reward the agent receives for performing action a in state s.

The most common task is to learn a policy $\pi :\, S \longrightarrow A$ that prescribes the agent how to act in each situation (state). More specifically, the goal is often defined as maximizing the expected sum of rewards (given the initial state s), with future rewards being discounted by a factor $\gamma \in (0,1]$:

$$\begin{aligned} V^\pi (s) \, = \, {\mathbb {E}} \left[ \sum _{t=0}^\infty \gamma ^t r(s_t, \pi (s_t)) \, \vert \, s_0 = s \right] \end{aligned}$$

(4)

With $V^*(s)$ the best possible value that can be achieved for (4), a policy $\pi ^*$ is called optimal if it achieves the best value in each state s.

The learning task, then, is to find an optimal policy, typically under the assumption that the process model (state transition and reward function) is not known. Therefore, the agent is supposed to learn an optimal policy through a proper exploration of its environment. Most approaches tackle the RL problem by estimating the expected reward in each state or in each state-action pair. Given such estimates, the agent can define an optimal policy by performing the action that leads to the state with the highest estimated reward (if the state transitions are known) or by picking the action that leads to the highest estimate among all state-action pairs in the current state. Alternatively, so-called policy-search algorithms learn a suitable policy more directly, for example, by representing policies in a parameterized form and estimating a gradient in the policy space.

2.2 Ranking

Ranking is one of the key tasks in the realm of preference learning. A ranking is a special type of preference structure, namely, a strict total order, that is, a binary relation $\succ$ on a set $\mathcal {A}$ of alternatives that is total, irreflexive, and transitive. In agreement with our preference semantics, $a \succ b$ suggests that alternative a is preferred to alternative b. However, in a wider sense, the term “preference” can simply be interpreted as any kind of order relation. For example, $a \succ b$ can also mean that a is an algorithm that outperforms b on a certain problem, or that a is a student finishing her studies more quickly than another student b.

In order to evaluate the predictive performance of a ranking algorithm, an accuracy measure (or loss function) is needed that compares a predicted ranking ${\hat{\tau }}$ with a given reference (“ground-truth”) ranking $\tau$. To this end, one can refer, for example, to distance measures commonly used in the literature, such as the Kendall distance

$$\begin{aligned} \ell _K(\tau , {\hat{\tau }}) = \# \big \{ (i,j) \, | \,\tau (i) < \tau (j) \wedge {\hat{\tau }}(i) > {\hat{\tau }}(j) \big \} \,, \end{aligned}$$

(5)

i.e., the number of discordant pairs of items, or the Spearman distance

$$\begin{aligned} \ell _S(\tau , {\hat{\tau }}) = \sum _i \big ( \tau (i) - {\hat{\tau }}(i) \big )^2 \,. \end{aligned}$$

(6)

A possible disadvantage of such measures is their equal treatment of all positions in a ranking, i.e., a mistake in the top is penalized in the same way as a mistake in the bottom part. In many applications, however, the top positions are more important than the rest of the ranking. Therefore, specialized measures like the (normalized) discounted cumulative gain have been proposed in fields such as information retrieval (Liu 2011). Sometimes, different assumptions are also made regarding the ground-truth that a predicted ranking is compared to. In document retrieval, for example, the ground-truth is not necessarily a ranking but could be a dichotomy: some documents are deemed relevant to a query while others are not. In a “good” ranking, the former should then be placed ahead of the latter.

Depending on the performance measure, finding an optimal prediction through expected or empirical loss minimization can become a difficult problem, especially because most measures are not (instance-wise) decomposable. For example, finding the generalized median

$$\begin{aligned} {\hat{\tau }} = \mathop {\textrm{argmin}}\limits _\tau \sum _{i=1}^m \ell ( \tau _i, \tau ) \,, \end{aligned}$$

i.e., the ranking that minimizes the sum of distances to given rankings $\tau _1, \ldots , \tau _m$, is known to be an NP-hard problem in the case where $\ell = \ell _K$ (Dwork et al. 2001).

Different types of ranking tasks have been studied in preference learning. In the following, we provide a compact overview of two important tasks referred to, respectively, as object ranking and label ranking.

2.3 Learning from object preferences

In so-called object ranking, the task is to induce a ranking function $r(\cdot )$ that is able to order any (finite) subset $\mathcal {O}$ of an underlying (possibly infinite) class $\mathcal {X}$ of objects. That is, $r(\cdot )$ assumes as input a subset $\mathcal {O} = \{ x_1, \ldots , x_m \} \subseteq \mathcal {X}$ of objects and returns as output a permutation $\tau$ of $\{1,\ldots , m \}$. The interpretation of this permutation is that, for objects $x_{i},x_{j} \in \mathcal {O}$, the former is preferred to the latter whenever $\tau (i) <\tau (j)$. The objects themselves are typically characterized by a finite set of n features, i.e., in terms of a feature vector (attribute-value representation)

$$\begin{aligned} x = \left( x^{(1)}, \ldots , x^{(n)} \right) \in \mathcal {X}= \mathcal {X}_1 \times \ldots \times \mathcal {X}_n \,. \end{aligned}$$

For example, an object $x = (7.4, 76, 0.997, \ldots , 0.56)$ could be a red wine characterized in terms of physicochemical properties such as acidity, chlorides, density, sulfates, etc., and $x \succ x'$ could mean that red wine x has a better quality (taste) than $x'$ (Cortez et al. 2009). A ranking task would be specified by a subset $\mathcal {O}$ of red wines, for which a ranking in terms of quality is sought.

2.3.1 Learning utility functions

One way to represent a ranking function r is via a (latent) value or utility function, i.e., a function $f:\, \mathcal {X}\longrightarrow \mathcal {U}$ that assigns a utility degree $u = f(x)$ to each object x. Typically, the utility scale $\mathcal {U}$ is the real number line ($\mathcal {U} = {\mathbb {R}}$) or a part thereof (e.g., $\mathcal {U} = [0,1]$), but ordinal utility scales (e.g., 1 to 5-star ratings) are also commonly used. Note that this representation implicitly assumes an underlying total order relation, since numerical (or at least totally ordered) utility scores enforce comparability of alternatives as well as transitivity. Applying the ranking function r (associated with f) to a subset $\mathcal {O} \subset \mathcal {X}$ then simply means scoring each $x_i \in \mathcal {O}$ in terms of $f(x_i)$ first and sorting the $x_i$ in decreasing order of their scores afterward. Evaluating alternatives in terms of a utility function is indeed a very natural way of representing preferences, which has a long tradition in economics and decision theory (Fishburn 1969).

Object ranking essentially reduces to a standard regression or ordinal regression problem (depending on the underlying utility scale) if the training data offers the utility scores (even if corrupted with noise) right away, i.e., if the data is of the form

$$\begin{aligned} \mathcal {D} = \big \{ (x_i, u_i ) \big \}_{i=1}^m \subset \mathcal {X} \times \mathcal {U} \,. \end{aligned}$$

Training a predictor (regression function) f on such data is sometimes called the “pointwise learning” approach. Yet, numerical information about the utility $u_i$ of individual objects $x_i$ can rarely be assumed. More commonly encountered is comparative preference information of the form $x_i \succ x_j$, which is often easier to elicit or can be induced from observations in an implicit way. For example, Joachims (2002) studies a scenario where the training information could be provided implicitly by the user who clicks on some of the links in a query result and not on others. This information can be turned into (noisy) binary preferences by assuming a preference of the selected pages over those nearby pages that are not clicked on.

A preference $x_i \succ x_j$ gives rise to a constraint on the (latent) utility function f and suggests that $f(x_i) > f(x_j)$, i.e., alternative $x_i$ should have a higher utility score than alternative $x_j$. Thus, the challenge for the learner is to find a value function that is as much as possible in agreement with a set of such constraints. For object ranking, this idea has first been formalized by Tesauro (1989) under the name comparison training. He proposed a symmetric neural network architecture that can be trained with representations of two states and a training signal that indicates which of the two states is preferable. The elegance of this approach comes from the property that one can replace the two symmetric components of the network with a single network, which can subsequently provide a real-valued evaluation of single states. Similar ideas have also been investigated for training other types of classifiers, in particular support vector machines. We already mentioned (Joachims 2002) who analyzed “click-through data” in order to rank documents retrieved by a search engine according to their relevance. The case where f is a linear function $x \mapsto \langle \theta , x \rangle$ is especially simple. As

$$\begin{aligned} \langle \theta , x_i \rangle> \langle \theta , x_j \rangle \quad \Leftrightarrow \quad \langle \theta , x_i - x_j \rangle > 0 \,, \end{aligned}$$

a preference $x_i \succ x_j$ can be transformed into a positive training example $(x_i - x_j, +1)$ and a negative example $(x_j - x_i, -1)$ for a linear classifier (which predicts a vector z as positive if $\langle \theta , z \rangle > 0$ and negative otherwise). Thus, ranking is essentially reduced to binary classification. In general, learning a (latent) utility function f from pairwise preferences between objects is called the “pairwise learning” approach.

Instead of learning from pointwise or pairwise training data, a latent utility function can also be induced from rankings $x_1 \succ x_2 \succ \ldots \succ x_m$ of any size. Directly learning from data of that kind (instead of decomposing a ranking into pairwise preferences) is referred to as the “listwise learning” approach (Cao et al. 2007). What this approach requires is a notion of how well a utility function fits an observed ranking. To this end, one can refer to probabilistic models of ranking data, such as the Plackett-Luce (PL) distribution, which assumes a parameter $v_i > 0$ for every choice alternative $x_i$ and models the probability of a ranking $\tau : x_1 \succ x_2 \succ \ldots \succ x_m$ as

$$\begin{aligned} p(\tau ) = \prod _{i=1}^m \frac{v_i}{v_i + \ldots + v_m} \,. \end{aligned}$$

Now, suppose the PL parameters are specified in a functional form as $v = f_\theta (x)$, where $\theta$ is a parameter vector; a simple example is a log-linear utility function $f_\theta (x) = \exp (\langle x, \theta \rangle )$. Then, given training data $\mathcal {D} = \{ \tau _j \}_{j=1}^N$ in the form of (i.i.d.) rankings $\tau _j: x_{j,1} \succ x_{j,2} \succ \ldots \succ x_{j,m_j}$, the log-likelihood of $\theta$ is given by

$$\begin{aligned} L(\theta ) = \sum _{j=1}^N \sum _{i=1}^{m_j} \log \big (f_\theta (x_{j,i}) \big ) - \sum _{j=1}^N \sum _{i=1}^{m_j} \log \left( \sum _{k=i}^{m_j} f_\theta (x_{j,k}) \right) \,. \end{aligned}$$

Invoking the statistical principle of maximum likelihood, learning can then be accomplished by finding the maximizer

$$\begin{aligned} {\hat{\theta }} = \mathop {\textrm{argmax}}\limits _\theta L(\theta ) \,. \end{aligned}$$

(7)

The parameter ${\hat{\theta }}$ can then be used to predict the ranking for any new set of objects $\{ x_1, \ldots , x_m \}$ (or, more specifically, to predict a probability distribution over the set of all rankings of these objects). Note that the likelihood will normally be a nonlinear function of $\theta$, so that the maximization problem (7) might not be easy to solve.

2.3.2 Learning preference relations

An alternative to learning latent utility functions consists of learning binary preference relations (Rigutini et al. 2011). Thus, the idea is to approach the object ranking problem by learning a binary preference predicate $h(x,x')$, which predicts whether x is preferred to $x'$ or vice versa. Such a predicate can be realized in the form of a binary classifier $\mathcal {X} \times \mathcal {X} \longrightarrow \{ -1, +1 \}$, which accepts the tuple $(x,x')$ as input and returns $+1$ if $x \succ x'$ and $-1$ if $x' \succ x$, More generally, h can also be a real-valued map $\mathcal {X} \times \mathcal {X} \longrightarrow {\mathbb {R}}$ expressing the strength of evidence $x \succ x'$; a special case could be a probabilistic classifier, where $h(x,x') \in [0,1]$ is the probability of $x \succ x'$. For training such a classifier, data in the form of pairwise preferences can be leveraged in a straightforward way: a preference $x_i \succ x_j$ gives rise to a positive training example $((x_i,x_j), +1)$ and a negative example $((x_j,x_i),-1)$.

Unlike a (unary) utility function f, which implies reflexivity, antisymmetry, and transitivity of the induced preference relation, a (binary) comparison function h trained in this way does not guarantee any of these properties, which are naturally required in the context of ranking. Technically, the classifier receives a concatenated vector $z = [x_i|x_j]$ as input, for which it produces an output h(z). A priori, however, there are no specific constraints between the outputs produced for inputs $[x_i|x_j]$ and $[x_j|x_i]$, or for $[x_i|x_j]$, $[x_j|x_k]$, and $[x_i|x_k]$. Reflexivity and antisymmetry could be assured by using a predictor

$$\begin{aligned} g(x_i, x_j) = \phi \big ( h(x_i, x_j) - h(x_j, x_i) \big ) \,, \end{aligned}$$

where $\phi$ is any function ${\mathbb {R}} \longrightarrow {\mathbb {R}}$ such that $\phi (0)=0$ and $\phi (x) = - \phi (-x)$. Then, $g(x_i, x_i) = 0$ and $g(x_i, x_j) = - g(x_j, x_i)$. The case of transitivity is not easily solvable, however.

In some situations, incomparability or even intransitivity might be desirable—in fact, intransitive behavior is commonly observed both for animals and humans (Tversky 1969; Roy 1996). The increased expressivity of a binary preference relation compared to a utility function can then be seen as an advantage. However, if a ranking of a set $\mathcal {Q} = \{ x_1, \ldots , x_m \}$ is eventually sought as a prediction, intransitivity does clearly pose a problem. The common approach, then, is to enforce a ranking by applying a ranking procedure to the binary preference relation $Q = (q_{i,j})_{1 \le i,j \le m}$, where $q_{i,j} = h(x_i, x_j)$ (or $= g(x_i, x_j)$). For example, the Borda ranking is obtained by assigning each alternative $x_i$ the Borda score

$$\begin{aligned} s_i = \sum _{j \ne i} q_{i,j} \,, \end{aligned}$$

and then sorting $x_1, \ldots , x_m$ in decreasing order of their respective scores $s_1, \ldots , s_m$.

2.4 Learning from label preferences

In addition to learning from object preferences, another important type of ranking problem is learning from label preferences. A key difference between object and label ranking concerns the formal representation of the preference context and the alternatives to be ordered. In object ranking, the context is (implicitly) assumed to be fixed, and hence not represented at all. What changes from one prediction task to the other is the set of objects to be ranked (e.g., red wines), and these objects are characterized in terms of associated properties. In label ranking, it is somehow the other way around: The alternatives to be ranked are always the same, and just identified by labels without properties (as in classification learning). It is now the ranking context that changes from task to task, which is characterized in terms of properties. For example, the task might be to rank a prespecified set of wines, say, $\{\text {Biferno Rosso DOC}, \text {Signature Malbec}, \text {Karia Chardonnay}, \text {Sauvignon Blanc} \}$, depending on the context, which could be described by the time of the day, the type of meal, etc.

Formally, in label ranking, preferences are contextualized by elements x of an instance space $\mathcal {X}$, and the goal is to learn a ranking function $\mathcal {X}\longrightarrow \mathcal {S}_{m}$ for a fixed $m \ge 2$, where $\mathcal {S}_{m}$ is the set of rankings (permutations) of $\{1, \ldots , m \}$. Thus, for any instance $x \in \mathcal {X}$, a prediction in the form of an associated ranking $\succ _{x}$ of a finite set $\mathcal {L} =\{\lambda _{1},\ldots ,\lambda _{m}\}$ of labels or alternatives is sought, where $\lambda _{i} \succ _{x}\lambda _{j}$ means that $\lambda _{i}$ is preferred to $\lambda _{j}$ in the context x. Again, the quality of a prediction of that kind is typically captured in terms of a rank distance or correlation measure such as (5) or (6). The training information consists of a set of instances for which (partial) knowledge about the associated preference relation is available. More precisely, each training instance x is associated with a subset of all pairwise preferences. Thus, despite the assumption of an underlying (“true”) target ranking, the training data is not expected to provide full information about such rankings (and may even contain inconsistencies, such as pairwise preferences that are conflicting due to observation errors).

Applications of this general framework can be found in various fields, for example, in marketing research; here, one might be interested in discovering dependencies between properties of clients and their preferences for products. Another application scenario is meta-learning, where the task is to rank learning algorithms according to their suitability for a new dataset, based on the characteristics of this dataset (Brazdil et al. 2022).

2.4.1 Learning utility functions

Just like the object ranking task, label ranking can be tackled by learning (latent) utility functions or binary preference relations. Recall that a utility function in the setting of object ranking is a mapping $f:\, \mathcal {X}\longrightarrow \mathcal {U}$ (where typically $\mathcal {U} = {\mathbb {R}}$) that assigns a utility degree f(x) to each object x and, thereby, induces a linear order on $\mathcal {X}$. As opposed to this, in the label preferences scenario, a utility function $f_{i}:\, \mathcal {X}\longrightarrow \mathcal {U}$ is needed for every label $\lambda _i$, $i = 1, \ldots , m$. Here, $f_i(x)$ is the utility assigned to alternative $\lambda _i$ in the context x. To obtain a ranking for x, the alternatives are ordered according to their utility scores, i.e., a ranking $\succ _{x}$ is derived such that $\lambda _i \succ _{x}\lambda _j$ implies $f_{i}(x) \ge f_{j}(x)$.

A corresponding method for learning the functions $f_{i}(\cdot )$ from training data has been proposed in the framework of constraint classification, which allows for reducing a label ranking to a single binary classification problem. The learning method proposed by Har-Peled et al. (2002) constructs two training examples, a positive and a negative one, for each given preference $\lambda _{i} \succ _{x}\lambda _{j}$, where the original d-dimensional training example (feature vector) $x = (x^{(1)}, \ldots , x^{(d)})$ is mapped into an $(m \times d)$-dimensional space:

$$\begin{aligned} {\bar{x}} = \left( 0, \ldots , 0, \underbrace{x^{(1)}, \ldots , x^{(d)}}_{i^{th} \text { block}}, 0, \ldots , 0, \underbrace{-x^{(1)}, \ldots , -x^{(d)}}_{j^{th} \text { block}}, 0, \ldots , 0 \right) \end{aligned}$$

This expanded vector is a positive example for the preference $\lambda _{i} \succ _{x}\lambda _{j}$ in the sense that $\langle {\bar{x}}, w \rangle > 0$ should hold for an $(m \times d)$-dimensional weight vector w; likewise, $-{\bar{x}}$ is a negative example for this preference. Any learning method for binary classification can be used for finding a suitable linear model w. Finally, the individual utility functions pertaining to the labels $\lambda _i$ are obtained by splitting w into m blocks, i.e., $f_i(x) = \langle x, w_i \rangle$, where $w_i$ is the $i^{th}$ block of vector w.

Another approach is to fit a PL model with the following parameterization (Cheng et al. 2010):

$$\begin{aligned} \theta _i = \exp \big ( \langle x, w_i \rangle \big ) \end{aligned}$$

Thus, the parameters of the model are now functions of the context $x$. Summarising the weight vectors $w_1, \ldots , w_m \in {\mathbb {R}}^d$ in a matrix $W \in {\mathbb {R}}^{m \times d}$, the entire weight vector $\theta$ is obtained as $\theta = \exp ( W x)$. As PL specifies a probabilistic model, $W$ can be learned by maximum likelihood. For example,, given training data $\mathcal {D} = \{ (x_i, \pi _i ) \}_{i=1}^N$, the estimate is of the form

$$\begin{aligned} \hat{W} = \mathop {\textrm{argmax}}\limits _{W} \sum _{i=1}^N \log p\big ( \pi _i \, | \,\theta = \exp ( W x_i ) \big ) \end{aligned}$$

This leads to a convex optimization problem that must be solved numerically.

Given a new query $x$, a prediction is obtained by computing $(\theta _1, \ldots , \theta _K) = \exp ( \hat{W} x)$ and setting

$$\begin{aligned} {\hat{\pi }} = {\mathrm{arg\,sort}} \{ \theta _1, \ldots , \theta _K \} \,. \end{aligned}$$

2.4.2 Learning preference relations

An alternative to learning latent utility functions consists of learning binary preference relations, which essentially amounts to reducing preference learning to binary classification. For object ranking, the pairwise approach has been pursued by Cohen et al. (1998). The authors propose to solve object ranking problems by learning a binary preference predicate $Q(x, x^\prime )$, which predicts whether x is preferred to $x^\prime$ or vice versa. A final ordering is found in the second phase by deriving a ranking that is maximally consistent with these (possibly conflicting) predictions.

The relational approach to label ranking has been introduced by Hüllermeier et al. (2008) as a natural extension of pairwise classification, a well-known class binarization technique. The idea is to train a separate model (base learner) $h_{i,j}$ for each pair of labels $(\lambda _{i},\lambda _{j}) \in \mathcal {L}^2$, $1 \le i <j \le m$; thus, a total number of $m(m - 1)/2$ models are needed. For training, a preference information of the form $\lambda _{i} \succ _{x}\lambda _{j}$ is turned into a (classification) example (x, y) for the learner $h_{a,b}$, where $a = \min (i, j)$ and $b = \max (i, j)$. Moreover, $y = 1$ if $i < j$ and $y= 0$ otherwise. Thus, $h_{a,b}$ is intended to learn the mapping that outputs 1 if $\lambda _{a} \succ _{x}\lambda _{b}$ and 0 if $\lambda _{b} \succ _{x}\lambda _{a}$. This mapping can be realized by any binary classifier. Instead of a {0, 1}-valued classifier, one can of course also employ a scoring classifier. For example, the output of a probabilistic classifier would be a number in the unit interval [0, 1] that can be interpreted as a probability of the preference $\lambda _{a} \succ _{x}\lambda _{b}$.

At classification time, a query $x_{0} \in \mathcal {X}$ is submitted to the complete ensemble of binary learners. Thus, a collection of predicted pairwise preference degrees $h_{i,j}(x)$, $1 \le i,j \le m$, is obtained. The problem, then, is to turn these pairwise preferences into a ranking of the label set $\mathcal {L}$. To this end, different ranking procedures can be used. The simplest approach is to extend the (weighted) voting procedure that is often applied in pairwise classification: For each label $\lambda _i$, a score

$$\begin{aligned} S_{i}\, =\,\sum _{1\le j\ne i\le m} h_{i,j}(x_{0}) \end{aligned}$$

is derived, where $h_{i,j}(x_{0}) = 1 -h_{j,i}(x_{0})$ for $i > j$, and then the labels are ordered according to these scores. Despite its simplicity, this ranking procedure has several appealing properties. Apart from its computational efficiency, it turned out to be relatively robust in practice, and, moreover, it possesses some provable optimality properties in the case where the Spearman distance (6) is used as an underlying loss function. Roughly speaking, if the binary learners are unbiased probabilistic classifiers, the simple “ranking by weighted voting” procedure yields a label ranking that minimizes the expected Spearman distance (Hüllermeier and Fürnkranz 2010). Finally, it is worth mentioning that, by changing the ranking procedure, the pairwise approach can also be adjusted to loss functions other than Spearman distance.

2.5 Other settings

A number of variants of the above ranking problems have been proposed and studied in the literature. For example, a setting referred to as instance ranking is very similar to object ranking. However, instead of relative (pairwise) comparisons, training data consists of absolute ratings of alternatives; typically these ratings are taken from an ordinal scale, such as 1 to 5 stars, but might even be binary in the simplest case. Moreover, a predicted ranking is not compared with another (ground-truth) ranking but with the partition induced by the rating of the alternatives (Hüllermeier and Vanderlooy 2009; Fürnkranz et al. 2009).

Attempts have also been made at combining object and label ranking, that is, to exploit feature representations of both the preference context and the alternatives to be ranked. For example, Schäfer and Hüllermeier (2018) propose a framework called dyad ranking. The basic idea is to combine both pieces of information by means of a joint feature map $\phi :\, \mathcal {X}\times \mathcal {Y}\longrightarrow \mathcal {Z}$ and to learn a value function $f:\, \mathcal {Z}\longrightarrow {\mathbb {R}}$; here, $\mathcal {Y}$ is a parametric or structured space of alternatives and $\mathcal {Z}\subseteq {\mathbb {R}}^{d}$ a joint feature space (Tsochantaridis et al. 2004).

2.6 Unsupervised preference learning

Problems in the realm of learning to rank can essentially be seen as supervised learning problems with specific characteristics, such as weak supervision and structured outputs. Yet, other learning and data analysis tasks can of course also be considered for preference data, including those that are commonly categorized as unsupervised learning. One example is cluster analysis, i.e., the clustering of ranking data. This problem can again be tackled on the basis of probabilistic models, for example assuming that observations are generated by a mixture of Mallows or Plackett-Luce distributions, and estimating the parameters of these distributions. However, since observed rankings might only be partial, models for complete rankings need to be extended correspondingly (Busse et al. 2007).

Another example is frequent pattern mining in preference data. Henzgen and Hüllermeier (2019) addresses this problem for rank data, that is, data in the form of (complete or incomplete) rankings of an underlying set of items. More specifically, two types of patterns are considered, namely frequent (sub-)rankings (e.g., on products A, B, C, 90% of the users share the relative preference $A \succ B \succ C$) and dependencies between such rankings in the form of association rules (e.g., users who prefer A to B are likely to prefer G to D, or expressed as a rule: If $A \succ B$ then $G \succ D$). The authors propose data structures and efficient algorithms for mining patterns of that kind in potentially very large databases.

2.7 Online preference learning and preference-based RL

Various problems in the realm of online machine learning have been extended to preference-based variants as well. An important example is the classical multi-armed bandits (MAB) problem, in which an agent is supposed to simultaneously explore and exploit a given set of choice alternatives in the course of a sequential decision process. In the standard setting, the agent learns from stochastic feedback in the form of real-valued rewards. In many applications, however, numerical reward signals are not readily available-instead, only weaker information is provided, in particular relative preferences in the form of qualitative comparisons between pairs of alternatives. This observation has motivated the study of variants of the multi-armed bandit problem, in which more general representations are used both for the type of feedback to learn from and the target of prediction.

The dueling bandits problem (Yue and Joachims 2009) describes an online learning scenario, in which the observed feedback consists of comparative preference information. In its basic form, there are m choice alternatives (options) $a_{1},\dots ,a_{m}$ (a.k.a. “arms” in analogy to the arms of a slot machine). At any time step t, the learner can choose to compare two of these arms as its action, say, $a_{i_{t}},a_{j_{t}}$, whereupon it observes preferential feedback $f_{t}$ over the chosen arms¹, which is either $a_{i_t} \succ a_{j_t}$ or $a_{j_t} \succ a_{i_t}.$ The feedback is typically assumed to be of stochastic nature and for sake of convenience, encoded by a binary variable such that $f_{t} \sim \textrm{Ber}(q_{i_{t},j_{t}})$ and $q_{i_t,j_t} \in [0,1]$ is the probability that $a_{i_t}$ is preferred over (“wins against”) $a_{j_t}.$ This way, the feedback is supposed to depend on the underlying reciprocal preference relation $Q {:=}(q_{i,j})_{1\le i,j\le m} \in [0,1]^{m\times m},$ the entries of which specify the probability that an arm will be preferred over another, which are, however, unknown to the learner.

Different goals and learning tasks have been considered in the literature for this basic learning scenario. Typically, the learner either tries to maximize a certain reward associated with its choice $(i_t,j_t)$ (or alternatively minimize a so-called regret incurred from its choice), or it tries to identify a feature of the underlying environmental parameters Q as quickly as possible, such as the best of all arms (perhaps assuming its existence) or a (partial) ranking over all arms. While multiple notions of “best arm” are conceivable, the arguably most natural one is the Condorcet winner (CW), which is defined as the arm $i^*$ that outperforms any other arm $j\not = i^*$ in the sense that $q_{i^*,j} \ge 1/2$ for all $j\not =i^*$. Whilst regret minimization usually requires a trade-off between exploration (trying unknown arms to avoid missing good ones) and exploitation (playing supposedly good arms to accumulate reward), the mere identification of the best arm or an underlying ranking can rather be seen as a pure exploration task.

Interesting research questions in this field include the development of efficient algorithms as well as the proof of theoretical upper and lower bounds on certain performance measures required to solve certain learning tasks. For the case of regret minimization, the performance is typically measured by means of the total regret incurred until the end of the learning process, whereas in pure exploration tasks, the sample complexity or the error probability of a learner are usually used. The former corresponds to the number of samples queried (or conducted duels) by the learner before termination, while the latter is the probability that the learner outputs a wrong decision after it terminates.

In this regard, theoretical assumptions made on the stochastic nature of the feedback mechanism play an important role, and such assumptions can either be parametric (e.g., a PL assumption) or non-parametric (e.g., certain types of transitivity). On the one side, these assumptions should facilitate learning such as decreasing the necessary sample complexity for achieving the task, on the other side, they may also ensure that the learning task set is actually well-defined. For example, the CW for a given preference relation Q may not exist, so the learning task of finding the CW is not always well-defined.

By considering more general variants of the action space or the feedback mechanism, one can obtain several generalizations of the basic dueling bandits scenario. In multi-dueling bandits (Haddenhorst et al. 2021), for instance, the learner chooses $k \ge 2$ arms $i_{1},\dots , i_{k}$ in each time step, which then compete with each other in a multi-duel and produce an observation in the form of a single winner. One can also consider a slight variant, where a pairwise preference is observed for every pair in the chosen subset (Brost et al. 2016; Saha and Gopalan 2018). In contextual dueling bandits, one assumes additional context information to be available in every iteration, which may influence the outcome of a duel. Again, this can be extended to the case of multi-duels. Since all these generalizations are still revolving around the issue of how to learn from the preferential feedback, it seems natural to refer to the induced class of learning problems as preference-based multi-armed bandits or preference-based bandits. Bengs et al. (2021) provides a comprehensive survey of the field.

2.8 Preference-based reinforcement learning

Reinforcement learning (RL) is closely connected to the MAB setting discussed in the previous section. While the conventional RL setting (cf. Sect. 2.1.4) relies on numeric evaluations of state-action pairs for task specification, preference-based extensions generally employ qualitative feedback, commonly in the form of pairwise trajectory comparisons. The most direct way to extend RL to a preference-based setting is to exploit the relationship to the bandit setting. This approach is taken by Busa-Fekete et al. (2014), who treat every possible policy as an arm and then, by solving the resulting dueling bandit problem, identify a preferred policy.

In addition to this way of directly learning a policy from preference feedback, Wirth et al. (2017) distinguishes two further classes of PbRL approaches. Both of them rely on first learning a predictive preference model, and then deriving a policy from that model. This split of preference- and policy learning can be beneficial since, in contrast to bandits, the RL problem cannot be reduced to identifying individual action values. This is because each action may influence the state of the environment and thereby the quality of future actions. Therefore, actions cannot be evaluated individually without taking the larger context of future actions (i.e., the policy) into account. Since the space of all possible policies is generally very large, learning preferences in this space can be challenging.

This limitation can be lifted with access to the dynamics of the environment, however. If we know which action will trigger which state transition, it is possible to compose individual action evaluations to estimate long-term quality, e.g., in the form of a $Q$-function (cf. Sect. 2.1.4). Due to the lower dimensionality, these local preferences are much easier to learn. Consider, for example, the relative difficulty of comparing two alternative chess strategies, as opposed to simply determining the winner based solely on two terminal board states. Although the dynamics are usually not known up-front, it is often possible to sample from them through interaction with the environment. We can gather these samples in the policy learning phase, requiring no additional human supervision. Therefore, by interleaving phases of preference learning with longer phases of policy learning, we can make more efficient use of human feedback.

The first class of preference-based approaches identified by Wirth et al. (2017) directly relies on a general preference model without assuming latent utilities. This is exemplified by Fürnkranz et al. (2012), who realize this approach by treating action evaluation as a label ranking (c.f. Sect. 2.4) problem. The learned label ranker can then be interpreted as a policy. The second class is similar to the first but learns a utility model instead of a general preference model. Such an approach is taken by Akrour et al. (2012), who propose to learn a policy return estimate with techniques related to utility-based object ranking (c.f. Sect. 2.3.1) and use this return to infer a policy using evolutionary strategies. We refer to Wirth et al. (2017) for a more extensive discussion of these approaches and other early work in preference-based reinforcement learning.

More recent works focus heavily on a particular paradigm based on this last, utility-based approach. This paradigm, started by Christiano et al. (2017), is characterized by learning utility estimates that can be used as a reward function and interleaving (non-exhaustive) preference learning with policy optimization. The policy is usually learned using conventional RL techniques, e.g., TRPO (Schulman et al. 2015). This type of approach, later commonly referred to as reinforcement learning from human feedback (RLHF) (Askell et al. 2021; Ouyang et al. 2022), has prominently been used as part of the training process of ChatGPT (OpenAI 2022). This, as well as other applications to generative models, is possible by interpreting a (usually pre-trained) generative model as a policy and optimizing it to take a series of actions (e.g., produce a piece of text) that satisfy human preferences.

2.9 Preference-based search and optimization

Consider a scenario in which an optimal alternative is sought among a possibly large (or even infinite) set of alternatives. In AI and operations research, problems of that kind are commonly tackled by means of systematic search methods—at least unless the space of feasible alternatives has a specific structure, making the problem amenable to more tailored techniques such as linear programming. To avoid a complete enumeration of the space, methods of that kind exploit information about the quality of individual candidates, either to prune complete portions of the solution space or to guide the search into promising regions. Feedback about the quality of solutions is collected over the course of the search process and is normally provided in the form of a numerical evaluation. More recently, preference-based variants of some of these methods have been proposed, motivated in much the same way as preference-based variants of the MAB problem: in many cases, numerical feedback is difficult to acquire, while relative comparisons between candidates are easier to obtain.

An important example is Bayesian optimization (BO), a black-box optimization method that has recently become quite popular in AI and machine learning. BO is commonly used for hyper-parameter optimization and algorithm configuration, that is, for searching good parameters of an algorithm: the solution space consists of all possible parameter configurations (e.g., the parameters of a SAT solver), and the performance to be optimized is the performance of the algorithm (e.g., the average runtime of the solver). More generally, denoting the solution space by $\Theta$ and the objective function by $g: \Theta \rightarrow {\mathbb {R}}$, the goal is to find

$$\begin{aligned} \theta ^* {:=}\arg \min _{\theta \in \Theta } g(\theta ) \,\,\,. \end{aligned}$$

(8)

BO samples the function g at a sequence of points $\theta _1, \theta _2, \ldots$, making use of (and successively improving) a surrogate model ${\hat{g}}$ in combination with a so-called acquisition function in order to achieve an optimal compromise between exploration and exploitation. Gonzalez et al. (2017) consider the case where g cannot be accessed directly, i.e., querying g at a point $\theta _i$ to observe $g(\theta _i)$ is not possible. Instead, only pairwise comparisons between two candidates $\theta _i$ and $\theta _j$ can be obtained. In other words, g is treated as a latent function that can only be queried through pairwise comparisons. This utility function is learned on the basis of a probabilistic choice model and a specifically designed acquisition function.

Monte Carlo Tree Search (MCTS) is a tree-based search method. Here, every solution is determined by an entire sequence of decisions as represented by a path from the root of the search tree to a leaf node. MCTS is commonly used in stochastic or adversarial environments, with the goal of identifying an agent’s best next move. To this end, methods such as UCT (a tree-based extension of the UCB algorithm for multi-armed bandits (Auer et al. 2002)) evaluate the quality of an inner node by averaging over several random completions, i.e., continuing search with random decisions until reaching a leaf node and assessing the quality of the corresponding path. However, there are also single-player versions of MCTS that can be used for classical minimal-cost path search, where every candidate solution corresponds to a path from the root of the search tree to a leaf node. Mohr et al. (2021) presents a preference-based extension of this approach, in which feedback is provided in the form of relative comparisons between random completions (instead of absolute assessments of individual completions). This feedback is used to learn a probabilistic choice model in each inner node of the tree, providing a ranking over the successor nodes from most to least promising.

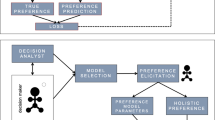
3 PL and MCDA: a systematic comparison

A comparison between PL and MCDA is possible at a methodological and conceptual rather than an experimental level. In fact, an empirical comparison with respect to the end results of PL and MCDA would not be meaningful, because there is no common context of their use and no objective truth is to be attained. Moreover, the methods of PL and MCDA are transforming the input preference information in a different way and introduce some instrumental bias in interactive steps, thus leading to different results. Furthermore, the concept of “learning” is implemented in PL and MCDA in different ways. In MCDA, especially in ROR, learning does not only concern the preference model but also the decision maker. Since the progress in learning of the DM is non-measurable, an experimental comparison of different methods is ill-founded. Consequently, instead of providing an empirical comparison, our aim is rather to identify methodological and conceptual differences as well as similarities, thereby revealing possible synergies and areas of mutual fertilization. In the following, we compare PL and MCDA according to several criteria—an overview is also provided in Table 1.

Table 1 Summary of the comparison of PL and MCDA

• Problem focus As detailed in Sect. 3, preference learning, like machine learning in general, covers a broad spectrum of different tasks and types of learning problems, including different levels of supervision (from fully unsupervised to fully supervised). Yet, it is probably fair to say that, in general, PL puts a strong emphasis on learning predictive models, typically in a supervised manner, and with the main objective of producing accurate predictions or prescriptions. The accuracy is measured in terms of an underlying (target) loss function and may depend on the concrete application at hand. In spite of this focus on predictive accuracy, it should also be mentioned that other criteria have come to the fore in the recent past, especially due to the growing interest in social aspects and trustworthiness of AI. One example is fairness of predictive models, which could mean, for instance, that predicted ranking should not be biased in favor of disfavor of certain subpopulations (Zehlike et al. 2021).

  The focus of MCDA is to recommend a satisfactory decision to the DM. This means that the recommendation should be consistent with the DM’s preferences represented by a model, usually built in the course of an interaction with the DM. The decision problems considered within MCDA concern the best choice, or ordinal classification, or a preference ranking of alternatives. Although the focus in MCDA is on finding a single decision rather than inducing an entire model (like in ML), formulating the problem requires a lot of preliminary work related to the definition of potential alternatives and the construction of a family of criteria for their evaluation (Roy 1996).

• User interaction Traditionally, user interaction has not been emphasized a lot in machine learning. Instead, the focus has been on the data, which, in the extreme case, was simply supposed to be given in the form of a static, pre-collected set of data stored in a database. At best, a human user was considered as a “labeler”, i.e., to provide supervision for training instances, e.g., in the setting of active learning or in crowdsourcing (Chen et al. 2013). With an increasing number of ML applications and the use of AI systems in everyday life, this started to change more recently, and machine learning “with the human in the loop” is now gaining popularity.

  MCDA is a process heavily involving the DM in the co-construction of their preferences by exploring, interpreting, and arguing, with the aim of recommending a course of action to increase the consistency between the evolution of the process and the DM’s objectives and value system (Roy 2000). MCDA tries to ensure that the DM, who is in the feedback loop of the decision support procedure, understands the impact of the provided preferential information on the shape of the preference model and, consequently, on the recommended decision (Corrente et al. 2024).

• Learning target Akin to statistical inference, the key interest in machine learning is model induction, that is, the induction of a model that generalizes well beyond the training data and allows for making accurate predictions on a population level. The model itself is “individualized” in the sense that predictions pertain to individuals of the population (and are obtained as functions of a suitable formal representation of individuals, most commonly in the form of a feature vector). Nevertheless, ML mainly aims at maximizing expected accuracy. That is, instead of targeting an individual instance, performance is averaged over the entire population.

  MCDA is more than just predictions based on examples. Its aim is to analyze the decision-making context by identifying the problem with its actors, potential alternatives and their consequences, and the stakes. The actors are stakeholders concerned by the decision. Their points of view are expressed through evaluation criteria. The DM is either an individual or a group that collectively makes a decision. Usually, in the decision-aiding process, there is an analyst who acts as an intermediary between the calculation procedure and the DM, organizing the interaction.

• Representation of alternatives In preference learning, the representation of choice alternatives strongly depends on the learning task. In the label ranking problem, for example, alternatives are merely identified by a label, but not represented in terms of any properties. In other settings, such as object ranking, properties—or features in ML jargon— are used, sometimes in the form of semantically meaningful (high-level) features, but often also in the form of more generic low-level features such as pixels in an image. These low-level features are especially common in the realm of deep learning, where the construction of meaningful (higher-level) representations is considered as a part of the learning process. In addition to feature representations, more structured representations such as graphs, trees, or sequences are also common in ML/PL.

  Alternatives considered in MCDA are potential actions with known or probabilistic consequences. Based on these consequences, a consistent family of evaluation criteria is built to characterize the alternatives. The set of considered alternatives may be either explicitly or implicitly known. In the former case, it is presented in the form of a finite list of alternatives with their performance matrix, where each alternative is represented by a vector of performances on the evaluation criteria. In the latter case, each alternative is characterized by a vector of decision variables subject to mathematical programming constraints or subject to a combinatorial generator. The decision variables are arguments of objective functions (criteria). The latter case of MCDA is called multiobjective optimization.

• Representation of users/DMs As already mentioned, instances in machine learning are most commonly represented in terms of features, and so are users in preference learning. Thus, a user is formally represented in terms of a vector, where each entry corresponds to the value of a certain feature. The latter can be mixed in their scaling and underlying domains, which can be numerical, binary, or (ordered) categorical. More complex, structured or multimodal representations have also become more common in the recent past—for example, in a medical context, a patient could be represented by a combination of numerical measurements, images, and textual data.

  In MCDA, the users are usually called decision-makers (DMs). They are the recipients of the decision-aiding service concerning a particular decision problem (best choice, ordinal classification, or preference ranking). They are not identified otherwise than through the family of criteria used to evaluate the alternatives. The construction of criteria is a pre-stage of preference modeling. Thus, instead of characterizing the DMs by some personal features, the family of evaluation criteria is tailored to a particular DM or a group of DMs. For example, when selecting the best holiday project, the family of criteria for parents with young children will be different from the one for a couple without children, even if the considered set of alternative projects is the same.

• Preference information In PL, preference information is typically holistic in the sense of referring to choice alternatives in their entirety. For example, a user may rate an alternative as a whole, or express a preference for one alternative over another one, though without referring to specific parts of properties of these alternatives. At the same time, preferences are often contextualized, most commonly by the user, but possibly also by other context variables specifying the choice situation.

  In MCDA, the preference information is necessary to build a DM’s preference model inducing a preference relation in the set of alternatives being richer than the dominance relation. The type of preference information depends on the aggregation procedure (preference model) and on the preference elicitation mode. When the preference elicitation is direct, the global preference information given by the DM concerns parameters of a value function or an outranking relation. When the preference information is indirect, it is composed of holistic decision examples or past decisions, e.g., pairwise comparisons or classifications of some alternatives. In the case of multiobjective optimization, when the search of the solution space is combined with preference modeling, the preference information is local, as it concerns the current stage of the search.

• Nature of the data In machine learning, training data is normally supposed to be produced by an underlying data-generating process, which is stochastic in nature. In other words, data is generated by an underlying though unknown (joint) probability distribution on properties of instances and outcomes. The stochastic nature of the data is important, because real data is always “noisy” in various ways, and a model fitting such data perfectly will normally not exist.

  In MCDA, the data used to construct the DM’s preference model is available either on request (directly or indirectly, as explained earlier) or from the observation of the DM’s past decisions. When decision examples or past decisions are inconsistent with respect to the dominance principle, they are either corrected or the rough set concept is used to handle them explicitly.

• Models and model assumptions Model assumptions in machine learning are normally weak in the sense that the learner can choose models (hypotheses) from a rich class of complex, nonlinear functions—deep neural networks can be mentioned as the most telling example. Obviously, to prevent the learner from overfitting the training data, such models need to be regularized. Since “black-box” function approximators such as neural networks are difficult to understand and lack interpretability, other types of models are sometimes preferred, notably symbolic models like rules or decision trees. But even these model classes are highly expressive, and models may become quite large (then again losing the advantage of intelligibility). Restrictively, however, it should also be mentioned that more standard statistical methods such as logistic regression, which do make strong (linearity) assumptions and are well interpretable, are also used in machine learning.

  In MCDA, the preference models are, generally, of three types: a real-valued value (utility) function, a system of binary relations (outranking), or a set of logical “if..., then...” statements (decision rules). They rely on different axiomatic foundations. The first model ranges from a simple weighted sum to integrals (Choquet, Sugeno) handling interactions among criteria. The second permits handling incomparability, and the third has the greatest capacity for preference representation of all three models. Moreover, decision rules identify values that drive DM’s decisions—each rule is an intelligible scenario of a causal relationship between performances on a subset of criteria and a comprehensive judgment.

• Model interpretation, usage, and expectations As already mentioned, models in ML/PL are mostly of predictive or prescriptive nature, i.e., they are mainly used for making predictions of outcomes in new contexts, or recommending decisions to a user in a new situation. The expectation is that a model generalizes well beyond the training data on which it has been learned, i.e., that predictions or prescriptions are accurate and incur a small loss or regret.

  In MCDA, the model interpretation and usage are either normative or constructive. It is normative when an ideal rationality of the DMs is assumed and the aim is to give an “objectively” best recommendation. This approach is typical for decision analysis based on expected utility theory. The “aiding” underlying the MCDA process assumes, however, that preferences of the DMs with respect to considered alternatives do not pre-exist in their minds. Thus, MCDA involves the DMs in the co-construction of their preferences. This implies that the concepts, models, and methods proposed by MCDA are seen as keys to doors giving access to elements of knowledge contributing to the acceptance of a final recommendation.

• Observational data availability and volume In ML/PL, data is normally assumed to be readily available, typically in large volume. Indeed, many learning algorithms, such as deep neural networks, require large amounts of data to guarantee good generalization, and the most impressive successes of machine learning can be found in data-rich domains. Typically, these are domains in which (behavioral) data can be collected easily in a systematic way, e.g., in social media or e-commerce. This being said, learning from “small data” has also gained attention more recently, as there are also domains in which the availability of data is much more limited, or producing (labeled) data is costly. Benchmark data abounds in ML/PL and plays an important role, e.g., in comparing the performance of new algorithms with the state of the art.

  In MCDA, the observational data concerning DMs’ preferences are not as massively available as in PL. When they are expressed by DMs in a direct dialogue, they are created during the decision-aiding process, and the volume of this data is limited by the fatigue of the DMs. They can be more when the preference information serving to build a preference model comes from observation of DMs’ routine acts before the model is built. Benchmark data on which various MCDA methods are compared are rare, however, with the exception of multiobjective optimization, for which rich benchmark data are available (Deb et al. 2002; Zitzler and Laumanns 2018).

• Validation, success criteria In ML/PL, the predictive accuracy of models learned on training data is commonly evaluated in terms of performance metrics and related loss functions. The main goal of the evaluation procedure is to get an idea of the model’s generalization performance. Yet, since the latter depends on the true but unknown data-generating process and hence cannot be computed, it is normally approximated by means of some internal evaluation procedure. To this end, only a part of the data is used for training, while the rest is used as test data. In so-called cross-validation, the data is divided into several folds, each fold is used for testing in turn, and the performances are averaged.

  In MCDA, user satisfaction is rather difficult to measure. The decision-aiding process is composed of preference elicitation, preference modeling, and DM’s analysis of the recommendation loops until the DM, or a group of DMs, accepts the recommendation or decides to change the problem setting. It is recommended to perform the robustness analysis (Roy 2010; Aissi and Roy 2010) which consists of checking how the recommendation changes when the preference model parameters are changed within the margins of ignorance. Experience indicates, moreover, that DMs wish to understand how their preference information influences the recommendation. To raise the DMs’ confidence in the received recommendation, MCDA methods try to implement the postulate of transparency and explainability. This is particularly important for interactive multiobjective optimization, where the answers given by DMs in the preference elicitation phase are translated into guidelines for the search algorithm in the optimization phase. Laboratory validation of multiobjective optimization methods is performed on publicly available benchmark problems. Success is measured by the closeness of the obtained set of non-dominated solutions to the known Pareto front. In the case of interactive multiobjective optimization, an artificial DM with a known utility function is used in a single-objective benchmark algorithm.

• Computational aspects Computational aspects play an important role in ML/PL, both in terms of time and space complexity, i.e., the time needed to train a model and the storage needed to store it (which may become an issue for large neural networks, for example). Scalability and sample efficiency of algorithms are especially important in domains where models must be trained on big data sets, but also in online settings, where models are trained, not in a batch mode, but incrementally on streaming data, perhaps even under real-time constraints. Moreover, efficiency may not only be required for training but also for prediction.

  In MCDA, scalability is, usually, less critical because the computation of a preference model involves a much smaller volume of data. In the case of multiobjective optimization concerning complex (nonlinear or combinatorial) problems, a short computation time is required between successive sessions of interactions with the DM.

• Application domains Preferences in general and preference learning in particular play an increasingly important role in various domains of application, ranging from computational advertising, recommender systems, electronic commerce, and computer games to adaptive user interfaces and personalized medicine. PL is also used in social media and platforms such as TikTok, YouTube, Spotify, LinkedIn, etc., again mainly for the purpose of personalization. More recently, PL has also been applied in the realm of generative AI, for example in ChatGPT. Although the scope is very broad, PL is less applied in safety-critical domains, unless predictions or recommendations can be checked and possibly corrected by a human expert.

  The application area of MCDM methods is very broad. This is evidenced by the large number of methods adapted to various applications. The choice of one of these many methods for a particular decision-making problem must correspond to the context of the application, the DM’s expectations for the form of the recommendation, and the type of preference information that can be obtained from the DM (Roy and Słowiński 2013). In (Cinelli et al. 2022), a new taxonomy-based system recommending MCDA methods has been described and made available online at https://mcda.cs.put.poznan.pl/. It includes a big collection of (>200) MCDA methods. It is also worth mentioning many safety-critical applications, and one-shot decision problems concerning the situations where a decision is experienced only once (Guo 2011).

4 Combining PL and MCDA

The combination of mathematical modeling of preferences with machine learning methods for model identification has received increasing attention in the recent past. In the following, we present two directions that have been pursued in this regard, the first taking preference models from MCDA as a point of departure and amending them by ML algorithms, the second proceeding from an ML methodology and tailoring it to the problem of learning preference models.

4.1 Multi-criteria preference learning

One way to combine PL with MCDA is to adopt preference models from MCDA and identify these models with algorithms from machine learning or, stated differently, to induce MCDA models in a data-driven way using machine learning methods. We refer to this approach as multi-criteria preference learning (MCPL). In principle, any of the three types of preference models considered in MCDA can be considered in this regard: utility (value) functions, outranking relations, or sets of decision rules. The ROR methodology presented in Part I is a good example of the initial inspiration of MCDA by PL [as argued in Corrente et al. (2013)], particularly DRSA (cf. Part I), which employs induction algorithms inspired by machine learning (Cendrowska 1987).

Fig. 1

Structure of a multi-criteria preference learning model combining a utility-based MCDA model with a stochastic response model

By combining MCDA models with ML algorithms, the hope is to get the best of both worlds. ML algorithms are scalable and robust toward noise and other data imperfections but are often difficult to interpret and do not guarantee to obey meaningful properties of decision models. MCDA models, on the other hand, are inherently interpretable and meaningful from of decision-making point of view. From an ML perspective, they provide a kind of representation bias, thereby incorporating important domain knowledge and enforcing consistency properties such as monotonicity. As for the amount and quality of the training data, different scenarios are conceivable:

• Like in standard ML, training data could be collected from an underlying population with possibly heterogeneous preferences. In this case, data will typically be more extensive, but also afflicted with noise and inconsistencies. Moreover, to capture the heterogeneity of the population, preferences should be modeled as functions, not only of properties of the decision alternatives but also of properties of the individuals.

• Like in MCDA, the data could still be assumed to come from the DMs for whom the decision aiding is performed, i.e., a single DM or a well-identified group of DMs. Even then, the data may be affected by inconsistencies, but will typically be so to a much lesser extent, especially if the group of DMs can be assumed to be somewhat homogeneous in the sense of sharing the same knowledge about decision alternatives. In this case, a single preference model can be expressed as a function of the properties of decision alternatives.

To cope with noisy data, an MCDA model needs to be extended by a stochastic component. Figure 1 sketches a possible architecture of an overall model for the case where the MCDA model is a utility function. Here, utility is treated as a latent variable that cannot be observed directly. Instead, the observation is a response by the DM, which depends on the utility in a non-deterministic way, and this dependence is captured by the response model. An example of such a model is the logistic noisy response model, where the DM provides a binary response $y \in \{ 0, 1 \}$ (e.g., like or dislike an alternative), and

$$\begin{aligned} P(y=1) = \frac{1}{1 + \exp \big ( - \gamma (U - \beta ) \big )} \,. \end{aligned}$$

Thus, the DM is more likely to answer positively if the (latent) utility exceeds a threshold $\beta$, and more likely to answer negatively, otherwise. However, the response is not precise but remains random to some extent: The higher U, the higher the probability of a positive response (with $P( y = 1) = 1/2$ for $U = \beta$). The precision of the DM is determined by the parameter $\gamma$: The larger $\gamma$, the more precisely the response depends on the latent utility. The latter itself is modeled as an aggregation (e.g., the Choquet integral) of local utilities pertaining to individual features (or criteria in MCDA terms).

Let us give some concrete examples of methods that can be covered under the label of MCPL, i.e., methods that are mutually inspired by PL and MCDA.

• Especially prevalent in the field of MCDA are approaches based on the Choquet integral (Grabisch and Labreuche 2005; Grabisch et al. 2008). In Sect. 2.8 of Part I, we already presented methods for estimating the parameters of this model from holistic preference information (extended from a flat structure of the set of criteria to a hierarchical structure in Section 2.10 of Part I). In general, extracting a Choquet integral (or, more precisely, the non-additive measure on which it is defined) from data is considered as a parameter identification problem and commonly formalized as a constraint optimization problem (Beliakov 2008), for example using the sum of squared errors as an objective function (Torra and Narukawa 2007; Grabisch 2003). To this end, Mori and Murofushi (1989) propose an early approach based on the use of quadratic forms, while an alternative heuristic method is introduced by Grabisch (1995). Meanwhile, the Choquet integral has been used for various problems in the realm of machine learning, including binary classification (Tehrani et al. 2012a), ordinal classification (Beliakov and James 2010; Tehrani and Hüllermeier 2013), ranking (Tehrani et al. 2012b), metric learning (Beliakov et al. 2011), multiple instance learning (Du et al. 2019), ensemble learning (Grabisch and Nicolas 1994), and transfer learning (Murray et al. 2019). More recently, Bresson et al. (2020) developed a method for learning hierarchical Choquet integrals, which is inspired by the (deep) neural network, thereby combining machine learning with hierarchical decision modeling (cf. Section 2.10 of Part I). The Choquet integral has also been used as a preference model in interactive evolutionary multiobjective optimization (Branke et al. 2016). Last but not least, more specialized learning methods have been developed for aggregation models that can be seen as special cases of Choquet, such as the OWA operator (Torra 2004; Melnikov and Hüllermeier 2019).

• There is also some work on learning the Sugeno integral as a qualitative counterpart of the Choquet integral. An early approach is (Prade et al. 2009), where the authors propose a procedure for eliciting the capacity underlying a Sugeno integral. Anderson et al. (2010) consider Sugeno integrals where both the integrand and the measure assume fuzzy numbers as values and propose a genetic algorithm for learning the underlying measure. Focusing on regression tasks, Gagolewski et al. (2019) develop a branch-refine-and-bound-type algorithm for fitting Sugeno integrals with respect to symmetric capacities. This algorithm is used to minimize the mean absolute error on the training data. Beliakov et al. (2020) express the learning problem as a difference of convex functions, making it amenable to DC (difference of convex) optimization methods and (local) linear programming. An approach based on linear programming is also proposed by Abbaszadeh and Hüllermeier (2021). An optimization technique based on the marginal contribution representation is explored by Beliakov and Divakov (2020). Thanks to this representation, the number of variables can be reduced, and the constraints can be simplified.

• Another important class of MCDA models—outranking instead of utility-based—is the ELECTRE family. An evolutionary algorithm has been used for learning the parameters of ELECTRE TRI-B, separating decision classes using a single boundary profile (Doumpos et al. 2009). Learning the parameters of MR-Sort, which is a simplified variant of ELECTRE TRI-B using a majority rule and boundary class profiles, has been tackled in various ways, e.g., using mixed-integer programming (Leroy et al. 2011), or linear programming combined with simulated annealing (Olteanu and Meyer 2014), or a dedicated metaheuristic (META) combining evolutionary algorithms with mathematical programming (Sobrie et al. 2013, 2019). Another non-compensatory sorting model learning was presented in Sobrie et al. (2015). Learning the parameters of ELECTRE TRI-rC, including a single characteristic profile to describe each decision class, has been accomplished by four methods based on different optimization techniques: an evolutionary algorithm, linear programming combined with a genetic approach, simulated annealing, and a dedicated heuristic (Kadziński and Szczepański 2022).

• Value function preference models have been learned within the regularization framework for sorting problems with multiple potentially non-monotonic criteria (Liu et al. 2019). Algorithms for learning the parameters of a value-based sorting model with diverse types of marginal value functions (including linear, piecewise-linear, splined, and general monotone ones) admitting value assignment examples in which a reference alternative can be classified into multiple classes with respective credibility degrees have been presented by Liu et al. (2020). Convex quadratic programming model for learning a value-based model with potentially interacting criteria, including novel methods for classifying non-reference alternatives to enhance the method’s applicability to different data sets was presented by Liu et al. (2021). MCPL has also been realized with value function models having a distance interpretation, like in TOPSIS. For example, Aggarwal et al. (2014) propose a method for learning of TOPSIS-like decision models, in which preference is a decreasing function of distance from an “ideal alternative”, and both the ideal alternative and the distance function are learned from data.

• Preference modeling has also been combined with rule induction as one of the most classical machine learning methods. For example, the MORE method learns rule ensembles subject to monotonicity constraints by minimizing cross-entropy as a loss function and treating a single rule as a subsidiary base classifier (Dembczyński et al. 2009). Moreover, Dembczyński et al. (2010) present a method for learning rule ensembles for multiple criteria ranking problems, and Kadziński et al. (2004) consider multiple criteria ranking and choice with all compatible minimal cover sets of decision rules.

• Inspired by the recent success of deep learning, MCDA has been combined with artificial neural networks. For example, the latter are used by Martyn and Kadziński (2023) to infer the parameters of threshold-based sorting procedures for various types of aggregation functions: the OWA aggregation operator, an additive value function, the Choquet integral, TOPSIS-based distances, and NetFlowScore procedures based on the principles of either PROMETHEE or ELECTRE.

4.2 Kernel-based preference learning

Instead of starting from preference modeling and using machine learning algorithms to induce MCDM models in a data-driven way, one can also proceed the other way around: Taking an algorithmic ML framework as a point of departure and adapting it for the purpose of preference modeling. An interesting example is the framework of kernel-based machine learning, which can serve as a unifying framework for learning and preferences modeling, thereby combining algorithmic features such as scalability and robustness through regularization with means for incorporating properties and domain knowledge into the modeling task.

Let us first recall some core concepts of kernel-based machine learning, notably the notion of a kernel. A function $k: \mathcal {X} \times \mathcal {X} \longrightarrow {\mathbb {R}}$ on a nonempty set $\mathcal {X}$ is a positive semi-definite kernel on $\mathcal {X}$ iff it is symmetric, i.e., $k(x,y) = k(y,x)$ for all $x,y \in \mathcal {X}$, and positive semi-definite, i.e.,

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^n c_i c_j k(x_i,x_j) \ge 0 \end{aligned}$$

for arbitrary n, $x_1, \ldots , x_n \in \mathcal {X}$, and $c_1, \ldots , c_n \in {\mathbb {R}}_+$. Given a kernel k on $\mathcal {X}$, an important theorem by Mercer (1909) implies the existence of a (Hilbert) space $\mathcal {H}$ and a map $\phi :\, \mathcal {X} \longrightarrow \mathcal {H}$, such that

$$\begin{aligned} k(x,y) = \langle \phi (x), \phi (y) \rangle \end{aligned}$$

for all $x,y \in \mathcal {X}$. Thus, computing the kernel k(x, y) in the original space $\mathcal {X}$ is equivalent to mapping x and y to the (typically high-dimensional) space $\mathcal {H}$ first, using the linearization or feature map $\phi$, and combining them in terms of the inner product in that space afterward.

This connection between a nonlinear combination of instances in the original space $\mathcal {X}$ and a linear combination in the induced feature space $\mathcal {H}$ provides the basis for the so-called “kernel trick”, which offers a systematic way to design nonlinear extensions of methods for learning linear models. The kernel trick has been applied to various methods and has given rise to many state-of-the-art machine learning algorithms, including support vector machines, kernel principle component analysis, and kernel Fisher discriminant, amongst others.

Applying the kernel trick essentially comes down to solving specific types of optimization problems. While a detailed discussion of such methods is beyond the scope of this paper, let us mention that solutions to such problems often admit an appealing interpretation. For example, in the most basic setting of binary classification, where training data is of the form $\mathcal {D} = \{ (x_i, y_i ) \}_{i=1}^N \subset \mathcal {X} \times \{ -1, +1 \}$, it can be shown that a predictor induced on $\mathcal {D}$ by loss minimization is of the form

$$\begin{aligned} f(x) = \sum _{i=1}^N \alpha _i \, y_i \, k(x,x_i) + \beta \,, \end{aligned}$$

with $\alpha _i \ge 0$ and $\beta \in {\mathbb {R}}$ a constant bias term. Those $x_i$ for which $\alpha _i > 0$ are called the support vectors—typically, solutions are sparse in the sense that $\alpha _i = 0$ for most of the training examples, and $\alpha _i > 0$ for only a few “important” examples. Thus, a new query instance is compared to each of the support vectors in terms of the kernel k, which can often be interpreted as a kind of similarity measure. The larger $k(x,x_i)$ and the more important the training example $(x_i,y_i)$, the more the class label $y_i$ is supported. All these evidences are summed up, so as to obtain overall evidence in favor of the positive ($f(x) > 0$) or the negative ($f(x) < 0$) class.

Waegeman et al. (2009) generalized the framework to the case where training information is given in the form of pairwise preferences $x_i \succ x_j$, encoded by the label $y_{i,j} = +1$ (and $y_{j,i} = -1$) attached to the tuple $(x_i,x_j)$. Making use of a generalized kernel

$$\begin{aligned} k^*: \, \mathcal {X}^2 \times \mathcal {X}^2 \longrightarrow {\mathbb {R}} \,, \end{aligned}$$

(9)

they obtain solutions of the form

$$\begin{aligned} f(x,x') = \sum _{i,j: y_{i,j} = 1} \alpha _{i,j} \, k^*(x_i,x_j, x, x') \,, \end{aligned}$$

expressing a degree of preference of x over $x'$. Intuitively, the tuple $(x,x')$ is compared to all “support preferences” $x_i \succ x_j$ in the training data, and similarity between $(x,x')$ and $(x_i,x_j)$ provides evidence in favor of the preference $x \succ x'$.

This approach comprises several interesting special cases. For example, if preferences $f(x_i,x_j)$ are derived from (one-dimensional) utilities $u(x_i)$ and $u(x_j)$, the kernel (9) effectively reduces to a two-dimensional kernel:

$$\begin{aligned} k^*(x_i,x_j,x,x') = k(x_i,x) - k(x_i,x') - k(x_j,x) + k(x_j,x') \end{aligned}$$

Another interesting special case is the aggregation of single-criterion preference relations, such as valued concordance relations used in ELECTRE methods. Consider a single-criterion outranking relation (for the $k^{th}$ criterion) of the form

$$\begin{aligned} s_k \left( x_i^{(k)}, x_j^{(k)} \right) = \frac{p_k(x_i^{(k)}) - \min \left( x_j^{(k)} - x_i^{(k)}, p_k(x_i^{(k)})\right) }{p_k(x_i^{(k)}) - \min \left( x_j^{(k)} - x_i^{(k)}, q_k(x_i^{(k)})\right) } \,, \end{aligned}$$

where $p_k$ and $q_k$ are threshold functions. From these single-criterion outranking relations, a concordance relation can then be built in terms of a weighted sum

$$\begin{aligned} S(x_i, x_j) = \sum _{k=1}^m w_k \, s_k \left( x_i^{(k)}, x_j^{(k)} \right) = \langle w, s \rangle \,. \end{aligned}$$

Embedding single-criterion preferences in feature space and expressing global preferences $f(x_i,x_j)$ as linear functions of $\phi (s(x_i,x_j))$ is then equivalent to applying the kernel-based approach with a kernel of the form

$$\begin{aligned} k^*(x_i,x_j,x,x') = K \big (s(x_i,x_j), s(x,x') \big ) \,, \end{aligned}$$

where $k: \mathcal {X}^2 \longrightarrow {\mathbb {R}}$ is a regular (two-dimensional) kernel. While the latter determines how single-criterion outranking relations are aggregated (e.g., linearly or nonlinearly), the construction of the vector s of these relations allows for incorporating domain knowledge.

5 Conclusion

Preference learning (PL) and multiple-criteria decision aiding (MCDA) have been developing over the last decades in rather separate communities. PL derives from machine learning and relies on statistical learning from usually massive data informing about user preferences through ratings or revealed choices. To a greater extent than machine learning in general, PL respects some background knowledge of the application domain and peculiarities of the data, such as their ordinal character. MCDA in turn derives from operational research, where the classic decision problems involving a single optimality criterion were replaced by consideration of multiple-criteria decision problems, which, philosophically, have no solution without involving the users’ preferences in the aggregation of the criteria.

Being convinced that PL and MCDA can complement and mutually benefit from each other, we undertook the task of showing opportunities for synergy based on the connection between these two research fields, hoping to attract interest from both communities and foster their rapprochement. To this end, we first reviewed both methodologies with the intention of highlighting their most common elements and characteristics—being aware that a certain level of subjectivity and personal bias of the two authors is unavoidable. Then, we compared the methodologies in a systematic way to enhance mutual understanding and to show that, in spite of different origins, PL and MCDA share the major goal of constructing practically useful decision models that either support humans in the task of choosing the best, classifying, or ranking alternatives from a given set, or even automating decision making by acting autonomously on behalf of the human.

We strongly believe that a close alliance of the decision sciences and machine learning is of utmost importance in the current era of modern AI, where decisions are increasingly automated and made by algorithms instead of humans. In fact, automated decision-making algorithms trained on data can already be found in various domains, such as hiring or placement decisions in employee recruitment (Pessach et al. 2020), the construction of individualized treatment rules in personalized medicine (Zhao et al. 2012), disaster management (Zagorecki et al. 2013), and even jurisdiction (Kleinberg et al. 2018). As shown by these examples, decision support and (partly) automated decision-making are gaining in societal significance and increasingly impact our daily life. Needless to say, this development also comes with increasing demands for the underlying methodology, which has to make sure that decisions are transparent, ethically justifiable and fair, as well as reliable and responsible (Lepri et al. 2018; Casteluccia and Métayer 2019). By joining efforts, PL and MCDA can contribute to a sound methodological foundation of data-driven and algorithmic decision support.