Exact distributional analysis of online algorithms with lookahead

Abstract

In online optimization, input data is revealed sequentially. Optimization problems in practice often exhibit this type of information disclosure as opposed to standard offline optimization where all information is known in advance. We analyze the performance of algorithms for online optimization with lookahead using a holistic distributional approach. To this end, we first introduce the performance measurement method of counting distribution functions. Then, we derive analytical expressions for the counting distribution functions of the objective value and the performance ratio in elementary cases of the online bin packing and the online traveling salesman problem. For bin packing, we also establish a relation between algorithm processing and the Catalan numbers. The paper shows that an exact analysis is strongly interconnected to the combinatorial structure of the problem and algorithm under consideration. Results further indicate that the value of lookahead heavily relies on the problem itself. The analysis also shows that exact distributional analysis could be used in order to discover key effects and identify related root causes in relatively simple problem settings. These insights can then be transferred to the analysis of more complex settings where the introduced performance measurement approach has to be used on an approximative basis (e.g., in a simulation-based optimization).

1 Introduction

Online optimization with lookahead deals with sequential decision making under incomplete information where each decision must be made based on a limited, but certain preview (lookahead) of future input data. In many applications, this optimization paradigm provides a better view of a decision maker’s informational state than pure offline and online optimization since not all may be known about the future, but information concerning the near future may be available.

The input of an online optimization problem – both with and without lookahead – consists of a sequence $\sigma = (\sigma _1, \sigma _2, \ldots , \sigma _n)$ of input elements $\sigma _1, \sigma _2, \ldots , \sigma _n$. One of the most prominent lookahead types is request lookahead where a new input element is revealed only when an old one has just been served (Allulli et al. 2008; Tinkl 2011). Under request lookahead of size $l \in {\mathbb {N}}$, an algorithm has access to a fixed number l of unserved input elements (or to all of the remaining unserved input elements if there are less than l of them). The first of these input elements would also be known in the pure online situation, but the remaining $l-1$ input elements are known only due to the lookahead capability. If an algorithm is allowed to process the known input elements in an arbitrary order, this type of lookahead corresponds to a buffer of size l where input elements can be reordered for subsequent processing. In stricter settings of online optimization with lookahead, buffers may be forbidden requiring to process input elements in the given order. In this paper, we will consider online optimization with lookahead where lookahead allows for buffering. An overview on various lookahead concepts throughout different applications can be found in Dunke (2014). Note that for $l = 1$, we obtain the setting without lookahead. Request lookahead construes the lookahead set as dependent on the processing statuses of the input elements and not in an independent process of release. There are other types of lookahead, e.g., time or property lookahead (Dunke 2014).

Basic online problems have been studied in the framework of competitive analysis (Borodin and El-Yaniv 1998; Fiat and Woeginger 1998): Algorithms for an online optimization problem have to compete with an optimal offline algorithm which knows the whole input in advance, and quality guarantees have to hold for all possible input sequences. Hence, competitive analysis is a worst-case analysis; results are overly pessimistic and do not reflect an algorithm’s practical abilities (Dorrigiv 2010; Fiat and Woeginger 1998). We conclude that more comprehensive analysis methods are required to display an algorithm’s overall behavior in a way supportive for decision makers in applications.

Advances in information technologies such as RFID, GPS, or GIS enable decision makers nowadays to obtain certain information about the near future. This information could be used algorithmically as a lookahead. However, lookahead is often still only considered an add-on to online optimization. The intermediate setting of lookahead has been addressed sporadically for a competitive analysis in the following areas: Routing and transportation (Allulli et al. 2008; Jaillet and Wagner 2006; Tinkl 2011), scheduling (Li et al. 2009; Mandelbaum and Shabtay 2011; Zheng et al. 2013), organization of data structures (Albers 1997, 1998; Breslauer 1998; Young 1991), data transfer (Imreh and Németh 2007), packing (Grove 1995), and metrical task systems (Ben-David and Borodin 1994; Koutsoupias and Papadimitriou 2000).

In this paper, we theoretically investigate what can be achieved through lookahead relative to the pure online case without lookahead. Since the choice of the right algorithm is most crucial to overall system performance, we assess algorithm performance with respect to practical needs. The following results and contributions are obtained in the paper: An exact distributional analysis is carried out for basic settings in two important classes of online problems (packing and routing). The analysis provides a holistic view of the performance of online algorithms; in particular, it yields considerably more information than conventional competitive analysis. To the best of our knowledge, such a comprehensive analysis has not been accomplished before in online optimization. Through our derivations, concrete explanations for observable lookahead effects in the classes of packing and routing problems are found which relate to the combinatorial structure of the problem settings. We also recognize that the human limits of grasping the combinatorial structure are likely to be reached soon when more complex settings need to be analyzed. Nonetheless, the validity of the methodological approach shown in this paper provides motivation to pursue this type of performance analysis on a sampling basis in more complex settings.

The remainder of the paper is organized as follows: In Sect. 2, we present a holistic distributional approach to performance measurement which allows comparing algorithms with different lookahead regimes to each other. Sections 3 and 4 validate the method in a theoretical analysis of the bin packing and traveling salesman problem. Exact analysis is possible because the implications of lookahead on the objective can be traced back to a combinatorial structure. We are aware that the considered problem settings are fairly simple. Yet, the performance analysis becomes quite involved. However, in the given problem settings we gain insight into why algorithms may substantially profit from additional information (in the case of the traveling salesman problem) or why not (in the case of bin packing). For more complex settings, the introduced approach of performance measurement is recommended to be used on an approximative basis (e.g., in a simulation-based optimization as carried out in Dunke 2014). The paper ends with a conclusion in Sect. 5.

2 Performance measurement in online optimization with lookahead

There are many perspectives on assessing algorithm performance: Worst-case analysis gives strong guarantees, but lacks in displaying the overall behavior. Average-case analysis addresses the overall behavior, but requires distributions on instances. Distributional analysis illustrates the whole performance spectrum and submits a fine-grained quality image. We first give an overview of existing performance measures which are related to our approach in Sect. 2.2. We denote an optimal offline algorithm which knows $\sigma$ in advance by Opt and the set of all input sequences by $\Sigma$; the cost of an algorithm Alg on input sequence $\sigma$ is denoted by ${\textsc {Alg}}[\sigma ]$. The discussion is restricted to minimization.

2.1 Literature review

Competitive analysis (Borodin and El-Yaniv 1998; Johnson 1973; Karlin et al. 1988; Sleator and Tarjan 1985) has become the standard for measuring the performance of online algorithms. Alg is called c-competitive if there is a constant a such that ${\textsc {Alg}}[\sigma ] \le c \cdot {\textsc {Opt}}[\sigma ] + a$ for all $\sigma \in \Sigma$. The competitive ratio $c_r$ of Alg is the greatest lower bound over all c such that Alg is c-competitive, i.e., $c_r =\inf \{c\ge 1 \,|\, {\textsc {Alg}} \text { is } c\text {-competitive}\}$. It states how much Alg deviates from Opt due to missing information in the worst case. However, there are notable disadvantages of the competitive ratio (Dorrigiv 2010; Fiat and Woeginger 1998): First, results are overly pessimistic because single worst-case instances, often pathologically construed, decide upon algorithm quality, and also competing with an omniscient offline algorithm may be irrelevant in practice. Second, competitive analysis is oblivious to overall algorithm behavior since performance is reduced to a single, worst-case-related figure; this makes discriminating algorithms with the same worst case, but different average case impossible. Third, a direct comparison between two algorithms is impossible. And fourth, the method often fails to reproduce the beneficial impact of lookahead.

Comparative analysis (Koutsoupias and Papadimitriou 2000) differs from competitive analysis as it relates the best objective value of a class of algorithm candidates to that of another class of algorithm candidates which are weaker than Opt, but stronger than those in the first class. Let ${\mathcal {A}}, {\mathcal {B}}$ be algorithm classes where ${\mathcal {B}}$ is more powerful than ${\mathcal {A}}$, e.g., due to lookahead, then the comparative ratio is

$$\begin{aligned} c^{comp}_r := \max _{{\textsc {B}} \in {\mathcal {B}}}\min _{{\textsc {A}} \in {\mathcal {A}}}\max _{\sigma \in \Sigma } \frac{{\textsc {A}}[\sigma ]}{{\textsc {B}}[\sigma ]}. \end{aligned}$$

To maximize $c^{comp}_r$, ${\mathcal {B}}$ chooses candidate B, whereupon ${\mathcal {A}}$ answers with A, whereupon B chooses the worst instance $\sigma \in \Sigma$ for A. Comparing algorithm classes with varying lookahead levels to each other (without reference to Opt) is also the foundation of our approach.

In an average-case analysis, stochasticity refers to probabilities for input sequence occurrences. Let D be a probability distribution over all input sequences, then Alg is called c-competitive under D if there is a constant a such that ${\mathbb {E}}_D({\textsc {Alg}}[\sigma ]) \le c \cdot {\mathbb {E}}({\textsc {Opt}}[\sigma ]) + a$. The expected competitive ratio of Alg under D is $c^D_r = \inf \{c \ge 1 \,|\, {\textsc {Alg}} \text { is } c\text {-competitive under } D\}$. The expectation can also be taken over all ratios: The expected performance ratio of Alg under D is $c'^D_r = \inf \Bigl \{c\ge 1 \,|\, {\mathbb {E}}_D\Bigl (\frac{{\textsc {Alg}}[\sigma ]}{{\textsc {Opt}}[\sigma ]}\Bigr ) \le c\Bigr \}$. According to Souza (2006), the expected performance ratio should be favored because sequences with small (large) objective would be underrepresented (overrepresented) in the isolated expectations. The expected performance ratio indicates which algorithm performs better on most sequences, and by Markov’s inequality the probability for a sequence with ratio far from the expectation can be bounded.

The main advantage of distributional performance analysis is that an algorithm is judged by a distribution instead of a single key figure. Relative interval analysis (Dorrigiv et al. 2009) is a preliminary stage of distributional analysis since it only considers the extreme values of a distribution for two algorithms. Define

$$\begin{aligned} \text {Min}_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(n):= & {} \min _{|\sigma |=n}\{{\textsc {Alg}}_1[\sigma ]-{\textsc {Alg}}_2[\sigma ]\}, \text {Max}_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(n) \\:= & {} \max _{|\sigma |=n}\{{\textsc {Alg}}_1[\sigma ]-{\textsc {Alg}}_2[\sigma ]\}, \end{aligned}$$

then the relative interval of ${\textsc {Alg}}_1$ and ${\textsc {Alg}}_2$ is

$$\begin{aligned} I_{{\textsc {Alg}}_1,{\textsc {Alg}}_2} = \Bigl [\liminf _{n \rightarrow \infty } \tfrac{\text {Min}_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(n)}{n}, \limsup _{n \rightarrow \infty } \tfrac{\text {Max}_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(n)}{n}\Bigr ]. \end{aligned}$$

The relative interval of an algorithm pair corresponds to its asymptotic range of amortized costs, and it allows for a direct comparison of two algorithms without reference to Opt.

Stochastic dominance (Müller and Stoyan 2002) origins from statistics where it is used to establish an order between distributions of two random variables. By interpreting the objective value obtained by an algorithm as a random variable, this concept has been transferred to online optimization (Hiller 2009) where the objective value distributions of two algorithms ${\textsc {Alg}}_1$ and ${\textsc {Alg}}_2$ are related to each other. Let $F_{{\textsc {Alg}}}: {\mathbb {R}} \rightarrow [0, 1]$ be the cumulative distribution function of the objective value of Alg: ${\textsc {Alg}}_1$ dominates ${\textsc {Alg}}_2$ stochastically at zeroth order if and only if ${\textsc {Alg}}_1[\sigma ] \ge {\textsc {Alg}}_2[\sigma ]$ for all $\sigma \in \Sigma$; ${\textsc {Alg}}_1$ dominates ${\textsc {Alg}}_2$ stochastically at first order if and only if $F_{{\textsc {Alg}}_2}(v) \ge F_{{\textsc {Alg}}_1}(v)$ for all $v \in {\mathbb {R}}$. If ${\textsc {Alg}}_1$ stochastically dominates ${\textsc {Alg}}_2$ at first order, then ${\mathbb {E}}({\textsc {Alg}}_1) \ge {\mathbb {E}}({\textsc {Alg}}_2)$. Unfortunately, stochastic dominance does not admit a total ordering among all distributions and we cannot expect a relation to hold for arbitrary algorithms. However, when comparing an algorithm without lookahead ${\textsc {Alg}}_1$ to one with lookahead ${\textsc {Alg}}_2$ (in minimization), ${\textsc {Alg}}_1 \ge _{st} {\textsc {Alg}}_2$ would illustrate the benefit of lookahead because ${\textsc {Alg}}_2$ attains smaller objective values on more instances than ${\textsc {Alg}}_1$.

Bijective analysis (Angelopoulos and Schweitzer 2013) is a special case of stochastic dominance where input sequences are uniformly distributed. The idea is to find a bijection $b: \Sigma \leftrightarrow \Sigma$ such that the objective value of ${\textsc {Alg}}_1$ on $\sigma$ is never worse than that of ${\textsc {Alg}}_2$ on the image $b(\sigma )$ of $\sigma$. Essentially, the approach consists in establishing an order of the elements in $\Sigma$ such that ${\textsc {Alg}}_1$ outperforms ${\textsc {Alg}}_2$ on every pair $(\sigma , b(\sigma ))$. ${\textsc {Alg}}_1$ is called no worse than ${\textsc {Alg}}_2$ (${\textsc {Alg}}_1 \preceq {\textsc {Alg}}_2$) if for all $n \ge n_0 \ge 1$ with some $n_0 \in {\mathbb {N}}$ there exists $b: \Sigma \leftrightarrow \Sigma$ with ${\textsc {Alg}}_1[\sigma ] \le {\textsc {Alg}}_2[b(\sigma )]$ for all $\sigma \in \Sigma$. ${\textsc {Alg}}_1$ is called better than ${\textsc {Alg}}_2$ if ${\textsc {Alg}}_1 \preceq {\textsc {Alg}}_2$ and not ${\textsc {Alg}}_2 \preceq {\textsc {Alg}}_1$. Hence, ${\textsc {Alg}}_1$ does not have to outperform ${\textsc {Alg}}_2$ on each sequence, but there has to be a relabeling of the sequences such that this relation holds between the original and relabeled sequences. We point out the advantages in Angelopoulos and Schweitzer (2013) for bijective analysis that can be transferred to any distributional approach: First, the idea is simple and intuitive, yet powerful. Second, algorithms can be compared directly without reference to an optimal offline algorithm. And third, typical algorithm properties are likely to be uncovered.

2.2 Counting distribution functions

Inspired by the bijective analysis of Angelopoulos and Schweitzer (2013), our analysis of algorithm performance is based on a distributional approach facilitating a comprehensive performance evaluation. We choose a performance measurement approach which summarizes the global behavior of an algorithm over all instances, but also takes into account local quality of algorithms in terms of comparing their performance on the same problem instance. The approach has been introduced in Dunke and Nickel (2013) and is further discussed in Dunke (2014).

In online optimization, nothing is known about the future. Likewise, in online optimization with lookahead, a limited amount of information about the future is available. Therefore, it is reasonable to impute this assumption also in the analysis method for algorithm performance. When no probabilities for instance occurrences are given, from the principle of insufficient reason the maximum entropy distribution is the best way to emulate the state of informational nescience as it minimizes the amount of a-priori information in the distribution (Jaynes 1957a, b). The uniform distribution over $\Sigma$ is the maximum entropy distribution among all distributions with support $\Sigma$ (which follows from Langrangian relaxation by the definition of the entropy together with the constraint that the sum over all probabilities equals 1). For finite $\Sigma$, this leads to counting results saying how many instances yield a certain objective value. The counting distribution function¹ subsumes these frequency information of objective values over $\Sigma$:

Definition 2.1

(Counting distribution function of objective value). Let $\sigma \in \Sigma$ be an input sequence, let ${\textsc {Alg}}$ be an algorithm, and let ${\textsc {Alg}}[\sigma ]$ be the objective value of ${\textsc {Alg}}$ on $\sigma$. If $\Sigma$ is a discrete set, then the function $F_{{\textsc {Alg}}}: {\mathbb {R}} \rightarrow [0, 1]$ with

$$\begin{aligned} F_{{\textsc {Alg}}}(v) := \frac{\displaystyle \sum _{\sigma \in \Sigma } {\mathbf {1}}_{[-\infty , v]}({\textsc {Alg}}[\sigma ])}{|\Sigma |} \end{aligned}$$

is called the counting distribution function of the objective value of ${\textsc {Alg}}$ over $\Sigma$. $\square$

For objective value $v \in {\mathbb {R}}$, the counting distribution function of the objective value $F_{{\textsc {Alg}}}(v)$ relates the number of input sequences with objective value smaller than or equal to v to the number of all possible input sequences. As every instance is considered with equal weight, this yields a counting result in the sense that $F_{{\textsc {Alg}}}(v)$ can be understood as the proportion among all input sequences leading to an objective value smaller than or equal to v.

A first step of comparing two algorithms ${\textsc {Alg}}_1$ and ${\textsc {Alg}}_2$ by their counting distribution functions of the objective value (see Fig. 1a) can be done by graphically examining the relative positions of their plots. For instance, when – in a minimization problem – the plot of $F_{{\textsc {Alg}}_1}(v)$ lies below that of $F_{{\textsc {Alg}}_2}(v)$ for a major proportion of objective values v, we can conclude as a first rule of thumb that $F_{{\textsc {Alg}}_1}(v)$ outperforms $F_{{\textsc {Alg}}_2}(v)$ on the majority of input sequences.

Fig. 1

a Counting distribution function of the objective value of ${\textsc {Alg}}_1$ and of the objective value of ${\textsc {Alg}}_2$. b Counting distribution function of the performance ratio of ${\textsc {Alg}}_1$ relative to ${\textsc {Alg}}_2$

The following definitions account for the relative performance of two algorithms to each other when both are restricted to operate on the same input sequence:

Definition 2.2

(Performance ratio). Let $\sigma \in \Sigma$ be an input sequence, and let ${\textsc {Alg}}_1$, ${\textsc {Alg}}_2$ be two algorithms for processing $\sigma$, respectively. $r_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(\sigma ) := \frac{ {\textsc {Alg}}_1[\sigma ] }{ {\textsc {Alg}}_2[\sigma ] }$ is called the performance ratio of ${\textsc {Alg}}_1$ relative to ${\textsc {Alg}}_2$ with respect to $\sigma$. $\square$

Definition 2.3

(Counting distribution function of performance ratio). Let $\sigma \in \Sigma$ be an input sequence, let ${\textsc {Alg}}$ be an algorithm, and let $r_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(\sigma )$ be the performance ratio of ${\textsc {Alg}}_1$ relative to ${\textsc {Alg}}_2$ on $\sigma$. If $\Sigma$ is a discrete set, then the function $F_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}: {\mathbb {R}} \rightarrow [0, 1]$ with

$$\begin{aligned} F_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(r) := \frac{\sum \nolimits _\sigma \in \Sigma {\mathbf {1}}_{[-\infty , r]}(r_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(\sigma ))}{|\Sigma |} \end{aligned}$$

is called the counting distribution function of the performance ratio of ${\textsc {Alg}}_1$ relative to ${\textsc {Alg}}_2$ over $\Sigma$.

In a first step, comparing ${\textsc {Alg}}_1$ and ${\textsc {Alg}}_2$ by their counting distribution function of the performance ratio (see Fig. 1b) can be done by partitioning all instances into subsets with ratio smaller than 1 (favoring ${\textsc {Alg}}_1$), with ratio larger than 1 (favoring ${\textsc {Alg}}_2$), and with ratio equal to 1 (displaying indifference between ${\textsc {Alg}}_1$ and ${\textsc {Alg}}_2$). The cardinalities of these subsets then can be put into relation to each other to provide a first impression about instance-wise algorithm qualities. Note that the competitive ratio of ${\textsc {Alg}}_1$ is obtained as $\max _{\sigma \in \Sigma }r_{{\textsc {Alg}}_1, {\textsc {Alg}}_2}(\sigma )$ if ${\textsc {Alg}}_2$ is ${\textsc {Opt}}$.

The two-sided approach has the following advantages: First, the objective value distribution gives a global view on algorithm quality over all instances; the performance ratio distribution offers a local view on the quality of both algorithms relative to each other on the same instance. Second, distribution-based analysis also yields information about ranges and variability. And third, algorithms with arbitrary lookahead levels can be compared.

In the sequel, we derive exact expressions for the counting distribution functions in two fundamental online optimization problems (bin packing in Sect. 3 and traveling salesman problem in Sect. 4) to assess the influence of lookahead on algorithm performance. The study shows that already in fairly easy problem settings, an exact analysis becomes quite involved. On the other hand, the analysis allows us to gain insight why lookahead does not prove that much beneficial in packing problems as compared to routing problems. To the best of our knowledge, an explicit consideration of all input sequences as conveyed by the exact distributional analysis has never been conducted before.

3 Online bin packing with lookahead

The bin packing problem is a fundamental combinatorial problem from the class of cutting and packing problems (Csirik and Woeginger 1998). It consists of packing the items (or more precisely their sizes) from input sequence $\sigma = (\sigma _1, \ldots , \sigma _n)$ into the least possible number of bins of capacity C. The online bin packing problem has been in the research focus of Computer Science ever since the 1970s (Johnson 1973, 1974) due to a series of appealing worst case analyses that could be established in this field. Surveys of the competitive analysis results on classical bin packing algorithms can be found in Borodin and El-Yaniv (1998), Csirik and Woeginger (1998) and Sgall (2014). In particular, it deserves mentioning that (in the limit) the well-known algorithms ${\textsc {BestFit}}$ and ${\textsc {FirstFit}}$ are $\frac{17}{10}$-competitive and their decreasing type (offline) variants where items are preordered by non-increasing size ${\textsc {BestFitDecreasing}}$ and ${\textsc {FirstFitDecreasing}}$ are $\frac{11}{9}$-competitive.

3.1 Problem setting and notation

In the online version, items are packed one after another without knowing any remaining item. In the online version with request lookahead of size l, items are packed sequentially with knowing l remaining items (or all remaining items if there are less than l of them); in particular, it is allowed to have a packing order different from the revelation order. Recall that the case $l = 1$ coincides with the pure online setting without additional lookahead. We now compare the pure online setting with the setting enhanced by lookahead: Online algorithm ${\textsc {BestFit}}$ puts the (only) known item into the fullest open bin that can accommodate it, if any; otherwise a new bin is opened and the item is put in it (Csirik and Woeginger 1998). Online algorithm ${\textsc {BestFit}}_l$ with request lookahead l first sorts the known items in order of non-increasing sizes and then puts the largest known item into the fullest open bin that can accommodate it, if any; otherwise a new bin is opened and the largest item is put in it (Csirik and Woeginger 1998). Observe that ${\textsc {BestFit}}_1$ conincides with ${\textsc {BestFit}}$.

Under lookahead of one additional item ($l=2$), we derive exact expressions for the counting distribution functions of the objective value and the performance ratio for the case of two item sizes $0.5 + \epsilon$ and $0.5 - \epsilon$ with arbitrary $\epsilon \in (0, \frac{1}{6})$ and $C=1$. Under these conditions at most two items fit into a single bin. A similar situation has been considered by Kenyon (1996) as a motivation to introduce the random order performance ratio as an alternative to competitive analysis.

Fig. 2

Counting distribution functions of a costs and b performance ratio of costs in the bin packing problem with 200 items

${{\textsc {BestFit}}}_2$ emulates ${{\textsc {BestFit}}}$ with the additional feature that the two known items are always sorted by decreasing size. From now on, we refer to ${{\textsc {BestFit}}}$ as ${{\textsc {Bf}}}$ and ${{\textsc {BestFit}}}_2$ as ${{\textsc {Bf}}}_2$. As stated above, the following analysis is restricted to item sequences $\sigma = (\sigma _1, \ldots , \sigma _n)$ with $\sigma _i \in \{0.5 + \epsilon$, $0.5 - \epsilon \}$, $\epsilon \in (0, \frac{1}{6})$, and $n \in {\mathbb {N}}$. The following additional notation is used:

• Large / small item: Item of size $0.5 + \epsilon$ / $0.5 - \epsilon$

• $n^l(\sigma$) / $n^s(\sigma$): Number of large / small items in $\sigma$

• ${\textsc {Bf}}(n, m)$ / ${\textsc {Bf}}_2(n, m)$: Number of item sequences of length n which need exactly m bins under ${{\textsc {BestFit}}}$ / ${{\textsc {BestFit}}}_2$

• $C_i$: ith Catalan number² given by $C_i = \left( {\begin{array}{c}2i\\ i\end{array}}\right) - \left( {\begin{array}{c}2i\\ i+1\end{array}}\right) = \frac{1}{i+1}\left( {\begin{array}{c}2i\\ i\end{array}}\right)$

As the main result of the analysis in this section, we find that the benefit attainable through lookahead in bin packing is of small magnitude which becomes evident in the plots of the counting distribution functions in Fig. 2. According to Sect. 3.2, this minor effect is attributable to rather restrictive conditions which have to hold for an input sequence in order to facilitate a saving of one bin through lookahead. Moreover, the combinatorial relation of the problem setting to the Catalan numbers becomes evident in the analysis, and it becomes clear that algorithm performance is closely related to the combinatorial structure of the problem. Exact expressions for the counting distribution functions of the number of bins used and the performance ratio are then derived in Sect. 3.3.

3.2 Combinatorial analysis of the lookahead effect

We analyze the behavior of ${\textsc {Bf}}$ and ${\textsc {Bf}}_2$ from a combinatorial perspective. The analysis shows that there is a close relation between the Catalan numbers and the extent of improved algorithm performance through lookahead. Additionally, we find that a bin saving through lookahead can only be achieved when several conditions on the item sequence are fulfilled at the same time. Hence, through our combinatorial analysis, we identify the core reason for the minor effect of lookahead in online bin packing.

Theorem 3.1

For any item sequence $\sigma = (\sigma _1, \sigma _2, \ldots )$ with $\sigma _i \in \{0.5+\epsilon , 0.5-\epsilon \}$, $\epsilon \in (0, \frac{1}{6})$, it holds that ${\textsc {Bf}}[\sigma ] - {\textsc {Bf}}_2[\sigma ] \in \{0, 1\}$.

Proof

The first difference in the packings of ${\textsc {Bf}}$ and ${\textsc {Bf}}_2$ occurs when item subsequence $(0.5-\epsilon , 0.5-\epsilon , 0.5+\epsilon )$ appears and there is no bin to accommodate any of these items. ${\textsc {Bf}}_2$ packs the first and third item into a single bin at full capacity and keeps the second (small) item unpacked in the lookahead until the end of the sequence (since items are homogenous), whereas ${\textsc {Bf}}$ packs the first two items in a bin at capacity $1-2\epsilon$ and the third item in a second bin. Thus, ${\textsc {Bf}}_2$ leads with one bin less used, but also one small item less packed. ${\textsc {Bf}}_2$ also loses its lookahead power as it holds the small item in the lookahead and will not change orders of two lookahead items ever again. Thus, both ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ will process the remaining items in parallel, but starting from a different bin configuration. The number of upcoming new bins for the remaining items by ${\textsc {Bf}}$ can only be the same or one less than that of ${\textsc {Bf}}_2$ (without considering the left-over small item) because items have to be packed in the same order and – as a result of the different bin configurations—${\textsc {Bf}}$ can pack one small item without opening a new bin, whereas ${\textsc {Bf}}_2$ has to open a new bin immediately. Finally, ${\textsc {Bf}}_2$ has to pack the left-over small item: When the number of new bins in the previous step is the same for ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ and in the packing of ${\textsc {Bf}}_2$ there is room for a small item, ${\textsc {Bf}}_2$ will end up with one bin less than ${\textsc {Bf}}$, otherwise ${\textsc {Bf}}_2$ will have to open a new bin resulting in a tie for the numbers of bins used. $\square$

From Theorem 3.1 it follows that ${\textsc {Bf}}_2$ dominates ${\textsc {Bf}}$ in the sense that for each item sequence it produces the same number of bins or even needs one bin less.

Definition 3.1

(Condensation of an input sequence). Let $\sigma = (\sigma _1, \sigma _2, \ldots )$ be an input sequence with $\sigma _i \in \{0.5+\epsilon , 0.5-\epsilon \}$, $\epsilon \in (0, \frac{1}{6})$. The condensation $\sigma ^c$ of $\sigma$ is the input sequence that arises by repetitively removing all pairs $(0.5-\epsilon , 0.5-\epsilon )$ starting in an odd position if the number of large items encountered previously is not larger than the number of small, unremoved items encountered previously. $\square$

A pair of removed small items in Definition 3.1 is also referred to as a condensed pair or as a condensation in an input sequence. Observe that condensed pairs of small items will be packed together in a single bin by ${\textsc {Bf}}$ with an unused capacity of $2\epsilon$, whereas for ${\textsc {Bf}}_2$ there remains hope that either of the two small items will be combined with a large item without any unutilized capacity. Hence, the term condensation will be helpful in the analysis.

Example 3.2

(Condensation of an input sequence). Consider for $\epsilon = 0.1$ the item sequences $\sigma _1 = (0.4, 0.4, 0.6, 0.6, 0.4, 0.6)$ and $\sigma _2 = (0.6, 0.4, 0.4,$ $0.6, 0.4, 0.4, 0.6, 0.4, 0.4, 0.4)$. The condensation of $\sigma _1$ is $\sigma _1^c = (0.6, 0.6, 0.4, 0.6)$; the condensation of $\sigma _2$ is $\sigma _2^c = (0.6, 0.4, 0.4, 0.6, 0.6, 0.4)$. $\square$

Theorem 3.2

For any item sequence $\sigma = (\sigma _1, \sigma _2, \ldots , \sigma _n)$ with $\sigma _i \in \{0.5+\epsilon , 0.5-\epsilon \}$, $\epsilon \in (0, \frac{1}{6})$ and $n \in {\mathbb {N}}$, it holds that ${\textsc {Bf}}[\sigma ] - {\textsc {Bf}}_2[\sigma ] = 1$ if and only if there is an odd $j\in {\mathbb {N}}$ such that the following conditions are satisfied:

• (i) $n^l((\sigma _1, \ldots , \sigma _{j-1})) = n^s((\sigma _1, \ldots , \sigma _{j-1})^c)$

• (ii) $(\sigma _j, \sigma _{j+1}, \sigma _{j+2}) = (0.5-\epsilon , 0.5-\epsilon , 0.5+\epsilon )$

• (iii) $n^s((\sigma _{j+3}, \ldots , \sigma _n)) = n^s((\sigma _{j+3}, \ldots , \sigma _n)^c)$

• (iv) $n^l((\sigma _{j+3}, \ldots , \sigma _n)) \ge n^s((\sigma _{j+3}, \ldots , \sigma _n)) + 1$

Proof

$\Rightarrow$: Let ${\textsc {Bf}}[\sigma ] - {\textsc {Bf}}_2[\sigma ] = 1$ for $\sigma =(\sigma _1, \ldots , \sigma _n)$. Then $\sigma$ can be split into $\sigma ^i=(\sigma _1, \ldots , \sigma _{j-1})$ and $\sigma ^{ii}=(\sigma _j, \ldots , \sigma _n)$ such that ${\textsc {Bf}}[\sigma ^i] - {\textsc {Bf}}_2[\sigma ^i] = 0$, ${\textsc {Bf}}[\sigma ^{ii}] - {\textsc {Bf}}_2[\sigma ^{ii}] = 1$ and both algorithms produce the same bin configurations (albeit in a different order) for $\sigma ^i$. In particular, this means that ${\textsc {Bf}}_2$ will pack $\sigma _{j-1}$ before $\sigma _j$. Among all these splits there exists one with longest $\sigma ^i$ which we refer to as $\sigma ^i$ from now on.

Recall that the first difference in the packings of ${\textsc {Bf}}$ and ${\textsc {Bf}}_2$ occurs when item subsequence $(0.5-\epsilon , 0.5-\epsilon , 0.5+\epsilon )$ appears and no open bin can accommodate any of these items. By definition, $\sigma ^i$ immediately precedes this subsequence. If $|\sigma ^i|$ was odd, any algorithm would leave a bin with space at least $0.5-\epsilon$ after packing the odd number of items in $\sigma ^i$. Hence, the first (small) item of the subsequence could also be added contradicting that no open bin can accommodate any of the items. Thus, $|\sigma ^i|$ is even and j is odd.

From Definition 3.1, it follows that $n^l(\sigma ^i) \ge n^s((\sigma ^i)^c)$ because any pair of small items that would lead to more small than large items immediately after this pair has been deleted in $n^s((\sigma ^i)^c)$ and $|\sigma ^i|$ is even. For $n^l(\sigma ^i) = n^s((\sigma ^i)^c)$, each large item has a matching small item which comes after or immediately before the large item. Thus, the configuration determined by ${\textsc {Bf}}$ is composed of $n^l(\sigma ^i)$ completely filled bins and $\frac{|\sigma ^i|-2n^l(\sigma ^i)}{2}$ bins with two small items. Clearly, this number of bins is optimal. From the proof of Theorem 3.1, both ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ attain the optimal number of bins by the same bin configurations for $n^l(\sigma ^i) = n^s((\sigma ^i)^c)$. For $n^l(\sigma ^i) > n^s((\sigma ^i)^c)$, we show by contradiction that $\sigma ^i$ cannot be a longest possible subsequence such that ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ produce the same bin configurations: Assume that $\sigma ^i$ is a longest possible subsequence such that ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ produce the same bin configurations and $n^l(\sigma ^i) > n^s((\sigma ^i)^c)$. Then there is at least one bin containing a large item without a matching small item. An additional small item will be put into such a bin, an additional large item will need a new bin, but the configurations of both algorithms will remain the same contradicting the definition of $\sigma ^i$. Thus, $n^l(\sigma ^i) = n^s((\sigma ^i)^c)$ which is (i).

According to (i) and the definition of $\sigma ^i$, there must be an odd j such that ${\textsc {Bf}}_2$ starts to exhibit an advantage over ${\textsc {Bf}}$ on $\sigma ^{ii}=(\sigma _j, \sigma _{j+1}, \sigma _{j+2}, \ldots )$ after $\sigma ^{i}$ has been packed resulting in the same bin configurations with no space left by both algorithms. Only $(\sigma _j, \sigma _{j+1})=(0.5-\epsilon , 0.5-\epsilon )$ potentially produces a difference. To make this happen, ${\textsc {Bf}}_2$ need not pack these two items into the same bin, whereas ${\textsc {Bf}}$ has to. This happens if and only if $\sigma _{j+2}=0.5+\epsilon$: ${\textsc {Bf}}_2$ will not pack $\sigma _{j+1}$ immediately, but delay it until the end of the item sequence, whereas $\sigma _{j+2}$ will be matched with $\sigma _{j}$. This establishes (ii).

To see (iii), note that the processing of ${\textsc {Bf}}_2$ on $\sigma ^{ii}=(0.5-\epsilon , 0.5-\epsilon , 0.5+\epsilon , \sigma _{j+3}, \ldots , \sigma _n)$ is emulated by ${\textsc {Bf}}$ on ${{\tilde{\sigma }}}^{ii}=(0.5-\epsilon , 0.5+\epsilon , \sigma _{j+3}, \ldots , \sigma _n, 0.5-\epsilon )$. Assume there is a condensed pair of small items in the subsequence starting with $\sigma _{j+3}$; if there is more than one condensation, consider the first one. Let $\sigma _{j'}$ be the first small item of this condensation. ${\textsc {Bf}}$ produces a bin with two small items for $\sigma _j$ and $\sigma _{j+1}$, but not for $\sigma _{j'}$ and $\sigma _{j'+1}$ since two small items starting in an even position of the original sequence cannot be put in the same bin by ${\textsc {Bf}}$. ${\textsc {Bf}}_2$ processes $(\sigma _j, \sigma _{j+1}, \sigma _{j+2}, \ldots , \sigma _{n-1}, \sigma _n)$ as $(\sigma _j, \sigma _{j+2}, \ldots , \sigma _{n-1}, \sigma _n, \sigma _{j+1})$ emulated by ${\textsc {Bf}}$, i.e., it does not produce a bin with two small items for $\sigma _j$ and $\sigma _{j+1}$, but for $\sigma _{j'}$ and $\sigma _{j'+1}$ since in $(\sigma ^i, {{\tilde{\sigma }}}^{ii})$ these items are condensed items. Between $\sigma _{j+3}$ and $\sigma _{j'}$, neither algorithm produces another bin with two small items since we consider the first condensation in the subsequence starting from $\sigma _{j+3}$. In particular, there cannot be a condensation of the original sequence starting in an odd position between $\sigma _{j+4}$ and $\sigma _{j'-1}$. If there was such a condensation, it would follow from (i) and (ii) that there must be another even index $j' < j+4$ starting a condensation in the subsequence starting with $\sigma _{j+3}$ contradicting to $j'$ being the first such index. Hence, both ${\textsc {Bf}}$ and ${\textsc {Bf}}_2$ produce one additional bin with two small items for ${{\tilde{\sigma }}}^{i}=(\sigma _1, \ldots , \sigma _{j-1}, \sigma _j, \sigma _{j+1}, \sigma _{j+2}, \ldots , \sigma _{j'})$ as compared to $\sigma ^{i}$, and $\sigma ^{i}$ could not have been the longest possible first part among all splits of $\sigma$.

From (i), (ii), (iii), we know that in ${\textsc {Bf}}_2$’s processing there is no bin with two small items from $\sigma _j$ onwards, whereas ${\textsc {Bf}}$ creates such a bin for $(\sigma _j, \sigma _{j+1})$. Hence, in order to pack $\sigma _{j+1}$ at the end of ${\textsc {Bf}}_2$’s processing into an already open bin and to save a bin as compared to ${\textsc {Bf}}$, we need an open bin with a large item only. This is the case if and only if in the subsequence starting from $\sigma _{j+3}$ at least one more large item exists, i.e., iv).

$\Leftarrow$: We have that for item sequence $\sigma$, there is an odd $j \in {\mathbb {N}}$ such that conditions (i) to (iv) are fulfilled. In the sequel, a bin is called matched if it contains a large and small item, otherwise it is called unmatched. From (ii) and (iii), we know that ${\textsc {Bf}}_2$ will not produce a bin with two small items from $\sigma _j$ onwards, whereas ${\textsc {Bf}}$ creates such a bin for $(\sigma _j, \sigma _{j+1})$. From iv), we conclude that the number of matched bins in ${\textsc {Bf}}_2$ is two higher than in ${\textsc {Bf}}$. From the pigeonhole principle, it follows that the number of unmatched bins in ${\textsc {Bf}}$ is three higher than in ${\textsc {Bf}}_2$. Thus, ${\textsc {Bf}}[(\sigma _j, \sigma _{j+1}, \ldots , \sigma _n)] - {\textsc {Bf}}_2[(\sigma _j, \sigma _{j+1}, \ldots , \sigma _n)] = 1$. (i) guarantees that in the bin configurations induced both by ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ there is a matching small item for any large item such that there is no bin with a large item only after $(\sigma _1, \ldots , \sigma _{j-1})$ have been processed. Since $|(\sigma _1, \ldots , \sigma _{j-1})|$ is even, there is no bin with a small item only after $(\sigma _1, \ldots , \sigma _{j-1})$ has been packed. Hence, the initial position for processing $(\sigma _j, \sigma _{j+1}, \ldots , \sigma _n)$ is the same for ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$ and can be viewed as restarting with no bins used so far. In particular, ${\textsc {Bf}}[(\sigma _1, \sigma _{2}, \ldots , \sigma _{j-1})] - {\textsc {Bf}}_2[(\sigma _1, \sigma _{2}, \ldots , \sigma _{j-1})] = 0$. $\square$

In Theorem 3.4, we characterize the number of item sequences of a given length which yield a saving of one bin by applying ${\textsc {Bf}}_2$ instead of ${\textsc {Bf}}$. To this end, we make use of the notion of (recurring) unit-sloped paths (Michaels and Rosen 1991).

Definition 3.3

((Recurring) unit-sloped path). A unit-sloped path of length 2i is a path in ${\mathbb {R}}^2$ from (0, 0) to $(2i, s_{2i})$ consisting only of line segments between $(k - 1, s_{k-1})$ and $(k, s_k)$ for $k = 1, 2, \ldots , 2i$ where $s_k = s_{k-1} + 1$ or $s_k = s_{k-1} -1$ and $s_0 = 0$. A recurring unit-sloped path of length 2i is a unit-sloped path of length 2i that ends in (2i, 0), i.e., it has $s_{2i} = 0$. $\square$

Note that if we restrict $s_k \ge 0$ for all $k = 0, 1, 2, \ldots , 2i$, this definition coincides with that of the well-known Dyck path (see, e.g., Deutsch 1999; Deutsch and Shapiro 2001). Figure 3 shows an example for a recurring unit-sloped path and a Dyck path, respectively.

Fig. 3

Recurring unit sloped paths. a General path and b Dyck path

The number of item sequences of length 2i without any condensation is equal to the Catalan number $C_{i+1}$ as a consequence of the following Lemma 3.3.

Lemma 3.3

• (a) The number of recurring unit-sloped paths of length 2i which have $s_k \ge 0$ for all $k = 0, 1, 2, \ldots , 2i$ is $C_i$.

• (b) The number of recurring unit-sloped paths of length 2i which have $s_k \ge -1$ for all $k = 0, 1, 2, \ldots , 2i$ is $C_{i+1}$.

Proof

See “Appendix A.1”. $\square$

We are now in a position to provide an expression for the number of item sequences of given length which lead to a a saving of one bin by applying ${\textsc {Bf}}_2$ instead of ${\textsc {Bf}}$.

Theorem 3.4

• (a) The number of item sequences $\sigma$ of odd length $|\sigma |=2n+1$ for $n \in {\mathbb {N}}$ with ${\textsc {Bf}}[\sigma ] - {\textsc {Bf}}_2[\sigma ] = 1$ is given by

  $$\begin{aligned} \sum _{p=1}^{n-1} \Bigl (2^{2(p-1)} - \sum _{i=1}^{p-1} C_i \cdot 2^{2(p-1-i)}\Bigr ) \Bigl (2^{2(n-p)} - \sum _{i=1}^{n-p} C_i \cdot 2^{2(n-p-i)} - C_{n-p+1}\Bigr ). \end{aligned}$$

• (b) The number of item sequences $\sigma$ of even length $|\sigma |=2n$ for $n \in {\mathbb {N}}$ with ${\textsc {Bf}}[\sigma ] - {\textsc {Bf}}_2[\sigma ] = 1$ is given by

  $$\begin{aligned} \sum _{p=1}^{n-1} \Bigl (2^{2(p-1)} - \sum _{i=1}^{p-1} C_i \cdot 2^{2(p-1-i)}\Bigr ) \Bigl (2^{2(n-p)-1} - \sum _{i=1}^{n-p-1} C_i \cdot 2^{2(n-p-i)-1} - C_{n-p}\Bigr ). \end{aligned}$$

Proof

• (a) We compute the number of item sequences $\sigma$ which can be brought into the form $\sigma = (\sigma _1, \ldots , \sigma _{j-1}, \sigma _{j}, \sigma _{j+1}, \sigma _{j+2}, \sigma _{j+3}, \ldots , \sigma _{2n+1})$ fulfilling (i) to (iv) from Theorem 3.2 with odd j. We can choose j to be any odd number with $|(\sigma _j, \sigma _{j+1}, \sigma _{j+2}, \ldots , \sigma _{2n+1})| \ge 4$. The largest j fulfilling this condition is $j = 2(n - 1)-1$ such that five items $(\sigma _{2(n-1)-1}, \sigma _{2(n-1)}, \sigma _{2n-1}, \sigma _{2n}, \sigma _{2n+1})$ remain. Hence, in the first sum, p runs from 1 to $n-1$ indicating that j runs from $2 \cdot 1 - 1 = 1$ to $2 \cdot (n-1) - 1$ with even j’s omitted.

  We first consider the first pair of parentheses: For fixed p, the number of item (sub-) sequences of length $2(p-1)$ satisfying condition (i) from Theorem 3.2, i.e.,

  $$\begin{aligned} n^l((\sigma _1, \ldots , \sigma _{j-1})) = n^s((\sigma _1, \ldots , \sigma _{j-1})^c) \end{aligned}$$

  (1)

  with $j-1 = 2(p-1)$ is $n_0 = 2^{2(p-1)} - \sum \nolimits _{i=1}^{p-1} C_i \cdot 2^{2(p-1-i)}$ which can be seen as follows: It holds that $n_0 = 2^{2(p-1)} - n_{viol}$ where $n_{viol}$ is the number of sequences of length $2(p-1)$ violating Equality 1. Since by definition $n^l((\sigma _1, \ldots , \sigma _{j-1})) \ge n^s((\sigma _1, \ldots , \sigma _{j-1})^c)$, we have $n_{viol} = |\Sigma ^{viol}|$ with $\Sigma ^{viol} := \{(\sigma _1, \ldots , \sigma _{j-1}) \,|\, n^l((\sigma _1, \ldots , \sigma _{j-1})) > n^s((\sigma _1, \ldots , \sigma _{j-1})^c)\}$. From the pigeonhole principle, we can only have $n^l((\sigma _1, \ldots , \sigma _{j-1})) = n^s((\sigma _1, \ldots , \sigma _{j-1})^c) + d$ where $d = 2, 4, 6, \ldots$ for $(\sigma _1, \ldots , \sigma _{j-1}) \in \Sigma ^{viol}$ because $|(\sigma _1, \ldots , \sigma _{j-1})^c|$ is even.

  Thus, there will be a last pair of large items occurring at positions $2(p-1-i)+1$ and $2(p-1-i)+2$ for some $i \in \{1, 2, \ldots , p-1\}$ which leads to

  $$\begin{aligned}&n^l((\sigma _{2(p-1-i)+1}, \ldots , \sigma _{j-1})) > n^s((\sigma _{2(p-1-i)+1}, \ldots , \sigma _{j-1})^c)\text {, i.e.,}\nonumber \\&n^l((\sigma _{2(p-1-i)+1}, \ldots , \sigma _{j-1})) = n^s((\sigma _{2(p-1-i)+1}, \ldots , \sigma _{j-1})^c) + 2. \end{aligned}$$

  (2)

  In this case, the conditions

  • $n^l((\sigma _{2(p-1-i)+3}, \ldots , \sigma _{2(p-1)})) = n^s((\sigma _{2(p-1-i)+3}, \ldots , \sigma _{2(p-1)})^c)$ and

  • $n^s((\sigma _{2(p-1-i)+3}, \ldots , \sigma _{2(p-1)})) = n^s((\sigma _{2(p-1-i)+3}, \ldots , \sigma _{2(p-1)})^c)$

  have to hold regardless of $\sigma _1, \ldots , \sigma _{2(p-1-i)}$ . Thus, we can choose $\sigma _1, \ldots , \sigma _{2(p -1-i)}$ freely giving the factor $2^{2(p-1-i)}$. The two itemized conditions are required in order to ensure that the two large items $\sigma _{2(p-1-i)+1}$ and $\sigma _{2(p-1-i)+2}$ represent the last pair of large items leading to Equality 2. In particular, if there was a condensed pair of small items, then at least one pair of two large items would follow which would lead to

  $$\begin{aligned} n^l((\sigma _{2(p-1-i')+1}, \ldots , \sigma _{j-1})) = n^s((\sigma _{2(p-1-i')+1}, \ldots , \sigma _{j-1})^c) + 2 \end{aligned}$$

  with $i' < i$. For fixed i, it remains to show that the number of item sequences of length $2(i-1)$ fulfilling the two itemized conditions is $C_i$.

  To this end, we make use of the concept of (recurring) unit-sloped paths (cf. Definition 3.3): In order to fulfill the two itemized conditions, observe the correspondences between the appearance of a large item and an up-move ($s_k = s_{k-1} + 1$) and between the appearance of a small item and a down-move ($s_k = s_{k-1} - 1$) in a unit-sloped path. Because the number of large items equals the number of small items and there are no condensations, this path is also recurring. The second itemized condition expresses that there are never two small items such that the number of large items minus the number of small items up to an arbitrary position in the item sequence would drop down to $-2$. Hence, the number of item sequences of length $2(i-1)$ fulfilling both conditions is equal to the number of recurring unit-sloped paths with $s_k \ge -1$ for all k. According to Lemma 3.3 b), this number is $C_i$.

  We now consider the second pair of parentheses: For fixed p, the number of item sequences of length $2(n-p)$ which fulfill conditions (iii) and (iv) from Theorem 3.2, i.e.,

  • $n^s((\sigma _{j+3}, \ldots , \sigma _{2n+1})) = n^s((\sigma _{j+3}, \ldots , \sigma _{2n+1})^c)$ and

  • $n^l((\sigma _{j+3}, \ldots , \sigma _{2n+1})) \ge n^s((\sigma _{j+3}, \ldots , \sigma _{2n+1})) + 1$

  with $j = 2p-1$ can be characterized as $2^{2(n-p)} - n_1 - n_2$ where $n_1$ is the number of item sequences of length $2(n-p)$ with at least one condensation and $n_2$ is the number of item sequences of length $2(n-p)$ without condensation that has the same number of small and large items.

  For $n_1$, let $i \in \{1, \ldots , n-p\}$ be fixed such that the first condensation consists of $\sigma _{2(p+i)}$ and $\sigma _{2(p+i)+1}$, then we need to have $n^l(\sigma _{j+3}, \ldots , \sigma _{2(p+i)-1}) = n^s(\sigma _{j+3}, \ldots , \sigma _{2(p+i)-1})$ and no condensation is allowed in $(\sigma _{j+3}, \ldots , \sigma _{2(p+i)-1})$. Structurally, we obtain the same two conditions as the two itemized conditions for the first pair of parentheses, i.e.,

  • $n^l((\sigma _{2(p+1)}, \ldots , \sigma _{2(p+i)-1})) = n^s((\sigma _{2(p+1)}, \ldots , \sigma _{2(p+i)-1}))$ and

  • $n^s((\sigma _{2(p+1)}, \ldots , \sigma _{2(p+i)-1})) = n^s((\sigma _{2(p+1)}, \ldots , \sigma _{2(p+i)-1})^c)$

  regardless of $\sigma _{2(p+i)+2}, \ldots , \sigma _{2n+1}$ because once a condensation occurs the rest is irrelevant. Since $\sigma _{2(p+i)+2}, \ldots , \sigma _{2n+1}$ are free, the factor $2^{2(n-p-i)}$ follows, and from Lemma 3.3, the number of item sequences of length $2(i-1)$ fulfilling the two itemized conditions is $C_i$. Thus, we obtain $n_1 = \sum \nolimits _{i=1}^{n-p} C_i \cdot 2^{2(n-p-i)}$. Also from Lemma 3.3, it follows that $n_2 = C_{n-p+1}$ gives the number of item sequences of length $2(n-p)$ where the number of large items equals the number of small items and no condensations occur.

• (b) The proof is analogous to part (a) with the only difference that the decomposition into $\sigma = (\sigma _1, \ldots , \sigma _{j-1}, \sigma _{j}, \sigma _{j+1}, \sigma _{j+2}, \sigma _{j+3}, \ldots , \sigma _{2n+1})$ now has odd $|(\sigma _{j+3}, \ldots , \sigma _{2n})|$. Thus, for a given $p \in \{1, \ldots , n-1\}$, the subsequence $(\sigma _{j+3}, \ldots , \sigma _{2n})$ now only has $2(n-p)-1$ elements, and the number of sequences of (longest possible even) length $2(n-p-1)$ without condensation and balanced number of small and large items is $C_{n-p}$. $\square$

3.3 Counting distribution functions

We go on to establish exact expressions for the counting distribution functions of the objective value and performance ratio related to algorithms ${\textsc {Bf}}$ and ${\textsc {Bf}}_2$. The analysis illustrates how a comprehensive assessment of algorithm quality can be obtained for the online bin packing setting under consideration. While the previous results on the number of item sequences for which ${\textsc {Bf}}_2$ incurs a bin saving over ${\textsc {Bf}}$ cannot be used directly for the counting distribution functions, many proof ideas are reused subsequently. The numbers $a_{n, k} = \frac{k+1}{n+1}\left( {\begin{array}{c}2n+2\\ n-k\end{array}}\right)$ with $k, n \in {\mathbb {N}}_0$, $n \ge k$ (cf. Deutsch and Shapiro 2001) will be used in several of the following results leading to the counting distribution functions for the objective value in Corollary 3.11 and for the performance ratio in Corollary 3.13.

Lemma 3.5

• (a) The number of item sequences $\sigma$ of length 2n where ${\textsc {Bf}}[\sigma ] = m$ is given by

  $$\begin{aligned} {\textsc {Bf}}(2n, m) = {\left\{ \begin{array}{ll} \displaystyle \sum _{k=m-n}^{n} a_{n,k} = \displaystyle \sum _{k=m-n}^{n} \frac{k+1}{n+1}\left( {\begin{array}{c}2n+2\\ n-k\end{array}}\right) &{} \text {if } n \le m \le 2n,\\ 0 &{} \text {otherwise.}\\ \end{array}\right. } \end{aligned}$$

• (b) The number of item sequences $\sigma$ of length $2n+1$ where ${\textsc {Bf}}[\sigma ] = m$ is given by

  $$\begin{aligned} {\textsc {Bf}}(2n+1, m) = {\left\{ \begin{array}{ll} 2\displaystyle \sum _{k=m-n}^{n} a_{n,k} + a_{n,m-1-n} &{} \text {if } n+1 < m \le 2n+1,\\ 3\displaystyle \sum _{k=0}^{n} a_{n,k} - a_{n, 0} &{} \text {if } m = n+1,\\ 0 &{} \text {otherwise.}\\ \end{array}\right. } \end{aligned}$$

Proof

By reverse induction. See “Appendix A.2”. $\square$

We now give another formula to compute the numbers ${\textsc {Bf}}(2n, m)$ and ${\textsc {Bf}}(2n+1, m)$.

Theorem 3.6

• (a) The number of item sequences $\sigma$ of length 2n where ${\textsc {Bf}}[\sigma ] = m$ is given by

  $$\begin{aligned} {\textsc {Bf}}(2n, m) = {\left\{ \begin{array}{ll} \left( {\begin{array}{c}2n+1\\ m+1\end{array}}\right) = \left( {\begin{array}{c}2n\\ m\end{array}}\right) + \left( {\begin{array}{c}2n\\ m+1\end{array}}\right) &{} \text {if } n \le m \le 2n,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

• (b) The number of item sequences $\sigma$ of length $2n+1$ where ${\textsc {Bf}}[\sigma ] = m$ is given by

  $$\begin{aligned} {\textsc {Bf}}(2n+1, m) = {\left\{ \begin{array}{ll} \left( {\begin{array}{c}2n+2\\ m+1\end{array}}\right) = \left( {\begin{array}{c}2n+1\\ m\end{array}}\right) + \left( {\begin{array}{c}2n+1\\ m+1\end{array}}\right) &{} \text {if } n+1 < m \le 2n+1,\\ \left( {\begin{array}{c}2n+3\\ n+2\end{array}}\right) - \left( {\begin{array}{c}2n+1\\ n+1\end{array}}\right) &{} \text {if }m = n+1,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Proof

By two-dimensional induction. See “Appendix A.3”. $\square$

Theorem 3.7

The number of item sequences $\sigma$ of length n where ${\textsc {Bf}}[\sigma ] = m$ and ${\textsc {Bf}}_2[\sigma ] = m-1$ is given by $\left( {\begin{array}{c}n\\ m+1\end{array}}\right)$ for $m = \lceil \frac{n}{2}\rceil + 1, \ldots , n-1$.

Proof

From Regev (2012), we have for $1 \le q \le p \le 2q-1$ the following expression for the binomial coefficient: $\left( {\begin{array}{c}p\\ q\end{array}}\right) = \sum \nolimits _{i\ge 0} C_i \left( {\begin{array}{c}p-1-2i\\ q-1-i\end{array}}\right)$.

For item sequence $\sigma$, assume that $|\sigma | = 2n$ and that $\sigma$ fulfills the conditions stated in Theorem 3.2. We further decompose $\sigma$ into three parts: For some $i \in \{1, \ldots , n-1\}$, let $(\sigma _1, \sigma _2, \ldots , \sigma _{2(i-1)})$ correspond to a recurring unit-sloped path with $s_k \ge -1$ for all $k = 1, 2, \ldots , 2(i-1)$, let $\sigma _{2i-1}, \sigma _{2i}$ be the first two small items which would be condensed, and let $(\sigma _{2i+1}, \sigma _{2(i+1)}, \ldots , \sigma _{2n})$ be the rest of $\sigma$. Note that $\sigma _{2i-1}, \sigma _{2i}$ are not necessarily responsible for the saving which can be accrued by ${\textsc {Bf}}_2$ over ${\textsc {Bf}}$.

According to Lemma 3.3, the number of item sequences fulfilling the properties of the first subsequence is $C_i$. The number of item subsequences $(\sigma _{2i+1}, \sigma _{2(i+1)}, \ldots , \sigma _{2n})$ leading to overall m bins for ${\textsc {Bf}}$ and overall $m-1$ bins for ${\textsc {Bf}}_2$ is $\left( {\begin{array}{c}2n-2i\\ m-i\end{array}}\right)$ which can be seen as follows: For $(\sigma _1, \sigma _2, \ldots , \sigma _{2(i-1)})$, $i-1$ bins were needed such that for $(\sigma _{2i-1}, \sigma _{2i}, \ldots , \sigma _{2n})$, $m-i+1$ and $m-i$ additional bins will be needed by ${\textsc {Bf}}$ and ${\textsc {Bf}}_2$, respectively. Since $\sigma _{2i-1}, \sigma _{2i}$ are small items, $m-i$ bins will be needed by ${\textsc {Bf}}$ for $(\sigma _{2i+1}, \sigma _{2(i+1)}, \ldots , \sigma _{2n})$ and in addition, conditions (ii), (iii) and (iv) of Theorem 3.2 have to hold for some $j \ge 2i-1$ to realize the saving of ${\textsc {Bf}}_2$. Because condition iv) of Theorem 3.2 has to hold, objective value m is attained by ${\textsc {Bf}}$ when $m-i$ out of the $2n - 2i$ items $(\sigma _{2i+1}, \sigma _{2(i+1)}, \ldots , \sigma _{2n})$ are large. However, this choice does not necessarily fulfill conditions (ii) and (iii) of Theorem 3.2 because it may be that $(\sigma _{2i+1}, \sigma _{2i+2})=(0.5-\epsilon , 0.5+\epsilon )$ or that condensations can be found in $(\sigma _{2i+2}, \sigma _{2i+3}, \ldots , \sigma _{2n})$. These two cases are resolved as follows: Whenever $(\sigma _{2i+1}, \sigma _{2i+2})=(0.5-\epsilon , 0.5+\epsilon )$, we find a bijective mapping from $\sigma$ to some $\sigma '$ where $\sigma '$ is identical to $\sigma$ except for $(\sigma _{2i+1}, \sigma _{2i+2})$ now being $(\sigma _{2i+1}, \sigma _{2i+2})=(0.5-\epsilon , 0.5-\epsilon )$. Hereby, another condensation is established which erases responsibility of the first condensation for the saving of ${\textsc {Bf}}_2$ and claims responsibility itself (by setting $j=2i+1$). Whenever we have another condensation in $(\sigma _{2i+2}, \sigma _{2i+3}, \ldots , \sigma _{2n})$, we recognize that it erases responsibility for the saving of ${\textsc {Bf}}_2$ of a previous condensation and claims responsibility itself (by setting j accordingly). Thus, for some i such that $(\sigma _{2i-1}, \sigma _{2i})$ is the first condensation, there are $\left( {\begin{array}{c}2n-2i\\ m-i\end{array}}\right)$ item subsequences $(\sigma _{2i+1}, \sigma _{2(i+1)}, \ldots , \sigma _{2n})$ fulfilling conditions (ii), (iii) and (iv) of Theorem 3.2. The next lemma is needed to complete the proof for even length 2n of $\sigma$.

Lemma 3.8

For $n \le m \le 2n$ it holds that $\sum \nolimits _{i\ge 1} C_i \left( {\begin{array}{c}2n-2i\\ m-i\end{array}}\right) = \sum \nolimits _{i\ge 1} C_{i-1} \left( {\begin{array}{c}2n-2i+1\\ m-i+1\end{array}}\right) .$

Proof

See “Appendix A.4”. $\square$

Using this result, the proof of Theorem 3.7 can be completed for even length 2n of $\sigma$ by

$$\begin{aligned} \sum _{i\ge 1} C_i \left( {\begin{array}{c}2n-2i\\ m-i\end{array}}\right)&= \sum _{i\ge 1} C_{i-1} \left( {\begin{array}{c}2n-2i+1\\ m-i+1\end{array}}\right) =\sum _{i\ge 1} \frac{1}{i}\left( {\begin{array}{c}2i-2\\ i-1\end{array}}\right) \left( {\begin{array}{c}2n-2i+1\\ m-i+1\end{array}}\right) \\&=\sum _{i\ge 0} \frac{1}{i+1}\left( {\begin{array}{c}2i\\ i\end{array}}\right) \left( {\begin{array}{c}2n-2i-1\\ m-i\end{array}}\right) = \sum _{i\ge 0} C_i \left( {\begin{array}{c}2n-2i-1\\ m-i\end{array}}\right) \\&=\left( {\begin{array}{c}2n\\ m+1\end{array}}\right) . \end{aligned}$$

where the last equality follows for $n < m \le 2n - 1$ from the proof of Lemma 9 in Regev (2012) and condition iv) from Theorem 3.2. For odd length $2n+1$ of $\sigma$, the proof is analogous with $2n-2i$ replaced by $2n-2i+1$. $\square$

Corollary 3.9

The number of item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m$ and ${\textsc {Bf}}_2[\sigma ] = m$ is given by $\left( {\begin{array}{c}n\\ m\end{array}}\right)$ for $m = \lceil \frac{n}{2}\rceil + 1, \ldots , n$.

Proof

See “Appendix A.5”. $\square$

We now state the central relation between the objective values attained by ${\textsc {Bf}}_2$ and ${\textsc {Bf}}$.

Theorem 3.10

The number of item sequences $\sigma$ of length n where ${\textsc {Bf}}_2[\sigma ] = m$ is given by

$$\begin{aligned} {\textsc {Bf}}_2(n, m) = {\left\{ \begin{array}{ll} 1 &{} \text {if } m = n,\\ {\textsc {Bf}}(n, m) + {\textsc {Bf}}(n, m+1) - 2 \left( {\begin{array}{c}n\\ m+1\end{array}}\right) &{} \text {if } m = \lceil \frac{n}{2}\rceil + 1, \ldots , n-1,\\ {\textsc {Bf}}(n, m) + {\textsc {Bf}}(n, m+1) - \left( {\begin{array}{c}n\\ m+1\end{array}}\right) &{} \text {if } m = \lceil \frac{n}{2}\rceil ,\\ 0 &{} \text {if } m \le \lceil \frac{n}{2}\rceil -1. \end{array}\right. } \end{aligned}$$

Proof

Because of item sizes in $\{0.5-\epsilon , 0.5+\epsilon \}$, at most two items can be packed in a bin so that packing n items in less than $\lceil \frac{n}{2}\rceil$ bins is infeasible. Likewise, each item of $\sigma$ is packed separately if and only if each item is large, and there is only one such item sequence $\sigma$.

The number of item sequences of length n for which ${\textsc {Bf}}_2$ attains objective value m can be computed as $n_1 + n_2 - n_3 - n_4$ where $n_1$ is the number of item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m$, $n_2$ is the number of item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m+1$, $n_3$ is the number of item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m$, ${\textsc {Bf}}_2[\sigma ] = m-1$, and $n_4$ is the number of item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m+1$, ${\textsc {Bf}}_2[\sigma ] = m+1$.

From Theorem 3.7, we have that the number of all item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m$ and ${\textsc {Bf}}_2[\sigma ] = m-1$ is $n_3 = \left( {\begin{array}{c}n\\ m+1\end{array}}\right)$ for $m = \lceil \frac{n}{2}\rceil + 1, \ldots , n-1$; from Corollary 3.9, we have that the number of all item sequences $\sigma$ of length n with ${\textsc {Bf}}[\sigma ] = m+1$ and ${\textsc {Bf}}_2[\sigma ] = m+1$ is $n_4 = \left( {\begin{array}{c}n\\ m+1\end{array}}\right)$ for $m = \lceil \frac{n}{2}\rceil , \ldots , n-1$, and the result follows. $\square$

From the previous results, we obtain expressions for the counting distribution functions of the objective value $F_{{\textsc {Bf}}}(v)$ and $F_{{\textsc {Bf}}_2}(v)$, respectively. We restrict ourselves to item sequences of even length since analogous conclusions can be drawn immediately in case of odd length.

Corollary 3.11

The counting distribution functions of the objective value $F_{{\textsc {Bf}}}(v)$ and $F_{{\textsc {Bf}}_2}(v)$ of Bf and ${\textsc {Bf}}_2$ for item sequences of length 2n are given by

$$\begin{aligned} F_{{\textsc {Bf}}}(v)= {\left\{ \begin{array}{ll} 0 &{} \text {if } v< n,\\ 2^{-2n}\displaystyle \sum _{m=n}^{\lfloor v \rfloor } \genfrac(){0.0pt}1{2n+1}{m+1} &{} \text {if } n \le v < 2n,\\ 1 &{}\text {if } v \ge 2n, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} F_{{\textsc {Bf}}_2}(v)= {\left\{ \begin{array}{ll} 0 &{} \text {if } v< n,\\ 2^{-2n}\Bigg (\displaystyle \sum _{m=n}^{\lfloor v \rfloor } \Bigl (\genfrac(){0.0pt}1{2n+1}{m+1}+\genfrac(){0.0pt}1{2n+1}{m+2}-2\genfrac(){0.0pt}1{2n}{m+1}\Bigr )+\genfrac(){0.0pt}1{2n}{m+1}\Bigg ) &{} \text {if } n \le v < 2n,\\ 1 &{}\text {if } v \ge 2n. \end{array}\right. } \end{aligned}$$

Proof

Direct consequence of Theorems 3.6 and 3.10. $\square$

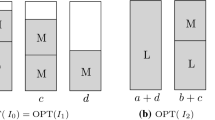
Figure 2a exemplarily plots $F_{{\textsc {Bf}}}(v)$ and $F_{{\textsc {Bf}}_2}(v)$ for all item sequences of length $n = 100$. We observe a rather small lookahead effect as a result of the (relatively restrictive) conditions in Theorem 3.2 which are collectively found only in a minor fraction of all item sequences.

Part (a) of the following corollary expresses ${\textsc {Bf}}_2$’s dominance over ${\textsc {Bf}}$. As seen from Theorem 3.1, stochastic dominance of all orders is established. As a consequence of part (b), knowing one additional item is worthless in the limit. Taking into account Theorem 3.1, this result was to be expected. The reason for this ineffectiveness lies in the total forfeiture of the power of the lookahead capability once a small item occurs and occupies the lookahead set.

Corollary 3.12

• (a) For item sequences of length 2n, we have $F_{{\textsc {Bf}}_2}(v) \ge F_{{\textsc {Bf}}}(v)$ for all $v \in {\mathbb {R}}$ and $F_{{\textsc {Bf}}_2}(v) - F_{{\textsc {Bf}}}(v) > F_{{\textsc {Bf}}_2}(v+1) - F_{{\textsc {Bf}}}(v+1)$ for all $v < 2n-1$.

• (b) For item sequences of length 2n, we have $\sup _{v \in {\mathbb {R}}}|F_{{\textsc {Bf}}_2}(v) - F_{{\textsc {Bf}}}(v)| \rightarrow 0$ as $n \rightarrow \infty$.

Proof

See “Appendix A.6”. $\square$

We next derive an expression for the counting distribution function of the performance ratio.

Corollary 3.13

The counting distribution function of the performance ratio $F_{{\textsc {Bf}},{\textsc {Bf}}_2}(r)$ of Bf relative to ${\textsc {Bf}}_2$ for item sequences of length 2n is given by

$$\begin{aligned} F_{{\textsc {Bf}},{\textsc {Bf}}_2}(r)= {\left\{ \begin{array}{ll} 0 &{} \text {if } r< 1,\\ \frac{1}{2} + \frac{\frac{1}{2}\left( {\begin{array}{c}2n\\ n\end{array}}\right) + \left( {\begin{array}{c}2n\\ n+1\end{array}}\right) }{2^{2n}} &{} \text {if } 1 \le r< \frac{2n-1}{2n-2} = 1 + \frac{1}{2n-2},\\ \frac{1}{2} + \frac{\frac{1}{2}\left( {\begin{array}{c}2n\\ n\end{array}}\right) + \left( {\begin{array}{c}2n\\ n+1\end{array}}\right) + \sum \limits _{i=0}^{n-2-k} \left( {\begin{array}{c}2n\\ 2n-i\end{array}}\right) }{2^{2n}} &{} \text {if } \frac{n+k+1}{n+k} = 1 + \frac{1}{n+k}\le r < \frac{n+k}{n+k-1}=1+\frac{1}{n+k-1}\\ &{} \text {for } k=1, \ldots , n-1,\\ 1 &{}\text {else.} \end{array}\right. } \end{aligned}$$

Proof

According to Theorem 3.7, we have:

• $\left( {\begin{array}{c}2n\\ n+2\end{array}}\right)$ is the number of sequences of length 2n with ${\textsc {Bf}}[\sigma ]=n+1$, ${\textsc {Bf}}_2[\sigma ]=n$

• $\left( {\begin{array}{c}2n\\ n+3\end{array}}\right)$ is the number of sequences of length 2n with ${\textsc {Bf}}[\sigma ]=n+2$, ${\textsc {Bf}}_2[\sigma ]=n+1$

• $\ldots$

• $\left( {\begin{array}{c}2n\\ 2n\end{array}}\right)$ is the number of sequences of length 2n with ${\textsc {Bf}}[\sigma ]=2n-1$, ${\textsc {Bf}}_2[\sigma ]=2n-2$

Apart from these item sequences, no other sequences change their objective due to application of ${\textsc {Bf}}_2$ instead of ${\textsc {Bf}}$. Thus, the performance ratio ranges in $[1, \frac{n+1}{n}]$ and the number of item sequences of length 2n which leave the number of bins unchanged in both algorithms is

$$\begin{aligned}&2^{2n} - \genfrac(){0.0pt}1{2n}{n+2} - \genfrac(){0.0pt}1{2n}{n+3} - \cdots - \genfrac(){0.0pt}1{2n}{2n}\\&\quad = \genfrac(){0.0pt}1{2n}{0} + \genfrac(){0.0pt}1{2n}{1} + \cdots + \genfrac(){0.0pt}1{2n}{n+1} =2^{2n-1} + \frac{1}{2} \genfrac(){0.0pt}1{2n}{n} + \genfrac(){0.0pt}1{2n}{n+1}. \end{aligned}$$

Exploiting this relation, we immediately get the given expression for the counting distribution function of the performance ratio as $F_{{\textsc {Bf}},{\textsc {Bf}}_2}(r)$. $\square$

In Fig. 2b, an exemplary plot of $F_{{\textsc {Bf}},{\textsc {Bf}}_2}(r)$ is given for $n = 100$ confirming that the lookahead effect is also relatively small with respect to an instance-wise comparison.

4 Online traveling salesman problem with lookahead

The traveling salesman problem (TSP) lies at the core of nearly every transportation or routing problem as it seeks to find a round trip (also called tour) for a given set of locations (also called requests) to be visited such that some cost function depending on the total travel distance or travel time is minimized (Lenstra and Rinnooy Kan 1975). The online TSP has been considered in several flavors for competitive analyses: A typical objective is makespan minimization. For this problem, a 2-competitive algorithm PlanAtHome is known (Ausiello et al. 1995) where the problem also involves request release dates. In an online variant with lookahead, customer requests pop up some time ahead of the earliest possible visit times. It is shown in Allulli et al. (2008) that lookahead leaves the competitive factor at 2, i.e., no better algorithm with respect to the optimal offline solution is found in competitive analysis. Another paper on the online TSP with lookahead is due to Jaillet and Wagner (2006). Here, lookahead is given by disclosure dates which differ from release dates. It is shown that the advanced information leads to improved competitive ratios.

4.1 Problem setting and notation

The setting considered in this paper refrains from request release dates and applies total distance as the objective criterion. We conduct an exact combinatorial analysis and explain the improvements that can be achieved through lookahead on typical input sequences. Hence, the TSP as considered in this paper is a pure sequencing problem. For input sequence $\sigma = (\sigma _1, \ldots , \sigma _n)$, let a request $\sigma _i$ with $i \in {\mathbb {N}}$ correspond to a point $x_i$ in a space ${\mathcal {M}}$ with metric $d: {\mathcal {M}} \times {\mathcal {M}} \rightarrow {\mathbb {R}}$, then the TSP consists of visiting the points of all requests – each one not before its release—with a server in a tour of minimum length starting and ending in some distinguished origin $o \in {\mathcal {M}}$.

A permutation $\pi (\sigma ) = (\pi _1(\sigma ), \pi _2(\sigma ), \ldots , \pi _n(\sigma ))$ of the set $\{\sigma _1, \sigma _2, \ldots , \sigma _n\}$ of requests represents a tour $(o, x_{\pi _1(\sigma )}, x_{\pi _2(\sigma )}, \ldots , x_{\pi _n(\sigma )}, o)$, i.e., a feasible solution to an instance of the TSP. The tour length of $\pi (\sigma )$ is given by the value

$$\begin{aligned} D(\pi (\sigma )) := d\big (o, x_{\pi _1(\sigma )}) + \displaystyle \sum _{i = 1}^{n-1} d(x_{\pi _i(\sigma )}, x_{\pi _{i+1}(\sigma )}\big ) + d\big (x_{\pi _n(\sigma )}, o\big ). \end{aligned}$$

The online version without lookahead is trivial: Requests are served in their order of appearance since no temporal aspects such as release dates are considered. In the online version with request lookahead of size l, requests are served sequentially with knowing l remaining requests (or all remaining requests if there are less than l of them); in particular, requests do not need to be served in their order of appearance. Recall that the case $l = 1$ coincides with the pure online setting without additional lookahead. We now compare the pure online setting with the setting enhanced by lookahead: Online algorithm ${\textsc {FirstComeFirstServed}}$ has no choices, i.e., the server has to visit the requests in their order of appearance in a first-come first-served manner. Online algorithm ${\textsc {NearestNeighbor}}_l$ with request lookahead l always moves the server to the closest known point in terms of distance from its current location.

Under lookahead of one additional request ($l=2$), we derive exact expressions for the counting distribution functions of the objective value and the performance ratio for the case of a metric space consisting of two points only, i.e., ${\mathcal {M}} = \{0, 1\}$ with $d(0,1) = d(1,0) = 1$, $d(0,0) = d(1,1) = 0$ and $o = 0$. Thus, this version of the TSP can also be recast as a 1-server problem on two points.

From now on, we refer to ${{\textsc {FirstComeFirstServed}}}$ as ${{\textsc {Fcfs}}}$ and ${{\textsc {NearestNeighbor}}}_2$ as ${{\textsc {Nn}}}$. We use the following additional terminology:

• A pass is the transition between two successive requests $(\sigma _i, \sigma _{i+1})$; a pass pair is a request subsequence $(\sigma _i, \sigma _{i+1}, \sigma _{i+2})$.

• A change (remain) pass is a pass $(\sigma _i, \sigma _{i+1})$ with $x_i \ne x_{i+1}$ ($x_i = x_{i+1}$).

• A free point at a given time is a point which is not occupied by the server at that time.

Note that because of the return to o, only even overall tour lengths are possible.

In contrast to bin packing, the analysis in this section will show significant reductions in overall tour lengths through lookahead. This becomes possible due to the large and irrevocable effect on the objective function that the resequencing of requests brings along. The major positive effect of lookahead in the TSP is seen in the plots of the counting distribution functions in Fig. 4. As presented in a stringent analysis in Sect. 4.2, the root cause for the advantage of Nn over Fcfs lies in its ability to crack pass pairs (0, 1, 0) or (1, 0, 1) in order to build pass pairs (0, 0, 1) or (1, 1, 0).

Fig. 4

Counting distribution functions of a costs and b performance ratio of costs in the TSP with 100 requests

4.2 Counting distribution functions

In this section, we derive expressions for the counting distribution functions of the objective values attained by algorithms ${\textsc {Fcfs}}$ and ${\textsc {Nn}}$, respectively, as well as an expression for the counting distribution function of the performance ratio of ${\textsc {Fcfs}}$ and ${\textsc {Nn}}$. The counting distribution functions thoroughly reflect the advantage of ${\textsc {Nn}}$ over ${\textsc {Fcfs}}$ which lies in the ability of pooling requests on the same location. The analysis is rather direct, i.e., we first provide a theorem giving the number of request sequences leading to a specific objective value or performance ratio, respectively, and then conclude with a corollary specifying the expression for the counting distribution function.

4.2.1 Counting distribution functions of the objective value

Theorem 4.1

• (a) The number of request sequences $\sigma$ of length n where ${\textsc {Fcfs}}[\sigma ] = m$ and m is even is given by ${\textsc {Fcfs}}(n, m) = \left( {\begin{array}{c}n+1\\ m\end{array}}\right) .$

• (b) The number of request sequences $\sigma$ of length n where ${\textsc {Nn}}[\sigma ] = m$ and m is even is given by

  $$\begin{aligned} {\textsc {Nn}}(n, m) = {\left\{ \begin{array}{ll} \left( {\begin{array}{c}n+1\\ 2m-2\end{array}}\right) + \left( {\begin{array}{c}n+1\\ 2m\end{array}}\right) &{}\text {if } m > 0,\\ 1 &{}\text {if } m = 0. \end{array}\right. } \end{aligned}$$

Proof

A sequence of n points starting and ending in o has $n+2$ requests including the two dummy requests at o and encounters $n+1$ passes to either the current or the free point.

• (a) For Fcfs in order to result in objective value m, a request sequence has to exhibit exactly m change passes out of the $n+1$ passes.

• (b) For $m = 0$, the formula obviously holds. Denote by $\sigma$ the original request sequence and by $\sigma '$ the visiting order under Nn. For $m > 0$, first observe that each resulting sequence $\sigma '$ after being processed by Nn exhibits a last change from 0 to 1 and a last change from 1 to 0 in the visiting order of requests which together contribute a total of 2 to the objective value. We conclude that a contribution of $\max \{0, m - 2\}$ is due to all previous passes that do not involve the 1 of the last change from 0 to 1. There are two cases how this 1 could be obtained: Either it was at the same position originally and remained there also under processing of Nn (case 1), or it had been shifted to that position as a result of the processing of Nn (case 2). For $n = 9$ and $m = 4$, we give an example of case 1 by

  • $\sigma = (\,\,0\,\,{\underrightarrow{,}}\,\,1\,\,,\,\,0\,\,,\,\,1\,\,{\underrightarrow{,}}\,\,0\,\,,\,\,0\,\,,\,\,0\,\,,\,\,0\,\,{\underline{,}}\,\,1\,\,,\,\,1\,\,{\underline{,}}\,\,0\,\,)$,

  • $\sigma ' = (\,\,0\,\,,\,\,0\,\,,\,\,1\,\,{\underleftarrow{,}}\,\,1\,\,,\,\,0\,\,{\underleftarrow{,}}\,\,0\,\,,\,\,0\,\,,\,\,0\,\,,\,\,1\,\,,\,\,1\,\,,\,\,0\,\,)$

  and of case 2 by

  • $\sigma = (\,\,0\,\,{\underrightarrow{,}}\,\,1\,\,,\,\,0\,\,,\,\,1\,\,{\underrightarrow{,}}\,\,0\,\,,\,\,0\,\,{\underrightarrow{\underrightarrow{,}}}\,\,1\,\,{\underline{,}}\,\,0\,\,,\,\,1\,\,,\,\,1\,\,{\underline{,}}\,\,0\,\,)$,

  • $\sigma ' = (\,\,0\,\,,\,\,0\,\,,\,\,1\,\,{\underleftarrow{,}}\,\,1\,\,,\,\,0\,\,{\underleftarrow{,}}\,\,0\,\,,\,\,0\,\,,\,\,1\,\,{\underleftarrow{\underleftarrow{,}}}\,\,1\,\,,\,\,1\,\,,\,\,0\,\,)$.

  For each of the $m-2$ changes incurred by Nn, of course, there must also have been a corresponding change pass in the original sequence (right arrow). Additionally, through the processing of Nn, this change pass can only be responsible for a change if in the processing order of Nn the (potentially shifted) destination of the original change pass is succeeded by another pass which has to be a remain-pass (left arrow).

  In the first case, $m-2$ change passes along with their affirmative remain-passes in the transformed sequence and two additional change passes (underlined) incur changes, i.e., $2(m-2) + 2 = 2m-2$ out of the $n+1$ passes have to be chosen. In the second case, because of the last change from 0 to 1, which resulted from a shifted change pass (left double arrow), and its affirmative remain-pass (right double arrow), $m-2+1=m-1$ change passes along with their affirmative remain-passes in the transformed sequence and two additional passes (underlined), whereof the first one is a pass from 1 to 0 ensuring that the 1 will be shifted to the right (cf. definition of case 2), incur changes, i.e., $2(m-1)+2=2m$ out of the $n+1$ passes have to be chosen. $\square$

From the previous result, we immediately obtain expressions for the counting distribution functions of the objective value $F_{{\textsc {Fcfs}}}(v)$ and $F_{{\textsc {Nn}}}(v)$, respectively. Note that Fcfs and Nn have possible tour lengths in $\{0, 2, 4, \ldots , 2\lceil \frac{n}{2}\rceil \}$ and $\{0, 2, 4, \ldots , 2\lceil \frac{n}{4}\}\rceil$, respectively, for $n+2$ requests including the first and last request to o (cf. proof of Theorem 4.1).

Corollary 4.2

The counting distribution functions of the objective value $F_{{\textsc {Fcfs}}}(v)$ and $F_{{\textsc {Nn}}}(v)$ of Fcfs and Nn for request sequences of length $n+2$ (including the first and last request to o) are given by

$$\begin{aligned} F_{{\textsc {Fcfs}}}(v)= {\left\{ \begin{array}{ll} 0 &{} \text {if } v< 0,\\ \displaystyle \sum _{i=0}^{n'} \genfrac(){0.0pt}1{n+1}{2i}\cdot \displaystyle 2^{-n} &{} \text {if } 2n' \le v < 2n' + 2 \text { for } n'=0,1,\ldots , \lceil \frac{n}{2}\rceil - 1,\\ 1 &{}\text {if } v \ge 2 \lceil \frac{n}{2}\rceil , \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} F_{{\textsc {Nn}}}(v)= {\left\{ \begin{array}{ll} 0 &{} \text {if } v< 0,\\ \displaystyle \sum _{i=0}^{n'} \Bigl (\genfrac(){0.0pt}1{n+1}{4i}+\genfrac(){0.0pt}1{n+1}{4i-2}\Bigr )\cdot \displaystyle 2^{-n} &{} \text {if } 2n' \le v < 2n' + 2 \text { for } n'=0,1, \ldots , \lceil \frac{n}{4}\rceil -1,\\ 1 &{}\text {if } v \ge 2 \lceil \frac{n}{4}\rceil . \end{array}\right. } \end{aligned}$$

Figure 4a exemplarily plots $F_{{\textsc {Fcfs}}}(v)$ and $F_{{\textsc {Nn}}}(v)$ for all item sequences of length $n = 100$. We observe a significant lookahead effect as a result of permuting request triples with two successive change passes such that these turn into one change pass and one remain pass.

4.2.2 Counting distribution function of the performance ratio

Theorem 4.3

Let $m_{{\textsc {Nn}}}(\sigma )$ and $m_{{\textsc {Fcfs}}}(\sigma )$ denote the objective values of algorithms Nn and Fcfs on request sequence $\sigma$, respectively, and let $n_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(n, a, b)$ be the number of request sequences $\sigma$ of length $n+2$ (including the first and last request to o) with $m_{{\textsc {Nn}}}(\sigma ) = a$ and $m_{{\textsc {Fcfs}}}(\sigma ) = b$ for $a = 0, 2, 4, \ldots , 2\lceil \frac{n}{4}\rceil$ and $b = 0, 2, 4, \ldots , 2\lceil \frac{n}{2}\rceil$, then it holds that

$$\begin{aligned} n_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(n, a, b)= {\left\{ \begin{array}{ll} 1 &{} \text {if } b = a = 0\\ \left( {\begin{array}{c}n+3-a\\ a\end{array}}\right) &{} \text {if } b = a \ne 0\\ \left( {\begin{array}{c}n+1-a\\ 2a\end{array}}\right) &{} \text {if } b = 3a\\ \left( {\begin{array}{c}n+2-a\\ 2a-1\end{array}}\right) + (a-1)\left( {\begin{array}{c}n+1-a\\ 2a-1\end{array}}\right) &{} \text {if } b = 3a-2\\ \left( {\begin{array}{c}a-2\\ \frac{b-a}{2}\end{array}}\right) \left( {\begin{array}{c}n+3-a\\ \frac{a+b}{2}\end{array}}\right) + \left( {\begin{array}{c}a-2\\ \frac{b-a}{2}-1\end{array}}\right) \left( {\begin{array}{c}n+2-a\\ \frac{a+b}{2}\end{array}}\right) + \left( {\begin{array}{c}a-1\\ \frac{b-a}{2}-1\end{array}}\right) \left( {\begin{array}{c}n+1-a\\ \frac{a+b}{2}\end{array}}\right) &{} \text {if } b = a+2, a+4, \ldots ,\\ &{} 3a-4\\ 0 &{} \text {else.} \end{array}\right. } \end{aligned}$$

Proof

Notice that Nn can never be worse than Fcfs because whenever Nn changes the order, a saving occurs without future drawbacks. Nn needs at least a third of the distance of Fcfs as seen by (0, 1, 0, 1, 0, 1, 0) which requires two units from Nn and six units from Fcfs. There are no sequences with a larger percentage of savings because at the end of this sequence only two requests on 0 are seen by Nn, i.e., there is no value of lookahead in this moment, and modifying the above sequence by additional requests cannot improve the advantage of Nn over Fcfs any further. Due to the return to o, both Fcfs and Nn lead to an even objective value. Therefore, it is sufficient to consider $n_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(n, a, b)$ with a, b as even numbers and $\frac{a}{b} \in [\frac{1}{3}, 1]$. For a request sequence with n points (apart from the dummy requests at the beginning and end), b can attain values up to $2\lceil \frac{n}{2}\rceil$ as seen by the worst-case sequences for Fcfs: Sequences of odd length consist only of change passes; sequences of even length consist only of change passes except for one remain pass. For a request sequence with n points (apart from the dummy requests at the beginning and end), a can attain values up to $2\lceil \frac{n}{4}\rceil$ as seen by the worst-case sequences for Nn as follows: In any visiting order under Nn, defined as $\sigma '$, an isolated 0 may only occur at the first and/or last request to $o = 0$; likewise, the only possible isolated 1 is the last request to 1. Hence, apart from these three requests, $\sigma '$ consists of a series of subsequences with minimum length 2 with requests on 1 only or 0 only. The largest objective value is incurred when the largest number of such subsequences appears in $\sigma '$ which is the case for subsequences in the form of pairs. Input sequences $\sigma '$ of this form result from $(0,(1,1,0,0)^c,x,0)$ with x being a request subsequence of minimum length 1 and maximum length 4 containing at least one 1 representing the last visit to 1.

${\varvec{b=a=0}}$::

The only sequence with $b = a = 0$ has $\sigma _i = 0$ for $i = 1, \ldots , n$.

${\varvec{b=a\ne 0}}$::

The visiting order of the points in $\sigma$ is identical for Fcfs and Nn because Nn has a lookahead of one additional request. In particular, we know that the pass immediately following each of the first $a-2$ change passes has to be a remain pass since otherwise Nn would have reorganized the order. (The last two change passes do not have to exhibit this structure because these changes cannot be extinguished by Nn due to the forced return to the origin.) Thus, since for $a-2$ passes we know the type of the immediate successor pass, we only have to choose a change passes out of $n+1-(a-2) = n+3-a$ passes.

${\varvec{b=3a}}$::

The largest possible advantage of Nn over Fcfs is achieved. A saving through Nn over Fcfs is obtained whenever the lookahead holds both a 0 and a 1 with the first request in the lookahead being different from the current location. Moreover, this saving will lead to another saving if the location of the first request in the lookahead is requested later again. Clearly, Nn could not anticipate the second saving as it involves a request not seen in the lookahead, but only got lucky that this request occurred. Hence, each time Fcfs requires a distance of 3, Nn only requires a distance of 1. Hence, it follows that the request sequence has to consist only of disjunct subsequences of the form $(0^{c_0},1,0^{c_1},1^{c_2},0,1^{c_3},0^{c_4})$ with $c_i \in {\mathbb {N}}$ for $i = 0, 1, 2, 3, 4$ where $x^c$ stands for a request on $x \in \{0, 1\}$ for c times in a row. The requests of each such subsequence will be visited in the order $(0^{c_0},0^{c_1},1,1^{c_2},1^{c_3},0,0^{c_4})$ by Nn producing two moves, whereas Fcfs needs six. In particular, we know that in the original sequence after the first pass from 0 to 1 a pass to 0 immediately follows and that the pass from 0 to $1^{c_3}$ is immediately preceded by a 1. Hence, for each pass in $\sigma$ that leads to one of the a moves of Nn, there is also another associated pass known in $\sigma$. Thus, we choose out of $n+1-a$ passes rather than out of $n+1$ passes. Within each such subsequence, we have to choose the ends of $0^{c_0}$, $0^{c_1}$, $1^{c_2}$, $1^{c_3}$ by selecting $c_0$, $c_1$, $c_2$, $c_3$. Since there are $\frac{a}{2}$ such subsequences for objective value a, in total we have to choose $4 \cdot \frac{a}{2} = 2a$ out of $n+1-a$ passes.

In the sequel, we call a subsequence (0, 1, 0) or (1, 0, 1) a change-change pass pair (c/c-pair) and a subsequence (0, 1, 1) or (1, 0, 0) a change-remain pass pair (c/r-pair). Moreover, observe that for a difference of $b-a$ in the outcome, one has to encounter exactly $\frac{b-a}{2}$ non-overlapping c/c-pairs before the final return to o.

${\varvec{b=3a-2}}$::

We need $\frac{3a-2-a}{2} = a-1$ non-overlapping c/c-pairs. Further, one additional (isolated) change pass has to occur within $\sigma$ because $a-1$ is odd and the server has to return to o. For each of the $a-1$ c/c-pairs (0, 1, 0) or (1, 0, 1), we also have to specify the position until which the sequence continues with 0 and 1, respectively. Hence, we have to choose $(a-1) + 1 + (a-1) = 2a - 1$ passes. There are two cases for the position of the isolated change pass:

Case 1::

The isolated change pass occurs after all non-overlapping c/c-pairs. Then we have to choose the first passes of the non-overlapping c/c-pairs and the isolated change pass out of $n + 1 - (a - 1) = n + 2 - a$ passes. There are $\left( {\begin{array}{c}n+2-a\\ 2a-1\end{array}}\right)$ possibilities to do so.

Case 2::

The isolated change pass occurs prior to all or within the sequence of non-overlapping c/c-pairs. Then we have to choose the first passes of the non-overlapping c/c-pairs and the isolated change pass out of $n + 1 - (a - 1) - 1 = n + 1 - a$ passes because we know that the isolated change pass is succeeded by a remain pass since otherwise it would not be an isolated change pass. There are $a-1$ positions to locate the isolated change pass prior to all or within the sequence of the $a-1$ non-overlapping c/c-pairs. Hence, there are $(a-1)\left( {\begin{array}{c}n+1-a\\ 2a-1\end{array}}\right)$ possibilities to choose the isolated change pass and the first passes of the non-overlapping c/c-pairs.

${\varvec{b=a+2i}}$ with ${\varvec{i = 1, 2, \ldots , a-2}}$ ::

Exactly i non-overlapping c/c-pairs occur before the final return to o because each such pair gives a saving of two. We conclude that at least $(a-2)-i$ pairs have to be c/r-pairs and two additional change passes are left over (which may come in an arbitrary form, i.e., as a c/c-pair or as two c/r-pairs). There are three cases for the positions and forms of the two left-over change passes:

Case 1::

Both left-over change passes appear at the end of $\sigma$, i.e., when all of the $a-2$ c/c- and c/r-pairs have occurred. We choose the first passes of the c/c- and c/r-pairs out of $n+1-(a-2)=n+3-a$ passes. Recall that for a difference of $b-a$ one has to encounter exactly $\frac{b-a}{2}$ non-overlapping c/c-pairs before the final return to o. In total, in order to obtain objective value pair (a, b) one has to choose $\frac{b-a}{2} + a = \frac{a+b}{2}$ change passes which are the first passes of the c/c- and c/r-pairs. Since the two left-over change passes appear at the end of $\sigma$, we have that the $\frac{b-a}{2}$ non-overlapping c/c-pairs appear somewhere among the $a-2$ known c/c- and c/r-pairs, i.e., we have to choose $\frac{b-a}{2}$ out of $a-2$. Overall, there are $\left( {\begin{array}{c}a-2\\ \frac{b-a}{2}\end{array}}\right) \left( {\begin{array}{c}n+3-a\\ \frac{a+b}{2}\end{array}}\right)$ possibilities to choose the first passes of the non-overlapping c/c-pairs and the first passes of both the c/c- and c/r-pairs.

Case 2::

One additional c/r-pair (containing a left-over change pass) appears before the last of the known $a-2$ c/c- and c/r-pairs, i.e., within the first $a-1$ c/c- and c/r-pairs. Then we have to choose $\frac{a+b}{2}$ change passes (which are the first passes of the c/c- and c/r-pairs) out of $n+1-(a-1)=n+2-a$ passes. Due to the additional c/r-pair, there are only $\frac{b-a}{2}-1$ c/c-pairs among the first $a-2$ c/c- and c/r-pairs, i.e., we have to choose $\frac{b-a}{2}-1$ first passes of the c/c-pairs out of $a-2$ first passes of the c/c- and c/r-pairs. Overall, there are $\left( {\begin{array}{c}a-2\\ \frac{b-a}{2}-1\end{array}}\right) \left( {\begin{array}{c}n+2-a\\ \frac{a+b}{2}\end{array}}\right)$ possibilities to choose the first passes of the non-overlapping c/c-pairs and the first passes of both the c/c- and c/r-pairs.

Case 3::

Two additional c/r-pairs (each containing a left-over change pass) appear before the last of the known $a-2$ c/c- and c/r-pairs, i.e., within the first a c/c- and c/r-pairs. Then we have to choose $\frac{a+b}{2}$ change passes (which are the first passes of the c/c- and c/r-pairs) out of $n+1-a$ passes. Due to the additional c/r-pairs, there are only $\frac{b-a}{2}-2$ or $\frac{b-a}{2}-1$ c/c-pairs among the first $a-2$ c/c- and c/r-pairs, i.e., we have to choose $\frac{b-a}{2}-2$ or $\frac{b-a}{2}-1$ first passes of the c/c-pairs out of $a-2$ first passes of the c/c- and c/r-pairs, i.e., $\left( {\begin{array}{c}a-2\\ \frac{b-a}{2}-2\end{array}}\right) + \left( {\begin{array}{c}a-2\\ \frac{b-a}{2}-1\end{array}}\right) = \left( {\begin{array}{c}a-1\\ \frac{b-a}{2}-1\end{array}}\right)$. Overall, there are $\left( {\begin{array}{c}a-1\\ \frac{b-a}{2}-1\end{array}}\right) \left( {\begin{array}{c}n+1-a\\ \frac{a+b}{2}\end{array}}\right)$ possibilities to choose the first passes of the non-overlapping c/c-pairs and the first passes of both the c/c- and c/r-pairs. $\square$

Corollary 4.4

With $n_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(n, i, j)$ defined as in Theorem 4.3, the counting distribution function of the performance ratio $F_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(r)$ of Fcfs and Nn for request sequences of length $n+2$ (including the first and last request to 0) is given by

$$\begin{aligned} F_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(r)=\displaystyle 2^{-n}\cdot \displaystyle \sum _{j=0, 2, \ldots , 2\lceil \frac{n}{2}\rceil }\displaystyle \sum _{\begin{array}{c} i=0, 2, \ldots , \min \{j, 2\lceil \frac{n}{4}\rceil \},\\ \frac{i}{j} \le r \end{array}} n_{{{\textsc {Nn}}},{{\textsc {Fcfs}}}}(n, i, j). \end{aligned}$$

In Fig. 4b, an exemplary plot of $F_{{\textsc {Nn}}},{{\textsc {Fcfs}}}(r)$ is given for $n = 100$ confirming that the lookahead effect is also enormous with respect to an instance-wise comparison.

5 Conclusion

We analyzed special cases of bin packing and the TSP using the concept of counting distribution functions. To the best of our knowledge, displaying exactly the algorithm behavior over all possible input sequences has never been done before. The derivations of the analytical expressions revealed that exact analysis in combinatorial online optimization is intertwined with the combinatorics of the problem setting (choice of parameter values) and the processing rules of algorithms. This could obviously be seen in bin packing with two item sizes where algorithm performance is described by the Catalan numbers. Clearly, these structures are recognizable by cognitively only when algorithms are simple and problems are elementary. However, even under this assumption the analysis became involved. To the best of our knowledge, our analysis is the first to give an exact image reproducing algorithm behavior over all input sequences in the respective problems. As a byproduct, the proofs yielded explanations for the magnitudes of the lookahead effects. For larger lookahead and general settings, it will be virtually impossible to track the effects of lookahead in the processing of an algorithm over all input sequences. Hence, we are led to conducting experimental analysis. Empirical results in further academic online optimization problems and in real world applications can be found in the author’s thesis (Dunke 2014). In particular, we emphasize that applying the performance measurement approach based on counting distribution functions has proven to be a powerful tool in the simulation-based analysis of real world problems.

Since an exact analysis in the style of this paper is likely to be out of scope for more complex settings, it has to be checked next which mathematical statements are realistic to be elicited in future works. An exact analysis of other lookahead types, e.g., time lookahead, and a subsequent comparison to the results of request lookahead represents a further step towards the general understanding of lookahead mechanisms. Likewise, an exact distributional analysis in other basic online optimization problems such as paging or scheduling is still missing.

Appendix A: Additional proofs for sect. 3

1.1 A.1: Proof of Lemma 3.3

• (a) See Michaels and Rosen (1991), chapter 7, pp. 115 and 116.

• (b) The proof is a straightforward consequence of the fact that the number of recurring unit-sloped paths of length 2i with $s_k \ge -1$ for $k = 0, 1, 2, \ldots , 2i$ is the number of all recurring unit-sloped paths of length 2i minus the number of all recurring unit-sloped paths of length 2i which hit the number $-2$ at least once. As a result of the reflection principle, counting the paths from (0, 0) to (2i, 0) hitting $-2$ at least once is the same as counting the paths from (0, 0) to $(2i,-4)$ hitting $-2$ at least once. But any such path must hit $-2$ at some point, i.e., we are computing the total number of paths from (0, 0) to $(2k,-4)$. In total, we obtain that the number of recurring unit-sloped paths of length 2i with $s_k \ge -1$ for $k = 0, 1, 2, \ldots , 2i$ is equal to the total number of paths from (0, 0) to (2i, 0) minus the total number of paths from (0, 0) to $(2i,-4)$ which is equal to

  $$\begin{aligned} \left( {\begin{array}{c}2i\\ i\end{array}}\right) -\left( {\begin{array}{c}2i\\ i+2\end{array}}\right)&= \frac{(2i)!}{(i!)^2} - \frac{(2i)!}{(i + 2)!(i - 2)!} = \frac{(2i)!}{(i!)^2}\Bigl (1 - \frac{i(i-1)}{(i+1)(i+2)}\Bigr )\\&= \frac{(2i)!}{(i!)^2} \frac{(i+1)(i+2)-i(i-1)}{(i+1)(i+2)} = \frac{(2i)!}{(i!)^2} \frac{4k+2}{(i+1)(i+2)}\\&= \frac{1}{i+2}\frac{1}{(i+1)!}\frac{(2i)!(4i+2)}{i!} \\&= \frac{1}{i+2}\frac{1}{(i+1)!}\frac{(2i)!(4i+2)(i+1)}{(i+1)!}\\&= \frac{1}{i+2}\frac{1}{(i+1)!}\frac{(2i)!(4i^2+6i+2)}{(i+1)!} \\&= \frac{1}{i+2}\frac{1}{(i+1)!}\frac{(2i)!(2i+1)(2i+2)}{(i+1)!}\\&= \frac{1}{i+2}\left( {\begin{array}{c}2i+2\\ i+1\end{array}}\right) = C_{i+1}. \end{aligned}$$

1.2 A.2: Proof of Lemma 3.5

• (a) Since for 2n items at least n and at most 2n bins are needed, ${\textsc {Bf}}(2n, m)=0$ for $m < n$ and $m > 2n$. For the remaining m, we perform a reverse induction on m. The base case $m = 2n$ is valid because the only item sequence which needs 2n bins has 2n large items and it holds that $\sum \nolimits _{k=2n-n}^{n} a_{n,k} = a_{n, n} = \frac{n+1}{n+1}\left( {\begin{array}{c}2n+2\\ 0\end{array}}\right) = 1$. For the inductive step, let ${\textsc {Bf}}(2n, m) = \sum \nolimits _{k=m-n}^{n} a_{n,k}$ be valid for some m with $2n \ge m > n$. We show that ${\textsc {Bf}}(2n, m - 1) = \sum \nolimits _{k = m - 1 -n}^{n} a_{n,k}$. Because of $m > n$, there must be a pair of large items starting at an odd position for which no matching small items follow in every item sequence with objective value m since otherwise these large items could be matched with small items and would fit into a bin contradicting $m > n$. Hence, we obtain for any item sequence with objective value m an item sequence with objective value $m-1$ by replacing the first pair of large items starting at an odd position for which no matching small items follow with a pair of small items which in turn lead to a condensation. As a result, we have ${\textsc {Bf}}(2n, m - 1) = {\textsc {Bf}}(2n, m) + |\Sigma _{add}|$ where $\Sigma _{add}$ are the additional item sequences leading to objective value $m-1$ which have not resulted from establishing a condensation in an item sequence with objective value m. These item sequences can be mapped to a unit-sloped path of length 2n not going below level $-1$ and ending at height $2(m-1-n)$.

  The next lemma is needed to complete the proof for even length 2n of $\sigma$.

Lemma A.1

• (a) The number $a_{n,k}$ of unit-sloped paths of length 2n with $s_{k'} \ge -1$ for all $k' = 0, 1, 2, \ldots , 2n$ which end at position (2n, 2k), i.e., at height 2k, is given by $a_{n, k} = \frac{k+1}{n+1}\left( {\begin{array}{c}2n+2\\ n-k\end{array}}\right) .$

• (b) The number of item sequences $\sigma$ of length 2n without condensations where ${\textsc {Bf}}[\sigma ] = m$ for $m \in \{n, n+1, \ldots , 2n\}$ is given by $a_{n, m-n}$.

Proof

• (a) The proof is an immediate consequence of the bijection between Dyck paths of length $2n+2$ and path pairs of length n given in Deutsch and Shapiro (2001) and the included remark concerning the relaxation of the restriction of path pairs having to end in the same point. To this end, we first modify the bijection by omitting the appended u-step at the beginning and the appended d-step at the end of the Dyck path in order to facilitate recurring unit-sloped paths that are allowed to hit the level of $-1$. Moreover, since the number of path pairs of length n having endpoints $k\sqrt{2}$ apart is $a_{n, k}$, it follows from the bijection that the number of unit-sloped paths ending at height 2k is $a_{n, k}$.

• (b) A total number of m bins with $m \in \{n, n+1, \ldots , 2n\}$ is obtained when in an item sequence without condensations $m-n$ out of the n pairs of successive items are pairs of large items for which no matching small items can be found afterwards. Each such item sequence corresponds to a unit-sloped path of length 2n with $s_k \ge -1$ for $k = 0, 1, 2, \ldots , 2n$ ending at height $2(m-n)$ because each pair of large items contributes an amount of 2 to the total height achieved at the end of the path, and the result follows. $\square$

From Lemma A.1, we have that $|\Sigma _{add}| = a_{n, m-n-1}$. Together with the induction hypothesis, we conclude that

$$\begin{aligned} {\textsc {Bf}}(2n, m - 1) = {\textsc {Bf}}(2n, m) + |\Sigma _{add}| = \displaystyle \sum _{k=m-n}^{n} a_{n,k} + a_{n, m-n-1} = \displaystyle \sum _{k=m-n-1}^{n} a_{n,k}. \end{aligned}$$

• (b) Since for $2n+1$ items at least $n+1$ and at most $2n+1$ bins are needed, ${\textsc {Bf}}(2n+1, m)=0$ for $m < n+1$ and $m > 2n+1$. Notice that whenever $m > n+1$ for an item sequence of length $2n+1$, we have $m > n$ for the same item sequence where the last item is deleted. Thus, there must be a pair of large items beginning at an odd position in the truncated sequence from the same reasoning as in part (a) of the proof. Objective value m with $n+1 < m \le 2n+1$ for an item sequence of length $2n+1$ can be attained in two ways: First, ${\textsc {Bf}}$ needed $m-1$ bins after 2n items and the $2n+1$st item leads to the mth bin. Second, ${\textsc {Bf}}$ needed m bins after 2n items and the $2n+1$st item needs no new bin. In the first case, we have ${\textsc {Bf}}(2n, m-1)$ item sequences which must incur a new bin upon appending a large item; appending a small item would leave the objective value at m because there are at least two large items which could be matched with the small item. In the second case, ${\textsc {Bf}}(2n, m)$ item sequences will not incur a new bin upon appending a small item as this item can be matched with one of the large items; appending a large item would lead to objective value $m+1$ since after 2n items there can never be a bin with a small item only. We obtain

  $$\begin{aligned} {\textsc {Bf}}(2n+1, m)&= {\textsc {Bf}}(2n, m-1) + {\textsc {Bf}}(2n, m)\\&= \displaystyle \sum _{k=m-1-n}^{n} a_{n,k} + \displaystyle \sum _{k=m-n}^{n} a_{n,k} = 2\displaystyle \sum _{k=m-n}^{n} a_{n,k} + a_{n,m-1-n}. \end{aligned}$$

  Objective value $n+1$ can be attained in three ways: First, ${\textsc {Bf}}$ needed n bins after 2n items and the $2n+1$st item is large leading to the $n+1$st bin. Second, ${\textsc {Bf}}$ needed n bins after 2n items and the $2n+1$st item is small leading to the $n+1$st bin. Third, ${\textsc {Bf}}$ needed $n+1$ bins after 2n items and the $2n+1$st item is small, but does not lead to a new bin. The first case is trivial. In the second case, we seek for the same item sequences because neither of them can exhibit a pair of large items starting in an odd position. In the third case, we seek for the item sequences of length 2n with objective value $n+1$ which have at least one pair of large items beginning at an odd position such that the appended small item does not incur a new bin. These item sequences are counted by ${\textsc {Bf}}(2n, n+1)$. We obtain

  $$\begin{aligned} {\textsc {Bf}}(2n+1, n+1)&= {\textsc {Bf}}(2n, n) + {\textsc {Bf}}(2n, n)+ {\textsc {Bf}}(2n, n+1)\\&= \displaystyle \sum _{k=0}^{n} a_{n,k} + \displaystyle \sum _{k=0}^{n} a_{n,k} + \displaystyle \sum _{k=1}^{n} a_{n,k} = 3\displaystyle \sum _{k=0}^{n} a_{n,k} - a_{n,0}. \end{aligned}$$

1.3 A.3: Proof of Theorem 3.6

• (a) We show by two-dimensional induction on n and m that $\sum \nolimits _{k=m-n}^{n} a_{n,k} = \left( {\begin{array}{c}2n+1\\ m+1\end{array}}\right)$. Recall that $n = 1, 2, \ldots$ and $m = n, n+1, \ldots , 2n$. The base case $n = 1$ and $m = n = 1$ is valid because it holds that $\sum \nolimits _{k=0}^{1} a_{1,k} = a_{1,0} + a_{1,1} = 2 + 1 = 3 = \left( {\begin{array}{c}2\cdot 1+1\\ 1+1\end{array}}\right) =\left( {\begin{array}{c}3\\ 2\end{array}}\right) =3.$ In the first inductive step (on n with fixed $m = n$), we show that $\sum \nolimits _{k=0}^{n} a_{n,k} = \left( {\begin{array}{c}2n+1\\ n+1\end{array}}\right)$ holds. From Shapiro (1976), we know that $\frac{1}{2} \left( {\begin{array}{c}2(n+1)\\ n+1\end{array}}\right) = \sum \nolimits _{k=0}^{n} a_{n,k}$. The result follows from

  $$\begin{aligned} \frac{1}{2} \left( {\begin{array}{c}2(n+1)\\ n+1\end{array}}\right) = \frac{1}{2} \frac{(2n+2)!}{(n+1)!(n+1)!} = \frac{(2n+2)(2n+1)!}{2(n+1)n!(n+1)!} = \left( {\begin{array}{c}2n+1\\ n+1\end{array}}\right) . \end{aligned}$$

  In the second inductive step (on m with arbitrary n), we show that $\sum \nolimits _{k=m-n}^{n} a_{n,k} = \left( {\begin{array}{c}2n+1\\ m+1\end{array}}\right)$ implies $\sum \nolimits _{k=m+1-n}^{n} a_{n,k} = \left( {\begin{array}{c}2n+1\\ m+2\end{array}}\right)$. This can be seen by the following calculations:

  $$\begin{aligned} \displaystyle \sum _{k=m+1-n}^{n} a_{n,k}&= \displaystyle \sum _{k=m-n}^{n} a_{n,k} - a_{n, m-n} = \left( {\begin{array}{c}2n+1\\ m+1\end{array}}\right) - \frac{m-n+1}{n+1}\left( {\begin{array}{c}2n+2\\ 2n-m\end{array}}\right) \\&= \frac{(2n+1)!(n+1)(m+2)-(m-n+1)(2n+2)!}{(2n-m)!(m+2)!(n+1)}\\&= \frac{(2n+1)!}{(m+2)!(2n-m-1)!}\frac{(n+1)(m+2)-(m-n+1)(2n+2)}{(2n-m)(n+1)}\\&= \frac{(2n+1)!}{(m+2)!(2n-m-1)!} \cdot 1 = \left( {\begin{array}{c}2n+1\\ m+2\end{array}}\right) . \end{aligned}$$

  The result now immediately follows from the formula given in part (a) of Lemma 3.5.

• (b) For $m = n+1$, we have

  $$\begin{aligned} 3\displaystyle \sum _{k=0}^{n} a_{n,k} - a_{n, 0}&\overset{a)}{=} 3\left( {\begin{array}{c}2n+1\\ n+1\end{array}}\right) - \frac{1}{n+1}\left( {\begin{array}{c}2n+2\\ n\end{array}}\right) \\&=\frac{(2n+1)!}{(n+2)!(n+1)!}(3n^2+7n+4) \end{aligned}$$

  and

  $$\begin{aligned} \left( {\begin{array}{c}2n+3\\ n+2\end{array}}\right) -\left( {\begin{array}{c}2n+1\\ n+1\end{array}}\right)&=\frac{(2n+1)!}{(n+2)!(n+1)!}(3n^2+7n+4). \end{aligned}$$

  which together yields the desired relation for $m = n+1$.

  For $n+1 < m \le 2n+1$, we have

  $$\begin{aligned} 2\displaystyle \sum _{k=m-n}^{n} a_{n,k} + a_{n,m-n-1}&\overset{a)}{=} 2\left( {\begin{array}{c}2n+1\\ m+1\end{array}}\right) + \frac{m-n}{n+1}\left( {\begin{array}{c}2n+2\\ 2n-m+1\end{array}}\right) \\&= \frac{(2n+2)!}{(m+1)!(2n-m+1)!}\Bigg (\frac{2(2n-m+1)}{2n+2}+\frac{m-n}{n+1}\Bigg )\\&= \frac{(2n+2)!}{(m+1)!(2n-m+1)!}\Bigg (\frac{2n+2}{2n+2}\Bigg )=\left( {\begin{array}{c}2n+2\\ m+1\end{array}}\right) . \end{aligned}$$

  The result now immediately follows from the formula given in part (b) of Lemma 3.5.

1.4 A.4: Proof of Lemma 3.8

We show that $\sum \nolimits _{i\ge 1} C_i \left( {\begin{array}{c}2n-2i\\ m-i\end{array}}\right) - \sum \nolimits _{i\ge 1} C_{i-1} \left( {\begin{array}{c}2n-2i+1\\ m-i+1\end{array}}\right) = 0.$ Notice that from the definition of the binomial coefficient, i ranges in $\{1, 2, \ldots , 2n-m\}$ in both terms. Hence,

$$\begin{aligned}&\sum _{i\ge 1} C_i \left( {\begin{array}{c}2n-2i\\ m-i\end{array}}\right) - \sum _{i\ge 1} C_{i-1} \left( {\begin{array}{c}2n-2i+1\\ m-i+1\end{array}}\right) \\&\quad = C_1 \left( {\begin{array}{c}2n-2\\ m-1\end{array}}\right) + C_2 \left( {\begin{array}{c}2n-4\\ m-2\end{array}}\right) + C_3 \left( {\begin{array}{c}2n-6\\ m-3\end{array}}\right) + \cdots + C_{2n-m} \left( {\begin{array}{c}2m-n\\ 2m-n\end{array}}\right) \\&\qquad - \Biggl (C_0 \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) + C_1 \left( {\begin{array}{c}2n-3\\ m-1\end{array}}\right) + C_2 \left( {\begin{array}{c}2n-5\\ m-2\end{array}}\right) + \cdots + C_{2n-m-1} \left( {\begin{array}{c}2m-n+1\\ 2m-n+1\end{array}}\right) \Biggr )\\&\quad = C_1 \left( {\begin{array}{c}2n-3\\ m-2\end{array}}\right) + C_2 \left( {\begin{array}{c}2n-5\\ m-3\end{array}}\right) + \cdots + C_{2n-m-1} \left( {\begin{array}{c}2m-n+1\\ 2m-2n\end{array}}\right) + C_{2n-m} - \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) \\&\quad = \sum _{i = 1}^{2n-m-1} C_i \left( {\begin{array}{c}2n-2i-1\\ m-i-1\end{array}}\right) + C_{2n-m} - \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) \\&\quad = \sum _{i = 0}^{2n-m-1} C_i \left( {\begin{array}{c}2n-2i-1\\ m-i-1\end{array}}\right) - \left( {\begin{array}{c}2n-1\\ m-1\end{array}}\right) + C_{2n-m} - \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) \\&\quad = \sum _{i = 0}^{2n-m} C_i \left( {\begin{array}{c}2n-2i-1\\ m-i-1\end{array}}\right) - C_{2n-m}\left( {\begin{array}{c}2m-2n-1\\ 2m-2n-1\end{array}}\right) - \left( {\begin{array}{c}2n-1\\ m-1\end{array}}\right) \\&\qquad + C_{2n-m} - \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) \\&\quad = \sum _{i \ge 0} C_i \left( {\begin{array}{c}2n-2i-1\\ m-i-1\end{array}}\right) - C_{2n-m} - \left( {\begin{array}{c}2n-1\\ m-1\end{array}}\right) + C_{2n-m} - \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) \\&\quad = \left( {\begin{array}{c}2n\\ m\end{array}}\right) - \left( {\begin{array}{c}2n-1\\ m-1\end{array}}\right) - \left( {\begin{array}{c}2n-1\\ m\end{array}}\right) = \left( {\begin{array}{c}2n\\ m\end{array}}\right) - \left( {\begin{array}{c}2n\\ m\end{array}}\right) = 0. \end{aligned}$$

1.5 A.5: Proof of Corollary 3.9

From Theorem 3.1, we know that ${\textsc {Bf}}_2[\sigma ]\in \{m, m-1\}$ whenever ${\textsc {Bf}}[\sigma ]=m$; from the previous Theorem 3.7, we know that $|\{\sigma \,|\, |\sigma | = n, {\textsc {Bf}}_2[\sigma ] = m-1, {\textsc {Bf}}[\sigma ] = m\}| = \left( {\begin{array}{c}n\\ m+1\end{array}}\right)$ for $m = \lceil \frac{n}{2}\rceil + 1, \ldots , n-1$. Hence, from Theorem 3.6 it immediately follows for these m that $|\{\sigma \,|\, |\sigma | = n, {\textsc {Bf}}_2[\sigma ] = m\}| = \left( {\begin{array}{c}n+1\\ m+1\end{array}}\right) - \left( {\begin{array}{c}n\\ m+1\end{array}}\right) = \left( {\begin{array}{c}n\\ m\end{array}}\right) .$ Clearly, $|\{\sigma \,|\, |\sigma | = n, {\textsc {Bf}}[\sigma ] = n\}| = |\{\sigma \,|\, |\sigma | = n, {\textsc {Bf}}_2[\sigma ] = n\}| = 1$.

1.6 A.6: Proof of Corollary 3.12

• (a) For $v < n$ and $v \ge 2n - 1$, $F_{{\textsc {Bf}}}(v) = F_{{\textsc {Bf}}_2}(v)$. For $n \le v < 2n-1$

  $$\begin{aligned} F_{{\textsc {Bf}}_2}(v) - F_{{\textsc {Bf}}}(v)&= \Biggl (\sum _{m=n}^{\lfloor v \rfloor } \Bigl (\genfrac(){0.0pt}1{2n+1}{m+2} - 2\genfrac(){0.0pt}1{2n}{m+1}\Bigr ) + \genfrac(){0.0pt}1{2n}{n+1}\Biggr ) \cdot (2^{-2n})\\&= \Biggl (\sum _{m=n}^{\lfloor v \rfloor } \Bigl (\genfrac(){0.0pt}1{2n}{m+2} - \genfrac(){0.0pt}1{2n}{m+1}\Bigr ) + \genfrac(){0.0pt}1{2n}{n+1}\Biggr ) \cdot (2^{-2n})\\&= \genfrac(){0.0pt}1{2n}{\lfloor v \rfloor +2} \cdot (2^{-2n}) > 0. \end{aligned}$$

  The second part follows immediately from Pascal’s triangle as a result of $\left( {\begin{array}{c}2n\\ v+2\end{array}}\right) > \left( {\begin{array}{c}2n\\ v+3\end{array}}\right)$ for $v = n, n+1, \ldots , 2n-3$.

• (b) Using the formula of Stirling ($n! \approx \sqrt{2\pi n}(\frac{n}{e})^n$, Königsberger (2001)), we get for $n \rightarrow \infty$ that

  $$\begin{aligned} F_{{\textsc {Bf}}_2}(n) - F_{{\textsc {Bf}}}(n)&= \left( {\begin{array}{c}2n\\ n+2\end{array}}\right) \cdot 2^{-2n}\\&\approx \frac{\sqrt{4\pi n} (\frac{2n}{e})^{2n}}{\sqrt{2\pi (n+2)}(\frac{n+2}{e})^{n+2}\sqrt{2\pi (n-2)}(\frac{n-2}{e})^{n-2} } \cdot 2^{-2n}\\&= \frac{\sqrt{n} 2^{2n}n^{2n}}{\sqrt{\pi (n^2 - 4)}(n+2)^{n+2} (n-2)^{n-2}}\cdot 2^{-2n} \in \Theta (\frac{1}{\sqrt{n}}).\\ \end{aligned}$$

  In addition, $\left( {\begin{array}{c}2n\\ v\end{array}}\right) > \left( {\begin{array}{c}2n\\ v+1\end{array}}\right)$ for $v \in {\mathbb {N}}$ with $v \ge n$, i.e., $F_{{\textsc {Bf}}_2}(v) - F_{{\textsc {Bf}}}(v)$ monotonously decreases for $v \ge n$. Since also $F_{{\textsc {Bf}}_2}(v) = F_{{\textsc {Bf}}}(v)$ for $v < n$ and $v \ge 2n-1$, the result follows.