1 Introduction

In maritime inventory routing problems (MIRPs), the routing and scheduling of ships is combined with inventory management at the loading and unloading ports (Agra et al. 2018). This problem is common in many vertically integrated companies that need to ship raw and intermediate materials to their downstream processing facilities, e.g., oil companies, chemical manufactures, liquified natural gas producers (Ronen 2002). With a single decision maker controlling both cargo and ships, MIRPs can be classified as industrial shipping problems (Christiansen et al. 2007).

Planning problems within maritime transportation can also be classified according to hierarchy levels (Christiansen et al. 2007): strategic planning is usually concerned with long-term decisions related to investing in transportation capacity and designing the transportation network. Typical examples are fleet size and mix problems (Pantuso et al. 2014) and liner shipping network design problems (Christiansen et al. 2020). On the tactical level, we find scheduling problems for industrial and tramp shipping (Christiansen and Fagerholt 2014). MIRPs usually belong to these problems. The tactical planning horizon often has a duration of 3–12 months. Operational planning problems have much shorter planning horizons and often address a wide variety of issues such as navigation and weather routing, speed selection, or the booking of single orders (Christiansen et al. 2007).

In this paper, we consider a tactical planning problem based on the shipping operations of one of the world’s largest aluminium producers. The producer needs to set up a shipment schedule for a planning horizon of 2–3 months to ensure that the aluminium production plants in Northern Europe are supplied with alumina from ports in South America. The producer controls a heterogeneous fleet of ships that can transport different types of alumina from the loading ports to the unloading ports. The operations at the loading ports however, are beyond the control of the producer and the port can only guarantee a ship’s departure within a week of the specified departure date in the shipment schedule. In addition to the uncertainty in departure time, there is uncertainty in the sailing time. The goal of the tactical planning process is to find the shipment plan that minimizes the costs of supplying the primary aluminium plants with alumina whilst satisfying the plants’ demand for alumina. The resulting optimization problem can be formulated as a MIRP where both the departure time and sailing time are uncertain.

MIRPs have been studied by the operations research community for decades. Numerous different applications have been studied: Christiansen and Nygreen (1998) and Christiansen (1999) for example, consider an application of shipping ammonia between production and consumption ports. Agra et al. (2013) study the problem of short sea fuel oil distribution in the archipelago of Cape Verde. Shao et al. (2015), Al-Haidous et al. (2016), and Li and Schütz (2020) are recent examples of setting up annual delivery plans for liquified natural gas. The papers by Christiansen and Fagerholt (2009), Christiansen and Fagerholt (2014), and Papageorgiou et al. (2014) provide a good overview over MIRPs and the existing literature. However, most of the literature reviewed in these papers considers deterministic problems despite various types of uncertainty affecting maritime transportation systems, for example uncertain sailing times due to changes in weather conditions.

Uncertainty, e.g. in travel times, has been considered in land-based vehicle routing and inventory routing problems for quite some time (see e.g., Laporte et al. 1992; Kleywegt et al. 2002; Kenyon and Morton 2003). In maritime inventory routing however, uncertainty has only recently started to attract the attention of the scientific community. Different approaches to handling uncertainty can be found in the literature: For example, Agra et al. (2012) who consider a robust vehicle routing problem with time windows and uncertain travel times and discuss its application to maritime transportation. Zhang et al. (2015) solve a robust maritime inventory routing problem with time windows and uncertain travel times by formulating it as a two-stage stochastic programming problem. The authors then solve the problem using a two-phase solution approach considering a set of disruptions and their recovery strategies. Agra et al. (2015) study a short sea maritime inventory routing problem with uncertainty in sailing times and waiting times at port. They formulate their problem as a two-stage stochastic programming problem and solve it using a decomposition approach similar to the L-shaped method. Agra et al. (2018) solve a robust maritime inventory routing problem with uncertain sailing times. The authors formulate their problem using the robust optimization approach introduced by Bertsimas and Sim (2004) to deal with the trade-off between the level of conservatism and the cost of robustness.

Simulation is another approach to dealing with uncertainty in maritime transportation. Halvorsen-Weare et al. (2013) solve a maritime inventory routing problem with the aim to create more robust routing and scheduling for LNG ships. They implement a simulation model with a recourse optimization procedure to evaluate solutions using a variation of policy strengthening strategies. Fischer et al. (2016) study the tactical fleet deployment problem in roll-on roll-off liner shipping. They use simulation to evaluate different strategies for handling disruptions in roll-on roll-off liner shipping. Medbøen et al. (2020) use an iterative approach that combines deterministic optimization with discrete-event simulation to solve a short sea liner network design problem with transshipment at sea.

In this paper, we provide a continuous-time formulation for a maritime inventory routing problem with uncertainty in both departure time from the loading port and sailing time. We develop a heuristic solution approach based on the iterative solution framework proposed by Acar et al. (2009). We combine deterministic optimization with simulation to find robust schedules specifying both ship type, departure time, and routes to the unloading ports as well as the unloading volumes at these ports. Note that it is possible to adapt the approach presented below to numerous different applications where the decision process can be split into two stages (similar to two-stage stochastic programming). Medbøen et al. (2020) for example, use a similar solution approach to solve a robust short sea feeder network design problem with transshipment, but the authors use a discrete-event simulation model to evaluate the performance of their solution instead of an optimization model. Still, to the best of our knowledge, our paper is the first paper to combine optimization and simulation to solve a continuous-time MIRP. We also test our solution approach on problem instances based on real-world data from one of world’s largest aluminium producers and show that we can increase the robustness of the solution considerably within acceptable runtimes.

The rest or the paper is organized as follows. First, we provide a more formal problem description in Sect. 2. Our solution approach combining optimization and simulation is presented in Sect. 3. In Sect. 4, we present the deterministic optimization model used in our solution approach. We introduce a case study based on real-world data in Sect. 5 and present the computational results from applying our solution approach. We conclude in Sect. 6.

2 Problem description

2.1 Real-world problem

The problem we consider in this paper is based on the shipping operations of one of the largest aluminium producers in the world. The producer produces alumina in South America and ships it from there to aluminium production plants across the world. In this paper we consider supplying the production plants located along the west coast of Norway from South America, see Fig. 1 for the supply and demand locations.

Fig. 1
figure 1

Alumina supply and demand locations

Full size image

To ensure that production at the plants in Norway is not interrupted due to lack of alumina, the producer sets up a tactical shipping schedule that specifies the departure dates from the different loading ports as well the unloading dates and volumes for the different aluminium production plants. The planning horizon for this problem is approximately 2–3 months with an underlying time resolution of 1 day.

Despite specifying the departure day for all scheduled voyages in the tactical shipping plan, the loading port can only guarantee a departure within a week from the specified departure day. In addition, ships may have to reduce speed along their voyage from South America to Norway. These delays may cause one or more of the production plants to run out of alumina and production stops. As stopping the production of aluminium is very costly, the shipping schedule has to ensure that the production plants never run out of alumina, despite delays in the arrival of planned shipments.

2.2 Optimization problem

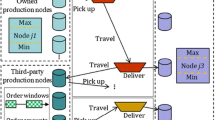
We consider this problem as MIRP with uncertain departure times and uncertain sailing times. A fleet of heterogeneous ships is to transport a product that may have different qualities from a set of loading ports to a set of customer ports. Each loading port provides one or more product qualities. The total quantity picked up during the planning horizon at each loading port is limited by a minimum and maximum quantity. Inventory management at the loading ports is not part of the problem as we consider storage at the loading ports and availability of products as unrestricted. It is therefore always possible to fully load a ship. Each customer has a constant demand rate and upper and lower limits for the permissible storage level. Each customer accepts only certain product qualities. Stock-outs at a customer, i.e. violating the lower storage limit, are to be avoided (if possible) and are subject to a penalty cost. All ports have one berth for loading or unloading a ship.

We only consider full shiploads from the loading ports, but do allow the ships to visit multiple customers during a voyage for unloading their cargo. The ships have different capacities and different costs and are chartered on a per voyage basis. We assume that the product owner does control the ships as the set of available ships is predefined through long-term agreements between the product owner and the ship owners. The long-term agreement also specifies the minimum and maximum number of voyages a ship has to carry out during the planning horizon. Note that selecting the set of available ships is not part of the problem discussed here.

Due to uncertainty in port admission time, departure times are uncertain and a ship leaves within a given time window from the planned departure date. In addition, the sailing time between the loading port and the first customer port is uncertain. The objective is to find the tactical shipment schedule that respects the product quantity requirements in all ports and minimizes the expected transportation costs over the planning horizon. The main decisions are which vessels to use, their planned departure times from the loading ports as well as their routes, i.e. which customers to visit on each voyage and when, as well as the loading and unloading quantities in each port.

3 Solution approach

To handle the uncertainty in departure time and sailing time, we combine optimization and simulation in a two-phase approach based on the hybrid optimization simulation framework proposed by Acar et al. (2009). Note that the approach presented here is in theory capable of finding the optimal solution to the true stochastic problem, but that we implement it as a heuristic to maintain computational tractability. Please see Sect. 4.4 for additional details regarding our implementation

In the first phase, we solve a deterministic MIRP to find an initial shipping plan for supplying the unloading ports with alumina from the loading ports. In the second phase, we assume a set of possible realizations of the uncertain parameters and simulate the performance of the shipping plan for each realization to estimate the shipping plan’s expected cost of uncertainty. We define the expected cost of uncertainty of a solution from phase 1 as the average of the additional costs this solution incurs during the simulations in phase 2. The simulation is carried out by re-optimizing the distribution of alumina to the unloading ports and calculating the increase in costs. The combined framework is illustrated in Fig. 2.

Fig. 2
figure 2

Overview of the combined of the optimization simulation approach

Full size image

Deterministic MIRPs are usually difficult to solve and considering uncertainty in some of the parameters only adds to the complexity of the problem. Attempting to solve a two-stage stochastic programming formulation of the problem may therefore result in considerable challenges regarding computational tractability. With the phase 2 optimization model, we can also easily reflect the level of flexibility the decision maker has once the uncertain parameters become known. This level of flexibility may range from no flexibility, i.e. having to sail the given routes and unload the given quantities, but at a delivery time that depends on the delay the ship has experienced, to having full flexibility, i.e. being allowed to change both the routes and delivery quantities at the unloading ports.

In phase 1 of our solution approach, we solve the deterministic version of our MIRP considering the entire transportation network, but assuming no delays. The resulting shipping plan specifies which of the available ships to charter, how much to load at the loading ports and when to depart for the unloading ports. The plan also determines which unloading ports the ship visits on its route as well as when and how much to unload at each of these ports.

For the problem considered in this paper, the loading ports are mainly located in South America, whereas all unloading ports are located along the west coast of Norway. All ships therefore need to sail through the North Sea on their way to the unloading ports. This assumption is utilized to create an artificial transit point (a location in the North Sea) in our transportation network that all routes must travel through. We use this artificial transit point to split the voyage into two parts: before reaching the transit point, the voyage is subject to uncertainty in departure date and sailing time. From the transit point and to the delivery ports, sailing times are considered to be deterministic, as illustrated in Fig. 3.

Fig. 3
figure 3

Illustration of the modified transportation network

Full size image

We exploit this assumption in our solution approach as the uncertainty in the problem is then only related to activities before arriving at the transit point. Thus, we replace the uncertainty in departure time and sailing time with an uncertain arrival time at the transit point. Compared to the total travel times, the sailing times from the transit point to the unloading ports are short. In phase 2 of the approach, we therefore solve a MIRP with deterministic sailing times on a smaller network to determine routes, delivery dates and quantities as well as the additional costs due to the delays of the simulated solution from phase 1. Please note that the general solution approach also works without this simplification exploiting the geographical properties of our case.

The solution from solving phase 1 is simulated in phase 2. We first use Monte Carlo sampling to draw a set of realizations of arrival times at the transit point for all voyages scheduled in the phase 1 solution. For each of the realizations we then solve the phase 2 model that only considers the network after the transit point. With the phase 2 model, we re-optimize the distribution of alumina from the transit point to the unloading ports throughout the planning horizon. We allow full flexibility on our phase 2 model, i.e. based on the arrival times at the transit point, the phase 2 model can change the route of a ship, both the sequence of port visits and which ports are visited, as well as the unloading quantities at the ports. Once the phase 1 solution has been simulated for all realizations, we calculate the solution’s expected cost of uncertainty from the objective functions from phase 2.

The expected cost of uncertainty is then associated with the corresponding phase 1 solution and included in the phase 1 model. The phase 1 model is then optimized again to generate a new best solution. If this new best solution has not yet been simulated, we pass it on to phase 2 to estimate its expected cost of uncertainty. This process continues until the phase 1 model for the first time produces an already simulated solution as best solution. At this point, our solution approach terminates as we have found the best solution to our MIRP for handling uncertainty in departure times and sailing times. Note that the expected cost of uncertainty needs to be defined such that it is always non-negative for the approach to converge to the optimal solution. Allowing for a negative expected cost of uncertainty may cause the approach to terminate before the optimal solution has been found.

The approach never excludes a previously simulated solution from the solution space of the phase 1 model. Including the expected cost of uncertainty only affects the solution’s objective function value, making it less attractive. Iteratively solving the phase 1 model, simulating the solution and updating the cost of this solution will therefore eventually reproduce a previously simulated solution.

4 Mathematical model

In this section, we present the optimization models used in phase 1 and phase 2 of our solution approach, solving the MIRP faced by a global aluminum producer. First, we introduce the notation used in both models in Sect. 4.1, before presenting the optimization models for phase 1 and phase 2 in Sects. 4.2 and 4.3 respectively. Lastly, we discuss how to associate the expected cost of uncertainty with a given solution and include it in the phase 1 model, see Sect. 4.4.

We use a continuous time formulation where the ships’ voyages are defined on a network where each node represents a pair (i, m), where i indicates the port and m indicates the visit number to port i (see e.g., Al-Khayyal and Hwang 2007; Agra et al. 2014). Furthermore, since the producer only charters a ship for sailing from the loading ports to the unloading ports, the return voyage is not considered.

4.1 Notation

We provide here the notation for the mathematical formulation of the deterministic MIRP solved in phase 1 of our solution approach.

Sets

\(\mathcal {V}\)

Set of ships

\(\mathcal {K}\)

Set of ship classes.

\(\mathcal {P}\)

Set of ports

\(\mathcal {P}^D\)

Set of demand ports, \(\mathcal {P}^D \subset \mathcal {P}\)

\(\mathcal {P}^S\)

Set of supply ports, \(\mathcal {P}^S \subset \mathcal {P}\)

\(\mathcal {M}_i\)

Set of possible visits to port i, \(i\in \mathcal {P}\)

\(\mathcal {Q}\)

Set of product qualities

\(\mathcal {S}^A\)

Set of nodes (i, m), where (i, m) is the \(m^{th}\) visit to port \(i, \in \mathcal {P},m\in \mathcal {M}_i\)

\(\mathcal {S}^A_v\)

Set of nodes (i, m) ship v can visit, \(\mathcal {S}^A_v \subset \mathcal {S}^A\)

\(\mathcal {S}^X_v\)

Set of sailing arcs (i, m, j, n) ship v can travel, where (i, m, j, n) means sailing from node (i, m) to node (j, n), \(i \in \mathcal {P},m\in \mathcal {M}_i,j \in \mathcal {P}^D,n\in \mathcal {M}_j\)

\(\mathcal {V}^k\)

Set of ships in class k, \(k\in \mathcal {K}\), \(\mathcal {V}^k \subset \mathcal {V}\)

Parameters

\(A_{iq}\)

1 if port \(i \in \mathcal {P}\) can accept or produce quality \(q \in \mathcal {Q}\), 0 otherwise

\(C^T_{k}\)

Cost per time period for using ship class \(k \in \mathcal {K}\)

\(C^P_{ik}\)

Fixed cost of visiting a port \(i \in \mathcal {P}\) by ship class \(k \in \mathcal {K}\)

\(K_k\)

Capacity of ship class \(k \in \mathcal {K}\)

\(K_v\)

Capacity of ship \(v \in \mathcal {V}\) (equal the class capacity \(K_k\) for all ships in class k, \(v \in \mathcal {V}^k \Rightarrow K_v = K_k\))

\(\overline{L}_i\)

Maximum level of total product collected from port \(i \in \mathcal {P}^S\)

\(\underline{L}_i\)

Minimum level of total product collected from port \(i \in \mathcal {P}^S\)

\(L_{i}^T\)

Maximum amount a ship in port \(i \in \mathcal {P}\) can (un)load in one time unit

\(\overline{N}\)

Upper bound on the number of shipments

\(\underline{N}\)

Lower bound on the number of shipments

\(Q^{O}_{vq}\)

Quantity of product quality \(q \in \mathcal {Q}\) loaded on ship \(v \in \mathcal {V}\) at the beginning of the planning horizon

\(R_i\)

Rate of consumption per day at port \(i \in \mathcal {P}^D\)

\(\overline{S}_i\)

Maximum stock level at port \(i \in \mathcal {P}^D\)

\(\underline{S}_i\)

Minimum stock level at port \(i \in \mathcal {P}^D\)

\(\underline{S}_i^T\)

Minimum stock level at port \(i \in \mathcal {P}^D\) at the end of the time horizon

\(S_i^O\)

Initial stock level at port \(i \in \mathcal {P}^D\)

T

Length of the time horizon

\(T_{ijv}\)

Time required to travel from port \(i \in \mathcal {P}\) to port \(j \in \mathcal {P}\) for ship \(v \in \mathcal {V}\)

\(T_{iv}^{O}\)

Travel time from initial position to port \(i\in \mathcal {P}\) for ship \(v \in \mathcal {V}\)

\(T_{iv}^S\)

Setup time required in port \(i \in \mathcal {P}\) for ship \(v \in \mathcal {V}\)

\(\overline{U}\)

Upper bound on total number of demand ports a ship can visit

Decision variables

\(f_{imjnvq}\)

Amount of product quality \(q \in \mathcal {Q}\) transported by ship \(v\in \mathcal {V}\) from node \((i,m) \in \mathcal {S}^A\) to node \((j,n) \in \mathcal {S}^A\)

\(l_{imvq}\)

Amount of product quality \(q\in \mathcal {Q}\) loaded or unloaded from ship \(v\in \mathcal {V}\) at port \(i \in \mathcal {P}\) during visit \(m\in \mathcal {M}_i\)

\(s_{im}\)

Stock level at start of visit \(m \in \mathcal {M}_i\) in port \(i \in \mathcal {P}^D\)

\(t_{im}\)

Start time of visit \(m \in \mathcal {M}_i\) in port \(i \in \mathcal {P}\)

\(t_{imv}^O\)

Time spent by ship \(v\in \mathcal {V}\) operating during visit \(m \in \mathcal {M}_i\) to port \(i \in \mathcal {P}\)

\(t_{imv}^W\)

Time spent by ship \(v\in \mathcal {V}\) waiting during visit \(m \in \mathcal {M}_i\) to port \(i \in \mathcal {P}\)

\(w_{imv}\)

1 if ship \(v\in \mathcal {V}\) visits port \(i \in \mathcal {P}\) for the m-th time, \(m \in \mathcal {M}_i\), 0 otherwise

\(x_{imjnv}\)

1 if ship \(v\in \mathcal {V}\) travels arc \((i,m,j,n) \in \mathcal {S}^X_v\), 0 otherwise

\(x_{imv}^O\)

1 if ship \(v\in \mathcal {V}\) travels from initial position to node \((i,m) \in \mathcal {S}^A\), 0 otherwise

\(y_{im}\)

1 if a ship visits port \(i \in \mathcal {P}\) for the m-th time, \(m \in \mathcal {M}_i\), 0 otherwise

\(z_{imv}\)

1 if ship \(v\in \mathcal {V}\) ends it route at \((i,m) \in \mathcal {S}^A\), 0 otherwise

\(z_v\)

1 if ship \(v \in \mathcal {V}\) is used, 0 otherwise

4.2 Model for phase 1

In this section, we present the optimization model used in phase 1 of our solution approach.

4.2.1 Objective function

The objective of the model in phase 1 is to minimize the total costs of transporting the product.

$$\begin{aligned}{} & {} \min \sum _{k\in \mathcal {K}} \sum _{v\in \mathcal {V}^{k}} C^T_k \cdot \left( \sum _{(i,m,j,n) \in \mathcal {S}_{v}^X} T_{ijv} \cdot x_{imjnv} + \sum _{(i,m) \in \mathcal {S}_{v}^A} T_{iv}^O \cdot x_{imv}^O \right) \nonumber \\{} & {} + \sum _{k\in \mathcal {K}} \sum _{v\in \mathcal {V}^{k}} \left( \sum _{(i,m) \in \mathcal {S}_v^A} C^T_k \cdot \left( t_{imv}^O + t_{imv}^W \right) + \sum _{(i,m) \in \mathcal {S}_{v}^A} C^P_{ik} \cdot w_{imv} \right) \end{aligned}$$
(1)

The first line in Eq. (1) represents the time charter cost when sailing between the ports and from origin. The first term in the second line is the time charter cost occuring during operation and waiting in a port, followed by the port fees.

4.2.2 Routing constraints

We use a continuous time formulation where the ship paths are defined on a network where each node represents a pair (i, m), where i indicates the port and m indicates the visit number to port i. Each ship must depart from its initial position, visit a series of demand and/or supply ports and end its voyage at an artificial end node. Split pickups are not allowed but each ship can split its delivery between a maximum of \(\overline{U}\) demand ports. Since the producer only charters a ship for sailing from the loading ports to the unloading ports, the return voyage is not considered.

The producer has long term contracts with several shipping companies stating an interval for number of shipments. As a simplification, the contracts are accumulated, creating a lower and upper bound for the total number of shipments.

$$\begin{aligned}&\sum _{(i,m) \in \mathcal {S}_v^A} x_{imv}^O = z_v, \quad v\in \mathcal {V} \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{(j,n) \in \mathcal {S}_v^A} x_{jnimv} + x_{imv}^O = w_{imv}, \quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{(j,n) \in \mathcal {S}_v^A} x_{imjnv} + z_{imv} = w_{imv}, \quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A \end{aligned}$$
(4)
$$\begin{aligned}&z_{imv} = 0, \quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A : i \in \mathcal {P}^S \end{aligned}$$
(5)
$$\begin{aligned}&\Bigg \lceil {\frac{\sum _{q\in \mathcal {Q}}Q_{vq}^0}{K_v}}\Bigg \rceil \le z_v, \quad v\in \mathcal {V} \end{aligned}$$
(6)
$$\begin{aligned}&\sum _{i \in \mathcal {P}^D}\sum _{m \in \mathcal {M}^D} x_{imv}^O = \Bigg \lceil \frac{\sum _{q \in \mathcal {Q}}Q_{vq}^O}{K_v}\Bigg \rceil , \quad v\in \mathcal {V} \end{aligned}$$
(7)
$$\begin{aligned}&\sum _{i \in \mathcal {P}^S} \sum _{m \in \mathcal {M}_i} w_{imv} \le z_v, \quad v\in \mathcal {V} \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{i \in \mathcal {P}^D} \sum _{m \in \mathcal {M}_i} w_{imv} \le \overline{U} z_v, \quad v\in \mathcal {V} \end{aligned}$$
(9)
$$\begin{aligned}&\underline{N} \le \sum _{v\in \mathcal {V}} z_v \le \overline{N} \quad \quad \end{aligned}$$
(10)
$$\begin{aligned}&\sum _{v\in \mathcal {V}} w_{imv} = y_{im}, \quad (i,m) \in \mathcal {S}^A \end{aligned}$$
(11)
$$\begin{aligned}&y_{i(m-1)} \ge y_{im}, \quad (i,m) \in \mathcal {S}^A: m > 1 \end{aligned}$$
(12)
$$\begin{aligned}&z_{v} \ge z_{v+1}, \quad k\in \mathcal {K}, v\in \mathcal {V}^k \setminus \{\text {|}V^k\text {|}\} \end{aligned}$$
(13)

Equations (2) make sure each ship that is used departs from its initial position for travelling to another node (i, m). Conservation of flow is handled by Eqs. (3) and (4). Constraints (5) ensure that a ship cannot end its route in a supply node. Further, constraints (6) and (7) make sure that each ship containing an initial load is used and visits a demand port. Equations (8) and (9) control that only one supply port and a maximum of \(\overline{U}\) demand ports are visited, respectively. Constraints (10) ensure that the total number of shipments are in the contracted interval \([\underline{N},\overline{N}]\). Moreover, Eq. () make sure that a ship can only visit node (i, m) if the variable \(y_{im}\) is one. Due to constraints (12) port i cannot be visited the \(m^{th}\) time if it is not visited in \(m-1\). Finally, we introduce the symmetry breaking constraints (13) for ship class k. It makes sure that if ship \(v+1\) in class \(k\in \mathcal {K}\) is used, then ship v in the same class must also be used.

4.2.3 Loading and unloading constraints

The network is divided into loading ports and unloading ports that can accept one or more product qualities with no ports serving both purposes. Each loading port has a supply interval for the total quantity loaded over the time horizon.

$$\begin{aligned}&Q_{vq}^O x_{imv}^O + l_{imvq} = \sum _{(j,n) \in \mathcal {S}_v^A} \left( f_{imjnvq} - f_{jnimvq} \right) , \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad v\in \mathcal {V}, q \in \mathcal {Q}, (i,m) \in \mathcal {S}_v^A: i \in \mathcal {P}^S \end{aligned}$$
(14)
$$\begin{aligned}&Q_{vq}^O x_{imv}^O - l_{imvq} = \sum _{(j,n) \in \mathcal {S}_v^A} \left( f_{imjnvq} - f_{jnimvq} \right) , \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad v\in \mathcal {V}, q \in \mathcal {Q}, (i,m) \in \mathcal {S}_v^A:i\in \mathcal {P}^D \end{aligned}$$
(15)
$$\begin{aligned}&\sum _{q \in \mathcal {Q}} f_{imjnvq} \le K_v x_{imjnv}, \quad v\in \mathcal {V}, (i,m,j,n) \in \mathcal {S}_v^X \end{aligned}$$
(16)
$$\begin{aligned}&\sum _{q \in \mathcal {Q}} l_{imvq} \le \min \{K_v, \overline{S}_i-\underline{S}_i\} w_{imv}, \quad v\in \mathcal {V},(i,m) \in \mathcal {S}_v^A: i \in \mathcal {P}^D \end{aligned}$$
(17)
$$\begin{aligned}&\sum _{q \in \mathcal {Q}} l_{imvq} = K_v w_{imv}, \quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A: i \in \mathcal {P}^S \end{aligned}$$
(18)
$$\begin{aligned}&{l_{imvq}} \le A_{iq} K_v w_{imv},\quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A, q \in \mathcal {Q} \end{aligned}$$
(19)

Equations (14) and (15) represent the mass conservation for node (i, m) in loading ports and unloading ports, respectively. Constraints (16) ensure that the flow of products between two nodes never exceeds the ship’s capacity. Further, constraints (17) ensure that quantity unloaded from ship v is never exceeding the ship’s capacity or the storage capacity at the unloading port. Since split pickups are disallowed, Eq. (18) ensure that each ship leaving a supply port is fully loaded. Furthermore, constraints (19) make sure that no ship can load or unload a quality that is either not produced in the loading port or not accepted in an unloading port.

4.2.4 Time constraints

Each ship has a fixed setup time in a given port and a variable (un)loading time, determined by the fixed (un)loading rate. Furthermore, all ports have one berth available for (un)loading.

$$\begin{aligned}&\frac{\sum _{q \in \mathcal {Q}}l_{imvq}}{L_i^T} + T_{iv}^S w_{imv} \le t_{imv}^O, \quad v \in \mathcal {V}, (i,m) \in \mathcal {S}_v^A \end{aligned}$$
(20)
$$\begin{aligned}&t_{imv}^W + t_{imv}^O \le T w_{imv}, \quad v \in \mathcal {V}, (i,m)\in \mathcal {S}_v^A \end{aligned}$$
(21)
$$\begin{aligned}&t_{i,m-1} + \sum _{v\in \mathcal {V}} t_{i,m-1,v}^o \le t_{im}, \quad (i,m) \in \mathcal {S}^A: m>1 \end{aligned}$$
(22)
$$\begin{aligned}&\sum _{v\in \mathcal {V}} \left( T_{iv}^O x_{imv}^O + t_{imv}^W \right) \le t_{im}, \quad (i,m) \in \mathcal {S}^A \end{aligned}$$
(23)
$$\begin{aligned}&(T - T_{iv}^O) x_{imv}^O + t_{imv}^W \le T - t_{im}\, \nonumber \\&\qquad \qquad \qquad \qquad (i,m) \in \mathcal {S}^A : i \in \mathcal {P}^D,v \in \mathcal {V} : \sum _{q \in \mathcal {Q}}Q_{vq}^O > 0 \end{aligned}$$
(24)
$$\begin{aligned}&t_{im} + \sum _{v \in \mathcal {V}} t_{imv}^O \le T, \quad (i,m) \in \mathcal {S}^A \end{aligned}$$
(25)
$$\begin{aligned}&t_{im} + \sum _{v\in \mathcal {V}}\left( t_{imv}^O+t_{jnv}^W + (T_{ijv}+T)\cdot x_{imjnv}\right) \le t_{jn} + T, \nonumber \\&\qquad \qquad \qquad \qquad (i,m), (j,n) \in \mathcal {S}^A \end{aligned}$$
(26)
$$\begin{aligned}&t_{im} + \sum _{v\in \mathcal {V}}\left( t_{imv}^O+t_{jnv}^W + (T_{ijv}-T)\cdot x_{imjnv}\right) \ge t_{jn} - T, \nonumber \\&\qquad \qquad \qquad \qquad (i,m), (j,n) \in \mathcal {S}^A \end{aligned}$$
(27)

Constraints (20) make sure that the operational time in a port is greater than the setup time in a port in addition to the time needed to (un)load the ship. Further, constraints (21) ensure that the operational and waiting time for ship v in port i are zero, if ship v is in use. Due to constraints (22), only one ship is allowed to be at port i at the same time. Constraints (23) assign the start time of ship v in the first node to be at least the travel time from ship v’s initial position to the first port. Constraints (24) make sure that ships that are in transit at the beginning of the horizon leave the origin at time zero. Constraints (25) ensure that the start time of visits and operational time for the visit is always within the time horizon. The last time constraints given by (26)–(27) connect the start time at node (i, m) to the start time in (j, n) given that ship v travels directly to (j, n).

4.2.5 Inventory constraints

Because the product is bought “free on board”, inventory management at the loading ports is not considered. However, inventory management is considered in each of the unloading ports. Since the cost associated with a stop in production is high, stock-outs (i.e. inventory levels falling below the minimum stock level) are not allowed. The consumption rate is treated as constant and known through the period.

$$\begin{aligned}&s_i^O - s_{i1} = R_i t_{i1},\quad i \in \mathcal {P}^D \end{aligned}$$
(28)
$$\begin{aligned}&s_{i(m-1)} + \sum _{q \in \mathcal {Q}} \sum _{v\in \mathcal {V}} l_{i,m-1,vq} - s_{im} = R_i \left( t_{im} - t_{i,m-1}\right) , \nonumber \\&\qquad \qquad \qquad \qquad i \in \mathcal {P}^D,m \in \mathcal {M}_i \setminus \{1\} \end{aligned}$$
(29)
$$\begin{aligned}&s_{im} + \sum _{q \in \mathcal {Q}} \sum _{v\in \mathcal {V}} l_{imvq} - \sum _{v\in \mathcal {V}} R_i t_{imv}^O \le \overline{S}_i, \quad i \in \mathcal {P}^D, m \in \mathcal {M}_i \end{aligned}$$
(30)
$$\begin{aligned}&s_{im} \ge \underline{S}_i, \quad i \in \mathcal {P}^D, m \in \mathcal {M}_i \end{aligned}$$
(31)
$$\begin{aligned}&s_{i\overline{M}_i} + \sum _{q \in \mathcal {Q}} \sum _{v\in \mathcal {V}} l_{i,\overline{M}_i,vq} - R_i \left( T - t_{i\overline{M}_i} \right) \ge \underline{S}_i^T, \quad i \in \mathcal {P}^D \end{aligned}$$
(32)
$$\begin{aligned}&\underline{L}_i \le \sum _{q \in \mathcal {Q}} \sum _{v\in \mathcal {V}} \sum _{m \in \mathcal {M}_i} l_{imvq} \le \overline{L}_i, \quad i\in \mathcal {P}^S \end{aligned}$$
(33)

Equations (28) set the initial stock levels. Further, the stock levels in the beginning of the \(m^{th}\) visit are related to the previous visit, see Eqs. (29). Constraints (30) make sure that the inventory capacity in unloading port i is not exceeded. Constraints (31) and (32) impose a lower inventory bound in unloading port i for the inventory level at the beginning of visit m and at the end of the time horizon, respectively. Lower bound \(\underline{S}_i\) can be interpreted as the port’s safety stock. The purpose of this safety stock is to ensure operations at the facility in case of unforeseen disruptions in deliveries. The lower bound at the end of the planning horizon \(\underline{S}_i^T\) also acts as safety stock, but additionally ensures that there are no end-of-horizon effects regarding deliveries late during the planning horizon. Lastly, constraints (33) ensure that the total volume supplied from supply port i is within the given interval \([ \underline{L}_i,\overline{L}_i]\).

4.2.6 Valid inequalities

We use three valid inequalities to strengthen the mathematical formulation in this article. The first two are similar to Agra et al. (2017) while the third is inspired by Agra et al. (2013).

4.2.6.1 Minimum visits and minimum operational time in each port

Let \(ND_i = \text {max} \{ T \cdot R_i - {S}_i^0 + \underline{S}_i, 0 \}, i \in \mathcal {P}^D\) be the net demand for each unloading port over the total planning horizon. The minimum number of visits in port \(i \in \mathcal {P}^D\) is then given by \(\underline{M}_i = \big \lceil \frac{ND_i}{\text {max} \{ K_k \} } \big \rceil\) and the minimum operational time in port \(i \in \mathcal {P}^D\) is given by \(\underline{T}_i^O = \frac{ND_i}{L_i^T } + \underline{M}_i\cdot T_i^F\). For the loading ports, the minimum number of visits is given as \(\underline{M}_i = \big \lceil \frac{\underline{L}_i}{{\text {max} \{ K_k \} } }\big \rceil\) while the minimum operational time is calculated as \(\underline{T}_i^O = \frac{\underline{L}_i}{L_i^T } + \underline{M}_i\cdot T_i^F\), where \(\underline{L}_i\) is the lower bound on the supplied quantity for port \(i \in \mathcal {P}^S\).

Constraints (34) ensure the minimum visits in port \(i \in \mathcal {P}\) while constraint (35) determines minimum operational time in port \(i \in \mathcal {P}\).

$$\begin{aligned} y_{im}&= 1, \quad i \in \mathcal {P}, m \le \underline{M}_i \end{aligned}$$
(34)
$$\begin{aligned} \sum _{m \in \mathcal {M}_i} \sum _{v \in \mathcal {V}} t^O_{imv}&\ge \underline{T}_i^O, \quad i \in \mathcal {P} \end{aligned}$$
(35)
4.2.6.2 Upper limit on time visited variables for each visit

The last valid inequalities imposes an upper bound on the time variables for visiting the unloading ports by utilizing the storage capacity as well as the consumption rate. Let \(T_{im}^{MAX}\) be the last possible time for visit \(m \in \mathcal {M}_i\) to port \(i \in \mathcal {P}^D\). \(T_{im}^{MAX}\) is defined as follows:

$$\begin{aligned} T_{im}^{MAX}=\text {min }\bigg \{ T\text { }, \frac{S_i^0+(m-1)\cdot \overline{S}_i - \underline{S}_i}{R_i} - T_i^F\bigg \}, (i,m) \in \mathcal {S}^A: i \in \mathcal {P}^D \end{aligned}$$

This gives the following inequality constraints:

$$\begin{aligned} t_{im}&\le T_{im}^{MAX}, \quad (i,m) \in \mathcal {S}^A: i \in \mathcal {P}^D \end{aligned}$$
(36)

Experience during the initial testing of these valid inequalities indicated that using both types of valid inequalities results in runtime reductions in the range 3–30% depending on problem instance. The effect of using these valid inequalities individually is difficult to predict, as using either type of valid inequality resulted in a reduction in runtime for one instance and an increase in runtime for the other.

4.2.7 Non-negativity and binary restrictions

$$\begin{aligned} f_{imjnvq}&\ge 0, \quad v\in \mathcal {V}, (i,m,j,n) \in \mathcal {S}_v^X, q \in \mathcal {Q} \end{aligned}$$
(37)
$$\begin{aligned} l_{imvq}&\ge 0, \quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A, q \in \mathcal {Q} \end{aligned}$$
(38)
$$\begin{aligned} t_{im}&\ge 0, \quad (i,m) \in \mathcal {S}^A \end{aligned}$$
(39)
$$\begin{aligned} t_{imv}^W, t_{imv}^O&\ge 0, \quad (i,m) \in \mathcal {S}^A, v \in \mathcal {V} \end{aligned}$$
(40)
$$\begin{aligned} x_{imjnv}&\in \{0, 1\}, \quad v\in \mathcal {V}, (i,m,j,n) \in \mathcal {S}_v^X \end{aligned}$$
(41)
$$\begin{aligned} x_{imv}^O, w_{imv}, z_{imv}&\in \{0, 1\}, \quad v\in \mathcal {V}, (i,m) \in \mathcal {S}_v^A \end{aligned}$$
(42)
$$\begin{aligned} y_{im}&\in \{0, 1\}, \quad (i,m) \in \mathcal {S}^A \end{aligned}$$
(43)
$$\begin{aligned} z_v&\in \{0, 1\}, \quad v\in \mathcal {V} \end{aligned}$$
(44)

Constraints (37)–(40) make sure that the loading, quantity and time variables are non-negative. Lastly, all binary routing variables are defined as binary in constraints (41)–(44).

4.3 Model for phase 2

The optimization model for phase 2 is essentially a simplified version of the phase 1 model presented above. The main simplifications result from the fact that the planned ship departures are known from the phase 1 solution. Combined with a realization for the uncertain parameters, i.e. departure times from the loading ports and sailing times, we calculate the arrival time at the transit point for all ships. The resulting MIRP then only focuses on distributing the product from the fully laden ships at the transit point to the unloading ports such that the total costs are minimized.

The most important change in the phase 2 model is that we need to include a shortfall variable in inventory constraints (31) as we may not be able to guarantee feasibility of this constraint for all possible realizations of delays. The shortfall variable is also included in the objective function with an associated penalty cost that is sufficiently large to discourage stock-outs.

The desired level of flexibility in the phase 2 model controls which variables are fixed when solving the problem. If no flexibility is allowed, variables w and x are fixed in phase 2 to their values in the phase 1 solution. The phase 2 model then only determines the timing of unloading operations and the associated costs. With full flexibility, none of the variables are fixed and the phase 2 model can choose freely which ports each ship should visit and how much to unload there.

It is also possible to introduce limited flexibility, e.g. restricting the deviation in number of port visits between phase 1 and phase 2 solutions. Let \(M_i^A\) be the actual number of visits to an unloading port in the phase 1 solution and \(\Delta V\) be the number of visits the phase 2 solution is allowed to deviate from \(M_i^A\). We can then easily implement limited flexibility in phase 2 by adding constraint (45):

$$\begin{aligned} \max \left\{ M_i^A - \Delta V, 0 \right\} \le \sum _{m \in \mathcal {M}_i} y_{im} \le \min \left\{ M_i^A + \Delta V, \text {|}\mathcal {M}_i\text {|} \right\} , \quad i \in \mathcal {P}^D \end{aligned}$$
(45)

If \(\Delta V = 1\), each port can be visited at most once more and once less than in the phase 1 solution. As this flexibility increases, the expected cost of uncertainty decreases. However, increasing flexibility also increases runtime in phase 2 as the problems become harder to solve. Based on some initial testing to assess the trade-off between solution quality and runtime, we use \(\Delta V=2\) to limit flexibility in phase 2.

4.4 Heuristic implementation of the solution approach

Similar to Acar et al. (2009) and Medbøen et al. (2020), our solution framework iterates between generating potential solutions in phase 1 and evaluating their performance under uncertainty in phase 2. Each simulated solution is then associated with an expected cost of uncertainty to each potential solution. Below, we describe how we use the proposed solution approach as a heuristic for finding solutions to our problem. We also show how feedback from phase 2 is included in the phase 1 model.

4.4.1 Identifying unique solutions

We use a continuous-time formulation for our MIRP in phase 1 of our solution approach. Achieving convergence of the continuous variables \(t_{im}\) can be challenging as associating the expected cost of uncertainty to a given solution may just cause a marginal change in departure time. We therefore discretize the planning horizon into intervals \(\tau \in \mathcal {T}\) with a duration \(\Delta T\). We then consider two departures as identical if their departures are planned during the same time interval. Consequently, a solution is identical, if the routing of the ships is identical and all departures are planned in the same time intervals. The downside of this discretization is that it might prevent us from finding the true optimal solution to the original problem, even if we simulate over all possible realizations of the uncertain parameters. Our solution approach therefore serves as a heuristic for finding solutions.

Note that the solution method is sensitive to the duration of the time intervals \(\Delta T\). Choosing a large \(\Delta T\) helps the method converge faster as fewer solutions need to be simulated. However, we also run the risk of overlooking good solutions as they may be considered identical to an already simulated solution. The choice of \(\Delta T\) thus represents a trade-off. If \(\Delta T\) is too large, certain areas of the solution space will go unexplored and there is the risk of missing good solutions. However, if \(\Delta T\) is too small, the framework will not converge because too many similar solutions are evaluated. Initial testing for our case indicates that \(\Delta T = 3\) provides an acceptable trade-off.

Our discretization might also be useful in a discrete-time formulation as the duration \(\Delta T\) can be longer than the duration of the discrete time period. In addition, we avoid the additional binary variables of the discrete-time formulation.

4.4.2 Modifying the phase 1 model

We show here how to extend the phase 1 model in order to associate the expected cost of uncertainty with a given solution. We first introduce the additional notation before presenting the additional constraints.

4.4.3 Additional notation

Sets

\(\mathcal {H}\)

Set of phase 1 solutions found in previous iterations

\(\mathcal {T}\)

Set of time intervals

Parameters

\(\Delta C_{\eta }\)

Expected cost of uncertainty for solution \(\eta \in \mathcal {H}\)

\(M_{i\eta }^A\)

Actual number of visits to in loading port \(i\in \mathcal {P}^S\) in phase 1 solution \(\eta \in \mathcal {H}\)

\(\Gamma _{im\tau \eta }\)

1 if node \((i,m) \in \mathcal {S}^A: i \in \mathcal {P}^S\) is served in time interval \(\tau\) in phase 1 solution \(\eta \in \mathcal {H}\), 0 otherwise

\(W_{imk\eta }\)

1 if ship class \(k \in \mathcal {K}\) is used to serve node \((i,m) \in \mathcal {S}^A: i \in \mathcal {P}^S\) in phase 1 solution \(\eta \in \mathcal {H}\), 0 otherwise

\(Z_{v\eta }\)

1 if ship v is used in stage 1 solution \(\eta \in \mathcal {H}\), 0 otherwise

\(\Delta T\)

Duration of each time interval

Decision variables

\(\lambda _{\eta }\)

1 if solution is identical to phase 1 solution \(\eta \in \mathcal {H}\), 0 otherwise

\(\gamma _{im\tau }\)

1 if node \((i,m) \in \mathcal {S}^A: i \in \mathcal {P}^S\) is visited in time interval \(\tau \in \mathcal {T}\), 0 otherwise

4.5 Model extensions

In order to discretize the time intervals for visits in loading ports constraints (46)–(48) are implemented. They ensure that the binary variable \(\gamma _{im\tau }\) is set to 1 if the port is visited during the time interval.

$$\begin{aligned} t_{im}&\ge (\tau - 1)\cdot \Delta T \cdot \gamma _{im\tau }, \quad i \in \mathcal {P}^S, m \in \mathcal {M}_i, \tau \in \mathcal {T} \end{aligned}$$
(46)
$$\begin{aligned} t_{im}-\tau \Delta T&\le (T-\tau \Delta T)(1-\gamma _{im\tau }), \quad i \in \mathcal {P}^S, m \in \mathcal {M}_i, \tau \in \mathcal {T} \end{aligned}$$
(47)
$$\begin{aligned} \sum _{\tau \in \mathcal {T}} \gamma _{im\tau }&= 1, \quad i \in \mathcal {P}^S, \eta \in \mathcal {H}, m \in 1,\ldots , M_{i\eta }^A \end{aligned}$$
(48)

Further, we need to check if a solution has been simulated before. Constraints (49)–(50) ensure that variable \(\lambda _\eta\) is set to 1 if the solution has been simulated during an earlier iteration.

$$\begin{aligned}&\quad \sum _{i \in \mathcal {P}^S} \sum _{m=1}^{M_{i\eta }^A+1} \left( \sum _{k \in \mathcal {K}}2 W_{imk\eta } \cdot \sum _{v \in \mathcal {V}^k} w_{imv} - W_{imk\eta } - \sum _{v \in \mathcal {V}^k} w_{imv} \right) \nonumber \\&\qquad + \sum _{v \in \mathcal {V}}\left( 2 Z_{v\eta } \cdot z_{v} - Z_{v\eta } - z_{v} \right) \nonumber \\&\qquad + \sum _{i \in \mathcal {P}^S} \sum _{m=1}^{M_{i\eta }^A+1}\sum _{\tau \in \mathcal {T}}\left( 2 \Gamma _{im\tau \eta } \cdot \gamma _{im\tau } - \Gamma _{im\tau \eta } - \gamma _{im\tau }\right) \ge M \cdot (\lambda _\eta -1), \nonumber \\&\qquad \qquad \qquad \qquad \eta \in \mathcal {H} \end{aligned}$$
(49)
$$\begin{aligned}&\quad \sum _{i \in \mathcal {P}^S} \sum _{m=1}^{M_{i\eta }^A+1} \left( \sum _{k \in \mathcal {K}}2 W_{imk\eta } \cdot \sum _{v \in \mathcal {V}^k} w_{imv} - W_{imk\eta } - \sum _{v \in \mathcal {V}^k} w_{imv} \right) \nonumber \\&\qquad + \sum _{v \in \mathcal {V}}\left( 2 Z_{v\eta } \cdot z_{v} - Z_{v\eta } - z_{v} \right) \nonumber \\&\qquad + \sum _{i \in \mathcal {P}^S} \sum _{m=1}^{M_{i\eta }^A+1}\sum _{\tau \in \mathcal {T}}\left( 2 \Gamma _{im\tau \eta } \cdot \gamma _{im\tau } - \Gamma _{im\tau \eta } - \gamma _{im\tau }\right) \le \lambda _\eta -1 , \nonumber \\&\qquad \qquad \qquad \qquad \eta \in \mathcal {H} \end{aligned}$$
(50)

The Big M-parameter in the constraints above is defined as:

$$\begin{aligned} M = 2 \cdot \min \left\{ \sum _{i \in \mathcal {P}^S} M_i, \overline{N}\right\} + \overline{N} \end{aligned}$$
(51)

In addition, we need to update the objective function Eq. (1) with the expected cost of uncertainty. Therefore, the new objective function is defined by Eq. (52).

$$\begin{aligned}{} & {} \min \sum _{k\in \mathcal {K}} \sum _{v\in \mathcal {V}^{k}} C^T_k \cdot \left( \sum _{(i,m,j,n) \in \mathcal {S}_{v}^X} T_{ijv} \cdot x_{imjnv} + \sum _{(i,m) \in \mathcal {S}_{v}^A} T_{iv}^O \cdot x_{imv}^O \right) \nonumber \\{} & {} \quad + \sum _{k\in \mathcal {K}} \sum _{v\in \mathcal {V}^{k}} \left( \sum _{(i,m) \in \mathcal {S}_v^A} C^T_k \cdot \left( t_{imv}^O + t_{imv}^W \right) + \sum _{(i,m) \in \mathcal {S}_{v}^A} C^P_{ik} \cdot w_{imv} \right) \nonumber \\{} & {} \quad + \sum _{\eta \in \mathcal {H}} \Delta C_{\eta }\cdot \lambda _{\eta } \end{aligned}$$
(52)

The last sum in the updated objective function (52) is the expected cost of uncertainty for a solution that has already been simulated.

5 Computational study

In this section, we present the results of applying our approach to problem instances based on real-world data. The solution approach is implemented in Python version 3.7.2. The optimization models are implemented in Mosel and solved using FICO Xpress version 8.5.10. The stopping criterion for Xpress is set to an optimality gap of \(1\%\). For our optimization-simulation approach we allow a runtime of 12 h. All calculations are carried out on a computer with two 2.4 GHz Intel Xeon Gold 5115 CPUs and 96 GB RAM.

5.1 Problem instances and input data

The problem instances are based on real-world data and chosen to mimic the tactical planning problem faced by one of the world’s largest producers of primary aluminium. To ensure that the production plants do not run out of alumina, shipments of alumina are planned up to 6 months ahead. Vessel class and shipment date are determined approx. 4 weeks ahead of departure. The deterministic model in phase 1 describes the current process of setting up the shipment schedule. The simulations in phase 2 of our solution approach represent the process of short term re-planning of shipments that has to be carried out in case of delays. By including this step in the initial planning process, we try to find more robust routes that require re-planning less often.

In order to test the solution framework, we introduce two problem instances, Small and Large, that differ in length of the planning horizon and the number of available ships. Only one product quality is considered. The main properties of the problem instances are summarized in Table 1.

Table 1 Properties of the problem instances
Full size table

We consider two sources of uncertainty in our case study. Firstly, departure times from the loading port deviate from the scheduled departure time by as much as 7 days. We assume a uniform distribution for the departure delay. Secondly, the sailing times vary due to the weather. We model the sailing in a simple way where the weather can be good, neutral or bad with equal probabilities, resulting in a sailing times of \(85 \%, 100 \%\) and \(115 \%\) of the deterministic sailing time, respectively. All realizations of uncertain parameters used in the simulation are drawn from their respective distributions by means of Monte Carlo sampling.

The costs used in our calculations for vessels, voyages as well as inventory are based on real-world costs from the case company, but can unfortunately not be disclosed due to reasons of confidentiality. Results are therefore discussed relative to each other. The penalty cost for violating the minimum inventory levels at the unloading ports has been set at a sufficiently high level to represent the cost of a rush order from the nearest loading port. In addition to the transportation and raw material cost, the cost of this rush order reflects that the alumina may have to be procured above market price and includes a risk premium as rush orders may not always be possible in the real world.

5.2 Performance of the solution approach

The convergence speed of our solution approach depends mainly on three factors: First, the time it takes to solve the phase 1 problem, secondly the time spent on phase 2 to simulate the solution from phase 1, and third, the number of required iterations before the solution approach terminates. We use different approaches for these three factors in our attempts to reduce runtime. We address the first issue with valid inequalities defined in Sect. 4.2. They reduce the solution time for the phase 1 model by up to 30% for the large problem instance. The phase 2 model is much simpler than the phase 1 model and solves approximately 10 times faster. Further reduction in runtime of phase 2 is achieved by running the simulations in parallel.

We reduce the number of required iterations by extracting and storing up to the 20 best solutions during the phase 1 solution process. We then simulate all of them using 50 scenarios in phase 2. Extracting multiple solutions reduces the runtime in phase 1 by approximately 25%. However, the time spent in phase 2 increases drastically as more solutions have to be simulated.

We further reduce the runtime of our approach by reducing the number of simulations used for each solution. Instead of simulating the phase 1 solution in a single step with 50 scenarios, we use a two-step simulation procedure where we first simulate all solutions with 10 scenarios to get a rough estimate on the expected cost of uncertainty. Once the approach has terminated, we evaluate up to the best 10 solution using 50 scenarios to provide a better estimate for the expected cost of uncertainty.

The impact of the different measures on the overall runtime is illustrated in Fig. 4. In particular, extracting multiple solutions and two-step simulation reduce the runtime by more than \(30\%\). The increase in phase 1 runtime for the single solution, two-step simulation setup is due to the approach requiring more iterations to converge to a previously simulated solution.

Fig. 4
figure 4

Runtime of our solution approach for the small problem instance

Full size image

5.3 Solution quality

The results from our optimization-simulation solution approach reported in this section are all obtained using the two-step simulation procedure, i.e. by first evaluating a solution’s expected cost of uncertainty using 10 realizations and then simulating the 10 best solutions over 50 realizations. The time interval \(\Delta T\) for distinguishing unique phase 1 solutions is set to \(\Delta T = 3\).

To evaluate the quality of the solution found using our solution approach, we first find the optimal solution to the deterministic problem instances (Small and Large). The objective function values of these solutions serve as our benchmarks and all other costs are presented relative to them. The expected costs of uncertainty for the deterministic solutions are then evaluated over the same 50 realizations used in the final evaluation of our solution approach.

The costs of the deterministic solutions and the solutions found by our solution approach are presented in Fig. 5 for the Small problem instance and in Fig. 6 for the Large problem instance. When comparing the different solutions, we first note that the deterministic solutions incur considerably higher expected costs of uncertainty than the solutions found by our optimization-simulation approach, especially for the Small problem instance. In the Small problem instance, the expected cost of uncertainty is 10.41% for the deterministic solution and only 0.04% for the solution found by our solution approach. The phase 1 solution our approach produces however, is 1.51% more expensive.

Fig. 5
figure 5

Costs for the small problem instance. Expected cost of uncertainty evaluated using 50 scenarios

Full size image

For the Large problem instance, the difference in the phase 1 cost between the deterministic solution and the solution found by our approach is even smaller at 0.29%. And similar to the Small problem instance, we see that the cost of uncertainty is substantially larger for the deterministic solution than for the solution from the optimization-simulation approach.

Fig. 6
figure 6

Costs for the large problem instance. Expected cost of uncertainty evaluated using 50 scenarios

Full size image

The expected cost of uncertainty for the deterministic solutions to both the Small and the Large instance are dominated by the penalty cost for violating the minimum inventory requirements. In case of the Small instance, the deterministic solution incurs this penalty cost 6 times, whereas the deterministic solution to the Large instance incurs this penalty cost 14 times. The best solutions found by our approach do not incur this penalty at all.

The results above show that our solutions are more robust with respect to delays in departure and sailing time, while being less than approx. 1.5% more expensive than the deterministic solution. We have also calculated the wait-and-see solutions (see e.g., Birge and Louveaux 2011) for both the Small and the Large problem instance and our solutions are within 0.3% of these. Hence, our approach is able to find solutions that are close to the optimal solutions of the two-stage stochastic programming version of the problems.

The results also emphasize the importance of finding and analyzing “sub-optimal” solutions. Different solutions can perform quite differently under uncertainty despite having almost equal deterministic objective functions values. The focus practitioners often have on finding the cheapest solution can therefore result in the opposite of the intended outcome due to the consequences of the delays.

Given that the underlying problem is of a tactical nature and will at most be solved once a week, the runtime of approximately 1.5 h for our solution approach is also considered acceptable.

6 Concluding remarks

In this paper, we combine optimization and simulation to solve a maritime inventory routing problem with uncertainty in departure time from the loading ports and sailing time. We use this solution approach as heuristic and iterate between solving a deterministic optimization problem in phase 1 to generate candidate solutions and simulating the performance of these solutions in phase 2. We apply our solution approach to problem instances based on real-world data from one of the world’s largest aluminium producers and show that we find solutions that perform considerably better under uncertainty than the solution based on the deterministic optimization model alone. More importantly, solutions found by the optimization-simulation approach are only marginally more expensive in the deterministic phase 1 model than the deterministic solution.

In addition, our solution approach evaluates multiple solutions and provides an estimate on these solutions perform under uncertainty. For many companies, this is often more desirable than determining a single optimal solution that the company might not be able to implement due to necessary abstractions and simplifications made during the modeling process. Having different solutions with similar objectives function values available thus provides an additional flexibility that is difficult to measure in terms of objective function value. The results also highlight the benefit of explicitly considering uncertainty during the planning process.

The true problem might best be described as a two-stage (or even multi-stage) stochastic programming problem. Unfortunately, we cannot solve that problem due to its size and computational complexity. Formulating and solving the stochastic programming problem is subject to future research.

The solution approach is intended to solve a tactical planning problem without strict requirements on runtime. Still, runtime can be considered as the main challenge that should be addressed. Several approaches can be considered to reduce the runtime (or increase the problem size our approach is capable of solving): First, solving the deterministic phase 1 model requires a lot of time. The use of heuristics might help speed up the process of solving this problem and thus reduce the overall runtime. Second, the largest part of the runtime is spent on simulations in phase 2. Reducing the number of simulations will also reduce the overall runtime. This might be achieved by (1) identifying poor solutions quickly to avoid spending too much on them and (2) generating solutions that will perform well under uncertainty in phase 1. How to make these approaches work will be addressed in future research.

The solution approach presented in this paper is general in nature and can also be applied problems other than maritime inventory routing problems. Similar to stochastic programming, it is particularly suitable for problems where decisions can be split in a deterministic first stage and a second stage where decisions depend on the realization of some uncertain parameters.