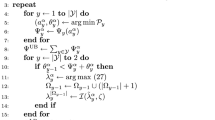Simplifying capacity planning for electricity systems with hydroelectric and renewable generation

Abstract

This work investigates approaches to simplify capacity planning for electricity systems with hydroelectric and renewable generators with three specific foci. First, we examine approaches to represent the efficiency of hydroelectric units. Next, we explore the effects of water-travel times and the representation of run-of-river units within cascaded hydroelectric systems. Third, we analyze the use of representative operating periods to capture electricity-system operations. We conduct these analyses using an archetypal planning models that is applied to the Columbia River system in the northwestern United States of America. We demonstrate that planning models can be simplified significantly, which improves model tractability with little loss of fidelity.

1 Introduction

Capacity planning for electricity systems is vitally important to ensure that electricity can be supplied to consumers at a socially desirable cost and reliability level. It is common for such planning exercises to have long model horizons, because capacity investments can require significant time. As such, capacity-planning decisions may have to be taken long in advance of when the capacity is needed to meet electricity needs. A key consideration in such modeling exercises is how capacity decisions impact electricity-system operations. Capturing such impacts can yield models that are extremely large-scale. Absent weather-dependent renewable energy, electricity-demand levels are the key factor that distinguish different operating periods. As such, the literature proposes computationally efficient approaches to capacity planning that rely upon analysis of an electricity system’s load-duration curve (Stoft 2002; Sioshansi 2016).

Another approach to capturing electricity-system operations, which is suited to the proliferation of weather-dependent renewable energy, is to model a small set of representative operating periods. Cohen et al. (2019) develop a model that uses 17 time slices—four for each season of the year and one for the overall peak-demand period—to represent electricity-system operations over a full year. The goal of such a modeling approach is to ensure that capacity levels can serve customer demands reliably and economically, even with variable and uncertain real-time availability of weather-dependent renewable energy. Capacity-planning models with insufficient operational resolution may be inadequate in capturing such impacts of weather-dependent renewable energy.

Thus, capacity-planning models that use a prescribed small set of representative operating periods are an improvement in capturing the effect of weather-dependent renewable energy on electricity-system operations (Cohen et al. 2019). These approaches are limited, however, in their ability to represent the chronology of electricity-system operations. Weather-dependent renewable energy can increase supply variability and uncertainty, which calls for more operational flexibility. Using a subset of days to represent electricity-system operations can result in different capacity mixes depending on whether generator-ramping constraints are modeled or not, which requires capturing the chronology of operating decisions (Liu et al. 2018b; Maluenda et al. 2018). The effect of ramping constraints on capacity decisions is pronounced particularly in the presence of weather-dependent renewable energy. Capturing intertemporal operations can be important in assessing electricity-system flexibility, e.g., from energy or natural-gas storage (Zhao et al. 2018). Common approaches to selecting representative operating periods include k-means (Boffino et al. 2019) or hierarchical (Nahmmacher et al. 2016; Liu et al. 2018a) clustering and optimization-based approaches (Poncelet et al. 2017).

There are many works that propose simplifications for capacity planning of electricity systems with thermal and renewable resources. The literature that examines capacity planning with hydroelectric, thermal, and renewable resources is more limited, however. Hydroelectric resources raise challenges that complicate electricity-system modeling.

For one, the efficiency of hydroelectric plants can have a non-linear and non-convex relationship with water flow and net head (Hidalgo et al. 2014; Hunter-Rinderle and Sioshansi 2021). These relationships raise trade-offs between representing plant operations accurately and model tractability. Non-linear models of hydroelectric-generator efficiency can be replaced with bi-linear or linear models that involve water flow and reservoir elevation (Conejo et al. 2002; Borghetti et al. 2008). Many electricity-system-planning models use linearizations, wherein reservoir elevation is fixed (Maluenda et al. 2018; Ramírez-Sagner and Muñoz 2019).

A second complication is that many hydroelectric generators are coupled by virtue of their being in a cascaded river system. As the penetration of weather-dependent renewable generation increases, it is important to assess the flexibility and limits of cascaded hydroelectric plants (Huertas-Hernando et al. 2017). Ibanez et al. (2014) find that modeling the details of cascaded hydroelectric plants yields better performance (e.g., less renewable-energy curtailment and operational cost) compared to not modeling such details.

A third complication is the capability of large hydroelectric reservoirs to provide seasonal or interannual water storage. Capacity-planning models that use a subset of days to represent electricity-system operations can capture short-duration energy storage (Liu et al. 2018b; Maluenda et al. 2018; Zhao et al. 2018). Methods to capture longer-duration seasonal or interannual energy storage are limited in the literature (Sioshansi et al. 2022). Indeed, using clustering techniques to select representative operating periods (Nahmmacher et al. 2016; Liu et al. 2018a; Boffino et al. 2019) may be inappropriate, because spring and autumn periods may have similar load and weather patterns (resulting in their being clustered), but very different reservoir water levels.

Given these limitations of the extant literature, we investigate three key aspects of capacity planning for electricity systems with hydroelectric, thermal, and renewable resources. We do this using an archetypal capacity-planning model and economic regret (Ramírez-Sagner and Muñoz 2019) as a performance metric. We apply our model to a case study that is based on the Columbia River system in the northwestern United States of America. The three aspects of capacity planning on which we focus yield three key contributions of our work. First, we examine different approaches to representing hydroelectric-generator efficiency and propose a regression-based linearization method, which gives good model performance compared to a non-linear efficiency function. Second, we analyze the impact of considering water-travel times and run-of-river storage capacities, demonstrating that these can be neglected with little impact on model results. Third, we use several variations of hierarchical clustering to select representative operating days and demonstrate that they can capture intraday, seasonal, and interannual time dynamics (including reservoir water levels). As a final contribution of our work, we demonstrate the limitations of relying upon objective-function value as a metric to assess the performance of a model reduction. Our results demonstrate that a key limitation of using objective-function value is its inability to capture extreme events (e.g., high-load or low-renewable-energy operating periods). Economic regret is a measure of model fidelity that is significantly more robust to such extremes.

The remainder of this paper is structured as follows. Section 2 provides the formulation of our archetypal capacity-planning model and Sect. 3 details the model reductions that we examine and the metric that is used to assess reduction quality. Section 4 summarizes case-study data and implementation. Section 5 provides our results. Section 6 concludes.

2 Model

This section provides the formulation of our archetypal capacity-expansion model. This model is not intended to capture every nuance of electricity-system planning. Rather, the goal is to explore a model that captures the key features of capacity planning with hydroelectric, renewable, and thermal resources.

2.1 Model notation

We begin by defining the following sets.

${\mathcal {H}}$	Set of hydroelectric dams
$\bar{{\mathcal {H}}}_c$	Set of dams that are upstream of dam c
${\mathcal {H}}^{\mathcal {L}}_n$	Set of dams that are located at transmission node n
${\mathcal {G}}$	Set of non-hydroelectric-generation technologies
${\mathcal {L}}$	Set of transmission lines
${\mathcal {L}}^\textrm{in}_n$	Set of transmission lines that flow into node n in the nominal direction
${\mathcal {L}}^\textrm{out}_n$	Set of transmission lines that flow out from node n in the nominal direction
${\mathcal {N}}$	Set of transmission nodes
${\mathcal {T}}^\textrm{H}$	Ordered set of hours during a year
${\mathcal {Y}}$	Ordered set of years
${\mathcal {Z}}$	Set of pieces of approximation of transmission losses

Next, we define the following indices.

c	Index for hydroelectric dams
g	Index for non-hydroelectric-generation technologies
h	Index for hours
l	Index for transmission lines
n	Index for transmission nodes
y	Index for years
z	Index of pieces of approximation of transmission losses

Next, we define the following parameters and functions.

$C^{{\mathcal {G}},\textrm{i}}_{y,g,n}$	Annualized year-y capital cost of non-hydroelectric-generation technology g that is located at node n ($/MW)
$C^{{\mathcal {G}},\textrm{V}}_{y,g,n,h}$	Operating cost during hour h of year y of a generator that uses non-hydroelectric-generation technology g and is located at node n ($/MWh)
$C^{\mathcal {L}}$	Annualized capital cost of transmission line ($/MW)
$C^\textrm{U}$	Value of lost load ($/MWh)
$D_z$	Coefficient for zth piece of flow-related transmission losses (p.u.)
$E_z$	Coefficient for zth piece of capacity-related transmission losses (p.u.)
$k^{{\mathcal {G}},\textrm{i}}_{0,g,n}$	Initial capacity that is installed at node n of non-hydroelectric-generation technology g (MW)
$k^{\mathcal {L}}_{0,l}$	Initial installed capacity of transmission line l (MW)
$L_{y,n,h}$	Node-n electric load during hour h of year y (MW)
$q^{\mathcal {G}}_{1,g,n,0}$	Initial production level of non-hydroelectric-generation technology g that is located at node n (MW)
$Q^{{\mathcal {H}},+}_c$	Maximum output of generator that is located at dam c (MW)
$q^{\mathcal {H}}_{1,c,0}$	Initial production level of generator that is located at dam c (MW)
$R_c$	Ramp rate of generator that is located at dam c (p.u.)
$R_g$	Ramp rate of non-hydroelectric-generation technology g (p.u.)
${\bar{W}}^{\mathcal {H}}_c$	Maximum water level of dam c (acre-feet)
$W^{{\mathcal {H}},-}_c$	Minimum water flow from dam c (acre-feet/h)
$W^{{\mathcal {H}},+}_c$	Maximum water flow from dam c (acre-feet/h)
$W^{{\mathcal {H}},f}_{y,c,h}$	Natural water inflow during hour h of year y into dam c (acre-feet)
$w^{{\mathcal {H}},\textrm{str}}_{1,c,0}$	Initial water level of dam c (acre-feet)
$\Gamma$	Discount rate (p.u.)
$\iota ^+$	Maximum interannual increase in capacity (p.u.)
$\iota ^-_g$	Maximum interannual decrease in capacity of non-hydroelectric-generation technology g (p.u.)
$\kappa ^\textrm{E}_g$	CO$_2$-equivalent-emission rate of non-hydroelectric-generation technology g (t/MWh)
$\kappa ^\textrm{T}$	Carbon-tax rate ($/t)
$\pi _c(\cdot ,\cdot )$	Output of generator that is located at dam c as a function of the water flow through the generator and the water level of its reservoir (MW)
$\rho$	Cost of retiring non-hydroelectric-generating capacity (p.u.)
$\sigma _{y,g}$	Energy-supply requirement during year y for non-hydroelectric-generation technology g (p.u.)
$\tau _{c,c'}$	Water-travel time from dam c to dam $c'$
$\Upsilon _{y,h}$	Weight on hour h of year y (h)
$\Phi _{y,g,n,h}$	Availability factor during hour h of year y of non-hydroelectric-generation technology g that is located at node n (p.u.)

Finally, we define the following set of decision variables.

$f^{\mathcal {L}}_{y,l,h}$	Net power flow during hour h of year y through transmission line l (MW)
$k^{{\mathcal {G}},\textrm{i}}_{y,g,n}$	Total capacity of non-hydroelectric-generation technology g that is available at node n during year y (MW)
$k^{{\mathcal {G}},\rho }_{y,g,n}$	Capacity of non-hydroelectric-generation technology g at node n that is retired during year y (MW)
$k^{\mathcal {L}}_{y,l}$	Total capacity of transmission line l that is available during year y (MW)
$q^{\mathcal {G}}_{y,g,n,h}$	Power output during hour h of year y of non-hydroelectric-generation technology g that is located at node n (MW)
$q^{\mathcal {H}}_{y,c,h}$	Power output during hour h of year y of generator that is located at dam c (MW)
$q^\textrm{U}_{y,n,h}$	Unserved node-n load during hour h of year y (MW)
$w^{{\mathcal {H}},\textrm{g}}_{y,c,h}$	Water flow during hour h of year y through generator that is located at dam c (acre-feet)
$w^{{\mathcal {H}},\textrm{spl}}_{y,c,h}$	Water spilled during hour h of year y from dam c (acre-feet)
$w^{{\mathcal {H}},\textrm{str}}_{y,c,h}$	Water level as of the end of hour h of year y of dam c (acre-feet)
$\mu ^{\mathcal {L}}_{y,l,h}$	Power losses during hour h of year y on transmission line l (MW)

2.2 Model formulation

The capacity-planning model is formulated as:

$$\begin{aligned}&\min \ \sum _{y \in {\mathcal {Y}}} \Gamma ^{y-1} \left\{ \sum _{l \in {\mathcal {L}}} C^{\mathcal {L}} k^{\mathcal {L}}_{y,l} + \sum _{n \in {\mathcal {N}}} \left\{ \sum _{g \in {\mathcal {G}}} \left[ C^{{\mathcal {G}},\textrm{i}}_{y,g,n} \cdot \left( k^{{\mathcal {G}},\textrm{i}}_{y,g,n} + \rho k^{{\mathcal {G}},\rho }_{y,g,n} \right) \right. \right. \right. \nonumber \\&\quad \left. \left. \left. + \sum _{h \in {\mathcal {T}}^\textrm{H}} \Upsilon _{y,h} \cdot \left( C^{{\mathcal {G}},\textrm{V}}_{y,g,n,h} + \kappa ^\textrm{T} \kappa ^\textrm{E}_g \right) q^{\mathcal {G}}_{y,g,n,h} \right] \right. \right. \nonumber \left. \left. + \sum _{h \in {\mathcal {T}}^\textrm{H}} \Upsilon _{y,h} C^\textrm{U} q^\textrm{U}_{y,n,h} \right\} \right\} \end{aligned}$$

(1)

$$\begin{aligned}&\mathrm {s.t.}\ k^{{\mathcal {G}},\rho }_{y,g,n} \ge k^{{\mathcal {G}},\textrm{i}}_{y-1,g,n} - k^{{\mathcal {G}},\textrm{i}}_{y,g,n}; \forall y \in {\mathcal {Y}}, g \in {\mathcal {G}}, n \in {\mathcal {N}}\end{aligned}$$

(2)

$$\begin{aligned}k^{{\mathcal {G}},\textrm{i}}_{y-1,g,n} - \iota ^-_g k^{{\mathcal {G}},\textrm{i}}_{0,g,n} \le k^{{\mathcal {G}},\textrm{i}}_{y,g,n} \le (1+\iota ^+) k^{{\mathcal {G}},\textrm{i}}_{y-1,g,n};&\;\forall y \in {\mathcal {Y}}, g \in {\mathcal {G}}, n \in {\mathcal {N}} \end{aligned}$$

(3)

$$\begin{aligned}&k^{\mathcal {L}}_{y-1,l} \le k^{\mathcal {L}}_{y,l} \le (1+\iota ^+) k^{\mathcal {L}}_{y-1,l}; \forall y \in {\mathcal {Y}}, l \in {\mathcal {L}} \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{n \in {\mathcal {N}}, h \in {\mathcal {T}}^\textrm{H}} \Upsilon _{y,h} q^{\mathcal {G}}_{y,g,n,h} \ge \sigma _{y,g} \sum _{n \in {\mathcal {N}}, h \in {\mathcal {T}}^\textrm{H}} \Upsilon _{y,h} L_{y,n,h}; \forall y \in {\mathcal {Y}}, g \in {\mathcal {G}} \end{aligned}$$

(5)

$$\begin{aligned}\sum _{g \in {\mathcal {G}}}q^{\mathcal {G}}_{y,g,n,h} + \sum _{c \in {\mathcal {H}}^{\mathcal {L}}_n} q^{\mathcal {H}}_{y,c,h} + \sum _{l \in {\mathcal {L}}^\textrm{in}_n} \left( f^{\mathcal {L}}_{y,l,h} - \frac{1}{2} \mu ^{\mathcal {L}}_{y,l,h} \right) + q^\textrm{U}_{y,n,h}&- \sum _{l \in {\mathcal {L}}^\textrm{out}_n} \left( f^{\mathcal {L}}_{y,l,h} + \frac{1}{2} \mu ^{\mathcal {L}}_{y,l,h} \right) = L_{y,n,h}; \forall y \in {\mathcal {Y}}, n \in {\mathcal {N}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(6)

$$\begin{aligned}&0 \le q^{\mathcal {G}}_{y,g,n,h} \le \Phi _{y,g,n,h} k^{{\mathcal {G}},\textrm{i}}_{y,g,n}; \forall y \in {\mathcal {Y}}, g \in {\mathcal {G}}, n \in {\mathcal {N}}, h \in {\mathcal {T}}^\textrm{H}\end{aligned}$$

(7)

$$\begin{aligned}-R_g k^{{\mathcal {G}},\textrm{i}}_{y,g,n} \le q^{\mathcal {G}}_{y,g,n,h} - q^{\mathcal {G}}_{y,g,n,h-1} \le R_g k^{{\mathcal {G}},\textrm{i}}_{y,g,n}; &\;\forall y \in {\mathcal {Y}}, g \in {\mathcal {G}}, n \in {\mathcal {N}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(8)

$$\begin{aligned}&q^{\mathcal {G}}_{y,g,n,0} = q^{\mathcal {G}}_{y-1,g,n,|{\mathcal {T}}^\textrm{H} |}; \forall y \in {\mathcal {Y}}, y > 1, g \in {\mathcal {G}}, n \in {\mathcal {N}} \end{aligned}$$

(9)

$$\begin{aligned}&0 \le q^\textrm{U}_{y,n,h} \le L_{y,n,h}; \forall y \in {\mathcal {Y}}; n \in {\mathcal {N}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(10)

$$\begin{aligned}q^{\mathcal {H}}_{y,c,h} &= \pi _c\left( w^{{\mathcal {H}},\textrm{g}}_{y,c,h},w^{{\mathcal {H}},\textrm{str}}_{y,c,h} \right) ; \forall y \in {\mathcal {Y}}, c \in {\mathcal {H}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(11)

$$\begin{aligned}-R_c Q^{{\mathcal {H}},+}_c \le q^{\mathcal {H}}_{y,c,h} - q^{\mathcal {H}}_{y,c,h-1} \le R_c Q^{{\mathcal {H}},+}_c;&\;\forall y \in {\mathcal {Y}}, c \in {\mathcal {H}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(12)

$$\begin{aligned}q^{\mathcal {H}}_{y,c,0} &= q^{\mathcal {H}}_{y-1,c,|{\mathcal {T}}^\textrm{H} |}; \forall y \in {\mathcal {Y}}, y > 1, c \in {\mathcal {H}}\end{aligned}$$

(13)

$$\begin{aligned}w^{{\mathcal {H}},\textrm{str}}_{y,c,h} &= w^{{\mathcal {H}},\textrm{str}}_{y,c,h-1} + \Upsilon _{y,h} \cdot \left( W^{{\mathcal {H}},f}_{y,c,h} - w^{{\mathcal {H}},\textrm{g}}_{y,c,h} - w^{{\mathcal {H}},\textrm{spl}}_{y,c,h} \right) \nonumber \\&\quad + \sum _{\zeta \in \bar{{\mathcal {H}}}_c} \Upsilon _{y,h-\tau _{\zeta ,c}} \cdot \left( w^{{\mathcal {H}},\textrm{g}}_{y,\zeta ,h-\tau _{\zeta ,c}} + w^{{\mathcal {H}},\textrm{spl}}_{y,\zeta ,h-\tau _{\zeta ,c}} \right) ; &\forall y \in {\mathcal {Y}}, c \in {\mathcal {H}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(14)

$$\begin{aligned}&w^{{\mathcal {H}},\textrm{str}}_{y,c,0} = w^{{\mathcal {H}},\textrm{str}}_{y-1,c,|{\mathcal {T}}^\textrm{H} |}; \forall y \in {\mathcal {Y}}, y > 1, c \in {\mathcal {H}} \end{aligned}$$

(15)

$$\begin{aligned}&0 \le w^{{\mathcal {H}},\textrm{str}}_{y,c,h} \le {\bar{W}}^{\mathcal {H}}_c; \forall y \in {\mathcal {Y}}, c \in {\mathcal {H}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(16)

$$\begin{aligned}&W^{{\mathcal {H}},-}_c \le w^{{\mathcal {H}},\textrm{g}}_{y,c,h} + w^{{\mathcal {H}},\textrm{spl}}_{y,c,h} \le W^{{\mathcal {H}},+}_c; \forall y \in {\mathcal {Y}}, c \in {\mathcal {H}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(17)

$$\begin{aligned}&w^{{\mathcal {H}},\textrm{str}}_{|{\mathcal {Y}}|,c,|{\mathcal {T}}^\textrm{H}|} \ge w^{{\mathcal {H}},\textrm{str}}_{1,c,0}; \forall c \in {\mathcal {H}} \end{aligned}$$

(18)

$$\begin{aligned}&-k^{\mathcal {L}}_{y,l} \le f^{\mathcal {L}}_{y,l,h} \le k^{\mathcal {L}}_{y,l}; \forall y \in {\mathcal {Y}}, l \in {\mathcal {L}}, h \in {\mathcal {T}}^\textrm{H} \end{aligned}$$

(19)

$$\begin{aligned}&\mu ^{\mathcal {L}}_{y,l,h} \ge E_z k^{\mathcal {L}}_{y,l} + D_z f^{\mathcal {L}}_{y,l,h}; \forall y \in {\mathcal {Y}}, l \in {\mathcal {L}}, h \in {\mathcal {T}}^\textrm{H}, z \in {\mathcal {Z}} \end{aligned}$$

(20)

$$\begin{aligned}&\mu ^{\mathcal {L}}_{y,l,h} \ge E_z k^{\mathcal {L}}_{y,l} - D_z f^{\mathcal {L}}_{y,l,h}; \forall y \in {\mathcal {Y}}, l \in {\mathcal {L}}, h \in {\mathcal {T}}^\textrm{H}, z \in {\mathcal {Z}} \end{aligned}$$

(21)

$$\begin{aligned}&k^{{\mathcal {G}},\rho }_{y,g,n} \ge 0; \forall y \in {\mathcal {Y}}, g \in {\mathcal {G}}, n \in {\mathcal {N}} \end{aligned}$$

(22)

$$\begin{aligned}&w^{{\mathcal {H}},\textrm{g}}_{y,c,h}, w^{{\mathcal {H}},\textrm{spl}}_{y,c,h} \ge 0; \forall y \in {\mathcal {Y}}, c \in {\mathcal {H}}, h \in {\mathcal {T}}^\textrm{H}. \end{aligned}$$

(23)

Objective function (1) minimizes the discounted sum of capacity and operational cost over the ordered set, ${\mathcal {Y}}$, of years. Electricity-system operations during each year are captured by an ordered set, ${\mathcal {T}}^\textrm{H}$, of representative operating hours. Objective function (1) contains four cost terms. The first represents the cost of adding transmission capacity—our model does not allow for transmission-capacity retirements. The second term represents the cost of adding or retiring generation capacity. Hydroelectric capacity is fixed but the capacity of other generation technologies can be adjusted. The third term is the cost of operating the generation fleet, which can include a carbon-emission cost. Operating hydroelectric generation is assumed to be costless. The final term is the cost of load curtailment.

Constraint sets (2)–(4) pertain to capacity decisions, which are made annually. The remaining constraints pertain to electricity-system operations, which are made during each representative hour of each year. Constraint set (2) defines generation-capacity retirements in terms of interannual decreases in generation capacity. Constraint sets (3) and (4) impose limits on interannual capacity changes.

Constraint set (5) imposes energy-based renewable-portfolio standards, which can be met only if sufficient capacity renewable-generation capacity is built. Constraint set (6) imposes hourly balance between energy that is supplied and consumed at each electricity-system node. Constraint sets (7) and (8) impose minimum and maximum bounds and ramping limits, respectively, on power output from non-hydroelectric generators. The parameter, $\Phi _{y,g,n,h}$, which appears in the right-hand side of (7) is an hourly p.u. capacity factor, e.g., to capture the variability of weather-dependent renewable generators. Constraint set (9) sets the production level of each non-hydroelectric generator as of the beginning of each year equal to its production as of the end of the previous year. Constraint set (10) limits curtailed load to be no greater than demand.

Constraint set (11) gives hydroelectric generation as a function of water flow and head level, which is related to the water level of the dam. Constraint set (12) imposes ramping limits on the hydroelectric generators. Constraint set (13) sets the production level of each hydroelectric generator as of the beginning of each year equal to its production as of the end of the previous year. Constraint set (14) enforces hourly water balance for each dam. The ending hour-h water level of a dam is defined as the sum of the hour-$(h-1)$ water level, natural inflows, and inflows from upstream dams, less the total of water that is released through the generator and for spillage. Constraint set (15) sets the water level of each dam as of the beginning of each year equal to its water level as of the end of the previous year. Constraint set (16) imposes minimum and maximum water-level limits on each dam. Constraint set (17) imposes minimum and maximum limits on water flows through each dam. Constraint set (18) forces the ending water level of each dam to be no less than its initial level.

Constraint set (19) imposes flow limits on transmission lines. Constraint sets (20) and (21) define transmission losses on each line as a piecewise-linear function of line capacity and flow. We use a pipeline model of the transmission network. However, our approach to modeling transmission losses can approximate a linearized power-flow model (Ahlhaus and Stursberg 2013). Constraint sets (22) and (23) impose non-negativity on generation-capacity retirements and water flows.

3 Model reductions and evaluation metric

We examine three types of model reductions that relate to representing the efficiency of hydroelectric generators through the choice of the form of $\pi _c(\cdot ,\cdot )$, simplifying the cascaded river system, and the selection of representative operating hours.

3.1 Functional Form of $\pi _c(\cdot ,\cdot )$

The function, $\pi _c(\cdot ,\cdot )$, can be complex and non-linear, especially if the plant has a large reservoir, e.g., due to head effects (Diniz et al. 2007; Hidalgo et al. 2014; Kong et al. 2019; Hunter-Rinderle and Sioshansi 2021). A common simplification to maintain tractability of capacity-planning models is to use a linear approximation of $\pi _c(\cdot ,\cdot )$. We examine different approximations of $\pi _c(\cdot ,\cdot )$ and propose a data-driven method that captures head effects.

We consider the following three functional forms of $\pi _c(\cdot ,\cdot )$, $\forall c \in {\mathcal {H}}$:

$$\begin{aligned}{} {} \pi _c\left( w^{{\mathcal {H}},\textrm{g}}_{y,c,h},w^{{\mathcal {H}},\textrm{str}}_{y,c,h} \right)& = \beta _{0,c} + \beta _{1,c} w^{{\mathcal {H}},\textrm{g}}_{y,c,h} + \beta _{2,c} w^{{\mathcal {H}},\textrm{str}}_{y,c,h} + \beta _{3,c} \cdot \left( w^{{\mathcal {H}},\textrm{g}}_{y,c,h} \right) ^2 \\&+ \beta _{4,c} \cdot \left( w^{{\mathcal {H}},\textrm{str}}_{y,c,h} \right) ^2 + \beta _{5,c} w^{{\mathcal {H}},\textrm{g}}_{y,c,h} w^{{\mathcal {H}},\textrm{str}}_{y,c,h}; \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \pi _c\left( w^{{\mathcal {H}},\textrm{g}}_{y,c,h},w^{{\mathcal {H}},\textrm{str}}_{y,c,h} \right) = \beta _{0,c} + \beta _{1,c} w^{{\mathcal {H}},\textrm{g}}_{y,c,h} + \beta _{2,c} w^{{\mathcal {H}},\textrm{str}}_{y,c,h}; \end{aligned}$$

(25)

and:

$$\begin{aligned} \pi _c\left( w^{{\mathcal {H}},\textrm{g}}_{y,c,h},w^{{\mathcal {H}},\textrm{str}}_{y,c,h} \right) = \beta _{1,c} w^{{\mathcal {H}},\textrm{g}}_{y,c,h}. \end{aligned}$$

(26)

Functional form (24) is the most complex, in that it captures non-linearities through quadratic and bi-linear terms. Form (25) is linear but captures head effects, through its dependence on the water level of the reservoir. Form (26) is linear and simpler than (25) because head effects are neglected completely by the former.

3.2 Cascaded river system

Our base case assumes non-zero times for water to flow from a dam to the one that is immediately downstream. Assuming zero water-travel times decouples (14) between different dams and hours. Model (1)–(23) can be simplified further if we assume that small dams have no water-storage capacity. Such an assumption simplifies the model because the $w^{{\mathcal {H}},\textrm{str}}_{y,c,h}$ variables for dams with no water-storage capacity can be eliminated and (14) and (16) for those dams can be replaced by:

$$\begin{aligned}{} & {} \Upsilon _{y,h} \cdot \left( w^{{\mathcal {H}},\textrm{g}}_{y,c,h} + w^{{\mathcal {H}},\textrm{spl}}_{y,c,h} \right) = \Upsilon _{y,h} \cdot \left( W^{{\mathcal {H}},f}_{y,c,h} \right) + \sum _{\zeta \in \bar{{\mathcal {H}}}_c} \Upsilon _{y,h} \cdot \left( w^{{\mathcal {H}},\textrm{g}}_{y,\zeta ,h} + w^{{\mathcal {H}},\textrm{spl}}_{y,\zeta ,h} \right) ;\nonumber \\{} & {} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \forall y \in {\mathcal {Y}}; h \in {\mathcal {T}}^\textrm{H}. \end{aligned}$$

(27)

In addition to it being more tractable, a model that replaces (14) and (16) with (27) is more amenable to the application of relaxation and decomposition techniques than a model with (14) and (16) is.

3.3 Selection of periods to represent system operations

The third model reduction that we explore is using hierarchical clustering to select a subset of days to represent power- and hydroelectric-system operations over each case-study year. Other clustering techniques (e.g., distribution-, density-, or centroid-based) can and are used in practice (Nahmmacher et al. 2016; Poncelet et al. 2017; Liu et al. 2018a; Boffino et al. 2019). Hierarchical clustering is used fairly commonly, though, meaning that our work examines the properties of a popular approach to selecting representative operating periods. Hierarchical clustering requires a metric between days and between clusters. To define such a metric, we represent each day as a vector, each of which consists of hourly load, solar-availability, and wind-availability features for each transmission node and hourly natural-water-inflow features for each dam.

We use Euclidean distance and minimax linkage as the metrics between days and clusters, respectively (Bien and Tibshirani 2011). Minimax linkage provides each cluster’s prototype, which is the day (from the unclustered data) that is closest to the cluster center. We use each cluster prototype in (1)–(23) to represent the days that are in the cluster and set the cluster weight equal to the number of days in the cluster. Using cluster prototypes in capacity planning tends to outperform using cluster centroids (Nahmmacher et al. 2016). Maintaining chronology of the prototypes captures some seasonal variability in natural water inflows.

We investigate eight clustering methods, which differ by the features that are used and how they are scaled. We examine two sets of features. The first consists of the aforementioned features (loads, solar and wind availabilities, and natural water inflows). The second consists of the aforementioned features except for natural water inflows, which are replaced by the day of the year.

We examine four approaches to scaling features. The first scales each feature linearly to the unit interval (i.e., minimum and maximum values for each feature are scaled to 0 and 1, respectively). The second selects the summer and winter days with the highest WECC-wide load as two representative days. The remaining representative days are selected by clustering the remaining days of the underlying data, using linear scaling. This technique is premised on the notion that peak-load days are important for capacity planning (Merrick 2016; Cohen et al. 2019). The third approach is the same as the first with ex post linear scaling of the electricity demands and natural water inflows of the prototypes so that total annual electricity demand and water inflows of the clustered and unclustered data are equal (Nahmmacher et al. 2016). The fourth technique uses capacity-based importance scaling and involves a two-step process (Nahmmacher et al. 2016; Sun et al. 2019; Limpens et al. 2019). We begin by applying the first scaling technique to select 30 representative operating days and solve (1)–(23) to determine the resultant optimal investments. Wind- and solar-availability features for each transmission node are scaled based on the proportion of total wind and solar capacity that is installed at each node with the 30 representative operating days. Natural water inflows and the day of the year (depending upon the set of features that is used) are scaled based on the capacity of each hydroelectric unit. Loads are scaled to the unit interval based on minimum and maximum values corresponding to each transmission node. These scaled values are multiplied by the maximum load that is observed at each node.

3.4 Reduction-evaluation metric

A common approach to assessing the quality of a solution that is obtained from a reduced model is to compare objective-function values of the full and reduced models (Merrick 2016). We use economic regret, which is computed using a three-step process, as a performance metric instead (Ramírez-Sagner and Muñoz 2019). First, a variant of (1)–(23) that has a model reduction is solved. Next, the investment decisions that are obtained from the reduced model are fixed and (1)–(23) is re-solved with the model reduction removed. Finally, the difference between the resultant objective-function value and the optimized objective-function value that is obtained from solving (1)–(23) without the model reduction is computed. This difference measures the economic cost (regret) of using the reduced model for investment planning.

4 Case-study data and implementation

Our case study optimizes, over a 20-year horizon that begins as of 2015, capacity expansion for Western Electricity Coordinating Council (WECC). WECC gets about a quarter of its electric energy and generating capacity from hydroelectric resources. The Columbia River system provides about half of WECC’s hydroelectric capacity.¹ Most of the case-study data are gathered from WECC’s 2024 and 2026 Production Cost Model Common Cases (PCMCCs).² Hourly load profiles are derived from 2026 PCMCC, which provides actual and simulated load profiles for 2009 and 2026, respectively. We use linear load-growth factors to interpolate and extrapolate these data to generate hourly load profiles for each case-study year. We assume a $$5\,000$/MWh penalty for load curtailment, a 7% annual discount rate, and 30% and 5% (on an energy basis) renewable-portfolio standards for wind and solar, respectively, during the final year of the optimization horizon (GE Energy 2010; Liu et al. 2018b).

4.1 Non-hydroelectric-generator data

Six generation technologies can have capacity added: coal-fired; natural-gas-fired steam (NGS), open-cycle (NGOC), and combined-cycle (NGCC); solar photovoltaic (PV); and wind units. We allow retirement of fossil-fueled but not renewable generation. We model hydroelectric, nuclear, geothermal, and biomass units, but do not allow capacity additions or retirements of these technologies. We use 2024 PCMCC to set starting capacity levels for all of the generation technologies. We assume an 80% availability factor for nuclear, geothermal, and biomass units. We limit ramp rates to 0.3 for all technologies, except for NGOC, PV, wind, and hydroelectric units that are not in the Columbia River system, which are assumed to have a ramp rate of 1.0 (Ibanez et al. 2014). We allow up to 30% interannual increase in generation-technology and transmission-line capacities and at most 20% interannual generation-capacity retirements. No energy storage, other than hydroelectric reservoirs, is considered.

Baseline generator-cost data, to which we apply learning rates and regional multipliers, are summarized in Table 1. Generator cost data are obtained from the works of Black and Veatch (2012); E3 (2012), to which interested readers are directed for complete details. Baseline PV and wind capital costs decrease to $$2\,226$/kW and $$1\,804$/kW, respectively, by the end of the optimization horizon. Capital and fixed operation and maintenance (O&M) costs at individual electricity-system nodes are up to 20% higher or 15% lower than baseline costs. Generator-retirement costs are 5% of capital cost. Generator-operating costs are computed using monthly estimates of coal and natural-gas prices for different WECC regions, which are taken from 2024 PCMCC, and the heat rates and variable O&M costs that are reported in Table 1. We assume a $58/t carbon tax, which is levied on carbon emissions from combusting fossil fuels to generate electricity. Hourly available wind and solar generation, which is assumed to be costless, is obtained from 2026 PCMCC. These data are for a single year only. Thus, we apply the same availability profiles for all case-study years.

Table 1 Baseline generator-cost data for case study

4.2 Transmission data

Figure 1 shows the assumed 15-node topology of the WECC transmission network. Transmission-network data are obtained from WECC’s 2034 Reference Case. The states of Washington and Oregon are aggregated into the Pacific Northwest node. 2034 Reference Case includes different transmission limits that depend upon season and the direction of flow. For simplicity, we use the maximum capacity that is reported in the dataset for each line. We assume that adding transmission capacity incurs a cost of $$614\,000$/MW (Mason and Curry 2012). In addition to modeling the 15-node network that is shown in Fig. 1, some of our cases model a three-zone simplification of the transmission system. The boundaries of the three zones are shown in Fig. 1.

Fig. 1

15-node and three-zone transmission-network models for the case study

4.3 Hydroelectric data

Figure 2 shows the topology of the 35-dam Columbia River system, which is aggregated minimally (a dam name that is followed by ‘$+x$’ indicates that the dam aggregates x additional dams). System-topology data are obtained from Northwest Power and Conservation Council³ and Bonneville Power Administration. All water flows to Bonneville, from which it flows into Pacific Ocean. Circles in the figure indicate hydroelectric generators, squares indicate significant reservoirs whereas dams without squares are run-of-river reservoirs that have at most 3.5 hours of storage, and crosses indicate dams with non-trivial natural water inflows. The red dashed rounded rectangles indicate the boundaries of six-dam aggregations that are used in some of our analysis. Dashed blue lines indicate state and provincial boundaries. We assume a one-hour water-flow time between upstream and downstream dams.

Fig. 2

Topology of Columbia River. Circles indicate hydroelectric generators, squares indicate significant reservoirs, crosses indicate dams with natural water inflows, and all water flows towards Bonneville. Red dashed rounded rectangles indicate boundaries of six-dam aggregations of the system. Dashed blue lines indicate state and provincial boundaries

Historical water-inflow, -outflow, and -storage and power-output data are obtained from United States Army Corps of Engineers⁴ and Government of Canada.⁵ Lower and upper bounds on water flows and reservoir levels are set to the minimum and maximum values that are observed in the historical data between 1999 and 2018. Historical water-inflow data for the same years, which exhibit seasonal and inter-annual variability, are applied to the 20-year case-study horizon.

Hydroelectric units at a transmission node that are not in the Columbia River system are aggregated into a single generic hydroelectric plant. We assume that such plants have fixed generation profiles, which are based on the historical generation profile of Lower Granite and scaled based on the aggregated nameplate capacity of the units. Lower Granite does not have a large upstream reservoir, meaning that its output reflects seasonal and annual variations of natural water inflows.

Natural-water-inflow features of dams are treated differently when applying hierarchical clustering to produce representative operating periods (cf. Sect. 3.3). Each dam that is part of the Columbia River system is represented by its natural water inflow that is in the historical data. Aggregated dams that are not part of the Columbia River system are represented by their generation profiles.

4.4 Case-study implementation

Depending upon which of (24), (25), or (26) is used for $\pi _c(\cdot ,\cdot )$, (1)–(23) can be linear or non-linear. Our case studies are implemented on a system with 270 GB of memory and two Intel Xeon E5-2697 v4 processors, each of which has 18 2.30-GHz cores.

The linear variants are programmed with Python 2.7 and solved using the barrier-method algorithm in Gurobi 7.5.1 with crossover disabled. Gurobi’s presolver is disabled or set to conservative and the homogeneous-barrier-method algorithm is used and presolver aggregation is disabled in some cases to improve algorithm performance. The default optimality tolerance of $10^{-8}$ is used. However, in some cases Gurobi stops barrier iterations close to but before reaching this tolerance.

The non-linear variants are programmed with Pyomo and solved using the interior/direct algorithm in Knitro 12.0.0 with HSL MA57. Knitro is given a solution of a corresponding linear variant as an initial point.

5 Case-study results

5.1 Functional Form of $\pi _c(\cdot ,\cdot )$

Figure 3 shows historical hourly power-output and water-flow data from 1999–2018 for Grand Coulee, which is the largest dam and reservoir on Columbia River. The observations are categorized by the reservoir’s water level. Overlaid on the scatterplot are ordinary-least-square (OLS) estimates of (24)–(26) to the underlying data. Two fits of (24) and (25), which correspond to different reservoir levels, are shown.

Fig. 3

Scatterplot of historical hourly power-output and water-flow data for the Grand Coulee reservoir and fits of (24)–(26) to the data

The adjusted $R^2$ of the OLS estimates of (24) and (25) are 0.9894 and 0.9862, respectively. Thus, (25) provides a relatively good linear approximation of (24) and can capture head effects. However, Fig. 3 shows deviations between (25) and the underlying observations with low head levels or water flows. Functional form (26) has the worst fit to the data, does not capture head effects, and is akin to the common linearization method that is used, wherein the water level is assumed fixed over the full optimization horizon (Maluenda et al. 2018; Ramírez-Sagner and Muñoz 2019).

We examine the effects of using (25) and (26) as linear approximations of (24) by computing economic regret, assuming that (24) is the true functional form of $\pi _c(\cdot ,\cdot )$ and (25) and (26) are reductions. We conduct this comparison using the three-zone transmission network, six-dam river system, and all 8760 hours of each year of the optimization horizon. The objective-function value with using (24) is $622.317 million. The objective-function values with using (25) and (26) to fix investments and re-solving the model with (24) are $622.441 million and $622.502 million, respectively. These yield economic regrets of 0.02% and 0.03%, respectively, with using each of (25) and (26) in place of (24). Thus, the choice of linear approximation has minuscule effects on capacity planning.

Figure 4 shows natural water inflows into and the optimized storage level of the Grand Coulee reservoir with the three different forms of $\pi _c(\cdot ,\cdot )$. The figure shows a significant difference in reservoir operations between (26) and the other two forms. Each of (24) and (25) capture head effects whereas (26) does not. Thus, the model keeps a higher reservoir level with (24) and (25) to increase hydroelectric-plant efficiency whereas it operates over a much wider range with (26). Given these results, we find (25) to be a good approximation of (24) that yields a linear variant of (1)–(23), low economic regret, and a reservoir-operation profile that is close to that which is obtained with (24). As such, we use (25) as the functional form of $\pi _c(\cdot ,\cdot )$ throughout our subsequent analysis.

Fig. 4

Natural water inflows into and optimized storage level of the Grand Coulee reservoir with different functional forms of $\pi _c(\cdot ,\cdot )$

5.2 Water-travel times and water-storage capacities of hydroelectric plants

Our base case assumes that water takes one hour to flow from a dam to the one that is immediately downstream, meaning that it can take nearly a day for water to flow from some dams to Pacific Ocean. Using the three-zone transmission network, 35-dam river system, and all 8760 hours of each year of the optimization horizon, we examine the effects of assuming zero water-travel time and that run-of-river dams have no water-storage capacity. Assuming zero water-travel times between adjacent dams yields zero economic regret, indicating that for the Columbia River system, water-flow times have no bearing on WECC capacity-planning decisions. Next, we simplify (1)–(23) further by assuming that run-of-river dams, of which there are 27 (cf. Fig. 2) have no water-storage capacity. This model reduction yields economic regret of 0.12%. Hereafter, we assume zero water-travel times but model water-storage capacity for all dams.

5.3 Selection of periods to represent system operations

To define a metric between days and clusters we represent each day as a vector. Each vector consists of $24 \cdot |{\mathcal {N}}|$ load, solar-availability, and wind-availability features, up to $24 \cdot |{\mathcal {H}}|$ natural-water-inflow features for each dam with non-trivial natural water inflows that is part of the Columbia River system, and 24 generation features for the hydroelectric plants that are not part of the Columbia River system. Thus, the vector that describes each day is in up to $24 \cdot (1+3\cdot |{\mathcal {N}}|+|{\mathcal {H}}|)$-dimensional space.

5.3.1 Cluster properties

Figures 5, 6, 7, 8 contrast the clustering techniques by showing thirty clusters that are selected for the year 2024 with three transmission nodes, a six-dam representation of the Columbia River system, and different combinations of features and scaling methods. The principal difference between the cluster choices is that having natural water inflows as a feature yields clusters that combine the beginning and end of the year and clusters that span seasons (cf. Figs. 5 and 6). Nevertheless, seasonal differences in natural water inflows yield some chronology in the resultant clusters. Having day of the year as a feature yields clusters that are chronologically closer (cf. Figs. 7 and 8).

Fig. 5

Thirty clusters selected for 2024 with three transmission nodes and six-dam representation of the Columbia River system using all features and linear scaling

Fig. 6

Thirty clusters selected for 2024 with three transmission nodes and six-dam representation of the Columbia River system using all features and capacity-based scaling

Fig. 7

Thirty clusters selected for 2024 with three transmission nodes and six-dam representation of the Columbia River system using day-of-year feature and linear scaling

Fig. 8

Thirty clusters selected for 2024 with three transmission nodes and six-dam representation of the Columbia River system using day-of-year feature and capacity-based scaling

5.3.2 Evaluating clusters

One approach to evaluating clustering techniques is to examine features, e.g., load- or renewable-availability-duration curves (Liu 2016; Merrick 2016; Nahmmacher et al. 2016; Limpens et al. 2019). This approach is premised on the notion that clustering performance is governed by matching the features of the clustered and unclustered data. However, matching features does not ensure that the clustered data yield desirable investment decisions (Teichgraeber and Brandt 2019). Thus, we focus our evaluation on comparing the performance of (1)–(23) with clustered and unclustered data.

Figure 9 shows differences in the values of (1) that are obtained from solving (1)–(23) with different numbers of clusters, compared to if it is solved using unclustered data. Figure 9 assumes three transmission nodes and a six-dam Columbia River system and the clustering methods are applied to each of the 20 case-study years separately. Increasing the number of clusters tends to reduce the difference in the optimized value of (1) between using clustered and unclustered data. Capacity-based scaling performs the best vis-à-vis the value of (1).

Fig. 9

Difference in optimized value of (1) from solving (1)–(23) with clustered data as opposed to solving it with unclustered data assuming three transmission nodes and six-dam representation of the Columbia River system

Figure 9 suggests that the clustered data introduce relatively small errors no greater than 6% even if each year is represented using only 10 days. This is a misleading interpretation of Fig. 9, because the clustered data are limited in capturing system operations under extreme conditions. As such, (1) does not provide an accurate representation of actual operation costs, especially if load must be curtailed. Figure 9 shows that using clustered data tends to underestimate the true value of (1) with unclustered data. This underestimation arises from capacity underinvestment if the clustered data provide a poor representation of the unclustered data.

Figure 10 summarizes economic regrets from using clustered data in (1)–(23). Figures 9 and 10 show very different magnitudes of the two performance metrics. Selecting 10 days to represent each year with natural water inflows as a feature and simple linear scaling yields the largest objective-function-value difference of 6% in Fig. 9. Yet, this cluster choice yields the highest economic regret of over 45% in Fig. 10. This economic regret arises due to less investment with the clustered data—a total of 66.8 GW and 34.8 GW of natural-gas-fired-generation and transmission capacity, respectively, as opposed to 101.7 GW and 41.1 GW with the unclustered data. As such, nearly 121.4 TWh of load is curtailed at a discounted cost of $315.8 billion if the optimized investments that are determined with the clustered data are undertaken. Conversely, if the unclustered data are used to determine investments, only 1.5 TWh of load is curtailed at a discounted cost of $3.9 billion.

Fig. 10

Economic regret from solving (1)–(23) with clustered data as opposed to solving it with unclustered data assuming three transmission nodes and six-dam representation of the Columbia River system

Figures 11 and 12 reinforce the limitation and benefit of using (1) and economic regret, respectively, as metrics for cluster-performance evaluation. Figure 11 summarizes the breakdown of the optimized value of (1) if (1)–(23) is solved with different numbers of clusters. The clusters are obtained using natural water inflows as a data feature and linear scaling and the case assumes three transmission nodes and a six-dam representation of the Columbia River system. The figure shows that the optimized objective-function value and its constituent components are very similar with different numbers of clusters. This finding is keeping with the results that are shown in Fig. 9.

Fig. 11

Breakdown of optimized value of (1) from solving (1)–(23) with different numbers of clusters that are obtained using natural water inflows as a data feature and linear scaling, assuming three transmission nodes and six-dam representation of the Columbia River system

Figure 12 summarizes the components of economic regret for the same set of clusters that are summarized in Fig. 11. Thus, Fig. 12 can be interpreted as giving the actual costs that are incurred if investment decisions are undertaken using each set of clusters to solve (1)–(23) and the resultant system is operated during each full year. With the exception of load-curtailment cost, the actual costs that are summarized in Fig. 12 are similar with different numbers of clusters and are similar to the values that are summarized in Fig. 11. The key difference between the costs that are summarized in Figs. 11 and 12 is that load-curtailment cost is much higher with fewer clusters. Moreover, load curtailment is not revealed if too few clusters are included in (1)–(23). Load curtailment is not revealed with a limited number of clusters because the clusters do not capture extreme events (e.g., days with high demand or low wind, solar, or hydroelectricity availability).

Fig. 12

Breakdown of components of economic regret from solving (1)–(23) with different numbers of clusters that are obtained using natural water inflows as a data feature and linear scaling, assuming three transmission nodes and six-dam representation of the Columbia River system

Figure 12 shows that underinvestment and resultant load curtailment persists. Simple linear scaling with 60 or fewer days results in underinvestment and significant load curtailment compared to unclustered data. Conversely, if capacity-based scaling is employed, 30 representative days are sufficient to yield investment and load-curtailment levels that are comparable to using unclustered data (Fig. 13 summarizes the breakdown of the components of economic regret for these sets of clusters). Specific generation and transmission investments have some variations between selecting 30, 60, and 120 days using capacity-based scaling. Nevertheless, economic regrets are very close to zero among all of these cases, which suggests that (1)–(23) with unclustered data has many near-optimal solutions with different capacity mixes.

Fig. 13

Breakdown of components of economic regret from solving (1)–(23) with different numbers of clusters that are obtained using natural water inflows as a data feature and capacity-based scaling, assuming three transmission nodes and six-dam representation of the Columbia River system

A second finding from comparing Figs. 9 and 10 is different relative performance of the clustering techniques. For instance, Fig. 9 suggests that if selecting 60 days, linear scaling with ex post load and water-inflow adjustments provides the worst-performing clusters. However, Fig. 10 shows that with respect to economic regret this clustering technique is second only to capacity-based scaling. These comparisons between Figs. 9 and 10 demonstrate the limitations of relying upon the value of (1) alone in evaluating the performance of clustering techniques.

With respect to economic regret, the first three scaling methods perform similarly (cf. Fig. 10). Capacity-based scaling has a clear performance advantage, especially if fewer than 120 representative days are being selected. Capacity-based scaling shows no significant difference between using natural water inflows and day of the year as data features. The two features perform similarly because both help to maintain chronology of the clusters (cf. Figs. 6 and 8). If capacity-based scaling is used, economic regret is near-zero with 60 or more days and only 0.5% with 30 days. Economic regret increases to up to 6% with fewer than 30 days.

A final comparison that we conduct, but exclude for sake of brevity, is the water-level profiles of reservoirs. Although clustered data yield some differences in water levels compared to unclustered data, the overall seasonal and interannual trends are captured. This is due to the clusters capturing seasonal chronology (cf. Figs. 5–8). Increasing the number of clusters reduces the differences in the resultant water-level profiles from using clustered and unclustered data.

5.4 Scaling performance of (1)–(23)

Figure 14 summarizes economic regrets from using our clustering methods with the full transmission and river-system topologies. Because the first three scaling methods perform similarly with the reduced networks, we consider only linear and capacity-based scaling. Figure 14 shows that our clustering methods scale well to a larger system, despite each day having significantly more features. As is the case with the smaller networks, selecting 60 operating days with capacity-based scaling yields economic-regret values of 0.47% or 0.58%, depending upon the features that are used. These economic-regret values increase to 1.15% and 1.45% if selecting 30 operating days.

Fig. 14

Economic regret from solving (1)–(23) with clustered data as opposed to solving it with unclustered data assuming the full transmission and river-system topologies

Table 2 summarizes how (1)–(23) scales with different numbers of transmission nodes, dams, and operating days. The reported solution times include reading input data and outputing model results. There are order-of-magnitude computation-time savings from reducing the number of operating days or nodes and dams that are modeled.

Table 2 Size of (1)–(23) and solution times with different model reductions, using natural water inflows as a data feature and linear scaling

6 Conclusions and discussion

We examine capacity planning for power systems with hydroelectric, thermal, and renewable generators. Such modeling is difficult, because of the need to capture reservoir water levels and seasonal and interannual variability of natural water inflows. We explore the use of three model reductions—simplifying the representation of (i) hydroelectric-plant efficiency, (ii) reservoirs and water-travel times, and (iii) system operations—to improve model tractability. Using economic regret as a metric, we demonstrate that these reductions can yield significant computation-time savings with little loss of model fidelity. The model reductions provide investments that are not unduly expensive and do not sacrifice system security, i.e., unserved energy is similar between the reduced and full models. Reservoir water levels of the hydroelectric plants are similar between the reduced and full models (Yagi 2020).

Although it is used commonly in the literature, we demonstrate the shortcomings of assessing the performance of a capacity-planning model solely based on comparing objective-function value. Specifically, objective-function value may not reveal the ‘brittleness’ of the system under extreme conditions. For instance, if only 10 days are used to represent system operations, those 10 days may not capture extremes or significant load curtailment that occur due to underinvestment. Economic regret is a performance metric that is robust to this type of effect.

The performance of the reductions may be specific to our case study and should be studied before being applied to other systems. For instance, we consider simple water-level constraints on reservoirs. More complex constraints (e.g., due to wildlife preservation, flood control, or irrigation) may interact with the reductions that we study. Our work demonstrates reductions that should be the foci of modelers who are undertaking these types of capacity-planning exercises. Among the model reductions that we examine, we surmise that the simplification of hydroelectric-plant efficiency and the selection of representative operating days is more generalizable to other system topologies and designs. Conversely, the detail with which a cascaded hydroelectric system should be represented may be more sensitive to its underlying topology.

Our work examines a deterministic planning model with continuous variables. Explicit uncertainty representation or discrete decisions (e.g., lumpy investments) may be important in some settings. To the extent that our proposed reductions improve tractability, they should ease including such uncertainties or discrete decisions in planning models.