1 Introduction

Pension schemes provide an important economic function in the society. They provide people with regular incomes after retirement from the productive labor workforce and incentivize sustainable consumption over a life time. With regards to benefit and contribution policies, there are two main categories of pension schemes: defined benefit schemes (DB schemes) and defined contribution schemes (DC schemes). In a DB scheme, pension benefits to be paid by the scheme after retirement are pre-defined. In this case, scheme members only need to pay contributions regularly and bear no investment risk. The scheme sponsor bears the risk of bad investment performance and may fail to deliver the benefits. In a DC scheme, the amount of contributions payable by scheme members is pre-determined rather than the benefit payments. The benefits depend on the size of the accumulated contributions and the scheme’s investment performance, and are uncertain until the retirement time. The sponsor bears no investment risk as its only responsibility is to pay joint contributions, while the employees face risks originating from market fluctuations. Historically, pension schemes were dominated by PAYGO DB schemes. However, DC schemes have become increasingly popular over the last decades. It is a consequence of the financial unsustainability of the DB schemes, especially in the presence of an ageing population.

In this paper, we focus our attention on DC schemes and study the optimal investment strategy for DC schemes from a theoretical point of view. In a DC scheme, members’ benefits rely heavily on the scheme’s investment performance. Therefore, it is crucial to study the optimal portfolio selection problem such that the scheme delivers satisfactory benefits at retirement. Gao (2008) used the dual approach to solve the optimal asset allocation problem for a DC scheme in a market with stochastic interest rates. Battocchio and Menoncin (2004) studied the optimal asset allocation problem for a DC pension plan manager who maximizes expected exponential utility of final wealth considering salary and inflation risk. However, Gao (2008) and Battocchio and Menoncin (2004) supposed that scheme members have full trust in the manager and do not take the attractiveness and effectiveness of the scheme management into consideration. Classically, DC schemes do not provide downside protections, leaving their members exposed to the risk of receiving insufficient benefits after retirement. DC schemes that do provide a minimum guarantee on the benefits however can also be more attractive to employers. Boulier et al. (2001) studied the optimal investment problem for a DC scheme in a framework with stochastic interest rates where a downside protection for the member’s benefits is provided. They obtained the optimal investment strategy which maximizes the expected terminal utility from the surplus between the scheme’s final wealth and the downside guarantee by applying the dynamic programming principle. Deelstra et al. (2003) extended their model to the case where the contribution process is stochastic. They modeled the manager’s remuneration as an increasing concave function of the surplus between the scheme’s terminal wealth and the minimum guarantee. The martingale method is used to find the optimal investment strategy that maximizes the manager’s expected utility from remuneration. Han and Hung (2012) further developed the model to consider inflation and labor income risks. They introduced a minimum guarantee on the purchase of an inflation-indexed annuity at retirement. To hedge the inflation risk, they included an inflation-indexed bond in the investment portfolio. Studies like Guan and Liang (2014), Chen et al. (2017) and Tang et al. (2018) investigated asset allocation problems for DC schemes with various types of guarantees on the terminal wealth. Nonetheless, these papers did not take the members’ stochastic mortality behavior into consideration and ignored the mortality risk.

In the context of insurance, life insurers also often include a number of guarantees in their products. Some of these products have similar downside protection structures to the DC schemes with minimum guarantees. For example, a guaranteed annuity option (GAO) gives its policyholder the right to convert the accumulated funds to a life annuity when the policy matures at a fixed conversion rate. A variable annuity (VA) with a guaranteed minimum maturity benefit (GMMB) rider guarantees the policyholder a certain minimum benefit at its maturity. A policyholder of a guaranteed minimum income benefit (GMIB) contract receives at least a pre-specified stream of lifetime income after annuitizing the VA. A guaranteed minimum withdrawal benefit (GMWB) ensures a steady stream of periodical withdrawals regardless of investment performance. There is a rich literature on the fair valuation and risk management of life insurance contracts with embedded guarantees, for example, Boyle and Hardy (2003), Pelsser (2003), Bauer et al. (2008), Van Haastrecht et al. (2010), Hyndman and Wenger (2014), Shen et al. (2016), Mamon et al. (2021) and Huang et al. (2022). Stochastic optimal control problems for insurance policies with various forms of guaranteed minimum benefits have been studied in the literature. See, for example, Dai et al. (2008), Chen and Forsyth (2008), Steinorth and Mitchell (2015), Horneff et al. (2015), Forsyth and Vetzal (2014), Lin et al. (2017), Wu et al. (2020), MacKay and Ocejo (2022). Dai et al. (2008) developed a singular stochastic control model for pricing GMWB contracts without considering mortality risk. Assuming the policyholder is fully rational, they investigated the optimal withdrawal strategy that maximizes the expected discounted value of the annuity policy. MacKay and Ocejo (2022) studied an optimal portfolio selection problem in a non-participating GMMB contract where the guaranteed amount is deterministic. The objective is to maximize the policyholder’s expected utility subject to a fair pricing constraint. Lin et al. (2017) studied the optimal investment strategies for an insurer that offers defaultable and fully protected participating contracts with a constant interest rate. The minimum guarantee appears as a constraint on the portfolio wealth. Wu et al. (2020) extended the work of Lin et al. (2017) studying the optimal management of participating contracts with mortality risk under a stochastic interest rate model. However, they used a deterministic force of mortality and ignored that the force of mortality can itself be stochastic and be exposed to shocks. In our work, we introduce life annuities as the guarantee target and incorporate stochastic interest rate and force of mortality. The annuity price and thus the value of the minimum guarantee are contingent on members’ expected remaining lifetime and future risk-free interest rate.

According to Cocco and Gomes (2012), the average life expectancy of a 65-year-old US (UK) male increases by 1.2 (1.5) years per decade. Consequently, a DB scheme for those populations in the US for example would have needed 29% more wealth in 2007 than in 1970. The increase in life expectancy in the UK is largely responsible for the underfunding of pay-as-you-go state pensions, defined benefit company pensions, and state-sponsored pension plans. Biffis and Blake (2014) mentioned that the estimate of the global amount of annuity- and pension-related longevity risk exposure amounts to $15 trillion. However, most articles studying optimal portfolio strategies for DC schemes focus on the financial risks (for example, interest rate risk, inflation risk) and leave longevity risk aside. Those studies that take longevity risk into account, mainly focus on optimal asset allocation problems for DB pension schemes, using time-varying but deterministic forces of mortality to implement longevity risk into their models. This approach ignores the fact that the force of mortality can itself be stochastic. In our work, we study an optimal portfolio problem for a DC scheme within the framework of a stochastic force of mortality as well as stochastic interest rates. Force of mortality, or the instantaneous rate of mortality, is often used within the context of survival analysis in actuarial science. Classical work, including De Moivre (1725) and Gompertz (1825), has studied deterministic force of mortality models. However, more recent research on mortality risk modeling considers discrete-time and continuous-time models with stochastic force of mortality. It is straightforward to model the force of mortality in a discrete-time setting since the mortality data are usually reported annually. Lee and Carter (1992) were among the earliest to model and estimate the force of mortality using time series methods. Other discrete-time models include, for example, the CBD model and Renshaw-Haberman cohort model (Cairns et al. 2006; Renshaw and Haberman 2006). Some studies, such as Milevsky and Promislow (2001) and Dahl (2004), found similarities in the methodology between interest rates and force of mortality; for example, that both are positive and have a term structure. Thus, drawing from the interest rate modeling literature, diffusion processes and jump processes are now used to study the impact of the force of mortality. In particular, affine mortality models are popular and are studied in works such as Dahl (2004), Biffis and Millossovich (2006a), Luciano and Vigna (2005), Russo et al. (2011) and Zeddouk and Devolder (2020). Russo et al. (2011) calibrated three different affine stochastic mortality models using term assurance premiums of three Italian insurance companies, and proposed that such affine models can be used for pricing mortality-linked securities. Luciano and Vigna (2005) described the force of mortality through affine models and calibrated the models using observed and projected UK mortality tables. Their results show that non-mean-reverting models outperform mean-reverting models for mortality modeling. Zeddouk and Devolder (2020) extended Luciano and Vigna (2005) to examine the impact of adding a time-dependent long-term mean reversion level to non-mean-reverting affine processes for the force of mortality. They assessed five affine mortality models by calibrating the processes to historical and projected Belgian mortality tables. Their results show that moving-target mean-reverting models describe the force of mortality more appropriately than fixed-target mean-reverting models as well as non-mean-reverting models. In this work, we assume that the evolution of the mortality rate of all the scheme members can be described by the same continuous-time stochastic process. We follow Menoncin (2009) and Zeddouk and Devolder (2020) and describe the force of mortality using an affine model which is analogous to the Cox-Ingersoll-Ross (CIR) process. The considered pension scheme is attractive to its members as it provides a minimum guarantee on purchasing lifetime annuities upon retirement. The longevity risk arises as the value of the minimum guarantee depends on members’ actual survival rate and expected remaining lifetime and is uncertain until retirement time. Besides, future contribution payments depend on members’ actual survival rate. As such, the manager invests in a security which allows to hedge the scheme’s exposure to the longevity risk.

Proposed by Blake and Burrows (2001), a longevity bond provides coupon payments based on the number of survivors in a chosen reference population. Therefore, investment in a longevity bond not only provides an efficient way to hedge the longevity risk, but also allows diversification of investment portfolios. Menoncin (2008) studied an optimal consumption and investment problem for an investor with a stochastic time of death. He maximized the investor’s inter-temporal consumption until the time of death and used a rolling longevity bond to hedge against the investor’s longevity risk. De Kort and Vellekoop (2017) modeled the force of mortality using the CIR process which guarantees the mortality rates to be non-negative. They argued that although there is no liquid market for such longevity bonds, it is not practical to put the market price of longevity risk at zero. Instead, they assumed a time-varying market price of longevity risk which is proportional to the square root of the mortality rate. Cocco and Gomes (2012) studied the optimal consumption and investment problem in a life-cycle model. By calibrating to US historical data and current projections, they showed considerable uncertainty with respect to future improvements in mortality rates. They also suggested that longevity linked securities can help in longevity risk management. Menoncin and Regis (2017) studied the optimal consumption and investment problem for an individual investor to hedge his longevity risk before retirement. They showed that the optimal proportion that should be invested in longevity bonds is higher than for other assets.

In this work, we consider a financial market that consists of three risky assets: a stock, a rolling bond and a rolling longevity bond. Our results show that the longevity bond provides an efficient way to hedge the longevity risk. Our main contribution is extending the works of Boulier et al. (2001), Gao (2008) and Menoncin and Regis (2017) by investigating the optimal portfolio allocation for DC schemes while hedging the longevity risk. The pension scheme promises that the scheme’s wealth level must be sufficient to allow the members to buy lifetime annuities at retirement, in this way providing a minimum guarantee. The scheme is exposed to longevity risk as the value of the minimum guarantee would be higher than anticipated if members’ life expectancy and actual survival rate exceeded expectations. At retirement time, the manager receives a fixed fraction of the surplus between the scheme wealth and the minimum guarantee as remuneration. The manager’s aim is then to maximize the expected utility from remuneration by controlling the investment strategy. To hedge the longevity risk, a rolling longevity bond as introduced in Menoncin (2008) is added to the investment portfolio. Our results show that the longevity risk plays an important role in the pension scheme’s risk management and reveals that the longevity bond can not only offer an efficient way to hedge future longevity risk, but also provide attractive risk premiums.

The rest of this paper is organized as follows. Section 2 presents the mathematical framework of the problem. We introduce the state variables, the financial market and the management of pension scheme. Moreover, the optimization problem in which the manager maximizes his utility of terminal wealth is defined. Section 3 gives our main results. In Sect. 3.1, we identify different components of the investment portfolio and reformulate the portfolio selection problem as a single investment portfolio optimization problem. We derive the analytical solution for the optimal investment strategy by using the dynamic programming principle in Sect. 3.2. Section 4 discusses several numerical studies including a sensitivity analysis with respect to different model parameters, which reveal the significance of introducing a rolling longevity bond in the investment portfolio.

2 Model

2.1 The state variables

Let \((\Omega , \mathscr {F}, \mathbb {F}, \mathbb {P})\) be a filtered probability space satisfying the usual conditions on an infinite time horizon \(\mathscr {T}=[0,\infty )\). \(\mathbb {P}\) is the physical (observable) probability measure and \(\mathscr {F}(t)\) signifies the information available to an investor at time t. On this probability space, we consider a friction-less financial market consisting of a stock, a rolling bond and a rolling longevity bond. For practical pricing of zero-coupon and longevity bonds, we consider a stochastic risk-free interest rate r(t) and a stochastic force of mortality \(\lambda (t).\) Furthermore, we denote by \(\bigl \{W(t)\mid t\in \mathscr {T}\bigr \}=\bigl \{\bigl [W_1 (t),W_2 (t),W_3 (t)\bigr ]^\prime \mid t\in \mathscr {T}\bigr \}\) a three-dimensional Brownian motion under \(\mathbb {P}.\) In addition, let \(\mathbb {G}=\{\mathscr {G}(t)\}_{t\ge 0}\) denote the sub-filtration of \(\mathbb {F}\) generated by W(t). We model the interest rate r(t) as a CIR process:

$$\begin{aligned} \textrm{d}r(t)=(a_r - b_r r(t))\textrm{d}t+\sigma _r \sqrt{r(t)}\textrm{d}W_1 (t),{} & {} {r(0)=r_0>0}, \end{aligned}$$

where \(a_r\), \(b_r\) and \(\sigma _r\) are positive constants. We further assume that the Feller condition \(2a_r \ge \sigma _r ^2\) is satisfied so that for any \(t\in \mathscr {T}\), \(r(t)>0,\) almost surely under \(\mathbb {P}\).

To model the pension scheme members, we consider a group of identical individuals with same age, gender, health condition, etc. Moreover, we assume that all the individuals from this group are homogeneous in their mortality behavior. Hence, we can describe the mortality behavior of the whole group using a single stochastic force of mortality process. A similar set-up is considered in Wong et al. (2017). As discussed earlier in Sect. 1, moving-target mean-reverting affine processes could appropriately model the evolution of the force of mortality. Thus, in the same spirit, we assume that \(\lambda (t)\) evolves as

$$\begin{aligned} \textrm{d}\lambda (t)=\left( a_{\lambda } (t)-b_{\lambda } \lambda (t)\right) \textrm{d}t +\sigma _{\lambda }\sqrt{\lambda (t)}\textrm{d}W_2 (t),{} & {} { \lambda (0)=\lambda _0>0 }, \end{aligned}$$
(1)

where \(a_\lambda (t)\) is a deterministic function, and, \(b_\lambda\) and \(\sigma _\lambda\) are positive constants. We impose the condition \(2a_\lambda (t)\ge \sigma _\lambda ^2,\) on the model parameters to ensure the strict positivity of \(\lambda (t)\). The analytical tractability of the affine model allows us to price mortality-linked securities, such as the longevity bond, using the arbitrage-free pricing framework developed for interest-rate derivatives.

The initial value of the mortality intensity \(\lambda _0\) is calculated according to the deterministic Gompertz-Makeham law and is given by

$$\begin{aligned} { \lambda _0 = \phi +\frac{1}{b} e^{\frac{t_0 -m}{b}}, } \end{aligned}$$
(2)

where \(t_0, m, \phi\) and b are positive constants. As in Menoncin (2009) and Zeddouk and Devolder (2020), we require that the expected value of \(\lambda (t)\) equals to the corresponding deterministic Gompertz-Makeham force of mortality to ensure at any time t,  \(\lambda (t)\) has a reasonable value. To achieve this, we require that \(a_{\lambda } (t)\) is of the following form

$$\begin{aligned}{ a_\lambda (t)=b_\lambda \left( \phi +\left( \frac{1}{b_\lambda b}+1\right) \frac{1}{b}e^{\frac{t-m}{b}}\right) . } \end{aligned}$$

Next, we measure the cumulative survival rate or survival probability in the group of individuals considered by tracking p(t),  the fraction of the group of individuals that survives from time 0 to t. Since the force of mortality measures the instantaneous rate of mortality, we can write

$$\begin{aligned} \frac{\textrm{d}p(t)}{p(t)}=-\lambda (t)\textrm{d}t, \quad p(0)=1. \end{aligned}$$

Suppose that there are n identical individuals in the group at the start. Then, by the homogeneity assumption of the mortality behavior, the number of individuals alive at time t is np(t). This follows from our conditionally independent and identically distributed (i.i.d.) assumption on the individual death occurrences. As such, given the force of mortality process \(\lambda (t),\) the mortality behaviour of the individuals in the considered group is independent of each other. Let \(\tau\) denote the remaining lifetime of an individual in the group. Given the individual is alive at t, the (conditional) expected survival probability from t to \(s>t\) can be computed using p(t) as follows

$$\begin{aligned}{ \mathbb {P}(\tau \ge s | \tau >t)=\mathbb {E}\left[ \frac{p(s)}{p(t)} \biggm | \mathscr {G}(t)\right] =\mathbb {E}\left[ e^{-\int _t^s\lambda (u)\textrm{d}u}\biggm | \mathscr {G}(t)\right] , } \end{aligned}$$

where \(\mathbb {E}[\cdot ]\) is the expectation operator under the physical measure \(\mathbb {P}\).

We define by \(H(t):= \mathbb {1}_{\{\tau \le t\}}, t \ge 0,\) the death occurrence process which records whether the individual has died at each time t. \(\mathbb {1}_{\{\cdot \}}\) denotes an indicator function. Let \(\mathbb {H}\) be the filtration whose \(\sigma\)-algebras \(\mathscr {H}(t)\) are generated by \(\{H(s):0\le s\le t\}.\) Then, \(\mathbb {H}\) collects information on the actual individual death occurrence. As the instantaneous rate of mortality is given by \(\lambda (t),\) it can be shown that the process \(\widetilde{H}(t)\) defined as

$$\begin{aligned}{ \widetilde{H}(t):=H(t)-\int _0^{t\wedge \tau } \lambda (u) \textrm{d}u, } \end{aligned}$$

is an \((\mathbb {H},\mathbb {P})\)-martingale. See, for example, Bielecki and Rutkowski (2013, Sect. 4.2).

Remark 1

There are two sources of longevity (mortality) risk in the model: systematic and idiosyncratic (unsystematic) longevity risk. Systematic longevity risk arises from the unexpected changes in population mortality that apply to all individuals in the population. Systematic longevity risk is non-diversifiable since it comes from the uncertainty in the path of mortality intensity (which is revealed by information in \(\mathbb {G}\)). Idiosyncratic longevity risk is the uncertainty in an individual’s survival, given known survival probability. It arises from the randomness of individual death occurrence. Idiosyncratic longevity risk can be diversified by pooling a large enough number of policyholders. We refer to: Duffie (2001, Chapter 11) for discussions on uncertainties regarding doubly stochastic default time; Dahl (2004), Luciano et al. (2012), and Hanewald et al. (2013) for systematic and unsystematic mortality risks.

2.2 The financial market

To discuss the prices of tradable financial risky assets in the market, we first characterize a risk-neutral pricing measure \(\widetilde{\mathbb {P}}\) that is equivalent to \(\mathbb {P}\) on \((\Omega , \mathscr {F}, \mathbb {F}, \mathbb {P})\). We set \(\mathbb {F}=\mathbb {G}\cup \mathbb {H}\) such that \(\mathbb {F}\) reveals all the information on past asset prices, mortality intensity evolution and actual individual death occurrence. Let \(\{\Theta (t)\mid t\in \mathscr {T}\}=\bigl \{\bigl [\theta _1(t),\theta _2(t),\theta _3(t)\bigr ]^\prime \bigm | t\in \mathscr {T}\bigr \}\) be an \(\mathbb {R}^3\)-valued, \(\mathscr {G}\)-adapted process such that process

$$\begin{aligned}{ Z(t)=\exp \left( -\int _{0}^{t}\Theta (s)^\prime \textrm{d}W(s)-\frac{1}{2}\int _{0}^{t}|\Theta (s)|^{2}\textrm{d}s \right) . } \end{aligned}$$

is a martingale under \(\mathbb {P}\), and \(\mathbb {E}[Z(t)]=1\). Let \(\{\phi (t)| t\in \mathscr {T}\}\) be a \(\mathscr {H}\)-predictable process with \(\int _0^t \phi (u)\lambda (u)\textrm{d}u<\infty\), and define

$$\begin{aligned}{ \widetilde{Z}(t)=1+\int _0 ^t \phi (u)\widetilde{Z}(u-)\textrm{d}\widetilde{H}(u), } \end{aligned}$$

Then, a new probability measure \(\widetilde{\mathbb {P}}\) that is equivalent to \(\mathbb {P}\) can be defined by

$$\begin{aligned}{ \frac{\textrm{d}\widetilde{\mathbb {P}}}{\textrm{d}\mathbb {P}}=Z(t)\widetilde{Z}(t). } \end{aligned}$$

By Girsanov’s theorem, under \(\widetilde{\mathbb {P}}\),

$$\begin{aligned}{ \widetilde{W}(t)=W(t)+\int _0 ^t \Theta (s)\textrm{d}s, } \end{aligned}$$

is a three-dimensional standard Brownian motion, and the instantaneous intensity of the death occurrence process H(t) is \((1+\phi (t))\lambda (t)\). We use the notation \(\bigl \{\widetilde{W}(t) \mid t \in \mathscr {T}\bigr \}=\bigl \{\bigl [\widetilde{W}_1 (t),\widetilde{W}_2 (t),\widetilde{W}_3 (t)\bigr ]^\prime \bigm | t \in \mathscr {T}\bigr \}\). We refer to Bielecki and Rutkowski (2013, Sect. 5.3) for further technical details.

The introduction of a risk-neutral measure also allows us to motivate the idea of a market price of risk or risk-premium through \(\Theta (t)\) and \(\phi (t)\) in our framework. In particular, \(\Theta (t)\) gives the market prices of interest rate risk, (systematic) longevity risk, stock price risk, and \(\phi (t)\) can be viewed as the market price of idiosyncratic longevity risk. Since the idiosyncratic longevity risk is diversifiable, pension scheme providers/insurers may have little interest in hedging this risk. Hence, as in Luciano et al. (2012), we assume that the market gives no value to the idiosyncratic longevity risk, i.e. there is zero risk premium for individual death occurrences. Under this assumption, the risk-neutral probability measure \(\widetilde{\mathbb {P}}\) is characterized via \(\frac{\textrm{d}\widetilde{\mathbb {P}}}{\textrm{d}\mathbb {P}}=Z(t)\).

The first financial asset in the market is a representative stock. We suppose that the stock price process S(t) under \(\mathbb {P}\) evolves as

$$\begin{aligned} \frac{\textrm{d}S(t)}{S(t)}=&\left( r(t)+\theta _r\sigma _S^r r(t)+\theta _S\sigma _S\right) \textrm{d}t + \sigma _S^r \sqrt{r(t)}\textrm{d}W_1 (t)+\sigma _S \textrm{d}W_3 (t),{} & {} {S(0)=S_0>0}, \end{aligned}$$

where \(\sigma _S, \sigma ^r_S, \theta _r, \theta _S\) are constants. Here, we have assumed that the market prices of interest rate risk and stock price risk are \(\theta _1(t)=\theta _r\sqrt{r(t)}\) and \(\theta _3(t)=\theta _S\), respectively. The instantaneous covariance between the stock price and risk-free interest rate is captured by \(\sigma _S^r\sqrt{r(t)}.\) The market price of stock price risk and different volatility coefficients (\(\sigma _S, \sigma _r\)) could be stochastic and take many different forms. However, as we mainly focus on the interest rate risk and longevity risk rather than investment risk, it is reasonable to suppose that they are constants.

For the pricing of a zero-coupon bond \(B(t,T_B)\) which pays one unit of currency at a fixed maturity time \(T_B,\) we first introduce a money market account R(t) via

$$\begin{aligned} \frac{\textrm{d}R(t)}{R (t)}=r(t)\textrm{d}t,{} & {} R(0)=1. \end{aligned}$$

The risk-neutral pricing formula then gives

$$\begin{aligned} B(t,T_B)=\widetilde{\mathbb {E}}\left[ \frac{R(t)}{R(T_B)} \Biggm | \mathscr {F}(t)\right] =\widetilde{\mathbb {E}}\left[ e^{-\int _t ^{T_B} r(u)\textrm{d}u} \biggm | \mathscr {F}(t) \right] , \end{aligned}$$

where \(\widetilde{\mathbb {E}}[\cdot ]\) is the expectation operator under the measure \(\widetilde{\mathbb {P}}\). As the interest rate r(t) follows an affine model, we can solve for the bond price as

$$\begin{aligned} { B(t,T_B)=e^{f_0 (t,T_B)-f_1(t,T_B) r(t)}, } \end{aligned}$$
(3)

where

$$\begin{aligned} f_0 (t,T_B)&=\frac{2a_r}{\sigma _r ^2}\log \left( \frac{2\eta _r e^{\frac{1}{2}(\tilde{b}_r + \eta _r)(T_B-t)}}{(\tilde{b}_r + \eta _r)(e^{\eta _r (T_B-t)}-1)+2\eta _r} \right) ,\\ f_1 (t,T_B)&=\frac{2(e^{\eta _r(T_B-t)} -1)}{(\tilde{b}_r + \eta _r )(e^{\eta _r(T_B-t)} -1)+2\eta _r},\\ \eta _r&=\sqrt{\tilde{b}_r ^2 +2\sigma _r ^2},\quad \quad \tilde{b}_r =b_r+\theta _r \sigma _r. \end{aligned}$$

The above result can be found in several sources, for example, Brigo and Mercurio (2007, Sect. 3.2.3), Cuchiero (2006, Sect. 3.1.2). The dynamics of \(B(t,T_B)\) under \(\mathbb {P}\) is given as

$$\begin{aligned} \frac{\textrm{d}B(t,T_B)}{B(t,T_B)}=\Big (r(t)+\theta _r\sqrt{r(t)}\sigma _B(t,T_B)\Big )\textrm{d}t+ \sigma _B(t,T_B)\textrm{d}W_1(t), \end{aligned}$$

where we denote \(\sigma _B(t,T_B)=-f_1(t,T_B)\sigma _r\sqrt{r(t)}.\)

As argued in Boulier et al. (2001), rolling bonds that can dynamically replicate other bonds in the market are useful and convenient for fund management. Thus, we also introduce a rolling zero-coupon bond B(t) with a constant time to maturity \(T_B\) in our analysis. A rolling bond can be viewed as a self-financing trading strategy which continuously reinvests in the bonds with a fixed time to maturity. For detailed a discussion on rolling bonds, we refer to Rutkowski (1999), Bielecki and Pliska (2004) and Bielecki et al. (2005). It is indeed possible to construct a suitable portfolio that dynamically adjusts its investment in the zero-coupon bonds to keep the portfolio a constant horizon \(T_B\). Using the results in Rutkowski (1999), it can be shown that B(t) satisfies the following stochastic differential equation

$$\begin{aligned} \frac{\textrm{d}B(t)}{B(t)}=\left( r(t)+\theta _r\sqrt{r(t)}\sigma _B(t,t+T_B)\right) \textrm{d}t+\sigma _B(t,t+T_B)\textrm{d}W_1(t). \end{aligned}$$
(4)

Since we use a one-factor CIR model for r(t), a zero-coupon bond with any maturity in the market can be replicated by rolling bonds and the money market account. Moreover, it can be shown that the zero-coupon bond \(B(t,T_B)\) is related to the rolling bond B(t) via

$$\begin{aligned} \frac{\textrm{d}B(t,T_B)}{B(t,T_B)}=\left( 1-\frac{\sigma _B(t,T_B)}{\sigma _B(t,t+T_B)}\right) \frac{\textrm{d}R(t)}{R(t)}+\frac{\sigma _B(t,T_B)}{\sigma _B(t,t+T_B)}\frac{\textrm{d}B(t)}{B(t)}. \end{aligned}$$

Hence, the use of the rolling bond B(t) via Eq. (4) is analogous to the use of a fixed maturity zero-coupon bond \(B(t,T_B)\).

The third and final asset in the market is a zero-coupon longevity bond, which is primarily used to hedge the longevity risk. A longevity bond is a financial security paying, at the expiration date, an amount equal to the fraction of survivors from time 0 to the maturity time in a reference population. The reference population can be a large number of similar individuals, e.g. a male generation born in the same year. We suppose that all individuals in the reference population have homogeneous mortality behavior and use (1) to model their mortality intensity. Let \(T_L\) be the fixed maturity time, then the payoff of the zero-coupon longevity bond is \(p(T_L)\). Suppose that the market price of longevity risk is \(\theta _2(t)=\theta _\lambda \sqrt{\lambda (t)}.\) Then, the arbitrage-free price \(L(t,T_L)\) of a zero-coupon longevity bond with fixed maturity time \(T_L\) is given as

$$\begin{aligned} L(t,T_L)&=\widetilde{\mathbb {E}}\left[ \frac{R(t)}{R(T_L)}p(T_L) \biggm | \mathscr {F}(t)\right] =e^{-\int _0 ^t \lambda (u)\textrm{d}u}\widetilde{\mathbb {E}}\left[ e^{-\int _t ^{T_L} \left( r(u)+\lambda (u)\right) \textrm{d}u} \biggm | \mathscr {F}(t)\right] . \end{aligned}$$

Due to the affine nature of r(t) and \(\lambda (t)\) and their independence, the longevity bond price can be expressed in the following form

$$\begin{aligned} L(t,T_L ) =&e^{-\int _0 ^t \lambda (u)\textrm{d}u}N(t,T_L), \end{aligned}$$
(5)

where

$$\begin{aligned} N(t,T_L)&= e^{f_0 (t,T_L )-f_1 (t,T_L )r(t)+h_0 (t,T_L )-h_1 (t,T_L )\lambda (t)},\\ h_1 (t,T_L)&=\frac{2(e^{\eta _\lambda (T_L-t)} -1)}{(\tilde{b}_\lambda + \eta _\lambda )(e^{\eta _\lambda (T_L-t)} -1)+2\eta _\lambda },\\ h_0 (t,T_L)&=-\int _t^{T_L} a_\lambda (u)h_1(u,T_L) \textrm{d}u,\\ \eta _\lambda&=\sqrt{\tilde{b}_\lambda ^2 +2\sigma _\lambda ^2}, \quad \quad \tilde{b_\lambda } =b_\lambda +\theta _\lambda \sigma _\lambda . \end{aligned}$$

By denoting \(\sigma _L^r (t,T_L)=-f_1 (t,T_L)\sigma _r \sqrt{r(t)}\) and \(\sigma _L^\lambda (t,T_L)=-h_1(t,T_L) \sigma _\lambda \sqrt{\lambda (t)}\), the evolution of \(L(t,T_L)\) is then described as

$$\begin{aligned} \frac{\textrm{d}L(t,T_L )}{L(t,T_L )}=&\Big (r(t)+\theta _r \sqrt{r(t)}\sigma _L^r (t,T_L ) +\theta _\lambda \sqrt{\lambda (t)}\sigma _L^\lambda (t,T_L)\Big )\textrm{d}t\\&+\sigma _L^r (t,T_L )\textrm{d}W_1 (t)+\sigma _L ^\lambda (t,T_L)\textrm{d}W_2 (t). \end{aligned}$$

In the same manner as for the zero-coupon bond, we consider a rolling longevity bond L(t) with a constant time to maturity \(T_L\) whose price process under \(\mathbb {P}\) is given as

$$\begin{aligned} \frac{\textrm{d}L(t)}{L(t)}=&\left( r(t)+\theta _r\sqrt{r(t)}\sigma _L^r(t,t+T_L)+\theta _\lambda \sqrt{\lambda (t)}\sigma _L^\lambda (t,t+T_L)\right) \textrm{d}t\nonumber \\&+\sigma _L^r(t,t+T_L)\textrm{d}W_1(t)+\sigma _L^\lambda (t,t+T_L)\textrm{d}W_2(t). \end{aligned}$$
(6)

We see that the rolling longevity bond correlates with the interest rate r(t) as well as the force of mortality \(\lambda (t)\). In fact, zero-coupon longevity bonds with any fixed maturity can be replicated using rolling bond, rolling longevity bond and cash via

$$\begin{aligned} \frac{\textrm{d}L(t,T_L)}{L(t,T_L)}=n_0(t)\frac{\textrm{d}R(t)}{R(t)}+n_B(t)\frac{\textrm{d}B(t)}{B(t)}+n_L(t)\frac{\textrm{d}L(t)}{L(t)}, \end{aligned}$$

where

$$\begin{aligned} n_L(t)&=\frac{\sigma _L^\lambda (t,T_L)}{\sigma _L^\lambda (t,t+T_L)}, n_B(t)=\frac{\sigma _L^r(t,T_L)}{\sigma _B(t,t+T_B)}-n_L(t)\frac{\sigma _L^r(t,t+T_L)}{\sigma _B(t,t+T_B)},\\ n_0(t)&=1-n_B(t)-n_L(t). \end{aligned}$$

Like earlier, the above relation also shows that the creation of the rolling longevity bond does not lead to any arbitrage. It is common in the literature in fact to use rolling bonds: Han and Hung (2012) introduced a rolling indexed bond to hedge the inflation risk for a DC scheme. Menoncin (2008) used a rolling longevity bond to transfer an individual’s longevity risk. In principle, the problems considered here can also be solved using a fixed term maturity zero-coupon longevity bond and a fixed term zero-coupon bond. However, the use of rolling longevity bond and rolling bond simplifies the calculations in Sect. 3 significantly.

Our choice of market price of risk \(\Theta (t)=\bigl [\theta _r\sqrt{r(t)},\theta _\lambda \sqrt{\lambda (t)},\theta _S \bigr ]^\prime\) ensures that Z(t) is a \(\mathbb {P}\)-martingale (see Shirakawa (2002), Theorem 3.2) due to the Novikov condition (see, for example, ?, Corollary 3.5.14). Hence, \(\widetilde{\mathbb {P}}\) is well defined. Moreover, the processes r(t) and \(\lambda (t)\) remain affine even after a change of measure to \(\widetilde{\mathbb {P}}.\) For any \(t,T_B,T_L\in \mathscr {T}\), we describe the risky asset prices in the form of a vector:

$$\begin{aligned} { \left[ \begin{array}{ccc} \frac{\textrm{d}B(t)}{B(t)}\\ \frac{\textrm{d}L(t)}{L(t)}\\ \frac{\textrm{d}S(t)}{S(t)} \end{array}\right] =\left( r(t)\mathbb {1}+M(t)\right) \textrm{d}t+\Sigma (t)^\prime \textrm{d}W(t), } \end{aligned}$$
(7)

where

$$\begin{aligned}&M(t)=\left[ \begin{array}{ccc} \theta _r \sqrt{r(t)}\sigma _B (t,t+T_B)\\ \theta _r \sqrt{r(t)}\sigma _L^r (t,t+T_L)+\theta _\lambda \sqrt{\lambda (t)}\sigma _L^\lambda (t,t+T_L)\\ \theta _r\sigma _S^r r(t)+\theta _S\sigma _S \end{array}\right] ,\\&\Sigma (t)^\prime =\left[ \begin{array}{ccc} \sigma _B (t,t+T_B) &{}\quad 0 &{}\quad 0\\ \sigma _L^r (t,t+T_L) &{}\quad \sigma _L^\lambda (t,t+T_L) &{}\quad 0 \\ \sigma _S^r\sqrt{r(t)} &{}\quad 0 &{}\quad \sigma _S \end{array}\right] . \end{aligned}$$

For ease of presentation, we also use the notation \(z(t)=[r(t), \lambda (t)]^\prime\) whose dynamics is given as

$$\begin{aligned} \textrm{d}z(t)=\mu (t,z(t))\textrm{d}t+\xi (t,z(t))^\prime \textrm{d}W(t), \quad z(0) = [r_0, \lambda _0]^\prime , \end{aligned}$$
(8)

where

$$\begin{aligned} \mu (t,z(t))=\left[ \begin{array}{ccc} a_r -b_r r(t)\\ a_\lambda (t)-b_\lambda \lambda (t) \end{array} \right] ,{} & {} \xi (t,z(t))^\prime =\left[ \begin{array}{ccc} \sigma _r\sqrt{r(t)} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \sigma _\lambda \sqrt{\lambda (t)} &{}\quad 0 \end{array}\right] . \end{aligned}$$

2.3 The pension scheme management

During the accumulation phase, scheme members continuously contribute to the pension scheme and delegate the scheme’s management to the scheme manager. That is to say, the manager is responsible for the investment. In return, the scheme promises a minimum guarantee at retirement in the form of lifetime annuities to its members. The scheme manager receives a fraction of the surplus between the scheme’s final wealth and the minimum guarantee as his one-off remuneration.

We suppose that there are n identical members (i.e. same age, gender, wage, etc.) in the scheme initially. Moreover, we assume that the scheme members’ mortality behavior correlates perfectly with the longevity bond’s underlying mortality experience, and the dynamics of the members’ mortality intensity is described by (1). Before retirement, each surviving member contributes a constant fraction of his instantaneous wage w(t). Previous studies, such as Han and Hung (2012) and Guan and Liang (2014), model the wage (or, contribution) as a stochastic process to study the optimal asset allocation problem for DC schemes. To simplify our calculations, the instantaneous wage in this work is assumed to be constant, that is, for any \(t\in [0,T]\), \(w(t)=w.\) Thus, the contribution \(c(t) = c\) is also constant, and the contribution rate is c/w. We note that our following analysis is also applicable when w(t) and c(t) are treated as independent stochastic processes or deterministic functions. In the case where a member dies before retirement time, we assume that he stops paying contribution immediately and his heirs receive nothing. For any \(t\in [0,T]\), the scheme manager invests the amounts \(\alpha _S (t), \alpha _B (t)\) and \(\alpha _L (t)\) of money in stock, rolling bond and rolling longevity bond, respectively. It then follows that the amount of money invested in the money market is \(\alpha _0(t) = F(t) - \alpha _B(t) - \alpha _L(t) -\alpha _S(t),\) where F(t) denotes the scheme’s wealth level. The dynamics of F(t) is given as

$$\begin{aligned} \textrm{d}F(t)=&\Big (r(t)F(t)+cnp(t)+\alpha (t)^\prime M(t)\Big )\textrm{d}t+\alpha (t)^\prime \Sigma (t)^\prime \textrm{d}W(t),{} & {} {F(0) = F_0>0}, \end{aligned}$$
(9)

where \(\big \{\alpha (t)\) \(\bigm | t\in [0,T]\big \}\) \(=\big \{\left[ \alpha _B (t),\alpha _L (t), \alpha _S (t)\right] ^\prime \bigm | t\in [0,T]\big \}\) denotes the investment in risky assets.

At retirement time T, the scheme manager promises that the pension wealth F(T) must exceed the lifetime annuities’ price, this acts as minimum guarantee G(T). Such minimum guarantee was also previously considered in works such as Boulier et al. (2001), Deelstra et al. (2003), Han and Hung (2012) and Guan and Liang (2014). Moreover, we suppose that the manager receives a constant fraction of the terminal surplus \(F(T)-G(T)\) as remuneration. Note that the manager’s remuneration will be positive only if \(F(T)-G(T)>0\). Deelstra et al. (2003) used a similar assumption on the manager’s remuneration. Here, we extend these works to the case where the death time is uncertain and the force of mortality is stochastic.

To compute the price of the lifetime annuity and G(T), we first need to decide the level of installments that the annuity delivers. Typically, the wage replacement ratio, the percentage of retirement income to pre-retirement income, is a good estimate of the income needed to maintain the living standard in retirement. We set the instantaneous installment of the annuity to be \(\pi\), which gives the wage replacement ratio as \(\pi /w\). As in Boulier et al. (2001), Boyle and Hardy (2003), Guan and Liang (2014), Menoncin and Regis (2017), we assume that the annuity is fairly priced, and its price is calculated using an expected discounted cash flow approach under the risk neutral measure \(\widetilde{\mathbb {P}}\). Assuming that the annuity provider also models the mortality behavior of members using \(\lambda (t)\), the price of a lifetime annuity a(T) at retirement time T is given as

$$\begin{aligned} a(T)=&\widetilde{\mathbb {E}}\left[ \int _T^\infty \pi \frac{R(T)}{R(s)}\frac{p(s)}{p(T)}\textrm{d}s \biggm | \mathscr {F}(T)\right] . \end{aligned}$$

More generally, the annuity providers’s risk-neutral probabilities concerning the evolution of mortality are different from those of the policyholders. However, we do not make such a distinction. The treatment of the more general problem as studied by Biffis and Millossovich (2006b) is beyond the scope of our work.

The minimum guarantee is met in purchasing lifetime annuities for surviving members at retirement time T. Therefore, its value at T is given as

$$\begin{aligned} G(T) =n p(T)a(T)=n\widetilde{\mathbb {E}}\left[ \int _T ^\infty \pi \frac{R(T)}{R(s)} p(s)\textrm{d}s \biggm | \mathscr {F}(T)\right] . \end{aligned}$$

As shown, the value of the minimum guarantee is contingent on the future risk-free interest rate and members’ survival rate, and it is unknown until the retirement time.

2.4 The utility maximization problem

We follow Merton (1969) and suppose the manager aims to maximize his expected utility of terminal remuneration. Hyperbolic absolute risk aversion (HARA) identifies a class of utility functions which is most commonly used. Constant relative risk aversion (CRRA), constant absolute risk aversion (CARA), and quadratic utility are all HARA type utility functions which have been used frequently in the past. For instance, Gao (2008) and Boulier et al. (2001) used CRRA utility function to study optimal asset allocation problems for DC schemes. Battocchio and Menoncin (2004) and Cairns (2000) adopted CARA and quadratic utilities, respectively. In this paper, we use a CRRA utility function in the form of

$$\begin{aligned} U(x)=\frac{x^{1-\gamma }}{1-\gamma }, \quad x>0, \end{aligned}$$
(10)

where \(\gamma >0\) and \(\gamma \not =1\). In the case when \(\gamma =1\), \(U(x)=\ln x\) is the log-utility function. This choice is motivated by two factors. First, pension schemes usually manage a large amount of money. With an increasing or decreasing relative risk aversion, the fraction of wealth invested in risky assets is affected by the total level of wealth. However, the CRRA utility function shows constant relative risk aversion and in conclusion the investment strategy is not affected by scale. Second, our optimization problem is analytically tractable when using CRRA utility. For other types of utility functions, we lose analytical tractability of the solutions and the ability to make precise qualitative statements, even if we were to numerically solve the optimization problem using our approach.

Using the CRRA utility function \(U(\cdot )\), maximizing the manager’s expected utility from remuneration is equivalent to maximizing the expected utility from the scheme’s terminal surplus. Therefore, we formulate the utility maximization problem as

$$\begin{aligned} \underset{ \alpha \in \mathscr {A}}{\sup }\ \, \mathbb {E}\left[ \frac{\left( F(T)-G(T)\right) ^{1-\gamma }}{1-\gamma }\right] \text { such that } F(T) \ge G(T) \, \text {a.s.}. \end{aligned}$$
(11)

In the above, the set \(\mathscr {A}\) denotes the set of all admissible strategies which are defined as below.

Definition 1

A portfolio strategy \(\{\alpha (t) \in \mathbb {R}^3\mid t \in [0,T] \}\) is called admissible if \(\alpha (t)\) is progressively measurable with respect to \(\mathscr {F}\) and \(\mathbb {E}\left[ \int _0^T |\alpha (t)|^2 \textrm{d}t\right] < \infty\).

In our setting, scheme members continuously contribute to the scheme during the accumulation phase. The term \(cnp(t)\textrm{d}t\) in (9) reveals that the wealth process F(t) is not self-financing. Besides, at the retirement time T, there is a minimum guarantee G(T) to be met. This means that the proposed problem (11) is not a classical Merton type optimal investment problem. To solve this non-self-financing constrained problem, we convert it into a self-financing investment portfolio optimization problem by introducing an auxiliary surplus process. We then solve the transformed problem using the dynamic programming principle.

3 Main results

3.1 Single investment portfolio optimization problem

Inspired by Boulier et al. (2001), we split the scheme’s wealth into two parts: one part is the future contributions to be paid by living members and the other part is a self-financing portfolio. For any \(t\in [0,T]\), denoting by D(t) the present value of future contributions until retirement time T, we can write

$$\begin{aligned} D(t) =\widetilde{\mathbb {E}}\left[ \int _t^T cn p(s)\frac{R(t)}{R(s)}\textrm{d}s\Biggm | \mathscr {F}(t)\right] . \end{aligned}$$
(12)

D(t) can be viewed as a coupon-paying bond that pays instantaneous coupon rate cnp(s) from time t to T. Next, we show that D(t) can be replicated by investing in the rolling bond, rolling longevity bond and money market.

Proposition 1

For any \(t\in [0,T]\), D(t) in (12) can be replicated as

$$\begin{aligned} \textrm{d}D(t) =\left( r(t)D(t)-cnp(t)+\alpha ^D(t)^\prime M(t) \right) \textrm{d}t+\alpha ^D(t)^\prime \Sigma (t)^\prime \textrm{d}W(t), \end{aligned}$$
(13)

where

$$\begin{aligned} \alpha ^D(t)=\left[ \begin{array}{ccc} \alpha _B^D(t)\\ \alpha _L^D(t)\\ 0 \end{array}\right] =\left[ \begin{array}{ccc} \frac{ cn\int _t ^TL(t,s)f_1 (t,s)\textrm{d}s}{f_1 (t,t+T_B )}-\frac{f_1(t,t+T_L)}{f_1(t,t+T_B)} \frac{cn\int _t^T L(t,s) h_1(t,s)\textrm{d}s}{h_1(t,t+T_L)}\\ \frac{cn\int _t^T L(t,s) h_1(t,s)\textrm{d}s}{h_1(t,t+T_L)}\\ 0 \end{array}\right] \end{aligned}$$
(14)

is the investment in risky assets. The holding in the money market is \(\alpha _0^D(t)=D(t)-\alpha _B^D(t)-\alpha _L^D(t)\).

See Appendix 1 for the proof.

Our next step is to construct a replicating portfolio for G(T). At time \(t\in [0,T]\), the present value of G(T) is given by

$$\begin{aligned} G(t) =&\widetilde{\mathbb {E}} \left[ G(T)\frac{R(t)}{R(T)}\Biggm | \mathscr {F}(t)\right] . \end{aligned}$$
(15)

Similar to replicating D(t), we show in the following proposition that G(t) can be replicated by investing in the bond, longevity bond and money market.

Proposition 2

For any \(t\in [0,T]\), G(t) in (15) can be replicated as

$$\begin{aligned} \textrm{d}G(t) =\left( r(t)G(t)+\alpha ^G(t)^\prime M(t) \right) \textrm{d}t+\alpha ^G(t)^\prime \Sigma (t)^\prime \textrm{d}W(t) \end{aligned}$$
(16)

where

$$\begin{aligned} \alpha ^G(t)=\left[ \begin{array}{ccc} \alpha _B^G(t)\\ \alpha _L^G(t)\\ 0 \end{array}\right] =\left[ \begin{array}{ccc} \frac{ \pi n\int _T^\infty L(t,s)f_1(t,s)\textrm{d}s}{f_1(t,t+T_B)}-\frac{f_1(t,t+T_L)}{f_1(t,t+T_B)}\frac{\pi n \int _T^\infty L(t,s)f_1(t,s)\textrm{d}s}{h_1(t,t+T_B)}\\ \frac{\pi n \int _T^\infty L(t,s)f_1(t,s)\textrm{d}s}{h_1(t,t+T_B)}\\ 0 \end{array}\right] \end{aligned}$$
(17)

is the investment in risky assets. The holding in the money market is \(\alpha _0^G(t)=G(t)-\alpha _B^G(t)-\alpha _L^G(t)\).

The proof is similar to Proposition 1 and is omitted here for the sake of brevity. Finally, we construct an auxiliary process \(Y(t)=F(t)+D(t)-G(t)\). At retirement time T, from (12), we see that \(D(T)=0\) and we have \(Y(T)=F(T)-G(T)\). That is, Y(T) is the surplus of the terminal scheme wealth over the minimum guarantee. From (9), (13) and (16), we obtain the following equation

$$\begin{aligned} \textrm{d}Y(t)&= \textrm{d}F(t)+\textrm{d}D(t)-\textrm{d}G(t)\nonumber \\&\quad =\left( r(t)Y(t)+\alpha ^Y(t)^\prime M(t) \right) \textrm{d}t+\alpha ^Y(t)^\prime \Sigma (t)^\prime \textrm{d}W(t) \end{aligned}$$
(18)

where

$$\begin{aligned} \alpha ^Y(t) = \alpha (t)+\alpha ^D(t)-\alpha ^G(t). \end{aligned}$$
(19)

Thus, our simplified portfolio optimization problem is given as

$$\begin{aligned}&\underset{\alpha ^Y \in \mathscr {A}}{\sup }\ \, \mathbb {E}\left[ \frac{Y(T)^{1-\gamma }}{1-\gamma } \right] \text { such that } Y(T) \ge 0 \, \text {a.s.}. \end{aligned}$$
(20)

Lemma 3

For any \(t\in [0,T]\), if \(\alpha ^Y(t)\in \mathscr {A}\), then \(\alpha (t)\in \mathscr {A},\) and the optimization problems (11) and (20) are equivalent.

See Appendix 2 for the proof.

We see that the wealth process (18) is self-financing. Once we are able to solve (20) and obtain the unique optimal control \({\alpha ^Y}^\star (t)\), we can use (14), (17) and (19) to obtain \(\alpha ^\star (t)\). We require that \(Y(0) =F(0)+D(0)-G(0)>0\) and suppose that Y(t) does not become negative before time T. If Y(t) hits zero, it stays there and no further investment takes place. Moreover, we assume that the manager is under the supervision of a regulator and choose the investment strategy as such that \(Y(T)=F(T)-G(T)\ge 0\) almost surely.

3.2 The optimal solution

We define the value function of our simplified problem (20) as

$$\begin{aligned} V(t,y,z):=\underset{\alpha ^Y \in \mathscr {A}}{\sup } \,\mathbb {E}\left[ \frac{Y(T)^{1-\gamma }}{1-\gamma } \Biggm | \mathscr {F}(t) \right] , \end{aligned}$$

with terminal condition \(V(T,y,z)=\frac{y^{1-\gamma }}{1-\gamma }\). We assume that \(V(t,y,z) \in C^{1,2,2}([0,T] \times \mathbb {R}^3_+).\) Then, by following the usual dynamic programming principle (see, for example, Pham (2009, Chapter 3)), V satisfies the following Hamilton-Jacobi-Bellman (HJB) equation

$$\begin{aligned} 0=V_t(t,y,z)+\underset{\alpha ^Y \in \mathbb {R}^3}{\sup }\mathscr {L}^{\alpha ^Y}V(t,y,z), \end{aligned}$$
(21)

where

$$\begin{aligned} \mathscr {L}^{\alpha ^Y}V = V_y (ry+{\alpha ^Y}^\prime M)+\mu ^\prime V_z+\frac{1}{2}\text {tr}(\xi ^\prime \xi V_{zz} )+\frac{1}{2}{\alpha ^Y}^\prime \Sigma ^\prime \Sigma \alpha ^Y V_{yy}+{\alpha ^Y}^\prime \Sigma ^\prime \xi V_{yz}. \end{aligned}$$

\(V_t\), \(V_y,\ V_{yy},\ V_z,\ V_{zz}\ \text {and}\ V_{yz}\) are the first and second order partial derivatives with respect to t, y, z. In particular, \(V_z=\left[ V_r, V_\lambda \right] ^\prime\), \(V_{yz}=\left[ V_{yr},V_{y\lambda } \right] ^\prime\) and \(V_{zz}=\left[ \left[ V_{rr},V_{\lambda r}\right] ^\prime ,\left[ V_{r\lambda }, V_{\lambda \lambda }\right] ^\prime \right]\). Solving the first order condition on \(\alpha ^Y\), we obtain the unique investment strategy as

$$\begin{aligned} {\alpha ^Y}^\star =-\frac{V_y}{V_{yy}} (\Sigma ^\prime \Sigma )^{-1} M-\frac{1}{V_{yy}} \Sigma ^{-1} \xi V_{yz}. \end{aligned}$$
(22)

Substituting (22) in (21), we obtain

$$\begin{aligned} 0=&V_t+V_y ry-\frac{1}{2}\frac{{V_y}^2}{V_{yy}} M^\prime (\Sigma ^\prime \Sigma )^{-1} M -\frac{V_y}{V_{yy}} M^\prime \Sigma ^{-1} \xi V_{yz}+\mu ^\prime V_z\nonumber \\&+\frac{1}{2}tr(\xi ^\prime \xi V_{zz})-\frac{1}{2} \frac{1}{V_{yy}} {V_{yz}}^\prime \xi ^\prime \xi V_{yz}. \end{aligned}$$
(23)

Once we solve for the value function V(t, y, z) in (23), we can obtain the optimal control \({\alpha ^Y}^\star (t)\). The following proposition provides the explicit optimal investment strategy for the transformed problem (20).

Proposition 4

For any \(t\in [0,T]\) and risk-aversion parameter

$$\begin{aligned} \gamma >\max \left\{ \frac{2\sigma _r^2+\sigma _r^2 \theta _r^2+2b_r \theta _r \sigma _r}{(b_r+\theta _r\sigma _r)^2+2\sigma _r^2},\ \frac{2b_\lambda \theta _\lambda \sigma _\lambda +\sigma _\lambda ^2 \theta _\lambda ^2}{(b_\lambda +\theta _\lambda \sigma _\lambda )^2}\right\} , \end{aligned}$$
(24)

under the financial market setting (7)–(8), the optimal solution to (20) is given as

$$\begin{aligned} {\alpha ^Y}^\star (t)=&\left[ \begin{array}{ccc} {\alpha ^Y_B}^\star (t)\\ {\alpha ^Y_L}^\star (t)\\ {\alpha ^Y_S}^\star (t) \end{array} \right] =\left[ \begin{array}{ccc} \frac{\theta _S\sigma _S^r -\theta _r\sigma _S-\sigma _S\sigma _rA_1(t,T)}{\sigma _S\sigma _r f_1 (t,t+T_B )}+\frac{f_1 (t,t+T_L ) }{f_1 (t,t+T_B )}\frac{\theta _\lambda +\sigma _\lambda A_2(t,T)}{\sigma _\lambda h_1 (t,t+T_L)}\\ -\frac{\theta _\lambda +\sigma _\lambda A_2(t,T)}{\sigma _\lambda h_1 (t,t+T_L)}\\ \frac{\theta _S}{\sigma _S } \end{array} \right] \frac{Y^\star (t)}{\gamma }, \end{aligned}$$

where

$$\begin{aligned}&\left\{ \begin{array}{ll} &{}A_1 (t,T)=\frac{a_{11} a_{12} \exp (-\sqrt{\Delta _1}(T-t)) -a_{11} a_{12}}{a_{12} \exp (-\sqrt{\Delta _1}(T-t))-a_{11}},\\ &{}\Delta _1 =b_r^2+\frac{\gamma -1}{\gamma }\left( 2\sigma _r^2 +\theta _r^2\sigma _r^2+2b_r\theta _r\sigma _r\right) ,\\ &{}a_{11,12}=\frac{(\gamma -1)\theta _r\sigma _r +b_r \gamma \pm \gamma \sqrt{\Delta _1}}{\sigma _r^2}, \end{array}\right. \nonumber \\&\left\{ \begin{array}{ll} &{}A_2 (t,T)=\frac{a_{21} a_{22} \exp (-\sqrt{\Delta _2}(T-t)) -a_{21} a_{22}}{a_{22} \exp (-\sqrt{\Delta _2}(T-t))-a_{21}},\\ &{}\Delta _2=b_\lambda ^2+\frac{\gamma -1}{\gamma }(2b_\lambda \theta _\lambda \sigma _\lambda +\theta _\lambda ^2\sigma _\lambda ^2),\\ &{}a_{21,22}=\frac{(\gamma -1)\theta _\lambda \sigma _\lambda +b_\lambda \gamma \pm \gamma \sqrt{\Delta _2}}{\sigma _\lambda ^2}, \end{array}\right. \nonumber \\&A_0(t,T)=\int _t^T \left( a_r A_1 (s,T)+a_\lambda (s) A_2(s,T)+\frac{1-\gamma }{2\gamma }\theta _S^2\right) \textrm{d}s. \end{aligned}$$

We include the proof in Appendix 1. Next, we show that \(Y^\star (t)\) obtained using \(\alpha ^{Y^\star }\) is always positive, and also verify the admissibility of the optimal control \({\alpha ^Y}^\star\).

Remark 2

For any \(t\in [0,T]\), let \(\tilde{\alpha }^{Y^\star } (t)=\frac{\alpha ^{Y^\star } (t)}{{Y^\star }(t)}\), we have

$$\begin{aligned} \textrm{d}{Y^\star }(t) = \left( r(t)+ \tilde{\alpha }^{Y^\star } (t)^\prime M(t) \right) {Y^\star }(t) \textrm{d}t+\tilde{\alpha }^{Y^\star } (t)^\prime \Sigma (t)^\prime {Y^\star }(t)\textrm{d}W(t). \end{aligned}$$

According to Proposition 4, we see that the optimal \(\tilde{\alpha }^{Y^\star }(t)\) is a well-defined vector of continuous (deterministic) functions. Thus, \(\mathbb {E}\left[ \int _0^T|\tilde{\alpha }^{Y^\star }(t) |^2 \textrm{d}t\right] <+\infty\), \(Y^\star (t)\) admits a unique solution and is bounded over [0, T]. Thereafter, we have \(\mathbb {E}\left[ \int _0^T|\alpha ^{Y^\star }(t) |^2 \textrm{d}t\right] <+\infty\) and \({\alpha ^Y}^\star (t) \in \mathscr {A}\). Besides, we get

$$\begin{aligned} \frac{Y^\star (t)}{Y(0)}=&\exp \Big ({\int _0^t \big ( r(u)+ \tilde{\alpha }^{Y^\star } (u)^\prime M(u) -\frac{1}{2}\tilde{\alpha }^{Y^\star } (u)^\prime \Sigma (u)^\prime \Sigma (u)\tilde{\alpha }^{Y^\star } (u) \big )\textrm{d}u }\\&+\int _0^t \tilde{\alpha }^{Y^\star } (u)^\prime \Sigma (u)^\prime \textrm{d}W(u) \Big ). \end{aligned}$$

From the above proposition, we observe a proportional relationship between \({\alpha _S^Y}^\star (t)\) and Y(t) for constant \(\theta _S\), \(\sigma _S\) and \(\gamma\). Namely, the optimal stock weight \(\frac{{\alpha ^Y_S}^\star (t)}{Y(t)}\) always stays the same throughout the investment horizon. This is similar to the classical Merton portfolio problem where the optimal portfolio weight on the risky asset is constant over time. The convention is that the constant market price of risk causes no change in the investment behavior. We also find that the optimal investment in the longevity bond \({\alpha _L^Y}^\star (t)\) is actually taken from the investment in the bond \({\alpha _B^Y}^\star (t)\) proportionally by a factor of \(-\frac{f_1 (t,t+T_L )}{f_1 (t,t+T_B )}\). From (3) and (5), we see that \(f_1 (t,t+T_B )\) and \(f_1 (t,t+T_L )\) are the duration of the rolling bond and rolling longevity bond, respectively. Since the duration is always positive, \(-\frac{f_1 (t,t+T_L )}{f_1 (t,t+T_B )}\) is negative. We conclude that there is a negative relationship between the optimal investments in bond and longevity bond. Besides, if the maturities of the rolling bond and the rolling longevity bond are the same (that is, \(T_B=T_L\)), we have \(f_1 (t,t+T_L )=f_1 (t,t+T_B )\) and \({\alpha _L^Y}^\star (t)\) is fully deduced from \({\alpha _B^Y}^\star (t)\). For any \(t<T\), \(h_1(t,t+T_L)\) stays constant and \(A_2(t,T)\) is negative and increases with t. Thus, it is easy to deduce that the optimal investment proportion in longevity bond \(\frac{{\alpha _L^Y}^\star (t)}{Y(t)}\) is decreasing over time. Even though the behavior of optimal proportions invested in bond and money market is not clear, it is apparent that greater the manager’s risk-aversion, lower the portfolio weights on the longevity bond and stock. Lemma 3 shows that Problem (11) and (20) are equivalent. According to (14), (17), (19) and Proposition 4, we obtain the solution to the initial problem (11) by straightforward calculations.

Proposition 5

For any \(t\in [0,T]\), under condition (24) and the financial market setting (7)–(8), the optimal solution to (11) is given as

$$\begin{aligned} \alpha _B^\star (t)=&\frac{\theta _S\sigma _S^r -\theta _r\sigma _S-\sigma _S\sigma _rA_1(t,T)}{\gamma \sigma _S\sigma _r f_1 (t,t+T_B )}Y(t) -\frac{ c n\int _t ^TL(t,s)f_1 (t,s)\textrm{d}s}{f_1 (t,t+T_B )}\\&+\frac{\pi n\int _T^\infty L(t,s)f_1(t,s)\textrm{d}s}{f_1(t,t+T_B)}-\frac{f_1(t,t+T_L)}{f_1(t,t+T_B)}\alpha _L^\star (t) ,\\ \alpha _L^\star (t)=&\, -\frac{\theta _\lambda +\sigma _\lambda A_2(t,T)}{\gamma \sigma _\lambda h_1 (t,t+T_L)}Y(t)-\frac{c n\int _t^T L(t,s) h_1(t,s)\textrm{d}s}{h_1(t,t+T_L)}+\frac{\pi n \int _T^\infty L(t,s)h_1(t,s)\textrm{d}s}{h_1(t,t+T_L)},\\ \alpha _S^\star (t)=&\frac{\theta _S}{\gamma \sigma _S }Y(t),\quad \alpha _0 ^\star (t)=F(t)-\alpha _B^\star (t)-\alpha _L^\star (t)-\alpha _S^\star (t). \end{aligned}$$

We find that the optimal amount invested in the stock does not depend directly on the fund’s wealth F(t) but on the process Y(t). Besides, the optimal stock weight \(\frac{\alpha _S^\star (t)}{F(t)}\) does not keep constant any more and depends on the ratio \(\frac{Y(t)}{F(t)}\). From the drift terms of F(t) and Y(t) in (9) and (18), we deduce that F(t) is expected to increase with t faster than Y(t). Thus, we conclude that the optimal stock weight falls over time. Similar to the result in Proposition 4, the optimal investments in bond and longevity bond correlate negatively. It is not possible to infer from the solution how the optimal weights in bond and longevity bond change over time. Section 4 shows the results of numerical simulations which allow us to observe the optimal investment strategy dynamically. However, it is not straightforward to detect from the optimal solution how the risk-aversion coefficient \(\gamma\), contribution rate c/w and wage replacement ratio \(\pi / w\) affect the optimal strategy. We provide a numerical analysis and comparative statics on these parameters in the following section.

4 Numerical applications

We first provide a base scenario to visualize the optimal proportions invested in risky assets and money market. Then, sensitivity analyses are provided to study the impact of model parameters on the optimal investment strategy. In what follows, we denote by \(w_B(t)\), \(w_L(t)\), \(w_S(t)\) and \(w_0(t)\) the investment proportions in rolling bond, rolling longevity bond, stock and money market, respectively.

4.1 The base scenario

The values of the parameters for the base scenario are given in Table 1. We do not use real market data but most of these parameter values are taken from Menoncin and Regis (2017) and Han and Hung (2012) and represent a consensus of the current literature. Here, we assume that there exists a rolling bond and a rolling longevity bond with constant maturity time (in years) \(T_B=10\) and \(T_L=10\), respectively. As the longevity bond is supposed to be issued based on the mortality index of an older population, we assume that the market consists of a rolling longevity bond whose underlying is the survival index of the 40-year-old population. The longevity risk tends to be largely ignored in very early ages. Hence, we suppose that the scheme manager considers to add the longevity bond to the investment portfolio after the scheme members reach the age of 40, that is, the initial age (in years) is \(t_0=40\). \(\lambda _0\) given in (2) is computed by using the parameters given in Table 1. The retirement age is chosen as 65 years old, in other words the retirement time is \(T=25\) years. \(\theta _\lambda\) is the parameter of the market price of longevity risk. It not easy to infer upon the value of \(\theta _\lambda\) as longevity bonds are traded over the counter (OTC) and not through an exchange. In our base scenario, we use \(\theta _\lambda =-0.10\). At time 0, the rolling bond offers a risk premium of about 0.01370 and the longevity bond provides a total risk premium of around 0.01372. The stock offers a total risk premium of around 0.01670. In this setting, the longevity risk premium is far less than the interest rate and stock risk premia. Later, we provide optimal investment strategies for different scenarios with different values of \(\theta _\lambda\). Without loss of generality, we normalize the size of membership of the fund to \(n=1\). Pension contribution rates differ widely among schemes and countries. According to HMRC (2018), in the UK, there is a limit on the amount of tax-free pension savings that an individual can pay into his pension account in each tax year. However, there is no cap on the contribution rate. As stated in DWP (2013), the Department for Work and Pensions requires that the minimum contribution rate for DC schemes is \(8\%\), which is UK legislation. We first consider \(c/ w=0.15\) then give a sensitivity analysis on the contribution rate. OECD (2019) shows that the net replacement rates vary across a large range from around \(30\%\) to \(90\%\) or more in OECD countries. The average net replacement rates of an average earner from mandatory schemes is \(59\%\). Since in the proposed scheme contributions are not returned to dead members, it is natural to set a replacement ratio that is above average. In our base scenario, we adopt \(\pi /w=0.75\). We set the instantaneous wage as \(w=15\), thus the instantaneous contribution and annuity installment are \(c=2.25\) and \(\pi =11.25\), respectively. We suppose the initial scheme wealth is \(F_0=20\) and the manager’s risk aversion coefficient is \(\gamma =2.5\).

Table 1 Values of parameters in the base scenario
Full size table

We obtain 1000 simulated paths and present the average paths of optimal investment proportions in Fig. 1. As discussed in Sect. 3.2, we see that the optimal stock weight \(w_S^\star (t)\) declines over time. The optimal weight in cash is initially negative and is increasing over time. In the beginning, the short position in the money market reveals that the scheme manager borrows money and invests in risky assets to obtain risk premia. It implies that the manager takes an aggressive approach to quickly increase the pension scheme’s wealth to a high level in the early stage. The reduction in the total proportion invested in risky assets shows that, when closer to retirement, the manager becomes more conservative and shifts the scheme’s wealth to safer assets.

The longevity bond dominates the portfolio in the second half of the management period. This implies that it plays an important role in the risk management of the scheme. Both bond and longevity bond provide interest rate hedging, but the optimal investments in the two assets act differently. Throughout the whole management period, the optimal bond weight is declining. The optimal weight in the longevity bond keeps increasing, though it drops slightly in the last few years. Besides, we see that the sum of bond and longevity bond weights declines over time. These observations reveal that, when approaching retirement, the need for interest rate hedging becomes lower while the need to hedge against longevity risk is still significant. Consequently, the manager cuts down the proportion of wealth invested in the bond while increasing the longevity bond’s weight. Generally, our base scenario implies that the longevity bond is an important element in the investment portfolio and provides an efficient way to hedge against both interest rate and longevity risks.

Fig. 1
figure 1

Average paths of optimal investment proportions

Full size image

4.2 Sensitivity analysis

In Sect. 3.2, we give some comments on the impact of model parameters on the optimal investment strategy. This section provides various scenarios to investigate the impact of model parameters numerically. We are interested in the following parameters: risk aversion coefficient (\(\gamma\)), market price of longevity risk parameter (\(\theta _\lambda\)), maturity of rolling longevity bond (\(T_L\)), contribution rate (c/w) and wage replacement ratio (\(\pi /w\)). Other factors such as the market prices of interest rate risk and stock risk may also affect the optimal investment strategy sufficiently. Nonetheless, we do not look into those factors as the focus of our study is on hedging longevity risk.

4.2.1 Risk-aversion

In the context of the CRRA utility function (10), \(\gamma\) measures the scheme manager’s aversion to risk. A higher value of \(\gamma\) signifies a higher risk aversion. Figure 2 shows the average paths of optimal investment proportions with different values of \(\gamma\). We observe that the investment proportions in bond and cash increase with \(\gamma ,\) whereas the investment proportions in longevity bond and stock decrease with \(\gamma\). A risk-averse investor tends to avoid relatively higher risk and prefers investments with lower risk but higher guaranteed returns. Although stock and longevity bond provide higher risk premiums, a high-risk-averse manager prefers to invest more in safer assets, i.e., bond and cash. This can also be explained by the optimal solution in Proposition 5. The optimal investment proportions in bond and longevity bond are negatively correlated. Since the longevity bond weight decreases with \(\gamma\), the bond weight increases accordingly. This behavior occurs as the bond is a safer asset than the longevity bond.

It is surprising that the optimal bond weight can become negative, meanwhile the holding in the money market is positive. This indicates that the manager chooses to short sell bonds when approaching retirement time T. Gao (2008) and Han and Hung (2012) also made similar findings. They showed that the pension portfolio would shift from investments into risky assets to the money market. The convention is that the bond guarantees a fixed amount of money at maturity. In the beginning, the weight put on the bond is relatively high and declines when moving closer to T. It also implies that the need to hedge interest rate risk becomes lower when approaching T.

Figure 2 shows that the longevity bond always suppresses other assets in the late management period, even for a high-risk-averse investor, as shown in the bottom right plot. Moreover, the longevity bond weight rises to around \(50\%\) by the end. Further, we find that the optimal weight for the longevity bond is almost always higher than for the stock, in all scenarios. Overall, we conclude that, even though highly risk-averse managers invest less in the longevity bond, the latter is always an important element in the scheme’s investment portfolio.

Fig. 2
figure 2

Average paths of optimal investment proportions with \(\gamma =2\), 3, 4 and 5

Full size image

4.2.2 Market price of longevity risk

Market price of risk parameters \(\theta _r\), \(\theta _\lambda\) and \(\theta _S\) all affect the optimal strategy. However, we are more interested in the impact of the longevity risk premium and therefore focus on the parameter \(\theta _\lambda\). From (6), we learn that the longevity risk premium offered by the rolling longevity bond increases with \(-\theta _\lambda\). Figure 3 shows the average optimal strategies for different values of \(\theta _\lambda\). In all these cases, the longevity risk premium is much smaller than the interest rate risk and stock risk premia determined by \(-\theta _r\) and \(\theta _s\), respectively. In general, we observe that the optimal weight for the longevity bond increases with \(-\theta _\lambda\) while the optimal bond weight decreases with \(-\theta _\lambda\). Besides, with increasing \(-\theta _\lambda ,\) the investment in the longevity bond suppresses other assets. This behavior is consistent with conventional thinking that an asset with higher risk premium is more attractive. The top left plot in Fig. 3 indicates that even in the case where the longevity risk premium is very low, the longevity bond dominates the portfolio over the last 8 years. It thus reveals that the kind of longevity bond considered in this work is a very efficient instrument to hedge the longevity risk.

Fig. 3
figure 3

Average paths of optimal investment proportions with \(\theta _\lambda =-0.06\), \(-0.08\), \(-0.12\) and \(-0.14\)

Full size image

We provide Fig. 4 to take a closer look at the impact of \(\theta _\lambda\) on the optimal investment strategies. Again, the higher the longevity risk premium, the higher the portfolio weight for the longevity bond. With other parameters unchanged, a higher \(-\theta _\lambda\) increases the longevity risk premium but does not increase the uncertainty in the longevity bond value. Thus, it makes the longevity bond more attractive. The opposite reaction of bond weight and longevity bond weight against \(\theta _\lambda\) is explained in the discussion of Proposition 5. It is not a surprise that the optimal weight for the stock is barely affected by \(\theta _\lambda\). The reason can be inferred from the optimal solution: the optimal stock weight is \(\frac{\theta _S}{\sigma _S \gamma }\frac{Y(t)}{F(t)}\). \(\frac{\theta _S}{\sigma _S \gamma }\) does not depend on \(\theta _\lambda\) and \(\frac{Y(t)}{F(t)}\) is only slightly affected by \(\theta _\lambda\). Besides, the weight for cash is not sensitive to \(\theta _\lambda\). This is because the changes in bond and longevity bond weights offset each other, and the total proportion in risky assets is not sensitive to \(\theta _\lambda\). In summary, we conclude that the longevity bond is an important element in the pension scheme’s investment portfolio and hedges the scheme’s longevity risk efficiently. Even when the longevity bond provides a relatively low longevity risk premium, it is optimal to invest a large proportion of the scheme’s wealth into the latter, especially during the late management period when the longevity risk is high.

Fig. 4
figure 4

Average paths of optimal investment proportions varying \(\theta _\lambda\)

Full size image

4.2.3 Maturity of the rolling longevity bond

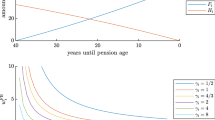
Now, we investigate the optimal strategy when \(T_L\) varies. Generally, Fig. 5 shows that the longer the rolling longevity bond’s maturity, the lower the investment proportions in bond and longevity bond, while more weight is shifted into cash. We observe that \(w_L\) shows an obvious decline when \(T_L\) rises from 5 to 10. No distinguishable change in \(w_L\) is observed when \(T_L\) takes the values 15, 20 and 25. Intuitively, this is because longer maturity times result in more uncertainty in the rolling longevity bonds. For a risk-averse investor, it is therefore better to have less portfolio weight attached to a longevity bond with a longer maturity. Figure 6 shows that \(\frac{1}{h_1(t,t+T_L)}\) is decreasing with \(T_L\) and \(\frac{1}{F(t)}\) does not change much when \(T_L\) changes. According to Proposition 5, this results in the decline of the longevity bond’s weights. At first, \(\frac{1}{h_1(t,t+T_L)}\) drops dramatically when \(T_L\) increases and later on it changes only slightly. Thereafter, we observe that the optimal longevity bond weight decreases with \(T_L\) but is not sensitive to longer maturities.

Fig. 5
figure 5

Average paths of optimal investment proportions varying \(T_L\)

Full size image
Fig. 6
figure 6

\(\frac{1}{h_1(t,t+T_L)}\) and \(\frac{f_1(t,t+T_L)}{f_1(t,t+T_B)}\) versus \(T_L\); Average path of \(\frac{1}{F(t)}\) varying \(T_L\)

Full size image

Compared to \(w_L\), \(w_B\) reacts stronger to changes in \(T_L\). This is apparent from the optimal solution as the changes in \(w_L\) are scaled up by the factor \(-\frac{f_1 (t,t+T_L ) }{f_1 (t,t+T_B)}\). Figure 6 shows that \(\frac{f_1 (t,t+T_L ) }{f_1 (t,t+T_B)}\) increases with \(T_L\). Therefore, the optimal weight for the bond decreases significantly with \(T_L\) due to decreasing \(-\frac{f_1 (t,t+T_L ) }{f_1 (t,t+T_B)}w_L(t)\). The optimal investment proportion in the bond becomes negative during the later years except for the case when \(T_L=5\). This is because the longevity bond is able to hedge longevity risk as well as interest rate risk. When nearing retirement, the need to hedge interest rate risk reduces while the longevity risk is still high. The negative position in the bond offsets the interest rate risk hedge provided by the longevity bond. Even though a negative position in the bond can be observed, the sum of the weights for longevity bond and bond are always positive. In addition, we observe that the longevity bond dominates the portfolio with higher \(T_L.\) Overall, longer maturity times may lessen the attractiveness of longevity bonds. Even though, longer maturity times might be detrimental to investment appeal, longevity bond’s always play an important role in the DC scheme’s risk management, dominating the portfolio during the late management period.

4.2.4 Contribution rate

The minimum requirement for contribution rates for DC schemes in the UK is \(8\%\), see DWP (2013) and OECD (2019). However, apart from the tax consideration, in principle, there is no upper limit on contribution rates. Figure 7 shows the optimal proportions when contribution rate c/w equals to 0.10, 0.20, 0.30 and 0.40. That is, the instantaneous contribution c equals to 1.5, 3, 4.5 and 6. In general, we observe that with increasing c/w, the total weight in risky assets increases while the weight in cash decreases. The intuition behind this observation is that with higher contribution rate, the present value of the scheme’s future income is higher. A high present value of the future income incentives the manager to increase the total investment into risky assets. Since there is guaranteed future income, the manager takes more risk in the hope of earning a higher risk premium. Moreover, the manager invests less in the longevity bond when the contribution rate is high. Although the manager reduces the longevity bond investment, it still remains an important element in the investment portfolio, eventually dominating the investments in other assets.

Fig. 7
figure 7

Average paths of optimal investment proportions varying contribution rate c/w

Full size image

4.2.5 Wage replacement ratio

The wage replacement ratio is a good tool when estimating retirement income needs. A high wage replacement ratio implies that a high fraction of the pre-retirement income is needed to maintain living standard in retirement. OECD (2019) reveals that the net replacement ratio varies from 30 to \(90\%\) among OECD countries. Accordingly, we set \(\pi /w\) equal to 0.30, 0.50, 0.70 and 0.90 to test the impact of wage replacement ratio. In Fig. 8, we observe that it is optimal to increase the fraction of wealth invested into the longevity bond when the wage replacement ratio is high. It is clear that with a higher wage replacement ratio, both the annuity installments \(\pi\) and the guarantee G(t) are higher. However, the wealth process F(t) and the discounted future contributions D(t) do not depend on the wage replacement ratio. Intuitively, a high wage replacement ratio implies that the members require high annuity installments (or, the minimum guarantee) and the scheme is exposed to greater longevity risk. As a consequence, the scheme manager invests a large proportion of the scheme’s wealth into the longevity bond to hedge the longevity risk.

Fig. 8
figure 8

Average paths of optimal investment proportions varying wage replacement ratio \(\pi /w\)

Full size image

5 Conclusion

We studied the optimal investment problem underlying the management of a DC pension scheme in a framework where both interest rate risk and longevity risk are considered. Our theoretical results and subsequent numerical studies showed evidence that the longevity bond plays an important role in DC scheme’s risk management. We observed that a scheme manager with high risk aversion, invests a low proportion in the longevity bond. However, even for a highly risk-averse manager, we showed that it is still optimal to invest a significant proportion of the scheme’s wealth into the longevity bond. Also, compared with the investment ratio’s of the other risky assets, the investment proportion for the longevity bond is shown to be relatively high even in the case where the longevity risk premium is relatively low. Moreover, we observed that longer maturity times could reduce the attractiveness of longevity bonds, however even longevity bonds with longer maturity dominate the other assets in the investment portfolio during the later periods of the scheme. Although the manager reduces investment into longevity bonds when the contribution rate is high, the longevity bond still remains an important element of the investment portfolio. Furthermore, we observed that a high wage replacement ratios incentivizes the scheme manager to invest a higher proportion of wealth into the longevity bond. We conclude that longevity bonds play an important role for DC pension schemes, in particular at times when the mortality risk is increased. They are very attractive to pension schemes and there is genuine potential in the development of mortality-linked derivatives and exchanges for longevity bonds.

There is scope for further research work. In this work, we assumed that the longevity bond’s reference population and the scheme members have the same mortality behavior. However, population basis risk arises when there is a mismatch between the hedging instrument’s underlying mortality experience and the hedging population’s mortality behavior. We investigate the impact of longevity basis risk on the asset allocation and longevity risk hedge in further work Agarwal et al. (2020).