Abstract
Modelling languages are intensively used in paradigms like model-driven engineering to automate all tasks of the development process. These languages may have variants, in which case the need arises to deal with language families rather than with individual languages. However, specifying the syntax and semantics of each language variant separately in an enumerative way is costly, hinders reuse across variants, and may yield inconsistent semantics between variants. Hence, we propose a novel, modular and compositional approach to describing product lines of modelling languages. It enables the incremental definition of language families by means of modules comprising meta-model fragments, graph transformation rules, and rule extensions. Language variants are configured by selecting the desired modules, which entails the composition of a language meta-model and a set of rules defining its semantics. This paper describes: a theory for checking well-formedness, instantiability, and consistent semantics of all languages within the family; an implementation as an Eclipse plugin; and an evaluation reporting drastic specification size and analysis time reduction in comparison to an enumerative approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Modelling languages are ubiquitous in many engineering disciplines, where models represent manageable abstractions of real, complex phenomena. This is no exception for software engineering, where paradigms like model-driven engineering (MDE) [6] make intensive use of modelling languages and models to conduct and provide automation for all phases of the development process. These models are specified via modelling languages, which are often domain-specific [33].
Modelling languages comprise abstract syntax (the concepts covered by the language), concrete syntax (their representation), and semantics (their meaning). In MDE, the abstract syntax of modelling languages is described by a meta-model; the concrete syntax by a model describing the rendering of the language elements; and the semantics by model transformations [71].
Sometimes, languages that share commonalities are organised into families. This is the case, for example, of the more than 120 variations of architectural languages reported in [45], and the many variants of Petri nets [49], access control languages [32] and symbolic automata [12] proposed in the literature. Likewise, language families can be defined to account for variants of a language directed to different kinds of users or contexts of use. For example, within UML, simple versions of class diagrams are suitable for novices; complete versions for experts; and restricted ones (e.g., with single inheritance) for detailed design targeting programming languages like Java. However, describing the syntax and semantics of each language variant separately is costly, does not benefit from reuse across variants, and may yield inconsistent semantics between variants.
To tackle this issue, product lines [58] have been applied to the engineering of modelling languages [48]. Product lines permit the compact definition of a potentially large set of products that share common features. This way, earlier works have created product lines of meta-models [14, 26] and model transformations [16, 66]. However, the former do not consider semantics [14, 26], while the latter do not support meta-model variants [66], are hard to extend [16], or are not based on formalisms that enable asserting consistency properties over the language family [16, 47].
In this work, we propose a novel modular approach for defining language product lines, which considers semantics and ensures semantic consistency across all of the members of the language family. The approach is based on the creation of modules encapsulating a meta-model fragment and graph transformation rules [23]. Modules can also declare different kinds of dependency on other modules, and extend the rules defined in those other modules. Overall, the proposed approach enables the definition of a large set of language variants in a compact way, with the underlying theory ensuring the syntactic well-formedness, instantiability and semantic consistency of each variant. To demonstrate the practicality of our proposal, we report on its realisation on a concrete tool called CaponeFootnote 1, and on an evaluation that shows its benefits over an enumerative approach.
This work extends our previous paper [15] as follows. We support a richer notion of meta-model, including element names, inheritance and OCL constraints. This is supported by a more detailed formalisation of models and meta-models (Sect. 4.1), which allows the analysis of conditions for structural well-formedness of the product line (Sect. 6.1). In addition, we propose a form of lifted instantiability analysis of the product line, to detect possible conflicts between the OCL constraints contributed by the modules of the product line (Sect. 6.2). Finally, we extend our previous evaluation with one more case study, and report on a new experiment that shows the efficiency of our lifted instantiability analysis with respect to a case-by-case analysis. Overall, the evaluations reported in this paper aim at answering the following research questions:
-
RQ1
What is the effort reduction of the approach with respect to an explicit definition of each language variant?
-
RQ2
What is the typical effort for adding a new feature to a language product line?
-
RQ3
In which scenarios is lifted instantiability analysis more efficient than a case-by-case analysis?
Three network language variants, and one example rule of each. (a) Simple links with node failures and acks. (b) Rich links with communication failures. (c) Rich links with communication failures and time. Rules use a compact notation with ++ denoting element creation, -- element deletion, and -> attribute change
The rest of the paper is organised as follows. Section 2 motivates the proposal via a running example, while Sect. 3 provides an overview of the approach. Section 4 introduces the structure of the resulting model of product lines. Section 5 expands them to consider behaviour using rules. Section 6 presents methods to analyse the product lines, including syntactic well-formedness, instantiability, and behaviour consistency. Section 7 reports on the supporting tool and Sect. 8 on an evaluation. Section 9 presents a discussion of the strong points and limitations of the approach. Section 10 compares our approach with related work, and Sect. 11 concludes the paper. An appendix includes the proofs of the proposed lemmas and theorems.
2 Motivation and running example
We motivate our approach based on a family of domain-specific languages (DSLs) to model communication networks, composed of nodes that exchange messages with each other. We would like to support different usages of the language family, such as: study the behaviour of networks with node failures, deal with message loss probabilities, or consider protocols and time performance, among others. As usual in MDE, we represent the language syntax with meta-models, and the semantics via (graph) transformation rules [23].
Figure 1 shows the meta-models of three language variants within the family, and, for each of them, one example rule capturing a small part of the associated behaviour (i.e., the forwarding of a message along nodes). Variant (a) is for a language with simple links between nodes (reference linkedTo), supporting node failures (broken) and a simple protocol (ack). Variant (b) features rich node links (class Link) with a probability simulating communication loss (lossProb). Variant (c), in addition, includes timestamps and size for messages, and considers the speed of links.
A naive approach would define separate meta-models and transformation rules for each language variant. However, as Fig. 1 shows, the various meta-models and the associated rules share commonalities which one may not want to replicate. Moreover, the language family may need to evolve and be extended over time, so adding new language features to it should be easy. However, in a naive approach, incorporating an optional feature (e.g., support for ad-hoc networks) implies duplicating each language variant and adding the new feature to the duplicates, entailing a combinatorial explosion of variants. Finally, evolving the rules of each variant separately may easily lead to inconsistencies between them.
An alternative solution would be to create one language that incorporates all possible features. However, this is not suitable either, as the language users would need to deal with an unnecessarily complex language, when a simpler variant would suffice. Moreover, some language features may be incompatible if they represent alternative options (e.g., a network should not have both simple and rich links at the same time).
We argue that a sensible solution to define and manage a family of languages, like the one described, should meet the following requirements:
-
R1.
Succinctness: Specifying a language family should require much less effort than specifying each language variant in isolation.
-
R2.
Extensibility: Adding a new language variant to the family should be easy, and should not require changing other existing variants, thus allowing incremental language construction.
-
R3.
Reusability: The specifications of language variants should be as reusable as possible, to minimise construction effort and avoid duplications within and across families.
-
R4.
Analysability: It should be possible to analyse a language family to ensure both syntactic (structural) correctness of each meta-model of the family—including their OCL invariants—and consistent behaviour of each language variant with the behaviour of the base language. The analysis should be efficient, and should not rely on a case-by-case examination of each language variant, due to a possibly exponential number of family members.
These requirements stem from our own experience building language families and techniques for their engineering [14, 16, 26], as well as on an analysis of the literature on language product line engineering [48] and compositional language engineering [55].
In the following, starting with an overview in Sect. 3, we propose a novel approach to modelling language variants that satisfies these requirements. The approach enables a compact, extensible specification of the syntax of a language family (Sect. 4), and provides analysis methods to ensure syntactic well-formedness of each meta-model in the family (Sect. 6.1), as well as its instantiability (Sect. 6.2). It also offers a compact, extensible specification of semantics (Sect. 5) that ensures consistency across all members of the family (Sect. 6.3).
3 Overview of the approach
Figure 2 depicts our approach to defining families of languages: each language feature is defined as a module comprising a meta-model fragment for the syntax, and a set of graph transformation rules for the semantics.
A set of modules M\(_1\),\(\dots \),M\(_n\) may extend another module M. In such a case, module M is said to be a dependency of M\(_1\),...,M\(_n\), and modules M\(_1\),\(\dots \),M\(_n\) are its extensions. The extensions M\(_1\),\(\dots \),M\(_n\) need to specify their role in the dependency (label 1 in Fig. 2). The possible roles are the standard variability options in feature modelling [31]: optional (the extension can be present or not in a language variant that includes the dependency), alternative (exactly one of the possible alternative extensions must be present), OR (one or more of the OR extensions can be present), or mandatory (if the dependency is present, so must be the extension). The extension also needs to specify how to merge its structure (i.e., its meta-model) with the one in the dependency module (label 2), and which of its rules extend rules in the dependency, if there is any (label 3).
Then, we define a modular language product line (LPL) as a tree of modules, with relations from the extensions to their dependencies, and one identified root module. A language variant can be obtained from the LPL by making a selection of modules that satisfy the dependencies. This induces proper compositions of the meta-models and rules in the selected modules.
With respect to requirements R1–R4 from Sect. 2, we observe the following.
-
R1.
Succinctness: Using product lines [50, 58] avoids defining each language variant in isolation. Instead, modules describe simpler language features that can be combined to obtain the desired language variant. In support to this claim, Sect. 8 describes an experiment reporting an 86–99% reduction on the specification sizes of language families built with our approach, with respect to defining each language in isolation.
-
R2.
Extensibility: Taking inspiration from practical component-based systems (e.g., Eclipse [22] or OSGI [53]), our modules encapsulate syntax and semantics, and can extend another module. This results in an extensible design of languages, since adding a new module to the LPL does not imply modifying a global structure – like a “monolithic” 150% meta-model overlapping the meta-model of all language variants [26], or a “global” feature model describing all language variants [31]. In addition, the experiment in Sect. 8 shows that the effort of extending by a new feature a language family built with our approach is much lower than relying on an explicit definition of each language in isolation (which may require duplicating the number of meta-models).
-
R3.
Reusability: Extension modules can reuse the syntax and semantics declared in their dependencies, as Sects. 4 and 5 will show.
-
R4.
Analysability: We provide techniques to ensure that each member of a product line is structurally well-formed (cf. Section 6.1), and that it does not present conflicts with the possible integrity constraints that are contributed by each module (cf. Section 6.2). In addition, we rely on graph transformation to express the semantics of modules. This enables consistency checking across all members of a language family (cf. Section 6.3). All of the analysis methods we propose do not rely on a case-by-case exploration of each family member, but are lifted analyses [68], which are applicable to the product-line level, thus generally resulting to be more efficient than a case-by-case analysis (cf. Section 8.2).
4 Language product lines: structure
We now proceed to formalise our approach, focusing on the abstract syntax of the languages. Section 5 will then expand the notion of module with rules to express behaviour. We start by introducing the basic concepts of models, meta-models, and morphisms in Sect. 4.1, which are then used to build the notion of language product line in Sect. 4.2.
4.1 Models, meta-models and morphisms
We use graphs to encode models and meta-models, using the notion of E-graph [23], enriched with labels [52] and inheritance [13]. As mentioned in Sect. 3, our modules are provided with a meta-model to represent the part of the language structure contributed by the module.
An E-graph is defined by two sets of nodes (graph and data nodes), a set of attributes, a set of labels, and a set of edges connecting two graph nodes (called references). Then, functions define the source and target of edges, the owner and values of attributes, and the labelling of nodes, attributes and references. In addition, inheritance is modelled as an acyclic relation between graph nodes. Definition 1 captures this notion.
Definition 1
[E-graph] An E-graph G is a tuple \(G\,{=}\,\langle V, E, A{,} D{,} L{,} owner_E{,} tar{,} owner_A{,} val{,} name_V{,} name_E{,} name_A, I \rangle \), where:
-
V, E, A are sets of vertices (or nodes), edges (or references), and attributes, respectively. We use F (fields) for the set \(E \cup A\).
-
D is a set of data nodes to be used for attribution, and L is a set of labels to be used as identifiers for nodes, references and attributes.
-
\(owner_E :E \rightarrow V\) and \(tar :E \rightarrow V\) are functions returning the source and target nodes of the edges in E, respectively.
-
\(owner_A :A \rightarrow V\) and \(val :A \rightarrow D\) are functions returning, for each attribute, its owner node and its value, respectively.
-
\(name_X :X \rightarrow L\) (for \(X \in \{V, E, A\}\)) are functions returning the name of nodes, references and attributes, respectively.
-
\(I \subseteq V \times V\) is a relation between nodes, representing inheritance: \((v_1,v_2)\in {I}\) means \(v_1\) inherits from \(v_2\).
Given a node \(v \in V\), we write \(sub(v)=\{v_s~|~(v_s, v)\in I^*\}\) for the set of nodes that inherit directly or indirectly from v (including v), with \(I^*\) the reflexive-transitive closure of I.
Remark 1
Given an E-graph G, we use V, E and so on, to refer to its components when no confusion can arise. When considering several graphs (e.g., M, MM), we use the graph name as superindex for the component name (e.g., \(V^M\), \(V^{MM}\), \(E^{M}\), \(E^{MM}\)). We also use owner for \(owner_E~\cup ~owner_A\), and name for \(name_E~\cup ~name_A\). Finally, we define the function \(fields :V \rightarrow E \cup A\) to obtain the set of defined and inherited fields of a node, as \(fields(v) = \{ f \in F~|~v \in sub(owner(f))\}\).
We will use E-graphs (from now on simply graphs) to represent both models and meta-models, where nodes denote either objects or classes, respectively. In the case of models, we require the inheritance relation to be empty. Graphs are often enriched with an algebra over a data signature [61], describing the data types (strings, integers, booleans) used for the attributes. Such graphs are called attributed graphs, and the set D is then defined as the union of the carrier sets of the algebra. In the case of meta-models, attributes specify a data type and do not hold values. This way, meta-models are attributed graphs over a final signature, where the carrier set of each sort has just one element.
Example 1
Figure 3 shows an example of two graphs representing a model and a meta-model. These are depicted using Definition 1 in part (a), and the UML notation in part (b). The meta-model MM contains just one class (v\(_1\)) with name Node, an attribute (a\(_1\)) with name broken of type bool, and a self-reference (e\(_1\)) with name linkedTo. The model M has two objects with names n1 and n2, whose broken attribute values are false and true, and which are connected via relation linkedTo.
Definition 2 gives some well-formedness conditions to be satisfied by graphs used to represent meta-models. The first condition for a meta-model to be well-formed (wff) states that inheritance should be acyclic, the second specifies that class names should be unique, while the third one asserts that the names of the (defined and inherited) fields of each class should not be repeated.
Definition 2
[Wff Meta-model] An E-graph G is said to be a wff meta-model—written wff(G)—if:
-
1.
I is acyclic.
-
2.
\(\forall v_1, v_2 \in V \cdot v_1 \ne v_2 \implies name_V(v_1) \ne name_V(v_2)\)
-
3.
\(\forall v \in V \cdot \forall f_1, f_2 \in fields(v) \cdot f_1 \ne f_2 \implies \) \(name(f_1) \ne name(f_2)\)
We also need to relate graphs to each other, for example, to specify a type relationship between a model and a meta-model, to identify a meta-model into a “bigger” one (which we use for extending the meta-model of a dependency module in extension modules), or to find an occurrence of a graph transformation rule within a model. For this purpose, we introduce graph morphisms, as a tuple of functions mapping the corresponding sets of elements in the two graphs, preserving all the functions within the graphs.
Definition 3
[Graph Morphism] Given two graphs G and H, a graph morphism \(f :G \rightarrow H\) is a tuple \(f=\langle f_X :X^G \rightarrow X^H \rangle \) (for \(X \in \{V, E, A, D, L\}\)) s.t.:
-
1.
Function \(owner_E\) and tar commute, taking into account inheritance:
$$\begin{aligned} \begin{aligned} \forall e \in E^G \cdot&f_V(owner_E^G(e)) \in sub(owner_E^H(f_E(e))~\wedge \\&f_V(tar^G(e)) \in sub(tar^H(f_E(e)) \end{aligned} \end{aligned}$$ -
2.
Function \(owner_A\) commutes, taking into account inheritance:
$$\begin{aligned}\forall a \in A^G \cdot f_V(owner_A^G(a)) \in sub(owner_A^H(f_A(a))\end{aligned}$$ -
3.
Functions val and \(name_X\) (for \(X \in \{V, E, A\}\)) commute: \(f_D \circ val^G = val^H \circ f_A\) and \(f_L \circ name_X^G = name^H_X \circ f_X\).
Remark 2
Note that, if the target graph H of a graph morphism has empty inheritance relation, conditions 1 and 2 in Definition 3 are equivalent to plain commutativity, since then \(sub(n)=\{n\}\) for every node \(n \in V\).
Example 2
Figure 3 shows an example morphism representing the conformance relation between model M and meta-model MM. The morphism maps each element in the sets V, E, A, D and L, making the functions satisfy conditions 1–3 in Definition 3. For example, \(f_V(owner_E^M(e_2))=v_1\), \(owner_E^{MM}(f_E(e_2))=v_1\), and \(v_1 \in sub(v_1)\) (as required by condition 1). We also have \(f_V(owner^{M}_A(a_2))=v_1\), \(owner_A^{MM}(f_A(a_2))=v_1\), and \(v_1 \in sub(v_1)\) (as required by condition 2). Finally, we have \(f_L(name^{M}_A(a_3))=broken=name^{MM}_A\) \((f_A(a_3))\) (as required by condition 3).
4.2 Language modules and product lines
We now define the notion of language module as a tuple containing a meta-model (as in Definition 1) that is wff (as in Definition 2), a dependency, the role of the module in the dependency, a spanFootnote 2 of morphisms (as in Definition 3) identifying elements of the module meta-model with those of its dependency, and a formula to restrict the choice of modules in configurations.
Definition 4
[Language Module] A language module is a tuple \(M=\langle {MM}, M_D, RO, IN, \Psi \rangle \), where:
-
MM is a well-formed meta-model.
-
\(M_D\) is a module, called dependencyFootnote 3.
-
\(RO \in \{ALT,OR,OPT,MAN\}\) is the role of M in the dependency, one among alternative, OR, optional, and mandatory.
-
\(IN= MM\longleftarrow {C}\longrightarrow {MM}(M_D)\) is an inclusion span between MM and the meta-model of M’s dependency, where C is a graph made of the common elements of MM and \(MM(M_D)\).
-
\(\Psi \) is a boolean formula using modules as variables.
M is said to be a top module if \(M_D=M\) and \(\Psi = true\). We use the predicate top(M) to identify top modules: \(top(M) \triangleq M_D(M)=M \wedge \Psi (M)=true\).
Remark 3
Based on Definition 4, we use the following notation. Given a module \(M_i\), we use MM\((M_i)\) for the meta-model of \(M_i\), and similarly for the other components of \(M_i\) (i.e., \(M_D\), RO, IN, \(\Psi \)). \(DEP^+(M_i)\) denotes the transitive closure of its dependencies (i.e., a set consisting of its dependency, the dependency of its dependency, etc.). \(DEP(M_i)=DEP^+(M_i) {\setminus } \{M_i\}\) is the transitive closure excluding itself, which is empty in top modules, and equal to \(DEP^+\) in non-top ones. \(DEP^*(M_i)=DEP^+(M_i) \cup \{M_i\}\) is the reflexive-transitive closure (i.e., including the module \(M_i\) as well). Typically, IN is the identity inclusion for top modules.
A language product line (LPL) is a set of modules with a single top module (1), closed under the modules’ dependencies (2), and without dependency cycles (3).
Definition 5
[Language Product Line] A language product line \(LPL = \{ M_i \}_{i \in I}\) is a set of modules s.t.:
Example 3
Figure 4 shows the LPL for the running example. It comprises 8 modules: Networking, NodeFailures, Ack, TimeStamped, SimpleLink, RichLink, Speed, and CommFailures, each showing its meta-model inside. Note that the LPL is just a collection of modules. Figure 4 represents the modules graphically, marked with a name, and related by the roles they declare in their dependencies, using the standard feature model notation shown in Fig. 2. That is to say, our LPLs do not include a separate feature model.
For extensibility, dependencies are expressed from a module (e.g., Ack) to its dependency (e.g., Networking). This permits adding new modules to the LPL without modifying existing ones. Figure 4 omits the dependency of the top module (Networking) and the span IN of each module is implicit, given by the equality of names of meta-model elements in both an extension module and its dependency. For example, class Message in module Ack is mapped to class Message in module Networking. Module TimeStamped has a formula \(\Psi \) stating that, if a language variant includes the module TimeStamped, then it must also include the module Speed. For clarity, the figure omits the formula \(\Psi \) when it is true, as is the case for all modules but TimeStamped.
We use TOP(LPL) to denote the only top module in LPL. Given a module \(M_i \in LPL\), we define the sets \(X(M_i)=\{M_j \in LPL~|~M_D(M_j)\) \(=M_i~\wedge ~RO(M_j)=X\}\), for \(X\in \{ALT,OR,OPT,MAN\}\), to obtain the extension modules of \(M_i\) with role X.
Example 4
The top module of the LPL of Fig. 4 is Networking. For this module, we have ALT(Networking) \(=\{\) SimpleLink, RichLink\(\}\), OPT(Networking) \(=\{\) NodeFailures, Ack, TimeStamped\(\}\), while MAN(Networking) and OR(Networking) are empty.
Given an LPL, a specific language of the family can be obtained by choosing a valid configuration of modules, as per Definition 6.
Definition 6
[Language Configuration] Given a language product line LPL, a configuration \(\rho \subseteq LPL\) is a set of modules s.t.:
We use CFG(LPL) to denote the set of all configurations of LPL.
A configuration \(\rho \) should contain the top module of the LPL (1) and, if \(\rho \) includes a module, then it should also include: all of its mandatory extension modules (2), exactly one of its alternative extension modules (3), at least one of its OR extension modules (4), and its dependency (5). Recall that the top module has itself as its only dependency. Finally, the formulae of all modules in the LPL should evaluate to true when substituting the modules that the configuration includes by true, and the rest by false (6).
Example 5
The LPL of Fig. 4 admits 24 configurations, including \(\rho _{0}=\{\) Networking, SimpleLink\(\}\) (the smallest configuration), \(\rho _{1}=\{\) Networking, SimpleLink, NodeFailures, Ack\(\}\), \(\rho _{2}=\{\) Networking, RichLink, CommFailures\(\}\), and \(\rho _{3}=\{\) Networking, RichLink, CommFailures, TimeStamped, Speed\(\}\). Due to \(\Psi \) (TimeStamped), a configuration that selects TimeStamped must select Speed as well. Configurations can include zero or more modules of OPT(Networking), and must include one or more modules of OR(RichLink) when RichLink is selected.
Given an LPL and a set \(S\subseteq {LPL}\), we use the predicate \(valid_{LPL}(S)\) to check if there is a language configuration on which the modules in S appear together: \(valid_{LPL}(S) \triangleq \exists \rho \in CFG(LPL) \cdot S \subseteq \rho \). In our example, we have, e.g., \(valid_{LPL}(\{\) Speed, Ack\(\})\), but \(\lnot valid_{LPL}(\{\) SimpleLink, RichLink\(\})\).
Given a configuration \(\rho \), we derive a product meta-model by merging the meta-models of all the modules in \(\rho \), using the inclusion spans as glueing points. This is formalised through the categorical notion of co-limit [40], which creates an E-graph using all the meta-models of the selected modules, and merging the elements that are identified by the morphisms.
Definition 7
[Derivation] Given a language product line LPL and a configuration \(\rho \in CFG(LPL)\), the product meta-model \(MM_\rho \) is given by the co-limit object of all meta-models and spans in the set \(\{IN(M_i)=\langle MM(M_i)\longleftarrow {C}\longrightarrow MM(M_D(M_i)) \rangle \mid {M}_i\in \rho \}\).
We use \(PR(LPL)=\{MM_\rho ~|~\rho \in CFG(LPL)\}\) for the set of all derivable product meta-models of LPL.
Example 6
Figures 1(a)–(c) from Sect. 2 show the product meta-models \(MM_{\rho _1}\), \(MM_{\rho _2}\) and \(MM_{\rho _3}\), respectively. Figure 5 details the calculation of \(MM_{\rho _1}\) using a co-limit. It shows the meta-model of each module in the configuration \(\rho _1\) (i.e., Networking, NodeFailures, Ack and SimpleLink), the intermediate E-graphs of the inclusion spans (\(C_{M_i,M_D(M_i)}\)), and the morphisms. The co-limit object \(MM_{\rho _1}\) includes all elements in the meta-models, merging those identified by the morphisms (i.e., those with the same name), and s.t. each triangle or square of morphisms commute. For readability, we omit the identity span of the top module Networking.
The behaviour associated with modules is specified through graph transformation rules (see Sect. 5.2). Hence, given a language product line LPL and a module \(M \in LPL\), we need to derive the meta-model used to type the rules of M. This meta-model—called the effective meta-model of M—is composed of the meta-models of the modules included in all configurations that include M. This way, we define the set \(CDEP(M)=\bigcap \{\rho \in CFG(LPL)~|~M\in \rho \}\), which is the intersection of all configurations that include M, and comprises the explicit module dependencies of M (i.e., \(DEP^*(M)\)) as well as the implicit dependencies due to the formula \(\Psi \) in modules. Then, the effective meta-model of M, noted EFF(M), is \(MM_{CDEP(M)}\), calculated as in Definition 7 but using CDEP(M) instead of a configuration \(\rho \). Intuitively, EFF(M) is the common slice of any product meta-model \(MM_\rho \) s.t. \(M \in \rho \).
Example 7
The effective meta-model of CommFailures is \(MM_{\rho _2}\) in Fig. 1(b), as CDEP(CommFailures\()=\{\) CommFailures, RichLink, Networking\(\}\). In turn, \(CDEP (\) TimeStamped\()=\{\) TimeStamped, Networking, Speed, RichLink\(\}\), since Speed appears in every configuration that includes TimeStamped—due to the formula in the latter module—while RichLink belongs to any configuration containing Speed.
In our formalisation of LPL, we purposely mix the product space (i.e., the modules) and the variability space (i.e., the feature model). One can see our modules as features, and derive a feature model from their dependencies, which then can be used to select a configuration, as shown in Sect. 7.
An important property to be analysed of an LPL is whether all its derivable meta-models \(MM_\rho \in PR(LPL)\) are well-formed meta-models. We defer the analysis of this property of LPLs to Sect. 6.1.
5 Language product lines: behaviour
Next, we extend LPLs with behaviour. First, Sect. 5.1 defines rules and extension rules, which Sect. 5.2 uses to extend modules and LPLs with behaviour.
5.1 Rules and extension rules
We use graph transformation rules to express module behaviour. Following the double pushout approach [23], a rule is defined by a span of three graphs: a left-hand side graph L, a right-hand side graph R, and a kernel graph K identifying the elements of L and R that the rule preserves. In addition, a rule has a set of negative application conditions (NACs), as Definition 8 shows.
Definition 8
[Graph Transformation Rule] A rule \(r=\langle L{\mathop {\longleftarrow }\limits ^{l}}K{\mathop {\longrightarrow }\limits ^{r}}R,\) \(NAC=\{L {\mathop {\longrightarrow }\limits ^{n_i}}N_i\}_{i \in I}\rangle \) consists of an injective span of (E-graph) morphisms and a set of negative application conditions, expressed as injective (E-graph) morphisms.
Remark 4
We use rules over typed E-graphs, with each of L, K, and R having a type morphism to a common meta-model.
Example 8
Figure 6(a) shows a rule example (depicting the transfer of a message from a sending node to a receiving one) according to Definition 8. Morphisms l, r identify elements with equal name. The rule is applicable on any model that contains two nodes, one of them having a message (graph L). Applying the rule deletes the edge from the message to the first node (graph K) and creates an edge from the message to the second node (graph R). We adopt a compact notation for rules, like that used in the Henshin [2] tool (cf. Fig. 6(b)), where all graphs L, K, R and \(N_i\) are overlapped. Elements in \(L \setminus K\) (those deleted) are marked with \(--\), those in \(R \setminus K\) (those created) are marked with \(++\), and those in a NAC (those forbidden) are marked with !! plus a subindex in case the rule presents several NACs.
(a) Rule move from module Networking using Definition 8. (b) Compact notation for rules
To enable the reuse of the rule-based behaviour defined for one module in its extensions, we propose a mechanism for rule extension that is based on higher-order rules [69]. Our extension rules add elements to a base rule. We support two kinds of extension rules: \(\Delta \)-rules, adding elements to L, K and R, and NAC-rules, adding extra NACs. Definition 9 starts with \(\Delta \)-rules.
Definition 9
[\(\Delta \)-rule] A \(\Delta \)-rule \(\Delta _r=\langle {L}{\mathop {\longleftarrow }\limits ^{l}}{K}{\mathop {\longrightarrow }\limits ^{r}}{R},\Delta {L}{\mathop {\longleftarrow }\limits ^{\Delta {l}}}\Delta { K}{\mathop {\longrightarrow }\limits ^{\Delta {r}}}\Delta {R},m=\langle m_X :X \rightarrow \Delta {X}\rangle ~\text {(for}~X\in \{L,K,R\})\rangle \) is composed of two spans and a triple \(m=\langle m_L, m_K, m_R \rangle \) of injective morphisms s.t. all squares commute (\(m_L \circ l = \Delta l \circ m_K\), \(m_R \circ r = \Delta r \circ m_K\)).
Example 9
Figure 7(a) shows an example \(\Delta \)-rule, augmenting any rule having two nodes in its left-hand side, with a link between them. We use a compact notation for \(\Delta \)-rules—illustrated by Fig. 7(b)—where the added elements are enclosed in regions labelled as \(\Delta \) followed by the place of addition: {preserve} for L, K and R; {delete} for L; {create} for R. Thus, the \(\Delta \)-rule in Fig. 7(a) adds a Link node and two edges to the L, K, and R components of a rule.
A \(\Delta \)-rule is applied to a standard rule via three injective morphisms, by calculating pushouts (POs), as per Definition 10. A PO is a glueing construction—a form of co-limit—that merges two graphs through the common elements identified via a third graph [40].
Definition 10
[\(\Delta \)-rule Application] Given a \(\Delta \)-rule \(\Delta _r\), a rule \(r'\), and a triple \(n=\langle n_X :X \rightarrow X' \rangle \) (for \(X\in \{L, K, R\}\)) of injective morphisms s.t. the back squares (1) and (2) in Fig. 8 commute, applying \(\Delta _r\) to \(r'\) (noted \(r' {\mathop {\Longrightarrow }\limits ^{\Delta _r}}r''\)) yields rule \(r''=\langle {L''}{\mathop {\longleftarrow }\limits ^{l''}}K''{\mathop {\longrightarrow }\limits ^{r''}}R'', NAC''=\{L''{\mathop {\longrightarrow }\limits ^{n''_i}}N''_i\}_{i\in I}\rangle \), built as follows:
-
1.
Span \(L'' {\mathop {\longleftarrow }\limits ^{l''}}K''{\mathop {\longrightarrow }\limits ^{r''}}R''\) is obtained by the POs of the spans \(X'{\mathop {\longleftarrow }\limits ^{n_X}}X{\mathop {\longrightarrow }\limits ^{m_X}}\Delta X\) (for \(X{\in }\{L, K, R\}\)), where morphisms \(l''\) and \(r''\) exist due to the universal PO property (over \(K''\))Footnote 4.
-
2.
The set \(NAC''\) is obtained by the POs of the spans \(N'_i {\mathop {\longleftarrow }\limits ^{n'_i}}L' {\mathop {\longrightarrow }\limits ^{ll}}L''\) (square (3) in Fig. 8) for every \(L'{\mathop {\longrightarrow }\limits ^{n'_i}}N'_i\) in \(NAC'\).
Example 10
Figure 9 illustrates the application of a \(\Delta \)-rule to a rule. In particular, the figure shows the application of the \(\Delta \)-rule \(\Delta \) move-rl (from RichLink) to rule move (from Networking), which were shown in Figs. 6 and 7. The \(\Delta \)-rule \(\Delta \) move-rl is applicable at match \(n=\langle n_L, n_K, n_R \rangle \), since move has two nodes in L, K and R. Applying \(\Delta \) move-rl produces another rule \(\langle {L''}{\mathop {\longleftarrow }\limits ^{l''}}K''{\mathop {\longrightarrow }\limits ^{r''}}R'', NAC''=\emptyset \rangle \) that increases rule move with the Link object connecting both nodes. Hence, the resulting rule can move the message between the nodes, only if they are connected by a Link.
A \(\Delta \)-rule \(\Delta '_r\) can also be applied to another \(\Delta \)-rule \(\Delta _r\) yielding a composed \(\Delta \)-rule that performs the actions of both \(\Delta \)-rules. The main idea is to match \(\Delta '_r\) on \(\Delta L \leftarrow \Delta K \rightarrow \Delta R\) of \(\Delta _r\), and compose the actions of both rules, as per Definition 11.
Definition 11
[\(\Delta \)-rule Composition] Let \(\Delta _r\) and \(\Delta _r'\) be two \(\Delta \)-rules, and \(n=\langle n_X :X' \rightarrow \Delta X \rangle \) (for \(X=\{L, K, R\}\)) be a triple of morphisms s.t. the squares (1) and (2) at the top of Fig. 10 commute. The composition of \(\Delta _r'\) and \(\Delta _r\) through n, written \({\Delta _r'} +_{n} {\Delta _r}\), is a \(\Delta \)-rule \(\langle L{\mathop {\longleftarrow }\limits ^{l}}K{\mathop {\longrightarrow }\limits ^{r}}R, \Delta L''{\mathop {\longleftarrow }\limits ^{\Delta l''}}\Delta K''{\mathop {\longrightarrow }\limits ^{\Delta r''}}\Delta R'', m''=\langle m''_L, m''_K, m''_R \rangle \rangle \) where the span \(\Delta L'' {\mathop {\longleftarrow }\limits ^{\Delta l''}}\Delta K''{\mathop {\longrightarrow }\limits ^{\Delta r''}} \Delta R''\) results from the POs of spans \(\Delta X {\mathop {\longleftarrow }\limits ^{n_X}}X'{\mathop {\longrightarrow }\limits ^{m'_X}}\Delta X'\) (for \(X{\in }\{L,K,R\}\))Footnote 5, and \(m''_X :X \rightarrow \Delta X=\Delta m_X \circ m_X\) (for \(X=\{L, K, R\}\)).
Given a \(\Delta \)-rule \(\Delta _r\) and a rule r (\(\Delta \)- or standard), we write \(n :\Delta _r \rightarrow r\) to denote the morphism triple between \(\Delta _r\) and r. NAC-rules rewrite standard rules by adding them a NAC, as per Definition 12.
Definition 12
[NAC-rule and application] A NAC-rule \(N_r=\langle {n}:{NL}\rightarrow {N}\rangle \) consists of an injective morphism. Given a NAC rule \(N_r\), a rule \(r=\langle L {\mathop {\longleftarrow }\limits ^{l}}K{\mathop {\longrightarrow }\limits ^{r}}R,NAC\rangle \), and an injective morphism \(m :NL \rightarrow L\), applying \(N_r\) to r via m (written \(r {\mathop {\Longrightarrow }\limits ^{N_r}}r'\)) yields \(r'=\langle L {\mathop {\longleftarrow }\limits ^{l}}K{\mathop {\longrightarrow }\limits ^{r}}R, NAC \cup \{L {\mathop {\longrightarrow }\limits ^{n'}}N'\}\rangle \), where \(N'\) is the PO object of \(N{\mathop {\longleftarrow }\limits ^{n}}NL{\mathop {\longrightarrow }\limits ^{m}}L\) (see diagram below).

Example 11
Figure 11 shows examples of applications of \(\Delta \)- and NAC-rules. \(\Delta \)-rule (a)—called \(\Delta \) move-cf—is provided by module CommFailures, and adds an attribute lossProb and a condition. NAC-rule (b)—called NAC-broken—is provided by module NodeFailures, and adds a NAC that forbids the Node from being broken. For illustration of Definition 11, \(\Delta \)-rule (c) is the result of the composition of the \(\Delta \)-rules \(\Delta \) move-rl (shown in Fig. 7) and \(\Delta \) move-cf, via the Link identified by l. Specifically, \(\Delta \) move-cf is applied on the \(\Delta \) {preserve} part of \(\Delta \) move-rl. The resulting \(\Delta \)-rule performs all actions of the two \(\Delta \)-rules.
(a) \(\Delta \)-rule from module CommFailures. (b) NAC-rule from module NodeFailures. (c) \(\Delta \)-rule resulting from composing \(\Delta \)-rules (a) and \(\Delta \) move-rl in Fig. 7. (d) Result of applying \(\Delta \)-rule (c) to rule move in Fig. 6. (e) Result of applying NAC-broken to rule (d) twice
Figure 11(d) is the rule resulting from applying \(\Delta \)-rule (c) to the rule move in Fig. 6, so that additional preserved elements are added to it (cf. Definition 10). Finally, the rule in Fig. 11(e) results from applying NAC-rule (b) to rule (d) twice (cf. Definition 12). This adds two NACs to (d) via two different morphisms: one identifying n with n1, and another identifying n with n2. These NACs are marked with \(!!_1\) and \(!!_2\).
Remark 5
The application of NAC- and \(\Delta \)-rules to a given rule, and the composition of \(\Delta \)-rules, are independent of the order of execution:
-
Given a rule r and a set \(D=\{m_i :\Delta _{r_i} \rightarrow r\}_{i\in I}\) of morphism triples from \(\Delta \)-rules into r, we can apply each \(\Delta \)-rule in D to r in any order, yielding the same result since \(\Delta \)-rules are non-deleting and there is no forbidding context for their application. We use the notation \(r{\mathop {\Longrightarrow }\limits ^{D}}r'\) for the sequential application \(r{\mathop {\Longrightarrow }\limits ^{\Delta _{r_0}}}r_0{\mathop {\Longrightarrow }\limits ^{\Delta _{r_1}}}\dots {r'}\) of each \(\Delta \)-rule in D starting from r.
-
The result of the composition of a set of \(\Delta \)-rules (\(\Delta _{r_i}\)) with a \(\Delta \)-rule (\(\Delta _{r}\)) is independent of the application order. Given a set \(D=\{m_i :\Delta _{r_i} \rightarrow \Delta _r\}_{i \in I}\), \(\amalg _D\) denotes the \(\Delta \)-rule that results from composing each \(\Delta _{r_i}\) (through \(m_i\)) to \(\Delta _r\) in sequence.
-
The result of the application of NAC-rules is independent of the application order. Given a set N of morphisms from NAC-rules into a rule r, we write \(r{\mathop {\Longrightarrow }\limits ^{N}}r'\) to denote the sequential application of each NAC-rule in N starting from r.
5.2 Behavioural language product lines
To add behaviour to LPLs, we incorporate into modules a set R of rules, two sets \(\Delta R\) and \( NR \) of extension rules (which are \(\Delta \)-rules and NAC-rules, respectively), and two sets EX and \( NEX \) of morphisms from the extension rules to (standard and \(\Delta \)-) rules in the module dependencies. This is captured by the next definition.
Definition 13
[Behavioural Module] A behavioural module extends Definition 4 of language module as follows. A behavioural module \(M=\langle MM, M_D, RO, IN,\) \(\Psi , R, \Delta R, NR ,EX, NEX \rangle \) consists of:
-
MM, \(M_D\), RO, IN and \(\Psi \) as in Definition 4.
-
Sets \(R=\{r_i\}_{i \in I}\) of rules, \(\Delta R=\{\Delta _{r_j}\}_{j \in J}\) of \(\Delta \)-rules, and \( NR =\{N_{r_h}\}_{h\in {H}}\) of NAC-rules, all typed by the effective meta-model of M, EFF(M).
-
A set \( EX =\{ m_{ij} :\Delta _{r_i} \rightarrow r_j~|~\Delta _{r_i} \in \Delta R \wedge r_j \in (R(M_j) \cup \Delta R(M_j)) \wedge M_j \in DEP(M) \}\) of morphism triples \(m_{ij}\) mapping each \(\Delta _{r_i} \in \Delta R\) to at least a (\(\Delta \)- or standard) rule \(r_j\) in some module \(M_j\) of M’s dependencies.
-
A set \( NEX =\{m_{ij} :NL_i \rightarrow L_j~|~N_{r_i} \in NR \wedge r_j \in R(M_j) \wedge M_j \in DEP(M) \}\) of morphisms \(m_{ij}\) mapping each NAC-rule \(N_{r_i}=\langle n_i :NL_i \rightarrow N_i\rangle \in NR \) to at least a rule \(r_j\) (with LHS \(L_j\)) in some module \(M_j\) of M’s dependencies.
Remark 6
Definition 13 uses \(R(M_j)\) (resp. \(\Delta R(M_j)\)) to refer to the set R (resp. \(\Delta R\)) within the behavioural module \(M_j\). In the following, we will use a similar notation for the other components of behavioural modules. Since the sets EX and \( NEX \) in Definition 13 contain morphisms to (\(\Delta \)-)rules in DEP(M), it follows that top modules cannot define extensions for their own rules.
We omit the definitions of behavioural LPL, configuration of a behavioural LPL and CFG since they are the same as in Definitions 5 and 6, but only considering behavioural modules instead of modules. However, we need to provide a new notion of behavioural derivation that complements that of Definition 7 (yielding a meta-model) with rule composition via the extension rules (yielding a set of rules).
First, Definition 14 characterises the sets of extension rules that apply to a given (standard or \(\Delta \)-) rule.
Definition 14
[Rule Extensions] Given a behavioural language product line BPL, a behavioural module \(M_i \in BPL\), a rule \(r \in R(M_i)\), and a \(\Delta \)-rule \(\Delta _r \in \Delta R(M_i)\), we define the sets:
-
\( EX (\Delta _r)=\{ m_j :\Delta _{r_j} \rightarrow \Delta _r~|~M_j\in BPL \wedge M_i\in DEP(M_j) \wedge m_j \in EX (M_j)\}\) of all morphism triples from every \(\Delta \)-rule \(\Delta _{r_j}\) rewriting \(\Delta _r\).
-
\( CEX (r)=\{ m_{j} :\amalg _{EX(\Delta _{r_j})} \rightarrow r~|~M_j\in BPL \wedge M_i\in DEP(M_j)\) \(\wedge ~\Delta _{r_j}\rightarrow r \in EX (M_j)\}\) of all morphism triples from every \(\Delta \)-rule \(\Delta _{r_j}\) (composed with all the extensions in \(EX(\Delta _{r_j})\)) rewriting r.
-
\( NEX (r)=\{ m :NL \rightarrow L~|~M_j\in BPL \wedge M_i\in DEP(M_j) \wedge m\in NEX (M_j)\}\) of all morphisms from every NAC-rule \(N_r\) adding a NAC to r.
Given a behavioural LPL and a configuration, we can perform a behavioural derivation. This yields the set of rules in the selected modules, extended by the rule extensions defined in those modules.
Definition 15
[Behavioural Derivation] Given a behavioural product line BPL and a configuration \(\rho \in CFG(BPL)\), we obtain the set \(R=\{r^{\prime \prime }_i\}_{i\in I}\), where each rule \(r^{\prime \prime }_i\) is obtained by the rewriting  of each rule \(r_i\in \bigcup _{M_j\in \rho }R(M_j)\) defined by the modules included in the configuration. We may also use the notation \(\rho (r_i)\) for the resulting rule \(r^{\prime \prime }_i\).
of each rule \(r_i\in \bigcup _{M_j\in \rho }R(M_j)\) defined by the modules included in the configuration. We may also use the notation \(\rho (r_i)\) for the resulting rule \(r^{\prime \prime }_i\).
Example 12
Consider the configuration \(\rho = \{\) Networking, NodeFailures, RichLink, CommFailures\(\}\) and the rules of Figs. 7 and 11. Then, \( EX (\Delta \) move-rl\()=\{\Delta \) move-cf\({\rightarrow }\Delta \) move-rl\(\}\), with the \(\Delta \)-rule \(\amalg _{EX(\Delta move-rl)}\) shown in Fig. 11(c). Now, \( CEX (\) move\()=\{\amalg _{EX(\Delta move-rl)}{\rightarrow }\) move\(\}\), and rule move’ in Fig. 11(d) results from the derivation move move’. Note that \( EX (\) Rich-Link) contains a morphism triple from \(\Delta \) move-rl to move. Composing \(\Delta \) move-rl with all extensions in \( EX (\Delta \) move-rl) preserves such morphism triples (since composition adds elements to the \(\Delta \) part of the rule only), which are then used in set \( CEX (\) move). Finally, \( NEX (\) move) contains two morphisms from NAC-broken in module NodeFailures to move. Thus, move” (cf. Figure. 11(e)) is obtained by move’
move’. Note that \( EX (\) Rich-Link) contains a morphism triple from \(\Delta \) move-rl to move. Composing \(\Delta \) move-rl with all extensions in \( EX (\Delta \) move-rl) preserves such morphism triples (since composition adds elements to the \(\Delta \) part of the rule only), which are then used in set \( CEX (\) move). Finally, \( NEX (\) move) contains two morphisms from NAC-broken in module NodeFailures to move. Thus, move” (cf. Figure. 11(e)) is obtained by move’ move”. The morphisms in \( NEX \), from NAC-broken to move, are also valid morphisms from NAC-broken into move’, since the derivation via \( CEX \) only adds elements to move.
move”. The morphisms in \( NEX \), from NAC-broken to move, are also valid morphisms from NAC-broken into move’, since the derivation via \( CEX \) only adds elements to move.
6 Language product lines: analysis
We now describe some analysis methods for LPLs. We start in Sect. 6.1 with the most basic structural property: well-formedness. Then, to enhance the applicability of our approach, Sect. 6.2 expands our notion of meta-model with OCL integrity constraints, and proposes methods to detect conflicts between the OCL constraints declared in different modules. Finally, Sect. 6.3 analyses behavioural consistency of the LPL, i.e., checking that the behaviour of every language does not contradict that of simpler language versions.
6.1 LPL well-formedness
A desirable property of LPLs is that every derivable meta-model be wff, according to Definition 2. Hence, we define the notion of well-formed LPL as follows.
Definition 16
[Wff Language Product Line] A language product line LPL is well-formed if \(\forall MM \in PR(LPL) \cdot \) wff(MM).
According to Definition 2, three conditions are required in a wff meta-model: unique class names, unique field names and acyclic inheritance. However, generating and checking the conditions in each product meta-model may be highly inefficient, since the number of derivable meta-models may be exponential in the number of modules. Therefore, this section proposes analysing those properties at the product-line level through a lifted analysis [68].
Our proposed analyses rely on the notion of 150% meta-model (150 MM in short),Footnote 6 which is the overlapping of the meta-models of all modules, where each element (class, attribute, reference, inheritance relation) is annotated with the module that produces it. We call such annotations presence conditions (PCs).
Definition 17
[150% Meta-model] Given a language product line LPL, its 150% meta-model 150 MM\(_{LPL}\) is a tuple 150 MM\(_{LPL}=\langle MM_{LPL}, \Phi _X :X^{MM_{LPL}} \rightarrow LPL \rangle \) (for \(X \in \{V, E, A, I\}\)) with:
-
\(MM_{LPL}=\) Co-limit of \(\{IN(M_i)=\langle MM(M_i)\longleftarrow {C_i}\longrightarrow MM(M_D(M_i)) \rangle \mid {M}_i\in LPL\}\)
-
\(\forall c \in X^{MM_{LPL}}\cdot \Phi _X(c)=M_i\) (for \(X \in \{V, E, A, I\}\)) iff \(\exists c' \in X^{MM(M_i)} \cdot f_i(c')=c~\wedge ~(\lnot top(M_i) \implies \not \exists z \in X^{C_i} \cdot g_i(z)=c)\), with \(f_i\) and \(g_i\) morphisms used to create \(MM_{LPL}\) (see diagram below).

Example 13
Figure 12 shows the 150 MM for the running example. Each element c in the 150 MM is tagged with the module originating it, \(\Phi _X(c)\), which is its PC. Since Networking is a top module, its elements (Message, Node, to, at, from) are tagged with [Networking]; for example, \(\Phi _V(\) Message) \(=\) Networking. Each non-top module M becomes the PC of the elements mapped from its meta-model, but not from the meta-model of its dependency. Intuitively, spans can be seen as graph transformation rules that add elements to the 150 MM, and those added elements receive the originating module as PC. For example, module Speed only adds the attribute speed, since it is the only element in morphism \(f_i\) which is not in \(g_i\) (cf. Figure 12), and so, the attribute is annotated with the PC Speed.
Remark 7
Each function \(\Phi _X\) is well defined. First, each element c in \(MM_{LPL}\) is mapped from some element in the meta-model of some module. This means that \(\Phi _X(c)\) has at least one candidate module. Actually, it has exactly one module, since c is produced either by a single top module, or by a non-top one. By the co-limit construction, no two different modules may introduce the same element, as this would then be replicated in \(MM_{LPL}\). Notationally, as with other functions, we use \(\Phi _F\) for \(\Phi _A \cup \Phi _E\), and omit the subindex when it is clear from the context.
As an additional remark, \(MM_{LPL}\) may not be a wff meta-model, since it may have repeated class and field names, as well as inheritance cycles. This is natural, since it is the overlap of all meta-models in the language family. Instead, we are rather interested in checking if all derivable meta-models are wff, hence, if the LPL itself is wff. We can exploit the 150 MM for this purpose.
For a start, Lemma 1 states the conditions for an LPL to produce meta-models with distinct class names.
Lemma 1
[Unique Class Names] Given a language product line LPL, each meta-model product \(MM_\rho \in PR(LPL)\) has unique class names iff:
Proof
In appendix. \(\square \)
Example 14
Figure 13(a) shows a variation of the running example to illustrate Lemma 1. Here, the modules MessageLength and MessageContent provide two pairs of classes with same name (Node and Message), as the 150 MM depicted in Fig. 13(b) shows. However, since both modules cannot belong together in a configuration (i.e., \(\lnot valid_{LPL}(\{\) MessageLength, MessageContent\(\})\)), the conditions for Lemma 1 are satisfied and the LPL does not generate meta-models with repeated class names.
One could observe that a more sensible design of the LPL would be to move the Message class and the at reference to module Networking’, leaving in MessageLength and MessageContent only the addition of the respective attributes length and body. This would minimise repetition across modules, and improve reuse of meta-model elements. We foresee the introduction of heuristics and guidelines for LPL designs in future work.
Lemma 2 deals with uniqueness of field names. The lemma ensures that any class in any derivable meta-model cannot have two fields with the same name within its set of declared and inherited fields. For this purpose, it creates the 150 MM and checks that if a class has two different fields with equal name, they come from incompatible modules (i.e., modules that cannot appear together in a configuration).
Lemma 2
[Unique Field Names] Given a language product line LPL, each derivable meta-model \(MM_\rho \in PR(LPL)\) has unique field names iff:
Proof
In appendix. \(\square \)
Example 15
Figure 14(a) shows another variation of the running example to illustrate Lemma 2. In this case, the optional module ServerFailure adds the attribute broken to class Server. Since its superclass Node also has an attribute with the same name, the meta-model product for configuration {Networking”, ServerFailure} is not wff. This can be detected using the 150 MM in Fig. 14(b). The condition in the lemma takes the modules supplying each attribute and, since we have \(valid_{LPL}(\) {Networking”, ServerFailure}), then we also have that the configuration {Networking”, ServerFailure} yields a non-wff meta-model product.
We now tackle inheritance cycles similarly as before: looking for cycles on the 150 MM and then checking that the modules contributing to each cycle cannot appear together in a configuration.
Lemma 3
[No Inheritance Cycles] Given a language product line LPL, each derivable meta-model \(MM_\rho \) \(\in PR(LPL)\) is free from inheritance cycles iff for each cycle \(C \subseteq I^{MM_{LPL}}\), we have \(\lnot valid_{LPL}(\{\) \(\Phi _{I}((v_1, v_2))~|\) \((v_1,v_2) \in C\})\).
Proof
In appendix. \(\square \)
Example 16
Figure 15(a) shows another variation of the running example to illustrate Lemma 3, where each module adds an inheritance relationship. Part (b) of the figure shows the 150 MM, which has one inheritance cycle C for the set of contributing modules \(S=\{\) Networking”’, AllNodesAreRouters, RoutersAreServers\(\}\). Since we have that \(valid_{LPL}(S)\), there is a cycle in every configuration that includes S.
Finally, we are ready to characterise wff LPLs in terms of the lifted analyses provided by Lemmas 1–3, instead of resorting to a case-by-case analysis of each derivable meta-model.
Theorem 1
[Wff Language Product Line] A language product line LPL is well formed iff it satisfies Lemmas 1–3.
Proof
Direct consequence of Lemmas 1–3. \(\square \)
6.2 LPL instantiability
In practice, meta-models are frequently assigned integrity constraints that restrict the models considered valid [6]. In MDE, such constraints are normally expressed in the Object Constraint Language (OCL) [51]. To keep the formalisation as simple as possible, we omitted OCL constraints so far, since they do not play a significant role in the structural and behavioural concepts we wanted to introduce. However, since OCL invariants are common within language engineering [6], we now consider them, and propose analysis techniques to detect possible inconsistencies among the constraints introduced by different modules of the LPL.
In the following, we first extend LPLs with OCL integrity constraints (Sect. 6.2.1), and then, we provide an overview of the analysis process (Sect. 6.2.2), which is based on an encoding of the LPL in a so-called feature-explicit meta-model (Sect. 6.2.3).
6.2.1 Extending LPLs with OCL constraints
We now extend meta-models within modules so that they may declare OCL invariants, as Definition 18 shows.
Definition 18
[Constrained Meta-model] A constrained meta-model \(CMM=\langle G, C, ctx\rangle \) consists of:
-
An E-graph G, as in Definition 1.
-
A set C of integrity constraints.
-
A function \(ctx :C \rightarrow V\) assigning a context vertex \(v \in V\) (i.e., a class) to each constraint \(c \in C\).
When using this notion to derive a meta-model product, the co-limit simply puts together the constraints defined in each class. Interestingly, cardinality constraints can be expressed using OCL constraints, and therefore, we use them in meta-models in the following. In the figures, we depict cardinality constraints using the standard UML notation, where absent cardinalities mean “exactly 1”. Moreover, we represent the function ctx by showing a link from a note with the name and text of the constraint, to the class to which it refers, as is customary in UML diagrams.
Example 17
Figure 16(a) shows a modification of the running example, where the meta-model of some modules declare OCL constraints. In particular, module RichLink adds the invariant nonRedundant to Link, which forbids the presence of two links with same from and to nodes. Module BiDir adds the invariant bidir, which demands each Link object to have some dual one connecting the same nodes but in the opposite direction. Finally, the invariant in HomeNodes demands each node to have a self-loop link. Please note that, in an LPL, invariants are typed by the effective meta-model EFF(M) of the module M in which they are included.
We observe that any configuration that includes modules {Networking, RichLink, BiDir, HomeNodes} (of which there are four) yields a meta-model product that is not instantiable: there is no valid non-empty model that satisfies all constraints (cf. Figure 16(b)). This instantiability problem originates from the fact that, when creating a Node, invariant loop requires a self-loop. But then, invariant BiDir requires a different link in the opposite direction, which in this case is also a self-loop. Finally, invariant nonRedundant forbids Link objects between the same nodes, hence rendering the model invalid. Since the from and to references of Link are mandatory, then there cannot be isolated Link objects either, and similarly for Message objects. This means that the meta-models of these four language variants are not instantiable due to the incompatibility of the three constraints. Removing the inequality l\(<>\) self from invariant BiDir would solve this problem.
6.2.2 Checking LPL instantiability: overview
The instantiability of a meta-model can be checked via model-finding [27, 38]. This technique encodes the meta-model and its constraints as a satisfaction problem, which is fed into a model finder. Then, the finder returns a valid model (i.e., conformant to the meta-model and satisfying its OCL constraints) if one exists within the search scope.
However, checking the instantiability of each derivable meta-model product of an LPL is costly, since there may be an exponential number of configurations, making it necessary to call the model finder for each one of them. Instead, we propose lifting instantiability analysis to the product-line level, in order to reduce the number of calls to the model finder. For this purpose, we use a technique similar to the one proposed in [26], but adapted to modular LPLs.
Figure 17 shows the steps in the instantiability analysis process. First, the process derives the 150 MM out of the LPL, as per Definition 17. We assume a wff LPL to start with, but recall that the resulting \(MM_{LPL}\) may contain repeated class or field names and inheritance cycles, whenever they are produced by modules belonging to different configurations. Hence, in step 2, the process suitably renames classes and fields having equal names to avoid duplicates, and modifies OCL invariants if needed. Note that the analysis of 150 meta-models with inheritance cycles is currently not supported.
In step 3, the 150 MM and the LPL are compiled into a so-called feature-explicit meta-model (FEMM) [26]. The latter is similar to the 150 MM, but, in addition, it embeds the structure of the feature space (i.e., the structure of the modules), and expresses the presence conditions of the 150 MM as OCL constraints. To this end, a class FMC contains as many boolean attributes as modules in the LPL, and an OCL constraint restricts the possible values that the attributes can take to be exactly those in CFG(LPL). Section 6.2.3 will provide more details on the construction of the FEMM.
In step 4, the process relies on a model finder to discover valid instances of the FEMM. These instances comprise two parts (cf. step 5): an FMC instance, whose boolean values yield a configuration \(\rho \), and a valid instance of the meta-model product \(MM_\rho \). This solving process can be iterated to find instantiations of other meta-model products by adding the negated found configuration as a constraint of FMC (step 6).
6.2.3 The feature explicit meta-model (FEMM)
Constructing the FEMM involves the logical encoding of the feature space of the LPL in a propositional formula \(\Lambda _{LPL}\) whose variables are the modules in the LPL, and such that \(\Lambda _{LPL}\) evaluates to true exactly on the configurations of the LPL [3].
Definition 19
[Logical Encoding of LPL] Given a language product line \(LPL = \{ M_i \}_{i \in I}\), its logical encoding \(\Lambda _{LPL}\) is given by:
with
where \(\oplus \) is the xor operation.
Example 18
The (simplified) logical encoding of the LPL in Fig. 16(a) is:
Networking \(\wedge \)
(Networking \(\implies \) SimpleLink \(\oplus \) RichLink) \(\wedge \)
(SimpleLink \(\implies \) Networking) \(\wedge \)
(RichLink \(\implies \) (Networking \(\wedge \)
(BiDir \(\vee \) Speed \(\vee \) CommFailures))) \(\wedge \)
(BiDir \(\implies \) RichLink) \(\wedge \)
(Speed \(\implies \) RichLink) \(\wedge \)
(CommFailures \(\implies \) RichLink) \(\wedge \)
(HomeNodes \(\implies \) RichLink)
Lemma 4 states the desired consistency between \(\Lambda _{LPL}\) and CFG(LPL).
Lemma 4
[Correctness of LPL Logical Encoding] Given a language product line LPL, then CFG(LPL) and \(\Lambda _{LPL}\) are consistent with each other:
Proof
In appendix. \(\square \)
Feature explicit meta-model for the LPL in Fig. 16(a). Numbers depict the step in the process where the elements are created
Next, we present the process to generate the FEMM, for which we adapt the procedure in [26]. We use as an example the generation of the FEMM for the LPL in Fig. 16(a), whose result is in Fig. 18.
-
1.
Merging of modelling and feature space. The FEMM includes the 150 MM and a mandatory class, called FMC, holding the information of the feature space. In particular, FMC has a boolean attribute for each module in the LPL, such that the values of these attributes indicate a selection of modules. In addition, FMC has an OCL constraint (the OCL encoding of the formula \(\Lambda _{LPL}\) from Definition 19) restricting the values the attributes can take to exactly the valid configurations of the LPL. Each class of the 150 MM with no superclasses is added a new (abstract) superclass BC with a reference fm to FMC, so that each class can access the configuration. Example In Fig. 18, the FEMM generation process creates classes BC and FMC. The latter declares seven boolean attributes corresponding to the seven modules in the LPL, as well as an OCL invariant corresponding to the logical encoding of the LPL formula (cf. Example 18). The interval [1..1] in class FMC stipulates that exactly one instance of the class is required.
-
2.
Emulating the PCs. The classes and fields (i.e., attributes and references) of the FEMM may only be instantiated in configurations where they appear. To this end, the PCs in the 150 MM are encoded as OCL constraints governing whether the classes can be instantiated, or whether the fields may hold values, depending on the value of FMC attributes. For optimisation purposes, no such OCL constraints are produced for the elements introduced by the top module, as they are available in all configurations. Example In Fig. 18, the invariants wc-speed and wc-lossProb in class Link control whether the attributes speed and lossProb should have a value or not. Specifically, they can only hold a value if modules Speed or CommFailures are selected, respectively. A similar approach is used for the references to and from of Link, and linkedTo of Node. All elements introduced by the top module (Networking) are available in all configurations, and so, no OCL constraints are included for them. Additionally, since module RichLink introduces class Link, class FMC is added the invariant wc-Link requiring zero instances of Link if the configuration does not select RichLink (i.e., the attribute RichLink is false).
-
3.
Invariants. Similar to classes and fields, modules can introduce invariants. To ensure such invariants are enforced only when the owner module M is in the configuration, they become prefixed by “fm.M implies...”. Example Invariants bidir and nonRedundant of Link, as well as loop of Node, get rewritten to be enforced only when modules BiDir, RichLink and HomeNodes are in the configuration, respectively.
-
4.
Inheritance. Modules may add inheritance relations. This is translated as an invariant in the subclass requiring that any field inherited through the added inheritance has no value when the module is not part of the configuration. For each incoming reference to the superclass or an ancestor, additional invariants are generated to check that the reference does not contain instances of the subclass in configurations where the module is not selected. Example Since Fig. 18 does not have inheritance, Fig. 19 illustrates this case. Part (a) of the figure depicts a simple LPL, where the optional module adds an inheritance relation between Server and Node. Part (b) shows the resulting FEMM, where class Server is added two invariants. Invariant wc-inh ensures that, if ServerAsNodes is not selected, then the broken attribute has no value (since Server would not inherit from Node). In turn, invariant wc-serves guarantees that, if ServerAsNodes is not selected, then reference serves contains no Server objects. The reader may consult more details of this step in [26].
As explained in Sect. 6.2.2, if the FEMM is instantiable, then the model finder will produce a model that encodes a valid configuration \(\rho \) in the attributes of the unique FMC object, and that includes an instance of \(MM_\rho \). Subsequently, the other configurations can be traversed by adding a new clause that negates the configuration found. This iterative process permits identifying all configurations that produce instantiable meta-models. When the process finishes—because the model finder does not find any more instances—then the configurations of the LPL not found in the process are those producing non-instantiable meta-models. Section 8.2 will illustrate the effectiveness of this technique to analyse the instantiability of the languages in an LPL.
6.3 Behavioural consistency
Regarding behavioural product lines, we would be interested in checking whether the behaviour of each language variant—given by configuration \(\rho \)—is consistent with the behaviour of any “smaller” language variant, i.e., defined by \(\rho ' \subseteq \rho \). This means that for any application of a rule \(\rho (r)\) in a language variant, which extends a base rule r, there is a corresponding application of r in the smaller language variant.
Hence, we distinguish a particular class of extension rules, called modular extensions, which only incorporate into another rule elements of meta-model types added by the module. That is, modular extensions do not add elements of types existing in the meta-model of a dependency, since this would risk changing the semantics of the extended rules. Instead, modular extensions “decorate” existing rules with elements reflecting the semantics of the new elements added to the meta-model.
Definition 20
[Modular Extension] Given a behavioural product line BPL and a behavioural module \(M=\langle {MM},M_D,RO,IN,\Psi ,R,\Delta R,NR,EX,NEX\rangle \in {BPL}\):
-
1.
A \(\Delta \)-rule \(\Delta _r \in \Delta R\) is a modular extension if each element in \(\Delta X {\setminus } X\) (for \(X\in \{L,K,R\}\)) is typed by \(MM {\setminus } C\) (for \(IN = \langle MM \leftarrow C \rightarrow MM(M_D) \rangle \)).
-
2.
A NAC-rule \(N_r \in NR\) is a modular extension if each element in \(N \setminus NL\) is typed by \(MM {\setminus } C\) (for \(IN = \langle MM \leftarrow C \rightarrow MM(M_D) \rangle \)).
-
3.
Given a rule \(r_i \in R\) and a rewriting
 , we say that \(\rho (r_i)\) is a modular extension of r if all rule extensions in \(CEX(r_i)\) and \(NEX(r_i)\) are modular extensions.
, we say that \(\rho (r_i)\) is a modular extension of r if all rule extensions in \(CEX(r_i)\) and \(NEX(r_i)\) are modular extensions.
Given a \(\Delta \)- or NAC-rule r, we use predicate \(mod-ext(r)\) to indicate that r is a modular extension.
Remark 8
The composition of two modular extensions is a modular extension, by transitivity of items 1 and 2 in Definition 20.
Example 19
The \(\Delta \)-rule \(\Delta \) move-rl in Fig. 7 is a modular extension, since it adds a node of type Link and edges of types from and to, belonging to the meta-model of RichLink but not to that of Networking. This \(\Delta \)-rule would not be a modular extension if it added, e.g., a Message node, as this may change the semantics of the base rule on models typed by the meta-model of Networking (so that the semantics of those models would be different in languages that include module RichLink and in those not including it). Instead, \(\Delta \) move-rl adds extra elements that only affect models typed by EFF(RichLink).
Similarly, the NAC-rule NAC-broken in Fig. 11(b) is a modular extension, since it adds an attribute of type broken, which belongs to the meta-model in NodeFailures but not to the one in Networking. Finally, rule move” in Fig. 11(e) is a modular extension of rule move (Fig. 6), since \(\Delta \) move-rl, \(\Delta \) move-cf and NAC-broken are modular extensions.
Modularly extended rules become of special interest in our setting, since they do not change the semantics of the base rule in models conformant to simpler language versions. Theorem 2 captures this property.
Theorem 2
[Consistent Extension Semantics] Let: BPL be a behavioural LPL; \(\rho \in CFG(BPL)\) be a configuration; \(r\in R(M_i)\) be a rule in some behavioural module \(M_i\) of the configuration \(\rho \); and \(G_\rho \) be a model typed by \(MM_\rho \). Then, for every direct derivation \(G_\rho {\mathop {\Longrightarrow }\limits ^{\rho (r)}} H_\rho \), there is a corresponding direct derivation \(G{\mathop {\Longrightarrow }\limits ^{r}}H\), if \(\rho (r)\) is a modular extension of r (and where G, \(G_\rho \), H and \(H_\rho \) are models related as Fig. 20 shows).
Proof
In appendix. \(\square \)
Example 20
Figure 21 shows a consistent extension. Given the configuration \(\rho _2=\{\) Networking, CommFailures, RichLink\(\}\), since the extended rule \(\rho _2(\) move) (Fig. 11(e)) is applicable to a model like \(G_{\rho _2}\) in the figure, the rule move (the base rule in Networking) is applicable to the model deprived of the elements introduced by \( MM _{\rho _2}\).
The next corollary summarises the implications of Theorem 2.
Corollary 1
Given a behavioural LPL BPL, a configuration \(\rho \in CFG(BPL)\), and a rule \(r\in R(M_i)\) with \(M_i\in \rho \) and \(mod-ext(\rho (r))\):
-
1.
\(\rho (r)\) does not delete more elements with types of \(EFF(M_i)\) than r (implied by item (2) in the proof of Theorem 2).
-
2.
\(\rho (r)\) does not create more elements with types of \(EFF(M_i)\) than r (implied by item (3) in the proof of Theorem 2).
-
3.
\(\rho (r)\) is not applicable more often than r (implied by item (1) in the proof of Theorem 2).
Finally, we define consistent behavioural LPLs as those where all extension rules of each module are modular extensions, and only the top module defines rules.
Definition 21
[Consistent Behavioural LPL] A behavioural LPL BPL is consistent if \(\forall M_i \in BPL \cdot \lnot top(M_i) \implies (R(M_i) = \emptyset \wedge \forall r_i \in \Delta R(M_i) \cup NR(M_i) \cdot mod-ext(r_i))\).
Consistent LPLs do not allow language variants to incorporate new actions (i.e., new rules) in the semantics of the top module, and all extensions are required to be modular. Even if this requirement might be too strong for some language families, the result permits controlling and understanding potential semantic inconsistencies between language variants. We leave for future work the investigation of finer notions of (in-)consistency.
Example 21
The running example (cf. Fig. 4) is not a consistent LPL. The top module declares three rules: send, move and receive. While all modules define modular extensions, module Ack needs to introduce a new rule to send back ack messages (cf. Fig. 23, label 2). Using our approach, the designer of the language family can identify the non-consistent variants with the base behaviour and the reasons for inconsistency.
7 Tool support
We have realised the presented concepts in a tool called Capone (Component-bAsed PrOduct liNEs), which is freely available at https://capone-pl.github.io/. It is an Eclipse plugin with the architecture depicted in Fig. 22.
Capone relies on EMF [65] as the modelling technology and Henshin [2] for the rules (standard, \(\Delta \)- and NAC-rules). In addition, it extends FeatureIDE [46] —a framework to construct product-line solutions— to support the composition of language modules, Henshin rules, and EMF meta-models, for a language configuration selection. This is performed by implementing the extension point composer offered by FeatureIDE.
We have designed a textual DSL to declare Capone modules, and built an editor for the DSL using the Xtext framework [76]. Modules may reference both Ecore meta-models and Henshin rules. The core of Capone supports all the analyses presented in Sect. 6. For the instantiability analysis, we rely on the USE Validator [38], a UML/OCL tool that permits finding valid object models (so called witnesses) when fed with a UML class model with OCL constraints. Generally, model-finders are configured with a search scope, so that if no solution is found within the given bounds, one may still exist outside (i.e., it is a semi-decidable analysis method). However, the widely accepted small-scope hypothesis in software testing argues that a high proportion of bugs can be found within a small search scope [28]. In practice, we heuristically set a search bound for the solver [9], but the user can modify it. Technically, to integrate the USE Validator, we needed to bridge between EMF and the format expected and produced by USE.
Figure 23 shows Capone in action. The view with label 1 shows the definition of a module using the DSL we have designed. The editor permits declaring the meta-model fragment referencing an existing ecore file, and instead of requiring explicit meta-model mappings, it relies on equality of names (of classes, attributes, references) for meta-model merging. Modules can also declare a formula and a dependency, and refer to a henshin file with their rules (see view with label 2 for an example henshin file). The editor suggests possible rules to extend, obtained from the module’s dependencies recursively (shown in the pop-up window with label a). To compose Henshin rules, Capone relies on equality of object identifiers. Interestingly, the implementation need not distinguish NAC- from \(\Delta \)-rules, since NACs in Henshin are expressed as elements tagged with forbid.
FeatureIDE contributes the views with labels 3 and 4. The view with label 3 contains the feature model capturing the module structure of the LPL. Our tool generates this model automatically out of the module structure. Feature models in FeatureIDE are more restricted than the ones we support. In particular, features cannot mix groups of OR/ALT children features with other types of features. Hence, the resulting feature model introduces intermediate features for this (cf. NetworkingALT in the view with label 3). Finally, the \(\Psi \) formulae of the modules are added as cross-tree constraints of the feature model (cf. label (b) in the figure).
Overall, users can select a specific configuration of the generated feature model (view 4). Then, Capone uses this configuration to merge the meta-models and rules corresponding to the language variant selected. Alternatively, it is possible to generate the meta-models and rules for all language variants.
8 Evaluation
In this section, our aim is answering three research questions (RQs), which assess the satisfaction of requirements R1–R4 stated in Sect. 2:
-
RQ1
What is the effort reduction of the approach with respect to an explicit definition of each language variant?
-
RQ2
What is the typical effort for adding a new feature to an LPL?
-
RQ3
In which scenarios is lifted instantiability analysis more efficient than a case-by-case analysis?
To answer these questions, we have used our module-based approach to build a synthetic language family plus five additional ones inspired by existing works in the literature [26, 43]. Then, we have compared the specification effort and the analysis time of our approach, with respect to an enumerative approach. In the following, Sect. 8.1 deals with RQ1 and RQ2, Sect. 8.2 answers RQ3, and Sect. 8.3 discusses threats to validity. The data of the experiments are available at https://capone-pl.github.io/examples.html.
8.1 RQ1 & RQ2: Specification effort
To answer RQ1 and RQ2, we have compared five LPLs built using our approach, with respect to an enumerative approach that would create each language variant separately from scratch.
Experiment setup. We have created five behavioural LPLs: Networking (the running example in Fig. 4); Graphs (with language variants like un-/directed edges and node hierarchy) along with a transformation implementing a breadth-first traversal; State machines (with variants like hierarchy, parallelism and time) plus a simulator; Petri nets (with variants like bounded places, inhibitor and read arcs, and attribute or object tokens) plus a simulator; and Automata (with variants like inputs, outputs, initial and final states, determinism, hierarchy and the availability of a stack) plus a simulator. The examples are from the product line literature [16, 43].
Results. Table 1 displays the results. The first two columns show the language family name and the number of configurations (i.e., language variants). The remaining ones show the size reduction of the structural part (meta-model) and the behavioural part (rules) achieved by the LPLs, compared to an enumerative approach.
For structure (columns 3–6), the table reports: number of modules in the LPL; total (and average) meta-model size in each module, as given by the number of classes, attributes and references in each meta-model; total (and average) meta-model size in each language variant of the enumerative approach; and total meta-model size reduction (%) that our approach brings.
For behaviour (columns 7–11), the table shows: number of Henshin rules in the LPL (and average per module); total (and average) size of the rules, as given by the number of objects, attributes and references in each rule; number of rules in the enumerative approach (and average per language variant); total (and average) added size of all rules; and total rule size reduction that the LPL approach brings.
Answering RQ1. In the study, our approach reduces the specification size of the structure by 86–99.82%, and the rules size by 91.7–99.87%. This reduction is correlated with the size of the language family (number of configurations/language variants).
Answering RQ2. In the study, adding a new module requires meta-models of size 3 to 5 (cf. column 4 of Table 1, value in parentheses). The effort is considerably larger in the enumerative approach, where meta-model sizes range between 12.5 and 31.3 (column 5) and adding a new optional module implies doubling the number of language variants. For the semantics, each module has between 1 and 2.07 rules on average (column 7), with size between 3.87 and 7.75 (column 8). Instead, each variant in the enumerative approach requires between 3.3 and 12 rules (column 9), with size between 7.16 and 14.45 (column 10). Hence, extending a language family built with an enumerative approach requires creating more and bigger rules.
8.2 RQ3: Instantiability analysis
Next, we investigate the performance of the lifted instantiability analysis presented in Sect. 6.2, in comparison with a case-by-case, enumerative approach.
Experiment setup. In this experiment, we have measured the time needed to assess whether a given LPL has instantiable meta-models, and to find a configuration that yields one of such. For this purpose, we have performed both lifted and enumerative instantiability analysis on the five case studies used in Sect. 8.1, and on an additional synthetic LPL example with 1295 configurations. In the lifted analysis, a single solving suffices to assess the LPL instantiability. In the enumerative case, instead, it is necessary to generate and analyse each product meta-model, until an instantiable one is found. In the best case, the first analysed product meta-model is instantiable, which finishes the analysis. In the worst case, there are no instantiable meta-models, which can only be assessed generating and instantiating each derivable product. To avoid spurious results, we repeated each lifted an enumerative analysis 20 times, and took the average. For the enumerative case, in addition, products were generated (and processed) in random order. The experiments were performed on a Windows 11 computer, with an i7-1260P processor and 16Gb of RAM memory.
Results. Table 2 summarises the results. It shows: name of the LPL (column 1); its number of configurations (column 2); lifted analysis time (column 3); time to process all meta-model products in the enumerative approach, which corresponds to the worst-case scenario (column 4); speedup of the lifted analysis in the worst-case scenario (column 5); time to process one meta-model by the enumerative approach, which corresponds to the best-case scenario (column 6); slow-down of the lifted analysis w.r.t. the enumerative approach in the best-case scenario (column 7); number of meta-models that the enumerative approach needs to process to be slower than the lifted analysis (column 8); and same information expressed as a percentage on the total number of configurations (column 9).
The lifted case only needs to find an instance of the FEMM to show that the LPL is instantiable, which requires from 94.65 to 706.75 ms for the analysed LPLs. For the enumerative case, we iterated on each configuration randomly, invoking the solver to analyse each product meta-model. This corresponds to the worst-case scenario, which requires visiting each configuration to find an instantiable meta-model. In this worst-case scenario for the enumerative approach, solving times vary between around 510 ms and 6.5 min, and so, the lifted analysis achieves speedups of 5\(\times \) up to 554.3\(\times \). The table also reports the first solving time of the enumerative approach, which corresponds to the best-case scenario (the first solving discovers an instantiable meta-model). In this case, the analysis times range from 31.4 to 76 ms, which means our lifted analysis entails a slow-down from 63.25 to 630.75 ms in the best-case scenario, compared to the enumerative approach. Finally, the last two columns report the number of configurations the enumerative approach needs to analyse to be slower than the lifted analysis. This value ranges from 2 to 10, which corresponds to 0.35% to 25% of the configurations.
Figure 24(a) shows a graphic comparing the analysis times of the enumerative and lifted approaches for the synthetic example. As expected, the time of the enumerative approach is linear on the number of configurations that need to be analysed (i.e., on the number of solvings required) to assess the LPL instantiability. Figure 24(b) zooms into the first 25 solvings, which shows a cut-off of 10 solvings, after which using the lifted approach is faster than the enumerative one.
Answering RQ3. We observe that, if we need to evaluate more than a few configurations (over the range of 2 to 10, representing between the 0.35% and the 25% of all configurations of the LPL) for instantiability, the lifted approach is faster. In the worst case, the lifted analysis achieves speedups of more than 5\(\times \), and up to 554.3\(\times \) for the Automata LPL. Since the analysis time in the enumerative approach is linear with the number of configurations, we can also observe that this speedup is larger the more configurations the LPL has.
If just one meta-model needs to be analysed (e.g., because we are interested in finding just one instantiable meta-model within the LPL, and the first product is instantiable) then the enumerative approach is slightly faster. This is so, since the lifted approach solves a more complicated problem: it contains all OCL expressions and all meta-models of the family overlapped. However, since this overhead is only up to around 630 ms in the worst case, we argue that using a lifted analysis is generally beneficial, since typically one does not know a-priori how many meta-models need to be tested before the first (un-)instantiable one is hit.
8.3 Threats to validity
Next, we analyse threats to the validity of our two experiments.
Construct validity. For RQ1 and RQ2, the results are very promising, evincing substantial size reduction when defining a language family with our proposal. However, experiments with real developers are needed to assess the correlation between this size reduction and the actual effort to build the LPLs.
Internal validity. For RQ3, we measured the solving time of processing each meta-model product in the enumerative case, and calculated the number of solvings necessary for the lifted case to become faster. For the enumerative approach, this measurement is dependent on the order in which the meta-model products are visited. To avoid spurious effects caused by particular meta-models being difficult or easy to analyse, we used a random order for generating the products, and 20 repetitions.
External validity. For RQ1 and RQ2, we have used five LPLs with 16 up to 1440 configurations. While we speculate that other language families may yield similar results (maintaining the correlation of size with number of configurations), more extensive experiments are needed for extra confidence in our claims. To reduce this risk, for RQ3, in addition, we created an additional synthetic LPL, which yielded similar results to the other ones.
9 Discussion
Next, we provide a discussion on the limitations, design choices and perspectives of our approach, along eight axes: encapsulation, reuse, module composition, cross-cutting language concerns, practical LPL design, analysis, behaviour correctness, and concrete syntax.
Encapsulation. Our approach does not include a mechanism to restrict which elements within a module may, may not, or should be extended. Instead, a module can extend any element in the meta-model of a dependency module. This is so as the meta-models (and rules) within modules lack a proper interface. Hence, our approach is white-box, since adding a module requires inspecting the existing modules to determine which of their elements are to be extended (and similarly for cross-tree constraints). Still, this constitutes an extensible mechanism, since adding a new feature to the language does not require modifying the existing specification. While at this stage, we opted for a simple, lightweight approach that favours flexibility, specifying such interfaces in modules can be done by identifying subsets of the meta-model elements that may, may not, or should receive extensions (and a similar mechanism could be followed for the module behaviour). Studying the suitability of this extension is up to future work.
Reuse. A module encapsulates structure and behaviour, and declares how it extends a given dependency module within the LPL. Therefore, it can reuse and extend the structure and behaviour of its dependency. To reuse a module in another LPL, its dependency should be modified to point to the new dependency module, and its extension role might also change, but its structure and behaviour can be reused as they are. We deem this small, required change as acceptable, compared to the effort needed to declare and maintain an explicit feature model externally (if the extension role is extracted from modules).
Module composition. As the evaluation shows, our merging construction for modules simplifies the construction of language families. Together with negative variability, this is one of the most used approaches in product lines [1]. Regarding other composition mechanisms [55], our approach can, e.g., emulate embedding (composing two meta-models by adding an association) by just extending a suitable class in the dependency module with the association. We cannot claim that our solution is the most appropriate one for all scenarios (cf. next point). In future work, we will explore the introduction of new mechanisms driven by the practical use of our approach.
Cross-cutting language concerns. Aspect orientation [34] claims that some concerns cross-cut software systems and cannot be easily embedded as standard object-oriented or procedural abstractions. Hence, it proposes modularity mechanisms (the aspects) that can be flexibly weaved into several places of a system. In our case, to use the same structure in several places of a language, the module realising it should be cloned and replicated in the LPL. We are currently working on generalising our approach to support extension modules with several dependencies, whereby an LPL may span a directed acyclic graph instead of a tree [64].
Practical LPL design. Proper engineering of effective modelling languages is not easy [71], especially in the case of language families. Our modular approach enables decomposing a language family into features, and describing the family as a product line of modules. Still, mechanisms facilitating its use in practice are required, including design guidelines (e.g., akin to [19], but in our setting), refactorings (as hinted at in Sect. 6.1), or techniques to reverse-engineer a set of language variants into an LPL (in the style of [47]).
Analysis. Section 6 has provided some methods to analyse LPL instantiability. However, if some language variant of the LPL is not satisfiable, the designer still needs to find the causes of inconsistency by analysing the constraints of the modules selected by the configuration. To facilitate this task, constraint debugging techniques [25, 74], e.g., based on finding the unsatisfiable core of the constraint set [59], could be used.
Behaviour correctness. Our analysis technique for behaviour consistency ensures that “bigger” languages of the family are consistent with “smaller” ones. Still, the behaviour of the LPL needs to be properly tested. Hence, we aim at developing efficient testing techniques for LPLs in the future, based on approaches to test software product lines [18].
Concrete syntax. This work has not covered the concrete syntax of LPLs, which is left for future work. We aim at graphical syntaxes, where modules include models of their graphical syntax, possibly with variants. Such models would be composed with the syntax models of the dependency modules, for which we are investigating suitable composition mechanisms.
10 Related work
We now examine related works on modelling language engineering (Sect. 10.1) and review approaches to transforming rewrite rules (Sect. 10.2) and analysing product lines (Sect. 10.3).
10.1 Modelling language engineering
Product lines have been used to define the abstract syntax of language families concisely. For example, Merlin [26] supports the definition of product lines of meta-models and the efficient analysis of their well-formedness properties. Merlin is not compositional, but it overlaps all meta-models in a 150 MM, where elements attach formulae stating the configurations they belong to. MetaDepth [14] uses multi-level modelling to define language families, and product lines for their customisation. The proposal is backed by a formal theory that guarantees correctness. None of these works considers semantics, and languages cannot be defined incrementally by composing modules.
Other proposals based on product lines consider semantics. Leduc et al. [41] define languages via extensible meta-models, and use the Visitor pattern (combined with Java or an action language) for the semantics, hampering analysis. They also lack means, like our configurations, to select between possible language extensions. In [16], a 150 MM captures variability within a domain, and defines transformations on top in a modular way. Being based on a 150 MM, extension is challenging, and analysis is complex since transformations are written in the Epsilon Object Language (EOL) [37]. Méndez et al. [47] reverse engineer LPLs from DSL variants. Their LPLs consider syntax and operational semantics. Compatibility of operations is checked by comparing their signatures and ASTs, but truly behavioural analyses are difficult since operations are expressed through Java-like methods.
Regarding language composition, Durán and Zschaler [20, 21] combine definitions of languages and their rule-based behaviour to build more complex languages. While this is achieved using an amalgamation construction, akin to our \(\Delta \)-rules, there is no notion of product line, language module, dependency, or configuration. Being based on graph transformation [77], their approach supports analysing whether the rule behaviour is protected at the level of traces, and not only on individual rules as we do. We will take inspiration on that approach for its application to LPLs, where languages are composed in more intricate ways out of fragments.
Concern-oriented design [36] (an evolution of the reusable aspect models approach [35]) supports components encapsulating design concerns plus a feature model as the configuration interface. Concerns are composed incrementally via configuration selections, but compositional semantics is not considered. Concern-Oriented Language Development (COLD) [10] is a conceptual proposal inspired by the latter trend of works. It fosters reusability in language development by the notion of language concern. Concerns are reusable language fragments consisting of abstract syntax, concrete syntax, and semantics, and which provide interfaces to support variability, customisation and use. In comparison, our modules are finer grained than concerns. Our LPLs offer a variability interface, but as discussed in Sect. 9, our modules lack a customisation interface stating the elements that need to be extended.
In the Kermeta language workbench [29], the operational semantics of languages is defined using the K3 meta-language in the form of aspects that are statically woven into the language syntax. While the Kermeta workbench enables a modular language definition, it lacks an explicit variability model, which prevents the construction of language families. GEMOC Studio/Melange [17] improves the Kermeta workbench by supporting language families and variation points, but the analysis of the composed language is limited to type checking to ensure type safety.
Jurack et al. [30] define algebraic component concepts for (EMF) models with well-defined interfaces, but components lack a specification of their semantics. LanGems [72] uses roles to define interfaces for language modules, but lacks product-line capabilities. Moreover, semantics is specified by operations in metaclasses, which is challenging to analyse.
Both MontiCore [8] and Neverlang [70] enable component-based language definition. MontiCore components encapsulate textual syntax, integrity constraints, semantics (via code generators), and can declare provided/required interfaces. Components can be organised into a product line (to support closed variability) and be customised through their interfaces (to support open variability). Language families explicitly declare a feature diagram, and provide bindings to specific components. In turn, Neverlang is a textual language workbench, in which modules encapsulate textual syntax and semantic actions on abstract syntax trees. Similar to MontiCore, it allows provided/required interfaces. Modules can be combined by slices, and language descriptors indicate which slices should be combined to generate a language interpreter. Neverlang is able to extract a feature model out of the language definitions [24], from which specific language configurations can be selected. In comparison to MontiCore and Neverlang, our approach is meta-model-based, supports the analysis of integrity constraints, and relies on graph transformation to define the language semantics. We target closed variability (language families), and so, our modules lack interfaces. Regarding MontiCore, our definition of product lines is slightly more direct—modules are features—which permits extending the family without changing existing definitions. Our modules are agnostic on the concrete syntax, which will facilitate incorporating several types of it (textual, graphical) to the LPL. Regarding semantics, we would like to explore the possibility to add code generators to modules, taking inspiration from [7].
Delta-oriented programming [62] permits building software products by defining a core module and a set of delta modules that specify changes to the core module. A software product is built by applying the delta modules to the core one. While this approach is highly expressive, ensuring confluence or semantic consistency is not possible in general. Hence, in the context of delta-oriented modelling, Pietsch et al. [56, 57] formalise delta operations as transformation rules and provide techniques for analysis, measurement and refactoring. Our approach works one meta-level up, but it would be interesting to consider their quality assurance techniques in our future work.
10.2 Rule transformation
Rule rewriting can be considered a particular realisation of rule inheritance/refinement (see [75] for a survey). It has been extensively studied in the literature. For instance, Parisi-Presicce [54] rewrites graph grammars by introducing high-level replacement systems where the productions are grammars and graph morphisms. Bottoni et al. [5] propose an incremental view on the syntax-directed construction of semantics of visual languages, which involves modifying triple graph rules where patterns declare conditions that a model must satisfy. The notion of higher-order transformation proposed in [44] permits applying transformations to rewriting rules, and obtain a valid graph rule. Our extension rules also rewrite rules, though their actions are limited to rule/NAC extension (i.e., they are non-deleting).
Differently from the approaches mentioned above, variability-based rules [66] encode several rules into a single specification. The authors also propose a merging algorithm to build a variability-based rule from several standard ones. While we could use variability-based rules to specify semantic variants, we opted for a modular approach to allow an incremental rule construction. In [73], regular outplace transformations are applied to models with variability, and this variability is propagated to the target models a-posteriori. In our case, variability is specified externally to meta-models via modules and dependencies, and rules are applied to models without variability.
Besides to rule rewriting, transformations have also been applied to product line rewriting. Taentzer et al. [67] use category theory to formalise the notion of transformation of software product lines, which combines modifications of feature models and product domain models. These transformations are proven to be sound. Instead, our extension rules modify rules, but preserve the domain meta-models and module dependencies.
10.3 Analysing product lines
Product lines are hard to analyse due to the possibly exponential number of derivable products. Hence, instead of a case-by-case approach, lifted analyses are often proposed [68]. These adapt techniques—originally developed to analyse a single product—to the product-line level, enabling the analysis of all products of the family at once, and avoiding the generation and analysis of each product in isolation.
In our case, we have lifted both syntactical analyses (cf. Sect. 6.1) and instantiability analysis based on model-finding (cf. Sect. 6.2) to the product-line level. For the latter, we follow an approach similar to the one in [26], where a feature-explicit meta-model is derived from a 150 MM, and then analysed with model finders. In our case, we derive a 150 MM from an LPL, and a logical encoding of its variability space. While [26] analysed further properties—beyond instantiability—and proposed the use of partial configurations for faster analysis, this is up to future work in our case.
Some works propose lifted analysis of well-formedness for product lines of models. For example, Lienhardt et al. [42] define product lines of statecharts using delta-modelling and analyse well-formedness of each derivable statechart at the product-line level. In a more general setting, Czarnecki and Pietroszek [11] propose a method to analyse product lines of models to check if each derivable one conforms to its meta-model, which includes OCL constraints. Our lifted instantiability analysis is defined at the meta-model level, and can be used to check if each product meta-model is instantiable.
In [16], a notion of transformation product line is proposed, following an annotative approach based on a 150 MM. Transformations are defined using EOL, complemented with contracts in OCL. Model finders can then be used to analyse the consistency of the contracts, but the transformations themselves are not analysed, since they are written in EOL. In contrast, via graph transformations, we are able to analyse semantic consistency for all members of the family (cf. Sect. 6.3).
11 Conclusions and future work
We have presented a new modular approach to defining modelling language families that considers both abstract syntax and semantics. The approach is based on product line techniques and involves the definition of language modules with interdependencies. Modules comprise a meta-model fragment (which may contain OCL constraints), rules, and extension rules that expand the rules of other dependency modules. We have developed analysis techniques for LPL syntactic well-formedness, instantiability, and behaviour consistency; demonstrated the applicability of the approach by an implementation atop Eclipse; and reported on an evaluation showing size and analysis time reductions.
In the future, on the practical side, we plan to apply the approach to industry cases and enhance our tooling, e.g., with refactoring suggestions to improve the quality of the product line. On the theoretical side, we plan to lift existing analysis techniques for graph transformation (e.g., conflicts, dependencies [39]) to the product-line level, develop finer granular analysis of (in-)consistency, devise effective testing techniques for LPLs, consider other satisfiability properties beyond instantiability, and improve satisfiability analyses with partial configurations, in the style of [26]. We will also consider generalising the approach to support extension modules with several dependencies, whereby an LPL may span a directed acyclic graph instead of a tree [64], and enable modules with several alternative/OR groups. In addition, we are studying the addition of module interfaces restricting the structural and behavioural elements within a module that may, may not, or should be extended. Finally, we are currently exploring the possibility to associate code generation templates to modules, in the style of [7], as well as (graphical) concrete syntax descriptions.
Notes
A span consists of two morphisms from a common graph.
Implicitly, modules are assigned a name (e.g., M, \(M_D\), Networking), which we use instead of the tuple contents to refer to them. This avoids the need to include explicitly an identifier label in the module tuple.
\(l''\) uniquely exists since we have \(K'\xrightarrow {ll \circ l'}L''\xleftarrow {n_L'\circ \Delta l}\Delta K\), and similarly for \(r''\).
Morphisms \(\Delta l''\) and \(\Delta r''\) uniquely exist by the universal PO property of \(\Delta K''\): \(\Delta l''\) uniquely exists since \(\Delta K \xrightarrow {\Delta m_L \circ \Delta l}\Delta L'' \xleftarrow {n'_L \circ \Delta l'}{\Delta K'}\), and similarly for \(\Delta r''\).
References
Apel, S., Batory, D., Kästner, C., Saake, G.: Basic concepts, classification, and quality criteria. In: Feature-Oriented Software Product Lines: Concepts and Implementation. Springer Berlin Heidelberg, Berlin, Heidelberg. pp 47–63 (2013)
Arendt, T., Biermann, E., Jurack, S., Krause, C., Taentzer, G.: Henshin: Advanced concepts and tools for in-place EMF model transformations. In MoDELS, volume 6394 of LNCS. pp 121–135. Springer (2010)
Benavides, D., Trinidad, P., Ruiz-Cortés, A.: Automated reasoning on feature models. In: CAiSE, volume 3520 of LNCS. Springer. pp 491–503 (2005)
Beuche, D., Schulze, M., Duvigneau, M.: When 150% is too much: supporting product centric viewpoints in an industrial product line. In: SPLC, ACM. pp 262–269 (2016)
Bottoni, P., Guerra, E., de Lara, J.: Enforced generative patterns for the specification of the syntax and semantics of visual languages. J. Vis. Lang. Comput. 19(4), 429–455 (2008)
Brambilla, M., Cabot, J., Wimmer, M.: Model-Driven Software Engineering in Practice, 2nd edn. Morgan & Claypool Publishers, San Rafael (2017)
Butting, A., Eikermann, R., Kautz, O., Rumpe, B., Wortmann, A.: Modeling language variability with reusable language components. In: SPLC, ACM, pp 65–75. (2018)
Butting, A., Pfeiffer, J., Rumpe, B., Wortmann, A.: A compositional framework for systematic modeling language reuse. In: MoDELS, ACM. pp 35–46 (2020)
Clarisó, R., González, C.A., Cabot, J.: Smart bound selection for the verification of UML/OCL class diagrams. IEEE Trans. Softw. Eng. 45(4), 412–426 (2019)
Combemale, B., Kienzle, J., Mussbacher, G., Barais, O., Bousse, E., Cazzola, W., Collet, P., Degueule, T., Heinrich, R., Jézéquel, J., Leduc, M., Mayerhofer, T., Mosser, S., Schöttle, M., Strittmatter, M., Wortmann, A.: Concern-oriented language development (COLD): fostering reuse in language engineering. Comput. Lang. Syst. Struct. 54, 139–155 (2018)
Czarnecki, K., Pietroszek, K.: Verifying feature-based model templates against well-formedness OCL constraints. In: GPCE. ACM. pp 211–220 (2006)
D’Antoni, L., Veanes, M.: Automata modulo theories. Commun. ACM 64(5), 86–95 (2021)
de Lara, J., Bardohl, R., Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Attributed graph transformation with node type inheritance. Theor. Comput. Sci. 376(3), 139–163 (2007)
de Lara, J., Guerra, E.: Language family engineering with product lines of multi-level models. Formal Aspects Comput. 33(6), 1173–1208 (2021)
de Lara, J., Guerra, E., Bottoni, P.: Modular language product lines: a graph transformation approach. In: MoDELS, ACM. pp 334–344 (2022)
de Lara, J., Guerra, E., Chechik, M., Salay, R.: Model transformation product lines. In: MoDELS, ACM. pp 67–77 (2018)
Degueule, T., Combemale, B., Blouin, A., Barais, O., Jézéquel, J.: Melange: a meta-language for modular and reusable development of DSLs. In: SLE, ACM. pp 25–36 (2015)
do Carmo Machado, I., McGregor, J.D., Cavalcanti, Y.C., de Almeida, E.S.: On strategies for testing software product lines: a systematic literature review. Inf. Softw. Technol. 56(10), 1183–1199 (2014)
Drux, F., Jansen, N., Rumpe, B.: A catalog of design patterns for compositional language engineering. J. Object Technol. 21(4), 1–13 (2022)
Durán, F., Moreno-Delgado, A., Orejas, F., Zschaler, S.: Amalgamation of domain specific languages with behaviour. J. Log. Algebraic Methods Program. 86(1), 208–235 (2017)
Durán, F., Zschaler, S., Troya, J.: On the reusable specification of non-functional properties in DSLs. In: SLE, volume 7745 of LNCS, Springer. pp 332–351 (2012)
Eclipse. https://www.eclipse.org/ (2022)
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Fundamentals of Algebraic Graph Transformation. Springer, Berlin (2006)
Favalli, L., Kühn, T., Cazzola, W.: Neverlang and FeatureIDE just married: integrated language product line development environment. In: SPLC, pp 1–11. ACM (2020)
Gómez-Gutiérrez, J.A., Clarisó, R., Cabot, J.: A tool for debugging unsatisfiable integrity constraints in UML/OCL class diagrams. In BPMDS/EMMSAD, volume 450 of LNBIP, Springer. pp 267–275 (2022)
Guerra, E., de Lara, J., Chechik, M., Salay, R.: Property satisfiability analysis for product lines of modelling languages. IEEE Trans. Softw. Eng. 48(2), 397–416 (2022)
Jackson, D.: Software Abstractions-Logic, Language, and Analysis. MIT Press, London (2006)
Jackson, D., Damon, C.: Elements of style: analyzing a software design feature with a counterexample detector. IEEE Trans. Softw. Eng. 22(7), 484–495 (1996)
Jézéquel, J., Combemale, B., Barais, O., Monperrus, M., Fouquet, F.: Mashup of metalanguages and its implementation in the Kermeta language workbench. Softw. Syst. Model. 14(2), 905–920 (2015)
Jurack, S., Taentzer, G.: A component concept for typed graphs with inheritance and containment structures. In: ICGT, volume 6372 of LNCS. Springer. pp 187–202 (2010)
Kang, K., Cohen, S., Hess, J., Novak, W., Peterson, A.: Feature-oriented domain analysis (FODA) feasibility study. Technical Report CMU/SEI-90-TR-021, Carnegie Mellon Universit (1990)
Kashmar, N., Adda, M., Atieh, M.: From access control models to access control metamodels: a survey. In FICC, volume 70 of LNNS. Springer. pp 892–911 (2020)
Kelly, S., Tolvanen, J.: Domain-Specific Modeling - Enabling Full Code Generation. Wiley, Hoboken (2008)
Kiczales, G., Lamping, J., Mendhekar, A., Maeda, C., Lopes, C. V., Loingtier, J., Irwin, J.: Aspect-oriented programming. In: ECOOP, volume 1241 of LNCS, Springer. pp 220–242 (1997)
Kienzle, J., Abed, W.A., Fleurey, F., Jézéquel, J., Klein, J.: Aspect-oriented design with reusable aspect models. LNCS Trans. Aspect Oriented Softw. Dev. 7, 272–320 (2010)
Kienzle, J., Mussbacher, G., Collet, P., Alam, O.: Delaying decisions in variable concern hierarchies. In: GPCE. ACM. pp 93–103 (2016)
Kolovos, D.S., Paige, R.F., Polack, F.: The Epsilon Object Language (EOL). In: ECMDA-FA, volume 4066 of LNCS, Springer. pp 128–142 (2006)
Kuhlmann, M., Gogolla, M.: From UML and OCL to relational logic and back. In: MoDELS, volume 7590 of LNCS, Springer. pp 415–431 (2012)
Lambers, L., Strüber, D., Taentzer, G., Born, K., Huebert, J.: Multi-granular conflict and dependency analysis in software engineering based on graph transformation. In: Proc. ICSE. ACM. pp 716–727 (2018)
Lane, S.M.: Categories for the Working Mathematician. Springer, Berlin (1971)
Leduc, M., Degueule, T., Combemale, B., van der Storm, T., Barais, O.: Revisiting visitors for modular extension of executable DSMLs. In: MoDELS, IEEE Computer Society. pp 112–122 (2017)
Lienhardt, M., Damiani, F., Testa, L., Turin, G.: On checking delta-oriented product lines of statecharts. Sci. Comput. Program. 166, 3–34 (2018)
Lopez-Herrejon, R.E., Batory, D.: A standard problem for evaluating product-line methodologies. In GCBSE. Springer, Berlin, Heidelberg. pp 10–24 (2001)
Machado, R., Ribeiro, L., Heckel, R.: Rule-based transformation of graph rewriting rules: towards higher-order graph grammars. Theor. Comp. Sci. 594, 1–23 (2015)
Malavolta, I., Lago, P., Muccini, H., Pelliccione, P., Tang, A.: What industry needs from architectural languages: a survey. IEEE Trans. Soft. Eng. 39(6), 869–891 (2013)
Meinicke, J., Thüm, T., Schröter, R., Benduhn, F., Leich, T., Saake, G.: Mastering Software Variability with FeatureIDE. Springer, Berlin (2017)
Méndez-Acuña, D., Galindo, J.A., Combemale, B., Blouin, A., Baudry, B.: Reverse engineering language product lines from existing DSL variants. J. Syst. Softw. 133, 145–158 (2017)
Méndez-Acuña, D., Galindo, J.A., Degueule, T., Combemale, B., Baudry, B.: Leveraging software product lines engineering in the development of external DSLs: a systematic literature review. Comput. Lang. Syst. Struct. 46, 206–235 (2016)
Murata, T.: Petri nets: properties, analysis and applications. Proc. IEEE 77(4), 541–580 (1989)
Northrop, L., Clements, P.: Software Product Lines: Practices and Patterns. Addison-Wesley Longman Publishing Co. Inc, Boston (2002)
OCL. http://www.omg.org/spec/OCL/ (2014)
Orejas, F., Lambers, L.: Lazy graph transformation. Fundam. Inf. 118(1–2), 65–96 (2012)
OSGi working group. OSGi: The dynamic module system for java. https://www.osgi.org/ (2022)
Parisi-Presicce, F.: Transformations of graph grammars. In: TAGT, volume 1073 of LNCS. Springer. pp 428–442 (1994)
Pfeiffer, J., Rumpe, B., Schmalzing, D., Wortmann, A.: Composition operators for modeling languages: a literature review. J. Comput. Lang. 76, 101226 (2023)
Pietsch, C., Kelter, U., Kehrer, T., Seidl, C.: Formal foundations for analyzing and refactoring delta-oriented model-based software product lines. In: SPLC, ACM. pp 30:1–30:11 (2019)
Pietsch, C., Reuling, D., Kelter, U., Kehrer, T.: A tool environment for quality assurance of delta-oriented model-based spls. In: VaMoS, ACM. pp 84–91 (2017)
Pohl, K., Böckle, G., Linden, F.J.: Software Product Line Engineering: Foundations, Principles and Techniques. Springer-Verlag, Berlin (2005)
Przigoda, N., Wille, R., Drechsler, R.: Analyzing inconsistencies in UML/OCL models. J. Circuits Syst. Comput. 25(3), 1640021:1-1640021:21 (2016)
Reuling, D., Pietsch, C., Kelter, U., Kehrer, T.: Towards projectional editing for model-based SPLs. ACM, In VaMoS (2020)
Sannella, D., Tarlecki, A.: Foundations of Algebraic Specification and Formal Software Development. Monographs in Theoretical Computer Science. An EATCS Series. Springer, Berlin (2012)
Schaefer, I., Bettini, L., Bono, V., Damiani, F., Tanzarella, N.: Delta-oriented programming of software product lines. In: SPLC, volume 6287 of LNCS, Springer. pp 77–91 (2010)
Schlie, A., Schulze, S., Schaefer, I.: Recovering variability information from source code of clone-and-own software systems. ACM, In VaMoS (2020)
Schobbens, P., Heymans, P., Trigaux, J., Bontemps, Y.: Generic semantics of feature diagrams. Comput. Networks 51(2), 456–479 (2007)
Steinberg, D., Budinsky, F., Paternostro, M., Merks, E.: EMF: Eclipse Modeling Framework, 2nd edn. Addison-Wesley Professional, Boston (2008)
Strüber, D., Rubin, J., Arendt, T., Chechik, M., Taentzer, G., Plöger, J.: Variability-based model transformation: formal foundation and application. Formal Asp. Comput. 30(1), 133–162 (2018)
Taentzer, G., Salay, R., Strüber, D., Chechik, M.: Transformations of software product lines: a generalizing framework based on category theory. In: MoDELS, IEEE. pp 101–111 (2017)
Thüm, T., Apel, S., Kästner, C., Schaefer, I., Saake, G.: A classification and survey of analysis strategies for software product lines. ACM Comput. Surv. 47(1), 6:1-6:45 (2014)
Tisi, M., Jouault, F., Fraternali, P., Ceri, S., Bézivin, J.: On the use of higher-order model transformations. In: ECMDA-FA, volume 5562 of LNCS. Springer. pp 18–33. (2009)
Vacchi, E., Cazzola, W.: Neverlang: a framework for feature-oriented language development. Comput. Lang. Syst. Struct. 43, 1–40 (2015)
Wasowski, A., Berger, T.: Domain-Specific Languages—Effective Modeling, Automation, and Reuse. Springer, Berlin (2023)
Wende, C., Thieme, N., Zschaler, S.: A role-based approach towards modular language engineering. In: SLE, volume 5969 of LNCS, Springer. pp 254–273 (2009)
Westfechtel, B., Greiner, S.: From single- to multi-variant model transformations: trace-based propagation of variability annotations. In: MoDELS, ACM. pp 46–56 (2018)
Wille, R., Soeken, M., Drechsler, R.: Debugging of inconsistent UML/OCL models. In: DATE, IEEE. pp 1078–1083 (2012)
Wimmer, M., Kappel, G., Kusel, A., Retschitzegger, W., Schönböck, J., Schwinger, W., Kolovos, D.S., Paige, R.F., Lauder, M., Schürr, A., Wagelaar, D.: Surveying rule inheritance in model-to-model transformation languages. J. Object Technol. 11(2), 1–46 (2012)
Xtext. https://www.eclipse.org/Xtext/ (2022)
Zschaler, S., Durán, F.: GTSMorpher: safely composing behavioural analyses using structured operational semantics. In: Composing Model-Based Analysis Tools. Springer International Publishing. pp 189–215 (2021)
Acknowledgements
We thank the reviewers for their useful comments. This work has been partially supported by Sapienza Visitor Programme, a visitor grant by Department of Computer Science at Sapienza, and the Spanish Ministry of Science (PID2021-122270OB-I00, PID2021-122270OB-I00, and RED2022-134647-T). P. Bottoni was partly supported by the Italian Ministry of University and Research (MUR) under PRIN grant B87G22000450001 (PINPOINT).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
Proof of Lemma 1: Unique Class Names.
Proof
- \(\Rightarrow )\):
-
We will proceed by contradiction. Assume there is a meta-model \(MM_\rho \in PR(LPL)\) having two classes \(v_i\) and \(v_j\) with the same name. Then, such classes are present in the 150 MM and therefore in \(V^{MM_{LPL}}\). This means that \(\{\Phi _V(v_i), \Phi _V(v_j)\} \subseteq \rho \), and therefore \(valid_{LPL}(\{\Phi _V(v_i), \Phi _V(v_j)\})\), in contradiction with the condition of the lemma.
- \(\Leftarrow )\):
-
Assume there are two distinct classes \(v_i\) and \(v_j\) in \(V^{MM_{LPL}}\) with the same name s.t. \(\lnot valid_{LPL}(\{\Phi _V(\) \(v_i), \Phi _V(v_j)\})\). But then, there cannot be any configuration \(\rho \in CFG(LPL)\) s.t. \(\{\Phi _V(v_i), \Phi _V(v_j)\}\) \(\subseteq \rho \); hence, no meta-model \(MM_\rho \in PR(LPL)\) can have classes with same name.
\(\square \)
Proof of Lemma 2: Unique Field Names.
Proof
The proof is similar to the one for Lemma 1:
- \(\Rightarrow )\):
-
We will proceed by contradiction. Assume there is a meta-model \(MM_\rho \in PR(LPL)\) having a class v that holds two fields \(f_1\) and \(f_2\) with the same name. Then, both v and \(f_1,f_2\) are present in the 150 MM and therefore in \(MM_{LPL}\). But then, \(\{\Phi _F(f_1), \Phi _F(f_2\) \()\} \subseteq \rho \), and so \(valid_{LPL}\) \((\{\Phi _F\) \((f_1), \Phi _F(f_2)\})\) holds, in contradiction with the condition of the lemma.
- \(\Leftarrow )\):
-
Assume any two distinct fields \(f_1\) and \(f_2\) with same name, belonging to the same class v, in \(MM_{LPL}\), s.t. \(\lnot valid_{LPL}(\{\Phi _F(f_1), \Phi _F(f_2)\})\). But then, there cannot be any configuration \(\rho \in CFG(LPL)\) s.t. \(\{\Phi _F(f_1), \Phi _F(f_2)\} \subseteq \rho \), and therefore no meta-model \(MM_\rho \in PR(LPL)\) can have a class with two fields with same name.
\(\square \)
Proof of Lemma 3: No Inheritance Cycles.
Proof
The proof is similar to those of Lemmas 1 and 2.
- \(\Rightarrow )\):
-
We will proceed by contradiction. Assume there is a meta-model \(MM_\rho \in PR(LPL)\) having an inheritance cycle \(C \subseteq I^{MM_\rho }\). Then, the cycle C is present in the 150 MM and therefore in \(MM_{LPL}\). This means that \(\{\Phi _I(v_1, v_2)~|~(v_1, v_2) \in C\} \subseteq \rho \), and therefore \(valid_{LPL}\) \((\{\Phi _I(v_1, v_2)~|~(v_1, v_2) \in C\})\), in contradiction with the condition of the lemma.
- \(\Leftarrow )\):
-
Assume there is an inheritance cycle \(C \in I^{MM_{LPL}}\) s.t. \(\lnot valid_{LPL}(\{\Phi _I(v_1, v_2)~|~(v_1, v_2) \in C\})\). But then, there cannot be any configuration \(\rho \in CFG(\) LPL) s.t. \(\{\Phi _I(v_1, v_2)~|~(v_1, v_2) \in C\} \subseteq \rho \), and therefore no meta-model \(MM_\rho \in PR(LPL)\) can have an inheritance cycle.
\(\square \)
Proof of Lemma 4: Correctness of Logical Encoding of LPL.
Proof
- \(\Rightarrow )\):
-
Any \(\rho \in CFG(LPL)\) should satisfy Definition 6, which means that:
- (1):
-
\(TOP(LPL) \in \rho \), hence the term TOP(LPL) of \(\Lambda _{LPL}\) evaluates to true,
- (2):
-
\(M \in \rho \implies \forall M_i \in MAN(M) \cdot M_i \in \rho \), hence the term \(M \implies \underset{M_i \in MAN(M)}{\bigwedge }M_i\) of \(\Lambda (M)\) evaluates to true,
- (3):
-
\(M \in \rho \implies (ALT(M) \ne \emptyset \implies \exists _1 M_i \in ALT(M) \cdot M_i \in \rho )\), hence the term \(M \implies \underset{M_i \in ALT(M)}{\bigoplus }M_i\) of \(\Lambda (M)\) evaluates to true,
- (4):
-
\(M \in \rho \implies (OR(M) \ne \emptyset \implies \exists M_i \in OR(M) \cdot M_i \in \rho )\), hence the term \(M \implies \underset{M_i \in OR(M)}{\bigvee }M_i\) of \(\Lambda (M)\) evaluates to true,
- (5):
-
\(M \in \rho \implies M_D(M) \in \rho \), hence the term \(M \implies M_D(M)\) of \(\Lambda (M)\) evaluates to true,
- (6):
-
\(\bigwedge _{M_i \in LPL} \Psi (M_i)[true/\rho , false/(LPL {\setminus } \rho )] = true\) makes the term \(\underset{M_i \in LPL}{\bigwedge }\Psi (M_i)\) of \(\Lambda (M)\) evaluate to true.
Conversely, if some \(\rho \not \in CFG(LPL)\), then some of the items 1–6 in Definition 6 evaluates to false, and so does the corresponding item in Definition 19.
- \(\Leftarrow )\):
-
Follows an analogous reasoning to \(\Rightarrow \), due to the 1-1 mapping between terms in Definitions 6 and 19.
\(\square \)
Proof of Theorem 2: Consistent Extension Semantics.
Proof
Model G in Fig. 20 is a pullback (PB) object, containing exactly the elements of \(G_\rho \) that are typed by the meta-model in module \(M_i\). The spans \(L \leftarrow K \rightarrow R\) and \(L_{\rho (r)} \leftarrow K_{\rho (r)} \rightarrow R_{\rho (r)}\) of rules r and \(\rho (r)\) are shown at the bottom, where morphisms \(l'\), \(k'\) and \(r'\) exist because \(\rho (r)\) is an extension of r (cf. Definition 10). Spans \(G \leftarrow D \rightarrow H\) and \(G_\rho \leftarrow D_\rho \rightarrow H_\rho \) result from the direct derivations of r and \(\rho (r)\). We need to show that: (1) morphism \(m :L \rightarrow G\) exists and r is applicable, i.e., NACs are satisfied, (2) morphisms \(d :D \rightarrow D_\rho \) and \(h :H \rightarrow H_\rho \) exist, and (3) square (1) is PB.
-
1.
Morphism \(m :L \rightarrow G\) exists since L is the PB object of \(G\rightarrow G_\rho \leftarrow L_{\rho (r)}\). Indeed, on the one hand, \(\rho (r)\) is a modular extension of r, so \(L_{\rho (r)}\setminus L\) is typed by \(MM_\rho \setminus MM(M_i)\). On the other hand, G only contains the elements of \(G_\rho \) typed by \(MM(M_i)\). Hence, the PB object of \(G\rightarrow G_\rho \leftarrow L_{\rho (r)}\) contains exactly the elements of \(L_{\rho (r)}\) typed by \(MM(M_i)\), i.e., L. If \(\rho (r)\) is applicable, all of its NACs are satisfied (\(G_\rho \) has no occurrence of them). NACs in \(\rho (r)\) may either have been added by a NAC-rule, or have existed in r. In the first case, the NAC-rule should be a modular extension adding elements typed by \(MM_\rho \setminus MM(M_i)\) and therefore not present in G. In the second case, the NAC of \(\rho (r)\) may have been enlarged by modular extensions, whose elements cannot be in G either.
-
2.
Since \(\rho (r)\) is a modular extension of r, both rules delete the same elements typed by \(MM(M_i)\). In addition, \(\rho (r)\) may delete more elements typed by \(MM_\rho \setminus MM(M_i)\). Therefore, there must be a morphism \(d :D \rightarrow D_\rho \). Morphism \(h :H \rightarrow H_\rho \) exists because of the universal pushout property. Since H is a pushout object, and we have \(K \rightarrow D \rightarrow D_\rho \rightarrow H_\rho \) and \(K \rightarrow R \rightarrow R_{\rho (r)} \rightarrow H_\rho \), there is a unique morphism \(H \rightarrow H_\rho \) as required.
-
3.
Square (1) would not be a PB if rule \(\rho (r)\) created elements typed by \(MM_\rho \setminus MM(M_i)\). However, this is not possible since \(\rho (r)\) is a modular extension.
\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
de Lara, J., Guerra, E. & Bottoni, P. Modular language product lines: concept, tool and analysis. Softw Syst Model (2024). https://doi.org/10.1007/s10270-024-01179-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10270-024-01179-9



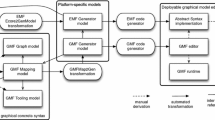




















 , we say that
, we say that 



