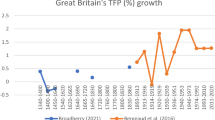
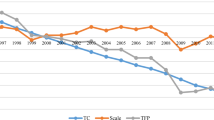
Abstract
Should intermediate consumption (IC), which historically accounts for around 50% of the value of production, be considered in growth accounting? The current growth accounting exercise does not model IC. This means that when IC experiences productivity gains, its capacity to transmit them to the whole economy is currently neglected. The rare current literature on this issue diverges substantially on the importance of the role of the IC as an explanatory factor of growth. We propose a bi-sectoral general equilibrium model that allows for an accounting where each productive sector contributes to growth in proportion to its weight in the economy. Our theoretical framework and the (proportional) growth accounting exercise it allows (i.e., calculating the contribution of technical change conveyed by IC and other usual key factors, such as: Global and sectoral TFP, Global and sectoral Capital deepening) are thoroughly presented. The proposed framework is autonomous and calibrated pedagogically. However, to illustrate empirically in a comparative way how it works, we have shown that it can also be reduced to a particular case of the literature and calibrated it on the US economy (1954–1990). Although this consistently improves the growth accounting accuracy, our results reveal that the IC has nevertheless contributed only 2% to US growth. We compared this result to the literature. The key factors influencing its magnitude were also highlighted and discussed.
Similar content being viewed by others
Notes
In our production functions, both are present, and the contributions of both to growth will be calculated as well as the contributions of technological change passing through each of these two channels.
In France, for instance, the works of Cette et al. (2004, 2005a, b, 2014) and Daw (2019). In the USA, e.g., Oliner and Sichel (2002) or Jorgenson et al. (2004, 2006, 2008); Van Ark et al. (2008) for a comparison between the USA and European Union or Oulton (2012) and Marrano et al. (2009) for the UK show, according to the authors or the year of publication, exogenous aggregated (macroeconomic) or more disaggregated growth accounting with a retrospective and prospective outlooks but without any technological progress bias (except Daw 2019 where these biases are encountered). In Japan, Sato and Tamaki (2009) illustrate an exogenous macroeconomic retrospective growth accounting exercise with biased technological progress. The works of Madsen (2010a, b), Fernald and Jones (2014), and Bergeaud et al. (2017, 2018a, b) for example, can also be considered as declensions but in which endogenous mechanisms are modeled explaining the evolution of factors contributing to growth without going however towards what is meant by general equilibrium modeling of evaluated economies.
However, the model used by each author is obviously its own.
As, for instance, in Byrne et al. (2013).
Which, in addition to the technological change that is common to both sectors, benefit from a specific one in their production. The latter will be at the origin of the incorporated and transmitted progress to standard sector via IC.
\({\widehat{q}}_{2}\) results from technical progress \({\widehat{q}}_{1}\), which is specific to the technological sector. The composite IC therefore has no technical change of its own, but the functioning of the economy, thanks to the specific change of the technological sector, diffuse through the production of the latter sector and its use to produce composite IC, a progress at a pace \({\widehat{q}}_{2}\) so called "derived progress". Its magnitude will depend on the value of the technological sector products in the composite IC. This is the reason why \({\widehat{q}}_{2}\) does not appear directly in the production functions but will be considered later in the evolutionary equations of the economy and in its growth accounting.
Since IC is a composite of products from standard and technological sectors. On the other hand, \({\widehat{q}}_{2}\) will be closer to 0 if IC is made up of standard sector products. This same idea applies if there were more than 2 sectors.
For instance: \({y}_{sprod}={TFP}_{s}{K}_{s}^{{\alpha }_{s}\left(1-{\gamma }_{s}\right)}{T}_{s}^{{\beta }_{s}\left(1-{\gamma }_{s}\right)}{H}_{s}^{\left(1-{\alpha }_{s}-{\beta }_{s}\right)\left(1-{\gamma }_{s}\right)-1}{IC}^{{\gamma }_{s}}\) then by developing the numerator of \({H}_{s}\) we see that this one is equal the opposite of the powers of \({K}_{s},{T}_{s}\;\text{and IC}\) hence the expression of \({y}_{sprod}.\) The output per hour of technological sector is treated by analogy.
The faster pace of progress in technological sector generates at the same time higher rate of technical obsolescence and that is the rational for higher depreciation rates in the technological sector. As an illustration, the latest version of EU-KLEMS (Stehrer et al. 2019 uses annual capital depreciation rates ranging from 31.5% for the category "Computer and communication equipment" to 1.1% for "Residential buildings", i.e., about 30 times lower depreciation for the latter category. "Other machinery and equipment" (excluding computer and communication equipment) is at 13.1% while "Transport equipment" is at 18.9%.
If, for instance: \({q}_{t}=1.1\), we have: \({I}_{s}=1.1*{I}_{t}\) and so: \(\frac{{I}_{s}}{{I}_{t}}=1.1\) which means that a standard investment unit equals 1.1 technological investment unit, which is written in terms of absolute prices: \({P}_{t}=\frac{1}{1.1}{P}_{s}\) and in terms of relative prices:: \({p}_{t}=\frac{{P}_{t}}{{P}_{s}}=0.91\).
With \(h={h}_{s}={h}_{t}=\frac{{p}_{ic}IC}{{Y}_{sprod}}=\frac{{p}_{ic}IC}{{p}_{t}{Y}_{tprod}}\).
We have to do: \({p}_{t}{y}_{tprod}^{{\prime}}\left({k}_{t}\right)={r}_{{k}_{t}}+{\delta }_{s}\) from where: \({\alpha }_{t}\left(1-{\gamma }_{t}\right)\frac{{{p}_{t}y}_{tprod}}{{k}_{t}}={r}_{{k}_{t}}+{\delta }_{s}\) and: \(\mathrm{ln}{k}_{t}+\mathrm{ln}\left({r}_{{k}_{t}}+{\delta }_{s}\right)=\mathrm{ln}{y}_{tprod}+\mathrm{ln}{p}_{t}\).
Given that the product of the standard sector is the numeraire, we will derive the stationary values of standard capital and technological capital by hours worked from the standard production function.
The level and downward trend in the relative price of technological products is the result of the upward trend in specific-technological sector progress: \({q}_{1}={- p}_{t}\) and \({\widehat{q}}_{1}=-{\widehat{p}}_{t}\). In the case of IC, the same hypothesis leads to: \({p}_{ic}=-{q}_{2}\) and \({\widehat{p}}_{ic}=-{\widehat{q}}_{2}\).
We have to do: \({{p}_{t}y}_{tprod}^{{\prime}}\left({t}_{t}\right)=\left({r}_{{t}_{t}}+{\delta }_{t}-{\widehat{p}}_{t}\right){p}_{t}\) from where: \({\beta }_{t}\left(1-{\gamma }_{t}\right)\frac{{{p}_{t}y}_{tprod}}{{t}_{t}}=\left({r}_{{t}_{t}}+{\delta }_{t}-{\widehat{p}}_{t}\right){p}_{t}\) and take the log-derivatives.
The Divisia index (here applied to gross output) over a period (t; t + 1), when the shares of the concerned values do not vary between t and t + 1, which is the case here, is written: \(\mathrm{ln}\left(\frac{{Y}_{t+1}}{{Y}_{t}}\right)=\sum_{i=s,t,ic}{\theta }_{i}ln\left(\frac{{Y}_{i, t+1}}{{Y}_{i,t}}\right)\) with \({Y}_{i}\) the production of the standard sector, technological one or the production of intermediates (for intermediates: \({Y}_{ic} \mathrm{is} IC\)). By reasoning directly with the indices \(\left(\frac{{Y}_{t+1}}{{Y}_{t}} \text{and }\frac{{Y}_{i,t+1}}{{Y}_{i,t}}\right)\) so directly using the Divisia index formula or replacing these indices with numbers – we would have in this case: \(\mathrm{ln}\left({Y}_{t}\right)=\sum_{i=s,t,ic}{\theta }_{i}ln\left({Y}_{i,t}\right)\) – then differentiating, in both cases, with respect to the time we obtain: \(\widehat{Y}={\theta }_{s}{\widehat{Y}}_{s}+{\theta }_{t}{\widehat{Y}}_{t}+{\theta }_{ic}\widehat{IC}\).
In this regime, the ratio between sectoral hours \(\left(\frac{{H}_{s}}{{H}_{t}}\right)\) must be constant. This does not necessarily mean fixed but simply identical rates of changes (numerator and denominator). If so, we have in steady state: \({\widehat{H}}_{s}={\widehat{H}}_{t}=\widehat{H}\).
E.g., the contribution of standard TFP to VA per hour is determined as follows: \({\widehat{TFP}}_{s}^{Cs}={\theta }_{s}\left({\widehat{y}}_{sprod}-\left(1-\gamma \right)\alpha {\widehat{k}}_{s}-\left(1-\gamma \right)\beta {\widehat{t}}_{s}-\gamma \widehat{ic}\right)\)
It is clear that if the first term of the parenthesis were that of the evolution of value added (and not that of production), the evolution of the TFP contribution of the standard sector would be 0 since the other 3 terms of this parenthesis correspond, in the steady state, to the evolution of this value-added. The empirical verification of the nullity of standard sector TFP is available in Appendix D (see TFP Standard sector).
For example, the sum of two growths of 5% is 10%, while the multiplication of two growth factors 1.05*1.05 gives 10.25%, or a difference of 0.0025. This difference goes to 0.031 if one has three growths of 10%.
There is a very slight difference of 0.0004, which, as already mentioned, can be misleadingly introduced when multiplying growth factors.
When trying to calculate the contribution of equipment-specific technological change to US growth from 1954 to 1990, GHK (p.351) find their figure of 58% (57.5% more precisely) by taking the ratio of specific technological change (0.77%) to productivity growth delivered by their model (1.34%) and not the one found empirically (1.24%). NS (p.18) uses the latter figure, however, to find that equipment-specific technological change accounts for near all the US growth from 1954 to 1990. Here, as already stated, we will work with 1.34%.
\(\left(\frac{\partial {\widehat{y}}_{va}}{\partial {\widehat{q}}_{2}}\right)*{\widehat{q}}_{2}=0.143*0.01=0.00143\) and \(\frac{0.00143}{0.0134}=10.67\%\).
References
Abramovitz M (1956) Resource and output trends in the US since 1870. Am Econ Rev 46(2):5–23
Acemoglu D (2002) Directed technical change. Rev Econ Stud 69(4):781–809
Bakhshi H, Larsen J (2005) ICT-Specific technological progress in the United Kingdom. J Macroecon 27(4):648–669
Barro RJ, Sala-i-Martin X (2004) Economic growth, 2nd end. The MIT Press
Bergeaud A, Cette G, Lecat R (2017) Total factor productivity in advanced countries: a long- term perspective. Int Prod Monitor 32:6–24
Bergeaud A, Cette G, Lecat R (2018a) The role of production factor quality and technology diffusion in twentieth-century productivity growth. Cliometrica 12(1):61–97
Bergeaud A, Cette G, Lecat R (2018b) Long-term growth and productivity trends: Secular stagnation or temporary slowdown? Revue de l’OFCE 0(3):37–54
Blanchard OJ (1997) The medium run. Brook Pap Econ Act 28(2):89–158
Byrne DM, Oliner SD, Sichel DE (2013) Is the information technology revolution over? Int Prod Monitor 25:20–36
Byrne DM, Corrado C (2017) ICT prices and ICT services: What do they tell us about productivity and technology. Int Prod Monitor 33:150–181
Caselli F, Coleman WJ (2006) The world technology frontier. Am Econ Rev 96(3):499–522
Cette G, Mairesse J, Kocoglu Y (2004) The spread of ICT and potential output growth. Revue D’économie Politique 114(1):77–97
Cette G, Kocoglu Y, Mairesse J (2005a) A century of total factor productivity in France. Bulletin de la Banque de France 139
Cette G, Mairesse J, Kocoglu Y (2005b) ICT and potential output growth. Econ Lett 87(2):231–234
Cette G (2014) Presidential conference: Does ICT remain a powerful engine of growth? Revue D’économie Politique 124(4):473–492
Cummins J, Violante GL (2002) Investment-specific technical change in the US (1947–2000): Measurement and macroeconomic consequences. Rev Econ Dyn 5(2):243–284
Davila A, Fernandez M, Zuleta H (2021) The natural resource boom and the uneven fall of the labor share. IZA Institute of Labor. Economic Discussion Paper Series, No. 14592
Daw G (2019) Total factor productivity: How to more accurately assess “our ignorance”? Revue Économique 70(2):239–283
Elsby MW, Hobijn B, Sahin A (2013) The decline of the US labor share. Brook Pap Econ Act 44(2):1–52
Fernald JG, Jones CI (2014) The future of US economic growth. Am Econ Rev 104(5):44–49
Fisher JDM (2006) The dynamic effects of neutral and investment-specific technology shocks. J Polit Econ 114(3):413–451
Greenwood J, Hercowitz Z, Krusell P (1997) Long-run implications of investment-specific technological change. Am Econ Rev 87(3):342–362
Growiec J, McAdam P, Mućk J (2018a) Endogenous labor share cycles: Theory and evidence. J Econ Dyn Control 87(C):74–93
Growiec J, McAdam P, Mućk J (2018b) Will the ‘true” labor share stand up? An applied survey on labor share measures. J Econ Surv 32(4):961–984
Horvath M (2000) Sectoral shocks and aggregate fluctuations. J Monet Econ 45(1):69–106
Hulten CR (1975) Technical change and the reproducibility of capital. Am Econ Rev 65(5):956–965
Hulten CR (1978) Growth accounting with intermediate inputs. Rev Econ Stud 45(3):511–518
Hulten CR (1979) On the importance of productivity change. Am Econ Rev 69(1):126–136
Hulten CR (1992) Growth accounting when technical change is embodied in capital. Am Econ Rev 82(4):964–980
Jäger K (2018) EU KLEMS growth and productivity accounts 2017 release, description of methodology and general notes. The Conference Board. http://www.euklems.net/index.html
Jones CI (2011) Intermediate goods and weak links in the theory of economic development. Am Econ J Macroecon 3(2):1–28
Jorgenson DW (1966) The embodiment hypothesis. J Polit Econ 74(1):1–17
Jorgenson DW, Ho MS, Stiroh KJ (2004) Will the U.S. Productivity Resurgence Continue? Current issues in economics and finance. Federal Reserve Bank of New York 10(3):1–7
Jorgenson DW, Ho MS, Stiroh KJ (2006) Potential growth of the U.S. economy: Will the productivity resurgence continue? Bus Econ 41(1):7–16
Jorgenson DW, Ho MS, Stiroh KJ (2008) A retrospective look at the US productivity growth resurgence. J Econ Perspect 22(1):3–24
Kahn J, Lim J (1998) Skilled labor-augmenting technical progress in U.S. manufacturing. Q J Econ 113(4):1281–1308
Karabarbounis L, Neiman B (2014) The global decline of the labor share. Q J Econ 129(1):61–103
Krueger A (1999) Measuring labor’s share. Am Econ Rev 89(2):45–51
Kydland FE, Prescott EC (1982) Time to build and aggregate fluctuations. Econometrica 50(6):1345–1370
Leontief W (1936) Quantitative input and output relations in the economic system of the United States. Rev Econ Stat 18(3):105–125
López JR, Torres JL (2012) Technological sources of productivity growth in Germany Japan, and the United States. Macroecon Dyn 16(1):133–150
Madsen JB (2010a) The anatomy of growth in the OECD since 1870. J Monet Econ 57(6):753–767
Madsen JB (2010b) Growth and capital deepening since 1870: is it all technological progress? J Macroecon 32(2):641–656
Marrano MG, Haskel JE, Wallis G (2009) What happened to the knowledge economy? ICT, intangible investment, and Britain’s productivity record revisited. Rev Income Wealth 55(3):686–716
Martínez D, Rodríguez J, Torres JL (2008) The Productivity paradox and the new economy: the Spanish case. J Macroecon 30(4):1569–1586
Ngai LR, Samaniego RM (2009) Mapping prices into productivity in multisector growth models. J Econ Growth 14(3):183–204
Ngai LR, Pissarides CA (2007) Structural change in a multi-sector model of growth. Am Econ Rev 97(1):429–443
Oliner S, Sichel D (2002) Information technology and productivity: Where are we Now and Where are we Going? Economic Review, Federal Reserve Bank of Atlanta 87(3):15–44
O’Mahony M, Vecchi M, Venturini F (2021) Capital heterogeneity and the decline of the labour share. Economica 88(350):271–296
Oulton N (2012) Long term implications of the ICT revolution: Applying the lessons of growth theory and growth accounting. Econ Model 29(5):1722–1736
Rodriguez F, Jayadef A (2013) The declining labor share of income. J Global Dev 3(2):1–18
Sachs JD, Kotlikoff LJ (2012) Smart machines and long-term misery. NBER WP, N°18629
Sato R, Tamaki M (2009) Quantity or quality: the impact of labour-saving innovation on US and Japanese growth rates 1960–2004. Jpn Econ Rev 60(4):407–434
Solow R (1956) A contribution to the theory of growth. Q J Econ 70(1):65–94
Solow R (1957) Technical change and the aggregate production function. Rev Econ Stat 39(3):312–320
Stehrer R, Bykova A, Jäger K, Reiter O, Schwarzhappel M (2019) Industry level growth and productivity data with special focus on intangible assets. wiiw Statistical Report 8
Sturgill B (2014) Back to the basics : Revisiting the development accounting methodology. J Macroecon 42(C):52–68
Sturgill B (2012) The relationship between factor shares and economic development. J Macroecon 34(4):1044–1062
Tamura R, Dwyer J, Devereux J, Baier S (2019) Economic growth in the long run. J Dev Econ 137(C):1–35
Turner C, Tamura R, Mulholland SE (2013) How Important are human capital, physical capital and total factor productivity for determining state economic growth in the United States, 1840–2000? J Econ Growth 18(4):319–371
Uzawa H (1963) On a two-sectors model of economic growth. Rev Econ Stud 29(1):40–47
Van Ark B, O’Mahony M, Timmer MP (2008) The Productivity gap between Europe and the United States: Trends and causes. J Econ Perspect 22(1):25–44
Whelan K (2003) A two-sector approach to modelling U.S. NIPA data. J Money Credit Bank 35 (4):627–656
Young AT (2010) One of the Things We Know that Ain’t so :is US labor’s share relatively stable ? J Macroecon 32(1):90–102
Zuleta H (2008) An empirical note on factor shares. J Int Trade Econ Dev 17(3):379–390
Acknowledgements
I am grateful to the Editor, Luís F. Costa, for beneficial guidance. I also thank two anonymous reviewers whose valuable and constructive comments and suggestions made it possible to improve an earlier draft of this manuscript. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
About this article
Cite this article
Daw, G. Impact of technical change via intermediate consumption: exhaustive general equilibrium growth accounting and reassessment applied to USA 1954–1990. Port Econ J 23, 55–87 (2024). https://doi.org/10.1007/s10258-022-00224-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10258-022-00224-z
Keywords
- General equilibrium models for growth accounting
- Technical change
- Relative prices
- Gross output, value-added, sectoral productions, and IC
- Growth Residual or Total Factor Productivity (TFP)