Abstract
For years, improving processes has been a prominent business priority for Chief Information Officers. As expressed by the popular saying, “If you can’t measure it, you can’t manage it,” process measures are an important instrument for managing processes and corresponding change projects. Companies have been using a value-based management approach since the 1990s in a constant endeavor to increase their value. Value-based business process management introduces value-based management principles to business process management and uses a risk-adjusted expected net present value as the process measure. However, existing analyses of this issue operate at a high (i.e., corporate) level, hampering the use of value-based business process management at an operational process level in both research and practice. Therefore, this paper proposes a valuation calculus that brings value-based business process management to the operational process level by showing how the risk-adjusted expected net present value of a process can be determined. We demonstrate that the valuation calculus provides insights into the theoretical foundations of processes and helps improve the calculation capabilities of an existing process-modeling tool.





Similar content being viewed by others
Notes
The text is italicized in the source. The symbol
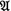 for the sigma-algebra and the symbol
for the sigma-algebra and the symbol 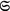 for the text’s sample space were replaced by the now more commonly used symbols \({\mathcal{F}}\) and Ω, respectively.
for the text’s sample space were replaced by the now more commonly used symbols \({\mathcal{F}}\) and Ω, respectively.
References
Abdellaoui M, Bleichrodt H, l’Haridon O, Paraschiv C (2013) Is there one unifying concept of utility? An experimental comparison of utility under risk and utility over time. Manage Sci 59(9):2153–2169. doi:10.1287/mnsc.1120.1690
Andersen S, Harrison GW, Lau MI, Rutström EE (2008) Eliciting risk and time preferences. Econometrica 76(3):583–618. doi:10.1111/j.1468-0262.2008.00848.x
Bai X, Padman R, Krishnan R (2007) A risk management approach to business process design. In: Rivard S, Webster J (eds) Proceedings of the 27th international conference on information systems (ICIS), Montreal, Canada, Paper 28
Bai X, Krishnan R, Padman R, Wang HJ (2013) On risk management with information flows in business processes. Inform Syst Res 24(3):731–749. doi:10.1287/isre.1120.0450
Bamberg G, Spremann K (1981) Implications of constant risk aversion. Math Method Oper Res 25(7):205–224
Becker J, Kahn D (2005) Der Prozess im Fokus. In: Becker J, Kugeler M, Rosemann M (eds) Prozessmanagement - Ein Leitfaden zur prozessorientierten Organisationsgestaltung. Springer-Verlag GmbH, Berlin
Beer M, Fridgen G, Müller H, Wolf T (2013) Benefits quantification in IT projects. In: Alt R, Franczyk B (eds) Proceedings of the 11th International Conference on Wirtschaftsinformatik (WI). Leipzig, Germany, pp 707–720
Bernoulli D (1954) Exposition of a new theory on the measurement of risk. Econometrica 22(1):23–36
Bolsinger M, Bewernik M, Buhl HU (2011) Value-based process improvement. In: Tuunainen VK, Rossi M, Nandhakumar J (eds) Proceedings of the 19th European conference on information systems (ECIS), Helsinki, Finland, Paper 21
Braunwarth K, Ullrich C (2010) Valuating business process flexibility achieved through an alternative execution path. In: Johnson R, De Villiers C, Kruger N, Bartmann D (eds) Proceedings of the 18th European conference on information systems (ECIS), Pretoria, South Africa, Paper 24
Braunwarth K, Kaiser M, Müller A (2010) Economic evaluation and optimization of the degree of automation in insurance processes. Bus Inf Syst Eng 2(1):29–39. doi:10.1007/s12599-009-0088-6
Buhl HU, Röglinger M, Stöckl S, Braunwarth K (2011) Value orientation in process management—research gap and contribution to economically well-founded decisions in process management. Bus Inf Syst Eng 3(3):163–172
Byers T, Waterman M (1984) Determining all optimal and near-optimal solutions when solving shortest path problems by dynamic programming. Oper Res 32(6):1381–1384
Coenenberg AG, Salfeld R (2007) Wertorientierte Unternehmensführung: Vom Strategieentwurf zur Implementierung. Schäffer-Poeschel, Stuttgart
Copeland TE, Koller T, Murrin J (1990) Valuation: measuring and managing the value of companies. Wiley, New York
Copeland TE, Weston JF, Shastri K (2005) Financial theory and corporate policy. Pearson Education Inc, Boston
Danielson MG, Heck JL, Shaffer DR (2008) Shareholder theory—how opponents and proponents both get it wrong. J Appl Finance 18(2):62–66
Datar S, Kulp SC, Lambert RA (2001) Balancing performance measures. J Account Res 39(1):75–92
Davamanirajan P, Kauffman RJ, Kriebel CH, Mukhopadhyay T (2006) Systems design, process performance, and economic outcomes in international banking. J Manage Inform Syst 23(2):65–90
Devaraj S, Kohli R (2001) The IT payoff: measuring the business value of information technology investments. Financial Times/Prentice Hall
Feiler PH, Humphrey WS (1993) Software process development and enactment: concepts and definitions. Proceedings of the 2nd International Conference on the Software Process. Continuous Software Process Improvement, Berlin, pp 28–40
Feller W (1971) An introduction to probability theory and its applications, vol 2. Wiley, New York
Franz P, Kirchmer M, Rosemann M (2011) Value-driven business process management—impact and benefits. http://www.accenture.com/SiteCollectionDocuments/PDF/Accenture-Value-Driven-Business-Process-Management.pdf. Accessed 2014-02-21
Freund RJ (1956) The introduction of risk into a programming model. Econometrica 24(3):253–263
Fridgen G, Müller H (2009) Risk/cost valuation of fixed price IT outsourcing in a portfolio context. In: Nunamaker J, Currie W, Chen H, Slaughter S (eds) Proceedings of the 30th international conference on information systems (ICIS). Phoenix, AZ, USA
Friedman M, Savage LJ (1948) The utility analysis of choices involving risk. J Polit Econ 56(4):279–304
Gartner (2013) Hunting and harvesting in a digital world: the 2013 CIO Agenda
Gibbons A (1985) Algorithmic graph theory. Cambridge University Press, Melbourne
Gibbons R (2005) Incentives between Firms (And within). Manage Sci 51(1):2–17
González LS, Rubio FG, González FR, Velthuis MP (2010) Measurement in business processes: a systematic review. BPMJ 16(1):114–134. doi:10.1108/14637151011017976
Grob HL (1993) Capital budgeting with financial plans: an introduction. Gabler, Wiesbaden
Gulledge TR, Hirschmann P, Scheer A (1997) Value-based management of inter-organizational business processes. In: Krallmann H (ed) Proceedings of the 3rd international conference on Wirtschaftsinformatik (WI), Berlin, Germany, pp 73–98
Hevner AR, March ST, Park J, Ram S (2004) Design science in information systems research. MISQ 28(1):75–105
Hillier FS (1963) The derivation of probabilistic information for the evaluation of risky investments. Manage Sci 9(3):443–457
Hollingsworth DC, WfMC (2003) The WfMC glossary. In: Fischer L (ed) Workflow handbook 2003. Future Strategies Inc., Lighthouse Point, Florida, pp 263–299
Hubbard DW (2007) How to measure anything: finding the value of intangibles in business. Wiley, New York
Ittner CD, Larcker DF (2001) Assessing empirical research in managerial accounting: a value-based management perspective. J Account Econ 32(1–3):349–410
Kasanen E, Trigeorgis L (1994) A market utility approach to investment valuation. Eur J Oper Res 74(2):294–309
Keeney RL (1994) Creativity in decision making with value-focused thinking. Sloan Manage Rev 35(4):33–41
Koller T, Goedhart M, Wessels D (2010) Valuation: measuring and managing the value of companies. Wiley, New Jersey
Kruschwitz L, Husmann S (2010) Finanzierung und Investition. Oldenburg Verlag, Munich
Kruschwitz L, Löffler A (2003) Semi-subjektive Bewertung. Z Betriebswirt 73(12):1335–1345
Kueng P, Kawalek P (1997) Goal-based business process models: creation and evaluation. BPMJ 3(1):17–38
Linderman K, McKone-Sweet KE, Anderson JC (2005) An integrated systems approach to process control and maintenance. Eur J Oper Res 164(2):324–340
Longley-Cook AG (1998) Risk-adjusted economic value analysis. N Am Actuar J 2(1):87–100
Meredith JR, Raturi A, Amoako-Gyampah K, Kaplan B (1989) Alternative research paradigms in operations. J Oper Manage 8(4):297–326
Mosteller F, Nogee P (1951) An experimental measurement of utility. J Polit Econ 59:371–404
Neiger D, Churilov L (2004a) Goal-oriented business process engineering revisited: a unifying perspective. In: Cordeiro J, Felipe J (eds) Proceedings of the 1st international workshop on computer supported activity coordination (CSAC) in conjunction with the 6th international conference on enterprise information systems (ICEIS). Porto, Portugal, pp 149–163
Neiger D, Churilov L (2004b) Goal-oriented business process modeling with EPCs and value-focused thinking. Business Process Management (LNCS) 3080:98–115
Neiger D, Churilov L, zur Muehlen M, Rosemann M (2006) Integrating risks in business process models with value focused process engineering. In: Ljungberg J, Andersson M (eds) Proceedings of the 14th European conference on information systems (ECIS). Gothenburg, Sweden, pp 1606–1615
Neuhuber LCN, Krause F, Roeglinger M (2013) flexibilization of service processes: toward an economic optimization model. In: Brinkkemper S, Batenburg R, van Hillegersberg J, van Heck E, Spiekermann S, Connolly R (eds) Proceedings of the 21st european conference on information systems (ECIS), Utrecht, The Netherlands, Paper 66
Object Management Group (2011) UML Superstructure Specification v 2.4.1. http://www.omg.org/spec/UML/2.4.1/Superstructure/PDF. Accessed 2014-02-21
Pearn W, Lin G, Chen K (1998) Distributional and inferential properties of the process accuracy and process precision indices. Commun Stat-Theor M 27(4):985–1000
Peffers K, Tuunanen T, Rothenberger MA, Chatterjee S (2008) A design science research methodology for information systems research. J Manage Inf Syst 24(3):45–77
Rappaport A (1986) Creating shareholder value: the new standard for business performance. Free Press, New York
Reijers HA, Liman Mansar S (2005) Best practices in business process redesign: an overview and qualitative evaluation of successful redesign heuristics. Omega 33(4):283–306. doi:10.1016/j.omega.2004.04.012
Rotaru K, Wilkin C, Churilov L, Neiger D, Ceglowski A (2011) Formalizing process-based risk with value-focused process engineering. Inf Syst E-Bus Manage 9(4):447–474. doi:10.1007/s10257-009-0125-5
Rubin V, Günther CW, van der Aalst WMP, Kindler E, van Dongen BF, Schäfer W (2007) Process mining framework for software processes. In: Wang Q, Pfahl D, Raffo DM (eds) Proceedings of the international conference on software process: software process dynamics and agility (ICSP). Minneapolis, MN, pp 169–181
Sampath P, Wirsing M (2011) Evaluation of cost based best practices in business processes. In: Halpin T, Nurcan S, Krogstie J (eds) Proceedings of the 12th international conference on business process modeling, development, and support (BPMDS) and 16th international conference on exploring modelling methods for systems analysis and design (EMMSAD) held at the 23rd international conference on advanced information systems engineering (CAiSE): enterprise. Business-Process and Information Systems Modeling, London, pp 61–74
Sedgewick R, Schidlowsky M (2003) Algorithms in Java, Part 5: graph algorithms. Addison-Wesley Longman Publishing Co., Inc, Boston
Sen S, Raghu T (2013) Interdependencies in IT infrastructure services: analyzing service processes for optimal incentive design. Inform Syst Res 24(3):822–841. doi:10.1287/isre.2013.0475
Sidorova A, Isik O (2010) Business process research: a cross-disciplinary review. BPMJ 16(4):566–597. doi:10.1108/14637151011065928
Sonnenberg C, vom Brocke J (2012) Evaluations in the science of the artificial-reconsidering the build-evaluate pattern in design science research. In: Peffers K, Rothenberger M, Kuechler B (eds) Proceedings of the 7th International conference on design science research in information systems: advances in theory and practice (DESRIST). Las Vegas, NV, pp 381–397
Stewart GB, Stern JM (1991) The quest for value: the EVA management guide. HarperBusiness, New York
Sun SX, Zhao JL, Nunamaker JF, Sheng ORL (2006) Formulating the data-flow perspective for business process management. Inform Syst Res 17(4):374–391
Swalm RO (1966) Utility theory—insights into risk taking. Harvard Bus Rev 44(6):123–136
Thome R, Müller T, Vogeler K (2011) Zukunftsthema Geschäftsprozessmanagement. http://www.pwc.de/de_DE/de/prozessoptimierung/assets/PwC-GPM-Studie.pdf. Accessed 2014-02-21
Tregear R (2012) Practical process: measuring processes. http://www.bptrends.com/publicationfiles/11-06-2012-Practical%20Process_Measuring%20Processes-Tregear.pdf. Accessed 2014-02-21
van der Aalst WMP (2001) Re-engineering knock-out processes. Decis Support Syst 30(4):451–468. doi:10.1016/S0167-9236(00)00136-6
van der Aalst WMP (2013) business process management: a comprehensive survey. ISRN Software Eng, vol. 2013, Article ID 507984, 37 pages. doi:10.1155/2013/507984
van der Aalst WMP, ter Hofstede AH, Kiepuszewski B, Barros AP (2003) Workflow patterns. Distrib Parallel Dat 14(3):5–51
van der Aalst WMP, van Hee KM, ter Hofstede AH, Sidorova N, Verbeek H, Voorhoeve M, Wynn MT (2011) Soundness of workflow nets: classification, decidability, and analysis. Form Asp Comput 23(3):333–363
van Hee K, Reijers H (2000) Using formal analysis techniques in business process redesign. In: van der Aalst WMP, Desel J, Oberweis A (eds) Business process management—models, techniques, and empirical studies. Springer, Berlin, pp 142–160
Venable J, Pries-Heje J, Baskerville R (2012) A comprehensive framework for evaluation in design science research. In: Peffers K, Rothenberger M, Kuechler B (eds) Proceedings of the 7th international conference on design science research in information systems: advances in theory and practice (DESRIST). Las Vegas, NV, pp 423–438
Vergidis K, Tiwari A, Majeed B (2008) Business process analysis and optimization: beyond reengineering. IEEE T Syst Man Cy C 38(1):69–82. doi:10.1109/TSMCC.2007.905812
vom Brocke J, Sonnenberg C, Simons A (2009) Wertorientiertes Prozessmanagement: State-of-the-Art und zukünftiger Forschungsbedarf. In: Hansen HR, Karagiannis D, Fill H (eds) Proceedings of the 9th international conference on Wirtschaftsinformatik (WI). Austria, Vienna, pp 253–262
vom Brocke J, Recker JC, Mendling J (2010) Value-oriented process modeling: integrating financial perspectives into business process re-design. BPMJ 16(2):333–356
vom Brocke J, Becker J, Braccini AM, Butleris R, Hofreiter B, Kapočius K, De Marco M, Schmidt G, Seidel S, Simons A, Skopal T, Stein A, Stieglitz S, Suomi R, Vossen G, Winter R, Wrycza S (2011a) Current, future issues in BPM research: a European perspective from the ERCIS meeting. CAIS 28(1):393–414
vom Brocke J, Sonnenberg C, Baumoel U (2011b) Linking accounting and process-aware information systems–towards a generalized information model for process-oriented accounting. In: Tuunainen VK, Rossi M, Nandhakumar J (eds) Proceedings of the 19th European conference on information systems (ECIS), Helsinki, Finland, Paper 23
Wolf C, Harmon P (2012) The state of business process management 2012. http://www.bptrends.com/bpt/wp-content/surveys/2012-_BPT%20SURVEY-3-12-12-CW-PH.pdf. Accessed 2014-02-21
Wynn MT, Low WZ, Nauta W (2013) A framework for cost-aware process management: generation of accurate and timely management accounting cost reports. In: Ferrarotti F, Grossmann G (eds) Proceedings of the ninth Asia-Pacific conference on conceptual modelling (APCCM). Adelaide, Australia, pp 79–88
Young SD, O’Byrne SF (2001) EVA and value-based management: a practical guide to implementation. McGraw-Hill, New York
Zimmermann S, Katzmarzik A, Kundisch D (2008) IT sourcing portfolio management for it service providers—a risk/cost perspective. In: Boland R, Limayem M, Pentland B (eds) Proceedings of 29th international conference on information systems (ICIS). France, Paris
zur Muehlen M, Shapiro R (2010) Business process analytics. In: vom Brocke J, Rosemann M (eds) Handbook on business process management 2: strategic alignment, governance, people and culture. Springer, Berlin, pp 137–158
Acknowledgments
Grateful acknowledgement is due to the DFG (German Research Foundation) for their support of the projects “Modeling, self-composition and self-configuration of reference processes based on semantic concepts (SEMPRO²)” (BU 809/7-2) and “Integrated Enterprise Balancing (IEB)” (BU 809/8-1) making this paper possible.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Determination of path probabilities
To determine the expected value of a process cash flow and its variance, it is essential to determine the path probabilities \(p_{k}\). This is presented in the following. During a process improvement project, a process is presented as a process model with a process-modeling tool. With the help of this formal presentation, it is possible to formally describe, how a path probability \(p_{k}\) is determined. In order to do so, the process model [as defined in Hollingsworth and WfMC (2003, p. 266)] of a process P is defined as a graph G.
The process model of a process P is a graph, because a process model is a set of nodes (vertices) that are interconnected by arrows (edges) (Gibbons 1985). The set of vertices is denoted by V and the set of edges by E and we write G = (V, E). Because the edges are arrows, a process is a directed graph (Gibbons 1985). More precisely, we assume that a process model of a process P is defined as a graph G as followed:
-
(D1)
A process model of a process P is a directed graph G = (V, E) with one root vertex \(a_{0}\) and one final vertex \(a_{D + 1}\), toward which all edges are directed. It is V the set of vertices and E the set of edges.
-
(D2)
The set V consists of the set of actions A united with the set RC of the routing constructs (van der Aalst et al. 2003) to denote control flow patterns of P, \(a_{0}\) and \(a_{D + 1}\), i.e., \(V\text{ := }A \cup RC \cup a_{0} \cup a_{D + 1}\).
-
(D3)
A contains all D actions of P, numbered from 1 to D.
-
(D4)
RC is the set of the routing constructs to denote the control flow patterns, e.g., XOR-split, XOR-join, AND-split and AND-join (van der Aalst et al. 2003). Each element has one distinct index. For example, in Fig. 2 (left process) these vertices are XOR-join 1, AND-split 2, AND-join 3 and XOR-split 4.
-
(D5)
The edge-set E contains all the directed edges between the vertices. The directed edge \((v_{i} , v_{j} , p_{ij} )\) is a member of the set E if and only if there is an arrow between vertex \(v_{i} \in V\) and \(v_{j} \in V\), pointing from \(v_{i}\) to \(v_{j}\) and having a probability for this transition (Hollingsworth and WfMC 2003, p. 282) of \(p_{ij}\), with \(0 < p_{ij} \le 1\), as weight. Each vertex in A has exactly one edge pointing toward it and exactly one edge pointing away from it.
The actions and routing constructs of a process path \(pp_{k}\) plus \(a_{0}\) and \(a_{D + 1}\) form (in a first step) a path multiset \(PS_{k}\), whose elements are out of V. The fact that it is a multiset is important to consider loops, as then the same vertices of G can occur several times. Each vertex \(v_{i}\) in \(PS_{k}\) that occurs more than once (in a second step) is given an index \(n \, \in \, {\mathbb{N}}\) in the form \(v_{i}^{(1)} , v_{i}^{(2)} , \ldots ,v_{i}^{\left( n \right)} , \ldots\). The index indicates the number of the iteration of a loop that the vertex is assigned to. This is to distinguish the vertices from one another because each of them is from different iterations that have different probabilities of being executed. In the left process in Fig. 2, there are the path sets.
PS 1 = {a 0 , a 1 , XOR-join (1)1 , AND-split (1)2 , a (1)2 , a (1)3 , AND-join (1)3 , XOR-split (1)4 , a 5 },
PS 2 = {a 0 , a 1 , XOR-join (1)1 , AND-split (1)2 , a (1)2 , a (1)3 , AND-join (1)3 , XOR-split (1)4 , a (1)4 , XOR-join (2)1 , AND-split (2)2 , a (2)2 , a (2)3 , AND-join (2)3 , XOR-split (2)4 , a 5 } and so on, with v 1: = a 0 , v 2: = a 1 , v (1)3 : = XOR-join (1)1 , v (2) 3 : = XOR-join (2)1 , …, v (1)4 : = AND-split (1)2 , v (2) 4 : = AND-split (2)2 , …, v (1)5 : = a (1)2 , v (2)5 : = a (2)2 , …, v (1)6 : = a (1)3 , v (2)6 : = a (2)3 , …, v (1)7 : = AND-join (1)3 , v (2)7 : = AND-join (2)3 , …, v (1)8 : = XOR-split (1)4 , v (2)8 : = XOR-split (2)4 , …, v (1)9 : = a (1)4 , …, and v 10: = a 5.
Every process path \(pp_{k}\) is executed with a certain path probability \(p_{k}\) that is the product of the transition probabilities of process path \(pp_{k}\):
The transition probability \(p_{{i^{\left( m \right)} j^{\left( n \right)} }}\) that \(v_{i}^{\left( m \right)}\) is followed by \(v_{j}^{\left( n \right)}\) can be estimated and is fixed. These transition probabilities could be estimated by an expert (Hubbard 2007) or by analyzing process log files (zur Muehlen and Shapiro 2010) using, for example, a process-mining framework like ProM (Rubin et al. 2007). In the left process in Fig. 2, for example, for the process path pp 1 there are the (non-zero) transition probabilities \(p_{12} = 1, p_{{23^{\left( 1 \right)} }} = 1, p_{{3^{\left( 1 \right)} 4^{\left( 1 \right)} }} = 1, p_{{4^{\left( 1 \right)} 5^{\left( 1 \right)} }} = 1, p_{{4^{\left( 1 \right)} 6^{\left( 1 \right)} }} = 1, p_{{5^{\left( 1 \right)} 7^{\left( 1 \right)} }} = 1, p_{{6^{\left( 1 \right)} 7^{\left( 1 \right)} }} = 1, p_{{7^{\left( 1 \right)} 8^{\left( 1 \right)} }} = 1\) and \(p_{{8^{\left( 1 \right)} ,10}} = 0.9\). All other transition probabilities are zero. Then it is
and
Expression (22) is not true in the event that a process model contains an OR-split (van der Aalst et al. 2003). This fact is important in Sect. 5.3, when showing how this valuation calculus helped to improve the calculation capabilities of a process-modeling tool. However, every OR-split can formally be transformed into a composition of XOR-splits and AND-splits, which allows the use of expression (22). Otherwise, the path probabilities need to be estimated.
Appendix 2: Process-probability-space
In probability theory, “a probability space is a triple (Ω, \({\mathcal{F}}\), P) of a sample space Ω, a [sigma]-algebra \({\mathcal{F}}\) and a probability measure P on \({\mathcal{F}}\)” (Feller 1971, p. 116). The sample space Ω is the set of all possibilities that the object under consideration can take; it is thus the set of all possible process paths, as these represent all possibilities of a process execution. A sigma-algebra has properties such that:
-
(1)
“If a set A is in \({\mathcal{F}}\) so is its complement [\(A^{C} = {\Omega }\backslash A\)].
-
(2)
If \(\left\{ {A_{n} } \right\}\) is any countable collection of sets in \({\mathcal{F}}\), then also their union \(\mathop {\bigcup }\nolimits A_{n}\) and intersection \(\mathop {\bigcap }\nolimits A_{n}\) belong to \({\mathcal{F}}\)” (Feller 1971, p. 112).
That the sigma-algebra in Definition 2 is the power set of the set of all process paths means that (i) and (ii) are fulfilled.
“A probability measure P on a [sigma]-algebra \({\mathcal{F}}\) of sets in Ω is a function assigning a value P{A} ≥ 0 to each set A in \({\mathcal{F}}\) such that P{Ω} = 1 and that for every countable collection of non-overlapping sets A n in \({\mathcal{F}}\) [it is] \({\bf P}\left\{ { \cup \,A_{n} } \right\} = \mathop \sum \nolimits_{n} {\bf P}\left\{ {A_{n} } \right\}\)” (Feller 1971, p. 115).
All process paths are mutually exclusive, and they represent all possibilities how a process can be executed. Every process path \(pp_{k}\) is executed with a certain path probability \(p_{k} > 0\). Given that there is exactly one process path taken if a process is executed and that they are mutual exclusive, the probabilities \(p_{k}\) sum up to 1, fulfilling P{Ω} = 1. The property \({\mathbf{P}}\left\{ {\mathop {\bigcup }\nolimits A_{n} } \right\} = \mathop \sum \nolimits_{n} {\mathbf{P}}\left\{ {A_{n} } \right\}\) also holds for every countable collection of non-overlapping sets A n in \({\mathcal{F}}\) since \({\mathcal{F}}\) is the power set of Ω.
Appendix 3: Expected value of the process cash flow
Let the probability that an action \(a_{d} \in AS,\) with \(AS:= \mathop {\bigcup }\nolimits_{k = 1}^{{\left| {\Omega } \right|}} AS_{k}\), is executed when executing a process be
with the indicator function
and the set \(PP_{{a_{d} }}\) of process paths in which the action \(a_{d}\) is
Then it is:
Appendix 4: Variance of the process cash flow
In the following first step, it is shown that \(Var\left[ {CF_{P} } \right] = - E\left[ {CF_{P} } \right]^{2} + \mathop \sum \nolimits_{k = 1}^{{\left| {\Omega } \right|}} p_{k} \cdot E\left[ {CF_{{pp_{k} }}^{2} } \right]\) in two ways. The first way is similar to the beginning of the calculation for the expected value in Appendix 3. The second way is more detailed and includes \(\mathop \sum \nolimits_{k = 1}^{{\left| {\Omega } \right|}} E\left[ {\left( {CF_{{pp_{k} }} - E\left[ {CF_{P} } \right]} \right)^{2} } \right]\cdot p_{k}\), a more intuitive expression for \(Var\left[ {CF_{P} } \right]\). This is why both ways are presented.
4.1 Way 1
4.2 Way 2
In the following second step, it is shown how \(Var\left[ {CF_{P} } \right]\) can be calculated only by using the expected values and variances of the cash flows of the actions of a process.
Let the probability that both actions \(a_{d} \in AS\) and \(a_{j} \in AS\), with \(AS\text{ := }\mathop {\bigcup }\nolimits_{k = 1}^{{\left| {\Omega } \right|}} AS_{k}\), are executed when executing a process be
with the set \(PP_{{a_{d} ,a_{j} }}\) of process paths, which contains the action \(a_{d}\) as well as the action \(a_{j}\):
Then it is:
Appendix 5: Probability of each action in process PR
In order to determine the expected value of \(CF_{PR}\) we first need to determine the probability of each action. This is:
Thus, it is for example
which is multiplied with \(E\left[ {CF_{{a_{2} }} } \right]\) since it is \(E\left[ {CF_{{a_{2}^{\left( i \right)} }} } \right] = E\left[ {CF_{{a_{2} }} } \right]\) for all \(i \in {\mathbb{N}}\).
Appendix 6: Details to determine the variance of \(\varvec{CF}_{{\varvec{PR}}}\)
In order to determine the variance of \(CF_{PR}\) with expression (21) it is necessary to calculate \(\mathop \sum \nolimits_{{a_{d} ,a_{j} \in AS,a_{d} \ne a_{j} }} E\left[ {CF_{{a_{d} }} } \right]E\left[ {CF_{{a_{j} }} } \right] \cdot Pr\left( {a_{d} ,a_{j} } \right)\). Hence, we need to determine the probabilities \(Pr\left( {a_{d} ,a_{j} } \right)\). According to expression (15) the process paths and the respective path probabilities need to be calculated. For example there are the process paths
with \(p_{1} = 0.9\); \(p_{2} = 0.09\); \(p_{3} = 0.009\); \(p_{4} = 0.0009\), and \(p_{5} = 0.00009.\) Considering this five paths Table 5 shows the probabilities \(Pr\left( {a_{d} ,a_{j} } \right)\). For example, the cell in row \(a_{2}^{\left( 1 \right)}\) and column \(a_{1}\) gives \(Pr\left( {a_{2}^{\left( 1 \right)} ,a_{1} } \right)\). Due to the fact that \(Pr\left( {a_{d} ,a_{j} } \right) = Pr\left( {a_{j} ,a_{d} } \right)\) it is enough to determine values of the lower triangular table. Since it is \(a_{d} \ne a_{j}\) in expression (21) and \(Pr\left( {a_{d} ,a_{d} } \right) = Pr\left( {a_{d} } \right)\) the values on the diagonal do not need to be determined. The process has potentially an infinite number of paths, which means that this table does not contain all relevant probabilities. However, it displays the structure how the values change, which makes it easy to consider all probabilities \(Pr\left( {a_{d} ,a_{j} } \right)\).
In Table 5, the values \(Pr\left( {a_{d} ,a_{j} } \right)\) for the same actions \(a_{d}\) and \(a_{j}\) are encircled. For example, the values in the cells of rows \(a_{3}^{\left( 1 \right)}\)to \(a_{3}^{\left( 5 \right)}\) and column \(a_{2}^{\left( 1 \right)}\)to \(a_{2}^{\left( 5 \right)}\)contain the values for \(Pr\left( {a_{d} ,a_{j} } \right)\) considering the appearance of the actions \(a_{2}\) and \(a_{3}\) in the process paths \(pp_{1}\) to \(pp_{5}\). All of these values have to be considered when calculating \(E\left[ {CF_{{a_{d} }} } \right]E\left[ {CF_{{a_{j} }} } \right] \cdot Pr\left( {a_{d} ,a_{j} } \right)\) in expression (21) for the actions \(a_{2}\) and \(a_{3}\). The different colors show areas with the same structure of the values, to know how to use the formula for a geometric series. With this it is possible to determine \(\mathop \sum \nolimits_{{a_{d} ,a_{j} \in AS,a_{d} \ne a_{j} }} E\left[ {CF_{{a_{d} }} } \right]E\left[ {CF_{{a_{j} }} } \right]\cdot Pr\left( {a_{d} ,a_{j} } \right)\) in expression (21).
Overall it is
Rights and permissions
About this article
Cite this article
Bolsinger, M. Bringing value-based business process management to the operational process level. Inf Syst E-Bus Manage 13, 355–398 (2015). https://doi.org/10.1007/s10257-014-0248-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10257-014-0248-1




 for the sigma-algebra and the symbol
for the sigma-algebra and the symbol 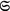 for the text’s sample space were replaced by the now more commonly used symbols
for the text’s sample space were replaced by the now more commonly used symbols