Skip to main content
SpringerLink
Log in

Integrability and Exact Solutions of the (2+1)-dimensional KdV Equation with Bell Polynomials Approach

  • Published:
Acta Mathematicae Applicatae Sinica, English Series Aims and scope Submit manuscript

Abstract

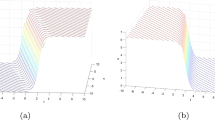
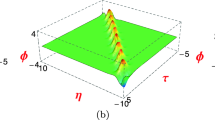
In this paper, the bilinear formalism, bilinear Bäcklund transformations and Lax pair of the (2+1)-dimensional KdV equation are constructed by the Bell polynomials approach. The N-soliton solution is derived directly from the bilinear form. Especially, based on the two-soliton solution, the lump solution is given out analytically by taking special parameters and using Taylor expansion formula. With the help of the multidimensional Riemann theta function, multiperiodic (quasiperiodic) wave solutions for the (2+1)-dimensional KdV equation are obtained by employing the Hirota bilinear method. Moreover, the asymptotic properties of the one- and two-periodic wave solution, which reveal the relations with the single and two-soliton solution, are presented in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bell, E.T. Exponential polynomials. Ann. Math., 35: 258–277 (1934)

    Article  MathSciNet  Google Scholar 

  2. Dubrovin, B. Integrable systems in topological field theory. Nucl. Phys. B, 379(3): 627–689 (1992)

    Article  MathSciNet  Google Scholar 

  3. Fan, E.G. Quasiperiodic waves and asymptotic behavior for Bogoyavlenskii’s breaking soliton equation in (2+1) dimensions. Phys. Rev. E, 78(3): 036607 (2008)

    Article  MathSciNet  Google Scholar 

  4. Fan, E.G. The integrability of nonisospectral and variable-coefficient KdV equation with binary Bell polynomials. Phys. Lett. A, 375(3): 493–497 (2011)

    Article  MathSciNet  Google Scholar 

  5. Furukawa, M., Tokuda, S. Mechanism of stabilization of ballooning modes by toroidal rotation shear in tokamaks. Phys. Rev. Lett., 94(17): 175001 (2005)

    Article  Google Scholar 

  6. Hasegawa, A., Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett., 23(3): 142–144 (1973)

    Article  Google Scholar 

  7. Hirota, R., Satsuma, J. A simple structure of superposition formula of the Bäcklund transformation. J. Phys. Soc. Japan, 45(5): 1741–1750 (1978)

    Article  Google Scholar 

  8. Hirota, R. Direct Methods in Soliton Theory. Springer-verlag, Berlin, 2004

    Book  Google Scholar 

  9. Iwao, M., Hirota, R. Soliton solutions of a coupled modified KdV equations. J. Phys. Soc. Japan, 66(3): 577–588 (1997)

    Article  MathSciNet  Google Scholar 

  10. Lambert, F., Loris, I., Springael, J., Willox, R. On a direct bilinearization method: Kaup’s higher-order water wave equation as a modified nonlocal Boussinesq equation. J. Phys. A: Math. Gen., 27(15): 5325–5334 (1994)

    Article  MathSciNet  Google Scholar 

  11. Lambert, F., Springael, J. Construction of Bäcklund transformations with binary Bell polynomials. J. Phys. Soc. Japan, 66(8): 2211–2213 (1997)

    Article  MathSciNet  Google Scholar 

  12. Lambert, F., Leble, S., Springael, J. Binary Bell polynomials and Darboux covariant Lax pairs. Glasgow Math. J., 43A: 53–63 (2001)

    Article  MathSciNet  Google Scholar 

  13. Lambert, F., Springael, J. On a direct procedure for the disclosure of Lax pairs and Bäcklund transformations. Chaos, Solitons and Fractals, 12(14–15): 2821–2832 (2001)

    Article  MathSciNet  Google Scholar 

  14. Lax, P.D. Integrals of nonlinear equations of evolution and solitary waves. Comm. Pure. Appl. Math., 21: 467–490 (1968)

    Article  MathSciNet  Google Scholar 

  15. Luo, L. New exact solutions and Bäcklund transformation for Boiti-Leon-Manna-Pempinelli equation. Phys. Lett. A, 375(7): 1059–1063 (2011)

    Article  MathSciNet  Google Scholar 

  16. Luo, L. Bäcklund transformation of variable-coefficient Boiti-Leon-Manna-Pempinelli equation. Appl. Math. Lett., 94: 94–98 (2019)

    Article  MathSciNet  Google Scholar 

  17. Ma, W.X., Zhou, R., Gao, L. Exact one-periodic and two-periodic wave solutions to hirota bilinear equations in (2+1) dimensions. Modern Phys. Lett. A, 24(21): 1677–1688 (2009)

    Article  MathSciNet  Google Scholar 

  18. Mckean, H.P., Moerbeke, P. van The spectrum of Hill’s equation. Invent. Math., 30(3): 217–274 (1975)

    Article  MathSciNet  Google Scholar 

  19. Miao, Q., Wang, Y.H., Chen, Y., Yang, Y.Q. PDEBellII: a Maple package for finding bilinear forms, bilinear Bäcklund transformations, Lax pairs and conservation laws of the KdV-type equations. Comput. Phys. Commun., 185(1): 357–367 (2014)

    Article  Google Scholar 

  20. Nakamura, A. A direct method of calculating periodic wave solutions to nonlinear evolution equations. I. Exact two-periodic wave solution. J. Phys. Soc. Japan, 47(5): 1701–1705 (1979)

    Article  MathSciNet  Google Scholar 

  21. Nakamura, A. A direct method of calculating periodic wave solutions to nonlinear evolution equations. II. Exact one and two-periodic wave solution of the coupled bilinear equations. J. Phys. Soc. Japan, 48(4): 1365–1370 (1980)

    Article  MathSciNet  Google Scholar 

  22. Novikov, S.P. The periodic problem for the Korteweg-de vries equation. Funct. Anal. Appl., 8(3): 236–246 (1975)

    Article  MathSciNet  Google Scholar 

  23. Osman, M.S., Ghanbari, B., Machado, J.A.T. New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity. Eur. Phys. J. Plus, 134(1): 20 (2019)

    Article  Google Scholar 

  24. Raissi, M., Perdikaris, P., Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys., 378: 686–707 (2019)

    Article  MathSciNet  Google Scholar 

  25. Satsuma, J. Higher conservation laws for the Korteweg-de Vries equation through Bäcklund transformation. Progr. Theoret. Phys., 52(4): 1396–1397 (1974).

    Article  Google Scholar 

  26. Satsuma, J., Ablowitz, M.J. Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys., 20(7): 1496–1503 (1979)

    Article  MathSciNet  Google Scholar 

  27. Tian, S.F., Zhang, H.Q. On the integrability of a generalized variable-coefficient Kadomtsev-Petviashvili equation. J. Phys. A: Math. Theor., 45(5): 055203 (2012)

    Article  MathSciNet  Google Scholar 

  28. Wang, Y.H., Chen, Y. Integrability of the modified generalised Vakhnenko equation. J. Math. Phys., 53(12): 123504 (2012)

    Article  MathSciNet  Google Scholar 

  29. Wang, Y.H., Chen, Y. Binary Bell polynomial manipulations on the integrability of a generalized (2+1)-dimensional Korteweg-de Vries equation. J. Math. Anal. Appl., 400(2): 624–634 (2013)

    Article  MathSciNet  Google Scholar 

  30. Wang, Y.H., Wang, H., Temuer, C. Lax pair, conservation laws, and multi-shock wave solutions of the DJKM equation with Bell polynomials and symbolic computation. Nonlinear Dyn., 78(2): 1101–1107 (2014)

    Article  MathSciNet  Google Scholar 

  31. Wang, Y.P., Tian, B., Wang, M., Wang, Y.F., Sun, Y., Xie, X.Y. Bäcklund transformations and soliton solutions for a (2+1)-dimensional Korteweg-de Vries-type equation in water waves. Nonlinear Dyn., 81(4): 1815–1821 (2015)

    Article  Google Scholar 

  32. Wang, Y.H., Chen, Y. Bell polynomials approach for two higher-order KdV-type equations in fluids. Nonlinear Anal. RWA, 31: 533–551 (2016)

    Article  MathSciNet  Google Scholar 

  33. Wazwaz, A.M. Two new Painlevé-integrable (2+1) and (3+1)-dimensional KdV equations with constant and time-dependent coefficients. Nucl. Phys. B, 954: 115009 (2020)

    Article  Google Scholar 

  34. Yu, S.J., Toda, K., Fukuyama, T. N-soliton solutions to a (2+1)-dimensional integrable equation. J. Phys. A: Math. Gen., 31(50): 10181–10186 (1998)

    Article  MathSciNet  Google Scholar 

  35. Zhang, Y., Ye, L.Y., Lv, Y.N., Zhao, H.Q. Periodic wave solutions of the Boussinesq equation. J. Phys. A: Math. Theor., 40(21): 5539–5549 (2007)

    Article  MathSciNet  Google Scholar 

  36. Zhang, Y., Wei, W.W., Cheng, T.F., Song, Y. Binary Bell polynomial application in generalized (2+1)-dimensional KdV equation with variable coefficients. Chin. Phys. B, 20(11): 110204 (2011)

    Article  Google Scholar 

Download references

Funding

The project is supported by the National Natural Science Foundation of China (No. 12175069 and No. 12235007) and Science and Technology Commission of Shanghai Municipality (No. 21JC1402500 and No. 22DZ2229014).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, East China Normal University, Shanghai, 200062, China

    Jun-cai Pu & Yong Chen

  2. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, China

    Yong Chen

Authors
  1. Jun-cai Pu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong Chen.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pu, Jc., Chen, Y. Integrability and Exact Solutions of the (2+1)-dimensional KdV Equation with Bell Polynomials Approach. Acta Math. Appl. Sin. Engl. Ser. 38, 861–881 (2022). https://doi.org/10.1007/s10255-022-1020-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10255-022-1020-9

Keywords

2000 MR Subject Classification

Search

Navigation