A modified Coulomb’s law for the tangential debonding of osseointegrated implants

Abstract

Cementless implants are widely used in orthopedic and dental surgery. However, debonding-related failure still occurs at the bone–implant interface. It remains difficult to predict such implant failure since the underlying osseointegration phenomena are still poorly understood. Especially in terms of friction and adhesion at the macroscale, there is a lack of data and reliable models. The aim of this work was to present a new friction formulation that can model the tangential contact behavior between osseointegrated implants and bone tissue, with focus on debonding. The classical Coulomb’s law is combined with a state variable friction law to model a displacement-dependent friction coefficient. A smooth state function, based on the sliding distance, is used to model implant debonding. The formulation is implemented in a 3D nonlinear finite element framework, and it is calibrated with experimental data and compared to an analytical model for mode III cleavage of a coin-shaped, titanium implant (Mathieu et al. in J Mech Behav Biomed Mater 8(1):194–203, 2012). Overall, the results show a close agreement with the experimental data, especially the peak and the softening part of the torque curve with a relative error of less than 2.25%. In addition, better estimates of the bone’s shear modulus and the adhesion energy are obtained. The proposed model is particularly suitable to account for partial osseointegration.

Appendices

Appendix 1

Contact formulation

In this section, the basic contact mechanics and the numerical discretization are briefly summarized. For the formulation of sliding contact, one can use elastoplasticity theory in order to incorporate friction response in the tangential direction (see, e.g., Laursen 2013; Wriggers 2006; Sauer and De Lorenzis 2015). In the context of this work, we use another approach that is based on the surface potential-based contact formulations of Duong and Sauer (2019) and Sauer and De Lorenzis (2013). The reader is referred to Corbett and Sauer (2014, 2015) for the NURBS-enriched contact finite element discretization.

1.1 Contact surface description

Considering a 3D body ${\mathcal {B}}$, its boundary $\partial {\mathcal {B}}$, such as its contact surface $\partial _{\text{c}}{{\mathcal {B}}}$, can be described by the mapping

$$\begin{aligned} \varvec{x}= \varvec{x}({\varvec{\xi }}), \quad {\varvec{\xi }}\in {\mathcal {P}}, \end{aligned}$$

(22)

which maps a point ${\varvec{\xi }}= \left\{ \xi ^1, \xi ^2 \right\}$ lying in the 2D parameter space ${\mathcal {P}}$ to the surface point $\varvec{x}\in \partial _{\text{c}}{{\mathcal {B}}}$. Then, a set of covariant tangent vectors on $\partial _{\text{c}}{{\mathcal {B}}}$ can be defined as

$$\begin{aligned} \varvec{a}_\alpha := \frac{\partial \varvec{x}}{\partial \xi ^\alpha }, \quad (\alpha =1,2) \end{aligned}$$

(23)

with the normal vector

$$\begin{aligned} \varvec{n}:= \frac{\varvec{a}_1 \times \varvec{a}_2}{||\varvec{a}_1 \times \varvec{a}_2||}. \end{aligned}$$

(24)

With Eqs. (23) and (24), the contact surface can then be characterized by the surface metric components

$$\begin{aligned} a_{\alpha \beta }&= \varvec{a}_\alpha \cdot \varvec{a}_\beta , \end{aligned}$$

(25)

The dual tangent vectors $\varvec{a}^\alpha$ defined by the relation $\varvec{a}^\alpha \cdot \varvec{a}_\beta = \delta ^\alpha _\beta$ can be related to the covariant tangent vectors in Eq. (23) by $\varvec{a}_\alpha = a_{\alpha \beta } \, \varvec{a}^\beta$. To track changes of $\partial _{\text{c}}{{\mathcal {B}}}$ during deformation, one chooses a reference configuration $\partial _{\text{c}}{{\mathcal {B}}}_0$, where the tangent vectors ${\varvec{A}}_\alpha$ and the surface metric tensor components $A_{\alpha \beta }$ can be defined as in Eqs. (23) and (25), respectively.

1.2 Contact kinematics and contact traction

To formulate frictional contact between two bodies ${\mathcal {B}}_1$ and ${\mathcal {B}}_2$, we consider interactions between a so-called slave point$\varvec{x}_k \in \partial _{\text{c}}{{\mathcal {B}}}_k$ ($k=$ 1 or 2) and a neighboring master surface $\partial _{\text{c}}{{\mathcal {B}}}_\ell$ ($l=$ 2 or 1). For the classical full-pass contact algorithm (see Laursen and Simo 1993), k is either set to 1 or 2. Further, we assume point interaction, i.e., $\varvec{x}_k$ can only interact with at most one point $\varvec{x}_\ell \in \partial _{\text{c}}{{\mathcal {B}}}_\ell$ at a given time.

Fig. 11

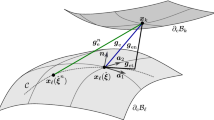
Frictional contact kinematics at current time $t_{n+1}$: current slave point $\varvec{x}_k$, current position of the previous interacting point $\displaystyle \varvec{x}_\ell ({\hat{{\varvec{\xi }}}}^n)$, current interacting point $\varvec{x}_\ell ({\hat{{\varvec{\xi }}}})$, the current elastic gap vector $\varvec{g}_{\text{e}}$ and its components, previous elastic gap $\varvec{g}_{\text{e}}^n$, and the sliding path ${\mathcal {C}}$. Adopted and modified from Duong and Sauer (2019)

In the following, for the sake of conciseness, all variables without superscript n are evaluated at the current time $t_{n+1}$, if not stated otherwise. To characterize the interaction between the two bodies, we consider a penalty formulation, with the penalty parameter $\epsilon$ (considered equal in normal and tangential direction). In order to determine the contact traction at the current time step, according to the contact formulation of Duong and Sauer (2019), a so-called interacting (elastic) gap vector $\varvec{g}_{\text{e}}({\hat{{\varvec{\xi }}}})$ is introduced (see Fig. 11). This gap vector is defined between the current slave point $\varvec{x}_k$ and the so-called current interacting point $\varvec{x}_\ell ({\hat{{\varvec{\xi }}}})$ on the master surface $\partial _{\text{c}}{{\mathcal {B}}}_\ell$ (defined below), i.e.,

$$\begin{aligned} \varvec{g}_{\text{e}}({\hat{{\varvec{\xi }}}}) := \varvec{x}_k - \varvec{x}_\ell ({\hat{{\varvec{\xi }}}}). \end{aligned}$$

(26)

The current gap vector can be further decomposed into a tangential and normal component $\varvec{g}_{\text{e}}({\hat{{\varvec{\xi }}}}) = \varvec{g}_{\text{en}}+ \varvec{g}_{\text{et}}$, with

$$\begin{aligned} \begin{aligned} \varvec{g}_{\text{en}}({\hat{{\varvec{\xi }}}})&:= \left( \varvec{n}\otimes \varvec{n}\right) \, \varvec{g}_{\text{e}},\\ \varvec{g}_{\text{et}}({\hat{{\varvec{\xi }}}})&:= \left( \varvec{a}_\alpha \otimes \varvec{a}^\alpha \right) \, \varvec{g}_{\text{e}}. \end{aligned} \end{aligned}$$

(27)

According to the penalty formulation, the total (normal and tangential) frictional contact traction is proportional to the interacting gap vector $\varvec{g}_{\text{e}}({\hat{{\varvec{\xi }}}})$, according to

$$\begin{aligned} \varvec{t}_{\mathrm{c}}= \epsilon \, \varvec{g}_{\text{e}}, \end{aligned}$$

(28)

which follows from using the contact potential $W:=\frac{1}{2}\epsilon \, \varvec{g}_{\text{e}}\cdot \varvec{g}_{\text{e}}$. At initial contact, the interacting point $\varvec{x}_\ell ({\hat{{\varvec{\xi }}}})$ is equal to the closest projection point of $\varvec{x}_k$. During sticking, the current interacting point is equal to the previous interacting point ${\hat{{\varvec{\xi }}}}^n$. Therefore, for sticking, the current contact gap vector $\varvec{g}_{\text{e}}$ is determined from Eq. (26) with ${\hat{{\varvec{\xi }}}} = {\hat{{\varvec{\xi }}}}^n$. During sliding, the current interacting point ${\hat{{\varvec{\xi }}}}$ is the solution of the kinematic constraint equation

$$\begin{aligned} {\varvec{f}}_{\varvec{g}}({\hat{{\varvec{\xi }}}}) := \varvec{g}_{\text{et}}- \varvec{g}_{\text{et}}^{{\max }}= {\mathbf {0}}, \end{aligned}$$

(29)

in the current configuration (see Duong and Sauer 2019). $\varvec{g}_{\text{e}}$ then follows from Eq. (26). The critical value during sliding $\varvec{g}_{\text{et}}^{{\max }}$ is defined by the chosen friction law. For example, for Coulomb’s friction, it is defined as

$$\begin{aligned} \varvec{g}_{\text{et}}^{{\max }}= \mu \left\| \varvec{g}_{\text{en}}\right\| {\varvec{\tau }}, \end{aligned}$$

(30)

where ${\varvec{\tau }}$ denotes the sliding direction and can be computed by projecting the previous interacting gap $\varvec{g}_{\text{e}}^n$ onto the tangent plane at the current interaction point $\varvec{x}_\ell ({\hat{{\varvec{\xi }}}})$, i.e.,

$$\begin{aligned} {\varvec{\tau }}= \frac{\left( \varvec{a}_\alpha \otimes \varvec{a}^\alpha \right) \, \varvec{g}_{\text{e}}^n}{\left\| \left( \varvec{a}_\beta \otimes \varvec{a}^\beta \right) \, \varvec{g}_{\text{e}}^n \right\| }, \end{aligned}$$

(31)

where $\varvec{a}_\alpha ,\,\varvec{a}^\alpha ,$ are evaluated at $\varvec{x}_\ell ({\hat{{\varvec{\xi }}}})$.

The computation of the friction coefficient $\mu$ in Eq. (13) requires the knowledge of the accumulated sliding distance $g_{\text{s}}$. Here, we approximate Eq. (12) by accumulating the distance from the initial interacting point to the current interacting point, i.e.,

$$\begin{aligned} g_{\text{s}}^{n+1} \approx \sum _{i=1}^{n+1} \left\| \varvec{x}_\ell \left( {\hat{{\varvec{\xi }}}}^i \right) - \varvec{x}_\ell \left( {\hat{{\varvec{\xi }}}}^{i-1} \right) \right\| . \end{aligned}$$

(32)

1.3 Finite element discretization

For the finite element formulation, the contact bodies are discretized into $n_{\mathrm{el}}$ elements. The geometry of an element e in the current configuration can be interpolated from the positions of the elemental nodes, or control points ${\mathbf {x}}_e$, as

$$\begin{aligned} \varvec{x}= {\mathbf {N}}_e({\varvec{\xi }}) \, {\mathbf {x}}_e, \quad {\varvec{\xi }}\in {\mathcal {P}}, \end{aligned}$$

(33)

where ${\mathbf {N}}_e := \left[ N_1\varvec{I}, N_2\varvec{I}, \ldots , N_{n_{\mathrm{el}}}\varvec{I}\right]$ denotes the element shape function array. Following the 3D contact enrichment approach of Corbett and Sauer (2014, 2015), the bulk of the bodies is discretized by linear elements with standard Lagrange interpolation following Sauer (2011), while the contact surfaces are discretized by non-uniform rational B-Splines (NURBS) interpolation (see, e.g., Hughes et al. 2005). The NURBS basis functions can be computed element-wise by employing the Bézier extraction operator ${\mathbf {C}}^e$ of Borden et al. (2011) and the Bernstein polynomials ${\mathbf {B}}$. Then, the shape function of control point A can be computed by

$$\begin{aligned} N_A(\xi ^1, \xi ^2) = \frac{w_A {\hat{N}}_A^e(\xi ^1,\xi ^2) }{\sum _{A=1}^{n} w_A {\hat{N}}_A^e(\xi ^1,\xi ^2)}, \end{aligned}$$

(34)

with the corresponding weight $w_A$, and the B-spline basis functions

$$\begin{aligned} \begin{aligned} {\hat{{\mathbf {N}}}}^e&= \{ {\hat{N}}_A^e \}^{n_e}_{A=1}, \\ {\hat{{\mathbf {N}}}}^e(\xi ^1,\xi ^2)&= {\mathbf {C}}^e_{\xi ^1} {\mathbf {B}}(\xi ^1) \otimes {\mathbf {C}}^e_{\xi ^2} {\mathbf {B}}(\xi ^2). \end{aligned} \end{aligned}$$

(35)

The finite element forces acting on the slave surface element e and the master surface element ${\hat{e}}$ are then given by

$$\begin{aligned} \begin{aligned} {\mathbf {f}}_c^e&:= \int _{\Gamma ^e} {\mathbf {N}}_e^{\mathrm{T}} \, \varvec{t}_{\mathrm{c}}\,{\mathrm{d}}a \quad {\text{(slave)}},\\ {\mathbf {f}}_c^{{\hat{e}}}&:=-\int _{\Gamma ^{{\hat{e}}}} {\mathbf {N}}_{{\hat{e}}}^{\mathrm{T}} ({\hat{{\varvec{\xi }}}}) \, \varvec{t}_{\mathrm{c}}\,{\mathrm{d}}a \quad {\text{(master)}}, \end{aligned} \end{aligned}$$

(36)

where $\Gamma$ denotes the surface element domains on the corresponding surfaces. As NURBS elements are at least $C^1$ continuous over the element boundaries, this gives us an accurate representation of the geometry, as well as an efficient and stable framework for contact computations.

Appendix 2: Derivation of the new analytical model with modified Coulomb’s friction

Given the modified Coulomb’s law in Sect. 2.2.3, a new analytical model can be derived. In general, the torque T, as a function of the rotation angle $\theta$, can be computed analytically, as

$$\begin{aligned} T(\theta ) = 2 \pi \int _{r} r^2 \cdot \sigma _{\theta z}(r,\theta ,g_{\text{s}}) \,{\mathrm{d}}r. \end{aligned}$$

(37)

Due to symmetry, the tangential traction component $\sigma _{\theta z}$ is distributed radially symmetric along the BII, while the radial traction component $\sigma _{zr}$ is zero. With the definition of the critical radius c from Eq. (17) we have $c(\theta _{\text{lin}}) = R$ and

$$\begin{aligned} \sigma _{\theta z}(\theta _{\text{lin}},c(\theta _{\text{lin}})) := t_{\text{t}}^{{\max }}. \end{aligned}$$

(38)

Assuming bone and implant to be linear elastic bodies, we know that for sticking, the tangential traction will be proportional to the applied rotation angle $\theta$ and the current radius r, i.e.,

$$\begin{aligned} \sigma _{\theta z}^{\text{stick}}(\theta ,r) = \lambda \theta r, \quad \lambda = {\text{const}}, \end{aligned}$$

(39)

where $\lambda$ is a constant stress per length. Thus, the torque for the sticking region becomes

$$\begin{aligned} T(\theta ) = 2 \pi \int ^{R}_{0} r^2 \cdot \lambda \theta r \,{\mathrm{d}}r = \frac{1}{2}\pi R^4 \lambda \theta , {\text{ for }} \theta \le \theta _{\text{lin}}. \end{aligned}$$

(40)

If we calculate the slope of the torque at $\theta = \theta _{\text{lin}}$ and $c(\theta _{\text{lin}})$, we get (Fig. 12)

$$\begin{aligned} \frac{\,{\mathrm{d}}T(\theta _{\text{lin}}, R)}{\,{\mathrm{d}}\theta _{\text{lin}}} = \frac{1}{2}\pi R^4 \lambda . \end{aligned}$$

(41)

Fig. 12

New analytical model: critical radius for stick/slip transition c as a function of the imposed rotation angle $\theta$ from Eq. (17)

We also know that for linear elasticity

$$\begin{aligned} \frac{\,{\mathrm{d}}T(\theta )}{\,{\mathrm{d}}\theta } = C, \quad \theta \le \theta _{\text{lin}}, \end{aligned}$$

(42)

where C is the effective shear stiffness of the system, that is approximately proportional to the shear modulus of bone. If we equate Eqs. (41) and (42), we obtain

$$\begin{aligned} \lambda = \frac{2C}{\pi R^4}, \end{aligned}$$

(43)

and inserting $\lambda$ into Eq. (39) yields

$$\begin{aligned} \sigma _{\theta z}^{\text{stick}}(\theta ,r) = \frac{2C}{\pi R^4} \theta r . \end{aligned}$$

(44)

Applying the definition in Eq. (38) to Eq. (44) yields

$$\begin{aligned} \sigma _{\theta z}^{\text{stick}}(\theta _{\text{lin}},R) = \frac{2C}{\pi R^4} \theta _{\text{lin}}R = t_{\text{t}}^{{\max }}, \end{aligned}$$

(45)

i.e.,

$$\begin{aligned} \frac{2C}{\pi R^3}=\frac{t_{\text{t}}^{{\max }}}{\theta _{\text{lin}}}. \end{aligned}$$

(46)

Together with Eq. (17), we finally obtain the tangential traction component for sticking

$$\begin{aligned} \sigma _{\theta z}^{\text{stick}}(\theta ,r) = \theta r \frac{t_{\text{t}}^{{\max }}}{\theta _{\text{lin}}R}=\frac{r}{c(\theta )} t_{\text{t}}^{{\max }}. \end{aligned}$$

(47)

In the sliding region $r \ge c$, the tangential traction follows the modified Coulomb’s law

$$\begin{aligned} \sigma _{\theta z}^{\text{slide}}=\mu p, \end{aligned}$$

(48)

with $\mu = \mu (g_{\text{s}})$ from Eq. (11). Here, we assume p to be homogeneously distributed along the contact surface. As long as a part of the interface remains sticking

$$\begin{aligned} g_{\text{s}}= 0, \quad {\text{otherwise}} \quad g_{\text{s}}= r \left( \theta - \theta _{{\max }}+ \theta _{\text{lin}}\right) . \end{aligned}$$

(49)

The tangential contact traction as a function of the rotation angle can then be summarized by combining Eqs. (47) and (48) to Eq. (18).

Appendix 3: Mesh and load step sensitivity

To analyze the convergence behavior, three different finite element meshes were constructed, denoted coarse, medium, and fine with 3390, 12,354, and 47,130 degrees of freedom, respectively. In addition, different load step sizes [$0.1^{\circ }$, $0.05^{\circ }$, $0.02^{\circ }$, $0.01^{\circ }$, $0.005^{\circ }$, $0.004^{\circ }$] were investigated, corresponding to a number of load steps of [100, 200, 500, 1000, 2000, 2500], respectively. For the parameters, data set 1 with $\mu _{{\mathrm{b}}}=0.4$ was chosen. To compare the different setups, we define the mean relative torque error

$$\begin{aligned} e_{T}^{\mathrm{rel}}= \underset{\theta \in \left[ 0,10^{\circ }\right] }{\mathrm{mean}} \left( \left\| \frac{T_{{\mathrm{exp}}}(\theta )-T(\theta )}{T_{\max }} \right\| \right) , \end{aligned}$$

(50)

where here $T_{\max }$ is the maximum torque obtained by the numerical solution.

Figure 13 shows the convergence behavior of the different meshes. It can be seen that $e_{T}^{\mathrm{mp}}$ reaches its limit for all meshes after 1000 load steps to 0.0175, 0.0171, and 0.017, respectively. This is also the case for the mean percentage error shown in Table 7, with its lowest value of 2.176% for the fine mesh and the highest value of 2.241% for the coarse mesh. In addition, the error is increasing with the number of load steps for the coarse mesh. This stems from the coarse resolution of the peak for larger load steps and thus leading to the torque values to be closer to the experimental data. It should be noted that the mesh size has a small effect on the outcome of the parameter study and thus, both $e_{T}^{\mathrm{mp}}$ and $e_{T}^{\mathrm{rel}}$ can be further minimized by performing a separate parameter estimation for each mesh.

Table 7 Mesh sensitivity: mean percentage error $e_{T}^{\mathrm{mp}}$ according to Eq. (19) for different configurations of data set 1 ($\mu _{{\mathrm{b}}}=0.4$)

Fig. 13

Mesh sensitivity: mean relative error $e_{T}^{\mathrm{rel}}$ according to Eq. (50) for different configurations of data set 1 ($\mu _{{\mathrm{b}}}=0.4$)