Abstract
We show that 3-Sasaki structures admit a natural description in terms of projective differential geometry. First we establish that a 3-Sasaki structure may be understood as a projective structure whose tractor connection admits a holonomy reduction, satisfying a particular non-vanishing condition, to the (possibly indefinite) unitary quaternionic group \({\text {Sp}}(p,q)\). Moreover, we show that, if a holonomy reduction to \({\text {Sp}}(p,q)\) of the tractor connection of a projective structure does not satisfy this condition, then it decomposes the underlying manifold into a disjoint union of strata including open manifolds with (indefinite) 3-Sasaki structures and a closed separating hypersurface at infinity with respect to the 3-Sasaki metrics. It is shown that the latter hypersurface inherits a Biquard–Fefferman conformal structure, which thus (locally) fibers over a quaternionic contact structure, and which in turn compactifies the natural quaternionic Kähler quotients of the 3-Sasaki structures on the open manifolds. As an application, we describe the projective compactification of (suitably) complete, non-compact (indefinite) 3-Sasaki manifolds and recover Biquard’s notion of asymptotically hyperbolic quaternionic Kähler metrics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A (pseudo-)Riemannian manifold (M, g) is said to be Sasaki, or Sasakian if its standard metric cone is (pseudo-)Kähler [14], and said to be Sasaki–Einstein if g is also Einstein. Inspired by the pioneering work of [5,6,7], we showed in [30] that projective geometry provides a natural unifying framework for treating many aspects of Sasaki and Sasaki–Einstein geometry. Recall that a projective structure on a manifold is an equivalence class \({\textbf {p}}\) of torsion-free affine connections that share the same unparametrized geodesics. Note that a (pseudo-)Riemannian manifold—and in particular a Sasaki manifold—thus induces a projective structure by its Levi–Civita connection. As shown in [30], a gain of this perspective is that it leads to natural smooth geometric compactifications of some complete non-compact (indefinite) Sasaki–Einstein structures, using tools from [21, 23].
Canonically associated to any projective manifold \((M,{\textbf {p}})\) of dimension \(n+1\ge 2\) is a projectively invariant connection \(\nabla ^{\mathcal {T}}\) on a natural vector bundle \({\mathcal {T}}\) of rank \(n+2\), the so-called tractor bundle with connection [8]. A result, with close links to the metric cone characterization of Sasaki-structures, is that a Sasaki–Einstein \((2m+1)\)-manifold of positive definite signature is exactly the same as a projective manifold for which the restricted holonomy of \(\nabla ^{\mathcal {T}}\) is contained in \({{\,\textrm{SU}\,}}(m+1)\). In the case of holonomy reductions of \(\nabla ^\mathcal {T}\) to the indefinite special unitary group \({{\,\textrm{SU}\,}}(p,q)\), the situation is more subtle and interesting, and these subtleties, not visible in the metric cone picture, are what is studied and exposed in [30]. Specifically, we showed in [30, Theorem B] that a projective holonomy reduction to \({{\,\textrm{SU}\,}}(p,q)\) induces in general a stratification
of the underlying projective manifold \((M, {\textbf {p}})\) into a disjoint union of submanifolds. Here, \(M_\pm \) are open submanifolds equipped with indefinite Sasaki–Einstein structures, and \(M_0\) is a smooth separating hypersurface equipped with an oriented conformal structure of signature \((2p - 1, 2q - 1)\) whose conformal holonomy is contained in \({{\,\textrm{SU}\,}}(p,q)\), making it (locally) what is called a Fefferman space (cf. [20, 37]). In fact \(M_0\) is the compactifying projective infinity of the Sasaki–Einstein spaces \(M_\pm \) [30, Theorem C]. To understand this picture fully, we explored in [30] the group identity
and the fact that \({{\,\textrm{U}\,}}(p, q)\) is the (compatible) intersection of any two of the groups on the right-hand side, at the level of projective holonomy reductions. We there treat the holonomy reductions for each group on the right-hand side separately, and then the implications of pairs of them holding simultaneously in a compatible way.
In this article, we develop the analogous theory for 3-Sasaki structures, meaning those (pseudo-)Riemannian manifolds (M, g) whose standard metric cone is hyperkähler, which implies in particular that \(\dim M \equiv 3 \pmod 4\). In recent decades, 3-Sasaki geometries have been the subject of considerable focus for a host of different reasons [1, 13,14,15, 31, 32]. From our current point of view, they are extremely interesting because, via the tools of projective geometry and the curved orbit theory of [23], we are able to link indefinite 3-Sasaki structures to Biquard–Fefferman conformal structures, which are conformal structures that fiber (locally) over quaternionic contact structures via a construction described by Biquard [10]; for a holonomy characterization of these conformal structures see [3]. Moreover, quaternionic contact structures were introduced by Biquard [10, 11] as geometric structures arising at the infinity of quaternionic Kähler manifolds, and our study recovers that fundamental relationship. Indeed all the geometries just mentioned are shown to be parts of a single smooth geometric structure and its leaf spaces. In more detail, the article proceeds as follows.
Following a recollection of both the algebraic preliminaries and the notions of quaternionic and hyperkähler structures in Sect. 2.1, in Definition 2.11 we recall the usual definition of a 3-Sasaki structure in terms of a triple of Killing vector fields. Proposition 2.12 then relates this description to the aforementioned definition via the metric cone. In Sect. 2.3, we review the necessary background on affine and projective differential geometry, including the standard tractor bundle \((\mathcal {T}, \nabla ^\mathcal {T})\) of a projective manifold.
The main results are presented in Sects. 3 and 4. In Theorem 3.1, we show that the projective tractor bundle \((\mathcal {T},\nabla ^\mathcal {T})\) of a 3-Sasaki manifold of dimension \(4m+3\) and of arbitrary signature \((4p-1,4q)\) admits a parallel Hermitian hypercomplex structure of signature (4p, 4q), equivalently a holonomy reduction to
where \(m:= p + q - 1\). Theorem 3.6 then considers the converse, namely a projective manifold \((M,{\textbf {p}})\) of dimension \(4m+3\ge 11\) equipped with a parallel Hermitian hypercomplex structure of signature (4p, 4q) on its tractor bundle. We show that, in general, this determines a stratification of M:
where \(M_\pm \) are open submanifolds equipped with indefinite 3-Sasaki structures of signature \((4p-1,4q)\) and \((4p,4q-1)\), respectively, and \(M_0\) is a smooth separating hypersurface equipped with a Biquard–Fefferman conformal structure of signature \((4p-1, 4q-1)\), as mentioned above and whose definition is recalled in Sect. 3.2. Theorem 3.7 then observes that \(M_0\) with its conformal structure is the boundary (“at infinity,” with respect to the 3-Sasaki metric) of a projective compactification of the 3-Sasaki structures on \(M_\pm \); see [21, 22] for the notion of projective compactification. In Sect. 4.1, we study oriented projective manifolds \((M,{\textbf {p}})\) of dimension \(4m+3\ge 11\) with a parallel hypercomplex structure on its tractor bundle, that is, with a projective holonomy reduction to
We show that such a reduction determines an integrable distribution D of rank 3 on M and that (locally) the corresponding leaf space \({\widetilde{M}}\) inherits a quaternionic structure \({\widetilde{Q}}\); see Theorem 4.3. Moreover, in Theorem 4.7 we prove that in this setting the projective tractor bundle of \((M,{\textbf {p}})\) descends, via the natural projection \(\pi : M\rightarrow {\widetilde{M}}\), to the canonical (normal) quaternionic tractor bundle of \(({\widetilde{M}}, {\widetilde{Q}})\)—a useful result of independent interest. Finally, that fact is used to show in Theorem 4.9 that, if the projective holonomy reduces from \({{\,\textrm{SL}\,}}(m + 1, \mathbb {H}) \) further to \({{\,\textrm{Sp}\,}}(p,q)\), then \({\widetilde{M}}\) admits in general a decomposition into submanifolds
where \(\widetilde{M}_{\pm }\) are open submanifolds with quaternionic Kähler structures of signatures \((4(p-1), 4q)\) and \((4p,4(q-1))\), respectively, and \(\widetilde{M}_0\) is a real separating hypersurface with a quaternionic contact structure of signature \((p-1, q-1)\) (see Definition 3.3). The quaternionic Kähler structures on \(\widetilde{M}_{\pm }\) coincide here with the canonical quaternionic Kähler quotients of the 3-Sasaki structures on \(M_\pm \) (induced by the defining triple of Killing fields), and the quaternionic contact structure on \(\widetilde{M}_0\) coincides with the one induced from the Biquard–Fefferman conformal structure on \(M_0\).
As a final point, here we remind the reader that the metric cone over a Sasaki–Einstein manifold carries a Ricci-flat Kähler structure. In dimension 4, however, a manifold carries such a structure if and only if it can be extended to a hyperkähler structure. Thus, a 3-dimensional Sasaki–Einstein structure can be extended to a 3-Sasaki structure. In that sense, the case of 3-dimensional 3-Sasaki structures was essentially treated in [30, §1]. In any case, as pointed out there, the metric underlying any Sasaki structure (and hence any 3-Sasaki structure) in that dimension is projectively flat. We will focus in this article on 3-Sasaki structures of dimension at least 11 and will discuss the 7-dimensional case, which is also special, only in remarks.
All objects herein are smooth, meaning \(C^\infty \).
2 Background
We start by recalling the notions of various geometric structures and some basic results about them that will be central for this article.
2.1 Quaternionic algebraic and geometric structures
For a uniform treatment of the quaternionically “flavored” structures in this section, see [2].
2.1.1 Quaternionic and hypercomplex vector spaces
Definition 2.1
Suppose \(\mathbb {V}\) is a real (finite-dimensional) vector space.
-
(a)
A hypercomplex structure on \(\mathbb {V}\) is a triple \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) of complex structures \(\mathbb {I},\mathbb {J},\mathbb {K}\in {\text {End}}\mathbb {V}\) on \(\mathbb {V}\) satisfying
$$\begin{aligned} \mathbb {I}\mathbb {J}\mathbb {K}= -\smash {{{\,\textrm{Id}\,}}_\mathbb {V}}. \end{aligned}$$ -
(b)
A quaternionic structure on \(\mathbb {V}\) is a 3-dimensional subspace
$$\begin{aligned} Q:= {\text {span}} \{\mathbb {I}, \mathbb {J}, \mathbb {K}\} \subseteq {\text {End}}\mathbb {V}, \end{aligned}$$where \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) is a hypercomplex structure
Note that, if \(Q \subseteq {\text {End}}\mathbb {V}\) is a quaternionic structure on a vector space \(\mathbb {V}\) and \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) a hypercomplex structure inducing it, then declaring \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) to be an oriented, orthonormal basis determines an orientation and inner product on Q. Moreover, the hypercomplex structures that induce Q are exactly the oriented bases of Q that are orthonormal with respect to that inner product.
If \(\mathbb {V}\) admits a hypercomplex or quaternionic structure, then \(\dim _\mathbb {R}\mathbb {V}= 4m + 4\) for some \(m \in \{0, 1, \ldots \}\). As for complex structures, a hypercomplex or quaternionic structure determines an orientation on \(\mathbb {V}\): Given a quaternionic basis of \(\mathbb {V}\), that is, an ordered \((m + 1)\)-tuple \((E_1, \ldots , E_{m+1})\) of vectors in \(\mathbb {V}\) such that
is a basis of \(\mathbb {V}\), declaring

to be positively oriented defines an orientation on \(\mathbb {V}\). This orientation is independent of the choice of vectors \(E_1, \ldots , E_{m+1}\) and the choice of representative triple \((\mathbb {I},\mathbb {J},\mathbb {K})\) in the quaternionic case, since any two such representatives are related by an action of \({{\,\textrm{SO}\,}}(3)\).
If \(\mathbb {V}\) is equipped with a hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) then, regarding it as a (right) \(\mathbb {H}\)-module—where \(\mathbb {H}\) is the quaternion algebra generated by \((\mathbb {I}, \mathbb {J}, \mathbb {K}\))—its automorphism group is
where \(\dim _\mathbb {R}\mathbb {V}= 4 m + 4\). The automorphism group of the induced quaternionic structure \(Q={\text {span}} \{\mathbb {I}, \mathbb {J}, \mathbb {K}\}\) on \(\mathbb {V}\) is
The factor \({{\,\textrm{Sp}\,}}(1)=\{q\in \mathbb {H}: |q|=1\}\) acts on \(\mathbb {V}\) by quaternionic scalar multiplication on the right, and \(\mathbb {Z}_2\) acts by multiplication by \(\pm \smash {{{\,\textrm{Id}\,}}}\) on both factors.
The maximal subgroups of these two groups characterized by fixing a volume form  compatible with the canonical orientation on \(\mathbb {V}\) are
compatible with the canonical orientation on \(\mathbb {V}\) are
Definition 2.2
Let \(\mathbb {V}\) be a real vector space equipped with an inner product h, that is, a symmetric non-degenerate bilinear form (here, and henceforth, not necessarily positive definite).
-
(a)
The inner product h is called Hermitian, with respect to a hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) on \(\mathbb {V}\), if
$$\begin{aligned} h(X, Y) = h(\mathbb {I}X, \mathbb {I}Y) = h(\mathbb {J}X, \mathbb {J}Y) = h(\mathbb {K}X, \mathbb {K}Y) \quad \text {for all} \quad X, Y \in \mathbb {V}, \end{aligned}$$(4)or, with respect to a quaternionic structure Q on \(\mathbb {V}\), if (4) holds for any, equivalently, every, hypercomplex structure inducing Q.
-
(b)
If an inner product h is Hermitian with respect to a hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) or a quaternionic structure Q, we call the respective pairs \((h, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) and (h, Q) a Hermitian hypercomplex structure and a Hermitian quaternionic structure on \(\mathbb {V}\).
If an inner product h on a real vector space \(\mathbb {V}\) is Hermitian with respect to a hypercomplex or quaternionic structure thereon, then its signature is (4p, 4q) for some \(p, q \in \{0, 1, \ldots \}\). Since the hypercomplex or quaternionic structure determines a natural orientation on \(\mathbb {V}\), a Hermitian inner product h determines a preferred volume form on \(\mathbb {V}\). Regarded as a (right) \(\mathbb {H}\)-module, a vector space \(\mathbb {V}\) equipped with a Hermitian hypercomplex structure \((h, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) has automorphism group
in the case where the signature of h is (4p, 4q), and the automorphism group of the induced Hermitian quaternionic structure (h, Q) on \(\mathbb {V}\) is
Figure 1 adapts from [2, Sect. 1] a diagram of the relationships of the above quaternionically flavored structures on a real vector space, giving for each the name, the defining data and its automorphism group. Arrows denote inclusions of automorphism groups, i.e., forgetting some of the data defining the structure.
2.1.2 Quaternionic and quaternionic Kähler structures
We now transfer the algebraic notions from Sect. 2.1 to the vector bundle setting.
Definition 2.3
-
(a)
A quaternionic structure on a vector bundle \(\mathcal {V}\) over a manifold M is a rank-3 subbundle \(Q \subset {\text {End}}(\mathcal {V})\) such that, locally around any point in M, there exists a local frame \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) of Q satisfying the quaternionic relations:
$$\begin{aligned} \mathbb {I}^2=\mathbb {J}^2=\mathbb {K}^2=-\smash {{{\,\textrm{Id}\,}}_{\mathcal {V}}} \quad \text {and} \quad \mathbb {I}\mathbb {J}\mathbb {K}=-\smash {{{\,\textrm{Id}\,}}_{\mathcal {V}}}, \end{aligned}$$where \({{\,\textrm{Id}\,}}_{\mathcal {V}}\) is the identity endomorphism. Such local frames \((\mathbb {I},\mathbb {J},\mathbb {K})\) of a quaternionic structure are called admissible. It follows that \({{\,\textrm{rank}\,}}\mathcal {V} \equiv 0 \pmod 4\).
-
(b)
An almost quaternionic structure on a manifold M of dimension \(4m+4\) is a quaternionic structure Q on TM, equivalently, a first-order \({{\,\textrm{G}\,}}\)-structure with structure group \({{\,\textrm{GL}\,}}(m + 1,\mathbb {H}) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\).
Note that an almost quaternionic manifold (M, Q) admits a canonical orientation, namely that determined by any admissible local frame \((\mathbb {I},\mathbb {J},\mathbb {K})\) of Q as in (3). Moreover, it is well-known, see Section 3.2 of [2], that an almost quaternionic manifold (M, Q) admits a distinguished class of linear connections on TM that preserve Q and have the same minimal torsion, which may be identified with the intrinsic torsion of the \({{\,\textrm{GL}\,}}(m + 1,\mathbb {H}) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\)-structure. This class of connections forms an affine space over the vector space of 1-forms on M. Specifically, any two such connections, \(\nabla \) and \(\widehat{\nabla }\), are related by a 1-form \(\Upsilon \in \Gamma (T^*M)\) according to the formula
where \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) is an admissible local frame of Q.
Definition 2.4
An almost quaternionic manifold (M, Q) of dimension \(4m+4 \ge 8\) is called quaternionic if it admits a torsion-free linear connection on TM preserving Q, equivalently, if the intrinsic torsion of the corresponding \({{\,\textrm{GL}\,}}(m + 1,\mathbb {H}) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\)-structure vanishes.
Definition 2.5
A quaternionic Kähler structure on a manifold M of dimension \(4m+4 \ge 8\) consists of a (pseudo-)Riemannian metric \(g \in \Gamma (S^2 T^*M)\) and an almost quaternionic structure \(Q \subset {\text {End}}(TM)\) such that
-
for each \(x \in M\), \((g_x, Q_x)\) is a Hermitian quaternionic structure on \(T_x M\);
-
Q is parallel with respect to the Levi–Civita connection of g.
In particular, Q is quaternionic.
A connected (pseudo-)Riemannian manifold (M, g) of signature (4p, 4q) admits a quaternionic Kähler structure if and only if the holonomy of g is contained in \({{\,\textrm{Sp}\,}}(p, q) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\). Quaternionic Kähler manifolds are known to be Einstein; see e.g., Corollary 12.2.14 in [14].
Remark 2.6
Note that in Definitions 2.4 and 2.5 we required the dimension to be at least 8. The reason is that dimension 4 is special and requires a separate treatment. Let us briefly explain this: Almost quaternionic structures in dimension 4 are known to be automatically quaternionic in the sense of Definition 2.4. Moreover, in dimension 4, due to the isomorphism \({{\,\textrm{Sp}\,}}(1) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\cong \text {SO}(4)\) (and thus also \({{\,\textrm{GL}\,}}(1, \mathbb H) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\cong \text {CSO}(4)\)), almost quaternionic structures are the same as oriented conformal structures, and Riemannian manifolds with holonomy in \({{\,\textrm{Sp}\,}}(1) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\) are simply oriented Riemannian manifolds. In view of that, the definition of quaternionic Kähler 4-manifolds needs to be adjusted: they are defined as oriented Riemannian 4-manifolds that are self-dual and Einstein. Similarly, the definition of quaternionic structures in dimension 4 is sometimes adjusted to mean self-dual oriented conformal structures; see e.g., Definition 12.2.12 in [14].
2.1.3 Hypercomplex and hyperkähler structures
Let us also recall the notion of a hyperkähler structure introduced by Calabi [17, 18].
Definition 2.7
-
(a)
A hypercomplex structure on a vector bundle \(\mathcal {V}\) over a manifold M consists of a triple \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) of sections \(\mathbb {I}, \mathbb {J}, \mathbb {K}\in \Gamma (\text {End}(\mathcal {V}))\) satisfying the quaternionic relations:
$$\begin{aligned} \mathbb {I}^2=\mathbb {J}^2=\mathbb {K}^2=-\smash {{{\,\textrm{Id}\,}}_{\mathcal {V}}} \quad \text {and} \quad \mathbb {I}\mathbb {J}\mathbb {K}=-\smash {{{\,\textrm{Id}\,}}_{\mathcal {V}}}, \end{aligned}$$where \({{\,\textrm{Id}\,}}_{\mathcal {V}}\) is the identity endomorphism.
-
(b)
A hypercomplex structure on a manifold M consists of a hypercomplex structure \((\mathbb {I},\mathbb {J},\mathbb {K})\) on TM, where \(\mathbb {I},\mathbb {J}\) and \(\mathbb {K}\) are integrable (as almost complex structures on M).
As for almost quaternionic structures, hypercomplex manifolds admit a natural orientation, which coincides with the orientation induced by any of the three complex structures.
Definition 2.8
-
(a)
A Hermitian hypercomplex structure on a vector bundle \(\mathcal {V}\) consists of a fiber metric g on \(\mathcal {V}\) and a hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) such that at each \(x \in M\), \((g_x, (\mathbb {I}_x, \mathbb {J}_x, \mathbb {K}_x))\) is a Hermitian hypercomplex structure on the fiber \(\mathcal {V}_x\).
-
(b)
A hyperkähler structure on a manifold M consists of a (pseudo-)Riemannian metric \(g \in \Gamma (S^2 T^*M)\) and a hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) on TM such that
-
\((g, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) is a Hermitian hypercomplex structure on TM;
-
\(\mathbb {I},\mathbb {J},\mathbb {K}\) are parallel with respect to the Levi–Civita connection of g.
In particular, since \(\mathbb {I}\), \(\mathbb {J}\) and \(\mathbb {K}\) are preserved by a torsion-free connection, they are necessarily integrable, i.e., \((\mathbb {I},\mathbb {J},\mathbb {K})\) is a hypercomplex structure on M.
-
Put another way, a hyperkähler structure on a manifold M is a quaternionic Kähler structure (g, Q) on M together with a global frame of Q that is parallel with respect to the Levi–Civita connection \(\nabla \) of g. Put yet another way, a hyperkähler structure on a manifold M consists of a metric \(g \in \Gamma (S^2 T^*M)\) together with a triple \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) of complex structures satisfying the quaternionic relations such that \((g, \mathbb {I})\), \((g, \mathbb {J})\), \((g, \mathbb {K})\) are Kähler structures.
A connected (pseudo-)Riemannian manifold (M, g) of signature (4p, 4q) admits a hyperkähler structure if and only if the holonomy of its Levi-Civita connection \(\nabla \) is contained in \({{\,\textrm{Sp}\,}}(p, q)\). Locally, hyperkähler structures are precisely the quaternionic Kähler structures that are Ricci-flat; see e.g., Corollary 12.2.14 in [14].Footnote 1
The sequel in particular treats Hermitian hypercomplex structures on a vector bundle parallel with respect to a connection on that vector bundle. These structures, that is, parallel Hermitian hypercomplex structures on vector bundles, are the vector bundle analogues of hyperkähler structures and in particular are characterized by containment of the holonomy of the connection in \({{\,\textrm{Sp}\,}}(p, q)\).
2.2 3-Sasaki structures
We recall some background on Sasaki and 3-Sasaki structures; for a comprehensive treatment we refer to the monograph [14].
Definition 2.9
A Sasaki structure on a manifold M consists of a (pseudo-)Riemannian metric \(g_{ab} \in \Gamma (S^2 T^*M)\) and a Killing field \(k^a \in \Gamma (TM)\) of g such that
-
(a)
\(g_{ab} k^a k^b = 1\)
-
(b)
\(\nabla _a\nabla _b k^c = -g_{ab} k^c + \delta ^c{}_a k_b.\)
The following equivalent characterization is well-known; see [13, 14].
Proposition 2.10
Let (M, g) be a (pseudo-)Riemannian manifold and
its metric cone, where t is the standard coordinate on \(\mathbb {R}_+\) and we identify \(M \leftrightarrow M \times \{1\}\).
-
(a)
If \(k \in \Gamma (TM)\) is a vector field such that (M, g, k) is a Sasaki manifold, define \(\mathbb {K}\in \Gamma ({\text {End}}(T\smash {\widehat{M}}))\) with respect to the splitting \(T\smash {\widehat{M}} = T(M \times \mathbb {R}_+) \cong TM \oplus T\mathbb {R}_+\) by declaring
$$\begin{aligned} \mathbb {K}(v):= \nabla _v k \quad \text {for}\; v \in \{k\}^{\perp } \cap TM, \qquad \mathbb {K}(k):= t \partial _t, \quad \text {and} \quad \mathbb {K}(t\partial _t):= -k. \end{aligned}$$Then, \(\mathbb {K}\) is a complex structure, and \((\smash {\widehat{M}}, {\hat{g}}, \mathbb {K})\) is a Kähler manifold.
-
(b)
Conversely, if \(\mathbb {K}\in \Gamma ({\text {End}}(T\smash {\widehat{M}}))\) is a complex structure for which \((\smash {\widehat{M}}, {\hat{g}}, \mathbb {K})\) is a Kähler structure, define \(k \in \Gamma (TM)\) by \(k:= \mathbb {K}\partial _t \vert _M\). Then, (M, g, k) is a Sasaki structure.
In particular, any manifold admitting a Sasaki structure has odd dimension.
Definition 2.11
A 3-Sasaki structure on a manifold M comprises a (pseudo-)Riemannian metric \(g_{ab} \in \Gamma (S^2 T^*M)\) and a triple (i, j, k) of Killing fields of g, where i, j, and k separately satisfy the conditions (a) and (b) of Definition 2.9 and together satisfy the following “quaternionic conditions”:
-
(c)
\(g_{ab}i^aj^b=g_{ab}j^ak^b=g_{ab}k^ai^b=0\)
-
(d)
\([i, j]=-2k, \quad [j, k]=-2i\), and \([k,i]=-2j\).
The collection (M, g, (i, j, k)) is together called a 3-Sasaki manifold.
It follows immediately from the definitions that for any 3-Sasaki manifold (M, g, (i, j, k)), each of (M, g, i), (M, g, j), and (M, g, k) are Sasaki manifolds.
Proposition 2.10 immediately implies an analogous result—a characterization via the metric cone—for 3-Sasaki manifolds vis-à-vis hyperkähler manifolds; see [13, 14].
Proposition 2.12
Let (M, g) be a (pseudo-)Riemannian manifold and
its metric cone, where t is the standard coordinate on \(\mathbb {R}_+\), and identify \(M \leftrightarrow M \times \{1\}\).
-
(a)
If (M, g, (i, j, k)) is a 3-Sasaki manifold, respectively, define \(\mathbb {I}, \mathbb {J}, \mathbb {K}\in \Gamma (T\smash {\widehat{M}})\) as in Proposition 2.10(a). Then, \((\smash {\widehat{M}}, {\hat{g}}, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) is a hyperkähler manifold.
-
(b)
For the converse, if \((\smash {\widehat{M}}, {\hat{g}}, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) is a hyperkähler manifold, respectively, define \(i, j, k \in \Gamma (TM)\) as in Proposition 2.10(b). Then, (M, g, (i, j, k)) is a 3-Sasaki structure.
In particular, if a manifold M admits a 3-Sasaki structure, then \(\dim M \equiv 3 \pmod 4\).
Given a 3-Sasaki structure on a manifold M, the identification \(M \leftrightarrow M \times \{1\}\), the canonical orientation on its hyperkähler cone, and the preferred unit normal vector field \(\partial _t \vert _M\) along M, together determine a canonical orientation and hence (via the metric) a preferred volume form on M. Moreover, a metric cone of a (pseudo-)Riemannian manifold (M, g) is Ricci-flat if and only g is Einstein [14, Lemma 11.1.15]. Thus Ricci-flatness of hyperkähler manifolds and Proposition 2.12 imply the following (see [14, Corollary 13.3.2]):
Proposition 2.13
Suppose (M, g, (i, j, k)) is a 3-Sasaki manifold. Then g is Einstein with Einstein constant \(\dim (M)-1\).
Finally, we recall in this section some important identities for 3-Sasaki manifolds; see e.g., [13, Proposition 1.2.4] taking our different sign conventions into account.
Proposition 2.14
Suppose (M, g, (i, j, k)) is a 3-Sasaki manifold. Then i, j, k satisfy the following identities and their cyclic permutations in i, j, k:
-
(a)
\(i^a\nabla _aj^b=-j^a\nabla _{a}i^b=-k^b;\)
-
(b)
\(\nabla _bi^c\nabla _a i^b-i_ai^c=-\delta _{a}{}^c;\)
-
(c)
\(\nabla _bi^c\nabla _aj^b-j_ai^c=-\nabla _bj^c\nabla _ai^b+i_aj^c=\nabla _ak^c.\)
2.3 Affine and projective geometry
We briefly review the notions from affine and projective geometry we need here. For more detailed background of these ideas with a view toward the present context, see [30, Sections 2 and 4.1].
A (torsion-free) affine connection on a manifold M is a (torsion-free) linear connection \(\nabla \) on its tangent bundle TM. For an affine manifold \((M,\nabla )\), we denote by

the curvature and by \({\text {Ric}}_{bd}:=R_{cb}{}^c{}_d\) the Ricci tensor of \(\nabla \). Two affine connections \(\nabla \) and \(\widehat{\nabla }\) are projectively equivalent if they have the same unparametrized geodesics. If both connections are torsion-free, this is well-known to be equivalent to the existence of a 1-form \(\Upsilon _a\in \Gamma (T^*M)\) such that
for any vector field \(\xi ^a\in \Gamma (TM)\).
Definition 2.15
A projective structure on a manifold M is an equivalence class \({\textbf {p}}\) of projectively equivalent torsion-free affine connections on M, and we call such a structure \((M, {\textbf {p}})\) a projective manifold.
In the following proposition, we record some well-known facts about certain important tensors in projective differential geometry (cf. [8, Section 3]):
Proposition 2.16
Suppose \((M,{\textbf {p}})\) is a projective manifold of dimension \(n+1\ge 2\). Let \(\nabla \in {\textbf {p}}\) be a connection in the projective class. Then the curvature R of \(\nabla \) admits the decomposition
Here: \(W_{ab}{}^c{}_d\) is the totally trace-free part of \(R_{ab}{}^{c}{}_d\), which is independent of the choice of \({\nabla \in {\textbf {p}}}\), and is called the projective Weyl curvature of \((M,{\textbf {p}})\); \(\textsf{P}_{ab}\) is the projective Schouten tensor of \(\nabla \) given by
Moreover,
where
is called the projective Cotton tensor of \(\nabla \). Finally, if \(\smash {\widehat{\nabla }}\in {\textbf {p}}\) is another connection in the projective class, related to \(\nabla \) via \(\Upsilon _a\) as in (6), then
Remark 2.17
If \(n=1\) in Proposition 2.16, that is, if \(\dim (M)=2\), then the symmetries of \(W_{ab}{}^c{}_d\) imply that \(W = 0\), and \(\smash {\widehat{C}}_{abc}=C_{abc}\).
Following [8], we fix the following notation for the line bundles on a projective manifold:
Notation 2.18
For a projective manifold \((M, {\textbf {p}})\) of dimension \(n + 1 \ge 2\), we define  . Note that \(\mathcal {K}\) enjoys a canonical orientation, and hence we may define preferred oriented roots \(\mathcal {E}(w):= \mathcal {K}^{w / (2 n + 4)}\) for any \(w\in \mathbb R\). For any vector bundle \(\mathcal {V} \rightarrow M\) we denote \(\mathcal {V}(w):= \mathcal {V}\otimes \mathcal {E}(w)\).
. Note that \(\mathcal {K}\) enjoys a canonical orientation, and hence we may define preferred oriented roots \(\mathcal {E}(w):= \mathcal {K}^{w / (2 n + 4)}\) for any \(w\in \mathbb R\). For any vector bundle \(\mathcal {V} \rightarrow M\) we denote \(\mathcal {V}(w):= \mathcal {V}\otimes \mathcal {E}(w)\).
An immediate consequence of (6) is:
Proposition 2.19
Suppose \((M, {\textbf {p}})\) is a projective manifold and \(0\ne w\in \mathbb R\). Then mapping a connection in \({\textbf {p}}\) to its induced connection on \(\mathcal {E}(w)\) induces an (affine) bijection between connections in \({\textbf {p}}\) and linear connections on \(\mathcal {E}(w)\). In particular, any trivialization of \(\mathcal {E}(w)\), viewed as a nowhere-vanishing section \(\sigma \in \mathcal {E}(w)\), gives rise to a connection \(\nabla \) in \({\textbf {p}}\) characterized by \(\nabla _a\sigma =0\).
Definition 2.20
Suppose \((M, {\textbf {p}})\) is a projective manifold of dimension \(n+1\). For \(0\ne w \in \mathbb {R}\), a nowhere-vanishing section of \(\mathcal {E}(w)\) as well as the corresponding connection \(\nabla \in {\textbf {p}}\) (as in Proposition 2.19) is called a scale of \((M,\textbf{p})\). Note that for a scale \(\nabla \in {\textbf {p}}\) one has \({\text {Ric}}_{[ab]}=\textsf{P}_{[ab]}=0\) and thus \({\text {Ric}}_{ab}={\text {Ric}}_{(ab)}=n\textsf{P}_{(ab)}=n\textsf{P}_{ab}\). Note that if \(\nabla , \widehat{\nabla }\in {\textbf {p}}\) are both scales then the \(\Upsilon \) in (6) is exact.
Any projective manifold \((M,\textbf{p})\) of dimension \(n + 1\) carries a canonical connection on a vector bundle of rank \(n+2\) over M, and the curvature of that connection is a (sharp) obstruction to \((M,\textbf{p})\) being locally projectively flat [8, Section 3]. Recall that a projective manifold is locally projectively flat if it is locally projectively equivalent to the standard projective structure on \(\mathbb {R}^{n + 1}\)—that is, the projective structure induced by the standard flat affine connection on \(\mathbb {R}^{n+1}\), whose geodesics are affine lines. Let us explain this in some more detail: the connection is defined on \(\mathcal {T}^{\,*}:= J^1\mathcal {E}(1)\rightarrow M\), the vector bundle of 1-jets of sections of \(\mathcal {E}(1)\). The natural projection \(J^1\mathcal {E}(1)\rightarrow \mathcal {E}(1)\) induces filtrations on \(\mathcal {T}\) and its dual \(\mathcal {T}^{\,*}\) given by the dual short exact sequences
We shall sometimes index sections of the bundles \(\mathcal {T}\) and \(\mathcal {T}^{\,*}\) of a projective manifold by upper, respectively, lower Latin capital letters, for example writing \(t^A\) for a section of \({\mathcal {T}}\). Using this notation, we identify the inclusion map \(\mathcal {E}(-1) \rightarrow \mathcal {T}\) above with a section
called the canonical (weighted) tractor, and the inclusion \(T^*M(1) \rightarrow \mathcal {T}^{\,*}\) with a section \(Z_A{}^a\).
Note that a splitting of the second sequence of (9) is the same as a linear connection on \(\mathcal {E}(1)\). Hence, by Proposition 2.19, connections of \({\textbf {p}}\) are in bijection to splittings of the exact sequences (9). Given a choice of connection \(\nabla \in {\textbf {p}}\), we write
for the bundle maps of the induced splitting of (9); thus,
Then the following fundamental result for projective manifolds holds; see [8, Section 3] (and for the last statement of the theorem [30, Section 4.1]).
Theorem 2.21
Suppose \((M, {\textbf {p}})\) is a projective manifold of dimension \(n+1\ge 2\).
-
(1)
The projective class \({\textbf {p}}\) induces on \(\mathcal {T}^{\,*}\) (and on all vector bundles arising from tensor operations of \(\mathcal {T}^{\,*}\) and its dual \(\mathcal {T}\)) a projectively invariant linear connection \(\nabla ^\mathcal {T}\), given by
$$\begin{aligned} \nabla ^{\mathcal {T}}_a (\mu _b\,,\, \sigma ) =(\nabla _a\mu _b+ \textsf{P}_{ab}\sigma ,\, \nabla _a\sigma - \mu _a) \end{aligned}$$in the splitting of \(J^1\mathcal {E}(1)\) determined by \(\nabla \in {\textbf {p}}\).
-
(2)
The curvature \(R^\mathcal {T}\) of \((\mathcal {T}, \nabla ^\mathcal {T})\) is a 2-form on M with values in the bundle \(\mathfrak {sl}(\mathcal {T})\) of trace-free endomorphisms of \(\mathcal {T}\), and it vanishes identically if and only if \((M,\textbf{p})\) is locally projectively flat. The latter is in turn the case if and only if the projective Weyl curvature vanishes identically for \(n\ge 2\), and if and only if the projective Cotton tensor vanishes identically for \(n=1\).
Moreover, if M is orientable, then an orientation on M induces a nowhere-vanishing section \(\varvec{\epsilon }\) of \( \mathcal {T}^{\ *}\) that is parallel for \(\nabla ^\mathcal {T}\) (and unique up to a non-zero constant factor).
Definition 2.22
Suppose \((M, {\textbf {p}})\) is projective manifold. Then the vector bundle \(\mathcal {T}\) and its dual \(\mathcal {T}^{\ *}\) equipped with the connection \(\nabla ^\mathcal {T}\) of Theorem 2.21 are called the (standard) tractor, respectively, cotractor bundle of \((M, {\textbf {p}})\), and \(\nabla ^\mathcal {T}\) the normal tractor (Cartan) connection of \((M, {\textbf {p}})\). Moreover, if \((M, {\textbf {p}})\) is orientable and oriented, we refer to  of Theorem 2.21 as the parallel tractor volume form of \((M,{\textbf {p}})\).
of Theorem 2.21 as the parallel tractor volume form of \((M,{\textbf {p}})\).
The tractor connection of a projective structure in Definition 2.22 is equivalent to the normal Cartan connection of a projective structure [25] and can alternatively also be encoded as an affine connection on a manifold of dimension \(n+2\) over M, as defined by Thomas in [41].
Another important tractor bundle is the following.
Definition 2.23
The vector bundle \(\mathcal {A}:=\mathfrak {sl}(\mathcal {T})\) of trace-free endomorphisms of \(\mathcal {T}\) (equipped with the connection \(\nabla ^\mathcal {T}\)) is called the adjoint tractor bundle of \((M,\textbf{p})\). It inherits, from (9), a filtration with a natural projection \(\Pi : \mathcal {A}\rightarrow TM\).
More explicitly, for a choice of connection \(\nabla \in {\textbf {p}}\) (giving rise to a splitting of (9)) the induced filtration of \(\mathcal {A}\) splits as:
where \(\mathfrak {sl}(TM)\) denotes the bundle of trace-free endomorphism of TM and \(\mathcal {E}=M\times \mathbb {R}\rightarrow M\) the trivial bundle. With respect to such a splitting, any section \(\mathbb A ^A {}_B\in \Gamma (\mathcal {A})\) decomposes as
for some \(\xi ^a \in \Gamma (TM)\), \(\phi ^a{}_b \in \Gamma ({\text {End}}TM)\), and \(\nu _b \in \Gamma (T^* M)\). We also write such a section more compactly in block matrix notation as:
The vector field
is, in particular, independent of the choice of \(\nabla \).
For later use, we recall that, with respect to a choice \(\nabla \in {\textbf {p}}\), the curvature  of \(\nabla ^{\mathcal {T}}\) may be written as
of \(\nabla ^{\mathcal {T}}\) may be written as
where \(W_{ab}{}^c{}_d\) is the projective Weyl curvature and \(C_{abd}\) the projective Cotton tensor of \(\nabla \), as defined in Proposition 2.16.
Parallel sections of \(\mathcal {A}\) are closely linked to projective symmetries of \((M,{\textbf {p}})\).
Definition 2.24
A vector field \(\xi \in \Gamma (TM)\) on a manifold M is called an affine symmetry (respectively, projective symmetry) of a torsion-free affine connection \(\nabla \), if its (local) flow preserves \(\nabla \) (respectively, the projective class \([\nabla ]\) of \(\nabla \)), equivalently, if \(\mathcal {L}_\xi \nabla =0\) (respectively the trace-free part of \(\mathcal {L}_\xi \nabla \) equals zero). Here, \(\mathcal {L}_\xi \nabla \) is the Lie derivative of \(\nabla \) along \(\xi \), that is, the (1, 2)-tensor given by
We recall the following result from [30, Section 4.4 and Theorem 4.4]:
Theorem 2.25
Suppose \((M,{\textbf {p}})\) is a projective manifold of dimension \(n+1\ge 3\). Then, for any choice \(\nabla \in {\textbf {p}}\), the differential operator \(L^{\mathcal {A}}: \Gamma (TM) \rightarrow \Gamma (\mathcal {A})\) given by
induces a bijection, with inverse \(\Pi : \Gamma (\mathcal {A})\rightarrow \Gamma (TM)\), between vector fields \(\xi \in \Gamma (TM)\) that satisfy
-
(a)
\(\xi \) is in the kernel of the projectively invariant differential operator
$$\begin{aligned} \mathcal {D}^{\mathcal {A}} : \Gamma (TM) \rightarrow&\,\Gamma ((S^2 T^*M \otimes TM)_{\circ }) \nonumber \\ \xi ^a \mapsto&\,(\nabla _{(b} \nabla _{c)} \xi ^a+ \textsf{P}_{(bc)} \xi ^a)_\circ , \end{aligned}$$(16)where \(\,\cdot \,_{\circ }\) denotes the totally trace-free part of \(S^2 T^*M \otimes TM\) or the projection thereto, and
-
(b)
\(W_{ab}{}^c{}_d \xi ^d= 0\) and \(C_{abd} \xi ^d=0\),
and parallel sections of \(\mathcal {A}\). Moreover, a solution \(\xi \) of \(\mathcal {D}^{\mathcal {A}}(\xi )=0\) (satisfying (b)) is a projective symmetry if and only if \(W_{d(a}{}^c{}_{b)} \xi ^d=0\) (respectively, \(W_{da}{}^c{}_{b} \xi ^d=0\)).
In view of Theorem 2.25, we fix the following notation:
Notation 2.26
With respect to a connection \(\nabla \in {\textbf {p}}\), of a projective manifold \((M,{\textbf {p}})\) of dimension \(n+1\), we write a parallel section \(\mathbb A^{A}{}_B\in \Gamma (\mathcal {A})\) of the adjoint tractor bundle as
Note that if \(\mathbb {I}^A{}_B\in {\text {End}}(\mathcal {T})\) is a complex structure on the tractor bundle \(\mathcal {T}\) of a projective manifold, that is, \(\mathbb {I}^A{}_B\mathbb {I}^B{}_C=-\delta ^A{}_C\), then necessarily one has \(\mathbb {I}^A{}_B\in \Gamma (\mathcal {A})\). In [30] we studied in detail the geometric implications of the existence of a parallel complex structure \(\mathbb {I}\in \Gamma (\mathcal {A})\), and those of a parallel Hermitian structure, on the tractor bundle of a connected oriented projective manifold. In this article we will investigate the geometric implications of parallel tractor hypercomplex and parallel tractor Hermitian hypercomplex structures.
3 Projective geometry of 3-Sasaki structures
We are now ready to present our first main results of this article.
3.1 Projective structures induced by 3-Sasaki structures
Since a 3-Sasaki manifold is Einstein, we have:
Theorem 3.1
Suppose (M, g, (i, j, k)) is a 3-Sasaki manifold of signature \((4p-1, 4q)\), and denote by \(\nabla \) the Levi–Civita connection of g. Then the tractor bundle \((\mathcal {T}, \nabla ^{\mathcal {T}})\) of the induced projective manifold \((M, [\nabla ])\) admits a parallel tractor Hermitian hypercomplex structure of signature (4p, 4q) given by:
-
(a)
a parallel tractor metric \(h \in \Gamma (S^2 \mathcal {T}^{\ *})\) of signature (4p, 4q) on \(\mathcal {T}\), and
-
(b)
a triple \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) of parallel tractor complex structures \(\mathbb {I}, \mathbb {J}, \mathbb {K}\in \Gamma ({\text {End}}\mathcal {T})\) on \(\mathcal {T}\) each Hermitian with respect to h and together satisfying
$$\begin{aligned} \mathbb {I}\mathbb {J}\mathbb {K}=-\smash {{{{\,\textrm{Id}\,}}}_{\mathcal {T}}}. \end{aligned}$$(17)
Proof
Suppose (M, g, (i, j, k)) is a 3-Sasaki manifold of signature \((4p-1, 4q)\). Then g is known to be Einstein (cf. Proposition 2.13). Hence, Theorem A of [30] implies that g induces a parallel tractor metric \(h \in \Gamma (S^2 \mathcal {T}^{\ *})\) of signature (4p, 4q) on \(\mathcal {T}\), and, from i, j and k, three parallel tractor complex structures \(\mathbb {I}:= L^\mathcal {A}(i), \mathbb {J}= L^\mathcal {A}(j), \mathbb {K}= L^\mathcal {A}(k)\) with respect to which h is Hermitian. It remains to show that \(\mathbb {I}\mathbb {J}\mathbb {K}=-\smash {{{\,\textrm{Id}\,}}_\mathcal {T}}\), equivalently that \(\mathbb {I}\mathbb {J}=\mathbb {K}\). Formula (15) for \(L^\mathcal {A}\) and the fact that i, j, and k are Killing fields of g (cf. the proof of [30, Theorem A]) imply that
in the scale of the Levi–Civita connection of the metric g. Hence, by Definition 2.11 and Proposition 2.14 one has
\(\square \)
Before we investigate the converse of Theorem 3.1, that is, the geometric implications of a parallel Hermitian hypercomplex structure on the tractor bundle of a projective manifold, we recall in the following section one more geometric structure; it will appear in results in Sect. 4.2.
3.2 Quaternionic contact structures
For a manifold N and a distribution \(H\subset TN\) we denote by \(\mathcal {L}: H\times H\rightarrow TN/H\) the Levi bracket, which for two sections \(\xi , \eta \) of H is defined as the projection of their Lie bracket \([\xi , \eta ]\) to TN/H. Then for any \(x\in N\), we may view \({\text {gr}}(T_xN)=H_x\oplus T_xN/H_x\) as a Lie algebra, where the bracket of two elements of \(H_x\) is given by \(\mathcal {L}_x\) and all other brackets are zero.
Definition 3.2
Suppose p, q are non-negative integers and \(p+q={\widetilde{m}}=m-1\). Regard \(\mathbb H^{{\tilde{m}}}\) as a (right) vector space over \(\mathbb H\), and denote by \(\langle \cdot ,\cdot \rangle : \mathbb H^{\widetilde{m}}\times \mathbb H^{\widetilde{m}}\rightarrow \mathbb H \) the standard quaternionic Hermitian inner product of signature (p, q), given by
Note that the imaginary part \(\text {Im}(\langle x,y\rangle )\in \text {Im}(\mathbb H)\) of \(\langle x,y\rangle \) is given by \(\text {Im}(\langle x,y\rangle )=\frac{1}{2}(\langle x,y\rangle -\langle y,x\rangle )\). The quaternionic Heisenberg algebra of signature (p, q) is the 2-step nilpotent graded Lie algebra
where the Lie bracket of two elements \((x,a), (y,b) \in \mathbb H^{\widetilde{m}}\oplus \text {Im}(\mathbb H)\) is given by
Definition 3.3
Suppose N is a manifold of dimension \(4{\widetilde{m}}+3\) (\({\widetilde{m}}\ge 1\)). Then a quaternionic contact structure of signature (p, q) (\(p+q={\widetilde{m}}\)) is given by a distribution \(H\subset TN\) of rank \(4{\widetilde{m}}\) such that such that the graded vector bundle \(\text {gr}(TN)=H\oplus TN/H\) is locally trivial as a bundle of Lie algebras \((\text {gr}(TN),\mathcal {L})\), with standard fiber isomorphic to the quaternionic Heisenberg Lie algebra of signature (p, q).
Note that the condition on \(\text {gr}(TN)=H\oplus TN/H\) in Definition 3.3 is equivalent to the existence of a quaternionic structure \(Q\subset \text {End}(H) \) on H and a conformal equivalence class [g] of Q-Hermitian (bundle) metrics of signature (p, q) on H (i.e., a \({{\text {CSp}}(p,q) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)}\)-structure on H) such that the Levi bracket  can be locally (for a local trivialization of the rank-3 bundle TN/H) written as \((g(I\,\cdot \,,\,\cdot \,), g(J\,\cdot \,,\,\cdot \,), g(K\,\cdot \,,\,\cdot \,))\) for a local frame (I, J, K) of Q and a metric \(g\in [g]\).
can be locally (for a local trivialization of the rank-3 bundle TN/H) written as \((g(I\,\cdot \,,\,\cdot \,), g(J\,\cdot \,,\,\cdot \,), g(K\,\cdot \,,\,\cdot \,))\) for a local frame (I, J, K) of Q and a metric \(g\in [g]\).
A compact homogeneous model for quaternionic contact manifolds of signature (p, q) is the quaternionic projectivization
of the cone of null vectors in the standard quaternionic Hermitian vector space \(\mathbb H^{p+1, q+1}\). It inherits from the quaternionic structure on \(\mathbb H P^{{\widetilde{m}}+1}\) an \({{\,\textrm{Sp}\,}}(p+1, q+1)\)-homogeneous quaternionic contact structure \(H\subset T\mathcal {N}^{4{\widetilde{m}}+3}\) of signature (p, q), where \(H_x\) is the maximal quaternionic subspace of \(T_x\mathcal {N}^{4{\widetilde{m}}+3}\subset T_x\mathbb H P^{{\widetilde{m}}+1}\) for any \(x\in \mathcal {N}^{4{\widetilde{m}}+3}\). In general, the following is known.
Theorem 3.4
[24, Section 4.3.3] There exists an equivalence of categories between quaternionic contact manifolds of signature (p, q) and regular normal parabolic geometries modeled on \({{\,\textrm{Sp}\,}}(p+1, q+1)/P\cong \mathcal {N}\), where P is the stabilizer of a null quaternionic line in \(\mathbb H^{p+1, q+1}\).
In particular, by Theorem 3.4, the so-called harmonic curvature of the corresponding normal parabolic geometry is a (sharp) obstruction for the local equivalence of a quaternionic contact manifold to its homogeneous model \({{\,\textrm{Sp}\,}}(p+1, q+1)/P\). For \({\widetilde{m}}\ge 2\) (that is, \(\dim N \ge 11\)) the harmonic curvature comprises a single irreducible component called the curvature of a quaternionic contact manifold, which can be viewed as a bundle map  . The case \({\widetilde{m}}= 1\) (\(\dim N = 7\)) is special, see e.g., [26, 27]. In particular, the harmonic curvature includes in this case an additional irreducible component, the torsion of a quaternionic contact manifold, which can be viewed as a bundle map \(H \times TN / H \rightarrow TN / H\); in higher dimensions the torsion vanishes. See [24, Section 4.3.3] for more details. Following the literature, we call a 7-dimensional quaternionic contact structure with vanishing torsion integrable.
. The case \({\widetilde{m}}= 1\) (\(\dim N = 7\)) is special, see e.g., [26, 27]. In particular, the harmonic curvature includes in this case an additional irreducible component, the torsion of a quaternionic contact manifold, which can be viewed as a bundle map \(H \times TN / H \rightarrow TN / H\); in higher dimensions the torsion vanishes. See [24, Section 4.3.3] for more details. Following the literature, we call a 7-dimensional quaternionic contact structure with vanishing torsion integrable.
Remark 3.5
The (aforementioned) homogeneous model of quaternionic contact manifolds \(\mathcal {N}\subset \mathbb H P^{{\widetilde{m}}+1}\) is a real hypersurface in a quaternionic manifold and inherits its quaternionic contact structure from the ambient quaternionic structure. Recall that any generic real hypersurface in a complex manifold inherits a non-degenerate CR-structure of hypersurface type from the ambient complex structure. The analogous statement in the quaternionic setting, however, is not true: If N is a generic real hypersurface of a quaternionic manifold (M, Q), then the maximal Q-invariant subbundle \(H\subset TN\) given by
where \((I_x, J_x, K_x)\) is a hypercomplex structure inducing \(Q_x\), is in general merely what is called a weakly quaternionic contact structure; see [28].
Quaternionic contact manifolds (in definite signature) were first studied by Biquard in [10, 11], where they arise as geometric structures at infinity of quaternionic Kähler manifolds. In fact, for \({\widetilde{m}}\ge 2\) Biquard showed in [10, Theorem D] that any real-analytic quaternionic contact structure of definite signature is locally the (conformal) infinity of a unique so-called asymptotically hyperbolic quaternionic Kähler (AHQK) metric. Duchemin [27, Theorem 1.4] showed that same holds for integrable structures with \({\widetilde{m}}=1\). Moreover, [10, Theorem C] and [27, Section 5] (see also [24, Proposition 4.5.5] for the indefinite case) imply that any quaternionic contact manifold (N, H) of signature (p, q) (assumed integrable if \({\widetilde{m}}=p+q=1\)) induces on the total of the \(S^2\)-subbundle \(S(Q)\rightarrow N\) (in \(Q\rightarrow N\)), of complex structures on H contained in Q, a non-degenerate CR-structure of hypersurface type and (Hermitian) signature \((2p+1, 2q+1)\). The subbundle S(Q) equipped with that structure is called the CR-twistor space of the quaternionic contact manifold.
Recall also that the classical Fefferman construction [12, 29] associates to any non-degenerate CR-structure of hypersurface type a conformal structure on the total space of a certain circle bundle over the CR-manifold and that conformal structures that arise via this construction are called Fefferman conformal structures. Combining the constructions of Biquard and Fefferman shows that any quaternionic contact manifold of signature (p, q) induces, on the total space of a certain \(S^3\)-bundle over it, a conformal structure of signature \((4p+3, 4q+3)\). We call conformal structures that arise (locally) via this construction from quaternionic contact manifolds Biquard–Fefferman conformal structures.
3.3 Projective structures with holonomy reduction to \({{\,\textrm{Sp}\,}}(p,q)\)
We are now ready to prove a result that includes a converse to Theorem 3.1—but also considerably more. We will restrict to dimension at least 11 and will comment later in Remark 3.8 briefly on what happens in the lowest possible dimension, namely 7, which is special.
Theorem 3.6
Let \((M, {\textbf {p}})\) be a projective manifold of dimension at least 11 equipped with a parallel Hermitian hypercomplex structure \((h, (\mathbb {I},\mathbb {J},\mathbb {K}))\) on its tractor bundle \((\mathcal {T}, \nabla ^{\mathcal {T}})\). Then, M is of dimension \(4m + 3\) and h has signature (4p, 4q) for some \(p, q, \in \{0, 1, \ldots \}\), where \(p+q-1 = m \ge 2\). The vector fields \(i:= \Pi (\mathbb {I}), j:= \Pi (\mathbb {J}), k:= \Pi (\mathbb {K})\) on M vanish nowhere, and M is stratified into a disjoint union of submanifolds
according to the strict sign of \(\tau := h(X,X) \in \Gamma (\mathcal {E}(2))\), where \(X \in \Gamma (\mathcal {T}(1))\) is the canonical tractor defined in (10). Furthermore, the components \(M_{\pm }\) and \(M_0\) are each equipped with a geometry canonically determined by \((M, {\textbf {p}}, h, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) as follows.
-
(a)
The submanifolds \(M_{\pm }\) are open and (if non-empty) are, respectively, equipped with 3-Sasaki structures \((g_{\pm }, (i, j, k))\) with Ricci curvature \({\text {Ric}}_\pm = (4m + 2) g_\pm \); \(g_+\) has signature \((4p-1, 4q)\), and \(g_-\) has signature \((4p,4q-1)\). The metrics \(g_{\pm }\) are compatible with the projective structure \({\textbf {p}}\) in the sense that their respective Levi–Civita connections \(\nabla ^{\pm }\) satisfy \(\nabla ^{\pm } \in {\textbf {p}}\vert _{M_{\pm }}\).
-
(b)
The submanifold \(M_0\) is (if non-empty) a smooth separating hypersurface and is equipped with an oriented (local) Biquard–Fefferman conformal structure \({\textbf {c}}\) of signature \((4p-1,4q-1)\) as defined in Sect. 3.2,
If h is definite, the stratification is trivial, that is, if h is ±-definite then, respectively, \(M = M_\pm \).
In Theorem 3.6(a), and in some places below, we have suppressed, for readability, the notation \(\cdot \,\vert _{M_{\pm }}\) specifying the restriction of the vector fields i, j, and k to \(M_{\pm }\).
Proof of Theorem 3.6
The existence of a parallel Hermitian hypercomplex structure on \(\mathcal {T}\) implies that the rank of \(\mathcal {T}\) equals \(4m+4\), implying that \(\dim M =4m+3\), and that h has signature (4p, 4q) for \(p+q-1 = m \ge 2\) (cf. (2)). By Proposition 5.23 of [30] the vector fields i, j, and k vanish nowhere on M, and by Theorem 5.1 of [30] the strict sign \(\tau =h(X,X)\) induces a decomposition of M as claimed.
-
(a)
Theorem B of [30] gives that \(M_\pm \) are both open and equipped with Einstein metrics \(g_\pm \) with Ricci tensor \((4m + 2) g_\pm \), whose Levi–Civita connection \(\nabla ^\pm \) lies in \({\textbf {p}}\vert _{M_\pm }\). Moreover, we know that i, j, and k are Killing fields for \(g_\pm \) satisfying (a) and (b) of Definition 2.9, so it remains to show that they also satisfy (c) and (d) of Definition 2.11. With respect to \(\nabla =\nabla ^\pm \) the tractor complex structures \(\mathbb {I}\) and \(\mathbb {J}\) are of the form (18), so the identity \(\mathbb {I}\mathbb {J}=\mathbb {K}\) and (19) imply that \(i_aj^a=0\) and that the first identity in Proposition 2.14(a), which is equivalent to \([i,j]=-2k\), both hold. Now, since (17) implies that \(\mathbb {I}\mathbb {K}=-\mathbb {J}\) and \(\mathbb {J}\mathbb {K}=\mathbb {I}\), one deduces similarly that \(i_ak^a=j_ak^a=0\), and that \([j,k]=-2i\) and \([k,i]=-2j\).
-
(b)
Theorem B of [30] also gives that \(M_0\) is a smooth separating hypersurface equipped with a conformal structure \({\textbf {c}}\) of signature \((4p-1,4q-1)\), and the proof thereof identifies \((\mathcal {T}\vert _{M_0}, h\vert _{M_0}, \nabla ^\mathcal {T}\vert _{M_0})\) with the conformal tractor bundle of \((M_0, {\textbf {c}})\) and its normal (conformal) tractor connection. Therefore, the parallel Hermitian hypercomplex structure \((h, (\mathbb {I}, \mathbb {J}, \mathbb {K}))\) on the projective tractor bundle \(\mathcal {T}\) induces a parallel Hermitian hypercomplex structure on \((\mathcal {T}\vert _{M_0}, h\vert _{M_0}, \nabla ^\mathcal {T}\vert _{M_0})\), and the claim follows from the characterization of Biquard–Fefferman conformal structures in [3, Theorem A]. \(\square \)
Theorem 3.7
Assume the setting of Theorem 3.6 and that \(M_0 \ne \emptyset \) (so \(p, q > 0\)). Then the projective manifold-with-boundary \((M {\setminus } M_\mp , {\textbf {p}}\vert _{M {\setminus } M_\mp })\) is, respectively, a smooth projective compactification (of order 2) of the 3-Sasaki manifold \((M_\pm , g_\pm , (i, j, k))\), with projective infinity the Biquard–Fefferman conformal structure \((M_0, \pm {{\textbf {c}}})\).
Proof
This follows immediately from Theorem 3.6 and [30, Theorem 5.1], which in turn use [21,22,23]. \(\square \)
Remark 3.8
Suppose now \((M, {\textbf {p}})\) is a projective manifold of dimension 7 equipped with a parallel Hermitian hypercomplex structure \((h, (\mathbb {I},\mathbb {J},\mathbb {K}))\) on its tractor bundle \((\mathcal {T}, \nabla ^{\mathcal {T}})\). Then Theorem 3.6 also holds, except that statement (b) needs to be modified, since the lowest dimension of a Biquard–Fefferman conformal structure (as it fibers over a quaternionic contact manifold) is 10. More specifically, h is in this case either of definite signature (8, 0), respectively, (0, 8), or signature (4, 4). In the definite cases, Theorem 3.6 holds without change: \(M_0=\emptyset \) and \(M=M_\pm \) admits a 3-Sasaki structure of definite signature (7, 0), respectively, (0, 7). In the indefinite case, \(M_\pm \) admit 3-Sasaki structures of signature (3, 4) and (4, 3), respectively, and \(M_0\) (if non-empty) is a real separating hypersurface, which is canonically equipped with an oriented conformal structure of signature (3, 3) with a holonomy reduction of its conformal tractor bundle to \({{\,\textrm{Sp}\,}}(1,1)\le {{\,\textrm{SO}\,}}(4,4)\). We will say later, in Remark 4.10, a bit more about the geometric interpretation of this reduction. With this modification, Theorem 3.7 also holds.
As a corollary of Theorems 3.1 and 3.6 one obtains the following characterization of 3-Sasaki manifolds, which also holds in dimension 7 by Remark 3.8:
Corollary 3.9
There is an equivalence of categories between 3-Sasaki structures (g, (i, j, k)) of signature \((4p-1, 4q)\) with \(4(p+q)-1\ge 7\) and projective structures of dimension \(4(p+q)-1\ge 7\) with a parallel Hermitian hypercomplex structure \((h,(\mathbb {I},\mathbb {J},\mathbb {K}))\) of signature (4p, 4q) on its tractor bundle \((\mathcal {T}, \nabla ^{\mathcal {T}})\) such that the canonical tractor X, as defined in (10), satisfies that h(X, X) is nowhere zero.
4 Geometry on the leaf space of the distribution spanned by i, j, k
In the following sections will see that the vector fields i, j, and k in the setting of Theorem 3.6 span an integrable distribution on M and will investigate the geometric structure on its local leaf space.
4.1 Projective structures with holonomy reduction to \({{\,\textrm{SL}\,}}(m+1, \mathbb {H})\)
We first study the geometric implications of a holonomy reduction of an oriented projective manifold of dimension \(4m+3\) to
that is, the tractor bundle \((\mathcal {T}, \nabla ^\mathcal {T})\) admits a parallel hypercomplex structure \(( \mathbb {I}, \mathbb {J},\mathbb {K})\) such that  and \(( \mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). We focus again on the case \(m\ge 2\), but comment on the case \(m=1\) in Remark 4.4.
and \(( \mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). We focus again on the case \(m\ge 2\), but comment on the case \(m=1\) in Remark 4.4.
Proposition 4.1
Suppose \((M,{\textbf {p}})\) is a connected oriented projective manifold of dimension \(4m+3\ge 7\) equipped with a parallel hypercomplex structure \(( \mathbb {I}, \mathbb {J},\mathbb {K})\) on its tractor bundle \((\mathcal {T}, \nabla ^\mathcal {T})\) such that  and \((\mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). Let \(i:= \Pi (\mathbb {I})\), \(j:= \Pi (\mathbb {J})\), \(k:= \Pi (\mathbb {K})\) denote the corresponding nowhere-vanishing vector fields on M. Then the following hold:
and \((\mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). Let \(i:= \Pi (\mathbb {I})\), \(j:= \Pi (\mathbb {J})\), \(k:= \Pi (\mathbb {K})\) denote the corresponding nowhere-vanishing vector fields on M. Then the following hold:
-
(a)
The distribution \(D:= {\text {span}}\{i,j,k\} \subset TM\) has rank 3 and is integrable.
-
(b)
Locally around any point in M there exists a scale \(\nabla \in {\textbf {p}}\) such that
$$\begin{aligned} \nabla _ai^a=\nabla _aj^a=\nabla _ak^a=0. \end{aligned}$$We refer to such a scale as an (i, j, k)-adapted scale. In view of (6) the freedom in the choice of an (i, j, k)-adapted scale in \({\textbf {p}}\) is addition of an exact 1-form \(\Upsilon _a\) satisfying \(\Upsilon _ai^a=\Upsilon _aj^a=\Upsilon _ak^a=0\).
-
(c)
The vector fields i, j, k are affine symmetries of any (i, j, k)-adapted scale and so, in particular, are projective symmetries of \((M, {\textbf {p}})\).
Proof
-
(a)
To see that D has rank 3, consider the compact flat homogeneous model of oriented projective manifolds of dimension \(4m+3\) given by the sphere
$$\begin{aligned} S^{4m+3}\cong {{\,\textrm{SL}\,}}(4m+4,\mathbb {R})/P, \end{aligned}$$viewed as the ray projectivization of \(\mathbb {R}^{4m+4}\) and equipped with its standard flat projective structure induced by the round metric, where P is the stabilizer of a ray. Since \({{\,\textrm{SL}\,}}(m+1,\mathbb {H})\) acts transitively on \(S^{4m+3}\) and preserves the parallel tractor
 , it follows from [23] that the curved orbit decomposition corresponding to the parallel tractor \(\mathbb {I}\wedge \mathbb {J}\wedge \mathbb {K}\) is trivial and that \(i\wedge j\wedge k\) is nowhere vanishing, since the zero set of any normal solution of a BGG operator (corresponding to a parallel tractor) is a union of curved orbits (see in particular, [23, Section 2.7]). Hence, D has rank 3. Now let us prove that D is integrable. We fix a scale \(\nabla \in {\textbf {p}}\) and use Notation 2.26. Then \(\mathbb {I}\mathbb {J}=\mathbb {K}\) implies that $$\begin{aligned} j^b\nabla _b i^a-j^a\phi (i)-i^a\phi (j)=k^a \quad \text {and}\quad i^b\nabla _b j^a-i^a\phi (j)-j^a\phi (i)=-k^a, \end{aligned}$$(21)
, it follows from [23] that the curved orbit decomposition corresponding to the parallel tractor \(\mathbb {I}\wedge \mathbb {J}\wedge \mathbb {K}\) is trivial and that \(i\wedge j\wedge k\) is nowhere vanishing, since the zero set of any normal solution of a BGG operator (corresponding to a parallel tractor) is a union of curved orbits (see in particular, [23, Section 2.7]). Hence, D has rank 3. Now let us prove that D is integrable. We fix a scale \(\nabla \in {\textbf {p}}\) and use Notation 2.26. Then \(\mathbb {I}\mathbb {J}=\mathbb {K}\) implies that $$\begin{aligned} j^b\nabla _b i^a-j^a\phi (i)-i^a\phi (j)=k^a \quad \text {and}\quad i^b\nabla _b j^a-i^a\phi (j)-j^a\phi (i)=-k^a, \end{aligned}$$(21)after which torsion-freeness of \(\nabla \) implies that \([i,j]=\nabla _i j-\nabla _j i=-2k\). Similarly, one deduces from \(\mathbb {I}\mathbb {K}=-\mathbb {J}\) and \(\mathbb {K}\mathbb {J}=-\mathbb {I}\) that \([k,i]=-2j\) and \([j,k]=-2i\). Therefore, the distribution \(D:= {\text {span}}\{i, j, k\}\) is involutive and hence integrable.
-
(b)
In Proposition 5.24 of [30] we have seen that locally around any point in M there exists an i-adapted scale, that is, a scale \(\nabla \in {\textbf {p}}\) with \(\nabla _ai^a=0\) (equivalently, \(\varphi (i)=0\)). According to (6) the freedom in the choice of an i-adapted scale is an exact 1-form \(\Upsilon _a\) satisfying \(\Upsilon _ai^a=0\). Hence, we need to show that an i-adapted scale can be modified, according to (6), by such a 1-form to a scale that is also adapted to j and k. So let us fix a local i-adapted scale \(\nabla \). First, \(\mathbb {I}^2=-\smash {{{\,\textrm{Id}\,}}}_\mathcal {T}\) implies that (in the i-adapted scale \(\nabla \))
$$\begin{aligned} \textsf{P}_{ab} i^ai^b=1 \quad \text {and}\quad i^a\nabla _ai^b=0. \end{aligned}$$(22)Moreover, \(\mathbb {I}\mathbb {J}=\mathbb {K}\) and \(\mathbb {I}\mathbb {K}=-\mathbb {J}\) imply that
$$\begin{aligned} \textsf{P}_{ab} i^aj^b=\textsf{P}_{ba} i^aj^b=\varphi (k)\quad \text {and}\quad \textsf{P}_{ab} i^ak^b= \textsf{P}_{ba} i^ak^b=-\varphi (j), \end{aligned}$$(23)and \(\mathbb {J}\mathbb {I}=-\mathbb {K}\), \(\mathbb {K}\mathbb {I}=\mathbb {J}\) and \(\mathbb {J}\mathbb {K}=-\mathbb {K}\mathbb {J}=\mathbb {I}\) that
$$\begin{aligned} i^a\nabla _a\varphi (j)=-2\varphi (k), \quad i^a\nabla _a\varphi (k)=2\varphi (j), \quad \text {and}\quad k^a\nabla _a\varphi (j)=j^a\nabla _a\varphi (k). \end{aligned}$$(24)Suppose \(\widehat{\nabla }\in {\textbf {p}}\) is another i-adapted scale which differs from \(\nabla \) by \(\Upsilon _a\) according to (6). Then the identity (7) shows that:
$$\begin{aligned} \smash {\widehat{\textsf{P}}}_{ab}i^b=\textsf{P}_{ab}i^b-(\nabla _a\Upsilon _b)i^b+\Upsilon _a\Upsilon _bi^b=\textsf{P}_{ab}i^b+\Upsilon _b \nabla _ai^b. \end{aligned}$$(25)By (21), (22) and (23), this implies:
$$\begin{aligned} \smash {\widehat{\textsf{P}}}_{ab}i^b j^a=\textsf{P}_{ab}i^bj^a+\Upsilon _b j^a\nabla _ai^b=\varphi (k)+ \Upsilon _b k^b. \end{aligned}$$(26)Analogously, one obtains:
$$\begin{aligned} \smash {\widehat{\textsf{P}}}_{ab}i^b k^a=\textsf{P}_{ab}i^bk^a+\Upsilon _b k^a\nabla _ai^b=-\varphi (j)-\Upsilon _b j^b. \end{aligned}$$(27)Therefore, the proof reduces to the question whether locally around any point there exists a smooth function f such that:
$$\begin{aligned} i\cdot f=0,\quad j\cdot f=-\varphi (j), \quad k\cdot f=-\varphi (k). \end{aligned}$$(28)By the Implicit Function Theorem and the Frobenius Theorem, it suffices to show that the rank-3 distribution on \(M\times \mathbb {R}\) spanned by \(\xi :=i\), \(\eta :=j+\varphi (j)\frac{\partial }{\partial t}\), and \(\zeta :=k+\varphi (k)\frac{\partial }{\partial t}\) is involutive (here, t denotes the standard coordinate on \(\mathbb {R}\)). The commutator relations of i, j, and k in the proof of (a) and (24) yield:
$$\begin{aligned}{}[ \xi , \eta ]=-2\zeta \quad [ \xi ,\zeta ]= 2\eta ,\quad [\eta ,\zeta ]=-2\xi , \end{aligned}$$which completes the proof.
-
(c)
Since, by assumption, \(\mathcal {T}\) is equipped with a \(\nabla ^\mathcal {T}\)-parallel hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\), the tractor curvature \(R_{ab}{}^C{}_D\) is a section of
 . Now consider
. Now consider 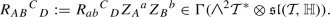
With respect to any scale \(\nabla \in {\textbf {p}}\), \(R_{AB}{}^C{}_D\) is, per (13),
$$\begin{aligned} R_{AB}{}^C{}_D=W_{ab}{}^c{}_d Z_{A}{}^aZ_{B}{}^b W^C{}_c Z_{D}{}^d-C_{abd} Z_{A}{}^aZ_{B}{}^bX^CZ_{D}{}^d. \end{aligned}$$Proposition 2.16 gives that \(W_{[ab}{}^c{}_{d]}=0\) and \(C_{[abd]}=0\), and so \(R_{[AB}{}^C{}_{D]}=0\). By (the proof of) Lemma 6.5 of [38] this implies
$$\begin{aligned} \mathbb {I}^{E}{}_{A}\, \mathbb {I}^{F}{}_{B}R_{EF}{}^C{}_D=\mathbb {J}^{E}{}_{A}\, \mathbb {J}^{F}{}_{B}R_{EF}{}^C{}_D=\mathbb {K}^{E}{}_{A}\, \mathbb {K}^{F}{}_{B}R_{EF}{}^C{}_D=R_{AB}{}^C{}_D. \end{aligned}$$(29)Hence \(X^A\mathbb {I}^{E}{}_{A}R_{EF}{}^C{}_D=X^A\mathbb {J}^{E}{}_{A}R_{EF}{}^C{}_D=X^A\mathbb {K}^{E}{}_{A}R_{EF}{}^C{}_D=0\), since \(X^AR_{AB}{}^C{}_D=0\). With respect to any scale \(\nabla \in {\textbf {p}}\) this says that \(i^a W_{ab}{}^c{}_{d}=j^a W_{ab}{}^c{}_{d}=k^a W_{ab}{}^c{}_{d}=0\) and \(i^a C_{abd}=j^a C_{abd}=k^a C_{abd}=0\). Thus, the claim follows from Proposition 5.27 of [30] and Theorem 2.25. \(\square \)
Using Theorem 2.25 straightforwardly yields the following identities:
Lemma 4.2
Assume the setting of Proposition 4.1, and let \(\nabla \in {\textbf {p}}\) be a local (i, j, k)-adapted scale. Then \(\mathbb {I}^2=\mathbb {J}^2=\mathbb {K}^2=-\smash {{{\,\textrm{Id}\,}}}\) and \(\mathbb {I}\mathbb {J}=-\mathbb {J}\mathbb {I}=\mathbb {K}\) imply:
-
(a)
\(i^a\nabla _a i^b=0,\quad \textsf{P}_{cd} i^c i^d=1,\quad \textsf{P}_{cd} i^d \nabla _b i^c=0,\quad \nabla _c i^a \nabla _b i^c - i^a \textsf{P}_{bc} i^c=-\delta ^a{}_b,\) and similarly for j and k;
-
(b)
\(\textsf{P}_{ab} i^a j^b=0,\quad \textsf{P}_{ab} i^a k^b=0,\,\text {and}\,\textsf{P}_{ab} j^a k^b=0;\)
-
(c)
\(i^a\nabla _a j^b=-j^a\nabla _a i^b=k^b,\,\text {and}\, \textsf{P}_{bc}i^c\nabla _a j^b=-\textsf{P}_{bc}j^c\nabla _a i^b=\textsf{P}_{bc} k^c;\)
-
(d)
\((\nabla _b i^c) \nabla _a j^b-\textsf{P}_{ad} j^d i^c=-(\nabla _b j^c ) \nabla _a i^b+\textsf{P}_{ad} i^d j^c=\nabla _a k^c,\)
and (c) and (d) also for their cyclic permutations of i, j, and k. Moreover, \(\nabla ^\mathcal {T}\mathbb {I}=\nabla ^\mathcal {T}\mathbb {J}=\nabla ^\mathcal {T}\mathbb {K}=0\) implies
and similarly for j and k.
Theorem 4.3
Suppose \((M,{\textbf {p}})\) is a connected oriented projective manifold of dimension \(4m+3\ge 11\) equipped with a parallel hypercomplex structure \((\mathbb {I}, \mathbb {J},\mathbb {K})\) on its tractor bundle \((\mathcal {T}, \nabla ^\mathcal {T})\) such that  and \( ( \mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). Then around any point in M there is an open set \(U \subseteq M\) such that the leaf space \({\widetilde{M}}\), of the restriction to U of the distribution \(D:= {\text {span}}\{i, j, k\}\) (in the notation of 4.1(a)), inherits a canonical quaternionic structure \({\widetilde{Q}} \subset {\text {End}}(T\widetilde{M})\).
and \( ( \mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). Then around any point in M there is an open set \(U \subseteq M\) such that the leaf space \({\widetilde{M}}\), of the restriction to U of the distribution \(D:= {\text {span}}\{i, j, k\}\) (in the notation of 4.1(a)), inherits a canonical quaternionic structure \({\widetilde{Q}} \subset {\text {End}}(T\widetilde{M})\).
Moreover, any (i, j, k)-adapted scale \(\nabla \) descends to a torsion-free affine connection \(\widetilde{\nabla }\) on \({\widetilde{M}}\) with respect to which the subbundle \({\widetilde{Q}}\) is parallel.
Proof
Given \((\mathbb {I},\mathbb {J},\mathbb {K})\) as in the statement of the theorem, let \(U\subset M\) be a sufficiently small open set so that \({\textbf {p}}\vert _U\) admits (i, j, k)-adapted scales and so that the natural projection \(\pi : U\rightarrow {\widetilde{M}}\) to the leaf space of D is a submersion. Moreover, fix an (i, j, k)-adapted scale \(\nabla \in {\textbf {p}}\vert _U\). By (a) and (c) of Lemma 4.2, the endmorphisms \(\nabla i\), \(\nabla j\), and \(\nabla k\) of TU vanish nowhere and map D to D. Hence, they induce endomorphisms I, J, and K of TU/D. From (a) and (d) of Lemma 4.2 we see that I, J, and K are complex structures on TU/D such that \(IJ=K\), which in particular implies that they span a subbundle \(Q\subset \text {End}(TU/D)\) of rank 3. Note that (6) implies that I, J, and K are independent of the choice of (i, j, k)-adapted scale in \({\textbf {p}}\vert _U\) and so is \(Q\subset \text {End}(TU/D)\). We now verify that Q descends to a subbundle of \(\text {End}(T{\widetilde{M}})\) by showing that the flows of i, j, and k preserve Q. By (c) of Proposition 4.1 we know that i, j and k are affine symmetries of \(\nabla \). Thus, (c) of Lemma 4.2 (cf. also the proof of (a) of Proposition 4.1) implies that one has \(\mathcal {L}_i\nabla i=\nabla \mathcal {L}_i i=0\) and similarly for j and k, and that
and its cyclic permutations in i, j and k hold. Hence, Q is preserved by the Lie derivatives \(\mathcal {L}_i\), \(\mathcal {L}_j\), and \(\mathcal {L}_k\), and so it descends to a subbundle \({\widetilde{Q}}\subset \text {End}(T{\widetilde{M}})\). Therefore, \(({\widetilde{M}},{\widetilde{Q}})\) is an almost quaternionic manifold; the quaternionic structure \({\widetilde{Q}}\) is independent of the choice of (i, j, k)-adapted scale \(\nabla \) because Q is.
To show that \(({\widetilde{M}},{\widetilde{Q}})\) is moreover quaternionic it remains to prove that it admits a torsion-free affine connection \(\widetilde{\nabla }\) preserving \({\widetilde{Q}}\). We show that any (i, j, k)-adapted scale induces such a connection. By (a) and (b) of Lemma 4.2, an (i, j, k)-adapted scale \(\nabla \) induces a decomposition
where H is the common kernel of the nowhere-vanishing 1-forms \(\textsf{P}_{ab}i^b\), \(\textsf{P}_{ab}j^b\) and \(\textsf{P}_{ab}k^b\). Via (31), I, J, and K may be identified with complex structures on H, and Q with a subbundle of \(\text {End}(H)\). Moreover, we may define a connection \(\nabla ^H\) on H by \(\nabla ^H_\eta \xi =p_H(\nabla _\eta \xi )\) for any \(\xi \in \Gamma (H)\) and \(\eta \in \Gamma (TU)\), where \(p_H: TU\rightarrow H\) denotes the natural projection defined by (31). From (30) one sees that \(\nabla ^H\) preserves I, J, and K and hence in particular Q. Now (c) of Proposition 4.1 implies that \(\nabla ^H\) descends to an affine connection \(\widetilde{\nabla }\) on \({\widetilde{M}}\), with \(\widetilde{\nabla }{\widetilde{Q}}=0\); \(\widetilde{\nabla }\) is torsion-free because \(\nabla \) is. \(\square \)
Remark 4.4
In fact Theorem 4.3 holds also in dimension 7 (note that the proof did not require dimension \(\ge 11\)). In this case, the proof of Theorem 4.3 shows that \(({\widetilde{M}}, {\widetilde{Q}})\) is an almost quaternionic 4-manifold, which, in view of Remark 2.6, may or may not be called quaternionic (depending on the chosen convention), and which in any case can be also interpreted as an oriented conformal manifold \(({\widetilde{M}}, [{\tilde{g}}])\).
Remark 4.5
In the setting of Theorem 4.3, suppose that \(\nabla '\) and \(\nabla \) are two (i, j, k)-adapted scales, which differ by the exact 1-form \(\Upsilon \) according to (6). Since \(\Upsilon \) is exact and annihilates \(D=\langle i,j,k\rangle \), it is invariant under the Lie derivative along i, j, and k. Hence, there exists a unique \({\tilde{\Upsilon }}\in \Gamma (T^*{\widetilde{M}})\) such that \(\pi ^*{\tilde{\Upsilon }}=\Upsilon \). Analogously, as in Theorem 5.31 [30], one may verify that \(\widetilde{\nabla }'\) and \(\widetilde{\nabla }\) are related by \({\tilde{\Upsilon }}\) (according to (5)).
Remark 4.6
There is also a converse to Theorem 4.3 associating to any quaternionic manifold an oriented projective manifold with a parallel hypercomplex structure on its tractor bundle, providing an analogue to the construction described in [6, Theorem 3.7] and [30, Theorem 5.32] that associates to any c-projective structure defined as in [16] a projective structure. We will not carry out this construction here, since it is well-known in other terms; see [38, 40], as well as [33, 34].
Suppose now that \({\widetilde{M}}\) is a manifold of dimension 4m equipped with an almost quaternionic structure \({\widetilde{Q}}\), which we recall is equivalent to a \(\text {GL}(m,\mathbb {H})\times _{\mathbb {Z}_2}{{\,\textrm{Sp}\,}}(1)\)-structure on \({\widetilde{M}}\). It is known that \(({\widetilde{M}}, {\widetilde{Q}})\) admits an equivalent description as a regular, normal parabolic geometry modeled on quaternionic projective space \(\text {PGL}(m+1,\mathbb {H})/P\cong \mathbb {H}P^m\), where P denotes here the stabilizer in \(\text {PGL}(m+1,\mathbb {H})\) of a point in \(\mathbb {H}P^m\), see [24, Section 4.1.8]. Provided that a certain topological obstruction vanishes [39], a \(\text {GL}(m,\mathbb {H})\times _{\mathbb {Z}_2}{{\,\textrm{Sp}\,}}(1)\)-structure admits a lift to a \(\text {GL}(m,\mathbb {H})\times {{\,\textrm{Sp}\,}}(1)\)-structure. In that case, a choice of such a lift is equivalent to an extension of the corresponding parabolic geometry of type \((\text {PGL}(m+1,\mathbb {H}), P)\) to a parabolic geometry of type \(({{\,\textrm{SL}\,}}(m+1,\mathbb {H}), {\widetilde{P}})\), where \({\widetilde{P}}\le {{\,\textrm{SL}\,}}(m+1,\mathbb {H})\) is the stabilizer of a quaternionic line in \(\mathbb {H}^{m+1}\). This implies that for any almost quaternionic manifold \(({\widetilde{M}}, {\widetilde{Q}})\) with a choice of a lift to a \(\text {GL}(m,\mathbb {H})\times {{\,\textrm{Sp}\,}}(1)\)-structure (which locally always exists) the normal Cartan connection can be viewed as a canonical linear connection \(\nabla ^{\widetilde{\mathcal {T}}}\) on the vector bundle \({\widetilde{\mathcal {T}}}\rightarrow {\widetilde{M}}\), which is the associated bundle to the Cartan bundle with standard fiber the standard representation of \({{\,\textrm{SL}\,}}(m+1,\mathbb {H})\); see [19]. Similarly as for projective structures, the vector bundle \((\widetilde{\mathcal {T}}, \nabla ^{\widetilde{\mathcal {T}}})\) with connection is called the quaternionic (standard) tractor bundle of \(({\widetilde{M}}, {\widetilde{Q}})\).
Theorem 4.7
Suppose \((M,{\textbf {p}})\) is a connected oriented projective manifold of dimension \(4m+3\ge 7\) equipped with a parallel hypercomplex structure \((\mathbb {I}, \mathbb {J},\mathbb {K})\) on its tractor bundle \((\mathcal {T}, \nabla ^\mathcal {T})\) such that  and \( ( \mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). As in Theorem 4.3 (and Remark 4.4) let \(({\widetilde{M}}, {\widetilde{Q}})\) be any leaf space of the integrable distribution \(D\subset TM\). Write \(\pi : M\rightarrow {\widetilde{M}}\) for the natural submersion, where M is replaced by a sufficiently small open subset if necessary.
and \( ( \mathbb {I}, \mathbb {J},\mathbb {K})\) induce the same orientation on \(\mathcal {T}\). As in Theorem 4.3 (and Remark 4.4) let \(({\widetilde{M}}, {\widetilde{Q}})\) be any leaf space of the integrable distribution \(D\subset TM\). Write \(\pi : M\rightarrow {\widetilde{M}}\) for the natural submersion, where M is replaced by a sufficiently small open subset if necessary.
-
(a)
Declare two elements \(t_x \in \mathcal {T}_x\) and \(t_{x'}\in \mathcal {T}_{x'}\) to be equivalent, if the following holds: \(\pi (x)=\pi (x')\) and \(t_{x'}\) is the result of parallel-transporting (with respect to \(\nabla ^\mathcal {T}\)) \(t_x\) along a curve connecting x and \(x'\) that is everywhere tangent to D. Then this defines an equivalence relation \(\sim \) on \(\mathcal {T}\).
-
(b)
The quotient \({\widetilde{\mathcal {T}}}:=\mathcal {T}/\sim \) of \(\mathcal {T}\) by the equivalence relation \(\sim \) as defined in (a) admits a natural structure of a vector bundle over \({\widetilde{M}}\) such that \(\pi ^*{\widetilde{\mathcal {T}}}\cong \mathcal {T}\). Moreover, the vector space of its sections \(\Gamma ({\widetilde{\mathcal {T}}})\) may be identified with the subspace of \(\Gamma (\mathcal {T})\) consisting of those sections \(t\in \Gamma (\mathcal {T})\) that satisfy \(\nabla ^\mathcal {T}_\xi t=0\) for any section \(\xi \) of D.
-
(c)
\(\nabla ^\mathcal {T}\) descends to a linear connection \(\nabla ^{{\widetilde{\mathcal {T}}}}\) on \({\widetilde{\mathcal {T}}}\rightarrow {\widetilde{M}}\).
-
(d)
The parallel hypercomplex structure \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) and the volume form \(\varvec{\epsilon }\) on \(\mathcal {T}\) descend to a \(\nabla ^{\widetilde{\mathcal {T}}}\)-parallel hypercomplex structure \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\) and to a \(\nabla ^{\widetilde{\mathcal {T}}}\)-parallel (real) volume form
 on \(\widetilde{\mathcal {T}}\), respectively. Moreover, \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) gives rise to a subbundle \({\widetilde{{\mathcal {S}}}}\subset \widetilde{\mathcal {T}}\) of rank 4 preserved by \({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}\) and \({\tilde{\mathbb {K}}}\).
on \(\widetilde{\mathcal {T}}\), respectively. Moreover, \((\mathbb {I}, \mathbb {J}, \mathbb {K})\) gives rise to a subbundle \({\widetilde{{\mathcal {S}}}}\subset \widetilde{\mathcal {T}}\) of rank 4 preserved by \({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}\) and \({\tilde{\mathbb {K}}}\). -
(e)
The vector bundle \(({\widetilde{\mathcal {T}}}, \nabla ^{{\widetilde{\mathcal {T}}}})\) with connection is the normal quaternionic (standard) tractor bundle of \(({\widetilde{M}}, {\widetilde{Q}})\).
Proof
-
(a)
In the proof of (c) of Proposition 4.1 we have seen that \(\xi ^aW_{ab}{}^c{}_d=0\) and \(\xi ^aC_{abd}=0\) for any section \(\xi \) of D. By the formula for the tractor curvature \(R^{\mathcal {T}}\) in (13), this implies that \(R^{\mathcal {T}}(\xi , \,\cdot \,)=0\) for any section \(\xi \) of D. Therefore, the parallel transport along curves with the same endpoints that are tangent to D is for all such curves the same, as the formula (3.1.13) in [9]—describing the dependence of the parallel-transport of a linear connection on a homotopy of curves with fixed endpoints in terms of curvature, shows. Hence, \(\sim \) is a well-defined equivalence relation on \(\mathcal {T}\).
-
(b)
We can proceed analogously to the argument in Section 5.4.5 of [30]. We equip \({\widetilde{\mathcal {T}}}\) with the initial topology with respect to the natural projection \({\tilde{p}}: {\widetilde{\mathcal {T}}}\rightarrow {\widetilde{M}}\). Then, choosing local sections of \(\pi \) shows that vector bundle charts of \(\mathcal {T}\) give rise to local trivializations of \({\widetilde{\mathcal {T}}}\), and hence \({\tilde{p}}: {\widetilde{\mathcal {T}}}\rightarrow {\widetilde{M}}\) can naturally be given the structure of a smooth vector bundle such that the following diagram commutes:

where \(\text {proj}:\mathcal {T}\rightarrow \widetilde{\mathcal {T}}=\mathcal {T}/\sim \) denotes the natural projection. The universal property of the pullback bundle and the fact that \(\text {proj}\vert _{\mathcal {T}_x}: \mathcal {T}_x\rightarrow \widetilde{\mathcal {T}}_{\pi (x)}\) is an isomorphism for all \(x\in M\) immediately imply that \(\pi ^*{\widetilde{\mathcal {T}}}\cong \mathcal {T}\). Moreover, it follows that for any section \({\tilde{t}}\in \Gamma (\widetilde{\mathcal {T}})\) the composition \({\tilde{t}}\circ \pi \) can be naturally interpreted as a section of \(\mathcal {T}\) and evidently the sections t of \(\mathcal {T}\) that arise in this way from sections \(\widetilde{\mathcal {T}}\) are precisely those that satisfy \(\nabla ^{\mathcal {T}}_\xi t=0\) for any section \(\xi \) of D.
-
(c)
Suppose \({\tilde{\xi }}\in \Gamma (T{\widetilde{M}})\) is any vector field on \({\widetilde{M}}\) and choose a lift of it to a vector field \(\xi \in \Gamma (TM)\) on M and let \({\tilde{t}}\) be section of \({\widetilde{\mathcal {T}}}\), which we view as a section of \(\mathcal {T}\) satisfying \((\nabla ^\mathcal {T}{\tilde{t}})\vert _D=0\). Note that \(\nabla _\xi ^{\mathcal {T}} {\tilde{t}}\) is independent of the choice of lift \(\xi \), since \((\nabla ^\mathcal {T}{\tilde{t}})\vert _D=0\). Moreover, for any section \(\eta \in \Gamma (D)\) we have \([\xi , \eta ]\in \Gamma (D)\), since \(\xi \) is projectable as a lift of \({\tilde{\xi }}\). Thus, for any \(\eta \in \Gamma (D)\) we have
$$\begin{aligned} \nabla _\eta ^\mathcal {T}\nabla _\xi ^\mathcal {T}{\tilde{t}}=R^{\mathcal {T}}(\eta , \xi )({\tilde{t}})+\nabla _\xi ^\mathcal {T}\nabla _\eta ^\mathcal {T}{\tilde{t}}+\nabla _{[\eta , \xi ]}^\mathcal {T}{\tilde{t}}=0, \end{aligned}$$since \(R^{\mathcal {T}}\) vanishes upon insertion of sections of D as we have seen in the proof of (a) and \((\nabla ^\mathcal {T}{\tilde{t}})\vert _D=0\). Therefore, \(\nabla ^\mathcal {T}_\xi {\tilde{t}}\) defines a section of \({\widetilde{\mathcal {T}}}\), which is independent of the choice of lift \(\xi \). Denoting this section by \(\nabla ^{\widetilde{\mathcal {T}}}_{\tilde{\xi }}{\tilde{t}}\), one verifies straightforwardly that \(\nabla ^{\widetilde{\mathcal {T}}}: \Gamma (\widetilde{\mathcal {T}})\rightarrow \Gamma (T^*{\widetilde{M}}\otimes \widetilde{\mathcal {T}})\) defines a linear connection on \(\widetilde{\mathcal {T}}\).
-
(d)
The first statement follows directly from the definition of \(\nabla ^{\widetilde{\mathcal {T}}}\) and \(\nabla ^\mathcal {T}\)-parallelism of \((\mathbb {I},\mathbb {J}, \mathbb {K})\) and \(\varvec{\epsilon }\). For the second statement denote by \({\mathcal {S}}\subset \mathcal {T}\) the subbundle given by the tensor product of \(\mathcal {E}(-1)\) with the subbundle of \(\mathcal {T}(1)\) generated by X, \(\mathbb {I}X\), \(\mathbb {J}X\), and \(\mathbb {K}X\), where X is the canonical (weighted) tractor \(X \in \Gamma (\mathcal {T}(1))\) defined by (9). By construction, \({\mathcal {S}}\subset \mathcal {T}\) is a subbundle of rank 4, which is invariant under the action of \(\mathbb {I}\), \(\mathbb {J}\) and \(\mathbb {K}\). We claim it descends to a rank-4 subbundle \({\widetilde{\mathcal {S}}}\subset \widetilde{\mathcal {T}}\) invariant under \({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}\) and \({\tilde{\mathbb {K}}}\). Hence, we have to verify that \(\nabla ^{\mathcal {T}}_\xi \) preserves \(\Gamma ({\mathcal {S}})\) for any section \(\xi \) of D. To do so, choose a (locally defined) (i, j, k)-adapted scale. With respect to such a scale, we have, by (12), that \(\mathbb {I}_{B}{}^AX^A=i^aW^A{}_a\), \(\mathbb {J}_{B}{}^AX^A=j^aW^A{}_a\) and \(\mathbb {K}_{B}{}^AX^A=k^aW^A{}_a\). Since \(\nabla _aX^A=W^A{}_a\), this implies that \(\xi ^a\nabla ^{\mathcal {T}}_a X^A\in \Gamma ({\mathcal {S}})\) for any \(\xi \in \Gamma (D)\). Moreover, contracting \(\nabla ^{\mathcal {T}}_a\mathbb {I}_{B}{}^A X^B=\mathbb {I}_{B}{}^A \nabla ^{\mathcal {T}}_aX^B\) with either \(i^a\), \(j^a\) or \(k^a\) gives \(-X^A\), \(\mathbb {K}_{B}{}^A X^B\) and \(-\mathbb {J}_{B}{}^A X^B\), respectively. Hence, also \(\xi ^a\nabla ^{\mathcal {T}}_a \mathbb {I}_{B}{}^A X^B\in \Gamma ({\mathcal {S}})\) for any \(\xi \in \Gamma (D)\) and the analogous statement for \(\nabla ^{\mathcal {T}}_a \mathbb {J}_{B}{}^A X^B\) and \(\nabla ^{\mathcal {T}}_a \mathbb {K}_{B}{}^A X^B\) follows similarly.
-
(e)
Set \({\tilde{\mathfrak {g}}}:=\mathfrak {sl}(m+1,\mathbb {H})\) and let \({\widetilde{P}}\le {{\,\textrm{SL}\,}}(m+1,\mathbb {H})\) be the stabilizer of a quaternionic line in \(\mathbb {H}^{m+1}\). By the characterization of tractor bundles and tractor connections in [19], we know that the normal (standard) quaternionic tractor bundle with connection of \(({\widetilde{M}}, {\widetilde{Q}})\) is (up to natural equivalence) the unique vector bundle with structure group \(\widetilde{P}\) and standard fiber the \(({\tilde{ \mathfrak {g}}}, \widetilde{P})\)-module \(\mathbb {H}^{m+1}\) and normal non-degenerate \({\tilde{\mathfrak {g}}}\)-connection. Hence, (e) can be proved by verifying all these properties for our pair \((\widetilde{\mathcal {T}}, \nabla ^{\widetilde{\mathcal {T}}})\). The proof is completely analogous to the proof of Proposition 5.35 of [30], so we will only sketch it here. That \((\widetilde{\mathcal {T}}, \nabla ^{\widetilde{\mathcal {T}}})\) is a vector bundle with structure group \(\widetilde{P}\) and standard fiber \(\mathbb {H}^{m+1}\) follows immediately from the existence of the hypercomplex structure \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\), the volume form \({\tilde{\varvec{\epsilon }}}\), and the filtration \({\tilde{\mathcal {S}}}\subset \widetilde{\mathcal {T}}\), where \({\tilde{\mathcal {S}}}\) corresponds to the quaternionic line in \(\mathbb {H}^{m+1}\) stabilized by \(\widetilde{P}\). Since \(\nabla ^{\mathcal {T}}\) has holonomy contained in \({{\,\textrm{SL}\,}}(m+1,\mathbb {H})<{{\,\textrm{SL}\,}}(4m+4,\mathbb {R})\), the construction of \(\nabla ^{\widetilde{\mathcal {T}}}\) implies that it is a \({\tilde{\mathfrak {g}}}\)-connection on \(\widetilde{\mathcal {T}}\). Moreover, normality of \(\nabla ^{\mathcal {T}}\) implies normality of \(\nabla ^{\widetilde{\mathcal {T}}}\), since the curvature \(R^{\widetilde{\mathcal {T}}}\) of \(\widetilde{\mathcal {T}}\) is the descent of \(R^{\mathcal {T}}\). Finally, an analogue of the proof of Claim 3 of [30, Proposition 5.35] implies the non-degeneracy of \(\nabla ^{\widetilde{\mathcal {T}}}\), since the vector bundle map
$$\begin{aligned} {\tilde{\Psi }}: T\widetilde{M}\rightarrow {{\,\textrm{Hom}\,}}({\tilde{\mathcal {S}}}, \widetilde{\mathcal {T}}/{\tilde{\mathcal {S}}}), \end{aligned}$$induced by the composition of \(\nabla ^{\widetilde{\mathcal {T}}}\) with the natural projection \(\Pi ^{\widetilde{\mathcal {T}}}: \widetilde{\mathcal {T}}\rightarrow \widetilde{\mathcal {T}}/{\tilde{\mathcal {S}}}\), defines an isomorphism between \(T\widetilde{M}\) and the vector subbundle \({{\,\textrm{Hom}\,}}_{({\tilde{\mathbb {I}}},{\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})}({\tilde{\mathcal {S}}}, \widetilde{\mathcal {T}}/{\tilde{\mathcal {S}}})\) of \({{\,\textrm{Hom}\,}}({\tilde{\mathcal {S}}}, \widetilde{\mathcal {T}}/{\tilde{\mathcal {S}}})\) of endomorphisms commuting with \({\tilde{\mathbb {I}}},{\tilde{\mathbb {J}}}\) and \({\tilde{\mathbb {K}}}\). \(\square \)
Remark 4.8
In the proof of Theorem 4.3 we have seen that the complex structures I, J, and K on TU/D are independent of the choice of (i, j, k)-adapted scale. Alternatively, this can be also seen more directly as follows: Let \({\mathcal {S}}\subset \mathcal {T}\) be as in the proof of (d) of Theorem 4.7. Since \(\mathbb {I}, \mathbb {J}, \mathbb {K}\) preserve \(\mathcal {S}\subset \mathcal {T}\), they induce complex structures on \(\mathcal {T}/\mathcal {S}\cong TM/D\otimes \mathcal {E}(-1)\) satisfying the quaternionic relations and thus on also on TM/D. The latter coincide with I, J, K.
4.2 The local leaf space of the distribution spanned by i, j, and k in Theorem 3.6
We return now to the setting of Theorem 3.6: Let \((M, {\textbf {p}})\) be a projective manifold of dimension at least 11 equipped with a parallel Hermitian hypercomplex structure \((h, (\mathbb {I},\mathbb {J},\mathbb {K}))\) on its tractor bundle \((\mathcal {T}, \nabla ^{\mathcal {T}})\). Let \(({\widetilde{M}}, {\widetilde{Q}})\) be the local leaf space of the 3-dimensional foliation D determined by (i, j, k) as in Theorem 4.3 and write \(\pi : M\rightarrow {\widetilde{M}}\) for the natural submersive projection (where M is replaced, if necessary, by a sufficiently small open subset).
By Theorem 4.7, the \((\mathbb {I},\mathbb {J},\mathbb {K})\)-Hermitian bundle metric h of signature (4p, 4q) on \(\mathcal {T}\) descends to a \(\nabla ^{\widetilde{\mathcal {T}}}\)-parallel bundle metric \({\tilde{h}}\) of signature (4p, 4q) on \(\widetilde{\mathcal {T}}\), which is Hermitian with respect to the \(\nabla ^{\widetilde{\mathcal {T}}}\)-parallel hypercomplex structure \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\) on \(\widetilde{\mathcal {T}}\). Hence, \({\tilde{h}}\) defines a holonomy reduction of the quaternionic standard tractor bundle to
By the theory of holonomy reductions of Cartan connections [23], this implies in particular that \(\widetilde{M}\) admits a decomposition into initial submanifolds, where each such submanifold corresponds to an \({{\,\textrm{Sp}\,}}(p,q)\)-orbit in \({{\,\textrm{SL}\,}}(m+1,\mathbb {H})/\widetilde{P}\cong \mathbb {H}P^m\) of the same dimension. Note that there are three \({{\,\textrm{Sp}\,}}(p,q)\)-orbits on \(\mathbb {H}P^m\) corresponding to the signature of a quaternionic line in \(\mathbb {H}^{m+1}\) being positive, negative, or null. The first two orbits are open, whereas the last defines a smooth embedded (real) hypersurface in \(\mathbb {H}P^m\) separating the two open orbits. Therefore, [23] implies that \(\widetilde{M}\) decomposes analogously as
where \(\widetilde{M}_\pm \subset \widetilde{M}\) are open submanifolds (if non-empty) and \(\widetilde{M}_0\subset \widetilde{M}\) is a smooth embedded (real) hypersurface. To describe these submanifolds more explicitly let us write \(S^2_+\widetilde{\mathcal {T}}^{\ *}\subset S^2\widetilde{\mathcal {T}}^{\ *}\) for the subbundle of \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\)-Hermitian forms on \(\widetilde{\mathcal {T}}\). Then, restricting a Hermitian form on \(\widetilde{\mathcal {T}}\) to the \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\)-invariant subbundle \({\widetilde{\mathcal {S}}}\) defines a surjection
from \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\)-Hermitian forms on \(\widetilde{\mathcal {T}}\) to the line bundle \(S^2_+{\widetilde{\mathcal {S}}}^*\) of \(({\tilde{\mathbb {I}}}, {\tilde{\mathbb {J}}}, {\tilde{\mathbb {K}}})\)-Hermitian forms on \({\widetilde{\mathcal {S}}}\). Then, \(\widetilde{M}_\pm \) and \(\widetilde{M}_0\) are the subsets of \(\widetilde{M}\), where \({\tilde{\tau }}=\Pi ^{S^2_+\widetilde{\mathcal {T}}^{\ *}}({\tilde{h}})\in \Gamma (S^2_+{\widetilde{\mathcal {S}}}^*)\) is positive, negative or zero, respectively. By definition of \({\tilde{h}}\), we must also have \(\pi ^*{\tilde{\tau }}=\tau =h(X,X)\) and hence
In particular, \(\widetilde{M}_0\) separates \(\widetilde{M}_\pm \) as \(M_0\) separates \(M_\pm \).
Theorem 4.9
Assume the setting of Theorem 3.6 and let \(({\widetilde{M}}, {\widetilde{Q}})\) be the local leaf space of the 3-dimensional foliation D determined by (i, j, k) as in Theorem 4.3. We write \(\pi : M\rightarrow {\widetilde{M}}\) for the natural submersion (where M is replaced, if necessary, by a sufficiently small open subset) and let \(\widetilde{M}_\pm =\pi (M_\pm )\) and \(\widetilde{M}_0=\pi (M_0)\) as in (32).
Then we have:
-
(a)
The submanifolds \(\widetilde{M}_{\pm }\) are open and (if non-empty) are, respectively, equipped with quaternionic Kähler structures \(({\widetilde{Q}}, {\tilde{g}}_{\pm })\) of signature \((4(p-1), 4q)\) and \((4p,4(q-1))\). The metrics \(g_\pm \) underlying the quaternionic Kähler structures have Ricci tensor \({\widetilde{{\text {Ric}}}}_\pm = (4m + 8){\tilde{g}}_\pm \).
-
(b)
The submanifold \(\widetilde{M}_0\) (if non-empty) is a smooth real hypersurface in \(({\widetilde{M}}, {\widetilde{Q}})\), and the maximal \({\widetilde{Q}}\)-invariant subbundle \({\widetilde{H}}_0\subset T{\widetilde{M}}_0\), as defined in (20), defines a quaternionic contact structure of signature \((p-1, q-1)\) on \({\widetilde{M}}_0\), with quaternionic structure on \({\widetilde{H}}_0\) equal to \({\tilde{Q}}\vert _{{\widetilde{H}}_0}\). Moreover, the conformal structure associated to \(({\widetilde{M}}_0, {\widetilde{H}}_0)\), via the Biquard–Fefferman construction (as explained in Sect. 3.2), equals \((M_0, \pm {\textbf {c}})\).
Proof
-
(a)
It is well-known that the local leaf space of the canonical rank-3 distribution of a 3-Sasaki structure admits a natural quaternionic Kähler structure; see [14, Theorem 13.3.13]. Hence, (a) follows directly from Theorem 3.6. For completeness and convenience of the reader, let us nevertheless give a proof of (a). Let \((g_\pm , (i,j,k))\) be the 3-Sasaki structure on \(M_\pm \) of Theorem 3.6, and denote by \(\nabla ^\pm \in {\textbf {p}}\vert _{M_\pm }\) the Levi–Civita connection of \(g_\pm \). Since i, j, and k are Killing fields of \(g_\pm \) (again we suppress the restriction notation \(\,\cdot \,\vert _{M_{\pm }}\)), the metric \(g_\pm \) descends to a metric \({\tilde{g}}_\pm \) on \({\widetilde{M}}_\pm \) characterized by
$$\begin{aligned} {\tilde{g}}_{\pm }(T\pi \cdot \xi , T\pi \cdot \eta )=g(\xi , \eta ) \quad \forall \, \xi ,\eta \in D^\perp , \end{aligned}$$where \(D^\perp \) denotes the orthogonal complement of D with respect to \(g_\pm \). The fact that i, j, and k are Killing fields of \(g_\pm \) also implies that \(\nabla ^\pm i\), \(\nabla ^\pm j\) and \(\nabla ^\pm k\) are \(g_\pm \)-skew. It follows from the construction of \({\widetilde{Q}}\) and \({\tilde{g}}_\pm \) that \({\tilde{g}}_\pm \) is \({\widetilde{Q}}\)-Hermitian. Moreover, by Theorem 4.3, \(\nabla ^\pm \) descends to a torsion-free affine connection \(\widetilde{\nabla }^\pm \) on \({\widetilde{M}}_\pm \) with \(\widetilde{\nabla }^\pm {\widetilde{Q}}=0\), which has to be the Levi–Civita connection of \({\widetilde{g}}_\pm \) by the definition of \({\tilde{g}}_\pm \) and the fact that \(\nabla ^\pm g_\pm =0\). Thus, \(({\widetilde{M}}_\pm , {\widetilde{Q}}, {\tilde{g}}_\pm )\) are quaternionic Kähler structures of signature \((4(p-1), 4q)\) and \((4p,4(q-1))\), respectively. By Theorem 3.6, we have \({\text {Ric}}_\pm =(4m+2) g_\pm \), from which one deduces by computation that \({\widetilde{{\text {Ric}}}}_\pm =(4m+8) {\tilde{g}}_\pm \); see [14, Theorem 13.3.13].
-
(b)
We have already seen that \({\widetilde{M}}_0\) is a smooth (real) hypersurface separating \({\widetilde{M}}_+\) and \({\widetilde{M}}_-\) in the quaternionic manifold \(({\widetilde{M}}, {\widetilde{Q}})\). We will show that the maximal quaternionic subbundle \({\widetilde{ H}}_0\subset T {\widetilde{M}}_0\) defines a quaternionic contact structure on \({\widetilde{M}}_0\) by identifying it with the quaternionic contact structure over which the Biquard–Fefferman conformal structure \((M_0, {\textbf {c}})\) fibers, by dint of its definition. To see this we proceed along the same lines as the proof of Theorem D in [30]. As we have seen there, \((\mathcal {T}\vert _{M_0}, h_0)\), where \(h_0:= h\vert _{M_0}\), is the conformal tractor bundle of \((M_0, \textbf{c})\) which is filtered as
$$\begin{aligned} \mathcal {T}\vert _{M_0} \supset \mathcal {T}^{\,0} \supset \mathcal {T}^{\,1}, \end{aligned}$$where \(\mathcal {T}^{\,1}\) is the restriction of the line bundle \(X\mathcal {E}(-1)\subset \mathcal {T}\) to \(M_0\) and \(\mathcal {T}^{\,0}:=(\mathcal {T}^{\,1})^\perp \) its orthogonal subspace with respect to \(h_0\). The containment \(\mathcal {T}^{\,1} \supset \mathcal {T}^{\,0}\) follows from the fact that the canonical weighted tractor \(X \in \Gamma (\mathcal {T}(1))\) is null on \(M_0\). In particular, in the notation of [8, Section 2] for line bundles \(\mathcal {E}[w]\) on conformal manifolds one has \(\mathcal {T}^{\,1}\cong \mathcal {E}[-1]\) and \(\mathcal {T}^{\,0}/\mathcal {T}^{\,1}\cong TM_0[-1]\), and the conformal structure \({\textbf {c}}\) on \(M_0\) is given by the non-degenerate bilinear form \({\textbf {g}}\in \Gamma (S^2 T^*M_0[2])\) which \(h_0\) induces on \(\mathcal {T}^{\,0}/\mathcal {T}^{\,1}\). The proof of Theorem D of [30] shows that the respective projecting parts i, j, and k of \(\mathbb {I}, \mathbb {J}\), and \(\mathbb {K}\) restrict on \(M_0\) to conformal Killing fields that are null. Moreover, the fact that h is Hermitian with respect to the hypercomplex structure \((\mathbb {I}, \mathbb {J},\mathbb {K})\), implies also that i, j, k are orthogonal to each other: for i and j we have
$$\begin{aligned} {\textbf {g}}(i,j)=h(\mathbb {I}X,\mathbb {J}X)=-h(X,\mathbb {K}X)=h(\mathbb {K}X, X)=h(X,\mathbb {K}X), \end{aligned}$$which thus has to vanish, and similarly for (k, i) and (j, k). Therefore, \({\textbf {g}}(i,\,\cdot \,)\), \({\textbf {g}}(j,\,\cdot \,)\), and \({\textbf {g}}(k,\,\cdot \,)\) descend to nowhere-vanishing linearly independent (weighted) 1-forms on \(TM_0/D_0\), where \(D_0:= D\vert _{M_0}\) is the distribution spanned by i, j, and k on \(M_0\). Let us denote the common kernel of these 1-forms by \(H_0\subset TM_0/D_0\). Note that, in the notation of Remark 4.8, \(H_0\) can be identified, up to a twist with a line bundle, with the bundle \(\mathcal {S}_0^\perp /\mathcal {S}_0\subset TM_0/D_0\otimes \mathcal {E}[-1]\), where \(\mathcal {S}_0:= \mathcal {S}\vert _{M_0}\) is the restriction of \(\mathcal {S}\subset \mathcal {T}\) (as defined in the proof of (d) of Proposition 4.7) to \(M_0\). Since \((h_0, (\mathbb {I}_0,\mathbb {J}_0,\mathbb {K}_0))\) is a parallel Hermitian hypercomplex structure on \(\mathcal {T}\vert _{M_0}\) (here \(\mathbb {I}_0:= \mathbb {I}\vert _{M_0}\) and analogously for \(\mathbb {J}_0\) and \(\mathbb {K}_0\)), the complex structures \(\mathbb {I}_0, \mathbb {J}_0, \mathbb {K}_0\) preserve \(\mathcal {S}_0\) and its orthogonal complement. Hence, they, (respectively), induce complex structures \(I_0, J_0, K_0\) on \(H_0\), and by construction they are the restrictions of the complex structures I, J, and K induced on TM/D; see Remark 4.8. By [3, Section 4.2] and [4], \(H_0\) and the quaternionic structure \(Q_0={\text {span}}\{I_0,J_0,K_0\}\) descend via \(\pi \) (the projection to the local leaf space of \(D_0\)) to the quaternionic contact structure \(({\widetilde{H}}_0', {\widetilde{Q}}_0')\) over which the Biquard–Fefferman conformal structure \((M_0, {\textbf {c}})\) fibers. By the definition of \({\widetilde{Q}}\), the subbundle \({\widetilde{H}}_0'\subset T{\widetilde{M}}_0\) must be \({\widetilde{Q}}\)-invariant and \({\widetilde{Q}}_0'\) must be the restriction of \({\widetilde{Q}}\) to \(\widetilde{H}_0'\). Since \({\widetilde{H}}_0\) is by definition (see statement (b)) the maximal \({\widetilde{Q}}\)-invariant subbundle of \(T{\widetilde{M}}_0\), we conclude \({\widetilde{H}}_0'\subset {\widetilde{H}}_0\) and hence for dimensional reasons \({\widetilde{H}}_0'={\widetilde{H}}_0\). \(\square \)
We finish with a few remarks.
Remark 4.10
Let us briefly comment on the analogue of Theorem 4.9 in the 7-dimensional case. Suppose \((M, {\textbf {p}})\) is a projective manifold of dimension 7 equipped with a parallel Hermitian hypercomplex structure \((h, (\mathbb {I},\mathbb {J},\mathbb {K}))\) on its tractor bundle \((\mathcal {T}, \nabla ^{\mathcal {T}})\). Then \(({\widetilde{M}}, {\widetilde{Q}})\) is 4-dimensional, which may be also viewed as an oriented conformal 4-manifold, as explained in Remark 4.4. By Theorem 13.3.13 of [14], it follows that on \({\widetilde{M}}_\pm \) one gets quaternionic Kähler 4-manifolds as defined in Remark 2.6. If \({\widetilde{M}}_0\ne \emptyset \), which implies \(p=q=1\), then \({\widetilde{M}}_0\) is a smooth hypersurface in \({\widetilde{M}}\), separating \({\widetilde{M}}_+\) and \({\widetilde{M}}_-\), with a conformal structure of definite signature. The latter is induced from the conformal structure on \(M_0\) with holonomy reduction to \({{\,\textrm{Sp}\,}}(1,1)\cong \text {Spin}(4,1)\) (cf. Remark 3.8). Recall in this context that LeBrun has shown in [35] that any real-analytic 3-dimensional conformal manifold is naturally the conformal infinity of a germ-unique real-analytic 4-dimensional Riemannian manifold that is self-dual and Einstein.
Remark 4.11
Note that in part (a) of Theorem 4.9, the underlying quaternionic Kähler structures \(({\widetilde{Q}}, {\tilde{g}}_{\pm })\) on \(\widetilde{M}_\pm \) are never hyperkähler, since hyperkähler structures are Ricci-flat.
Remark 4.12
In principle one can adapt the methods of [30, §6] to use quaternionic contact structures to construct examples of projective structures with holonomy reductions to \({{\,\textrm{Sp}\,}}(p, q)\), including ones with a non-empty hypersurface curved orbit. In that reference, for a CR structure to produce (along with some other choices) a smooth projective structure with special unitary holonomy reduction, it was necessary that the Fefferman–Graham ambient obstruction tensor \(\mathcal {O}\) of the induced conformal structure vanishes. For Biquard–Fefferman conformal structures, however, \(\mathcal {O}\) vanishes automatically [36, Corollary 1.1(4)].
Remark 4.13
One could weaken the hypothesis of Theorem 3.6 and instead ask for the curved orbit decomposition determined by a parallel Hermitian quaternionic structure (that is, as holonomy reduction of the normal projective tractor connection to \({{\,\textrm{Sp}\,}}(p, q) \times _{\mathbb {Z}_2} {{\,\textrm{Sp}\,}}(1)\)) rather than a parallel Hermitian hypercomplex structure (a reduction to \({{\,\textrm{Sp}\,}}(p, q)\)). But [5, Theorem 4.5.1] or [6, Proposition 4.15] implies that if a projective structure admits a parallel Hermitian quaternionic structure, then locally around each point (or globally, if M is simply connected) it also a parallel Hermitian hypercomplex structure, so (locally) the weaker structure has the same geometric consequences. This result mirrors the fact explained in Section 5.5 of [30] that a reduction to \({{\,\textrm{U}\,}}(p', q')\)) (locally) entails a reduction to \({{\,\textrm{SU}\,}}(p', q')\).
Notes
Some sources define quaternionic Kähler structures to exclude hyperkähler structures.
References
Agricola, I., Friedrich, T.: 3-Sasakian manifolds in dimension seven, their spinors and \(\operatorname{G}_2\)-structures. J. Geom. Phys. 60(2), 326–332 (2010). arXiv:0812.1651
Alekseevsky, D.V., Marchiafava, S.: Quaternionic structures on a manifold and subordinated structures. Ann. Mat. Pura Appl. (4) 171, 205–273 (1996). https://doi.org/10.1007/bf01759388
Alt, J.: On quaternionic contact Fefferman spaces. Differ. Geom. Appl. 28, 376–394 (2010). arXiv:1003.1849
Alt, J.: On the twistor space of a quaternionic contact manifold. J. Geom. Phys. 61, 1783–1788 (2011). arXiv:1104.2705
Armstrong, S.: Holonomy of Cartan connections. University of Oxford Thesis (2006)
Armstrong, S.: Projective holonomy I: principles and properties. Ann. Glob. Anal. Geom. 33, 47–69 (2008). arXiv:math/0602620
Armstrong, S.: Projective holonomy II: cones and complete classifications. Ann. Glob. Anal. Geom. 33, 137–160 (2008). arXiv:math/0602621
Bailey, T.N., Eastwood, M.G., Gover, A.R.: Thomas’s structure bundle for conformal, projective and related structures. Rocky Mt. J. Math. 24, 1191–1217 (1994)
Ballmann, W.: Vector Bundles and Connections. Lecture notes, available at http://people.mpim-bonn.mpg.de/hwbllmnn/archiv/conncurv1999.pdf
Biquard, O.: Métriques d’Einstein asymptotiquement symétriques. Astérisque 265, 115 pp (2000)
Biquard, O.: Quaternionic contact structures. In: Marchiafava, S., Piccinni, P., Pontecorvo, M. (eds.) Proceedings of the Second Meeting on Quaternionic Structures in Mathematics and Physics, Roma (1999). World Scientific, pp. 23–30 (2001)
Burns, D., Diederich, K., Shnider, S.: Distinguished curves in pseudoconvex boundaries. Duke Math. J. 44, 407–431 (1977)
Boyer, C.P., Galicki, K.: 3-Sasakian manifolds. Surv. Differ. Geom. 6, 123–184 (1999). arXiv:hep-th/9810250
Boyer, C.P., Galicki, K.: Sasakian Geometry. Oxford Mathematical Monographs. Oxford University Press, Oxford, xii+613 pp (2008)
Boyer, C.P., Galicki, K., Mann, B.M.: The geometry and topology of 3-Sasakian manifolds. J. Reine Angew. Math. 455, 183–220 (1994)
Calderbank, D.M.J., Eastwood, M.G., Matveev, V.S., Neusser, K.: C-projective geometry. Memoirs AMS 267(1299), 137 pp (2020)
Calabi, E.: Métriques Kähleriénnes et fibrés holomorphes. Ann. Scient. École Norm. Sup., Ser. 4, 12(2), 269–294 (1979)
Calabi, E.: Isometric Families of Kähler Structures. The Chern Symposium 1979. Springer, Berlin (1980)
Čap, A., Gover, A.R.: Tractor calculi for parabolic geometries. Trans. Am. Math. Soc. 354, 1511–1548 (2002)
Čap, A., Gover, A.R.: A holonomy characterisation of Fefferman spaces. Ann. Glob. Anal. Geom. 38, 399–412 (2010). arXiv:math/0611939
Čap, A., Gover, A.R.: Projective compactifications and Einstein metrics. J. Reine. Angew. Math. 717, 47–75 (2016). arXiv:1304.1869
Čap, A., Gover, A.R., Hammerl, M.: Projective BGG equations, algebraic sets, and compactifications of Einstein geometries. J. Lond. Math. Soc. (2) 86, 433–454 (2012). https://doi.org/10.1112/jlms/jds002. arXiv:1005.2246
Čap, A., Gover, A.R., Hammerl, M.: Holonomy reductions of Cartan geometries and curved orbit decompositions. Duke Math. J. 163, 1035–1070 (2014). arXiv:1103.4497
Čap, A., Slovák, J.: Parabolic Geometries I: Background and General Theory. Math. Surveys Monogr., vol. 154. Amer. Math. Soc., Providence (2009)
Cartan, É.: Sur les variétés à connexion projective. Bulletin de la Soc. Math. France 52, 205–241 (1924)
Conti, D., Fernández, M., Santisteban, J.A.: On seven dimensional quaternionic contact solvable Lie groups. Forum Math. 26(2), 547–576 (2014)
Duchemin, D.: Quaternionic contact structures in dimension 7. Annales de l’institut Fourier 56(4), 851–885 (2006). arXiv:math/0311436
Duchemin, D.: Quaternionic-contact hypersurfaces. arXiv:math/0604147
Fefferman, C.: Monge–Ampère equations, the Bergman Kernel, and geometry of Pseudoconvex domains. Ann. Math. (2) 103, 395–416 (1976)
Gover, A.R., Neusser, K., Willse, T.: Projective Geometry of Sasaki–Einstein structures and their compactification. Dissertationes Math. 546, 64 pp. (2019). arXiv:1803.09531
Galicki, K., Salamon, S.: Betti numbers of 3-Sasakian manifolds. Geom. Dedicata 63, 45–68 (1996)
Grove, K., Wilking, B., Ziller, W.: Positively curved cohomogeneity one manifolds and 3-Sasakian geometry. J. Differ. Geom. 78, 33–111 (2008). arXiv:math/0511464
Joyce, D.: The hypercomplex quotient and the quaternionic quotient. Math. Ann. 290, 323–340 (1991)
Joyce, D.: Compact quaternionic and hypercomplex manifolds. J. Differ. Geom. 35, 743–761 (1992)
LeBrun, C.R.: \(\cal{H} \)-spaces with a cosmological constant. Proc. R. Soc. Lond. A 380, 171–185 (1982)
Leistner, T., Lischewski, A.: The ambient obstruction tensor and conformal holonomy. Pac. J. Math. 290, 403–436 (2017). arXiv:1511.07214
Leitner, F.: On transversally symmetric pseudo-Einstein and Fefferman–Einstein spaces. Math. Z. 256, 443–459 (2007). arXiv:math/0502287
Pedersen, H., Poon, Y.S., Swann, A.F.: Hypercomplex structures associated to quaternionic manifolds. Differ. Geom. Appl. 9, 273–292 (1998)
Salamon, S.M.: Differential geometry of quaternionic manifolds. Ann. Scient. École Norm. Sup. Ser. 4 19(1), 31–55 (1986)
Swann, A.F.: Hyper-Kähler and quaternionic Kähler geometry. Math. Ann. 289, 421–450 (1991)
Thomas, T.Y.: A projective theory of affinely connected manifolds. Math. Zeitschrift 25, 723–733 (1926)
Acknowledgements
A.R.G. acknowledges support by the Royal Society of New Zealand via Marsden Grants 16-UOA-051 and 19-UOA-008. K.N. was supported by the grant GA19-06357S from Czech Science Foundation (GAČR). T.W. acknowledges support and hospitality from Centro de Investigación en Matemáticas (Mexico), and support from Guilford College. Moreover, we would like to thank the referee for several helpful comments and suggestions.
Funding
Open access publishing supported by the National Technical Library in Prague.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is dedicated to Eugenio Calabi on the occasion of his 100th birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gover, A.R., Neusser, K. & Willse, T. Compactifications of indefinite 3-Sasaki structures and their quaternionic Kähler quotients. Annali di Matematica 203, 875–902 (2024). https://doi.org/10.1007/s10231-023-01385-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-023-01385-0
Keywords
- Projective differential geometry
- Einstein manifolds
- Sasaki manifolds
- Hyper-Kähler and quaternionic Kähler geometry
- Holonomy
- Geometric compactifications




 , it follows from [
, it follows from [ . Now consider
. Now consider 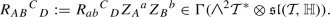
 on
on 