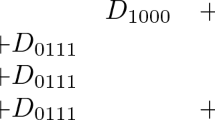1 Introduction

Beauville has shown in [6] that if the image of the canonical map \(\Phi _{K_S}\) of a surface has dimension 2, then its degree d is bounded as follows:

$$\begin{aligned} d:=\deg (\Phi _{K_S}) \le 9+\frac{27-9q}{p_g-2}\le 36. \end{aligned}$$

Note that the bound \(d\le 36\) was shown first by Persson in [21, Proposition 5.7]. Here, q is the irregularity and \(p_g\) the geometric genus of S. In particular, \(28 \le d\) is only possible if \(q=0\) and \(p_g=3\).

Motivated by this observation, the construction of surfaces with \(p_g=3\) and canonical map of degree d for every value \(2 \le d \le 36\) is an interesting, but still widely open problem [16, Question 5.2]. For a long time, the only examples with \(10\le d\) were the surfaces of Persson [21], with canonical map of degree 16, and Tan [27], with degree 12. In recent years, this problem attracted the attention of many authors, putting an increased effort in the construction of new examples. As a result, we have now examples in the literature for all degrees \(2\le d \le 12\) and \(d=14,16, 20, 24, 27, 32\) and 36, see [11, 13, 14, 16,17,18, 22,23,24,25] and [19].

In this paper, we construct surfaces as quotients of a product of two curves \(C_1\times C_2\) modulo an action of the group \(S_3\times \mathbb {Z}_3^2\). Here \(C_1\) is a fixed curve of genus 10 while \(C_2\) is a curve of genus 19 varying in a one-dimensional family. Varying the action of \(S_3\times \mathbb {Z}_3^2\), we get four different one-dimensional families of canonical models of surfaces of general type with \(K_S^2=24\), \(p_g=3\) and \(q=0\).

We write the canonical system of each of them in terms of invariant holomorphic two forms on the product \(C_1\times C_2\). It turns out that for none of them \(\vert K_{S}\vert \) is base point-free, i.e., the canonical map \(\Phi _{K_{S}} :S \dashrightarrow {\mathbb {P}}^2\) is just a rational map. To compute its degree, we resolve the indeterminacy by a sequence of blowups and compute the degree of the resulting morphism via elementary intersection theory. It turns out that the degree of the canonical map is not always constant in a family, and in fact, it assumes five different values: \(d=12,13,15,16\) and 18. To our knowledge, there are no other examples in the literature of surfaces with canonical map of degree 13, 15 and 18.Footnote 1

We point out that our surfaces are examples of product–quotient surfaces, i.e., quotients of product of two curves modulo an action of a finite group. In our cases, the action is diagonal and non-free, arising surfaces with 8 rational double points as singularities of type \(\frac{1}{2}(1,1)\). Product–quotient surfaces are studied for the first time by Catanese in [9]. They are revealed to being a very useful tool for building new examples of algebraic surfaces and studying their geometry in an accessible way. Apart from other works that mainly deal with irregular surfaces, we want to mention the complete classification of surfaces isogenous to a product with \(p_g=q=0\) [1] and the classification for \(p_g=1\) and \(q=0\) under the assumption that the action is diagonal [12], and the rigid but not infinitesimally rigid manifolds [5] of Bauer and Pignatelli that gave a negative answer to a question of Kodaira and Morrow [15, p.45].

Notation: An algebraic surface S is a canonical model if it has at most rational double points as singularities and ample canonical divisor. Recall that each surface of general type is birational to a unique canonical model. In particular, the minimal resolution of the singularities of S is its minimal model.

Let us denote by \(\sigma \) and \(\tau \) a rotation (3-cycle) and a reflection (transposition) of \(S_3\), respectively. Consider also the three irreducible characters of \(S_3\), so the trivial character 1, the character \(\textit{sgn}\) computing the sign of a permutation, and the only two-dimensional irreducible character \(\mu :=\frac{1}{2}\left( \chi _{reg}-sgn-1\right) \), where \(\chi _{reg}\) is the character of the regular representation of \(S_3\).

Let us fix a basis \(e_1, e_2\) of \({\mathbb {Z}}_3^2\) and consider the dual characters \(\epsilon _1\), \(\epsilon _2\) of \(e_1\) and \(e_2\), i.e., the characters defined by

$$\begin{aligned} \epsilon _i(ae_1+be_2):=\zeta _3^{a\delta _{1i}+b\delta _{2i}}, \qquad \zeta _3:=e^{\frac{2\pi i }{3}}, \end{aligned}$$

where \(\delta _{ij}\) is the Kronecker delta.

Given a representation \(\rho \) on a vector space V and an isotypic component W of V of character \(\chi \), we can sometimes write \(W_\chi \) instead of W for specifying its character.

When we write \(\root n \of {\lambda }\) we mean the first root of the complex number \(\lambda \), i.e., if \(\lambda =\vert \lambda \vert \cdot e^{i\theta }\), then \(\root n \of {\lambda }=\root n \of {\vert \lambda \vert }\cdot e^{i\frac{\theta }{n}}\).

Finally, denote by \([j]\in \{0,1\}\) the class of the integer number j modulo 2.

2 The surfaces

In this section, we construct a series of surfaces S, as quotients of a product of two curves \(C_1\) and \(C_2\), modulo a suitable diagonal action of the group \(S_3\times {\mathbb {Z}}_3^2\). For any surface S, we determine the canonical map \(\Phi _{K_S}\) and compute its degree.

We consider the projective space \(\mathbb {P}^3\) with homogeneous coordinates \(x_0, \ldots , x_3\) and the weighted projective space \(\mathbb {P}^3(1,1,1,2)\) with homogeneous coordinates \(y_0, \ldots , y_3\). Here \(y_3\) is the variable of weight 2. We take the curves \(C_1\subseteq \mathbb {P}^3\) and \(C_2\subseteq \mathbb {P}^3(1,1,1,2)\) as follows:

$$\begin{aligned} C_1 :{\left\{ \begin{array}{ll} x_2^3=x_0^3-x_1^3 \\ x_3^3=x_0^3+x_1^3 \end{array}\right. }, \qquad C_2 :{\left\{ \begin{array}{ll} y_2^3=y_0^3+y_1^3 \\ y_3^3=y_0^6+y_1^6-2\lambda y_0^3y_1^3 \end{array}\right. }, \lambda \ne -1,1 \end{aligned}$$

Both curves are smooth; in fact, this is the reason why we assume \(\lambda \ne -1,1\) in the definition of \(C_2\).

On the first curve \(C_1\), we consider the action of \(S_3\times {\mathbb {Z}}_3^2\) given by

$$\begin{aligned}{} & {} \phi _1:S_3\times {\mathbb {Z}}_3^2 \rightarrow {\text {Aut}}(C_1), \quad \left( \sigma ^i\tau ^j, (a,b)\right) \\{} & {} \quad \mapsto [(x_0:x_1:x_2: x_3) \mapsto (\zeta _3^ix_{[j]}:x_{[j+1]}: (-1)^j\zeta _3^{2a+2i} x_2: \zeta _3^{2b+2i} x_3)]. \end{aligned}$$

We leave to the reader to checking that this defines an action.

Note that the automorphisms \(\phi _1(\sigma ^i\tau ^j,(a,b))\) are precisely the deck transformations of the cover

$$\begin{aligned} \pi _1 :C_1 {\mathop {\longrightarrow }\limits ^{9: 1}} {\mathbb {P}}^1 {\mathop {\longrightarrow }\limits ^{6: 1}} {\mathbb {P}}^1, \qquad (x_0:x_1:x_2:x_3) \mapsto (x_0:x_1)\mapsto \left( x_0^3x_1^3: (x_0^6+x_1^6)/2\right) . \end{aligned}$$

In particular, \(C_1/\left( S_3\times {\mathbb {Z}}_3^2\right) \simeq {\mathbb {P}}^1\) and \(\pi _1\) is the quotient map. The cover is branched along \(p_1:=(1:1)\), \(p_2:=(0:1)\) and \(p_3:=(-1:1)\), corresponding to the three orbits of the points with non-trivial stabilizer, of respective length 9, 18 and 9. A representative of each orbit and a generator of the stabilizer is given by:

figure a

On the second curve \(C_2\), the action \(\phi _2\) is defined as

$$\begin{aligned}{} & {} \phi _2 :S_3\times {\mathbb {Z}}_3^2 \rightarrow {\text {Aut}}(C_2), \quad \left( \sigma ^i\tau ^j, (a,b)\right) \\{} & {} \quad \mapsto [(y_0:y_1:y_2: y_3) \mapsto (\zeta _3^iy_{[j]}:y_{[j+1]}: \zeta _3^{a+2b+2i} y_2: \zeta _3^{2a+2b+i} y_3)]. \end{aligned}$$

As in the previous case, we leave to the reader to checking that this defines a group action and note that the automorphisms \(\phi _2(\sigma ^i\tau ^j,(a,b))\) are precisely the deck transformations of the cover

$$\begin{aligned} \pi _2:C_2 {\mathop {\longrightarrow }\limits ^{9:1}}{\mathbb {P}}^1 {\mathop {\longrightarrow }\limits ^{6:1}} {\mathbb {P}}^1, \qquad (y_0:y_1:y_2:y_3) \mapsto (y_0:y_1)\mapsto \left( y_0^3y_1^3: (y_0^6+y_1^6)/2\right) . \end{aligned}$$

Hence, \(C_2/\left( S_3\times {\mathbb {Z}}_3^2\right) \simeq {\mathbb {P}}^1\) and \(\pi _2\) is the quotient map. The cover is branched along \(q_1:=(1:1)\), \(q_2:=(0:1)\), \(q_3:=(1:\lambda )\) and \(q_4:=(-1:1)\), corresponding to the four orbits of the points with non-trivial stabilizer, of respective length 27, 18, 18 and 9. Note that the points \(q_j\) are pairwise distinct under the assumption \(\lambda \ne -1,1\).

A representative of each orbit and a generator of the stabilizer is given by:

figure b

We compute the action of \(S_3\times \mathbb {Z}_3^2\) on \(H^0(C_i,\Omega _{C_i}^1)\).

By standard adjunction theory, \(H^0(C_1,\Omega _{C_1}^1)\) is isomorphic to \(H^0(C_1,{\mathcal {O}}_{C_1}(2))\), isomorphism mapping a monomial \(x_0^{2-\alpha -\beta -\gamma }x_1^\alpha x_2^\beta x_3^\gamma \) to the 1-form \(\omega _{\alpha \beta \gamma }\) that in affine coordinates is

$$\begin{aligned} \omega _{\alpha \beta \gamma }:=u^\alpha v^{\beta -2} t^{\gamma -2}du, \qquad \hbox {where} \qquad u:=\frac{x_1}{x_0} \quad v:=\frac{x_2}{x_0} \quad \hbox {and} \qquad t:=\frac{x_3}{x_0}. \end{aligned}$$

The character of the canonical representation of \(C_1\), the action of \(S_3\times {\mathbb {Z}}_3^2\) on \(H^0(C_1,\Omega _{C_1}^1)\), can be computed by the standard Chevalley–Weil formula and is amount to

$$\begin{aligned} \chi _{can}^1=\epsilon _1^2\cdot \epsilon _2^2+sgn\cdot \epsilon _1\cdot \epsilon _2 +sgn\cdot \epsilon _2+sgn\cdot \epsilon _1+\mu \cdot \epsilon _1\cdot \epsilon _2+\mu \cdot \epsilon _1^2\cdot \epsilon _2+\mu \cdot \epsilon _1\cdot \epsilon _2^2. \end{aligned}$$

We give an explicit decomposition into irreducible subspaces. Using the expression in affine coordinates we obtain

$$\begin{aligned} \begin{aligned}&(\sigma ^i\tau ^j,(a,b))\cdot \omega _{\alpha \beta \gamma } = \phi _1(\left( \sigma ^i\tau ^j,(a,b)\right) ^{-1})^{*}(\omega _{\alpha \beta \gamma }) \\ {}&\quad =(-1)^{j(\beta -1)}\zeta _3^{a(\beta -2)+b(\gamma -2)+\left( \alpha -(2\alpha +\beta +\gamma -2) [j]+2\beta +2\gamma -7\right) i}\\&\quad \omega _{(\alpha -(2\alpha +\beta +\gamma -2)[j])\beta \gamma }. \end{aligned} \end{aligned}$$

A tedious but straightforward computation gives the following decomposition:

$$\begin{aligned} \begin{aligned} H^0(C_1,\Omega _{C_1}^1)=&\langle \omega _{011}\rangle _{\epsilon _1^2\cdot \epsilon _2^2} \oplus \langle \omega _{100}\rangle _{sgn\cdot \epsilon _1\cdot \epsilon _2} \oplus \langle \omega _{020}\rangle _{sgn\cdot \epsilon _2} \oplus \langle \omega _{002}\rangle _{sgn\cdot \epsilon _1} \oplus \\&\langle \omega _{000},\omega _{200}\rangle _{\mu \cdot \epsilon _1\cdot \epsilon _2}\oplus \langle \omega _{010},\omega _{110}\rangle _{\mu \cdot \epsilon _1^2\cdot \epsilon _2}\oplus \langle \omega _{001},\omega _{101}\rangle _{\mu \cdot \epsilon _1\cdot \epsilon _2^2}. \end{aligned} \end{aligned}$$

Similarly, adjunction theory gives an isomorphism among \(H^0(C_2,\Omega _{C_2}^1)\) and \(H^0(C_2,{\mathcal {O}}_{C_2}(4))\) mapping a monomial \(y_0^{4-\alpha -\beta -2\gamma }y_1^\alpha y_2^\beta y_3^\gamma \) to the 1-form \(\omega '_{\alpha \beta \gamma }\) that in affine coordinates is

$$\begin{aligned} \omega '_{\alpha \beta \gamma }:=(u')^{\alpha }(v')^{\beta -2} (t')^{\gamma -2}du', \qquad \hbox {where} \qquad u':=\frac{y_1}{y_0} \quad v':=\frac{y_2}{y_0} \quad \hbox {and} \qquad t':=\frac{y_3}{y^2_0}. \end{aligned}$$

We obtain a basis of the 19-dimensional space \(H^0(C_2, {\mathcal {O}}_{C_2}(4))\) by taking the 22 monomials of degree 4 in the variables \(y_j\) and removing \(y_0y_2^3\), \(y_1y_2^3\) and \(y_2^4\) that can be expressed in terms of the other monomials using the cubic equation defining \(C_2\). Accordingly we get a basis of \(H^0(C_2,\Omega _{C_2}^1)\) by removing from that set \(\omega '_{\alpha \beta \gamma }\) the 1-form \(\omega '_{040}, \omega '_{030}\) and \(\omega '_{130}\). The canonical character of \(C_2\) is given by Chevalley–Weil as

$$\begin{aligned}{} & {} \chi _{can}^2=sgn \cdot \epsilon _1^2\cdot \epsilon _2+sgn\cdot \epsilon _1^2\cdot \epsilon _2^2+sgn\cdot \epsilon _1\cdot \epsilon _2+sgn\cdot \epsilon _1+sgn\cdot \epsilon _2^2+\mu \cdot \epsilon _1+\mu \cdot \epsilon _2\\{} & {} \quad +2\mu \cdot \epsilon _2^2+sgn\cdot \epsilon _1^2+\epsilon _1^2+\mu \cdot \epsilon _1^2+\mu \cdot \epsilon _1\cdot \epsilon _2, \end{aligned}$$

and the action on \(H^0(C_2,\Omega _{C_2}^1)\) computed in affine coordinates as above is

$$\begin{aligned} \begin{aligned} (\sigma ^i\tau ^j,(a,b))\cdot \omega '_{\alpha \beta \gamma }&= \phi _2(\left( \sigma ^i\tau ^j,(a,b)\right) ^{-1})^{*}(\omega '_{\alpha \beta \gamma }) \\ {}&=(-1)^{j}\zeta _3^{a(2\beta +\gamma )+b(\beta +\gamma -4)+\left( \alpha -(2\alpha +\beta +2\gamma -4)[j] +2\beta +\gamma +1\right) i}\\&\qquad \times \omega '_{(\alpha -(2\alpha +\beta +2\gamma -4)[j])\beta \gamma }. \end{aligned} \end{aligned}$$

Another tedious computation gives the decomposition

$$\begin{aligned} \begin{aligned} H^0(C_2,\Omega _{C_2}^1)=&\langle \omega '_{002}\rangle _{sgn\cdot \epsilon _1^2\cdot \epsilon _2} \oplus \langle \omega '_{021}\rangle _{sgn\cdot \epsilon _1^2\cdot \epsilon _2^2}\oplus \langle \omega '_{120}\rangle _{sgn\cdot \epsilon _1\cdot \epsilon _2} \\&\oplus \langle \omega '_{101}\rangle _{sgn\cdot \epsilon _1}\oplus \langle \omega '_{200}\rangle _{sgn\cdot \epsilon _2^2}\oplus \langle \omega '_{001},\omega '_{201}\rangle _{\mu \cdot \epsilon _1} \oplus \langle \omega '_{011},\omega '_{111}\rangle _{\mu \cdot \epsilon _2} \\ {}&\oplus \left( \langle \omega '_{000},\omega '_{400}\rangle \oplus \langle \omega '_{100},\omega '_{300}\rangle \right) _{\mu \cdot \epsilon _2^2}\oplus \langle \omega '_{010}+\omega '_{310}\rangle _{sgn\cdot \epsilon _1^2}\oplus \langle \omega '_{010}-\omega '_{310}\rangle _{\epsilon _1^2} \\ {}&\oplus \langle \omega '_{110},\omega '_{210}\rangle _{\mu \cdot \epsilon _1^2} \oplus \langle \omega '_{220},\omega '_{020}\rangle _{\mu \cdot \epsilon _1\cdot \epsilon _2}. \end{aligned} \end{aligned}$$

We consider unmixed quotients \(S:=(C_1\times C_2)/\left( S_3\times {\mathbb {Z}}_3^2\right) \) modulo a diagonal action \(\phi _1\times \left( \phi _2\circ \Psi \right) \), where \(\Psi \) is one of the automorphisms of \(S_3\times \mathbb {Z}_3^2\).

Firstly we study the singularities of S. We observe that \(C_1\) and \(C_2\) have stabilizers of order 6, 3 and 6 and 2, 3, 3 and 6, respectively. Hence, 18 points of \(C_1\) and 36 points of \(C_2\) have stabilizer of even order. However, \(S_3\times \mathbb {Z}_3^2\) has only three elements of order 2 and they are in the same conjugacy class. This means that each of these three elements fix exactly \(6\cdot 12=72\) points of \(C_1\times C_2\). Thus, S can never be smooth, and if it admits only nodes, then they are in total \(3\cdot 72 /27=8\).

Now let us consider the following automorphisms of \(S_3\times \mathbb {Z}_3^2\)

$$\begin{aligned} \begin{aligned} \Psi _1&=Id,&\Psi _2&= \left( {\left\{ \begin{array}{ll} \sigma \mapsto \sigma \\ \tau \mapsto \tau \sigma \\ \end{array}\right. }, \begin{pmatrix} 0&{}1 \\ 2 &{} 0\end{pmatrix} \right) ,&\\ \Psi _3&= \left( {\left\{ \begin{array}{ll} \sigma \mapsto \sigma ^2 \\ \tau \mapsto \tau \\ \end{array}\right. }, \begin{pmatrix} 0&{}2 \\ 1 &{} 0\end{pmatrix} \right) ,&\Psi _4&= \left( {\left\{ \begin{array}{ll} \sigma \mapsto \sigma ^2 \\ \tau \mapsto \tau \\ \end{array}\right. }, \begin{pmatrix} 0&{}2 \\ 2 &{} 0\end{pmatrix} \right) .&\end{aligned} \end{aligned}$$
(1)

A direct computation shows us that for these four choices of \(\Psi \) the surface S has exactly 8 nodes and no other singularities.

Remark 2.1

The first example has been found by using the database [10]. Later on, we have run a systematic search over all automorphisms of \(S_3\times \mathbb {Z}_3^2\), proving that the obtained surfaces having only nodes are isomorphic to the four surfaces presented in this note.

The vector space \(H^0(K_{S})\) is isomorphic to the invariant subspace \(\big (H^0(\Omega _{C_1}^1) \otimes H^0(\Omega _{C_2}^1) \big )^{S_3\times {\mathbb {Z}}_3^2}\), where the action on the tensor product is diagonal, i.e., \(\left( \sigma ^i\tau ^j,(a,b)\right) \in S_3\times {\mathbb {Z}}_3^2\) acts via

$$\begin{aligned} \phi _1(\left( \sigma ^i\tau ^j,(a,b)\right) ^{-1})^{*} \otimes \phi _2(\Psi (\left( \sigma ^i\tau ^j,(a,b)\right) ^{-1}))^{*}. \end{aligned}$$
(2)

For each character, \(\eta \) of \(S_3\times \mathbb {Z}_3^2\) defines its twist by \(\Psi \) as

$$\begin{aligned} \eta _\Psi :=\eta \circ \Psi ^{-1}. \end{aligned}$$

Pulling back \(H^0(K_S)\) to \(C_1\times C_2\), we obtain

Lemma 2.2

A basis of \(H^0(K_S)\) is given by the \(\left( S_3\times {\mathbb {Z}}_3^2\right) \)-invariant 2 forms of \(H^0(\Omega _{C_1}^1) \otimes H^0(\Omega _{C_2}^1) \) with respect to the action (2). Hence,

$$\begin{aligned} \big (H^0(\Omega _{C_1}^1) \otimes H^0(\Omega _{C_2}^1) \big )^{S_3\times {\mathbb {Z}}_3^2}=\bigoplus _{\eta \ne 0} \big (H^0(\Omega _{C_1}^1)_{\eta }\otimes H^0(\Omega _{C_2}^1)_{\overline{\eta _\Psi }}\big )^{S_3\times {\mathbb {Z}}_3^2}, \end{aligned}$$

where \(H^0(\Omega _{C_i}^1)_{\eta }\) is the isotypic component of \(H^0(\Omega _{C_i}^1)\) of character \(\eta \). Moreover,

$$\begin{aligned} p_g=\langle \chi _{can}^1\cdot \chi _{can}^2,1\rangle =\sum _{\eta \ne 0} \langle \chi _{can}^1,\eta \rangle \cdot \langle \chi _{can}^2, \overline{\eta _\Psi }\rangle . \end{aligned}$$

Denote by \(\omega _{jklmrs}:=\omega _{jkl}\otimes \omega '_{mrs}\). We can now state and prove our main result:

Theorem 2.3

For all \(\Psi \in {\text {Aut}}(S_3\times {\mathbb {Z}}_3^2)\) in (1), the diagonal action \(\phi _1 \times (\phi _2 \circ \Psi )\) of \(S_3\times {\mathbb {Z}}_3^2\) on the product of the two curves \(C_1\) and \(C_2\) is not free. The quotient is a canonical model of a regular surface S of general type with \(K_S^2=24\), \(p_g=3\) and with 8 rational double points as singularities of type \(\frac{1}{2}(1,1)\). A basis of \(H^0(K_S)\), the canonical map \(\Phi _{K_S}\) in projective coordinates and its degree are stated in the table:

figure c

Proof

We have already mentioned that for all \(\Psi \) in (1) the action is not free and the quotient S has 8 singularities of type \(\frac{1}{2}(1,1)\) and no other singularities. The genus of the two curves is \(g(C_i)\ge 2\); hence, \(C_1\times C_2\) has ample canonical divisor, and so, S has ample canonical divisor too. It follows that S is a canonical model.

The self-intersection of the canonical divisor of each S is amount to

$$\begin{aligned} K_S^2=\frac{8(g(C_1)-1)(g(C_2)-1)}{\vert S_3\times {\mathbb {Z}}_3^2\vert }=24. \end{aligned}$$

They are regular surfaces, because they do not possess any nonzero holomorphic one forms, since \(C_i/\left( S_3\times {\mathbb {Z}}_3^2\right) \) is biholomorphic to \({\mathbb {P}}^1\). The geometric genus of each S is therefore equal to (compare [4])

$$\begin{aligned} p_g= \chi ({\mathcal {O}}_{S})- 1 = \frac{(g(C_1)-1)(g(C_2)-1)}{\vert S_3\times {\mathbb {Z}}_3^2\vert }+\frac{1}{12}\left( 8\cdot \frac{3}{2}\right) -1=3. \end{aligned}$$

Using Lemma 2.2, we have computed a basis of \(H^0(K_S)\). In fact, since we have proved that \(p_g=3\) it is enough to verify that the given elements of the table are invariant for the corresponding action. Applying the explicit isomorphisms from \(H^0(C_1,\Omega _{C_1}^1)\) to \(H^0(C_1,{\mathcal {O}}_{C_1}(2))\) and from \(H^0(C_2,\Omega _{C_2}^1)\) to \(H^0(C_2,{\mathcal {O}}_{C_2}(4))\), we obtain the product of quadrics and quartics defining the canonical map in the table.

It remains to determine the degree of \(\Phi _{K_S}\) for each surface S. Instead to work on S, it is convenient to work on \(C_1\times C_2\), which is smooth:

Note that the map \(\Phi _{K_S}\circ \lambda _{12}\) is induced by the sublinear system \(\vert T \vert \) of \(\vert K_{C_1\times C_2}\vert \) generated by the three invariant 2 forms defining \(\Phi _{K_S}\). In particular, the self-intersection of T is amount to

$$\begin{aligned} T^2=\left( \lambda _{12}^* K_S\right) ^2=\vert S_3\times {\mathbb {Z}}_3^2\vert \cdot K_S^2=54\cdot 24. \end{aligned}$$

We resolve the indeterminacy of \(\Phi _T=\Phi _{K_S}\circ \lambda _{12}\) by a sequence of blowups, as explained in the textbook [7, Theorem II.7]:

Here the morphism \(\Phi _{\widehat{M}}\) is induced by the base point-free linear system \(\vert \widehat{M} \vert \) obtained as follows:

We blow up the base points of \(\vert T\vert \), take the pullback of the mobile part \(\vert M \vert \) of \(\vert T\vert \) and remove the fixed part of this new linear system. We repeat the procedure, until we obtain a base point-free linear system \(\vert \widehat{M}\vert \).

The self-intersection \(\widehat{M}^2\) is positive if and only if \(\Phi _{\widehat{M}}\) is not composed with a pencil. In this case, \(\Phi _{\widehat{M}}\) is onto and it holds:

$$\begin{aligned} \deg (\Phi _{K_S})=\frac{1}{\vert S_3\times \mathbb {Z}_3^2 \vert }\deg (\Phi _{\widehat{M}})=\frac{1}{54}\widehat{M}^2. \end{aligned}$$

For the computation of the resolution, it is convenient to write the divisors of the product of quadrics and quartics defining \(\Phi _{K_S}\) (and hence \(\Phi _T\) ) as linear combinations of the curves \(F_j:=\lbrace x_j=0\rbrace \) and \(G_k:=\lbrace y_k=0\rbrace \) on \(C_1\times C_2\). We point out that these curves are reduced and intersect pairwise transversally thanks to the assumption \(\lambda \ne -1,1\). In particular, \((F_j,F_k)=(G_j,G_k)=0\) and \((F_j, G_k)=81\), for \(k\ne 3\), while \((F_j, G_3)=162\).

Consider the first surface in the table. Here, the divisors of the three products of quadrics and quartics spanning the subsystem \(\vert T\vert \) are:

$$\begin{aligned} F_0+F_1+ 2G_2+G_3, \qquad 2F_2+2G_0+2G_1 \qquad \hbox {and} \qquad 2F_3+4G_2. \end{aligned}$$

Here \(\vert T\vert \) has not fixed part and it has precisely 81 (non-reduced) base points \(F_2\cap G_2\). We can perform the computation of the difference \(T^2- \widehat{M}^2\) by applying Lemma 2.4 (for a proof see [11, Lemma 2.3]) recursively for each base point of \(\vert T \vert \):

Lemma 2.4

Let \(\vert M \vert \) be a two-dimensional linear system on a surface S spanned by \(D_1\), \(D_2\) and \(D_3\). Assume that \(\vert M \vert \) has only isolated base points, smooth for S, and that in a neighborhood of a base point p we can write the divisors \(D_i\) as

$$\begin{aligned} D_1=aH, \quad D_2=bK \quad \hbox {and} \quad D_3= cH+d K. \end{aligned}$$

Here H and K are reduced, smooth and intersect transversally at p and a, b, c, d are nonnegative integers, \(b\le a\). Assume that

  • \(d\ge b\) or

  • \(b\ne 0\) and \(c+md\ge a\), where \(a=mb+q\) with \(0\le q<b\).

Then after blowing up at most (ab)-times, we obtain a new linear system \(\vert \widehat{M} \vert \) such that no infinitely near point of p is a base point of \(\vert \widehat{M} \vert \). Moreover, \(\widehat{M}^2 =M^2-ab\).

In a neighborhood of each of these base points, the three divisors are, respectively,

$$\begin{aligned} 2G_2, \qquad 2F_2 \qquad \hbox {and} \qquad 4G_2. \end{aligned}$$

Since \(F_2\) and \(G_2\) are transversal, we are in the situation of the Lemma 2.4 with \(H=G_2\) and \(K=F_2\), \(a=b=2\) and \(c=4\), \(d=0\). So \(b\ne 0\) and \(c+md\ge a\) and Lemma 2.4 applies. The correction term is \(ab=4\) for each of the 81 base points. Thus,

$$\begin{aligned} T^2- \widehat{M}^2=4\cdot 81. \end{aligned}$$

The degree of the canonical map is therefore given by

$$\begin{aligned} \deg (\Phi _{K_S})=\frac{1}{54}\widehat{M}^2=\frac{1}{54}\left( T^2 - (T^2-\widehat{M}^2)\right) =\frac{1}{54}\left( 54 \cdot 24- 4\cdot 81\right) =18. \end{aligned}$$

Now we take in exam the second surface in our table. Here the subsystem \(\vert T\vert \) is spanned by:

$$\begin{aligned} D_1:= 2F_2+G_0+G_1+G_3, \quad D_2:=2F_3+2G_0+2G_1 \quad \hbox {and} \quad D_3:= F_2+2G_2+\Delta , \end{aligned}$$

where \(\Delta =(\zeta _3x_0y_0^2-x_1y_1^2)\). The (set-theoretical) base locus is

$$\begin{aligned} F_2\cap G_0, F_2\cap G_1, \quad \Delta \cap G_0, \Delta \cap G_1, \quad \hbox {and} \quad \Delta \cap F_3\cap G_3. \end{aligned}$$

We remark that the other pieces of the base locus are empty. In fact, those points would belong to some \(F_i\cap F_j\) or \(G_i\cap G_j\) and we have already mentioned that they are pairwise disjoint.

We determine the correction term to the self-intersection number for each of these base points of \(\vert T\vert \).

We consider first the 81 points \(F_2\cap G_i\), for \(i=0,1\). Here \(F_2\) and \(G_i\) intersect transversally at each of them. Around one of these points, the divisors \(D_k\) are given by \(G_i+2F_2\), \(2G_i\) and \(F_2\). We are in the situation of the Lemma 2.4 with \(H=G_i\) and \(K=F_2\), \(a=d=2\) and \(b=c=1\). Hence, \(d\ge b\) and Lemma 2.4 applies, which yields \(ab=2\) as correction term.

We consider now the 81 base points \(\Delta \cap G_i\). The local coordinates around one of these points are \(X:=x_j/x_i\) and \(Y:=y_i/y_j\), where \(j=0,1, j\ne i\). So the divisors \(D_k\) are, respectively, given by

$$\begin{aligned} \lbrace Y=0\rbrace , \qquad 2\lbrace Y=0 \rbrace \qquad \hbox {and} \qquad \lbrace \zeta _3^{1+i}Y^2-X=0 \rbrace . \end{aligned}$$

Thus, \(D_1\) and \(D_3\) intersect transversally in (0, 0) and we fall down once more in the situation of the Lemma 2.4. Here \(H=D_3\) and \(K=D_1\), \(a=b=1\), \(c=0\) and \(d=2\). Since \(d\ge b\), then Lemma 2.4 is fulfilled and the correction term is amount to \(ab=1\).

We consider finally the points \(\Delta \cap F_3\cap G_3\). These points satisfy the equations

$$\begin{aligned} {\left\{ \begin{array}{ll} y_3^3 =y_0^6+y_1^6-2\lambda y_0^3y_1^3 &{}=0 \\ x_3^2 =x_0^3+x_1^3 &{} =0 \\ \zeta _3x_0y_0^2-x_1y_1^2 &{} =0 \end{array}\right. }. \end{aligned}$$
(3)

The last two equations imply that \(x_1^3=-x_0^3\) and

$$\begin{aligned} x_0^3y_0^6 =(\zeta _3x_0y_0^2)^3=(x_1y_1^2)^3 =x_1^3y_1^6=-x_0^3y_1^6. \end{aligned}$$

Thus, \(y_0^6+y_1^6=0\), and comparing it with the first equation of  3, we get \(\lambda y_0^3y_1^3=0\). Therefore, \(\Delta \cap F_3\cap G_3\) is non-empty only if \(\lambda =0\).

Let us suppose \(\lambda \ne 0\). Then

$$\begin{aligned} T^2-\widehat{M}^2=2\cdot 2 \cdot 81+2\cdot 81=6\cdot 81, \end{aligned}$$

and the degree of the canonical map is amount to

$$\begin{aligned} \deg (\Phi _{K_S})=\frac{1}{54}\left( T^2 - (T^2-\widehat{M}^2)\right) =\frac{1}{54}\left( 54\cdot 24- 6\cdot 81\right) =15. \end{aligned}$$

It remains to consider the case when \(\lambda =0\). The base points \(\Delta \cap F_3\cap G_3\) are the following 54 ones:

$$\begin{aligned} t_k:= \left( \left( 1:-\zeta _3^{k_1}\root 3 \of {2}{\zeta }_3^{k_2}:0\right) ,\left( 1:e^{\frac{\pi i }{6}}\zeta _6^{k_3}:\root 6 \of {2}e^{\frac{\pi i}{12}\left( 1-2[k_3]\right) }\zeta _3^{k_4}:0\right) \right) ,\\ {}{} & {} \qquad k_1+k_3\equiv 2 \mod 3, \end{aligned}$$

where \(k_i=0,1,2\), for \(i\ne 3\), and \(k_3=0, \dots , 5\). Fix coordinates \(X:=x_1/x_0+\zeta _3^2\) and \(Y:=y_1/y_0-e^{\frac{\pi i }{6}}\) around one of these points, for example that one for \(k=(2,0,0,0)\). The divisors \(D_k\) are locally given by

$$\begin{aligned} \lbrace Y=0 \rbrace , \qquad 2\lbrace X=0 \rbrace \qquad \hbox {and} \qquad \lbrace Y(2e^{\frac{\pi i 5}{6}}+Y-2e^{\frac{\pi i 5}{6}}X-XY)=0\rbrace =\lbrace Y=0\rbrace . \end{aligned}$$

In this case, \(H=\{X=0\}\) and \(K=\{Y=0\}\) and \(a=2\) and \(b=d=1\), \(c=0\). The correction term is \(ab=2\).

Hence,

$$\begin{aligned} T^2-\widehat{M}^2=2\cdot 2 \cdot 81+2\cdot 81+2 \cdot 54=6\cdot 81+2\cdot 54. \end{aligned}$$

The degree of the canonical map is therefore given by

$$\begin{aligned} \deg (\Phi _{K_S})=\frac{1}{54}\left( T^2 - (T^2-\widehat{M}^2)\right) =\frac{1}{54}\left( 54\cdot 24- 6\cdot 81-2\cdot 54\right) =13. \end{aligned}$$

We leave to the reader to verifying with the same approach that the degree of the canonical map of the remaining two surfaces is amount to that ones stated in the table. \(\square \)