Introduction

Maximisation of net present value (NPV) and/or reduction of the net present cost (NPC) in the mining industry has traditionally targeted the optimisation of the orebody knowledge, economics (commodity price, operating and fixed costs, discount rate, etc.), technical capacities (slope requirements, metallurgical recoveries, etc.), and operational capacities (mine, processing plant, stockpiling, etc.).

Development of frameworks to allow simultaneous optimisation of a mining operation began in the mid-1990s. Newmont Mining Corporation promoted the development of an in-house optimizer based on a mixed integer programming formulation to maximize discounted cash flows by simultaneously optimizing material movement from a set of open pit and underground mines to multiple destinations (Hoerger et al. 1999). BHP followed by developing Blasor mine planning software (Stone et al. 2007) to maximise NPV. In addition, Whittle (2010) describes a global optimizer, designed to incorporate mining, processing, and blending components into the optimization process, and Saliba and Dimitrakopoulos (2019) developed a stochastic framework that simultaneously optimizes mining, destination, and processing decisions for a multi-pit, multi-processor gold mining complex. While these methods employ sophisticated techniques and an integrated approach, they all neglect or minimally consider the water management component.

Development of iron ore deposits below the water table is increasing in the Pilbara region of Western Australia as high-quality iron ore resources above the water table are depleted. Dewatering of deposits below the water table can generate large volumes of water that exceeds the needs of the mining operation. Historically, management of surplus water produced by dewatering in the Pilbara has been managed primarily through discharge to nearby water courses, subject to quality. However, continuous discharge has been increasingly seen by environmental regulators as inappropriate for ephemeral environments like the Pilbara, irrespective of water quality. Consequently, there is an increasing expectation that mining companies will demonstrate stewardship of water resources to secure environmental approvals and maintain the social licence to operate (DWER 2020).

Lévy et al. (2006), Gunson et al. (2012), and Miller et al. (2021) discuss the importance of the threats and opportunities linked to water management in the mining industry and how newly developed water treatment technologies and assessment tools can be incorporated to enhance the recovery and reuse of water on site. This can reduce the risks associated with securing long-term water supply and further improve production, environment, and safety.

All mining companies in the Pilbara region of Western Australia are currently adopting management strategies to maximise the inherent value of water resources for positive economic, social, and environmental outcomes. For example, Rio Tinto Iron Ore developed an integrated surplus water management solution to enable the below water table expansion of the Marandoo iron ore mine, where surplus water is used for agricultural irrigation (Field and Harold 2013); Fortescue Metal Group (FMG) manages their surplus water volumes via re-injection into the aquifers in their Cloudbreak, Christmas Creek, and Solomon mines (FMG 2010, 2011, 2015); and BHP developed a regional water resource management plan for the central and eastern Pilbara regions to minimise potential impacts to receiving receptors (BHP 2015, 2016). In all of these instances, the optimisation of the various water users and minimisation of the impacts to the environmentally sensitive receptors were performed with individual and independent modelling that could potentially result in conflict; hence, the desire to resolve the issue and utilise Roy Hill Mine as a case study.

The Roy Hill Mine Case Study

The Roy Hill Mine (Roy Hill) is a world-class mining operation located on the eastern part of the Upper Fortescue Valley near the eastern perimeter of the Fortescue Marsh in Western Australia’s Pilbara region, between approximately 60 and 120 km north of Newman. Roy Hill represents the next generation of integrated iron ore mining, rail and port projects and currently delivers 60 million tonnes per annum (Mtpa) of iron ore to international markets, with recent approval to increase to 70 Mtpa.

Iron ore deposits at Roy Hill have been identified in the Nammuldi Member of the Marra Mamba Iron Formation (Lascelles 2000). The component of the Marra Mamba Iron Formation below the water table is in hydraulic connection to a regionally extensive aquifer system, where water quality plays a crucial role. Consequently, mining operations must manage substantial volumes of surplus water while also taking water quality into account.

Roy Hill maintains a Water Management Strategy (RHWMS) for dewatering, water supply, and surplus water disposal to ensure alignment with business, environmental, and stakeholder objectives. The primary goals of the RHWMS are to minimise the surplus water disposal and water supply and maximise the re-use of process water and dewatering volumes. For water balance planning purposes, the RHWMS defines seven primary ‘water balance’ tasks that describe the water inputs and outputs for the parts of the operation that comprise the overall mine site water balance:

  • Mining and Dewatering task (MDT): this includes ore moisture (pore water) and mine dewatering streams, i.e. fresh, brackish, saline, and hypersaline water streams. The mine dewatering infrastructure consists of 10 regions where the waters are collected and blended. Each region was identified based on similar water quality that was evaluated during borefield development, historic groundwater analysis, and preliminary model simulations.

  • Ore Processing Task (OPT): this is where the ore is processed and washed using water. The water inputs are wash, raw, and decant water, whilst the outputs are the tailings and product moisture.

  • Water Treatment Plant Task (WTPT): this is where some of the brackish dewatering volumes are treated to produce wash water for the OPT. The plant can also accept water volumes from the water supply task (described below), when not enough brackish water is available from the MDT. The by-product of the water treatment is the reject water.

  • Tailing Storage Facility Task (TSFT): this task groups together all of the tailing storage facilities available on site. This is fed with the tailings from the OPT; its main output is the decant water of the tailing storage facilities.

  • Dust Suppression Task (DST): in this task, water is sourced from mine dewatering or water supply for dust suppression.

  • Water Supply Task (WST): this represents the supplementary fresh water inputs for the system. This task consists of outputs that could feed the OPT, WTPT, and/or DST.

  • Surplus Water Disposal Task (SWDT): this is where surplus water is disposed of and has multiple components. In particular, Roy Hill has developed:

    • two managed aquifer recharge (MAR) projects for disposing and storing surplus groundwater close to the mining area, referred to as the South-west Injection Borefield (SWIB) and Stage 1 Borefield (S1B);

    • two conceptual remotely located MAR projects, referred to as remote MAR north (RMARN) and remote MAR south (RMARS), and;

    • as a contingency plan, Roy Hill is evaluating the potential construction and use of an evaporation pond (EP).

Tasks may comprise one or multiple components. For example, the mining and dewatering task comprises multiple pit regions and water quality streams. Various models have been developed to simulate the time-variant water balance for some of the tasks described above. These include:

  • Groundwater model (GWM): the Roy Hill mine is located in the vicinity of an evapo-concentrating basin (Fortescue Marsh) that has caused the underlying aquifer to be hypersaline (Skrzypek et al. 2013). Mine dewatering will affect the mobilisation of salinity and a groundwater model was fundamental to predict not only the dewatering requirements to meet the mine plan, but more importantly its salinity concentration for the “Mine and Dewatering Task”. The groundwater model was also used to assess the aquifer injection capacities and the groundwater supply sustainability. The model has been currently developed with the software FEFLOW v7.4 (Diersch 2014) and maintained by the company’s hydrogeology team.

  • Ore Processing model (OPM): this model determines the required water and the maximum salinity concentration to be used to process the ore (OPT) and depends on the mine plan. The current model has been developed with a Microsoft Excel spreadsheet and is currently owned and maintained by the company’s metallurgic team.

  • Tailing Storage Facility modelling (TSFM): This modelling was necessary to evaluate the most economical options for storage of the tailings (TSF task). The critical results of this modelling exercise are the calculations of the decant water available from the storage facilities and their salinity concentrations. This model was developed using Goldsim software (GoldSim Technology Group 2021) by an external consultant and maintained by the company’s metallurgic team.

The OPM and the TSFM models are coupled together, i.e. the results of the TSF (GoldSim) model are directly written in the Ore Processing spread-sheet model that, in turn, assesses whether it is possible to use the available decant water from the storage facilities, based on the modelled salinity concentration for each simulated month. The main objective of this modelling is to calculate the optimum decant rate to maximise the life of the TSF.

The water balance for all other tasks, except for the DST (which can be set with a pre-defined time series), cannot be easily determined for this case study. The calculations have been traditionally analysed by studying and modelling the abovementioned tasks individually and independently from each other (FMG 2011), especially for those projects where groundwater quality is not an issue (Field and Harold 2013). However, for this specific case study, where the water quality of the abstracted water volumes plays an important role in the water use, this type of approach would require the formulation of some assumptions for each task that might conflict with the results of the other modelling tasks. Conflicts identified are summarised below:

  • OPM could assume a specific water supply from dewatering that may not be available according to the GWM predictions.

  • The GWM would not be able to predict the TSF decant water volumes and qualities that are calculated with a more sophisticated model that accounts for beaching and consolidation of the tailings.

  • Not all available decant water could be re-used; this means that an individual use of the TSFM could conflict with the OPM and the GWM.

  • Water demands from the OPT cannot be handled with the GWM too, because they consider parameters such as ore density that are not accounted for in the groundwater model.

  • Re-injection water volumes and qualities would be impossible to calculate with the GWM without coupling it with the OPM.

  • The utilisation of the various injection borefields in the GWM also depends on the background natural salinity. Without the availability of custom-made packages for the GWM, which would require the development of functions that could intervene during the simulations via software source code modifications or call-back interactions, re-injection volume routing for the different borefields would be impossible to determine.

The purpose of this work was to develop a mathematical tool that could perform an integrated water management analysis, post-processing the results of all the water modelling activities (GWM, OPT, and TSFM) and calculate the optimal water balance rates for each task, maximise the water usage, and minimise the disposal and NPC.

The tool was developed with the coding language Python with the idea to make it licence-free and fully customisable in case of future development of the mine water infrastructures. Python offers the advantage of being totally open source and in constant evolution. This enables Python users to access the most up-to-date routines for solving complex mathematical problems.

The biggest advantage of a solution that employs independent software is the capability to run scenario simulations in a few seconds and keep the various expertise and sophistications of each individual model separated, without sacrificing the conceptual representation of the physical system. Injection and water supply solutions found with this tool are then tested with the GWM to verify if the aquifers can sustain the abstraction for supply and whether the injections comply with the environmental constraints (mounding limitations). This simple scheme, which required no more than one or two iterations with the GWM, avoided the development of convoluted and time-consuming GWM call-back functions, and provided a very practical way to assess the economic value of the water management.

In compliance with Roy Hill's confidentiality policies, it is important to note that it was not possible to divulge water management volume modelling results or provide more in-depth infrastructural and geographical details of the mine site. As a result, this work primarily focuses on showcasing the methodological approach to the problem and its successful application in the Roy Hill case. This approach aided the decision-making process for water infrastructure upgrades, which ultimately contributed to minimizing the NPC.

Mathematical Framework and Software Development

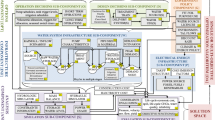
Figure 1 shows a simplified flow chart of the various tasks, modelling activities, and their connections. These are wrapped by the integrated water management tool described in this work. A more detailed and complete flow chart showing the connection between all of the water tasks modelled with the integrated water balance tool is shown in supplemental Fig. S-1.

Fig. 1
figure 1

Color-coded water balance tasks – Light blue: introducing water; Orange: using water; Dark Red: receiving water

Full size image

The software described in this work was built using a linear programming simplex optimisation algorithm (Dantzig 1963) to minimise an objective function. The software was coded with the language Python 3.6 (Van Rossum and Drake 2009) using the module “scipy.optimise.linprog” (Jones et al. 2001) to solve the linear programming problem.

The problem identified 43 independent decision variables represented in the flow chart of Figure S-1 and described in supplemental Table S-2. However, the following should be noted:

  • the optimisation problem was set up to allow the optional use of a second water treatment plant task (WTPT2), but the water supply task is not allowed to feed this task, i.e. only mine dewatering volumes can feed this task;

  • reject water from the water treatment plants can be disposed of in SWIB or EP only; and

  • the water supply was distinguished in two time-dependent sources. For all the dates before mid-2024, the water supply is sourced from S1B, whilst for the remainder simulation, the water supply source is unknown and generic. The purpose of the simulation was to demonstrate the probability that a water supply would be required after June 2024. This exercise was necessary as the S1B will not be available for water supply after June 2024. Therefore, the variables WSx and WSS1Bx are actually alternatives in the solution, i.e. the problem is solved for a generic WSx and the result is assigned to WSS1Bx if the date is before the end of June 2024.

The problem is further defined with the declaration of the inputs and constants (assumptions) described in supplemental Table S-3. The optimisation consists in minimising the following objective function:

$$F={C}_{WS}TWS+{C}_{WTPT}{WT}_{1}+{C}_{WTPT2}{WT}_{2} +{C}_{S1B}S1B+{C}_{SWIB}SWIB+{C}_{RMARN}RMARN+{C}_{RMARS}RMARS+{C}_{EP}EP$$

where:

  • \(TWS=WSP+WSWT+WSDS\)

  • \({WT}_{1}=WW\)

  • \({WT}_{2}=WW2+WW2S1B+WW2RMARS\)

  • \(S1B=MDFS1B+MDBS1B+NRPWS1B\)

  • \(SWIB=MDFSWIB+MDBSWIB+MDSSWIB+MDHSSWIB+NRPWSWIB+RWSWIB+RW2SWIB\)

  • \(RMARN=MDFRMARN+MDBRMARN+MDSRMARN+MDHSRMARN\)

  • \(RMARS=MDFRMARS+MDBRMARS+WW2RMARS\)

  • \(EP=MDFEP+MDBEP+MDSEP+MDHSEP+NRPWEP+RWEP+RW2EP\)

  • CWS, CWTPT, CWTPT2, CS1B, CSWIB, CRAMARN, CRAMARS and CEP are the cost/penalty coefficients defined in Table S-3 (supplemental file).

The cost/penalty coefficients should represent the operational costs (OPEX). Therefore, the algorithm will minimise the operational costs if a feasible solution can be found. This type of optimisation will not, however, prevent the utilisation of infrastructures with a very high capital cost but a very low operational cost, such as an evaporation pond. In this case and in order to force the system to avoid the utilisation of very expensive assets from the investment point of view (i.e. capital expenditure or CAPEX), the operational costs were intentionally manipulated in the preliminary phase of the optimisation. In other words, the cost/penalty coefficients were conveniently defined in a way to prioritise the cheapest existing infrastructures from the capital investment point of view and to prioritise their utilisation. It is only after this first pass optimisation that the cost analysis is recalculated with realistic cost coefficients to evaluate actual costs.

The minimisation of the objective function is constrained by equality and inequality constraints (Table 1 and 2) that were defined from the water balance, input assumptions, and physical limitations of each water task. In particular, the equality constraints ensure that the water balance of each task is maintained by requiring that the volumes of water entering and leaving the task are equal. On the other hand, the inequality constraints represent the physical limitations of the infrastructures, such as the maximum capacities of the injection borefields.

Table 1 Equality constraints
Full size table
Table 2 Inequality constraints
Full size table

The constraints are incorporated into the software using matrix and vector inputs. Two matrices are created to represent the right-hand and left-hand sides of the expressions displayed in Tables 1 and 2, respectively. In these matrices, each column corresponds to the coefficient applied to one of the 43 variables to be optimized (see supplemental Table S-2), and each row represents a constraint. Additionally, two vectors are generated to signify the values of the left- and right-hand sides of the expressions found in Tables 1 and 2. The matrix representation allows us to simplify the formulation of the problem in:

$$\underset{{\varvec{x}}\in {\mathbb{R}}}{{\text{min}}}F({\varvec{x}})$$

subject to:

$$\left\{\begin{array}{c}{\varvec{A}}{\varvec{x}}={\varvec{b}}\left(t\right)\\ {{\varvec{A}}}^{\boldsymbol{^{\prime}}}{\varvec{x}}\le {{\varvec{b}}}^{\boldsymbol{^{\prime}}}\left(t\right)\end{array}\right.$$

where: x is the vector defining the variables described in Table S-2, A is the coefficient matrix used to define the equality constraints, A’ is the coefficient matrix used to define the inequality constraints, b(t) is the time variant vector defining the known terms of the equality constraints, and b’(t) is the time variant vector defining the known terms of the inequality constraints. The matrices A and A' remain constant over time since they do not depend on time. In contrast, the vectors b and b' exhibit varying values because the software uses time-variant inputs, such as mine dewatering volumes. As a result, it is necessary to perform individual minimization of the objective function for each simulated time instance (the simulation is run in monthly increments).

These matrices and vectors with the objective function definition are then used to solve the linear programming problem for each simulated time period using the Python module “scipy.optimise.linprog” (Jones et al. 2001). The core of the algorithm lies in defining the objective function, input matrices, and vectors. Any modification to the hydraulic infrastructure would necessitate a change in the configuration.

Dewatering infrastructures at Roy Hill are aggregated in 10 different regions that were conveniently defined based on the pits’ geographical locations and their expected water quality from dewatering. For each region, the water volumes, calculated with the GWM for mine dewatering, were distinguished in four different “quality” streams defined based on the total dissolved solid (TDS) concentration predicted by the GWM:

  • Fresh water (TMDF): Conc. < 2,450 mg/L (TDS)

  • Brackish water (TMDB): 2,450 < Conc. < 5,000 mg/L (TDS)

  • Saline water (TMDS): 5,000 < Conc. < CHS mg/L (TDS)

  • Hypersaline water (TMDHS): Conc. > CHS mg/L (TDS)

where CHS is a threshold concentration between saline and hypersaline that is also optimised during the simulation. The software tests different CHS values ranging from 20,000 to 45,000 mg/L. The optimal CHS concentration was chosen by minimising the disposal (S1B, SWIB, RMARN, RMARS, and EP) and water supply (TWS) volumes. Increasing the threshold concentration reduces the discharges volumes. However, this iteration eventually stops once the optimal concentration is reached since higher concentrations would not provide any additional benefit. This optimisation is required for scenarios that include WTPT2 to provide the engineers with the input parameters for its construction (water balance and concentration).

NPC Calculations

Roy Hill was interested in developing a cost/benefit analysis to evaluate the construction of a second water treatment plant that was capable of processing dewatering abstraction with higher concentrations than the existing water treatment plant, which is only able to process TDS concentrations up to 5,000 mg/L. To allow a multiple scenario comparison, a full cost analysis was also implemented in the software. This comprised the calculation of the NPC, considering the following factors:

  • Evaluation of the OPEX as a sum of the variables (that depends on the actual water rates) and fixed costs (e.g. maintenance).

  • Evaluation of CAPEX of the new infrastructures to be used. The software provides the option to select either a lumped cost for each infrastructure or a cost proportional to the maximum rate predicted for each infrastructure.

  • Consideration of the consumer price index (CPI, 2.5% for this case study).

  • Inclusion of the discount rate (d) with a pre-tax discount rate of 21.47%–(WAAC(R)) for this case study.

The mathematical formulation of the NPC is as follows:

$$NPC=CAPEX+OPEX$$

where:

$$CAPEX=\sum_{i}^{n}\sum_{j}^{{m}_{i}}{C}_{j}^{CAPEX}{\left(\frac{1+CPI/12}{1+d/12}\right)}^{i}$$

with:

$${C}_{j}^{CAPEX}=\left\{\begin{array}{c}{C}_{j}^{Lump\_C} \,if \,{\delta }_{j}=1\\ {C}_{j}^{Rate\_C}\times {max(rate)}_{j}\, if\, {\delta }_{j}=0\end{array}\right.$$

and:

$$OPEX= \sum_{i=1}^{n}\sum_{j=1}^{{m}_{i}{\prime}}{C}_{ij}^{OPEX}{\left(\frac{1+CPI/12}{1+d/12}\right)}^{i}$$

with:

$${C}_{ij}^{OPEX}={{\rho }_{i}C}_{j}^{Fixed\_O}\times {days}_{i}+{C}_{j}^{Rate\_O}\times {rate}_{i}$$
$${\rho }_{i}=\left\{\begin{array}{c}1 \quad if\, {rate}_{i}>0\\ 0 \quad if\, {rate}_{i}=0\end{array}\right.$$

In the above: n is the total number of months of the simulation and i is the ith month; \({m}_{i}\) is the number of infrastructures built in the ith month and j is the jth infrastructure; CPI and d are expressed in decimal form and divided by 12, assuming that the input values are annual; \({C}_{j}^{Lump\_C}\) is the current lumped cost of construction of the jth infrastructure; \({C}_{j}^{Rate\_C}\) is the current cost of construction of the jth infrastructure per unit of discharge rate; max(rate)j is the maximum discharge rate predicted for the infrastructure over the entire period of simulation; \({\delta }_{j}\) is an input parameter to indicate whether the jth infrastructure was assigned with a lumped cost or a cost proportional to the maximum rate predicted for the infrastructure; \({m}_{i}{\prime}\) is the number of infrastructures operating in the ith month; \({C}_{j}^{Fixed\_O}\) is the current fixed daily operating cost of the jth infrastructure (\({C}_{j}^{Fixed\_O}\) is 0 when the infrastructure is not operating in the ith month, i.e. when the rate is 0); and \({C}_{j}^{Rate\_O}\) is the variable operating cost of the jth infrastructure per unit of discharge rate.

At the end of each optimised simulation, OPEX and CAPEX are calculated and used to estimate the NPC. This enables the user to assess the most cost-effective scenarios. For this calculation, realistic cost/penalty coefficients were used to recalculate the OPEX costs. Effective CAPEX and OPEX costs are not explicitly reported in this work due to confidentiality.

For this case study, the NPC calculations used the following assumptions:

  • The evaporation pond (EP) was assigned with a CAPEX cost proportional to the maximum rate predicted for the infrastructure, whilst a fixed cost was assigned for the other infrastructures.

  • No fixed daily costs were used for the OPEX calculation.

  • S1B, SWIB, S1WS, and WTPT have no CAPEX cost as the infrastructures already exist.

  • It was assumed that surplus water disposal in the borefields close to the mining area and the evaporation pond would occur by gravity with a very negligible cost. Therefore EP, S1B, and SWIB have no OPEX cost in this calculation.

  • A small OPEX cost due to energy consumption for the pumps was assigned to the S1B water supply (WSS1x). This was doubled for the unknown water supply source (WSx) after June 2024.

  • OPEX costs of the same order of magnitude of the WSx were assigned to the disposal volumes routed to the remote MARs (RMARS and RMARN). The cost in this case was a function of the distance from the mine.

  • The greatest and most important OPEX costs (an order of magnitude higher than the rest) were assigned to the water treatment plant for the high energy consumption (WT1 and WT2). WT2 was assigned the highest OPEX cost due to the higher TDS concentrations to process.

  • OPEX and CAPEX costs were estimated with the help of the Roy Hill engineers and the previous experience of the consultants engaged by Roy Hill.

It is essential to emphasize once more that the actual OPEX and CAPEX costs used for calculating the NPC were sourced from Roy Hill's engineering team and consultants who have experience with similar projects. Although confidentiality policies prevent the publication of these values, the data used is considered highly reliable for the following reasons:

  • The knowledge of the OPEX costs for existing infrastructures is derived directly from actual observations of operational costs over the last eight years of operations.

  • The CAPEX cost estimate for the second water treatment plant is based on the previous design and construction of the existing water treatment plant. Additionally, external consultants provided Roy Hill with detailed cost estimate reports that cannot be shared due to confidentiality reasons.

  • The CAPEX cost for the evaporation pond was evaluated based on three key factors: (i) historical meteorological data used to assess potential evaporation rates throughout the year, and the unit costs for (ii) lining and (iii) earthworks. While the last two factors were easy to estimate with very minimal uncertainties, the first factor is subject to a degree of uncertainty. However, no uncertainty analysis was conducted for this aspect, as the cost difference between the second water treatment plant and the evaporation pond was so great that any perturbation of those parameters would not have affected the outcome presented in this paper.

Calculation of the Maximum Saline Concentration for WTPT2

The software was further developed to minimise the input salinity for the WTPT2 in the scenarios that used it. Given that WTPT2 does not currently exist, Roy Hill had the requirement to evaluate the cost benefit to build this infrastructure. One of the key input parameters for design purposes was the maximum input salinity concentration, together with the water balance for this task.

Considering that the dewatering volumes are sourced from different regions of the mine with individual hydraulic infrastructures, the optimisation process evaluated the opportunity to modulate the flux from each active region in order to get the minimum concentration possible for the saline volumes required in WTPT2 for each simulated period, i.e. we implemented a “cherry-pick” method.

This cherry-pick optimisation uses a mathematical “cost” function assessment, where the cost, in this case, is a function of the concentration and the parameters that change are the fluxes from the regions to minimize the concentration of the blended water. Indeed, the current infrastructure at the mine site theoretically allows the possibility of modulating the flows from each region to source the water treatment plant. This was an important exercise that allowed the engineers to design a new plant that could treat the lowest possible concentration. The concentration of the saline water directed to WTPT2, can be defined as follows:

$${C}_{MDSWT2}(t)=\frac{\sum_{i=1}^{N}{w}_{i}(t){q}_{i}^{s}(t){C}_{i}(t)}{MDSWT2(t)}$$

where:

  • N is the number of regions (10 in this case study);

  • \({q}_{i}^{s}(t)\) is the discharge rate of saline water available from region i at time t;

  • \({C}_{i}(t)\) is the concentration of the saline water at time t available from region i;

  • \(MDSWT2(t)\) is the saline discharge rate required at WTPT2 at time t;

  • \({w}_{i}(t)\) is the regional weight to be optimised that will determine the contribution of each region in the composition of the discharge rate required at WTPT2 at time t.

Even this type of optimisation was solved with the simplex method (Dantzig 1963), given the linear nature of the problem, and consisted in the minimisation of \({C}_{MDSWT2}(t)\) with the following constraints:

$$\left\{\begin{array}{l}\sum_{i}^{N}{w}_{i}\left(t\right){q}_{i}^{s}\left(t\right)=MDSWT2\left(t\right)\\ \sum_{i=1}^{N}{w}_{i}(t)=1\end{array}\right.$$

Software Workflow

The entire simulation workflow is shown in Fig. 2 and summarised as follows:

  1. 1.

    Each scenario is run with preliminary cost/penalty coefficients with a tentative saline/hypersaline concentration threshold pre-assigned for each attempt.

  2. 2.

    1. is repeated with other threshold saline/hypersaline concentration thresholds (CHS).

  3. 3.

    The simulation that results with the lowest water supply and surplus water disposal corresponding to the lowest saline/hypersaline threshold concentration is selected.

  4. 4.

    The “cherry-pick” optimization method described above is run to calculate the minimum saline concentration routed to the second treatment plant.

  5. 5.

    In the end, the NPC is calculated with realistic cost/penalty coefficients.

Fig. 2
figure 2

Optimized Software Workflow: Light Blue – Optimization Phase; Red – Objective Achievement Control Check; Purple – Water Treatment Input Concentration Optimization Phase; Yellow – NPC Calculation Phase

Full size image

Model Predictive Scenarios and Results

Adopting a traditional water balance approach that ignored the other water tasks and the water quality component by using the following inequality equation:

$$TMD-(FRESH+WASH+DS)\le S1B+SWIB+ RMARN+RMARS$$

did not identify any issue, i.e. the existing MARs were apparently sufficient to manage the surplus water volumes. This, however, contrasted with the observations of the site staff who were having issues with disposal of surplus water volumes in MARs such as at S1B where only brackish water could be injected. The new water balance tool correctly identified issues with the surplus water management.

The risks were flagged to the decision makers together with the proposal to investigate optimisation of two infrastructural configuration upgrades. Table 3 summarises the optimised scenarios: Scenario 2 uses WTPT2 to process saline water to get wash water, whilst Scenario 1 does not. The commissioning date of WTPT2 was estimated based on the earliest possibility, considering the time required for internal approvals and construction.

Table 3 Predictive scenarios and cumulative discounted NPC calculations
Full size table

Some assumptions were made on the injection capacity of SWIB, S1B, and RMARN (see supplemental file, Table S-3). These assumptions are compatible with the GWM results in terms of the maximum capacity that the aquifer can accept. However, a further consideration was required to account for the actual hydraulic infrastructure limits and the performance of the injection infrastructure. Table 3 and Fig. 3 shows the NPC analysis of two scenarios that were run from March 2021 and June 2032. In summary, the results show that:

  • Scenario 1 (without WTPT2) would require a fresh/brackish water supply with a capacity of ≈34 ML/d and would trigger the construction and commissioning of an evaporation pond in December 2022 with a maximum capacity of 69 ML/d.

  • Although Scenario 2, including WTPT2, resulted in some EP rates, they were drastically less than in Scenario 1. Given the very conservative borefield injection capacity constraints assigned for RMARN (a recent update of the groundwater model predicts twice as much than assigned in this case study that could accommodate the predicted EP rates), it may be possible to exclude the EP OPEX and CAPEX costs in Scenario 2 for decision-making purposes.

  • In both scenarios, the OPEX cost was negligible compared to the CAPEX. However, Scenario 2, with a second water treatment plant, was more favourable because it minimises the NPC.

Fig. 3
figure 3

Discounted NPC calculations for the scenario without WTPT2 (blue) and with WTPT2 (orange)

Full size image

In terms of water quality, the difference in the hypersaline TDS concentration threshold (CHS) optimisation between Scenarios 1 and 2 was 6,000 mg/L with a difference in the peak for the saline streams of 4,222 mg/L. A concentration below the threshold optimised for Scenario 1 would trigger a greater water supply volume requirement to satisfy the dust suppression demand and increase the surplus water for disposal.

The input concentration for WTPT2 in Scenario 2 was further optimised with the “cherry-pick” method described above. This optimisation demonstrates that with opportunistic management of the regional volumes, it is possible to reduce the maximum concentration that feed WTPT2 of ≈ 3,300 mg/L.

Conclusions

A custom-made linear programming optimisation software was developed and used to optimise the Roy Hill water management on site. The software is based on a simplex algorithm developed with the coding language Python 3.6.

Implementation of this software tool at Roy Hill has significantly improved the management of the hydrogeology team's workflow, resulting in a more efficient and reliable approach to water balance calculation. This tool has facilitated better collaboration with other teams within the company, enabling more informed decision-making in identifying risks associated with surplus water management, and identifying potential cost savings through optimization of the NPC. Its successful implementation has revolutionized the way Roy Hill approaches water management, enhancing productivity and sustainability.

Previously, Roy Hill water balance calculations were estimated without considering water quality and using the results of the GWM independently from other water tasks. While this approach was acceptable in the early years of mining when water quality was not a concern, over time, dewatering abstractions mobilized saline water from the nearby hypersaline aquifer (Skrzypek et al. 2013). This necessitated a re-evaluation of the water management strategy, which was successfully resolved by implementing this software solution.

The tool was initially adopted to evaluate the cost effectiveness of two infrastructure upgrade configurations. The first one included all the existing infrastructures and allowed the possibility to utilise a remote water supply and an evaporation pond to discharge surplus water. The second configuration adopted an additional water treatment plant. The results of this exercise showed that implementation of a second water treatment plant reduces disposal of surplus saline water and additional water supply volumes, both of which require high CAPEX. Also, the cost comparison shows that implementation of a second treatment plant is favourable.

A further optimisation exercise on the saline concentrations highlighted the opportunity to reduce the concentration for the WTPT2 demands. This optimisation benefitted from the fact that not all the available saline water will be used in WTPT2 at each simulated time. This means that the lower the demand, the greater the benefit in concentration reduction and vice versa.

This example application showcases the tool's ability to generate cost projections over time by integrating infrastructure investments with water management. It also highlights the tool's potential to optimize cost-effectiveness in water management while ensuring sustainable infrastructure development. It is also important to stress the fact that model simulations were executed within a matter of seconds, allowing for comprehensive scenario evaluation, and reporting to be completed in just half a day's work. This demonstrates the tool's exceptional ability to provide rapid analysis while maintaining the distinct expertise and complexity of individual water modelling tasks. Furthermore, it achieves this without compromising the conceptual representation of the physical system, demonstrating its efficiency and effectiveness in handling diverse water management challenges.

The algorithm is now an integral component of recurring water balance assessments, conducted whenever the mine planning team releases a new mine plan. The primary objective of this routine modelling is to identify potential risks associated with surplus water disposal using the existing hydraulic infrastructure. This process supplies vital information to the company’s decision-makers in a timely manner, enabling them to adapt the mine plan and prevent severe delays or disruptions in ore production.

A potential advancement of this work involves implementing a two-way coupling with the GWM. Each solution generated by the Python optimizer should be verified using the GWM to ensure aquifer capacity and water supply sustainability. Importantly, the GWM also considers environmental constraints, such as the mounding caused by reinjections, which must be verified. Currently, this verification process is conducted manually rather than automatically following each optimization. Implementing a two-way coupling would streamline this process and enhance overall efficiency.

Another limitation of the current solution is the absence of an uncertainty analysis. This could be addressed by implementing a multiple scenario analysis, such as using a Monte Carlo simulation approach, assuming that the inputs are not deterministic. This method would depend on the availability of uncertainty calculations derived from the results of various modelling tasks. An initial assessment could focus on the models with the greatest uncertainties and the most marked effect on surplus water calculations, such as the GWM. The Roy Hill hydrogeology team is currently working on this.