Provision of health care services and regional diversity in Germany: insights from a Bayesian health frontier analysis with spatial dependencies

Abstract

The German health care system is among the most patient-oriented systems in Europe. Nevertheless, distinct utilisation patterns, access barriers due to socio-economic profiles, and potentials of misallocation of medical resources lead to disparities in the provision of health care services. We analyse how a possible over- and undersupply of services and the utilisation of and the access to the health care system relate to regional variations in the population’s well-being. For this purpose, we employ a recent Bayesian stochastic frontier approach that allows for spatial dependence structures. Our results indicate that patient migration plays an important role in contributing to regional differences in the utilisation of the medical infrastructure. As a consequence, policy should take spatial patterns of health care utilisation into account to improve the allocation of medical resources.

Appendices

Appendix

The following appendices provide further details on the Bayesian estimation procedure and the derivation of the marginal effects of the $z$ variables.

The Bayesian stochastic frontier model

Prior specification

In a fully Bayesian approach, the general form of a normal regularisation-type prior with penalisation term and smoothing variance for a vector of unknown regression coefficients ${\varvec{\upzeta}}$ is given by:

$$\begin{array}{*{20}r} \hfill {p(\varvec{\zeta}|\tau^{2} ) \propto \left( {\frac{1}{{\tau^{2} }}} \right)^{{\frac{{rk\left( \varvec{K} \right)}}{2}}} \exp \left\{ { - \frac{1}{{2\tau^{2} }}\varvec{\zeta^{\prime}K\zeta }} \right\}} \\ \end{array}$$

(6)

In (6), $\varvec{K}$ is a known penalty matrix which is chosen a priori and the smoothing variance is $\tau^{2} = 1/\lambda$ where $\lambda \ge 0$ is an unknown smoothing component that determines the strength of the regularisation to avoid overfitting.¹⁹ To obtain a data-driven degree of smoothness, we assign an inverse gamma hyperprior to $\tau^{2}$, i.e., $\tau^{2} \sim IG\left( {a,b} \right)$ with $a = b = 0.001$, which is the common choice in Bayesian estimation [21]. In summary, the general form of (6) offers a practical and flexible way to deal with any unknown regression coefficients by an adequate choice of $\varvec{K}$.

Linear and nonlinear effects

In (1) and (4) the coefficient $\varvec{\beta}$ and $\varvec{\delta}$ describe the linear influences of the covariate vectors $x_{it}$ and $z_{it}$, respectively. For estimation purpose, we replace the variance components of $u_{it}^{*}$ and $v_{it}$ by $\sigma_{u}^{2} = { \exp }\left\{ {c_{u} } \right\}$ and $\sigma_{v}^{2} = { \exp }\left\{ {c_{v} } \right\}$, respectively, where $c_{u}$and $c_{v}$ are coefficients to be estimated. We restrict (6) with $\varvec{K} = 0$ to obtain completely non-informative priors. Therefore, the joint prior distributions for $\beta$, $\delta$, $c_{u}$, $c_{v}$ and $\mu$ are flat, i.e. $p\left( \beta \right)$, $p\left( \delta \right)$, $p\left( {c_{u} } \right)$, $p\left( {c_{v} } \right)$, $p\left( \mu \right) \propto const$.

We model the nonlinear effect of a covariate $\tilde{x}_{it}$ by means of a smooth function $f\left( {\tilde{x}_{it} } \right)$. We apply P-splines as introduced by Eilers and Marx [20], and approximate the unknown function by a polynomial spline of degree 3 with 20 equidistantly spaced knots over the domain of $\tilde{x}_{it}$: $f\left( {\tilde{x}_{it} } \right) = \varvec{W\tilde{\beta }}$, where $\varvec{W}$ is the design matrix comprising the basis functions at the observed covariate values and $\tilde{\varvec{\beta }}$ is a vector of regression coefficients to be estimated. Following Eilers and Marx [20] and Belitz et al. [6], for $\varvec{\zeta}= \tilde{\varvec{\beta }}$ in (6) the matrix $\varvec{K}$ comprises a second-order random walk penalty term to obtain a regularised function $f\left( {\tilde{x}_{it} } \right)$.²⁰

Spatial components

To model spatial dependencies, we consider structured spatial effects in the production function ($\gamma_{i}$) and in the scaling function ($\theta_{i}$). We assign a Markov random field prior to the joint distribution of $\varvec{\gamma}$ and $\varvec{\theta}$ [22]. To obtain the representation in (6) for $\varvec{\zeta}=\varvec{\gamma}$ and $\varvec{\zeta}=\varvec{\theta}$, respectively, we define a first-order neighbourhood structure on the set of German districts. Thus, the we set $\varvec{K}$ equal to an adjacency matrix $\varvec{A}$, which takes the form of an indicator matrix, where the off-diagonal elements are equal to unity if two districts share a common border, and zero otherwise.

As the district-specific effects $\alpha_{i}$ are independent of the neighbourhood structure in $\varvec{A}$, one can interpret them as structured spatial effects. In that way, the joint prior distribution of $\varvec{\alpha}$ corresponds to a Markov random field without neighbourhood structure. We specify the distribution in (6) for $\varvec{\zeta}=\varvec{\alpha}$ by setting $\varvec{K}$ equal to an identity matrix $\varvec{I}$. In summary, the decomposition into structured and unstructured spatial components allows for additional flexibility in the model to recover more general spatial dependencies.²¹

Estimation

The MCMC estimation algorithm is implemented in a developer version of the freely available software BayesX [6, 40] provide a detailed description of thse sampling algorithms which we adopt. Bayesian inference is based on the posterior density functions of the model given by $p\left( {\zeta |y} \right) \propto p\left( {y|\zeta } \right)p\left( \zeta \right)$, which are obtained from the sampling paths to easily draw inferential results. For simplicity, $\zeta$ denotes the collection of all unknown model parameters, and $p\left( \zeta \right)$ are the respective prior distributions which are all of the type of (6), but differ from each other due to the different specifications of $\varvec{K}$.

Quantile residuals

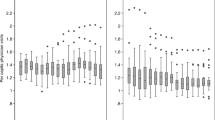
See Fig. 5,

Fig. 5

QQ-Plots. The figures show the standarised quantile residuals of the Models 0-III

Since SFA’s fit into the class of distributional regression models, quantile residuals are commonly used to check if the model has been correctly specified [41]. Quantile residuals are defined as $\hat{r}_{i} = {\varvec{\Phi}}^{ - 1} ( {F( {y_{i} \left| {\hat{\varvec{\vartheta }}_{i} } \right.} )} )$, with the inverse cumulative distribution function (c.d.f.) of a standard normal distribution $\varPhi^{ - 1}$ and $F\left( {. |\hat{\varvec{\vartheta }}} \right)$ denoting the c.d.f. with model specific parameters, i.e., $\hat{\varvec{\vartheta }}_{0} = \left( {\varvec{\alpha}, \varvec{\beta}, \tilde{\varvec{\beta }}_{1} , \ldots , \tilde{\varvec{\beta }}_{\varvec{J}} ,\varvec{\delta}, \sigma_{v}^{2} , \sigma_{{u^{*} }}^{2} , \mu } \right)^{\prime }$, $\hat{\vartheta }_{I} = \left( {\varvec{\alpha}, \varvec{\beta}, \tilde{\varvec{\beta }}_{1} , \ldots ,\tilde{\varvec{\beta }}_{\varvec{J}} ,\varvec{ \delta },\varvec{\gamma}, \sigma_{v}^{2} , \sigma_{{u^{*} }}^{2} , \mu } \right)^{\prime } , \hat{\vartheta }_{II} = \left( {\varvec{\alpha}, \varvec{\beta}, \tilde{\varvec{\beta }}_{1} , \ldots ,\tilde{\varvec{\beta }}_{\varvec{J}} ,\varvec{ \delta },\varvec{\theta},\sigma_{v}^{2} , \sigma_{{u^{*} }}^{2} , \mu } \right)^{\prime } , \hat{\vartheta }_{II} = \left( {\varvec{\alpha}, \varvec{\beta}, \tilde{\varvec{\beta }}_{1} , \ldots , \tilde{\varvec{\beta }}_{\varvec{J}} ,\varvec{ \delta },\varvec{\theta},\sigma_{v}^{2} , \sigma_{{u^{*} }}^{2} , \mu } \right)^{\prime } ,$ where the indices are used to distinguish the model specifications ‘0′ to ‘III’ as outlined in Sect. 3.2.1. Based on the SFA specification, $F\left( {. |\hat{\vartheta }} \right)$ is a mixed normal-half normal distribution [44]. According to Dunn and Smyth [18], the quantile residuals should at least approximately be standard normally distributed if the correct model has been specified. In practice, the residuals can be subjected to eyeball inspection in terms of QQ-plots.

Bayesian R²

In Bayesian inference one obtains a set of posterior simulation draws $l = 1, \ldots , L$. For each draw, one obtains the vector of predicted values $\hat{\varvec{y}}^{\left( l \right)}$ and residuals $\varvec{e}^{\left( l \right)} = \varvec{y} - \hat{\varvec{y}}^{\left( l \right)}$ over all cross-sectional $i = 1, \ldots , N$ and time instances $t = 1, \ldots , T$. For each posterior draw $l$, we calculate the proportion of variance explained as:

$${\text{Bayesian }}R^{2} = \frac{{\frac{1}{NT}\mathop \sum \nolimits_{i = 1}^{N} \mathop \sum \nolimits_{i = 1}^{T} \left( {\hat{y}_{it}^{\left( l \right)} - \hat{y}^{\left( l \right)} } \right)^{2} }}{{\frac{1}{NT}\mathop \sum \nolimits_{i = 1}^{N} \mathop \sum \nolimits_{i = 1}^{T} \left( {\hat{y}_{it}^{\left( l \right)} - \hat{y}^{\left( l \right)} } \right)^{2} + \frac{1}{NT}\mathop \sum \nolimits_{i = 1}^{N} \mathop \sum \nolimits_{i = 1}^{T} \left( {\hat{e}_{it}^{\left( l \right)} - \hat{e}^{\left( l \right)} } \right)^{2} }}$$

Since an R²_l obtains for each posterior draw l = 1,…, L, we summarise this sample information by its posterior mean. The Bayesian R² can be interpreted as a data-based estimate of the proportion of variance explained by the model [27, 28].

Marginal effects

In (4), the scaling function $h_{it} = { \exp }\left\{ {z_{it}^{'} \delta + \theta_{i} } \right\}$ translates the effects of $z_{it}$, denoted by $\delta$, to both the mean and the variance of $u_{it}^{*}$. The parametrisation of $u_{it} = h_{it} u_{it}^{*}$ with $u_{it}^{*} \sim N^{ + } \left( {\mu ,\sigma^{2} } \right)$ is equivalent to $u_{it} \sim N^{ + } (\mu_{it}^{*} ,\left( {\sigma_{it}^{2} )^{*} } \right)$ where $\mu_{it}^{*} = \mu { \exp }\left\{ {z_{it}^{'} \delta + \theta_{i} } \right\}$ and $(\sigma_{it}^{2} )^{*} = \sigma^{2} { \exp }\left\{ {2z_{it}^{'} \delta + 2\theta_{i} } \right\}.$ According to Wang [68], the first two moments of $u_{it}$read as

$$\begin{aligned} {\mathbb{E}}\left[ {u_{it} } \right] &= \sigma_{it}^{*} \left[ {a + \frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right] \hfill \\ Var\left[ {u_{it} } \right] &= (\sigma_{it}^{2} )^{*} \left[ {1 - a\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right] - \left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right]^{2} } \right], \hfill \\ \end{aligned}$$

where $a = \frac{{\mu_{it}^{*} }}{{\sigma_{it}^{*} }}$ and $\varphi ( \cdot )$ and $\varPhi \left( \cdot \right)$ denote the probability density function and the cumulative

density function of the standard normal distribution, respectively. Then, the marginal effect of a change in the $d$-th variable in $z_{it}$ on the respective moments of $u_{it}$ is given by the partial first derivatives:

$$\begin{aligned} &\begin{aligned}\frac{{\partial {\mathbb{E}}\left[ {u_{it} } \right]}}{{\partial z^{d} }} & = \delta^{d} \left[ {1 - a\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right] - \left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right]^{2} } \right] + 2\delta^{d} \sigma_{it}^{*} \\&\quad\times\left[ {\left( {1 + a^{2} } \right)\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right] - \left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right]^{2} } \right]\end{aligned} \\& \begin{aligned}\frac{{\partial Var\left[ {u_{it} } \right]}}{{\partial z^{d} }} & = \frac{{\delta^{d} }}{{\sigma_{it}^{*} }}\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right]\left( {\left( {{\mathbb{E}}\left[ {u_{it} } \right]^{2} } \right)\left( {{\mathbb{E}}\left[ {u_{it} } \right]^{2} - Var\left[ {u_{it} } \right]} \right)} \right) \\ & \quad + 2\delta^{d} (\sigma_{it}^{2} )^{*} \left\{ {1 - \frac{1}{2}\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right]\left( {a + a^{3}}\right.}\right.\\&\quad\left.{\left.{ + \left( {2 + 3a^{2} } \right)\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right] + 2a\left[ {\frac{\phi \left( a \right)}{\varPhi \left( a \right)}} \right]^{2} } \right)} \right\}, \\\end{aligned} \end{aligned}$$

where $\delta^{d}$ is the coefficient of the $d$-th variable in $\delta$.