An asynchronous proximal bundle method

Abstract

We develop a fully asynchronous proximal bundle method for solving non-smooth, convex optimization problems. The algorithm can be used as a drop-in replacement for classic bundle methods, i.e., the function must be given by a first-order oracle for computing function values and subgradients. The algorithm allows for an arbitrary number of master problem processes computing new candidate points and oracle processes evaluating functions at those candidate points. These processes share information by communication with a single supervisor process that resembles the main loop of a classic bundle method. All processes run in parallel and no explicit synchronization step is required. Instead, the asynchronous and possibly outdated results of the oracle computations can be seen as an inexact function oracle. Hence, we show the convergence of our method under weak assumptions very similar to inexact and incremental bundle methods. In particular, we show how the algorithm learns important structural properties of the functions to control the inaccuracy induced by the asynchronicity automatically such that overall convergence can be guaranteed.

1 Introduction

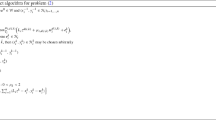
We consider an optimization problem of the form

$$\begin{aligned} \min _{x \in \mathbb {R}^n} \quad f(x) := \sum _{i=1}^m f_i(x) \end{aligned}$$

(P)

where the $f_i :\mathbb {R}^n \rightarrow \mathbb {R}$, $i=1, \dotsc , m$, are non-smooth convex functions. We assume that each $f_i$ is Lipschitz-continuous with a possibly unknown Lipschitz constant $L_i$, i.e.,

$$\begin{aligned} \forall \,x, x' \in \mathbb {R}^n :\left| f_i(x) - f_i(x') \right| \le L_i \cdot \left\| x - x' \right\| . \end{aligned}$$

Each function $f_i$ is given by a first-order oracle, i.e., given a point $x \in \mathbb {R}^n$ the oracle returns the function value $f_i(x)$ and a subgradient $g_i \in \partial f_i(x)$ at x where $\partial f_i(x)$ denotes the subdifferential of $f_i$ at x. One well-established method to solve these problems are bundle methods [2, 10]. In a nutshell, bundle methods are iterative algorithms that collect subgradient information for each function $f_i$ from the set

$$\begin{aligned} W_i:= \mathop {\textrm{conv}}\limits \left\{ (c, l) :c = f(x) - \left\langle l, x \right\rangle , l \in \partial f_i(x), x \in \mathbb {R}^n \right\} . \end{aligned}$$

In iteration $k = 0,1,2, \dotsc$ starting from a current center of stability $\hat{x}^k$, they form a cutting plane model $\hat{f}_i^k(x)$ for each $f_i(\cdot )$ using finite subsets $\mathcal {B}_i^k \subseteq W_i$ via

$$\begin{aligned} \hat{f}_i^k(x):= \max \left\{ c + \left\langle l, x \right\rangle :(c, l) \in \mathcal {B}_i^k \right\} . \end{aligned}$$

Then a (proximal) bundle method computes a new candidate $\bar{x}^k$ by solving a master problem

$$\begin{aligned} \bar{x}^k = \mathop {\mathrm {\arg \,\min }}\limits \left\{ \hat{f}^k(x) + \frac{u^k}{2} \left\| x - \hat{x}^k \right\| ^2 :x \in \mathbb {R}^n \right\} , \hat{f}^k(x):= \sum _{i=1}^m \hat{f}_i^k(x) \end{aligned}$$

where the weight $u^k > 0$ penalizes the distance to $\hat{x}^k$. Afterwards, the function oracles compute the function values and subgradients at the candidate $\bar{x}^k$ and the actual decrease $f(\hat{x}^k) - f(\bar{x}^k)$ is compared to the predicted decrease

$$\begin{aligned} \Delta ^k = f(\hat{x}^k) - \hat{f}^k(\bar{x}^k) \ge 0. \end{aligned}$$

If the actual decrease achieves a fraction of at least $\varrho \in (0,1)$ of the predicted decrease, the algorithm performs a descent step (or serious step) choosing the candidate as the new center $\hat{x}^{k+1} \leftarrow \bar{x}^k$. Otherwise, the center remains unchanged $\hat{x}^{k+1} \leftarrow \hat{x}^k$ but the subgradient information at $\bar{x}^k$ is added to the bundles $\mathcal {B}_i^k$.

In this paper we aim at the development of a fully asynchronous proximal bundle method. Here fully asynchronous means that the evaluation of each subfunction $f_i(\cdot )$ at some point x as well as the computation of the master problem is done in separate processes. Each process is started at some time and once the computation is finished the results are communicated to the other processes. The order in which the computations are started and when the results are available is not defined. The only assumption is that each process finishes its computation in finite time. In particular, only a finite number of other processes may start or finish between the time when a certain process is started and the time its results become available.

The algorithm to be designed should be usable as drop-in replacement for standard proximal bundle methods. In particular, oracles that can be used in a standard method should be applicable for the asynchronous method as well (given that the implementation is suitable to be used in a parallel and distributed computational environment). Specifically, we have the following goals:

• 1. Each oracle only needs to provide the same information a standard bundle method requires, i.e., for each point $x \in \mathbb {R}^n$ the oracle computes the function value $f_i(x)$ and a subgradient $g_i(x) \in \partial f_i(x)$. In particular, no additional information like the Lipschitz constant $L_i$ needs to be known.

• 2. If the results for some oracle call $f_i(x)$ are not available, yet (because of the asynchronous nature), the algorithm needs to use an approximation of that value. A natural choice is the value computed by the current cutting plane model (although other models are possible). The algorithm should work when using the cutting plane model to determine approximate values as needed.

• 3. In many applications not all subfunctions $f_i(\cdot )$, $i \in \{1, \dotsc , m\}$, depend on all components $x_j$, $j \in \{1, \dotsc , n\}$, of the variables (e.g., $f_i$ is constant on the subspace $\left\{ x + \delta e_j :\delta \in \mathbb {R} \right\}$ for each $x \in \mathbb {R}^n$). The algorithm should automatically exploit these properties.

1.1 Literature overview

Bundle methods are a well-established tool for solving non-smooth convex (and non-convex) optimization problems, see, e.g., [10, 15]. The main computational burden in a bundle method is typically the evaluation of the function oracles, which may itself involve solving some inner optimization problems. Even if the oracle calls are evaluated in parallel, the whole iterative method has to wait until each (possibly slow) oracle has finished. Hence, a single expensive oracle may dominate the overall running time. In order to reduce the overall running times, different variants of bundle methods have been proposed that try to reduce either the number of oracle calls, replace them with cheaper approximations or simply do not wait for the slowest oracles to complete. In this paper we will combine and extend several of these ideas to develop our new asynchronous bundle method.

The idea of incremental bundle methods [5] is to skip the evaluation of some $f_i(\cdot )$ and replace their function value by an approximation, e.g., the model value. Our method also uses an approximation of the real function value (the “guess model”, see Sect. 2.2) of those $f_i(\cdot )$ that have not been evaluated, yet. In fact, similar to incremental methods it is also possible to use the cutting plane model to obtain approximate function values (see Sect. 6). One main difference between synchronous incremental methods and asynchronous methods is that the evaluation results in the former setting are still obtained in a well-defined order. In an asynchronous setting the evaluations may have varying running times, hence there is no implicit guarantee that the functions are evaluated regularly (e.g., every N iterations). Although it is a valid strategy to enforce such a regular evaluation explicitly in an asynchronous setting, our algorithm does not use it.

Using the cutting plane model as approximation implies that the approximated values always underestimate the real function values. This may be disadvantageous and may lead to ineffective descent steps. In [19] the authors extended the incremental approach and used upper models to obtain upper bounds on the real function values. This approach required the knowledge of the Lipschitz constants for each $f_i(\cdot )$. Only if the upper bounds were not sufficient to decide on a null step or descent step, the function is evaluated. In our approach it is also possible to use upper models for the approximate function values, but other models not requiring explicit knowledge of the Lipschitz constants are possible as well (see Sect. 6.2).

Another idea to reduce the running time required for exact oracle calls is to replace the oracles with inexact ones, see [3] for a comprehensive overview. Instead of computing the function values and subgradients exactly only approximated values are computed. The asynchronous setting is somehow similar to the inexact setting. In fact, we replace the notion of “inexact” values by “outdated” values, i.e., we do not know the exact function values in the current point but in some older (hopefully close) point. In order to get exact results from inexact oracles one typically requires controlling the inexactness in some way, e.g., to use so called “asymptotically exact” oracles, which provide increasingly better approximations during the run of the algorithm. In fact, the authors in [5] already realized that incremental bundle methods can be interpreted as inexact oracles and analyzed their algorithm within an inexact framework. Because the asynchronous setting is so closely related to incremental methods, the same could be done for our algorithm. However, there are some important differences. The algorithm developed in this paper learns the amount of inaccuracy introduced by the asynchronicity during the run and automatically adjusts the inaccuracy of future evaluations in order to guarantee convergence. We will show that this allows to interpret the guess model in our approach as an asymptotically exact oracle which has vanishing approximation errors.

In a recent work [4] the authors show how solving multiple master problems in parallel with different constant proximal parameters can be used to achieve optimal convergence rates. However, besides solving the master problems in parallel their method is synchronized.

There are currently only few papers discussing asynchronous bundle methods. A recent publication is [11], where the authors consider level bundle methods (instead of proximal bundle methods). The authors discuss two approaches to ensure convergence in the asynchronous setting. Their first approach requires knowledge of the Lipschitz constants. We will get an analogous result for our algorithm if the Lipschitz constants are known (see Sect. 6.1). Their second approach gets rid of this assumption but requires scarce synchronized steps from time to time, where all function oracles are evaluated at the same point. At the same time, the algorithm computes a guess of the Lipschitz constant. Our algorithm does not require synchronized steps at all (in fact, there might not be a single point except for the starting point at which all functions $f_i$ are evaluated) but we also compute a guess of the Lipschitz constant during the algorithm. The difference is that knowing a reasonably good guess of the Lipschitz constant allows to judge whether the current approximations are “good enough” which allows getting rid of forced synchronized steps completely. An older paper considering asynchronous proximal bundle methods is [6]. That paper focused on the specialized setting of Lagrangian relaxation (see [7, 13, 14]). There the idea was to select certain subspaces of variables that influence only few of the functions $f_i(\cdot )$ and to optimize on several such subspaces in parallel. Convergence had been guaranteed by tracking which function depends on which variables. An interesting but unusual property of that work is that the algorithm solves several master problems in parallel (on disjoint subspaces). The setting of the algorithm in this paper is more general and not restricted to Lagrangian relaxation. However, we will also present a variant that is able to track dependencies between variables and functions and to exploit these dependencies in the algorithm (see Sect. 6.4). Furthermore, our algorithm also allows having parallel processes that solve (different) master problems to compute new candidate points.

1.2 Outline of this paper

This paper is structured as follows. In Sect. 2 we introduce the notation and present the basic asynchronous framework and all major building blocks, which will be discussed in later sections. In Sect. 3 we start with the computation of new candidate points using the typical master problem of proximal bundle methods, and we discuss the adaptions made for descent steps in Sect. 4. We analyze the convergence of our algorithm in Sect. 5 which resembles the steps of convergence proofs for bundle methods for our asynchronous method. The basic algorithm and its analysis are presented without explicit guess models. We give some possible guess models in Sect. 6. In order to adjust the accuracy of these guess models accordingly, the Lipschitz constants must be known. However, we also show how the algorithm can be extended to the case of unknown Lipschitz constants in Sect. 6.2. Furthermore, we extend the algorithm to the case where some functions are constant along some coordinate directions in Sect. 6.4. The final algorithm with all extensions is shown in Sect. 7. Finally, we present some preliminary computational tests in Sect. 8 and give some directions for future work in Sect. 9.

2 Asynchronous framework and notation

In this section we describe the basic asynchronous algorithmic framework. In a classic, synchronous bundle method each iteration roughly does the following steps:

• 1. The master problem is solved relative to the current center $\hat{x}^k$ computing a new candidate $\bar{x}^k$.

• 2. Each function is evaluated at $\bar{x}^k$ obtaining the function value and subgradient information and the cutting plane model is updated.

• 3. A descent test decides whether a descent step ($\hat{x}^{k+1} \leftarrow \bar{x}^k$) or a null step ($\hat{x}^{k+1} \leftarrow \hat{x}^k$) is performed.

In particular, the order of the computational steps and the available information is fixed, i.e., in each step the full information of the previous steps is available. In our asynchronous setting we relax this property. Each iteration of the algorithm now corresponds to one of these steps but not necessarily in the same order: a new candidate becomes available, some (but not necessarily each) function $f_i(\cdot )$ has been evaluated at some former candidate, the center is updated. The most common case is that the evaluation of some functions $f_i(\cdot )$ takes longer. The algorithm does not need to wait until the results of all functions are available but may decide to do a descent step earlier. Similarly, subgradient information for some function $f_i(\cdot )$ can be added to the function model as soon as it is available so that new candidates can be computed immediately before all oracles have finished their computation at the old candidate.

In order to formalize our setting, we split the computation into three classes of parallel running processes communicating only by sending messages to each other.

• (P1) Supervisor process: The supervisor process maintains the data/state of the algorithm. It receives candidate points from master problem processes and sends them to oracle processes for evaluation, and function values and subgradients from the oracle processes and sends them to the master processes. Furthermore, the supervisor decides when a descent step should be done and sends the center point to all master processes.

• (P2) Master problem process(es): A master problem process computes new candidates by solving a master problem. It sends its solution as new candidate to the supervisor. It receives subgradient information and possibly a new center point from the supervisor, see Algorithm 1.

• (P3) Oracle process(es): An oracle process for some subfunction $f_i(\cdot )$ receives candidate points $\bar{x}\in \mathbb {R}^n$ from the supervisor and computes a function value $f_i(\bar{x})$ and a subgradient $g_i \in \partial f_i(\bar{x})$ and sends them back to the supervisor, see Algorithm 2.

The central process is the supervisor process, which handles the current global state of the algorithm. Its task corresponds to the main loop of a classic bundle method. Although the processes run in parallel, each single process does its work sequentially. In particular, the supervisor process has a well-defined order in which it obtains and updates information. It will therefore be convenient to equip all global data with a unique iteration counter $k\in K= \{0, 1, 2, \dotsc \}$ corresponding to the iterations of the supervisor process (which we will denote by a superscript k). Indeed, the basic global data of the supervisor process is the same as in a sequential algorithm:

• The center of stability $\hat{x}^k$, $k \in K$.

• The next candidate point $\bar{x}^k$, $k \in K$, and model value $\hat{f}_i^k(\bar{x}^k)$ for all $i \in \{1, \dotsc , m\}$ in the candidate.

• The bundle of cutting planes $\mathcal {B}^k = (\mathcal {B}^k_i)_{i=1,\dotsc ,m}$.

The difference to a classic bundle method is that, when deciding on a descent step or not, not all function values $f_i(\bar{x}^k)$ and subgradients $g_i^k \in \partial f_i(\bar{x}^k)$ are available. Therefore, the algorithm has to use something else. In the literature different ideas have been proposed [5] for the case that exact information is not available. In incremental bundle methods the cutting plane model $\hat{f}_i^k(\cdot )$ is used to approximate the function value. Another related idea is to use an inexact function oracle that only returns an approximation of the exact function value but may be computed faster [3]. We will combine and extend ideas from both approaches in the sense that we use a model (not necessarily the cutting plane model $\hat{f}_i^k(\cdot )$) to approximate the function value and that model should be built from the information obtained in earlier iterations. This model is called the guess model of $f_i(\cdot )$ in iteration k and is denoted by $\tilde{f}^k_i(\cdot )$. Note that in contrast to inexact function oracles, our function oracles provide exact values but the guess model $\tilde{f}^k_i(\cdot )$ may only use information already available in iteration k. Therefore, the inexactness in our case comes from the fact that the information used by $\tilde{f}^k_i(\cdot )$ is outdated (the values at the current candidate $\bar{x}^k$ are not known, yet, but only the values of earlier candidates). Nevertheless, the similarity between both concepts (“inexact” and “outdated” information) is apparent and will carry over to the analysis.

The guess model $\tilde{f}^k_i(\cdot )$ is only used to approximate the function value in the candidate. A classic bundle method also needs the function value in the current center $\hat{x}^k$. For them, we use another idea from inexact methods [3] and do not use the guess model but the best known lower bound on the function value in $\hat{x}^k$ that can be derived from the cutting plane model. We will see in Sect. 4 why we choose those two approaches.

In addition to the candidate, center and bundles, the supervisor process also keeps track of the following two objects:

• The best known lower bound $\bar{f}_i^k$ on $f_i(\hat{x}^k)$ in the current center $\hat{x}^k$ for all $i=1, \dotsc , m$, $k \in K$.

• The current guess model $\tilde{f}_i^k(\cdot )$, $i=1, \dotsc , m$, $k \in K$.

Putting all together, there are three possibilities for each iteration step from k to $k+1$:

• New candidate: a new candidate point $\bar{x}$ with model values $\hat{f}_i$ has been received from a master process. The global data is changed $\bar{x}^{k+1} \leftarrow \bar{x}$ and $\hat{f}_i^{k+1} \leftarrow \hat{f}_i$, $i=1, \dotsc , m$.

• New cutting plane: a function $f_i(\cdot )$ for some $i \in \{1, \dotsc , m\}$ has been evaluated at some earlier candidate $\bar{x}^l$, $l \le k$, given the function value $f_i(\bar{x}^l)$ and a subgradient $g^k_i \in \partial f_i(\bar{x}^l)$. The subgradient is appended to the bundle $\mathcal {B}^{k+1}_i \leftarrow \mathcal {B}^k_i \cup \{(c, g^k_i)\}$ with $c:= f_i(\bar{x}^l) - \left\langle g^k_i, \bar{x}^l \right\rangle$. Furthermore, the guess model $\tilde{f}^k_i(\cdot )$ as well as the best lower bound in the center $\bar{f}^{k+1}_i \leftarrow \max \{\bar{f}^k_i, c + \left\langle g^k_i, \hat{x}^k \right\rangle \}$ are updated using the new information. The subgradient information is also sent to all master problem processes (that will add them to their model for their next computation).

• A descent step: the supervisor accepts the candidate as the new center of stability $\hat{x}^{k+1} \leftarrow \bar{x}^{k}$. The new center is sent to all master processes, and the guess models $\tilde{f}^k_i(\cdot )$ and the best known lower bounds in the center $\bar{f}^k_i$, $i=1, \dotsc , m$, will be updated for the new center.

Note that in contrast to a classic bundle method, receiving new candidates, new cutting planes and doing a descent step are separate “iterations” in our setting (i.e., going from k to $k+1$ only one of these steps is done). The supervisor process tests if a descent step can be done after either a new candidate or a new cutting plane has been received (see Sect. 4). If the supervisor decides for a null step (i.e., to not perform a descent step) then nothing changes, thus we do not count it as an iteration. A first basic version of the algorithm can be seen in Algorithm 3 (the descent conditions (D1) and (D2) will be discussed later in Sect. 4). It already contains all main steps, but we will later extend it to get the final algorithm.

We want to emphasize that there is no limit on the number of master processes or evaluation processes running in parallel as long as there is at least one of each. A standard setup would be to have exactly one master problem process and exactly one evaluation process for each $f_i(\cdot )$, $i=1, \dotsc , m$. However, if, e.g., the evaluation of some function $f_i$ takes significantly longer than the others, then there might be several processes evaluating $f_i(\cdot )$ at different candidate points at the same time. Furthermore, not all functions $f_i$, $i=1, \dotsc , m$, may be evaluated at all candidates. If the computation of some oracle $f_{\hat{\imath }}(\cdot )$, $\hat{\imath } \in \{1, \dotsc , m\}$, takes too long, the supervisor may perform some descent steps before the oracle process can be evaluated at a new candidate, so effectively skipping the evaluation of $f_{\hat{\imath }}(\cdot )$ for some candidates. However, we make the general assumption, that each oracle call finishes in finite time.

Assumption 1

(called “finite response assumption” in [11]) Suppose there is an infinite number of global iterations. Then for each $i \in \{1, \dotsc , m\}$ there is an infinite number of indices corresponding to a new cutting plane for function $f_i(\cdot )$.

This assumption alone is not sufficient to prove convergence of our algorithm. The reason is that it allows that the time between two successive evaluations of the same function $f_i(\cdot )$ could grow arbitrarily. Therefore, we will later make a few additional technical assumptions (that are not difficult to fulfill in practice).

2.1 Notation

In order to simplify the notation a bit, we will use the following convention throughout the rest of the paper:

• Items associated with iteration $k \in K$ of the supervisor process get a superscript k.

• Items associated with a function $f_i$ get a subscript i.

• Items associated with a function f but with no subscript i denote the sum over all i, e.g., $f(x) = \sum _{i=1}^m f_i(x)$, $\bar{f}^k = \sum _{i=1}^m \bar{f}^k_i$.

• If the algorithm needs the value of some function at some specific point (the center or some candidate), we shorten the notation by dropping the point if it is clear from the context. In detail:

  • $f^k_i:= f^k_i(\bar{x}^k)$, the function value at the candidate,

  • $\hat{f}^k_i:= \hat{f}^k_i(\bar{x}^k)$, the model value at the candidate,

  • $\tilde{f}^k_i:= \tilde{f}^k_i(\bar{x}^k)$, the guess model value at the candidate,

  If we refer to the model itself we write $\hat{f}_i^k(\cdot )$ or $\tilde{f}^k_i(\cdot )$.

• The set $\hat{K}\subseteq K$ denotes the global indices corresponding to a descent step, i.e.  $\hat{x}^{k+1} = \bar{x}^k$. Each candidate $\bar{x}^k$ is computed relative to an earlier center (not necessarily $\hat{x}^{k-1}$ because of the asynchronicity), respectively candidate $\bar{x}^{k^-}$. In other words, $k^-\in \hat{K}$ is the preceding descent step.

• Let $k \in K$ be an arbitrary iteration and $i \in \{1, \dotsc , m\}$ a function index. The candidate $\bar{x}^k$ has been generated by some master problem process. We will often use the notation $k_i$ to refer to the last index $k_i \le k$ whose information (function value $f_i(\bar{x}^{k_i})$ and subgradient $g^{k_i}_i \in \partial f_i(\bar{x}^{k_i})$) has been received by the supervisor process and is contained in the guess model $\tilde{f}^k_i(\cdot )$. Note that for fixed k the index $k_i$ may be different for each $i \in \{1, \dotsc , m\}$.

2.2 The guess model

The guess model is used to approximate the function value in the current candidate. In order to give a useful approximation, the guess model must be a reasonably good approximation of the real value. Formally we make the following assumption:

Assumption 2

Let $i \in \{1, \dotsc , m\}$, $k \in K$ be an iteration and $k_i \le k$, $k_i \in K$, the last preceding candidate at which $f_i(\cdot )$ has been evaluated. Then

$$\begin{aligned} \left| \tilde{f}^k_i(x) - f_i(x) \right| \le \gamma _i L_i \left\| x - \bar{x}^{k_i} \right\| \hbox { for all}\ x \in \mathbb {R}^n, \end{aligned}$$

(1)

from some constant $\gamma _i \ge 1$.

Note that a valid guess model can easily be built without actually knowing $L_i$ or whether $f_i(\cdot )$ is bounded from below. For instance $\tilde{f}_i^k(x) \equiv f_i(\bar{x}^{k_i})$ is already a valid model with $\gamma _i:= 1$. In Sect. 6 we will present and discuss a few possible choices for the guess model including this one.

The guess model can be seen as an inexact oracle for the functions $f_i(\cdot )$, $i=1, \dotsc , m$. Indeed, we will exploit Assumption 2 such that $\tilde{f}^k(\cdot )$ gets approximately exact when the algorithm approaches an optimal solution. Therefore, the concept and also its analysis is closely related to the notion “asymptotically exact oracles” of [3]. The main difference here is that the inexactness is not a property of the function oracle itself (we assume that all oracles are exact) but due to the way the algorithm uses the evaluation results to estimate the function values at some other point.

3 The master problem

In this section we shortly describe some important properties of the master problem. These results are well-known (see, e.g., [10], Chapter XV). The master problems solved in our algorithm are exactly the same as in classic bundle methods and need not be modified.

The master problem in a proximal bundle method has the form

$$\begin{aligned} \min \left\{ \hat{f}^k(x) + \frac{u^k}{2} \left\| x - \bar{x}^{k^-} \right\| ^2 :x \in \mathbb {R}^n \right\} \end{aligned}$$

where $u^k\in [u^{\text {lb}}, u^{\text {ub}}]$, $0 < u^{\text {lb}}\le u^{\text {ub}}$, is a bounded parameter penalizing the distance to the center $\bar{x}^{k^-}$. Note that choosing an appropriate sequence of parameters $u^k$ is quite crucial for practical performance in synchronized bundle methods and our asynchronous method as well (see, e. g. [12, 16, 18]).

Each master problem process manages its own cutting plane model $\hat{f}^k(\cdot )$. With a slight abuse of notation we do not indicate that this model may be different for each master problem process (it would be correct to write $\hat{f}^{\pi , k}$ where $\pi$ denotes a specific process). This includes the parameter $u^k$ (as a shorthand for $u^{\pi ,k}$), which may be different for each master problem process. In particular, each master problem process may choose a different strategy for managing $u^k$ depending on its cutting plane model or even different parameters may be used for the same model (in [4] authors show how running multiple parallel master problems with different prox parameters $u_k$ can be used to achieve optimal convergence rates in a synchronized setting). Furthermore we denote by $\bar{K}^\pi \subseteq K$ the subset of indices associated with process $\pi$. The master problem is a strictly convex optimization problem with a unique optimal solution $\bar{x}^k \in \mathbb {R}^n$. The optimal solution gives rise to an aggregated subgradient $\bar{g}^k \in \partial \hat{f}^k(\bar{x}^k)$ such that (see, e.g., [10], Lemma 3.1.1)

$$\begin{aligned} \bar{x}^k = \bar{x}^{k^-} - \tfrac{1}{u^k} \bar{g}^k. \end{aligned}$$

(2)

If the master problem process receives new cutting plane information $x_i \in \mathbb {R}^n$, $f_i(x_i)$ and $g_i \in \partial f_i(x_i)$ for some $i \in \{1, \dotsc , m\}$, this information is added to the local bundle and the cutting plane model. In contrast to a standard synchronized method there may not be even a single cutting plane that has been received since the previous computation of the master problem has started (in particular, no cutting plane at the previous candidate point). In fact, any number of cutting planes for any $f_i(\cdot )$, $i\in \{1, \dotsc , m\}$, belonging to different evaluation points may have been received.

Remark 1

The above setting implies that each master process should manage separate cutting plane models $\hat{f}^k_i(\cdot )$ for each $f_i(\cdot )$, $i \in \{1, \dotsc , m\}$. This indicates that disaggregated cutting plane models should be used, i.e.,

$$\begin{aligned} \hat{f}^k(x) = \sum _{i=1}^m \hat{f}^k_i(x) = \sum _{i=1}^m \max \left\{ c + \left\langle g, x \right\rangle :(c,g) \in \mathcal {B}^k_i \right\} . \end{aligned}$$

However, this is not enforced. A master problem process may also use an aggregated model of the form

$$\begin{aligned} \hat{f}^k(x) = \max \left\{ \sum _{i=1}^m (c_i + \left\langle g_i, x \right\rangle ) :(c_1, \dotsc , c_m, g_1, \dotsc , g_m) \in \mathcal {B}^k \right\} . \end{aligned}$$

Note that in an asynchronous setting it is not clear which cutting planes should be aggregated: only few functions $f_i(\cdot )$ may have been evaluated at some candidate (yet), hence only few $g_i$ are available. Therefore, a practical implementation requires a strategy to fill the missing $g_i$ in order to form an aggregated cutting plane. Possible strategies are, e.g., reusing the result of an earlier evaluation $g^l_i$ or the aggregated subgradient $\bar{g}^l_i$ for some $l < k$. Furthermore, fully aggregated and fully disaggregated models are only two extreme examples of cutting plane models. More general approaches have been proposed as well (see, e.g., [9]).

The disaggregated model is usually a much better approximation of $f(\cdot )$ and thus leads to fewer null steps, but the latter is generally easier to solve. If the number of subfunctions m is large, solving a fully disaggregated master problem may be too expensive. However, our parallel setting would even allow having multiple parallel processes solving master problems with different models simultaneously, so using more expensive master problems may be feasible. For the remainder of this paper we will assume that a fully disaggregated model is used, which makes the analysis a little easier.

As in the classic bundle method we assume that at least the cutting plane received last for each function $f_i(\cdot )$ is contained in the master process’ cutting plane model. In particular, the model of the master problem is exact at the last candidate at which each function has been evaluated.

Assumption 3

Let $i \in \{1, \dotsc , m\}$, $k \in \bar{K}^\pi$ and $k_i$ denote the index of the last candidate $\bar{x}^{k_i}$ at which $f_i(\cdot )$ has been evaluated and whose cutting plane information has been received by the master process. Then $\hat{f}^k_i(\bar{x}^{k_i}) = f_i(\bar{x}^{k_i})$.

The master problem in our algorithm is the same as for synchronous methods. In fact, any master problem satisfying the following assumption can be used. We formulate this as an assumption in order to emphasize that different variants of master problems can be used.

Assumption 4

Assume $\hat{x}^k = \hat{x}$ for all $k \ge k_0$, $k \in \bar{K}^\pi$. Then there is an $\bar{x}\in \mathbb {R}^n$ such that $\lim _{k \ge k_0} \bar{x}^k = \bar{x}$ and, under assumptions 1 and 3, $\bar{x}\in \mathop {\mathrm {\arg \,\min }}\limits _{x \in \mathbb {R}^n} f(x) + \frac{\bar{u}}{2} \left\| x - \hat{x} \right\| ^2$ for some weight $\bar{u} \in [u^{\text {lb}}, u^{\text {ub}}]$.

A simple way to satisfy Assumptions 4 is to ensure the following conditions:

• (M1) $u^k \ge u^{k-1}$ as long as the center does not change (i.e., during any sequence of nullsteps),

• (M2) $\hat{f}^{k+1}(x) \ge \hat{f}^k(\bar{x}^k) + \left\langle \bar{g}^k, x - \bar{x}^k \right\rangle$.

The first condition can obviously be satisfied by choosing an appropriate update rule for the $u^k$, the latter by ensuring $(\hat{f}_i^k(\bar{x}^k) - \left\langle \bar{g}^k_i, \bar{x}^k \right\rangle , \bar{g}^k_i) \in \mathcal {B}_i^{k+1}$ for all $i=1, \dotsc , m$. Because the sequence $u^k$ is non-decreasing and bounded, it has an accumulation point $\bar{u}$. Classic arguments ( [10], Theorem XV.3.2.4 and its proof) show that then sequence $\bar{x}^k$ has an accumulation point $\bar{x}$ (and actually converges to $\bar{x}$). Assumption 1 and 3 establish that $\hat{f}^k(\bar{x}) \approx f(\bar{x})$ for k large enough.

Remark 2

• 1. The condition $u^k \le u^{\text {ub}}$ can sometimes be relaxed in synchronized methods, for instance to $\sum _{k \ge 1} \frac{u^{k-1}}{(u^k)^2} = \infty$ (see, e.g., [10], Theorem XV.3.2.4), which means the $u^k$ should not grow “too fast”. This relies on the property of synchronized methods of adding the cutting plane of $f(\cdot )$ at $\bar{x}^k$ immediately to the bundle. However, this is difficult to establish in our asynchronous setting because the cutting plane information at $\bar{x}^k$ is not available right away, but there might be several iterations until the relevant information is available. In fact, Assumption 1 only guarantees that all functions $f_i(\cdot )$ will be evaluated sufficiently close to $\bar{x}$ eventually, and Assumption 3 gives $\hat{f}^k(\bar{x}) \approx f(\bar{x})$ for k large enough.

• 2. Condition (M2) allows that the bundles $\mathcal {B}^k_i$ can be compressed, i.e., the sizes of the bundle can be reduced to contain only two cutting planes, which is important to limit the size of the bundles in practice. In fact, it is well-known that the aggregated linear function (the right-hand side in (M2)) and a cutting plane in $\bar{x}^k$ (i.e., $(f_i(\bar{x}^k) - g^k_i, f_i(\bar{x}^k)) \in \mathcal {B}_i^k$ for some $g^k_i \in \partial f_i(\bar{x}^k)$) are enough to establish convergence (see, e.g., [2], Algorithmic Pattern 4.2). The cutting plane in $\bar{x}^k$ is replaced in the asynchronous setting by Assumption 3, i.e., each bundle $\mathcal {B}_i^k$ must contain the latest available cutting plane at $x^{k_i}$.

4 The descent step

A classic proximal bundle method performs a descent step if the actual decrease of the function value from the current center to the candidate is large compared to the expected decrease predicted by the cutting plane model. In detail, given a parameter $\varrho \in (0,1)$, the algorithm does a descent step if

$$\begin{aligned} f(\bar{x}^{k^-}) - f(\bar{x}^k) \ge \varrho \cdot (f(\bar{x}^{k^-}) - \hat{f}^k). \end{aligned}$$

The problem in the asynchronous setting is that we do not know the function values $f(\bar{x}^{k^-})$ and $f(\bar{x}^k)$ exactly. Therefore, we use the best known lower bound $\bar{f}^k \le f(\bar{x}^{k^-})$ to approximate the function value in the center and the guess model value $\tilde{f}^k$ to approximate the function value in the candidate. Denoting the predicted decrease by

$$\begin{aligned} \Delta ^k := \bar{f}^k - \hat{f}^k, \end{aligned}$$

(3)

the descent test condition for the asynchronous setting is

$$\begin{aligned} \bar{f}^k - \tilde{f}^k \ge \varrho \cdot \Delta ^k. \end{aligned}$$

The problem of this descent test is that the step might not give sufficient decrease even if the test is satisfied. Whereas using $\bar{f}^k$ instead of $f(\bar{x}^{k^-})$ is not a problem (because using a too small center value would only underestimate the decrease), using the approximated value $\tilde{f}^k$ is a problem: if $\tilde{f}^k \ll f(\bar{x}^k)$ the algorithm would overestimate the decrease and do a “bad” descent step. In order to overcome this problem we use Assumption 2 for the guess model: if each $f_i(\cdot )$ has been evaluated at some point $\bar{x}^{k_i}$, $k_i < k$, sufficiently close to (although not exactly at) the candidate $\bar{x}^k$, we know that $\left| \tilde{f}_i^k - f_i(\bar{x}^k) \right|$ is arbitrarily small for each $i \in \{1, \dotsc , m\}$. Therefore, we augment the descent test with the following precondition: let $\bar{\delta } > 0$ and $\bar{R}> 0$ be two arbitrarily large constants (say $\sim 10^{10}$), $\delta _i^k \in (0, \bar{\delta })$, $i=1, \dotsc , m$, be non-negative values (to be determined later) and denote by $k_i \le k$ the last index before k at which $f_i$ has been evaluated. A descent step is only performed if

$$\begin{aligned} \left\| \bar{x}^k - \bar{x}^{k_i} \right\| < \min \{\delta _i^k \Delta ^k, \bar{R}\} \text { for all } i \in \{1, \dotsc , m\}. \end{aligned}$$

In other words, a candidate $\bar{x}^k$ can only be accepted as new center if all functions $f_i(\cdot )$ have been evaluated sufficiently close to $\bar{x}^k$ relative to the predicted decrease ($\bar{\delta }$ can be thought of an initial estimate for $\delta ^k_i$, but can indeed be really huge so that it has no impact in practice).

Let $\bar{x}^k$ be a candidate computed by a master problem process relative to the preceding center $\bar{x}^{k^-}$ and let $\bar{g}^k$ denote the aggregated subgradient. Then the predicted decrease can be expressed as

$$\begin{aligned} \Delta ^k := \bar{f}^k - \hat{f}^k(\bar{x}^{k^-}) + \frac{1}{u^k} \left\| \bar{g}^k \right\| ^2 \ge \bar{f}^k - \hat{f}^k(\bar{x}^{k^-}) + \frac{1}{u^{\text {ub}}} \left\| \bar{g}^k \right\| ^2. \end{aligned}$$

(4)

An important consequence of this expression is that the predicted decrease is also non-negative (because $\hat{f}^k(\bar{x}^{k^-}) \le \bar{f}^k$ by definition of $\bar{f}^k$). Putting all together, the supervisor process performs a descent step if and only if the following two conditions are satisfied:

• (D1) $\left\| \bar{x}^k - \bar{x}^{k_i} \right\| < \min \left\{ \delta _i^k \Delta ^k, \bar{R}\right\}$ for all $i=1, \dotsc , m$,

• (D2) $\bar{f}^k - \tilde{f}^k \ge \varrho \cdot \Delta ^k$.

The predicted decrease $\Delta ^k$ is also a measure for the progress of the algorithm. A bundle method drives the expected progress to zero, eventually proving that the model value converges to the function value in the center and the aggregated subgradient goes to zero as well, proving optimality. We will show the same in our asynchronous setting. Furthermore, we will see that $\Delta ^k$ is also a measure for the accuracy of the guess model (and for the best known lower bound in the center as well), hence the closer we get to an optimal solution, the more precise the guess model will become.

The following is a simple but important observation that follows directly from the $\bar{R}$ bound in (D1). In fact, the validity of this result is the reason for the $\bar{R}$ bound (other assumptions could be made as well, e.g., if all $f_i(\cdot )$ have bounded level sets).

Observation 3

Assume the sequence $(f(\bar{x}^k))_{k \in K}$ is bounded from below. Then

$$\begin{aligned}\liminf _{k \in K} \tilde{f}^k > -\infty .\end{aligned}$$

In other words, if the sequence of exact function values at all evaluation points $\bar{x}^k$, $k \in K$, is bounded, then the values obtained from the guess model are also bounded.

Proof

By Assumption 2

$$\begin{aligned} \tilde{f}^k&= \sum _{i=1}^m \tilde{f}^k_i(\bar{x}^k) = \sum _{i=1}^m \Big (\underbrace{(\tilde{f}^k_i(\bar{x}^k) - f_i(\bar{x}^k))}_{{\mathop {\ge }\limits ^{\text {(1)}}} - \gamma _i L_i \left\| \bar{x}^k - \bar{x}^{k_i} \right\| } + f_i(\bar{x}^k)\Big ) \\&\ge \sum _{i=1}^m \Big (f_i(\bar{x}^k) - \gamma _i L_i \left\| \bar{x}^k - \bar{x}^{k_i} \right\| \Big ) \ge f(\bar{x}^k) - \sum _{i=1}^m \gamma _i L_i \bar{R}\end{aligned}$$

and the claim follows because the last term is bounded from below. $\square$

Another consequence of the $\bar{R}$-bound in (D1) is that, together with Assumption 2, the guess model can be interpreted as an inexact oracle with bounded error for all descent steps (i.e., $E^g = 0, E^f \le E_{\max }$ in the setting of [5]). Hence, the convergence results from there can be applied. A simple way to obtain an asymptotically exact oracle (with vanishing errors) would be to simply let $\delta ^k_i \xrightarrow {k \rightarrow \infty } 0$. However, it might not be clear in general how fast these $\delta ^k_i$ should go to zero, which certainly depends on the functions to be optimized. Hence, our goal is to manage the accuracy of the guess model automatically. In our analysis we will prove that with our accuracy management the guess model becomes asymptotically exact and the sequence of centers converges to an optimal solution.

5 Convergence analysis

The convergence analysis for bundle methods usually distinguishes two cases: whether the algorithm does only a finite number of descent steps, proving that the final center is an optimal solution, or it does an infinite number of descent steps. We will do the same and adapt the classic analysis to our asynchronous setting.

5.1 Finite number of descent steps

In this section we deal with the first case that the algorithm does only a finite number of descent steps. The following is a classic result for proximal bundle methods but extended to the asynchronous setting.

Theorem 4

Assume there is a $\bar{k} \in K$ such that the algorithm performs only null-steps, i.e., $\hat{x}^k = \hat{x}$ for some $\hat{x}\in \mathbb {R}^n$ and all $k \ge \bar{k}$. Then

$$\begin{aligned}\hat{x}\in \mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f. \end{aligned}$$

Proof

Fix an arbitrary master process $\pi$ and denote by $\bar{K}^\pi \subseteq \bar{K}$ the subsequence of candidates generated by $\pi$ for the final center. For every $k \in \bar{K}^\pi$ let $\hat{f}^k(\cdot )$ denote the cutting plane model of $\pi$ used to generate $\bar{x}^k$. By Assumption 4 this sequence of candidates converges to some limit point $\lim _{k \in \bar{K}^\pi } \bar{x}^k = \bar{x}$ and

$$\begin{aligned} \lim _{k \in \bar{K}^\pi } \hat{f}^k(\bar{x}^k) = f(\bar{x}). \end{aligned}$$

(5)

Because each $f_i(\cdot )$ is guaranteed to be evaluated infinitely often (Assumption 1), this implies that eventually conditions (D1) will be satisfied for all $k \ge k_0$ for some $k_0 \ge \bar{k}$. However, no descent step occurs, so (D2) must not be satisfied, and we know

$$\begin{aligned} \varrho \Delta ^k = \varrho (\bar{f}^k - \hat{f}(\bar{x}^k)) > \bar{f}^k - \tilde{f}^k(\bar{x}^k) \end{aligned}$$

(6)

for all $k \ge k_0$. The sequence of lower bounds in the center $\bar{f}^k$ is non-decreasing and bounded, hence converging to some value $\bar{f}^k \uparrow \bar{f}\le f(\hat{x})$. Furthermore, the guess models must become arbitrarily exact at $\bar{x}$, too:

$$\begin{aligned}&\left| \tilde{f}_i^k(\bar{x}^k) - f_i(\bar{x}) \right| = \left| \tilde{f}_i^k(\bar{x}^k) - f_i(\bar{x}^k) + f_i(\bar{x}^k) - f_i(\bar{x}) \right| \\&\qquad \le \underbrace{\left| \tilde{f}_i^k(\bar{x}^k) - f_i(\bar{x}^k) \right| }_{\le \gamma _i L_i\left\| \bar{x}^k - \bar{x}^{k_i} \right\| } + \underbrace{\left| f_i(\bar{x}^k) - f_i(\bar{x}) \right| }_{\le L_i\left\| \bar{x}^k - \bar{x} \right\| } \le \gamma _i L_i \left\| \bar{x}^{k_i} - \bar{x}^k \right\| + L_i \left\| \bar{x}^k - \bar{x} \right\| , \end{aligned}$$

and the right-hand side converges to zero. Because this holds for all $i=1, \dotsc , m$, we may conclude

$$\begin{aligned} \lim _{k \in \bar{K}^\pi } \tilde{f}^k(\bar{x}^k) = f(\bar{x}). \end{aligned}$$

(7)

Using (5)-(7) as well as $\varrho \in (0,1)$ and $\Delta ^k \ge 0$ we get

$$\begin{aligned} \lim _{k \in \bar{K}^\pi } \varrho \Delta ^k = \varrho (\bar{f}- f(\bar{x})) \ge \bar{f}- f(\bar{x}), \end{aligned}$$

which can only be true if $\lim _{k \in \bar{K}^\pi } \Delta ^k = 0$. By (2) and (4) $\hat{x}= \bar{x}= \lim _{k \in \bar{K}^\pi } \bar{x}^k$.

By Assumption 3 the model is exact at the last candidate, i.e., $\hat{f}_i^k(\bar{x}^{k_i}) = f_i(\bar{x}^{k_i})$ for all $i=1, \dotsc , m$, therefore

$$\begin{aligned} \left| \hat{f}_i^k - f_i(\bar{x}^k) \right| \le \underbrace{\left| \hat{f}_i^k(\bar{x}^k) - \hat{f}_i^k(\bar{x}^{k_i}) \right| }_{\rightarrow 0} + \underbrace{\left| \hat{f}_i^k(\bar{x}^{k_i}) - f_i(\bar{x}^{k_i}) \right| }_{=0} + \underbrace{\left| f_i(\bar{x}^{k_i}) - f_i(\bar{x}^k) \right| }_{\rightarrow 0} \xrightarrow {k \in \bar{K}^\pi } 0. \end{aligned}$$

Because $\bar{g}^k \in \partial \hat{f}^k(\bar{x}^k)$ and $\left\| \bar{g}^k \right\| \rightarrow 0$ by (4) this proves $0 \in \partial f(\hat{x})$ and thus $\hat{x}\in \mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f$. $\square$

Note that the proof actually shows that the sequence of candidates generated by each single master problem process converges to the center and the model of each master process shows the optimality of the center. Therefore, the sequences of all (independent) master problem processes converge to the same point.

5.2 Infinite number of descent steps

In this section we deal with the case that the algorithm performs an infinite number of descent steps. For this, let $\hat{K}\subseteq K$ denote the global iterates corresponding to the update of the center, i.e., $\forall \,k \in \hat{K}:\hat{x}^{k+1} = \bar{x}^k$. In particular, for these iterates the descent condition must be satisfied

$$\begin{aligned} 0 \le \varrho \cdot \Delta ^k \le \bar{f}^k - \tilde{f}^k \end{aligned}$$

for some $\varrho \in (0,1)$. For a given $k \in \hat{K}$ we denote by $k^-\in \hat{K}$ the index of the descent step that led to the center relative to which $\bar{x}^k$ has been computed (i.e.  $\hat{x}^{(k^-) + 1} = \bar{x}^{k^-}$). Let $\hat{K}_{k_0}^l:= \left\{ k_1, \ldots , k_p \in \hat{K} :k_0< k_1< \cdots < k_p = l \right\}$ be a consecutive sequence of descent steps such that $k^-_j = k_{j-1}$ for $j=1, \dotsc , p$, i.e., each candidate $\bar{x}^{k_j}$ has been computed relative to $\bar{x}^{k_{j-1}}$. If we sum up the predicted decrease of all steps in such a consecutive sequence we get

$$\begin{aligned} \begin{aligned} \varrho \sum _{k \in \hat{K}_{k_0}^l} \Delta ^k&\le \sum _{k \in \hat{K}_{k_0}^l} (\bar{f}^k - \tilde{f}^k) = \sum _{k \in \hat{K}_{k_0}^l} (\bar{f}^k - \tilde{f}^{k^-}) + \sum _{k \in \hat{K}_{k_0}^l} (\tilde{f}^{k^-} - \tilde{f}^k) \\&= (\tilde{f}^{k_0} - \tilde{f}^{l}) + \sum _{k \in \hat{K}_{k_0}^l} (\bar{f}^k - \tilde{f}^{k^-}). \end{aligned} \end{aligned}$$

(8)

This inequality has a nice interpretation: the sum of the expected decreases is bounded by the total decrease $(\tilde{f}^{k_0} - \tilde{f}^{l})$ and the sum of “errors” made for the center values: let $\hat{x}= \hat{x}^k$ be the center at a descent step $k \in \hat{K}$ that was the candidate at iteration $k^-$. The error made in this center is the difference between the best known lower bound $\bar{f}^{k}$ at iteration k (when $\hat{x}$ is the current center) and the guessed value $\tilde{f}^{k^-}$ at iteration $k^-$ (when $\hat{x}$ was the candidate to be made the new center). If we can show that the above sum is bounded, we can conclude that $\Delta ^k \rightarrow 0$ and, similar to the previous section, that $\tilde{f}^k$ gets asymptotically exact, i.e., $\tilde{f}^k \rightarrow f(\bar{x}^k)$. The problematic part is the sum of the errors made for the center values. In a classic bundle method with exact evaluations this term is zero. However, because we use inexact or outdated information we have to take measures to ensure that the sum of errors remains bounded. The following Lemma makes this more precise. In fact, it suffices to ensure that the errors are small compared to the expected progress (such that the errors cannot obliterate the progress completely).

Lemma 5

Let $\alpha \in (0,1)$ and assume that there is a $k_0 \in \hat{K}$ such that for the guess value $\tilde{f}^{k^-}$ of $f(\bar{x}^{k^-})$ at the preceding descent step $k^-$ (when $\bar{x}^{k^-}$ became the new center) and the best known lower bound $\bar{f}^{k}$ of $f(\bar{x}^{k^-})$ at the current descent step (when $\bar{x}^{k^-}$ is left and $\bar{x}^k$ becomes the center)

$$\begin{aligned} \bar{f}^{k} - \tilde{f}^{k^-} \le \alpha \cdot \varrho \cdot \Delta ^{k^-} \end{aligned}$$

(9)

for all k with $k^-\ge k_0$ and $\lim _{k \in K} \tilde{f}^k$ is bounded from below. Then there is a constant $C_{k_0} \in \mathbb {R}$ such that for any consecutive sequence of center points $\hat{K}' \subseteq \hat{K}$ the sum of predicted decreases is bounded $\sum _{k \in \hat{K}'} \Delta ^k \le C_{k_0} < \infty$.

Proof

Let $\hat{K}'\subseteq \hat{K}$ be a consecutive sequence of points and $\hat{K}_{l_0}^l \subseteq \hat{K}'$ a finite consecutive subsequence of $\hat{K}'$ such that $l_0 \ge k_0$ is as small as possible. Note that $l_0$ only depends on $k_0$ because there is only a finite number of master processes and for each master process there is a unique smallest index $\ge k_0$ at which it is started. From (8) and (9) we get

$$\begin{aligned} \varrho \sum _{k \in \hat{K}_{l_0}^l} \Delta ^{k}&\le \tilde{f}^{l_0} - \tilde{f}^{l} + \sum _{k \in \hat{K}_{l_0}^l} \alpha \varrho \Delta ^{k^-} = \tilde{f}^{l_0} - \tilde{f}^{l} + \sum _{k \in \hat{K}_{l_0}^{l}} \alpha \varrho \Delta ^{k} + \alpha \varrho \Delta ^{l_0} - \alpha \varrho \Delta ^{l}. \end{aligned}$$

Rearranging terms gives

$$\begin{aligned} (1 - \alpha ) \varrho \sum _{k \in \hat{K}_{k_0}^l} \Delta ^{k} \le \tilde{f}^{l_0} - \tilde{f}^{l} + \alpha \varrho \Delta ^{l_0} - \alpha \varrho \Delta ^l. \end{aligned}$$

Using $\Delta ^k \ge 0$ for all $k \in \hat{K}$ and the assumption that $\tilde{f}^k$ is bounded from below shows $\lim _{l \rightarrow \infty } \sum _{k \in \hat{K}_{l_0}^l} \Delta ^k \le C_{k_0} < \infty$ because the right-hand side only depends on $k_0$. $\square$

Although condition (9) looks quite simple, it cannot be tested directly: at the moment the algorithm has to decide whether a descent step is made, only $\Delta ^k$ and $\tilde{f}^k$ are known but the future $\bar{f}^{l}$ with $l^- = k$ will not be known definitely before the succeeding descent step $l \in \hat{K}$. In Sect. 6.1 we will see how to overcome this problem.

Lemma 6

Suppose there is an infinite number of descent steps and $f(\bar{x}^k) \ge f(\hat{x})$ for some $\hat{x}\in \mathbb {R}^n$ and all $k \in \hat{K}$ and $\bar{f}^{k} - \tilde{f}^{k^-} \le \alpha \cdot \varrho \cdot \Delta ^{k^-}$ for all $k \ge k_0$. Then the $\bar{x}^k$ converge to a minimizer of f. In particular, $\mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f \ne \emptyset$.

Proof

(This proof is along the lines of [8, Lemma 5.3.5]) First, note that the lower bound in the center gets asymptotically exact. Let $k \in \hat{K}$ be a descent step and $k^-\in \hat{K}$ the preceding descent step. Then by (D1) and because $\hat{f}^{k^-}_i$ is exact at the point $\bar{x}^{k^-_i}$ of the last evaluation of $f_i$ before iteration $k^-$ (i.e.  $\hat{f}_i^{k^-}(\bar{x}^{k^-_i}) = f_i(\bar{x}^{k^-_i})$) we get

$$\begin{aligned} \nonumber f_i(\bar{x}^{k^-}) - \bar{f}^{k}_i&= \underbrace{f_i(\bar{x}^{k^-}) - f_i(\bar{x}^{k^-_i})}_{\le L_i\left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| } + \underbrace{\hat{f}^{k^-}_i(\bar{x}^{k^-_i}) - \hat{f}^{k^-}_i(\bar{x}^{k^-})}_{\le L_i \left\| \bar{x}^{k^-_i} - \bar{x}^{k^-} \right\| } + \underbrace{\hat{f}^{k^-}_i(\bar{x}^{k^-}) - \bar{f}^{k}_i}_{\le 0} \\&\le 2L_i\left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| {\mathop {\le }\limits ^{\text {(D1)}}} 2L_i\delta ^{k^-}_i\Delta ^{k^-} \le 2 L_i \bar{\delta } \Delta ^{k^-} \end{aligned}$$

(10)

for all $i=1, \dotsc , m$. By the subgradient inequality

$$\begin{aligned} f(\bar{x}^{k^-}) \ge f(\hat{x}) \ge \hat{f}^k(\bar{x}^k) + \left\langle \bar{g}^k, \hat{x}- \bar{x}^k \right\rangle \end{aligned}$$

and by (2) (and because $\bar{x}^{k^-}$ is the center relative to which $\bar{x}^k$ has been computed)

$$\begin{aligned} \bar{g}^k = u^k \cdot (\bar{x}^{k^-} - \bar{x}^k). \end{aligned}$$

(11)

Using $\hat{f}^k(\bar{x}^{k}) = \hat{f}^{k^-}$ the distance of $\bar{x}^k$ to $\hat{x}$ can be bounded

for some constant $C > 0$. Let $\hat{K}_{l_0}^k$ be a consecutive sequence of descent steps eventually generating center $\hat{x}^k$ with $l_0 \ge k_0$ as small as possible. Iterating the argument above for all descent steps $l \in \hat{K}_{l_0}^k$

$$\begin{aligned} \left\| \hat{x}- \bar{x}^k \right\| ^2 \le \left\| \hat{x}- \bar{x}^{l_0} \right\| ^2 + 2C \sum _{l \in \hat{K}_{l_0}^k} \Delta ^l + \Delta ^{l_0} < \infty . \end{aligned}$$

(12)

The sum in (12) is finite because $f(\hat{x}^k) \ge f(\hat{x})$ implies by Observation 3 that the $\tilde{f}^k$ are bounded from below as well, so we can apply Lemma 5. This shows that the sequence of centers is bounded and therefore has an accumulation point $\tilde{x}$.

Next we show that each limit point is a minimizer of f. By (D1) and $\hat{f}^k_i(\bar{x}^{k_i}) = f_i(\bar{x}^{k_i})$ we know for the model value for each $i=1, \dotsc , m$

$$\begin{aligned} \nonumber \left| \hat{f}^k_i(\bar{x}^k) - f_i(\bar{x}^k) \right|&\le \underbrace{\left| \hat{f}^k_i(\bar{x}^k) - \hat{f}^k_i(\bar{x}^{k_i}) \right| }_{\le L_i \left\| \bar{x}^k - \bar{x}^{k_i} \right\| } + \underbrace{\left| \hat{f}^k_i(\bar{x}^{k_i}) - f_i(\bar{x}^{k_i}) \right| }_{=0} + \underbrace{\left| f_i(\bar{x}^{k_i}) - f_i(\bar{x}^k) \right| }_{\le L_i \left\| \bar{x}^{k_i} - \bar{x}^k \right\| } \\&\le 2L_i \left\| \bar{x}^k - \bar{x}^{k_i} \right\| \le 2 L_i \bar{\delta } \Delta ^k. \end{aligned}$$

(13)

Let $x \in \mathbb {R}^n$ be an arbitrary point. The subgradient inequality states

$$\begin{aligned} f(x) \ge \hat{f}^k(\bar{x}^k) + \left\langle \bar{g}^k, x - \bar{x}^k \right\rangle \end{aligned}$$

and (4) and (13) imply that the right-hand side of this inequality converges to $f(\tilde{x})$ for a proper subsequence of center points converging to $\tilde{x}$, hence $\tilde{x} \in \mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f$.

Finally, we may replace $\hat{x}$ with $\tilde{x}$ in inequality (12) and choose $k_0$ so that the right-hand side is smaller than some arbitrary $\varepsilon > 0$. This shows $\bar{x}^k \rightarrow \tilde{x}$ completing the proof. $\square$

Putting all together we can prove now that in case of an infinite number of descent steps the sequence of centers minimizes the function and converges to an optimal solution if one exists.

Theorem 7

Suppose there is an infinite number of descent steps and $\bar{f}^k - \tilde{f}^{k^-} \le \alpha \cdot \varrho \cdot \Delta ^{k^-}$ for all $k \ge k_0$. Then $\lim _{k \in \hat{K}} \tilde{f}^k = \lim _{k \in \hat{K}} \bar{f}^k = \lim _{k \in \hat{K}} f(\bar{x}^k) = \inf f$ and $\lim _{k \in \hat{K}} \bar{x}^k \in \mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f$ if $\mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f \ne \emptyset$.

Proof

If there is an $x \in \mathbb {R}^n$ with $f(\bar{x}^k) \ge f(x)$ for all $k \in \hat{K}$, then by Lemma 6 the sequence of centers converges to a minimizer of f. In particular this is the case if $\mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f \ne \emptyset$. Otherwise $\mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits f = \emptyset$ and $f(\bar{x}^k) < f(x)$ for each $x \in \mathbb {R}^n$ and infinitely many $k \in \hat{K}$. Hence $\lim _{k \in \hat{K}} f(\bar{x}^k) = \inf f$. $\square$

6 The guess model

The guess model is a central feature of our algorithm. It determines approximate function values at candidate points $\bar{x}^k$ if a function $f_i(\cdot )$ has not been evaluated at $\bar{x}^k$, yet. We have already discussed basic properties of the guess model in Sect. 2.2 but we did not present actual possible implementations of the guess model. In this section we will first prove a central claim that states that the requirements for the convergence results of the previous section (namely condition (9) are indeed satisfied if we use a valid guess model). In particular, we will specify the missing piece of descent condition (D1), namely the precise values of the $\delta ^k_i$, $i=1, \dotsc , m$, $k \in K$. We start with the assumption that the Lipschitz constants are known and then extend to the case where the Lipschitz constants are not known. Finally, we present different possibilities for choosing the guess model.

6.1 The descent step radius with known Lipschitz constants

Knowing the Lipschitz constants, $L_i$, $i=1, \dotsc , m$, easily allows adjusting the $\delta ^k_i$ so that the error made by the guess model is small compared to the predicted decrease $\Delta ^k$.

Observation 8

Let $\alpha \in (0,1)$, set $\delta ^k_i:= \min \left\{ \frac{\alpha \varrho }{(1 + \gamma _i) m L_i}, \bar{\delta }\right\}$ for all $k \in K$ and $i=1, \dotsc , m$. Then $\bar{f}^k - \tilde{f}^{k^-} \le \alpha \cdot \varrho \cdot \Delta ^{k^-}$ for all $k \in K$ whenever (D1) holds at $k^-$.

Proof

Each $\bar{f}^k_i$ is a lower bound on $f_i(\bar{x}^{k^-})$, hence

$$\begin{aligned} \sum _{i=1}^m (\bar{f}^k_i - \tilde{f}^{k^-}_i)&= \sum _{i=1}^m \Big (\underbrace{(\bar{f}_i^k - f_i(\bar{x}^{k^-_i}))}_{\le f_i(\bar{x}^{k^-}) - f_i(\bar{x}^{k^-_i}) \le L_i\left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| } + \underbrace{(f_i(\bar{x}^{k^-_i}) - \tilde{f}^{k^-}_i))}_{\le \gamma _i L_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| \text { by Ass.~ (2)}} \Big ) \\&\le \sum _{i=1}^m (1 + \gamma _i) L_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| \\ \text {(by (D1))} \quad&\le \sum _{i=1}^m (1 + \gamma _i) L_i \frac{\alpha \varrho }{(1 + \gamma _i) m L_i} \Delta ^{k^-} \le \alpha \varrho \Delta ^{k^-}. \end{aligned}$$

$\square$

If the Lipschitz constants $L_i$ are known, the convergence of the algorithm follows. However, we will show in the next section that if these constants are not known, the algorithm can compute a suitable approximation during the run.

6.2 The descent step radius with unknown Lipschitz constants

If the Lipschitz constants $L_i$, $i=1, \dotsc , m$, are not known, the algorithm can determine a suitable approximation during its run. Intuitively it is sufficient to compare function values computed by the oracle calls and to derive the Lipschitz constants from them. For this, observe that in the proof of Observation 8 the Lipschitz constant $L_i$ is used to bound two terms: $\bar{f}^k_i - f_i(\bar{x}^{k^-_i}) \le L_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\|$ and $f_i(\bar{x}^{k^-_i}) - \tilde{f}^{k^-}_i \le \gamma _i L_i \left\| \bar{x}^{k^-_i} - \bar{x}^{k^-} \right\|$. In particular, all values taking part in these estimations ($\bar{f}^k_i$, $f_i(\bar{x}^{k^-_i})$, $\tilde{f}^{k^-}_i$) are known at some point in the algorithm. Hence, the main idea is to keep a lower bound $L^k_i \le L_i$, $i=1, \dotsc , m$, $k \in K$, of each Lipschitz constant $L_i$ and increase this lower bound as soon as condition (9) is observed as not satisfied. Formally, let $k \in \hat{K}$ be a descent step (i.e., the descent conditions have been satisfied) with old center $\bar{x}^{k^-}$ and candidate $\bar{x}^k$. We will first check if an update of the Lipschitz constants is necessary ((L1) and (L2)) and if this is the case, then enlarge the $L_i^k$ in two steps to an intermediate value $L_i^{k+1/2}$ and the new value $L_i^{k+1}$ ((L3) and (L4)).

• (L1) If $k \in K$ is not a descent step, set $L^{k+1}_i \leftarrow L^k_i$, $i=1, \dotsc , m$.

• (L2) If $\bar{f}^k - \tilde{f}^{k^-} \le \alpha \varrho \Delta ^{k^-}$, set $L^{k+1}_i \leftarrow L^k_i$, $i=1, \dotsc , m$.

• (L3) If $\left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| > 0$, then $L^{k+1/2}_i \leftarrow \max \left\{ L^k_i, (\bar{f}_i^{k^-} - f_i(\bar{x}^{k^-_i})) / \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| \right\}$, otherwise $L_i^{k+1/2} \leftarrow L^k_i$.

• (L4) If $\left\| \bar{x}^{k^-} {-} \bar{x}^{k^-_i} \right\| {>} 0$, then $L^{k+1}_i {\leftarrow } \max \left\{ L^{k+1/2}_i, (f_i(\bar{x}^{k^-_i}) {-} \tilde{f}^k_i) / (\gamma _i\left\| \bar{x}^{k^-} {-} \bar{x}^{k^-_i} \right\| )\right\}$, otherwise $L^{k+1}_i \leftarrow L^{k+1/2}_i$.

Only descent steps are important for this estimation (step (L1)). When we leave center $\hat{x}^k$ we know the final value of $\bar{f}^k$, and we can verify if (9) was satisfied in the previous descent step (step (L2)). If not, then at least one of the inequalities

$$\begin{aligned} \bar{f}^k_i - f_i(\bar{x}^{k^-_i})&\le L^{k^-}_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\|{} & {} \text {and}&f_i(\bar{x}^{k^-_i}) - \tilde{f}^{k^-}_i \le \gamma _i L^{k^-}_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| \end{aligned}$$

for some $i=1, \dotsc , m$ must be violated. We then enlarge $L^{k+1}_i$ so that those inequalities would be satisfied with these larger constants (steps (L3)and (L4)). Note that test (L2) ensures that the $L_i^k$ are only updated if the error made over all functions has been too large. It might be the case that some functions had a too large error (i.e., $L_i^k$ has been too small) but the overall error was small enough.

Although the constants $L^{k}_i$ are only increased in the next descent step, which may seem to be too late, they will become increasingly better approximations of the real Lipschitz constant $L_i$ and this will be sufficient for convergence. In order to show this, note first that the sequence $(L_i^k)_{k \in K}$ is non-decreasing and bounded (by $L_i$), so it has a limit $\bar{L}_i \le L_i$ and $L^k_i \le \bar{L_i}$ for all $i=1, \dotsc , m$ and all $k \in K$.

Theorem 9

Let $\alpha \in (0,1)$, set $\delta ^k_i:= \min \left\{ \frac{\alpha \varrho }{(1 + \gamma _i) m L^k_i}, \bar{\delta }\right\}$ for all $k \in K$ and $i=1, \dotsc , m$. Then there is a $k_0 \in K$ such that $\bar{f}^k - \tilde{f}^{k^-} \le \frac{1 + \alpha }{2} \cdot \varrho \cdot \Delta ^{k^-}$ for all $k \in K$, $k \ge k_0$, whenever (D1) holds.

Proof

Because $\bar{L}_i = \lim _{k \in K} L^k_i$ for each $\varepsilon > 0$ there is a $k_\varepsilon \in K$ such that $\bar{L}_i - \varepsilon \le L_i^k$ for all $i \in \{1, \dotsc , m\}$ and all $k \in K$ with $k \ge k_\varepsilon$.

$$\begin{aligned} \sum _{i=1}^m (\bar{f}^k_i - \tilde{f}^{k^-}_i)&= \sum _{i=1}^m \big (\underbrace{(\bar{f}^k_i - f_i(\bar{x}^{k^-_i}))}_{\le \bar{L}_i\left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| } + \underbrace{(f_i(\bar{x}^{k^-_i}) - \tilde{f}^{k^-}_i)}_{\le \gamma _i \bar{L}_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| } \big ) \le \sum _{i=1}^m (1 + \gamma _i) \bar{L}_i \left\| \bar{x}^{k^-} - \bar{x}^{k^-_i} \right\| \\ \text {(by (D1))} \quad&\le \sum _{i=1}^m (1 + \gamma _i) \bar{L}_i \frac{\alpha \varrho }{(1 + \gamma _i) m L^{k^-}_i} \Delta ^{k^-} \le \sum _{i=1}^m (1 + \gamma _i) \bar{L}_i \frac{\alpha \varrho }{(1 + \gamma _i) m (\bar{L}_i - \varepsilon )} \Delta ^{k^-} \\&\le \alpha \varrho \Delta ^{k^-} \left( \frac{1}{m} \sum _{i=1}^m \frac{\bar{L}_i}{\bar{L}_i - \varepsilon }\right) . \end{aligned}$$

By choosing $\varepsilon = \frac{1 - \alpha }{1 + \alpha } \cdot \min \{\bar{L}_1, \dotsc , \bar{L}_m\}$ the right-hand term can be bounded by

$$\begin{aligned} \alpha \varrho \Delta ^{k^-} \cdot \left( \frac{1}{m} \sum _{i=1}^m \frac{\bar{L}_i}{\bar{L}_i - \frac{1-\alpha }{1+\alpha } \bar{L}_i} \right) = \frac{1+\alpha }{2} \varrho \Delta ^{k^-}. \end{aligned}$$

$\square$

6.3 Possible guess models

In this section we describe possible choices for valid guess models. The simplest choice for $\tilde{f}^k_i(\cdot )$ is to use the function value at another (possibly close) point, i.e.,

$$\begin{aligned} \tilde{f}^{1,k}_i(x) := f_i(\bar{x}^{k_i}) \hbox { for all}\ x \in \mathbb {R}^n. \end{aligned}$$

Obviously, this model satisfies Assumption 2 with $\gamma _i = 1$ for all $i=1, \dotsc , m$:

$$\begin{aligned} \left| f_i(x) - \tilde{f}^{1,k}_i(x) \right| = \left| f_i(x) - f_i(\bar{x}^{k_i}) \right| \le 1 \cdot L_i \left\| x - \bar{x}^{k_i} \right\| . \end{aligned}$$

Another natural choice for the guess model $\tilde{f}^k_i(\cdot )$ is the cutting model $\hat{f}_i^k$ itself, i.e.,

$$\begin{aligned} \tilde{f}^{2,k}_i(x):= \hat{f}^k_i(x). \end{aligned}$$

This is basically the idea of the incremental bundle method presented in [5]. Then (because $f_i(\bar{x}^{k_i}) = \hat{f}_i^k(\bar{x}^{k_i})$)

$$\begin{aligned} \left| f_i(x) - \tilde{f}^{2,k}_i(x) \right|&= \left| f_i(x) - \hat{f}^k_i(x) \right| \le \underbrace{\left| f_i(x) - f_i(\bar{x}^{k_i}) \right| }_{\le L_i \left\| x - \bar{x}^{k_i} \right\| } + \underbrace{\left| \hat{f}^k_i(x^{k_i}) - \hat{f}^k_i(x) \right| }_{\le L_i \left\| x - \bar{x}^{k_i} \right\| } \\&\le 2 L_i \left\| x - \bar{x}^{k_i} \right\| , \end{aligned}$$

hence the cutting plane model is a valid guess model with $\gamma _i = 2$ for all $i=1, \dotsc , m$. Interestingly, the simple model provides the smaller constant $\gamma _i$. The reason is that the cutting plane model underestimates the true function value more easily than the simple model. A third possible model is therefore a combination of both

$$\begin{aligned} \tilde{f}^{3,k}_i(x):= \max \{ \tilde{f}^{1,k}_i(x), \tilde{f}^{2,k}_i(x) \}, \end{aligned}$$

which is also valid with $\gamma _i = 1$ for all $i=1, \dotsc , m$.

Remark 10

An important motivation for using the cutting plane guess model $\tilde{f}^{2,k}(\cdot )$ are Lagrangian relaxation approaches of combinatorial optimization problems [7, 13, 14]. Here the functions $f_i(x)$ are defined as

$$\begin{aligned} f_i(x):= \max \left\{ (c - A_i^T x)^T z :z \in Z_i \right\} \end{aligned}$$

where $Z_i$ is a combinatorial, often finite set. A subgradient $g \in \partial f_i(x)$ is given by an optimal solution $z_i^* \in \mathop {\mathrm {{\text {*}}{Arg}\,\max }}\limits \left\{ (c - A_i^T x)^T z_i :z_i \in Z_i \right\}$ via $g = (-A_i z_i)$. The optimal value of this problem typically changes for each evaluation of $f_i(\cdot )$ because the candidate x changes. However, because the $Z_i$ are finite, the optimal solution $z_i^*$ does not change very frequently. In fact, the set of optimal solutions generated throughout the algorithm is often quite small (in particular in the later iterations when the candidates $\bar{x}^k$ do not change that much between evaluations). Hence, as soon as these solutions and the corresponding subgradients are contained in the cutting plane model, the model is in fact exact (i.e., $\tilde{f}^k_i(\bar{x}^k) = f_i(\bar{x}^k)$) in many cases. In this situation evaluating the function $f_i$ does not lead to new cutting plane information (the guess model is equally good) in most iteration but merely verifies that the guess model is indeed exact or catches the few cases where it is not.

Remark 11

Note that the guess model does not give a valid upper bound on the function value in general. In particular, the cutting plane model $\tilde{f}^{2,k}_i(\cdot )$ is a lower model and does not provide upper bounds at all. The problem is that guess models are guaranteed to be exact only at the evaluation points (at the last preceding candidate point at which $f_i(\cdot )$ has been evaluated to be precise) and this may be different for each $i=1, \dotsc , m$. This is a problem when the algorithm terminates as, e.g., the final result is not guaranteed to be a valid upper bound for the Lagrangian relaxation problem. However, there is a simple work-around: when the algorithm is about to stop at a certain point $\hat{x}^k$, all oracles must be evaluated once at this point, also see Remark 13 below.

6.4 Restriction to active subspaces

The main motivation of [6] was that in Lagrangian relaxation approaches many functions $f_i(\cdot )$ only depend on few variables. The algorithm presented in [6] basically detected these dependencies by observing which components of the subgradients $g_i \in \partial f_i(\bar{x}^k)$ are non-zero: as long as all observed subgradients have a zero entry in some component, the function $f_i(\cdot )$ is assumed to be constant along the subspace corresponding to this component. Furthermore, because the cutting plane model is built from the observed subgradients, the cutting plane model is constant along these subspaces, too.

A similar observation led to the development of Dynamic Bundle Methods [1]. The idea here is to maintain a set of active constraints in a Lagrangian relaxation approach in order to keep the number of (non-zero) dual variables small. If some formerly inactive constraints become violated during the algorithm, they are added to the set of active constraints.

We want to show how this idea can be incorporated into our algorithm. The main motivation for this is that condition (D1) is a global condition, restricting the distance of the last evaluation point $\bar{x}^{k_i}$ for some $i=1, \dotsc , m$ from the candidate $\bar{x}^k$ in all components $x_j$, $j=1, \dotsc , n$. However, if some function $f_i(\cdot )$ does not depend on some variable $x_j$, such a global condition seems too strong. Indeed, if $f_i(\cdot )$ does not depend on $x_j$ at all, a non-zero difference $(\bar{x}^k - \bar{x}^{k_i})_j \ne 0$ should not impede the acceptance of the candidate. Although the information whether a certain $f_i(\cdot )$, $i=1, \dotsc , m$, depends on some variable $x_j$, $j=1, \dotsc , n$, might be known from the problem structure, it can be detected automatically using an active set strategy like in [1] or [6]. We show how (D1) can be relaxed to obtain a weaker condition that exploits the detected active sets.

For this, let $J_i^k \subseteq \{1, \dotsc , n\}$, $i=1,\dotsc ,m$, $k \in K$, denote the subset of indices for which some subgradient of function $f_i(\cdot )$ with a non-zero entry in that component has been observed until iteration $k \in K$, i.e.,

$$\begin{aligned} J_i^k:= \bigcup _{\begin{array}{c} l \le k \\ l \in K_i \end{array}} \mathop {\textrm{supp}}\limits (g^l_i) \end{aligned}$$

where $K_i \subseteq K$ denotes the global indices corresponding to a new evaluation result of $f_i(\bar{x}^{k_i})$ and $g^k_i \in \partial f_i(\bar{x}^{k_i})$. Obviously, these sets can easily be tracked by the supervisor process.

The main idea now is that for function $f_i(\cdot )$ we only need to consider the components on the subspace $J^k_i$. For each vector $x \in \mathbb {R}^n$ and $J\subseteq \{1, \dotsc , n\}$ denote by $x_{J}$ the subvector consisting only of the components of $J$. We replace (D1) by

• (D1’) $\left\| \bar{x}^k_{J_i^k} - \bar{x}^{k_i}_{J_i^k} \right\| < \delta _i^k\Delta ^k$ and $\left\| \bar{x}^k - \bar{x}^{k_i} \right\| < \bar{R}$ for all $i=1, \dotsc , m$,

and the update conditions (L3) and (L4) for the $L_i^k$ by

• (L3’) If $\left\| \bar{x}_{J^{k^-}_i}^{k^-} - \bar{x}_{J^{k^-}_i}^{k^-_i} \right\| > 0$, then

  $$\begin{aligned} L^{k+1/2}_i \leftarrow \max \left\{ L^k_i, (\bar{f}_i^{k^-} - f_i(\bar{x}^{k^-_i})) / \left\| \bar{x}^{k^-}_{J^{k^-}_i} - \bar{x}^{k^-_i}_{J^{k^-}_i} \right\| \right\} , \end{aligned}$$

  otherwise $L_i^{k+1/2} \leftarrow L^k_i$.

• (L4’) If $\left\| \bar{x}_{J^{k^-}_i}^{k^-} - \bar{x}_{J^{k^-}_i}^{k^-_i} \right\| > 0$, then

  $$\begin{aligned} L^{k+1}_i \leftarrow \max \left\{ L^{k+1/2}_i, (f_i(\bar{x}^{k^-_i}) - \tilde{f}^{k^-}_i) / (\gamma _i\left\| \bar{x}_{J^{k^-}_i}^{k^-} - \bar{x}_{J^{k^-}_i}^{k^-_i} \right\| )\right\} , \end{aligned}$$

  otherwise $L^{k+1}_i \leftarrow L^{k+1/2}_i$.

This way a function $f_i(\cdot )$ only restricts the movement of the candidate along the subspace of variables it depends on.

In order to see that all convergence results still hold, denote the largest subspace $f_i(\cdot )$ depends on (according to all observations of the algorithm) by $J_i:= \bigcup _{k \in K}J_i^k$ for $i=1,\dotsc ,m$. Note that there is some $k_0 \in K$ such that $J_i = J^k_i$ for all $i=1, \dotsc , m$, $k \ge k_0$, because the number of variables n is finite. Define

$$\begin{aligned} F_i(x):= \sup _{k \in K_i} \left( f_i(\bar{x}^{k_i}) + \left\langle g_i^k, x - \bar{x}^{k_i} \right\rangle \right) , \end{aligned}$$

i.e., $F_i(\cdot )$ is the function defined by all subgradients ever obtained for $f_i(\cdot )$ by the algorithm. Note that $F_i(\cdot )$ is constant along the components $\bar{J}_i:= \{1, \dotsc , n\} {\setminus } J_i$ by definition and $F_i(\cdot )$ is consistent with all function values and subgradients computed by the algorithm. In particular, we may assume that the algorithm optimized $F(x) = \sum _{i=1}^m F_i(x)$ instead of f(x). Using the notation

$$\begin{aligned} (x_{|J})_j:= {\left\{ \begin{array}{ll} x_j, &{} j \in J, \\ 0, &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

($x_{|J}$ denotes the projection of x onto the subspace $\left\{ y \in \mathbb {R}^n :y_{\bar{J}} = 0 \right\}$) we have $F_i(x) = F_i(x_{|J_i})$ for all $x \in \mathbb {R}^n$. Hence, we may replace all $\bar{x}^k$ by $\bar{x}^k_{|J_i}$ in all proofs, e.g.,

$$\begin{aligned} \left| F_i(x) - F_i(y) \right| = \left| F_i(x_{|J_i}) - F_i(y_{|J_i}) \right| \le L_i \left\| x_{|J_i} - y_{|J_i} \right\| = L_i \left\| x_{J_i} - y_{J_i} \right\| \end{aligned}$$

(Lemma 6, Observation 8 and Theorem 9). With this observation all arguments remain valid for all indices $k \ge k_0$. Consequently, the algorithm computes (an approximation of) an optimal solution $x^* \in \mathop {\mathrm {{\text {*}}{Arg}\,\min }}\limits F$ and by $F(x) \le f(x)$ (by definition) and $F(x^*) = f(x^*)$ this is also a minimizer of $f(\cdot )$.

7 The final algorithm

We are now almost ready to present the final algorithm or, more precisely, the final supervisor process. It remains to specify the termination criterion. A typical choice is a bound on the predicted decrease: the algorithm terminates as soon as $\Delta ^k \le \varepsilon$ for some $\varepsilon \ge 0$ (see, e.g., [12]). Indeed, Theorem 7 implies that this condition will be met after a finite number of iterations if $f(\cdot )$ is bounded from below.

Corollary 12

Let $\varepsilon > 0$ and assume $\inf _{x \in \mathbb {R}^n} f(x) > -\infty$, then there is a $k \in K$ such that $\Delta ^k < \varepsilon$.

We will use this as termination criterion. The final algorithm of the supervisor process is shown in Algorithm 4.

Remark 13

It is well-known that the above termination criterion is quite weak: the distance from a true optimal solution may be arbitrarily large, e.g., if $f(\cdot )$ is a function that decreases very slowly. The criterion is even weaker in our asynchronous setting: because $\Delta ^k = \bar{f}^k - \hat{f}^k$ and the value $\bar{f}^k$ is only a lower bound on the true function value in the center $f(\bar{x}^{k^-})$, the value $\Delta ^k$ may be much smaller than the “real” predicted decrease of a classic bundle method $f(\bar{x}^{k^-}) - \hat{f}^k$. Furthermore, without knowing the real value of the Lipschitz constants the difference between $\bar{f}^k$ and $f(\bar{x}^{k^-})$ is hard to estimate. Hence, the algorithm may stop too early.

A simple way around this in practice is to enforce an exact evaluation of all oracles at the final center (ensuring $\bar{f}^k = f(\bar{x}^{k^-})$) and only terminate if the (then correct) predicted decrease is small enough. This could lead to numerous exact evaluations during the final iterations of the algorithm. An implementable strategy could therefore be as follows: First test if $\Delta ^k \le \frac{\varepsilon }{2}$. Only if this is the case, evaluate $f(\bar{x}^{k^-})$ exactly and then terminate if $f(\bar{x}^{k^-}) - \hat{f}^k \le \varepsilon$. Furthermore, the synchronized evaluations can be done by additional processes independent of the main algorithm, so the main algorithm can continue independently. When the synchronized evaluation is done and verified to meet the stopping condition, the algorithm terminates with that point as solution, otherwise the main algorithm adds the cutting planes obtained by the synchronized processes to the bundles and continues.

Other stopping conditions based on the aggregated subgradient or linearization errors can be used in the same way. In order to keep the presentation simple we do not use this strategy in Algorithm 4.

8 Preliminary computational experiments

In this section we present a few first computational experiments. The experiments are focused on one property of the asynchronous method, namely that few slow oracles might not slow down the overall computation because the algorithm may proceed with the results of the other, faster oracles. This is indeed one of our main motivations for the development of the algorithm.

The experiments solve the Lagrangian relaxation of multi-commodity-flow test instances [17]. Each instance consists of 11 commodities, hence has 11 subproblems. In order to simulate slow oracles, we randomly picked $N=1, \dotsc , 5$ of these oracles and artificially slowed down the evaluation of these subproblems by 0.1 s. For each instance and N we computed 10 runs each with a different subset of slowed subproblems.

Our test implementation runs on a single compute node with an Intel Xeon CPU 2.20GHz and 40 cores. The algorithm uses only a single master problem in disaggregated form. We implemented a synchronous and an asynchronous bundle method in Rust 1.66 sharing large parts of the code (i.e., the master problem and oracle implementations are identical). The difference between both implementations is basically the supervisor process. In the synchronous method the supervisor process waits for all oracles to finish their computation. The asynchronous method uses the mechanism described in this paper (see Algorithm 4). The reason why we choose such relatively small problems is that our implementation only runs on a single compute node and not on a distributed computer cluster, yet.

We measured the running time in seconds for our implementation to reach the final solution and compared the running times of the synchronous and the asynchronous methods. Table 1 shows the running times of both algorithms if no oracle is slowed down. As expected, the synchronous method in this case is usually much faster than the asynchronous method. This is expected because the oracles are very fast and the solution time of the master problem is significant. The asynchronous method, in contrast, starts the solution of new master problem processes as soon as a few oracles finish their computation, potentially solving several unnecessary master problems (because all oracles have almost the same very short computation time, waiting for the remaining oracles would be the better choice, which is what the synchronous method basically does).

Table 1 Running times in seconds for the synchronous and asynchronous algorithms without slow down

Table 2 Ratio of synchronous and asynchronous running times, $t_{\text {async}} / t_{\text {sync}}$

Table 3 Factor by which the running time increases compared with no slow down of the same algorithm

However, if we slow down some oracles, the computation time of the oracles becomes much larger and dominates the computation time for the master problem. Table 2 shows for each instance and number N of slowed oracles the ratio of the running time of the asynchronous method divided by the running time of the synchronous method (i.e., a value $<1$ means the asynchronous method is faster, otherwise the synchronous method is faster). Our asynchronous method is now faster than the synchronized method on average. In particular, Table 3 shows the factor by which the running time of the synchronous and the asynchronous method has changed compared with the running time without slow down. For the synchronous method the running time is increased significantly (independent of the number of oracles being slowed down because all oracles are evaluated in parallel). However, for the asynchronous one there is almost no change in the running time.

These experiments are, of course, very preliminary, yet quite promising. They show that the asynchronous method may have a significant advantage over the synchronous method if some oracles require a much higher computation time than others. Unfortunately, if the computation times of all oracles are close to each other, the synchronous method clearly wins. However, it should be noted that the current preliminary implementation of the supervisor process is the simplest possible, e.g., new master problem computations are started as soon as the result of the oracle is available. Therefore, a possible improvement would be that the supervisor actually measures the computation time of each oracle and performs an asynchronous update only if the computations of some oracles take significantly longer than others (effectively turning the algorithm into a synchronous method if all oracles require roughly the same computation time).

9 Summary and future research

In this paper we presented a fully asynchronous proximal bundle method for solving non-smooth, convex optimization problems given by first order oracles. The presented algorithm can be used as a drop-in replacement for a classic method without requiring additional information like Lipschitz constants. The algorithm may use an arbitrary number of processes evaluating the functions at certain candidate points and may also use an arbitrary number of master problem processes producing new candidate points. All processes communicate with a single supervisor process that manages the global iterations. Instead of using the exact function values the algorithm uses a guess model to obtain approximate function values. Convergence is guaranteed by learning the Lipschitz constants during the algorithm and by ensuring that all functions are evaluated sufficiently close to the current candidate point depending on the expected decrease. In particular, the algorithm does not have (scarce) coordination steps. We proved that the sequence of center points generated by the algorithm converges to an optimal solution of the problem (if one exists) under quite weak assumptions. This convergence theory is similar to inexact bundle methods and incremental bundle methods.

Starting from this basic algorithm, there are several interesting next steps. First, the algorithm allows using multiple master problems, which is very untypical for bundle methods. However, the asynchronous method presented in [6] can also be interpreted as a bundle method with multiple master problems, one for each selected subspace. These master problems were partially disaggregated models where only the functions active on the subspace get their own cutting plane model whereas all other functions are collected in a single aggregated model. It would be interesting to investigate whether a number of similar master problems can indeed produce better candidates. The simplest idea would be to have m master problems where master problem i uses two cutting plane models, one for $f_i(\cdot )$ and one for $\sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^m f_j(\cdot )$. Another would be to select appropriate subsets of functions similar to the subspace selection in [6]. The advantage is that each of these master problems is a partially disaggregated model and much faster to solve than a fully disaggregated model, but also a possibly better approximation than a fully aggregated model, thus potentially producing good candidate points rather quickly.

Another research direction would be the incorporation of inexact oracles. This has been done for the asynchronous level bundle method in [11] and the results should carry over. We deliberately did not investigate this setting in order to keep the already complicated presentation of our approach reasonably simple.

Finally, this paper focuses only on the theoretic aspects of the algorithm. We only present very preliminary numerical results. The reason is that a full implementation of the algorithm requires a lot of additional details to be specified, e.g., the number and kind of master problems processes (as discussed above), the number of oracle processes for each function $f_i(\cdot )$, the scheduling strategy (in a practical implementation the supervisor might track the computation times for each function oracle and either collect the results of oracles with short computation times or might decide to spawn additional processes for the slower oracles), etc.. A full investigation and numerical analysis of this algorithm would lengthen this paper significantly and will therefore be the topic of a future paper.