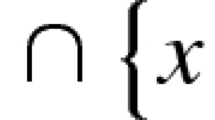Intersecting and dense restrictions of clutters in polynomial time

Abstract

A clutter is a family of sets, called members, such that no member contains another. It is called intersecting if every two members intersect, but not all members have a common element. Dense clutters additionally do not have a fractional packing of value 2. We are looking at certain substructures of clutters, namely minors and restrictions. For a family of clutters we introduce a general sufficient condition such that for every clutter we can decide whether the clutter has a restriction in that set in polynomial time. It is known that the sets of intersecting and dense clutters satisfy this condition. For intersecting clutters we generalize the statement to k-wise intersecting clutters using a much simpler proof. We also give a simplified proof that a dense clutter with no proper dense minor is either a delta or the blocker of an extended odd hole. This simplification reduces the running time of the algorithm for finding a delta or the blocker of an extended odd hole minor from previously ${\mathscr {O}}(n^4)$ to ${\mathscr {O}}(n^3)$ filter oracle calls.

1 Introduction

A clutter is a family of sets, called members, over a finite ground set V such that no member contains another [7]. Clutters are isomorphic if they can be obtained from each other by relabeling the ground set. A cover of ${\mathscr {C}}$ is a set $B \subseteq V$ such that $B \cap C \ne \emptyset$ for all members $C \in {\mathscr {C}}$. It is called minimal if it does not contain another cover. The covering number $\tau ({\mathscr {C}})$ is the minimum cardinality of a cover. A packing of a clutter is a set of pairwise disjoint members. The packing number $\nu ({\mathscr {C}})$ is the maximum cardinality of a packing. Clearly, $\tau ({\mathscr {C}}) \ge \nu ({\mathscr {C}})$. The blocker $b({\mathscr {C}})$ is the clutter given by the minimal covers of ${\mathscr {C}}$. Edmonds and Fulkerson [7] observed that $b(b({\mathscr {C}}))={\mathscr {C}}$.

Consider the following example of a clutter. Take the edge set of a graph as the ground set and the s-t-paths as members. The minimal covers are the inclusion-wise minimal s-t-cuts and $\tau ({\mathscr {C}})=\nu ({\mathscr {C}})$ by Menger’s theorem [10].

A clutter ${\mathscr {C}}$ is ideal if the polyhedron $\{{{\textbf {x}}} \ge 0 :x(C) \ge 1 \;\forall C \in {\mathscr {C}}\}$ is integral. The notion of idealness was introduced by Cornuéjols and Novick [5]. The above clutter is ideal, which can be shown by using the famous Max-Flow Min-Cut theorem by Ford and Fulkerson [8]. Lehman [9] proved that a clutter is ideal if and only if its blocker is ideal.

As one might expect, not every clutter is ideal. In fact, Ding, Feng and Zang [6] showed that the problem to decide whether a clutter is ideal is co-NP-complete.

Definition 1

([2]) Let ${\mathscr {C}}$ be a clutter over ground set V. A fractional packing of value two is a vector $y \in {\mathbb {R}}^{{\mathscr {C}}}_{\ge 0}$ with $\sum _{C \in {\mathscr {C}}} y_C = 2$ such that

$$\begin{aligned} \sum _{C \in {\mathscr {C}}:v \in C} y_C \le 1 \quad \forall v \in V . \end{aligned}$$

(1)

A simple reason why a clutter is not ideal is that it has covering number at least 2, but no fractional packing of value two. Clutters with this property are called dense [2].

Fig. 1

Deletion and contraction of a single element v

An important notion needed to study clutters is that of minors. These minors are built upon the concept of deletion and contraction of a single element v. In both cases, the element v is removed from the ground set. For a deletion, all members containing v are removed from the clutter. For a contraction, the members are kept, but members that contain another member are removed to satisfy the minimality condition of members. See Fig. 1 for an illustration.

Definition 2

([11]) Let ${\mathscr {C}}$ be a clutter over a ground set V and $I, J \subseteq V$ disjoint subsets. The minor of ${\mathscr {C}}$ obtained after deleting I and contracting J is the clutter ${\mathscr {C}} \backslash I / J$ over the ground set $V - (I \cup J)$ whose members are the inclusion-wise minimal sets of $\{C-J: C~\in ~{\mathscr {C}},\, C~\cap ~I = \emptyset \}$. If $I \cup J \ne \emptyset$ the minor is called proper.

One can easily show that the minor ${\mathscr {C}}\backslash I /J$ is the clutter obtained by deleting elements in I and contracting elements in J one by one in any order.

Seymour [12] showed that $b({\mathscr {C}}\backslash I/J) = b({\mathscr {C}})\backslash J/I$. He also proved that every minor of an ideal clutter is ideal. It therefore suffices to find a non-ideal minor to certify that the clutter is not ideal. This motivates the problem to decide whether a clutter has a dense minor. Abdi, Lee and Cornuéjols [2] showed that this problem can be solved in polynomial time. This is quite surprising as from the hardness result of Ding, Feng and Zang [6], one can conclude that this problem is NP-complete if the input is the blocker of the clutter [2].

For the study of dense minors, the following two examples (see Fig. 2) are fundamental. Let $n \ge 3$ be an integer. Take the clutter over the ground set $\{1,2,\ldots ,n\}$ with members $\{1,2\},\{1,3\},\ldots ,\{1,n\}$ and $\{2,3,\ldots ,n\}$. This clutter is denoted as $\varDelta _n$ and a clutter isomorphic to this clutter is called a delta of dimension n. Observe that $b(\varDelta _n)=\varDelta _n$.

Let $n\ge 5$ be an odd integer. Consider the clutter ${\mathscr {C}}$ over the ground set $\{1,2\ldots ,n\}$ with minimum cardinality members $\{1,2\},\{2,3\},\ldots ,\{n-1,n\}$ and $\{n,1\}$. A clutter that is isomorphic to ${\mathscr {C}}$ is an extended odd hole of dimension n.

Fig. 2

$\varDelta _6$ and an extended odd hole of dimension 7

Abdi and Lee [4] proved that every dense clutter has a delta or the blocker of an extended odd hole minor. They also showed that this minor in a dense clutter can be found in polynomial time.

A nontrivial clutter is called k-wise intersecting if it has no cover of size 1 and every k (not necessarily distinct) members have a common element. Abdi, Cornuéjols, Huynh and Lee [1] conjectured that for $k\ge 4$ these clutters are non-ideal.

The 2-wise intersecting clutters are also called intersecting clutters. They satisfy $\tau ({\mathscr {C}})\ge 2$ and $\nu ({\mathscr {C}})=1$. Note that dense clutters are intersecting. Abdi, Cornuéjols and Lee [2] showed that one can decide in polynomial time whether a clutter has an intersecting minor.

As we do not allow covers of size 1 in many cases, we occasionally consider only special kinds of minors.

Definition 3

([2]) Let ${\mathscr {C}}$ be a clutter over a ground set V and $I \subseteq V$. Let

$$\begin{aligned} J:= \{u \in V-I: \{u\} \text { is a cover of } {\mathscr {C}} \backslash I\} . \end{aligned}$$

(2)

The minor ${\mathscr {C}} \backslash I / J$ is the restriction of ${\mathscr {C}}$ after restricting I.

The following are our main contributions:

• We introduce the concept for a family of clutters ${\mathscr {S}}$ to be k-unifying (Sect. 2). This gives a sufficient condition to decide whether a clutter has a restriction in ${\mathscr {S}}$ in polynomial time. The abstract unifying theorem could also be applied to other sets of clutters and might therefore be of independent interest.

• Abdi, Cornuéjols and Lee [2] showed that the set of intersecting clutters is 3-unifying. We generalize this result and show that k-wise intersecting clutters are $(k+1)$-unifying (Sect. 3). This is achieved by a much simpler proof.

• We give a streamlined proof that dense clutters with no proper dense minors are deltas or the blocker of extended odd holes (Sect. 4). This is also the main step to show that the set of dense clutters is 3-unifying. Conceptually, one has to find a vertex with certain properties in a graph. While Abdi and Lee [4] first decompose the graph into 2-connected blocks, we show that one can find such a vertex directly.

• This allows us to formulate a faster algorithm to find a delta or the blocker of an extended odd hole minor (Sect. 5). The running time is improved from previously ${\mathscr {O}}(n^4)$ [4] to ${\mathscr {O}}(n^3)$ filter oracle calls.

2 The unifying theorem

We will present a sufficient condition to decide whether a clutter has a restriction with a certain property in polynomial time.

Definition 4

Let ${\mathscr {S}}$ be a family of clutters. A clutter ${\mathscr {C}} \in {\mathscr {S}}$ is called restriction-minimal in ${\mathscr {S}}$ if no proper restriction of ${\mathscr {C}}$ is in ${\mathscr {S}}$.

Definition 5

A family of clutters is called k-unifying if every restriction-minimal clutter in this set has k members whose union is the ground set of that clutter.

We are ready to formulate the main theorem of this section.

Theorem 1

(Unifying theorem) Let ${\mathscr {S}}$ be a k-unifying family of clutters and ${\mathscr {C}}$ be a clutter over a ground set V. Then the following two statements are equivalent:

• (i) ${\mathscr {C}}$ has a restriction in ${\mathscr {S}}$;

• (ii) there are k members $C_1, C_2, \ldots , C_k$ of ${\mathscr {C}}$ such that the clutter obtained from ${\mathscr {C}}$ after restricting $V - \bigcup _{i=1}^k C_i$ is in ${\mathscr {S}}$.

Proof

($\Longleftarrow$) is immediate. ($\implies$) Since clutters have a finite ground set, ${\mathscr {C}}$ has a restriction-minimal restriction ${\mathscr {C}}\backslash I / J$ in ${\mathscr {S}}$. As ${\mathscr {S}}$ is k-unifying, we find k members $C_1', C_2', \ldots , C_k'$ in this restriction such that $\bigcup _{i=1}^k C_i' = V - (I \cup J)$. Let $C_i = C_i' \cup J$, which are members of ${\mathscr {C}}$ by the definition of a restriction. That yields $I=V-\bigcup _{i=1}^k C_i$.$\square$

Corollary 1

Let ${\mathscr {C}}$ be a clutter over a ground set V with n elements and m members. Let ${\mathscr {S}}$ be a k-unifying family of clutters for a fixed $k\ge 2$. Furthermore, there is an oracle given, which decides whether a given clutter is in ${\mathscr {S}}$ in polynomial time. Then one can decide in polynomial time depending on n and m whether ${\mathscr {C}}$ has a restriction in ${\mathscr {S}}$.

Proof

For each set of not necessarily different k members of ${\mathscr {C}}$, consider the restriction of the complement of the union of these members. If any of these restrictions is a clutter in ${\mathscr {S}}$, a restriction is found. Otherwise, there is no such restriction by Theorem 1. Since there are $m^k$ possibilities to choose the members, all possible restrictions can be calculated in polynomial time dependent on n and m. The oracle decides whether the restriction is actually in ${\mathscr {S}}$, so this entire process can be done in polynomial time. $\square$

In Sect. 3, we will apply this corollary to the family of intersecting clutters and in Sect. 4 to the family of dense clutters. We get polynomial time algorithms to decide whether a clutter has an intersecting/dense restriction as long as the members of the clutter are given explicitly.

3 k-wise intersecting clutters

This section gives a simplified proof for the statement that intersecting clutters with no proper intersecting restriction have three members whose union is the ground set ([2]). Abdi, Cornuéjols and Lee used a tool for finding delta minors. We will instead utilize a simple minimality argument. The statement is generalized for k-wise intersecting clutters and formulated in the language of the unifying theorem.

Theorem 2

For $k\ge 2$ the set of k-wise intersecting clutters is $(k+1)$-unifying.

Proof

Let ${\mathscr {C}}$ be k-wise intersecting such that no proper restriction is k-wise intersecting. We have to show that ${\mathscr {C}}$ has $(k+1)$ members whose union is the ground set. Choose $(k+1)$ members $C_1, C_2, \ldots , C_{k+1}$ of ${\mathscr {C}}$ such that $|\bigcap _{i=1}^{k+1} C_i|$ is minimal. Assume for a contradiction there is a $v \in V$ such that $v \not \in C_i$ for $i=1,2, \ldots , k+1$. Consider the restriction ${\mathscr {C}}'={\mathscr {C}} \backslash \{v\} / J$. We get $J \subseteq \bigcap _{i=1}^{k+1} C_i$.

Since ${\mathscr {C}}'$ is not k-wise intersecting and ${\mathscr {C}}'=\{\emptyset \}$ or $\tau ({\mathscr {C}}')\ge 2$, we find k not necessarily different members $C_1',\ldots , C_k'$ of ${\mathscr {C}}'$ with empty intersection. They imply k members $C_1^*, C_2^*,\ldots , C_k^*$ in ${\mathscr {C}}$ with $\bigcap _{i=1}^k C_i^* \subseteq J$. Note that the intersection of these k members is not empty since ${\mathscr {C}}$ is k-wise intersecting. We find an element $u \in \bigcap _{i=1}^k C_i^*$. Since $\{u\}$ is not a cover, there is a member $C_{k+1}^*$ with $u \not \in C_{k+1}^*$. We conclude

$$\begin{aligned} \bigcap _{i=1}^{k+1} C_i^* \subsetneq J \subseteq \bigcap _{i=1}^{k+1} C_i , \end{aligned}$$

(3)

contradicting the minimality assumption.$\square$

For intersecting clutters we get the following consequence:

Corollary 2

(Reformulation of [2], Proposition 3.3) The set of intersecting clutters is 3-unifying.

By Corollary 1, we can therefore decide in polynomial time whether a clutter has an intersecting restriction.

Remark 1

([2], Remark 1.2) A clutter has an intersecting restriction if and only if it has an intersecting minor.

Proof

If a clutter has an intersecting restriction, this restriction is by definition a minor.

Let ${\mathscr {C}}$ be clutter and ${\mathscr {C}} \backslash I /J$ be an intersecting minor. Let ${\mathscr {C}}'={\mathscr {C}} \backslash I /J'$ be the minor obtained after restricting I. By the definition of a restriction and $\tau ({\mathscr {C}} \backslash I /J) \ge 2$, we get $J' \subseteq J$. If ${\mathscr {C}}'$ was trivial, so would ${\mathscr {C}} \backslash I / J$. If ${\mathscr {C}}'$ had two disjoint members, so would ${\mathscr {C}} \backslash I /J$ because it is not trivial. Since both are not the case, ${\mathscr {C}}'$ is intersecting.$\square$

As a consequence thereof, given a clutter explicitly with its members, we can decide in polynomial time whether the clutter has an intersecting minor. It is conjectured that ideal clutters with no intersecting minor also have the max-flow min-cut property [2].

4 Dense clutters

Abdi, Cornuéjols and Lee showed that dense clutters with no proper dense restriction have three members whose union is the ground set [2]. This is equivalent to the set of dense clutters being 3-unifying. They used a tool to find a delta or an extended odd hole minor presented by Abdi and Lee [4]. They also used the fact that dense clutters have a delta or the blocker of an extended odd hole minor, which is also given by [4].

Instead of using these tools, we will give an alternate proof for them using the structure of minimally dense clutters. These are clutters with no proper dense minor. We will use similar ideas translated to this slightly different setting, but also some new ones. The focus will be on the structure of covers of size 2 in clutters with a fractional packing of value 2 provided by Lemma 1.

In one of the proof steps, one essentially has to show that a graph has a vertex with certain properties. Abdi and Lee [4] decompose the graph into 2-connected blocks. We show that this step is not necessary, by choosing an approriate vertex directly.

This also turns into an improvement in the running time of the algorithm for finding a delta or the blocker of an extended odd hole minor. This improved algorithm will be discussed in Sect. 5.

The remaining proof of the statement that the set of dense clutters is 3-unifying is also slightly simplified by using the structure of minimally dense clutters.

Abdi and Lee considered clutters with $\min \{|C|:C\in {\mathscr {C}}\}=2$ and the graph with vertex set V with the members of cardinality 2 as edges [4]. We will consider this graph of the blocker.

Definition 6

Let ${\mathscr {C}}$ be a clutter over a ground set V with $\tau ({\mathscr {C}})=2$. The covering graph of ${\mathscr {C}}$ is the graph with vertex set V and the covers of size two of ${\mathscr {C}}$ as edges.

Fig. 3

Covering graphs of $\varDelta _6$ and a blocker of an extended odd hole

The covering graph of a delta is a single vertex connected to all other vertices and the covering graph of a blocker of an extended odd hole is an odd cycle (Fig. 3).

Conversely, a clutter with a covering graph of an odd cycle is a blocker of an extended odd hole.

The following lemma analyzes the structure of covers of size 2 in clutters with a fractional packing of value 2. The key observation is that each member in the fractional packing intersects each cover of size 2 in exactly one element.

Lemma 1

Let ${\mathscr {C}}$ be a clutter over a ground set V with $\tau ({\mathscr {C}})=2$, a connected covering graph, and a fractional packing of value 2. Then the covering graph is bipartite and ${\mathscr {C}}$ has two members representing the colour classes. In particular there are members L and K of ${\mathscr {C}}$ with $K \cap L = \emptyset$ and $K \cup L = V$.

Proof

For $C \in {\mathscr {C}}$ let $x_C$ be the value assigned to C in the fractional packing of value 2. Let $B=\{b_1,b_2\}$ be an arbitrary cover of size 2 of ${\mathscr {C}}$ and C be an arbitrary member of ${\mathscr {C}}$ with $x_{C} > 0$. Since B is a cover, we have $|B\cap C| \ge 1$. Assume $|B \cap C| > 1$. We conclude

$$\begin{aligned} 2\ge & {} \sum _{C':b_1 \in C'} x_{C'} + \sum _{C':b_2 \in C'} x_{C'} = \sum _{C':b_1 \in C' \text { or } b_2 \in C'} x_{C'} \nonumber \\{} & {} + \sum _{C':b_1 \in C' \text { and } b_2 \in C'} x_{C'} \ge 2 + x_C > 2 , \end{aligned}$$

(4)

a contradiction. Therefore $|B\cap C| = 1$.

Since the cover of size 2 was arbitrary, each member C with $x_C>0$ has exactly one element with each of these covers in common. In the covering graph G, such a member is a stable set and vertex cover. Let s and t be two arbitrary vertices of G. As G is connected, there is an s-t-path in G. Such a path has to be alternating between vertices in C and vertices not in C. In particular, the covering graph cannot contain an odd cycle, since that would result in two paths between the same vertices of different parity in length. Thus, the covering graph is bipartite and we get two colour classes.

In a connected bipartite graph, the only sets of vertices that are a stable set and a vertex cover, are the two colour classes.

It is impossible that all members with $x_C > 0$ are only one of the two colour classes, because that would be the only member in the fractional packing and a value of 2 would not be possible. Therefore, each colour class is represented by a member, so there are members K and L with $K \cap L = \emptyset$ and $K \cup L = V$.$\square$

Definition 7

A clutter is called minimally dense if it is dense and no proper minor is dense. A clutter is called strictly dense if it is dense and no proper restriction is dense.

Given a minimally dense clutter, we will consider proper minors with covering number at least 2. Such a minor then has a fractional packing of value 2. The idea is to construct minors with a connected covering graph and then apply Lemma 1 to deduce specific members of that minor. They will imply members of the original clutter such that in total we get a delta or the blocker of an extended odd hole.

The first step is to show that the covering graph of the original clutter is actually connected.

We will use the following lemma to get a certificate for a dense clutter.

Lemma 2

([2], Lemma 1.6) Let ${\mathscr {C}}$ be a clutter with $\tau ({\mathscr {C}})\ge 2$ over a ground set V. Then the following are equivalent:

• (i) ${\mathscr {C}}$ is dense,

• (ii) there is a $w \in {\mathbb {R}}_{\ge 0}^V$ with ${{\textbf {1}}}^{T}w=1$ such that $\sum _{u \in C} w_u > \frac{1}{2}$ for all $C \in {\mathscr {C}}$.

Proof

Consider the following dual pair of linear programs:

Observe that (i) holds if and only if the optimal value of (D) is greater than $\frac{1}{2}$. Statement (ii) holds if and only if the optimal value of (P) is greater than $\frac{1}{2}$. From strong duality we get the equivalence.$\square$

Lemma 3

A minimally dense clutter has $\tau ({\mathscr {C}})=2$ and a connected covering graph.

Proof

If an element $v \in V$ does not appear in a cover of size two of ${\mathscr {C}}$, the proper minor ${\mathscr {C}} \backslash v$ has covering number at least 2. Thus, this minor has a fractional packing of value 2 which is also a fractional packing of value 2 for ${\mathscr {C}}$, a contradiction. Therefore, $\tau ({\mathscr {C}}) = 2$ and each element of the ground set appears in a cover of size 2.

Let G be the covering graph of ${\mathscr {C}}$. Assume G is not connected. Let A be the vertex set of one component of G and $B = V - A$. Let H be the subgraph of G induced by A. Note that A is a cover of ${\mathscr {C}}$ since it contains at least one cover.

Consider the minor ${\mathscr {C}}'={\mathscr {C}}/B$. If ${\mathscr {C}}'$ has a cover of size 1, this would also be a cover of ${\mathscr {C}}$, since no member is entirely contracted as A is a cover. Hence, ${\mathscr {C}}'$ has a fractional packing of value 2. The covering graph $H'$ of ${\mathscr {C}}'$ contains the edges of H and is thus connected. By applying Lemma 1 on ${\mathscr {C}}'$, we get that $H'$ is bipartite and the two colour classes K and L are members in ${\mathscr {C}}'$, implying that K and L are not covers in ${\mathscr {C}}'$ and ${\mathscr {C}}$.

Since ${\mathscr {C}}$ is dense, by Lemma 2 there is a $w \in {\mathbb {R}}^V_{\ge 0}$ such that $\sum _{u\in C} w_u > \frac{w(V)}{2}$ for all $C \in {\mathscr {C}}$. Let without loss of generality $w(K) \ge w(L)$. Each member of ${\mathscr {C}} \backslash K / L$ then has weight greater than

$$\begin{aligned} \frac{w(V)}{2} - w(L) \ge \frac{w(V)-w(K)-w(L)}{2} = \frac{w(V-A)}{2} . \end{aligned}$$

(5)

Hence, the certificate for ${\mathscr {C}}$ also implies a certificate for ${\mathscr {C}}\backslash K /L$. Since that minor cannot be dense, we have $\tau ({\mathscr {C}}\backslash K /L)<2$. Thus, this minor has a cover of size 1. Let this cover be $\{b\}$. The proper minor ${\mathscr {C}}''={\mathscr {C}} \backslash b / (B-\{b\})$ has no cover of size 1 since there is no edge between the vertex sets A and B. Using the same argument as for ${\mathscr {C}}'$, the covering graph of ${\mathscr {C}}''$ contains the edges of H, is bipartite, and has the colour classes as members. Therefore, K and L are members of ${\mathscr {C}}''$, but not covers. That yields that $K \cup \{b\}$ is not a cover of ${\mathscr {C}}$, a contradiction.$\square$

We will use the following tool to find delta minors.

Lemma 4

([3], Corollary 2.2, see also [4], Theorem 5) Let ${\mathscr {C}}$ be a clutter over a ground set V. Let $u,v,w \in V$ be distinct elements and such that $\{u,v\}$ and $\{u,w\}$ are members of ${\mathscr {C}}$. Let $C \in {\mathscr {C}}$ such that $\{u,v,w\}\cap C = \{v,w\}$. Then ${\mathscr {C}}$ has a delta minor.

Proof

Let $I=V-(C \cup \{u\})$. Let $C_1 = \{x \in C: \{u,x\} \in {\mathscr {C}}\}$. Note that $|C_1|\ge 2$ as $v,w \in C_1$. Starting with the minor ${\mathscr {C}} \backslash I$, contract elements x of $C - C_1$ one by one as long as $\{u,x\}$ is not a member of the current minor. We get a clutter ${\mathscr {C}}'={\mathscr {C}} \backslash I/C_2$ where $C_2 \subseteq C - C_1$. Note that due to the definition of $C_2$, $\{u\}$ is not a member of this clutter as it is not a member of ${\mathscr {C}} \backslash I$. As C is a member of ${\mathscr {C}}$, we get that $C-C_2$ contains a member of ${\mathscr {C}}'$. Actually, $C-C_2$ is a member in ${\mathscr {C}}'$ because there is no member $C' \subsetneq C-C_2$ as it would imply a member $C^* \subsetneq C$ of ${\mathscr {C}}$. Therefore, ${\mathscr {C}}'$ has the members $C-C_2$ and $\{u,x\}$ for all $x \in C-C_2$. There cannot be further members due to the definition of a clutter. Therefore, ${\mathscr {C}}'$ is a delta and ${\mathscr {C}}$ has a delta minor.$\square$

We are now ready to prove a key result of this section, namely that a minimally dense clutter is already a delta or the blocker of an extended odd hole. We provide a simplified proof in comparison to Abdi and Lee [4]. First, we will outline the proof idea and point out the key difference to the original proof.

By Lemma 3, a minimally dense clutter ${\mathscr {C}}$ has a connected covering graph G. We can further assume that G is bipartite, as it is the blocker of an extended odd hole (or a delta if $|V|=3$) otherwise. This leads to two colour classes X and Y, where without loss of generality Y is a cover.

The idea is to delete and contract elements from ${\mathscr {C}}$, such that no cover of size 1 results, deleting these vertices from G does not disconnect the graph and Y still contains a cover. Finding such elements then enables the use of Lemma 1 to derive a contradiction. We then show that one can find such elements unless ${\mathscr {C}}$ is a delta.

One can remove an element of X such that no cover of size 1 arises by contracting it. Elements of Y cannot be contracted because Y needs to contain a cover in the minor.

Abdi and Lee [4] use this observation to check for all $x \in X$, whether removing x keeps Y connected ( [4], Claim 1 of Theorem 7) and can assume that there is no such vertex otherwise. Then they proceed by decomposing G into 2-connected blocks.

We show that it is not necessary to perform this step, by directly considering a vertex $x \in X$ such that removing x keeps the other vertices in X connected.

As Claim 1 of Theorem 7 in [4] also dominates the running time of the implied algorithm for finding a delta or the blocker of an extended odd hole minor, this is the reason for our improvement of the running time.

We proceed by giving a formal proof.

Theorem 3

(Reformulation of [4], Theorem 3) A minimally dense clutter is a delta or the blocker of an extended odd hole.

Fig. 4

We can remove an $x \in X$ such that all elements of $X\setminus \{x\}$ are in the same component. Otherwise we could remove $x'$ for a larger component

Fig. 5

Situation of the covering graph. The set of isolated vertices in Y incident to x is Z

Proof

By Lemma 3, the covering graph G of the minimally dense clutter ${\mathscr {C}}$ is connected. If G contains an odd cycle, contracting all other elements leads to a minor with covering number at least 2, but the covering graph is not bipartite. If the minor has a fractional packing of value 2, Lemma 1 implies a contradiction. Therefore, the minor is dense and thus not proper. In conclusion, G does not properly contain an odd cycle and thus is an odd cycle with no additional chords. Therefore, ${\mathscr {C}}$ is the blocker of an extended odd hole or a delta if $|V|=3$.

We can now assume that G is bipartite. Let X and Y be the colour classes of G.

One of them is a cover, otherwise we would have disjoint members. So let without loss of generality Y be a cover and $B \subseteq Y$ be a minimal cover. We get $|Y|\ge 3$ as there is no edge in G[Y].

Remove an $x \in X$ from G such that the number of vertices from X in the same component of the resulting graph is maximal (see Fig. 4). Let this maximal component be $M_x$. If $|M_x| \ne |X|-1$, take an $x' \in X$ that is not in $M_x$. Removing $x'$ instead of x does not disconnect $M_x$. Furthermore, x is connected to $M_x$, a contradiction to the maximality. Therefore, removing x from G does not disconnect the other vertices in X.

Let $G'$ be the graph resulting from G after removing x. The components of $G'$ consist of one component containing all other vertices in X and some vertices from Y. All other components have to be a single vertex from Y, because there are no edges between vertices in Y. Let this set of isolated vertices be Z.

We are now in the situation shown in Fig. 5. Since G is connected, $\{x,z\}$ is an edge of G for all $z \in Z$. Assume that there is a $y \in Z-B$. Consider the minor ${\mathscr {C}} / y$. This minor is not dense and has a connected covering graph. By Lemma 1, this minor has a member $C' \subseteq X$. It implies a member $C \subseteq X \cup \{y\}$ in ${\mathscr {C}}$, a contradiction to B being a cover. So $Z \subseteq B$.

If $|Z|\ge 2$, the blocker of ${\mathscr {C}}$ has members $\{x,z_1\},\{x,z_2\}$. As B is a minimal cover of ${\mathscr {C}}$, it is a member of $b({\mathscr {C}})$. Furthermore, we have $B \cap \{x,z_1,z_2\}=\{z_1,z_2\}$. Applying Lemma 4 yields that $b({\mathscr {C}})$ has a delta minor. Let $b({\mathscr {C}})\backslash I /J=\varDelta _n$. We get ${\mathscr {C}} \backslash J / I = b(\varDelta _n)=\varDelta _n$. Thus, ${\mathscr {C}}$ has a delta minor. As deltas are dense, ${\mathscr {C}}$ is a delta itself.

If $|Z|<2$ consider the minor ${\mathscr {C}}\backslash Z /\{x\}$. This minor has no cover of size 1 because even if $|Z|=1$ there is no edge incident to $z \in Z$ other than $\{x,z\}$. Furthermore, this minor is not trivial as we would have $|V|\le 2$. As that minor also has a connected covering graph and is not dense, by Lemma 1, we find a member $C' \subseteq X$. This implies a member $C \subseteq X$ of ${\mathscr {C}}$, a contradiction to Y being a cover.

In conclusion, each case led to a contradiction or a delta or the blocker of an extended odd hole.$\square$

Note that a similar result is known for minimally non-ideal clutters. These are non-ideal clutters such that every proper minor is ideal.

Theorem 4

([13], see also [9] and [3], Theorem 4.6) Let ${\mathscr {C}}$ be a minimally non-ideal clutter with $\tau ({\mathscr {C}})=2$. Then ${\mathscr {C}}$ is a delta or the blocker of an extended odd hole.

Of course, the assumption that every proper minor is ideal is much stronger than the assumption that every proper minor with covering number at least 2 has a fractional packing of value 2.

In the rest of this section, we will prove that the set of dense clutters is 3-unifying.

Lemma 5

A minimally dense clutter over a ground set V has three members $C_1, C_2$ and $C_3$ with empty intersection whose union is the ground set.

Proof

We will prove that such a clutter ${\mathscr {C}}$ has two members $C_1$ and $C_2$ whose union is the ground set and $|C_1 \cap C_2|=1$. We can then choose an arbitrary $C_3$ not containing the common element to complete the proof.

If ${\mathscr {C}}$ is a delta, choose $C_1=\{1,2\}$ and $C_2=\{2,3,\ldots ,n\}$.

If ${\mathscr {C}}$ is the blocker of an extended odd hole, take an arbitrary $v \in V$ and consider the minor ${\mathscr {C}} / v$. The covering graph of this minor is connected and bipartite since it is a path. By Lemma 1, we find two disjoint members K and L of this minor with $K \cup L = V-\{v\}$. Since ${\mathscr {C}}$ has no disjoint members, they both contain v in ${\mathscr {C}}$.$\square$

The following lemma bridges the gap from minimally dense to strictly dense clutters.

Lemma 6

Let ${\mathscr {C}}$ be a strictly dense clutter over a ground set V and $J \subseteq V$ such that ${\mathscr {C}} / J$ is dense. Then for each $v \in J$, there is a $w \in V-J$ such that $\{v,w\}$ is a cover of size 2 in ${\mathscr {C}}$.

Proof

Assume there is a $v \in J$ such that no such cover of size 2 exists. Then the minor ${\mathscr {C}} \backslash \{v\}/ (J-\{v\})$ has no cover of size 1 and thereby covering number at least 2. Furthermore, this minor has no fractional packing of value 2 since every member of the minor contains a member of ${\mathscr {C}} / J$. Therefore this minor is dense. The restriction obtained from ${\mathscr {C}}$ after restricting v contracts a subset of $J-\{v\}$ since $\tau ({\mathscr {C}} \backslash v/ (J-\{v\}))\ge 2$. This implies that that restriction is also dense, a contradiction.$\square$

We are now ready to prove the main result of this section.

Theorem 5

([2], Proposition 4.5) The family of dense clutters is 3-unifying.

Proof

Let ${\mathscr {C}}$ be a strictly dense clutter over a ground set V. We will show that there are three members $C_1,C_2$ and $C_3$ whose union is V. Choose U such that ${\mathscr {C}} / U$ is dense but no proper contraction minor is. Let ${\mathscr {C}} \backslash I / (U \cup U')$ be a proper minor of ${\mathscr {C}} /U$ with covering number at least 2. If $I \ne \emptyset$, the restriction ${\mathscr {C}} \backslash I / J$ is not dense and therefore has a fractional packing of value 2. Since $J \subseteq (U \cup U')$, the minor ${\mathscr {C}} \backslash I / (U \cup U')$ also has a fractional packing of value 2. If $I=\emptyset$, we get the same conclusion by the definition of U.

Hence, ${\mathscr {C}}/U$ is minimally dense. By Lemma 5, we find three members $C_1', C_2'$ and $C_3'$ in ${\mathscr {C}}/U$ with empty intersection and union $V - U$.

Let $C_1, C_2, C_3 \in {\mathscr {C}}$ such that $C_i' \subseteq C_i \subseteq C_i' \cup U$ for $i=1,2,3$. Suppose there is a $v \in V-(C_1 \cup C_2 \cup C_3)$. Clearly, $v \in U$. By Lemma 6, there is a cover $\{v,w\}$ with $w \in V-U$. Since none of the three members contains U, they all contain w, a contradiction.$\square$

By Corollary 1, given a clutter explicitly with its members, we can find a dense restriction in polynomial time or state that there is none. Similarly to Remark 1, having a dense restriction is equivalent to having a dense minor. Furthermore, this is also equivalent to having a delta or the blocker of an extended odd hole minor.

Remark 2

([2], Remark 4.4) Let ${\mathscr {C}}$ be a clutter over a ground set V. Then the following statements are equivalent:

• (i) ${\mathscr {C}}$ has a dense restriction.

• (ii) ${\mathscr {C}}$ has a delta or the blocker of an extended odd hole minor.

• (iii) ${\mathscr {C}}$ has a dense minor.

To finish this section, we will prove that the fundamental theorem of [4], Theorem 7, can be easily deduced from the results of this chapter. This will show the connection of the proofs given in [4] and this section.

Theorem 6

(Reformulation of [4], Theorem 7) Let ${\mathscr {C}}$ be a clutter over ground set V where

$$\begin{aligned} \min \{|C|: C \in {\mathscr {C}}\} = 2 \end{aligned}$$

and the minimum cardinality members correspond to the edges of a connected graph G over vertex set V. Then at least one of the following statements holds:

• (i) G is bipartite with colour classes R and B such that B is a cover.

• (ii) ${\mathscr {C}}$ has a delta or an extended odd hole minor.

Proof

Consider the blocker $b({\mathscr {C}})$. If $b({\mathscr {C}})$ is dense, it has a delta or the blocker of an extended odd hole minor. Therefore, ${\mathscr {C}}$ has a delta or an extended odd hole minor.

Otherwise, $b({\mathscr {C}})$ has a fractional packing of value 2 and a connected covering graph as the covering graph of $b({\mathscr {C}})$ is just G. By Lemma 1, the covering graph is bipartite and we find members K and L of $b({\mathscr {C}})$ that correspond to the colour classes. They correspond to minimal covers of ${\mathscr {C}}$, so G is bipartite and one of the colour classes is a cover.

In each case, one of the statements holds.$\square$

5 Finding delta or blocker of extended odd hole minors

We will discuss an algorithm which finds a delta or the blocker of an extended odd hole minor of a dense clutter.

The clutter ${\mathscr {C}}$ over the ground set V is given by a filter oracle [13]. This oracle returns in time $\theta$ whether a set $A \subseteq V$ contains a member of ${\mathscr {C}}$. A clutter can have an exponential number of members. The idea of filter oracles is to avoid the problem, that the input of the clutter could already be exponential in the size of the ground set. Instead of a constant time oracle used by [4], we specify the time required to run the oracle. The algorithm implied by the proofs given in Sect. 4 has a running time of ${\mathscr {O}}(n^3(\theta +n))$. This improves the running time of the algorithm by Abdi and Lee in [4] with a running time of ${\mathscr {O}}(n^4)$ oracle calls.

We will start with some basic properties about filter oracles.

Lemma 7

([4], Remark 9) Let ${\mathscr {C}}$ be a clutter over a ground set V given by a filter oracle. Let $n=|V|$ and $\theta$ be the time required to run the oracle. Then the following statements hold:

• (i) The members of cardinality 1 can be computed in ${\mathscr {O}}(n\theta )$ time.

• (ii) The members of cardinality 2 can be computed in ${\mathscr {O}}(n^2\theta )$ time.

• (iii) Given a set $C \subseteq V$, it can be checked in ${\mathscr {O}}(n\theta )$ time, whether $C \in {\mathscr {C}}$.

• (iv) Given a set $A \subseteq V$ that contains a member, such a member can be found in ${\mathscr {O}}(n^2\theta )$ time.

Proof

• (i) We check whether $\{\}$ contains a member. If this is the case, there is no member of cardinality 1. Otherwise, check whether A contains a member for all $A \subseteq V$ with $|A|=1$.

• (ii) First, compute all members of cardinality 0 and 1. For all A with $|A|=2$ that do not contain a member of cardinality 0 or 1, check whether A contains a member. If it does, it has to be a member of cardinality 2.

• (iii) Check whether C contains a member. Then for all $C' \subseteq C$ with $|C'|=|C|-1$, check whether $C'$ contains a member. If at least one $C'$ contains a member, C cannot be a member. Otherwise it is.

• (iv) We can decide in ${\mathscr {O}}(n\theta )$ time whether A is a member or return an $A' \subseteq A$ with one element less by (iii). Repeating this process with the obtained subset iteratively leads to a member. There are at most |A| such iterations. Hence, a member can be found in ${\mathscr {O}}(n^2\theta )$ time.

$\square$

Lemma 8

([13], Theorem 5.1) Let ${\mathscr {C}}$ be a clutter over a ground set V given by a filter oracle, which runs in time $\theta$. Then the filter oracle also implies a filter oracle for the blocker $b({\mathscr {C}})$ running in $\theta +{\mathscr {O}}(|V|)$ time.

Proof

If we want to decide whether $B \subseteq V$ contains a member in $b({\mathscr {C}})$, we can instead check whether B is a cover in ${\mathscr {C}}$. This is equivalent to $V-B$ containing a member in ${\mathscr {C}}$. By the filter oracle for ${\mathscr {C}}$, this can be done in $\theta +{\mathscr {O}}(|V|)$ time, as we need linear time to compute the complement.$\square$

Lemma 9

([13], Theorem 5.2) Let ${\mathscr {C}}$ be a clutter over a ground set V given by a filter oracle, which runs in time $\theta$. Let $I,J \subseteq V$ be disjoint. Then the filter oracle implies a filter oracle for the minor ${\mathscr {C}} \backslash I /J$, which runs in time $\theta +{\mathscr {O}}(|V|)$.

Proof

By the definition of a minor, $A'$ containing a member in ${\mathscr {C}} \backslash I / J$ is equivalent to $A = A' \cup J$ containing a member in ${\mathscr {C}}$, so we get a filter oracle for ${\mathscr {C}} \backslash I / J$. We need linear time to compute the union $A' \cup J$.$\square$

The input of the final algorithm is a dense clutter including a certificate $w \in {\mathbb {R}}^V_{\ge 0}$ as in Lemma 2. We allow a scaled certificate, meaning that it only has to satisfy $w(C) > \frac{w(V)}{2}$ for all members $C \in {\mathscr {C}}$. The certificate is necessary because, in the proof of Lemma 3, we considered the minor ${\mathscr {C}} \backslash K / L$. Without the certificate, we would also need to consider the minor ${\mathscr {C}}\backslash L / K$. That could lead to an exponential runtime because the algorithm works recursively.

Note that the certificate can be calculated with a linear program, if the members are explicitly given.

We will formulate an algorithm that, given a dense clutter including a certificate, computes a delta, the blocker of an extended odd hole minor, or a proper dense minor. If the output is a proper dense minor, we will call the algorithm again. We need to make sure that a certificate for the proper dense minor can be computed easily.

Lemma 10

Let ${\mathscr {C}}$ be a dense clutter over a ground set V with $\tau ({\mathscr {C}})=2$ and connected bipartite covering graph. The clutter is inputted via a filter oracle running in time $\theta$. Let $n=|V|$. Then a certificate $w \in {\mathbb {R}}^V_{\ge 0}$ such that $w(C)>\frac{w(V)}{2}$ for all members $C \in {\mathscr {C}}$ can be computed in ${\mathscr {O}}(n^2(\theta +n))$ time.

Proof

All members of cardinality 2 of the blocker can be computed in ${\mathscr {O}}(n^2(\theta +n))$ time. Hence, the covering graph G of ${\mathscr {C}}$ can be computed in that time. Let X and Y be the colour classes of the bipartition, which can also be calculated in quadratic time. For $v \in V$ let w(v) be the degree of v in G. This defines an initial certificate with $w(V) = 2m$ where m is the number of edges. Each member $C \in {\mathscr {C}}$ contains at least one element of each cover of size 2. Thus, C as a vertex set is incident to all edges, implying $w(C) \ge m$. If a member contains more than one element of a cover, at least one edge has to be counted twice and therefore $w(C) \ge m+1$. By the same argument as in Lemma 1, the only possible members incident to at most one element of each cover of size 2 are X and Y. Check whether X or Y are members of ${\mathscr {C}}$. This can be done in linear time. Only one of them can be a member since ${\mathscr {C}}$ is dense. If none of them is a member, return w as the certificate. If without loss of generality X is a member, let $x \in X$ and $y \in Y$. Increase w(x) by $\frac{1}{2}$ and decrease w(y) by $\frac{1}{2}$ to get a certificate $w'$. This does not change the total sum and each member then fulfils $w'(C) \ge m + \frac{1}{2}$, so $w'$ is indeed a certificate and can be returned.$\square$

We are now ready to formulate the main algorithm, see Algorithm 1.

Algorithm 1

Finding a delta or the blocker of an extended odd hole minor

Theorem 7

The algorithm works correctly. It runs in ${\mathscr {O}}(n^2(\theta +n))$ time. If it returns a proper dense minor, a certificate for this minor being dense can be calculated in ${\mathscr {O}}(n^2(\theta +n))$ time.

Proof

The correctness of the algorithm is given by the proof of Lemma 3 and Theorem 3. Whenever we get a contradiction or an excluded case in the proof due to the clutter being minimally dense, the algorithm outputs the proper dense minor. Note that in almost all cases where a proper dense minor is returned, we have the situation of Lemma 10 with the minor ${\mathscr {C}}\backslash v$ in the first step and ${\mathscr {C}} \backslash K / L$ as the only exceptions.

In both cases, we can take the projection of the certificate of the original clutter on the new ground set. For ${\mathscr {C}} \backslash v$ this is a certificate because w(C) does not change for members C, but $w(V) \ge w(V-\{v\})$. For ${\mathscr {C}} \backslash K / L$ the argument is given in the proof of Lemma 3. The running time for the certificate is satisfied in both cases. It remains to show that the running time of the algorithm is indeed ${\mathscr {O}}(n^2(\theta +n))$.

The covers of size 2 can be computed in ${\mathscr {O}}(n^2(\theta +n))$ time since they are minimal covers and members of cardinality 2 in the blocker can be computed in that time. Therefore, we find a $v \in V$ that does not appear in a cover of size 2 or obtain the covering graph G in ${\mathscr {O}}(n^2(\theta +n))$ time.

In each connected component of G, we can find an odd cycle or a bipartition in quadratic time.

Checking whether K and L are members of ${\mathscr {C}}/B$ can be done in a linear number of oracle calls. By finding all minimal covers of size 1 in the blocker, we can decide whether $\tau ({\mathscr {C}}\backslash K / L)\ge 2$ is satisfied in a linear number of oracle calls. If there is a cover of size 1, we can use it as the cover $\{b\}$ of ${\mathscr {C}}\backslash K / L$.

We can decide in one oracle call whether X or Y is a cover. The minimal cover $B \subseteq Y$ can be obtained in ${\mathscr {O}}(n^2(\theta +n))$ time by Lemma 7. The $x \in X$ such that removing x from G does not disconnect $X - \{x\}$ can be computed in quadratic time as we can start with any element and find a better one given by the proof in Theorem 3 in linear time.

The set Z is calculated in linear time since these are just components of a graph. Checking $Z \subseteq B$ and possibly finding $y \in Z-B$ can also be done in linear time as an order of the elements can be assumed.

The computation of the delta minor in Lemma 4 can also be implemented to run in ${\mathscr {O}}(n(\theta +n))$ time. The sets I and $C_1$ of the proof can be determined in that time. Let X denote the set of elements of $C-C_1$ that are already contracted when considering $x \in C-C_1$. We query the oracle whether $\{u,x\} \cup X$ contains a member in ${\mathscr {C}}$. As C is a member of ${\mathscr {C}}$ and $\{u\}$ is not a member of ${\mathscr {C}}\backslash I/X$, this is by construction of X equivalent to $\{u,x\}$ being a member of ${\mathscr {C}}\backslash I/X$. Hence, each element $x \in C-C_1$ can be processed in ${\mathscr {O}}(\theta +n)$ time. In conclusion, every single step of the algorithm can be implemented in ${\mathscr {O}}(n^2(\theta +n))$ time, concluding the proof.$\square$

By applying the algorithm recursively and calculating the new certificate, the cardinality of the ground set decreases in each iteration. As an immediate consequence, we get the following corollary as the main result of this section.

Corollary 3

There is an algorithm that, given a dense clutter over the ground set V by a filter oracle and a certificate w for that clutter being dense, finds a delta or the blocker of an extended odd hole minor in ${\mathscr {O}}(|V|^3(\theta +|V|))$ time, where $\theta$ is the time required for an oracle call.

In conclusion, given a clutter ${\mathscr {C}}$ over a ground set V explicitly with its members, we can decide in polynomial time (in $|{\mathscr {C}}|$ and |V|) whether ${\mathscr {C}}$ has a dense restriction. Recall that this is equivalent to ${\mathscr {C}}$ having a delta or the blocker of an extended odd hole minor.

If ${\mathscr {C}}$ has a dense restriction, we can find it and compute a certificate in polynomial time.

Given a set $A \subseteq V$, we can decide in ${\mathscr {O}}(|V||{\mathscr {C}}|)$ time whether A contains a member by checking all members. Therefore, we have a polynomial time filter oracle and can find a delta or the blocker of an extended odd hole minor in polynomial time.