The role of rationality in integer-programming relaxations

Abstract

For a finite set $X \subset \mathbb {Z}^d$ that can be represented as $X = Q \cap \mathbb {Z}^d$ for some polyhedron Q, we call Q a relaxation of X and define the relaxation complexity ${\text {rc}}(X)$ of X as the least number of facets among all possible relaxations Q of X. The rational relaxation complexity ${\text {rc}}_\mathbb {Q}(X)$ restricts the definition of ${\text {rc}}(X)$ to rational polyhedra Q. In this article, we focus on $X = \Delta _d$, the vertex set of the standard simplex, which consists of the null vector and the standard unit vectors in $\mathbb {R}^d$. We show that ${\text {rc}}(\Delta _d) \le d$ for every $d \ge 5$. That is, since ${\text {rc}}_\mathbb {Q}(\Delta _d)=d+1$, irrationality can reduce the minimal size of relaxations. This answers an open question posed by Kaibel and Weltge (Math Program 154(1):407–425, 2015). Moreover, we prove the asymptotic statement ${\text {rc}}(\Delta _d) \in O(\nicefrac {d}{\sqrt{\log (d)}})$, which shows that the ratio $\nicefrac {{\text {rc}}(\Delta _d)}{{\text {rc}}_\mathbb {Q}(\Delta _d)}$ goes to 0, as $d \rightarrow \infty$.

1 Introduction

Finding compact representations of a large set of integer points in a high-dimensional space is a recurring theme in combinatorial optimization, where these points usually describe the feasible solutions to a discrete problem. A classical approach is, given a set of points of interest $X\subseteq \mathbb {Z}^d$, to find a polyhedron $Q\subseteq \mathbb {R}^d$ whose integer points are exactly those in X, i.e., such that $Q\cap \mathbb {Z}^d = X$. Such a polyhedron is called a relaxation of X. By feeding a relaxation of X to an integer programming solver, one can optimize a linear objective function over X. The relaxation complexity of X, denoted by ${\text {rc}}(X)$, is the smallest number of facets of a relaxation of X. This concept was introduced by Kaibel and Weltge [1] (see also Weltge [2]) as a measure of the complexity of a set of integer points.

A basic question is to determine the relaxation complexity of simple sets like the vertices of a hypercube or a simplex. For instance, one has ${\text {rc}}(\{0,1\}^d)\le 2d$ by counting the number of facets of the 0/1 hypercube. However, a relaxation with only $d+1$ facets exists [1]. Moreover, it is easy to see that any bounded relaxation of a full-dimensional set $X\subseteq \mathbb {Z}^d$ must have at least $d+1$ facets, and one can further show that the 0/1 hypercube does not admit any unbounded relaxation [1], implying ${\text {rc}}(\{0,1\}^d)= d+1$. In general, however, a finite set of points can admit an unbounded relaxation. Notice that such a relaxation must have irrational rays only (assuming $X\ne \emptyset$): indeed, starting from a point of X and applying a rational ray would produce infinitely many integer points. As a prominent example, the authors of [1] describe a 5-dimensional simplex (that is unimodularly equivalent to the standard simplex) and an unbounded, irrational relaxation of its vertex set, which however has at least six facets. Inspired by this result, they pose the following questions.

Questions 1

Let $\Delta _d$ be the set consisting of the null vector and the canonical unit vectors in $\mathbb {R}^d$, and let ${\text {rc}}_\mathbb {Q}(\cdot )$ be the restriction of ${\text {rc}}(\cdot )$ to rational relaxations.

• (Q1) Does ${\text {rc}}(\Delta _d) = {\text {rc}}_\mathbb {Q}(\Delta _d) = d+1$ hold for all positive integers d?

• (Q2) If $X \subseteq \mathbb {Z}^d$ is finite, does ${\text {rc}}(X) \ge \dim (X) + 1$ hold? Here, $\dim (X)$ is the dimension of the affine hull of X.

• (Q3) If $X \subseteq \mathbb {Z}^d$ is finite, does ${\text {rc}}(X) = {\text {rc}}_\mathbb {Q}(X)$ hold?

In this paper, we show that ${\text {rc}}(\Delta _d)<{\text {rc}}_\mathbb {Q}(\Delta _d)$ for $d\ge 5$. This gives negative answers to all the three questions above. The starting point is an example in dimension 5.

Theorem 1

We have ${\text {rc}}(\Delta _5)=5$.

From this example, we can easily show that irrationality helps to reduce the relaxation complexity also in higher dimensions. Thus, Questions 1– have a negative answer for every $d \ge 5$.

Corollary 1

For every $d \in \mathbb {Z}_{>0}$, one has

$$\begin{aligned} {\text {rc}}(\Delta _d) \le 5 \left\lfloor \frac{d+1}{6}\right\rfloor + \Bigl ((d+1) \bmod 6\Bigr ), \end{aligned}$$

where $\left\lfloor .\,\right\rfloor$ denotes the rounding-down operation and $(d+1) \bmod 6$ is the remainder of the division of $(d+1)$ by 6.

Since the relaxation complexity and rational relaxation complexity differ, one might wonder about the ratio ${\text {rc}}(\Delta _d)/ {\text {rc}}_\mathbb {Q}(\Delta _d)$ of these two quantities. By Corollary 1, this ratio is bounded from above by $\frac{5}{6} + o(d),$ as $d \rightarrow \infty$. With a significantly more involved construction, we can show that ${\text {rc}}(\Delta _d)/ {\text {rc}}_\mathbb {Q}(\Delta _d) \rightarrow 0,$ as $d \rightarrow \infty$, by providing the following asymptotic estimate:

Theorem 2

We have ${\text {rc}}(\Delta _d)\in O\left( \frac{d}{\sqrt{\log d}}\right)$.

The remainder of this article is structured as follows. First, we mention related literature (Sect. 1.1) and introduce the notation and terminology that we use throughout the article (Sect. 1.2). In Sect. 2, we prove Theorem 1 and Corollary 1, and, based on the proof of Theorem 1, we derive our strategy for proving Theorem 2. The proof of the latter theorem is then presented in Sect. 4. Finally, we list some open problems in Sect. 5.

1.1 Related literature

The relaxation complexity has been formally introduced by Kaibel and Weltge in [1], where it is also shown how to derive lower bounds for it. Among others, this lower bound shows that any relaxation of a natural encoding of Hamiltonian cycles via binary vectors needs exponentially many inequalities in general. For $X \subseteq \{0,1\}^d$, an upper bound on the minimal number of inequalities needed to separate X and $\{0,1\}^d \setminus X$ has been derived by Jeroslow [3]. Complementing the upper and lower bounds, Averkov and Schymura [4] derived criteria that guarantee that ${\text {rc}}(X)$ can be computed by solving a mixed-integer program. More sophisticated mixed-integer programming techniques to compute ${\text {rc}}(X)$ have been discussed recently by Averkov, Hojny, and Schymura [5]. Independently from the criteria in [4] that guarantee computability in arbitrary dimensions, Weltge [2] shows that ${\text {rc}}(X)$ for $X \subseteq \mathbb {Z}^d$ is computable if $d = 2$, and [4] extends this result to $d = 3$. Averkov, Hojny, and Schymura [6] showed that, if $d = 2$, then ${\text {rc}}(X)$ can be found in polynomial time. Furthermore, [6] also addresses issues behind the computability of ${\text {rc}}(X)$ and ${\text {rc}}_\mathbb {Q}(X)$ for an arbitrary dimension and reveals that having ${\text {rc}}(X)<{\text {rc}}_\mathbb {Q}(X)$ is an additional obstacle on the way to computing ${\text {rc}}(X)$ and ${\text {rc}}_\mathbb {Q}(X)$, as certain natural computational procedures fail to stop and so do not give finite algorithms in this case. For more details, see Sect. 5.

Extension complexity is a related, but more well studied concept than relaxation complexity (see [7] for a survey). The extension complexity of a polyhedron $P\subseteq \mathbb {R}^d$ is the minimum number of facets of a polyhedron $Q\subseteq \mathbb {R}^{d+d'}$ that projects down to P. If P is the convex hull of our set of integer points X, the extension complexity of P measures how compactly one can describe X using a linear formulation with additional variables, while the relaxation complexity of X allows to use integer formulations, but with no additional variables. The existence of small extended formulations for a given polyhedron P is related to the existence of small non-negative factorizations of a matrix related to P by the celebrated Yannakakis’ Theorem [8]. Finding non-negative factorizations of (non-negative) matrices is a problem of independent interest, and in 1993 it was asked [9] whether using irrational numbers could lead to smaller factorizations of rational matrices. This was recently answered in [10] and [11]: irrational numbers indeed help, as there are rational matrices whose minimum size factorizations require irrational numbers. As far as the authors know, the examples given in the aforementioned papers do not correspond to polyhedra, hence it is open whether using irrational numbers leads to smaller extended formulations for rational polyhedra.

Despite the lower bounds and the computability results mentioned above, the existence of small relaxations for a given set of points does not have a general characterization similar to what is known for extended formulations in terms of non-negative factorizations and communication protocols [8, 12]. Moreover, we lack general approaches to construct relaxations, while several efficient constructions for extended formulations are known [13,14,15,16,17]. This paper can be seen as one step forward in this direction.

Interestingly, sets of points like those corresponding to the spanning trees of a graph do not admit relaxations of subexponential size [1], but do admit polynomial-sized extended formulations [18,19,20]; the opposite happens for other sets, for instance those corresponding to stable sets or matchings in a graph, which admit simple, linear-sized relaxations, but no extended formulation of subexponential size [21, 22].

1.2 Notation, terminology, and background

We use $\subseteq$ and $\subset$ to denote inclusion and strict inclusion, respectively. As usual, we define $[m] {:}{=}\{1,\ldots ,m\}$ for $m \in \mathbb {Z}_{>0}$ and $[m] {:}{=}\emptyset$ for $m =0$. We denote by $\textbf{0}_a$ (resp. $\textbf{0}_{a, b}$) the all-zero vector (resp. all-zero matrix) of size a (resp. $a \times b$), writing only ${\varvec{0}}$ when the dimension is clear from the context. We denote the standard unit vectors in $\mathbb {R}^d$ by $e_1,\dots ,e_d$. Using this notation, $\Delta _d = \{\textbf{0},e_1,\dots ,e_d\}$. The dimension $\dim (X)$ of $X \subseteq \mathbb {R}^d$ is the dimension of its affine hull. The cardinality of X is denoted by |X| and its convex hull is denoted by ${\text {conv}}(X)$. For two sets X and Y, we denote by $Y^X$ the set of all maps from X to Y. If X is finite, then $\mathbb {R}^X$ is a |X|-dimensional vector space over $\mathbb {R}$ and, thus, it has the standard Euclidean topology. As usual, for $\phi :X \rightarrow Z$ and $Y \subseteq X$, the notation $\phi |_Y$ is used to denote the restriction of the map $\phi$ to Y.

We call elements of $\mathbb {Z}^d$ integer points/vectors and we call elements of $\ \mathbb {Z}^d \times \mathbb {R}^m$ mixed-integer points/vectors. An affine transformation $\phi :\mathbb {R}^d \rightarrow \mathbb {R}^d$ is said to be unimodular if it maps the integer lattice onto itself, that is, $\phi (\mathbb {Z}^d) = \mathbb {Z}^d$. It is known and easy to check (see, e.g., [23]) that $\phi$ is unimodular if and only if it can be represented as $\phi (x) = U x + v$ where $v \in \mathbb {Z}^d$ and $U \in \mathbb {Z}^{d \times d}$ is a unimodular matrix, which is an integer matrix with determinant equal to one in absolute value.

The recession cone ${\text {rec}}(P)$ of a nonempty polyhedron $P \subseteq \mathbb {R}^d$ is the set of all $u \in \mathbb {R}^d$ satisfying $p+u \in P$ for each $p \in P$. The recession cone of a polyhedron $P\ne \emptyset$ given by an inequality description $A x \le b$ is a polyhedral cone, which can be given by the inequality description $A x \le \textbf{0}$.

For $X \subseteq Y \subseteq \mathbb {R}^k$, a polyhedron P satisfying $X = P \cap Y$ is called a (polyhedral) relaxation of X within Y. By ${\text {rc}}(X,Y)$ we denote the minimal k such that $X = P \cap Y$ holds for some polyhedron P with k facets. If such k does not exist, we let ${\text {rc}}(X,Y ) =\infty$. We call ${\text {rc}}(X,Y)$ the relaxation complexity of X within Y. It is clear that ${\text {rc}}(X,Y)$ is monotonically non-decreasing with respect to Y in the sense that $X \subseteq Y \subseteq Z$ implies ${\text {rc}}(X,Y) \le {\text {rc}}(X,Z)$. For $X \subseteq \mathbb {Z}^d$, we call ${\text {rc}}(X){:}{=}{\text {rc}}(X,\mathbb {Z}^d)$ the (integer) relaxation complexity while, for $X \subseteq \mathbb {Z}^d \times \mathbb {R}^n$, we call ${\text {rc}}(X,\mathbb {Z}^d \times \mathbb {R}^n$) the (d, n)-mixed-integer relaxation complexity or the mixed-integer relaxation complexity with respect to d integer and n real variables. Similarly, a (d, n)-mixed-integer relaxation of X is a relaxation of X within $\mathbb {Z}^d \times \mathbb {R}^n$.

We also provide some necessary background from the theory of irrational numbers. The field $\mathbb {R}$ is a vector space over $\mathbb {Q}$ and it can be seen in different ways that $\mathbb {R}$ is infinite-dimensional over $\mathbb {Q}$. One easy non-constructive way to see this is to observe that $\mathbb {R}$ is uncountable, whereas $\mathbb {Q}$ and by this also every finite-dimensional vector space over $\mathbb {Q}$ is countable. This observation shows that for every $k \in \mathbb {Z}_{>0}$ there exists numbers $a_1,\ldots ,a_k \in \mathbb {R}$ that are linearly independent over $\mathbb {Q}$. As a consequence, we also see that for every $k \in \mathbb {Z}_{>0}$ there exist numbers $b_1,\ldots ,b_k \in \mathbb {R}$ such that $1,b_1,\ldots ,b_k$ are linearly independent over $\mathbb {Q}$. To show the latter, one can start with numbers $a_0,\ldots ,a_k \in \mathbb {R}$ linearly independent over $\mathbb {Q}$ and fix $b_i {:}{=}a_i/a_0$ for $i\in [k]_0$. Alternatively, the sequence $b_0=1,b_1,\ldots ,b_k$ of numbers linearly independent over $\mathbb {Q}$ can also be obtained by choosing an arbitrary algebraic number $c \in \mathbb {R}$ of algebraic degree $k+1$ and fixing $b_i = c^i$ for $i\in [k]_0$. See [24, Sect. 4] for more details.

2 The projection approach

In this section, we prove Theorem 1 and Corollary 1. Then, we will discuss how our proof strategy can be generalized to show Theorem 2.

2.1 The counterexample in dimension five

Define

$$\begin{aligned} \Delta {:}{=}\{{\varvec{0}}, e_1,e_2, e_3, (1,0,1,1,0), (0,1,1,0,1)\}\subset \mathbb {Z}^5. \end{aligned}$$

$\Delta$ is the vertex set of a 5-dimensional simplex and is unimodularly equivalent to $\Delta _5$. We work with $\Delta$ instead of $\Delta _5$ because this simplifies the calculations: giving a relaxation of $\Delta$ will imply the existence of a relaxation of $\Delta _5$ of the same size.

Let $\ell \subset \mathbb {R}^5$ be the line spanned by the vector $(0,0,0,1,\sqrt{2})$. In [1] it is shown that ${\text {conv}}(\Delta )+\ell$ is an (unbounded) relaxation of $\Delta$. However, such a relaxation has more than five facets. In order to give our relaxation, it is easier to reduce ourselves to a 4-dimensional space by projecting on a suitable hyperplane along line $\ell$, and looking for a relaxation of the projection of $\Delta$ within the projection of $\mathbb {Z}^5$. In particular, we use the following observation:

Observation 1

Let $\pi :\mathbb {R}^5 \rightarrow \mathbb {R}^4$ be the projection

$$\begin{aligned} \pi (x_1,x_2,x_3,x_4,x_5) {:}{=}\left( x_1,x_2,x_3, x_4 - \frac{1}{\sqrt{2}} x_5\right) \end{aligned}$$

and $P \subseteq \mathbb {R}^4$ be a polyhedron satisfying $P\cap (\mathbb {Z}^3 \times \mathbb {R}) = \pi (\Delta )$. Then $Q{:}{=}(P\times \{0\}) + \ell$ is a relaxation of $\Delta$. In other words, one has ${\text {rc}}(\Delta ,\mathbb {Z}^5)\le {\text {rc}}(\pi (\Delta ),\mathbb {Z}^3\times \mathbb {R})$.

Proof

By the choice of $\pi$, $\pi (\mathbb {Z}^5)$ is a subset of $\mathbb {Z}^3 \times \mathbb {R}$. Moreover, $\ell$ is the kernel of $\pi$ and Q is the pre-image of P under $\pi$.

We show that $Q\cap \mathbb {Z}^5=\Delta$. If $q\in Q\cap \mathbb {Z}^5$, then $\pi (q) \in P\cap (\mathbb {Z}^3 \times \mathbb {R}) = \pi (\Delta )$. The condition $\pi (q) \in \pi (\Delta )$ implies $q\in \Delta + \ell$. But since $\ell$ is an irrational line, its only integer point is $\textbf{0}$. Hence the points of $\Delta$ are the only integer points in $\Delta +\ell$. As $q \in \mathbb {Z}^5$, we conclude that $q \in \Delta$. Conversely, if $q \in \Delta$, then $\pi (q) \in \pi (\Delta ) \subseteq P$. Thus, q is in the pre-image of P under $\pi$, that is, $q \in Q$. This shows $Q \cap \mathbb {Z}^5 = \Delta$ and yields the assertion. $\square$

Based on Observation 1, for deriving ${\text {rc}}(\Delta ,\mathbb {Z}^5) \le 5$ it is sufficient to find a (3, 1)-mixed-integer relaxation of $\pi (\Delta )$ with five facets. To this end, let $\varepsilon \in (0,1)$ and consider the inequalities

$$\begin{aligned} x_1&\ge x_4, \end{aligned}$$

(1)

$$\begin{aligned} x_3&\ge x_4, \end{aligned}$$

(2)

$$\begin{aligned} \varepsilon x_1 + x_2 + \frac{1-\varepsilon }{1+\sqrt{2}} x_3 + \frac{(1-\varepsilon )\sqrt{2}}{1+\sqrt{2}} x_4&\le 1, \end{aligned}$$

(3)

$$\begin{aligned} x_3 + \sqrt{2}x_4&\ge 0, \end{aligned}$$

(4)

$$\begin{aligned} x_1 - (1+\varepsilon ) x_2 + x_3 - x_4&\le 1. \end{aligned}$$

(5)

We use these inequalities to define the polyhedron $P_\varepsilon {:}{=}\{ x \in \mathbb {R}^4: x \text { satisfies~(1)--(5)}\}$. Moreover, let

$$\begin{aligned} \Delta ' {:}{=}\pi (\Delta )=\left\{ {\varvec{0}}, e_1,e_2, e_3, (1,0,1,1), \left( 0,1,1,-\frac{1}{\sqrt{2}}\right) \right\} . \end{aligned}$$

Fig. 1

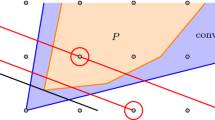
The projection of $\Delta '$ onto the first three components, with the fourth component of the elements of $\Delta '$ indicated in the boxes (left), and the sets of elements of $\Delta '$ on which inequalities (1)–(5) are active (right). The colors indicate that (1)–(3) provide upper bounds on $x_4$, while (4)–(5) provide lower bounds on $x_4$. Inequalities (1), (2) and (4) are facet-defining for ${\text {conv}}(\Delta ')$, as each of them is active on four affinely independent vertices. Inequalities (3) and (5) define two-dimensional faces of ${\text {conv}}(\Delta ')$

Proposition 1

The polyhedron $P_{\nicefrac {1}{8}}$ satisfies $P_{\nicefrac {1}{8}} \cap (\mathbb {Z}^3 \times \mathbb {R}) = \Delta '$.

Proof

We only provide a sketch of the proof and refer the reader to Appendix 1 for all details. An illustration of the geometry behind our proof is given in Fig. 1. Moreover, a computer-assisted proof can be found at github.¹

Consider the coordinate projection map $\phi (x_1,x_2,x_3,x_4) {:}{=}(x_1,x_2,x_3)$. The inequality description of the polytope $T{:}{=}\phi (P_{\nicefrac {1}{8}})$ can be determined from the inequality description of $P_{\nicefrac {1}{8}}$ via Fourier-Motzkin elimination, see, e.g., the book [23]. Inspecting this inequality description, we show $T \cap \mathbb {Z}^3 = \{(0,0),(1,0),(0,1)\} \times \{0,1\} = \phi (\Delta ')$. Once this verification is done, by plugging in an arbitrary $(x_1,x_2,x_3) \in T \cap \mathbb {Z}^3$ into the system (1)–(5) one obtains a system of linear constraints for $x_4$. These constraints provide lower and upper bounds on $x_4$. It turns out that for each choice of $(x_1,x_2,x_3) \in T \cap \mathbb {Z}^3$, the respective best lower and upper bound on $x_4$ match and thus give exactly one choice of $x_4$ corresponding to $(x_1,x_2,x_3,x_4) \in \Delta '$. That is, for $(x_1,x_2,x_3) \in \{(0,0,0),e_1,e_2,e_3\}$, one obtains inequalities $x_4 \le 0$ and $x_4 \ge 0$, for $(x_1,x_2,x_3) = (1,0,1)$, one obtains $x_4 \le 1$ and $x_4 \ge 1$, while for $(x_1,x_2,x_3) = (0,1,1)$, one obtains $x_4 \le - \frac{1}{\sqrt{2}}$ and $x_4 \ge - \frac{1}{\sqrt{2}}$. This shows the asserted equality $P_{\nicefrac {1}{8}} \cap (\mathbb {Z}^3 \times \mathbb {R}) = \Delta '$. $\square$

We observe that the sequence of the values ${\text {rc}}(\Delta _d)$ is monotonically non-decreasing.

Proposition 2

${\text {rc}}(\Delta _d) \le {\text {rc}}(\Delta _{d+1})$.

Proof

A relaxation of $\Delta _{d+1}$ with k inequalities restricted to the coordinate subspace $\mathbb {R}^d \times \{0\}$ gives a relaxation of $\Delta _d$ with at most k inequalities. This shows the desired assertion. $\square$

Our use of Proposition 2 is two-fold. We need it as an ingredient in the proof of Theorem 1, on the one hand. On the other hand, since ${\text {rc}}(\Delta _d)$ grows with respect to d, we are justified to study the asymptotic growth of this quantity.

We are ready to prove Theorem 1,

Proof of Theorem 1

By Proposition 1 and Observation 1, $(P_{\nicefrac {1}{8}}\times \{0\})+\ell$ is a relaxation of $\Delta$. Since $P_{\nicefrac {1}{8}}$ is defined by five inequalities, we have ${\text {rc}}(\Delta ) \le 5$. On the other hand, by Proposition 2 we have ${\text {rc}}(\Delta ) = {\text {rc}}(\Delta _5) \ge {\text {rc}}(\Delta _4) = 5$, where ${\text {rc}}(\Delta _4)=5$ has been verified in [4]. $\square$

Remark 1

(Computer-assisted studies) The system (1)–(5) has been discovered and validated using a computer. For the separation of $\Delta '$ from $\mathbb {Z}^4$ with five inequalities, a mixed-integer programming model has been established, akin to the model suggested in [4]. In the established model, instead of $\mathbb {Z}^4$ a finite sufficiently large subset of $\mathbb {Z}^4$ has been used as an “approximation” of $\mathbb {Z}^4$. The model was represented and solved in floating-point arithmetic. The values that have been produced as a result have been inspected and manually converted to exact algebraic numbers in the field $\mathbb {Q}[\sqrt{2}]{:}{=}\left\{ a + b\sqrt{2} \, :\, a,b \in \mathbb {Q} \right\}$; for values that were very close to 0 or 1 but could not be rounded to integers without losing the exactness of the relaxation, we introduced the value $\varepsilon >0$.

As a post-processing step, for the validation of the system, along with the manual verification, we also used the computer algebra system SageMath [25]. Notably, SageMath can carry out exact polyhedral computations over the field of algebraic numbers. So, in SageMath it is possible to carry out all of the computational steps described in the above proof by working with polyhedra over the algebraic numbers. In particular, we used SageMath to determine an appropriate choice of $\varepsilon >0$ in (1)–(5).

2.2 Extensions of the five-dimensional counterexample

To prove Corollary 1, we show that ${\text {rc}}(\Delta _d)$ is sub-additive in the cardinality $d+1$ of $\Delta _d$. To this end, we introduce the free join of non-empty finite sets $X \subset \mathbb {Z}^k$ and $Y \subset \mathbb {Z}^\ell$ and study its properties. For $k, \ell \in \mathbb {Z}_{>0}$, we define the free join by

$$\begin{aligned} X *Y {:}{=}\left\{ (x,\textbf{0},0) \, :\, x \in X \right\} \cup \left\{ (\textbf{0},y,1) \, :\, y \in Y \right\} \subset \mathbb {Z}^k \times \mathbb {Z}^\ell \times \mathbb {Z}. \end{aligned}$$

This operation corresponds to the free join of polytopes, as ${\text {conv}}(X *Y)$ is the free join of the polytopes ${\text {conv}}(X)$ and ${\text {conv}}(Y)$, as defined in [26, 15.1.3]. It is also useful to define the free join in the case when k or $\ell$ is zero, which means that one takes the free join with $\Delta _0 {:}{=}\{\textbf{0}\} \subseteq \mathbb {R}^0$. This is naturally defined as $X *\Delta _0 {:}{=}(X \times \{0\}) \cup \{e_{k+1}\} \subset \mathbb {Z}^k \times \mathbb {Z}$ and $\Delta _0 *Y {:}{=}\{\textbf{0}\} \cup ( Y \times \{1\}) \subset \mathbb {Z}^\ell \times \mathbb {Z}$. The analogy for passing from X to $X *\Delta _0$ within the theory of polyhedra is building a pyramid over a given polytope. Note that $(X+u) *(Y+v)$ coincides with $X *Y$ up to a unimodular transformation for all $u \in \mathbb {Z}^k$ and $v \in \mathbb {Z}^\ell$. Indeed, $(X+u) *(Y+v)$ is the image of $X *Y$ under the affine unimodular map $\phi (x,y,z) {:}{=}(x + (1-z) u,y+ z v,z)$.

In order to handle special cases uniformly, it will we also be convenient to fix $X *\emptyset {:}{=}X$, $\emptyset *Y {:}{=}Y$, ${\text {rc}}(\Delta _0){:}{=}1$, $\Delta _{-1} {:}{=}\emptyset$ and ${\text {rc}}(\Delta _{-1}){:}{=}0$.

Lemma 1

Let $k, \ell \in \mathbb {Z}_{\ge 0}$ with $k>0$ or $\ell >0$. Then, for non-empty finite sets $X \subset \mathbb {Z}^k$ and $Y \subset \mathbb {Z}^\ell$ with $\dim (X)=k$ and $\dim (Y)=\ell$, one has ${\text {rc}}(X *Y ) \le {\text {rc}}(X) + {\text {rc}}(Y)$.

Proof

We may assume w.l.o.g. that both X and Y admit a relaxation, i.e., ${\text {rc}}(X)$ and ${\text {rc}}(Y)$ are finite, as otherwise the statement holds trivially. We first consider the case $k> 0$, $\ell >0$. Without loss of generality we may assume that both X and Y contain the null vector. Let $Ax \le b$ and $Cy \le d$ be inequality systems defining relaxations P and Q of X and Y, respectively, having ${\text {rc}}(X)$ and ${\text {rc}}(Y)$ inequalities, respectively. Since both X and Y contain the origin, b and d are non-negative vectors. In particular, there needs to be at least one strictly positive entry in b and d, as otherwise, P or Q would be a full-dimensional cone and would contain infinitely many integer points.

To verify the inequality, it suffices to show that the polyhedron

$$\begin{aligned} R = \{ (x,y,z) \in \mathbb {R}^k \times \mathbb {R}^\ell \times \mathbb {R}: Ax \le b\cdot (1 - z),\; Cy \le d\cdot z\}, \end{aligned}$$

defined by ${\text {rc}}(X) + {\text {rc}}(Y)$ inequalities, is a relaxation of $X *Y$.

Let $(x,y,z) \in R \cap \mathbb {Z}^{k+\ell +1}$. If $z = 0$, then y is contained in the recession cone ${\text {rec}}(Q)$ of Q. Since Q is a relaxation of Y, we conclude $y = \textbf{0}$ as otherwise there are infinitely many integer points in Q. Moreover, setting $z=0$ gives the original system $Ax \le b$, i.e., $x \in X$ follows. Analogously, if $z=1$, then $x \in {\text {rec}}(P)$ and $y \in Y$. Thus, $(x,y,z) \in X *Y$ follows in both cases.

If $z \le -1$, then $\{y\in \mathbb {R}^\ell : Cy \le d\cdot z\}$ is a subset of ${\text {rec}}(Q)$, since decreasing the right-hand side makes the system more restrictive as d is non-negative. Since there exists at least one entry of d that is positive, $Cy \le d\cdot z$ excludes the null vector if $z < 0$. Hence, $\{y\in \mathbb {R}^\ell : Cy \le d\cdot z\}$ does not contain any integer point. Since we can argue analogously for $z \ge 2$ and the system $Ax \le b\cdot (1-z)$, we conclude $R \cap \mathbb {Z}^{k+\ell +1} \subseteq X *Y$. The reverse inclusion $X *Y \subseteq R \cap \mathbb {Z}^{k+\ell +1}$ is straightforward.

When k or $\ell$ is zero, the argument is similar. Without loss of generality, let $\ell =0$. Then $Y = \Delta _0$ and $X *Y = (X \times \{0\}) \cup \{e_{k+1}\}$. Again, we can assume that $\textbf{0} \in X$ and fix a system $Ax \le b$ of ${\text {rc}}(X)$ inequalities that defines a relaxation of X. One can see that the system $Ax \le b \cdot (1-z)$, $z \ge 0$ of ${\text {rc}}(X)+1 = {\text {rc}}(X)+{\text {rc}}(Y)$ inequalities defines a relaxation of $X *Y$ following the proof strategy we used in the case $k>0,\ell >0$. $\square$

Using Lemma 1, Corollary 1 follows easily.

Proof of Corollary 1

Note that ${\text {rc}}(\Delta _{k+\ell +1}) = {\text {rc}}(\Delta _k *\Delta _\ell )$ because $\Delta _{k+\ell +1}$ and $\Delta _k *\Delta _\ell$ are unimodularly equivalent.

Let m and r be the quotient and the remainder of the division of $d+1$ by 6. By the above observation, $\Delta _d$ is equivalent to the free join of m copies of $\Delta _5$ and one copy of $\Delta _{r-1}$ for $r>0$. Thus, using Lemma 1 and Theorem 1, we obtain ${\text {rc}}(\Delta _d) \le m {\text {rc}}(\Delta _5) + {\text {rc}}(\Delta _{r-1}) \le 5\,m + r$. $\square$

Remark 2

Combining Proposition 2 and the inequality ${\text {rc}}(\Delta _{d+1}) \le {\text {rc}}(\Delta _d *\Delta _0) \le {\text {rc}}(\Delta _d) + 1$, which follows from Lemma 1, we conclude that, for any given $d \in \mathbb {Z}_{>0}$, the value ${\text {rc}}(\Delta _{d+1})$ either stays equal to ${\text {rc}}(\Delta _d)$ or grows with respect to ${\text {rc}}(\Delta _d)$ by exactly one unit. Thus, for the determination of the exact behavior of ${\text {rc}}(\Delta _d)$ in d, the frequency of the jumps by one unit would have to be estimated from below and above.

As a consequence of our proof approach for Theorem 1, we also obtain the following.

Corollary 2

For every dimension $d \in \mathbb {Z}_{\ge 5}$, up to identification with respect to unimodular transformations, there exist infinitely many sets $X \subset \mathbb {Z}^d$ with $\dim (X)=d$ and ${\text {rc}}(X) < d+1$.

Proof

We first settle the case $d=5$. For each $a \in \mathbb {Z}_{>0},$ we consider the one-parametric generalization

$$\begin{aligned} X_a {:}{=}\{\textbf{0},e_1,e_2,e_3, (1,0,1,1,0), (0,1,1,0,a) \} \end{aligned}$$

of the set $\Delta$, with $\Delta =X_a$ for $a=1$. The projection of $X_a$ along the irrational line $\ell _a$ spanned by $(0,0,0, 1, a \sqrt{2})$ under the map $\pi _a:\mathbb {R}^5 \rightarrow \mathbb {R}^4$,

$$\begin{aligned} \pi _a(x_1,x_2,x_3,x_4,x_5) = \left( x_1,x_2,x_3,x_4 - \frac{1}{a \sqrt{2}} x_5\right) . \end{aligned}$$

is the same set $\Delta '$ as the projection of $\Delta$ under the projection map $\pi$ considered in the analysis of $\Delta$. It is clear that $\pi _a$ maps $\mathbb {Z}^5$ into $\mathbb {Z}^3 \times \mathbb {R}$. Consequently, in the same way as we showed that $\pi ^{-1}(P_{\nicefrac {1}{8}})$ is a five-facet relaxation of $\Delta$ within $\mathbb {Z}^5$ relying on Observation 1 and Proposition 1, we can also show that $\pi _a^{-1}(P_{\nicefrac {1}{8}})$ is a five-facet relaxation of $X_a$ within $\mathbb {Z}^5$ relying on a straightforward generalization of Observation 1 (with $\Delta$ and $\pi$ replaced by $X_a$ and $\pi _a$, respectively) and Proposition 1.

Distinct sets $X_{a'}$ and $X_{a''}$ with $a',a'' \in \mathbb {Z}_{>0}$ and $a' \ne a''$ do not coincide up to unimodular transformations when $a' \ne a''$, since $X_a$ is the vertex set of a simplex of volume $\frac{1}{5!} a$ and unimodular transformations preserve volume. This completes the proof of the assertion for $d=5$.

For higher dimensions $d \ge 6$, we use $Y_a {:}{=}X_a *\Delta _{d-6}.$ The set $Y_a$ is the vertex set of a simplex of volume $\frac{1}{d!} a$. Thus, all of the sets $Y_a$ with $a \in \mathbb {Z}_{>0}$ are pairwise distinct up to unimodular transformations. Lemma 1 yields ${\text {rc}}(Y_a) \le {\text {rc}}(X_a) + {\text {rc}}(\Delta _{d-6}) \le 5 + d-5 = d < d+1$. $\square$

3 The project-lift-relax approach

In this section, we set preliminary grounds for the proof of Theorem 2 by generalizing our approach to proving Theorem 1. The core steps to find our 5-dimensional counterexample consist of a projection of (a unimodular transformation of) $\Delta _5$ to a lower dimensional space and a determination of a (3, 1)-mixed-integer relaxation of the projection. As we will see below, the continuous coordinate of such a relaxation can be interpreted as a lifting from a 3-dimensional space. For this reason, to be able to generalize our proof strategy to prove Theorem 2, we provide two lemmas that explain how the relaxation complexity behaves under these two operations: projection and lifting. Afterwards, we will review our approach to prove Theorem 1 in the light of these two lemmas, which will motivate our strategy to prove Theorem 2.

The following can be seen as a generalization of Observation 1.

Lemma 2

(On injective projections) Let $X \subseteq Z \subseteq \mathbb {R}^d$ and let $\pi :\mathbb {R}^d \rightarrow \mathbb {R}^n$ be an affine map such that $\pi |_Z$ is injective. Then,

$$\begin{aligned} {\text {rc}}(X,Z) \le {\text {rc}}(\pi (X),\pi (Z)). \end{aligned}$$

Proof

Let $k = {\text {rc}}(\pi (X),\pi (Z))$. We may assume that k is finite, as otherwise the assertion is trivial. Consider a polyhedron Q with k facets, which is a relaxation of $\pi (X)$ within $\pi (Z)$, which means that $Q \cap \pi (Z) = \pi (X)$ holds. It is clear that the polyhedron $P = \pi ^{-1}(Q)$ has at most k facets. For verifying the asserted inequality, it suffices to show that P is a relaxation of X within Z, which means that $P \cap Z = X$.

To check the inclusion $P \cap Z \subseteq X$, we consider an arbitrary $y \in P \cap Z$. From the definition of P, we see that $\pi (y) \in Q \cap \pi (Z)$. In view of $Q \cap \pi (Z) = \pi (X)$, we obtain $\pi (y) \in \pi (X)$. As $\pi |_Z$ is injective and $X \subseteq Z$, we conclude that $y \in X$.

For showing the converse inclusion $X \subseteq P \cap Z$, we consider an arbitrary $y \in X$. Since $X \subseteq Z$, we have $y \in Z$. The condition $y \in P$, which remains to be verified, is equivalent to $\pi (y) \in Q$. Since $Q \cap \pi (Z) = \pi (X)$ and $\pi (y) \in \pi (X)$, we see that $\pi (y)$ is indeed in Q. $\square$

Next, we show how we can derive upper bounds on the (k, 1)-mixed-integer relaxation complexity of finite sets by means of lifting. To formalize this, we introduce, for $h:X \rightarrow \mathbb {R}$,

$$\begin{aligned} {\text {lift}}_h(X)&{:}{=}\left\{ (x,h(x)) \, :\, x \in X \right\} ,\\ {\text {clift}}_h(X)&{:}{=}{\text {conv}}({\text {lift}}_h(X)), \end{aligned}$$

and call these sets the lift (resp. convex lift) of X with respect to the height function h.

Consider a $(k+1)$-dimensional polytope P in $\mathbb {R}^{k+1}$. The facet-defining inequalities for this polytope are inequalities in $(x,y) \in \mathbb {R}^k \times \mathbb {R}$, which can be brought into one of the three forms $y \le u^\top x + v$, $y \ge u^\top x +v$ or $0 \le u^\top x + v$, where $u \in \mathbb {R}^k$ and $v \in \mathbb {R}$. We call the respective facets of Q the upper facets, the lower facets, and the lateral facets.

Proposition 3

Let $P\subset \mathbb {R}^{k+1}$ be a full-dimensional polytope, $h:T\rightarrow \mathbb {R}$ be a function from a finite non-empty set $T\subset \mathbb {Z}^k$. Then P is a relaxation of ${\text {lift}}_h(T)$ within $\mathbb {Z}^k\times \mathbb {R}$ if and only if

• 1. every $p\in {\text {lift}}_h(T)$ is contained in an upper and lower facet of P, and

• 2. the projection of P onto the first k components is a relaxation of T within $\mathbb {Z}^k$.

Proof

First, suppose that P is a relaxation of ${\text {lift}}_h(T)$ within $\mathbb {Z}^k\times \mathbb {R}$. If, by contradiction, there is $(x,h(x))\in {\text {lift}}_h(T)$ that is not contained in any upper facet of P, then there is some $y>h(x)$ such that $(x,y)\in P$, contradicting the fact that $P\cap (\mathbb {Z}^k\times \mathbb {R}) = {\text {lift}}_h(T)$. Arguing similarly for lower facets, one checks Condition 1. Condition 2 follows immediately from the definition of relaxation.

For the opposite direction, let P satisfy Conditions 1 and 2. Condition 1 easily implies that $P\cap (\mathbb {Z}^k\times \mathbb {R}) \supseteq {\text {lift}}_h(T)$. For the reverse inclusion, let $(x,y)\in P\cap (\mathbb {Z}^k\times \mathbb {R})$. We need to show that $(x,y) \in {\text {lift}}_h(T)$. By Condition 2, one has $x \in T$. If (x, y) were not in ${\text {lift}}_h(T)$, one would have $y\ne h(x)$. Then, if $y > h(x)$ (resp. $y<h(x)$), we conclude that (x, y) violates every upper facet (resp. lower facet) inequality of P, in particular those that are active on (x, h(x)), a contradiction. $\square$

Motivated by a free-sum operation for polytopes [26, 15.1.3], we introduce the free sum of $X \subseteq \mathbb {Z}^m$ and $Y \subseteq \mathbb {Z}^n$ as

$$\begin{aligned} X \oplus Y {:}{=}\left\{ (x,\textbf{0}) \, :\, x \in X \right\} \cup \left\{ (\textbf{0},y) \, :\, y \in Y \right\} . \end{aligned}$$

This operation will be useful, because $\Delta _k \oplus \Delta _m = \Delta _{k+m}$.

Lemma 3

Let X, Y be two disjoint finite subsets of $\mathbb {Z}^k$ with $\textbf{0} \in X$ and $|Y|=m$. Let $h:X \cup Y \rightarrow \mathbb {R}$ be such that $h(p) =0$ for every $p \in X$ and the values h(p) with $p \in Y$ are linearly independent over $\mathbb {Q}$. Then ${\text {rc}}(X \oplus \Delta _m) \le {\text {rc}}({\text {lift}}_h(X \cup Y), \mathbb {Z}^k \times \mathbb {R}).$

Proof

Let $Y = \{p_1,\ldots ,p_m\}$. The map $\phi :\mathbb {R}^k\times \mathbb {R}^m \rightarrow \mathbb {R}^k\times \mathbb {R}^m$ which is defined as $\phi (a,b) {:}{=}\left( a + \sum _{i=1}^m b_i p_i, b\right)$ is unimodular (because it is associated with an upper-triangular matrix with only 1 s on the diagonal) and it satisfies

$$\begin{aligned} \phi (X \oplus \Delta _m) = \left\{ (x,\textbf{0}) \, :\, x \in X \right\} \cup \left\{ (p_i, e_i ) \, :\, i \in \{1,\ldots ,m\} \right\} . \end{aligned}$$

(6)

We combine this map with the map $\psi (a,b) {:}{=}\left( a, \sum _{i=1}^m h(p_i) b_i \right)$. Since $h(p_1),\ldots ,h(p_m)$ are linearly independent over $\mathbb {Q}$, the map $\psi |_{\mathbb {Z}^{k+m}}$ is injective. Consequently $(\psi \circ \phi )|_{\mathbb {Z}^{k+m}}$ is injective as well, so we obtain

$$\begin{aligned} {\text {rc}}\,(X \oplus \Delta _m, \mathbb {Z}^{k+m})&\le {\text {rc}}( \psi (\phi ( X \oplus \Delta _m)), \psi (\phi (\mathbb {Z}^{k+m})){} & {} \text {(by Lemma}\,\,2).\\&= {\text {rc}}({\text {lift}}_h(X \cup Y), \psi ( \mathbb {Z}^{k+m} )){} & {} \hbox { by } (6)\ \hbox {and unimodularity of}\ \phi \\&\le {\text {rc}}({\text {lift}}_h(X \cup Y), \mathbb {Z}^k \times \mathbb {R}).{} & {} \text {(since}\, \psi ( \mathbb {Z}^{k+m} ) \subseteq \mathbb {Z}^k \times \mathbb {R}) \end{aligned}$$

$\square$

Having Lemmas 2 and 3 in mind, the summary of the proof of the upper bound ${\text {rc}}(\Delta _5) \le 5$ is as follows. First, we find it convenient to go from $\Delta _5$ to $\Delta$. One can represent these two sets as columns of two matrices (see Fig. 2a and b), which easily allows to check that they are unimodularly equivalent. Second, we apply the projection $\pi$ on $\mathbb {R}^4$ along line $\ell$, as defined in Observation 1. This corresponds to applying Lemma 2, where $X=\Delta$, $Z=\mathbb {Z}^5$. The points in $\pi (\Delta )$ are listed as columns of the matrix in Fig. 2c. Now, in light of Lemma 3, we see the points in $\pi (\Delta )$ as coming from a lift of points in $\mathbb {Z}^3$. Let $X=\Delta _3$ and $Y=\{(1,0,1), (0,1,1)\}$, and h such that $h(p)=0$ for $p\in X$, $h(1,0,1)= 1$, and $h(0,1,1)= -1/\sqrt{2}$. Then, by Lemma 3, we have that ${\text {rc}}(\Delta _5)={\text {rc}}(X \oplus \Delta _2) \le {\text {rc}}({\text {lift}}_h(X \cup Y), \mathbb {Z}^3 \times \mathbb {R})$.

Fig. 2

Visualization of the reductions in the proof of Theorem 1

In order to obtain Theorem 1, it now remains to show that P, defined as in Sect. 2.1, is a relaxation of ${\text {lift}}_h(X \cup Y)$ within $\mathbb {Z}^3 \times \mathbb {R}$. One can do that by setting $T=X\cup Y$ and verifying Conditions 1 and 2 in Proposition 3. Condition 1 can be easily verified by the reader (notice that inequalities (1), (2), (3) define upper facets of P, and inequalities (4),(5) define lower facets). Verifying Condition 2 can be done directly via Fourier-Motzkin elimination, as mentioned in the proof of Theorem 1.

In summary, our proof of Theorem 1 consists of three steps: project (a unimodular transformation of) the simplex to a lower dimensional space; lift the projection into a space with one continuous coordinate; relax the mixed-integer point set by finding a small relaxation. To prove Theorem 2, we once again utilize this project-lift-relax strategy. That is, the steps of our proof are:

• S1 Find a suitable unimodular copy of $\Delta _d$ and project this copy onto $\mathbb {Z}^k$ via a map $\pi$.

• S2 Construct a suitable height function $h:\pi (\tilde{\Delta }_d) \rightarrow \mathbb {R}$

• S3 Derive a relaxation P of ${\text {lift}}_h(\pi (\tilde{\Delta }_d))$ within $\mathbb {Z}^k \times \mathbb {R}$.

By a variation of Lemma 3, which we formulate below as Lemma 5, the number of facets of P will provide an upper bound on ${\text {rc}}(\tilde{\Delta }_d)$ and thus on ${\text {rc}}(\Delta _d)$ since $\Delta _d$ and $\tilde{\Delta }_d$ are unimodularly equivalent, provided the height function h satisfies all assumptions. In the following subsections, we discuss each of these three steps in detail.

4 The Proof of Theorem 2

This section is devoted to proving Theorem 2.

4.1 Project: Selecting the Right Simplex and Its Projection

Step  requires us to select a set $\tilde{\Delta }_d$ that is unimodularly equivalent to $\Delta _d$ as well as a projection $\pi :\mathbb {R}^d \rightarrow \mathbb {R}^k$. To this end, consider the following $d\times (d+1)$ matrix

$$\begin{aligned} M = \begin{pmatrix} \textbf{0}_k &{} I_k &{} B \\ \textbf{0}_{d-k} &{} \textbf{0}_{d-k, k} &{} I_{d-k} \end{pmatrix}, \end{aligned}$$

where $I_k$ denotes the identity matrix of order k, and B is the $k \times (d-k)$ matrix whose columns are all the vectors in $\{0,1\}^k$ with at least two 1-entries. Note that this definition requires $d = 2^k - 1$. Although this assumption might look restrictive, we can reduce the proof of Theorem 2 to this special case as we will see later.

Let $\tilde{\Delta }_d\subset \mathbb {R}^d$ be the set of columns of M. It is easy to see that $\tilde{\Delta }_d$ and $\Delta _d$ are unimodularly equivalent. We select $\pi$ to be the orthogonal projection of $\mathbb {R}^d$ onto the first k coordinates. In the spirit of Lemma 3, we then let $X\subset \mathbb {Z}^k$ be the set containing the first $k+1$ columns of M (truncated to the first k coordinates), i.e., $X =\Delta _k$, and $Y\subset \mathbb {Z}^k$ be the set containing the truncation of the other columns of M, so that $T {:}{=}X\cup Y= \{0,1\}^k$.

4.2 Lift: finding the right height function

Our next goal is to find a suitable height function h for Step . In view of Step , we need to select h in such a way that the we can easily derive a mixed-integer relaxation of ${\text {lift}}_h(T)$. By Proposition 3, such a relaxation can be obtained by taking the 2k box constraints $z \in [0,1]^k \times \mathbb {R}$ and selecting upper and lower facets of ${\text {clift}}_h(Y)$ that cover all points (z, h(z)) for $z \in T$. Our strategy for finding a small relaxation is thus

• S3a to find a small covering of the points (z, h(z)) for $z \in T$ consisting of upper and lower facets, respectively.

To be able to quantify the minimum size of a covering by upper and lower facets, respectively, we need to derive combinatorial properties of the facet structure of ${\text {clift}}_h(T)$. In our analysis in the next subsection, it will thus be convenient to have a function h that satisfies $h(z) \in \mathbb {Q}$ for all $z \in T$. In view of Lemma 3, however, we require that the values h(y) for all $y \in Y$ are linearly independent over $\mathbb {Q}$. To achieve this, we will slightly perturb h, but note that this may change the combinatorial structure of the facets of ${\text {clift}}_h(T)$. As we show next, simplicial facets of ${\text {clift}}_h(T)$ remain simplicial after small perturbations of h. Thus, we can still pursue our strategy if we restrict ourselves to cover the points (z, h(z)) in Step  by simplicial facets.

Therefore, we define the simplicial upper (resp. lower) covering numbers of ${\text {lift}}_h(T)$, denoted by ${\text {sucn}}_h(T)$ (resp. ${\text {slcn}}_h(T)$), as the minimum number of simplicial upper (resp. lower) facets that cover all vertices of the upper (resp. lower) part of ${\text {clift}}_h(T)$. If no covering by simplicial facets exist, the respective number is set to be $\infty$.

Lemma 4

(On semi-continuity) Let T be an m-dimensional subset of $\{0,1\}^m$.

Then, for every $h \in \mathbb {R}^T$ which is not a restriction of an affine function, there exists an open neighborhood $U \subseteq \mathbb {R}^T$ of h with the property that for every ${\tilde{h}}\in U$ one has

$$\begin{aligned} {\text {sucn}}_{{\tilde{h}}}(T)&\le {\text {sucn}}_h (T),\\ {\text {slcn}}_{{\tilde{h}}}(T)&\le {\text {slcn}}_{h} (T). \end{aligned}$$

Proof

We only prove the first inequality, since the proof of the second inequality is completely analogous. Let $Q{:}{=}{\text {clift}}_h(T)$. Notice that Q is full-dimensional, since $h \in \mathbb {R}^T$ is not a restriction of an affine function. Every simplicial upper facet of Q is given by

$$\begin{aligned} F_h {:}{=}{\text {conv}}\left\{ \begin{pmatrix} v_0 \\ h(v_0) \end{pmatrix}, \ldots , \begin{pmatrix} v_m \\ h(v_m) \end{pmatrix} \right\} , \end{aligned}$$

where $v_0,\ldots ,v_m \in T$ are affinely independent. By standard linear algebra, with an appropriate ordering of $v_0,\ldots ,v_m$, the respective facet-defining inequality for Q is given by

$$\begin{aligned} \text {det}\begin{pmatrix} 1 &{} \cdots &{} 1 &{} 1 \\ v_0 &{} \cdots &{} v_m &{} x \\ h(v_0) &{} \cdots &{} h(v_m) &{} y \end{pmatrix} \le 0. \end{aligned}$$

(7)

By expanding the determinant with respect to the last column, one can see that the fact that $F_h$ is an upper facet can be expressed as

$$\begin{aligned} \text {det}\begin{pmatrix} 1 &{} \cdots &{} 1 \\ v_0 &{} \cdots &{} v_m \end{pmatrix} > 0\end{aligned}$$

and the strict validity of the inequality on ${\text {vert}}(Q) {\setminus } \left\{ \left( {\begin{array}{c}v_i\\ h(v_i)\end{array}}\right) \, :\, i\in \{0,\ldots ,m\} \right\}$:

$$\begin{aligned} \underbrace{ \text {det}\begin{pmatrix} 1 &{} \cdots &{} 1 &{} 1\\ v_0 &{} \cdots &{} v_m &{} x\\ h(v_0) &{} \cdots &{} h(v_m) &{} h(x) \end{pmatrix} }_{=:\phi _{h}(x)}&< 0{} & {} \text {for all} \ x \in T \setminus \{v_0,\ldots ,v_m\}. \end{aligned}$$

(8)

Since $\phi _h(x)$ is linear in h, the set

$$\begin{aligned} H {:}{=}\left\{ {\tilde{h}}\in \mathbb {R}^T \, :\, \phi _{{\tilde{h}}}(x) < 0 \text { for all } x \in T \setminus \{v_0,\ldots ,v_m\} \right\} \end{aligned}$$

is open (it is the interior of a polyhedron) and it satisfies $h \in H$. By construction, for every ${\tilde{h}}\in H$, the set $F_{\tilde{h}}$ is an upper facet of ${\text {clift}}_{{\tilde{h}}}(T)$.

Thus, whenever t simplicial upper facets $F_h^1,\ldots ,F_h^t$ cover the vertex set of ${\text {clift}}_h(T)$ we see there exist t respective open sets $H^1,\ldots ,H^t$ with $h \in H^i$ for every $i\in \{1,\ldots ,t\}$. It follows that, for every ${\tilde{h}}$ in the open set $H^1\cap \cdots \cap H^t$, the sets $F_{\tilde{h}}^1,\ldots ,F_{\tilde{h}}^t$ are simplicial upper facets of ${\text {clift}}_{\tilde{h}}(T)$ that cover the vertex set of ${\text {clift}}_{\tilde{h}}(T)$. In particular, the latter holds for every ${\tilde{h}}$ in a sufficiently small neighborhood of h. $\square$

Another difficulty arises in the tools that we have available for Step , because Lemma 3 requires a height function h with $h(x) = 0$ for all $x \in X$. We were not able to find such a height function that allows us to find a small relaxation in Step . For this reason, we need a strengthening of Lemma 3, which we give in Lemma 5 below. In preparation for this, we provide the following proposition, which is actually a classical observation used in the theory of regular polyhedral subdivisions. For the sake of completeness, we give a short proof.

Proposition 4

Let $X \subseteq \mathbb {Z}^m$ and $h, {\tilde{h}}:X \rightarrow \mathbb {R}$ be such that $h(x) - {\tilde{h}}(x)=f(x)$ for every $x\in X$, where $f:\mathbb {R}^m\rightarrow \mathbb {R}$ is an affine function. Then

$$\begin{aligned} {\text {rc}}( {\text {lift}}_h(X), \mathbb {Z}^m \times \mathbb {R}) = {\text {rc}}({\text {lift}}_{\tilde{h}}(X), \mathbb {Z}^m \times \mathbb {R}). \end{aligned}$$

Proof

The affine map $\phi (x,y) = (x, y + f(x))$ maps both $\mathbb {R}^m\times \mathbb {R}$ and $\mathbb {Z}^m \times \mathbb {R}$ bijectively onto themselves and it satisfies $\phi (x,{\tilde{h}}(x)) = (x,h(x))$, which means that $\phi$ maps ${\text {lift}}_{{\tilde{h}}}(X)$ bijectively onto ${\text {lift}}_h(X)$. Thus every relaxation of ${\text {lift}}_{{\tilde{h}}}(X)$ within $\mathbb {Z}^m \times \mathbb {R}$ is bijectively mapped to a relaxation of ${\text {lift}}_h(X)$ within $\mathbb {Z}^m \times \mathbb {R}$ and vice versa. This yields the desired assertion. $\square$

Lemma 5

Let X be an affinely independent subset of $\mathbb {Z}^k$ with $\textbf{0} \in X$, let Y be a finite m-element subset of $\mathbb {Z}^k$ disjoint with X, and let $h:X \cup Y \rightarrow \mathbb {R}$ be such that

• (a) $h(x) \in \mathbb {Q}$ for every $x \in X$ and

• (b) the values h(y) with $y \in Y$ together with 1 are linearly independent over $\mathbb {Q}$.

Then ${\text {rc}}(X \oplus \Delta _m) \le {\text {rc}}({\text {lift}}_h(X \cup Y), \mathbb {Z}^k \times \mathbb {R})$.

Proof

Since X is affinely independent, there exists an affine function f that coincides with h on X. Since $h(x) \in \mathbb {Q}$ for every $x \in X$, we can choose f with rational coefficients. Then the function $h - f$ is equal to 0 on X.

We now verify that the assumptions of Lemma 3 are fulfilled by checking that the values $h(y) - f(y)$ with $y \in Y$ are linearly independent over $\mathbb {Q}$. By the choice of f, we have $f(y) \in \mathbb {Q}$ for every $y \in Y$. Hence, since the values h(y) with $y \in Y$ together with 1 are linearly independent over $\mathbb {Q}$, it follows the values $h(y)-f(y)$ with $y \in Y$ are linearly independent over $\mathbb {Q}$. Thus, using Lemma 3 and then Proposition 4, we obtain

$$\begin{aligned} {\text {rc}}(X \oplus \Delta _m) \le {\text {rc}}({\text {lift}}_{h-f}(X \cup Y), \mathbb {Z}^k \times \mathbb {R}) = {\text {rc}}({\text {lift}}_h(X \cup Y, \mathbb {Z}^k \times \mathbb {R}). \end{aligned}$$

$\square$

Equipped with these tools, we are able to provide a statement that allows us to bound the relaxation complexity in terms of simplicial upper and lower covering numbers.

Lemma 6

Let $X\subseteq \{0,1\}^k$, let Y be an m-element subset of $\{0,1\}^k$ disjoint with X, and let $h:X \cup Y \rightarrow \mathbb {R}$ be any function which is not a restriction of an affine function and satisfies $h(x) \in \mathbb {Q}$ for all $x \in X$. Then

$$\begin{aligned} {\text {rc}}(X \oplus \Delta _m) \le {\text {rc}}(X \cup Y) + {\text {sucn}}_h(X \cup Y ) + {\text {slcn}}_h(X \cup Y). \end{aligned}$$

Proof

One can approximate h arbitrarily well by ${\tilde{h}}:X \cup Y \rightarrow \mathbb {R}$ for which ${\tilde{h}}(x) = h(x)\in \mathbb {Q}$ for every $x \in X$ and the values ${\tilde{h}}(y)$ with $y \in Y$, together with 1, are linearly independent over $\mathbb {Q}$. Thus, the assertion follows by combining Proposition 3 with $T=X\cup Y$ and Lemmas 5 and 4. $\square$

Recall from the previous subsection that we want to apply a lifting to the set $T = X \cup Y$ with $X = \Delta _k$ and $Y = \{0,1\}^k {\setminus } X$. Due to Lemma 6, we can use in Step  of our strategy any height function h such that $h|_T$ is not the restriction of an affine function and such that $h(x) \in \mathbb {Q}$ for all $x \in X$. Towards proving Theorem 2, we select

$$\begin{aligned} h:\{0,1\}^k \rightarrow \mathbb {R},\qquad h(x_1,\dots ,x_k) = (2x_k - 1) \cdot r(x_1,\dots ,x_{k-1}), \end{aligned}$$

where $r:\{0,1\}^{k-1} \rightarrow \mathbb {R}$ is defined by $r(x_1,\dots , x_{k-1})=(\sum _{i=1}^{k-1} x_i)^2$.

Remark 3

Function r is the height function that defines the so-called staircase triangulation of $[0,1]^{k-1}$, see, e.g., [27, Sect. 16.7.2]. That is, the statements about simplicial facets of ${\text {lift}}_h(X \cup Y, \mathbb {Z}^k \times \mathbb {R})$, which we will make in the following section, can be related to a triangulation of $[0,1]^{k-1}$ if we fix $x_k$ to 0 or 1.

4.3 Relax: constructing a small mixed-integer relaxation

To complete Step , we use the height function h from the preceding subsection and bound ${\text {sucn}}_h(\{0,1\}^k)$ and ${\text {slcn}}_h(\{0,1\}^k)$ from above. First, we show that the two values are equal, i.e., it is sufficient to investigate the upper or lower facets.

Proposition 5

One has

$$\begin{aligned} {\text {slcn}}_h(\{0,1\}^k) = {\text {sucn}}_h(\{0,1\}^k). \end{aligned}$$

Proof

The affine map $\phi (x_1,\ldots ,x_k,y) {:}{=}(x_1,\ldots ,x_{k-1},1-x_k, -y)$ is an affine involution on $\mathbb {R}^{k+1}$. Furthermore, $\phi$ can be restricted to an involution on ${\text {lift}}_h(\{0,1\}^k)$ since

$$\begin{aligned}&\phi \bigl ( x_1,\ldots ,x_{k-1},x_k, (2 x_k - 1) \cdot r(x_1,\ldots ,x_{k-1}) \bigr ) \\ =&\bigl ( x_1,\ldots , x_{k-1},1-x_k, - (2 x_k - 1) \cdot r(x_1,\ldots ,x_{k-1}) \bigr ), \\ =&\bigl (x_1,\ldots ,x_{k-1}, 1- x_k , (2 (1-x_k) - 1) \cdot (r(x_1,\ldots ,x_{k-1}) \bigr ) \\ \in&{\text {lift}}_h(\{0,1\}^k) \end{aligned}$$

for each $(x_1,\ldots ,x_k) \in \{0,1\}^k$. This implies that a subset $F\subseteq {\text {clift}}_h(\{0,1\}^k)$ defines a facet of ${\text {clift}}_h(\{0,1\}^k)$ if and only if the set $\phi (F)$ does. Now, in order to obtain the identity in the thesis it thus suffices to show that F is an upper facet if and only if $\phi (F)$ is a lower facet. Indeed, let $f:\mathbb {R}^{k+1} \rightarrow \mathbb {R}$ be the affine function defining an upper facet F of ${\text {clift}}_h(\{0,1\}^k)$, so that $f(x)\le 0$ is valid for each $x\in {\text {clift}}_h(\{0,1\}^k)$, equality is attained for $x\in F$, and the coefficient of $x_{k+1}$ is positive. Then $f(\phi (x))\le 0$ is valid for each $x\in {\text {clift}}_h(\{0,1\}^k)$, with equality attained for $x\in \phi (F)$, and the coefficient of $x_{k+1}$ is negative, hence the facet $\phi (F)$ given by the affine function $f(\phi (x))$ is a lower facet of ${\text {clift}}_h(\{0,1\}^k)$. The reverse implication holds by an analogous argument. $\square$

Proposition 5 allows us to focus on the upper facets of ${\text {clift}}_h(\{0,1\}^k)$. We will consider two families of simplicial (upper) facets: one will cover vertices with $x_k=0$ and the other will cover vertices with $x_k=1$. For simplicity we denote a vertex of ${\text {clift}}_h(\{0,1\}^k)$ by $(x,x_{k+1})$, where $x\in \{0,1\}^k$ and $x_{k+1}=h(x)$. We now define the facets that we will use in our covering. Let $\pi$ be a permutation of $[k-1]$, $B\subseteq [k-1]$, $b=|B|$, and let $\pi ':[k-1-b] \rightarrow [k-1]{\setminus } B$ be a bijection. Let

$$\begin{aligned} F_\pi ={\text {conv}}\left( \{(\textbf{0},0), (e_k,0)\}\cup \Big \{ (e_k + \sum _{i = 1}^t e_{\pi (i)}, t^2): t\in \{1,\dots , k-1\}\Big \}\right) , \end{aligned}$$

and

$$\begin{aligned}&F_{B,\pi '}= {\text {conv}}\Big (\{(e(B),-b^2), (e(B) + e_k, b^2)\} \cup \{(e(B\setminus j),-(b-1)^2), j\in B\}\\&\quad \cup \Big \{ (e(B)+e_k + \sum _{i = 1}^{t} e_{\pi '(i)}, (b+t)^2) : t\in \{1,\dots , k-1-b\}\Big \}\Big ), \end{aligned}$$

where $e(B)=\sum _{i\in B} e_i$.

Proposition 6

$F_\pi$ and $F_{B,\pi '}$ as defined above are simplicial upper facets of ${\text {clift}}_h(\{0,1\}^k)$.

Proof

$F_\pi$ can be easily seen to contain exactly $k+1$ affinely independent vectors, hence in order to show that it is a facet, it suffices to exhibit a valid inequality for ${\text {clift}}_h(\{0,1\}^k)$ that is satisfied at equality precisely by the points of $F_\pi$. One can argue in the same way for $F_{B,\pi '}$.

Consider the inequality

$$\begin{aligned} x_{k+1}\le \sum _{i=1}^{k-1} (2i-1)x_{\pi (i)}. \end{aligned}$$

(9)

Let $(x,x_{k+1})$ be a vertex of ${\text {clift}}_h(\{0,1\}^k)$. If $x_k=0$, then (9) is trivially satisfied, as the left-hand side is non-positive and the right-hand side would be non-negative, and it is satisfied with equality only if $x=\textbf{0}$. Now, let $x_k=1$, hence $x_{k+1}=(\sum _{i=1}^{k-1} x_i)^2=\ell ^2$ for some $\ell \in \mathbb {Z}_{\ge 0}$. Then the right-hand side of (9) is the sum of $\ell$ odd numbers, i.e., at least $\sum _{i=1}^\ell (2i-1)= \ell ^2=x_{k+1}$, and equality holds exactly when $(x,x_{k+1})\in F_{\pi }$.

Now, consider the inequality

$$\begin{aligned} x_{k+1}\le b^2-b - (2b-1)x(B)+\sum _{i=1}^{k-1-b} (2b+2i-1)x_{\pi '(i)} +2b^2x_k, \end{aligned}$$

(10)

where $x(B)= \sum _{i\in B} x_i$ similarly as before. Let $h_1=x(B)$ and $h_2=x([k-1]\setminus B)$. Suppose $x_k=1$. Then $x_{k+1}=(h_1+h_2)^2$ and the right-hand side of (10) becomes

$$\begin{aligned} b^2-b - (2b-1)h_1+\sum _{i=1}^{k-1-b} (2b+2i-1)x_{\pi '(i)} +2b^2\ge & {} b^2-b - (2b-1)h_1 \\{} & {} \quad + 2bh_2+ h_2^2+2b^2 \end{aligned}$$

by lower bounding the summation $\sum _{i=1}^{k-1-b} (2i-1)x_{\pi '(i)}$ with the sum of the first $h_2$ odd numbers. The expression above is at least $(h_1+h_2)^2$ if and only if

$$\begin{aligned} h_1^2 + 2h_1h_2 + (2b-1)h_1 - 2bh_2 \le 3b^2-b. \end{aligned}$$

The latter is easily seen to hold, since $h_1\le b$.

The case $x_k=0$ follows from the previous case by noticing that the left-hand side of (10) decreases by $2(h_1+h_2)^2$ and the right-hand side decreases by $2b^2\le 2(h_1+h_2)^2$.

Finally, one can easily verify that the inequality is satisfied with equality exactly when $(x,x_{k+1}) \in F_{B,\pi '}$, which concludes the proof. $\square$

We now give our covering. The idea is to cover all vertices of ${\text {clift}}_h(\{0,1\}^k)$ that have $x_k=1$ with facets of the form $F_\pi$, and the other vertices with facets of the form $F_{B,\pi '}$.

Proposition 7

There is a set $\Pi _k$ of $O(2^k/\sqrt{k})$ permutations on $[k-1]$ such that the facets in ${\mathcal {F}}_1{:}{=}\{F_\pi : \pi \in \Pi _k\}$ cover all vertices of ${\text {clift}}_h(\{0,1\}^k)$ with $x_k=1$.

To prove Proposition 7, we derive an upper bound on the number of simplices needed in a triangulation of the hypercube $[0,1]^k$. Specifically, we consider the triangulation arising from permutations contained in the symmetric group $S_k$ of the set [k]. This triangulation is ${\mathcal {T}}_k = \{ \Delta ^\pi : \pi \in S_k\}$ with $\Delta ^\pi = \{x \in \mathbb {R}^k: 1 \ge x_{\pi (1)} \ge \dots \ge x_{\pi (k)} \ge 0\}$.

Proposition 8

The minimum number of simplices from ${\mathcal {T}}_k$ needed to cover all vertices of $[0,1]^k$ is $\left( {\begin{array}{c}k\\ \lfloor \nicefrac {k}{2} \rfloor \end{array}}\right)$.

Proof

With each vertex x of $[0,1]^k$, we associate the set $A(x) = \{ i \in [k]: x_i = 1\}$. Moreover, let $a(x) = | A(x) |$. Then, a simplex $\Delta ^\pi \in {\mathcal {T}}_k$ contains x if and only if $A(x) = \{\pi (1), \dots , \pi (a(x))\}$. The minimum number of simplices needed to cover all vertices of $[0,1]^k$ is thus equivalent to the minimum cardinality of a set $\Pi \subseteq S_k$ of permutations such that, for each vertex x of $[0,1]^k$, there is a permutation $\pi \in \Pi$ with $A(x) = \{\pi (1), \dots , \pi (a(x))\}$.

To characterize such a minimum set $\Pi$, consider the poset of all subsets of [k] ordered by inclusion. Note that there is a one-to-one correspondence between permutations $\pi$ of [k] and chains $\emptyset \subseteq \{i_1\} \subseteq \{i_1,i_2\} \subseteq \dots \subseteq \{i_1, \dots , i_k\}$ in this poset via $\pi (1) = i_1,\dots , \pi (k) = i_k$. Consequently, since subsets of [k] correspond to vertices of $[0,1]^k$, the minimum number of simplices needed to cover all vertices of $[0,1]^k$ is the same as the minimum number of chains needed to cover all elements of the poset. By Dilworth’s theorem, see, e.g., the book [28], this number is the same as the length of a largest antichain in the poset. Since all subsets of [k] of cardinality $\lfloor \frac{k}{2} \rfloor$ are pairwise incomparable, the length of a largest antichain is at least $\left( {\begin{array}{c}k\\ \lfloor \nicefrac {k}{2} \rfloor \end{array}}\right)$. Moreover, this bound is tight due to a result by Sperner [29]. $\square$

Proposition 7 thus follows, because $\left( {\begin{array}{c}k\\ \lfloor \frac{k}{2} \rfloor \end{array}}\right) \in \Theta (\frac{2^k}{\sqrt{k}})$, see [30, Sect. 4].

Now, to cover the vertices of ${\text {clift}}_h(\{0,1\}^k)$ with $x_k=0$, we will select facets of the form $F_{B,\pi '}$. Notice that only the choice of the set B determines which vertices with $x_k=0$ are in $F_{B,\pi '}$, hence the choice of the bijection $\pi '$ is irrelevant. We then fix one such bijection $\pi _B$ for each B, and simply write $F_{B}{:}{=}F_{B,\pi _B}$.

Proposition 9

There is a family ${\mathcal {B}}$ of $O(2^k\frac{\log (k)}{k})$ subsets of $[k-1]$ such that the facets in ${\mathcal {F}}_0{:}{=}\{F_{B}: B \in {\mathcal {B}}\}$ cover all vertices of ${\text {clift}}_h(\{0,1\}^k)$ with $x_k=0$.

Proof

Notice that a vertex of ${\text {clift}}_h(\{0,1\}^k)$ with $x_k=0$ is in $F_B$ if and only if the support of $(x_1,\dots ,x_{k-1})$ is either equal to B or to a subset of B of size $b-1$ (where again $b=|B|$). Consider the Hasse diagram $D=(V,A)$ of the poset $2^{[k-1]}$, ordered by inclusion. It suffices to give a family ${\mathcal {B}}$ of vertices of D with the property that, for any set $X\subseteq [k-1]$, either $X\in {\mathcal {B}}$ or X “points” to a set in ${\mathcal {B}}$, i.e., $(X,B)\in A$ for some $B \in {\mathcal {B}}$. We construct this family, which we call “dominating”, using the probabilistic method, similarly as done in [31, Theorem 1.2.2] for bounding the domination number of undirected graphs.

Let ${\mathcal {X}}\subseteq V$ be formed by picking each subset of $[k-1]$ with a probability $p_i$ (to be specified later) that depends on its size i. Let ${\mathcal {Y}}\subseteq V$ contain the sets of $V\setminus {\mathcal {X}}$ that do not point to any set in ${\mathcal {X}}$. Notice that the family ${\mathcal {X}}\cup {\mathcal {Y}}$ is dominating. We now bound its expected size. We have that

$$\begin{aligned} \mathbb {E}(|{\mathcal {X}}|)&=\sum _{i=1}^{k-1} {k-1 \atopwithdelims ()i} p_i,\\&\mathbb {E}(|{\mathcal {Y}}|)\le \sum _{i=1}^{k-1} {k-1 \atopwithdelims ()i-1} (1-p_i)^{k-i}, \end{aligned}$$

where for the latter we used the fact that a set of size $i-1$ points to exactly $k-i$ sets, none of which has to be picked in ${\mathcal {X}}$. We now set $p_i=\frac{\ln (k-i)}{k-i}$, and use the fact that $1-p\le e^{-p}$ for all reals p. We then get

$$\begin{aligned}&\mathbb {E}(|{\mathcal {X}}\cup {\mathcal {Y}}|) \le \sum _{i=1}^{k-1}\Big ( {k-1 \atopwithdelims ()i} \frac{\ln (k-i)}{k-i}+{k-1 \atopwithdelims ()i-1} \frac{1}{k-i}\Big )\\&\quad \le 2\ln (k) \sum _{i=1}^{k-1} \frac{{k \atopwithdelims ()i}}{k-i}= 2\ln (k) \sum _{i=1}^{k-1} \frac{{k \atopwithdelims ()k-i}}{k-i}\\&\quad =2\ln (k) \sum _{i=1}^{k-1} \frac{{k+1 \atopwithdelims ()k-i+1}}{k+1}\cdot \frac{k-i+1}{k-i}\le 4\frac{\ln (k)}{k+1} \sum _{i=1}^{k-1} {k+1 \atopwithdelims ()k-i+1}\le 2^{k+3}\frac{\ln (k)}{k+1}, \end{aligned}$$

where the second equality follows from the known identity $\frac{{k \atopwithdelims ()\ell }}{\ell +1}=\frac{{k+1 \atopwithdelims ()\ell +1}}{k+1}$, and the last inequality from the binomial expansion.$\square$

We can now obtain our bound on ${\text {sucn}}_h(\{0,1\}^k)$ (hence, on ${\text {slcn}}_h(\{0,1\}^k)$) by putting together Propositions 7 and 9.

Corollary 3

We have ${\text {sucn}}_h(\{0,1\}^k)\in O(\frac{2^k}{\sqrt{k}})$.

4.4 Putting all pieces together

With the preparatory work of the preceding sections, we are able to provide a proof of Theorem 2.

Proof of Theorem 2

First, assume that there is a positive integer k such that $d = 2^{k}-1$. Let $m = d - k$. Furthermore, let $\tilde{\Delta }_d$ as well as $T = X \cup Y$ be defined as in Sect. 4.1. Then, $X = \Delta _k$ and $Y = \{0,1\}^k \setminus X$. Moreover, as defined at the end of Sect. 4.2, let $h:\{0,1\}^k \rightarrow \mathbb {R}$ be given by $h(x_1, \dots , h_k) = (2x_k - 1) \cdot r(x_1,\dots ,r_{k-1})$. By Lemma 6,

$$\begin{aligned} {\text {rc}}(\Delta _d) = {\text {rc}}(\Delta _k \oplus \Delta _m) \le {\text {rc}}(X \cup Y) + {\text {sucn}}_h (X \cup Y) + {\text {slcn}}_h (X \cup Y). \end{aligned}$$

As $X \cup Y = \{0,1\}^k$ and ${\text {rc}}(\{0,1\}^k) \le 2k$, we derive from Proposition 5 and Corollary 3 the upper bound ${\text {rc}}(\Delta _d) \in O(\frac{2^k}{\sqrt{k}})$. Because $k = \log _2(d+1)$, the assertion follows.

If there is no positive integer k with $d = 2^k - 1$, then let $d'$ be the smallest integer greater than d that admits such a representation. Note that $d < d' \le 2d$ and ${\text {rc}}(\Delta _d) \le {\text {rc}}(\Delta _{d'})$. Thus, by the above argumentation,

$$\begin{aligned} {\text {rc}}(\Delta _d) \le {\text {rc}}(\Delta _{d'}) \in O\left( \tfrac{d'}{\sqrt{\log (d')}}\right) = O\left( \tfrac{d}{\sqrt{\log (d)}}\right) . \square \end{aligned}$$

5 Outlook

In light of our new results, we formulate the following open problems:

• (P1) For given $d \in \mathbb {Z}_{>0},$ characterize all finite subsets X of $\mathbb {Z}^d$ satisfying ${\text {rc}}(X) < {\text {rc}}_\mathbb {Q}(X)$. The first open case is $d=5$.

• (P2) Improve the asymptotic upper bound on ${\text {rc}}(\Delta _d)$. The best known lower bound on ${\text {rc}}(\Delta _d)$ is of asymptotic order $\Omega (\log d)$, see [4]. In contrast, our asymptotic upper bound $O( \frac{d}{\sqrt{\log d}})$ is only mildly sublinear in d. It is widely open what asymptotic behavior for ${\text {rc}}(\Delta _d)$ one should expect, but it is quite likely that our upper bound is not tight.

• (P3) As ${\text {rc}}(X)$ and ${\text {rc}}_\mathbb {Q}(X)$ do not coincide in general, there are two algorithmic problems that one can ask, for every fixed dimension d as well as for an unspecified d: Determine whether ${\text {rc}}(X)$ and ${\text {rc}}_\mathbb {Q}(X)$ are algorithmically computable. The existence of sets X satisfying ${\text {rc}}(X) < {\text {rc}}_\mathbb {Q}(X)$ is an additional complication that makes an algorithmic computation of these two values quite an intricate task, as explained in [5]. The authors of [6] introduce a non-increasing sequence $(u_k)_{k \in \mathbb {N}}$ of upper bounds on ${\text {rc}}_\mathbb {Q}(X)$, which are computable for each given k. This sequence stabilizes by attaining the value ${\text {rc}}_\mathbb {Q}(X)$ after finitely many steps. However, it is open whether one can decide for fixed k whether $u_k = {\text {rc}}_\mathbb {Q}(X)$. One way to decide this is by providing a computable matching lower bound. In [1], a mechanism to derive lower bounds via so-called hiding sets is presented. Deriving a lower bound $\ell$ via hiding sets yields $\ell \le {\text {rc}}(X) \le {\text {rc}}_\mathbb {Q}(X) \le u_k$. Thus, this approach can only work if ${\text {rc}}(X) = {\text {rc}}_\mathbb {Q}(X)$. In [4] it is shown that ${\text {rc}}(X)={\text {rc}}_\mathbb {Q}(X)$ for any $X\subseteq \mathbb {Z}^d$ when $d\le 4$, and for other special cases. In this case, one might wonder about a computable lower bound on ${\text {rc}}(X)$ that is tight. Due to Corollary 1 and Theorem 2, however, ${\text {rc}}(X)$ can be strictly smaller than ${\text {rc}}_\mathbb {Q}(X)$, and thus, matching upper bounds on ${\text {rc}}_\mathbb {Q}(X)$ and lower bounds on ${\text {rc}}(X)$ do not exist in general.

• (P4) Determine the minimum of ${\text {rc}}(X)$ over all sets $X \subseteq \mathbb {Z}^d$ of dimension $d=\dim (X)$. This quantity can be analyzed asymptotically, for $d \rightarrow \infty$, as well as for concrete choices of d. It would be interesting to see if the minimum is attained for $X= \Delta _d$.

• (P5) Study the relaxation complexity with respect to arbitrary sub-fields of $\mathbb {R}$. One can introduce the relaxation complexity ${\text {rc}}_{\mathbb {F}}(X)$ of $X \subseteq \mathbb {Z}^d$ with respect to relaxations of X described by inequalities with coefficients in ${\mathbb {F}}$. It is clear that ${\text {rc}}_{\mathbb {F}}(X)$ is monotone in ${\mathbb {F}}$ with respect to inclusion. Our arguments show that the estimate ${\text {rc}}_{\mathbb {F}}(X) \in O(\frac{d}{\sqrt{\log (d)}})$ holds for every field of dimension at least $d+1$ over $\mathbb {Q}$, as we only need $d+1$ numbers in $\mathbb {R}$ that are linearly independent over $\mathbb {Q}$ to prescribe appropriate heights. For $d=5$, our construction shows ${\text {rc}}_{\mathbb {Q}[\sqrt{2}]}(\Delta _5)=5$, where the field $\mathbb {Q}[\sqrt{2}]$ has dimension two over $\mathbb {Q}$. This is the smallest dimension of ${\mathbb {F}}$ over $\mathbb {Q}$ with ${\text {rc}}_{{\mathbb {F}}}(\Delta _5)=5$, as the only one-dimensional field over $\mathbb {Q}$ is $\mathbb {Q}$ itself. It is likely that ${\text {rc}}_{\mathbb {F}}(\Delta _5)=5$ holds for every field ${\mathbb {F}}\subset \mathbb {R}$ of dimension two over $\mathbb {Q}$, which just means that ${\text {rc}}_{\mathbb {Q}[r]}(\Delta _5) = 5$ should be true for every $r \in \mathbb {R}\setminus \mathbb {Q}$.

• (P6) When ${\mathbb {F}}$ is the field of real algebraic numbers, determine if ${\text {rc}}_{\mathbb {F}}(X)$ is computable for a given finite $X \subset \mathbb {Z}^d$ and if the equality ${\text {rc}}_{{\mathbb {F}}}(X) = {\text {rc}}(X)$ holds for every finite$X \subset \mathbb {Z}^d$. Indeed, our results show that the choice between rationals and arbitrary reals makes a difference, but the reals in their whole generality include numbers that one cannot even approximate algorithmically, so it makes sense to ask if some reasonably constructive subfield of the reals would be enough for computing the relaxation complexity. The field of algebraic numbers could be a good candidate.

Appendix: Proof of Proposition 1

In this appendix, we provide the missing details to prove Proposition 1. For $\varepsilon = \frac{1}{8}$, System (1)–(5) describing the polyhedron $P_{\nicefrac {1}{8}}$ can be compactly written as $A\bar{x} \ge 0$, where

and $\bar{x} = (1,x_1,x_2,x_3,x_4)^\top$. Our proof consists of two steps. First, we show that any $x \in \mathbb {Z}^3\times \mathbb {R}$ satisfying (1)–(5) satisfies $(x_1,x_2,x_3)^\top \in \Delta _2 \times \{0,1\}$. That is, the first three coordinates of any mixed-integer point in $P_{\nicefrac {1}{8}}$ correspond to the first three coordinates of a point in $\Delta '$. Second, we prove that, for every of the six possible combinations for the first three coordinates, there is a unique fourth coordinate such that $x \in P_{\nicefrac {1}{8}}$, and that this coordinate is such that $x \in \Delta '$.

Fig. 3

The projection on the first three components of $\Delta '$ (convex hull in orange) and the polytope $P_{\nicefrac {1}{8}}$ (green). The inequality description of the projection of $P_{\nicefrac {1}{8}}$ can be derived from the inequality description (1)–(5) of $P_{\nicefrac {1}{8}}$ using Fourier-Motzkin elimination, which combines the three upper bounds (1)–(3) on $x_4$ with the two lower bounds (4)–(5) on $x_4$. As a result, one obtains $3 \times 2 =6$ inequalities for $x_1,x_2,x_3$, and it turns out that each of these inequalities defines a facet of the projected polytope

To prove the first part, we used Fourier-Motzkin elimination (FME) to project $P_{\nicefrac {1}{8}}$ onto a polyhedron in 3-dimensional and 2-dimensional space, respectively. Inspecting these systems, we could show that indeed every $x \in P_{\nicefrac {1}{8}}$ satisfies $(x_1,x_2,x_3)^\top \in \Delta _2 \times \{0,1\}$. For the sake of conciseness, we do not provide all details of FME. Instead, we only provide systems of linear inequalities that can be derived using FME and which suffice to prove our claim, namely $B_1\bar{x} \ge 0$ and $B_2\bar{x} \ge 0$ with

Both systems can be derived from $A\bar{x} \ge 0$ by combining some non-negative multiples of these inequalities. Concretely, $B_1 = C_1A$ and $B_2 = C_2A$ for the non-negative matrices

respectively. That is, $B_1\bar{x} \ge 0$ and $B_2\bar{x} \ge 0$ are conic combinations of the inequalities in $A\bar{x} \ge 0$.

From system $B_2\bar{x} \ge 0$, we derive

$$\begin{aligned} -\frac{8}{9} \le x_2 \le \frac{2 + \frac{1}{8}\sqrt{2}}{2 - \frac{9}{64}\sqrt{2}}. \end{aligned}$$

Since we require $x_2 \in \mathbb {Z}$, rounding the bounds yields $x_2 \in \{0,1\}$ as desired. This observation allows us to find the possible values for $x_1$ and $x_3$ based on a case distinction.

Lemma 7

For any $x \in P_{\nicefrac {1}{8}} \cap \mathbb {Z}^3 \times \mathbb {R}$ with $x_2 = 0$, we have $x_1,x_3 \in \{0,1\}$.

Proof

Substituting $x_2=0$ in $B_1\bar{x} \ge 0$, we obtain

This system contains inequalities $0 \le x_3 \le 1$ and the inequality $x_1 \le 1$. For providing a lower bound on $x_1$ we can combine $\sqrt{2} x_1 + x_3 \ge 0$ with $x_3 \le 1$, yielding $x_1 \ge -\frac{1}{\sqrt{2}}$. Taking integrality of $x_1$ into account, we conclude $x_1 \ge 0$, which proves the assertion.$\square$

Lemma 8

For any $x \in P_{\nicefrac {1}{8}} \cap \mathbb {Z}^3 \times \mathbb {R}$ with $x_2 = 1$, we have $x_1 = 0$ and $x_3 \in \{0,1\}$.

Proof

Substituting $x_2=1$ in $B_1\bar{x} \ge 0$, we get

The second and the fourth inequality provide bounds on $x_3$. Combining the bounds with $x_3 \in \mathbb {Z}$ yields $x_3 \in \{0,1,2\}$. The third inequality gives $x_1 \le 0$. In order to obtain a lower bound on $x_1$, we combine the first inequality $\sqrt{2} x_1 + x_3 \ge 0$ with the bound $x_3 \le 2$ and obtain $x_1 \ge - \frac{2}{\sqrt{2}}$. By integrality of $x_1$, we thus have $x_1 \ge -1$. Consequently, $(x_1,x_3)^\top \in \{-1,0\} \times \{0,1,2\}$. Inserting all points in the above system shows that only the choices with $x_1=0$ and $x_3 \in \{0,1\}$ are valid.$\square$

Combining these two lemmata and $x_2 \in \{0,1\}$ shows the first part of our proof, i.e., any $x \in P_{\nicefrac {1}{8}}$ satisfies $(x_1,x_2,x_3)^\top \in \Delta _2 \times \{0,1\}$.

For the second part, we investigate the implications of inserting $\bar{x}$ with $(x_1,x_2,x_3)^\top \in \Delta _2 \times \{0,1\}$ into system $A\bar{x} \ge 0$. To this end, let $A'$ be the matrix consisting of the first four columns of A and let $A''$ be the matrix containing the last column of A. System $A\bar{x} \ge 0$ is thus equivalent to

$$\begin{aligned} A' \begin{pmatrix} 1\\ x_1\\ x_2\\ x_3 \end{pmatrix} + A''x_4 \ge 0. \end{aligned}$$

For any $x' = (1,x_1,x_2,x_3)^\top \in \{1\}\times \Delta _2 \times \{0,1\}$, the vector $g = A'x'$ is one of the six columns of matrix

Denote by $g^0,\dots ,g^5$ the columns of G. To show that, for any $x'$, there is a unique choice for the missing coordinate $x_4$, we analyze $g + A''x_4 \ge 0$. Straightforward calculations show that $x_4=0$ is valid when $g \in \{g^0,\dots ,g^3\}$, that $x_4=1$ is valid for $g = g^4$, and $x_4 = - \frac{1}{\sqrt{2}}$ is valid for $g = g^5$. That is, every point in $\Delta '$ is also contained in $P_{\nicefrac {1}{8}}$. To conclude the proof, we need to show that the choice for $x_4$ is unique. This is done in a straightforward manner by finding a pair of matching upper and lower bounds, which we derive from $A\bar{x} \ge 0$:

$g=g_0$::

first and fourth inequality confirm that $x_4=0$

$g=g_1$::

second and fourth inequality confirm that $x_4=0$.

$g=g_2$::

second and fourth inequality confirm that $x_4=0$.

$g=g_3$::

first and fifth inequality confirm that $x_4=0$

$g=g_4$::

first and the fifth inequality confirm that $x_4=1$.

$g=g_5$::

third and the fourth inequality confirm that $x_4 = - \frac{1}{\sqrt{2}}$.

This concludes the proof of Proposition 1.