Abstract
Proximal methods are known to identify the underlying substructure of nonsmooth optimization problems. Even more, in many interesting situations, the output of a proximity operator comes with its structure at no additional cost, and convergence is improved once it matches the structure of a minimizer. However, it is impossible in general to know whether the current structure is final or not; such highly valuable information has to be exploited adaptively. To do so, we place ourselves in the case where a proximal gradient method can identify manifolds of differentiability of the nonsmooth objective. Leveraging this manifold identification, we show that Riemannian Newton-like methods can be intertwined with the proximal gradient steps to drastically boost the convergence. We prove the superlinear convergence of the algorithm when solving some nondegenerated nonsmooth nonconvex optimization problems. We provide numerical illustrations on optimization problems regularized by \(\ell _1\)-norm or trace-norm.




Similar content being viewed by others
Notes
We choose the term “Newton acceleration” to emphasize the similarity with the celebrated Nesterov acceleration [34]. Indeed both methods add an acceleration step after the proximal gradient iteration. But, unlike Nesterov’s method where the acceleration is provided by an inertial step, the Newton acceleration comes from a second-order step on a smooth substructure, as we detail in this paper.
The weaker assumption of prox-boundedness (ie. \(g+r\Vert \cdot \Vert ^2\) is bounded below for some r) implies that \( \mathbf {prox}_{\gamma g}(y) \) is non-empty when \(\gamma \) is taken sufficiently small; see [36, Chap. 1.G].
The following example shows that in the nonconvex setting, ii) and iii) do not necessarily imply i). Take f null and g as follows, then the proximity operator of g at 0 writes:
$$\begin{aligned} g(x) = {\left\{ \begin{array}{ll} x^{2}/2 &{} \text {if } |x| \le 1\\ 1-3x/2 &{} \text {if } x \ge 1\\ 1+3x/2 &{} \text {if }x \le -1 \end{array}\right. }, \qquad \mathbf {prox}_{\gamma g}(0) = {\left\{ \begin{array}{ll} 0 &{} \text {if } \gamma \in (0, 8/9) \\ \{-3\gamma / 2, 0, 3\gamma / 2\} &{} \text {if } \gamma = 8/9 \\ \{-3\gamma / 2, 3\gamma / 2\} &{} \text {if } \gamma > 8/9. \end{array}\right. } \end{aligned}$$The function g is 1-prox-regular at 0, there holds \(0 \in {{\,\mathrm{ri}\,}}\partial g(0) = \{0\}\), and yet 0 is not a fixed point of the proximal operator with stepsizes close to 1.
Each CG iteration requires one Hessian-vector product, avoiding to form the Hessian matrix. A test on this ratio is used to detect a direction of quasi-negative curvature for the (Riemannian) Hessian, which is a stopping criterion of the Conjugate Gradient. In our implementation, we require this quantity to be smaller than \(10^{-15}\) for the Newton method. For the truncated version, we reduce the threshold when getting close to the solution: initialized at 1, the threshold is decreased by a factor 10 each time the unit-step is accepted by the line search.
References
Absil, P.A., Baker, C.G., Gallivan, K.A.: Trust-region methods on riemannian manifolds. Found. Comput. Math. 7(3), 303–330 (2007)
Absil, P.A., Mahony, R., Sepulchre, R.: Optimization algorithms on matrix manifolds. Princeton University Press, NJ (2009)
Absil, P.A., Malick, J.: Projection-like retractions on matrix manifolds. SIAM J. Optim. 22, 135–158 (2012)
Agarwal, N., Boumal, N., Bullins, B., Cartis, C.: Adaptive regularization with cubics on manifolds. Mathematical Programming (2020)
Aravkin, A.Y., Baraldi, R., Orban, D.: A proximal quasi-newton trust-region method for nonsmooth regularized optimization. SIAM J. Optim. 32(2), 900–929 (2022)
Bach, F., Jenatton, R., Mairal, J., Obozinski, G.: Optimization with sparsity-inducing penalties. Foundations and Trends® in Machine Learning 4(1), 1–106 (2012)
Bareilles, G., Iutzeler, F.: On the interplay between acceleration and identification for the proximal gradient algorithm. Comput. Optim. Appl. 77, 351–378 (2020)
Beck, A.: First-order methods in optimization, vol. 25. SIAM (2017)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2(1), 183–202 (2009)
Becker, S., Fadili, J., Ochs, P.: On quasi-newton forward-backward splitting: Proximal calculus and convergence. SIAM J. Optim. 29(4), 2445–2481 (2019)
Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: A fresh approach to numerical computing. SIAM Rev. 59(1), 65–98 (2017)
Bolte, J., Nguyen, T.P., Peypouquet, J., Suter, B.W.: From error bounds to the complexity of first-order descent methods for convex functions. Mathematical Programming (2015)
Bonnans, J.F., Gilbert, J.C., Lemaréchal, C., Sagastizábal, C.A.: Numerical optimization: theoretical and practical aspects. Springer Science & Business Media, Berlin (2006)
Boumal, N.: An introduction to optimization on smooth manifolds. To appear with Cambridge University Press (2022). URL http://www.nicolasboumal.net/book
Briant, O., Lemaréchal, C., Meurdesoif, P., Michel, S., Perrot, N., Vanderbeck, F.: Comparison of bundle and classical column generation. Math. Program. 113(2), 299–344 (2008)
Burke, J.V., Moré, J.J.: On the identification of active constraints. SIAM J. Numer. Anal. 25(5), 1197–1211 (1988)
Daniilidis, A., Hare, W., Malick, J.: Geometrical interpretation of the predictor-corrector type algorithms in structured optimization problems. Optimization 55(5–6), 481–503 (2006)
Dembo, R.S., Steihaug, T.: Truncated-newtono algorithms for large-scale unconstrained optimization. Math. Program. 26(2), 190–212 (1983)
Dennis Jr, J.E., Schnabel, R.B.: Numerical methods for unconstrained optimization and nonlinear equations. SIAM (1996)
Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91(2), 201–213 (2002)
Drusvyatskiy, D., Lewis, A.S.: Optimality, identifiability, and sensitivity. Math. Program. 147(1–2), 467–498 (2014)
Hare, W., Sagastizábal, C.: Computing proximal points of nonconvex functions. Math. Program. 116(1–2), 221–258 (2009)
Iutzeler, F., Malick, J.: Nonsmoothness in machine learning: specific structure, proximal identification, and applications. Set-Valued and Variational Analysis 28(4), 661–678 (2020)
Lee, C.p.: Accelerating inexact successive quadratic approximation for regularized optimization through manifold identification. arXiv preprint arXiv:2012.02522 (2020)
Lee, J.D., Sun, Y., Saunders, M.A.: Proximal newton-type methods for minimizing composite functions. SIAM J. Optim. 24(3), 1420–1443 (2014)
Lemaréchal, C., Oustry, F., Sagastizábal, C.: The u-lagrangian of a convex function. Trans. Am. Math. Soc. 352(2), 711–729 (2000)
Lewis, A., Wylie, C.: A simple newton method for local nonsmooth optimization. arXiv preprint arXiv:1907.11742 (2019)
Lewis, A.S.: Active sets, nonsmoothness, and sensitivity. SIAM J. Optim. 13(3), 702–725 (2002)
Lewis, A.S., Liang, J., Tian, T.: Partial smoothness and constant rank. SIAM J. Optim. 32(1), 276–291 (2022)
Lewis, A.S., Wright, S.J.: A proximal method for composite minimization. Math. Program. 158(1), 501–546 (2016). https://doi.org/10.1007/s10107-015-0943-9
Liang, J., Fadili, J., Peyré, G.: Activity identification and local linear convergence of forward-backward-type methods. SIAM J. Optim. 27(1), 408–437 (2017)
Mifflin, R., Sagastizábal, C.: A VU-algorithm for convex minimization. Math. Program. 104(2–3), 583–608 (2005)
Miller, S.A., Malick, J.: Newton methods for nonsmooth convex minimization: connections among U-lagrangian, riemannian newton and sqp methods. Math. Program. 104(2–3), 609–633 (2005)
Nesterov, Y.: A method of solving a convex programming problem with convergence rate O\((1/k^2)\). Soviet Mathematics Doklady 27(2), 372–376 (1983)
Poliquin, R., Rockafellar, R.: Prox-regular functions in variational analysis. Trans. Am. Math. Soc. 348(5), 1805–1838 (1996)
Rockafellar, R.T., Wets, R.J.B.: Variational analysis, vol. 317. Springer, Berlin (2009)
Wright, S.J.: Identifiable surfaces in constrained optimization. SIAM J. Control. Optim. 31(4), 1063–1079 (1993)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is partly funded by the ANR JCJC project STROLL (ANR-19-CE23-0008).
Appendices
Preliminary results on the proximal gradient
The first result shows the local Lipschitz continuity of the proximity operator. It can be proven by applying [35, Th. 4.4] with the assumption that \({\bar{x}}=\mathbf {prox}_{{{\bar{\gamma }}} g}({\bar{y}})\), following the arguments of [22, Th. 1]. We provide here a self-contained proof.
Lemma A.1
Consider a function \(g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\), a pair of points \({\bar{x}}, {\bar{y}}\) and a step length \({\bar{\gamma }}>0\) such that \({\bar{x}}=\mathbf {prox}_{{{\bar{\gamma }}} g}({\bar{y}})\) and \(g\) is r prox-regular at \({\bar{x}}\) for subgradient \({\bar{v}} \triangleq ({\bar{y}}-{\bar{x}}) / {\bar{\gamma }}\).
Then, for any \(\gamma \in (0, \min (1/r, {{\bar{\gamma }}}))\), there exists a neighborhood \({\mathcal {N}}_{{\bar{y}}}\) of \({\bar{y}}\) over which \(\mathbf {prox}_{\gamma g}\) is single-valued and \((1-\gamma r)^{-1}\)-Lipschitz continuous. Furthermore, there holds
for \(y\in {\mathcal {N}}_{{\bar{y}}}\) and x near \({\bar{x}}\) in the sense \(\Vert x-{\bar{x}}\Vert <\varepsilon \), \(|g(x)-g({\bar{x}})|<\varepsilon \) and \(\Vert (y-x)/\gamma - {\bar{v}}\Vert <\varepsilon \).
Proof
One can easily check that prox-regularity of \(g\) at \({\bar{x}}\) for subgradient \({\bar{v}}\) is equivalent to prox-regularity of function \({\tilde{g}}\) around 0 for subgradient 0, with \({\tilde{g}} = g(\cdot + {\bar{x}}) - \langle {\bar{v}}, \cdot \rangle - g({\bar{x}})\) and a change of variable \({\tilde{x}} = x-{\bar{x}}\). Similarly, \({\bar{x}}=\mathbf {prox}_{{{\bar{\gamma }}} g}({\bar{y}})\) is characterized by its global optimality condition
which we may write as
Under that same change of variables, since \({\tilde{g}}(0) = 0\), this optimality condition rewrites as
We may thus apply Theorem 4.4 from [35] to get the claimed result on \({\tilde{g}}\), which transfers back to \(g\) as our change of function and variable is bijective. We thus obtain that for \(\gamma \in (0, \min (1/r, {{\bar{\gamma }}}))\), on a neighborhood \({\mathcal {N}}_{{\bar{y}}}\) of \({\bar{y}}\), \(\mathbf {prox}_{\gamma g}\) is single-valued, \((1-\gamma r)^{-1}\)-Lipschitz continuous and \(\mathbf {prox}_{\gamma g}(y)=[I+\gamma T]^{-1}(y)\), where T denotes the \(g\)-attentive \(\varepsilon \)-localization of \(\partial g\) at \({\bar{x}}\). Taking y near \({\bar{y}}\) and x near \({\bar{x}}\) such that \(\Vert x-{\bar{x}}\Vert <\varepsilon \), \(|g(x)-g({\bar{x}})|<\varepsilon \) and \(\Vert (y-x)/\gamma - {\bar{v}}\Vert <\varepsilon \) allows to identify the localization of \(\partial g(x)\) with \(\partial g(x)\), so that
Note that the proof of [35, Th. 4.4] includes a minor error relative to the Lipschitz constant computation, we report here a corrected value. \(\square \)
Now, we show that critical points of prox-regular functions are strong local minimizers; this result appears more or less explicitly in some articles, including [17].
Lemma A.2
Let f and g denote two functions and \({\bar{x}}\), \({\bar{y}}\) two points such that f is differentiable at \({\bar{y}}\) and g is r-prox-regular at \({\bar{x}}\) for subgradient \(\frac{1}{\gamma }({\bar{y}}-{\bar{x}}) - \nabla f({\bar{y}}) \in \partial g({\bar{x}})\) with \(\gamma \in (0, 1/r)\). Then, the function \(\rho _{{\bar{y}}} : x\mapsto g(x) + \frac{1}{2\gamma }\Vert {\bar{y}}-\gamma \nabla f({\bar{y}}) - x\Vert ^2\) satisfies
Proof
Prox-regularity of g at \({\bar{x}}\) with subgradient \(\frac{1}{\gamma } ({\bar{y}}-\gamma \nabla f({\bar{y}}) - {\bar{x}}) \in \partial g({\bar{x}})\) writes
The identity \( 2\langle b-a, c-a\rangle = \Vert b-a\Vert ^2 + \Vert c-a\Vert ^2 - \Vert b-c\Vert ^2 \) applied to the previous scalar product yields:
which rewrites
which is the claimed inequality. \(\square \)
Technical results on Riemannian methods.
In this section, we provide basic results on Riemannian optimization that simplify our developments and that we have not been able to find in the existing literature.
1.1 Euclidean spaces and manifolds, back and forth
We establish here a connection between the Riemannian and the Euclidean distances.
Lemma B.1
Consider a point \({\bar{x}}\) of a Riemannian manifold \({\mathcal {M}}\), equipped with a retraction \({\text {R}}\) such that \({\text {R}}_{{\bar{x}}}\) is \({\mathcal {C}}^2\). For any \(\varepsilon >0\), there exists a neighborhood \({\mathcal {U}}\) of \({\bar{x}}\) in \({\mathcal {M}}\) such that

where \({\text {R}}^{-1}_{{\bar{x}}}:{\mathcal {M}}\rightarrow T_{{\bar{x}}} {\mathcal {M}}\) is the smooth inverse of \({\text {R}}_{{\bar{x}}}\) defined locally around \({\bar{x}}\).
Proof
The retraction at \({\bar{x}}\) can be inverted locally around 0. Indeed, as \({\text {D}}{\text {R}}_{{\bar{x}}}(0_{T_{{\bar{x}}} {\mathcal {M}}})=I\) is invertible and \({\text {R}}_{{\bar{x}}}\) is \({\mathcal {C}}^2\), the implicit function theorem provides the existence of a \({\mathcal {C}}^2\) inverse function \({\text {R}}^{-1}_{{\bar{x}}}:{\mathcal {M}}\rightarrow T_{{\bar{x}}} {\mathcal {M}}\) defined locally around \({\bar{x}}\). Furthermore, one shows by differentiating the relation \({\text {R}}_{{\bar{x}}}\circ {\text {R}}_{{\bar{x}}}^{-1}\) that the differential of \({\text {R}}^{-1}_{{\bar{x}}}\) at \({\bar{x}}\) is the identity.
We consider the function \(f:{\mathcal {M}}\rightarrow {\mathbb {R}}\) defined by \(f(x)=\Vert \log _{{\bar{x}}}(x)\Vert -\Vert {\text {R}}_{{\bar{x}}}^{-1}(x)\Vert \). Clearly \(f({\bar{x}})=0\), and \({\text {D}}f({\bar{x}})=0\) as the differentials of both \({\text {R}}_{{\bar{x}}}^{-1}\) and logarithm at \({\bar{x}}\) are the identity. In local coordinates \({\hat{x}}=\log _{{\bar{x}}}{x}\) around \({\bar{x}}\), f is represented by the function \({\hat{f}}=f\circ \exp _{{\bar{x}}}: T_{{\bar{x}}} {\mathcal {M}}\rightarrow {\mathbb {R}}\). As \({\hat{f}}(\hat{{\bar{x}}})=0\), \({\text {D}}{\hat{f}}(\hat{{\bar{x}}})=0\) and \({\hat{f}}\) is \({\mathcal {C}}^2\), there exists some \(C>0\) such that
For any \(\varepsilon >0\), by taking a small enough neighborhood \({\hat{{\mathcal {U}}}}'\subset {\hat{{\mathcal {U}}}}\), there holds
Thus for all x in \({\mathcal {U}}= {\text {R}}_{{\bar{x}}}({\hat{{\mathcal {U}}}}')\),
as \({\hat{x}}=\log _{{\bar{x}}}(x)\), \(\hat{{\bar{x}}}=0\). We conclude with  . \(\square \)
. \(\square \)
We recall a slightly specialized version of [33, Th. 2.2], which is essentially the application of the implicit function theorem around a point of a manifold.
Proposition B.1
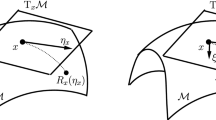
Consider a p-dimensional \({\mathcal {C}}^k\)-submanifold \({\mathcal {M}}\) of \({\mathbb {R}}^n\) around a point \({\bar{x}}\in {\mathcal {M}}\). The mapping \({\text {R}}: T {\mathcal {B}}\rightarrow {\mathcal {M}}\), defined for \((x, \eta )\in T {\mathcal {B}}\) near \(({\bar{x}}, 0)\) by \(\mathrm {proj}_x({\text {R}}(x, \eta )) = \eta \) defines a second-order retraction near \(({\bar{x}}, 0)\). The point-wise retraction, defined as \({\text {R}}_x = {\text {R}}(x, \cdot )\), is locally invertible with inverse \({\text {R}}_{x}^{-1}=\mathrm {proj}_{x}\).
Proof
Let \(\varPsi : {\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n-p}\) denote a \({\mathcal {C}}^k\) function defining \({\mathcal {M}}\) around \({\bar{x}}\): for all x close enough to \({\bar{x}}\), there holds \(x\in {\mathcal {M}}\Leftrightarrow \varPsi (x)=0\), and \({\text {D}}\varPsi (x)\) is surjective. Consider the equation \(\varPhi (x, \eta _t, \eta _n) = 0\) around \(({\bar{x}}, 0, 0)\), with

The partial differential \({\text {D}}_{\eta _n}\varPhi ({\bar{x}}, 0, 0)\) is, for  ,
,
Since \({\bar{x}}\in {\mathcal {M}}\), \({\text {D}}_{\eta _n}\varPhi ({\bar{x}}, 0, 0)\) is surjective from  to \({\mathbb {R}}^{n-p}\) so its a bijection. The implicit function theorem provides the existence of neighborhoods \({\mathcal {N}}_{{\bar{x}}}^1\subset {\mathcal {M}}\),
to \({\mathbb {R}}^{n-p}\) so its a bijection. The implicit function theorem provides the existence of neighborhoods \({\mathcal {N}}_{{\bar{x}}}^1\subset {\mathcal {M}}\),  ,
,  and a unique \({\mathcal {C}}^k\) function \(\eta _n : {\mathcal {N}}_{{\bar{x}}}^1 \times {\mathcal {N}}_0^2 \rightarrow {\mathcal {N}}_0^3\) such that, for all \(x\in {\mathcal {N}}_{{\bar{x}}}^1\), \(\eta _t\in {\mathcal {N}}_0^2\) and \(\eta _n\in {\mathcal {N}}_0^3\), \(\eta _n({\bar{x}}, 0) = 0\) and
and a unique \({\mathcal {C}}^k\) function \(\eta _n : {\mathcal {N}}_{{\bar{x}}}^1 \times {\mathcal {N}}_0^2 \rightarrow {\mathcal {N}}_0^3\) such that, for all \(x\in {\mathcal {N}}_{{\bar{x}}}^1\), \(\eta _t\in {\mathcal {N}}_0^2\) and \(\eta _n\in {\mathcal {N}}_0^3\), \(\eta _n({\bar{x}}, 0) = 0\) and
It also provides an expression for the partial derivative of \(\eta _n\) at (x, 0) along \(\eta _t\): for  ,
,
As noted before, \({\text {D}}_{\eta _n}\varPhi (x, 0, 0)\) is bijective since \(x\in {\mathcal {M}}\). Besides, \({\text {D}}_{\eta _t} \varPhi (x, 0, 0) = {\text {D}}\varPhi (x)[\xi _t]=0\) since  identifies as the kernel of \({\text {D}}\varPhi (x)\). Thus \({\text {D}}_{\eta _t} \eta _n(x, 0) = 0\).
identifies as the kernel of \({\text {D}}\varPhi (x)\). Thus \({\text {D}}_{\eta _t} \eta _n(x, 0) = 0\).
Now, define a map \({\text {R}}:{\mathcal {N}}_{{\bar{x}}}^1\times {\mathcal {N}}_0^2 \rightarrow {\mathcal {M}}\) by \({\text {R}}(x, \eta _t) = x + \eta _t + \eta _n(x, \eta _t)\). This map has degree of smoothness \({\mathcal {C}}^k\) since \(\eta _n\) is \({\mathcal {C}}^k\), satisfies \({\text {R}}(x, 0) = x\) since \(\eta _n(x, 0)=0\) and satisfies \({\text {D}}_{\eta _t}\eta _n(x, 0) = I + {\text {D}}_{\eta _t}(x, 0) = I\). Thus \({\text {R}}\) defines a retraction on a neighborhood of \(({\bar{x}}, 0)\).
We turn to show the second-order property of \({\text {R}}\). Consider the smooth curve \(c\) defined as \(c(t) = {\text {R}}(x, t\eta )\) for some \(x\in {\mathcal {N}}_{{\bar{x}}}^1\),  . It’s first derivative writes
. It’s first derivative writes
The acceleration of the curve c is obtained by computing the derivative of \(c'(\cdot )\) in the ambient space and then projecting onto  . Thus \(c''(t)=0\) and in particular, \(c''(0)=0\) which makes \({\text {R}}\) a second-order retraction. \(\square \)
. Thus \(c''(t)=0\) and in particular, \(c''(0)=0\) which makes \({\text {R}}\) a second-order retraction. \(\square \)
Lemma B.2
Consider a point \({\bar{x}}\) of a Riemannian manifold \({\mathcal {M}}\). For any \(\varepsilon >0\), there exists a neighborhood \({\mathcal {U}}\) of \({\bar{x}}\) in \({\mathcal {M}}\) such that, for all \(x\in {\mathcal {U}}\),

where \(\Vert x-{\bar{x}}\Vert \) is the Euclidean distance in the ambient space.
Proof
Let \({\bar{x}}\), x denote two close points on \({\mathcal {M}}\). Consider the tangential retraction introduced in Proposition B.1. As a retraction, it satisfies:
Taking \(x={\text {R}}_{{\bar{x}}}(\eta )\) allows to write \(x = {\bar{x}} + {\mathcal {O}}(\Vert {\text {R}}_{{\bar{x}}}^{-1}(x)\Vert ^2)\), so that for any small \(\varepsilon _1>0\), there exists a small enough neighborhood \({\mathcal {U}}_1\subset {\mathcal {U}}\) of \({\bar{x}}\) in \({\mathcal {M}}\) such that
By Lemma B.1, for \(\varepsilon _2>0\) small enough, there exists a neighborhood \({\mathcal {U}}_2\subset {\mathcal {U}}\) of \({\bar{x}}\) such that,

With \(\varepsilon _1\), \(\varepsilon _2\) such that \(1-\varepsilon =(1-\varepsilon _1)(1-\varepsilon _2)\), we combine the two estimates to conclude. \(\square \)
1.2 Two technical results on Riemannian descent algorithms
We provide here two technical results used in the proofs of Sect. 4. First, Theorem B.1 adapts [13, Th. 4.16] to the Riemannian setting. Second, Lemma B.3 adapts the proof of [18, Lemma A.2] to the Riemannian setting.
Theorem B.1
(Soundness of the Riemannian line search) Consider a manifold \({\mathcal {M}}\) equipped with a retraction \({\text {R}}\) and a twice differentiable function \(F:{\mathcal {M}}\rightarrow {\mathbb {R}}\) that admits a strong local minimizer \(x^\star \), that is, a point such that \(\hbox {Hess }F(x^\star )\) is positive definite. If x is close to \(x^\star \), \(\eta \) brings a superlinear improvement towards \(x^\star \), that is  as \(x\rightarrow x^\star \), and \(0<m_1<1/2\), then \(\eta \) is acceptable by the Armijo rule (4.1) with unit stepsize \(\alpha =1\).
as \(x\rightarrow x^\star \), and \(0<m_1<1/2\), then \(\eta \) is acceptable by the Armijo rule (4.1) with unit stepsize \(\alpha =1\).
Proof
Let \(x, \eta \in T {\mathcal {B}}\) denote a pair such that x is close to \(x^\star \) and  . For convenience, let \(x_+ = {\text {R}}_x(\eta )\) denote the next point.
. For convenience, let \(x_+ = {\text {R}}_x(\eta )\) denote the next point.
Following [2] (see e.g. the proof of Th. 6.3.2), we work in local coordinates around \(x^\star \), representing any point \(x\in {\mathcal {M}}\) by \({\widehat{x}} = \log _{x^\star }(x)\) and any tangent vector  by \({\widehat{\eta }}_x = {\text {D}}\log _{x^\star }(x)[\eta ]\). The function \(F\) is represented by
by \({\widehat{\eta }}_x = {\text {D}}\log _{x^\star }(x)[\eta ]\). The function \(F\) is represented by  . Defining the coordinates via the logarithm grants the useful property that the Riemannian distance of any two points \(x, y\in {\mathcal {M}}\) matches the euclidean distance between their representatives:
. Defining the coordinates via the logarithm grants the useful property that the Riemannian distance of any two points \(x, y\in {\mathcal {M}}\) matches the euclidean distance between their representatives:  . Besides, there holds
. Besides, there holds
Indeed, \({\text {D}}F(x)[\eta ] = (F\circ \gamma )'(0)\) and \(\hbox {Hess }F(x)[\eta , \eta ] = (F\circ \gamma )''(0)\), where \(\gamma \) denotes the geodesic curve defined by \({\widehat{\gamma }}(t) = {\widehat{x}} + t{\widehat{\eta }}\). Using \(F\circ \gamma ={\widehat{F}}\circ {\widehat{\gamma }}\), one obtains the result.
Step 1. We derive an approximation of \({\text {D}}F(x)[\eta ] = \langle \hbox {grad }F(x), \eta \rangle \) in terms of \({\text {D}}^2 {\widehat{F}}(\widehat{x^\star })[{\widehat{x}}-\widehat{x^\star }]^2\). To do so, we go through the intermediate quantity \({\text {D}}{\widehat{F}}({\widehat{x}}) [\widehat{x_+}-{\widehat{x}}]\), and handle precisely the \(o(\cdot )\) terms. By smoothness of \({\widehat{F}}\) and since \({\text {D}}{\widehat{F}}(\widehat{x^\star })=0\), Taylor’s formula for \({\text {D}}{\widehat{F}}\) writes
where, in the last step, we used that \(\Vert \widehat{x_+}-\widehat{x^\star }\Vert = o(\Vert {\widehat{x}}-\widehat{x^\star }\Vert )\) to get that \(\Vert {\text {D}}^2 {\widehat{F}}(\widehat{x^\star })[\widehat{x_+}-\widehat{x^\star }, {\widehat{x}}-\widehat{x^\star }]\Vert = \Vert {\text {D}}^2 {\widehat{F}}(\widehat{x^\star })\Vert \Vert \widehat{x_+}-\widehat{x^\star }\Vert \Vert {\widehat{x}}-\widehat{x^\star }\Vert = o(\Vert {\widehat{x}}-\widehat{x^\star }\Vert ^2)\). We now turn to show that \({\text {D}}{\widehat{F}}({\widehat{x}}) [\widehat{x_+}-{\widehat{x}}]\) behaves as \({\text {D}}F(x)[\eta ]\) up to \(o(\Vert \widehat{x_+}-{\widehat{x}}\Vert ^2)\). Since \({\text {D}}F(x)[\eta ]={\text {D}}{\widehat{F}}({\widehat{x}})[{\widehat{\eta }}]\) by (B.1), there holds:
As \(F\) is twice differentiable and \(\exp \) is \({\mathcal {C}}^\infty \), \({\widehat{F}}\) is twice differentiable as well. In particular its derivative is locally Lipschitz continuous, so that for \({\widehat{x}}\) near \(\widehat{x^\star }\), we obtain a first estimate:
Besides, the following estimate holds \(\Vert {\widehat{\eta }} - (\widehat{x_+} - {\widehat{x}})\Vert = o (\Vert {\widehat{x}}-\widehat{x^\star } \Vert )\). Indeed, as the function  is differentiable, there holds for
is differentiable, there holds for  small,
small,
which simplifies to \(\widehat{x_+} = {\widehat{x}} + {\widehat{\eta }} + o(\Vert \eta \Vert )\). Lemma B.1 allows to write  . Using the triangular inequality and the assumption that
. Using the triangular inequality and the assumption that  we get
we get

so that the second estimate holds.
Combining the two above estimates allows to conclude that
so that overall,
Using that  and \({\text {D}}^2 {\widehat{F}}(\widehat{x^\star }) = \hbox {Hess }F(x^\star )\) (B.1), we obtain
and \({\text {D}}^2 {\widehat{F}}(\widehat{x^\star }) = \hbox {Hess }F(x^\star )\) (B.1), we obtain

Step 2. The function \(F\) admits a second-order development around \(x^\star \): applying Eq. (2.3) with the exponential map \(\exp _{x^\star }\) as a second-order retraction yields

where we used that  . Denote \(0 < l \le L\) the lower and upper eigenvalues of \(\hbox {Hess }F(x^\star )\). The combination (B.3) \(+ m_1\) (B.2) writes
. Denote \(0 < l \le L\) the lower and upper eigenvalues of \(\hbox {Hess }F(x^\star )\). The combination (B.3) \(+ m_1\) (B.2) writes

Let \(\varepsilon >0\) such that \(\frac{1}{2}L \varepsilon ^2 < (\frac{1}{2}-m_1) l\). As  , for x close enough to \(x^\star \) there holds
, for x close enough to \(x^\star \) there holds  . Combining this with the second-order development of f at \(x_+\), there holds:
. Combining this with the second-order development of f at \(x_+\), there holds:

Subtracting the two estimates yields

which ensures that the Armijo condition is satisfied. \(\square \)
Lemma B.3
(Riemannian Newton-CG a descent direction) Let Assumption 1 hold and consider a manifold \({\mathcal {M}}\) and a point \(x\in {\mathcal {M}}\). If \(F\) is twice differentiable on \({\mathcal {M}}\) at x and x is not a stationary point of \(F\), then there holds:
where d was obtained solving (Inexact Newton eq.) with any forcing parameter \(\eta \).
Proof
The result is obtained by applying the analysis of [18, Lemma A.2] to the approximate resolution of (Inexact Newton eq.) on the euclidean space  , with constant specified according to the proof. \(\square \)
, with constant specified according to the proof. \(\square \)
Complements to the experimental section
1.1 Oracles of section 5.1
We detail here the oracles of \(f(x)\triangleq 2x_1^2+x_2^2\) and \(g(x) \triangleq |x_1^2-x_2|\):
-
proximity operator: For \(\gamma <1/2\), there holds
$$\begin{aligned} \mathbf {prox}_{\gamma g}(x) = {\left\{ \begin{array}{ll} (\frac{x_1}{1+2\gamma }, x_2+\gamma ) &{}\text { if } x_2 \le \frac{x_1^2}{(1+2\gamma )^2} - \gamma \\ (\frac{x_1}{1+4\gamma t-2\gamma }, x_2 + 2\gamma t - \gamma ) &{}\text { if } \frac{x_1^2}{(1+2\gamma )^2} - \gamma \le x_2 \le \frac{x_1^2}{(1-2\gamma )^2} + \gamma \\ (\frac{x_1}{1-2\gamma }, x_2-\gamma ) &{}\text { if } \frac{x_1^2}{(1-2\gamma )^2} + \gamma \le x_2 \end{array}\right. } \end{aligned}$$where t solves \(x_2^2 + (-2\gamma t + \gamma - x_2)(1+4\gamma t -2\gamma )^2 = 0\).
-
Riemannian gradient and Hessian: Since \(g\) is identically null on \({\mathcal {M}}\), for any point \((x, \eta )\in T {\mathcal {B}}\), \( \hbox {grad }g(x) = 0 \text { and } \hbox {Hess }g(x)[\eta ] = 0 \). Moreover, Euclidean gradient and Hessian-vector product are converted to Riemannian ones using Eqs. (2.1) and (2.2):
$$\begin{aligned} \hbox {grad }f(x)&= \mathrm {proj}_{x}(\nabla f(x)) \\ \hbox {Hess }f(x)[\eta ]&= \mathrm {proj}_{x}\left( \nabla ^2 f(x)[\eta ] - \begin{pmatrix} 2\eta _1 \\ 0 \end{pmatrix} \left\langle \nabla f(x), \begin{pmatrix} 2x_1 \\ -1 \end{pmatrix}\right\rangle \frac{1}{1+4x_1^2} \right) , \end{aligned}$$and the orthogonal projection onto
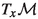 writes $$\begin{aligned} \mathrm {proj}_{x}(d) = d - \left\langle d, \begin{pmatrix} 2x_1 \\ -1 \end{pmatrix}\right\rangle \frac{1}{1+4x_1^2} \begin{pmatrix} 2x_1 \\ -1 \end{pmatrix}. \end{aligned}$$
writes $$\begin{aligned} \mathrm {proj}_{x}(d) = d - \left\langle d, \begin{pmatrix} 2x_1 \\ -1 \end{pmatrix}\right\rangle \frac{1}{1+4x_1^2} \begin{pmatrix} 2x_1 \\ -1 \end{pmatrix}. \end{aligned}$$
1.2 Differentiating the singular-value decomposition
We establish the expressions of the derivative of the matrices involved in the singular value decomposition. These results may be seen as part of folklore, but, up to our knowledge, there are not explicitly written in the literature. We need them for the computations related to trace-norm regularized problems.
Lemma C.1
Consider the manifold of fixed rank matrices \({\mathcal {M}}_r\), a pair \(x, \eta \in T {\mathcal {B}}\) and a smooth curve \(c: I\rightarrow {\mathcal {M}}_r\) such that \(c(0)=x\), \(c'(0)=\eta \). Besides, let U(t), \(\varSigma (t)\), V(t) denote smooth curves of St(m, r), \({\mathbb {R}}^{r\times r}\), St(n, r) such that \(\gamma (t) = U(t)\varSigma (t) V(t)^\top \). The derivatives of the decomposition factors at \(t=0\) write
where \(I_k\) is the identity of \({\mathbb {R}}^{k\times k}\), \(\circ \) denotes the Hadamard product and \(F\in {\mathbb {R}}^{r\times r}\) is such that \(F_{ij} = 1 / (\varSigma _{jj}^2 - \varSigma _{ii}^2)\) if \(\varSigma _{jj} \ne \varSigma _{ii}\), and \(F_{ij}=0\) otherwise. Equivalently, when the tangent vector is represented as \(\eta = UMV^\top + U_pV^\top + UV_p^\top \), the above expressions simplify to
Proof
We consider the curve \(\gamma \) and all components and derivatives at \(t=0\), therefore we don’t mention evaluation time. Differentiating \(\gamma = U\varSigma V^\top \) yields
As a tangent vector to the Stiefel manifold at point U, \(U'\) can be expressed as [2, Ex. 3.5.2]
where \(\varOmega _U\in {\mathbb {R}}^{r\times r}\) is a skew-symmetric matrix, \(B_U\in {\mathbb {R}}^{m-r \times m-r}\), and \(U_\perp \) is any matrix such that \(U^\top U_\perp = 0\) and \(U_\perp ^\top U_\perp = I_{m-r}\). Similarly, \(V' = V\varOmega _V + V_\perp B_V\), where \(\varOmega _V\in {\mathbb {R}}^{r\times r}\) is skew-symmetric, \(B_V\in {\mathbb {R}}^{n-r \times n-r}\), and \(V_\perp \) is any matrix such that \(V^\top V_\perp = 0\) and \(V_\perp ^\top V_\perp = I_{n-r}\).
Computing \(U^\top \times \) (C.1) \(\times V\) yields
Looking at the diagonal elements of this equation yields the derivative of the diagonal component of \(\eta \). This is done by taking the Hadamard product of both sides of previous equation with the identity matrix of \({\mathbb {R}}^{r\times r}\), and writes
The off-diagonal elements of this equation write
where \({{\bar{I}}}_r\) has zeros on the diagonal and ones elsewhere. Adding (C.3)\(\varSigma \) and \(\varSigma \)(C.3)\(^\top \) yields
which decouples coefficient-wise. At coefficient (ij), with \(i\ne j\),
hence \(\varOmega _U = F \circ \left[ U^\top \eta V \varSigma + \varSigma V^\top \eta ^\top U \right] \), where \(F\in {\mathbb {R}}^{m-r\times r}\) has zeros on the diagonal and for \(i\ne j\), \(F_{ij} = 1/(\varSigma ^2_{jj} - \varSigma ^2_{ii})\) if \(\varSigma ^2_{jj} \ne \varSigma ^2_{ii}\), 0 otherwise. Besides, left-multiplying (C.1) by \(U_\perp ^\top \) yields \(U_\perp ^\top \eta = U^\top _\perp U'\varSigma V^\top \), which rewrites, using the decomposition (C.2) of \(U'\), as \(U_\perp ^\top \eta = B_U \varSigma V^\top \). Hence \(B_U = U_\perp ^\top \eta V \varSigma ^{-1}\) and we get the complete expression for \(U'\) by assembling the expressions of \(\varOmega _U\) and \(B_U\) with the decomposition (C.2). The term \(U_\perp ^\top U_\perp \) is eliminated using that \(U^\top U + U_\perp ^\top U_\perp = I_m\).
Let’s follow the same steps to get expressions for \(V'\). Adding \(\varSigma \)(C.3) and (C.3)\(^\top \varSigma \) yields
from which we get \(\varOmega _V = F \circ \left[ \varSigma U^\top \eta V + V^\top \eta ^\top U \varSigma \right] \). Besides, right-multiplying (C.1) by \(V_\perp \) yields \(\eta V_\perp = U \varSigma V'^\top V_\perp \), which rewrites using the decomposition \(V' = V\varOmega _V + V_\perp B_V \) as \(\eta V_\perp = U \varSigma B_V^\top \). Hence \(B_V = V_\perp ^\top \eta ^\top U \varSigma ^{-1}\), and we get the claimed formula by eliminating the \(V_\perp \) terms with \(V^\top V + V_\perp ^\top V_\perp = I_n\). The simplified expressions are obtained using that \(U^\top U=I_m\), \(U^\top U_p=0\), \(V^\top V=I_n\) and \(V^\top V_p=0\). \(\square \)
We are now ready to give the expression of the Riemannian gradient and Hessian of the nuclear norm.
Proposition C.1
The nuclear norm \(g=\Vert \cdot \Vert _*\) restricted to \({\mathcal {M}}_r\) is \({\mathcal {C}}^2\) and admits a smooth second-order development of the form (2.3) near any point \(x = U\varSigma V^\top \in {\mathcal {M}}_r\). Denoting  a tangent vector, there holds:
a tangent vector, there holds:
where \(\circ \) denotes the Hadamard product and \({\tilde{F}}\in {\mathbb {R}}^{r\times r}\) is such that \({\tilde{F}}_{ij} = 1 / (\varSigma _{jj} + \varSigma _{ii})\) if \(\varSigma _{jj} \ne \varSigma _{ii}\), and \({\tilde{F}}_{ij}=0\) otherwise.
Proof
Let \(c: I\rightarrow {\mathcal {M}}_r\) denote a smooth curve over \({\mathcal {M}}_r\) such that \(\gamma (0)=x\) and \(\gamma '(0)=\eta \), and consider \(\varphi = \Vert c(\cdot )\Vert _* : I\rightarrow {\mathbb {R}}\). Writing the decomposition \(c(t) = U(t)\varSigma (t) V(t)^\top \), for U(t), \(\varSigma (t)\), V(t) smooth curves of St(m, r), \({\mathbb {R}}^{r\times r}\), St(n, r) allows to write \(\varphi (t) = {{\,\mathrm{Tr}\,}}(\varSigma (t))\). Applying Lemma C.1 yields
so that  .
.
In order to obtain the Riemannian Hessian, let \({{\bar{Z}}} : I\rightarrow {\mathbb {R}}^n\) denote a smooth extension of \(\hbox {grad }g(c(\cdot ))\), defined by \({{\bar{Z}}}(t) = U(t)V(t)^\top \). The Riemannian Hessian is then obtained as \(\hbox {Hess }g(x)[\eta ] = \mathrm {proj}_x {{\bar{Z}}}'(0)\). The derivative of \({{\bar{Z}}}\) at 0 is simply \({{\bar{Z}}}'(0) = U' V^\top + U V'^\top \) and thus writes, applying Lemma C.1
This expression simplifies to the statement by using the fact that F is antisymmetric and applying the identity \((A\circ B)^\top = A^\top \circ B^\top \). \(\square \)
1.3 Additional numerical experiment
We illustrate in this appendix the robustness of the Newton acceleration on several instances of the same problem. More precisely, in the set-up of Sect. 5.3, we compare the 4 algorithms on 20 random instances of the tracenorm problem, in terms of wallclock time required to reach a suboptimality of \(10^{-9}\). We then provide in Fig. 5 a performance profile (i.e. the ordinate of a curve at absciss \(t \ge 1\) indicates the proportion of problems for which the corresponding algorithm was able to satisfy the criterion within t times the best algorithm time for each problem; see [20]).
We observe the following on Fig. 5. The ordinate at origin of a curve gives the proportion of problems for which the corresponding algorithm performed best: methods with Newton acceleration are the most efficient in \(95\% (= 75\%+20\%)\) of the instances. Furthermore, they require about \(2.5\times \) less time to converge in half of the instances. Note also that the proximal gradient is completely outperformed by the others algorithms since it takes \(5\times \) more time than the best algorithm, for all instances.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bareilles, G., Iutzeler, F. & Malick, J. Newton acceleration on manifolds identified by proximal gradient methods. Math. Program. 200, 37–70 (2023). https://doi.org/10.1007/s10107-022-01873-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-022-01873-w
Keywords
- Nonsmooth optimization
- Riemannian optimization
- Proximal Gradient
- Identification
- Partial Smoothness
- Sparsity-inducing regularization



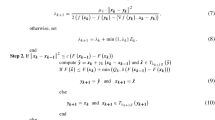
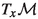 writes
writes 