Bound-constrained global optimization of functions with low effective dimensionality using multiple random embeddings

Abstract

We consider the bound-constrained global optimization of functions with low effective dimensionality, that are constant along an (unknown) linear subspace and only vary over the effective (complement) subspace. We aim to implicitly explore the intrinsic low dimensionality of the constrained landscape using feasible random embeddings, in order to understand and improve the scalability of algorithms for the global optimization of these special-structure problems. A reduced subproblem formulation is investigated that solves the original problem over a random low-dimensional subspace subject to affine constraints, so as to preserve feasibility with respect to the given domain. Under reasonable assumptions, we show that the probability that the reduced problem is successful in solving the original, full-dimensional problem is positive. Furthermore, in the case when the objective’s effective subspace is aligned with the coordinate axes, we provide an asymptotic bound on this success probability that captures its polynomial dependence on the effective and, surprisingly, ambient dimensions. We then propose X-REGO, a generic algorithmic framework that uses multiple random embeddings, solving the above reduced problem repeatedly, approximately and possibly, adaptively. Using the success probability of the reduced subproblems, we prove that X-REGO converges globally, with probability one, and linearly in the number of embeddings, to an $\epsilon$-neighbourhood of a constrained global minimizer. Our numerical experiments on special structure functions illustrate our theoretical findings and the improved scalability of X-REGO variants when coupled with state-of-the-art global—and even local—optimization solvers for the subproblems.

1 Introduction

In this paper, we address the bound-constrained global optimization problem

$$\begin{aligned} \begin{aligned} f^* := \min _{{{\varvec{x}}}\in {\mathcal {X}}}&\;\; f({{\varvec{x}}}), \end{aligned} \end{aligned}$$

(P)

where $f: {\mathbb {R}}^D \rightarrow {\mathbb {R}}$ is continuous, possibly non-convex and deterministic,¹ and where, without loss of generality,²${\mathcal {X}} := [-1,1]^D\subseteq {\mathbb {R}}^D$.

In an attempt to alleviate the curse of dimensionality of generic global optimization, we focus on objective functions with ‘low effective dimensionality’ [58], namely, those that only vary over a low-dimensional subspace (which may not necessarily be aligned with standard axes), and remain constant along its orthogonal complement. These functions are also known as objectives with ‘active subspaces’ [14] or ‘multi-ridge’ [25, 55]. They are frequently encountered in applications, typically when tuning (over)parametrized models and processes, such as in hyper-parameter optimization for neural networks [3], heuristic algorithms for combinatorial optimization problems [34], complex engineering and physical simulation problems [14] as in climate modelling [37], and policy search and dynamical system control [26, 61].

When the objective has low effective dimensionality and the effective subspace of variation is known, it is straightforward to cast (P) into a lower-dimensional problem which has the same global minimum $f^*$ by restricting it to and solving (P) only within this important subspace. Typically, however, the effective subspace is unknown, and random embeddings have been proposed to reduce the size of (P) and hence the cost of its solution, while attempting to preserve the problem’s (original) global minimum values. In this paper, we investigate the following feasible formulation of the reduced randomised problem,

where ${{\varvec{A}}}$ is a $D\times d$ Gaussian random matrix (see Definition A.1) with $d \ll D$, and where ${{\varvec{p}}} \in {\mathcal {X}}$ is user-defined and provides additional flexibility that we exploit algorithmically. Our approach needs the following clarification.

Definition 1.1

We say that (${\mathrm{RP}}{\mathcal {X}}$) is successful if there exists ${{\varvec{y}}}^* \in {\mathbb {R}}^d$ such that $f({{\varvec{A}}}{{\varvec{y}}}^*+{{\varvec{p}}}) = f^*$ and ${{\varvec{A}}}{{\varvec{y}}}^* + {{\varvec{p}}} \in {\mathcal {X}}$.

We derive a lower bound on the probability that (${\mathrm{RP}}{\mathcal {X}}$) is successful in the case when d lies between $d_e$ and $D-d_e$, where $d_e$ is the dimension of the effective subspace. We show that this success probability is positive and that it depends on both the effective subspace and the ambient dimensions.³ However, in the case when the effective subspace is aligned with the coordinate axes, we show that the dependence on D in this lower bound is at worst polynomial. We then propose X-REGO (${\mathcal {X}}$-Random Embeddings for Global Optimization), a generic algorithmic framework for solving (P) using multiple random embeddings. Namely, X-REGO solves (${\mathrm{RP}}{\mathcal {X}}$) repeatedly with different ${{\varvec{A}}}$ and possibly different ${{\varvec{p}}}$, and can use any global optimization algorithm for solving the reduced problem (${\mathrm{RP}}{\mathcal {X}}$). Using the computed lower bound on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$), we derive a global convergence result for X-REGO, showing that as the number of random embeddings increases, X-REGO converges linearly, with probability one, to an $\epsilon$-neighbourhood of a global minimizer of (P).

Existing relevant literature Optimization of functions with low effective dimensionality has been recently studied primarily as an attempt to remedy the scalability challenges of Bayesian Optimization (BO), such as in [17, 21, 28, 41, 58]. Investigations of these special-structure problems have been extended beyond BO, to derivative-free optimization [48], multi-objective optimization [47] and evolutionary methods [15, 50]. As the effective subspace is generally unknown, some existing approaches learn the effective subspace beforehand [17, 21, 25, 55], while others estimate it during the optimization, updating the estimate as new information becomes available on the objective function [13, 15, 28, 61]. We focus here on an alternative approach, bypassing the subspace learning phase, and optimizing directly over random low-dimensional subspaces, as proposed in [6, 7, 36, 58].

Wang et al. [58] propose the REMBO algorithm, that solves, using Bayesian methods, a single reduced subproblem,

$$\begin{aligned} \begin{aligned} \min _{{{\varvec{y}}}}&\;\; f({{\varvec{A}}}{{\varvec{y}}}) \\ \text {subject to}&\;\; {{\varvec{y}}} \in {\mathcal {Y}} = [-\delta , \delta ]^d, \end{aligned} \end{aligned}$$

(RP)

where ${{\varvec{A}}}$ is as above, and $\delta > 0$. They evaluate the probability that the solution of (RP) corresponds to a solution of the original problem (P) in the case when the effective subspace is aligned with coordinate axes and when $d=d_e$, where $d_e$ denotes the dimension of the effective subspace; they show that this probability of success of (RP) depends on the parameter $\delta$ (the size of the ${\mathcal {Y}}$ box), and it decreases as $\delta$ shrinks. Conversely, setting $\delta$ large may result in large computational costs to solve (RP). Thus, a careful calibration of $\delta$ is needed for good algorithmic performance. The theoretical analysis in [58] has been extended by Sanyang and Kabán [50], where the probability of success of (RP) is quantified in the case $d \ge d_e$; an algorithm, called REMEDA, is also proposed in [50] that uses Gaussian random embeddings in the framework of evolutionary methods for high-dimensional unconstrained global optimization.

In the recent preprint [9], we further extend these analyses to arbitrary effective subspaces (i.e., not necessarily aligned with the coordinate axes) and random embeddings of dimension $d\ge d_e$, and consider the wider framework of generic unconstrained high-dimensional global optimization. We propose the REGO algorithm, that replaces the high-dimensional problem (P) (with ${\mathcal {X}} = {\mathbb {R}}^{D})$, by a single reduced problem (RP), and solves (RP) using any global optimization algorithm. Instead of estimating solely the norm of an optimal solution of (RP), as in [50, 58], we derive its exact probability distribution. Furthermore, we show that its squared Euclidean norm (when appropriately scaled) follows an inverse chi-squared distribution with $d - d_e +1$ degrees of freedom, and use a tail bound on the chi-squared distribution to get a lower bound on the probability of success of (RP). Our theory and numerical experiments indicate that, under suitable assumptions, the success of (RP) is essentially independent on D, but depends mainly on two factors: the gap between the subspace dimension d and the effective dimension $d_e$, and the ratio between $\delta$ (the size of the low-dimensional domain), and the distance from the origin (the centre of the original domain ${\mathcal {X}}$) to the closest affine subspace of global minimizers.

In contrast to [9, 50], the present case of the constrained problem (P) poses a new challenge: a solution ${{\varvec{y^*}}}$ of (RP) is not necessarily feasible for the full-dimensional problem (P) (i.e., ${{\varvec{A}}} {{\varvec{y}}}^* \notin {\mathcal {X}}$). To remedy this, Wang et al. [58] endow REMBO with an additional step that projects ${{\varvec{A}}} {{\varvec{y}}}^*$ onto ${\mathcal {X}}$. However, the lack of injectivity of the projection may not be beneficial to the proposed Bayesian optimization algorithm as some parts of the domain might be over-explored when using a classical kernel (such as the squared exponential kernel) directly on the low-dimensional domain ${\mathcal {Y}}$. The design of kernels avoiding this over-exploration has been tackled in [6, 7]. Binois et al. [7] further advances the discussion regarding the choice of the low-dimensional domain ${\mathcal {Y}}$ in (RP) and computes an ‘optimal’ set ${\mathcal {Y}}^* \subset {\mathbb {R}}^d$, i.e., a set that has minimum (here, infimum) volume among all the sets ${\mathcal {Y}} \subset {\mathbb {R}}^d$ for which the image of the mapping ${\mathcal {Y}} \rightarrow {\mathcal {X}}: {{\varvec{y}}} \mapsto p_{\mathcal {X}}({{\varvec{A}}} {{\varvec{y}}})$ contains the ‘maximal embedded set’ $\{ p_{\mathcal {X}}({{\varvec{A}}} {{\varvec{y}}}) : {{\varvec{y}}} \in {\mathbb {R}}^d \}$, where $p_{{\mathcal {X}}}({{\varvec{x}}})$ is the classical Euclidean projection of ${{\varvec{x}}}$ on ${\mathcal {X}}$. They show that $\mathcal {Y^*}$ has an intricate representation when the dimension of the full-dimensional problem is large, and propose to replace the Euclidean projection map $p_{{\mathcal {X}}}$ suggested by Wang et al. [58] by an alternative mapping for which an ‘optimal’ low-dimensional domain has nicer properties. Nayebi et al. [43] circumvent the projection step by replacing the Gaussian random embeddings of (RP) by random embeddings defined using hashing matrices, and choose ${\mathcal {Y}} = [-1,1]^d$. This choice guarantees that any solution of the low-dimensional problem provides an admissible solution for the full-dimensional problem in the case ${\mathcal {X}} = [-1,1]^D$.

The need to combine optimization algorithms that rely on random Gaussian embeddings with a projection step has also been recently discussed in [40], where it is suggested to replace the formulation (RP) by (${\mathrm{RP}}{\mathcal {X}}$), that we also consider in this paper. However, Letham et al. [40] do not provide analytical estimates of the probability of success of this new formulation, solely evaluating it numerically using Monte-Carlo simulations; they also do not use multiple random embeddings as proposed in Wang et al. [58] and employed here as well. Our proposed X-REGO algorithmic framework (and more precisely, the adaptive variant A-REGO described in Sect. 5) is closely related to the sequential algorithm proposed by Qian et al. [48], in the framework of unconstrained derivative-free optimization of functions with approximate low-effective dimensionality, and to the algorithm proposed in [36] for constrained Bayesian optimization of functions with low-effective dimension, using one-dimensional random embeddings. However, our results rely on the assumption that the subspace dimension d is larger than the effective dimension $d_e$, and so our approach significantly differs from [36]. Very recently, Tran-The et al. [54] have proposed an algorithm that uses several low-dimensional (deterministic) embeddings in parallel for Bayesian optimization of high-dimensional functions.

Randomized subspace/projections methods have recently attracted much interest for local or convex optimization problems; see for example, [30, 33, 38, 42, 44, 57]; no low effective dimensionality assumption is made in these works. Finally, we note that the main step in our convergence analysis consists in deriving a lower bound on the probability that a random subspace of given dimension intersects a given set (the set of approximate global minimizers), which is an important problem in stochastic geometry, see, e.g., the extensive discussion by Oymak and Tropp [46]. Unlike the results presented in [46], our results do not involve statistical dimensions of sets, which are unknown and, in our case, problem dependent.

We have recently explored the applicability of X-REGO to global optimization of Lipschitz-continuous objectives, that do not necessarily have low effective dimension, for arbitrary (non-empty) domain ${\mathcal {X}}$ and arbitrary d. We prove in [12] that X-REGO converges almost surely to an $\epsilon$-neighbourhood of a (constrained) global minimizer of (P), relying on tools from conic integral geometry to bound the probability of success of the random subproblem. The latter bound is understandably exponential in the big problem dimension and does not provide a distributional result for the size of the reduced minimizer. Even asymptotically, the general success bound is exponential in D while when there is an effective subspace aligned with coordinate axes, the bound here is polynomial. We also address in [12] the unconstrained case when the objective has low effective dimension but the effective dimension $d_e$ is unknown, and propose a variant of X-REGO that explores random subspaces of increasing dimension until finding the effective dimension of the problem.

Our contributions Here we investigate a general random embedding framework for the bound-constrained global optimization of functions with low effective dimensionality. This framework replaces the original, potentially high-dimensional problem (P) with several reduced and randomized subproblems of the form (${\mathrm{RP}}{\mathcal {X}}$), which directly ensures feasibility of the iterates with respect to the constraints.

Using various properties of Gaussian matrices and a useful result from [9], we derive a lower bound on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) when $d_e \le d \le D-d_e$. To achieve this, we provide a sufficient condition for the success of (${\mathrm{RP}}{\mathcal {X}}$) that depends on a random vector ${{\varvec{w}}}$, which in turn, is a function of the embedding matrix ${{\varvec{A}}}$, the parameter ${{\varvec{p}}}$ of (${\mathrm{RP}}{\mathcal {X}}$) and an arbitrary global minimizer ${{\varvec{x}}}^*$ of (P). We show that ${{\varvec{w}}}$ follows a $(D-d_e)$-dimensional t-distribution with $d - d_e +1$ degrees of freedom, and provide a lower bound on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) in terms of the integral of the probability density function of ${{\varvec{w}}}$ over a given closed domain. In the case when the effective subspace is aligned with the coordinate axes, the closed domain simplifies to a $(D-d_e)$-dimensional box, and we provide an asymptotic expansion of the integral of the probability density function over the box, when $D\rightarrow \infty$ (and d and $d_e$ are fixed). Our theoretical analysis, backed by numerical testing, indicates that the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) decreases with the dimension D of the original problem (P). However, in the case when the effective subspace is aligned with the coordinate axes, we show that it decreases at most in a polynomial way with the ambient dimension D for some useful choices of ${{\varvec{p}}}$.

We also propose the X-REGO algorithm, a generic framework for the constrained global optimization problem (P) that sequentially or in parallel solves multiple subproblems (${\mathrm{RP}}{\mathcal {X}}$), varying ${{\varvec{A}}}$ and also possibly ${{\varvec{p}}}$. We prove global convergence of X-REGO to a set of approximate global minimizers of (P) with probability one, with linear rate in terms of the number of subproblems solved. This result requires mild assumptions on problem (P) (f is Lipschitz continuous and (P) admits a strictly feasible solution) and on the algorithm used to solve the reduced problem (namely, it must solve (${\mathrm{RP}}{\mathcal {X}}$) globally and approximately, to required accuracy), and allows a diverse set of possible choices of ${{\varvec{p}}}$ (random, fixed, adaptive, deterministic). Our convergence proof crucially uses our result that the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) is positive and uniformly bounded away from zero with respect to the choice of ${{\varvec{p}}}$, and hence, assumes that $d_e \le d \le D-d_e$.

We provide an extensive numerical comparison of several variants of X-REGO on a set of test problems with low effective dimensionality, using three different solvers for (${\mathrm{RP}}{\mathcal {X}}$), namely, BARON [49], DIRECT [24] and (global and local) KNITRO [8]. We find that X-REGO variants show significantly improved scalability with most solvers, as the ambient problem dimension grows, compared to directly using the respective solvers on the test set. Notable efficiency was obtained in particular when local KNITRO was used to solve the subproblems and the points ${{\varvec{p}}}$ were updated to the ‘best’ point (with the smallest value of f) found so far.

Paper outline In Sect. 2, we recall the definition of functions with low effective dimensionality and some existing results that we will use in our analysis. Section 3 derives lower bounds for the probability of success of (${\mathrm{RP}}{\mathcal {X}}$). The X-REGO algorithm and its global convergence are then presented in Sect. 4, while in Sect. 5, different X-REGO variants are compared numerically on benchmark problems using three optimization solvers (DIRECT, BARON and KNITRO) for the subproblems. Our conclusions are drawn in Sect. 6.

Notation We use bold capital letters for matrices (${{\varvec{A}}}$) and bold lowercase letters (${{\varvec{a}}}$) for vectors. In particular, ${{\varvec{I}}}_D$ is the $D \times D$ identity matrix and ${{\varvec{0}}}_D$, ${{\varvec{1}}}_D$ (or simply ${{\varvec{0}}}$, ${{\varvec{1}}}$) are the D-dimensional vectors of zeros and ones, respectively. We write $a_i$ to denote the ith entry of ${{\varvec{a}}}$ and write ${{\varvec{a}}}_{i:j}$, $i<j$, for the vector $(a_i \; a_{i+1} \cdots a_{j})^T$. We let ${{\,\mathrm{range}\,}}({{\varvec{A}}})$ denote the linear subspace spanned in ${\mathbb {R}}^D$ by the columns of ${{\varvec{A}}} \in {\mathbb {R}}^{D \times d}$. We write $\langle \cdot , \cdot \rangle$, $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ for the usual Euclidean inner product, the Euclidean norm and the infinity norm, respectively. Where emphasis is needed, for the Euclidean norm we also use $\Vert \cdot \Vert _2$.

Given two random variables (vectors) x and y (${{\varvec{x}}}$ and ${{\varvec{y}}}$), the expression $x {\mathop {=}\limits ^{law}} y$ (${{\varvec{x}}} {\mathop {=}\limits ^{law}} {{\varvec{y}}}$) means that x and y (${{\varvec{x}}}$ and ${{\varvec{y}}}$) have the same distribution. We reserve the letter ${{\varvec{A}}}$ for a $D\times d$ Gaussian random matrix (see Definition A.1) and write $\chi ^2_n$ to denote a chi-squared random variable with n degrees of freedom (see Definition A.5).

Given a point ${{\varvec{a}}} \in {\mathbb {R}}^D$ and a set S of points in ${\mathbb {R}}^D$, we write ${{\varvec{a}}}+S$ to denote the set $\{ {{\varvec{a}}}+{{\varvec{s}}}: {{\varvec{s}}} \in S \}$. Given functions $f(x):{\mathbb {R}}\rightarrow {\mathbb {R}}$ and $g(x):{\mathbb {R}}\rightarrow {\mathbb {R}}^+$, we write $f(x) = \Theta (g(x))$ as $x \rightarrow \infty$ to denote the fact that there exist positive reals $M_1,M_2$ and a real number $x_0$ such that, for all $x \ge x_0$, $M_1g(x)\le |f(x)| \le M_2g(x)$.

2 Preliminaries

2.1 Functions with low effective dimensionality

Definition 2.1

(Functions with low effective dimensionality [58]) A function $f : {\mathbb {R}}^D \rightarrow {\mathbb {R}}$ has effective dimension $d_e$ if there exists a linear subspace ${\mathcal {T}}$ of dimension $d_e$ such that for all vectors ${{\varvec{x}}}_{\top }$ in ${\mathcal {T}}$ and ${{\varvec{x}}}_{\perp }$ in ${\mathcal {T}}^{\perp }$ (the orthogonal complement of ${\mathcal {T}}$), we have

$$\begin{aligned} f({{\varvec{x}}}_{\top } + {{\varvec{x}}}_{\perp }) = f({{\varvec{x}}}_{\top }), \end{aligned}$$

(2.1)

and $d_e$ is the smallest integer satisfying (2.1).

The linear subspaces ${\mathcal {T}}$ and ${\mathcal {T}}^{\perp }$ are called the effective and constant subspaces of f, respectively. In this paper, we make the following assumption on the function f.

Assumption 2.2

The function $f:{\mathbb {R}}^D \rightarrow {\mathbb {R}}$ is continuous and has effective dimensionality $d_e$ such that $d_e < D$, with effective subspace⁴${\mathcal {T}}$ and constant subspace ${\mathcal {T}}^{\perp }$ spanned by the columns of the orthonormal matrices ${{\varvec{U}}} \in {\mathbb {R}}^{D \times d_e}$ and ${{\varvec{V}}} \in {\mathbb {R}}^{D\times (D-d_e)}$, respectively. We let ${{\varvec{x}}}_\top = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}$ and ${{\varvec{x}}}_\perp = {{\varvec{V}}} {{\varvec{V}}}^T {{\varvec{x}}}$, the unique Euclidean projections of any vector ${{\varvec{x}}} \in {\mathbb {R}}^D$ onto ${\mathcal {T}}$ and ${\mathcal {T}}^\perp$, respectively.

We define the set of feasible global minimizers of problem (P),

$$\begin{aligned} G := \{{{\varvec{x}}} \in {\mathcal {X}}: f({{\varvec{x}}}) = f^* \}. \end{aligned}$$

(2.2)

Note that, for any ${{\varvec{x}}}^* \in G$ with Euclidean projection ${{\varvec{x}}}_\top ^*$ on the effective subspace ${\mathcal {T}}$, and for any $\tilde{{{\varvec{x}}}} \in {\mathcal {T}}^\perp$, we have

$$\begin{aligned} f^* = f({{\varvec{x}}}^*) = f({{\varvec{x}}}^*_{\top } + \tilde{{{\varvec{x}}}}) = f({{\varvec{x}}}_{\top }^*). \end{aligned}$$

(2.3)

The minimizer ${{\varvec{x}}}_{\top }^*$ may lie outside ${\mathcal {X}}$, and furthermore, there may be multiple points ${{\varvec{x}}}_{\top }^*$ in ${\mathcal {T}}$ satisfying $f^* = f({{\varvec{x}}}^*_\top )$ as illustrated in [9, Example 1.1]. Thus, the set G is (generally)⁵ a union of (possibly infinitely many) ($D-d_e$)-dimensional simply-connected polyhedral sets, each corresponding to a particular ${{\varvec{x}}}_{\top }^*$. If ${{\varvec{x}}}_{\top }^*$ is unique, i.e., every global minimizer ${{\varvec{x}}}^* \in G$ has the same Euclidean projection ${{\varvec{x}}}_\top ^*$ on the effective subspace, then G is the $(D-d_e)$-dimensional set $\{ {{\varvec{x}}} \in {\mathcal {X}} : {{\varvec{x}}} \in {{\varvec{x}}}_{\top }^* + {\mathcal {T}}^{\perp } \}$.

Definition 2.3

Suppose Assumption 2.2 holds. For any global minimizer ${{\varvec{x}}}^* \in G$, let $G^* := \{ {{\varvec{x}}} \in {\mathcal {X}} : {{\varvec{x}}} \in {{\varvec{x}}}_{\top }^* + {\mathcal {T}}^{\perp } \}$ be the simply connected subset of G that contains ${{\varvec{x}}}_{\top }^* = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}^*$, and ${\mathcal {G}}^* := \{ {{\varvec{x}}} \in {\mathbb {R}}^D: {{\varvec{x}}} \in {{\varvec{x}}}_{\top }^* + {\mathcal {T}}^{\perp } \}$, the ($D-d_e$)-dimensional affine subspace that contains $G^*$.

We can express $G^* = {\mathcal {G}}^* \cap {\mathcal {X}} = \{{{\varvec{x}}}_{\top }^*+{{\varvec{V}}} {{\varvec{g}}}: -{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* + {{\varvec{V}}} {{\varvec{g}}} \le {{\varvec{1}}}, {{\varvec{g}}} \in {\mathbb {R}}^{D-d_e} \}$, where ${{\varvec{V}}}$ is defined in Assumption 2.2. For each $G^*$, we define the corresponding set of “admissible” $(D-d_e)$-dimensional vectors as

$$\begin{aligned} {\bar{G}}^* := \{{{\varvec{g}}} \in {\mathbb {R}}^{D-d_e} : {{\varvec{x}}}_{\top }^* + {{\varvec{V}}} {{\varvec{g}}} \in G^*\}. \end{aligned}$$

(2.4)

Note that the set $G^*$ is $(D-d_e)$-dimensional if and only if the volume of the set ${\bar{G}}^*$ in ${\mathbb {R}}^{D-d_e}$, denoted by ${{\,\mathrm{Vol}\,}}({\bar{G}}^*)$, is non-zero. In some particular cases, when the global minimizer ${{\varvec{x}}}^*$ in Definition 2.3 is on the boundary of ${\mathcal {X}}$, the corresponding simply connected component $G^*$ may be of dimension strictly lower than $(D-d_e)$ and, hence, ${{\,\mathrm{Vol}\,}}({\bar{G}}^*) = 0$; a case we need to sometimes exclude from our analysis.

Definition 2.4

Let $G^*$ and ${\bar{G}}^*$ be defined as in Definition 2.3 and (2.4), respectively. We say that $G^*$ is non-degenerate if ${{\,\mathrm{Vol}\,}}({\bar{G}}^*) > 0$.

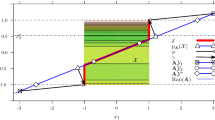
The definitions and assumptions introduced in this section are illustrated next in Fig. 1.

Fig. 1

Abstract illustration of the embedding of an affine d-dimensional subspace ${{\varvec{p}}}+{{\,\mathrm{range}\,}}({{\varvec{A}}})$ into ${\mathbb {R}}^D$. The red line represents the feasible set of solutions along ${{\varvec{p}}}+{{\,\mathrm{range}\,}}({{\varvec{A}}})$ and the blue line represents the set $G^*$. The random subspace intersects ${\mathcal {G}}^*$ at ${{\varvec{x}}}^*$, which is infeasible

Geometric description of the problem Figure 1 sketches the linear mapping ${{\varvec{y}}} \rightarrow {{\varvec{A}}}{{\varvec{y}}} + {{\varvec{p}}}$ that maps points from ${\mathbb {R}}^d$ to points in the affine subspace ${{\varvec{p}}}+{{\,\mathrm{range}\,}}({{\varvec{A}}})$ in ${\mathbb {R}}^D$. This figure also illustrates the case of a non-degenerate simply-connected component $G^*$ of global minimizers (blue line; Definition 2.3), which here has dimension $D-d_e=1$. Degeneracy of $G^*$ (Definition 2.4) would occur if ${{\varvec{x}}}^*_{\top }$ was a vertex of the domain ${\mathcal {X}}$, in which case the corresponding $G^*$ would be a singleton.

For (${\mathrm{RP}}{\mathcal {X}}$) to be successful in solving the original problem (P), Fig. 1 illustrates it is sufficient that the red line segment (the feasible set of (reduced) solutions in ${\mathbb {R}}^d$ mapped to ${\mathbb {R}}^D$) intersects the blue line segment (the set $G^*$). If $G^* = G$, this sufficient condition is also necessary, so that (${\mathrm{RP}}{\mathcal {X}}$) is not successful; else, we need to check the other simply connected components of G to decide whether (${\mathrm{RP}}{\mathcal {X}}$) is successful or not.

Note that, while the blue and red line segments do not intersect in Fig. 1, their prolongations outside ${\mathcal {X}}$ (${\mathcal {G}}^*$ and ${{\varvec{p}}}+{{\,\mathrm{range}\,}}({{\varvec{A}}})$) do. This is related to [58, Theorem 2], which says that if the dimension of the embedded subspace (d) is greater than the effective dimension ($d_e$) of f then ${\mathcal {G}}^*$ and ${{\varvec{p}}}+{{\,\mathrm{range}\,}}({{\varvec{A}}})$ intersect with probability one. Wang et al. [58] have shown this result for the case ${{\varvec{p}}} = {{\varvec{0}}}$, but it can easily be generalized to arbitrary ${{\varvec{p}}}$. In other words, in the unconstrained setting when ${\mathcal {X}} = {\mathbb {R}}^D$ and $d \ge d_e$, it is known that the reduced problem (${\mathrm{RP}}{\mathcal {X}}$) is successful with probability one [9, 58]: one random embedding typically suffices to solve the original problem (P). The main contribution of this paper is to quantify the probability of the random embedding to contain a feasible solution of the original problem, in the bound-constrained setting. For this, we rely on results of [9] that characterize the distribution of a random reduced minimizer ${{\varvec{y}}}^*$ such that ${{\varvec{A}}}{{\varvec{y}}}^*+{{\varvec{p}}}$ is an (unconstrained) minimizer of f, thus quantifying a specific intersection between the random subspace and ${\mathcal {G}}^*$. We recall these results in Sect. 2.2, and use this characterization in Sect. 3 to derive a lower bound on the probability of ${{\varvec{A}}} {{\varvec{y}}}^* + {{\varvec{p}}}$ to belong to $G^*$, namely, to be feasible for the original problem (P).

2.2 Characterization of (unconstrained) minimizers in the reduced space

Let ${\mathcal {S}}^* := \{ {{\varvec{y}}}^* \in {\mathbb {R}}^d : {{\varvec{A}}}{{\varvec{y}}}^* + {{\varvec{p}}} \in {\mathcal {G}}^* \}$, with ${\mathcal {G}}^*$ defined in Definition 2.3, be a subset of points ${{\varvec{y}}}^*$ corresponding to solutions of minimizing f over the entire ${\mathbb {R}}^D$. With probability one, ${\mathcal {S}}^*$ is a singleton if $d = d_e$ and has infinitely many points if $d>d_e$ [9, Corollary 3.3]. It is sufficient to find one of the reduced minimizers in ${\mathcal {S}}^*$, ideally one that is easy to analyse, and that is close to the origin (i.e., the centre of the domain ${\mathcal {X}}$) in some norm so as to encourage the feasibility with respect to ${\mathcal {X}}$ of its image through ${{\varvec{A}}}$. An obvious candidate is the minimal Euclidean norm solution,

$$\begin{aligned} \begin{aligned} {{\varvec{y}}}_2^{*} = \mathop {\mathrm{arg~min}}\limits _{{{\varvec{y}}} \in {\mathbb {R}}^d} \;\;&\Vert {{\varvec{y}}} \Vert _2 \\ \text {s.t.}\;\;&{{\varvec{y}}} \in {\mathcal {S}}^*. \end{aligned} \end{aligned}$$

(2.5)

The following result provides a useful characterization of ${{\varvec{y}}}_2^*$ as the minimum Euclidean norm solution to a random linear system.

Theorem 2.5

[9, Theorem 3.1] Suppose Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be any global minimizer of (P) with Euclidean projection ${{\varvec{x}}}_\top ^*$ on the effective subspace, and ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector. Let ${{\varvec{A}}}$ be a $D \times d$ Gaussian matrix, with $d \ge d_e$. Then ${{\varvec{y}}}_2^{*}$ defined in (2.5) is given by

$$\begin{aligned} {{\varvec{y}}}_2^* := {{\varvec{B}}}^T({{\varvec{B}}}{{\varvec{B}}}^T)^{-1}{{\varvec{z}}}^*, \end{aligned}$$

(2.6)

which is the minimum Euclidean norm solution to the system

$$\begin{aligned} {{\varvec{B}}} {{\varvec{y}}}^* = {{\varvec{z}}}^*, \end{aligned}$$

(2.7)

where ${{\varvec{B}}} = {{\varvec{U}}}^T {{\varvec{A}}}$ and ${{\varvec{z}}}^* \in {\mathbb {R}}^{d_e}$ is uniquely defined by

$$\begin{aligned} {{\varvec{U}}}{{\varvec{z}}}^* = {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }, \,\,\text {with}\, {{\varvec{p}}}_{\top } = {{\varvec{U}}}{{\varvec{U}}}^T{{\varvec{p}}}. \end{aligned}$$

(2.8)

Proof

The full proof is given in the technical report version of this paper, see [11]. $\square$

Remark 2.6

Note that ${{\varvec{B}}} = {{\varvec{U}}}^T{{\varvec{A}}}$ is a $d_e \times d$ Gaussian matrix, since ${{\varvec{U}}}$ has orthonormal columns (see Theorem A.2). Also, (2.8) implies $\Vert {{\varvec{z}}}^* \Vert _2 = \Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert _2$.

Using (2.6) and various properties of Gaussian matrices, [9] shows that the squared Euclidean norm of ${{\varvec{y}}}_2^*$ follows the (appropriately scaled) inverse chi-squared distribution. We rely on this result in the next section (see the proof of Theorem 3.3) to quantify the probability of success of (${\mathrm{RP}}{\mathcal {X}}$), which we will lower bound by the probability that ${{\varvec{A}}} {{\varvec{y}}}_2^* + {{\varvec{p}}} \in {\mathcal {X}}$, i.e., that ${{\varvec{A}}}{{\varvec{y}}}_2^* + {{\varvec{p}}}$, the representation of ${{\varvec{y}}}_2^*$ in the high-dimensional domain, is feasible for (P).

Theorem 2.7

([9, Theorem 3.7]) Suppose Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be any global minimizer of (P) and ${{\varvec{p}}}\in {\mathcal {X}}$ a given vector, with respective projections ${{\varvec{x}}}_\top ^*$ and ${{\varvec{p}}}_\top$ on the effective subspace. Let ${{\varvec{A}}}$ be a $D \times d$ Gaussian matrix, with $d \ge d_e$. Then, ${{\varvec{y}}}^*_2$ defined in (2.5) satisfies

$$\begin{aligned} \frac{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top } \Vert ^2_2}{\Vert {{\varvec{y}}}^*_2 \Vert ^2_2} \sim \chi ^2_{d-d_e+1} \quad \text {if } {{\varvec{x}}}_{\top }^* \ne {{\varvec{p}}}_{\top }. \end{aligned}$$

If ${{\varvec{x}}}_{\top }^* = {{\varvec{p}}}_{\top }$, then ${{\varvec{y}}}^*_2 = {{\varvec{0}}}$ .

3 Estimating the success of the reduced problem

This section derives lower bounds on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$). Lemma 3.1 lower bounds this probability by that of a non-empty intersection between the random subspace ${{\varvec{p}}}+{{\,\mathrm{range}\,}}({{\varvec{A}}})$ and an arbitrary simply-connected component $G^*$ of the set of global minimizers (Definition 2.3). This probability is further expressed in Corollary 3.4 in terms of a random vector ${{\varvec{w}}}$ that follows a multivariate t-distribution. From Sect. 3.1 onwards, we derive positive and/or quantifiable lower bounds on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$), while also trying to eliminate, wherever possible, the dependency of the lower bounds on the choice of ${{\varvec{p}}}$ and $G^*$.

Lemma 3.1

Suppose Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix with $d \ge d_e$. Let ${{\varvec{y}}}_2^*$ be defined in (2.5). The reduced problem (${\mathrm{RP}}{\mathcal {X}}$) is successful in the sense of Definition 1.1 if ${{\varvec{A}}}{{\varvec{y}}}_2^*+{{\varvec{p}}} \in {\mathcal {X}}$, namely

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}] \ge {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}} \le {{\varvec{A}}}{{\varvec{y}}}_2^* + {{\varvec{p}}}\le {{\varvec{1}}}]. \end{aligned}$$

(3.1)

Proof

This is an immediate consequence of Definition 1.1 and (2.5), as the latter implies ${{\varvec{A}}} {{\varvec{y}}}_2^* + {{\varvec{p}}} \in {\mathcal {G}}^*$ and so $f({{\varvec{A}}} {{\varvec{y}}}_2^* + {{\varvec{p}}}) = f^*$. $\square$

Let us further express (3.1) as follows. Let ${{\varvec{Q}}} = ({{\varvec{U}}} \; {{\varvec{V}}})$, where ${{\varvec{U}}}$ and ${{\varvec{V}}}$ are defined in Assumption 2.2. Since ${{\varvec{Q}}}$ is orthogonal, we have

$$\begin{aligned} {{\varvec{A}}}{{\varvec{y}}}_2^*= {{\varvec{Q}}}{{\varvec{Q}}}^T{{\varvec{A}}}{{\varvec{y}}}_2^*= {{\varvec{Q}}} \begin{pmatrix} {{\varvec{U}}}^T \\ {{\varvec{V}}}^T \end{pmatrix} {{\varvec{A}}} {{\varvec{y}}}_2^*. \end{aligned}$$

(3.2)

Using (2.6), we get ${{\varvec{U}}}^T{{\varvec{A}}} {{\varvec{y}}}_2^* = {{\varvec{z}}}^*$. Letting

$$\begin{aligned} {{\varvec{w}}} := {{\varvec{V}}}^T{{\varvec{A}}} {{\varvec{y}}}_2^*, \end{aligned}$$

(3.3)

we get

$$\begin{aligned} {{\varvec{A}}}{{\varvec{y}}}_2^* = {{\varvec{Q}}} \begin{pmatrix} {{\varvec{z}}}^* \\ {{\varvec{w}}} \end{pmatrix} = \begin{pmatrix} {{\varvec{U}}}&{{\varvec{V}}} \end{pmatrix} \begin{pmatrix} {{\varvec{z}}}^* \\ {{\varvec{w}}} \end{pmatrix} = {{\varvec{U}}}{{\varvec{z}}}^* + {{\varvec{V}}}{{\varvec{w}}} = {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top } + {{\varvec{V}}}{{\varvec{w}}}, \end{aligned}$$

(3.4)

where in the last equality, we used (2.8). By substituting ${{\varvec{p}}} = {{\varvec{p}}}_{\top }+{{\varvec{p}}}_{\perp }$ and (3.4) in (3.1), we obtain

$$\begin{aligned} \begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}]&\ge {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}}\le {{\varvec{A}}}{{\varvec{y}}}_2^* + {{\varvec{p}}} \le {{\varvec{1}}}] \\&= {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* -{{\varvec{p}}}_{\top } + {{\varvec{V}}}{{\varvec{w}}} + {{\varvec{p}}}_{\top }+{{\varvec{p}}}_{\perp } \le {{\varvec{1}}}] \\&= {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* + {{\varvec{p}}}_{\perp } + {{\varvec{V}}}{{\varvec{w}}} \le {{\varvec{1}}}]. \end{aligned} \end{aligned}$$

(3.5)

According to this derivation, all the randomness within the lower bound (3.5) is contained in the random vector ${{\varvec{w}}}$. The next theorem, derived in Appendix B, provides the probability density function of this random vector.

Remark 3.2

Suppose that Assumption 2.2 holds and recall (2.2). If there exists ${{\varvec{x}}}^*\in G$ such that ${{\varvec{x}}}_{\top }^* = {{\varvec{p}}}_{\top }$, where the subscript represents the respective Euclidean projections on the effective subspace, then $f({{\varvec{p}}}) = f({{\varvec{p}}}_{\top }+{{\varvec{p}}}_{\perp }) = f({{\varvec{x}}}_{\top }^* + {{\varvec{p}}}_{\perp }) = f^*$, where ${{\varvec{p}}}_{\perp }$ is the Euclidean projection of ${{\varvec{p}}}$ on the constant subspace ${\mathcal {T}}^{\perp }$ of the objective function. Thus ${{\varvec{p}}}\in G$ so that, for any embedding ${{\varvec{A}}}$, (${\mathrm{RP}}{\mathcal {X}}$) is successful with the trivial solution ${{\varvec{y}}}^* = {{\varvec{0}}}$. Therefore, in our next result, without loss of generality, we make the assumption ${{\varvec{x}}}_{\top }^* \ne {{\varvec{p}}}_{\top }$.

Theorem 3.3

(The p.d.f. of ${{\varvec{w}}}$) Suppose that Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix with $d_e \le d \le D-d_e$. Assume that ${{\varvec{p}}}_\top \ne {{\varvec{x}}}_\top ^*$, where the subscript represents the Euclidean projection on the effective subspace. The random vector ${{\varvec{w}}}$ defined in (3.3) follows a $(D-d_e)$-dimensional t-distribution with parameters $d-d_e+1$ and $\frac{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2}{d-d_e+1}{{\varvec{I}}}$, and with p.d.f. $g({{\varvec{{\bar{w}}}}})$ given by

$$\begin{aligned} g({{\varvec{{\bar{w}}}}}) = \frac{1}{(\sqrt{\pi } \Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert )^m} \left[ \frac{\Gamma (\frac{m+n}{2})}{\Gamma (\frac{n}{2})} \right] \left( 1 + \frac{{{\varvec{{\bar{w}}}}}^T{{\varvec{{\bar{w}}}}}}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2} \right) ^{-(m+n)/2}, \end{aligned}$$

(3.6)

where $m = D-d_e$ and $n = d-d_e+1$.

Proof

See Appendix B. $\square$

Let us now summarize the above analysis in the following corollary.

Corollary 3.4

Suppose that Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix with $d_e \le d \le D-d_e$. Assume that ${{\varvec{p}}}_\top \ne {{\varvec{x}}}_\top ^*$, where the subscript represents the Euclidean projection on the effective subspace. Then

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge {{\,\mathrm{{\mathbb {P}}}\,}}(-{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* + {{\varvec{p}}}_{\perp } + {{\varvec{V}}}{{\varvec{w}}} \le {{\varvec{1}}}), \end{aligned}$$

(3.7)

where ${{\varvec{w}}}$ is a random vector that follows a $(D-d_e)$-dimensional t-distribution with parameters $d-d_e+1$ and $\frac{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2}{d-d_e+1}{{\varvec{I}}}$.

Proof

The result follows from derivations (3.1)–(3.5) and Theorem 3.3. $\square$

Here is a roadmap for the results in the remainder of this section. We aim to answer the following two questions:

• Is the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) positive for any ${{\varvec{p}}}$? In other words: Does the random subspace $\mathrm {range}({{\varvec{A}}}) + {{\varvec{p}}}$ intersect a subspace of (unconstrained) global minimizers of (P) inside ${\mathcal {X}}$ with positive probability for all ${{\varvec{p}}}$? Answering this question allows to quantify the number of random embeddings required for finding a global minimizer of (P) when ${{\varvec{p}}}$ is chosen arbitrarily and kept fixed (if several embeddings are used, they all share the same ${{\varvec{p}}}$). We show that this question can be answered positively, and provide a lower bound on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) that depends on ${{\varvec{p}}}$ in Theorem 3.6.

• Furthermore, can we derive a positive lower bound on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) that does not depend on ${{\varvec{p}}}$? Ideally, we aim to prove convergence of X-REGO irrespectively of the choice of ${{\varvec{p}}}$. Indeed, it could be useful algorithmically to let ${{\varvec{p}}}$ vary from one random embedding to another, for example by setting ${{\varvec{p}}}$ to the best point found so far as proposed in Sect. 4. In the specific case where the effective subspace is aligned with the coordinate axes, we provide in Theorem 3.8 a lower bound that is independent of ${{\varvec{p}}}$, and asymptotically quantify its dependence on D, $d_e$ and d. Deriving such a bound for arbitrary effective subspaces seems, unfortunately, too challenging; we bypass this difficulty by assuming Lipschitz-continuity of f and providing in Theorem 3.15 a uniform lower bound on the probability of $\epsilon$-success of (${\mathrm{RP}}{\mathcal {X}}$), a weaker condition that requires the random subspace to contain an $\epsilon$-minimizer, i.e., a feasible point ${{\varvec{x}}}$ such that $f(x) \le f^*+ \epsilon$. This key result will allow us to prove almost sure convergence of X-REGO to an $\epsilon$-minimizer in Sect. 4, for any choice of ${{\varvec{p}}} \in {\mathcal {X}}$, including adaptive ones.

3.1 Positive probability of success of the reduced problem (${\mathrm{RP}}{\mathcal {X}}$)

To prove that the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) is strictly positive, we need the following additional assumption, that says that the function has low effective dimension and there exists a set of feasible optimal solutions of (P) that is “large enough”, i.e., of dimension at least $D-d_e$; a counter-example of this assumption would be a case when the feasible global minimizers of (P) are isolated (for an illustration, translate the set ${\mathcal {G}}^*$ in Fig. 1 to the upper right so that the blue line segment shrinks to the upper right corner of the box).

Assumption 3.5

Assume that Assumption 2.2 holds, and that there is a set $G^*$ defined in Definition 2.3 that is non-degenerate according to Definition 2.4.

The next result then proves that for all ${{\varvec{p}}}$, with a strictly positive probability, the random embedding contains a feasible global minimizer of (P).

Theorem 3.6

Suppose that Assumption 3.5 holds, and let ${{\varvec{A}}}$ be a $D \times d$ Gaussian matrix with $d_e \le d \le D-d_e$. Then, for any ${{\varvec{p}}} \in {\mathcal {X}}$,

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] > 0. \end{aligned}$$

(3.8)

Proof

We consider two cases, ${{\varvec{p}}}\in G$ and ${{\varvec{p}}} \in {\mathcal {X}}\setminus G$. Firstly, assume that ${{\varvec{p}}} \in G$. Then, ${{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] = 1$ since taking ${{\varvec{y}}} = {{\varvec{0}}}$ in (${\mathrm{RP}}{\mathcal {X}}$) yields $f({{\varvec{p}}}) = f^*$.

Assume now that ${{\varvec{p}}}\in {\mathcal {X}}\setminus G$. Assumption 3.5 implies that there exists a global minimizer ${{\varvec{x}}}^*$ and associated $G^*$ for which ${{\,\mathrm{Vol}\,}}({\bar{G}}^*) > 0$, where $G^*$ and ${\bar{G}}^*$ are defined in Definition 2.3 and (2.4), respectively. Using (3.7) with this particular ${{\varvec{x}}}^*$ and noting that ${{\varvec{p}}}_{\perp } = {{\varvec{V}}}{{\varvec{V}}}^T{{\varvec{p}}}$ gives us

$$\begin{aligned} \begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}]&\ge {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* + {{\varvec{V}}}({{\varvec{V}}}^T{{\varvec{p}}} + {{\varvec{w}}}) \le {{\varvec{1}}}] \\&= {{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{V}}}^T{{\varvec{p}}} + {{\varvec{w}}} \in \{{{\varvec{g}}} \in {\mathbb {R}}^{D-d_e} : -{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* + {{\varvec{V}}}{{\varvec{g}}} \le {{\varvec{1}}} \}] \\&= {{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{V}}}^T{{\varvec{p}}} + {{\varvec{w}}} \in {\bar{G}}^*] \\&= {{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{w}}} \in -{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*] \\&= \int _{-{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*} g({{\varvec{{\bar{w}}}}}) d{{\varvec{{\bar{w}}}}}, \end{aligned} \end{aligned}$$

(3.9)

where $g({{\varvec{{\bar{w}}}}})$ is the p.d.f. of ${{\varvec{w}}}$ given in (3.6). The latter integral is positive since $g({{\varvec{{\bar{w}}}}}) > 0$ for any ${{\varvec{{\bar{w}}}}} \in {\mathbb {R}}^{D-d_e}$ and since ${{\,\mathrm{Vol}\,}}(-{{\varvec{V}}}^T{{\varvec{p}}}+{\bar{G}}^*) = {{\,\mathrm{Vol}\,}}({\bar{G}}^*) > 0$ (invariance of volumes under translations) by Assumption 3.5. $\square$

Note that the proof of Theorem 3.6 illustrates that the success probability of (${\mathrm{RP}}{\mathcal {X}}$), though positive, depends on the choice of ${{\varvec{p}}}$.⁶ Next, under additional problem assumptions, we derive lower bounds on the success probability of (${\mathrm{RP}}{\mathcal {X}}$) that are independent of ${{\varvec{p}}}$ and/or quantifiable.

3.2 Quantifying the success probability of (${\mathrm{RP}}{\mathcal {X}}$) in the special case of coordinate-aligned effective subspace

Provided the effective subspace ${\mathcal {T}}$ is aligned with coordinate axes and without loss of generality, we can write the orthonormal matrices ${{\varvec{U}}}$ and ${{\varvec{V}}}$, whose columns span ${\mathcal {T}}$ and ${\mathcal {T}}^\perp$, as ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e} \; {{\varvec{0}}}]^T$ and ${{\varvec{V}}} = [{{\varvec{0}}} \; {{\varvec{I}}}_{D-d_e}]^T$. The following result quantifies the probability of the random embedding to contain a feasible global solution of (P) in this case, in terms of the cumulative distribution function of ${{\varvec{w}}}$.

Theorem 3.7

Let Assumption 2.2 hold with ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e} \; {{\varvec{0}}}]^T$ and ${{\varvec{V}}} = [{{\varvec{0}}} \; {{\varvec{I}}}_{D-d_e}]^T$. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix with $d_e \le d \le D-d_e$. Assume that ${{\varvec{p}}}_\top \ne {{\varvec{x}}}_\top ^*$, where the subscript represents the Euclidean projection on the effective subspace. Then

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}}- {{\varvec{p}}}_{d_e+1:D} \le {{\varvec{w}}} \le {{\varvec{1}}}- {{\varvec{p}}}_{d_e+1:D}], \end{aligned}$$

(3.10)

where ${{\varvec{w}}}$ is a random vector that follows a $(D-d_e)$-dimensional t-distribution with parameters $d-d_e+1$ and $\frac{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2}{d-d_e+1}{{\varvec{I}}}$.

Proof

For ${{\varvec{x^*}}}\in G^*$, we have

$$\begin{aligned} {{\varvec{x}}}_{\top }^* = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}^* = \begin{pmatrix} {{\varvec{I}}} &{}\quad {{\varvec{0}}} \\ {{\varvec{0}}} &{}\quad {{\varvec{0}}} \end{pmatrix} {{\varvec{x}}}^* = \begin{pmatrix} {{\varvec{x}}}^*_{1:d_e} \\ {{\varvec{0}}} \end{pmatrix}. \end{aligned}$$

(3.11)

Furthermore,

$$\begin{aligned} {{\varvec{p}}}_{\perp } = {{\varvec{V}}} {{\varvec{V}}}^T {{\varvec{p}}} = \begin{pmatrix} {{\varvec{0}}} &{}\quad {{\varvec{0}}} \\ {{\varvec{0}}} &{}\quad {{\varvec{I}}} \end{pmatrix} {{\varvec{p}}} = \begin{pmatrix} {{\varvec{0}}} \\ {{\varvec{p}}}_{d_e+1:D} \end{pmatrix}. \end{aligned}$$

Note that ${{\varvec{x}}}^* \in [-1,1]^{D}$ implies that ${{\varvec{x}}}^*_{1:d_e} \in [-1,1]^{d_e}$. Corollary 3.4 then yields

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}]&\ge {{\,\mathrm{{\mathbb {P}}}\,}}(-{{\varvec{1}}} \le {{\varvec{x}}}_{\top }^* + {{\varvec{p}}}_{\perp }+ {{\varvec{V}}} {{\varvec{w}}} \le {{\varvec{1}}}) \\&= {{\,\mathrm{{\mathbb {P}}}\,}}\left[ \begin{pmatrix} -{{\varvec{1}}} \\ -{{\varvec{1}}} \end{pmatrix} \le \begin{pmatrix} {{\varvec{x}}}^*_{1:d_e} \\ {{\varvec{0}}} \end{pmatrix} + \begin{pmatrix} {{\varvec{0}}} \\ {{\varvec{p}}}_{d_e+1:D} \end{pmatrix} + \begin{pmatrix} {{\varvec{0}}} \\ {{\varvec{I}}} \end{pmatrix} {{\varvec{w}}} \le \begin{pmatrix} {{\varvec{1}}} \\ {{\varvec{1}}} \end{pmatrix}\right] \\ (\text {since}\, {{\varvec{x}}}^*_{1:d_e} \in [-1,1]^{d_e})&= {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}} \le {{\varvec{p}}}_{d_e+1:D} + {{\varvec{w}}} \le {{\varvec{1}}}], \end{aligned}$$

which immediately gives (3.10). $\square$

Note that the right-hand side of (3.10) can be written as the integral of the p.d.f. of ${{\varvec{w}}}$ over the hyperrectangular region $-{{\varvec{1}}} - {{\varvec{p}}}_{d_e+1:D} \le {{\varvec{w}}} \le {{\varvec{1}}} - {{\varvec{p}}}_{d_e+1:D}$. Instead of directly computing this integral, we analyse its asymptotic behaviour for large D, assuming that $d_e$ and d are fixed. We obtain the following main result, with its proof provided in Appendix C.

Theorem 3.8

Let Assumption 2.2 hold with ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e} \; {{\varvec{0}}}]^T$ and ${{\varvec{V}}} = [{{\varvec{0}}} \; {{\varvec{I}}}_{D-d_e}]^T$. Let $d_e$ and d be fixed, with $d_e \le d \le D-d_e$, and let ${{\varvec{A}}}$ be a $D \times d$ Gaussian matrix. For all ${{\varvec{p}}} \in {\mathcal {X}}$, we have

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge \tau > 0, \end{aligned}$$

(3.12)

where $\tau$ satisfies

$$\begin{aligned} \tau = \Theta \left( \frac{\log (D-d_e+1)^{\frac{d-1}{2}}}{2^{D-d_e} \cdot (D-d_e+1)^{d_e}}\right) \,\text {as}\, D \rightarrow \infty , \end{aligned}$$

(3.13)

and the constants in $\Theta (\cdot )$ depend only on $d_e$ and d.

Proof

See Appendix C. $\square$

The next result shows that, in the particular case when ${{\varvec{p}}} = {{\varvec{0}}}$, the center of the full-dimensional domain ${\mathcal {X}}$, the probability of success decreases at worst in a polynomial way⁷ with the ambient dimension D.

Theorem 3.9

Let Assumption 2.2 hold with ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e} \; {{\varvec{0}}}]^T$ and ${{\varvec{V}}} = [{{\varvec{0}}} \; {{\varvec{I}}}_{D-d_e}]^T$. Let $d_e$ and d be fixed, with $d_e \le d \le D-d_e$, and let ${{\varvec{A}}}$ be a $D \times d$ Gaussian matrix. Let ${{\varvec{p}}} = {{\varvec{0}}}$. Then

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge \tau _{{{\varvec{0}}}} > 0, \end{aligned}$$

(3.14)

where

$$\begin{aligned} \tau _{{{\varvec{0}}}} = \Theta \left( \frac{\log (D-d_e+1)^{\frac{d-1}{2}}}{(D-d_e+1)^{d_e}}\right) \,\text {as}\, D \rightarrow \infty , \end{aligned}$$

(3.15)

and where the constants in $\Theta (\cdot )$ depend only on $d_e$ and d.

Proof

See Appendix C. $\square$

Remark 3.10

Unlike Theorem 3.6, the above result does not require Assumption 3.5. In this specific case, as the effective subspace is aligned with the coordinate axes, Assumption 3.5 is satisfied. The latter follows from ${{\bar{G}}}^* = \{ {{\varvec{g}}} \in {\mathbb {R}}^{D-d_e} : -{{\varvec{1}}} \le {{\varvec{x}}}_\top ^* + {{\varvec{V}}} {{\varvec{g}}} \le {{\varvec{1}}}\} = \{ {{\varvec{g}}} \in [-1,1]^{D-d_e}\}$, as ${{\varvec{V}}} = [{{\varvec{0}}} \; {{\varvec{I}}}_{D-d_e}]^T$ and the last $D-d_e$ components of the vector ${{\varvec{x}}}_\top ^*$ are zero; see the proof of Theorem 3.7.

Remark 3.11

We note that (3.10) holds with equality if $d=d_e$ and $G = G^*$. Our numerical experiments in Sect. 5 also clearly illustrate that the success probability decreases with growing problem dimension D.

Remark 3.12

Our particular choice of asymptotic framework here is due to its practicality as well as to the ready-at-hand analysis of a similar integral to (C.2) in [60]. The scenario ($d_e$ and d fixed, D large) is a familiar one in practice, where commonly, $d_e$ is small compared to D, and d is limited by computational resources available to solve the reduced subproblem. Other asymptotic frameworks that could be considered in the future are $d_e = O(1)$, $d = O(\log (D))$ or $d_e = O(1)$, $d = \beta D$ where $\beta$ is fixed. For more details on how to obtain asymptotic expansions similar to (3.13) and (3.15) for such choices of $d_e$ and d, refer to [53, 60].

3.3 Uniformly positive lower bound on the success probability of (${\mathrm{RP}}{\mathcal {X}}$) in the general case

As mentioned in the last paragraph of Sect. 3.1, it is difficult to derive a uniformly positive lower bound on the probability of success of (${\mathrm{RP}}{\mathcal {X}}$) that does not depend on ${{\varvec{p}}}$. However, assuming Lipschitz continuity of the objective function, we are able to achieve such a guarantee for (${\mathrm{RP}}{\mathcal {X}}$) to be approximately successful, a weaker notion that is defined as follows.

Definition 3.13

For a(ny) $\epsilon >0$, we say that (${\mathrm{RP}}{\mathcal {X}}$) is $\epsilon$-successful if there exists ${{\varvec{y}}}^* \in {\mathbb {R}}^d$ such that $f({{\varvec{A}}}{{\varvec{y}}}^*+{{\varvec{p}}}) \le f^* + \epsilon$ and ${{\varvec{A}}}{{\varvec{y}}}^* + {{\varvec{p}}} \in {\mathcal {X}}$.

Let

$$\begin{aligned} G_\epsilon := \{ {{\varvec{x}}} \in {\mathcal {X}} : f({{\varvec{x}}}) \le f^* + \epsilon \} \end{aligned}$$

(3.16)

be the set of feasible $\epsilon$-minimizers. The reduced problem (${\mathrm{RP}}{\mathcal {X}}$) is thus $\epsilon$-successful if it contains a feasible $\epsilon$-minimizer.

Assumption 3.14

The objective function $f : {\mathbb {R}}^D \rightarrow {\mathbb {R}}$ is Lipschitz continuous with Lipschitz constant L, that is, $|f({{\varvec{x}}}) - f({{\varvec{y}}})| \le L\Vert {{\varvec{x}}} - {{\varvec{y}}} \Vert _2$ for all ${{\varvec{x}}}$ and ${{\varvec{y}}}$ in ${\mathbb {R}}^D$.

The next theorem shows that the probability that (${\mathrm{RP}}{\mathcal {X}}$) is $\epsilon$-successful is uniformly bounded away from zero for all ${{\varvec{p}}} \in {\mathcal {X}}$.

Theorem 3.15

Suppose that Assumption 3.5 and Assumption 3.14 hold. Let ${{\varvec{A}}}$ be a $D \times d$ Gaussian matrix with $d_e \le d \le D-d_e$ and $\epsilon >0$, an accuracy tolerance. Then there exists a constant $\tau _{\epsilon } > 0$ such that, for all ${{\varvec{p}}} \in {\mathcal {X}}$,

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({\mathrm{RP}}{\mathcal {X}}) \ \text {is}\, \epsilon \text {-successful}] \ge \tau _{\epsilon }. \end{aligned}$$

(3.17)

Proof

Assumption 3.5 implies that there exists a global minimizer ${{\varvec{x}}}^* \in {\mathcal {X}}$, with corresponding sets $G^*$ (Definition 2.3) and ${\bar{G}}^*$ in (2.4) such that ${{\,\mathrm{Vol}\,}}({\bar{G}}^*) > 0$. Let $N_{\eta }(G^*):= \{ {{\varvec{x}}} \in {\mathcal {X}}: \Vert {{\varvec{x}}}_{\top }^* - {{\varvec{U}}}{{\varvec{U}}}^T {{\varvec{x}}}\Vert _2 \le \eta \}$ be a neighbourhood of $G^*$ in ${\mathcal {X}}$, for some $\eta > 0$, where as usual, ${{\varvec{x}}}_{\top }^* = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}^*$ is the Euclidean projection of ${{\varvec{x}}}^*$ on the effective subspace.

Firstly, assume that ${{\varvec{p}}} \in N_{\epsilon /L}(G^*)$. Then, $\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top } \Vert \le \epsilon /L$, and by Assumption 3.14, $|f({{\varvec{p}}}) - f^*| = |f({{\varvec{p}}}_{\top }) - f({{\varvec{x}}}_{\top }^*)| \le L\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top } \Vert \le \epsilon$. Thus ${{\varvec{p}}} \in G_{\epsilon }$ and, hence, ${{\,\mathrm{{\mathbb {P}}}\,}}[({\mathrm{RP}}{\mathcal {X}}) \ \text {is}\,\epsilon \text {-successful}] = 1$.

Otherwise, ${{\varvec{p}}}\in {\mathcal {X}}\setminus N_{\epsilon /L}(G^*)$. Using the proof of Theorem 3.6, we have

$$\begin{aligned} \begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is}\, \epsilon \text {-successful}] \ge {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}]&\ge \int _{-{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*} g({{\varvec{{\bar{w}}}}}) d{{\varvec{{\bar{w}}}}}, \end{aligned}\nonumber \\ \end{aligned}$$

(3.18)

where $g({{\varvec{{\bar{w}}}}})$ is the p.d.f. of ${{\varvec{w}}}$ given by (3.6), and where the first inequality is due to the fact that (${\mathrm{RP}}{\mathcal {X}}$) being successful implies that (${\mathrm{RP}}{\mathcal {X}}$) is $\epsilon$-successful (by letting $\epsilon := 0$ in Definition 3.13). To prove (3.17), it is thus sufficient to lower bound $g({{\varvec{{\bar{w}}}}})$ by a positive constant, independent of ${{\varvec{p}}}$. Since ${{\varvec{p}}} \notin N_{\epsilon /L}(G^*)$, we have

$$\begin{aligned} \frac{\epsilon }{L} < \Vert {{\varvec{x}}}^*_{\top } - {{\varvec{p}}}_{\top }\Vert _2 = \Vert {{\varvec{U}}}{{\varvec{U}}}^T({{\varvec{x}}}^* - {{\varvec{p}}}) \Vert _2 \le \Vert {{\varvec{U}}}{{\varvec{U}}}^T\Vert _2\cdot \Vert {{\varvec{x}}}^* - {{\varvec{p}}}\Vert _2 \le 2\sqrt{D},\nonumber \\ \end{aligned}$$

(3.19)

where the last inequality follows from $\Vert {{\varvec{U}}}{{\varvec{U}}}^T\Vert _2 = 1$, since ${{\varvec{U}}}$ has orthonormal columns, and from $-{{\varvec{2}}} \le {{\varvec{x}}}^* - {{\varvec{p}}} \le {{\varvec{2}}}$ since ${{\varvec{x}}}^*,{{\varvec{p}}} \in [-1,1]^D$. Furthermore, note that, for any ${{\varvec{{\bar{w}}}}} \in -{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*$, we have

$$\begin{aligned} -{{\varvec{1}}}-{{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\perp } \le {{\varvec{V}}}{{\varvec{{\bar{w}}}}} \le {{\varvec{1}}} - {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\perp }, \end{aligned}$$

and, hence,

$$\begin{aligned} \begin{aligned} \Vert {{\varvec{V}}}{{\varvec{{\bar{w}}}}} \Vert _{\infty }&\le \max (\Vert -{{\varvec{1}}}-{{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\perp }\Vert _{\infty },\Vert {{\varvec{1}}}-{{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\perp }\Vert _{\infty }) \\&\le \Vert {{\varvec{1}}}\Vert _{\infty } + \Vert {{\varvec{x}}}_{\top }^* \Vert _{\infty } + \Vert {{\varvec{p}}}_{\perp }\Vert _{\infty } \\&\le 1 + \Vert {{\varvec{x}}}_{\top }^* \Vert _{2} + \Vert {{\varvec{p}}}_{\perp }\Vert _{2} \\&= 1 + \Vert {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}^* \Vert _{2} + \Vert {{\varvec{V}}} {{\varvec{V}}}^T{{\varvec{p}}}\Vert _{2} \\&\le 1 + \Vert {{\varvec{U}}} {{\varvec{U}}}^T \Vert _2 \cdot \Vert {{\varvec{x}}}^* \Vert _{2} + \Vert {{\varvec{V}}} {{\varvec{V}}}^T\Vert _2 \cdot \Vert {{\varvec{p}}}\Vert _{2} \\&\le 1+2\sqrt{D}, \end{aligned} \end{aligned}$$

where the last inequality follows from $\Vert {{\varvec{U}}}{{\varvec{U}}}^T\Vert _2 = 1$ and $\Vert {{\varvec{V}}}{{\varvec{V}}}^T\Vert _2 = 1$ (as ${{\varvec{U}}}$ and ${{\varvec{V}}}$ are orthonormal) and from ${{\varvec{x}}}^*, {{\varvec{p}}} \in [-1,1]^D$. Thus,

$$\begin{aligned} \Vert {{\varvec{{\bar{w}}}}}\Vert _2 = \Vert {{\varvec{V}}}{{\varvec{{\bar{w}}}}} \Vert _2 \le \sqrt{D}\Vert {{\varvec{V}}}{{\varvec{{\bar{w}}}}} \Vert _{\infty } \le \sqrt{D} (1+2\sqrt{D}) \le 3D. \end{aligned}$$

(3.20)

By combining (3.6), (3.19) and (3.20), we finally obtain

$$\begin{aligned} \begin{aligned} \int _{-{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*} g({{\varvec{{\bar{w}}}}}) d{{\varvec{{\bar{w}}}}}&= C(m,n) \int _{-{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*} \frac{1}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^m} \left( 1 + \frac{\Vert {{\varvec{{\bar{w}}}}}\Vert ^2}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2} \right) ^{-(m+n)/2} d{{\varvec{{\bar{w}}}}} \\&> C(m,n) (2\sqrt{D})^{-m} (1+9D^2L^2/\epsilon ^2)^{-(m+n)/2} \int _{-{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*} d {{\varvec{{\bar{w}}}}} \\&= C(m,n) (2\sqrt{D})^{-m} (1+9D^2L^2/\epsilon ^2)^{-(m+n)/2} {{\,\mathrm{Vol}\,}}(-{{\varvec{V}}}^T {{\varvec{p}}} + {\bar{G}}^*) \\&= C(m,n) (2\sqrt{D})^{-m} (1+9D^2L^2/\epsilon ^2)^{-(m+n)/2} {{\,\mathrm{Vol}\,}}({\bar{G}}^*), \end{aligned} \end{aligned}$$

where $C(m,n) = \Gamma ((m+n)/2)/(\pi ^{m/2}\Gamma (n/2))$ and where in the last equality we used the fact ${{\,\mathrm{Vol}\,}}(-{{\varvec{V}}}^T{{\varvec{p}}}+{\bar{G}}^*) = {{\,\mathrm{Vol}\,}}({\bar{G}}^*)$ for any ${{\varvec{p}}} \in {\mathbb {R}}^D$ (invariance of volumes under translations). The result follows from the assumption that ${{\,\mathrm{Vol}\,}}({\bar{G}}^*)~>~0$. $\square$

4 The X-REGO algorithm and its global convergence

In the case of random embeddings for unconstrained global optimization, the success probability of the reduced problem is independent of the ambient dimension [9]. However, in the constrained case of problem (P), the analysis in Sect. 3 shows that the probability of success of the reduced problem (${\mathrm{RP}}{\mathcal {X}}$) decreases with D. It is thus imperative in any algorithm that uses feasible random embeddings in order to solve (P) to allow multiple such subspaces to be explored, and it is practically important to find out what are efficient and theoretically-sound ways to choose these subspaces iteratively. This is the aim of our generic and flexible algorithmic framework, X-REGO (Algorithm 1). Furthermore, as an additional level of generality and practicality, we allow the reduced, random subproblem to be solved stochastically, so that a sufficiently accurate global solution of this problem is only guaranteed with a certain probability. This covers the obvious case when a (convergent) stochastic global optimization algorithm would be employed to solve the reduced subproblem, but also when a deterministic global solver is used but may sometimes fail to find the required solution due to a limited computational budget, processor failure and so on.

In X-REGO, for $k\ge 1$, the kth embedding is determined by a realization $\tilde{{{\varvec{A}}}}^k = {{\varvec{A}}}^k({{\varvec{\omega }}}^k)$ of the random Gaussian matrix ${{\varvec{A}}}^k$, and it is drawn at the point $\tilde{{{\varvec{p}}}}^{k-1} = {{\varvec{p}}}^{k-1}({{\varvec{\omega }}}^{k-1}) \in {\mathcal {X}}$, a realization of the random variable ${{\varvec{p}}}^{k-1}$ (which, without loss of generality, includes the case of deterministic choices by writing ${{\varvec{p}}}^{k-1}$ as a random variable with support equal to a singleton).

X-REGO can be seen as a stochastic process, so that in addition to $\tilde{{{\varvec{p}}}}^k$ and $\tilde{{{\varvec{A}}}}^k$, each algorithm realization provides sequences $\tilde{{{\varvec{x}}}}^k = {{\varvec{x}}}^k({{\varvec{\omega }}}^k)$, $\tilde{{{\varvec{y}}}}^k = {{\varvec{y}}}^k({{\varvec{\omega }}}^k)$ and ${\tilde{f}}_{min}^k = f_{min}^k({{\varvec{\omega }}}^k)$, for $k \ge 1$, that are realizations of the random variables ${{\varvec{x}}}^k$, ${{\varvec{y}}}^k$ and $f_{min}^k$, respectively. Each iteration of X-REGO solves—approximately and possibly, with a certain probability—a realization ($\widetilde{\text {RP}{\mathcal {X}}^k}$) of the random problem

To calculate $\tilde{{{\varvec{y}}}}^k$, ($\widetilde{\text {RP}{\mathcal {X}}^k}$) may be solved to some required accuracy using a deterministic global optimization algorithm that is allowed to fail with a certain probability; or employing a stochastic algorithm, so that $\tilde{{{\varvec{y}}}}^k$ is only guaranteed to be an approximate global minimizer of ($\widetilde{\text {RP}{\mathcal {X}}^k}$) (at least) with a certain probability.

Several variants of X-REGO can be obtained by specific choices of the random variable ${{\varvec{p}}}^k$ (assumed throughout the paper to have support contained in ${\mathcal {X}}$). A first possibility consists in simply defining ${{\varvec{p}}}^k$ as a random variable with support $\{{{\varvec{0}}}\}$, so that $\tilde{{{\varvec{p}}}}^{k} = {{\varvec{0}}}$ for all k. It is also possible to preserve the progress achieved so far by defining ${{\varvec{p}}}^k = {{\varvec{x}}}_{opt}^k$, where

$$\begin{aligned} {{\varvec{x}}}_{opt}^k := \arg \min \{ f({{\varvec{x}}}^1), f({{\varvec{x}}}^2), \dots , f({{\varvec{x}}}^k)\}, \end{aligned}$$

(4.2)

the random variable corresponding to the best point found over the k first embeddings. We compare numerically several choices of ${{\varvec{p}}}$ on benchmark functions in Sect. 5.

The termination in Line 2 could be set to a given maximum number of embeddings, or could check that no significant progress in decreasing the objective function has been achieved over the last few embeddings, compared to the value $f(\tilde{{{\varvec{x}}}}^k_{opt})$. For generality, we leave it unspecified here.

4.1 Global convergence of the X-REGO algorithm to the set of global $\epsilon$-minimizers

For a(ny) given tolerance $\epsilon >0$, let $G_\epsilon$ be the set of approximate global minimizers of (P) defined in (3.16). We show that ${{\varvec{x}}}_{opt}^k$ in (4.2) converges to $G_{\epsilon }$ almost surely as $k \rightarrow \infty$ (see Theorem 4.7).

Intuitively, our proof relies on the fact that any vector $\tilde{{{\varvec{x}}}}^k$ defined in (4.1) belongs to $G_\epsilon$ if the following two conditions hold simultaneously: (a) the reduced problem ($\text {RP}{\mathcal {X}}^k$) is $(\epsilon - \lambda )$-successful in the sense of Definition 3.13,⁸ namely,

$$\begin{aligned} f_{min}^k \le f^* + \epsilon -\lambda ; \end{aligned}$$

(4.3)

(b) the reduced problem ($\widetilde{\text {RP}{\mathcal {X}}^k}$) is solved (by a deterministic/stochastic algorithm) to an accuracy $\lambda \in (0,\epsilon )$ in the objective function value, namely,

$$\begin{aligned} f({{\varvec{A}}}^k {{\varvec{y}}}^k + {{\varvec{p}}}^{k-1}) \le f_{min}^k + \lambda \end{aligned}$$

(4.4)

holds (at least) with a certain probability. We introduce two additional random variables that capture the conditions in (a) and (b) above,

$$\begin{aligned} R^k&= \mathbbm {1}\{({\text {RP}{\mathcal {X}}^k}) \,\text {is}\, (\epsilon -\lambda )\,\text {-successful in the sense of}\, (4.3)\}, \end{aligned}$$

(4.5)

$$\begin{aligned} S^k&= \mathbbm {1}\{({\text {RP}{\mathcal {X}}^k}) \,\text {is solved to accuracy}\, \lambda \,\text {in the sense of}\, (4.4)\}, \end{aligned}$$

(4.6)

where $\mathbbm {1}$ is the usual indicator function for an event.

Let ${\mathcal {F}}^k = \sigma ({{\varvec{A}}}^1, \dots , {{\varvec{A}}}^k, {{\varvec{y}}}^1, \dots , {{\varvec{y}}}^k, {{\varvec{p}}}^0, \dots , {{\varvec{p}}}^k)$ be the $\sigma$-algebra generated by the random variables ${{\varvec{A}}}^1, \dots , {{\varvec{A}}}^k, {{\varvec{y}}}^1, \dots , {{\varvec{y}}}^k, {{\varvec{p}}}^0, \dots , {{\varvec{p}}}^k$ (a mathematical concept that represents the history of the X-REGO algorithm as well as its randomness until the kth embedding),⁹ with ${\mathcal {F}}^0 = \sigma ({{\varvec{p}}}^0)$. We also construct an ‘intermediate’ $\sigma$-algebra, namely,

$$\begin{aligned} {\mathcal {F}}^{k-1/2} = \sigma ({{\varvec{A}}}^1, \dots , {{\varvec{A}}}^{k-1}, {{\varvec{A}}}^{k}, {{\varvec{y}}}^1, \dots , {{\varvec{y}}}^{k-1}, {{\varvec{p}}}^0, \dots , {{\varvec{p}}}^{k-1}), \end{aligned}$$

with ${\mathcal {F}}^{1/2} = \sigma ({{\varvec{p}}}^0, {{\varvec{A}}}^{1})$. Note that ${{\varvec{x}}}^k$, $R^k$ and $S^k$ are ${\mathcal {F}}^{k}$-measurable,¹⁰ and $R^k$ is also ${\mathcal {F}}^{k-1/2}$-measurable; thus they are well-defined random variables.

Remark 4.1

The random variables ${{\varvec{A}}}^1, \dots , {{\varvec{A}}}^k$, ${{\varvec{y}}}^1, \dots , {{\varvec{y}}}^k$, ${{\varvec{x}}}^1, \dots , {{\varvec{x}}}^k$, ${{\varvec{p}}}^0, {{\varvec{p}}}^1, \dots , {{\varvec{p}}}^k$, $R^1$, $\dots$, $R^k$, $S^1, \dots , S^{k}$ are ${\mathcal {F}}^{k}$-measurable since ${\mathcal {F}}^0 \subseteq {\mathcal {F}}^1 \subseteq \cdots \subseteq {\mathcal {F}}^{k}$. Also, ${{\varvec{A}}}^1, \dots , {{\varvec{A}}}^k$, ${{\varvec{y}}}^1, \dots , {{\varvec{y}}}^{k-1}$, ${{\varvec{x}}}^1, \dots , {{\varvec{x}}}^{k-1}$, ${{\varvec{p}}}^0, {{\varvec{p}}}^1, \dots , {{\varvec{p}}}^{k-1}$, $R^1$, $\dots$, $R^k$, $S^1, \dots , S^{k-1}$ are ${\mathcal {F}}^{k-1/2}$-measurable since ${\mathcal {F}}^0 \subseteq {\mathcal {F}}^{1/2} \subseteq {\mathcal {F}}^1 \subseteq \cdots \subseteq {\mathcal {F}}^{k-1} \subseteq {\mathcal {F}}^{k-1/2}$.

A weak assumption is given next, that is satisfied by reasonable techniques for the subproblems; namely, the reduced problem ($\text {RP}{\mathcal {X}}^k$) needs to be solved to required accuracy with some positive probability.

Assumption 4.2

There exists $\rho \in (0,1]$ such that, for all $k \ge 1$,¹¹

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[ S^k = 1 | {\mathcal {F}}^{k-1/2}]={\mathbb {E}}[S^k | {\mathcal {F}}^{k-1/2}] \ge \rho , \end{aligned}$$

i.e., with (conditional) probability at least $\rho > 0$, the solution ${{\varvec{y}}}^k$ of ($\text {RP}{\mathcal {X}}^k$) satisfies (4.4).

Remark 4.3

If a deterministic (global optimization) algorithm is used to solve ($\widetilde{\text {RP}{\mathcal {X}}^k}$), then $S^k$ is always ${\mathcal {F}}_k^{k-1/2}$-measurable and Assumption 4.2 is equivalent to $S^k\ge \rho$. Since $S^k$ is an indicator function, this further implies that $S^k\equiv 1$, provided a sufficiently large computational budget is available.

The results of Sect. 3 provide a lower bound on the (conditional) probability of the reduced problem ($\text {RP}{\mathcal {X}}^k$) to be $(\epsilon -\lambda )$-successful, with the consequence given in the first part of the next corollary.

Corollary 4.4

If Assumptions 3.5 and 3.14 hold and if $d_e \le d \le D-d_e$, then

$$\begin{aligned} {\mathbb {E}}[R^k | {\mathcal {F}}^{k-1}] \ge \tau , \quad \mathrm{for}\quad k\ge 1. \end{aligned}$$

(4.7)

If Assumption 4.2 holds, then

$$\begin{aligned} {\mathbb {E}}[R^k S^k | {\mathcal {F}}^{k-1/2}] \ge \rho R^k, \quad \mathrm{for}\quad k\ge 1. \end{aligned}$$

(4.8)

Proof

Recall that the support of the random variable ${{\varvec{p}}}^k$ is contained in ${\mathcal {X}}$. For each embedding, we apply Theorem 3.15 (setting ${{\varvec{p}}} = \tilde{{{\varvec{p}}}}^{k-1}$ and replacing $\epsilon$ by $\epsilon -\lambda$) to deduce that there exists $\tau \in (0,1]$ such that ${{\,\mathrm{{\mathbb {P}}}\,}}[R^k = 1 | {\mathcal {F}}^{k-1} ] \ge \tau$, for $k\ge 1$. Then, in terms of conditional expectation, we have ${\mathbb {E}}[R^k | {\mathcal {F}}^{k-1}] = 1 \cdot {{\,\mathrm{{\mathbb {P}}}\,}}[ R^k = 1 | {\mathcal {F}}^{k-1}] + 0 \cdot {{\,\mathrm{{\mathbb {P}}}\,}}[ R^k = 0 | {\mathcal {F}}^{k-1} ] \ge \tau$.

If Assumption  4.2 holds, then ${\mathbb {E}}[R^k S^k | {\mathcal {F}}^{k-1/2}] = R^k {\mathbb {E}}[ S^k | {\mathcal {F}}^{k-1/2}] \ge \rho R^k$, where the equality follows from the fact that $R^k$ is ${\mathcal {F}}^{k-1/2}$-measurable (see [20, Theorem 4.1.14]). $\square$

4.1.1 Global convergence proof

A useful property is given next.

Lemma 4.5

Let Assumptions 3.5, 3.14 and 4.2 hold, and let $d_e \le d \le D-d_e$. Then, for $K\ge 1$, we have

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}\left[ \bigcup _{k=1}^K \left\{ \{R^k = 1\} \cap \{ S^k = 1 \} \right\} \right] \ge 1 - (1-\tau \rho )^K. \end{aligned}$$

Proof

We define an auxiliary random variable, $J^K := \mathbbm {1} \Big (\bigcup _{k=1}^K \big \{ \{R^k = 1\} \cap \{ S^k = 1 \} \big \} \big ).$ Note that $J^K = 1- \prod _{k=1}^{K} (1-R^k S^k)$. We have

where

• $(*)$ follow from the tower property of conditional expectation (see (4.1.5) in [20]),

• $(\circ )$ is due to the fact that $R^1, \dots , R^{K-1}$ and $S^1,\dots ,S^{K-1}$ are ${\mathcal {F}}^{K-1/2}$-  and ${\mathcal {F}}^{K-1}$-measurable (see Theorem 4.1.14 in [20]),

• the inequalities follow from (4.8) and (4.7), respectively.

We repeatedly expand the expectation of the product for $K-1$, $\ldots$, 1, in exactly the same manner as above, to obtain the desired result. $\square$

In the next lemma, we show that if ($\text {RP}{\mathcal {X}}^k$) is $(\epsilon -\lambda )$-successful and is solved to accuracy $\lambda$ in objective value, then the solution ${{\varvec{x}}}^k$ must be inside $G_{\epsilon }$; thus proving our intuitive statements (a) and (b) at the start of Sect. 4.1.

Lemma 4.6

Suppose Assumptions 3.5, 3.14 and 4.2 hold, and let $d_e \le d \le D-d_e$. Then

$$\begin{aligned} \{R^k = 1\}\cap \{S^k = 1\} \subseteq \{{{\varvec{x}}}^{k} \in G_{\epsilon }\}. \end{aligned}$$

Proof

By Definition 3.13, if ($\text {RP}{\mathcal {X}}^k$) is $(\epsilon -\lambda )$-successful, then there exists ${{\varvec{y}}}^k_{int} \in {\mathbb {R}}^d$ such that ${{\varvec{A}}}^k {{\varvec{y}}}^k_{int} + {{\varvec{p}}}^{k-1} \in {\mathcal {X}}$ and

$$\begin{aligned} f({{\varvec{A}}}^k{{\varvec{y}}}^k_{int} + {{\varvec{p}}}^{k-1}) \le f^* + \epsilon - \lambda . \end{aligned}$$

(4.9)

Since ${{\varvec{y}}}^k_{int}$ is in the feasible set of ($\text {RP}{\mathcal {X}}^k$) and $f^k_{min}$ is the global minimum of ($\text {RP}{\mathcal {X}}^k$), we have

$$\begin{aligned} f^k_{min} \le f({{\varvec{A}}}^k{{\varvec{y}}}^k_{int} + {{\varvec{p}}}^{k-1}). \end{aligned}$$

(4.10)

Then, for ${{\varvec{x}}}^k$, (4.4) gives the first inequality below,

$$\begin{aligned} f({{\varvec{x}}}^k) \le f^k_{min} + \lambda \le f({{\varvec{A}}}^k{{\varvec{y}}}^k_{int} + {{\varvec{p}}}^{k-1}) + \lambda \le f^* + \epsilon , \end{aligned}$$

where the second and third inequalities follow from (4.10) and (4.9), respectively. This shows that ${{\varvec{x}}}^k \in G_\epsilon$. $\square$

In the following theorem, we show that X-REGO converges almost surely to an $\epsilon$-minimizer of (P), i.e., a feasible solution of (P) with cost at most $f^*+\epsilon$.

Theorem 4.7

(Global convergence) Suppose Assumptions 3.5, 3.14 and 4.2 hold, and let $d_e \le d \le D-d_e$. Then

$$\begin{aligned} \lim _{k\rightarrow \infty } {{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{x}}}^k_{opt} \in G_{\epsilon }]=\lim _{k\rightarrow \infty } {{\,\mathrm{{\mathbb {P}}}\,}}[f({{\varvec{x}}}^k_{opt}) \le f^* + \epsilon ] = 1 \end{aligned}$$

where ${{\varvec{x}}}^k_{opt}$ and $G_{\epsilon }$ are defined in (4.2) and (3.16), respectively.

Furthermore, for any $\xi \in (0,1)$,

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[ {{\varvec{x}}}^k_{opt} \in G_{\epsilon } ]= {{\,\mathrm{{\mathbb {P}}}\,}}[f({{\varvec{x}}}^k_{opt}) \le f^* + \epsilon ]\ge \xi \,\text {for all}\, k \ge K_{\xi }, \end{aligned}$$

(4.11)

where $K_\xi := \Big \lceil {\frac{|\log (1-\xi )|}{\tau \rho }}\Big \rceil$.

Proof

Lemma 4.6 and the definition of ${{\varvec{x}}}^k_{opt}$ in (4.2) provide

$$\begin{aligned} \{ R^k = 1 \} \cap \{ S^k = 1 \} \subseteq \{ {{\varvec{x}}}^k \in G_{\epsilon } \} \subseteq \{ {{\varvec{x}}}_{opt}^k \in G_{\epsilon } \} \end{aligned}$$

for $k = 1, 2,\dots , K$ and for any integer $K\ge 1$. Hence,

$$\begin{aligned} \bigcup _{k=1}^K \{ R^k = 1 \} \cap \{ S^k = 1 \} \subseteq \bigcup _{k=1}^K \{ {{\varvec{x}}}^k_{opt} \in G_{\epsilon } \}. \end{aligned}$$

(4.12)

Note that the sequence $\{ f({{\varvec{x}}}^1_{opt}), f({{\varvec{x}}}^2_{opt}), \dots , f({{\varvec{x}}}^K_{opt})\}$ is monotonically decreasing. Therefore, if ${{\varvec{x}}}^k_{opt} \in G_{\epsilon }$ for some $k \le K$ then ${{\varvec{x}}}^i_{opt} \in G_{\epsilon }$ for all $i = k, \dots , K$; and so the sequence $(\{ {{\varvec{x}}}^k_{opt} \in G_{\epsilon } \})_{k = 1}^K$ is an increasing sequence of events. Hence,

$$\begin{aligned} \bigcup _{k=1}^K \{ {{\varvec{x}}}^k_{opt} \in G_{\epsilon } \} = \{ {{\varvec{x}}}^K_{opt} \in G_{\epsilon } \}. \end{aligned}$$

(4.13)

From (4.13) and (4.12), we have for all $K\ge 1$,

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[\{ {{\varvec{x}}}^K_{opt} \in G_{\epsilon } \}] \ge {{\,\mathrm{{\mathbb {P}}}\,}}\left[ \bigcup _{k=1}^K \{ R^k = 1 \} \cap \{ S^k = 1 \} \right] \ge 1 - (1- \tau \rho )^K, \end{aligned}$$

(4.14)

where the second inequality follows from Lemma 4.5. Finally, passing to the limit with K in (4.14), we deduce $1 \ge \lim _{K \rightarrow \infty } {{\,\mathrm{{\mathbb {P}}}\,}}[\{ {{\varvec{x}}}^K_{opt} \in G_{\epsilon } \}] \ge \lim _{K \rightarrow \infty } \left[ 1 - (1- \tau \rho )^K\right] = 1$, as required.

Note that if

$$\begin{aligned} 1-(1-\tau \rho )^k \ge \xi \end{aligned}$$

(4.15)

then (4.14) implies ${{\,\mathrm{{\mathbb {P}}}\,}}[ {{\varvec{x}}}^k_{opt} \in G_{\epsilon } ] \ge \xi$. Since (4.15) is equivalent to $k \ge \displaystyle \frac{\log (1-\xi )}{\log (1-\tau \rho )}$, (4.15) holds for all $k\ge K_\xi$ since $K_\xi \ge \displaystyle \frac{\log (1-\xi )}{\log (1-\tau \rho )}$. $\square$

Remark 4.8

Crucially, we note that X-REGO (Algorithm 1) is a generic framework that can be applied to a general, continuous objective f in (P). Furthermore, the convergence result in Theorem 4.7 also continues to hold in this general case provided (4.7) can be shown to hold; this is where we crucially use the special structure of low effective dimensionality of the objective that we investigate in this paper. In [12], we apply X-REGO to global optimization of Lipschitz continuous objectives, under no special structure assumption and for arbitrary values of d and arbitrary domains; there, we also prove almost sure convergence to $\epsilon$-minimizers using tools from conic integral geometry.

Remark 4.9

If f is a convex function (and known a priori to be so), then clearly, a local (deterministic or stochastic) optimization algorithm may be used to solve ($\widetilde{\text {RP}{\mathcal {X}}^k}$) and achieve (4.4). Apart from this important speed-up and simplification, it is difficult to exploit this additional special structure of f in our analysis, in order to improve the success bounds and convergence.

Quantifiable rates of convergence when the effective subspace is aligned with coordinate axes Using the estimates for $\tau$ in Theorem 3.8, we can estimate precisely the rate of convergence of X-REGO as a function of problem dimension, assuming that ${\mathcal {T}}$ is aligned with coordinate axes.

Theorem 4.10

Suppose Assumption 2.2 holds with ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e} \; {{\varvec{0}}}]^T$ and ${{\varvec{V}}} = [{{\varvec{0}}} \; {{\varvec{I}}}_{D-d_e}]^T$, as well as Assumption 4.2. Let $\xi \in (0,1)$, and $d_e$ and d be fixed with $d_e \le d \le D-d_e$. Then (4.11) holds with

$$\begin{aligned} K_\xi = \frac{\left| \log (1-\xi )\right| }{\rho } O\left( \frac{2^{D-d_e} \cdot (D-d_e+1)^{d_e}}{\log (D-d_e+1)^{\frac{d-1}{2}}}\right) \,\text {as}\, D \rightarrow \infty . \end{aligned}$$

(4.16)

If ${{\varvec{p}}}^k = {{\varvec{0}}}$ for $k\ge 0$, then (4.11) holds with

$$\begin{aligned} K_\xi = \frac{\left| \log (1-\xi )\right| }{\rho } O\left( \frac{ (D-d_e+1)^{d_e}}{\log (D-d_e+1)^{\frac{d-1}{2}}}\right) \,\text {as}\, D \rightarrow \infty . \end{aligned}$$

(4.17)

Proof

Firstly, note our remark regarding assumptions below. The result follows from Theorem 4.7, (3.13) and (3.15). $\square$

Remark 4.11

Assumptions 3.5 and 3.14 were required to prove Theorem 3.15 and, consequently, (4.7). If the effective subspace is aligned with coordinate axes, we no longer need Assumptions 3.14 and 3.5 to prove (4.7). In this case, (4.7) follows from Theorem 3.8, together with the fact that ($\text {RP}{\mathcal {X}}^k$) being successful implies ($\text {RP}{\mathcal {X}}^k$) is $\epsilon$-successful for any $\epsilon \ge 0$.

5 Numerical experiments

5.1 Setup

Algorithms We test different variants of Algorithm 1 against the no-embedding framework, in which (P) is solved directly without using random embeddings and with no explicit exploitation of its special structure. Each variant of X-REGO corresponds to a specific choice of ${{\varvec{p}}}^k$, $k \ge 0$:

• Adaptive X-REGO (A-REGO). In X-REGO, the point ${{\varvec{p}}}^k$ is chosen as the best point found up to the kth embedding: if $f({{\varvec{A}}}^k {{\varvec{y}}}^k+{{\varvec{p}}}^{k-1}) < f({{\varvec{p}}}^{k-1})$ then ${{\varvec{p}}}^{k} := {{\varvec{A}}}^k {{\varvec{y}}}^k+{{\varvec{p}}}^{k-1}$, otherwise, ${{\varvec{p}}}^k := {{\varvec{p}}}^{k-1}$.

• Local Adaptive X-REGO (LA-REGO). In X-REGO, we solve ($\widetilde{\text {RP}{\mathcal {X}}^k}$) using a local solver (instead of a global one as in N-REGO). Then, if $|f({{\varvec{A}}}^k {{\varvec{y}}}^k+{{\varvec{p}}}^{k-1}) - f({{\varvec{p}}}^{k-1})| > \gamma$ for some small $\gamma$ (here, $\gamma = 10^{-5}$), we let ${{\varvec{p}}}^{k} := {{\varvec{A}}}^k {{\varvec{y}}}^k+{{\varvec{p}}}^{k-1}$, otherwise, ${{\varvec{p}}}^k$ is chosen uniformly at random in ${\mathcal {X}}$.

• Nonadaptive X-REGO (N-REGO). In X-REGO, all the random subspaces are drawn at the origin: ${{\varvec{p}}}^k := {{\varvec{0}}}$ for all k.

• Local Nonadaptive X-REGO (LN-REGO). In X-REGO, the low-dimensional problem ($\widetilde{\text {RP}{\mathcal {X}}^k}$) is solved using a local solver, and the point ${{\varvec{p}}}^k$ is chosen uniformly at random in ${\mathcal {X}}$ for all k.

Solvers We test the aforementioned X-REGO variants using three solvers for solving the reduced problem ($\widetilde{\text {RP}{\mathcal {X}}^k}$)—or for solving the original problem (P) in the no-embedding case—namely, DIRECT ([24, 27, 35]), BARON ([49, 52]) and KNITRO ([8]).

DIRECT ([24, 27, 35]) version 4.0 (DIviding RECTangles) is a deterministic¹² global optimization solver, that does not require information about the gradient nor about the Lipschitz constant.

BARON ([49, 52]) version 17.10.10 (Branch-And-Reduce Optimization Navigator) is a state-of-the-art branch- and-bound type global optimization solver for nonlinear and mixed-integer programs, that is highly competitive [45]. However, it accepts only a few (general) classes of functions (e.g., no trigonometric functions, no black box functions).

KNITRO ([8]) version 10.3.0 is a large-scale nonlinear local optimization solver that makes use of objective derivatives. KNITRO has a multi-start feature, referred here as mKNITRO, allowing it to aim for global minimizers.

We refer to [9] for a detailed description of the solvers. We test A-REGO and N-REGO using DIRECT, BARON and mKNITRO and test LA-REGO and LN-REGO using only local KNITRO, with no multi-start.

In addition to the comparison with ‘no embedding’, we compare X-REGO with the REMBO approach proposed in [58], which we modify so that it matches our present framework. Namely, we replace the Bayesian solver used in REMBO with (m)KNITRO (in its local and global incarnations). Our proposal is tested within the N-REGO (with mKNITRO) and LN-REGO (with KNITRO) frameworks where instead of solving ($\widetilde{\text {RP}{\mathcal {X}}^k}$) we solve the following problem

where ${\mathcal {P}}_{{\mathcal {X}}}({{\varvec{x}}}) := \arg \min _{{{\varvec{z}}} \in {\mathcal {X}}} \Vert {{\varvec{z}}} - {{\varvec{x}}} \Vert _2$ is the standard projection operator that projects an infeasible ${{\varvec{x}}}$ (that is outside ${\mathcal {X}}$) onto the nearest feasible point in ${\mathcal {X}}$; note that ${\mathcal {P}}_{{\mathcal {X}}}$ ensures that the computed solutions are feasible and thus there is no need for linear constraints as in ($\widetilde{\text {RP}{\mathcal {X}}^k}$). However, to restrict the search space, we follow the original REMBO proposal [58] and impose the bound constraint ${{\varvec{y}}} \in [-\delta , \delta ]^{d_e}$, where $\delta = \delta _{opt} := 8 \times \sqrt{d_e}$—an optimal value for $\delta$ determined based on the theoretical bounds in [9]. Note that $\delta _{opt}$ is not the same for every problem in the test set as $\delta _{opt}$ depends on $d_e$.

Test set The methodology of these constructions is given in [9, 58] and summarized here in Appendix D. Our synthetic test set contains 19 D-dimensional functions with low effective dimension, with $D = 10,100$ and 1000. We construct these high-dimensional functions from 19 global optimization problems (Table 4, of dimensions 2–6) with known global minima [5, 22, 29], some of which are in the Dixon-Szego test set [16]. The construction process consists in artificially adding coordinates to the original functions, and then applying a rotation to ensure that the effective subspace is not aligned with the coordinate axes.

Experimental setup We solve the entire test set with each version of X-REGO and its paired solvers. Let f be a function from the test set with the global minimum $f^*$. When applying any version of X-REGO to minimize f, we let $d=d_e$ for the size of the random embedding. We terminate either after $K = 100$ embeddings, or earlier, as soon as¹³

$$\begin{aligned} f(\widetilde{{{\varvec{A}}}}^k \tilde{{{\varvec{y}}}}^k + \tilde{{{\varvec{p}}}}^{k-1})-f^* \le \epsilon = 10^{-3}. \end{aligned}$$

(5.1)

Table 1 The table outlines the experimental setup for the solvers, used both in the ‘no-embedding’ algorithm and for solving the low-dimensional problems ($\widetilde{\text {RP}{\mathcal {X}}^k}$) and ($\widetilde{\text {CP}{\mathcal {X}}^k}$) (as usually, f denotes the D-dimensional function to minimize, $f^*$ is its global minimum, and $\epsilon$ in (5.1) is set to $10^{-3}$). At each internal iteration, DIRECT stores $f_D^*$—the minimal value of f found so far, while BARON stores $f_B^U$ and $f_B^L$—the smallest upper bound and largest lower bound found found so far. Note that, for BARON, $f_B^U = f({{\varvec{x}}}^k)$ in ($\widetilde{\text {RP}{\mathcal {X}}^k}$)

We then record the computational cost, which we measure in terms of either function evaluations or CPU time in seconds. To compare with ‘no-embedding’, we solve the full-dimensional problem (P) directly with DIRECT, BARON and mKNITRO with no use of random embeddings. The budget and termination criteria used for each solver to solve ($\widetilde{\text {RP}{\mathcal {X}}^k}$) within X-REGO, or to solve (P) in the ‘no-embedding’ framework are outlined in Table 1.

Remark 5.1

The experiments are done not to compare solvers but to contrast ‘no-embedding’ and REMBO with the X-REGO variants. All the experiments were run in MATLAB on the 16 cores (2 $\times$ 8 Intel with hyper-threading) Linux machines with 256 GB RAM and 3300 MHz speed.

We compare the results using performance profiles (Dolan and Moré [18]), which measure the proportion of problems solved by the algorithm in less than a given budget defined based on the best performance among the algorithms considered. More precisely, for each solver (BARON, DIRECT and KNITRO), and for each algorithm ${\mathcal {A}}$ (the above-mentioned variants of X-REGO and ‘no-embedding’), we record ${\mathcal {N}}_p({\mathcal {A}})$, the computational cost (see Table 1) of running algorithm ${\mathcal {A}}$ to solve problem p within accuracy $\epsilon$. Let ${\mathcal {N}}^*_p$ be the minimum computational cost required for problem p by any algorithm ${\mathcal {A}}$. The performance (probability) of algorithm ${\mathcal {A}}$ on the problem set ${\mathcal {P}}$ is defined as

$$\begin{aligned} \pi _{{\mathcal {A}}}(\alpha ) = \frac{| \{p \in {\mathcal {P}} : {\mathcal {N}}_p({\mathcal {A}}) \le \alpha {\mathcal {N}}^*_p\} |}{|{\mathcal {P}}|}, \end{aligned}$$

with performance ratio $\alpha \ge 1$.

Fig. 2

Comparison between X-REGO variants and ‘no-embedding’ using DIRECT

5.2 Numerical results

DIRECT Figure 2 compares the adaptive and non-adaptive random embedding algorithms (A-REGO and N-REGO) to the no-embedding framework, when using the DIRECT solver for the reduced problem ($\widetilde{\text {RP}{\mathcal {X}}^k}$) (and for the full-dimensional problem in the case of the no-embedding framework). We find that the no-embedding framework outperforms the two X-REGO variants. We also note that this behaviour is more pronounced when the dimension of the problem (P) is small. In that regime, it is also difficult to determine which version of X-REGO performs the best. When D is large, the no-embedding framework still outperforms the two variants of X-REGO, but among these two, the adaptive one (A-REGO) performs generally better than N-REGO. The average number of function evaluations and random embeddings/subspaces required by the algorithms are given in Tables 2 and 3, respectively.

Table 2 Average number of function evaluations or CPU time spent by each algorithm-solver pair

Table 3 Average number of embeddings for each algorithm-solver pair

BARON Figure 3 compares A-REGO and N-REGO to the no-embedding framework, when using BARON to solve the reduced problem ($\widetilde{\text {RP}{\mathcal {X}}^k}$). We find that the no-embedding framework is clearly outperformed by the two variants of X-REGO in the large-dimensional setting. Then, it is also clear that the adaptive variant of X-REGO outperforms the non-adaptive one. Table 2 also indicates that the CPU time used by the different algorithms increases with the dimension of the problem, and that the increase is most rapid for ’no-embedding’.

Fig. 3

Comparison between X-REGO variants and ‘no-embedding’ using BARON

KNITRO The comparison between the X-REGO variants, using mKNITRO to solve ($\widetilde{\text {RP}{\mathcal {X}}^k}$), is given in Fig. 4. Here, we also compare the local variants of X-REGO (namely, LA-REGO and LN-REGO), for which the reduced problem is solved using local KNITRO, with no multi-start feature, and the REMBO framework described above with (m)KNITRO. We find that the local variants outperform the global ones, and the no-embedding framework when the dimension of the problem is sufficiently large. Figure 4 also indicates that the local non-adaptive variant (LN-REGO) outperforms the adaptive one in this high-dimensional setting. This behaviour can also be observed in Tables 2 and 3, which indicate that less function evaluations and embeddings are needed for LA-REGO compared to LN-REGO for large D; this may be a feature of the test set we used/devised. Finally, the modified REMBO framework behaves comparatively well on this problem set. We note however, that its performance depends on the choice of a domain in the reduced space whose size $\delta$ needs careful choosing and it is typically not known a priori.¹⁴ By contrast, such careful reduced domain choices are not needed for X-REGO; which is a clear practical advantage for the latter. Furthermore, to the best of our knowledge, the convergence of the REMBO framework (with multiple embeddings) still needs to be developed, and we delegate this question to future work.

Fig. 4

Comparison between X-REGO variants, modified REMBO and ‘no-embedding’ using KNITRO. Here and in the following tables, modified REMBO refers to the combination of REMBO with N-REGO framework and modified REMBO(L) refers to the combination of REMBO with LN-REGO framework

Conclusions to numerical experiments The numerical experiments presented in this paper indicate that, as expected, the X-REGO algorithm is mostly beneficial for high-dimensional problems, when D is large. In this setting, X-REGO variants paired with the BARON and mKNITRO solvers outperform the ‘no-embedding’ approach, of applying these solvers directly to the problems. It is less obvious to decide which variant of X-REGO is best, but it seems that, at least on the problem set considered, the local variants outperform the global ones.

We have conducted additional numerical experiments where d is chosen to be strictly greater than $d_e$ (for example, $d=d_e+2$ is reasonable for our test set given the small dimension of the original Dixon-Szëgo test set); the performance of methods—particularly with BARON and (m)KNITRO—was similar to the $d=d_e$ presented here, as can be seen in the results given in Appendix E. Furthermore, we also considered five different realizations of the test set (namely, a different random rotation of the effective subspace was performed); again, similar results to the ones presented here were observed as illustrated in Appendix E and in the ArXiv version (arXiv:2009.10446) of this paper.

We also compared X-REGO (paired with KNITRO) with the simplest version of Random Search—uniform sampling inside the domain ${\mathcal {X}}$. The maximum budget of samples is set to $10^5$ in our experiment. We sample until either we have successfully found a global minimum (i.e. $f({{\varvec{x}}}_{sample}) \le f^* + 10^{-3}$) or we have exhausted the budget. The results of this experiment (including average number of samples by Random Search) are provided in Appendix E in Fig. 8. As expected, our X-REGO variants perform reassuring well by comparison.

Finally, since for our test set, we know the effective subspace/exact embedding of each test function, we have also checked how optimizing directly in this important subspace compares to using randomly drawn subspaces. Figure 9 in Appendix E displays our findings when comparing A-REGO and N-REGO (with mKNITRO) against direct optimization with mKNITRO in the respective effective subspace of each test function. As expected, mKNITRO usually manages to solve the given problems using a substantially smaller number of function evaluations when the effective subspace of each test objective is known. However, we emphasize again that the main aim of developing X-REGO is to allow the solution of such special structure global optimization problems when the low-dimensional effective subspace is unknown.

6 Conclusions and future work

We studied a generic global optimization framework, X-REGO, that relies on multiple random embeddings, for bound-constrained global optimization of functions with low effective dimensionality. For each random subspace, a lower-dimensional bound-constrained subproblem is solved, using a global or even local algorithm. Theoretical guarantees of convergence and encouraging numerical experiments are presented, which are particularly quantified in terms of their problem dimension dependence for the case when the effective subspace is aligned with the coordinate axes. We note that the X-REGO algorithmic framework (Algorithm 1) can be applied to a general, continuous objective f in (P) as the effective dimensionality assumption is not used; furthermore, our main global convergence result continues to hold under some assumptions (see Remark 4.8). Indeed, in [12], we explore the use of X-REGO for global optimization of Lipschitz continuous objectives, under no low effective dimension assumption, for arbitrary non-empty domain ${\mathcal {X}}$ and subspace dimension d [12]. We prove the convergence of X-REGO to an $\epsilon$-minimizer of (P), i.e., a point with cost at most $f^*+ \epsilon$, by providing a lower bound on the probability of the random subspace to contain an $\epsilon$-minimizer (analogously to Theorem 3.15) using tools from conic integral geometry.

Note also that our analysis relies on the assumption that the dimension of the random subspace satisfies $d_e \le d \le D-d_e$, with $d_e$ the dimension of the effective subspace. As the latter may be unknown in practice, this is a strong prerequisite. One possibility is to estimate the effective dimension $d_e$ numerically, as in [50]. Alternatively, we propose in [12] a variant of X-REGO that explores successively random subspaces of increasing dimension until finding the effective dimension of the problem, and prove almost sure convergence of this algorithmic framework to an $\epsilon$-minimizer of (P) in the unconstrained case (${\mathcal {X}} = {\mathbb {R}}^D$).

Appendices

A Technical definitions and results

1.1 A.1 Gaussian random matrices

Definition A.1

(Gaussian matrix, see [31, Definition 2.2.1]) A Gaussian (random) matrix is a matrix ${{\varvec{A}}} = (a_{ij})$, where the entries $a_{ij} \sim {\mathcal {N}}(0,1)$ are independent (identically distributed) standard normal variables.

Gaussian matrices have been well-studied with many results available at hand. Here, we mention a few key properties of Gaussian matrices that we use in the analysis; for a collection of results pertaining to Gaussian matrices and other related distributions refer to [31, 56].

Theorem A.2

(see [31, Theorem 2.3.10]) Let ${{\varvec{A}}}$ be a $D \times d$ Gaussian random matrix. If ${{\varvec{U}}} \in {\mathbb {R}}^{D \times p}$, $D \ge p$, and ${{\varvec{V}}} \in {\mathbb {R}}^{d \times q}$, $d \ge q$, are orthonormal, then ${{\varvec{U}}}^T{{\varvec{A}}}{{\varvec{V}}}$ is a Gaussian random matrix.

Theorem A.3

(see [31, Theorem 2.3.15]) Let ${{\varvec{A}}}$ be a $D \times d$ Gaussian random matrix, and let ${{\varvec{X}}} \in {\mathbb {R}}^{r \times D}$ and ${{\varvec{Y}}} \in {\mathbb {R}}^{q \times D}$ be given matrices. Then, ${{\varvec{X}}}{{\varvec{A}}}$ and ${{\varvec{Y}}}{{\varvec{A}}}$ are independent if and only if ${{\varvec{X}}}{{\varvec{Y}}}^T = {{\varvec{0}}}$.

Theorem A.4

(see [31, Theorem 3.2.1]) Let ${{\varvec{A}}}$ be a $D \times d$ Gaussian random matrix with $D \ge d$. Then, the Wishart matrix ${{\varvec{A}}}^T{{\varvec{A}}}$ is positive definite, and hence nonsingular, with probability one.

1.2 A.2 Other relevant probability distributions

Definition A.5

(Chi-squared distribution) Given a collection $Z_1, Z_2, \dots , Z_n$ of n independent standard normal variables, the random variable $W = Z_1^2+Z_2^2+\cdots Z_n^2$ is said to follow the chi-squared distribution with n degrees of freedom (see [39, A.2]). We denote this by $W \sim \chi _n^2$.

Theorem A.6

(see [31, Theorem 3.3.12]) Let ${{\varvec{M}}}$ be an $n \times l$ Gaussian matrix with $n \ge l$, ${{\varvec{y}}}$ be an $l \times 1$ random vector distributed independently of ${{\varvec{M}}}^T{{\varvec{M}}}$, and ${{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{y}}} \ne {{\varvec{0}}}] = 1$. Then,

$$\begin{aligned} \frac{{{\varvec{y}}}^T {{\varvec{M}}}^T{{\varvec{M}}}{{\varvec{y}}}}{{{\varvec{y}}}^T{{\varvec{y}}}} \sim \chi ^2_n \end{aligned}$$

and is independent of ${{\varvec{y}}}$.

Definition A.7

(Inverse chi-squared distribution) Given $X \sim \chi _n^2$, the random variable $Y = 1/X$ is said to follow the inverse chi-squared distribution with n degrees of freedom. We denote this by $Y \sim 1/\chi _n^2$ (see [39, A.5]).

Definition A.8

An l-dimensional random variable ${{\varvec{t}}}$ is said to have t-distribution with parameters $\nu$ and ${{\varvec{\Sigma }}}$ if its joint p.d.f. is given by (see [31, Chapter 4])

$$\begin{aligned} f({{\varvec{t}}}) = \frac{1}{(\pi \nu )^{l/2}}\left[ \frac{\Gamma \left( \frac{l+\nu }{2}\right) }{\Gamma \left( \frac{\nu }{2}\right) } \right] \det ({{\varvec{\Sigma }}})^{-1/2} \left( 1+\frac{1}{\nu } {{\varvec{t}}}^T {{\varvec{\Sigma }}}^{-1}{{\varvec{t}}} \right) ^{-(l+\nu )/2}, \end{aligned}$$

(A.1)

where $\Gamma$ is the usual gamma function.

Definition A.9

(F-distribution) Let $W_1 \sim \chi _{\nu _1}^2$ and $W_2 \sim \chi _{\nu _2}^2$ be independent. A random variable X is said to follow an F-distribution with degrees of freedom $\nu _1$ and $\nu _2$ if

$$\begin{aligned} X \sim \frac{W_1/\nu _1}{W_2/\nu _2}. \end{aligned}$$

We denote this by $X \sim F(\nu _1,\nu _2)$. The p.d.f. of X is given by (see [39, A.19])

$$\begin{aligned} f(x) = \frac{\Gamma (\frac{\nu _1+\nu _2}{2})}{\Gamma (\frac{\nu _1}{2})\Gamma (\frac{\nu _2}{2})} \left( \frac{\nu _1}{\nu _2} \right) ^{\nu _1/2} x^{\nu _1/2-1} \left( 1+\frac{\nu _1}{\nu _2}x \right) ^{-\frac{\nu _1+\nu _2}{2}} \,\text {for}\, x>0. \end{aligned}$$

(A.2)

1.3 A.3 Additional relevant results

Lemma A.10

[23, p. 13] Let ${{\varvec{x}}}$ and ${{\varvec{y}}}$ be random vectors such that ${{\varvec{x}}} {\mathop {=}\limits ^{law}} {{\varvec{y}}}$ and let $f_i(\cdot )$, $i=1,2,\dots ,m$, be measurable functions. Then,

$$\begin{aligned} \begin{pmatrix} f_1({{\varvec{x}}})&f_2({{\varvec{x}}})&\dots&f_m({{\varvec{x}}}) \end{pmatrix}^T {\mathop {=}\limits ^{law}} \begin{pmatrix} f_1({{\varvec{y}}})&f_2({{\varvec{y}}})&\dots&f_m({{\varvec{y}}}) \end{pmatrix}^T. \end{aligned}$$

The last results apply to spherical probability distributions, defined as follows (for more details regarding spherical distributions, refer to [4, 23, 31]).

Definition A.11

An $n\times 1$ random vector ${{\varvec{x}}}$ is said to have a spherical distribution if for every orthogonal $n \times n$ matrix ${{\varvec{U}}}$,

$$\begin{aligned} {{\varvec{U}}}{{\varvec{x}}} {\mathop {=}\limits ^{law}} {{\varvec{x}}}. \end{aligned}$$

Theorem A.12

(see [32, Theorem 2.1.]) Let ${{\varvec{x}}} {\mathop {=}\limits ^{law}} r{{\varvec{u}}}$ be a spherically distributed $n \times 1$ random vector with ${{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{x}}} = {{\varvec{0}}}] = 0$, where r is independent of ${{\varvec{u}}}$ with p.d.f. $h(\cdot )$. Then, the p.d.f. $g(\hat{{{\varvec{x}}}})$ of ${{\varvec{x}}}$ is given by

$$\begin{aligned} g(\hat{{{\varvec{x}}}}) = \frac{\Gamma (n/2)}{2\pi ^{n/2}} h(\Vert \hat{{{\varvec{x}}}} \Vert ) \Vert \hat{{{\varvec{x}}}} \Vert ^{1-n}. \end{aligned}$$

B Derivation of the probability density function of ${{\varvec{w}}}$

We derive the probability density function of the random vector ${{\varvec{w}}}$ defined in (3.3) following a similar line of argument as in [9]: we first derive the distribution of $\Vert {{\varvec{w}}} \Vert _2^2$ and then show that ${{\varvec{w}}}$ follows a spherical distribution, which then allows us to derive the exact distribution of ${{\varvec{w}}}$.

Theorem B.1

(Distribution of $\Vert {{\varvec{w}}}\Vert _2^2$) Suppose that Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix, with $d_e \le d \le D-d_e$. Assume that ${{\varvec{p}}}_\top \ne {{\varvec{x}}}_\top ^*$, where the subscript represents the Euclidean projection on the effective subspace. Let ${{\varvec{w}}}$ be defined in (3.3). Then,

$$\begin{aligned} \left( \frac{1}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2_2} \cdot \frac{d-d_e+1}{D-d_e}\right) \Vert {{\varvec{w}}}\Vert _2^2 \sim F(D-d_e,d-d_e+1), \end{aligned}$$

where $F(v_1,v_2)$ denotes the F-distribution with degrees of freedom $v_1$ and $v_2$.

Proof

We write ${{\varvec{w}}}$ as ${{\varvec{C}}}{{\varvec{y}}}_2^*$, where ${{\varvec{C}}} = {{\varvec{V}}}^T{{\varvec{A}}}$. We first establish three facts: a) ${{\varvec{B}}}$ defined in Theorem 2.5 and ${{\varvec{C}}}$ are independent; b) ${{\varvec{y}}}_2^*$ and ${{\varvec{C}}}$ are independent; c) ${{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{y}}}_2^* \ne {{\varvec{0}}}] = 1$.

• (a) Since ${{\varvec{V}}}$ is orthonormal, Theorem A.2 implies that ${{\varvec{C}}}$ is a Gaussian matrix. Moreover, the fact ${{\varvec{U}}}^T{{\varvec{V}}} = {{\varvec{0}}}$ implies that ${{\varvec{B}}}$ and ${{\varvec{C}}}$ are independent, see Theorem A.3.

• (b) Since ${{\varvec{y}}}_2^*$ is measurable as a function of ${{\varvec{B}}}$ (see proof [9, Lemma A.16]), ${{\varvec{y}}}_2^*$ and ${{\varvec{C}}}$ must be independent.

• (c) We have ${{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{y}}}_2^* \ne {{\varvec{0}}}] = 1 - {{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{y}}}_2^* = {{\varvec{0}}}] = 1 - {{\,\mathrm{{\mathbb {P}}}\,}}[\Vert {{\varvec{y}}}_2^* \Vert _2^2 = 0] = 1-0,$ where the last equality is due to the fact that $\Vert {{\varvec{y}}}_2^*\Vert _2^2$ follows the (appropriately scaled) inverse chi-squared distribution (Theorem 2.7), which is a continuous distribution.

Now, we apply Theorem A.6 to obtain

$$\begin{aligned} \frac{\Vert {{\varvec{w}}}\Vert _2^2}{\Vert {{\varvec{y}}}_2^* \Vert _2^2} = \frac{({{\varvec{y}}}_2^*)^T {{\varvec{C}}}^T {{\varvec{C}}} {{\varvec{y}}}_2^*}{\Vert {{\varvec{y}}}_2^* \Vert _2^2} \sim \chi ^2_{D-d_e}, \end{aligned}$$

(B.1)

which together with Theorem 2.7 yields

$$\begin{aligned} \frac{\Vert {{\varvec{w}}}\Vert _2^2}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert _2^2} \sim \frac{\chi ^2_{D-d_e}}{\chi ^2_{d-d_e+1}}, \end{aligned}$$

(B.2)

where $\chi ^2_{D-d_e}$ and $\chi ^2_{d-d_e+1}$ are independent.¹⁵ Using the definition of the F-distribution (see Definition A.9), we obtain the desired result. $\square$

Using Theorem B.1, it is straightforward to derive the p.d.f of $\Vert {{\varvec{w}}}\Vert$.

Theorem B.2

(The p.d.f. of $\Vert {{\varvec{w}}}\Vert$) Suppose that Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix, with $d_e \le d \le D-d_e$. Assume that ${{\varvec{p}}}_\top \ne {{\varvec{x}}}_\top ^*$, where the subscript represents the Euclidean projection on the effective subspace. The p.d.f. $h({\hat{w}})$ of $\Vert {{\varvec{w}}}\Vert$, with ${{\varvec{w}}}$ defined in (3.3), is given by

$$\begin{aligned} h({\hat{w}}) = \frac{2\Gamma (\frac{m+n}{2})}{\Gamma (\frac{m}{2})\Gamma (\frac{n}{2})} \cdot \frac{{\hat{w}}^{m-1}}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^m} \left( 1+\frac{{\hat{w}}^2}{\Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert ^2}\right) ^{-(m+n)/2}, \end{aligned}$$

(B.3)

where $m = D-d_e$, $n=d-d_e+1$, and where $\Gamma$ is the usual gamma function.

Proof

Let $X \sim F(D-d_e, d-d_e+1)$. Theorem B.1 implies that

$$\begin{aligned} \Vert {{\varvec{w}}}\Vert {\mathop {=}\limits ^{law}} K \sqrt{X}, \end{aligned}$$

(B.4)

where

$$\begin{aligned} K = \Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top } \Vert \sqrt{\frac{D-d_e}{d-d_e+1}}. \end{aligned}$$

(B.5)

For the p.d.f. of $\Vert {{\varvec{w}}}\Vert$, we have

$$\begin{aligned} h({\hat{w}})= & {} \frac{d}{d{\hat{w}}} {{\,\mathrm{{\mathbb {P}}}\,}}[\Vert {{\varvec{w}}}\Vert< {\hat{w}}] = \frac{d}{d{\hat{w}}} {{\,\mathrm{{\mathbb {P}}}\,}}[K\sqrt{X}< {\hat{w}}] = \frac{d}{d{\hat{w}}} {{\,\mathrm{{\mathbb {P}}}\,}}[X < {\hat{w}}^2/K^2]\nonumber \\= & {} \frac{2{\hat{w}}}{K^2} f({\hat{w}}^2/K^2), \end{aligned}$$

(B.6)

where f(x) denotes the p.d.f of an F-distributed random variable with degrees of freedom $m = D-d_e$ and $n = d-d_e+1$. By substituting (A.2) in (B.6), we obtain the desired result. $\square$

To derive the p.d.f. of ${{\varvec{w}}}$ we rely on the fact that ${{\varvec{w}}}$ has a spherical distribution (see Definition A.11), as we show next.

Theorem B.3

(${{\varvec{w}}}$ has a spherical distribution) Suppose that Assumption 2.2 holds. Let ${{\varvec{x}}}^*$ be a(ny) global minimizer of (P), ${{\varvec{p}}}\in {\mathcal {X}}$, a given vector, and ${{\varvec{A}}}$, a $D \times d$ Gaussian matrix, with $d_e \le d \le D-d_e$. Assume that ${{\varvec{p}}}_\top \ne {{\varvec{x}}}_\top ^*$, where the subscript represents the Euclidean projection on the effective subspace. The random vector ${{\varvec{w}}}$, defined in (3.3), has a spherical distribution.

Proof

Our proof is similar to the proof of Lemma A.16 in [9]. Let ${{\varvec{S}}}$ be any $(D-d_e) \times (D-d_e)$ orthogonal matrix. To prove that ${{\varvec{w}}}$ has a spherical distribution, we need to show that

$$\begin{aligned} {{\varvec{w}}} {\mathop {=}\limits ^{law}} {{\varvec{S}}}{{\varvec{w}}}. \end{aligned}$$

(B.7)

Using (2.6), we write ${{\varvec{w}}} = {{\varvec{C}}}{{\varvec{B}}}^T({{\varvec{B}}}{{\varvec{B}}}^T)^{-1}{{\varvec{z}}}^*$, where ${{\varvec{C}}} = {{\varvec{V}}}^T{{\varvec{A}}}$ and ${{\varvec{B}}}={{\varvec{U}}}^T{{\varvec{A}}}$ are Gaussian matrices independent of one another by the point a) of the proof of Theorem B.1. Let $f : {\mathbb {R}}^{Dd \times 1} \rightarrow {\mathbb {R}}^{(D-d_e) \times 1}$ be a vector-valued function defined as

$$\begin{aligned} f({{\,\mathrm{vec}\,}}[{{\varvec{C}}}^T \; {{\varvec{B}}}^T]) = {{\varvec{C}}}{{\varvec{B}}}^T({{\varvec{B}}}{{\varvec{B}}}^T)^{-1}{{\varvec{z}}}^*, \end{aligned}$$

(B.8)

where ${{\,\mathrm{vec}\,}}[{{\varvec{C}}}^T \; {{\varvec{B}}}^T]$ denotes the vector of the concatenated columns of $({{\varvec{C}}}^T \; {{\varvec{B}}}^T)$. We can express f as

$$\begin{aligned} f({{\,\mathrm{vec}\,}}[{{\varvec{C}}}^T \; {{\varvec{B}}}^T]) = \begin{pmatrix} \frac{p_1({{\varvec{C}}},{{\varvec{B}}})}{q({{\varvec{B}}})}&\frac{p_2({{\varvec{C}}},{{\varvec{B}}})}{q({{\varvec{B}}})}&\dots&\frac{p_{D-d_e}({{\varvec{C}}},{{\varvec{B}}})}{q({{\varvec{B}}})} \end{pmatrix}^T, \end{aligned}$$

where $p_i({{\varvec{C}}},{{\varvec{B}}})$ for $1 \le i \le D-d_e$ are some polynomials in the entries of ${{\varvec{C}}}$ and ${{\varvec{B}}}$ and $q({{\varvec{B}}}) = \det ({{\varvec{B}}}{{\varvec{B}}}^T)$. Since q and $p_i$’s are polynomials in Gaussian random variables, they are all measurable. Furthermore, since ${{\varvec{B}}}$ is Gaussian, by Theorem A.4, ${{\,\mathrm{{\mathbb {P}}}\,}}[q = 0] = 0$; this implies that $p_i/q$ is a measurable function for each $i = 1,2,\dots ,D-d_e$ (see [59, Theorem 4.10]).

We have

$$\begin{aligned} {{\varvec{w}}} = f({{\,\mathrm{vec}\,}}[{{\varvec{C}}}^T \; {{\varvec{B}}}^T]) \,\text {and}\, {{\varvec{S}}}{{\varvec{w}}} = f({{\,\mathrm{vec}\,}}[({{\varvec{S}}}{{\varvec{C}}})^T \; {{\varvec{B}}}^T]). \end{aligned}$$

(B.9)

From Theorem A.2 it follows that ${{\varvec{C}}} {\mathop {=}\limits ^{law}} {{\varvec{S}}}{{\varvec{C}}}$; hence ${{\,\mathrm{vec}\,}}[{{\varvec{C}}}^T \; {{\varvec{B}}}^T] {\mathop {=}\limits ^{law}} {{\,\mathrm{vec}\,}}[({{\varvec{S}}}{{\varvec{C}}})^T \; {{\varvec{B}}}^T]$. We can now apply Lemma A.10 to conclude that

$$\begin{aligned} {{\varvec{w}}} = f({{\,\mathrm{vec}\,}}[{{\varvec{C}}}^T \; {{\varvec{B}}}^T]) {\mathop {=}\limits ^{law}} f({{\,\mathrm{vec}\,}}[({{\varvec{S}}}{{\varvec{C}}})^T \; {{\varvec{B}}}^T]) = {{\varvec{S}}}{{\varvec{w}}}. \end{aligned}$$

(B.10)

$\square$

We are now ready to derive the p.d.f. of ${{\varvec{w}}}$, and hence prove Theorem 3.3.

Proof of Theorem 3.3

We show that the p.d.f. of ${{\varvec{w}}}$ is given by (3.6). The identification with the t-distribution follows from (A.1). Let us first show that ${{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{w}}} = {{\varvec{0}}}] = 0$. Let $X \sim F(D-d_e,d-d_e+1)$. We have

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{w}}} = {{\varvec{0}}}] = {{\,\mathrm{{\mathbb {P}}}\,}}[\Vert {{\varvec{w}}}\Vert ^2 = 0] = {{\,\mathrm{{\mathbb {P}}}\,}}[X = 0], \end{aligned}$$

(B.11)

where in the last equality we applied Theorem B.1. Since the F-distributed X is a continuous random variable, the last probability in (B.11) is equal to zero.

Since ${{\,\mathrm{{\mathbb {P}}}\,}}[{{\varvec{w}}} = {{\varvec{0}}}] = 0$ and ${{\varvec{w}}}$ has a spherical distribution (Theorem B.3), Theorem A.12 implies that the p.d.f. $g({{\varvec{{\bar{w}}}}})$ of ${{\varvec{w}}}$ satisfies

$$\begin{aligned} g({{\varvec{{\bar{w}}}}}) = \frac{\Gamma (m/2)}{2\pi ^{m/2}} h(\Vert {{\varvec{{\bar{w}}}}} \Vert ) \Vert {{\varvec{{\bar{w}}}}} \Vert ^{1-m}, \end{aligned}$$

(B.12)

where $h(\cdot )$ denotes the p.d.f. of $\Vert {{\varvec{w}}}\Vert$. By substituting (B.3) into (B.12), we obtain the desired result. $\square$

C Proof of Theorem 3.8 and Theorem 3.9

A crucial Lemma is given first.

Lemma C.1

In the conditions of Theorem 3.8, we have

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge I({{\varvec{p}}},\Delta ), \end{aligned}$$

(C.1)

where $\Delta := \Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top }\Vert$ and

$$\begin{aligned} I({{\varvec{p}}},\Delta ) := \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \prod _{i=d_e+1}^D \frac{1}{\sqrt{2\pi }} \int _{s(-1-p_i)/\Delta }^{s(1-p_i)/\Delta }e^{-x^2/2} dx \right) s^{n-1} e^{-s^2/2} ds.\nonumber \\ \end{aligned}$$

(C.2)

Proof

Theorem 3.7 implies that

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}})\,\text {is successful}\,] \ge {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}}-{{\varvec{p}}}_{d_e+1:D} \le {{\varvec{w}}} \le {{\varvec{1}}}-{{\varvec{p}}}_{d_e+1:D}], \end{aligned}$$

where ${{\varvec{w}}}$ follows a $(D-d_e)$-dimensional t-distribution with parameters $n= d-d_e+1$ and ${{\varvec{\Sigma }}} = (\Delta ^2/n){{\varvec{I}}}$. According to [31, p. 133],

$$\begin{aligned} {{\varvec{w}}} {\mathop {=}\limits ^{law}} \frac{\Delta }{s} \begin{pmatrix} Z_1 \\ \vdots \\ Z_m \end{pmatrix}, \end{aligned}$$

(C.3)

with $s \sim \sqrt{\chi ^2_{n}}$, $m = D-d_e$ and $Z_1, \dots , Z_m$ i.i.d standard Gaussian random variables. Then, (C.3) yields

$$\begin{aligned}&{{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge {{\,\mathrm{{\mathbb {P}}}\,}}[-{{\varvec{1}}}-{{\varvec{p}}}_{d_e+1:D} \le {{\varvec{w}}} \le {{\varvec{1}}}-{{\varvec{p}}}_{d_e+1:D}] \nonumber \\&\quad = {{\,\mathrm{{\mathbb {P}}}\,}}\left[ \frac{s}{\Delta }(-1-p_{d_e+1}) \le Z_1 \le \frac{s}{\Delta }(1-p_{d_e+1}), \dots , \frac{s}{\Delta }(-1-p_D) \le Z_m \le \frac{s}{\Delta }(1-p_D)\right] ,\nonumber \\ \end{aligned}$$

(C.4)

which can be written as (see [19, p. 1])

$$\begin{aligned} \int _{0}^{\infty } G({{\varvec{p}}},\Delta ,s) h(s) ds, \end{aligned}$$

(C.5)

where

$$\begin{aligned} \begin{aligned} G({{\varvec{p}}},\Delta ,s)&= \int _{s(-1-p_{d_e+1})/\Delta }^{s(1-p_{d_e+1})/\Delta } \dots \int _{s(-1-p_D)/\Delta }^{s(1-p_D)/\Delta } \frac{1}{(2\pi )^{m/2}} e^{-\frac{1}{2}(x_1^2 + \cdots + x_m^2)} dx_1 \dots dx_m \\&= \prod _{i=d_e+1}^D \frac{1}{\sqrt{2\pi }} \int _{s(-1-p_{i})/\Delta }^{s(1-p_{i})/\Delta }e^{-x^2/2} dx, \end{aligned} \end{aligned}$$

(C.6)

and where h(s) is the pdf of s given by

$$\begin{aligned} h(s) = \frac{1}{2^{\frac{n}{2}-1} \Gamma (\frac{n}{2})} s^{n-1} e^{-s^2/2}. \end{aligned}$$

(C.7)

By combining (C.4) – (C.7), we obtain (C.1)–(C.2). $\square$

It is easier to show Theorem 3.9 first, when ${{\varvec{p}}} = {{\varvec{0}}}$.

1.1 C.1 Proof of Theorem 3.9

The next result is a direct corollary of Lemma C.1 when ${{\varvec{p}}} = {{\varvec{0}}}$, allowing us to replace $I({{\varvec{p}}},\Delta )$ in (C.1) with a new integral $J_{m,n}(\Delta )$ that will be easier to manipulate.

Corollary C.2

In the conditions and notation of Lemma C.1, let ${{\varvec{p}}} = {{\varvec{0}}}$. Then

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge J_{m,n}(\Vert {{\varvec{x}}}_{\top }^*\Vert ), \end{aligned}$$

(C.8)

where

$$\begin{aligned} J_{m,n}(\Delta ) := \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \sqrt{\frac{2}{\pi }} \int _{0}^{s/\Delta } e^{-x^2/2} dx \right) ^m s^{n-1} e^{-s^2/2} ds. \end{aligned}$$

(C.9)

Proof

Let ${{\varvec{p}}}={{\varvec{0}}}$. Then Lemma C.1 implies that ${{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge I({{\varvec{0}}},\Vert {{\varvec{x}}}_{\top }^*\Vert ),$ where

$$\begin{aligned} \begin{aligned} I({{\varvec{0}}},\Vert {{\varvec{x}}}_{\top }^*\Vert )&= \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \prod _{i=d_e+1}^D \frac{1}{\sqrt{2\pi }} \int _{-s/\Vert {{\varvec{x}}}_{\top }^*\Vert }^{s/\Vert {{\varvec{x}}}_{\top }^*\Vert }e^{-x^2/2} dx \right) s^{n-1} e^{-s^2/2} ds \\&= \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \sqrt{\frac{2}{\pi }} \int _{0}^{s/\Vert {{\varvec{x}}}_{\top }^*\Vert } e^{-x^2/2} dx \right) ^m s^{n-1} e^{-s^2/2} ds \\&= J_{m,n}(\Vert {{\varvec{x}}}_{\top }^*\Vert ). \\ \end{aligned} \end{aligned}$$

(C.10)

$\square$

We need to introduce the following three results on the integral $J_{m,n}(\Delta )$ in (C.9).

Lemma C.3

The integral $J_{m,n}(\Delta )$ in (C.9) is a monotonically decreasing function of $\Delta$.

Proof

Let $\Delta _1, \Delta _2$ be any positive reals that satisfy $\Delta _1 \le \Delta _2$. We need to show that $J_{m,n}(\Delta _1) \ge J_{m,n}(\Delta _2)$. This relation follows immediately from the observation that, for any $s \ge 0$,

$$\begin{aligned} \sqrt{\frac{2}{\pi }} \int _{0}^{s/\Delta _1} e^{-x^2/2} dx \ge \sqrt{\frac{2}{\pi }} \int _{0}^{s/\Delta _2} e^{-x^2/2} dx \end{aligned}$$

since the integrand is positive. $\square$

Lemma C.4

The integral $J_{m,n}(\Delta )$ defined in (C.9) satisfies $J_{m,n}(\Delta ) \le 1$ for all $\Delta > 0$.

Proof

Note that, for any $s \ge 0$, we have

$$\begin{aligned} \sqrt{\frac{2}{\pi }} \int _{0}^{s/\Delta } e^{-x^2/2} dx \le \sqrt{\frac{2}{\pi }} \int _{0}^{\infty } e^{-x^2/2} dx = 1. \end{aligned}$$

Hence,

$$\begin{aligned} J_{m,n}(\Delta ) \le \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } s^{n-1} e^{-s^2/2} ds = 1. \end{aligned}$$

$\square$

The following theorem provides an asymptotic expansion of $J_{m,n}(\Delta )$ for large m, that has polynomial dependence on m.

Theorem C.5

Let $J_{m,n}(\Delta )$ be the integral defined in (C.9). Let n and $\Delta$ be fixed and let $r = (n+\Delta ^2-2)/2$. If $r \ne 0$ then, for large m,

$$\begin{aligned} J_{m,n}(\Delta )= & {} \frac{C(n,\Delta )}{(m+1)^{\Delta ^2}} \left( (\log (m+1))^r - \frac{r}{2} \log (\log (m+1)) \cdot (\log (m+1))^{r-1}\right. \nonumber \\&\bigg . + O( (\log (m+1))^{r-1}) \bigg ), \end{aligned}$$

(C.11)

where

$$\begin{aligned} C(n,\Delta ) = \pi ^{\frac{\Delta ^2}{2}}\Delta ^n \frac{ \Gamma (\Delta ^2)}{\Gamma (n/2)}. \end{aligned}$$

If $r=0$, then $J_{m,n}(\Delta ) = J_{m,1}(1) = 1/(m+1)$.

Proof

The proof of this lemma is similar to the derivations in [60, Section 2, Chapter 2], and is deferred to the end of this appendix. $\square$

Proof of Theorem 3.9

Corollary C.2 implies that

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge I({{\varvec{0}}},\Vert {{\varvec{x}}}_{\top }^*\Vert ) \ge J_{m,n}(\Vert {{\varvec{x}}}_{\top }^*\Vert ). \end{aligned}$$

(C.12)

By definition of ${{\varvec{x}}}_\top ^*$, there exists ${{\varvec{x}}}^* \in G$ such that ${{\varvec{x}}}_\top ^* = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}^*$ with ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e}; \; {{\varvec{0}}}]$. Then ${{\varvec{x}}}^*_\top = [{{\varvec{x}}}^*_{1:d_e}; {{\varvec{0}}}]$ which implies $\Vert {{\varvec{x}}}_{\top }^*\Vert \le \sqrt{d_e}$. By monotonic decrease of $J_{m,n}$ (see Lemma C.3), (C.12) yields

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge J_{m,n}(\sqrt{d_e}) \end{aligned}$$

for all ${{\varvec{x}}}^*, {{\varvec{p}}} \in {\mathcal {X}}$ such that ${{\varvec{x}}}_{\top }^* \ne {{\varvec{p}}}_{\top }$. If ${{\varvec{x}}}_{\top }^* = {{\varvec{p}}}_{\top }$, then

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] = 1 \ge J_{m,n}(\sqrt{d_e}), \end{aligned}$$

where the inequality follows from Lemma C.4. Thus, (3.12) is satisfied for $\tau _{{{\varvec{0}}}} = J_{m,n}(\sqrt{d_e})$, and (3.15) follows from Theorem C.5. $\square$

1.2 C.2 Proof of Theorem 3.8

Unlike the case ${{\varvec{p}}} = {{\varvec{0}}}$, we cannot rewrite directly the integral $I({{\varvec{p}}},\Delta )$ in terms if the integral $J_{m,n}(\Delta )$ (i.e., Corollary C.2 does not hold) for ${{\varvec{p}}} \in {\mathcal {X}}$ arbitrary. However, we derive a lower bound on $I({{\varvec{p}}},\Delta )$ in terms of the simpler integral $J_{m,n}(\Delta )$ that is valid for all ${{\varvec{p}}} \in {\mathcal {X}}$.

Lemma C.6

For any ${{\varvec{p}}} \in {\mathcal {X}}$ and for any $\Delta > 0$, we have

$$\begin{aligned} I({{\varvec{p}}},\Delta ) \ge \frac{1}{2^m}J_{m,n}(\Delta /2). \end{aligned}$$

Proof

Let us define the function

$$\begin{aligned} g(z,\Delta ,s) = \frac{1}{\sqrt{2\pi }} \int _{s(-1-z)/\Delta }^{s(1-z)/\Delta }e^{-x^2/2} dx, \end{aligned}$$

(C.13)

and note that

$$\begin{aligned} I({{\varvec{p}}},\Delta ) = \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \prod _{i=d_e+1}^D g(p_i,\Delta ,s)\right) s^{n-1} e^{-s^2/2} ds. \end{aligned}$$

(C.14)

Next we find the minimizers of $g(z,\Delta ,s)$ over $z \in [-1,1]$. Introducing the notation $l(z,\Delta ,s) := s(1-z)/\Delta$, and using Leibniz integral rule, we obtain

$$\begin{aligned} \begin{aligned} \frac{d g(z,\Delta ,s)}{d z}&= e^{\frac{-l(z,\Delta ,s)^2}{2}}\frac{d (l(z,\Delta ,s))}{d z}-e^{\frac{-l(-z,\Delta ,s)^2}{2}}\frac{d(-l(-z,\Delta ,s))}{d z} \\&= e^{\frac{-s^2(1-z)^2}{2\Delta ^2}}\left( \frac{-s}{\Delta }\right) - e^{\frac{-s^2(-1-z)^2}{2\Delta ^2}}\left( \frac{-s}{\Delta }\right) \\&= \frac{s}{\Delta }e^{-\frac{s^2}{2\Delta ^2}(1+z^2)}\left( e^{-\frac{s^2z}{\Delta ^2}}-e^{\frac{s^2z}{\Delta ^2}}\right) . \end{aligned} \end{aligned}$$

(C.15)

Hence, $d g(z,\Delta ,s)/d z$ is equal to zero if and only if

$$\begin{aligned} e^{-\frac{s^2z}{\Delta ^2}}-e^{\frac{s^2z}{\Delta ^2}} = 0, \end{aligned}$$

(C.16)

which occurs only at $z = 0$. The sign of $d g(z,\Delta ,s)/d z$ changes from negative to positive at $z=0$ implying that the function is concave and so $g(z,\Delta ,s)$ attains its maximum at $z=0$ and its minimum at the boundaries. Since $g(z,\Delta ,s)$ is symmetric around $z=0$, the minimum is attained at $z = \pm 1$. Thus, for all $z \in [-1,1]$,

$$\begin{aligned} g(z,\Delta ,s) \ge g(-1,\Delta , s) = \frac{1}{\sqrt{2\pi }} \int _{-l(1,\Delta ,s)}^{l(-1,\Delta ,s)}e^{-x^2/2} dx = \frac{1}{\sqrt{2\pi }} \int _{0}^{\frac{2s}{\Delta }}e^{-x^2/2} dx.\nonumber \\ \end{aligned}$$

(C.17)

By combining (C.17) with (C.14), we obtain

$$\begin{aligned} \begin{aligned} I({{\varvec{p}}},\Delta )&\ge \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \prod _{i=d_e+1}^D \frac{1}{\sqrt{2\pi }} \int _{0}^{\frac{2s}{\Delta }}e^{-x^2/2} dx \right) s^{n-1} e^{-s^2/2} ds \\&= \frac{1}{2^m}\cdot \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \sqrt{\frac{2}{\pi }} \int _{0}^{\frac{2s}{\Delta }} e^{-x^2/2} dx \right) ^m s^{n-1} e^{-s^2/2} ds \\&= \frac{1}{2^m}J_{m,n}(\Delta /2). \end{aligned} \end{aligned}$$

(C.18)

$\square$

Proof of Theorem 3.8

Lemmas C.1 and C.6 provide

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge I({{\varvec{p}}},\Delta ) \ge \frac{1}{2^m} J_{m,n}(\Delta /2). \end{aligned}$$

(C.19)

Let us now show that $\Delta \le 2\sqrt{d_e}$ for all ${{\varvec{x}}}^*,{{\varvec{p}}}\in [-1,1]^D$. Since ${{\varvec{U}}} = [{{\varvec{I}}}_{d_e} \; {{\varvec{0}}}]^T$, for any global minimizer ${{\varvec{x}}}^*$, we have ${{\varvec{x}}}_{\top }^* = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{x}}}^* = [{{\varvec{x}}}_{1:d_e}^*; \; {{\varvec{0}}}]$, and for any ${{\varvec{p}}}$, we have ${{\varvec{p}}}_{\top } = {{\varvec{U}}} {{\varvec{U}}}^T {{\varvec{p}}} = [{{\varvec{p}}}_{1:d_e}; \; {{\varvec{0}}}]$. Since ${{\varvec{x}}}^*,{{\varvec{p}}} \in [-1,1]^D$, there holds $\Vert {{\varvec{x}}}_{\top }^*\Vert \le \sqrt{d_e}$ and $\Vert {{\varvec{p}}}_{\top }\Vert \le \sqrt{d_e}$, and hence, $\Delta = \Vert {{\varvec{x}}}_{\top }^* - {{\varvec{p}}}_{\top } \Vert \le \Vert {{\varvec{x}}}_{\top }^*\Vert + \Vert {{\varvec{p}}}_{\top }\Vert \le 2\sqrt{d_e}.$

Using the fact that $J_{m,n}(\Delta )$ is a monotonically decreasing function (see Lemma C.3), (C.19) yields

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}}) \,\text {is successful}\,] \ge \frac{1}{2^m} J_{m,n}(\sqrt{d_e}) \end{aligned}$$

(C.20)

for all ${{\varvec{x}}}^*, {{\varvec{p}}} \in {\mathcal {X}}$ such that ${{\varvec{x}}}_{\top }^* \ne {{\varvec{p}}}_{\top }$. If ${{\varvec{x}}}_{\top }^* = {{\varvec{p}}}_{\top }$, then

$$\begin{aligned} {{\,\mathrm{{\mathbb {P}}}\,}}[({{\mathrm{RP}}{\mathcal {X}}})\,\text {is successful}\,] = 1 \ge \frac{1}{2^m}J_{m,n}(\sqrt{d_e}), \end{aligned}$$

where the inequality follows from Lemma C.4. Thus, (3.12) is satisfied for $\tau = J_{m,n}(\sqrt{d_e})/2^m$, and (3.13) follows from Theorem C.5. $\square$

1.3 C.3 Proof of Theorem C.5

We rewrite $J_{m,n}(\Delta )$ as follows

$$\begin{aligned} \begin{aligned} J_{m,n}(\Delta )&= \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \sqrt{\frac{2}{\pi }} \int _{0}^{s/\Delta } e^{-x^2/2} dx \right) ^m s^{n-1} e^{-s^2/2} ds \\&= \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } \left( \frac{2}{\sqrt{\pi }} \int _{0}^{\frac{s}{\sqrt{2}\Delta }} e^{-x^2} dx \right) ^m s^{n-1} e^{-s^2/2} ds \\&= \frac{1}{2^{\frac{n}{2}-1}\Gamma (\frac{n}{2})} \int _0^{\infty } {{\,\mathrm{{\mathrm{erf}}}\,}}^m\left( \frac{s}{\sqrt{2}\Delta }\right) s^{n-1} e^{-s^2/2} ds, \end{aligned} \end{aligned}$$

where ${{\,\mathrm{{\mathrm{erf}}}\,}}(\cdot )$ denotes the usual error function. After making an appropriate transformation, the integral becomes

$$\begin{aligned} J_{m,n}(\Delta ) = \frac{2 \Delta ^n}{\Gamma (\frac{n}{2})} \int _0^{\infty } {{\,\mathrm{{\mathrm{erf}}}\,}}^m(s) s^{n-1} e^{-\Delta ^2s^2} ds \end{aligned}$$

In [60, Section 2, Chapter 2], Wong derives an asymptotic expansion of a similar integral; our derivations are based on his method.

As s varies from 0 to $\infty$, ${{\,\mathrm{{\mathrm{erf}}}\,}}(s)$ increases monotonically from 0 to 1. So, for m large almost all the mass of the integrand is concentrated at $\infty$. We make the substitution $e^{-t} = {{\,\mathrm{{\mathrm{erf}}}\,}}(s)$ to bring the integral to the form:

$$\begin{aligned} J_{m,n}(\Delta ) = \frac{\sqrt{\pi }\Delta ^n }{\Gamma (\frac{n}{2})} \int _{0}^{\infty } e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt, \end{aligned}$$

(C.21)

where $K = 1-\Delta ^2$ and $s(t) = {{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(e^{-t})$. Due to monotonicity of ${{\,\mathrm{{\mathrm{erf}}}\,}}$, s(t) is uniquely defined for every t. As ${{\,\mathrm{{\mathrm{erf}}}\,}}$ varies from 0 to 1, t varies from $\infty$ to 0. So the mass of the transformed integrand is now concentrated around 0.

We will derive the asymptotic expansion for (C.21) in three steps:

• 1. First, we will derive the asymptotic expansion of $e^{Ks(t)^2} s(t)^{n-1}$.

• 2. Then, we will show that, for any $0<c<1$, the integral

  $$\begin{aligned} \int _c^{\infty } e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt \end{aligned}$$

  is exponentially small.

• 3. Finally, we will derive the asymptotic expansion of

  $$\begin{aligned} \int _{0}^c e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt. \end{aligned}$$

1.3.1 Step 1

Lemma C.7

(see [60, Lemma 1, p. 67]) For small positive t, $s(t) = {{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(e^{-t})$ satisfies

$$\begin{aligned} s(t)^2= & {} -\log (t) - \frac{1}{2} \log (-\log (t)) - \log (\sqrt{\pi }) + \frac{\log (-\log (t))}{4(-\log (t))} - \frac{\log (e/\sqrt{\pi })}{2(-\log (t))} \\&+ O\left( \frac{\log ^2(-\log (t))}{(\log (t))^2} \right) . \end{aligned}$$

Proof

The asymptotic expansion of ${{\,\mathrm{{\mathrm{erf}}}\,}}(s)$ at infinity is given by

$$\begin{aligned} {{\,\mathrm{{\mathrm{erf}}}\,}}(s) \sim 1 - \frac{e^{-s^2}}{\sqrt{\pi }s}\left( 1- \frac{1}{2s^2} + \frac{3}{4s^4} - \cdots \right) \end{aligned}$$

By writing $1 - e^{-t} = 1-{{\,\mathrm{{\mathrm{erf}}}\,}}(s)$ and using Taylor’s expansion for $e^{-t}$ at 0, we obtain

$$\begin{aligned} t(1+O(t)) = \frac{e^{-s^2}}{\sqrt{\pi }s}\left( 1- \frac{1}{2s^2} + \frac{3}{4s^4} - \cdots \right) . \end{aligned}$$

By taking logs on both sides and using the Taylor’s expansion for $\log (1+x)$, we have

$$\begin{aligned} \log (t) + O(t) = -s^2-\log (\sqrt{\pi }) - \log (s) - \frac{1}{2s^2} + O\left( \frac{1}{s^4}\right) . \end{aligned}$$

(C.22)

The dominant terms are $\log (t)$ and $s^2$, hence

$$\begin{aligned} s^2 \sim -\log (t), \,\text {as}\, t \rightarrow 0^{+}. \end{aligned}$$

(C.23)

To obtain higher order approximations, we write

$$\begin{aligned} s(t)^2 = -\log (t) + \epsilon _1(t) \end{aligned}$$

and substitute this into (C.22). We have

$$\begin{aligned} \begin{aligned} \log (t) + O(t)&= \log (t)-\epsilon _1(t) - \log (\sqrt{\pi }) - \frac{1}{2}\log (-\log (t)) -\frac{1}{2}\log \left( 1+ \frac{\epsilon _1(t)}{-\log (t)} \right) \\&\quad + O\left( \frac{1}{-\log (t)+\epsilon _1(t)} \right) \end{aligned}\nonumber \\ \end{aligned}$$

(C.24)

Note that by (C.23), as $t \rightarrow 0^{+}$

$$\begin{aligned} \frac{\epsilon _1(t)}{-\log (t)} \rightarrow 0. \end{aligned}$$

(C.25)

By using (C.25) in (C.24), we obtain

$$\begin{aligned} \epsilon _1(t) = - \frac{1}{2}\log (-\log (t))- \log (\sqrt{\pi }) + o(1). \end{aligned}$$

(C.26)

To obtain the following leading terms in the approximation we write

$$\begin{aligned} s^2(t) = -\log (t) - \frac{1}{2}\log (-\log (t))- \log (\sqrt{\pi }) + \epsilon _2(t) \end{aligned}$$

(C.27)

and repeat the above procedure. We substitute (C.27) into (C.22) and after a little manipulation obtain

$$\begin{aligned} O(t)= & {} -\epsilon _2(t) -\frac{1}{2} \log \left( 1 - \frac{1}{2} \frac{\log (-\log (t))}{-\log (t)} - \frac{\log (\sqrt{\pi })}{-\log (t)} + \frac{\epsilon _2(t)}{-\log (t)} \right) \nonumber \\&-\frac{1}{2} \cdot \frac{1}{-\log (t)} \cdot \frac{1}{1-\frac{1}{2}\frac{\log (-\log (t))}{-\log (t)} - \frac{\log (\sqrt{\pi })}{-\log (t)} + \frac{\epsilon _2(t)}{-\log (t)}} + O((-\log (t))^{2})\nonumber \\ \end{aligned}$$

(C.28)

Using the fact (by (C.26)) that $\epsilon _2(t) = o(1)$ and Taylor’s expansions for $\log (1+x)$ and $1/(1-x)$, we obtain

$$\begin{aligned} \begin{aligned} O(t)&= -\epsilon _2(t) - \frac{1}{2}\left( - \frac{1}{2} \frac{\log (-\log (t))}{-\log (t)} + O\left( \frac{1}{-\log (t)} \right) \right) \\&\quad -\frac{1}{2} \cdot \frac{1}{-\log (t)} \left( 1 + O\left( \frac{\log (-\log (t))}{-\log (t)} \right) \right) , \end{aligned} \end{aligned}$$

which yields

$$\begin{aligned} \epsilon _2(t) = \frac{\log (-\log (t))}{4(-\log (t))} + O\left( \frac{1}{-\log (t)} \right) . \end{aligned}$$

(C.29)

To obtain the following leading terms in the expansion of $\epsilon _2(t)$, we use (C.29) in (C.28) leaving the first term ($-\epsilon _2(t)$) as is:

$$\begin{aligned} \begin{aligned} O(t)&= -\epsilon _2(t) -\frac{1}{2} \log \left( 1 - \frac{1}{2} \frac{\log (-\log (t))}{-\log (t)} - \frac{\log (\sqrt{\pi })}{-\log (t)} + O\left( \frac{\log (-\log (t))}{(-\log (t))^2}\right) \right) \\&\quad -\frac{1}{2} \cdot \frac{1}{-\log (t)} \cdot \frac{1}{1-\frac{1}{2}\frac{\log (-\log (t))}{-\log (t)} - \frac{\log (\sqrt{\pi })}{-\log (t)} + O\left( \frac{\log (-\log (t))}{(-\log (t))^2}\right) } + O((-\log (t))^{2}) \end{aligned} \end{aligned}$$

Now, using Taylor’s expansions for $\log (1+x)$ and $1/(1-x)$, we obtain

$$\begin{aligned} \begin{aligned} O(t)&= -\epsilon _2(t) - \frac{1}{2}\left( - \frac{1}{2} \frac{\log (-\log (t))}{-\log (t)} - \frac{\log (\sqrt{\pi })}{-\log (t)} + O\left( \frac{\log ^2(-\log (t))}{(-\log (t))^2}\right) \right) \\&\quad -\frac{1}{2} \cdot \frac{1}{-\log (t)} \left( 1 + O\left( \frac{\log (-\log (t))}{-\log (t)} \right) \right) , \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \epsilon _2(t) = \frac{\log (-\log (t))}{4(-\log (t))} - \frac{\log (e/\sqrt{\pi })}{2(-\log (t))} + O\left( \frac{\log ^2(-\log (t))}{(-\log (t))^2} \right) . \end{aligned}$$

$\square$

Corollary C.8

Let $l(t) = -\log (t)$. Then, as $t \rightarrow 0^{+}$,

$$\begin{aligned} \begin{aligned} e^{Ks(t)^2}s(t)^{n-1}&= e^{Kl(t)}\pi ^{-K/2} l(t)^{\frac{n-1-K}{2}} \left( 1 - \left( \frac{n-1-K}{4}\right) \frac{\log (l(t))}{l(t)} \right. - \frac{\log (e^{K/2}\pi ^{\frac{n-1-K}{4}})}{l(t)} \\&\quad \left. + O{\left( \frac{\log ^2(l(t))}{l(t)^2}\right) } \right) \end{aligned} \end{aligned}$$

(C.30)

Proof

From Lemma C.7 it follows that

$$\begin{aligned} e^{Ks(t)^2} = e^{Kl(t)}l(t)^{-K/2}\pi ^{-K/2}\exp \left( \frac{K\log (l(t))}{4l(t)} - \frac{K\log (e/\sqrt{\pi })}{2l(t)} + O\left( \frac{\log ^2(l(t))}{l(t)^2} \right) \right) . \end{aligned}$$

By using Taylor’s expansion for $\exp$ we obtain

$$\begin{aligned} e^{Ks(t)^2} = e^{Kl(t)}l(t)^{-K/2}\pi ^{-K/2}\left( 1+\frac{K\log (l(t))}{4l(t)} - \frac{K\log (e/\sqrt{\pi })}{2l(t)} + O\left( \frac{\log ^2(l(t))}{l(t)^2}\right) \right) .\nonumber \\ \end{aligned}$$

(C.31)

Similarly, using Lemma C.7 and binomial expansion, for $s(t)^{n-1}$, we have

$$\begin{aligned} (s(t)^2)^{\frac{n-1}{2}} = l(t)^{\frac{n-1}{2}}\left( 1- \frac{(n-1)\log (l(t))}{4l(t)}-\frac{(n-1)\log (\sqrt{\pi })}{2l(t)} + O\left( \frac{\log ^2(l(t))}{l(t)^2}\right) \right) \nonumber \\ \end{aligned}$$

(C.32)

By multiplying the leading terms in (C.31) and (C.32), we obtain the desired result. $\square$

1.3.2 Step 2

Let $0<c<1$. We will show that, for large m,

$$\begin{aligned} \int _c^{\infty } e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt = O\left( \frac{e^{-c(m+n)}}{m+n}\right) . \end{aligned}$$

Let ${{\,\mathrm{{\mathrm{erf}}}\,}}(s) = e^{-t}$. First, we establish that

$$\begin{aligned} \text {there exists a positive constant}\, \text {A such that}\, s(t) = {{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(e^{-t}) \le Ae^{-t} \,\text {for all}\, t \in [c,\infty ).\nonumber \\ \end{aligned}$$

(C.33)

Note that (C.33) holds if there exists an $A>0$ such that ${{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(x) \le Ax$ for all $x \in [0,e^{-c}]$. To prove this, we apply the Mean Value Theorem to ${{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}$ over [0, x]; by the Mean Value Theorem there exists $y\in (0,x)$ such that

$$\begin{aligned} \frac{{{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(x) - {{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(0)}{x-0} = ({{\,\mathrm{{\mathrm{erf}}}\,}}^{-1})^{'}(y) \end{aligned}$$

(C.34)

Using the following formula for the derivative of the inverse of the error function [1, Eq. (2.4), p. 192],

$$\begin{aligned} ({{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(x))' = \frac{\sqrt{\pi }}{2} e^{({{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(x))^2}, \end{aligned}$$

from (C.34), we obtain

$$\begin{aligned} \frac{{{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(x)}{x} = \frac{\sqrt{\pi }}{2} e^{({{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(y))^2}. \end{aligned}$$

(C.35)

Since ${{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}$ is an increasing function and $y < x \le e^{-c}$, (C.35) gives

$$\begin{aligned} {{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(x) \le \frac{\sqrt{\pi }}{2} e^{({{\,\mathrm{{\mathrm{erf}}}\,}}^{-1}(e^{-c}))^2} x, \end{aligned}$$

which proves (C.33).

Now, since s(t) is a monotonically decreasing function with $s(\infty ) = 0$, we have¹⁶

$$\begin{aligned} e^{Ks(t)^2} \le \max \{1,e^{Ks(c)^2}\} \,\text {for}\, t \ge c. \end{aligned}$$

(C.36)

Using (C.33) and (C.36), we finally obtain

$$\begin{aligned} \begin{aligned} \int _c^{\infty } e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt&\le A^{n-1} \max \{1,e^{Ks(c)^2}\} \int _c^{\infty } e^{-(m+n)t} dt \\&= A^{n-1} \max \{1,e^{Ks(c)^2}\} \frac{e^{-c(m+n)}}{m+n}. \end{aligned} \end{aligned}$$

1.3.3 Step 3

Let $L(\lambda ,\mu ,z)$ and $G(\lambda ,\mu ,z)$ be defined as follows

$$\begin{aligned} L(\lambda ,\mu ,z) = \int _0^c t^{\lambda - 1} (-\log (t))^{\mu } e^{-zt} dt \end{aligned}$$

and

$$\begin{aligned} G(\lambda ,\mu ,z) = \int _0^c t^{\lambda - 1} (-\log (t))^{\mu } \log (-\log (t)) e^{-zt} dt, \end{aligned}$$

where $0<c<1$. The expansion of $e^{Ks(t)^2}s(t)^{n-1}$ in Theorem C.8 gives

$$\begin{aligned} \begin{aligned} \int _{0}^{c} e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt&= \pi ^{-K/2}L\left( 1-K,\frac{n-1-K}{2},m+1\right) \\&\quad - \pi ^{-K/2} \left( \frac{n-1-K}{4}\right) G\left( 1-K,\frac{n-3-K}{2},m+1 \right) \\&\quad - \pi ^{-K/2} \log (e^{K/2}\pi ^{\frac{n-1-K}{4}}) L\left( 1-K,\frac{n-3-K}{2},m+1\right) + \cdots , \end{aligned} \end{aligned}$$

(C.37)

The following theorem provides the asymptotic expansion for $L(\lambda ,\mu ,z)$.

Theorem C.9

(see [60, Theorem 2, p. 70]) Let $0<c<1$ and let $\lambda$ and $\mu$ be any real numbers with $\lambda > 0$. We have

$$\begin{aligned} L(\lambda ,\mu ,z) \sim z^{-\lambda }(\log (z))^{\mu } \sum _{r=0}^{\infty } (-1)^r \left( {\begin{array}{c}\mu \\ r\end{array}}\right) \Gamma ^{(r)}(\lambda ) (\log (z))^{-r} \end{aligned}$$

as $z \rightarrow \infty$, where $\Gamma ^{(r)}$ denotes the rth derivative of the gamma function.

In the following theorem we derive the asymptotic expansion for $G(\lambda ,\mu ,z)$ based on the proof of [60, Theorem 2, p. 70].

Theorem C.10

Let $0<c<1$ and let $\lambda$ and $\mu$ be any real numbers with $\lambda > 0$. We have

$$\begin{aligned} \begin{aligned}&G(\lambda ,\mu ,z) \sim z^{-\lambda }(\log (z))^{\mu } \log (\log (z)) \sum _{r=0}^{\infty } (-1)^r \left( {\begin{array}{c}\mu \\ r\end{array}}\right) \Gamma ^{(r)}(\lambda ) (\log (z))^{-r} \\&\quad + z^{-\lambda } (\log (z))^{\mu } \sum _{r=1}^{\infty } a_r \Gamma ^{(r)} (\lambda ) (\log (z))^{-r}, \end{aligned} \end{aligned}$$

as $z \rightarrow \infty$, where

$$\begin{aligned} a_r = -\sum _{i=0}^{r-1} \left( {\begin{array}{c}\mu \\ i\end{array}}\right) \frac{(-1)^i}{r-i} \,\text {for}\, r = 1,2,\dots . \end{aligned}$$

(C.38)

Proof

With the substitution $u = zt$, we obtain

$$\begin{aligned} \begin{aligned} G(\lambda ,\mu ,z)&= z^{-\lambda }\int _{0}^{cz} u^{\lambda - 1} (\log (z) - \log (u))^{\mu } \log (\log (z)-\log (u)) e^{-u} du \\&= z^{-\lambda } (\log (z))^{\mu } \int _{0}^{cz} u^{\lambda -1} \left( 1 - \frac{\log (u)}{\log (z)} \right) ^{\mu } \left( \log (\log (z)) + \log \left( 1-\frac{\log (u)}{\log (z)}\right) \right) e^{-u}du \\&= z^{-\lambda } (\log (z))^{\mu } (\log (\log (z))G_1 + G_2), \end{aligned}\nonumber \\ \end{aligned}$$

(C.39)

where

$$\begin{aligned} G_1 = \int _{0}^{cz} u^{\lambda -1} \left( 1 - \frac{\log (u)}{\log (z)} \right) ^{\mu } e^{-u}du \end{aligned}$$

and

$$\begin{aligned} G_2 = \int _{0}^{cz} u^{\lambda -1} \left( 1 - \frac{\log (u)}{\log (z)} \right) ^{\mu }\log \left( 1-\frac{\log (u)}{\log (z)}\right) e^{-u}du. \end{aligned}$$

(C.40)

We first derive the asymptotic expansion for $G_2$, the asymptotic expansion for $G_1$ can then be derived in a similar manner.

Let N be an arbitrary positive integer such that $N+1 \ge \mu$. By Taylor’s expansion,

$$\begin{aligned} \begin{aligned} \left( 1 - \frac{\log (u)}{\log (z)} \right) ^{\mu }&= \sum _{r=0}^{N} (-1)^r\left( {\begin{array}{c}\mu \\ r\end{array}}\right) \left( \frac{\log (u)}{\log (z)} \right) ^r + R_{1,N} \\ \log \left( 1-\frac{\log (u)}{\log (z)}\right)&= - \sum _{r=1}^{N} \frac{1}{r} \left( \frac{\log (u)}{\log (z)} \right) ^r + R_{2,N}, \end{aligned} \end{aligned}$$

for all $0<u<cz$, where

$$\begin{aligned} |R_{i,N}| \le C_{i,N} \frac{|\log (u)|^{N+1}}{|\log (z)|^{N+1}} (i = 1,2) \end{aligned}$$

for some fixed constants $C_{1,N},C_{2,N} > 0$. Hence,

$$\begin{aligned} \left( 1 - \frac{\log (u)}{\log (z)} \right) ^{\mu } \log \left( 1-\frac{\log (u)}{\log (z)}\right) = \sum _{r=1}^{2N} a_r \left( \frac{\log (u)}{\log (z)} \right) ^r + R_{2N}, \end{aligned}$$

(C.41)

for all $0< u < cz$, where $a_r$’s are defined as in (C.38) and

$$\begin{aligned} |R_{2N}| \le C_{2N} \frac{|\log (u)|^{2N+1}}{|\log (z)|^{2N+1}} \end{aligned}$$

for some fixed $C_{2N} > 0$. By substituting (C.41) in (C.40), we obtain

$$\begin{aligned} G_2 = \sum _{r=1}^{2N} a_r (\log (z))^{-r} \int _0^{cz} u^{\lambda - 1} (\log (u))^r e^{-u} du + r_{2N}, \end{aligned}$$

where

$$\begin{aligned} r_{2N} = \int _0^{cz} u^{\lambda -1} e^{-u} R_{2N} du. \end{aligned}$$

Wong showed in [60, p. 71] that, as $z \rightarrow \infty$,

$$\begin{aligned} \int _0^{cz} u^{\lambda - 1} (\log (u))^r e^{-u} du = \Gamma ^{(r)}(\lambda ) + O(e^{-\epsilon c z}), \end{aligned}$$

where $\epsilon \in (0,1/2)$. Furthermore,

$$\begin{aligned} \begin{aligned} |r_{2N}|&\le C_{2N} |\log (z)|^{-2N-1} \int _{0}^{cz} |u^{\lambda -1} \log (u)^{2N+1} e^{-u}|du \\&\le C_{2N} |\log (z)|^{-2N-1} \int _{0}^{\infty } |u^{\lambda -1} \log (u)^{2N+1} e^{-u}|du \end{aligned} \end{aligned}$$

It can be shown that the latter integral is bounded (see [60, Eq. (2.27), p. 71]; thus, $r_{2N} = O(\log (z)^{-2N-1})$. Hence,

$$\begin{aligned} G_2 = \sum _{r=1}^{2N} a_r \Gamma ^{(r)}(\lambda ) (\log (z))^{-r} + O(\log (z)^{-2N-1}). \end{aligned}$$

(C.42)

In a similar manner, one can show that

$$\begin{aligned} G_1 = \sum _{r=0}^{N} (-1)^r \left( {\begin{array}{c}\mu \\ r\end{array}}\right) \Gamma ^{(r)}(\lambda ) (\log (z))^{-r} + O(\log (z)^{-N-1}). \end{aligned}$$

(C.43)

Combining (C.39), (C.42) and (C.43), we obtain the desired result. $\square$

1.3.4 Conclusions

$$\begin{aligned} \begin{aligned} J_{m,n}(\Delta )&= \frac{2 \Delta ^n}{\Gamma (\frac{n}{2})} \int _0^{\infty } {{\,\mathrm{{\mathrm{erf}}}\,}}^m(s) s^{n-1} e^{-\Delta ^2s^2} ds \\&= \frac{\sqrt{\pi }\Delta ^n }{\Gamma (\frac{n}{2})} \int _{0}^{\infty } e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt \\&= \frac{\sqrt{\pi }\Delta ^n }{\Gamma (\frac{n}{2})} \int _{0}^{c} e^{Ks(t)^2} s(t)^{n-1} e^{-(m+1)t} dt + O\left( \frac{e^{-c(m+n)}}{m+n}\right) . \end{aligned} \end{aligned}$$

(C.44)

By using Theorem C.9 and Theorem C.10 in (C.37) and substituting $K = 1- \Delta ^2$, we obtain (C.11). Note that if $r = 0$ then $n=1$ and $\Delta = 1$ and so $K=0$. In this case, $e^{Ks(t)^2} s(t)^{n-1} = 1$ and direct integration yields $J_{m,1}(1) = 1/(m+1)$.

D The problem test set

Table 4 contains the explicit formula, domain and global minimum of the functions used to generate the high-dimensional test set. The problem set contains 19 problems taken from [22, 29, 51]. Problems that cannot be solved by BARON are marked with ‘$^*$’. Problems that will not be solved by KNITRO are marked with ‘$^\circ$’.

We briefly describe the technique we adapted from Wang et al. [58] to generate high-dimensional functions with low effective dimensionality, which was first applied to the above test set in [9]. Let ${\bar{g}}(\bar{{{\varvec{x}}}})$ be any function from Table 4; let $d_e$ be its dimension and let the given domain be scaled to $[-1, 1]^{d_e}$. We create a D-dimensional function $g({{\varvec{x}}})$ by adding $D-d_e$ fake dimensions to ${\bar{g}}(\bar{{{\varvec{x}}}})$, $g({{\varvec{x}}}) = {\bar{g}}(\bar{{{\varvec{x}}}}) + 0\cdot x_{d_e+1} + 0 \cdot x_{d_e+2} + \cdots + 0\cdot x_{D}$. We further rotate the function by applying a random orthogonal matrix ${{\varvec{Q}}}$ to ${{\varvec{x}}}$ to obtain a non-trivial constant subspace. The final form of the function we test is

$$\begin{aligned} f({{\varvec{x}}}) = g({{\varvec{Q}}}{{\varvec{x}}}). \end{aligned}$$

(D.1)

Table 4 The problem set listed in alphabetical order

Note that the first $d_e$ rows of ${{\varvec{Q}}}$ now span the effective subspace ${\mathcal {T}}$ of $f({{\varvec{x}}})$.

For each problem in the test set, we generate three functions f as defined in (D.1), one for each $D = 10$, 100, 1000.

E Additional numerical results

In this section we provide additional numerical results for X-REGO.

Fig. 5

Comparison between X-REGO variants with the parameter $d = d_e + 2$ and ‘no-embedding’, using DIRECT to solve the subproblem ($\widetilde{\text {RP}{\mathcal {X}}^k}$)

Fig. 6

Comparison between X-REGO variants with the parameter $d = d_e + 2$ and ‘no-embedding’, using BARON to solve the subproblem ($\widetilde{\text {RP}{\mathcal {X}}^k}$)

Fig. 7

Comparison between X-REGO variants with the parameter $d = d_e + 2$ and ‘no-embedding’, using KNITRO to solve the subproblem ($\widetilde{\text {RP}{\mathcal {X}}^k}$)

Fig. 8

Comparison between X-REGO variants and Random Search with the parameter $d = d_e$ and ‘no-embedding’, using KNITRO to solve the subproblem ($\widetilde{\text {RP}{\mathcal {X}}^k}$). Average number (averaged over the test set of KNITRO) of function evaluations (samples) for Random Search are given as follows: 79,172 (D = 10), 83,947 (D=100) and 86,708 (D = 1000)

Fig. 9

Performance profile comparing the proposed algorithms (A-REGO and N-REGO, equipped with mKNITRO) with the optimization of the objective directly in the effective subspace

Firstly, we compare the X-REGO framework with no-embedding when setting $d = d_e+2$ for the size of the random embeddings. We also consider five different realizations of the test set (namely, a different random rotation of the effective subspace was performed) to check the robustness of our approaches (see Figs. 5, 6, 7).

Next we compare X-REGO variants with Random Search (see Fig. 8); see our associated comments in the penultimate paragraph of Sect. 5, just before/above Sect. 6.

Finally, Fig. 9 shows the performance profiles obtained when comparing X-REGO variants A-REGO and N-REGO (with mKNITRO) with the case when each test function is minimized directly in the exact embedding/effective subspace (using mKNITRO); see our associated comments in the last paragraph of Sect. 5, just above Sect. 6.