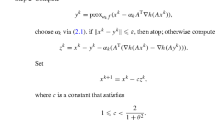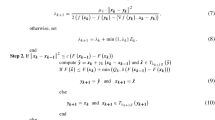Skip to main content
SpringerLink
Log in

A globally convergent proximal Newton-type method in nonsmooth convex optimization

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

The paper proposes and justifies a new algorithm of the proximal Newton type to solve a broad class of nonsmooth composite convex optimization problems without strong convexity assumptions. Based on advanced notions and techniques of variational analysis, we establish implementable results on the global convergence of the proposed algorithm as well as its local convergence with superlinear and quadratic rates. For certain structured problems, the obtained local convergence conditions do not require the local Lipschitz continuity of the corresponding Hessian mappings that is a crucial assumption used in the literature to ensure a superlinear convergence of other algorithms of the proximal Newton type. The conducted numerical experiments of solving the \(l_1\) regularized logistic regression model illustrate the possibility of applying the proposed algorithm to deal with practically important problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/.

  2. The code is downloaded from https://github.com/ZiruiZhou/IRPN.

References

  1. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 83–202 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Nesterov, Yu.: Lectures on Convex Optimization, 2nd edn. Springer, Cham, Switzerland (2018)

    Book  MATH  Google Scholar 

  3. Schmidt, M., Roux, N., Bach, F.: Convergence rates of inexact proximal-gradient methods for convex optimization. In: Shawe-Taylor, J., et al. (eds.) Advances in Neural Information Processing Systems 24, pp. 1458–1466. Curran Associates, New York (2011)

    Google Scholar 

  4. Li, G., Pong, T.K.: Calculus of the exponent of Kurdyka-Łojasiewicz inequality and its applications to linear convergence of first-order methods. Found. Comput. Math. 18, 1199–1232 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Luo, Z.-Q., Tseng, P.: On the linear convergence of descent methods for convex essentially smooth minimization. SIAM J. Control. Optim. 30, 408–425 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  6. Necoara, I., Nesterov, Yu., Glineur, F.: Linear convergence of first order methods for non-strongly convex optimization. Math. Progr. 175, 69–107 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  7. Tseng, P.: Approximation accuracy, gradient methods, and error bound for structured convex optimization. Math. Progr. 125, 263–295 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Ye, J.J., Yuan, X., Zeng, S., Zhang, J.: Variational analysis perspective on linear convergence of some first order methods for nonsmooth convex optimization problems. Set-Valued Var. Anal. (2021). https://doi.org/10.1007/s11228-021-00591-3

    Article  MathSciNet  MATH  Google Scholar 

  9. Lee, J.D., Sun, Y., Saunders, M.A.: Proximal Newton-type methods for minimizing composite functions. SIAM J. Optim. 24, 1420–1443 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Fukushima, M., Mine, H.: A generalized proximal point algorithm for certain non-convex minimization problems. Int. J. Syst. Sci. 12, 989–1000 (1981)

    Article  MATH  Google Scholar 

  11. Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control. Optim. 14, 877–898 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  12. Facchinei, F., Pang, J.-S.: Finite-Dimesional Variational Inequalities and Complementarity Problems. Springer, New York (2003)

    MATH  Google Scholar 

  13. Izmailov, A.F., Solodov, M.V.: Newton-Type Methods for Optimization and Variational Problems. Springer, New York (2014)

    Book  MATH  Google Scholar 

  14. Friedman, J., Hastie, T., Höfling, H., Tibshirani, R.: Pathwise coordinate optimization. Ann. Appl. Stat. 1, 302–332 (2007)

  15. Yuan, G.-X., Ho, C.-H., Lin, C.-J.: An improved GLMNET for L1-regularized logistic regression. J. Mach. Learn. Res. 13, 1999–2030 (2012)

    MathSciNet  MATH  Google Scholar 

  16. Hsieh, C., Dhillon, I.S., Ravikumar, P.K., Sustik, M.A.: Sparse inverse covariance matrix estimation using quadratic approximation. In: Shawe-Taylor, J., et al. (eds.) Advances in Neural Information Processing Systems 24, pp. 2330–2338. Curran Associates, New York (2011)

    Google Scholar 

  17. Oztoprak, F., Nocedal, J., Rennie, S., Olsen, P.A.: Newton-like methods for sparse inverse covariance estimation. In: Pereira, F., et al. (eds.) Advances in Neural Information Processing Systems 25, pp. 755–763. Curran Associates, New York (2012)

    Google Scholar 

  18. Sra, S., Nowozin, S., Wright, S.J. (eds.): Optimization for Machine Learning. MIT Press, Cambridge (2011)

    Google Scholar 

  19. Robinson, S.M.: Generalized equations and their solutions, Part II: applications to nonlinear programming. Math. Program. Stud. 19, 200–221 (1982)

    Article  MATH  Google Scholar 

  20. Mordukhovich, B.S.: Variational Analysis and Applications. Springer, Cham, Switzerland (2018)

    Book  MATH  Google Scholar 

  21. Dontchev, A.L., Rockafellar, R.T.: Implicit Functions and Solution Mappings: A View from Variational Analysis, 2nd edn. Springer, New York (2014)

    Book  MATH  Google Scholar 

  22. Fischer, A.: Local behavior of an iterative framework for generalized equations with nonisolated solutions. Math. Progr. 94, 91–124 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  23. Byrd, R.H., Nocedal, J., Oztoprak, F.: An inexact successive quadratic approximation method for L-1 regularized optimization. Math. Progr. 157, 375–396 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Lee, C., Wright, S.J.: Inexact successive quadratic approximation for regularized optimization. Comput. Optim. Appl. 72, 641–0674 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Scheinberg, K., Tang, X.: Practical inexact proximal quasi-Newton method with global complexity analysis. Math. Progr. 160, 495–529 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  26. Yue, M.-C., Zhou, Z., So, A.M.-C.: A family of inexact SQA methods for non-smooth convex minimization with provable convergence guarantees based on the Luo-Tseng error bound property. Math. Progr. 174, 327–358 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  27. Themelis, A., Stella, L., Patrinos, P.: Forward-backward envelope for the sum of two nonconvex functions: further properties and nonmonotone linesearch algorithms. SIAM J. Optim. 28, 2274–2303 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  28. Mordukhovich, B.S., Nam, M.N.: An Easy Path to Convex Analysis. Morgan & Claypool Publishers, San Rafael, CA (2014)

    MATH  Google Scholar 

  29. Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (1998)

    Book  MATH  Google Scholar 

  30. Aragón Artacho, F.J., Geoffroy, M.H.: Characterization of metric regularity of subdifferentials. J. Convex Anal. 15, 365–380 (2008)

    MathSciNet  MATH  Google Scholar 

  31. Aragón Artacho, F.J., Geoffroy, M.H.: Metric subregularity of the convex subdifferential in Banach spaces. J. Nonlin. Convex Anal. 15, 35–47 (2015)

    MathSciNet  MATH  Google Scholar 

  32. Drusvyatskiy, D., Mordukhovich, B.S., Nghia, T.T.A.: Second-order growth, tilt stability, and metric regularity of the subdifferential. J. Convex Anal. 21, 1165–1192 (2014)

    MathSciNet  MATH  Google Scholar 

  33. Gaydu, M., Geoffroy, M.H., Jean-Alexis, C.: Metric subregularity of order \(q\) and the solving of inclusions. Cent. Eur. J. Math. 9, 147–161 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  34. Li, G., Mordukhovich, B.S.: Hölder metric subregularity with applications to proximal point method. SIAM J. Optim. 22, 1655–1684 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  35. Zheng, X.Y., Ng, K.F.: Hölder stable minimizers, tilt stability sand Hölder metric regularity of subdifferentials. SIAM J. Optim. 120, 186–201 (2015)

    MATH  Google Scholar 

  36. Mordukhovich, B.S., Ouyang, W.: Higher-order metric subregularity and its applications. J. Global Optim. 63, 777–795 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  37. Khanh, P.D., Mordukhovich, B.S., Phat, V.T.: A generalized Newton method for subgradient systems. arXiv:2009.10551v1 (2020)

  38. Mordukhovich, B.S., Sarabi, M.E.: Generalized Newton algorithms for tilt-stable minimizers in nonsmooth optimization. arXiv:2004.02345 (2020)

  39. Drusvyatskiy, D., Lewis, A.S.: Error bounds, quadratic growth, and linear convergence of proximal methods. Math. Oper. Res. 43, 919–948 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  40. Beck, A.: First-Order Methods in Optimization. SIAM, Philadelphia (2017)

    Book  MATH  Google Scholar 

  41. Chen, X., Fukushima, M.: Proximal quasi-Newton methods for nondifferentiable convex optimization. Math. Progr. 85, 313–334 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  42. Dan, H., Yamashita, N., Fukushima, M.: Convergence properties of the inexact Levenberg-Marquardt method under local error bound conditions. Optim. Meth. Softw. 17, 605–626 (2002)

  43. Chang, C.C., Lin, C.J.: LIBSVM?: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2, 27:1–27:27 (2011)

Download references

Acknowledgements

The authors are very grateful to two anonymous referees for their helpful suggestions and remarks that allowed us to significantly improve the original presentation. The alphabetical order of the authors indicates their equal contributions to the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Wayne State University, Detroit, MI, USA

    Boris S. Mordukhovich

  2. Department of Mathematics, The University of Hong Kong, Hong Kong, China

    Xiaoming Yuan

  3. Department of Mathematics and Statistics, University of Victoria, Victoria, Canada

    Shangzhi Zeng

  4. Department of Mathematics, Southern University of Science and Technology, National Center for Applied Mathematics Shenzhen, Shenzhen, 518055, China

    Jin Zhang

Authors
  1. Boris S. Mordukhovich
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaoming Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shangzhi Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Boris S. Mordukhovich or Jin Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Boris S. Mordukhovich: Partly supported by the USA National Science Foundation under grants DMS-1512846 and DMS-1808978, by the USA Air Force Office of Scientific Research grant #15RT04, and by Australian Research Council Under Grant DP-190100555.

Xiaoming Yuan: Supported by the General Research Fund 12302318 from the Hong Kong Research Grants Council.

Shangzhi Zeng: Supported by the Pacific Institute for the Mathematical Sciences (PIMS)

Jin Zhang: Supported by National Science Foundation of China 11971220, by Shenzhen Science and Technology Program (No. RCYX20200714114700072), and by the Stable Support Plan Program of Shenzhen Natural Science Fund (No. 20200925152128002)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mordukhovich, B.S., Yuan, X., Zeng, S. et al. A globally convergent proximal Newton-type method in nonsmooth convex optimization. Math. Program. 198, 899–936 (2023). https://doi.org/10.1007/s10107-022-01797-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-022-01797-5

Keywords

Mathematics Subject Classification

Search

Navigation