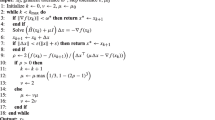Abstract
For a given matrix subspace, how can we find a basis that consists of low-rank matrices? This is a generalization of the sparse vector problem. It turns out that when the subspace is spanned by rank-1 matrices, the matrices can be obtained by the tensor CP decomposition. For the higher rank case, the situation is not as straightforward. In this work we present an algorithm based on a greedy process applicable to higher rank problems. Our algorithm first estimates the minimum rank by applying soft singular value thresholding to a nuclear norm relaxation, and then computes a matrix with that rank using the method of alternating projections. We provide local convergence results, and compare our algorithm with several alternative approaches. Applications include data compression beyond the classical truncated SVD, computing accurate eigenvectors of a near-multiple eigenvalue, image separation and graph Laplacian eigenproblems.







Similar content being viewed by others
Notes
Here and in the following, the error constant behind \(O(\Vert E\Vert _F)\) depends mainly on the condition of \({\varSigma }_*\), which can be very large, but is fixed in this type of local analysis.
From a polar decomposition \(Z^T=UP\) one gets \(Z^TZ-I = (Z^T-U)(P+I)U^T\), and since the singular values of \((P+I)U^T\) are all at least 1, it follows that \(\Vert Z-U^T\Vert _F\le \Vert Z^TZ-I\Vert _F\).
We thank Yuichi Yoshida for this observation.
References
Abolghasemi, V., Ferdowsi, S., Sanei, S.: Blind separation of image sources via adaptive dictionary learning. IEEE Trans. Image Process. 21(6), 2921–2930 (2012)
Ames, B.P.W., Vavasis, S.A.: Nuclear norm minimization for the planted clique and biclique problems. Math. Program. 129(1 Ser. B), 69–89 (2011)
Andersson, F., Carlsson, M.: Alternating projections on nontangential manifolds. Constr. Approx. 38(3), 489–525 (2013)
Bai, Z., Demmel, J., Dongarra, J., Ruhe, A., van der Vorst, H. (eds.): Templates for the solution of algebraic eigenvalue problems. A practical guide. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2000)
Barak, B., Kelner, J.A., Steurer, D.: Rounding sum-of-squares relaxations. In: Proceedings of the 46th Annual ACM Symposium on Theory of Computing, pp. 31–40 (2014)
Bell, A.J., Sejnowski, T.J.: An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 7(6), 1129–1159 (1995)
Bühlmann, P., van de Geer, S.: Statistics for High-Dimensional Data. Methods, Theory and Applications. Springer, Heidelberg (2011)
Cai, J.-F., Candès, E.J., Shen, Z.: A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 20(4), 1956–1982 (2010)
Candès, E.J.: The restricted isometry property and its implications for compressed sensing. C. R. Math. Acad. Sci. Paris 346(9–10), 589–592 (2008)
Candès, E.J., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9(6), 717–772 (2009)
Candes, E.J., Tao, T.: Near-optimal signal recovery from random projections: universal encoding strategies? IEEE Trans. Inform. Theory 52(12), 5406–5425 (2006)
Candès, E.J., Tao, T.: The power of convex relaxation: near-optimal matrix completion. IEEE Trans. Inform. Theory 56(5), 2053–2080 (2010)
Carroll, J.D., Chang, J.-J.: Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition. Psychometrika 35(3), 283–319 (1970)
Cichocki, A., Mandic, D., De Lathauwer, L., Zhou, G., Zhao, Q., Caiafa, C., Phan, H.A.: Tensor decompositions for signal processing applications: from two-way to multiway component analysis. IEEE Signal Proc. Mag. 32(2), 145–163 (2015)
Coleman, T.F., Pothen, A.: The null space problem. I. Complexity. SIAM J. Algebraic Discrete Methods 7(4), 527–537 (1986)
De Lathauwer, L.: A link between the canonical decomposition in multilinear algebra and simultaneous matrix diagonalization. SIAM J. Matrix Anal. Appl. 28(3), 642–666 (2006). (electronic)
De Lathauwer, L.: Decompositions of a higher-order tensor in block terms. II. Definitions and uniqueness. SIAM J. Matrix Anal. Appl. 30(3), 1033–1066 (2008)
De Lathauwer, L., De Moor, B., Vandewalle, J.: A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 21(4), 1253–1278 (2000). (electronic)
De Lathauwer, L., De Moor, B., Vandewalle, J.: Computation of the canonical decomposition by means of a simultaneous generalized Schur decomposition. SIAM J. Matrix Anal. Appl. 26(2), 295–327 (electronic) (2004/2015)
Demanet, L., Hand, P.: Scaling law for recovering the sparsest element in a subspace. Inf. Inference 3(4), 295–309 (2014)
Demmel, J.W.: Applied Numerical Linear Algebra. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (1997)
Domanov, I., De Lathauwer, L.: Canonical polyadic decomposition of third-order tensors: reduction to generalized eigenvalue decomposition. SIAM J. Matrix Anal. Appl. 35(2), 636–660 (2014)
Drusvyatskiy, D., Ioffe, A.D., Lewis, A.S.: Transversality and alternating projections for nonconvex sets. Found. Comput. Math. 15(6), 1637–1651 (2015)
Edmonds, J.: Systems of distinct representatives and linear algebra. J. Res. Nat. Bur. Stand. Sect. B 71B, 241–245 (1967)
Fazel, M.: Matrix rank minimization with applications. Ph.D. thesis, Electrical Engineering Deptartment Stanford University (2002)
Fazel, M., Hindi, H., Boyd, S.P.: A rank minimization heuristic with application to minimum order system approximation. In: Proceedings of the 2001 American Control Conference, pp. 4734–4739 (2001)
Golub, G.H., Van Loan, C.F.: Matrix Computations. Johns Hopkins University Press, Baltimore, MD (2013)
Grant, M., Boyd, S.: CVX: Matlab Software for Disciplined Convex Programming, version 2.1, March 2014. http://cvxr.com/cvx
Gurvits, L.: Classical complexity and quantum entanglement. J. Comput. Syst. Sci. 69(3), 448–484 (2004)
Harshman, R.A.: Foundations of the PARAFAC procedure: models and conditions for an “explanatory” multi-modal factor analysis. UCLA Working Papers in Phonetics 16, 1–84 (1970)
Harvey, N.J.A., Karger, D.R., Murota, K.: Deterministic network coding by matrix completion. In: Proceedings of the 16th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 489–498 (2005)
Harvey, N. J. A., Karger, D. R., Yekhanin, S.: The complexity of matrix completion. In: Proceedings of the 17th Annual ACM-SIAM Symposium on Discrete Algorithm, pp. 1103–1111 (2006)
Håstad, J.: Tensor rank is NP-complete. J. Algorithms 11(4), 644–654 (1990)
Helmke, U., Shayman, M.A.: Critical points of matrix least squares distance functions. Linear Algebra Appl. 215, 1–19 (1995)
Hillar, C.J., Lim, L.-H.: Most tensor problems are NP-hard. J. ACM 60(6), Art. 45, 39 (2013)
Hitchcock, F.L.: The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 6, 164–189 (1927)
Huang, G.B., Ramesh, M., Berg, T., Learned-Miller, E.: Labeled faces in the wild: a database for studying face recognition in unconstrained environments. Technical report 07-49, University of Massachusetts, Amherst (2007)
Ivanyos, G., Karpinski, M., Qiao, Y., Santha, M.: Generalized Wong sequences and their applications to Edmonds’ problems. In: Proceedings of the 31st International Symposium on Theoretical Aspects of Computer Science, vol. 117543, pp. 397–408 (2014)
Kindermann, S., Navasca, C.: News algorithms for tensor decomposition based on a reduced functional. Numer. Linear Algebra Appl. 21(3), 340–374 (2014)
Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51(3), 455–500 (2009)
Leurgans, S.E., Ross, R.T., Abel, R.B.: A decomposition for three-way arrays. SIAM J. Matrix Anal. Appl. 14(4), 1064–1083 (1993)
Lewis, A.S., Luke, D.R., Malick, J.: Local linear convergence for alternating and averaged nonconvex projections. Found. Comput. Math. 9(4), 485–513 (2009)
Lewis, A.S., Malick, J.: Alternating projections on manifolds. Math. Oper. Res. 33(1), 216–234 (2008)
Li, N., Kindermann, S., Navasca, C.: Some convergence results on the regularized alternating least-squares method for tensor decomposition. Linear Algebra Appl. 438(2), 796–812 (2013)
Liu, Y.-J., Sun, D., Toh, K.-C.: An implementable proximal point algorithmic framework for nuclear norm minimization. Math. Program. 133(1—-2, Ser. A), 399–436 (2012)
Liu, Z., Vandenberghe, L.: Interior-point method for nuclear norm approximation with application to system identification. SIAM J. Matrix Anal. Appl. 31(3), 1235–1256 (2009)
Lovász, L.: Singular spaces of matrices and their application in combinatorics. Bol. Soc. Brasil. Math. 20(1), 87–99 (1989)
Mohlenkamp, M.J.: Musings on multilinear fitting. Linear Algebra Appl. 438(2), 834–852 (2013)
Motwani, R., Raghavan, P.: Randomized Algorithms. Chapman and Hall/CRC, Routledge (2010)
Noll, D., Rondepierre, A.: On local convergence of the method of alternating projections. Found. Comput. Math. 16(2), 425–455 (2016)
Oxley, J.: Infinite matroids. In: White, N. (ed.) Matroid Applications, pp. 73–90. Cambridge University Press, Cambridge (1992)
Qu, Q., Sun, J., Wright, J.: Finding a sparse vector in a subspace: linear sparsity using alternating directions. In: Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K. (eds.) Advances in Neural Information Processing Systems, pp. 3401–3409. Curran Associates, Inc, Red Hook (2014)
Qu, Q., Sun, J., Wright, J.: Finding a sparse vector in a subspace: linear sparsity using alternating directions. arXiv:1412.4659 (2014)
Recht, B.: A simpler approach to matrix completion. J. Mach. Learn. Res. 12, 3413–3430 (2011)
Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 52(3), 471–501 (2010)
Sorber, L., Van Barel, M., De Lathauwer, L.: Tensorlab v2.0. http://www.tensorlab.net/
Spielman, D.A., Wang, H., Wright, J.: Exact recovery of sparsely-used dictionaries. In: Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, IJCAI ’13, pp. 3087–3090. AAAI Press (2013)
Stewart, G.W.: Matrix Algorithms. Vol. II. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2001)
Stewart, G.W., Sun, J.G.: Matrix Perturbation Theory. Computer Science and Scientific Computing. Academic Press, Inc., Boston, MA (1990)
Sun, J., Qu, Q., Wright, J.: Complete dictionary recovery over the sphere I: Overview and the geometric picture. arXiv:1511.03607 (2015)
Sun, J., Qu, Q., Wright, J.: Complete dictionary recovery over the sphere II: Recovery by Riemannian trust-region method. arXiv:1511.04777 (2015)
Uschmajew, A.: Local convergence of the alternating least squares algorithm for canonical tensor approximation. SIAM J. Matrix Anal. Appl. 33(2), 639–652 (2012)
Uschmajew, A.: A new convergence proof for the higher-order power method and generalizations. Pac. J. Optim. 11(2), 309–321 (2015)
Wang, L., Chu, M.T.: On the global convergence of the alternating least squares method for rank-one approximation to generic tensors. SIAM J. Matrix Anal. Appl. 35(3), 1058–1072 (2014)
Wedin, P.-Å.: Perturbation bounds in connection with singular value decomposition. Nordisk Tidskr. Informationsbehandling (BIT) 12, 99–111 (1972)
Xu, Y., Yin, W.: A block coordinate descent method for regularized multiconvex optimization with applications to nonnegative tensor factorization and completion. SIAM J. Imaging Sci. 6(3), 1758–1789 (2013)
Zhao, X., Zhou, G., Dai, W., Xu, T., Wang, W.: Joint image separation and dictionary learning. In: 18th International Conference on Digital Signal Processing (DSP), pp. 1–6. IEEE (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by JST CREST (Iwata team), JSPS Scientific Research Grants No. 26870149 and No. 26540007, and JSPS Grant-in-Aid for JSPS Fellows No. 267749.
Appendix: Finding rank-one bases via tensor decomposition
Appendix: Finding rank-one bases via tensor decomposition
In this appendix, we describe the rank-one basis problem as a tensor decomposition problem. Recall that in this problem, we are promised that the given subspace \({\mathcal {M}}\) is spanned by rank-one matrices. Thus we can apply Algorithm 3 (Phase II) with the precise rank guess directly. Alternatively, we can also stop after Algorithm 2 (Phase I), which in practice performs well (see Sect. 5.1). The following tensor decomposition viewpoint leads to further algorithms.
Let \(M_1,\ldots ,M_d\) be an arbitrary basis of \({\mathcal {M}}\), and let \({\mathcal {T}}\) be the \(m\times n\times d\) tensor whose 3-slices are \(M_1,\ldots ,M_d\). The fact that \({\mathcal {M}}\) possesses a rank-one basis is equivalent to the existence of d (and not less) triplets of vectors \(({\mathbf {a}}_\ell ^{}, {\mathbf {b}}_\ell ^{}, {\mathbf {c}}_\ell ^{})\) where \({\mathbf {a}}_\ell ^{}\in {\mathbb {R}}^{m}, {\mathbf {b}}_\ell ^{}\in {\mathbb {R}}^{n}, {\mathbf {c}}_\ell ^{}\in {\mathbb {R}}^{d}, \) such that
(here \(c_{k,\ell }\) denotes the kth entry of \({\mathbf {c}}_\ell \)). Namely, if such triplets \(({\mathbf {a}}_\ell ^{}, {\mathbf {b}}_\ell ^{}, {\mathbf {c}}_\ell ^{})\) exist, then the assumed linear independence of the \(M_k\) automatically implies that rank-one matrices \( {\mathbf {a}}_\ell ^{} {\mathbf {b}}_\ell ^T\) belong to \({\mathcal {M}}\). Using the outer product of vectors (denoted by \(\circ \)), we may express this relation in terms of the tensor \({\mathcal {T}}\) as
This type of tensor decomposition into a sum of outer products is called the CP decomposition, and is due to Hitchcock [36] (although the term CP decomposition appeared later). In general, the smallest d required for a representation of the form (25) is called the (canonical) rank of the tensor \({\mathcal {T}}\). We refer to [40] and references therein for more details. In summary, we have the following trivial conclusion.
Proposition 8
The d-dimensional matrix space \({\mathcal {M}} = {{\mathrm{{span}}}}(M_1,\ldots ,M_d)\) possesses a rank-one basis if and only if the tensor \({\mathcal {T}}\) whose 3-slices are the \(M_1,\ldots ,M_d\) has (canonical) rank d. Any CP decomposition (25) of \({\mathcal {T}}\) provides a rank-one basis \({\mathbf {a}}_1^{} {\mathbf {b}}_1^T, \ldots , {\mathbf {a}}_d^{} {\mathbf {b}}_d^T\) of \({\mathcal {M}}\).
We remark that computing the rank of a general third-order tensor is known to be NP-hard [33, 35]. Therefore, it is NP-hard to check whether a matrix space \({\mathcal {M}}\) admits a rank-one basis. Nevertheless, we might try to find a rank-one basis by trying to calculate a CP decomposition (25) from linearly independent \(M_1,\ldots ,M_d\). We outline two common algorithms.
1.1 Simultaneous diagonalization
If the tensor \({\mathcal {T}} \in {\mathbb {R}}^{m \times n \times r}\) is known to have rank d and \(d\le \min (m,n)\), it is “generically” possible to find a CP decomposition (25) in polynomial time using simultaneous diagonalization [16, 19, 41].
Let us introduce the factor matrices \({\mathbf {A}} = [{\mathbf {a}}_1,\ldots ,{\mathbf {a}}_d] \in {\mathbb {R}}^{m\times d}\), \({\mathbf {B}} = [{\mathbf {b}}_d,\ldots ,{\mathbf {b}}_d] \in {\mathbb {R}}^{n\times d}\), and \({\mathbf {C}} = [{\mathbf {c}}_1,\ldots ,{\mathbf {c}}_d] \in {\mathbb {R}}^{d\times d}\). Then (24) reads
where \(D_k = {{\mathrm{{diag}}}}({\mathbf {c}}_k^T)\), in which \({\mathbf {c}}_k^T\) denotes the kth row of \({\mathbf {C}}\). In other words, a rank-one basis exists, if the \(M_1,\ldots ,M_d\) can be simultaneously diagonalized. The basic idea of the algorithm of Leurgans, Ross, and Abel in [41] is as follows. One assumes \({{\mathrm{rank}}}({\mathbf {A}}) = {{\mathrm{rank}}}({\mathbf {B}}) = d\). Pick a pair \((k,\ell )\), and assume that \(D_k\) and \(D_\ell \) are invertible, and that \(D_k^{} D_\ell ^{-1}\) has d distinct diagonal entries. Then it holds
where superscript \(^+\) denotes the Moore-Penrose inverse. In other words, \({\mathbf {A}}\) contains the eigenvectors of \(M_k^{} M_\ell ^+\) to distinct eigenvalues, and is essentially uniquely determined (up to scaling and permutation of the columns). Alternatively, for more numerical reliability, one can compute an eigenvalue decompositions of a linear combination of all \(M_k^{} M_\ell ^+\) instead, assuming that the corresponding linear combination of \(D_k^{} D_\ell ^{-1}\) has distinct diagonal entries. Similarly, \({\mathbf {B}}\) can be obtained from an eigendecomposition, e.g. of \(M_k^T (M_\ell ^T)^+\) or linear combinations. Finally,
which gives \({\mathbf {C}}\). The algorithm requires the construction of Moore-Penrose inverses of matrices whose larger dimension is at most \(\max (m,n)\). Hence, the complexity is \(O(mn^2)\).
The condition that the \(D_k^{} D_\ell ^{-1}\) or a linear combination of them should have distinct diagonal entries is not very critical, since it holds generically, if the matrices \(M_1,\ldots ,M_d\) are randomly drawn from \({\mathcal {M}}\), or, when this is not possible, are replaced by random linear combination of themselves. The condition \({{\mathrm{rank}}}({\mathbf {A}}) = {{\mathrm{rank}}}({\mathbf {B}}) = d\) on the other hand, is a rather strong assumption on the rank-one basis \({\mathbf {a}}^{}_1{\mathbf {b}}_1^T,\ldots ,{\mathbf {a}}_d^{} {\mathbf {b}}_d^T\). It implies uniqueness of the basis, and restricts the applicability of the outlined algorithm a priori to dimension \(d \le \min (m,n)\) of \({\mathcal {M}}\). There is an interesting implication on the condition (14) that we used for the local convergence proof of our algorithms. Theorem 4 and Corollary 5 therefore apply at every basis element \({\mathbf {a}}_\ell ^{} {\mathbf {b}}_\ell ^T\) in this setting.
Proposition 9
Let \({\mathbf {a}}^{}_1{\mathbf {b}}_1^T,\ldots ,{\mathbf {a}}_d^{} {\mathbf {b}}_d^T\) be a rank-one basis such that \({{\mathrm{rank}}}({\mathbf {A}}) = {{\mathrm{rank}}}({\mathbf {B}}) = d\). Then (14) holds at any basis element \(X_* = X_\ell = {\mathbf {a}}_\ell ^{} {\mathbf {b}}_\ell ^T\).
Proof
This follows immediately from Lemma 7 by taking \(\tilde{{\mathcal {M}}} = {{\mathrm{span}}}\{ {\mathbf {a}}_k^{} {\mathbf {b}}_k^T :k \ne \ell \}\). \(\square \)
De Lathauwer [16] developed the idea of simultaneous diagonalization further. His algorithm requires the matrix \({\mathbf {C}}\) to have full column rank, which in our case is always true as \({\mathbf {C}}\) must contain the basis coefficients for d linearly independent elements \(M_1,\ldots ,M_d\). The conditions on the full column rank of \({\mathbf {A}}\) and \({\mathbf {B}}\) can then be replaced by some weaker conditions, but, simply speaking, too many linear dependencies in \({\mathbf {A}}\) and \({\mathbf {B}}\) will still lead to a failure. A naive implementation of De Lathauwer’s algorithm in [16] seems to require \(O(n^6)\) operations (assuming \(m=n\)).
Further progress on finding the CP decomposition algebraically under even milder assumptions has been made recently in [22]. It is partially based on the following observation: denoting by \(m_\ell =\text{ vec }(M_\ell )\) the \(n^2\times 1\) vectorization of \(M_\ell \) (which stacks the column on top of each other), and defining \(\text{ Matr }({\mathcal {T}}) = [m_1,\ldots , m_r]\in {\mathbb {R}}^{mn\times d}\), we have
where \( {\mathbf {B}} \odot {\mathbf {A}} = [{\mathbf {a}}_1 \otimes {\mathbf {b}}_1,\ldots ,{\mathbf {a}}_d \otimes {\mathbf {b}}_d] \in {\mathbb {R}}^{mn \times d} \) is the so called Khatri-Rao product of \({\mathbf {B}}\) and \({\mathbf {A}}\) (here \(\otimes \) is the ordinary Kronecker product). If \({\mathbf {C}}\) (which is of full rank in our scenario) would be known, then \({\mathbf {A}}\) and \({\mathbf {B}}\) can be retrieved from the fact that the matricizations of the columns of \( \text{ Matr }({\mathcal {T}}){\mathbf {C}}^{-T} = {\mathbf {B}} \odot {\mathbf {A}} \) must be rank-one matrices. In [22] algebraic procedures are proposed that find the matrix \({\mathbf {C}}\) from \({\mathcal {T}}\).
Either way, by computing the CP decomposition for \({\mathcal {T}}\) we can, at least in practice, recover the rank one basis \(\{{\mathbf {a}}_\ell ^{}{\mathbf {b}}_\ell ^T\}\) in polynomial time if we know it exists. This is verified in our MATLAB experiments using Tensorlab’s cpd in Sect. 5.1.1.
1.2 Alternating least squares
An alternative and cheap workaround are optimization algorithms to calculate an approximate CP decomposition of a given third-order tensor, a notable example being alternating least squares (ALS), which was developed in statistics along with the CP model for data analysis [13, 30]. In practice, they often work astonishingly well when the exact rank is provided.
Assuming the existence of a rank-one basis, that is, \({{\mathrm{rank}}}({\mathcal {T}}) = d\), the basic ALS algorithm is equivalent to a block coordinate descent method applied to the function
The name of the algorithm comes from the fact that a block update consists in solving a least squares problem for one of the matrices \({\mathbf {A}}\), \({\mathbf {B}}\) or \({\mathbf {C}}\), since f is quadratic with respect to each of them. It is easy to derive the explicit formulas. For instance, fixing \({\mathbf {A}}\) and \({\mathbf {B}}\), an optimal \({\mathbf {C}}\) with minimal Frobenius norm is found from (26) as \( {\mathbf {C}} = \text{ Matr }({\mathcal {T}})^T ({\mathbf {B}}^T \odot {\mathbf {A}}^T)^+. \) The updates for the other blocks look similar when using appropriate reshapes of \({\mathcal {T}}\) into a matrix; the formulas can be found in [40].
The question of convergence of ALS is very delicate, and has been subject to many studies. As it is typical for these block coordinate type optimization methods for nonconvex functions, convergence can, if at all, ensured only to critical points, but regularization might be necessary, see [44, 48, 62–64, 66] for some recent studies, and [40] in general. Practical implementations are typically a bit more sophisticated than the simple version outlined above, for instance the columns of every factor matrix should be rescaled during the process for more numerical stability. Also a good initialization of \({\mathbf {A}}\), \({\mathbf {B}}\), and \({\mathbf {C}}\) can be crucial for the performance. For instance one may take the leading HOSVD vectors [18] or the result of other methods [39] as a starting guess for ALS.
Rights and permissions
About this article
Cite this article
Nakatsukasa, Y., Soma, T. & Uschmajew, A. Finding a low-rank basis in a matrix subspace. Math. Program. 162, 325–361 (2017). https://doi.org/10.1007/s10107-016-1042-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-016-1042-2
Keywords
- Low-rank matrix subspace
- \(\ell ^1\) relaxation
- Alternating projections
- Singular value thresholding
- Matrix compression