Designing a dairy supply chain network considering sustainability and resilience: a multistage decision-making framework

Abstract

The crucial role of sustainable development and resiliency strategies is undeniable in today’s competitive market space, especially after the Coronavirus outbreak. Hence, this research develops a multistage decision-making framework to investigate the supply chain network design problem considering the sustainability and resiliency dimensions. In this way, the scores of the potential suppliers based on the sustainability and resilience dimensions were calculated using the MADM methods, and then, these scores were applied as inputs in the proposed mathematical model (the second stage), which determined which supplier should be selected. The proposed model aims to minimize the total costs, maximize the suppliers' sustainability and resiliency, and maximize the distribution centers' resiliency. Then, the proposed model is solved by the preemptive fuzzy goal programming method. Overall, the main objectives and aims of the current work are to present a comprehensive decision-making model that can incorporate the sustainability and resilience dimensions into the supplier selection and supply chain configuration processes. In general, the main contributions and advantages of this work can be summarized as follows: (i) this research simultaneously investigates the sustainability and resiliency concepts in the dairy supply chain, (ii) the current work develops an efficient multistage decision-making model that can evaluate the suppliers based on the resilience and sustainability dimensions and configure the supply chain network, simultaneously. Based on the obtained results, the responsiveness and facilities reinforcement indicators are the most important indicators for the resilient aspect. On the other hand, reliability and quality are the most important indicators of sustainability aspect. Also, the results show that a large percentage of supply chain costs are related to purchasing and production costs. Besides, according to the outputs, the total cost of supply chain increases by enhancing the demand.

Graphical abstract

Introduction

Nowadays, the crucial role of supply chain management (SCM) has been bolded due to technological growth, market competitiveness, and population growth (Nayeri et al. 2023). Nowadays, the managers of supply chains (SCs) know that to improve their market share and enhance efficiency, they need an optimal plan for their SC network (SCN). In the traditional approach, researchers and managers only considered the economic aspects of the SCNs design problem. However, by increasing environmental concerns, the tendency of researchers has shifted toward configuring the SCN considering environmental issues, or Green SC (GrSC) (Nayeri et al. 2020). Moreover, to reach the dimensions of sustainability, as one of the most crucial concepts in modern businesses, researchers tried to integrate the social, environmental, and features in the SCN design problem that led to born the sustainable SC (SSC) problem (Sazvar et al. 2021b).

Natural and man-made disasters always threaten supply chains. For example, in 2019, the Coronavirus disease outbreak led to obstructing the movement of materials from Wuhan, which was a global center for automotive, biomedicine, and electronics in industries that resulted in many disruptions and losses in related businesses (Akbari-Kasgari et al. 2022). There is an efficient concept to tackle disruptions, called resiliency in the literature. Based on the definition, resilience means the ability of SCN to deal with disruptions to satisfy customer demands (Ahranjani et al. 2020). For another example, we can refer to the earthquake in Japan (On March 11, 2011). This earthquake led to suspending the production line of the majority of automobile manufacturers. According to evidence, among the automobile manufacturers, the most damage was by Nissan Motor Company (Rezapour et al. 2017). However, this company had a better recovery process in comparison with its competitors. Six months after the incident, the reduction rate of Nissan’s production was only 3.8%, while those of other competitors were 24.8% on average (Rezapour et al. 2017). This example demonstrates the key role of resilience in the business environment.

Motivated by the above-mentioned concerns, incorporating resilience and sustainability features has become a trending topic in recent years. In this regard, in the nowadays competitive and modern business environment, customers not only evaluated the companies based on their price and quality but also they are considered environmental and social dimensions (Breque et al. 2021; Sazvar et al. 2021a; Nayeri et al. 2022). Therefore, incorporating the sustainable development pillars into the supply chain is a necessary action. Although the sustainability concept may seem like an extra cost, it increases the loyalty of customers, which leads to enhancing profits (Sazvar et al. 2021a). On the other side, due to several man-made and natural disruptions and disasters that have occurred in recent years (e.g., the COVID-19 pandemic and the Turkey earthquake), incorporating the resilience concept into the supply chain can lead to improving the capability of company to deal with disruptions and gaining competitive advantage (Namdar et al. 2021). On the other hand, given the crucial role of sustainability and resilience, these concepts have been introduced as the two main pillars of Industry 5.0 in which resilience and sustainability are integrated to configure the SCNs in the future (Breque et al. 2021; Nayeri et al. 2023). Besides, owing to the importance of sustainability and resiliency, these features are considered the major parts of the viable supply chain (Ivanov 2020; Rostami et al. 2022) as a post-pandemic supply chain, which demonstrates their crucial role. Hence, this research attempts to incorporate both of these crucial features in designing the SCN for the selected case study.

Nowadays, dairy products are an important part of people's daily diet. In this regard, Fig. 1 shows the per capita dairy consumption between 1980 and 2022. Based on the report of IBSI world, it is expected that per capita dairy consumption grows at an annualized rate of 0.3% to 651.2 pounds per person. Dairy products are crucial for maintaining a healthy weight and building bones. Also, these products are very important for the health of gums and teeth. In addition, dairy products are rich in vitamin A, vitamin D, calcium, and protein. On the other side, based on the report of McKinsey & Company, demand for dairy products has increased during the Coronavirus outbreak. Therefore, motivated by the mentioned points and due to the importance of dairy products, the present work aims at studying the logistic system of dairy products.

Fig. 1

The per capita dairy consumption between 1980 and 2022 (IBSI world)

In the current study, the preventive approach for resiliency has been incorporated into the research problem using two strategies: (i) considering the resilience indicators in the supplier selection phase and (ii) maximizing the probability of not facing disruption in the distribution centers. Regarding the importance of the first strategy, we can give the following example. On 17 March 2000, the production capacity of Philips company, a supplier of Ericsson and Nokia companies, was disrupted by fire. At that time, Nokia At that time, Nokia decided to sign a new contract with the backup suppliers, but Ericsson believed that Philips could handle this issue and did not do anything. After several weeks, Ericsson faced a loss of over 400 million dollars (Zsidisin and Wagner 2010). This example demonstrates the importance of considering the resiliency strategies in the supplier selection phase. On the other side, regarding the importance of the second strategy, we can refer to the recent pandemic (COVID-19). This pandemic originated in Wuhan, which was a global distribution center for the medical devices, optical electronics, automotive, and biomedicine industries. This pandemic led to a drastic disruption in distributing the raw materials of the mentioned industries and caused severe losses to these industries. For example, Hyundai company decided to suspend its production lines in Korea because of the delay in the raw material supply caused by the COVID-19 pandemic in China (Namdar et al. 2021). The provided example shows the crucial role of the resilience strategy in distribution centers. Hence, the current work aimed to adopt the preventive resilience strategy so that in the first stage, the resilience indicators have been considered in the supplier selection process. Then, the probability of not facing disruption in the distribution centers is maximized.

This study attempts to develop a multistage decision-making framework for planning a sustainable-resilient SCN. For this purpose, the Fuzzy Decision Making and Trial Evaluation Laboratory (FDEMATEL), Fuzzy Multi-Objective Optimization model based on the Ratio Analysis (FMOORA), and the mathematical model approaches are integrated. Afterward, the proposed multi-objective model is solved employing the preemptive fuzzy goal programming method. The following points are the main contributions of this work: (i) presenting a comprehensive study to integrate the sustainability and resiliency measures in the SCN design problem for the dairy industry, (ii) applying the multiple-attribute decision-making methods to calculate the values of the sustainability and resiliency indicators, (iii) incorporating the resilience concept in the research problem with a preventive approach, (iv) considering the interrelationships among sub-criteria of sustainability and resiliency aspects, and (v) investigating a real-world case study.

The rest of this study is organized as follows: The literature review and research methodology are presented in Sects. "Literature review" and "Research methodology", respectively. The computational results are presented in Sect. "Computational results". Finally, conclusions are provided in Sect. "Conclusion".

Literature review

Sustainable and resilient supply chain

Mari et al. (2014) presented a mathematical model to configure a Sustainable-Resilient SCN (SRSCN). They considered disruption risks as the resiliency indicator and environmental impacts as the sustainability indicator. They solved the offered model using the weighted goal programming (GP) method. Fahimnia and Jabbarzadeh (2016) configured an SRSCN by proposing a multi-objective programming (MOP) model. Their model aimed at maximizing the sustainability measures while minimizing the total costs. They investigated a real application in the sports clothes industry and solved the problem by employing the fuzzy GP (FGP) approach. Zahiri et al. (2017) studied the SCND problem by considering sustainability and resiliency dimensions for the pharmaceutical case study. They suggested a model to minimize environmental damages the costs and non-resiliency measures. They employed a metaheuristic algorithm to solve the research problem. A stochastic programming model was suggested by Jabbarzadeh et al. (2018) to configure an SCN with simultaneous consideration of resiliency and sustainability indicators. Then, they obtained the Pareto front by employing the $\varepsilon$-constraint approach. Fazli-Khalaf et al. (2020) configured an SRSCN by proposing a possibilistic MOP for the tire industry. The suggested model tried to optimize the sustainability dimensions. Also, the authors maximized the reliability of network facilities as the resilience strategy. Finally, the $\varepsilon$-constraint method is applied to solve the suggested MOP model.

Mehrjerdi and Shafiee (2020) suggested a multistage model for configuring an SCN with sustainability and resiliency features for the tire industry. They first applied the TOPSIS method to rank the resilience strategies. Afterward, a MOP model was suggested to design an SRSCN. Hosseini-Motlagh et al. (2020) develop a hybrid model to design an SCN for the wheat industry considering the resiliency and sustainability indicators, simultaneously. To this end, the authors proposed a MOP model that maximized the social impact and resilience of the SC and minimized the total costs. Mishra and Singh (2020) studied the sustainable-resilient reverse logistics system considering big data in an uncertain environment. The obtained results showed that the dynamic allocation and flexible capacity increased the capability of the supply chain to deal with disruptions. Kaur et al. (2020) tried to configure a sustainable and resilient production and procurement system. They proposed an independent and integrated model. The obtained results showed that the integrated model provided better solutions. A reverse logistics with resiliency and sustainability features for the vehicles industry was designed by Govindan and Gholizadeh (2021). They offered a scenario-based mathematical model by considering the impact of big data. Eventually, they solved the offered model using a metaheuristic algorithm. Shabbir et al. (2021) suggested a MOP to maximize the resiliency and sustainability measures in the SCND problem. They applied the robust counterpart model to tackle uncertainty. Sazvar et al. (2021a, b) studied the SRSCN design problem for the vaccine case study using a capacity planning approach. The authors offered a MOP model to optimize the resiliency and sustainability dimensions. They applied multi-choice GP to achieve the solution. Nayeri et al. (2021) configured an SCN with sustainability and resiliency features using a mathematical model. In that research, a new version of goal programming was developed to obtain the optimal solution. Vali-Siar and Roghanian (2022) designed a sustainable and resilient SC in which the responsiveness metric was considered. It should be noted that they selected the tire industry as a real application. The authors used the Lagrangian relaxation method to solve the research problem. Taleizadeh et al. (2022) studied the pricing decision in the resilient SC problem considering the sustainability factors. They considered the manufacturer as the follower and the government as the leader and then employed Stackelberg's game approach. Akbari-Kasgari et al. (2022) designed a resilient and sustainable SC for the copper industry. The authors considered the social, environmental, and financial aspects as the sustainability factors and adopted the backup supplier strategy as the resiliency factor. Mohammed et al. (2021a, b) employed the decision-making methods to investigate the supply and demand resilience. In this regard, the authors developed a hybrid method based on the DEMATEL and technique for order of preference by similarity to ideal solution (TOPSIS) approaches to quantify the resilience of suppliers and their performance. Then, they used the obtained weights as a input in a possibilistic bi-objective mathematical model. Mohammed et al. (2021a) focused on the green and resilient supplier selection and order allocation problem by employing a hybrid method based on the analytical hierarchy process (AHP), TOPSIS, and $\varepsilon$-constraint approaches. The authors first evaluated the performance of the suppliers using the AHP-TOPSIS approach and then proposed a multi-objective model to determine the quantity of orders. Finally, they solved the proposed model using the $\varepsilon$-constraint method. Mohammed (2020) conducted a quantitative study to overcome several issues regarding identifying, quantifying, and exploring greenness and resiliency performance in the supplier selection problem. For this purpose, the author employed the DEMATEL and VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) methods. Mohammed et al. (2019) studied the green and resilient supply chain network design problem by using the decision-making methods. In this regard, the authors obtained the importance of the indicators using the fuzzy AHP method and then proposed a multi-objective fuzzy programming model to configure a supply chain network. In the next step, they solved the proposed model by the $\varepsilon$-constraint method and then applied the TOPSIS method to rank the Pareto solutions. Nayeri et al. (2022) investigated the sustainable and resilient supply chain network design problem by considering the role of global factors. The authors proposed a multi-objective mathematical model and solved it employing the weighted Tchebycheff. Zhang and Yu (2023) tried to investigate the low-carbon closed-loop supply chain problem using the dynamic decision-making approach. The authors considered government double subsidies and different power structures. Sazvar et al. (2022) focused on sustainable and resilient supplier selection using decision-making and data mining methods. In this way, they developed a data-driven decision-making framework based on the fuzzy Best–Worst Method (BWM) and fuzzy inferences system approaches. Abbasian et al. (2023) proposed a mathematical programming model to configure a sustainable and resilient supply chain network considering the location, inventory, and routing decisions. Then, they developed a heuristic-based goal programming method to solve the research problem. Also, several studies investigated the SRSCN problem with other approaches such as simulation and system dynamics (Fahimnia et al. 2018; Ivanov 2018; Rajesh 2018; Ramezankhani et al. 2018; Pavlov et al. 2019; Souza et al. 2019). To better understand, Table 1 categorizes the reviewed literature, and Table 2 shows the considered indicators for sustainability and resiliency in previous papers.

Table 1 Categorizing the most related previous papers

Table 2 The sustainability and resiliency indicators in the previous studies

The dairy supply chain

In this section, we report some relevant articles in the dairy SC area. In this area, Yang et al. (2015) offered a new model to configure an SC network for the dairy industry. They used an approximation method to solve the offered model. Yavari and Geraeli (2019) suggested a mathematical model for designing a closed-loop supply chain network considering the environmental concerns of the dairy industry. They developed a heuristic method to compute the value of the objective function. Jouzdani et al. (2020) investigated the SC network design problem for dairy products. The authors proposed a robust optimization model to configure a multi-product dairy SC considering multiple transportation modes. Jouzdani and Govindan (2021) configured a sustainable SC for dairy products. The authors proposed a MOP that optimized the social, financial, and environmental goals. A model was proposed by Yavari and Ajalli (2021) to design a resilient and green SC for a dairy company. The authors showed that the average carbon emissions and total costs decreased when the resiliency and greenness aspects were considered. Cakar and Çavuş (2021) evaluated the performance of the suppliers for the dairy industry by employing the fuzzy TOPSIS method. In this regard, first, they determined the related criteria and alternatives. Then, they measured the indicators’ weights and ranked the alternatives. Gholizadeh et al. (2021) suggested a multi-objective model for configuring an SC network considering the sustainability aspect. They used the $\varepsilon$-constraint method to achieve Pareto solutions. Munien and Telukdarie (2021) tried to model resilience in the supply chain for the dairy case study. For this purpose, the authors developed a system dynamic model to investigate the role of digitalization and localization factors. The results indicated that by enhancing digitalization and localization, employment and inventory levels also increased. Kazancoglu et al. (2021) investigated the dairy supply chain problem by proposing a fuzzy-based hybrid decision framework. In this regard, the authors combined the fuzzy methods to identify and evaluate the main barriers in the dairy supply chain. Prakash (2022) focused on the role of resilience in the dairy supply chain. In this regard, the authors conducted an empirical study in India to identify the sources of the disruptions. The results showed that disruptions have a negative effect on flexibility, efficiency, quality, and responsiveness. Behzadianfar et al. (2022) proposed a model to design an SC under a fuzzy environment for the dairy industry. The authors considered three targets involving economic, social, and environmental objective functions to incorporate the sustainable development pillars into the research problem. Moreno-Camacho et al. (2022) investigated the supply chain problem considering the sustainable development pillars for the dairy industry. The suggested model could make optimal decisions regarding supplier selection, facility location, transportation mode selection, and materials flow. Lagarda-Leyva et al. (2023) focused on the food supply chain problem considering the sustainability concept by proposing a methodological framework based on the system dynamic approach to transform this waste into co-products and generate business opportunities.

Research gap and contributions

The literature shows that the sustainable-resilient SCND problem has become a trending topic among researchers, recently. In this regard, although recently several works have been conducted in this field, the simultaneous incorporation of the resiliency and sustainability dimensions into the dairy industry has been ignored by the previous papers. However, dairy products are among the most consumed food products, especially after the Coronavirus outbreak, and considering the mentioned concepts can enhance the efficiency of the SCs. Moreover, due to the high importance of resiliency and sustainability, these concepts have been introduced as the main pillars of the viable supply chain and Industry 5.0, which shows the essential role of these concepts in modern businesses. On the other hand, the preventive approach for resiliency has been rarely addressed by the previous papers, and the majority of studies were focused on the recovery aspect of resilience and used some strategies such as the extra capacity to recoil from disruptions. In this regard, the current work applies a preventive approach to incorporate the resiliency aspect into the research problem. Another point, the present research investigates the interrelationships among the sub-criteria of sustainability and resiliency aspects in the sustainable-resilient supply chain planning problem that was ignored by the previous papers. Regarding the difference between this work and most related studies, for example, in comparison with (Mohammed et al. 2021a), they considered green and resilience criteria, but this work considers green, social, and resilience criteria. Also, the model proposed by Mohammed et al. 2021a only determined the number of products ordered from suppliers, but the model proposed in this study determines the number of orders from suppliers, the number of manufactured products, the quantity of lost sales, and also the quantity of inventory. In addition, in comparison with Mohammed et al. (2019), they did not consider the social impacts in their work, which has been considered in the current study. Also, the current work considers lost sales and inventory levels, which did not consider by Mohammed et al. (2019).

In general, based on the mentioned points, the main contributions of this study can be summarized as follows:

• This research is among the first ones that simultaneously investigates the sustainability and resiliency concepts in the dairy supply chain by considering the interrelationships among the indicators.

• This research develops an efficient multistage decision-making framework that can evaluate the suppliers based on sustainability and resiliency measures and set an optimal plan for the supply chain, simultaneously.

• This study incorporates the resiliency dimension into the problem by a preventive approach.

• This study considers the interrelationships among the sub-criteria of the resiliency and sustainability aspects.

Research methodology

This research develops a multistage decision-making framework to evaluate the performance of the suppliers based on the resilience and sustainability indicators and configure a supply chain network for the dairy industry. The considered supply chain network includes three echelons, namely suppliers, production plants, and distribution centers. The performance of suppliers is assessed in the first stage, and the supply chain configuration is determined in the second stage. In this regard, the proposed research methodology of the research consists of two phases. At the beginning of the first phase, the considered products and facilities are selected. In other words, the case study is identified. Then, the potential suppliers and distribution centers are specified. In the next step, the main indicators for evaluating the suppliers’ performance are identified. Then, the fuzzy DEMATEL and fuzzy MOORA approaches are utilized to measure the weight of the criteria and the coefficients of resiliency and sustainability of suppliers, respectively. Regarding the distribution centers, the probability of disruption (e.g., floods and earthquakes) is determined by collecting data on the occurrence of such natural disasters at the location of these facilities. The outputs of the first stage are utilized as the input of the second stage. Finally, the model is solved by employing the preemptive fuzzy goal programming method. The flowchart of the described research methodology is depicted in Fig. 2. Although the current work does not develop a new method or technique, it has provided a novel application of a multistage method in the dairy industry (Stage I: FDEMATEL and FMOORA methods, Stage II: Mathematical model and Preemptive fuzzy goal programming).

Fig. 2

The flowchart of the research methodology

The main reasons for employing the FDEMATEL method are as follows: (i) it is one of the best approaches to identify the cause and effect relationship between indicators (Akyuz and Celik 2015), (ii) using the DEMATEL method leads to decreasing the number of chosen criteria for the evaluation, which can beneficial for organizations to increase the efficiency of particular factors (Tzeng et al. 2007), (iii) this method helps experts to deal with uncertainty/imprecision of the business environment (Muhammad and Cavus 2017), (iv) it has widely used in the previous papers and showed good performance (for example, see Fallahpour et al. 2021; Alamroshan et al. 2022). On the other hand, the main reasons for using the FMOORA method are as follows: (i) It is very simple, robust, and stable (Karande and Chakraborty 2012), (ii) it requires minimum computational time and mathematical calculations (Brauers and Zavadskas 2012), (iii) it is widely employed in the previous papers and showed appropriate performance (for example, see Arabsheybani et al. 2018; Arslankaya and Çelik 2021).

Problem description

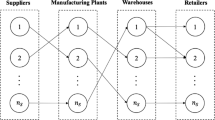
Motivated by the crucial role of the sustainability and resilience factors, which are introduced as the main pillars of Industry 5.0 (Breque et al. 2021; Nayeri et al. 2023) and a viable supply chain (Ivanov 2020; Lotfi et al. 2021), this research focuses on the simultaneous evaluation of resiliency and sustainability in a supply chain of dairy products. The SCN that is considered in the present study consists of three echelons involving suppliers, a production plant, and distribution centers. In this SCN, first, the required milk for the production process is provided by animal husbandry and sent to the production plant. Afterward, the other raw materials are bought from the suppliers. The production plant produces different types of products such as various flavors of milk, yogurt, ayran, cheese, ice cream, and faloodeh. After completing the production process and packaging, the products would be transferred to different distribution centers. So, the main costs of the considered supply chain are as follows: The purchasing costs, the contracting costs, the holding costs, the production costs, and the transportation costs. Figure 3 shows the considered supply chain network.

Fig. 3

The configuration of considered three echelons supply chain

The resiliency and sustainability dimensions help supply chain leaders to deal with unpredictable disruptions and increase supply chain efficiency. Hence, the current work has incorporated the resiliency concept into the considered supply chain network to improve its performance. In this regard, the present paper proposes four objective functions (OFs). The first OF attempts to reduce the cost of the network. The resiliency and sustainability indicators of suppliers are addressed in the second and third objective functions. Finally, the last objective function focuses on the resiliency of distribution centers. In general, the current work incorporates the resilience concept into the research problem in two steps. In the first step, the suppliers are evaluated according to the resilience indicators (see stage 1). Moreover, in the next step, the resiliency of the suppliers and distribution centers is maximized in Stage 2 (mathematical model). Hence, by evaluating the suppliers based on the resiliency indicators and maximizing the resiliency of the distribution centers, the designed supply chain becomes resilience against potential disruptions.

Stage one

Phase one focuses on calculating the coefficient of resiliency and sustainability scores of supplier using a multi-level approach. Various criteria and factors are considered in calculating the scores. The three steps of phase one are explored in the following.

Step one: identifying the criteria

In this step, various criteria are studied and analyzed, and then, the decision-maker selects the most practical criteria for evaluating suppliers. Suppliers are evaluated based on both resiliency and sustainability criteria. In this regard, according to the experts’ opinions and the literature, the following criteria are identified for sustainability (Table 3) and resiliency (Table 4). It should be noted that to extract the indicators, in this research, we first determine the potential indicators based on the literature. Then, the experts of the considered company selected the indicators that they think were most relevant to the selected industry. Hence, although factors such as flexibility and communications were among the initial potential indicators, they did not select them as the final indicators. The profile of the experts is presented in Table 5. In addition, it should be noted that although the cost is one of the most important economic factors, we did not consider it as an indicator in stage I because it has been considered and incorporated into the mathematical programming model in Stage II.

Table 3 The considered criteria for sustainability

Table 4 The considered criteria for resiliency

Table 5 Respondents' profile

Step two: determining the weights of the criteria

Determining the weight of criteria is one of the essential steps of decision-making problems. This study aims to address various criteria for the sustainability and resilience of suppliers, and the FDEMATEL is chosen for this end. Even though employing the quantitative approaches might present more precise results, since humans are involved in the decision-making process, using these methods would not work in the best way possible. This is because of the ambiguity, uncertainty, and different perception of different people from a specific situation, affecting the final results of the problem. Hence, it would be more practical to use the fuzzy sets logic suggested by Zadeh (1965).

Fontela and Gabus (1976) presented the DEMATEL, which is a decision-making approach based on pairwise comparison and the opinion of experts used for solving complicated problems. The method was extended to fuzzy DEMATEL by Wu and Lee (2007). Since the final results of the problem depend on the opinion of experts, inviting an acceptable number of experts would help reach more accurate results and close to real situations. The steps of the fuzzy DEMATEL approach are explored in detail by Lin and Wu (2008).

Step three: determining the coefficient score of alternatives

Different methods are utilized to compute the coefficient of considered factors of suppliers in decision-making problems. Multi-criteria problems mainly consist of qualitative and quantitative factors. Qualitative factors are mostly hard to translate into quantitative factors due to the ambiguity in the perception of experts and the unavailability of precise information. The FMOORA, which is a simple and understandable approach addressing a large number of criteria, could be one of the most practical approaches to use in these situations (Siddiqui and Tyagi 2016). This approach is explored in detail by Siddiqui and Tyagi (2016).

Stage two

Phase two focuses on incorporating the calculated information from phase one into a MOP model. It should be noted that the scores of suppliers that were calculated based on the sustainability and resiliency indicators using the FMOORA method are employed as inputs for the mathematical programming model (parameters γ_sr and θ_sr). The assumptions used in shaping the mathematical model and the notations used in presenting the model are presented in the following.

Assumptions

• According to the considered case study, the dairy production plant is responsible for managing the whole supply chain.

• Since the considered company produces multiple products that require purchasing multiple raw materials, in this study, multiple raw materials and products are considered.

• Inspired by many papers in the literature and also based on the request of the considered case study, the model is based on a multi-period problem with a one-month planning horizon.

• According to real-world conditions, each supplier can only provide one type of raw material, and multiple suppliers can be used for acquiring the required amount of one type of raw material.

• Inspired by real-world conditions and related papers, the production capacity and holding capacity of raw materials and products are limited.

• According to the considered case study, all transportation is done using trucks and roads.

• Inspired by the literature and according to the selected case study, the profit margin of selling products is a portion of the price they are sold.

• Based on the related papers in the literature and also according to the conditions of the considered case study, lost sales are considered in presenting the model.

Notations

s:

Suppliers

r:

Raw materials (RM)

p:

Products

d:

Distribution centers (DC)

t:

Periods

γ_sr:

The resiliency score for supplier s that provided raw material r

θ_sr:

The sustainability score for supplier s that provided raw material r

CP_srt:

The cost of purchasing RM r from supplier s in period t

OD_st:

Fixed purchasing cost from supplier s in period t

HR_r:

Holding cost of RM r in production plant

HP_p:

Holding cost of product p in production plant

CTO_pt:

The unit of manufacturing cost for product p in period t

TR_sr:

The cost for shipping raw material r between supplier and manufacturer

TL_dp:

The cost for shipping product p from plant to DC d

PR_d:

Disruption probability in distribution center d

SA_pt:

Profit margin of selling product p in period t

Z_rt:

Capacity of production plant for holding raw material r in period t

ZN_pt:

Capacity of production plant for holding product p in period t

ZK_pt:

Capacity of production plant for producing product p in period t

ZS_srt:

Capacity of supplier s for providing raw material r in period t

N_rp:

The utilization rate of raw material r to manufacture product p

TM_p:

Required time for manufacturing a product p

DE_dpt:

Demand of distribution center d for product p in period t

F_dpt:

Cost of lost sales of product p in period t

Q_srt:

The amount of RM r transported to production plant from supplier s in period t

Y_srt:

A binary variable that equal to 1 if supplier s is selected to purchase RM r in period t

TO_pt:

The quantity of produced product p in period t

QL_dpt:

The quantity of product p transported to DC d from production plant

IR_rt:

Inventory of RM r

IP_pt:

Inventory of product p

LS_dpt:

Lost sell of product p in DC d

Mathematical model

Equation (1) calculates the purchasing costs and relation (2) computes the cost of working with suppliers.

$$\text{PeC} = \sum\limits_{s} {\sum\limits_{r} {\sum\limits_{t} {{\text{CP}}_{srt} \times Q_{srt} } } }$$

(1)

$$\text{FPeC} = \sum\limits_{s} {\sum\limits_{r} {\sum\limits_{t} {{\text{OD}}_{srt} \times Y_{srt} } } }$$

(2)

Relation (3) calculates the cost of producing goods.

$$\text{ProC} = \sum\limits_{p} {\sum\limits_{t} {{\text{CTO}}_{pt} \times {\text{OT}}_{pt} } }$$

(3)

Relations (4) and (5) compute the holding costs.

$${\text{HCR}} = \sum\limits_{r} {\sum\limits_{t} {{\text{HR}}_{r} \times {\text{IR}}_{rt} } }$$

(4)

$${\text{HCP}} = \sum\limits_{p} {\sum\limits_{t} {{\text{HP}}_{p} \times {\text{IP}}_{pt} } }$$

(5)

The transportation costs are calculated in Eqs. (6) and (7).

$${\text{TCSP}} = \sum\limits_{s} {\sum\limits_{r} {\sum\limits_{t} {TR_{sr} \times Q_{srt} } } }$$

(6)

$${\text{TCPD}} = \sum\limits_{d} {\sum\limits_{p} {\sum\limits_{t} {{\text{TL}}_{dp} \times {\text{QL}}_{dpt} } } }$$

(7)

Relation (8) calculates the cost of lost sales.

$${\text{CLS}} = \sum\limits_{d} {\sum\limits_{p} {\sum\limits_{t} {F_{dpt} \times {\text{LS}}_{dpt} } } }$$

(8)

$$\begin{aligned} {\text{Min}}\,\,{\text{TC}} & = {\text{PeC}} + {\text{FPeC}} + {\text{ProC}} + {\text{HCR}} \\ & \quad + {\text{HCP}} + {\text{TCSP}} + {\text{TCPD}} + {\text{CLS}} \\ \end{aligned}$$

(9)

Equation (9) is the first objective function that aims to minimize the total cost. In this regard, the total cost includes fixed and variable purchasing cost of raw materials, production cost, holding cost of raw materials and products, transportation cost of raw materials and products, and lost sale costs.

$${\text{Max}}\,{\text{SUS}} = \sum\limits_{s} {\sum\limits_{r} {\sum\limits_{t} {\gamma_{sr} \times Q_{srt} } } }$$

(10)

$${\text{Max}}\,{\text{RES}} = \sum\limits_{s} {\sum\limits_{r} {\sum\limits_{t} {\theta_{sr} \times Q_{srt} } } }$$

(11)

Equation (10) (the second objective function) aims to maximize the sustainability of suppliers. Moreover, relation (11) (the third objective function) attempts to maximize the resiliency of suppliers.

$${\text{Max}}\,{\text{RED}} = \sum\limits_{d} {\sum\limits_{p} {\sum\limits_{t} {\left( {1 - {\text{PR}}_{d} } \right) \times {\text{SA}}_{pt} \times {\text{QL}}_{dpt} } } }$$

(12)

The expected disruption cost (EDC), which is one of the resilient SC factors, is considered for distribution centers (Mari et al. 2014). The EDC can be defined as the cost of lost opportunity in the on-time delivery of products to the customers in case of disruption occurrence (Mari et al. 2014). Maximizing the probability of not facing disruption and, subsequently, the lost sales is presented in Eq. (12). This maximization would work in favor of having a resilient supply chain.

Constraints:

$$Q_{srt} \le {\text{ZS}}_{srt} \times Y_{srt} \quad \forall s,r,t$$

(13)

$${\text{IR}}_{rt} \le Z_{rt} \quad \forall r,t$$

(14)

$${\text{TM}}_{p} \times {\text{TO}}_{pt} \le {\text{ZK}}_{pt} \quad \forall p,t$$

(15)

$${\text{IP}}_{pt} \le {\text{ZN}}_{pt} \quad \forall p,t$$

(16)

Relations (13)–(16) are the capacity constraints of the research problem. In this regard, Eq. (13) shows that only the selected suppliers can provide the required raw materials and in a limited amount restricted by their capacity. The limited capacity of the production plant for holding raw materials is presented in Eq. (14). Equation (15) represents the capacity constraint for the production centers. The limited capacity of the production plant in holding different products is shown in Eq. (16).

$$\begin{aligned} & {\text{IR}}_{{r\left( {t - 1} \right)}} + \sum\limits_{s} {Q_{srt} } \\ & \quad = {\text{IR}}_{rt} + \sum\limits_{p} {N_{rp} \times {\text{TO}}_{pt} } \quad \forall r,t \\ \end{aligned}$$

(17)

$${\text{IP}}_{{p\left( {t - 1} \right)}} + {\text{TO}}_{pt} = {\text{IP}}_{pt} + \sum\limits_{d} {{\text{QL}}_{dpt} } \quad \forall p,t$$

(18)

Equation (17) guarantees the equality of inventory of raw materials from the previous period and purchased raw material in the current period to the inventory of raw material at the end of the current period and the used raw materials in the produced products. Relation (18) shows the flow balance constraint in the distribution center.

$${\text{DE}}_{dpt} = {\text{QL}}_{dpt} + {\text{LS}}_{dpt} \quad \forall d,p,t$$

(19)

Relation (19) calculates the amount of product sent to distribution centers and also the quantity of lost sales.

$$Q_{srt} ,{\text{QL}}_{dpt} ,{\text{TO}}_{pt} ,{\text{LS}}_{dpt} ,{\text{IR}}_{rt} ,{\text{IP}}_{pt} \ge 0$$

(20)

$$Y_{srt} \in \left\{ {0,1} \right\}$$

(21)

Equations (20) and (21) show the range of variables (i.e., the positive and binary variables).

Preemptive fuzzy GP

GP is known as efficient method to solve the MOP models (Nayeri et al. 2018). In formulating goal programming approaches, the aspiration levels of objective functions should be precisely determined (Mamashli et al. 2021). However, in real-life situations finding these aspiration levels would be almost impossible for decision-makers because of the existing uncertainty in data (Khan and Mahmood 2019). The fuzzy sets theory is one of the most practical tools used to address the uncertainty of the data decision-making process (Kim et al. 2000). Hence, integrating it with goal programming and developing the FGP method would be a practical idea. Mirzaee et al. (2018) presented a new extension of FGP and named it preemptive FGP. Preemptive FGP was presented by extending FGP with different importance and priorities to fix its limitation. In general, the FGP has been applied in the current work for the following reasons: (i) it can tackle the uncertainty of the data decision-making process, (ii) it is widely used in the related literature and showed good performance (see Selim and Ozkarahan 2008; Subulan et al. 2015; Kilic and Yalcin 2020; Zandkarimkhani et al. 2020), (iii) this approach considers different importance and priorities. This approach can be formulated as follows (Mirzaee et al. 2018).

μ_i:

Achievement degree of objective i

f_i:

Value of objective function i

Low_i:

Lower bound of goal i

Up_i:

Upper bound of goal i

Goal_i:

Specified goal for objective function i

${d}_{i}^{+}$,${d}_{i}^{-}$:

Deviation of objective function o from the specified goal

The general configuration of PFGP:

$${\text{Max}}\,Z = \mathop \sum \limits_{i} \mu_{i}$$

(22)

Subject to:

$$co_{m} \left( x \right) \le = \ge 0\quad \forall m$$

(23)

$$\mu_{i} + \frac{1}{{{\text{Goal}}_{i} - {\text{Low}}_{i} }} \times d_{i}^{ - } \le 1\quad {\text{Maximizing objective functions}}$$

(24)

$$f_{i} + d_{i}^{ - } \ge {\text{Goal}}_{i}$$

(25)

$$\mu_{i} + \frac{1}{{{\text{Up}}_{i} - {\text{Goal}}_{i} }} \times d_{i}^{ + } \le 1\quad {\text{Maximizing objective functions}}$$

(26)

$$f_{i} - d_{i}^{ + } \le {\text{Goal}}_{i}$$

(27)

$$\mu_{i} \ge \mu_{{i^{\prime}}} \quad \forall i \ne i^{\prime}$$

(28)

$$X,\mu_{i} ,d_{i}^{ + } ,d_{i}^{ - } \ge 0$$

(29)

Equation (22) maximizes the summation of all achievement degrees of objectives. Equation (23) shows the system constraints of the problem. It should be noted that $c{o}_{m}\left(x\right)$ shows the constraints of the original model. For maximizing objective functions Eqs. (24) and (25), and for minimizing objective functions Eqs. (26) and (27) compute the achievement degree of objectives. Each objective function with a higher priority according to the decision maker should achieve a higher achievement degree. This condition is presented in the model using Eq. (28). In other words, this constraint determines the priority of objective functions. Equation (29) shows the variation range of decision variables. Also, it should be noted that in the employed method, the linear membership function for the $i$-th goal is defined as follows.

For maximization

$$\mu = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{if}}\;f_{i} \ge {\text{Goal}}_{i} } \hfill \\ {\frac{{f_{i} - {\text{Low}}_{i} }}{{{\text{Goal}}_{i} - {\text{Low}}_{i} }}} \hfill & {\quad {\text{if}}\;{\text{Low}}_{i} \le f_{i} \le {\text{Goal}}_{i} } \hfill \\ 0 \hfill & {\quad {\text{if}}\;f_{i} \le {\text{Low}}_{i} } \hfill \\ \end{array} } \right.$$

(30)

For minimization

$$\mu = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{if}}\;f_{i} \le {\text{Goal}}_{i} } \hfill \\ {\frac{{{\text{Up}}_{i} - f_{i} }}{{{\text{Up}}_{i} - {\text{Goal}}_{i} }}} \hfill & {\quad {\text{if}}\;{\text{Goal}}_{i} \le f_{i} \le {\text{Up}}_{i} } \hfill \\ 0 \hfill & {\quad {\text{if}}\;f_{i} \ge {\text{Up}}_{i} } \hfill \\ \end{array} } \right.$$

(31)

Presented mathematical model after using the solution approach

The mathematical model using the PFGP is changed as follows:

$${\text{Max}}\;Z = \mu_{1} + \mu_{2} + \mu_{3} + \mu_{4}$$

(32)

Subject to: (13)–(21) and (29)

$$\mu_{1} + \frac{1}{{{\text{Up}}_{1} - {\text{Goal}}_{1} }} \times d_{1}^{ + } \le 1$$

(33)

$$f_{1} - d_{1}^{ + } \le {\text{Goal}}_{1}$$

(34)

$$\mu_{2} + \frac{1}{{{\text{Goal}}_{2} - {\text{Low}}_{2} }} \times d_{2}^{ - } \le 1$$

(35)

$$f_{2} + d_{2}^{ - } \ge {\text{Goal}}_{2}$$

(36)

$$\mu_{3} + \frac{1}{{{\text{Goal}}_{3} - {\text{Low}}_{3} }} \times d_{3}^{ - } \le 1$$

(37)

$$f_{3} + d_{3}^{ - } \ge {\text{Goal}}_{3}$$

(38)

$$\mu_{4} + \frac{1}{{{\text{Goal}}_{4} - {\text{Low}}_{4} }} \times d_{4}^{ - } \le 1$$

(39)

$$f_{4} + d_{4}^{ - } \ge {\text{Goal}}_{4}$$

(40)

$$\mu_{1} \ge \mu_{2}$$

(41)

$$\mu_{2} \ge \mu_{3}$$

(42)

$$\mu_{3} \ge \mu_{4}$$

(43)

This research applies the lexicographic approach to calculate the values of the lower bound and upper bound of the objective functions (OFs) (see Table 6). Also, for the minimization objective functions, ${\mathrm{goal}}_{i}$ is calculated by solving the model to minimize the ith OF. On the other side, for the maximization of OFs, ${\mathrm{goal}}_{i}$ is computed by solving the model to maximize the i-th objective function. It should be noted that $Zi$ shows the $i$-th OF of the proposed model (i.e., ${Z}_{1}=TC,{Z}_{2}=\mathrm{SUS},{Z}_{3}=\mathrm{RES},$ and ${Z}_{4}=\mathrm{RED}$).

Table 6 The way of calculating the upper bound and lower bound of each OF

Computational results

Case study

To demonstrate the application of the developed decision-making framework, this research has considered a case study in the dairy industry. Zarrin Ghazal Company with the brand of Daity is one of the popular firms in the dairy industry in Iran. This company is located in Shiraz city and produces different types of dairy products such as milk, cheese, cream, yogurt, dough, faloodeh, and ice cream. Information about the bill of materials (BOM) is given in Table 7. Also, Fig. 4 depicts the potential suppliers and distribution centers of this company.

Table 7 The utilization rate of raw materials in each product

Fig. 4

The location of facilities of the supply chain of the considered case study

On the other side, based on the collected data, the disruption probability for each DC is reported in Table 8. In this regard, to estimate the probability of disruption, at the outset, we sent an email to the Seismological Center of Iran (http://irsc.ut.ac.ir/index.php?lang=fa), and they sent us the total number of earthquakes that occurred in each location that we considered as the potential location for establishing the distribution centers. Then, we used the following relation where ${Y1}_{d}$ is the number of earthquakes in location $d$ whose magnitude was between 5 to 6, ${Y2}_{d}$ shows the number of earthquakes in location $d$ whose magnitude was between 6 to 7 and demonstrates the total number of earthquakes in location $d$. Also, $w1$ shows the weight of the earthquakes whose magnitude was between 5 to 6, and $w2$ demonstrates the weight of the earthquakes whose magnitude was between 6 to 7. In this study, we considered $w1$ equal to 0.25 and $w1$ equal to 0.75.

$${\mathrm{PR}}_{d}= \frac{w1.{Y1}_{d}+w2.{Y2}_{d}}{{YT}_{d}}$$

(44)

To better understand, we calculate the probability of disruption in location #4 (Gilan), which is equal to 0.05. In this regard, based on the gathered data, for this location, $Y1=6$, $Y2=1$, and $YT=45$. Hence, the probability of disruption for this location is calculated as follows:

$${\mathrm{PR}}_{4}= \frac{0.25\times 6+0.75\times 1}{45}=0.05$$

The time horizon considered by this research is included four periods, and the production capacity for each period for Cream, Dough, Ice cream, and Faloodeh is equal to 201,650 and for Yogurt, Cheese, and Milk is equal to 101,650. See the Supplementary Materials (Part A) to find other data.

Table 8 The disruption probability for each DC

Reporting the results

Results of the first stage

This section is dedicated to presenting the obtained results from the first stage. First, the scores of the suppliers according to the resiliency and sustainability aspects are measured by applying the FDEMATEL and FMOORA methods. The obtained results by the FDEMATEL method are given in Tables 9 and 10. It should be noted that the calculating flow is provided in the Supplementary Materials (part B). As shown in Table 9, CR2 (responsiveness) and CR3 (facilities reinforcement) are the most important indicators for the resilient aspect. Moreover, according to Table 10, CS1 (reliability) and CS3 (quality) are the most important indicators for sustainability aspect. On the other hand, the obtained results by the FMOORA method are provided in Table 11 (for the resilience criteria) and Table 12 (for the sustainability criteria). See Supplementary Materials (part B) to find the calculation process.

Table 9 The weight of the resilience criteria

Table 10 The weight of the sustainability criteria

Table 11 The results of FMOORA for the resilience criteria (parameter $\gamma_{sr}$)

Table 12 The results of FMOORA for the sustainability criteria (parameter $\theta_{sr}$)

Results of the second stage

Here, the outputs of the second stage are reported. To do this, the model has been implemented in LINGO software and solved on an Intel(R) Core(TM) i7 CPU Q740 @1.73 GHz PC with 4 RAM. For solving the proposed MOP, the importance of the objective functions has been considered as $\mathrm{TC}>\mathrm{SUS}>\mathrm{RES}>\mathrm{RED}$ (based on the experts’ opinions). The outputs are presented in Table 13. As shown in this table, the highest achievement degree belongs to the first OF. The higher achievement degree shows that the obtained objective function is close to the goal determined by the managers. Table 14 shows the selected suppliers for each raw material and their scores, and Table 15 presents the amount of production in each period. The obtained results about the amount of purchased raw materials, the quantity of inventories and lost sales, and the number of products shipped to DCs are provided in Supplementary Materials (part C). To better understand, the costs of SCN are categorized and depicted in Fig. 5, and the percentage of purchasing of each raw material from the selected suppliers is given in Fig. 6. Based on Fig. 5, the highest cost of SCN is related to purchase costs and then production costs, and finally ordering costs have the lowest percentage.

Table 13 The results of solving the proposed MOP

Table 14 The selected suppliers and their score

Table 15 The amount of production in each period

Fig. 5

Classifying the costs of supply chain

Fig. 6

The percentage of purchasing of each raw material from the selected suppliers

Sensitivity analyses

The impact of sustainability and resilience

Here, we have solved the problem under different modes, namely (i) traditional (without sustainability and resiliency concepts), (ii) sustainable, (iii) resilience, and (iv) sustainable-resilient in order to see the impact of resiliency and sustainability. The obtained results are given in Table 16. In this regard, for calculating the goal value of each OF, we solved the model by considering the related OF, separately. As shown in the last row of this table, for every objective function, the goal value is better than all modes. On the other side, regarding the four modes, in the first mode, we just considered the first objective function and as shown in Table 16, the value of TC is equal to its goal value. In mode 2, we considered the first and second objective functions (TC and SUS), jointly. For this reason, the value of both objective functions has been worse than their goal value. On the other hand, in mode 3, we considered the third and fourth objective functions (RES and RED), jointly. Based on the obtained results, the values of both objective functions were less than their goal values. Finally, in mode 4, we have considered all of the objective functions together. In this mode, although the obtained values for the second, third, and fourth objective functions (SUS, RES, and RED) are better than other modes, their values still worse than their goal values. Actually, the value of every objective function in every mode never became better than their goal values. The obtained results show the interaction between resiliency and sustainability features. According to the outputs, by simultaneous consideration of the financial, resiliency, and sustainability indicators, the behavior of the model shifts to create a trade-off between the mentioned measures. For example, the total costs have increased, but the resilience measure is improved. To better understand, Fig. 7 illustrates the behavior of the different measures under the different modes.

Table 16 Comparing the results of different modes for supply chain

Fig. 7

The behavior of the different measures under the different modes

Sensitivity analysis on the OFs’ importance

The impact of the importance of the OFs on the results is investigated in this section. Table 17 shows the results of the sensitivity analysis. The results show that if the manager decides to reduce the total costs but wants to add sustainability and resilience to its SCN, the best prioritization of the objective functions is (1) TC, (2) RED, (3) RES, and (4) SUS.

Table 17 Comparing the results of different modes according to the importance of the objective functions

Demand

Figure 8 shows the behavior of the proposed model according to demand changes. As shown in Fig. 8, by enhancing the demand, all of the costs have increased. According to the outputs, by 30% increasing the demand, the shortage, transportation, production, and purchasing costs have increased by 24, 23, 21, 43, and 42%, respectively. Also, when the demand decreases by 30%, the shortage, transportation, production, and purchasing costs have decreased by 100, 28, 30, 50, and 45%, respectively. It should be noted that by 30% decreasing the demand size, the shortage costs are equal to zero (100% decreasing).

Fig. 8

Sensitivity analysis of the total costs based on demand changes

Robustness and validation of the employed method

This section evaluates the performance of the developed integrated approach. For this purpose, first, we have compared the results of the first stage with a traditional method (Analytic Hierarchy Process-AHP), and then, the results of the second stage are assessed.

Comparing with the traditional methods

Table 18 makes a comparison between the indicators’ weights obtained by the employed method (the outputs of the first stage) with the results of the AHP approach. According to this table, both methods have achieved similar results, which confirms the validity of the employed method. In this regard, as can be seen in Table 18, for all indicators, the weight obtained by the employed method is completely close to the weight obtained by the AHP method. Hence, the achieved results are valid and reliable. Regarding the rationale behind such survey, it should be noted that in the literature to show the performance and efficiency of the outputs of a decision-making method, researchers usually make a comparison between the results of the employed method and a traditional method such as AHP. It should be noted that to implement the AHP method, questionnaires (pairwise comparisons) are dispatched among the experts and then the average of their opinions is used to calculate the weights of the indicators. Also, the consistency ratio (CR) for this method is equal to 0.0676 that close to zero and an acceptable value.

Table 18 Comparing with the AHP method

Evaluating the results of the second stage

To show the efficiency of the applied approach, we have solved several test problems using the employed method (EM) and the traditional fuzzy GP (TFGP). Table 19 compares the obtained results. As shown in Table 19, in all instances, the achievement degree (${\mu }_{i}$) of the EM is higher than TFGP, which demonstrates its better performance.

Table 19 Comparing the employed method with the TFGP

Validating the obtained results

This section aims at validating the outputs of the current work based on the results of the previous related studies. Based on the results of this work, by increasing the amount of demand, the total cost has increased, this behavior also observed in Jouzdani et al. (2020) and Moreno-Camacho et al. (2022), which investigated the dairy supply chain problem. Besides, according to the literature (for example, see Jouzdani and Govindan 2021; Nayeri et al. 2021), by increasing the importance of an objective function, its value in the outs of the goal programming should be improved. The mentioned behavior has been observed in the results of the current work. Also, the behavior of the first objective function under different modes was similar to Jouzdani et al. (2020). The mentioned points can confirm the validity of the obtained results.

Managerial insights

In the nowadays complex and competitive business environment, setting an appropriate plan to configure the supply chain is a crucial task for managers. Today, managers know that the customers not only evaluate the performance of a company based on traditional indicators like cost and quality but also consider other criteria such as sustainability. On the other hand, since supply chains have always faced various man-made and natural disruptions, incorporating strategies called resilience that can improve the capability of supply chains to deal with disruptions seems so necessary. Hence, owing to the key role of the above-mentioned points in the practice, the current work has focused on incorporating the sustainability and resiliency into the supply chain network design problem. In this regard, this paper can give a comprehensive perspective on the sustainable-resilient supply chain network problem to managers, especially in the dairy industry. In this way, by reading this work, managers can be familiar with the most important indicators related to sustainability and resilience concepts and incorporate these indicators into their businesses. Also, since this work simultaneously investigated the supplier selection and supply chain network design problems, it can help managers to understand these problems appropriately and improve the activities of their supply chain accordingly. Moreover, the outputs can be helpful for managers to see the behavior of their supply chain due to changing the critical parameters. For example, according to the sensitivity analysis results, with increasing demand, the total cost including the shortage cost has increased. In this regard, some strategies like sub-contracting or outsourcing can be useful to reduce the number of shortages and consequently decrease the total costs.

Conclusion

This study addressed the panning of the SRSCN problem for the dairy industry. In this way, a multistage model was developed based on the FDEMATEL, FMOORA, and multi-objective mathematical model methods. The first stage calculated the scores of the suppliers based on the resiliency and sustainability aspects, and the second stage tried to set a plan for the supply chain network. The objective functions of the proposed model minimized the total costs and maximized the system's resiliency. Then, the proposed multi-objective model was solved by employing the preemptive FGP approach and the results are reported. In this research, to achieve the sustainability objective, the suppliers were evaluated based on the sustainability measures in the first stage and also the score of suppliers in the terms of sustainability was maximized in the second stage. On the other hand, to achieve the resiliency objectives, the performance of the suppliers according to the resiliency concept was assessed in the first stage, and then, their scores in the terms of resiliency were maximized in the second stage. Based on the obtained results, the simultaneous consideration of the sustainability and resiliency features led to improving the performance of the supply chain. Besides, the results showed that when the importance of an objective function increased, its value improved, too. Also, the results confirm the performance and efficiency of the developed multistage decision-making model.

Future studies can employ heuristic/metaheuristic algorithms to solve the proposed model in large-sized test problems. On the other side, the present paper did not consider the perishability of dairy products, which can be incorporated into future papers. In this regard, future authors can see Govindan et al. (2014) Sinha and Anand (2018) and Kumar Sinha and Anand (2020). Also, one of the directions for future studies is to add other concepts such as viability and agility to the current study. Moreover, future studies can incorporate the dimensions of Industry 4.0, such as digitalization, into the research problem. Finally, future researchers can add reverse logistics to the current work and configure a closed-loop supply chain for the research problem.