Rock slope stability analysis under Hoek–Brown failure criterion with different flow rules

Abstract

The stability analysis of homogeneous rock slope following the Hoek–Brown failure criterion under the hypothesis of different flow rules is performed based on limit equilibrium and finite element methods. The applied failure criterion is the generalized Hoek–Brown that can be introduced as a shear/normal function in analysis applying different flow rules. The results are compared with those obtained by the application of equivalent shear strength parameters of the Mohr–Coulomb criterion, considering that this is still the most widely used criterion in rock slope stability analysis and is still the base for the shear strength reduction method applied in finite element modelling. Different proposals for estimating the equivalent strength parameters based on confining stress level are evaluated. The limitation of stress-dependent linear Mohr–Coulomb parameters is emphasized by analysing the vertical cut problem, for which, depending on the chosen stress level, different critical heights are obtained for the same material. Sensitivity analysis of geotechnical parameters used as input for failure criterion is performed to determine their influence on slope stability. Probabilistic analysis is conducted to determine the probability of failure when different flow rules are applied. If slope stability analysis is performed with an assumption of associative flow rule, the probability of failure is within the acceptable limits for the considered case study, while employing non-associative flow rule, the probability of failure is rather high. The chart is presented that could be readily used to estimate the combination of σ_ci, GSI, and m_i values that produce failure for the analysed case study.

Introduction

The estimation of the factor of safety (FS) value in rock slope stability is one of the most important tasks for the design of different geotechnical works, i.e. infrastructures, mining, dams, etc.

The most widely used failure criterion in the study of the behaviour of rock masses is the generalized non-linear empirical Hoek–Brown (HB) criterion (Hoek et al. 2002; Hoek and Brown 2019). This failure criterion is widely accepted for the study of homogeneous and isotropic types of rock media as an equivalent continuum, which includes weak rock mass and heavily fractured rock mass where the governing failure pattern is along a rotational failure surface rather than through intact rock and joints.

In the state of the art of rock slope stability analysis, both by limit equilibrium method (LEM) and finite element method (FEM), the Mohr–Coulomb (MC) linear failure criterion is still the most widely used one considering that the material strength is expressed in terms of normal and shear stresses rather than in terms of principal stresses. In the past, most of the commercial numerical software did not use the HB failure criterion, and for this reason, the need arose to know the equivalent MC shear strength parameters (cohesion and friction angle) of the rock mass deduced from the HB criterion that should depend on the range of confining stress (${\sigma }{\prime}_{3{\text{max}}}$) governing the results of analysis. Nowadays, modern commercial software has introduced the HB criterion; therefore, it seems unnecessary to continue using the equivalent MC parameters, although the conversion of the parameters is still used for many geotechnical applications. For the equivalent parameters to be valid, it is important to choose the appropriate stress range for the failure mechanism depending on the geotechnical problem at hand. There are a lot of proposals for the estimation of equivalent MC parameters for tunnelling problems (Hoek et al. 2002; Sofianos 2003; Sofianos and Nomikos 2006; Jiménez et al. 2008), rock slope stability (Hoek et al. 2002; Yang and Yin 2010; Li et al. 2008; Wei et al. 2018, Rafiei Renani and Martin 2020), strip footing on rock mass (Yang and Yin 2010), etc. Anyway, the majority of the proposed solutions for determination of equivalent MC parameters provide great discrepancies due to different estimations of confining stress level $\left({\sigma }{\prime}_{3{\text{max}}}\right)$.

The plasticity flow rule describes the relation between the plastic strain increment and stress tensor following yielding. The associative flow rule is the condition for which the normality criterion is satisfied (e.g. for MC criterion dilatancy angle is equal to friction angle). In the slope stability analysis of homogeneous and isotropic rock mass obeying HB failure criterion, the flow rule is usually not well defined. In the study performed by Melentijevic (2005) and Melentijevic et al. (2017), the analysis of the influence of flow rule on rock slope stability is studied in detail. These results confirm the overestimation of FS by the application of the hypothesis of the associative flow rule in comparison to the non-associative flow rule with the corresponding dilatancy angle $\left(\psi \right)$ depending on the rock mass quality.

Also, another problem arises in FEM considering that stability problems are based on the shear strength reduction technique (SSR method) where the values of cohesion and friction angle $\left({c}{\prime}and {\phi }{\prime}\right)$ are reduced by an iterative process until reaching the FS. Further on, as a consequence of strength envelope linearization over the stress range of interest, the same material can have different equivalent shear strength parameters $\left({c}{\prime}and {\phi }{\prime}\right)$. In this paper, the implication of stress-dependent linear parameters is analysed from the vertical cut slope perspective (upper and lower bound solution).

There are a lot of charts still being elaborated and used by many researchers for the preliminary quick assessment of the stability of rock slopes (Hoek and Bray 1981; Carranza-Torres 2004; Melentijevic 2005; Jiménez et al. 2008; Li et al. 2008; Li et al. 2009; Li et al. 2011; Shen et al. 2013; Melentijevic et al. 2017; Zuo and Shen 2020; etc.). In this study, the stability of the rock slope presented is evaluated by taking into account different flow rules introduced in the generalized HB criterion.

Nowadays, probabilistic slope stability assessment is often used to address uncertainties originating from input parameters. In recent years, many researchers have studied different probabilistic aspects applied to rock slope stability (e.g. Serrano and Castillo 1973; Griffiths and Fenton 2004; Zhang et al. 2010; Javankhoshdel and Bathurst 2016; Javankhoshdel et al. 2017; Zhou et al. 2017; Rafiei Renani et al. 2019; Wang et al. 2020; Guo et al. 2020; Johari et al. 2020). Probabilistic and statistical concepts are implemented in Eurocodes (in particular Eurocode 7—European standard for geotechnical design), where, for example, characteristic values of geotechnical parameters could be determined by statistical procedures (Tietje et al. 2014). The analysis considered in this study is extended to account for the probability of failure for associative and non-associative flow rules. For the considered case study, when the slope stability analysis is performed under the assumption of the associative flow rule, the probability of failure is within acceptable limits, while under the non-associative flow rule, the probability of failure is rather high, whereas the deterministic factor of safety is close to unity.

For the application of the HB criterion, it is important to take into account the uncertainty in the estimation of basic input parameters σ_ci, GSI and m_i and its effect on the study of a particular geotechnical problem. For that purpose, sensitivity analysis is performed to produce charts for the analysed case study showing the range of input parameters within the realistic values of parameters for rock material considered (σ_ci, GSI and m_i) for associative and non-associative flow rule that would lead to failure of rock slope.

Failure criterion

Hoek and Brown failure criterion

The HB failure criterion (2002, 2019) is the empirical criterion most widely used in rock mechanics, based on the GSI classification system. Its applicability to the rock mass considers intact rock, blocky, and heavily jointed rock mass (Fig. 1). These groups can be considered homogeneous and isotropic, i.e. mainly applicable to soft and highly fractured rocks.

Fig. 1

Scale effect and applicability of the HB failure criterion (modified after Hoek and Brown 2019)

The formulation of the latest version of the HB criterion, which has undergone different modifications throughout its development, is the following:

$$\sigma {^{\prime}}_{1}=\sigma {^{\prime}}_{3}+{\sigma }_{ci}{\left({m}_{b}\frac{\sigma {^{\prime}}_{3}}{{\sigma }_{ci}}+s\right)}^{a}$$

(1)

where ${\sigma }_{1}^{\mathrm{^{\prime}}}$ and ${\sigma }_{3}^{\mathrm{^{\prime}}}$ are the major and minor principal stresses at failure; ${\sigma }_{ci}$ is the uniaxial compressive strength of the intact rock; m_b is the reduced value of the intact rock mass constant m_i; and s and a are the rock mass material constants. Where:

$${m}_{b}={m}_{i}{\text{exp}}\left(\frac{GSI-100}{28-14D}\right)$$

(2)

$$s={\text{exp}}\left(\frac{GSI-100}{9-3D}\right)$$

(3)

$$a=\frac{1}{2}+\frac{1}{6}\left({e}^{-GSI/15}-{e}^{-20/3}\right)$$

(4)

Deformation modulus of the rock mass is defined based on the availability of data on the elastic modulus of intact rock (E_i):

$${E}_{rm}\left(MPa\right)=100000\left(\frac{1-D/2}{1+{\text{exp}}\left(\left(75+25D-GSI\right)/11\right)}\right)\mathrm{or}\ {E}_{rm}={E}_{i}\left(0.02+\frac{1-D/2}{1+{\text{exp}}\left(\left(60+15D-GSI\right)/11\right)}\right)$$

(5)

where GSI is the geological strength index, and D is the disturbance factor taking into account the effect of blasting and stress relaxation (varying from 0 for undisturbed rock mass to 1 for completely disturbed rock mass) (Hoek and Brown 2019).

Rafiei Renani and Cai (2022) comprehensively reviewed the evolution of the HB criterion and emphasized its advantages and disadvantages and the effect of parameter uncertainty on the reliability of estimated rock mass properties.

Shear/normal function of HB failure criterion

The HB criterion can be presented alternatively as a shear/normal function as given in Serrano and Olalla (1994) for the original HB (Hoek and Brown 1980) and by Serrano et al. (2000) for the generalized HB (Hoek et al. 1992).

The stresses exerted on the failure surface (Coulomb type failure criterion) can be parametrically obtained from the Mohr failure criterion type (envelope of stress circles), setting the value of the instantaneous friction angle ($\phi$) as a parameter, defined as the slope of Mohr’s envelope. These stresses $(\tau \mathrm{and }\sigma )$, referred to the point R representing the state of stress exerted on the failure plane (Fig. 2), in the dimensionless form $\left({\tau }^{*}\mathrm{ and }{{\sigma }_{n}}^{*}\right)$, are given according to:

Fig. 2

Types of failure criteria (modified from Serrano et al. 2005)

$${\tau }^{*}\equiv \tau /{\beta }_{a}={q}^{*}\left(\phi \right){\text{cos}}\psi$$

(6)

$${\sigma }_{n}^{*}\equiv {\sigma }_{n}/{\beta }_{a}={p}^{*}\left(\phi \right)-{q}^{*}\left(\phi \right){\text{sin}}\psi$$

(7)

A general flow rule for rock masses, which is necessary to define a Coulomb type failure criterion can be of linear type, establishing the relation between the instantaneous friction angle $\left(\phi \right)$ with the dilatancy angle $\left(\psi \right)$:

$${\text{sin}}\psi =\chi \cdot {\text{sin}}\varphi +k$$

(8)

where χ and k are the parameters of a general equation of linear type.

Specific cases of this general flow rule given in Eq. (8) are: (a) the associative rule with χ = 1 and k = 0 that gives a dilatancy angle equal to instantaneous friction angle $(\psi \equiv \phi )$ and (b) the non-associative rule with a constant value of dilatancy angle $(\psi \equiv {\psi }_{0})$ for χ = 0 and $k=sin {\psi }_{0}$.

When analysing rock slope stability in two-dimensional form, the case is of the plane strain. The HB failure criterion can be simplified using Lambe’s variables ($p=\left({\sigma }_{1}+{\sigma }_{3}\right)/2$,$q=\left({\sigma }_{1}-{\sigma }_{3}\right)/2$), which is given in the dimensionless form $\left({p}_{0}^{*}=p/{\beta }_{a}+{\zeta }_{a} \mathrm{and }{q}^{*}=q/{\beta }_{a}\right)$ in Serrano et al. (2000):

$$\frac{p}{{\beta }_{a}}+{\zeta }_{a}=\left[1+\left(1-a\right){\left(\frac{q}{{\beta }_{a}}\right)}^{k}\right]\frac{q}{{\beta }_{a}}$$

(9)

which becomes:

$${p}_{0}^{*}\equiv {p}^{*}+{\zeta }_{a}=\left[1+\left(1-a\right){{q}^{*}}^{k}\right]{q}^{*}$$

(10)

Parameters ${\beta }_{a}$ and ${\zeta }_{a}$ are two basic material constants that establish the rock strength, based on the HB parameters a, m_i, and s as well as on the uniaxial compressive strength of the intact rock (${\sigma }_{ci}$) as follows:

$${\beta }_{a}={A}_{a}{\sigma }_{ci}$$

(11)

$${\zeta }_{a}=s/({m}_{b}{A}_{a})$$

(12)

where

$$k=\left(1-a\right)/a\mathrm{ and }{A}_{a}^{k}={m}_{b}\left(1-a\right)/{2}^{1/a}$$

(13)

The strength modulus ${\beta }_{a}$ is used to scale the failure criterion, while the coefficient of toughness ${\zeta }_{a}$ represents the relative quality and strength of the rock mass; i.e., it inherits the type of rock mass and extent to which it is fractured and disturbed representing the “dimensionless isotropic tensile strength” of the rock mass and can be regarded as the “tensile strength coefficient of the rock mass”.

The instantaneous friction angle $\left(\phi \right)$ is defined as the tangent line of the Mohr’s envelope expressed as:

$${\text{sin}}\rho =d{q}^{*}/d{p}_{0}^{*}=1/\left(1+k{{q}^{*}}^{k}\right)$$

(14)

Depending on the instantaneous friction angle $\left(\phi \right)$, Lambe’s dimensionless variables that follow the HB criterion are as follows:

$${q}^{*}\equiv q/{\beta }_{a}={\left[\frac{1-{\text{sin}}\phi }{k{\text{sin}}\phi }\right]}^{1/k}$$

(15)

$${p}_{0}^{*}\equiv p/{\beta }_{a}+{\zeta }_{a}=a\left[\frac{1+k{\text{sin}}\phi }{{\text{sin}}\phi }\right]{\left[\frac{1-{\text{sin}}\phi }{k{\text{sin}}\phi }\right]}^{1/k}$$

(16)

The advantage of representing the shear/normal stress function in this form is that it does not require the range of principal stresses to be determined for its application in the analysis of slope stability.

Associative and non-associative flow rule

In the slope stability analysis of rock masses obeying the HB failure criterion for homogeneous and isotropic rock mass, the application of the associative flow rule results in an overestimation of the FS in comparison to the analysis with the application of the non-associative flow rule (Melentijevic 2005; Melentijevic et al. 2005, 2017). The usually proposed and applied values of dilatancy angle $\left(\psi \right)$ in the non-associative flow rule for different geotechnical problems are conditioned by the rock mass quality defined by GSI and the friction angle (ϕ′), being defined: for poor-quality rock mass (GSI = 25) ψ = 0°, for average-quality rock mass (GSI = 50) ψ = 4° (ϕ′/8), and for good-quality rock mass (GSI = 75) ψ = 11.5° (ϕ′/4), as proposed by Hoek and Brown (1997), although other types of the general flow rule can be proposed.

Other studies included the analysis of the flow rule by the introduction of the dilatancy angle such as those given for infinite rock slopes (Manzanas 2002; Serrano et al. 2005) and planar failure (Serrano et al. 2002; Serrano and Olalla 2004; Melentijevic 2005; Melentijevic et al. 2006).

The influence of the flow rule on other geotechnical problems in rock mechanics is given for tunnelling (Reig 2004; Alejano and Alonso 2005; Serrano et al. 2011), anchors (García Wolfrum, 2005), footings on rock mass (Alencar et al. 2019, 2021), etc., confirming the importance for incorporation of non-associative flow rule into the analysis.

Equivalent Mohr–Coulomb failure parameters

Different commercial geotechnical software still widely uses the linear MC criterion for the analysis of different geotechnical problems making this methodology a general engineering approach. For that purpose, it is necessary to obtain values of equivalent MC parameters, i.e. c′ and ϕ′, by the linearization of Eq. (1) in the range of minor principal failure stress ${\sigma }_{1}{\prime}<{\sigma }_{3}{\prime}<{\sigma }_{3{\text{max}}}{\prime}$ (Fig. 3) (Hoek et al. 2002):

$${\varphi }{\prime}={{\text{sin}}}^{-1}\left[\frac{6a{m}_{b}{\left(s+{m}_{b}{\sigma }_{3n}{\prime}\right)}^{a-1}}{2\left(1+a\right)\left(2+a\right)+6a{m}_{b}{\left(s+{m}_{b}{\sigma }_{3n}{\prime}\right)}^{a-1}}\right]$$

(17)

$${c}{\prime}=\frac{{\sigma }_{ci}\left[\left(1+2a\right)s+\left(1-a\right){m}_{b}{\sigma }_{3n}{\prime}\right]\cdot {\left(s+{m}_{b}{\sigma }_{3n}{\prime}\right)}^{a-1}}{\left(1+a\right)\left(2+a\right)\sqrt{1+\left(6a{m}_{b}{\left(s+{m}_{b}{\sigma }_{3n}{\prime}\right)}^{a-1}\right)/\left(\left(1+a\right)\cdot \left(2+a\right)\right)}}$$

(18)

where ${\sigma }_{3n}{\prime}={\sigma }_{3{\text{max}}}{\prime}/{\sigma }_{ci}$, and ${\sigma }_{t}$ tensile strength.

Fig. 3

Relation between major and minor principal stress at failure of the HB criterion and equivalent MC parameters (Hoek et al. 2002)

The value of ${\sigma }_{3{\text{max}}}{\prime}$ is the upper limit of the confining stress for which the relationship between the MC and the HB failure criteria is considered, and it should be defined for various geotechnical applications (tunnels, slopes, foundations, etc.). The determination of the value of ${\sigma }_{3{\text{max}}}{\prime}$ in the case of slopes must correspond to the adjustment of the value of the FS against slope failure, including the shape and location of the failure line. Hoek et al. (2002) proposed the following relationship determined for different ranges of slope geometries and rock mass properties based on Bishop’s method:

$$\frac{{\sigma }_{3{\text{max}}}{\prime}}{{\sigma }_{cm}{\prime}}=0.72{\left(\frac{{\sigma }_{cm}{\prime}}{\gamma H}\right)}^{-0.91}$$

(19)

where $\gamma$ and H are the unit weight and the slope height, respectively; ${\sigma }_{cm}{\prime}$ is the rock mass compressive (or “global”) strength, defined by the following Eq. (20), for the stress range ${\sigma }_{t}<{\sigma }_{3}{\prime}<{\sigma }_{ci}/4$ (Hoek et al. 2002):

$${\sigma }_{cm}{\prime}={\sigma }_{ci}\frac{\left({m}_{b}+4s-a\left({m}_{b}-8s\right)\right)\cdot {\left({m}_{b}/4+s\right)}^{a-1}}{2\cdot \left(1+a\right)\cdot \left(2+a\right)}$$

(20)

Li et al. (2008) have defined three zones as can be seen in Fig. 4. If the stress conditions of the rock material fall within zones 1 and 3, overestimation of the ultimate shear strength can be considered using the equivalent MC parameters instead of the HB curve.

Fig. 4

Linearization of the HB failure criterion (Li et al. 2008)

According to Li et al. (2008), for very steep slopes, the stresses along the failure surface fall within the zone 1 (Fig. 4), producing the maximum difference between the HB and MC failure criterion. Therefore, the shear stress obtained using the HB criterion is less than that obtained using the MC criterion by applying Eq. (19).

A better adjustment of the equivalent parameters is required in order not to overestimate the FS, especially on slopes with an angle of inclination $\left(\delta \right)$ greater than 45° (Li et al. 2008). The following modified formulations are proposed based on the slope inclination angle $\left(\delta \right)$, to try to provide a better fit of the linearization of the HB curve in zone 1 (Fig. 4):

$$\frac{{\sigma }_{3{\text{max}}}{\prime}}{{\sigma }_{cm}{\prime}}=0.2{\left(\frac{{\sigma }_{cm}{\prime}}{\gamma H}\right)}^{-1.07}\delta (\ge {45}^\circ )$$

(21)

$$\frac{{\sigma }_{3{\text{max}}}{\prime}}{{\sigma }_{cm}{\prime}}=0.41{\left(\frac{{\sigma }_{cm}{\prime}}{\gamma H}\right)}^{-1.23}(\delta <{45}^\circ )$$

(22)

Rafiei Renani and Martin (2020) performed numerical analysis for over 100 slopes to investigate the influence of ${\sigma }_{3{\text{max}}}{\prime}$ on FS and failed material area by applying the proposed original HB Eq. (19) and modified Eqs. (21) and (22). Based on numerical analysis, they obtained the following relation between ${\sigma }_{3{\text{max}}}{\prime}$ and slope angle $\left(\delta \right)$:

$$\frac{{\sigma }_{3{\text{max}}}{\prime}}{\gamma H}=\frac{0.175}{{\text{tan}}\left(\delta \right)}$$

(23)

Anyway, the best adjustment of the value of the minor principal stress $\sigma_{3\max }{\prime}$ considering the analysis of the non-linear correlation of the HB failure criterion and the derived equivalent MC parameters should correspond to the maximum thickness of the failed material area.

Applied methodology

Charts

Chart-based slope stability analysis is still widely used in everyday practice for the quick estimation of the geometry of the slope based on geotechnical parameters. The most used stability chart for slope stability is presented by Taylor (1937) which requires the MC shear resistance parameters. There are different stability charts presented for rock slope design, such as Hoek and Bray (1981) that uses equivalent MC parameters, as well as others that use generalized HB failure criterion (Carranza-Torres 2004, Jiménez et al. 2008, Li et al. 2008, Li et al. 2009, Li et al. 2011, Zuo and Shen 2020; Kumar et al. 2021). The charts presented by Melentijevic (2005) and Melentijevic et al. (2017) incorporate different assumptions of flow rules in the HB failure criterion. These charts were developed for the original HB criterion (1980) applying the parametric form of shear/normal stress given by Serrano and Olalla (1994), taking into account different flow rules. If the associative flow rule is applied by these charts, the slope stability (i.e. the general slope angle) is overestimated in comparison to the application of the non-associative flow rule. An example of the application of these charts is presented in Fig. 5 confirming the influence of different flow rules on results by the estimation of the necessary slope angle for FS = 1.0.

Fig. 5

Relationship between dimensionless height (H*) and slope angle (${\varvec{\delta}}$) for FS = 1.0 and different flow rules with constant values of ${\varvec{\psi}}$ for a ${\varvec{\xi}}$=0.01 and b ${\varvec{\xi}}$=0.1 (Melentijevic et al. 2017)

Fig. 6

Uniform homogeneous slope in mudstone rock mass (Berisavljević et al., 2018)

Limit equilibrium method

The LEM is the most widely used and preferred method for slope stability, due to its simplicity (compared to the more rigorous approaches such as FEM) and good understanding of its outcomes. The commercial code Slide2 v9.020 (RocScience 2022a) is used for the analysis in this study. The location of the critical failure surface with the lowest FS value is determined by the automated grid search for the general circular failure surface. The Morgenstern-Price method is used which satisfies both the equilibrium of forces and moments (Morgenstern and Price 1965).

Critical slope height

The vertical cut problem is well known within the framework of the theory of plasticity, namely the collapse load theorem. This theorem can produce upper and lower bound solutions to the problem at hand and is usually termed limit analysis. The well-known equation to determine a lower bound solution for critical height H_L of vertical cut (Davis and Selvadurai 2002) is the following:

$${H}_{L}=\frac{2c}{\gamma }\sqrt{N}$$

(24)

where N is defined as: ${\text{N}}=\frac{\text{1+sin}\phi {\prime}}{\text{1-sin}\phi {\prime}}$

Upper bound solution for critical height H_U of vertical cut (Davis and Selvadurai 2002) is:

$${H}_{U}\text{=}\frac{4c}{\gamma }\sqrt{N}$$

(25)

Finite element method

The commercial code RS2 v11.013 (Rocscience Inc. 2022) is used for FEM analysis. The location of the failure surface is automatically determined by the analysis of deformations, i.e. the maximum shear strains, without a requirement to make any hypothesis on the shape and position of the failure surface.

The initial stress field is considered by the gravity loading option. The adopted initial value of lateral earth pressure coefficient (K₀) is 1.0, considering the findings from the study done by Rafiei Renani and Martin (2020). The deformation modulus is introduced according to Eq. (5). It should be noted that it has no influence on the value of FS, as previously discussed by different authors (Cheng et al. 2007; Griffiths and Lane 1999; Hammah et al. 2005).

The lateral boundaries of the model are sufficiently large in order not to influence the results of analysis. Left- and right-side model boundaries are restrained only in the y-direction, while the bottom boundary is completely restrained (x- and y-direction). The uniform mesh with 6-noded triangular elements (total no 2767 elements) is used.

When the generalized HB criterion is applied, the associative and non-associative flow rule is introduced by the value of the dilation parameter (m_dil), ranging from 0 for the non-associative flow rule with ψ = 0° (m_dil = 0) to m_b for the associative flow rule (m_dil = m_b) (Rocscience Inc. 2022, Naznin 2007).

When an equivalent linear MC criterion is used, the associative flow rule is introduced by the equivalence of the dilation to the friction angle $\left(\psi =\phi \right)$ and the non-associative flow rule by $\psi$=variable.

The FS is determined by the SSR method which reduces the shear strength until instability occurs. The application of the SSR method for the MC criterion (by the introduction of equivalent parameters) includes the iterative application of FS on shear strength parameters (c and $\phi$). It is supposed that in both cases of associative $\left(\psi =\phi \right)$ and non-associative flow ($\psi$=variable) rule the same FS is applied during the iterative process on the dilatancy angle $(\psi )$.

In the case of the HB failure criterion, the SSR method is introduced based on the formulation presented by Benz et al. (2008), in which an intrinsic shear strength factor is included in the shear strength criterion.

When the shear/normal function is introduced to define the failure criterion, it permits the introduction of arbitrary function and the construction of a non-linear MC strength envelope. In this case, shear/normal function is introduced by Eqs. (6) and (7) that already involve the flow rule, thus being unnecessary to introduce the dilation parameter (m_dil). The SSR method is applied directly to the value of shear strength (Rocscience Inc. 2022b).

Probabilistic analysis

In the next step, a reliability analysis was performed to investigate the influence of applied flow rule on the probability of failure (P_f). In terms of universal definition, the P_f is the likelihood that the structure will fail during operational life and is an important part of risk analysis. The P_f, calculated together with the consequence of failure (CoF), helps in establishing the risk level for a particular problem at hand.

In slope stability analysis, P_f is defined as (Rocscience Inc. 2022a):

$${P}_{f}=(total no. of analyses)/(no. of analyses with FS<1.0)$$

(26)

Another commonly used measure of safety in probabilistic analysis is the reliability index (RI) which is defined, for an assumption of normal distribution of FS after probabilistic analysis, as follows:

$$RI=\frac{\mu -1}{SD}$$

(27)

where μ is mean value of the FS and SD is standard deviation of FS.

As can be seen from Eq. (27), the RI represents the number of standard deviations that separate the mean FS from the critical FS.

For an assumption of lognormal distribution of FS, the RI can also be determined.

Before analysis, one has to assign a statistical distribution to random variables (input parameters). In the case of MC failure criterion, random variables usually represent shear strength parameters (c′ and $\phi$′).

However, in the case of nonlinear criterion, namely shear/normal function, statistical distribution has to be assigned directly to the shear strength of the material. In this way, the variation of shear strength in the analysis is defined by the coefficient of variation (CoV). The CoV is the ratio of the SD to the mean value and shows the extent of variability to the mean of the population. The higher CoV implies greater dispersion, and vice versa. According to Eurocode 7 (EN 2004), CoV for shear strength of material varies in the range of 15 to 25%, being in this study the value of CoV = 20% assumed.

Regarding the number of analysed failure surfaces, two different probability analyses could be performed, namely the Overall slope and Global minimum. In the case of global minimum analysis, probability of failure is determined only for critical deterministic failure surface. Therefore, the P_f and the RI are only based on the analysis of one slip surface. For the Overall slope method, the entire slip surface search is repeated within a prescribed number of samples. In this case, each iteration of the probabilistic analysis can locate a different global minimum slip surface.

After defining random variables, and their distributions, the sampling method has to be determined. The sampling method determines how the statistical input distributions for the random variables will be sampled. The theoretical background of these methods can be found in Robert and Casella 2004; El-Ramly et al. 2002; McKay et al. 1979; and Iman et al. 1980. Three sampling techniques are available in software, namely Monte Carlo simulation, Latin Hypercube technique, and Response surface. It is important to mention that the Latin Hypercube sampling technique gives comparable results to the Monte Carlo technique but with fewer samples. This is why the Latin Hypercube sampling technique is chosen in this study.

Case study of failed slope

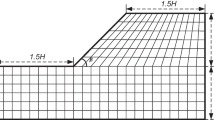
The case study analysed is presented by Berisavljevic et al. (2018). The slope is 12 m high with a uniform inclination of 45°. During highway construction, the failure occurred. The rock mass is classified as poor-quality mudshale. Groundwater was not detected during and after geotechnical investigations, so the analysis is performed without consideration of pore-water pressures. The geometry of the slope and view of the mudstone material is shown in Fig. 6.

Table 1 summarizes geotechnical parameters of the material defined in situ and derived by formulations presented in Serrano et al. (2000) and Melentijevic (2005) (see the “Failure criterion” section), which are further necessary for the analysis performed by charts, LEM, FEM, and probabilistic and sensitivity analyses.

The constant value of disturbance factor of D = 0.7 is assumed (mechanical excavation due to stress relaxation according to Hoek and Brown 2019) in the whole model. Other assumptions on the distribution of disturbance factor D are possible, i.e. different linearly varying distribution, according to Silva-Guzmán and Gómez (2015), Rose et al. (2018), and Ma et al. (2022), but this assumption of constant value of D is considered to be on the safe side from the practical point of view.

In the following section, results of analyses, considering the influence of flow rules, are shown.

At first, the preliminary estimation of slope stability by application of charts given in Melentijevic (2005) and Melentijevic et al. (2017) is performed. Nevertheless, as expected, the original HB overestimates the rock mass strength, so the evaluation of the stability of the rock slope is performed additionally to take into account the generalized HB criterion. Then, the FEM and LEM analyses with generalized HB criterion in its parametric form (Serrano et al. 2000; Melentijevic 2005) are discussed. The comparison is made between the results obtained with generalized HB and equivalent MC criteria both in LEM and FEM. The dependence of the MC parameters on the ${\sigma }_{3{\text{max}}}{\prime}$ level (refer to the “Application of equivalent MC parameters” section) is used to analyse the vertical cut problem, common for limit analysis. The probabilistic analysis is performed to investigate the influence of different flow rules on the probability of failure. Finally, the sensitivity analysis is done to obtain the failure charts applicable to this case study. These failure charts reproduce a combination of HB parameters (namely m_i, σ_ci, and GSI), derived from a shear/normal function, that would lead to the failure of analysed slope, both for associative and non-associative flow rule.

Results and discussion

Application of charts

For preliminary analysis of slope stability, the dimensionless charts presented in Fig. 5 are used. These charts are also used to evaluate the influence of the flow rule on results by the estimation of the necessary slope angle for FS = 1.0. Considering that graphs are developed for particular values of $\zeta$(0.01 and 0.1), the interpolation is done to match the value given in Table 1 for the analysed case study. The overestimation of the slope angle can be observed if the associative flow rule is adopted, while the non-associative flow rule with ψ = 0° (corresponding to poor quality of the rock mass) matches approximately limit equilibrium for the existing adopted geometry of the case study, as summarized in Table 2. It can be observed from Fig. 5 that in general, the application of the associative flow rule represents the unconservative approach in the rock slope stability analysis.

Application of equivalent MC parameters

Table 3 summarizes the results of LEM and FEM by employing equivalent MC parameters (c′ and ϕ′) determined by different authors (chapter “Equivalent Mohr–Coulomb failure parameters”). To simulate the associative and non-associative flow rule in FEM, the value of the dilation angle (ψ) is introduced either by ψ=$\rho$ (associative) or ψ = 0° (non-associative).

From Table 3, it can be observed that the shear strength parameters (c′ and ϕ′), obtained for different ${\sigma }_{3{\text{max}}}{\prime}$ values, have significant influence on the factor of safety. The greater the ${\sigma }_{3{\text{max}}}{\prime}$, the greater the FS. If the result calculated for the non-associative flow rule by FEM (Eq. 21) is considered as reference (FS = 1.58), all other assumptions provide errors in the estimation of FS. The maximum difference is up to 12.72%.

Additional analyses are performed to investigate the influence of the K₀ value on ${\sigma }_{3{\text{max}}}{\prime}$. The K₀ is varied from 0.5 to 3.0, which is considered the common range for rock slope engineering problems. Depending on the position of the critical sliding surface from LEM (obtained for shear/normal function of the HB criterion under associative flow rule assumption), ${\sigma }_{3{\text{max}}}{\prime}$ varied from 41 and 70 kPa for K₀ = 0.5 and 3.0, respectively. The critical sliding surface obtained in LEM by the application of shear/normal function with non-associative flow rule is much shallower (refer to section “Application of HB criterion”) producing ${\sigma }_{3{\text{max}}}{\prime}$ values between 26 and 35 kPa, for K₀ = 0.5 and 3.0, respectively. Even though the selection of K₀ produces differences, they are not considered significant from the practical point of view. These findings are in agreement with the conclusions of Rafiei Renani and Martin (2020).

Analysis of critical slope height

As shown in Table 3, the same material can have different shear strength parameters (c′ and ϕ′) based on proposed formulations by different authors. Shear strength parameters are also dependent on strength envelope linearization over the stress range of interest.

In the following, the dependence of shear strength on the stress level will be used to investigate its influence on the critical height of vertical cut.

For different sets of c′ and ϕ′ parameters from Table 3, critical cut heights H_L and H_U are calculated and presented in Table 4 and Fig. 7.

The exact collapse height for this problem, if we assume that the material cannot support tension, is precisely equal to H_L. If we assume that the material cannot support tensile stress, then a vertical tension crack can develop behind the cut’s face and, rather than the failure wedge, a thin slab of soil can collapse leaving a new, near vertical face. If the material supports tension, then H_U will be closer to the true collapse load. The reason H_U is twice the exact value of H_L is due to the choice of collapse mechanism (planar failure surface) (Davis and Selvadurai 2002).

Collapse load theorems were originally developed for elastic-perfectly plastic materials that obey the associative flow rule. Regardless of this, one can try to determine the vertical cut height (FS = 1.0) within the LEM framework.

It is well known that for the planar (wedge) failure surface LEM calculation will produce the vertical cut height identical to H_U (with the same c′/ϕ′ material considered). In the case of a lower bound solution, the H_L value should be matched to the LEM analysis by introducing a tension crack of a certain depth.

Next, one could try to determine the vertical cut height by introducing a nonlinear shear/normal function in LEM for the set of parameters summarized in Table 1. If a nonlinear strength envelope is applied, the critical height of the vertical cut is stress independent and should have constant value over the entire stress level.

Results of limit analyses (Eqs. (24) and (25)) and LEM analyses with nonlinear shear/normal function (for associative and non-associative flow rule with ψ = 0°) are reproduced in the form of a graph in Fig. 7.

Fig. 7

Critical height of the vertical cut for different σ′_3max levels

Fig. 8

Overlapped FEM vs LEM failure surfaces for a shear/normal function for associative flow rule, b shear/normal function for non-associative flow rule with ψ = 0°, c generalized HB with associative flow rule, and d generalized HB with non-associative flow rule with m_dil = 0

Fig. 9

FEM contours of minor principal stress $\left({\sigma }_{3}^{\mathbf{^{\prime}}}\right)$ with the position of failure surfaces for a shear/normal function for associative flow rule, b shear/normal function for non-associative flow rule with ψ = 0°, c generalized HB with associative flow rule, and d generalized HB with non-associative flow rule with m_dil = 0

Fig. 10

P_f convergence plot for a associative and b non-associative flow rule with ψ = 0°

Fig. 11

Distribution of FS values for a associative and b non-associative flow rule with ψ = 0°

Fig. 12

Shear strength factor vs FS for associative and non-associative flow rule with ψ = 0°

Fig. 13

Shear/normal function of HB criterion by Serrano et al. (2000) for the analysed case study

Fig. 14

Correlation between m_i, ${\sigma }_{{\text{ci}}}$, and GSI for the slope failure (FS = 1.0) of the case study for a associative and b non-associative flow rule with ψ = 0°

Fig. 15

Relationship between m_i, ${\sigma }_{{\text{ci}}}$, and GSI for FS = 1.0 of the case study for a associative and b non-associative flow rule with ψ = 0°

As expected, the critical cut height for the nonlinear strength envelope has a constant value over the stress range of interest and is lower than the corresponding results of limit analysis.

Although this analysis seems rather simple, it leads to one very important conclusion. For realistic materials (for which shear strength parameters are stress dependent), critical cut height is variable and depends on the choice of strength parameters for a particular stress range. If the nonlinear nature of the strength envelope is employed in the analysis by LEM, constant critical cut height is obtained.

Application of HB criterion

Table 5 summarizes results obtained by the application of LEM and FEM under different hypotheses for the failure criterion and flow rule. If LEM and FEM calculations are performed by the application of shear/normal function under the hypothesis of associative and non-associative flow rule (Eqs. (6) and (7)), the higher values of FS are observed for the case of associative flow rule compared to the non-associative (with ψ = 0°). If the generalized HB criterion is applied considering the dilation parameter (m_dil), a small difference is observed in FS under the assumption of associative and non-associative flow rule. In general, the approximate error between FS values obtained under the hypothesis of associative and non-associative flow rule is in the order of 45%, considering that the reference value is the one with the minimum FS (the shear/normal function with non-associative flow in FEM).

The failure surfaces obtained by LEM and FEM are compared in Fig. 8. The FEM failure surfaces are represented by the maximum shear strain band, while the failure surfaces obtained by LEM are introduced as red lines in Fig. 8. In general, failure surfaces obtained by LEM for associative and non-associative flow rule cover less failure area than the ones obtained by FEM. It can also be observed that the position of failure surfaces (for the generalized HB criterion) obtained by LEM for associative flow rule matches quite well with the ones obtained by FEM. The failure surfaces for the non-associative flow rule in LEM are shallower than those of the associative flow rule.

Figure 9 shows the contours of minor principal stress $\left({{\varvec{\sigma}}}_{3}^{\mathrm{^{\prime}}}\right)$, obtained from FEM analysis, along with superimposed LEM failure surfaces for associative and non-associative flow rules. The ${\sigma }_{3{\text{max}}}{\prime}$ value obtained by FEM is compared to the values obtained by different authors listed in Table 3. It can be observed that the value of ${\sigma }_{3{\text{max}}}{\prime}$ (for K₀ = 1.0) ranges from 30 to 60 kPa under different assumptions of the non-associative and the associative flow rule, respectively. This is in accordance with the values provided by Rafiei Renani and Martin (2020) and Li et al. (2008) for $\delta$≥45° (Table 3).

Probabilistic analysis

P_f was determined for the associative and the non-associative flow rule of the shear/normal functions defined by Eqs. (6) and (7) (Table 5). For both scenarios, 1000 analyses (sampling iterations) were performed. The convergence plot of the P_f, as shown in Fig. 10a, indicates that convergence in the case of associative flow rule is achieved after approx. 600 iterations. The second scenario (non-associative flow rule) reached a constant value of P_f = 28.14% after approx. 400 iterations (Fig. 10b). It is interesting to note that the P_f, in the case of the non-associative flow rule, decreases abruptly to the minimum value after less than 50 iterations, while in the case of the associative flow rule P_f steadily increases towards the maximum value (of more than 4%) and then, after sufficient number of iterations reduces to the constant value of 2.70%.

Figure 11 shows the distribution of FS values for the two cases analysed (failure criterion introduced by the shear/normal function defined by Eqs. (6) and (7) with the associative and the non-associative flow rule as given in Table 5). A statistical distribution that best fits the FS data is a normal distribution. Highlighted green bars indicate FS values less than 1.0. It is obvious that for the non-associative scenario P_f is much higher and unacceptable for conventional geotechnical practice (0.1% < P_f < 3% or 2 < RI < 3) (US Army Corps of Engineers 1997).

Figure 12 shows the relation between the shear strength factor (being defined as the factor for which the FS of each trial has to be multiplied to obtain FS = 1.0) and the factor of safety (FS). Dark grey dots indicate analyses with FS < 1.0, while light grey dots indicate analyses with FS > 1.0. In the case of the associative flow rule, the shear strength factor for the failure surface with the lowest FS value, after probabilistic analysis, is equal to 0.61, while in the case of the non-associative flow rule strength factor equals 0.88.

Analysis of shear/normal function of HB criterion

Figure 13 summarizes the shear/normal functions of the generalized HB criterion in the form presented by Serrano et al. (2000) for associative and non-associative flow rule (with ψ = 0°). The correlating curves are presented for the set of initially adopted parameters, as summarized in Table 1 (GSI = 30, ${\sigma }_{{\text{ci}}}=10.5$ MPa, and m_i = 7). Figure 13 also shows the failure criteria range both for associative and non-associative flow rule that leads to rock slope failure (FS = 1.0) according to probabilistic analysis whose summary is given in Fig. 12 (estimated as 0.61 for associative and 0.88 for non-associative flow rule with ψ = 0°).

Figure 14 shows the relationship between different HB parameters (m_i, ${\sigma }_{{\text{ci}}}$, and GSI) that would produce the failure under certain combinations. Input parameters were varied until they produced the shear strength envelope reasonably well matched to the weighted failure envelope (for associative and non-associative flow rule, represented as dotted lines in Fig. 13). For example, it can be observed that for the same m_i value, the corresponding range of ${\sigma }_{{\text{ci}}}$ and GSI values is almost the same for different flow rules; however, the higher GSI value to obtain FS = 1.0 is necessary in the case of the non-associative flow rule.

Figure 15 presents the relationship between ${\sigma }_{{\text{ci}}}$ and GSI for different m_i values for limit state condition FS = 1, shown both for associative and non-associative flow rule. If the combination of these parameters is introduced into shear/normal function, it would lead to failure of the rock slope.

Several important assumptions and conclusions can be derived from previous considerations:

• (i) The associative flow rule overestimates the rock mass strength, overestimating FS of the rock slope, in comparison to the non-associative flow rule.

• (ii) For the analysed slope case study to reach the state of failure, the shear/normal function should be factored by 0.88 and 0.61, for the case of non-associative and associative flow rules, respectively (Fig. 13).

• (iii) The variability of GSI and ${\sigma }_{{\text{ci}}}$ in relation to m_i value (for the weighted failure criteria that leads to slope failure) is presented in Fig. 14. It can be observed that with an increase of m_i, the range of ${\sigma }_{{\text{ci}}}$ values practically remains unchanged, while the variation of GSI is more pronounced. It can be observed that for the same combination of m_i and ${\sigma }_{{\text{ci}}}$, values of GSI are lower for the associative flow rule. With an increasing value of m_i and corresponding range of ${\sigma }_{{\text{ci}}}$, the value of GSI decreases.

• (iv) It is possible to determine the combination of GSI and ${\sigma }_{{\text{ci}}}$ values for constant m_i, necessary to reach the rock slope failure for associative and non-associative scenario, as summarized in Fig. 15.

• (v) The charts presented in Fig. 15 are valid for considered case study and could be used for the quick estimation of the combination of input parameters that would lead to rock slope failure taking into account the extent of uncertainty in defining initial values of input parameters GSI, m_i, and ${\sigma }_{{\text{ci}}}$.

• (vi) The shear/normal function is dependent on the initially estimated geotechnical parameters GSI, m_i, and ${\sigma }_{{\text{ci}}}$. The variability of values of these influencing parameters on the failure criterion (Fig. 15) can be defined by the coefficient of variation (CoV). Table 6 summarizes the CoV for associative and non-associative flow rule with ψ = 0° that leads to failure, observing that CoV is greater for GSI and ${\sigma }_{{\text{ci}}}$ parameters for associative than that of the non-associative flow rule, being negligible the difference for m_i. Nevertheless, these CoV values are in accordance with the values summarized in Rafiei Renani and Cai (2022).

Conclusions

Based on the analysis and results given in this study, the following conclusions can be derived:

• (i) The alternative application of the generalized HB failure criterion by the shear/normal function (valid both for the associative and non-associative flow rule) and its simple incorporation into commercial codes for slope stability analysis is presented. This shear/normal stress failure criterion is independent of the estimated ${\sigma }_{3{\text{max}}}{\prime}$ value omitting the need for calculating equivalent MC parameters.

• (ii) If the associative flow rule is applied through the shear/normal function for the generalized HB failure criterion, both in LEM and FEM, the FS value is overestimated compared to the non-associative flow rule. This is in agreement with the findings of Melentijevic (2005) and Melentijevic et al. (2017).

• (iii) The comparison between the failure patterns obtained by LEM and FEM shows that the corresponding failed area from LEM is smaller compared to the one obtained by FEM. Also, the different assumption on the flow rule influences the position of the failure surface within the slope. The hypothesis of the non-associative flow rule produces shallower failure surfaces.

• (iv) Careful choice of ${\sigma }_{3{\text{max}}}{\prime}$ value for the estimation of equivalent MC parameters is of prime importance for proper slope stability analysis. The limitation of stress-dependent linear Mohr–Coulomb parameters is emphasized by analysing the vertical cut problem, for which, depending on the chosen stress level, different critical heights are obtained for the same material.

• (v) The best estimation of the maximum minor principal stress level ${\sigma }_{3{\text{max}}}{\prime}$ should be related to the thickness of the failed material.

• (vi) A cautious estimate of initial input geotechnical parameters (GSI, m_i, ${\sigma }_{{\text{ci}}}$) for HB failure criterion should be done. It is necessary to define the range of input parameters instead of unique value in order to take into account the variability of the possible subjective choice of in situ rock mass properties. In this sense, probabilistic analysis should be performed to properly consider possible variability of rock mass properties estimated in situ.

• (vii) If slope stability analysis for the considered case study is performed with an assumption of associative flow rule, the P_f is less than 3% which is considered acceptable. If the non-associative flow rule is employed, the probability of failure is rather high with P_f = 27.8%, whereas the deterministic safety factor value is close to 1. This is in accordance with the field observations.

• (viii) Charts are developed for the analysed case study for quick initial estimation of rock mass parameters σ_ci, GSI, and m_i, both for associative and non-associative flow rule that would lead to slope failure. Similar charts should be developed for each case study to reduce the subjective engineering choice on the value of GSI since ${\sigma }_{{\text{ci}}}$ and m_i could be more reliably determined by means of laboratory tests.

• (ix) With the same values of m_i and ${\sigma }_{{\text{ci}}}$, the higher GSI values lead to failure under the hypothesis of the non-associative flow rule compared to the associative one.

• (x) The necessary incorporation of non-associative flow rule into slope stability analysis is emphasized.

Table 1 Summary of geometrical and geotechnical parameters necessary for slope stability analysis

Table 2 Necessary slope angle $\left(\delta \right)$ for the limit stability FS = 1.0 for the case study

Table 3 Summary of results of FS for analysed case study under different assumptions for equivalent c′ and ϕ′

Table 4 Summary of values of H_L and H_U

Table 5 Summary of FS under different assumptions for the case study applying shear/normal function

Table 6 CoV of parameters GSI, m_i, and${{\varvec{\sigma}}}_{\mathbf{c}\mathbf{i}}$for different flow rules