Multispectral hyperbolic incoherent holography

Abstract

This paper presents a new method of multispectral hyperbolic incoherent holography in which a hyperbolic volume interferogram was directly measured by an appropriate designed interferometer. This method enables to obtain a set of spectral components of three-dimensional images and continuous spectra for spatially incoherent, polychromatic objects. We introduced a calibration method of a phase aberration of the interferometer. The spectral resolution and spatial resolutions are investigated based on analytical solution of impulse response function of hyperbolic holography. From experimental results and theoretical predictions, the validity of the calibration method was confirmed. Experimental results agree with the theoretical ones. Consequently, the retrieved images obtained by the method are shown to demonstrate the performance of the method.

1 Introduction

Digital holographic technique has been extending its application area in recent years [1]. For incoherent holography [2] in which object to be imaged are incoherent in space, only light emits from each point on an object interfere itself. Various types of techniques have proposed. One technique is based on diffraction theory which can be implemented by making use of spatial light modulator [3,4,5] or concave mirror [6] and other technique uses radial shearing [7] or rotational shearing [8] interferometric systems.

In our conventional work of incoherent digital holographic spectrometry, the two-wavefront folding interferometer [9,10,11,12,13,14] and the synthetic aperture technique enables us to generate a volume interferogram. By choosing the appropriate selection rule used in the synthetic aperture technique, several types of volume interferogram have been created such as spherical type (S-type) volume interferogram [9, 10], hyperbolic type (H-type) volume interferogram [11], rotated hyperbolic type (RH-type) volume interferogram [12], and others [14]. In S-type method, the analytical solution of four-dimensional (4D) impulse response function (IRF) defined over $(x,\;y,\;z,\;\omega )$ space was derived [13]. This agrees well with experimental results in spectral resolution and three-dimensional (3D) spatial imaging properties.

In this paper, we present a new method, called multispectral hyperbolic incoherent holography. The present method is based on alternated design of two-wavefront folding interferometer. This method has three advanced features; first, we can obtain directly the hyperbolic volume interferogram from measurement of optical intensity on the optical axis. Because a single detector can be used instead of image sensor, it is possible to achieve high sensitivity and high dynamic range interferometric measurement. Second, unlike the previous method, no synthetic aperture technique is required. Third, the object to be measured does not need to be set on stage. This means that the application area of this method is wider than previous methods in which translation of object is necessary.

Furthermore, the spectral resolution and spatial resolutions are investigated based on new analytical solution of IRF of hyperbolic holography. These results are compared with the experimental results.

In Sect. 2, we begin by summarizing the procedure of the present method in connection with the retrieval process of multispectral components of 3D images. The principle of method is based on the Wiener–Khinchine theorem and a modified version of generalized Van Cittert–Zernike theorem. In Sect. 3, we show the experimental condition, interferometric measurement, and non-calibrating experimental results. From these experimental results, we find that the phase aberration cause by non-ideal properties of interferometer is introduced. It degrades quality of retrieved image. To resolve this issue, we present an in-situ phase calibration method. The experimental results of retrieved image after calibration of phase aberration are shown to demonstrate improvement of image quality. In Sect. 4, we investigate 3D imaging properties of hyperbolic holography by making use of a novel analytical solution of IRF defined over the 4D space. The primary result obtained in this section is a full description of the 4D IRF expressed mathematically in closed form. Theoretical predictions obtained from the analytical solution of IRF are also shown, for comparison with experimental results. These results lead to the final conclusion of the present article, stated in Sect. 5.

2 Description of method

2.1 Measurement of 3D volume interferogram

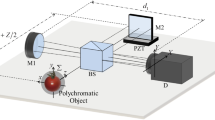
Figure 1 shows a schematic of experimental system. The measured 3D object is spatially incoherent and polychromatic. The propagated light is split by a beam splitter (BS). Each split wavefront is reversed from up to down by prism P or from left to right by prism P’, and then superposed on BS again. After passing through the lens, only optical intensity on the optical axis at apex of prism P’ is detected by a single detector. In this interferometer, the lateral shears, denoted $(X,\;Y)$, are introduced by x- and y-stages. The longitudinal shear, denoted Z, is introduced by piezoelectric translator (PZT). The optical path length between one of apex of prism P’ and the origin of the Cartesian coordinate system $(x,\;y)$ is denoted by ${z_0}$. During interferometric measurement, the x- and y-stages and PZT are moved stepwise, and the optical intensities at the same position on the optical axis are recorded. After all measurements, we arrange sequentially obtained optical intensity in 3D array $(X,\;Y,\;Z)$ according as motions of stages. In this way, one obtains the hyperbolic volume interferogram directly.

Fig. 1

(Color online) Schematic of experimental system

The superposed points of the optical fields reflected by the prisms P and P’ are expressed as ${\bf r} =(x,\;Y - y,\;{z_0}+Z)$ and ${{\bf r}^\prime }=(X - x,\;y,\;{z_0})$, respectively. The optical intensity of 3D interferogram, $I(X,\;Y,\;Z)$ is expressed in the following form:

$$I(X,\;Y,\;Z)=\frac{1}{4}\left[ {\Gamma ({\bf r},\;{\bf r})+\Gamma ({{\bf r}^\prime },\;{{\bf r}^\prime })+\Gamma ({{\bf r}^\prime },\;{\bf r})+{\Gamma ^*}({{\bf r}^\prime },\;{\bf r})} \right],$$

(1)

where * denotes a complex conjugate. In this equation, the time t in $\Gamma$ is suppressed, because the optical field is stationary in time. In Eq. (1), $\Gamma ({\bf r},\;{\bf r})=\left\langle {|V({\bf r},\;t)|{{\kern 1pt} ^2}} \right\rangle$ and $\Gamma ({{\bf r}^\prime },\;{{\bf r}^\prime })=\left\langle {|V({{\bf r}^\prime },\;t)|{{\kern 1pt} ^2}} \right\rangle$ are the optical intensities of the optical field $V({\bf r},\;t)$ at points ${\bf r}$ and ${{\bf r}^\prime }$ respectively, and $\langle {\rm ...} \rangle$ stands for the ensemble average. In the present method, we detect only intensities on the optical axis, then the 3D position vectors are rewritten by setting $x=y=0$, as ${\bf r}=(0,\;Y,\;{z_0}+Z)$ and ${{\bf r}^\prime }=(X,\;0,\;{z_0})$.

For stationary field, the spatial correlation function $\Gamma (X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)$ recorded in the 3D volume interferogram may be expressed as a superposition of the cross-spectral density ${W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)$ in the form

$$\Gamma (X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)=\int\limits_{0}^{\infty } {{W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)} {\text{d}}\omega ,$$

(2)

where $\omega =ck$ is the angular frequency with c being the speed of light in free space, $k={{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }$ is the wavenumber with the wavelength $\lambda$. Equation (2) means that for a stationary optical filed, spectral components of the optical fields of different frequencies are mutually uncorrelated. Under the paraxial approximation and the assumptions ${z_0}>>{\text{}}Z$ and ${z_0}>>{\text{}}{z_s}$, the cross-spectral density ${W_\omega }$ appeared in the right-hand-side of Eq. (2) can be written as in the following form:

$${W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)=\exp (ikZ){W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}),$$

(3)

On substituting Eq. (3) into Eq. (2), we obtain the relationship between the measured spatial correlation function $\Gamma$ and the cross-spectral density ${W_\omega }$,

$$\Gamma (X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)=c\int_{0}^{\infty } {\exp (ikZ){W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0})} {\text{d}}k.$$

(4)

It is then clear that Eq. (4) may be inverted to express the cross-spectral density ${W_\omega }$ as the Fourier transform of the spatial correlation function $\Gamma$:

$${W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0})=\frac{1}{{2\pi c}}\int {\Gamma (X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)\exp ( - ikZ){\text{d}}Z} .$$

(5)

The integrand has taken over the actual extension of the interferogram with respect to the thickness Z. The cross-spectral density ${W_\omega }\left( {X,\;0,\;{z_0};\;0,\;Y,\;{z_0}} \right)$ is defined as the cross-correlation between the monochromatic component of the optical field ${U_\omega }(X,\;0,\;{z_0})$ and ${U_\omega }(0,\;Y,\;{z_0})$. It is expressed as in the following form (Details see in Eq. (29) of Appendix):

$$\begin{aligned} {W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}) & =\left\langle {U_{\omega }^{*}(X,\;0,\;{z_0}){U_\omega }(0,\;Y,\;{z_0})} \right\rangle , \\ & ={S^\prime }({x_s},\;{y_s},\;{z_s}) \otimes \frac{1}{{{\lambda ^2}{z^2}}}\exp \left[ {i\frac{k}{{2z}}\left( { - {X^2}+{Y^2}} \right)} \right], \\ \end{aligned}$$

(6)

where ${S^\prime }({x_s},\;{y_s},\;{z_s})$ denotes the product of the spectral density of the object at point $({x_s},\;{y_s},\;{z_s})$ and the phase factor depending on the point, the symbol $\otimes$ stands for two-dimensional convolution, and $z={z_0} - {z_s}$ is the optical depth distance of the light source. Figure 2 shows typical hyperbolic volume interferogram, obtained by the present method. This interferogram corresponds to a monochromatic point source located at the upper left (${x_s}<0\;$ and ${y_s}>0\;$) of the Cartesian coordinate system. As shown in Eq. (6), the sign of the quadratic phase factors of X and Y are opposite. Therefore, the fringe patterns within the volume interferogram are arranged as hyperbolic surface as shown in Fig. 2.

Fig. 2

Example of a typical hyperbolic volume interferogram for a monochromatic point source located at the upper left of the Cartesian coordinate system

2.2 Retrieval of 3D images for many spectral components

From the hyperbolic volume interferogram, we may retrieve spectral components of 3D images of the object by applying a similar method to the inverse propagation of optical field based on Fresnel diffraction formula. Generally, there are two methods to obtain retrieved images from hyperbolic holograms, one is one-time Fourier transform method (1-FT method) and the other is two-times Fourier transform method (2-FT method). The 1-FT method treats light propagation as a unit of spherical wave based on Huygens’ principle. The 2-FT method treats light propagation as a unit of plane wave based on propagation of the angular spectrum. The advanced feature of 2-FT method is that the field of view is not depending on the depth distance. Therefore, we can obtain correct intensity distribution along z-axis and the size of retrieved image does not change. On the other hand, 1-FT method keeps the same field of view, while the size of retrieved image changes. In this paper, we present retrieved process of hyperbolic holography base on 2-FT method. We begin by writing the cross-spectral density ${W_\omega }$ across a reference plane $z={z_0}$ as

$$\begin{aligned} W_{\omega }^{{({z_0})}}(X,\;0;\;0,\;Y) & ={W_\omega }(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}) \\ & =\left\langle {U_{\omega }^{*}(X,\;0,\;{z_0}){U_\omega }(0,\;Y,\;{z_0})} \right\rangle , \\ \end{aligned}$$

(7)

where superscript in the left-hand-side of Eq. (7) specifies the position of the reference plane. By taking Fourier transforms of the cross-spectral density in Eq. (7), the angular cross-spectral density in Fourier space, denotes $\tilde {W}_{\omega }^{{({z_0})}}$, is defined by

$$\begin{aligned} \tilde {W}_{\omega }^{{({z_0})}}({k_x},\;0;\;0,\;{k_y}) & =\frac{1}{{2\pi }}\int {W_{\omega }^{{({z_0})}}(X,\;0;\;0,\;Y)\exp [ - i( - {k_x}X+{k_y}Y)]{\text{d}}} X{\text{d}}Y \\ & =\left\langle {\tilde {U}_{\omega }^{*}({k_x},\;0,\;{z_0}){{\tilde {U}}_\omega }(0,\;{k_y},\;{z_0})} \right\rangle . \\ \end{aligned}$$

(8)

From Eq. (8), the angular cross-spectral density defined in the Fourier space $\tilde {W}_{\omega }^{{({z_0} - {z^\prime })}}$ across a certain source plane $z={z^\prime }<{z_0}$ can be retrieved. By multiplying the inverse of the optical transfer function (OTF), we obtain the relationship between the angular cross-spectral densities at $z={z_0} - {z^\prime }$ and $z={z_0}$ as

$$\tilde {W}_{\omega }^{{({z_0} - {z^\prime })}}({k_x},\;0;\;0,\;{k_y})=\lambda z\exp \left[ {i\frac{{{z^\prime }}}{{2k}}( - {k_x}^{2}+{k_y}^{2})} \right]\tilde {W}_{\omega }^{{({z_0})}}({k_x},\;0;\;0,\;{k_y}),$$

(9)

where ${k_x}$ and ${k_y}$ are the lateral components of the wavenumber vector ${\varvec{k}}$. By taking inverse Fourier transform of both side of Eq. (9), the cross-spectral density across the source plane $W_{\omega }^{{({z_0} - {z^\prime })}}$ is retrieved, that is [details see in Eq. (36) of “Appendix”].

$$W_{\omega }^{{({z_0} - {z^\prime })}}(X,\;0;\;0,\;Y)=W_{\omega }^{{({z_0})}}(X,\;0;\;0,\;Y) \otimes \exp \left[ { - i\frac{k}{{2{z^\prime }}}\left( { - {X^2}+{Y^2}} \right)} \right].$$

(10)

As is seen in Eqs. (6), (7) and (10), this cross-spectral density $W_{\omega }^{{({z_0} - {z^\prime })}}$ is proportional to the spectral density ${S^\prime }({x_s},\;{y_s},\;{z_s})$ at an object plane $z={z_s}$. It is then possible to retrieve the spectral component of a 3D image of the light source by a similar method to conventional angular spectrum technique. In this manner, the 3D spatial distribution of the spectral density, namely the 3D image at each spectral component, can be obtained.

3 Experiment and in-situ calibration method

3.1 Experimental condition

In this section, we demonstrate the experiment to obtain the hyperbolic volume interferogram. The measured object is a mask screen of number 5 that is illuminated by white light source; metal halide lamp (MHL), so that, the object under measurement is planar polychromatic object. Figure 3 shows continuous spectral profile of the MHL that is obtained by Fourier transforms spectroscopy. The spectral resolution is 61.09 ${\text{c}}{{\text{m}}^{ - 1}}$ and spectral range is 3.13 × 10⁴ ${\text{c}}{{\text{m}}^{ - 1}}$. Figure 4 shows a photograph of illuminated mask screen of number 5 of size 0.3 mm × 0.5 mm. The depth distance z of the object is measured from one of apex of prism P’. It is set 115 or 135 mm. The object light propagates into the two-wavefront folding interferometer. The x- and y-stages moved stepwise, each interval of step is 12.9 µm, respectively. The PZT moved stepwise in z-direction, each interval of step is 0.08 µm. According to the movement of x-, y-stages and PZT, the single detector records light intensities 64 × 64 × 64 times.

Fig. 3

Continuous spectral profile of primary light source (metal halide lamp) measured by Fourier transform spectrometry

Fig. 4

Photograph of mask screen of number 5. This object is illuminated by a metal halide lamp and the size is horizontal 0.3 mm and vertical 0.5 mm

3.2 Experimental results

Figure 5 shows hyperbolic volume interferogram obtained from the experiment. The quarter part of the interferogram is removed to show inner fringe arrangement. The lateral size of recorded volume interferogram in x and y direction is 825.6 µm and the thickness is 5.12 µm, respectively. Figure 6 shows the continuous spectral profile of the object. This spectral profile is obtained by Fourier transform respect to thickness Z along the center of the volume interferogram. The circle legend is the original data obtained from spectrum channel of the Fourier transform. The numbers of data is 13, which is choosing so that there are cover the wavelength range of the visible light. The spectral resolution is limited by interval and number of steps of movement of PZT. In this experimental condition, the spectral peak in Fig. 6 located around 560 nm and the spectral resolution at this wavelength is 31.11 nm. Within the spectral resolution, this spectral profile agrees with that of MHL, as shown in Fig. 3. Thus, we will treat the retrieved results at this spectral peak in the following consideration.

Fig. 5

Hyperbolic volume interferogram obtained by experiment

Fig. 6

Continuous spectral profile recorded on the observation plane obtained by taking the Fourier transform along the center of the volume interferogram with respect to the thickness Z

Figure 7 shows the phase distributions of the measured hyperbolic complex holograms (cross-spectral densities) at the spectral peak 560 nm, where the object depth distance is $z=115$ mm or $z=135$ mm, respectively. Figure 8a, c shows the in-focus images that are retrieved from corresponding holograms over x–y plane. Figure 8b, d show the intensity distribution over y–z plane at $x=0$. We find that the images at the object depths shown in Fig. 8a, c are not correct images of measured object because the phase distributions in Fig. 7 are distorted by the phase aberration introduced by unwanted motions of x- and y-stages. This reflects the image distortion in Fig. 8 and, so, we cannot retrieve the correct image of number 5. In the next subsection, we will present in-situ calibration method to eliminate phase aberration.

Fig. 7

Phase distribution of measured object at the spectral peak 560 nm, the object depth distance is a $z=115$ mm, and b $z=135$ mm

Fig. 8

(Color online) The retrieved image that the measured object is located at $z=115$ mm (above) and $z=135$ mm (below). The in-focus image over x–y plane at retrieved distance a ${z^\prime }=115$ mm and c ${z^\prime }=140$ mm. The intensity distribution over y–z plane are shown (b, d)

3.3 In-situ calibration method

From Fig. 8, we find that the retrieved images are not correct. We expect that, during measurement of volume interferogram, the phase distribution may be affected by unwanted motion of x- and y-stages. This results in phase aberration. In principle, the correct phase distribution of hyperbolic hologram can be obtained by subtracting the phase aberration from the phase distribution of measured hyperbolic hologram.

To calibrate this phase aberration, we inserted the other BS and image sensor between lens and single detector to perform a simultaneous measurement of volume interferogram which records fringe patterns of phase aberration only. Figure 9 shows a schematic of an optical setup for in-situ calibration method. By choosing the pixel at $(x,\;y)=({X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2})$ and arranging the pixel values according to the positions of stages $(X,\;Y,\;Z)$, we obtain another volume interferogram that records different spatial correlation function of the form:

Fig. 9

(Color online) Schematic of an optical setup for in-situ calibration method

$$\Gamma ({X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2},\;{z_0};\;{X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2},\;{z_0}+Z)=\frac{1}{{{\lambda ^2}{z^2}}}\int {{S_\omega }({{\bf r}_s})} \exp (ikZ){d^3}{r_s}{\text{d}}\omega .$$

(11)

From Eq. (11), we see that this special correlation function contains only an interference term related to longitudinal shear, whose drift results in phase aberration. It does not include a linear and quadratic phase factor. Thus, it does not record the 3D information of the object. According to motions of x- and y-stages, if there is no drift of longitudinal shear between two arms of interferometer, the spatial correlation function in Eq. (11) is almost constant. But if there is unwanted motion of x- and y-stages that introduce phase aberration, this spatial correlation function records it. The spectral decomposition of this spatial correlation function $\Gamma$ gives a set of cross-spectral density ${W_\omega }({X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2};\;{X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2})$, which includes information of phase aberration at each spectral component. In this way, we may obtain phase aberration separately form the originally measured phase distribution.

In-situ calibration of phase aberration can be performed by subtracting the phase distribution of cross-spectral density ${W_\omega }({X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2};\;{X \mathord{\left/ {\vphantom {X 2}} \right. \kern-0pt} 2},\;{Y \mathord{\left/ {\vphantom {Y 2}} \right. \kern-0pt} 2},\;{z_0})$ from the phase distribution of original cross-spectral density ${W_\omega }(X,\;0;\;0,\;Y,\;{z_0})$. By applying this calibration method, we can eliminate phase aberration at each cross-spectral density, namely incoherent hyperbolic hologram.

Figure 10 shows the phase aberration of two experimental set up, at object depth distance $z=115$ mm and $z=135$ mm. From both figures, we see that the phase aberrations are almost same. Thus, we may regard that the phase aberration has reproducibility if we do not change the alignment of interferometer.

Fig. 10

Phase aberration of two experiments condition at object depth distance a $z=115$ mm, and b $z=135$ mm

3.4 Performance of calibration

We have calibrated the phase aberration by the method that presented in Subsect. 3.3. First, the calibrated phase distribution at the spectral peak, 560 nm, of the measured object for both experimental conditions are shown in Fig. 11. We find that hyperbolic curve appear in the phase distributions.

Fig. 11

Phase distribution of measured object after calibration of phase aberration at object depth distance a $z=115$ mm, and b $z=135$ mm

Next, we show in Fig. 12a the in-focus image retrieved from the complex hologram shown in Fig. 11a, where the object depth is $z=115$ mm. From the intensity distribution of in-focus image along x- and y-axes, the sizes of the retrieved object in Fig. 12a is 0.32 and 0.50 mm, respectively. Thus, we find that the results agree well with the actual size of the measured object. Figure 12b shows the intensity distribution over y–z plane at $x=0$. The intensity peak appears close to the retrieved distance ${z^\prime }=115$ mm.

Fig. 12

(Color online) The retrieved image after calibration of phase aberration that the measured object is located at $z=115$ mm (above) and $z=135$ mm (below). The in-focus image over x–y plane at retrieved distance a ${z^\prime }=115$ mm and c ${z^\prime }=140$ mm. The intensity distribution over y–z plane are shown (b, d)

Then, we show the in-focus image retrieved from the complex hologram shown in Fig. 11b, where the object depth is $z=135$ mm. Figure 12c shows the in-focus image over x–y plane. From the intensity distribution of in-focus image along x- and y-axes, the sizes of the retrieved object in Fig. 12c is 0.34 and 0.52 mm, respectively. Thus, we find that the results agree well with the actual size of the measured object. Figure 12d shows the intensity distribution over y–z plane at $x=0$. The intensity peak appears close to the ${z^\prime }=140$ mm. The retrieved distance and object depth are almost same in both experimental results. Thus, we can retrieve the correct images by applying the phase calibration method, and the sizes of the retrieved object are almost same as the size of the measured object. Although the measured object is planar polychromatic object, but we can obtain 3D image by changing the retrieval distance as show in Fig. 12b, d.

4 Mathematical analysis and comparison

In this section, we investigate imaging properties of hyperbolic holography by deriving an analytical solution of IRF. We also demonstrate the comparisons of the theoretical prediction based on analytical solution of IRF with the experimental result for monochromatic point source.

4.1 Analytical solution of impulse response function of multispectral hyperbolic holography

In this subsection, we derive an analytical solution of 4D IRF. Let us first assume that the object to be measured is monochromatic point source, having angular frequency ${\omega _s}=c{k_s}={{2\pi c} \mathord{\left/ {\vphantom {{2\pi c} {{\lambda _s}}}} \right. \kern-0pt} {{\lambda _s}}}$. Here, subscript s indicates that the parameters are source parameters [See in Eq. (12)], and the spatial correlation function is measured along x-, y-, and z-axes within a baseline length of ${l_x}$, ${l_y}$ and ${l_z}$ [See in Eq. (13)]. We write

$$S({x_s},\;{y_s},\;{z_s},\;\omega )={\delta ^3}({x_s} - x_{s}^{\prime },\;{y_s} - y_{s}^{\prime },\;{z_s} - z_{s}^{\prime })\delta (\omega - {\omega _s}){\text{,}}$$

(12)

$$A(X,\;Y,\;Z)={\text{rect}}({X \mathord{\left/ {\vphantom {X {{l_x}}}} \right. \kern-0pt} {{l_x}}}){\text{rect}}({Y \mathord{\left/ {\vphantom {Y {{l_y}}}} \right. \kern-0pt} {{l_y}}}){\text{rect}}({Z \mathord{\left/ {\vphantom {Z {{l_z}}}} \right. \kern-0pt} {{l_z}}})=A(X,Y){\text{rect}}({Z \mathord{\left/ {\vphantom {Z {{l_z}}}} \right. \kern-0pt} {{l_z}}}).$$

(13)

Here, $S({x_s},\;{y_s},\;{z_s},\;\omega )$ denotes the spectral density of the monochromatic point source and the 3D window function $A(X,\;Y,\;Z)$ specify the size of volume interferogram. It takes unit value in the measured area and zero outside.

We begin by noting that, from Eq. (5), the actually measured cross-spectral density across observation plane is obtained by taking the Fourier transform of the 3D spatial correlation function $\Gamma (X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)$ with respect to the thickness $Z$. Then, the actually measured cross-spectral density, denoted ${W_M}$, is expressed as a Fourier transform of the product of the window function $A$ in Eq. (13) and the spatial correlation function $\Gamma$:

$$\begin{aligned} {W_M} & (X,\;0,\;{z_0};\;0,\;Y,\;{z_0};\;{\omega _i}) \\ & =\frac{1}{{2\pi c}}\int {A(X,\;Y,\;Z)\Gamma (X,\;0,\;{z_0};\;0,\;Y,\;{z_0}+Z)\exp ( - i{k_i}Z){\text{d}}Z{\kern 1pt} } \\ & =\frac{{{l_z}}}{{2\pi }} \text{sinc}\left[ {\frac{{{l_z}}}{2}({k_s} - {k_i})} \right]{\kern 1pt} A(X,\;Y)W(X,\;0,\;{z_0};\;0,\;Y,\;{z_0};\;{\omega _s}), \\ \end{aligned}$$

(14)

where we write ${\text{sinc}}\,x={{(\sin x)} \mathord{\left/ {\vphantom {{(\sin x)} x}} \right. \kern-0pt} x}$. The subscript i indicates that the parameters are used for the retrieval, and angular frequency for retrieval is ${\omega _i}=c{k_i}={{2\pi c} \mathord{\left/ {\vphantom {{2\pi c} {{\lambda _i}}}} \right. \kern-0pt} {{\lambda _i}}}$. In Eq. (14), the product of the coefficient ${{{l_z}} \mathord{\left/ {\vphantom {{{l_z}} {2\pi }}} \right. \kern-0pt} {2\pi }}$ and the sinc function represents the spectral IRF determined by the limited baseline length ${l_z}$. The actually measured cross-spectral density ${W_M}$ is extended within the width of the spectral IRF.

Next, we obtain the 3D object information from the cross-spectral density. According to the 2-FT method, the cross-spectral density ${W_M}(X,\;0,\;{z_0};\;0,\;Y,\;{z_0};\;{\omega _i})$ is converted to the angular cross-spectral density ${\tilde {W}_M}({k_x},\;0,\;{z_0};\;0,\;{k_y},\;{z_0};\;{\omega _i})$. Then, it is multiplied by OTF to produce ${\tilde {W}_M}({k_x},\;0,\;{z_0} - {z^\prime }\;;\;0,\;{k_y},\;{z_0} - {z^\prime }\;;\;{\omega _i})$, and inverse conversion to the cross-spectral density ${W_M}(X,\;0,\;{z_0} - {z^\prime }\;;\;0,\;Y,\;{z_0} - {z^\prime }\;;\;{\omega _i})$. Therefore, finally obtained cross-spectral density is expressed as

$$\begin{aligned} &{W_M}(X,\;0,\; {z_0} - {z^\prime };\;0,\;Y,\;{z_0} - {z^\prime };\;{\omega _i}) \\&\quad= \frac{{{\lambda _i}{z_i}}}{{4{\pi ^2}}}\int {{W_M}(X,\;0,\;{z_0};\;0,\;Y,\;{z_0};\;{\omega _i})} \\ &\quad\quad \times \exp \left\{ {i\left[ {(X - {x_i}){k_{ix}} - (Y - {y_i}){k_{iy}}} \right]+i\frac{{{z_i}}}{{2{k_i}}}( - k_{{ix}}^{2}+k_{{iy}}^{2})} \right\}{\text{d}}{k_{ix}}{\text{d}}{k_{iy}}{\text{d}}X{\text{d}}Y. \\ \end{aligned}$$

(15)

The cross-spectral density ${W_M}(X,\;0,\;{z_0} - {z^\prime }\;;\;0,\;Y,\;{z_0} - {z^\prime }\;;\;{\omega _i})$ is proportional to the spectral density ${S^\prime }({x_s},\;{y_s},\;{z_s})$ at a source plane. Thus, the retrieved 3D image $O({x_i},\;{y_i},\;{z_i},\;{\omega _i})$ is rewritten after standard but slightly tedious calculation as

$$\begin{aligned} O({x_i},\;{y_i},\; & {z_i},\;{\omega _i}) \\ & =\frac{{{l_z}}}{{2\pi {\lambda _s}^{2}{z^2}}}{\text{sinc}}\left[ {\frac{{{l_z}}}{2}({k_s} - {k_i})} \right]\exp \left[ { - i\frac{{{k_i}}}{{2{z_i}}}( - {x_i}^{2}+{y_i}^{2})} \right] \\ &\quad \times \int\limits_{{{\kern 1pt} - {{{\kern 1pt} {l_x}} \mathord{\left/ {\vphantom {{{\kern 1pt} {l_x}} 2}} \right. \kern-0pt} 2}}}^{{{{{\kern 1pt} {\kern 1pt} {l_x}} \mathord{\left/ {\vphantom {{{\kern 1pt} {\kern 1pt} {l_x}} 2}} \right. \kern-0pt} 2}}} {\exp \left[ {i\frac{{{k_i}}}{{{z_i}}}\left( {m{x_s} - {x_i}} \right)X} \right]\exp \left[ { - i\frac{{{k_i}}}{{2{z_i}}}(m - 1){X^2}} \right]} {\text{d}}X \\ &\quad \times \int\limits_{{{\kern 1pt} - {{{\kern 1pt} {l_y}} \mathord{\left/ {\vphantom {{{\kern 1pt} {l_y}} 2}} \right. \kern-0pt} 2}}}^{{{{{\kern 1pt} {\kern 1pt} {l_y}} \mathord{\left/ {\vphantom {{{\kern 1pt} {\kern 1pt} {l_y}} 2}} \right. \kern-0pt} 2}}} {\exp \left[ { - i\frac{{{k_i}}}{{{z_i}}}\left( {m{y_s} - {y_i}} \right)Y} \right]} \exp \left[ {i\frac{{{k_i}}}{{2{z_i}}}(m - 1){Y^2}} \right]{\text{d}}Y. \\ \end{aligned}$$

(16)

Because in the linear-optical system, the output image is represented by the superposition integral of the input image and IRF:

$$O({x_i},\;{y_i},\;{z_i},\;{\omega _i})=\int {S({x_s},\;{y_s},\;{z_s},\;\omega )h({x_i},\;{y_i},\;{z_i},\;{\omega _i};\;{x_s},\;{y_s},\;{z_s},\;{\omega _s}){d^3}{r_s}{\text{d}}\omega } .$$

(17)

Therefore, using Eqs. (12), (16), and (17), the detail of calculation can be found in Ref. [13]. The final expression of 4D IRF of the present method is written as

$$\begin{aligned} h({x_i},\;{y_i},\;{z_i},\; & {\omega _i};\;{x_s},\;{y_s},\;{z_s},\;{\omega _s}) \\ & =\frac{{m{l_z}}}{{2\pi c{\lambda _s}z|m - 1|}}\text{sinc}\left[ {\frac{{{l_z}}}{2}({k_s} - {k_i})} \right]\exp \left[ { - i\frac{{{k_i}}}{{2{z_i}}}\left( { - x_{i}^{2}+y_{i}^{2}} \right)} \right] \\ &\quad \times \exp {}^{{(*)}}\left\{ { - i\frac{{{k_i}}}{{2{z_i}|m - 1|}}[ - {{(m{x_s} - {x_i})}^2}+{{(m{y_s} - {y_i})}^2}]} \right\} \\ &\quad \times {\left\{ {[{F^*}({\alpha ^+}) - {F^*}({\alpha ^ - })][F({\beta ^+}) - F({\beta ^ - })]} \right\}^{(*)}}, \\ \end{aligned}$$

(18)

where (*) appear only if $0<m<1$ and the magnification $m={{{k_s}{z_i}} \mathord{\left/ {\vphantom {{{k_s}{z_i}} {({k_i}z)}}} \right. \kern-0pt} {({k_i}z)}}={{{\lambda _i}{z_i}} \mathord{\left/ {\vphantom {{{\lambda _i}{z_i}} {({\lambda _s}z)}}} \right. \kern-0pt} {({\lambda _s}z)}}$ that represents the ratio of the product of wavelength and depth of object and retrieved image. The function $\text{F}(a)$ is defined as in the following form [15] expressed in terms of real component $\text{C}(a)$ and imaginary component $\text{S}(a)$ of Fresnel integrals [16].

$$\text{F}(a)=\frac{1}{{\sqrt 2 }}\exp \left( { - i\frac{\pi }{4}} \right)\left\{ {\frac{1}{2}+\text{C}(a)+i\left[ {\frac{1}{2}+\text{S}(a)} \right]} \right\},$$

(19)

and $\alpha$, $\beta$ are

$${\alpha ^ \pm }=\sqrt {\frac{{{k_i}|m - 1|}}{{\pi {z_i}}}} \left( { \pm \frac{{{l_x}}}{2} - \frac{{m{x_s} - {x_i}}}{{m - 1}}} \right),$$

(20)

$${\beta ^ \pm }=\sqrt {\frac{{{k_i}|m - 1|}}{{\pi {z_i}}}} \left( { \pm \frac{{{l_y}}}{2} - \frac{{m{y_s} - {y_i}}}{{m - 1}}} \right).$$

(21)

In Eq. (18), if we take the limit of $m \to 1$, Eq. (18) reduces to

$$\begin{aligned} h({x_i},\;{y_i},\;{z_i},\; & {\omega _i};\;{x_s},\;{y_s},\;{z_s},\;{\omega _s}) \\ & =\frac{{{l_x}{l_y}{l_z}}}{{2\pi {\lambda _s}^{2}{z^2}}}\exp \left[ { - i\frac{{{k_i}}}{{2{z_i}}}\left( { - x_{i}^{2}+y_{i}^{2}} \right)} \right] \\ &\quad \times \text{sinc}\left[ {\frac{{{l_z}}}{2}({k_s} - {k_i})} \right]{\kern 1pt} {\kern 1pt} \text{sinc}\left[ {\frac{{{l_x}{k_i}}}{{2{z_i}}}({x_s} - {x_i})} \right]{\kern 1pt} {\kern 1pt} \text{sinc}\left[ {\frac{{{l_y}{k_i}}}{{2{z_i}}}({y_s} - {y_i})} \right]. \\ \end{aligned}$$

(22)

This function corresponds to diffraction-limited in-focus image of the monochromatic point source.

Equation (18) is the 4D IRF in the present method defined over $(x,\;y,\;z,\;\omega )$ space and Eq. (22) corresponds to diffraction-limited in-focus image of the monochromatic point source. As we suggested for IRF of S-type method previously [13], the recorded fringe patterns of S-type method correspond directly to the phase distributions of the wavefront of many spectral components propagated from the object being measured. Accordingly, the complex holograms derived from an S-type method corresponds to the ordinary phase distribution as obtained by inline phase-shifting holography. In hyperbolic holography, the recorded fringe patterns do not correspond simply to the wavefront propagated from the object. However, these analytical solutions of 4D IRF in this method and S-type method have similar mathematical form. The diffraction-limited in-focus image is consistent in particular except for the difference in coefficients. The difference in coefficients is caused by retrieval process. In the analytical solution of the S-type method, the convolution integral is directly calculated. On the other hand, the analytical solution of the hyperbolic holography is calculated by a Fourier transforms and inverse Fourier transform. Therefore, although the recorded fringe patterns do not correspond simply to the wavefront propagated from the object, the spectral resolution and spatial resolution are determined in the same manner as S-type method.

4.2 Comparison of imaging properties predicted by IRF and experiment

In the experiment of validation of IRF, the measured object is monochromatic point source composed of optical fiber and He–Ne laser with wavelength 543.5 nm. It locates near the origin of the coordinate system. The object depth distance is 67 mm. Then, light propagates through the two-wavefront folding interferometer. Prism P and P’ were moved stepwise. The numbers of steps of movement of x- and y-stage is 32 × 32, each interval is 12.9 µm. The numbers of steps of movement of PZT is 64, each interval is 0.08 µm.

The spectral profile obtained from volume interferogram is shown in Fig. 13. The intensity peak is located around 531 nm, ones, agrees well with the wavelength of He–Ne laser within the spectral resolution. Next, we demonstrate the comparison between experimental and analytical results. Figure 14 shows the phase distribution of the each cross-spectral density at the spectral peak 531 nm; Fig. 14a shows phase distribution of the cross-spectral densities at the spectral peak appeared in Fig. 13. This is an original cross-spectral density that includes the phase aberration. Figure 14b shows distribution of phase aberration at the spectral peak obtained by the calibration method in Sect. 3.3. Figure 14c shows phase distribution of the cross-spectral density after application of the calibration method. And Fig. 14d shows theoretical phase distributions of the cross-spectral density in this experiment that is calculated from the analytical solution of 4D IRF.

Fig. 13

Spectral profile obtained from volume interferogram. The measured object is the monochromatic point source with wavelength 543.5 nm

Fig. 14

a Phase distributions of the cross-spectral densities at the spectral peak appeared in Fig. 13. b Phase aberration distributions at the spectral peak recovered from the other cross-spectral densities. c Phase distributions of the cross-spectral density after application of the calibration method. d Theoretically phase distributions of the cross-spectral density in this experimental condition

In Fig. 14a the phase distribution is not a hyperbolic curve because it contains the phase aberration. Then after application of the calibration method we can obtain the phase distribution in a hyperbolic curve, which is shown in Fig. 14c. Comparison between the calibrated phase distributions in Fig. 14c, which is obtained by experiment and the phase distribution in Fig. 14d, which is obtained by analytical solution of 4D IRF, we found that they are in good agreement. Thus, we can see that the phase aberration is largely eliminated by the proposed calibration method.

Figure 15 shows the in-focus image over x–y plane at $\lambda =531$ nm and retrieved distance is ${z^\prime }=67$ mm. Figure 15a is obtained from original phase distribution, Fig. 15b is obtained from the phase distributions after application of the calibration method, and Fig. 15c is calculated from the analytical solution of 4D IRF in Eq. (18). In Fig. 15a, the image is blurred and we cannot retrieve the image of point source. After application of calibration method we can retrieve the corrected image as shown in Fig. 15b. Comparison between the retrieved images in Fig. 15b, which is obtained by experiment and the retrieved image in Fig. 15c, which is obtained by analytical solution of 4D IRF, we find that there are also in good agreements.

Fig. 15

(Color online) The in-focus image over x–y plane at $\lambda =531$ nm and retrieved distance ${z^\prime }=67$ mm. Each image is obtained from a original phase distributions shown in Fig. 14a, b phase distributions after application of the calibration method shown in Fig. 14c, and c analytical solution of 4D IRF in Eq. (18)

Figure 16 shows the intensity distributions over x–z plane. Figure 16a is obtained from original phase distribution, Fig. 16b is obtained from the phase distribution after application of the calibration method, and Fig. 16c is calculated from the analytical solution of 4D IRF in Eq. (18). Comparison between the experimental result shown in Fig. 16b and the theoretical prediction shown in Fig. 16c, we find that the intensity peak is located at the same position, and the spread of the longitudinal direction also agree well. Finally, details can be clearly seen from the next figure. Figure 17 shows the comparison of intensity profiles of retrieved images along z-axis: original phase distributions (dashed curve), the phase distributions after application of the calibration method (dotted curve), and the theoretical prediction (solid curve). From Fig. 17, we find that the curve that calculate by the analytical solutions of 4D IRF agree well with experimental results. All in all, it is concluded that the results obtained from application of the phase calibration method enable to retrieve the correct 3D information of the measured object, and the 4D IRF specifies spectral resolution and 3D spatial resolution in multispectral hyperbolic digital holography.

Fig. 16

(Color online) The intensity distribution over x–z plane. Each image is obtained from a original phase distributions shown in Fig. 14a, b phase distributions after application of the calibration method shown in Fig. 14c, and c analytical solution of 4D IRF in Eq. (18)

Fig. 17

Comparison of intensity profiles of retrieved images along z-axis: original phase distributions (dashed curve), phase distributions after application of the calibration method (dotted curve), and the analytical solution of 4D IRF (solid curve)

5 Conclusions

We have proposed a new method to obtain multispectral 3D images. In this method a hyperbolic volume interferogram is directly measured by an appropriately designed interferometer. In this interferometer, only intensity on the optical axis is measured and, so we can use single detector with high sensitivity and high dynamic range. Therefore, it is possible to achieve high sensitivity interferometric system. However, The phase aberration occurred during an experiment. We proposed a calibration method to correct the phase distribution. Basically, the measured interferogram is affected mainly by path difference drift caused by misalignments and unwanted motion of stages. Then all phase aberration is included in interferogram. The phase aberration caused by these factors can be obtained separately form one-time experiment. Moreover, we investigate imaging properties of multispectral hyperbolic incoherent holography based on a novel analytical solution of impulse response function defined over 4D space.

From our work, it has been shown that the spectral resolution and 3D imaging properties obtained experimentally by applying the in-situ calibration method agree well with theoretical ones predicted based on the novel 4D IRF. We also find that the spectral resolution and 3D spatial resolutions are determined in the same manner as ordinary holography. In general, based on the advanced features of this method, it is expected to have wider application area and higher dynamic range of interferometric system than author’s conventional works. In the proposed method, the measurement time is not concerned. The method can be applying to investigate refractive index distribution or spectral of opaque objects. In future work, we may reduce the measurement time by using galvanic mirror system instead of the states where the system moves synchronies to the recording time of the single detector.

Appendix: Derivation of Eqs. (6) and (10)

We think the relationship between the spectral density $S({x_s}\;,{y_s}\;,{z_s})$ and the cross-spectral density $W(X\;,0\;,{z_0};\;0\;,Y\;,{z_0})$ at the observation plane. We suppress $\omega$ since we consider a monochromatic component of optical field. First, the spectral density $S({x_s}\;,{y_s}\;,{z_s})$ is expressed in the following form:

$$S({x_s}\;,{y_s}\;,{z_s})=\langle {\kern 1pt} U_{s}^{*}({x_s}\;,{y_s}\;,{z_s}){U_s}({x_s}\;,{y_s}\;,{z_s})\rangle ,$$

(23)

where $\langle {\mathbf{...}}\rangle$ stands for the ensemble average, * denotes complex conjugate, and ${U_s}$ is the monochromatic component of optical fields at the light source plane $z={z_s}$. From Fresnel diffraction formula, the monochromatic component of optical fields at any points $(X\;,Y)$ on the observation plane $z={z_0}$ are expressed as

$$\begin{gathered} U(X,\;Y,\;{z_0}) \hfill \\ \quad =\frac{{\exp (ikz)}}{{i\lambda z}}\int {{U_s}({x_s},\;{y_s},\;{z_s})} \exp \left\{ {i\frac{k}{{2z}}\left[ {{{(X - {x_s})}^2}+{{(Y - {y_s})}^2}} \right]} \right\}{\text{d}}{x_s}{\text{d}}{y_s}{\text{d}}{z_s}, \hfill \\ \end{gathered}$$

(24)

where $z={z_0} - {z_s}$ is optical depth of the object, as measured from the observation plane. In the present method, the superposed points of the wavefronts are sheared along either x- or y-axes. By setting $X=0$ and $Y=0$, we may rewrite Eq. (24) in the forms:

$$\begin{gathered} U(X,\;0,\;{z_0}) \hfill \\ \quad =\frac{{\exp (ikz)}}{{i\lambda z}}\int {{U_s}({x_s},\;{y_s},\;{z_s})} \exp \left\{ {i\frac{k}{{2z}}\left[ {{{(X - {x_s})}^2}+{y_s}^{2}} \right]} \right\}{\text{d}}{x_s}{\text{d}}{y_s}{\text{d}}{z_s}, \hfill \\ \end{gathered}$$

(25)

$$\begin{gathered} U(0,\;Y,\;{z_0}) \hfill \\ \quad =\frac{{\exp (ikz)}}{{i\lambda z}}\int {{U_s}(x_{s}^{\prime },\;y_{s}^{\prime },\;{z_s})} \exp \left\{ {i\frac{k}{{2z}}\left[ {x_{s}^{{\prime 2}}+{{(Y - y_{s}^{\prime })}^2}} \right]} \right\}{\text{d}}x_{s}^{\prime }{\text{d}}y_{s}^{\prime }{\text{d}}{z_s}, \hfill \\ \end{gathered}$$

(26)

The measured cross-spectral density $W(X\;,0\;,{z_0};\;0\;,Y\;,{z_0})$ may be defined as the cross-correlation between the monochromatic components of the optical fields $U(0\;,Y\;,{z_0})$ and $U(X\;,0\;,{z_0})$. It is expressed as

$$\begin{aligned} W(X,\;0,\; & {z_0};\;0,\;Y,\;{z_0}) \\ & =\langle {\kern 1pt} {U^*}(X,\;0,\;{z_0})U(0,\;Y,\;{z_0})\rangle \\ & =\frac{1}{{{\lambda ^2}{z^2}}}\int {\langle {\kern 1pt} U_{s}^{*}(x,\;y_{s}^{\prime },\;{z_s}){U_s}({x_s},\;{y_s},\;{z_s})\rangle } \\ & \times \exp \left\{ {i\frac{k}{{2z}}\left[ {x_{s}^{{\prime 2}}+{{(Y - y_{s}^{\prime })}^2} - {{(X - {x_s})}^2} - {y_s}^{2}} \right]} \right\}{\text{d}}{x_s}{\text{d}}{y_s}{\text{d}}{z_s}{\text{d}}x_{s}^{\prime }{\text{d}}y_{s}^{\prime }. \\ \end{aligned}$$

(27)

Because the object is a spatially incoherent, the optical fields from different positions on the object are mutually uncorrelated. Thus,

$$\langle {\kern 1pt} U_{s}^{*}(x_{s}^{\prime },\;y_{s}^{\prime },\;{z_s}){U_s}({x_s},\;{y_s},\;{z_s})\rangle =S({x_s},\;{y_s},\;{z_s}){\delta ^2}({x_s} - x_{s}^{\prime },\;{y_s} - y_{s}^{\prime }).$$

(28)

On substituting Eq. (28) into Eq. (27), we obtain the following expression for the cross-spectral density in terms of the spectral density of the objects:

$$\begin{aligned} W(X,\; & 0,\;{z_0};\;0,\;Y,\;{z_0}) \\ & =\frac{1}{{{\lambda ^2}{z^2}}}\int {S({x_s},\;{y_s},\;{z_s})} \exp \left[ { - i\frac{k}{{2z}}\left( { - {x_s}^{2}+{y_s}^{2}} \right)} \right] \\ & \times \exp \left\{ {i\frac{k}{{2z}}\left[ { - {{(X - {x_s})}^2}+{{(Y - {y_s})}^2}} \right]} \right\}{\text{d}}{x_s}{\text{d}}{y_s}{\text{d}}{z_s} \\ & ={S^\prime }({x_s},\;{y_s},\;{z_s}) \otimes \frac{1}{{{\lambda ^2}{z^2}}}\exp \left[ {i\frac{k}{{2z}}\left( { - {X^2}+{Y^2}} \right)} \right]. \\ \end{aligned}$$

(29)

Here,

$$S^{\prime}({x_s},\;{y_s},\;{z_s})=S({x_s},\;{y_s},\;{z_s})\exp \left[ { - i\frac{k}{{2z}}( - {x_s}^{2}+{y_s}^{2})} \right],$$

(30)

is the product of the spectral density $S({x_s}\;,{y_s}\;,{z_s})$ and the phase factor depending on source point, and the symbol $\otimes$ stands for two-dimensional convolution. The angular cross-spectral density in the Fourier space $\tilde {W}({k_x},\;0,\;{z_0};\;0,\;{k_y},\;{z_0})$ is defined as

$$\begin{gathered} \tilde {W}({k_x},\;0,\;{z_0};\;0,\;{k_y},\;{z_0}) \hfill \\ \quad =\frac{1}{{2\pi }}\int {W(X,\;0,\;{z_0};\;0,\;Y,\;{z_0})\exp \left[ { - i( - {k_x}X+{k_y}Y)} \right]{\text{d}}X{\text{d}}Y} . \hfill \\ \end{gathered}$$

(31)

Now, Fourier transforms of the second terms of last expression in Eq. (29) is expressed as

$$\begin{aligned} F & \left\{ {\frac{1}{{{\lambda ^2}{z^2}}}\exp \left[ {i\frac{k}{{2z}}\left( { - {X^2}+{Y^2}} \right)} \right]} \right\} \\ & =\frac{1}{{2\pi {\lambda ^2}{z^2}}}\int {\exp \left[ {i\frac{k}{{2z}}\left( { - {X^2}+{Y^2}} \right)} \right]\exp \left[ { - i( - {k_x}X+{k_y}Y)} \right]{\text{d}}X{\text{d}}Y} \\ & =\frac{1}{{2\pi \lambda z}}\exp \left[ { - i\frac{z}{{2k}}\left( { - {k_x}^{2}+{k_y}^{2}} \right)} \right]. \\ \end{aligned}$$

(32)

This last expression is the OTF defined in 2D Fourier space. Accordingly, on substituting Eq. (29) into Eq. (31) and using convolution theorem, the angular cross-spectral density $\tilde {W}({k_x},\;0,\;{z_0};\;0,\;{k_y},\;{z_0})$ is expressed as the following form:

$$\tilde {W}({k_x},\;0,\;{z_0};\;0,\;{k_y},\;{z_0})=\frac{1}{{\lambda z}}F\left[ {{S^\prime }({x_s},\;{y_s},\;{z_s})} \right]\exp \left[ { - i\frac{z}{{2k}}\left( { - {k_x}^{2}+{k_y}^{2}} \right)} \right].$$

(33)

For calculating inverse propagation, we multiply the both sides of Eq. (33) by complex conjugate of OTF. It is expressed as

$$\tilde {W}({k_x},\;0,\;{z_0};\;0,\;{k_y},\;{z_0})\lambda z\exp \left[ {i\frac{z}{{2k}}\left( { - {k_x}^{2}+{k_y}^{2}} \right)} \right]=F[{S^\prime }({x_s},\;{y_s},\;{z_s})].$$

(34)

Now, inverse Fourier transforms of OTF defined in 2D Fourier space is expressed as

$$\begin{aligned} {F^{ - 1}} & \left\{ {\lambda z\exp \left[ {i\frac{z}{{2k}}\left( { - {k_x}^{2}+{k_y}^{2}} \right)} \right]} \right\} \\ & =\frac{{\lambda z}}{{2\pi }}\int {\exp \left[ {i\frac{z}{{2k}}\left( { - {k_x}^{2}+{k_y}^{2}} \right)} \right]\exp \left[ {i( - {k_x}X+{k_y}Y)} \right]{\text{d}}{k_x}{\text{d}}{k_y}} \\ & =2\pi \exp \left[ { - i\frac{k}{{2z}}( - {X^2}+{Y^2})} \right], \\ \end{aligned}$$

(35)

Finally, by taking inverse Fourier transforms of both sides of Eq. (34), we obtained the final relationship between the spectral density ${S^\prime }({x_s},\;{y_s},\;{z_s})$ and the cross-spectral density $W(X\;,0\;,{z_0};\;0\;,Y\;,{z_0})$ at the observation plane:

$$W(X,\;0,\;{z_0};\;0,\;Y,\;{z_0}) \otimes \exp \left[ { - i\frac{k}{{2z}}\left( { - {X^2}+{Y^2}} \right)} \right]=\int {{S^\prime }({x_s},\;{y_s},\;{z_s}){\text{d}}{x_s}{\text{d}}{y_s}{\text{d}}{z_s}} ,$$

(36)

From these, we will find that the absolute value of the left-hand-side of Eq. (36) proportional to the spectral density at the particular light source at $z=$ constant. Therefore, it is possible to retrieve the spectral component of a 3D image of the light source by this similar method to conventional angular spectrum technique.