Introduction

Groundwater is the largest source of freshwater on Earth since it represents 99% of usable freshwater resources (Fisher et al. 2017) and is used to meet the global water supply demand (i.e., drinking, industrial and irrigation). In addition, aquifers exchange water with surface-water bodies, which is essential to maintain water-dependent ecosystems and river flow during drought periods. The chemical nature of the recharge waters that feed aquifers is highly variable, and there are large differences in flow and solute composition associated with the different recharge mechanisms (diffuse or point source), including natural, induced or artificial recharge. Thus, it is important to preserve the state of groundwater bodies since their deterioration has deleterious effects on human and environmental health and ecosystem services and ultimately causes economic losses.

Groundwater quality can be conditioned by several factors, and its deterioration is commonly associated with anthropic activities (Belkin et al. 2000; Sapek 2014; Burri et al. 2019). Acquiring knowledge on groundwater pollution is difficult and fragmented due to the variable sources, types, and processes that influence the recharge into aquifers; however, groundwater quality can also be threatened by natural processes such as chemical and/or biological processes induced by the mixing of different waters (McArthur et al. 2001, Swartz et al. 2004; Lapworth et al. 2017). Identifying the pollutant sources and understanding pollutant dynamics in groundwater requires the development and application of methods to identify and quantify the recharge sources and the occurrence and fate of the pollutants, namely, source apportioning identification and quantification.

Multivariate data analysis is performed to determine the origin and the proportion of each polluted recharge source (end-member) within a groundwater sample (mixture). These calculations are needed to identify recharge from polluted sources to groundwater.

Mixing calculations have been applied successfully in previous investigations. For instance, Beyerle et al. (1999) quantified surface-water/groundwater interactions by mixing calculations considering 3H/3He, noble gases and chlorofluorocarbons (CFCs) in Switzerland. Nakaya et al. (2007) applied a mixing model and inversion analysis of the ratios of stable isotopes of oxygen (δ18O) and hydrogen (δD) to discern between shallow flow paths and deep groundwater flow paths in the Matsumoto Basin (Japan). Similarly, Ramos-Leal et al. (2007) utilized mixing methods to differentiate between shallow groundwater and deep groundwater and to understand the geochemical composition of an aquifer located in central Mexico, and Jørgensen et al. (2008) employed mixing calculations in the mixing zone of a coastal aquifer in Denmark to investigate the seawater contribution. Vázquez-Suñé et al. (2010) computed mixing ratios to estimate the contribution of recharge in the aquifers of Barcelona (Spain), while Chen et al. (2002) applied mixing calculations in a coal-mining context in China by using conventional hydrogeochemical data and environmentally stable isotopes. Jurgens et al. (2014) applied mixing models to determine the age distribution of groundwater in the Middle Rio Grande Basin (New Mexico), and Jurado et al. (2015) quantified chemical processes affecting organic pollutants by using mixing calculations in Barcelona (Spain).

The complexity of mixing calculations increases as more end-members become involved. In the case of two end-members, mixing ratios can be relatively easily calculated by using conservative tracers (e.g., Cl) as the concentration between the conservative solutes (i.e., in the absence of chemical reactions) of two end-members follows a linear relation (Wigley and Plummer 1976; Tubau et al. 2014). In contrast, as the number of involved end-members increases, the calculation becomes more complex due to the consideration of conservative and nonconservative compounds, ions or parameters (hereafter termed ‘compounds’ for convenience) and as the uncertainty of the model increases. Moreover, most mixing models assume that the chemical composition of end-members are different and accurately known, which is debatable (Vázquez-Suñé et al. 2010). To solve uncertainties associated with a large number of end-members and their composition, Carrera et al. (2004) and Vázquez-Suñe et al. (2010) proposed a methodology based on the use of multivariate statistical analysis (MSA) for computing mixing ratios with uncertain end-members. This methodology maximizes the likelihood of concentration measurements with respect to both mixing ratios and end-member concentrations and has been successfully applied to address different problems.

Another benefit of using MSA is the capacity to identify geochemical reactions that could occur in groundwater related to nonconservative compounds and when deviations from the theoretical mixing line exist. Redox processes, carbonate dissolution/precipitation, ion exchange and other processes may be identified and quantified. Jurado et al. (2013) and Tubau et al. (2014) applied MSA methods to identify and quantify sources and reactions that influence the quality of the urban groundwater in the aquifers of Barcelona (Spain). Cánovas et al. (2012) investigated the impact of discharges from a freshwater reservoir and identified the involved metal transport mechanisms into the acidic Tinto River (Spain). Martinez et al. (2017) employed MSA methods combined with 3D geological modelling to characterize the alluvial aquifer recharge sources in the upper Condamine River catchment (Australia). Scheiber et al. (2018) applied MSA methods to quantify the contributions of different water sources in a mining context. Behrouj-Peely et al. (2020) estimated the mixing ratios in a karst system under different hydrogeological conditions, and Scheiber et al. (2020) assessed the hydrochemical apportioning of irrigation groundwater sources in an alluvial aquifer in Australia. These successful applications suggest that MSA methods can provide essential information in the context of groundwater management, as MSA allows for the identification and characterization of the sources (end-members) involved in the mixing process, apportioning groundwater sources and quantifying the reactions that occur. In general, MSA methods allow one to ascertain the fate of the observed compounds and to evaluate possible management strategies. However, despite the great potential of MSA methods, very few investigations have applied them to quantify hydrochemical reactions, and to the authors’ knowledge, they have not yet been utilized in the context of rural aquifers, such as the Niebla-Posadas (NP) aquifer in the Guadalquivir Valley (Spain).

In this context, the main objective of this report is to apply MSA methods to the NP aquifer to acquire knowledge about the mixing processes and their consequences for groundwater quality by considering the apportionment of different groundwater sources. This analysis will enable (1) an understanding of the processes that affect the groundwater quality of the NP aquifer and (2) improvement in the water management strategies of this specific region. Despite the local focus of this investigation, the application of MSA methods will also serve as an example for their application to other aquifers worldwide.

This report extends previous work by Scheiber et al. 2018 by (1) estimating the total recharge at the regional scale, (2) source apportionment, identification and quantification, and (3) using MSA to quantify the occurrence of chemical reactions in groundwater.

Materials and methods

Site description

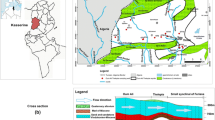
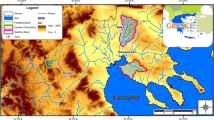
The study area is located near Seville, Spain (≈20 km in northern Spain; Fig. 1). This zone forms part of the Neogene basin of the Guadalquivir River, has an extension of 57 km2 and is located between the Betic range and the Iberian massif. The climate is Mediterranean (temperate-warm) and is influenced by the Atlantic Ocean and the surrounding main relief units. The average annual temperature ranges between 15 and 18 °C in the valley region, and the precipitation is very irregular, ranging from 500 to 600 mm/year (CHG 2015).

Fig. 1
figure 1

Location map showing the position and geology of the study area

Full size image

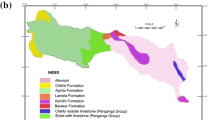
The Niebla-Posadas hydrogeological unit (HU) is formed by conglomerate, detrital limestone and sandstone with abundant marine micro- and macrofauna. The HU constitutes the base of the Cenozoic and outcrops in the northern area and dips southward, where it is confined by the Cenozoic overlying the marine blue marls that are rich in planktonic, benthic microfauna and organic matter. This unit overlies a Paleozoic basement that is fractured and weathered in its upper part, constituting a zone of relatively high permeability. The basement is also affected by two fault systems with SW–NE and NW–SE orientations.

Hydrodynamically, at the regional scale, groundwater flows from the northwest (NW) to the southeast (SE) following the local topography. Chemical changes along flow lines have been identified by Scheiber et al. 2016. The main recharge source of the aquifer is the direct rainfall in the outcropping area located in the NW region. It has been estimated that this recharge is approximately 25 mm/year and occurs in an area of 1,300 km2, which is the total extension of the water body (Gerena-Posadas) to which the NP HU belongs. The water outlets of the aquifer system reach up to 34 hm3/year (without considering the extractions for mining use) and are mainly related to agricultural and domestic consumption extractions (CHG 2015; Navarro et al. 1993).

Previous investigations

Scheiber et al. (2018) identified several recharge sources (end-members) in the NP HU by applying MSA and the MIX code (Carrera et al. 2004) to a large hydrochemical dataset obtained from one field campaign undertaken in February 2012. Three different end-members were identified based on nine compounds (dissolved inorganic carbon (DIC), Cl, NH4, Na, B, Ca, I, Br and SC). In addition, the composition of the potential end-members was identified by using end-member mixing analysis (EMMA) combined with Piper diagrams. The three identified end-members were the rainfall recharge (R), the groundwater originating at the Basal Miocene aquifer (Mb), and the groundwater that flows through the Palaeozoic and reaches the NP aquifer (PZ). The main characteristics of the three end-members are described as follows:

  • End-member R has a Ca–HCO3 composition and is related to the direct rainfall recharge that takes place in the outcropping area (NW) of the Cenozoic materials in the NP aquifer. This end-member has low concentrations of Cl, NH4, Na, B, I and Br and a high Ca concentration.

  • End-member Mb has a Na–HCO3 composition and is associated with water reaching the NP aquifer from the Basal Miocene HU, where Ca–Na exchange processes occur. This end-member is characterized by a low concentration of Ca (≈1 mg/L).

  • End-member PZ has a Na–Cl composition and is related to the groundwater that reaches the NP aquifer after flowing along the fractures of the Paleozoic HU. This groundwater feeds the NP aquifer through the principal fault. The PZ end-member is rich in DIC, Cl, NH4, Na, B, I and Br.

According to Scheiber et al. (2018), end-member R was consistently present in sampling points near the recharge area (NW). When this water flows along the NW–SE flow lines, the contribution of the end-member Mb increases. Sampling points located in the deepest area (SE) had a composition that was compatible with water flowing from the Paleozoic formation.

Sampling and analytical methods

This investigation is based on data from 38 water samples analysed during the field campaign carried out in September 2014 with the objective of determining general chemistry features and isotope composition. Sampling points included wells, piezometers, drains, and springs, and only those whose characteristics (e.g., screen depth in the case of wells or piezometers) were well known were chosen; thus, the sampled HU (i.e., the formation from which the sampled water belonged) was known. All sampled points were purged until the stabilization of the parameters prior to sampling. A closed flow cell was selected to measure in situ physico-chemical parameters, such as temperature (°C), pH, specific conductance (SC, μS cm–1), Eh and dissolved oxygen (DO, mg L–1). In addition, the major and trace solutes were determined (Scheiber et al. 2016).

Statistical analysis

Cluster analysis

Cluster Analysis (CA) was applied to group samples into statistically distinct hydrochemical groups. CA uses several techniques to perform sample classification by assigning observations to groups so that each group is relatively homogeneous and distinct from other groups (Hussain et al. 2008). Numerous studies have utilized this technique to successfully classify water samples (Javadi et al. 2017; Jiang et al. 2015; Majolagbe et al. 2016; Pacheco Castro et al. 2018; Rotiroti et al. 2017; Venkatramanan et al. 2015; Yidana et al. 2008). Hence, in this study, the Q-mode agglomerative hierarchical clustering (HCA) method is employed to classify samples into distinct hydrochemical groups by applying the Ward method (Ward Jr 1963), which is based on the distance between two observations. In this case, the Euclidean distance process was applied to determine the proximity between observations by drawing a straight line between pairs of observations.

Factor analysis

Factor analysis is a multivariate analytical technique that explains the variance observed in the original dataset. This analysis uses principal component analysis (PCA), which is aimed at converting a set of observations of possibly correlated variables to a set of values of linearly uncorrelated variables referred to as principal components and at originating a separation of uncorrelated variables referred to as factors. The objective of PCA is to convert a set of observations of possibly correlated variables to a set of values of linearly uncorrelated variables referred to as principal components. Factor analysis can be applied to establish a pattern of variation among variables or to reduce large datasets into factors. The number of factors obtained from this analysis indicates the number of possible sources of variation in the data.

Certain hydrogeological research investigations have utilized factor analysis with different objectives—for example, factor analysis has been performed to trace groundwater circulation (Join et al. 1997), to evaluate the temporal evolution of groundwater composition (Helena et al. 2000), to assess groundwater salinization (Morell et al. 1996), or to determine the number of end-members in a mixing problem (Christophersen and Hooper 1992).

End-member mixing analysis

End-member mixing analysis (EMMA) applies PCA to determine (1) the minimum number of end-members (sources) necessary to explain the chemical composition of each sampling point, considering only mixing processes (Tubau et al. 2014) and (2) the tracers needed for MIX calculation (Carrera et al. 2004; Fig. 2). EMMA employs a constrained least squares solution that is based on the linearity of mixing processes, the conservative behaviours of tracers, and the invariance of the composition of end-members (Christophersen et al. 1990; Hooper 2003; Hooper et al. 1990).

Fig. 2
figure 2

The three groundwater groups identified by PCA

Full size image

EMMA does not identify specific sources but provides an arbitrary number that must be supported by a good conceptual model. The goal is to maximize the cumulative amount of data variance that can be described with the fewest possible principal components (Doctor et al. 2006). EMMA analyses have been previously utilized to ascertain the sources in mixing problems (Christophersen and Hooper 1992; Doctor et al. 2006; James and Roulet 2006; Martinez et al. 2017; Tubau et al. 2014). The components were defined based on the Kaiser criterion (Kaiser 1960); eigenvalues greater than 1 were accepted as possible sources of variance in the datasets. Complete data used for mixing analysis can be found in the supplementary information (Tables S1 and S2 of the ESM).

Source apportionment

In mixing problems, the commonly performed MSA assumes that the end-member concentrations are well known, which is inconsistent with reality. In many cases, the concentrations of different species in the end-members are unknown, and they are extremely variable in both space and time. The MIX code (Carrera et al. 2004) is used to address these difficulties. The MIX code is an extended approach of that of Kent et al. (1990), which quantifies source apportionment (mixing ratios) from groundwater sample composition. The objective of this method is to calculate the proportions in which ne end-member waters are mixed in np samples, measuring ns species in each of the mixtures. This objective is achieved by maximizing the likelihood of concentration measurements with respect to both mixing ratios and source concentrations. This process is repeated iteratively until the mixing model is calibrated; furthermore, this method improves the estimation of source concentrations, thus expanding the potential of this calculation. Recently, Serrano-Juan et al. (2020) created a user-friendly interface for the MIX code following the methodology proposed by Carrera et al. (2004)

Results and discussion

This section shows the results of applying different methods to characterize the groundwater at the NP aquifer. First, the end-members are identified and characterized using CA, PCA, EMMA methodology and the MIX code; second, the mixing processes and the contribution of the different end-members are determined using the MIX code; third, the chemical reaction processes are assessed by MSA and by comparing the estimated and calculated groundwater composition; and, lastly, the isotopic composition of groundwater is evaluated.

Identification and characterization of the end-members

Cluster analysis: ascertaining the number of end-members

Figure 3 shows a dendrogram that was constructed by applying cluster analysis to the groundwater samples. Three different groundwater groups are clearly identified. Based on the dendrogram diagram (Fig. 3), group 1 consists of 17 sampling points, corresponding to 45% of the samples. These samples have a Na–HCO3 composition and low concentrations of Ca and SC (ca. 2,100 μS/cm). Samples included in group 1 are related to groundwater from the Cenozoic aquifer (Mb) and then to the groundwater hosted in the confined part of the NP aquifer. Group 2 comprises 19 sampling points, representing 50% of the water samples. Samples included in group 2 show a Ca–HCO3 composition and the lowest SC value (approximately 800 μS/cm); thus, this water corresponds to the recharge water of the NP aquifer (R). It is worth mentioning that direct rainfall recharge occurs in the outcropping area located in the NW part of the study site. Group 3 is formed by two sampling points, thus, by the remaining 5% of the samples. These samples have a Na–Cl composition and rich concentrations of SC (4,900 μS/cm), NH4, B and I. This water flows through the fractures of the Paleozoic (PZ) formation and reaches the NP aquifer in the distal area (Fig. 1).

Fig. 3
figure 3

a Dendrogram made with 38 samples, which identified three groundwater groups and b results of the principal component analysis (PCA) using 38 samples and 10 compounds (Test 4)

Full size image

End-member mixing analysis: identification of end-members

End-member mixing analysis was performed to identify the necessary number of end-members to be retained and the selection of the compounds. A total of four tests were conducted using 38 samples and considering different compounds. The results of these tests are sensitive to the selected compounds. The characteristics and the results of the tests are described as follows:

  • First EMMA test (T1). This test considered 14 compounds (DIC, Cl, NH4, Na, B, Ca, δ13C, I, Br, δ2H, 87Sr/86Sr, specific conductivity (SC), δ34SSO4 and δ18OSO4), and a total variance of 82% was obtained with three eigenvectors. The first eigenvector explained 57% of the variance, and most of the components contributed positively, with the exception of Ca, δ13C, δ2H and δ18O; the more contributory tracers were Na, Cl, NH4 and B. The second eigenvector explained 16% of the variance, and Ca, δ34SSO4, δ18O, I, δ2H and DIC were the tracers that contributed the most. The third eigenvector offers 9% of the total variance, and its contributions are attributable to δ13C, 87Sr/86Sr and DIC.

  • Second EMMA test (T2). 87Sr/86Sr is not included, and three eigenvectors explain 83% of the total variance. A minor increase in the main contributing tracers for each eigenvector produces an increase in the total variance of 60% (first eigenvector), 13% (second eigenvector) and 10% (third eigenvector).

  • Third EMMA test (T3). 87Sr/86Sr, δ2H and δ18O are not included, and the total variance increases to 84% with three end-members. In general, this increase is attributed to a greater contribution of tracers, such as Cl, Na, HCO3, Ca, and NH4.

  • Fourth EMMA test (T4). This test was carried out considering 10 tracers (SC, DIC, Cl, Na, Ca, NH4, Br, I, B, δ34SSO4) and explained a total variance of 85% obtained with three components. The first eigenvector explains 59% of the variance and is contributed by SC, Cl, Na, NH4, I and B. The second eigenvector explains 16% of the variance and mainly participates in δ34SSO4, Ca and I. The third eigenvector, with 10% of the variance, includes Ca, NH4 and B.

An analysis of the EMMA results concluded that the most appropriate test is the fourth EMMA test with eigenvalues greater than 1 (Fig. 3), which explains 85% of the chemical variability of the groundwater in the study area. Ten compounds (SC, DIC, Cl, Na, Ca, NH4, Br, I, B, and δ34SSO4) and three end-members were identified.

Principal component analysis (PCA) was performed to determine the differences among the principal components identified by EMMA and was applied to the three principal components identified in the fourth EMMA test. Figure 2 indicates that the three principal components differ in SC and in the content of Cl and Na.

Composition of the end-members and temporal evolution

Scheiber et al. (2018) also defined three end-members to explain a total of 83% of the variance, which is similar to the calculated value in this work (85%). They also applied the MIX code to calculate the end-member composition, including their associated uncertainties; however, this previous investigation was only based on one field campaign (28 samples from C1 PCA).

In the present report, the composition of the end-members is recalculated by considering data from the field campaign carried out in September 2014 (38 samples). Figure 4 shows a comparison between the end-member compositions by considering the two field campaigns (C1 and C2). The composition of the R end-member did not change considerably over time, and only a slight decrease (from C1 to C2) in the concentration of NH4 (–30%) was detected. The Mb end-member shows an increase (from C1 to C2) in the concentration of NH4 (+100%). In contrast, the concentration of Br decreases (–60%) over time. The remaining species were practically constant throughout the field campaigns. The composition of the PZ end-member was fairly constant, with only an increase in the concentration of Ca (+100%). Overall, it can be assumed that the compositions of end-members are constant over time since considerable differences were not observed and only small variations in NH4, Br and Ca occur. The rise in the concentration of NH4 in the Mb end-member might be related to greater degradation of the organic matter of the bluish marls covering the NP aquifer (Scheiber et al. 2016); however, the variation in the concentration of Ca in the PZ end-member may be caused by a larger interaction between the groundwater and the rocks of the Paleozoic basement.

Fig. 4
figure 4

End-member compositions in two field campaigns (C1 and C2)

Full size image

Mixing processes and contribution of the end-members

Mixing ratios are evaluated with the MIX code integrating ten compounds (SC, DIC, Cl, Na, Ca, NH4, Br, I, B, and 34SSO4), three end-members (R, Mb and PZ) and 38 observation points. This code requires introducing the measurement uncertainties assuming a standard deviation (Table 1). Based on previous works, the standard deviation values were defined depending on the conservative behaviours of each species. The standard deviations assigned to groundwater samples (between 10 and 30%, depending on the compound) were lower than those assigned to the end-members (100%), as the composition of the latter is uncertain. Once the composition of the end-members was recalculated, the standard deviation associated with the end-members was reduced to 5%, and the composition of the end-members and mixing ratios at the observation points could be evaluated. The calibration of this analysis was performed by introducing the compounds from the lowest deviation values to the highest and by adjusting the standard deviation until the measured and calculated values were as similar as possible.

Table 1 Standard deviation value applied to each compound. SD standard deviation
Full size table

The measured and calculated concentrations and mixing ratios were obtained from this analysis. Figure 5 displays the scatter diagrams of the measured vs. calculated concentrations. The following observations can be drawn from their comparison:

  1. 1.

    The measured and calculated concentrations for SC, Cl, and Na, both in the end-members and in the observation points, fall close to the 1:1 line. This finding means that the concentration of these species is the result of mixing among the three end-members. These conservative compounds facilitate the calculation of mixing ratios.

  2. 2.

    In general, the measured concentrations of NH4, Br, I and B are higher than those calculated by the MIX code. For compound I, the difference between the measured concentration and the calculated concentration is very small. The increase in these species is related to organic matter degradation, which acts as a reducing agent in the NP aquifer (Scheiber et al. 2016, 2015). The greatest differences are observed in the observation points located in the confined part of the NP aquifer and screened in the Cenozoic materials. In the case of B and I, the highest concentrations are registered in the observation points placed in the most southeastern areas, which have further reducing conditions.

  3. 3.

    The measured DIC concentrations for some observation points are higher than the computed concentrations due to the dissolution of carbonated materials. In contrast, the observation points influenced by the PZ end-member are affected by several chemical processes. Reductive dissolution of FeOOH by organic matter degradation contributes HCO3 to the system; whereas on the other hand, the precipitation of siderite (FeCO3) expanding HCO3 (Eq. 1) takes place simultaneously with the previously described reactions.

    $$\textrm{C}{\mathrm{H}}_2\textrm{O}+4\ \textrm{FeOOH}+7\ {\mathrm{H}}^{+}\to 4\ {\textrm{Fe}}^{2+}+{\mathrm{H}\textrm{CO}}_3^{-}+6{\textrm{H}}_2\mathrm{O}$$
    (1)
  4. 4.

    Ca behaviour is highly variable. The measured concentrations are higher than those calculated at the observation points located near the recharge area (NW). The excess Ca in this area could be related to the dissolution of carbonates as a result of the interaction between the recharge water and the carbonate materials. The measured Ca was smaller than the calculated Ca at many of the observation points located in the confined part of the aquifer. This finding can be associated with cation exchange processes occurring in clayish materials, where Ca is replaced by Na in the groundwater. This process is not reflected in the Na values calculated by MIX, since the increase in this species is integrated into the Mb end-member.

Fig. 5
figure 5

Calibration of the analyses using the MIX code

Full size image

The spatial distribution of the mixing ratios is shown in Fig. 6. The calculated mixing ratios show significant variability; however, the main trends can be discerned. R is the main end-member at these observation points near the recharge aquifer area. As one moves further from this area in the flow direction, the Mb end-member becomes more prominent and increases progressively. The deepest observation points located in the southeast have different proportions of the PZ end-member. Differences between them (i.e., observation points located in the southeast area) depend on the positions (i.e., depth relative to the top of the formation) of their screens and, thus, on the relative depth at which samples are obtained.

Fig. 6
figure 6

Spatial distribution of the mixing ratios obtained with the MIX calculation for each sampling point

Full size image

Overall, mixing ratio analysis allows characterization of the recharge and determines that most samples have a high proportion of water due to rainfall recharge. The R end-member and Mb end-member represent 41 and 48%, respectively, and they correspond to recharged rainwater. The remaining 11% belongs to water that flows through Paleozoic materials and discharges into the Cenozoic aquifer system.

Quantification of chemical processes

After identifying the end-members, selecting the appropriate compounds and evaluating the mixing ratios, the chemical reactions are quantified by MSA. Note that chemical reactions were identified, but not quantified, in previous research (Scheiber et al. 2016, 2015).

Excess NH 4 and B is observed in 37% of the observation points and 50% of the observation points, respectively. The enrichment factor is then calculated by comparing the measured and calculated values and by considering the results of applying the MIX code. Enrichment factors of 36 and 37% are estimated for NH4 and B, respectively, by averaging the observation points that have an excess of these compounds. The observation points that have excess NH4 and B are located in the confined part of the aquifer (red circles in Fig. 7a, b). The calculated enrichment factors agree with the enrichment factor calculated for I (36%). The similarity among the three enrichment factors proves the high correlation that exists among the three compounds and their interdependence. As determined by Scheiber et al. (2016), the high concentrations of NH4, B and I are attributed to the degradation of marine solid organic matter by the sulfate dissolved in the recharge water.

Fig. 7
figure 7

a Plot of measured against calculated values by MIX for B and b plot of measured against calculated values by MIX for NH4

Full size image

The cation exchange process between Na and Ca has a significant role in the evolution of groundwater chemistry (Scheiber et al. 2015). The occurrence of this process is supported by the notion that (1) groundwater in the confined aquifer is rich in Na and poor in Ca and (2) the concentration of Ca decreases in the flow direction as groundwater becomes increasingly Na-dominated. Cation exchange takes place when the remaining pore water contained in sediments deposited in marine environments is replaced by freshwater via freshening (Fig. 8).

Fig. 8
figure 8

Piper diagram, showing that a Ca–Na exchange process takes place in the aquifer

Full size image

The Ca–Na exchange reaction can be written as:

$${\textrm{Ca}}^{2+}+2\mathrm{X}-\textrm{Na}\to {\textrm{X}}_2-\textrm{Ca}+2{\textrm{Na}}^{+}$$
(2)

According to Gaines and Thomas (Gaines Jr and Thomas 1953), the selectivity coefficient (K) may be expressed as:

$$K=\frac{\left[{\textrm{X}}_2-\textrm{Ca}\right]\times {\left[{\textrm{Na}}^{+}\left(\textrm{aq}\right)\right]}^2}{\left[{\textrm{Ca}}^2\left(\textrm{aq}\right)\right]\times {\left[\textrm{X}-\textrm{Na}\right]}^2}$$
(3)

where X2–Ca and X–Na are the equivalent fractions of Ca and Na in the clay and Na+(aq) and Ca(aq) are the activities of Na and Ca, respectively, in the external aqueous solution. The MIX calculation allows the determination of the Ca and Na fractions in the clay by comparing the measured and estimated concentrations of Ca and Na. Consequently, K can be calculated for clay materials present in the NP aquifer. Based on the results obtained from the MIX calculation, the average selectivity coefficient value for the NP clays is 5.7 (ranging between 1.7 and 12.4). The computed K values agree with those calculated by other authors (Robbins and Carter 1983; Griffioen 1993; Bruggenwert and Kamphorst 1979).

Isotopic composition of groundwater at the investigation site

Isotopic composition of end-members

Based on the computed mixing ratios, the isotopic composition of δ2H and δ18OH2O were recalculated (Fig. 9a). The recharge end-member (R) has the heaviest isotopic composition for δ2H and δ18OH2O (–27.3 and –4.7‰, respectively). The isotopic composition of the Miocene end-member (Mb) falls between the composition of R and the composition of Pz (–29.0 and –4.9‰) but shows an isotopic composition closer to Pz than to R. The Pz end-member has the lightest isotopic values (–29.5 and –5.0‰). The isotopic composition of all observation points is aligned and falls within those of the three end-members. The tendency of groundwater samples to have depleted values of δ2HH2O and δ18OH2O indicates long residence times and suggests that the recharge of the sampled groundwater could have occurred under climatic conditions colder than those of the current groundwater (Scheiber et al. 2015).

Fig. 9
figure 9

a δ18O vs. δ2H recalculated content applying the mixing ratios and b representation of the end-member isotopic content of sulfate

Full size image

The sulfate isotopic composition (Fig. 9b) also shows variations among the three end-members. The R end-member has the lightest isotopic composition, with values of +3.7 and 4.1‰ for δ34SSO4 and δ18OSO4, respectively. This composition agrees with the oxidation of sulfides occurring in granites or massive sulfide deposits or in sedimentary materials. The Mb and PZ end-members present a heavier isotopic composition than the R end-member. The isotopic composition for Mb is δ34SSO4 = +12 and +17‰, while for PZ, it is δ18OSO4 = +5.3 and +6.5‰. The isotopic composition of groundwater samples from observation points trend towards heavy values of δ34SSO4 and δ18OSO4, suggesting that sulfate-reduction processes are occurring, which can be deduced from the results in Scheiber et al. (2015).

Assessment of the fate of the environmental isotopes in groundwater samples

Once the mixing ratios and isotopic compositions of the end-members were estimated, the fate of the isotopes in the NP aquifer was assessed. The theoretical isotopic composition (δ34SSO4 and δ18OSO4) of groundwater at the observation points is calculated by considering the previously estimated mixing ratios and is compared with the measurements (Fig. 5).

Only a few observation points fell relatively close to the 1:1 line, indicating that the isotopic composition is the result of mixed end-members (i.e., R, Mb and PZ). This finding is not valid for most observation points in which the measured δ34SSO4 is generally higher than the calculated value. This behaviour could be related to geochemical processes associated with bacterial reduction, as when these processes occur, it is observed that there is (1) a general trend of increasing δ34SSO4, (2) slopes between 0.22 and 0.28 in the δ34SSO4 vs. δ18OSO4 plot, and (3) the depletion of sulfate concentration (Grassi and Cortecci 2005; Thode and Monster 1970). The minimum extent value and maximum extent value for δ34SSO4 were 0.2 and 8.0‰, respectively. The largest increases correspond to the observation points located in the confined part of the NP aquifer, where the sulfate concentration is low (Fig. 10a). One of the most relevant results of this research is the quantification of SO2–4 reduction processes at the observation points located in the confined part of the NP aquifer (Table 2).

Fig. 10
figure 10

a Plot of δ34SSO4 against SO–24 and b plot of δ34SSO4 against δ18OSO4 as calculated (grey circles) and measured (yellow circles)

Full size image
Table 2 Quantification of SO2–4 reduction at 16 points located in the confined part of the aquifer
Full size table

Figure 10 shows δ18OSO4 vs. δ34SSO4 for the observation points considering both the measured composition and computed isotopic composition. The slope of the line defined by the points had a slope of nearly 2. Although this value is lower than those calculated by other authors in experimental investigations, which have obtained slope values ranging from 2.5 to 4 (Aquilina et al. 1997; Cecile et al. 1983; Mizutani and Rafter 1973), it agrees with reported results by different researchers from investigations based on fieldwork (Knöller et al. 2004; Strebel et al. 1990).

The depleted concentrations due to SO4 reduction are assessed by comparing the theoretical (i.e., estimated) composition at each observation point by considering only mixing processes and the mixing ratios calculated with the MIX code and the measured ratios (Table 3). The comparison shows that dissolved SO4 is reduced by a maximum of 20 mg/L in the confined part of the NP aquifer by considering only observation points affected by the sulfate reduction process (16 points) and located in the confined part of the NP aquifer (Table 3).

Table 3 Sulfate reduction quantification
Full size table

Conclusions

MSA methods are successfully applied in the NP aquifer (southern Spain) to quantify the chemical processes that control groundwater quality. This research surpasses previous research developed in the same study area, such as Scheiber et al. 2018, and has contributed to improving knowledge about crucial aspects related to the groundwater quality at the NP aquifer as follows:

  • This global assessment based on MSA methods confirms that groundwater quality issues associated with the NP aquifer are not related to anthropogenic activities, as pointed out by Scheiber et al. (2015, 2016). Groundwater quality issues are the result of geogenic and mixing water processes.

  • The assessment of the temporal evolution of the composition of the end-members shows that they do not vary significantly over time. It is possible to assume that the composition of the identified end-members is invariant over time.

  • Three end-members and 10 tracers are needed to explain 85% of the chemical variability in the groundwater of the NP aquifer considering only mixing processes. This conclusion is based on the combination of multiple analyses such as EMMA, PCA and cluster analysis.

  • The recharge of the aquifer in terms of percentage has been estimated by using the MIX code.

  • The chemical reactions identified in previous works have been quantified by comparing the calculated and measured concentrations. Enrichment factors of 36, 37 and 36% were estimated for NH4, B and I, respectively.

  • The selectivity coefficient (K) for the NP clays was calculated by using the MIX code. This result is meaningful since K is an essential parameter for the calculation of cation exchange processes. The value obtained (K = 5.7) is consistent with values reported by other authors.

  • The isotopic contents (δ2HH2O/δ18OH2O and δ34SSO4/δ18OSO4) were recalculated by using the MIX calculations, and it was deduced that the measured δ34SSO4/δ18OSO4 was affected by sulfate reduction processes.

  • Bacterial reduction and sulfate reduction processes that take place in the confined area of the NP aquifer have been identified and quantified.

Overall, the proposed methodology is a useful tool for quality groundwater management in aquifers that are fed by water from different sources or with different compositions. To the authors’ knowledge, this research entails the first application of this methodology, consisting of the combination of different analyses and techniques, to calculate aspects such as recharge and the selectivity coefficient. The quality and quantity of the obtained results confirm that the proposed methodology, or a part of it, could be applied to address similar problems in other aquifers worldwide.