Introduction

Measurement of water levels in wells is a necessary task for understanding groundwater resources (Taylor and Alley 2001). Developing water-level elevation maps is a major use of water-level measurements in wells (e.g., Hart and McAda 1985; Bexfield and Anderholm 2000; Land and Newton 2008; Rawling 2015). Such maps convey vital information about an aquifer, such as groundwater flow directions, locations of recharge and discharge, groundwater/surface-water interactions, and the influence of lithology and geologic structure on groundwater occurrence and flow. These maps can be used to infer aquifer hydraulic properties and their spatial variation, and assess the impacts of groundwater pumping on water resources (Freeze and Cherry 1979; Fetter 2001).

Sequential water-level maps through time are useful for understanding factors relevant to changing groundwater levels such as climatic variations relating to recharge and the impact of groundwater management strategies. Derivative products from sequential water-level maps include maps of water-level change (Bexfield and Anderholm 2002; Tillery 2008a, b; Galanter and Curry 2019; Falk et al. 2011; Powell and McKean 2014; Ritchie et al. 2019), estimates of groundwater storage change (e.g., McGuire et al. 2012; Haacker et al. 2016; Rinehart et al. 2016) and maps of projected usable lifetimes of an aquifer (Mulligan et al. 2008; Rawling and Rinehart 2018).

Manual water-level measurements are labor-intensive, time-consuming, and expensive. Emphasizing these facts, recent research has focused on the optimal design of new monitoring networks (Júnez-Ferreira and Herrera 2013) and streamlining existing water-level measurement networks to reduce costs, while preserving the essential data needed to characterize an aquifer (Fisher 2013; Ohmer et al. 2019; Ritchie and Pepin 2020). It is clearly prudent to analyze and interpret water-level data collected at such a great expense with methods that will extract the most useful information.

Both manual measurements and continuous time-series of water levels from automated recorders are point data in space. The geostatistical interpolation method of kriging is frequently used to generate continuous surfaces from point data. It was originally developed in the mining industry and has a strong theoretical background (Cressie 2015). It is applied regularly across the gamut of earth and environmental sciences (Webster and Oliver 2007), and groundwater hydrology in particular (Kitanidis 1997), including in recent studies in New Mexico (Rinehart et al. 2016; Rawling and Rinehart 2018; Ritchie et al. 2019). Spatiotemporal kriging is an extension of spatial kriging to include the additional dimension of time, and it derives from an equally well-developed theory (Cressie and Wikle 2011; Montero et al. 2015; Gräler et al. 2016; Wikle et al. 2019). It has also seen use in earth and environmental sciences (e.g., Huevelink and Griffith 2010; Gasch et al. 2015; Varouchakis et al. 2021), but applications to groundwater hydrology have been limited. Varouchakis and Hristopulos (2019) and Varouchakis (2018) compared different spatiotemporal variogram models to a sparse dataset of water-level data at 11 wells, spanning 22 years in a 26-km2 basin on the island of Crete, and produced maps of the groundwater surface and maps of the uncertainty (standard deviation). In a recent application to a regional-scale aquifer, Ruybal et al. (2019) applied spatiotemporal kriging to 27 years of water-level data from 118 wells in the variably confined Arapahoe aquifer, which covers ~11,135 km2 in the Denver Basin, Colorado, USA. There are no theoretical or hydrogeologic limitations to the application of spatiotemporal kriging relative to spatial kriging other than the necessity of time series data sufficient to characterize the temporal correlation structure.

The present study addresses water levels in the topographically closed Mimbres Basin of the Basin and Range geologic province in southwestern New Mexico, USA (Figs. 1 and 2). The region has an arid continental climate with low humidity and large diurnal temperature variations. The average annual precipitation at Deming is 24 cm, while the average annual temperature is 16 °C (Malm 2003; Western Regional Climate Center 2021). Groundwater is the principal water source for agricultural, domestic, and industrial needs, yet the number of water-level measurements has declined steadily since 1980 (Fig. 3). One hundred and seven new water-level measurements collected during early 2020 were combined with 40 years of data at over 600 wells. Spatiotemporal kriging was applied to these data after removal of the regional water-level trend. Sequential water-level maps, comparison with spatial kriging, and interpretation of the water-level changes in the context of the regional geology, climate and land use are presented. The emphasis is on the practical application of spatiotemporal kriging and demonstration of its benefits in a geologically complex regional-scale aquifer.

Fig. 1
figure 1

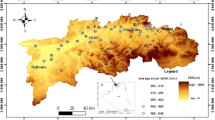
Location of the Mimbres Basin in southwest New Mexico, USA. Thickness of the basin fill from Heywood (2002)

Full size image
Fig. 2
figure 2

Geologic map of the Mimbres Basin. Geology simplified from New Mexico Bureau of Geology and Mineral Resources (2003). Colored groups of outlier wells (A, B, C, D) are described in the text. Red box shows extent of the spatiotemporal maps in section ‘Spatiotemporal variogram and model’

Full size image
Fig. 3
figure 3

a Count of water-level measurements in the Mimbres Basin; b Area of irrigated land; c Volume of water withdrawn for irrigation; d Annual precipitation at three stations, locations shown in Fig. 1. b–c Data compiled from Sorenson (1977), (1982); Wilson (1986), (1992); Wilson and Lucero (1997); Wilson et al. (2003); Longworth et al. (2008), (2013); and Magnuson et al. (2019). Missing values estimated as described in Rawling (2021). d Data from Western Regional Climate Center (2021)

Full size image

The topographic setting and geologic framework of the Mimbres Basin aquifer system are more complex than that of the Arapahoe aquifer studied by Ruybal et al. (2019), yet the regional water-level trend and spatiotemporal covariance structure in the Mimbres Basin are well-characterized by a polynomial trend model and a single spatiotemporal variogram model, respectively. Known aspects of the regional hydrogeology are reflected in the results, and water-level changes can be related to spatiotemporal trends of precipitation and land use, offering new insights as to the influences of these factors on groundwater resources. This study illustrates that the spatiotemporal approach offers improved precision and accuracy compared to spatial kriging, yields these benefits over a larger area than spatial kriging at any given time period, leverages historical data in a way that spatial kriging cannot, and produces fewer artifacts due to changing well networks over time.

Geology and hydrology

The Mimbres Basin is characterized by steep and rugged fault-block mountains that bound low-relief desert plains. The latter formed on structurally down-dropped basins filled with Cenozoic sedimentary rocks, and lesser amounts of volcaniclastic and volcanic rocks (Clemons and Mack 1988). The basin-fill units host the aquifer system that is the focus of this study (Clemons and Mack 1988; Hanson et al. 1994; Seager 1995; Hawley et al. 2000). North–northwest-trending basin axes, with sediment thicknesses of 500 to >1,000 m, are separated by saddles of shallow bedrock; large areas of the Mimbres Basin have a total basin-fill thickness of less than 100 m (Fig. 1; Heywood 2002).

An upper, poorly consolidated basin-fill sedimentary unit with a thickness ranging from 100 to 300 m can be distinguished from a lower unit that is as much as 1,000 m thick and composed of conglomerate, sandstone, and mudstone. The lower unit is usually correlated with the well-indurated Gila Conglomerate and/or Gila Group, which is widely exposed at the northern margins of the Mimbres Basin and in the mountains to the north (Hawley et al. 2000). The majority of the wells in this study are completed in the upper unit or the uppermost part of the lower unit. Quaternary near-surface deposits across the basin are unconsolidated and can have saturated thicknesses up to 30 m. Darton (1916) and White (1931) described the Mimbres Basin aquifer as overall phreatic or unconfined, with local zones of partial confinement and subartesian conditions. Many irrigation wells have multiple screens and access more than one water-bearing zone. Water levels do not show distinct trends with depth of wells. It is assumed that the water levels analyzed here are derived from one complex yet hydrologically continuous, regional, and unconfined aquifer system.

Most recharge comes from the infiltration of the Mimbres River water and mountain front recharge (Wilson and Guan 2004) along the northern margins of the basin. Small amounts of perennial flow in San Vicente Arroyo derive from urban irrigation, leakage, and treated effluent discharge from Silver City sewage treatment and infiltrates upstream of the Mimbres River confluence (Fig. 1; Hawley et al. 2000). Intermittent drainages sourced in intrabasin and basin-bounding mountains contribute small amounts of recharge (Hanson et al. 1994; Hawley et al. 2000; Finch et al. 2008). Potential evapotranspiration is high and areal recharge across the basin floors is negligible. Hanson et al. (1994) estimated total recharge to the United States portion of the Mimbres Basin at 35.6 × 106 m3/year, only a few percent of the total precipitation over the basin, which rarely exceeds 38 cm annually (Fig. 3). Luna County encompasses about two-thirds of the Mimbres Basin and the majority of the irrigated area; estimated groundwater withdrawals in the county in 2015 were 102 × 106 m3, roughly three times the total estimated recharge (Magnusson et al. 2019; Fig. 3). Groundwater pumping and evapotranspiration from playas are the main discharges. The latter has largely been replaced by the former since groundwater pumping for irrigated agriculture began in 1908 (Hawley et al. 2000). Contaldo and Mueller (1991) and Haneberg and Friesen (1995) described land subsidence and measured earth fissure formation in the Mimbres Basin, a highly visible consequence of ongoing groundwater pumping in the basin.

Methods

Data collection and filtering

Water-level measurements were made in 107 wells in January and February 2020 with a steel tape or an electric water-level sounder if the well was unequipped. Water level data since 1980 collected by the New Mexico Bureau of Geology and Mineral Resources (NMBGMR), US Geological Survey (USGS), and New Mexico Office of the State Engineer (NMOSE) were obtained from the NMBGMR Aquifer Mapping program database. Hydrographs for each well were viewed interactively and all measurements during the normal irrigation season, March–October inclusive, were removed. The exception was year 2012, in which there were many March measurements, which were kept unless there was a clear signal of drawdown due to actively pumping wells. Measurements with a USGS data quality flag were removed as were 18 measurements that appeared to be significant outliers, based on the users’ judgement during inspection of the hydrographs. Five wells with 73–127 measurements, with 5–10 in a year instead of the more typical 1–2, were downsampled evenly in time to 40 measurements each, removing 379, mostly redundant, measurements—see section S1 of the electronic supplementary material (ESM1). The resulting dataset consists of 2,997 measurements from 663 wells. The land surface elevation at each well was determined from a 4.5-m digital elevation model, and the water-level elevation was then determined from the depth-to-water measurements.

Regional trend model

The water-table configuration of an unconfined aquifer is often a subdued replica of the land surface topography (King 1899; Tόth 1963; Desbarats et al. 2002). There is a strong north-to-south regional trend in land surface elevation in the Mimbres Basin, and thus a regional water level trend. The water-level surface model used here is spatiotemporal regression kriging (Kyriakidis and Journel 1999; Hengl et al. 2007; Huevelink and Griffith 2010; Ruybal et al. 2019) where the water-level elevation at any point Z(s,t) is a function of space (s) and time (t), and consists of two parts:

$$Z\left(s,t\right)=m\left(s,t\right)+\varepsilon \left(s,t\right)$$
(1)

where m(s,t) is a deterministic trend and ɛ(s,t) is the stochastic residual with a normal distribution and zero mean. The trend is modelled as controlled by factors that are constant in time; i.e., m(s), but variable in space on a large scale such as land surface elevation and regional geology. Residuals from the trend account for the local geometry of water levels and how they change with smaller-scale spatial patterns of discharge, recharge, and variations of these processes in time.

Experimental spatial variograms calculated from residuals of a polynomial trend surface based on the easting and northing coordinates of wells did not reach a constant sill, but rather showed continuous increase with increasing spatial lag, indicating nonstationarity (Webster and Oliver 2007). Therefore, the regional trend was modelled with a third-order polynomial function of the first two principal components of the easting, northing, and elevation coordinates of the wells (Abdi and Williams 2010; section S2 of ESM1). The first two principal components explain 96% of the variation in the three-dimensional (3D) coordinates of the wells. All three spatial coordinates contribute to all three of the principal components. The analysis was not extended to the northern terminus of the basin due to the lack of data.

Water-level elevations whose standardized residuals were greater than two standard deviations (SD) from zero, and had a Cook’s Distance value greater than 4/n (0.0013) where n is the number of data, were flagged as outliers (Schuenemeyer and Drew 2011; Glen 2020). These 138 water-level measurements were dropped from further analysis, and were not used in the spatiotemporal kriging. After removal of these outliers, the residuals from the principal component polynomial trend model form a minimally skewed, approximately normal distribution with near zero mean (section S3 of ESM1).

Spatiotemporal variogram and model

The spatial and temporal correlation of the residuals of the water-level measurements from the time-invariant trend model were quantified via the sample spatiotemporal variogram:

$$\gamma \left(h,u\right)=\frac{1}{2\bullet N\left(h,u\right)}{\sum}_{i=1}^{N\left(h,u\right)}{\left[\varepsilon \left(s,t\right)-\varepsilon \left(s+h,t+u\right)\right]}^2$$
(2)

where h is the spatial separation (lag), u is the time lag, and N(h,u) is the number of paired residuals separated by spatiotemporal lag (h,u) (Heuvelink and Griffith 2010; Ruybal et al. 2019). Because the water-level measurements are not regularly arranged in space or time, they are grouped into bins of spatial and temporal lags. The variogram value, γ, is thus the average squared difference in residuals at each combination of spatial and temporal lag (Fig. 4).

Fig. 4
figure 4

Sample spatiotemporal variogram of residuals from the regional trend model and fitted sum-metric model

Full size image

The sum-metric model (Snepvangers et al. 2003) was chosen from the available spatiotemporal variogram models available in the gstat package in R (Gräler et al. 2016; R Core Team 2018), based on (1) better values of the fit parameters generated by the numerical optimization scheme in R and (2) comparison of “leave-one-out” cross-validation statistics generated for each model in turn (Cressie and Wikle 2011; section S4 of ESM1). The sum-metric model is the sum of separate spatial, temporal, and joint spatio-temporal variogram components. The joint component is a metric variogram, where κ is the space–time anisotropy ratio (space/time) that relates spatial and temporal distances into a single space-time distance (Kyriakidis and Journel 1999; Snepvangers et al. 2003). κ less than one means that, for example, the correlation at 1-m distance equals the correlation at 5-days time, and vice-versa if the anisotropy is greater than one (Gasch et al. 2015).

The best fitting sum-metric model is shown in Fig. 4 and is given by:

$${\gamma}_{\mathrm{S}}(h)\left(\mathrm{Circular}\right)=\left\{\begin{array}{c}{\sigma}_{\mathrm{S}}^2\left(1-\frac{2}{\pi }{\cos}^{-1}\left(\frac{h}{a_{\mathrm{S}}}\right)+\frac{2h}{\pi {a}_{\mathrm{S}}}\sqrt{1-\frac{h^2}{{a_{\mathrm{S}}}^2}}\right)+{\sigma}_{\mathrm{nS}}^2,\kern0.5em 0<h\le {a}_{\mathrm{S}}\\ {}{\sigma}_{\mathrm{S}}^2+{\sigma}_{\mathrm{nS}}^2,\kern0.5em h>{a}_{\mathrm{S}}\\ {}0,\kern0.5em h=0\end{array}\right.$$
(3)
$$\gamma_{\mathrm T}(u)\left(\mathrm{Nugget}\right)=\sigma_{\mathrm{nT}}^2\left[1-\delta(h)\right]$$
(4)

and

$$\gamma_{\mathrm J}\left(h,u\right)\left(\mathrm{Exponential}\right)=\left\{\begin{array}{c}\sigma_{\mathrm J}^2\left[1-\exp\left(-\frac{\sqrt{h^2+\left(\kappa\bullet u\right)^2}}{a_{\mathrm J}}\right)\right]+\sigma_{\mathrm{nJ}}^2,\;0<\sqrt{h^2+\left(\kappa\bullet u\right)^2}\\0,\;\sqrt{h^2+\left(\kappa\bullet u\right)^2}=0\end{array}\right.$$
(5)

where \({\sigma}_{\mathrm{S},\mathrm{J}}^2\) and aS,J are the variance and range of the spatial and joint components of the sum-metric variogram, \({\sigma}_{\mathrm{nS},\mathrm{nT},\mathrm{nJ}}^2\) is the nugget variance, and δ(h) is the Kronecker delta, which equals 1 when h = 0 and 0 otherwise. The nugget variance is present in all three components, but has different magnitudes for each, and is the sum of spatio-temporal variation in the data at ranges smaller than the smallest lag distance and measurement errors (Cressie and Wikle 2011). Note that the temporal component γT(u) is a pure nugget variogram; all of the spatiotemporal correlation is accounted for in the joint component.

The structure of the sample spatio-temporal variogram and fitted model in Fig. 4 suggests the utility of the spatiotemporal approach. In the spatial domain, the variogram rises rapidly to a well-defined sill value (sum of spatial and joint components)) of about 190 m2 at a range of 15–21 km (Table 1). Well pairs separated by a distance larger than this have uncorrelated measurements, and a measurement at one provides no information about the other. The results shown in Figs. 5, 6, 7, and 8 are clipped to the extent of a buffer defined by this spatial range around each well regardless of the time of measurement. As separations decrease the residuals of the water-level data are progressively more strongly correlated. In the time domain, the variogram rises very slowly, indicating a strong temporal correlation of water levels to the largest temporal lags of nearly 22 years. Many years of data can thus aid in the prediction of water levels at unmeasured times.

Table 1 Parameters of fitted sum-metric model
Full size table
Fig. 5
figure 5

Maps of kriging results at four time periods in the region of irrigated agriculture, which shows the largest water level changes in the study area: a 1985, b 2000, c–d 2012, and e–f 2020. There were insufficient data in 1985 and 2000 to perform spatial kriging. Area of maps shown as red box in Fig. 2. Contour lines are at 5-m intervals. Uplands and mountains of lithified Cenozoic sedimentary rocks and older sedimentary, igneous, and metamorphic rocks, undivided, shown as gray overlay

Full size image
Fig. 6
figure 6

Maps of the standard error of kriging: a 1985, b 2000, c–d 2012, and e–f 2020. The data in 1985 and 2000 are insufficient to perform spatial kriging, as shown by the sparse number of wells (crosses) (a– b). Extent of maps in Fig. 5 shown by grey box

Full size image
Fig. 7
figure 7

Net water-level change from 2012 to 2020 calculated with spatiotemporal and spatial kriging, and the confidence factor (see text). Note the different scales for the water-level change. Numbered wells are discussed in the text. Pink areas (a–b) are regions of sparse data in steep terrain where the trend surface plus kriging model predicts water levels above the ground surface, and thus is not valid. Black outline (d) is the intersection of the range buffers around the wells from spatial kriging at the two different time periods. Extent of maps in Fig. 5 shown by grey box (a–b)

Full size image
Fig. 8
figure 8

Net water-level change from 1980–2020, calculated with spatiotemporal kriging. Pink areas are regions of sparse data in steep terrain where the trend surface plus kriging model predicts water levels above the ground surface, and thus is not valid. Uplands and mountains of lithified Cenozoic sedimentary rocks and older sedimentary, igneous, and metamorphic rocks, undivided, shown as gray overlay

Full size image

The Mimbres Basin covers over 10,000 km2, and is geologically and topographically diverse, with great variations in basin-fill thickness (Fig. 1), and with a variety of land uses. One may ask if it is appropriate to use a single sample variogram and fitted model, or “global” model, to describe the spatiotemporal correlation structure of the water-level data across the entire region. To investigate this, the data were subsetted into the San Vicente, Deming, and Florida hydrogeologic regions identified by Finch et al. (2008; Fig. 2), with an overlap of 5 km along the boundaries. The Upper Mimbres region was not investigated separately due to the paucity of data. Sample spatiotemporal variograms were calculated for each region and a best fitting model was chosen using the same optimization criteria described previously. Based on cross-validation statistics, in all cases, the “global” model performed as well or better than any of the region-specific models; thus, only it was used in further analyses (section S5 of ESM1).

Spatiotemporal kriging

Spatiotemporal kriging was implemented at 5-year intervals from 1980 to 2020, and 2012, the last year with abundant water level measurements (Fig. 3). A local neighborhood in spacetime of the 200 most correlated measurements around each well was used during kriging, which relaxes strict stationarity assumptions, and smooth variations in the mean can be accommodated (Gräler et al. 2016). The shape of the neighborhood is defined by the fitted space-time anisotropy ratio of 2.24; measurements at numerically equivalent space and time lags are more correlated in time than in space, which is evident from inspection of the fitted model (Fig. 4). The predicted water level elevation (Fig. 5) is the sum of the temporally constant trend function and the predicted residual from the spatiotemporal kriging, which is unique to each prediction instance. The prediction standard error is the square root of the prediction variance and varies in space and time (Fig. 6; Hengl et al. 2007; Cressie and Wikle 2011; Cressie 2015; Ruybal et al. 2019). The standard error of the trend surface is shown in Fig. S2d of ESM1.

Discussion

Spatial vs. spatiotemporal kriging

This study illustrates several benefits of spatiotemporal kriging relative to purely spatial kriging. Within the time span of the data (1980–2020), a water-level surface may be generated for any time instance, even those with very few measurements when spatial kriging is not possible (e.g., 1985, 2000; Figs. 5 and 6). For any time instance of prediction, a standard error map can be generated to assess the quality of the results and its spatial variation (Fig. 6). Integration of the temporal and spatial correlation structures results in standard errors that are lower for any time instance when compared to purely spatial kriging, regardless of the spatial data density. In addition, there is very little change in the spatiotemporal kriging standard error between time instances with abundant data (2012, 2020) versus those years with few data (1985, 2000). These last two facts are a direct consequence of the strong temporal correlation of water levels in the Mimbres Basin, and lend confidence to predictions made in data-sparse years.

The spatial distribution of predicted water-level rises and declines from 2012 to 2020 is similar using both methods, but the magnitudes are unrealistically large in the spatial kriging case, with maximum predicted increases about three times larger than in spatiotemporal kriging (Fig. 7). For example, the water-level rise of 49 m predicted southeast of Faywood by spatial kriging is unsupported by the limited data from well 7358, which changed less than 1 m from 1982 to 2012. Spatiotemporal kriging predicts a water-level rise here of 3.5 m. Well 2466 between Whitewater and Faywood showed an approximately linear rise of 1.3 m/year from 1992 to 2012, which, if it continued to 2020, would yield a 2012–2020 water level rise of 10.6 m. Spatiotemporal kriging predicts a decline here of less than 7.6 m. The largest water-level rises, along a northwest-trending line from Akela to Faywood (from wells 5950–2466), have measurements at only one of the two time instances (Fig. 7); thus, the leveraging of the temporal correlation in the spatiotemporal method should produce more accurate predictions. Note, however, that the predicted maximum water level rise near Akela is controlled by well 5950 and is similar in both kriging types, 15–20 m. The 2020 measurement at this well may be in error as previous measurements showed very little change. No interpolation or prediction method can account for poor quality data.

Ruybal et al. (2019) showed that changing well networks through time is a major source of uncertainty when comparing spatial kriging maps of water levels made at different times. Calculating water level changes from 2012 to 2020 using spatial kriging necessitates comparing predictions with low standard error to predictions with high standard error. Conversely, as noted above, for the same time instances in the spatiotemporal kriging case, the standard error maps are very similar in spatial distribution and lower in magnitude despite the quite different well networks, even at times with few data (e.g., 1985 and 2000, Fig. 6). This results in less uncertainty in calculated water-level changes. This can be quantified with a confidence factor defined as:

$$1-0.5\left[\frac{\mathrm{variance}\ \mathrm{of}\ \mathrm{older}\ \mathrm{surface}}{\mathrm{maximum}\ \mathrm{variance}\ \mathrm{of}\ \mathrm{older}\ \mathrm{surface}}+\frac{\mathrm{variance}\ \mathrm{of}\ \mathrm{younger}\ \mathrm{surface}}{\mathrm{maximum}\ \mathrm{variance}\ \mathrm{of}\ \mathrm{younger}\ \mathrm{surface}}\right]$$
(6)

and shown in map form (Fig. 7; Rawling and Rinehart 2018). Statistics from leave-one-out cross validation also confirm the improvements gained by accounting for the temporal correlation in the data (Table S7 of ESM1). The ability to generate maps at time periods of the user’s choice is complemented by the ability to “fill out” hydrographs at individual wells (Rawling 2021). Both approaches could be useful in calibrating numerical groundwater flow models as the interpolated values are data-based and with quantified uncertainty, and are not dependent on any parameterization of the flow model itself.

The standard error contributed by the regional trend model is the same for both the spatial and spatiotemporal kriging cases (Fig. S2d of ESM1). It is added to the standard error from kriging to result in the total standard error of prediction. The temporally constant trend model was calculated using all of the well location data from 1980–2020; however, for the spatial case, one should strictly calculate a trend surface for 2012 and 2020 separately using only the well locations for those 2 years. The fewer available data would result in significantly more uncertainty in the trend surface, and a larger total standard error of the prediction for either year. The use of data through time improves both aspects of the water level prediction, the regional trend surface and the kriging results.

Furthermore, when comparing the results of spatial kriging at two different times, the range (correlation length) of the correlation structure at each time period must be considered. No benefit is gained from kriging in regions outside of the intersection of range buffers defined by the correlation length at each time instance around each well (Fig. 7). In these areas, water-level measurements are spaced at a distance larger than the correlation length at any time and so water-level changes predicted in these areas should be considered spurious. This is a significant disadvantage of spatial kriging, as water-level networks are rarely consistent through time. Depending on the data density, the intersection of the range buffers at two different times may result in highly discontinuous areas of kriging prediction, allowing only incomplete, lower-bound estimates on derivative quantities such as storage change to be calculated (e.g., Rinehart et al. 2016). In section ‘Spatiotemporal variogram and model’ the investigation of potential variation in the spatiotemporal correlation structure was discussed. This was motivated by the consideration of a lack of spatial stationarity due to the large size, variations in land use, and geologic and topographic complexity of the Mimbres Basin. It is also possible that the purely temporal correlation structure has changed over time, in part or all of the study area. This may be suggested by large changes in water levels and the decrease in the frequency of measurements. Both have occurred in the Mimbres Basin. Change in temporal correlation was not specifically addressed in this study, but it may be possible to investigate in the future as over 100 years of water level data exist for the basin.

Outliers, geology, and patterns of water-level change

137 measurements from 43 wells were poorly fit by the regional trend model and flagged as outliers, as discussed in section ‘Regional trend model’ (Fig. 2). Wells with outliers tend to be on the perimeter of the study area, and 20 of the 43 wells with outlier measurements are located on outcrops of Gila Group or older pre-Cenozoic bedrock and are likely not completed in the basin-fill aquifer. Example outlier well groups shown in Fig. 2 have water levels that plot distinctly below (groups A and D) or above (groups B and C) regional trends of water-level versus land surface elevation or latitude. Well groups A–C are completed in Gila Group or older bedrock, and group D wells are completed in basin fill. Confining layers in the group D area and/or the low local topographic relief compared to areas to the west may affect the water levels in in the group D wells.

The areas of net water-level rise from 1980 to 2020 include two centers at Whitewater and Faywood (Fig. 8). These are due to infiltration of streamflow in San Vicente Arroyo and emergence of deep-sourced water at springs near Faywood, including Faywood Hot Spring, which discharges from fractured volcanic rocks along the Silver City fault (Hanson et al. 1994; Hawley et al. 2000; Heywood 2002; Fig. 2). Although the net water-level change since 1980 is positive (Fig. 8), both of these areas have experienced water-level declines from 2012–2020 (Fig. 7). The precipitation trend in the Mimbres Basin (Fig. 3) shows a steady decline since the 1980s, and this is likely to negatively affect stream flow and spring discharge.

Net water-level declines of up to 24 m and expanding cones of depression dominate the region from Deming south to Columbus (Figs. 5 and 8). This is the region of the most abundant groundwater pumping for irrigation (Hawley et al. 2000), and where Contaldo and Mueller (1991) documented land subsidence and earth fissure formation. The predevelopment water table map of Hanson et al. (1994, based largely on data of Darton 1916) depicting conditions in 1910–1911 shows no closed basin or cone of depression in this area, but it covers at least 71 km2 and is over 5 m deep in 1985 (Fig. 5). White (1931) noted that 15 years after irrigation pumping began in 1908, maximum water level declines in wells were about 5 m with an average of less than 2 m. Thus water-level declines have increased after 1985 as compared to the previous ~60 years. Conover and Akin (1942) mapped a cone of depression at least 10 m deep in 1941 between Deming and Akela at the terminus of the Mimbres River and just east of the bedrock saddle (Fig. 1). This closed depression is not apparent on any of the maps in this study (Fig. 5) and water levels have in fact risen here over the past 40 years (Fig. 8), yet they remain lower than the bottom of the 1941 depression. Conover and Akin (1942) stated that groundwater pumping was much in excess of any potential recharge, and high recharge from infiltration of Mimbres River flow in infrequent wet years would at best temporarily slow ongoing water level declines due to pumping.

Areas of water-level rise southwest of Deming, in the Florida Graben, and northeast of Columbus all likely represent (partial) recovery of water levels and flattening of cones of depression after abandonment of most irrigation in these areas. Irrigated acreage and estimated groundwater withdrawals have declined since 1970, but have increased in the last 10 years (Fig. 3). This may be the cause of the large water-level declines around Columbus and Hermanas since 2012 (Figs. 7 and 8). Delineating spatial and temporal trends of irrigated acreage in the Mimbres Basin as a proxy for groundwater pumping using repeat satellite imagery, and relating these patterns to water-level trends, would be a fruitful topic of future research.

The transition from water-level rise to decline northeast of Columbus is along the strike with southeast-trending faults at the south end of the 76 Subbasin. Water-level change gradients along the east side of the Florida Graben show some association with the bounding faults (Fig. 8). The largest water-level declines have occurred in areas with large (southern 76 Subbasin) and small (Columbus region) basin-fill thicknesses (Figs. 1 and 8). Many of the earth fissures mapped in the 76 Subbasin form polygonal patterns which may be due to areally extensive dewatering of fine-grained sediment due to regional groundwater pumping (Contaldo and Mueller 1991; Haneberg and Friesen 1995). This is in contrast to linear trends of earth fissures along mapped faults which occur due to differential subsidence across a buried bedrock discontinuity (e.g., Holzer et al. 1979). Overall, geologic heterogeneity, such as variations in basin-fill thickness, vertical and lateral lithologic changes, and intra-basin faulting together, do not appear to create hydrologic discontinuities, such as compartmentalization or confinement, significant enough to strongly affect the patterns of water level change. This allowed the use of the global model of the water-level spatiotemporal correlation structure in this study. Vertical integration of hydraulic head in deep irrigation wells with long and/or multiple screens is likely an important factor in the homogeneous spatiotemporal correlation structure but, outside the areas of irrigated agriculture, most of the data are from shallower stock wells with much shorter screen intervals. To date, the spatiotemporal pattern of water-level changes in the Mimbres Basin is due to the interplay of variation in precipitation and land use/groundwater extraction, whereas basin-fill thickness, stratigraphy, and geologic structure are secondary controls.

Conclusions

This study has extended the long history of water-level measurements in the Mimbres Basin and used the geostatistical method of spatiotemporal kriging to create maps of water levels and water-level changes from 1980 to 2020. Compared to spatial kriging, the spatiotemporal approach offers improved precision and accuracy, predictions at times with no data as well as at locations with no data, fewer artifacts due to changing well networks over time, the ability to exploit historical data in a way that spatial kriging alone cannot, and overall greater confidence in predictions. Despite the geologic and topographic complexity of the Mimbres Basin, a single, global model was able to describe the spatiotemporal correlation structure of the water-level data.

In the areas of the most abundant groundwater pumping for irrigation, from Deming to Columbus, water levels have declined up to 24 m and cones of depression have expanded greatly. In other areas, water levels have risen, presumably as a result of declining irrigation resulting in the flattening of cones of depression. Water-level declines have occurred in concert with declining regional precipitation over the past 10 years near Whitewater and Faywood, both identified as areas of groundwater recharge in previous studies.

The spatiotemporal kriging approach is more mathematically complex than spatial kriging, demanding of computational resources, and multidimensional space-time datasets with hundreds or thousands of data must be manipulated to implement it. The user must be familiar enough with the theory, methodology, and potential pitfalls to make informed decisions at several points during the analysis that will affect the final results. There is no substitute for field measurements of aquifer water-levels, yet the cost in funds and staff hours to gather these data has always been high and continues to rise. Data collected at such great expense should be analyzed with methods that will extract the most useful information. This study in a geologically heterogeneous aquifer system builds on the recent studies of Ruybal et al. (2019) and Varouchakis (2018) to demonstrate that spatiotemporal kriging of water level data is superior to spatial kriging in many ways. Any hydrogeologic analysis that is dependent on water-level maps should benefit from the improvements offered by spatiotemporal kriging if time series of data are available. This includes the assessment of water-level changes (as demonstrated here), calculation of storage changes, calibration of numerical groundwater-flow models, and design and updating of water-level monitoring networks.