1 Introduction

Debris flows are a subset of gravity-driven slope hazards comprising a mixture of grains (rocks, soils) and water. The high fluid volume fraction and elevated relative density of the grains results in the forces developed in both phases significantly contributing to the dynamics of the mass movement [1]. The granular phase may also comprise a wide range of particle sizes [2], leading to complexity at both the grain- and macro-flow scales. With debris flows representing a significant geophysical hazard across the world [3], gaining an understanding of the roles of these different components in controlling outcomes may help to effectively model and mitigate their destructive potential.

Information from naturally occurring debris flows is typically limited by the fact that initial and boundary conditions of the mass movement are generally unknown and material parameters obtained from the final flow morphology are poorly constrained [4]. In contrast, laboratory experiments offer a way to control all characteristics of the flow and contacting boundaries for the duration of the mass movement. Hence, data resulting from laboratory-scale flow experiments is repeatable and can be used to understand the influence of individual parameters on the flow’s behaviour.

One experimental configuration that has received significant attention, because it replicates the unsteady nature of many geophysical flows, is the collapse of a granular step [5]. Generally performed on a granular column with an axisymmetric [5, 6] or quasi-two-dimensional [7] geometry, the column is suddenly released from its initial configuration and collapses until it reaches a stationary final deposit. While dry [5,6,7,8], fully-submerged [9] and wetted [10] granular material have all been used, fewer studies have investigated a situation more reminiscent of debris flows where the column is filled with fluid to a comparable depth to that of the granular material, which we term fully saturated.

The high travel speeds of full scale debris flows mean that even small particles exhibit inertial behaviour where the interaction between grain and fluid can be complex [2]. Dimensional analysis of a simple granular-fluid system suggests that the effects of surface tension are small compared to gravitational forces and fluid viscosity at the macro-scale of geophysical flows [11]. However, it has been found that the flow regime of a collapsing fluid-saturated granular column is primarily determined by the degree of capillary effects between the granular phase and the interstitial fluid due to surface tension [12].

However, as implied by the laboratory experiments, surface tension undoubtedly contributes to granular-scale flow mechanics, particularly at the flow’s surface, and it remains possible that these processes can control mechanisms such as the build-up and dissipation of pore fluid pressure through capillary forces affecting macro-scale flow outcomes [13]. Several studies [e.g. 14, 15] have shown that the inclusion of high concentrations of fine granular material, like clays and silts, enhance the development of excess pore pressures which reduces the frictional resistance exerted on the bulk flow by the terrain bed. Coupled with the small number of physical studies investigating this phenomenon, the fact that recent numerical models [e.g. 16, 17, 18] have not reached a consensus on the most appropriate way to tractably model the mechanisms driving spatio-temporal variations in the grain size distribution suggests that we do not comprehensively understand the mechanisms at play or how their influence scales. Given the comparative micro-scale over which the interactions between the granular fines and the interstitial fluid occur, provided that a sufficient concentration of granular fines is present in the flow, it seems reasonable to suggest that surface tension may play a role in the development of these excess pore pressures and, hence, influence the macro-scale behaviour of the flow.

One way to try and replicate the stress-dependent processes present in natural scale flows within a laboratory model is to utilise a physical modelling method commonly used in the field of Geotechnical Engineering called Centrifuge modelling. By spinning a laboratory-scale model on an arm, the centripetal acceleration from the rotation becomes an effective gravitational acceleration. Thus, the effects of gravity on large ‘prototype’ structures can be replicated at a small physical scale through enhancing the effective gravitational acceleration [19]. The laboratory model is submitted to the required gravitational acceleration in order to replicate the stress profile within the modelled prototype scenario. The stress-similarity is achieved by attaching the model to the end of a centrifuge beam and submitting it to an elevated gravitational acceleration G which is N times larger than Earth’s gravity g [20].

In the past two decades, there have been a number of significant works where centrifuge modelling has been used to physically investigate the scaling of the kinematic processes driving granular flows [e.g. 21, 22, 23]. More recently, the focus has shifted to the design of granular flow mitigation structures and the impact forces developed by the flow-structure collision [e.g. 24, 25]. However, the added complexity of a fluid phase has meant that the use of centrifuge modelling to study debris flows, to date, has been quite limited mainly focusing on debris flow initiation [20] and propagation [26].

The current study aims to provide a platform to investigate the role of micro-scale surface tension effects on macro-scale debris flow behaviour by first characterising the collapse response of grain-fluid mixtures with inertial grains by performing axisymmetric fluid-saturated granular column collapse tests using a geotechnical centrifuge. The use of the centrifuge allows a parameter space of particle size, surface tension and fluid viscosity to be explored in regimes where the grains are inertial and surface tension effects should have little influence on macro-scale flow outcomes.

Fig. 1
figure 1

Schematic of the initial configuration of a just saturated granular column collapse

Full size image

2 Dimensional analysis

Fig. 2
figure 2

Schematic of experimental setup

Full size image

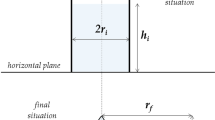
The initial geometry of an axisymmetric, fluid saturated, granular column collapse (see Fig. 1), can be described by two parameters; the initial height of the shared free-surface of the granular-fluid mixture \(h_0\), and the radius of the column prior to collapse initiation \(r_0\). Assuming that the granular phase is comprised of identical spherical particles situated in a homogeneous packing, the granular phase of the column can be characterised by the particle diameter d, the particle density \(\rho _p\) and the mean solid volume fraction of the column \(\phi _p\). Similarly, a Newtonian fluid phase can be characterised by the fluid density \(\rho _f\), the fluid dynamic viscosity \(\mu _f\), and the fluid surface tension \(\sigma _f\). While the initial system is fully saturated, as the collapse progresses, it is possible to obtain flow regions where the depth of the fluid phase is different to that of the granular phase. This can lead to the degree of saturation, the porosity of the granular media, and the surface tension of the fluid phase to significantly influence collapse dynamics.

The current analysis is interested in analysing the evolution of the phase front velocities \(u_x\), where subscript x can refer to the fluid f or particle p phases, and the basal fluid pressure gradient at the centre of the column \({\dot{P}}\) with time t throughout the duration of the column collapse. A promising place to start to understand this complex system is by utilising Buckingham’s \(\Pi\) theorem [27] to systematically identify dimensionless variables, termed \(\Pi\) groups, that provide a homogeneous solution to the physical relationships between key geometric and material parameters, and measured test data. Assuming a constant of gravitational acceleration \(G=Ng\), where N is a constant and g is Earth’s constant of gravitational acceleration, it is hypothesised that a relationship between \(u_x\) and the other defined variables can be postulated as

$$\begin{aligned} u_x = f_1(h_0,r_0,d,\rho _p,\phi _p,\rho _f,\mu _f,\sigma _f,{\dot{P}},t,G) \end{aligned}$$
(1)

where \(f_1\) is an unknown function. The primary difference between Eq. 1 and other relationships used in previous analyses to describe simplified debris flow motion [e.g. 1, 11], is the inclusion of fluid surface tension as a parameter. In contrast to previous analyses, we include fluid surface tension here as a controlling parameter to understand how, in a regime where particle inertia can dilate the granular phase, micro-scale interactions in the pore space may influence macro-scale outcomes.

Temporarily excluding \(\phi _p\) as it is a dimensionless quantity, the other 11 variables within Eq. 1 are derived from combinations of three fundamental physical dimensions: mass, length and time. Hence, Buckingham’s \(\Pi\) theorem dictates that the variables can be connected by \(11-3=8\) independent dimensionless \(\Pi\) groups. Following a previously described mathematical process [11], Eq. 1 can be rewritten as

$$\begin{aligned} \frac{u_x}{\sqrt{GL}}=f_2 \left( \frac{h_0}{r_0}, \frac{r_0}{d}, \frac{(\rho _p-\rho _f)N}{\rho _f}, \frac{t}{\sqrt{L/G}}, \right. \nonumber \\ \left. \frac{\dot{P}}{\rho _f\sqrt{G^3h_0}}, \frac{\rho Gh_0d}{\sigma _f}, \frac{\mu _f\sqrt{G{h_0}^3}}{\sigma _f d}, \phi _p \right) \end{aligned}$$
(2)

where \(f_2\) is an unknown function, L is a characteristic length scale and \(\rho\) is the effective density of the granular-fluid column calculated as \(\rho =\phi _p\rho _p+(1-\phi _p)\rho _f\). The characteristic length scale L has been intentionally left arbitrary allowing us to explore this dimensionless space over both the column and grain scales (see Sect. 6).

The left-hand side of Eq. 2 takes the form of a phase Froude number \(\text{ Fr}_x\) where again, the subscript x refers to the phase of interest. \(\text{ Fr}_x\) compares the influence of inertial and gravitational forces at the phase flow front over the length scale of interest. The right-hand side is comprised of eight dimensionless groups that are used to determine \(\text{ Fr}_x\). The first parameter is the column aspect ratio a which has been shown to be the dominant parameter in the scale analysis of dry granular column collapses. The second parameter was defined as the system size [8] \(r^*\) and was shown to have some influence on the evolution of the dry collapse case. The third parameter is the relative granular-fluid density ratio accounting for acceleration-scale buoyancy \(\rho ^*\). When \(N=\) 1, \(\rho ^*\) reduces to the simple mass ratio found in traditional fluid-granular flow scale analyses [e.g. 1]. Whereas, when \(N>\) 1, the enhanced gravitational field acts on the difference in densities, normalised as a reference density, as a buoyancy. The fourth parameter, \({t}^*\), is the ratio between t and a characteristic inertial timescale \(\sqrt{L/G}\) where, again, L refers to the characteristic length scale of interest. The fifth parameter, \({\dot{P}}^*\), is the ratio between \(\dot{P}\) and the equivalent hydrostatic pressure gradient down the initial height of the column. The sixth parameter is the column Bond number \(\text{ Bo }\) and is defined as the ratio between the inertial forces at the column scale that drive the collapse of the column and the capillary forces at the grain scale induced by deformation of the fluid-air interface. Its influence over the collapse regime of a fluid-saturated granular material under Earth’s gravitational acceleration has already been highlighted [12]. The seventh parameter is known as the Capillary number \(\text{ Ca }\) and relates the viscous forces within the fluid at the column scale to surface tension effects at the grain scale. The final parameter is \(\phi _p\) which remains unchanged since it is already dimensionless. The inclusion of both \(\textrm{Bo}\) and \(\textrm{Ca}\) as \(\Pi\) groups of interest is crucial for ensuring that macro-scale inertial and viscous forces are scaled appropriately in relation to grain-scale surface tension effects in order to obtain a granular phase whose behaviour is primarily governed by particle inertia. Here, we use centrifuge modelling to extend the accessible model parameter space for a simple axisymmetric, fluid-saturated, column collapse configuration. Hence, we are able to perform a multi-scale analysis of the problem by varying G rather than adapting the physical size of the experimental configuration.

It is important to note that the solution to Eq. 2 is not unique. The resulting \(\Pi\) groups could have been recast into alternative forms. In particular, Ca could be replaced by other previously studied dimensionless quantities like the Stokes St (characteristic particle timescale against characteristic fluid timescale) or Reynolds Re (inertial forces against viscous forces in the fluid) numbers. Ca was determined as the most useful parameter out of this group given that the influence of surface tension has been shown to vary with scale [11].

Crucially, four of the dimensionless groups within Eq. 2 contain N or G suggesting that the behaviour of the analysed system is highly scale dependent. Hence, to sufficiently determine the contributions of these dimensionless groups to collapse behaviour, a multi-scale analysis would be required. Given that the size of an experimental configuration is often limited in a laboratory setting, this type of analysis is unworkable with most laboratory-scale granular-flow test configurations.

Table 1 Summary of experimental test parameters
Full size table

3 Model apparatus

Experiments were conducted using the University of Nottingham’s GT50/1.7 geotechnical beam centrifuge. The centrifuge has a platform radius of 2 m and is attached to a swinging platform capable of supporting a payload up to 0.9 m high, 0.6 m circumferential and 0.8 m wide [30]. The machine is capable of applying a maximum centripetal acceleration of 150 g to a payload up to 335 kg in mass.

Within a wind-proof strong box, a steel cylinder with an inner radius \(r_0=\) 54 mm was positioned in the centre of a 490 mm by 485 mm flat plexiglass sheet (see Fig. 2). A foam o-ring was fixed to the base of the steel cylinder allowing a seal to form between the cylinder and the plexiglass when downward pressure was applied to the cylinder. The cylinder was held in a fixed position by two steel rods that were screwed into the top of the column and tightly pressed against a forked steel plate.

Throughout testing, the cylinder was filled to an initial height \(h_0=\) 50 mm of both grains and fluid, creating a just-saturated column with \(a=\) 0.93. Several previous studies have investigated the effects of varying a in both the axisymmetric [5, 6, 8] and quasi-two-dimensional [7, 31] collapse. So here, we focus on column configurations where \(a\approx\) 1, matching a number of reviewed geophysical collapse events [32]. A 12 V LED lightsheet was installed beneath the plexiglass sheet, which acted as a diffuser, creating even back-lighting of the test surface.

The fluid-saturated granular column was comprised of spherical soda lime glass beads and an interstitial fluid consisting of a miscible glycerol-water mixture. Table 1 details the range of values used for all test parameters of interest. The tested centrifuge rotational speeds were selected such that the tested values of N relative to the centrifuge cradle were 1, 5, 15 and 30. These values were then adjusted so that they were relative to a height of \(\frac{2}{3}h_0\) above the horizontal plane to account for variations in centrifugal acceleration across the height of the column. Higher rotational speeds were not explored as the resolution of the recorded videos were limited by the frame rates of the cameras.

Table 2 provides a summary of the parameter space obtained across testing for the dimensionless groups from Eq. 2 calculable from the geometric and material property information given in Table 1. Given that the Bond number is always significantly larger than unity while the tested Capillary numbers cover a range of magnitudes smaller and larger than unity, it is evident that the parameter space explored by the current experiments includes flow states that are largely dominated by gravitational forces at the column-scale while the relative influence of surface tension at the grain-scale and viscous forces at the column-scale vary depending on the geometry of the initial column and test material properties.

It should be noted that previous studies [8, 33] have concluded that axisymmetric column collapse experiments conducted over the specified range of \(r^*\) are highly susceptible to grain-size effects which can significantly influence the mobility and duration of the collapses. However, by not adhering to the geometric reality of the natural scale, we are able to ensure that the behaviour of the spherical particles is primarily governed by their inertia. As such, the current study complements previous work by focusing on a collapse regime where the influence of particle inertia is promoted instead of grain scale.

Table 2 Summary of the dimensionless parameter space calculable from the geometric and material property information in Table 1
Full size table
Fig. 3
figure 3

Snapshots of the collapse sequence downstream of centrifuge motion for two columns, both with \(d=\) 8 mm, with gravitational acceleration coefficient \(N=\) 1 [(a)–(e)] and \(N=\) 14 [(f)–(j)]. The averaged radial position of the fluid (red) and particle (white) phase fronts, where the top left of each image is the point of origin, are shown (colour figure online)

Full size image

3.1 Test procedure

The fully-saturated granular column was prepared after the model was loaded onto the centrifuge. A predefined mass of granular material \(M_{p}\) was poured into the tube which had been previously filled by a predefined volume of interstitial fluid \(V_{f}\) where the respective mass of water \(M_w\) and glycerol \(M_g\) used was defined by the glycerol mass concentration required for that test. The column was compacted from the top using a steel rod until the desired initial column height \(h_0=50\) mm was achieved, and the surface of the fluid was level with the top of the grains. The repeatability of this preparation method is demonstrated by the small range of \(\phi _p\) values achieved across all tests as stated in Table 2. While the achieved packing fractions suggest that the column packing configuration can be described as a poured random packing [34], we follow the logic of previous authors [e.g. 13, 17] by assuming that the granular column is initially in a dense configuration as \(\phi _p\) is greater than the critical solid volume fraction \(\phi _c=\) 0.6 which is generally used as a criteria to assess whether a granular flow is going to contract or dilate.

Prior to initiating collapse, the centrifuge with the experiment mounted on it was spun up to a speed submitting the model to an enhanced gravitational acceleration \(G=Ng\) where \(g=\) 9.81 m s\(^{-2}\). Once spun up, a weighted pulley system was triggered by an air-powered actuator to lift the cylinder and initiate the collapse of the fully-saturated granular column over the horizontal test plane. From analysis of the raw basal pressure data and the high-speed camera footage, the time scale for the cylinder to be lifted up to a height of \(h_0\), \(t_{col}\), can be approximately calculated as \(t_{col}\approx 2.5\sqrt{h_0/(Ng)}\). This equates to a mean release velocity that obeys Sarlin et al.’s [35] criterion for a release process that has no influence on the dynamics of a quasi-two-dimensional collapse consisting of dry spherical glass beads. Li et al. [36] suggested that a lower release velocity may be satisfactory to achieve this effect for wetted granular material given the potential build-up of cohesive forces between adjacent grains. Further investigation is required to confirm this theory and extend it to the fully saturated regime, as well as considering other collapse geometries like the axisymmetric case. However, we deem the dry criterion to be sufficient for the current study.

3.2 Front measurement

Lifting the steel cylinder initiated the collapse of the fluid-saturated granular column. The temporal evolution of the collapse was recorded by two Go-Pro cameras at a resolution of 1080 \(\times\) 1920 pixels and an acquisition rate of 240 frames per second. The images were first treated for fisheye distortion effects [37]. The experimental spatial domain within the images is then calibrated using black markers positioned around the edge of the lightsheet. The markers are used within the digital image correlation (DIC) scheme developed by Blaber et al. [38] to produce an orthonormal image plane. Radial distance values could be taken from the post-processed images at a spatial resolution of 0.5 mm. The upstream and downstream directions, which refers to whether the flow is propagating with (upstream) or against (downstream) the relative motion of the centrifuge, of the collapse are recorded on separate cameras to improve image resolution. This also allows for the contributions of Coriolis acceleration and the Eötvös effect to be considered [19] with respect to the upstream and downstream directions of motion as shown in Fig. 2.

Figure 3 shows the collapse evolution of two test cases, both with \(d=\) 8 mm, at \(N=\) 1 [(a)–(e)] and \(N=\) 14 [(f)–(j)] from the downstream direction. A multi-threshold image analysis scheme was developed to create masks of the individual fluid and particle phases for each image frame. These calibrated masks were then used to obtain the averaged instantaneous front positions, \(r_{f,i}\) and \(r_{g,i}\), and the final front positions, \(r_{f,F}\) and \(r_{g,F}\), of the fluid and particle phases, respectively. Tracking the phase fronts separately was necessary in order to evaluate how variations in the chosen parameter space affected phase front interactions.

For tests that remained within the measurement domain [(a)–(e)], \(r_{f,F}\) and \(r_{g,F}\) are defined as the position of the phase fronts when the collapsing material ceases to move which is formalised as an average fluid front velocity less than 2.4 \(\times\) 10\(^{-3}\) m s\(^{-1}\) (0.01 mm per frame). However, for tests at elevated G, \(N>\) 1, [(f)–(j)] the propagation of the two phases extended beyond the measurement area. In these cases, \(r_{f,i}\) and \(r_{g,i}\) were taken as the average radial distance of the respective phase fronts from the final image frame, where the entirety of both phase fronts remained inside the measurement area.

3.3 Pore pressure measurement

Fig. 4
figure 4

Time evolution of basal fluid pressure at the centre of the column, P, for \(d=\) 2 mm, \(N=\) 4.61 and \(C_m=\) 0. The column collapse was initiated at time \(t=\) 0. The raw signal (black), the reconstructed signals filtered with \(f_c=\) 1000 Hz (blue), and \(f_c=\) 100 Hz (red) are all shown. The inset shows the magnified initial pressure evolution of the test demonstrating how well the reconstructed signal with \(f_c=\) 1000 Hz captures the early pressure drop and recovery (colour figure online)

Full size image

The evolution of basal fluid pressure under the centre of the granular column was measured with a miniature pressure transducer (PT) which was covered by a sheet of filter paper. The sensor had a pressure range of 200 kPa and recorded data at a frequency of 125 kHz. Measurement accuracy was found to be ± 0.1 kPa by calculating the average reading error when supplying a known pressure to the transducer. Figure 4 provides an example of the filtering strategies implemented to clean the signal for a collapse test where \(d=\) 2 mm, \(N=\) 4.6 and \(C_m=\) 0. From the data, a number of different effects can be seen. In particular, the large spike in pressure located around 0.16 − 0.17 s after collapse initiation is a result of the vibrations across the run out surface emanating from the weight used to lift the steel column colliding with the actuator located at the bottom of its housing. Given that signal noise comprised a number of identifiable elements such as this vibration, Fourier transformations of the signal were used to define a cutoff frequency \(f_c\) for a low-pass filtering scheme.

The overall trend of the signal, highlighted in red in Fig. 4, from collapse initiation through to run out completion, was approximated using a fourth-order low-pass digital Butterworth filter with \(f_c=\) 100 Hz within the Matlab [39] signal processing toolbox. Pressure changes relating to column dilation occurring over the first few milliseconds of the collapse were also of interest and were captured using a higher cutoff frequency equal to \(f_c=\) 1000 Hz. The inset of Fig. 4 demonstrates the filtering schemes ability to capture the significant pressure drop and recovery at the onset of collapse. Pore pressure measurements were only considered for tests where \(N>\) 1 to ensure that the noise of the signal was less significant than the total drop in pressure. Pressure measurements were also not recorded for tests undertaken at \(N=28.1\).

4 Column mobility

The influence of particle size d and gravitational acceleration N on the temporal evolution of the collapse front was investigated by examining the temporal evolution of \(r_{f,i}\) from time \(t=0\) until the time where \(r_{f,F}\) is achieved \(t_F\). Figure 5 presents the evolution of the difference between the instantaneous fluid phase front position and the initial fluid phase front position normalised by the initial fluid phase front position, known as the normalised fluid run out length, \((r_{f,i}-r_{f,0})/r_{f,0}\) for particle diameters \(d=\) 2 mm, \(d=\) 4 mm, \(d=\) 6 mm, and \(d=\) 8 mm, at \(N=\) 1, \(N=\) 4.61 and \(N=\) 14, downstream of centrifuge motion. Figure 5 also includes data from a set of experiments where the column had no grains, just the fluid phase, illustrating the limiting case (i.e. \(d=\) 0 mm) for each N. The selected tests have a constant \(\mu _f\) at each value of N with \(\mu _f/\mu _w=[\) 1, 6.7, 21.5 ] for \(N=\) 1, \(N=\) 4.61 and \(N=\) 14.

Fig. 5
figure 5

Temporal evolution of the normalised fluid run out length \((r_{f,i}-r_{f,0})/r_{f,0}\) in time t for particle sizes \(d=\) 2 mm (green), \(d=\) 4 mm (blue), \(d=\) 6 mm (red), \(d=\) 8 mm (black) at \(N=\) 1 (line), \(N=\) 4.6 (dashed) and \(N=\) 14 (dot-dashed) downstream of centrifuge motion. Collapses of a grain-free fluid phase (cyan) at all values of N are also shown (colour figure online)

Full size image
Fig. 6
figure 6

Temporal evolution of the normalised distance between the phase fronts \((r_{f,i}-r_{p,i})/r_{f,0}\) against normalised time \(t/t_F\) for particle sizes \(d=\) 2 mm (green), \(d=\) 4 mm (blue), \(d=\) 6 mm (red), \(d=\) 8 mm (black) at \(N=\) 1 (line), \(N=\) 4.6 (dashed), \(N=\) 14 (dot-dashed) and \(N=\) 28.1 (triangles) upstream (a) and downstream (b) of centrifuge motion (colour figure online)

Full size image

Tests at \(N=1\) appear to follow the three distinct collapse stages described by previous authors [5, 6, 8]. On initiation, the flow front initially accelerates to reach a state of quasi-steady flow. In the run out phase, the flow retards until movement ceases and the final deposit is formed where \(r=r_{f,F}\). The time at which \(r=r_{f,F}\), \(t_{f,F}\), for these test cases increases with grain size d, similar to the relationship found by Bougouin et al. [12]. That study reasoned that the capillary forces between grains, whose magnitude is controlled by the level of surface tension between the interstitial fluid and the ambient air, was the key contributor to this phenomena. Larger capillary forces are present within granular mixtures with smaller pore spaces, an allegory of particle size, which restricts the mobility of grains and results in a lower \(t_{f,F}\) value. Even though the particle sizes used in the current study are at the top end of the particle sizes used by Bougouin et al., suggesting that the current regime is primarily controlled by inertial forces, the influence of surface tension is still identifiable in this run out stage. This may result from a number of factors including; fluid seepage scaling more strongly with N than grain scale inertia [40, 41], the high free surface energy of plexiglass which increases its wettability and aids the propagation of a fluid film across its surface [42] and, particle clustering that can lead to localised capillary effects which reduces the speed of the granular phase.

In contrast, for \(N>\) 1, \(t_{f,F}\) primarily decreases with increasing pore space. This trend tends towards the edge case of the collapse of the singular fluid phase. Similarly to the case of \(N=\) 1, the retardation present in the temporal evolution of the tests containing a granular phase is due to surface tension giving rise to capillary forces which reduces flow mobility. Crucially, by comparing to the edge case, it is evident that the level of retardation reduces with increasing N, suggesting that the influence of capillary forces on the temporal evolution of the collapse reduces with increased scale. This result is reassuring as the macro-scale behaviour of geophysical-scale debris flows are predominantly controlled by gravitational and viscous forces [11].

Given that the interaction between the granular and fluid phases has been shown to significantly affect flow mobility, it is logical to consider the temporal evolution of both constitutive phases through their relative positions to one another. Figure 6 shows the evolution of the normalised distance between the fluid and granular phase fronts \((r_{f,i}-r_{p,i})/r_{f,i}\) with normalised time \(t/t_F\) for particle diameters \(d=\) 2 mm, \(d=\) 4 mm, \(d=\) 6 mm, and \(d=\) 8 mm, at \(N=\) 1, \(N=\) 4.61, \(N=\) 14 and \(N=\) 28.1 for the upstream and downstream propagation directions. Similarly to Fig. 5, tests have been selected so all tests conducted at the same N use interstitial fluids with the same viscosity. \(\mu _f/\mu _w=\) 44.8 for the tests conducted at \(N=\) 28.1.

Initially, all collapses exhibited a drainage phase where the fluid front accelerates away from the granular material. For a given value of N, the maximum distance between the two phase fronts increases with pore space as the space for the fluid to exit the granular structure increases while the influence of capillary effects reduce. For a given value of d, the maximum relative distance increases with N until \(N=\) 14. Increasing N to 28.1 sees a reduction in the maximum relative distance possibly resulting from the reduced impact of solid–fluid interactions as the flow becomes dominated by inertia.

Figure 6 also shows how the granular front’s ability to catch up to the fluid front varies with d and N. The two fronts were considered to be approximately aligned when the normalised relative distance was less than 0.05. For all tests conducted with \(N=\) 1, the granular front was able to completely catch up to the fluid front by the end of the run out phase. The granular front did not overtake the fluid fronts over the duration of these tests which is likely due to the significant impact that surface tension has on laboratory-scale granular-fluid flows.

For a given \(d>\) 2 mm and \(N>\) 1, the final separation between the two phase fronts reduced with increasing N. For collapses propagating in the downstream direction, the granular front was even able to overtake the fluid front for \(N=\) 28.1. It is clear that the enhanced gravitational acceleration field is supplying more kinetic energy to the granular phase which allows it to catch up to the fluid front. Hence, the separation between the two phase fronts reduces when a larger acceleration field (N) is applied.

Figure 6 also shows the influence of the Coriolis acceleration on the mobility of the flow. During the initial stages of the post-collapse propagation, the maximum separation between the two phase fronts for each test was generally greater for the collapsing section propagating in the downstream direction. This was somewhat expected as the Coriolis acceleration will promote the drainage and subsequent propagation of the fluid away from the centre of the test area in the downstream direction while impeding it in the upstream direction. Similarly, during the latter stages of recorded motion, the ability of the granular front to catch up to the fluid front, resulting in a lower final separation, also increased when aided by the Coriolis acceleration. Similar effects have been noted in recent numerical works [43, 44] where the density of the flow is highly dependent on the flow propagation direction relative to centrifuge motion. Naturally, the magnitude of these effects increased with N, as the magnitude of the Coriolis acceleration also increases with N.

While the influence of the Coriolis acceleration does vary with particle size, it only appears to have a significant affect on flow dynamics when the collapses containing smaller particle sizes (i.e. \(d=\) 2 mm) enter a ‘creep-like’ flow regime where, in the downstream direction, the fluid front is again able to accelerate away from the granular front. Whereas, for the larger particle sizes, the Coriolis force only further propagates the reduction of \((r_{f,i}-r_{p,i})/r_{f,i}\) with normalised time. Similarly, the influence of the Eötvös effect appeared to be negligible on flow dynamics prior to the creep phase which is likely due to the fact that natural scale particle inertia has been preserved. Given that the current study focuses on debris flow mechanics, which are best replicated within the experiment prior to the flow entering a monolayer (i.e. the initial acceleration phase), we have deemed the asymmetry induced by the Coriolis acceleration and the Eötvös effect to be negligible for the particular collapse period of interest (see Sect. 6).

5 Fluid pressure evolution

Fig. 7
figure 7

Temporal evolution of the dimensionless basal fluid pressure at the centre of the column \(P/\rho _fGh_0\), filtered using \(f_c=\) 100 Hz with time t for particle sizes \(d=\) 2 mm (green), \(d=\) 4 mm (blue), \(d=\) 6 mm (red), \(d=\) 8 mm (black) at (a) \(N=\) 4.61 (line) and (b) \(N=\) 14 (dashed). (c) Basal fluid pressure at the centre of the column P, filtered at \(f_c=\) 1000 Hz, against \(t/t_I\) immediately after the release of the column (colour figure online)

Full size image

As well as having a dominant effect on the possible separation between the two phase fronts, the drainage phase of the collapse is key to the dissipation of pore pressure from the initially static column configuration. Figure 7 details the evolution of the normalised basal fluid pressure at the centre of the column P with time t for particle diameters, \(d=\) 2 mm, \(d=\) 4 mm, \(d=\) 6 mm, and \(d=\) 8 mm, at (a) \(N=\) 4.61, and (b) \(N=\) 14, respectively. Again, tests have been selected that have a shared \(\mu _f\) value for every value of N. In this case, the time-frame shown has been restricted to the first 0.5 s of each collapse at which point the residual normalised pressure is referred to as \({P_F}^*\).

At the beginning of each test conducted at both \(N=\) 4.61 and \(N=\) 14, \(P\approx \rho _fGh_0\) which illustrates that pressures within the column are hydrostatic prior to the collapse. Upon release, the height of fluid above the pressure sensor reduces throughout the collapse as the granular-fluid mixture propagates out away from the column centre. This results in a progressive reduction of P until \(P=P_F\).

The influence of d on the temporal evolution of P can be illustrated through its influence of \({P_F}^*\). For a given N, \({P_F}^*\) increases with decreasing d and \({P_F}^*\) for particle sizes \(d=\) 6 mm and \(d=\) 8 mm is approximately equal to 0 kPa where no fluid remains above the PT. This demonstrates the reduced influence of the granular phase on \({P_F}^*\) as d increases. It can be reasoned that the increased pore space improves the fluid’s ability to displace from the centre of the measurement domain over the test duration. Conversely, a smaller pore space limits the fluid’s ability to exit the granular material which itself has reduced mobility due to capillary effects. A similar particle size dependency has been observed in the case of post-depositional seepage in natural scale debris flows [e.g. 45]. The influence of d also appears to slightly increase with N.

Figure 7c focuses on another characteristic feature of the evolution of P, which is the reduction and recovery of basal pore pressure observed over the inertial column timescale \(t_I=\sqrt{h_0/G}\) immediately after collapse initiation. While the magnitude of this initial pressure reduction increases with N, the more interesting variation is largely controlled by d with the magnitude of the pressure drop generally increasing as d decreases for a given N. This effect is more pronounced when \(N=\) 14. The recovery of this initial pressure reduction also appears to reduce as N increases. As this variation in pressure reduction occurs immediately after the release of the column, it is likely to be the result of initial particle rearrangement. It has been found previously that the critical solid volume fraction for spherical grains \(\phi _{p,c}\approx\) 0.57 [13]. This suggests that all tests in the current study were conducted with dense granular packings which means that, upon the onset of the collapse, the granular structure must initiate its displacement by first dilating. This allows the interstitial pore fluid to move into the additional pore space created by the dilation which, based on the pore pressure feedback loop described by Iverson et al. [46], causes a reduction in basal fluid pressure. Rondon et al. [13] demonstrated the presence of the pore pressure feedback loop for a quasi-two-dimensional fully-submerged granular column collapse configuration exposed to the acceleration field of Earth’s gravity. The study was carried out using only a singular particle size ten times smaller than the smallest particle used in the current work. A submerged collapse would not experience any influence from surface tension so any differences in behaviour based on particle size would emanate from viscous interactions between the fluid and the grains. In the current configuration, capillary forces arising from the presence of surface tension will cause a further reduction in P.

6 Scale analysis

As collapse dynamics clearly depend on N, dimensionless parameters used previously in the literature, a and \(\phi _p\), are not enough to characterise the phenomena governing the behaviour of the fluid-saturated granular column collapse in the current test configuration. The observed interplay between the fluid and particle fronts also suggests that the viscous nature of the interstitial fluid must also be recognised to explain these flow states.

Fig. 8
figure 8

\({\dot{P}_m}^*\) normalised by \(D=(\rho ^*)^\beta (r^*)^\gamma\) against \(\text{ Bo }/\text{Ca }\) for particle sizes \(d=\) 2 mm (green), \(d=\) 4 mm (blue), \(d=\) 6 mm (red), \(d=\) 8 mm (black) at \(N=\) 4.61 (triangle) and \(N=\) 14 (star). The black line indicates the power law fit provided in Eq. 4 using the exponents found in Table 3 (colour figure online)

Full size image

To characterise the acceleration phase of each collapse, the maximum velocities of the two phase fronts \(u_{f,m}\) and \(u_{p,m}\), and the time after collapse initiation that these maximum velocities were achieved \(t_{f,m}\) and \(t_{p,m}\), were evaluated. A linear approximation of the pressure gradient over the first significant pressure drop at the centre of the column, \(\dot{P}_m\), was recorded as indicative of the pore pressure response in the early collapse stages. Using these terms, Eq. 2 can be rewritten into the following form

$$\begin{aligned} \frac{u_{x,m}}{\sqrt{GL}}=f_3 \left( \frac{h_0}{r_0}, \frac{r_0}{d}, \frac{(\rho _p-\rho _f)N}{\rho _f}, \frac{t_{x,m}}{\sqrt{L/G}}, \right. \nonumber \\ \left. \frac{\dot{P}_m}{\rho _f\sqrt{G^3h_0}}, \frac{\rho Gh_0d}{\sigma _f}, \frac{\mu _f\sqrt{G{h_0}^3}}{\sigma _f d} \right) \end{aligned}$$
(3)

where \(f_3\) is an unknown function and, again, the subscript x refers to the phase of interest. Noting that \(\phi _p\) remained approximately constant throughout the experiments, this parameter was disregarded from all further analyses. Thus eight dimensionless groups are defined: \(\text{ Fr}_{x,L}\), a, \(r^*\), \(\rho ^*\), \({t_{x,L}}^*\), \({\dot{P}_m}^*\), \(\text{ Bo }\) and \(\text{ Ca }\), where subscript x, again, refers to the phase of interest and subscript L is equal to d or \(h_0\) depending on the characteristic length scale of interest.

Values of \(\text{ Fr}_{x,L}\) and \({t_{x,L}}\) were obtained for each test by averaging the upstream and downstream values of \(V_x\) and \(t_x\), respectively. This had the added benefit of limiting the contributions of Coriolis acceleration and the Eötvös effect on the scale analysis. The significance of each parameter in Eq. 3 was tested through the implementation of a non-linear regression scheme with a weighting that favoured power-law fits that minimised the degrees of freedom to reasonably portray the data set. Given that we do not have an a priori understanding of the combined and relative influence of each \(\Pi\) group within the dimensionless parameter space, a generalised power-law fit provides a reasonable starting point for this process. The outcome is that all measured quantities, meaning \({\dot{P}_m}^*\), \(\text{ Fr}_{x,L}\) and \({t_{x,L}}^*\), appear to be independent of each other for all phases and scales. Figs. 8, 9 and 10 show the finalised fits for \(\dot{P}^*\), \(\text{ Fr}_{x,L}\) and \({t_{x,L}}^*\) against \(\text{ Bo }/\text{Ca }\), respectively. The low measurement error for the majority of points in Figs. 8 and  9 further highlights the minimal influence that the Coriolis acceleration had over the collapse period of interest. In the case of \({\dot{P}_m}^*\), the absolute measurement error for each data point lies within each respective marker. It is important to note that this error differs from the fluctuations in pressure gradient throughout the signal which is significantly larger. The variation of all measured quantities of interest Q can be described by the following relation

$$\begin{aligned} Q= \left( \frac{\text{ Bo }}{\text{ Ca }}\right) ^\alpha {(\rho ^*)}^\beta {(r^*)}^\gamma \end{aligned}$$
(4)

where \(\alpha\), \(\beta\) and \(\gamma\) are constants that are summarised in Table 3. Equation 4 demonstrates that the selected characteristic quantities associated with the initial acceleration phases of the granular and fluid flow fronts and the initial post-collapse pressure gradient can be reasonably well predicted by a simplistic power law model consisting of three dimensionless parameters.

Table 3 Summary of exponents used to fit Eq. 4 for all characteristic dimensionless quantities of interest. The normalised root mean squared error RMSE\(_N\) of each fit is also detailed
Full size table

6.1 Quantification of scaling parameter influence

Fig. 9
figure 9

\(\text{ Fr}_{x,L}\) normalised by \(D=(\rho ^*)^\beta (r^*)^\gamma\) against \(\text{ Bo }/\text{Ca }\) for particle sizes \(d=\) 2 mm (green), \(d=\) 4 mm (blue), \(d=\) 6 mm (red), \(d=\) 8 mm (black) at \(N=\) 1 (cross), \(N=\) 4.61 (triangle), \(N=\) 14 (star) and \(N=\) 28.1 (circle). (a) \(x=f\) and \(L=d\), (b) \(x=f\) and \(L=h_0\), (c) \(x=p\), and \(L=d\) and (d) \(x=p\) and \(L=h_0\). The black line indicates the power law fit provided in Eq. 4 using the exponents found in Table 3. Error bars signify the absolute measurement error of the independent variable (colour figure online)

Full size image
Fig. 10
figure 10

\(t_{x,L}\) normalised by \(D=(\rho ^*)^\beta (r^*)^\gamma\) against \(\text{ Bo }/\text{Ca }\) for particle sizes \(d=\) 2 mm (green), \(d=\) 4 mm (blue), \(d=\) 6 mm (red), \(d=\) 8 mm (black) at \(N=\) 1 (cross), \(N=\) 4.61 (triangle), \(N=\) 14 (star) and \(N=\) 28.1 (circle). (a) \(x=f\) and \(L=d\), (b) \(x=f\) and \(L=h_0\), (c) \(x=p\), and \(L=d\) and (d) \(x=p\) and \(L=h_0\). The black line indicates the power law fit provided in Eq. 4 using the exponents found in Table 3. Error bars signify the absolute measurement error of the independent variable (colour figure online)

Full size image
Fig. 11
figure 11

(a) \({(\text{ Bo }/\text{Ca})}^\alpha\) against \(\text{ Bo }/\text{Ca }\). (b) \({\rho ^*}^\beta\) against \(\rho ^*\). (c) \({r^*}^\gamma\) against \(r^*\). Fits for \(\text{ Fr}_{f,d}\) (black), \(\text{ Fr}_{f,h_0}\) (black dashed), \(\text{ Fr}_{p,d}\) (red), \(\text{ Fr}_{p,h_0}\) (red dashed), \({t_{f,d}}^*\) (blue), \({t_{f,h_0}}^*\) (blue dashed), \({t_{p,d}}^*\) (cyan), and \({t_{p,h_0}}^*\) (cyan dashed) are shown (colour figure online)

Full size image

Equation 4 provides significant insight into the factors governing the behaviour of these characteristic flow states. The relative influence of each parameter on the right-hand side of Eq. 4 on the mobility of the granular and fluid phases is investigated further in Fig. 11 where each parameter to the power of its exponent is plotted against itself for all variations of \(\text{ Fr}_{x,L}\) and \({t_{x,L}}^*\).

Considering \(\text{ Bo }/\text{Ca }\) as a single parameter within Eq. 4 means that the fits of Q are decoupled from the influence of surface tension at the grain-scale. Instead, it is the balance of column-scale gravitational and viscous forces that influence flow behaviour. While the influence of surface tension at varying levels of N was discussed previously, the relatively large particle sizes used has allowed all cases of Q to be surface tension independent at all scales. Figure 11a shows that \((\text{ Bo }/\text{Ca})^\alpha\) decreases as \(\text{ Bo }/\text{Ca }\) increases for all cases of \(\text{ Fr}_{x,L}\). Given that column collapses are gravity-driven processes, the rate at which gravitational forces increase will dominate the rate at which inertial forces increase for all phases and scales. This means that column mobility, and therefore \({t_{x,L}}^*\), increases as gravitational force contributions increase with respect to viscous effects.

Figure 11b demonstrates that \(({\rho ^*})^\beta\) increases with \(\rho ^*\) in all cases. According to Bougouin and Lacaze [9], the range of \(\rho _p/\rho _f\) values used categorises the observed flow states into the inertial regime where inertial fluid forces have a significant impact on flow behaviour. However, the influence of particle inertia still dominates, which causes \(\beta\) to vary depending on the phase of the flow. Generally, the magnitude of \(\beta\) is greater for the particle phase for both quantities of interest at both the column- and granular-scales. It would be interesting to achieve higher values of \(\rho ^*\) by either reducing \(\rho _f\) or increasing \(\rho _p\) and see how flow states where fluid inertial effects are no longer important (i.e. the free-fall regime) scale with Eq. 4.

Warnett et al. [8] found that increasing \(r^*\) increased the mobility of the collapse in the dry case. In the current study, Fig. 11c shows that the influence of \(r^*\) is predominantly dependent on the scale of interest. Generally, increasing \(r^*\) reduced the mobility of the column at the column-scale while increasing it at the grain-scale with respect to velocity and collapse duration. This outcome is logical as \(r^*\) is a ratio between the column- and grain-scales. Previously, this effect was found to saturate when \(r^*\approx\) 107, a value that is significantly higher than what is covered by the parameter space of the current study. As \(r^*\) was varied by changing the particle size, we are unable to determine whether \(r_0\), and other parameters defining the column geometry, have a significant impact on the evolution of the flow as N increases.

7 Discussion

The wide particle size distribution in debris flows coupled with comparatively high fluid volume fraction leads to macro-scale flow features that can originate from micro-scale processes. This makes similitude between laboratory experiments and geophysical-scale movement events particularly difficult. For example, surface tension can not be important in the geophysical flow when considering overall flow scale, but becomes important in a laboratory prototype with reduced geometric scale. This means that the true role of surface tension through fines in the geophysical flow may actually be masked by these scaling artefacts in the laboratory. This research attempts to evaluate laboratory flows where the particles are inertial, in an attempt to isolate the response of those grains as differentiated from fine grains in a debris flow.

To mimic debris flows, we used a just-saturated granular column collapse configuration, consisting of glass grains in a size range where their inertia was significant, facilitated by using a geotechnical centrifuge. Grain size, gravitational acceleration and fluid viscosity were systematically varied to analyse their influence on the front evolution of grain and fluid phases alongside the basal pore pressure.

The drainage phase, where the fluid front accelerates away from the granular front, was found to be accentuated by both increasing the granular pore space and, increasing the level of gravitational acceleration up until \(N=\) 14. Larger tested values of N resulted in collapse dynamics becoming less dependent on grain-fluid interactions and particle inertia dominating the dynamics of the granular phase. Without enhanced gravitational acceleration, just-saturated granular columns evolved in a similar way to previous experiments (dry, underwater, saturated); comprising acceleration, quasi-steady and retardation phases. The duration of these run out events primarily decreased with particle size as larger capillary forces, which limit grain mobility, developed within the granular materials with smaller pore spaces. In contrast, the collapse duration of tests exposed to elevated levels of gravitational acceleration decreased with both increasing pore space and increasing N for a given particle size. The latter showing that the influence of capillary forces on the evolution of the collapse reduces with increased scale.

Analysis of the temporal evolution of the basal pore pressure at the centre of the column also highlighted the major influence of pore space as N increases, particularly during the initial drainage phase post-collapse initiation. The magnitude of the initial pressure drop increases with decreasing particle size at a given level of elevated gravitational acceleration. Similarly to the conclusions of previous authors [13, 46], this pore size dependent pressure drop is surmised to emanate from the pore-pressure feedback loop for a dense granular configuration. The presence of capillary forces within the just-saturated column configuration caused the pore pressure to drop further when the particle size was smaller.

Buckingham’s \(\Pi\) theorem was used to postulate a relationship between 11 fundamental test variables that characterise the acceleration phase of each column collapse using 8 independent dimensionless \(\Pi\) groups. A non-linear regression scheme was used to evaluate the influence of each parameter and found that all measured quantities of interest, specifically, \({\dot{P}_m}^*\), \(\text{ Fr}_{x,L}\) and \({t_{x,L}}^*\), are independent of each other at all scales and are well described by \(Q=(\text{ Bo }/\text{Ca})^\alpha {(\rho ^*)}^\beta {(r^*)}^\gamma\) where \(\alpha\), \(\beta\) and \(\gamma\) are dependent on Q. Crucially, the inclusion of both \(\text{ Bo }\) and \(\text{ Ca }\) within a single parameter means that all quantities of interest are decoupled from grain-scale surface tension effects and it is the balance of column-scale gravitational and viscous forces that govern acceleration phase collapse behaviour as seen in natural-scale debris flows with a granular phase including inertial particles.

The current study has been effective in highlighting the collapse response of grain-fluid mixtures with inertial grains. This provides a start point for exploring separately the role of fines, where their effect may be negligible on the inertial/flow scale, but which may nevertheless control processes within the much smaller pore spaces. This work is timely given the findings of Kaitna et al. [15] highlighting the importance of fine granular material to the maintenance of excess pore pressures in steady-state granular-fluid flows. Developing a large dataset of unsteady granular-fluid flow experiments, where the impact of including fine granular material can be quantified, will be crucial to the development of a more mechanically precise pore pressure evolution model.