Impedance control based on error feedback for the manipulator of an underwater vehicle-manipulator system

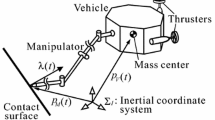
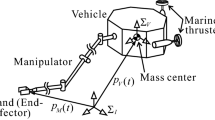
Abstract

This paper deals with the design of a motion and force control scheme for underwater vehicles, each of which has a manipulator. For a subsea operation that requires a contact between the manipulator’s tip (e.g., the hand) and various types of environments, it is desirable that the mechanical impedance of the manipulator is adjusted according to the contact surface. From this point of view, the paper focuses on the design of an impedance control scheme. Several impedance controllers have been developed. Most of them were designed on the assumption that the control capability of the vehicle is the same as that of the manipulator. However, it has been pointed out in the literature that for a real underwater robot, its vehicle control is more challenging than its manipulator control, because the vehicle has much larger inertia, and many more inaccurate position sensors and actuators than the manipulator. In view of this fact, we develop an impedance control scheme for the manipulator under the condition that the vehicle is independently controlled by a motion controller with poor performance. Moreover, we provide the results of simulations for comparing an existing controller with the proposed one.

Appendices

Appendix 1: derivation of (3) with (4) to (8)

Replacing $a_\textrm{CV}(t)\lambda (t)$ by $J_{V}(\phi )^{\textrm{T}}f_{S}(t)$ in the vehicle’s dynamic model (15) with (16) and (17) of [33], we can acquire the vehicle’s dynamic model (3) with (4) to (8). The signal $\lambda (t)\in R$ is a contact force perpendicular to the tangent plane of the contact surface, and $a_{CV}(t)\in R^{6}$ is expressed as

$$\begin{aligned} a_\textrm{CV}(t)=[1/\Vert n_{C}(t)\Vert ] J_{V}(\phi )^{\textrm{T}}n_{C}(t), \end{aligned}$$

(53)

where $n_{C}(t)\in R^{3}$ is a normal vector of the tangent plane of the contact surface. Moreover, the derivations of the vehicle’s dynamic models of [33] and this paper are similar to that of [23]. The detailed derivation of the dynamic model of the vehicle is shown in Appendix 1 of [23]. In this paper, we provide the following equations utilized in the derivation of (3) with (4) to (8):

$$\begin{aligned} \left. \begin{array}{l} M_{V}(\phi )\ddot{x}_{V}(t)+M_{VM}(\phi )\ddot{q}(t) +n_{V}(\phi ,\dot{\eta })+d_{V}(t)\\ \quad =f_{V} (t)+J_{V}(\phi )^{\textrm{T}}f_{S}(t),\\ f_{V}(t)=T(\phi _{V})C_{3}D(v)v(t),\\ \dot{v}(t)=-(1/2)C_{1}D(v)v(t)+(1/2)C_{2}\tau _{V}(t). \end{array} \right\} \end{aligned}$$

(54)

It should be noted that the first Eq. (54) is a standard type of dynamic model of the vehicle (e.g., the Eq. (1.52) of [1]), whereas the second and third equations of (54) are dynamic models of marine thrusters [50].

Appendix 2: derivation of (9) with (10) to (12)

Solving the model (3) for $\ddot{x}_{V}(t)$, and then substituting it into the standard type of manipulator’s dynamic model (e.g., the Eq. (1.52) of [1])

$$\begin{aligned} \begin{array}{l} M_\textrm{VM}(\phi )^{\textrm{T}}\ddot{x}_{V}(t) +M_{M}(\phi )\ddot{q}(t)+n_{M}(\phi ,\dot{\eta })+d_{M}(t)\\ \quad =\tau _{M}(t)+J_{M}^{V}(q)^{\textrm{T}} R(\phi _{V})^{\textrm{T}}f_{S}(t), \end{array} \end{aligned}$$

(55)

we obtain the following dynamic model:

$$\begin{aligned} \begin{array}{l} M_{Q}(\phi )\ddot{q}(t)+z_{Q}(t)+w_{Q}(t)\\ \quad =\tau _{M}(t)+J_{M}^{V}(q)^{\textrm{T}} R(\phi _{V})^{\textrm{T}}f_{S}(t). \end{array} \end{aligned}$$

(56)

It is noteworthy that $M_{V} (\phi )$ is a non-singular matrix, because it is a symmetric and positive definite matrix (as shown in the property P2 of [23]). The manipulator’s dynamic model (56) is represented in a joint space [i.e., q(t) ]. However, a control objective is generally established in a task space [i.e., $p_{M}^{V}(t)$], and hence we transform the dynamic model (56) from the joint space to the task space. Solving the time derivative of (11) for $\ddot{q}(t)$ [on the assumption that $J_M^V (q)$ is a non-singular (full rank) matrix], then substituting it into the dynamic model (56) for $\ddot{q}(t)$, and then multiplying both its sides by $J_{M}^{V}(q)^{-\textrm{T}}$, we can acquire the manipulator’s dynamic model (9).

Appendix 3: derivation of (17) with (18)

Substituting the constants $\bar{c}_{6}$ and $\bar{c}_{15}$ into 0 in the inequalities (74) of [33], and then replacing $|\lambda (t)|$ by $\Vert f_{S}(t) \Vert$ in the Eqs. (76) and (79) of [33], we can acquire the inequality (17) with (18). The signal $\lambda (t)$ is a contact force perpendicular to the tangent plane of the contact surface. The detailed derivation of the inequality of $\Vert z_{P}(t)\Vert$ with the filter $z_\textrm{Pf}(t)$ is shown in Appendix 3 of [33].

Appendix 4: derivation of second inequality of (19)

In the derivation of the second inequality of (19), we utilize the following inequalities:

$$\begin{aligned} \left. \begin{array}{l} \Vert \dot{M}_{V}(\phi ,\dot{\phi })\Vert \le \bar{c}_{1} \Vert \dot{\phi }(t) \Vert ,\; \Vert M_{VM}(\phi )\Vert \le \bar{c}_{2},\\ \Vert \dot{M}_\textrm{VM}(\phi ,\dot{\phi })\Vert \le \bar{c}_{3} \Vert \dot{\phi }(t)\Vert ,\; \Vert M_{V}(\phi )^{-1}\Vert \le \bar{c}_{4}, \end{array} \right\} \end{aligned}$$

(57)

where $\bar{c}_{1}$ to $\bar{c}_{4}$ are positive constants. Moreover, the assumptions of the boundedness of the disturbances and their time derivatives lead to the following inequalities:

$$\begin{aligned} \left. \begin{array}{l} \Vert d_{V}(t)\Vert \le \bar{c}_{D1},\; \Vert d_{M}(t)\Vert \le \bar{c}_{D2},\; \Vert \dot{d}_{V}(t)\Vert \le \bar{c}_{D3},\\ \Vert \dot{d}_{M}(t)\Vert \le \bar{c}_{D4}, \end{array} \right\} \end{aligned}$$

(58)

where $\bar{c}_{D1}$ to $\bar{c}_{D4}$ are positive constants.

Solving the first filter of (6), and then taking its norm, we obtain

$$\begin{aligned} \Vert w_\textrm{VF1}(t)\Vert =\Vert \exp (-\rho t)w_\textrm{VF1}(0)\Vert \le \Vert w_\textrm{VF1}(0)\Vert . \end{aligned}$$

(59)

Taking the norm of the first filter of (6), and then applying (59) to it, we have

$$\begin{aligned} \Vert \dot{w}_\textrm{VF1}(t)\Vert =\Vert -\rho w_\textrm{VF1}(t)\Vert \le \rho \Vert w_\textrm{VF1}(0)\Vert . \end{aligned}$$

(60)

Similarly, solving the second filter of (6), then taking its norm, and then applying the first inequality of (58) to it, we obtain

$$\begin{aligned} \begin{array}{l} \Vert w_\textrm{VF2}(t)\Vert =\left\| \int _{0}^{t}\exp (-\rho (t-\bar{\tau })) [-\rho d_{V}(\bar{\tau })]d\bar{\tau }\right\| \\ \quad \le \rho \exp (-\rho t)\int _{0}^{t}\exp (\rho \bar{\tau }) \Vert d_{V}(\bar{\tau })\Vert d\bar{\tau }\\ \quad \le \bar{c}_{D1}\rho \exp (-\rho t)\int _{0}^{t} \exp (\rho \bar{\tau })d\bar{\tau }\\ \quad \le \bar{c}_{D1}[1-\exp (-\rho t)]\\ \quad \le \bar{c}_{D1}. \end{array} \end{aligned}$$

(61)

Taking the norm of the second filter of (6), and then applying (61) and the first inequality of (58) to it, we have

$$\begin{aligned} \Vert \dot{w}_\textrm{VF2}(t)\Vert =\Vert -\rho w_\textrm{VF2}(t)-\rho d_{V}(t)\Vert \le 2\bar{c}_{D1}\rho . \end{aligned}$$

(62)

Representing the second Eq. (4) in the form of a norm, and then applying (59), (61) and the first inequality of (58) to it, we obtain

$$\begin{aligned} \Vert w_{C}(t)\Vert =\Vert d_{V}(t)+w_\textrm{VF1}(t)+w_\textrm{VF2}(t)\Vert \le \bar{c}_{5}, \end{aligned}$$

(63)

where $\bar{c}_{5}\in R^{+}$ is provided by the following equation:

$$\begin{aligned} \bar{c}_{5}=2\bar{c}_{D1}+\Vert w_\textrm{VF1}(0)\Vert . \end{aligned}$$

(64)

Differentiating the second Eq. (4) with respect to time, then taking its norm, then applying (60), (62) and the third inequality of (58) to it, and then substituting (64) into it, we have

$$\begin{aligned} \Vert \dot{w}_{C}(t)\Vert =\Vert \dot{d}_{V}(t)+\dot{w}_\textrm{VF1}(t) +\dot{w}_\textrm{VF2}(t)\Vert \le \bar{c}_{D3}+\bar{c}_{5}\rho . \end{aligned}$$

(65)

Taking the norm of the third Eq. (12), and then applying (63), the second and fourth inequalities of (57), and the second inequality of (58) to it, we obtain

$$\begin{aligned} \Vert w_{Q}(t)\Vert =\Vert d_{M}(t) -M_\textrm{VM}(\phi )^{\textrm{T}}M_{V}(\phi )^{-1}w_{C}(t)\Vert \le \bar{c}_{6}, \end{aligned}$$

(66)

where $\bar{c}_{6}\in R^{+}$ is written as

$$\begin{aligned} \bar{c}_{6}=\bar{c}_{D2}+\bar{c}_{2}\bar{c}_{4}\bar{c}_{5}. \end{aligned}$$

(67)

Differentiating the third Eq. (12) with respect to time, then taking its norm, and then applying (63), (65), the first to fourth inequalities of (57) and the fourth inequality of (58) to it, we have

$$\begin{aligned} \begin{array}{l} \Vert \dot{w}_{Q}(t)\Vert =\Vert \dot{d}_{M}(t)-\dot{M}_{VM} (\phi ,\dot{\phi })^{\textrm{T}}M_{V}(\phi )^{-1}w_{C}(t)\\ \qquad -M_\textrm{VM}(\phi )^{\textrm{T}}\dot{M}_{V} (\phi ,\dot{\phi })^{-1}w_{C}(t)\\ \qquad -M_\textrm{VM}(\phi )^{\textrm{T}}M_{V}(\phi )^{-1} \dot{w}_{C}(t)\Vert \\ \quad =\Vert \dot{d}_{M}(t) -\dot{M}_\textrm{VM}(\phi ,\dot{\phi })^{\textrm{T}} M_{V}(\phi )^{-1}w_{C}(t)\\ \qquad +M_\textrm{VM}(\phi )^{\textrm{T}}M_{V}(\phi )^{-1} \dot{M}_{V}(\phi ,\dot{\phi })M_{V}(\phi )^{-1}w_{C}(t)\\ \qquad -M_{VM}(\phi )^{\textrm{T}}M_{V}(\phi )^{-1} \dot{w}_{C}(t)\Vert \\ \quad \le \bar{c}_{7}+\bar{c}_{8}\rho +\bar{c}_{9}\Vert \dot{\phi }(t)\Vert , \end{array} \end{aligned}$$

(68)

where $\bar{c}_{7}\in R^{+}$, $\bar{c}_{8}\in R^{+}$ and $\bar{c}_{9}\in R^{+}$ are, respectively, provided by the following equations:

$$\begin{aligned} \bar{c}_{7}=\bar{c}_{D4}+\bar{c}_{2}\bar{c}_{4}\bar{c}_{D3},\; \bar{c}_{8}=\bar{c}_{2}\bar{c}_{4}\bar{c}_{5},\; \bar{c}_{9}=(\bar{c}_{3}+\bar{c}_{1}\bar{c}_{2}\bar{c}_{4})\bar{c}_{4}\bar{c}_{5}. \end{aligned}$$

(69)

Differentiating the third Eq. (10) with respect to time, then taking its norm, and then applying (66), (68), the first and second inequalities of (15) and the inequality $\Vert \dot{q}(t)\Vert \le \Vert \dot{\phi }(t)\Vert$ to it, we obtain

$$\begin{aligned} \begin{array}{l} \Vert \dot{w}_{P}(t)\Vert =\Vert \dot{J}_{M}^{V}(q,\dot{q})^{-\textrm{T}} w_{Q}(t)+J_{M}^{V}(q)^{-\textrm{T}}\dot{w}_{Q}(t)\Vert \\ \quad \le c_{J10}\bar{c}_{6}\Vert \dot{q}(t)\Vert +c_{J9}[\bar{c}_{7} +\bar{c}_{8}\rho +\bar{c}_{9}\Vert \dot{\phi }(t)\Vert ]\\ \quad \le \bar{c}_{7}c_{J9}+\bar{c}_{8}c_{J9}\rho +(\bar{c}_{6}c_{J10}+\bar{c}_{9}c_{J9}) \Vert \dot{\phi }(t)\Vert . \end{array} \end{aligned}$$

(70)

The inequality (70) leads to the second inequality of (19).

Appendix 5: derivations of inequalities of (20)

The condition of all the revolute joints of the manipulator leads to the first inequality of (20). Solving (11) for $\dot{q}(t)$ [on the assumption that $J_{M}^{V}(q)$ is a non-singular (full rank) matrix], then taking its norm, and then applying the first inequality of (15) to it, we obtain the second inequality of (20). Taking the norm of the kinematic equation (e.g., the Eq. (2.17) of [47])

$$\begin{aligned} p_{M}(t)=p_{V}(t)+R(\phi _{V})p_{M}^{V}(t), \end{aligned}$$

(71)

and then applying the eighth inequality of (13) and the first inequality of (20) to it, we acquire the third inequality of (20). We can rewrite (5) as

$$\begin{aligned} \begin{array}{l} \dot{p}_{M}(t)=\dot{p}_{V}(t)-S(R(\phi _{V})p_{M}^{V})J_{R}(\phi _{V}) \dot{\phi }_{V}(t)\\ \quad\qquad +R(\phi _{V})\dot{p}_{M}^{V}(t), \end{array} \end{aligned}$$

(72)

where the meaning of the skew-symmetric matrix $S(\cdot )$ is described in Table 1. Representing (72) in the form of a norm, then utilizing the property $\Vert S(\bar{x})\Vert = 6\Vert \bar{x}\Vert$ for any vector $\bar{x}\in R^{3}$, and then applying the fifth and eighth inequalities of (13) and the first inequality of (20) to it, we acquire the fourth inequality of (20).

Appendix 6: derivations of equations of (29)

Replacing $p_{M}(t)$ and $p_{M}^{V}(t)$ by $p_\textrm{MR}(t)$ and $p_\textrm{MR}^{V}(t)$ in (71) of Appendix 5, respectively, and then solving it for $p_\textrm{MR}^{V}(t)$, we acquire the first equation of (29). In this derivation, we utilize the property $R(\phi _{V})^{-1} = R(\phi _{V})^{\textrm{T}}$ (e.g., the Eq. (2.7) of [47]). Substituting (14) into (72) of Appendix 5 for $J_{R}(\phi _{V})\dot{\phi }_{V}(t)$, we have

$$\begin{aligned} \begin{array}{l} \dot{p}_{M}(t)=\dot{p}_{V}(t)-S(R(\phi _{V})p_{M}^{V})\omega _{V}(t) +R(\phi _{V})\dot{p}_{M}^{V}(t). \end{array} \end{aligned}$$

(73)

Applying the skew-symmetric property $S(\bar{x})\bar{z}=-S(\bar{z})\bar{x}$ for any vectors $\bar{x}\in R^{3}$ and $\bar{z}\in R^{3}$ (e.g., the Eq. (A.32) of [48]) to (73), then replacing $p_{M}^{V}(t)$, $\dot{p}_{M}^{V}(t)$ and $\dot{p}_{M}(t)$ by $p_\textrm{MR}^{V}(t)$, $\dot{p}_\textrm{MR}^{V}(t)$ and $\dot{p}_\textrm{MR}(t)$, respectively, and then solving it for $\dot{p}_\textrm{MR}^{V}(t)$, we obtain the second Eq. (29).

Appendix 7: derivations of inequalities of (30)

Taking the norms of (14) and its time derivatives, and then applying the fifth to seventh inequalities of (13) to them, we have

$$\begin{aligned} \left. \begin{array}{l} \Vert \omega _{V}(t)\Vert \le c_{J5}\Vert \dot{\phi }_{V}(t)\Vert ,\\ \Vert \dot{\omega }_{V}(t)\Vert \le c_{J6}\Vert \dot{\phi }_{V}(t)\Vert ^{2} +c_{J5} \Vert \ddot{\phi }_{V}(t)\Vert ,\\ \Vert \ddot{\omega }_{V}(t)\Vert \le c_{J7}\Vert \dot{\phi }_{V}(t)\Vert ^{3} +\bar{c}_{10}\Vert \dot{\phi }_{V}(t)\Vert \Vert \ddot{\phi }_{V}(t)\Vert \\ \quad +c_{J5}\Vert \phi _{V}^{(3)}(t)\Vert , \end{array} \right\} \end{aligned}$$

(74)

where $\bar{c}_{10}\in R^{+}$ is provided by the following equation:

$$\begin{aligned} \bar{c}_{10}=2c_{J6}+c_{J8}. \end{aligned}$$

(75)

Representing the first Eq. (29) in the form of a norm, and then applying the eighth inequality of (13), the first inequality of (26) and the boundedness of $p_{V}(t)$ (in the assumption A3) to it, we acquire the first inequality of (30). Taking the norm of the second Eq. (29), then utilizing the property $\Vert S(\bar{x})\Vert = 6\Vert \bar{x}\Vert$ for any vector $\bar{x}\in R^{3}$, and then applying the eighth inequality of (13), the second inequality of (26), the first inequality of (30), the first inequality of (74) and the boundedness of $\dot{p}_{V}(t)$ and $\dot{\phi }_{V}(t)$ (in the assumption A3) to it, we obtain the second inequality of (30). We consider the following differential kinematic Eq. (e.g., the Eq. (6.10) of [47]):

$$\begin{aligned} \begin{array}{l} \ddot{p}_\textrm{MR}^{V}(t)=R(\phi _{V})^{\textrm{T}} \{ \ddot{p}_\textrm{MR}(t)-\ddot{p}_{V}(t)\\ \quad\qquad -[S(\dot{\omega }_{V})+S(\omega _{V})S(\omega _{V})] R(\phi _{V})p_\textrm{MR}^{V}(t)\\ \quad \qquad-2S(\omega _{V})R(\phi _{V})\dot{p}_\textrm{MR}^{V}(t)\}. \end{array} \end{aligned}$$

(76)

Representing (76) in the form of a norm, then utilizing the property $\Vert S(\bar{x})\Vert = 6\Vert \bar{x}\Vert$ for any vector $\bar{x}\in R^{3}$, and then applying the eighth inequality of (13), the third inequality of (26), the first and second inequalities of (30), the first and second inequalities of (74) and the boundedness of $\ddot{p}_{V}(t)$, $\dot{\phi }_{V}(t)$ and $\ddot{\phi }_{V}(t)$ (in the assumption A3) to it, we attain the third inequality of (30). Differentiating (76) with respect to time, and then using the property $\dot{R}(\phi _{V},\dot{\phi }_{V})=S(\omega _{V})R(\phi _{V})$ (e.g., the Eq. (5.36) of [47]), we obtain

$$\begin{aligned} \begin{array}{l} p_{MR}^{V(3)}(t)=R(\phi _{V})^{\textrm{T}}\{ p_\textrm{MR}^{(3)}(t) -p_{V}^{(3)}(t)-[S(\ddot{\omega }_{V})\\ \quad\qquad +2S(\dot{\omega }_{V})S(\omega _{V}) +S(\omega _{V})S(\dot{\omega }_{V})\\ \quad\qquad +S(\omega _{V})S(\omega _{V})S(\omega _{V})] R(\phi _{V})p_\textrm{MR}^{V}(t)\\ \quad\qquad -3[S(\dot{\omega }_{V})+S(\omega _{V})S(\omega _{V})] R(\phi _{V})\dot{p}_\textrm{MR}^{V}(t)\\ \quad\qquad -3S(\omega _{V})R(\phi _{V})\ddot{p}_\textrm{MR}^{V}(t)\}. \end{array} \end{aligned}$$

(77)

Taking the norm of (77), then utilizing the property $\Vert S(\bar{x})\Vert = 6\Vert \bar{x}\Vert$ for any vector $\bar{x}\in R^{3}$, and then applying the eighth inequality of (13), the fourth inequality of (26), the first to third inequalities of (30), the first to third inequalities of (74) and the boundedness of $p_{V}^{(3)}(t)$, $\dot{\phi }_{V}(t)$, $\ddot{\phi }_{V}(t)$ and $\phi _{V}^{(3)}$ (in the assumption A3) to it, we attain the fourth inequality of (30).

Appendix 8: derivation of (35)

Taking the norm of (33), then applying (17), the third and eighth inequalities of (13) and the first inequality of (16) to it, and then substituting (34) into it, we have

$$\begin{aligned} \begin{array}{l} \Vert \tau _{M}(t)\Vert = \Vert J_{M}^{V}(q)^{\textrm{T}} \{-M_{P}(\phi )M_{T}^{-1} [\alpha e_{I}(t)+e_{S}(t)]\\ \qquad +z_{P}(t)-R(\phi _{V})^{\textrm{T}}f_{S}(t)\}\Vert \\ \quad \le c_{J3} \{ c_{M1}\Vert M_{T}^{-1}\Vert [\alpha \Vert e_{I}(t)\Vert +\Vert e_{S}(t)\Vert ]+c_{Z1}\\ \qquad +c_{Z2}\rho \Vert \dot{\eta }(t)\Vert +c_{Z3}\Vert \dot{\eta }(t)\Vert ^{2}+c_{Z4}\Vert f_{S}(t)\Vert \\ \qquad +c_{Z5}z_\textrm{Pf}(t)+c_{R1}\Vert f_{S}(t)\Vert \}\\ \quad \le c_{J3}\{ c_{M1}\Vert M_{T}^{-1}\Vert [\alpha \Vert e_{I}(t)\Vert +\Vert D_{T}\Vert \Vert \dot{e}_{P}^{V}(t)\Vert \\ \qquad +\Vert K_{T}\Vert \Vert e_{P}^{V}(t)\Vert +\Vert F_{T}\Vert \Vert R(\phi _{V})\Vert \Vert e_{F}(t)\Vert ]\\ \qquad +c_{Z1}+c_{Z2}\rho \Vert \dot{\eta }(t)\Vert +c_{Z3}\Vert \dot{\eta }(t)\Vert ^{2}+c_{Z4}\Vert f_{S}(t)\Vert \\ \qquad +c_{Z5}z_\textrm{Pf}(t)+c_{R1}\Vert f_{S}(t)\Vert \}. \end{array} \end{aligned}$$

(78)

Applying the eighth inequalities of (13) to (78), and then rearranging it, we obtain

$$\begin{aligned} \begin{array}{l} \Vert \tau _{M}(t)\Vert \le c_{J3}\{ c_{M1}\Vert M_{T}^{-1}\Vert [\alpha \Vert e_{I}(t)\Vert +\Vert D_{T}\Vert \Vert \dot{e}_{P}^{V}(t)\Vert \\ \qquad +\Vert K_{T}\Vert \Vert e_{P}^{V}(t)\Vert +c_{R1}\Vert F_{T}\Vert \Vert e_{F}(t)\Vert ]\\ \qquad +c_{Z1}+c_{Z2}\rho \Vert \dot{\eta }(t)\Vert +c_{Z3}\Vert \dot{\eta }(t)\Vert ^{2}+c_{Z4}\Vert f_{S}(t)\Vert \\ \qquad +c_{Z5}z_\textrm{Pf}(t)+c_{R1}\Vert f_{S}(t)\Vert \}\\ \quad \le c_{J3}c_{Z1}+c_{J3}c_{Z2}\rho \Vert \dot{\eta }(t)\Vert +c_{J3}c_{Z3}\Vert \dot{\eta }(t)\Vert ^{2}\\ \qquad +(c_{J3}c_{Z4}+c_{J3}c_{R1})\Vert f_{S}(t)\Vert +c_{J3}c_{Z5}z_\textrm{Pf}(t)\\ \qquad +\Vert M_{T}^{-1}\Vert [c_{J3}c_{M1}\Vert K_{T}\Vert \Vert e_{P}^{V}(t)\Vert \\ \qquad +c_{J3}c_{M1}\Vert D_{T}\Vert \Vert \dot{e}_{P}^{V}(t)\Vert +c_{J3}c_{M1}c_{R1}\Vert F_{T}\Vert \Vert e_{F}(t)\Vert \\ \qquad +c_{J3}c_{M1}\alpha \Vert e_{I}(t)\Vert ]. \end{array} \end{aligned}$$

(79)

The inequality (79) leads to the inequality (35).

Appendix 9: proof of Theorem 1

We choose the following positive definite function:

$$\begin{aligned} V_{1}(t)=(1/2)e_{I}(t)^{\textrm{T}}e_{I}(t). \end{aligned}$$

(80)

Differentiating (80) with respect to time, then substituting the closed-loop error model (36) into it, and then applying the third inequality of (16), the first inequality of (19), the third inequality of (30) and the inequality $\bar{a}\bar{b}\le \bar{c}\bar{a}^{2}+\bar{b}^{2}/(4\bar{c})$ for any scalars $\bar{a}\in R$, $\bar{b}\in R$ and $\bar{c}\in R^{+}$ to it, we have

$$\begin{aligned} \begin{array}{l} \dot{V}_{1}(t)=e_{I}(t)^{\textrm{T}}\dot{e}_{I}(t)\\ \quad \le -\alpha e_{I}(t)^{\textrm{T}}e_{I}(t) +[\Vert M_{P}(\phi )^{-1}\Vert \Vert w_{P}(t)\Vert \\ \qquad +\Vert \ddot{p}_{MR}^{V}(t)\Vert ]\Vert M_{T}\Vert \Vert e_{I}(t)\Vert \\ \quad \le -\alpha e_{I}(t)^{\textrm{T}}e_{I}(t) +\bar{c}_{11}\Vert M_{T}\Vert \Vert e_{I}(t)\Vert \\ \quad \le -(\alpha /2)e_{I}(t)^{\textrm{T}}e_{I}(t) +\bar{c}_{11}^{2}\Vert M_{T}\Vert ^{2}/(2\alpha ), \end{array} \end{aligned}$$

(81)

where $\bar{c}_{11}\in R^{+}$ is provided by the following equation:

$$\begin{aligned} \bar{c}_{11}=c_{M3}c_{W1}+c_\textrm{PR7}. \end{aligned}$$

(82)

In the application of the inequality $\bar{a}\bar{b}\le \bar{c}\bar{a}^{2}+\bar{b}^{2}/(4\bar{c})$ to $\dot{V}_{1}(t)$, we choose $\bar{a}$, $\bar{b}$ and $\bar{c}$ as $\Vert e_{I}(t)\Vert$, $\bar{c}_{11}\Vert M_{T}\Vert$ and $\alpha /2$, respectively. Substituting (80) into (81), we obtain

$$\begin{aligned} \dot{V}_{1}(t)\le -\alpha V_{1}(t) +\bar{c}_{11}^{2}\Vert M_{T}\Vert ^{2}/(2\alpha ). \end{aligned}$$

(83)

Moreover, applying Lemma 3.2.4 of [51] to (83), we have

$$\begin{aligned} \begin{array}{l} V_{1}(t)\le \exp (-\alpha t)V_{1}(0) +\bar{c}_{11}^{2}\Vert M_{T}\Vert ^{2}/(2\alpha ^{2})\\ \quad \le (c_{V1}/2)\exp (-\alpha t) +(c_{V2}/2)\Vert M_{T}\Vert ^{2}/\alpha ^{2}, \end{array} \end{aligned}$$

(84)

where $c_{V1}=2V_{1}(0)$ and $c_{V2}=\bar{c}_{11}^2$. Utilizing (80) and (84), we acquire the inequality (38), which means the ultimate boundedness of $e_{I}(t)$.

We apply the following signals to the differential Eq. (24):

$$\begin{aligned} \left. \begin{array}{l} z_{I}(t)=\left[ \begin{array}{c} \int _{0}^{t} e_{P}^{V}(\bar{\tau })d\bar{\tau }\\ e_{P}^{V}(t) \end{array} \right] ,\\ u_{I}(t)=\int _{0}^{t}R(\phi _{V}(\bar{\tau }))^{\textrm{T}} e_{F}(\bar{\tau })d\bar{\tau },\; w_{I}(t)=e_{I}(t). \end{array} \right\} \end{aligned}$$

(85)

In this case, the differential Eq. (24) is valid, and furthermore $u_{I}(t)$ and $w_{I}(t)$ are bounded, because of the boundedness of $e_{I}(t)$ and the assumption A10. Therefore, it follows from Lemma 1 that $z_{I}(t)$ is bounded. This is equivalent to the boundedness of $e_{P}^{V}(t)$ and $\int _{0}^{t} e_{P}^{V}(\bar{\tau })d\bar{\tau }$.

Solving (31) for $\dot{e}_{P}^{V}(t)$ [in view of the positive definiteness of $M_{T}$ (i.e., the non-singularity of $M_{T}$)], then taking its norm, and then applying the assumption A10 and the boundedness of $e_{I}(t)$, $e_{P}^{V}(t)$ and $\int _{0}^{t} e_{P}^{V}(\bar{\tau })d\bar{\tau }$ to it, we can show that $\dot{e}_{P}^{V}(t)$ is bounded. Differentiating the first Eq. (22) with respect to time, then representing its time derivative $\dot{p}_{M}^{V}(t)$ in the form of a norm, and then applying the second inequality of (30) and the boundedness of $\dot{e}_{P}^{V}(t)$ to it, we can indicate the boundedness of $\dot{p}_{M}^{V}(t)$. Utilizing the second inequality of (20) and the boundedness of $\dot{p}_{M}^{V}(t)$, we can show that $\dot{q}(t)$ is bounded. The assumption A3 and the boundness of $\dot{q}(t)$ lead to the boundedness of $\dot{\phi }(t)$ and $\dot{\eta }(t)$, whose meanings are described in Table 1. Utilizing the third inequality of (20) and the assumption A3, we can show that $p_{M}(t)$ is bounded. Similarly, using the fourth inequality of (20), the boundedness of $\dot{p}_{M}^{V}(t)$ and the assumption A3, we can indicate the boundedness of $\dot{p}_{M}(t)$. Therefore, the assumption A2 and the boundedness of $p_{M}(t)$ and $\dot{p}_{M}(t)$ lead to the boundedness of $f_{S}(t)$. Taking the norm of the second equation of (22), and then applying (27) and the boundedness of $f_{S}(t)$ to it, we can indicate the boundedness of $e_{F}(t)$. In view of the fact that the filter (18) is a stable one, it follows from the assumption A3 and the boundedness of $\dot{\eta }(t)$ and $f_{S}(t)$ that $z_\textrm{Pf}(t)$ is bounded. Applying the boundedness of $\dot{\eta }(t)$, $f_{S}(t)$, $z_\textrm{Pf}(t)$, $e_{P}^{V}(t)$, $\dot{e}_{P}^{V}(t)$, $e_{F}(t)$ and $e_{I}(t)$ to (35), we can show that $\tau _{M}(t)$ is bounded. We can prove that all the closed-loop signals are bounded. This completes the proof.

Appendix 10: proof of theorem 2

We choose the following positive definite function:

$$\begin{aligned} V_{2}(t)=(1/2)\dot{e}_{I}(t)^{\textrm{T}}\dot{e}_{I}(t). \end{aligned}$$

(86)

Differentiating (86) with respect to time, then substituting the closed-loop error model (37) into it, and then applying the second and third inequalities of (16), the first and second inequalities of (19), the fourth inequality of (30) to it, we have

$$\begin{aligned} \begin{array}{l} \dot{V}_{2}(t)=\dot{e}_{I}(t)^{\textrm{T}}\ddot{e}_{I}(t)\\ \quad \le -\alpha \dot{e}_{I}(t)^{\textrm{T}} \dot{e}_{I}(t)\\ \qquad +[\Vert M_{P}(\phi )^{-1}\Vert ^{2}\Vert \dot{M}_{P} (\phi ,\dot{\phi })\Vert \Vert w_{P}(t)\Vert \\ \qquad +\Vert M_{P}(\phi )^{-1}\Vert \Vert \dot{w}_{P}(t)\Vert +\Vert p_\textrm{MR}^{V(3)}(t)\Vert ]\Vert M_{T}\Vert \Vert \dot{e}_{I}(t)\Vert \\ \quad \le -\alpha \dot{e}_{I}(t)^{\textrm{T}}\dot{e}_{I}(t) +\{ c_{M2}c_{M3}^{2}c_{W1}\Vert \dot{\phi }(t)\Vert \\ \qquad +c_{M3}[c_{W2}+c_{W3}\rho +c_{W4}\Vert \dot{\phi }(t)\Vert ]\\ \qquad +c_\textrm{PR8}\} \Vert M_{T}\Vert \Vert \dot{e}_{I}(t)\Vert . \end{array} \end{aligned}$$

(87)

In view of the stability properties of Theorem 1 and the assumption A3 [i.e., the boundedness of $\dot{\phi }(t)$], the constant $c_{\phi }\in R^{+}$ is defined as

$$\begin{aligned} c_{\phi }=\sup _{t\ge 0}\{ \Vert \dot{\phi }(t)\Vert \}, \end{aligned}$$

(88)

where $\sup _{t\ge 0}\{\Vert \bar{z}(t)\Vert \}$ means the supremum of $\Vert \bar{z}(t)\Vert$ for any vector signal $\bar{z}(t)$. Applying the inequality $\Vert \dot{\phi }(t)\Vert \le c_{\phi }$ to (87), and then rearranging it, we obtain

$$\begin{aligned} \begin{array}{l} \dot{V}_{2}(t) \le -\alpha \dot{e}_{I}(t)^{\textrm{T}} \dot{e}_{I}(t) +\bar{c}_{12}\Vert M_{T}\Vert \Vert \dot{e}_{I}(t)\Vert \\ \quad +\bar{c}_{13}\rho \Vert M_{T}\Vert \Vert \dot{e}_{I}(t)\Vert , \end{array} \end{aligned}$$

(89)

where $\bar{c}_{12}\in R^{+}$ and $\bar{c}_{13}\in R^{+}$ are, respectively, provided by the following equations:

$$\begin{aligned} \left. \begin{array}{l} \bar{c}_{12}=c_{M2}c_{M3}^{2}c_{W1}c_{\phi } +c_{M3}(c_{W2}+c_{W4}c_{\phi })+c_\textrm{PR8},\\ \bar{c}_{13}=c_{M3}c_{W3}. \end{array} \right\} \end{aligned}$$

(90)

Applying the inequality $\bar{a}\bar{b}\le \bar{c}\bar{a}^{2}+\bar{b}^{2}/(4\bar{c})$ for any scalars $\bar{a}\in R$, $\bar{b}\in R$ and $\bar{c}\in R^{+}$ to the second and third terms of the right-hand side of (89), and then substituting (86) into it, we have

$$\begin{aligned} \dot{V}_{2}(t) \le -\alpha V_{2}(t)+(\bar{c}_{12}^{2} +\bar{c}_{13}^{2}\rho ^{2})\Vert M_{T}\Vert ^{2}/\alpha . \end{aligned}$$

(91)

In the application of the inequality $\bar{a}\bar{b}\le \bar{c}\bar{a}^{2}+\bar{b}^{2}/(4\bar{c})$ to the second term of the right-hand side of (89), we choose $\bar{a}$, $\bar{b}$ and $\bar{c}$ as $\Vert \dot{e}_{I}(t)\Vert$, $\bar{c}_{12}\Vert M_{T}\Vert$ and $\alpha /4$, respectively. Similarly, in the application of its third term, we select $\bar{a}$, $\bar{b}$ and $\bar{c}$ as $\Vert \dot{e}_{I}(t)\Vert$, $\bar{c}_{13}\rho \Vert M_{T}\Vert$ and $\alpha /4$, respectively. Moreover, applying Lemma 3.2.4 of [51] to (91), we obtain

$$\begin{aligned} \begin{array}{l} V_{2}(t) \le \exp (-\alpha t) V_{2}(0)+(\bar{c}_{12}^{2} +\bar{c}_{13}^{2}\rho ^{2})\Vert M_{T}\Vert ^{2}/\alpha ^{2}\\ \quad \le (c_{V3}/2)\exp (-\alpha t)\\ \qquad +[(c_{V4}+c_{V5}\rho ^{2})/2] \Vert M_{T}\Vert ^{2}/\alpha ^{2}, \end{array} \end{aligned}$$

(92)

where $c_{V3}=2V_{2}(0)$, $c_{V4}=2\bar{c}_{12}^2$ and $c_{V5}=2\bar{c}_{13}^2$. Utilizing (86) and (92), and then multiplying both its sides by 2, we have

$$\begin{aligned} \begin{array}{l} \Vert \dot{e}_{I}(t)\Vert ^{2} \le c_{V3}\exp (-\alpha t)+(c_{V4} +c_{V5}\rho ^{2})\Vert M_{T}\Vert ^{2}/\alpha ^{2}. \end{array} \end{aligned}$$

(93)

Differentiating (31) with respect to time, and then substituting it into (93) for $\dot{e}_{I}(t)$, we acquire the inequality (39). This completes the proof.