1 Introduction

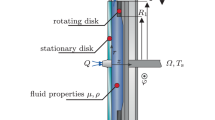
Open wet clutches, used in systems like dedicated hybrid transmissions (DHT) and battery electric vehicles (BEV) as separation clutches or power shift clutches, in electronic limited slip differentials (eLSDs) and in torque vectoring modules, have losses in the disengaged state that contribute in the range of one digit percentage to the energy losses in the drive train. Therefore, causing additional energy consumption, which causes increased \(\mathrm{CO_{2}}\) emission and further wear on parts in the drive train. The losses induced in the wet clutch in its open state are caused by the hydrodynamic drag torque \(T_{s}\) between the decoupled disks, spinning at dissimilar speeds. Consequently the prediction of the drag torque – and hence the associated potential for energy loss minimization – is a core requirement in the design of such clutches [13].

A variety of different attempts to model the single and two-phase flow within the clutch was already conducted, where mainly three different approaches were used: (i) the assumption of a turbulent flow [12, 19], the assumption of a laminar flow [15, 20, 39] and the approach to capture the most influencing effects by means of an analytical description with the option to state an equation for drag torque \(T_{\mathrm{s}}\) [30, 33, 35]. However, these prediction models are based on strong simplifications regarding the velocity field. In consequence, the velocity fields in these models could not be verified experimentally [35].

One of the most reliable types of prediction models are based on the analytical solution of the Navier-Stokes equations [30, 32, 33], whereby for the analytical solution, simplifications have to be made. Such simplifications are e.g. the assumption of laminar flow as well as rotational symmetry, thus only allowing for the characterization of smooth ungrooved disks [15, 17, 18], like used in practical applications. Consequently, these models can not provide insight on more complex flow typologies induced by rough and grooved disks. Furthermore, the validity is restricted to a small range of parameter combinations between the radial velocity \(u_{r}\), the gap height \(h\), the kinematic viscosity \(\nu\) and the disk radius \(R\) in the form of \(\frac{u_{r}h^{2}}{\nu R}\ll 1\) [25].

More insight into the more complex flow topology of grooved disks were just recently provided by laser optical measuring techniques [6, 9, 41] modified for the given problem [7, 10] and successfully applied on the gap flow in the open wet clutch [21, 22, 26]. These experimental studies could quantify the local wall shear stress. Additionally the volumetric flow topology within the investigated groove geometries and their local influence on the wall shear stress distribution in the surrounding of the groove was identified. These findings successfully concluded a first step towards the derivation of a cause-effect-relationship between flow phenomena and the drag torque. Despite this promising approach towards novel data and information, the large variety of different parameters describing the problem, constitute a major challenge for the derivation of more general phenomenological relations. One promising method for the direct reduction of measurement parameters and influencing factors can be provided by dimensional analysis [38, 42]. This was already conducted for the open wet clutch [24, 25]. Latest efforts to gain more insights into the flow phenomena where conducted by Neupert et al. (2019) [28] with a thoroughly-conducted numerical study for more complex groove geometries and an additional experimental study [29], where the pressure at different radial positions was measured for a wider understanding of the involved flow phenomena in the gap, which generated some substantial progress.

Despite the above-outlined variety of (partly combined) analytical, numerical and experimental investigations into both clutch-flow and resulting drag-torque, the direct comparison of velocity fields and corresponding flow topology as revealed from experimental and numerical approaches is still pending for the given flow scenario. As a first attempt to address this pending quantitative flow-field comparison, the current work conducts both experiments using defocusing particle tracking (DPTV) for the measurement of the flow field in six different groove geometries and numerical simulations so as to achieve a comparative framework to study the flow in proximity of various groove geometries. Overall six different groove geometries were investigated:

  • radial groove

  • inclined groove (rotated clockwise)

  • inclined groove (rotated counterclockwise)

  • radially contracting groove

  • radially expanding groove

  • radial groove with overprinted waffle pattern

The groove geometries are shown and further specified in Fig. 1. Note that the pumping or blocking effect of inclined grooves depends on the resulting force components in the direction of the groove, which depends on the relative rotation of the disks (friction and steel disks). In the present case of braking operation, this depends only on the rotation of the disk, such that the inclined geometry of Fig. 1b serves for both pumping and blocking clutch operation. The results of the measurements and the simulations are compared and the potential to complement each other is discussed.

Fig. 1
figure 1

Experimentally and numerically investigated disks with 32 circumferential evenly distributed grooves; inner radius \(R_{1}=82.5\) mm, outer radius \(R_{2}=93.75\) mm, groove width \(W=2\) mm (at the mean radius \(R_{m}=(R_{1}+R_{2})/2=88.125\) mm), groove depth \(H=0.75\) mm, gap height \(h=400\) \(\upmu\)m; \({}^{\ast}\) both rotational directions investigated (pumping/blocking), inclination angle \(\alpha=22.5^{\circ}\) oriented with respect to the radial direction; \({}^{\Delta}\) min/max groove width \(W_{\text{min}}=1.35\) mm/\(W_{\text{max}}=2.70\) mm \({}^{\diamond}\) only experimentally investigated, depth/width of the overprint \(0.25/1.2\) mm, imprinting width \(d=5.5\) mm. a radial, b inclined\({}^{\ast}\), c contracting\({}^{\Delta}\), d expanding\({}^{\Delta}\), e embossed\({}^{\diamond}\)

Full size image

2 DPTV experiments

2.1 Defocusing particle tracking velocimetry (DPTV)

Particle imaging velocimetry (PIV) and particle tracking velocimetry (PTV) are popular laser-optical measurement techniques, which provide quantitative velocity field information on a flow field [34]. While in PIV the displacement of an ensemble of particles is determined, in PTV the displacement of individual particles is tracked over two or more images in a Lagrangian frame of reference, thus providing deeper physical insight. In planar PTV the in-plane displacement is directly derived from the distance a particle traveled in a known time interval between two images. However, planar PTV only provides two dimensional velocity information.

Defocusing particle tracking velocimetry (DPTV) [41] can additionally provide velocity information of the out-of-plane component and was already successfully applied for investigations on open wet clutches by Leister et al. [23]. The working principle for DPTV is the deliberate defocusing of the particles in the field of view. When moving a particle away form the focal plane the particle image turns from a point into a defocus ring. The defocus ring diameter grows with increased distance from the focal plane. Consequently the out-of-plane position \(z^{*}\) of the particle can be derived form the ring diameter, as shown in Fig. 2. The relation between the particle image diameter \(d_{\mathrm{i}}\) and the \(z^{*}\) position is given in Eq. (1) [31].

$${d_{\mathrm{i}}}^{2}=\!\!\!\underbrace{M^{2}d_{\mathrm{p}}^{2}}_{\substack{\text{geom.\leavevmode\nobreak\ image}}}\!\!\!+\underbrace{5.95(M+1)^{2}\lambda^{2}f_{\#}^{2}}_{\substack{\text{diffraction}}}+\underbrace{\frac{M^{2}{z^{*}}^{2}D_{a}^{2}}{(s_{0}+z^{*})^{2}}}_{\substack{\text{defocusing}}}$$
(1)
Fig. 2
figure 2

Principle of defocusing visualized: A particle closer to the focal plane (orange) appears a smaller defocused ring compared to a particle further away from the focal plane (green). This way the out-of-plane position can be determined form the ring diameter. Adopted from [22]

Full size image

The particle image diameter depends on the magnification \(M\), the particle diameter \(d_{\mathrm{p}}\), the wavelength of the used light \(\lambda\), the focal length of the imaging lens \(f_{\#}\), the aperture diameter \(D_{\mathrm{a}}\) and the distance of the imaging optics to the focal plane \(s_{0}\). For a fixed measurement setup the first two terms describing the geometrical image and the diffraction become constant and the particle image diameter depends solely on the third (defocusing) term of Eq. (1).

For microscopic applications the distance of the imaging optics from the focal plane is much larger than the distance of the particle from the focal plane so that \(s_{0}\gg z^{*}\) applies and Eq. (1) can be further simplified to the proportional relationship

$$d_{i}\propto\left(\text{const.}+{z^{*}}^{2}\right)^{\frac{1}{2}}.$$
(2)

Furthermore, with sufficient distance of the particle to the focal plane the hyperbolic relation in Eq. (2) can be approximated as linear \(d_{\mathrm{i}}\,\propto\,z^{*}\) [10]. In the following the out-of-plane position of the particle is normalized with respect to the gap height of the open wet clutch \(h\) to that \(z=z^{*}/h\).

2.2 Experiments

The experiments conducted in this work are in analogy with the experiments on an open wet clutch from Leister et al. [22]. The test rig, shown in Fig. 3, consists of a transparent stator plate and a rotating disk. The stator plate is made from anti-reflection float glass to provide optical access for both the laser for illumination and the camera for imaging purposes. The disk on the rotating counterpart can be replaced to vary the measured disk geometry. The used disks were additive-manufactured models, by means of stereo-lithography, of the scale \(1:1\), with an inner radius of \(R_{1}=82.5\) mm and an outer radius of \(R_{1}=93.75\) mm. It is important to note in this context, that additive manufactured disks have proven to resemble the original disks sufficiently accurately with respect to comparable roughness properties of the respective materials [1, 27], which are accordingly considered as hydraulically smooth throughout the present study. Each investigated disk geometry had 32 grooves, with the groove geometry varying between the individual disks. Further specification is provided in Fig. 1.

Fig. 3
figure 3

Clutch test rig and positioning of the DPTV measurement setup. The oil is pumped through the central black tube into the open wet clutch. The laser and camera are positioned in a back scatter setup due to the single optical access through the transparent stator plate

Full size image

The gap between the the rotating disk (measured in the ungrooved region of the disk) was \(h=400\,\upmu\)m and the disks were rotated with an angular velocity of \(\Omega=1\) Hz to ensure a single phase flow without the onset of aeration. The rotor was rotated by a ADDA TFC 80A‑2 electrical motor, which was coupled with a WL100L-F2231 optical sensor to ensure a constant rotational speed.

White mineral oil (density \(\rho_{o}\,=\,850\) kg/m3, dynam. viscosity \(\mu=0.0136\) kg/ms at 40 \({}^{\circ}\)C, CAS No: 8042-47-5) was pumped into the middle of the rotor-stator gap with a volumetric flow rate of \(\dot{V}=3.6\pm 0.1\) l/min (see Fig. 3), which corresponds to a specific volume flow of 9.63 mm3/(mm2s) for the given geometry. This high flow rate was chosen to ensure single phase flow and avoid the onset of aeration. The oil was seeded with fluorescent particles for the DPTV measurement (diameter \(d_{p}=9.84\) \(\upmu\)m, density \(\rho_{p}=9.8\)4 \(\upmu\)m, wavelength of the emitted light \(\lambda=584\) nm) to avoid reflections of the laser light into the camera. An increased pumped flow rate compared to the numerical simulations was chosen deliberately to compensate the influence of gravity as elaborated by Leister et al. [25].

The measurement volume was illuminated by a Quantel Evergreen Nd:YAG Laser (\(\lambda=532\) nm, 200 mJ/pulse, pulse distance \(\Delta t=40\) \(\upmu\)s) in a double-pulse configuration. The particles were recorded at the same groove position once every revolution in double-frame single-exposure configuration [34]. For each investigated groove geometry 1,000 double frames were recorded with an ILA.PIV.sCMOS camera (sensor \(2560\times 2160\) pixel, 16 bit) equipped with a Questar QM 100 lens. With the given imaging setup an in-plane resolution of 151 pixel/mm could be achieved. For the out-of-plane resolution, the used optical system provided a resolution of 40 px/mm by defocusing in axial direction [10, 22].

The recorded images were processed in a similar manner to Leister et al. [22]. In the first step the raw images were pre-processed by means of mean-image subtraction and subsequent intensity amplification. Subsequently, a coherent Hough transform [2,3,4], which is a variation of the original Hough transform [14], was applied to detect the defocused ring shaped particle images. In post-processing the determined ring-diameter values were afterwards corrected for the error introduced by field curvature. The underlying in-situ calibration was done following the treatise of Fuchs et al. [10].

3 Numerical simulations

The numerical study is carried out using the open-source finite-volume-based simulation framework OpenFOAM Version 9 from the OpenFOAM foundation release [40]. Incompressible steady state solver simpleFoam is utilized for the solution of the Navier-Stokes equation for the flow in the ring segment taking into account the centrifugal accelerations and Coriolis effects into the fluid through the multiple reference frame (MRF) method:

$$\begin{gathered}\displaystyle\nabla\cdot\left(\vec{u}_{R}\otimes\vec{u}_{I}\right)+\vec{\Omega}\times\vec{u}_{I}=-\nabla\left(p/\rho\right)+\nu\nabla\cdot\nabla\left(\vec{u}_{I}\right),\\ \displaystyle\nabla\cdot\vec{u}_{I}=0,\end{gathered}$$
(3)

where \(\vec{\Omega}\) is the rotational vector, \(\vec{r}\) is the vector from the origin of rotation, and \(\vec{u}_{R}\) and \(\vec{u}_{I}\) denote the velocity in rotating and inertial reference frames, respectively, so \(\vec{u}_{I}=\vec{u}_{R}+\vec{\Omega}\times\vec{r}\).

Fig. 4 presents the sketch of simulation domain with boundary conditions applied at the domain patches. The fluid domain is defined by subtracting the 3D-geometry of a structured disk from a ring segment within a range of \(\varphi=-5.625^{\circ}\) to \(5.625^{\circ}\), which represents 1/32 of the entire disk geometry (as shown in Fig. 5). The final mesh is generated using the background mesh created with blockMesh and is locally refined and snapped to specific groove geometries using snappyHexMesh. The near-wall region is refined in the background mesh using simpleGrading coefficients that fit the structure geometry (as shown in Fig. 6). The background mesh consists of \(N_{r}\times N_{\phi}\times N_{z}=120-200\times 200-300\times 50\) cells, depending on the investigated groove geometry, resulting in a final mesh of 1‑2.5 million cells. A constant volumetric flow rate of \(2.25\) l/min is prescribed utilizing flowRateInletVelocity boundary condition for the velocity, while zero-gradient condition is applied for the pressure at the inlet of the domain. At the outlet, the fixed-value pressure condition is set, while the zero-gradient velocity condition is applied. The grooved wall velocity is prescribed to the fixed value corresponding to the angular velocity of \(\Omega=2\pi\) rad/s and the no-slip boundary condition is applied at the flat stationary wall. A zero-gradient condition is applied on both, rotating and static walls, while periodicity is prescribed at the sides of the ring segment. The fluid properties are chosen in correspondence to that of the synthetic oil utilized in the experiment (\(\nu=16\times 10^{-6}\) m2/s). The iterative solution algorithm is terminated after the normalized residuals reach \(1\times 10^{-6}\) and \(1\times 10^{-5}\) for the velocity and the pressure field, respectively.

Fig. 4
figure 4

Sketch of the simulation domain with applied boundary conditions

Full size image
Fig. 5
figure 5

Definition of the simulations domain: fluid domain (green) and the subtracted disk geometry (yellow)

Full size image
Fig. 6
figure 6

The background mesh with local cell grading (a) and the final mesh (b)

Full size image

Five numerical simulations were conducted using the boundary conditions and geometry variations listed above. The simulation of the inclined groove was conducted in both rotational directions. However, the radial groove geometry with the waffle pattern was not simulated due to the significantly higher complexity and larger computational requirements of the mesh generation (as shown in Fig. 1). Exemplary, the simulation results for the straight radial groove are visualized using streamlines in Fig. 7. As pointed out by Leister et al. [22], the radial vortex inside the radial groove can be identified in the visualization.

Fig. 7
figure 7

Vortex visualization through stream lines in the radially grooved disk

Full size image

4 Comparison of numerical and experimental investigations

The velocity field of the radial, circumferential and axial component are directly compared for the experimentally measured velocity fields and the numerically determined ones. Note that the depicted cross section is a top view of the \(\varphi-z\) plane in radial direction at the height of the mean radius \(R_{m}=(R_{1}+R_{2})/2\). This particular display style is chosen to provide also immediate comparability to the investigations by Leister et al. [21, 22, 26]. The results for a radially grooved disk are shown in Fig. 8. The depicted velocity fields show good agreement with the already published phenomena as occur in a radial groove [22]. The figure saliently demonstrates that the numerical data is in good agreement with the experimental data for the circumferential and axial velocity components. The radial velocity component also demonstrates the same trend for the numerical and experimental case, except having different overall magnitudes. This demonstrates the influence gravity on the radial velocity, as shown by Leister et al. [25] as well as the importance of the inflow and outflow conditions on the given problem.

Fig. 8
figure 8

Experimentally (left) and numerically (right) determined velocity fields in a radially grooved disk – see Fig. 1a; normalized circumferential velocity \(u_{\varphi}/\Omega R_{\text{m}}\) (top), normalized radial velocity \(u_{r}/\Omega R_{\text{m}}\) (middle), normalized axial velocity \(u_{z}/\Omega R_{\text{m}}\) (bottom). The rotational direction is indicated by the arrow

Full size image

The results on the inclined grooves for counterclockwise and clockwise rotation are shown in Figs. 9 and 10, respectively, in what the arrow on the top of the figure indicates the direction of rotation. For this case there is also good agreement for the circumferential and axial velocity component. The different inclination relative to the rotational direction becomes apparent in the interpretation of the radial velocity component, since the conveying direction is inverted depending on the sign of the rotation. The inversion of the convening direction is consistent between the numerical simulations and the experimental investigations.

Fig. 9
figure 9

Experimentally (left) and numerically (right) determined velocity fields in a included groove (rotation counterclockwise – pumping outwards flow) – see Fig. 1b; normalized circumferential velocity \(u_{\varphi}/\Omega R_{\text{m}}\) (top), normalized radial velocity \(u_{r}/\Omega R_{\text{m}}\) (middle), normalized axial velocity \(u_{z}/\Omega R_{\text{m}}\) (bottom). The rotational direction is indicated by the arrow

Full size image
Fig. 10
figure 10

Experimentally (left) and numerically (right) determined velocity fields in a included groove (rotation clockwise – blocking outwards flow) – see Fig. 1b; normalized circumferential velocity \(u_{\varphi}/\Omega R_{\text{m}}\) (top), normalized radial velocity \(u_{r}/\Omega R_{\text{m}}\) (middle), normalized axial velocity \(u_{z}/\Omega R_{\text{m}}\) (bottom). The rotational direction is indicated by the arrow

Full size image

Variations in the radial opening angle of the groove – see for comparison Figs. 11 and 12 – have shown to have only little effect on the flow topology. However, based on the order of magnitude lower radial velocity component in combination with a lower signal to noise ratio compared to the experiment from Fig. 8, it can be hypothesized that the conveying rate in the groove at the smallest cross section at \(R_{1}\) or \(R_{2}\) is restricted. Consequently, any assumptions as built upon the stream-filament theory and the resulting determinations in this context have limited accuracy.

Fig. 11
figure 11

Experimentally (left) and numerically (right) determined velocity fields in a radially contracting groove – see Fig. 1c; normalized circumferential velocity \(u_{\varphi}/\Omega R_{\text{m}}\) (top), normalized radial velocity \(u_{r}/\Omega R_{\text{m}}\) (middle), normalized axial velocity \(u_{z}/\Omega R_{\text{m}}\) (bottom). The rotational direction is indicated by the arrow

Full size image
Fig. 12
figure 12

Experimentally (left) and numerically (right) determined velocity fields in a radially expanding groove – see Fig. 1d; normalized circumferential velocity \(u_{\varphi}/\Omega R_{\text{m}}\) (top), normalized radial velocity \(u_{r}/\Omega R_{\text{m}}\) (middle), normalized axial velocity \(u_{z}/\Omega R_{\text{m}}\) (bottom). The rotational direction is indicated by the arrow

Full size image

Despite the missing comparison with numerical data, the shown data in Fig. 13 from the DPTV-experiment on the radial groove overprinted with a waffle pattern, demonstrate a similarly sensitive impact on the radial velocity component. The elevated radial velocity component in the overprinted case indicates, that the structuring of the previously smooth surface neighboring the groove leads to a more concentrated volume flow in the groove over the whole disk radius.

Fig. 13
figure 13

Experimentally determined velocity fields in a radially groove with overprinted waffle pattern – see Fig. 1e; normalized circumferential velocity \(u_{\varphi}/\Omega R_{\text{m}}\) (top), normalized radial velocity \(u_{r}/\Omega R_{\text{m}}\) (middle), normalized axial velocity \(u_{z}/\Omega R_{\text{m}}\) (bottom). The rotational direction is indicated by the arrow

Full size image

5 Discussion

Currently, the disk geometry, material and operating parameters are main focus when optimizing an open wet clutch. However, it becomes clear that for a better understanding and, therefore, prediction of the drag torque, also the fluid mechanical influences need to be considered. The flow topology has an immediate influence on the drag torque in the single-phase state (before the onset of aeration). The flow along the groove forms a cavity-roller vortex, but in addition functions as a conveying flow conduit. This, in fact, has several consequences:

The conveying characteristic of the flow topology can hence be evaluated by the volume flow along the groove. This is an important factor as the radial outflow affects the aeration onset, which in turn causes a drop in drag torque [30]. Therefore, the volume flow in radial direction is an important parameter for the evaluation of a disk geometry and to characterize the end of the single phase flow regime.

The second characteristic of the flow topology, as predominated by a vortex inside the groove, impacts the drag torque directly, since the wall shear stress changes depending on the flow topology. To better understand the function as a vortex tube and its interplay with the drag torque various (local) Eulerian vortex-identification criteria [8, 11, 16, 36] can be utilized to obtain quantitative information like the vorticity, circulation and spacial expansion of the vortex. One such example has already been outlined by Leister et al. [22], who applied the \(\Gamma_{1}\) criterion in order to emphasize strength and location of the cavity roller inside a purely radial groove.

Generally, such approaches are considered as capable to derive three additional parameters to describe the flow topology the respective flow topologies. Furthermore, in the case of sufficiently time resolved investigations of the disengagement process of the clutch, for instance, the identifications of Lagrangian structures [5, 37] can provide supplementary information on system latencies. This would be especially useful for all unsteady processes like the clutch engagement, disengagement and also the change of flow topology towards the aeration.

The very good agreement between the circumferential and axial velocity components from the DPTV experiments and the numerical simulations emphasize the value of complementary experimental and numerical investigations for better understanding of the flow topology and ultimately also drag-torque estimations. However, the limited quantitative agreement between the DPTV experiments and the numerical simulation for the radial velocity component also demonstrates the importance of the boundary conditions to the problem at hand. Two aspects, which are not considered in the simulation, are the influence of the gravity as well as the two-phase surrounding of the single-phase flow region. The direction of the gravitational vector changes constantly in the rotor-fixed frame of reference, thus constantly changing the flow topology within the groove. The discrepancy between the experimental and numerical investigation is in accordance with analytical considerations on the gravitational influence [25]. The other influence factor is the two-phase plenum being not considered in the numerical simulation, which influences the inflow and outflow boundary conditions. However, a detailed modeling of complex side conditions requires comprehensive investigations that could lead to higher quality boundary conditions for simulations, which however is beyond the scope of the present comparative study. Consequently, a straight-forward applicable first step towards better drag torque prediction could be to research the spatially resolved correlation of the radial flow magnitude with the drag torque.

Another important observation is the increased sensitivity of the radial flow velocity with the added overprint of the waffle pattern. This phenomenon can be interpreted in two different ways, leading to separate approaches. First, the overprinted pattern can be interpreted as causing micro-flow structures in the gap between the grooves, thus changing the flow inside the groove. This would consequently lead to a significantly more complex flow topology. The second approach is the interpretation of the waffle pattern as a sort of quasi-roughness. This added roughness in the gap would also influence the radial flow between the grooves and would in turn potentially lead to increased flow rate inside the grooves. This insight reveals a need for more research on this topic, since both interpretations lead to categorically different optimization strategies. In both ways, however, the overprint reveals an additional degree of freedom for optimization efforts.

6 Concluding remarks

The present work presents the investigation of varying clutch-disk groove geometries as influential factors for the resulting the flow topology in the rotor-stator gap of an open wet clutch. To address the overarching goal of improved predictability of the adverse drag torque, it has been shown in the present work that numerical simulations can predict the circumferential and axial velocity components sufficiently well and therefore present a valuable tool for the analysis of the flow structure in an open wet clutch. However, for the radial velocity component, differences in the determined flow magnitude only allow the qualitative comparison between the experiments and the numerical simulations, which in turn demonstrates the careful choice of accurately prescribed boundary conditions to be of utmost importance for an optimal prediction of the resulting effects of the problem at hand. Especially since the radial flow rate is critical to predict the onset of aeration, further research on the two-phase plenum (clutch housing) and its influence on the in- and outflow is needed, for more accurately optimized boundary conditions. Here the DPTV method can operate as a valuable tool for the validation of simulated flow typologies. For the relationship between the flow topology and the resulting drag torque, additional degrees of freedom and optimization parameters for clutch design have been identified. However, this relationship is highly complex, hence a possible development is the correlation of these parameters with the drag torque. In this context, also the application of regression or machine learning methods can be envisioned for an improved prediction of drag torque and, therefore, also a general identification of further directions for optimization strategies in the open wet clutch design.