1 Introduction

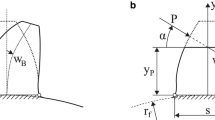
If rotary movements and torque have to be transmitted angularly in a drive train, bevel gears are of particular importance. A cone represents the basic body of bevel gears (see Fig. 1a). A bevel gear stage consists of an input gear (pinion) and an output gear (wheel). The input gear usually has a fewer number of teeth than the output gear [2]. Due to their tapered basic body, various shaft angles can be realized. The most commonly used shaft angle is 90°. An axis offset (also called hypoid offset) is also possible in order to optimally adapt the gear set to the respective application (see Fig. 1b). Due to the geometric flexibility regarding shaft angle and hypoid offset, bevel gears have a very wide range of applications. A typical large field of application are axle drive systems for passenger cars or commercial vehicles. But also, bevel and hypoid gears are widely used in industrial, marine and aeronautical applications. In the following, within the term bevel gear hypoid gears are included.

Fig. 1
figure 1

Exemplary bevel gear set without axis offset (a) and with axis offset (b)

Full size image

The maximum transferable torque is mainly limited by the load carrying capacity of the gear set. Typical failure modes affecting the flanks of a bevel gear set are pitting, tooth flank fracture and scuffing. Furthermore, the phenomenon micropitting also affects the load carrying capacity of the tooth flank since it may change the load distribution on the flank. Fig. 2 shows the above-mentioned failure modes on a bevel gear flank without offset and with a shaft angle of 90°.

Fig. 2
figure 2

Different tooth flank failure modes at a bevel gear pinion flank. a Pitting. b Tooth flank fracture. c Scuffing. d Micropitting. (Picture sources: [3,4,5])

Full size image

In order to ensure a reliable operation of a bevel gear set, the load carrying capacity of the tooth flank has to be taken into account within the gear design process. Due to the complex geometry of a bevel gear a virtual cylindrical gear is used as substitute gearing according to the current state of the art [6]. The substitute gearing represents the meshing conditions of a bevel gear with sufficient accuracy. Therefore, it is possible to determine the load carrying capacity of bevel gears regarding pitting, scuffing, micropitting and tooth flank fracture in an early stage of design by use of few, reliable input variables.

The load carrying capacity regarding scuffing, micropitting and tooth flank fracture can be determined by use of the virtual cylindrical gear geometry along the path of contact [5, 7,8,9,10,11]. In contrast to this the determination of the pitting load carrying capacity is only carried out on a single, representative point on the path of contact of the virtual cylindrical gear [12].

Within this paper a new extended calculation method is provided to calculate the pitting load carrying capacity along the entire path of contact of the virtual cylindrical gear, analogous to the current calculation methods for determining scuffing, micropitting and tooth flank fracture load carrying capacities.

In scope of this paper calculation methods comply in assumptions, structure and conditions with the standard calculation method B of ISO 10300:2014 are termed as calculation methods of standard category B. Analogous calculation methods comply with the standard calculation method A of ISO 10300:2014 are termed as calculation methods of standard category A.

2 State of the art

2.1 Failure mode pitting

The failure mode pitting occurs if the material strength is exceeded by the occurring stress [13, 14]. The damage usually starts at or near the gear surface, preferred on areas with negative specific sliding [15,16,17]. The crack is initiated at or near the tooth flank surface and grows into the depth. Consequences are shell-shaped material eruptions [18], which can lead to unfavorable NVH-behavior and additional dynamic forces [19]. Pitting often shows a progressive damage development and may cause other failure modes such as tooth breakage. Fig. 2 shows a typical pitting on a bevel gear flank.

2.2 Calculation methods according to the state of the art

The pitting safety factor SH of gears is defined as the ratio of the permissible contact stress σHP and the contact stresses σH [12, 20].

$$S_{H}=\frac{\sigma _{HP}}{\sigma _{H}}$$
(1)

Based on experimental investigations, Wirth [21] developed a local calculation method of standard category A and additionally a calculation approach of standard category B to determine the pitting load carrying capacity of bevel gears (see Fig. 3). By use of the local calculation method, a local safety against pitting on the tooth flank is determined, using the exact description of the macro and micro geometry of a bevel gear set. For calculating the load carrying capacity according the calculation method of standard category B only information about the macro geometry is necessary. The standard-capable method by Wirth [21, 22] is to a large extend adopted in ISO 10300-2:2014 method B1 [12].

Fig. 3
figure 3

Overview of relevant standard calculation methods and their origin

Full size image

Klein [8, 23] extended the calculation method of standard category B by Wirth [21, 22] to the effect of a greater resolution of the stress along the path of contact of the virtual cylindrical gear. Klein [8, 23] concentrates his researches on scuffing for bevel and hypoid gears and in 2021 his findings were documented as an international technical specification [9]. Figure 3 illustrates the relationship between the calculation methods described above.

In the following subchapters, the calculation methods that constitute the state of the art and form the basis of the new extended calculation approach are discussed in more detail.

2.2.1 Local calculation method

The local calculation method of standard category A is based on the real bevel gear geometry (macro and micro geometry) and uses local contact stresses to determine the safety factors against pitting. The local contact stresses σH,i can be calculated by the multiplication of the calculated Hertzian stresses σH,lok,i and the square root of the dynamic factor KV according to ISO 10300-1:2014 [6] in order to take load increases due to internal dynamic effects into account. The local contact stresses σH,lok,i are usually determined using a loaded tooth contact analysis (LTCA), BECAL [24] was used here for this purpose [25].

$$\sigma _{H{,}i}=\sigma _{H{,}\mathrm{lok}{,}i}\cdot \sqrt{K_{v}}$$
(2)

The local permissible contact stress σHP,i is calculated on the basis of the strength numbers according to ISO 6336-5:2016 [26] using the corresponding equations according to ISO 10300-2:2014 [12], whereas the bevel specific influence on the permissible contact stress is taken into account by the additional slip factor ZS [25].

$$\sigma _{HP{,}i1{,}2}=\sigma _{H{,}\lim }\cdot Z_{NT}\cdot Z_{X}\cdot Z_{L}\cdot Z_{V}\cdot Z_{R}\cdot Z_{W}\cdot Z_{\mathrm{Hyp}{,}i}\cdot Z_{S{,}i}$$
(3)

The life factor ZNT, the size factor ZX, the lubricant factors ZL ZV ZR and the work hardening factor ZW, determined according to ISO 10300-2:2014 [12], are considered constant over the entire tooth mesh. The hypoid factor ZHyp,i as well as the slip factor ZS,i are local values.

The hypoid factor ZHyp,i takes into account the influence of longitudinal sliding on the pitting load carrying capacity. It is based on the sum of velocities vertical to the contact line \(v_{\Sigma {,}\text{vert}{,}i}\) and the sliding velocity parallel to the contact line \(v_{g{,}\mathrm{par}{,}i}\). [25].

$$Z_{\mathrm{Hyp}{,}i}=1-0.3\cdot \left(\frac{v_{g{,}\mathrm{par}{,}i}}{v_{\Sigma {,}\text{vert}{,}i}}-0.15\right)\ with\colon \;0.6\leq Z_{\mathrm{Hyp}{,}i}\leq 1$$
(4)

The slip factor ZS,i considers the influence of the slip on the permissible contact stress. It is determined for pinion and wheel by the slip perpendicular to the contact line ζvert,i [25].

$$Z_{S{,}i1{,}2}=\frac{7}{24}\zeta _{\mathrm{vert}{,}i1{,}2}+\frac{47}{40}\ with\colon \;1\leq Z_{S{,}i1{,}2}\leq 1.175$$
(5)

Recalculation of experimental tests showed a very good correlation between the predicted and the real pitting areas on the damaged gear flanks, see Fig. 9. Not only the place of the initial pitting is calculated correctly, also the pitting growth is predicted reasonably [21].

The local calculation method is applicable for case hardened gears which meet the state-of-the-art regarding material and heat treatment and represents the reference for the development of the calculation methods of standard category B. It can only be applied in combination with a loaded tooth contact analysis based on the real tooth flank geometry (macro and micro-geometry).

2.2.2 Standard calculation method

For practical reasons also a calculation method of standard category B was developed by Wirth [22]. This approach allows an estimation of the pitting load carrying capacity of a bevel or hypoid gear set at a very early design stage of the gear development. Due to the complex geometry of bevel and hypoid gears, the calculation method is based on a virtual gear geometry. The bevel gear geometry is transferred to a virtual tooth system, which represents the tooth contact conditions and thus forms the basis for determining the load carrying capacity regarding different failure modes.

Initially, a virtual cylindrical gear for bevel gears without offset and a virtual crossed helical gear or a virtual bevel gear for hypoid gears were used [27,28,29]. Wirth [21] developed a virtual cylindrical gear, which can be used for bevel and hypoid gears. The virtual cylindrical gear also forms the basis of the international standard ISO 10300 series and represents the state-of-the-art for calculation methods according to the standard category B. The virtual cylindrical gear geometry is structured according to the schematic diagram in Fig. 4. The virtual cylindrical gear is derived from the reference cone of the bevel gear or rather the hypoid gear. Detailed information regarding the representation of a bevel or hypoid gear as a virtual cylindrical gear are available in Annex A of ISO 10300-1:2014 [6].

Fig. 4
figure 4

Schematic diagram of a hypoid gear according

Full size image

A comparable plane of action is essential for a reasonable calculation of the load carrying capacity by using the virtual cylindrical gear. Wirth [21] has shown that the zone of action can be described with sufficient accuracy by a parallelogram. Fig. 5 shows the schematic representation of the zone of action according to Wirth [21]. More detailed information on determining the relevant zone of action for bevel gears can be found in ISO 10300-1:2014 [6]. Based on this, the load distribution between several meshing teeth is determined by the length ratios of the contact lines lb in the zone of action. As shown schematically in Fig. 5, a parabolic load distribution along the line of action and an elliptical load distribution along the contact lines lb are assumed. In total, a maximum of three simultaneously meshing teeth are considered.

Fig. 5
figure 5

Zone of action according to Wirth [30]

Full size image

Based on the virtual cylindrical gear set and the operating conditions, a global pitting safety factor according to ISO 10300-2:2014 [12] or Wirth [21] can be determined. The nominal contact stress σH0 can be calculated with Eq. 6 according to ISO 10300-2:2014 [12], where Fn is the nominal force of the virtual cylindrical gear at the mean point P. The formula of the nominal contact stress σH0 according to Wirth [21] is given in Eq. 7.

$$\sigma _{H0}=\sqrt{\frac{F_{n}}{l_{bm}\cdot \rho _{\mathrm{rel}}}}\cdot Z_{M-B}\cdot Z_{LS}\cdot Z_{E}\cdot Z_{K}$$
(6)
$$\sigma _{H0}=\sqrt{\frac{F_{n}}{l_{bm}\cdot \rho _{\mathrm{rel}}}}\cdot Z_{M-B}\cdot Z_{LS}\cdot Z_{E}$$
(7)

According to ISO 10300-2:2014 [12] and Wirth [21], the pitting load carrying capacity is determined at one decisive point, which lies between the inner point of single contact and the midpoint of the path of contact, depending on the face contact ratio of the virtual cylindrical gear. The mid zone factor ZM−B is used to convert the radii of curvature at the design point P to the radii of curvature at the point which is decisive for the failure mode pitting.

The contact stress can be calculated by use of Eq. 8.

$$\sigma _{H}=\sigma _{H0}\cdot \sqrt{K_{A}\cdot K_{v}\cdot K_{H\beta }\cdot K_{H\alpha }}\leq \sigma _{HP}$$
(8)

To avoid pitting, the occurring contact stress σH has to be lower than the permissible contact stress σHP, which can be calculated according to ISO 10300-2:2014 [12] as given in Eq. 9 and according to Wirth [21] as specified in Eq. 10.

$$\sigma _{HP}=\sigma _{H{,}\lim }\cdot Z_{NT}\cdot Z_{X}\cdot Z_{L}\cdot Z_{V}\cdot Z_{R}\cdot Z_{W}\cdot Z_{\mathrm{Hyp}}\cdot S_{\mathrm{Hmin}}$$
(9)
$$\sigma _{HP}=\sigma _{H{,}\lim }\cdot Z_{NT}\cdot Z_{X}\cdot Z_{L}\cdot Z_{V}\cdot Z_{R}\cdot Z_{W}\cdot Z_{\mathrm{Hyp}}\cdot Z_{S}\cdot S_{\mathrm{Hmin}}$$
(10)

Analogous to the local calculation method, Wirth [30] uses an additional slip factor ZS1,2, given in Eq. 11, to determine the permissible flank stress σHP, as quoted in Eq. 10.

$$\begin{array}{l} Z_{S1}=1.175;Z_{S2}=1\:forZ_{M-B}< 0.98\\ Z_{S1}=1;Z_{S2}=1.175\:forZ_{M-B}> 1 \end{array}$$
(11)

Finally, the occurring contact stress calculated according to Eq. 8 and the permissible contact stress, calculated according to Eq. 9, can be used for determining a global safety value against pitting according to Eq. 1.

The essential difference between the standard calculation method ISO 10300-2:2014 [12] and the calculation method of standard category B provided by Wirth [21] regards the consideration of the positive and negative sliding zones on the tooth flank. Within ISO 10300-2:2014 [12] the slip factor ZS is not used in the calculation method whereas the bevel factor ZK is used to considerate among other differences the specific sliding conditions for bevel gears in comparison to cylindrical gears. Subsequently for the standard-capable calculation method according to Wirth [21], the permissible contact stress is increased by the slip factor ZS. In the standard calculation method ISO 10300-2:2014 [12] the nominal contact stress is decreased by the bevel gear factor ZK. In sum both considerations of the slip conditions resulting in nearly the same safety factors. On a physical point of view the increasing of the permissible contact stress σHP is more comprehensible than the reduction of the nominal contact stress σH0 due to the slip conditions on the tooth flank. This issue is discussed in more detail in Sect. 6.2.

2.2.3 Extended standard calculation method to determine the Hertzian contact stresses along the path of contact

Based on the virtual cylindrical gear geometry the Hertzian contact stress can be calculated along the path of contact of the virtual cylindrical gear according to ISO/DTS 10300-4:2019 [10], ISO/TS 10300-20:2021 [9] or Klein [8, 31]. Therefore, the transverse path of contact between pinion and wheel of the virtual cylindrical gear set is divided in a number of sections (e.g. n = 10) to determine the local safety factors for n + 1 points of contact. To define the contact points the coordinate gY is established, which originates in the pitch point C (= design point P of the bevel gear set). Towards the pinion tip gY is defined as positive, towards the pinion root it is defined as negative. Fig. 6 shows an exemplary path of contact including the coordinate gY. In the boundary points A and E on the transverse path of contact gY is determined as follows [9].

$$g_{Y}\left(A\right)=-g_{va2}$$
(12)
$$g_{Y}\left(E\right)=g_{va1}$$
(13)
Fig. 6
figure 6

Transverse path of contact [30]

Full size image

The length of the transverse path of contact can be subdivided in a number of sections i. For a contact point Y on the transverse path of contact of the virtual cylindrical gear the corresponding coordinate gY(Y) can be calculated as follows [9].

$$g_{Y}\left(Y\right)=\left(g_{Y}\left(A\right)+k_{s}g_{v\alpha }\right)+Y\frac{\left(1-2k_{s}\right)g_{v\alpha }}{i}$$
(14)

Where:

\(k_{s}\):

0 for bevel gears with \(\beta _{vb}> 0;\)

\(k_{s}\):

0.001 for bevel gears with \(\beta _{vb}=0\);

\(g_{v\alpha }\):
$$g_{va1}+g_{va2}=\frac{1}{2}\left[\left(\sqrt{{d}_{va1}^{2}-{d}_{vb1}^{2}}-d_{v1}\sin \alpha _{\mathrm{vet}}\right)+\left(\sqrt{{d}_{va2}^{2}-{d}_{vb2}^{2}}-d_{v2}\sin a_{\mathrm{vet}}\right)\right]$$
\(g_{v\alpha }\):

the length of path of contact of the virtual cylindrical gear.

In the next step the length of each contact line lb,Y can be calculated at each contact point Y of the virtual cylindrical gear by using Eq. 15. Fig. 7 shows the general definition of the length of the contact lines lb,Y according to ISO/TS 10300-20:2021 [9].

$$l_{b{,}Y}=l_{b0{,}Y}\left(1-C_{lb{,}Y}\right)$$
(15)
Fig. 7
figure 7

General definition of length of contact lines [9]

Full size image

The theoretical length of a contact line at a contact point lb0,Y of the virtual cylindrical gear can be calculated by use of the following equation [9].

$$l_{b0{,}Y}=\sqrt{\left(x_{1{,}Y}-x_{2{,}Y}\right)^{2}+\left(y_{1{,}Y}-y_{2{,}Y}\right)^{2}}$$
(16)

The contact line lengths are trimmed at the edges by the elliptical correction function Clb [9].

$$C_{lb{,}Y}=\sqrt{\left(1-\left(f_{Y}/f_{\max }\right)^{2}\right)\left(1-\sqrt{b_{v{,}\mathrm{eff}}/b_{v}}\right)^{2}}$$
(17)
$$l_{b{,}Y}=l_{b0{,}Y}\cdot (1-C_{lb{,}Y})$$
(18)

Based on the contact line lengths and the assumption of load distribution shown in Fig. 5, a local load distribution factor ZLS,Y can be determined. For this purpose, the area of the semi-ellipse of the middle contact line is set in relation to the total area consisting of the semi-ellipse areas over all contact lines [9].

$$Z_{LS{,}Y}=\sqrt{\frac{A_{m}}{A_{t}+A_{m}+A_{r}}}$$
(19)
$$A=0.25\cdot \pi \cdot p_{Y}\cdot l_{b{,}Y}$$
(20)

Using the curvature factor XY the local equivalent radius of relative curvature ρrel,Y can be calculated for each considered contact point Y [9].

$$\rho _{\mathrm{rel}{,}Y}=\rho _{\mathrm{rel}}/{X}_{Y}^{2}$$
(21)
$$X_{Y}=\frac{\tan \alpha _{\mathrm{vet}}}{\sqrt{\frac{\left(d_{v1}/2\cdot \sin \alpha _{\mathrm{vet}}+g_{Y}\right)}{d_{vb1}/2}}\cdot \sqrt{\frac{\left(d_{v2}/2\cdot \sin \alpha _{\mathrm{vet}}-g_{Y}\right)}{d_{vb2}/2}}}$$
(22)

The conversion of the maximum line load at point M to the contact point Y is calculated by use of the local face load factor KHβ,Y, according Eq. 23–25 [9].

$$K_{H\beta {,}Y}=K_{H\beta }\cdot \left\lfloor 1-\left(b_{Y}\cdot z_{Y}\right)^{a}\right\rfloor$$
(23)
$$z_Y=\sqrt{\begin{aligned}&\left(\frac{b_{v{,}\mathrm{eff}}}{2}-\frac{x_{1{,}Y}+x_{2{,}Y}}{2}\right)^{2} \\ & +\left(g_{va2}-\frac{g_{v\alpha }}{2}+g_{Y}-\frac{y_{1{,}Y}+y_{2{,}Y}}{2}\right)^{2}\end{aligned}}$$
(24)
$$a=\frac{1}{K_{H\beta }-1};\;b_{Y}=\frac{2}{l_{bm{,}Y}}$$
(25)

The modified Hertzian contact stress at contact point Y \(\sigma _{H{,}\mathrm{mod}{,}Y}\) can be calculated based on the Hertzian contact stress σH,Y. The Hertzian contact stress σH,Y is calculated by use of the described load sharing and curvature factors according Eq. 27. Within the determination of the modified Hertzian contact stress σH,mod,Y the profile crowning of the gear set is taken into account by use of the exponent e according to ISO 10300-2:2014 [9, 12]

$$\sigma _{H{,}\mathrm{mod}{,}Y}=\sigma _{H{,}Y}+\left(\frac{1}{6}\cdot e+0.25\right)\cdot max\left(\sigma _{H{,}Y}\right)\cdot \left(\frac{\left| g_{Y}\right| }{g_{va{,}\max }}\right)^{4}$$
(26)
$$\sigma _{H{,}Y}=\sqrt{\frac{F_{n}\cdot K_{A}\cdot K_{v}\cdot K_{H\beta {,}Y}\cdot K_{H\alpha }}{l_{b{,}Y}\cdot \rho _{\mathrm{rel}{,}Y}}}\cdot Z_{E}\cdot Z_{LS{,}Y}$$
(27)

3 Description of the methodical approach

In the following the calculation methods used within this paper and their relation between each other are presented to obtain a better overview about the discussed calculation methods.

The suggested extended calculation method of the load capacity against pitting of bevel gears combines the localized calculation method of the contact stresses given in ISO/TS 10300-20:2021 [9] and the calculation method by Wirth [21] enhanced by localized calculation factors. Therefore, within the presented extended calculation method, the load capacity against pitting can be calculated along the path of contact of the virtual cylindrical gear, similar to the given standard of ISO/TS 10300-20:2021 [9]. Fig. 8 shows graphical the connection between the calculation methods.

Fig. 8
figure 8

Visualization of the connections between the calculation methods regarding the load carrying capacities of bevel gears discussed in this paper

Full size image

As visualized in Fig. 8 the local calculation method of standard category A, provided by Wirth [21], is used to validate the new extended calculation method. This approach is reasonable due to the fact, that the local calculation method is based on experimental investigations and is able to predict the areas on the tooth flank with a safety factor against pitting less than 1.0. In Fig. 9 the red dots represent the calculation points with a safety factor against pitting less than 1.0, which match very good with the early pitting damage on the related tooth flank. Additionally, the local calculation method is widely, successfully used with application in practice. Therefore, the validation of the extended calculation method of standard category B based on a proven calculation method of standard category A is considered to be sufficient.

Fig. 9
figure 9

Comparison of predicted safety factors against pitting on the tooth flank and real pitting damage occurred by experimental investigations [1]. a Pitting on the tooth flank of the pinion after 3 ⋅ 106 load cycles at pinion [1]. b Calculation result of the safety factor against pitting according to local calculation method

Full size image

4 New extended calculation approach for the pitting load carrying capacity of bevel and hypoid gears

Based on extensive experimental studies within the research projects by Wirth [22] and Boiadjiev [3] as well as the findings of Klein [8], a new extended approach of standard category B for calculation of the pitting safety factor for bevel gears was developed by one of the co-authors. This approach is described in the following.

The new extended calculation approach offers the possibility to determine the pitting load carrying capacity of bevel gears over the entire length of the path of contact of the corresponding virtual cylindrical gear. Thus, purely on the basis of the macro geometry, the user has more information about the pitting load carrying capacity of the tooth flank compared to the current standard at an early stage of gear design. For this purpose, the Hertzian contact stresses as well as the permissible contact stresses have to be determined along the path of contact of the virtual cylindrical gear pair.

To determine the modified Hertzian contact stresses σH,Y,mod along the path of contact of the virtual cylindrical gear the calculation method according to Klein [8] and ISO/TS 10300-20:2021 [9] is applied.

Unlike to the known calculation methods of standard category B according to Wirth [21] as well as according to ISO 10300-2:2014 [12], the safety factor against pitting is not determined at a decisive point, but locally for each considered point Y on the path of contact of the virtual cylindrical gear. Based on Wirth [21] the permissible contact stress is determined according to Eq. 28 with the extended, localized hypoid factor ZHyp,Y, slip factor ZS,Y and speed factor ZV,Y for each point of contact Y along the path of contact considered.

$$\sigma _{HP1{,}2{,}Y}=\frac{{\sigma _{H{,}\lim 1{,}2}}\cdot Z_{NT1{,}2}}{S_{\mathrm{Hmin}}}\cdot Z_{X1{,}2}\cdot Z_{W}\cdot Z_{L}\cdot Z_{R}\cdot Z_{V{,}Y}\cdot Z_{\mathrm{Hyp}{,}Y}\cdot Z_{S{,}Y}$$
(28)

The life factor ZNT, the size factor ZX, the work hardening factor ZW, the lubricant factor ZL and the roughness factor ZR represent global values, that are constant along the path of contact. They are calculated according to ISO 10300-2:2014 [12]. The speed factor ZV,Y, hypoid factor ZHyp,Y and slip factor ZS,Y depend on the local velocity conditions at the considered point of contact Y along the path of contact and have to be modified in comparison to the equations given in ISO 10300-2:2014 [12].

The speed factor ZV,Y depends on the tangential speed at mid face width of the reference cone of the wheel vmt2 and can be calculated by using Eq. 29.

$$Z_{V{,}Y}=C_{ZV}+\frac{2\cdot \left(1-C_{ZV}\right)}{\sqrt{0.8+32/v_{mt2{,}Y}}}$$
(29)

The local tangential speed vmt2,Y can be calculated as a function of the coordinate for transverse path of contact gY.

$$v_{mt2{,}Y}=v_{mt2}-2\cdot v_{mt2}\cdot g_{Y}\cdot \sin (\alpha _{\mathrm{vet}})/d_{v2}$$
(30)

With:

$$v_{mt2}=\frac{d_{m2}\cdot n_{2}}{19098}$$
(31)

Fig. 10 shows the speed factor along the path of contact of the virtual cylindrical gear for different test gear sets (the macro geometries are listed in Table 1). The speed factor shows an almost constant behavior along the path of contact of the virtual cylindrical gears. The value of the speed factor depends on gear size and the field of action. Although the speed factor for the test gearings used here show only very small fluctuations in value over the path of contact, the speed factor is used in the new extended calculation method in localized form according to Eq. 29 to establish a conclusive calculation method. For gears of larger sizes, greater fluctuations in the speed factor over the path of contact are expected.

Fig. 10
figure 10

Exemplary speed factor ZV,Y determined for test gear sets

Full size image
Table 1 Basic geometry data
Full size table

By use of the hypoid factor ZHyp,Y the influence of longitudinal sliding on the pitting load carrying capacity is taken into account. The hypoid factor ZHyp,Y can be calculated for each considered contact point with Eq. 32:

$$Z_{\mathrm{Hyp}{,}Y}=1-0.3\cdot \left(\frac{v_{g{,}\mathrm{par}}}{v_{\Sigma {,}\mathrm{vert}{,}Y}}-0.15\right)$$
(32)

With:

$$0.6\leq Z_{\mathrm{Hyp}{,}Y}\leq 1$$

It is assumed that the sliding velocity parallel to the contact line vg,par shows constant values along the whole path of contact [5, 8, 9, 21]. Therefore, the sliding velocity vg,par is determined at the mean point P by use of the following equations.

$$h_{1}=\frac{d_{m1}/\cos \delta _{1}}{d_{m1}/\cos \delta _{1}+d_{m2}/\cos \delta _{2}}\cdot a{,}h_{2}=a-h_{1}$$
(33)
$$\varphi _{1}=\arccos \left(2\cdot \frac{h_{1}}{d_{m1}}\right){,}\varphi _{2}=\arccos \left(2\cdot h_{2}/d_{m2}\right)$$
(34)
$$v_{g}=\sqrt{\begin{aligned} & \left(v_{mt2}\cdot cos\varphi _{2}\right)^{2}+\left(v_{mt1}\cdot cos\varphi _{1}\right)^{2}+ \\ & \left(v_{mt1}\cdot sin\varphi _{1}-v_{mt2}\cdot sin\varphi _{2}\right)^{2}\end{aligned}}$$
(35)
$$v_{g{,}\mathrm{par}}=v_{g}\cdot \cos \left| \omega _{\mathrm{bel}}\right|$$
(36)

The absolute local surface velocities are required for the determination of the local sum of velocities vertical to the contact line \(v_{\Sigma {,}\text{vert}{,}Y}\). It should be noted that hypoid gears have an additional velocity component in the tooth width direction due to the hypoid offset. However, it can be assumed that this is constant over the line of contact [5, 8, 9]. The surface velocity in lengthwise direction of the tooth wt1,2s is determined at the mean point P. The surface velocity in profile direction of the tooth is calculated locally over the path of contact of the virtual cylindrical gear.

$$w_{t1{,}2s}=v_{mt1{,}2}\cdot \sin \beta _{m1{,}2}$$
(37)
$$w_{t1h{,}Y}=v_{mt1}\cdot \cos \beta _{m1}\cdot \left(\sin \alpha _{n}+2\cdot g_{Y}/d_{v1}\right)$$
(38)
$$w_{t2h{,}Y}=v_{mt2}\cdot \cos \beta _{m2}\cdot \left(\sin \alpha _{n}-2\cdot g_{Y}/d_{v2}\right)$$
(39)

The total surface velocity can be determined by vectorially addition of the velocity components in lengthwise and profile direction of the tooth. Using the inclination angle of contact line βB, the absolute surface velocity vertical to the contact line can be calculated.

$$w_{t1{,}2{,}Y}=\sqrt{{w}_{t1{,}2s}^{2}+{w}_{t1{,}2h{,}Y}^{2}}$$
(40)
$$\omega _{wt1{,}2{,}Y}=\arctan \left(w_{t1{,}2h{,}Y}/w_{t1{,}2s}\right)$$
(41)
$$w_{t1{,}2\mathrm{vert}{,}Y}=w_{t1{,}2{,}Y}\cdot \sin \left(\left| \beta _{B}\right| +\left| \omega _{wt1{,}2{,}Y}\right| \right)$$
(42)

The local sum of velocities vertical to the contact line \(v_{\Sigma {,}\text{vert}{,}Y}\) consists of the local surface velocity of pinion and wheel oriented vertically to the contact line.

$$v_{\Sigma {,}\mathrm{vert}{,}Y}=w_{t1\mathrm{vert}{,}Y}+w_{t2\mathrm{vert}{,}Y}$$
(43)

The localized slip factor ZS,Y considers the influence of the specific slip conditions on the tooth flank on the permissible contact stress. It is defined according to the local calculation method.

$$Z_{S{,}Y1{,}2}=\frac{7}{24}\zeta _{\mathrm{vert}{,}Y1{,}2} + \frac{47}{40} \text{mit:} \;1\leq Z_{S{,}Y1{,}2}\leq 1.175$$
(44)

The slip perpendicular to the contact line is calculated for pinion and gear separately according to the following formulae.

$$\zeta _{\mathrm{vert}{,}Y1}=1.0-\frac{\left| w_{t2{,}\mathrm{vert}{,}Y}\right| }{\left| w_{t1{,}\mathrm{vert}{,}Y}\right| }$$
(45)
$$\zeta _{\mathrm{vert}{,}Y2}=1.0-\frac{\left| w_{t1{,}\mathrm{vert}{,}Y}\right| }{\left| w_{t2{,}\mathrm{vert}{,}Y}\right| }$$
(46)

Finally, the local safety factor against pitting SH1,2,Y can be determined for each considered contact point Y along the path of contact of the virtual cylindrical gear based on the local permissible contact stress σHP1,2,Y calculated according to Eq. 28 and the local contact stress σH,Y calculated according to Eq. 26.

$$S_{H1{,}2{,}Y}=\sigma _{HP1{,}2{,}Y}/\sigma _{H{,}Y}$$
(47)

5 Validation of the new extended calculation approach

For validation of the new extended calculation approach of standard category B, a comparison between the local calculation method of standard category A and the new extended calculation approach is presented. For this purpose, the same test gear sets G0, G15, G31.75 and G44 used by Wirth [21, 22] are considered. The basic geometry data of these investigated gear sets are given in Table 1. All test gears show a typical ease off design and were ground and blast cleaned after heat treatment. The recalculations were carried out for a torque of 500 Nm and a rotational speed of 4500 min−1 at pinion.

As described, the extended calculation approach is based on the virtual cylindrical gear geometry. The virtual cylindrical gear geometry is calculated in the mean section of the bevel gear. In Fig. 11 the calculation points along the path of contact are illustrated exemplarily as red dots for the proposed extended calculation approach. Unlike the extended calculation, the local calculation considers the whole flank of the gear by use of tooth sections, which are distributed over the whole flank. The tooth sections are shown as black dashed lines in Fig. 11. The following comparisons between the results of the extended calculation approach, the standard calculation method according to ISO 10300-2:2014 [12] and the local calculation method (method A) are performed along the mean section.

Fig. 11
figure 11

Definition of tooth sections and path of contact gY [32]

Full size image

5.1 Comparison of radius of relative curvature

Within the newly developed calculation method, the radii of relative curvature are calculated in accordance with ISO/TS 10300-20:2021 [9] at the considered contact points Y of the virtual cylindrical gear. Exemplary values of the local radius of relative curvature along the path of contact are shown in Fig. 12. The dashed lines in Fig. 12 represent the values determined within a tooth contact analysis by use of the software BECAL [24]. The solid lines show the values calculated by the extended approach according to ISO/TS 10300-20:2021 [9], which is based on the approach of Shtipelman [33].

Fig. 12
figure 12

Comparison of radii of relative curvature according to extended approach of standard category B and loaded tooth contact analysis LTCA of standard category A. a G0—drive side. b G15—drive side. c G31.75—drive side. d G44—drive side

Full size image

The results of the extended calculation approach based on the virtual cylindrical gear geometry correlate well with the results of the tooth contact analysis based on the real flank geometry. The small deviations can be explained by the fact, that the microgeometry of the bevel gears cannot be represented in detail by the virtual cylindrical gear geometry.

5.2 Comparison of Hertzian contact stresses

The modified Hertzian contact stress σH,Y,mod represents a significant factor on the load carrying capacity of gears regarding pitting. Therefore, the correlation between the new extended approach and a LTCA was investigated. In Fig. 13 the results of the described comparison are shown. The dashed lines show the values determined within a LTCA by use of the software BECAL [24, 34]. The solid lines show the values for Hertzian contact stresses calculated according to the extended calculation approach of standard category B. The dotted lines within the following figures present the calculated nominal contact stress according to the standard calculation method ISO 10300-2:2014 [12].

Fig. 13
figure 13

Comparison of Hertzian contact stress according to extended approach of standard category B and loaded tooth contact analysis LTCA of standard category A. a G0—drive side. b G15—drive side. c G31.75—drive side. d G44—drive side

Full size image

All in all, the Hertzian stresses calculated by the extended approach of standard category B and the LTCA of standard category A are in good accordance. However, it can be seen that the geometry of the test gears can only be represented roughly, but sufficiently accurate, by use of a virtual cylindrical gear geometry. The extended calculation approach shows slightly higher stresses than the local calculation method for all considered examples. In summary, it can be stated that the assessment of the risk of pitting failure is conservative if the new extended approach of standard category B is used for the herein investigated test gear sets. For a more accurate consideration of the real flank geometry the described local calculation approach of standard category A should be used.

In Fig. 13 it is visible that the Hertzian contact stress according to the standard calculation method ISO 10300-2:2014 [12] is located at a significant lower level in comparison to the extended approach of standard category B and the LTCA. This lower level can be traced back to the consideration of the bevel gear factor ZK within calculation method of ISO 10300-2:2014 [12], which is not considered within other given calculation methods.

With Fig. 13 the given statement in Sect. 3.2.2, that the calculated Hertzian contact stress σH0 by use of the slip factor ZS is a better representation of the reality than by use of the bevel gear factor ZK, can be underlined. This can be seen in the better correlation of the calculated Hertzian contact stresses σH0 by use of the extended calculation method with the results of the LTCA.

5.3 Comparison of hypoid factor

In comparison with ISO 10300-2-2014 [12], the newly developed calculation method is based on a hypoid factor determined along the path of contact of the virtual cylindrical gear. In Fig. 14, the hypoid factor determined according to the new extended calculation approach of standard category B is compared with the hypoid factor determined using the local calculation method of standard category A. The dashed lines represent the values determined within local calculation method. The solid lines show the values calculated by use of the new extended approach.

Fig. 14
figure 14

Comparison of hypoid factor according to the new extended calculation approach of standard category B and local calculation method of standard category A. a G0—drive side. b G15—drive side. c G31.75—drive side. d G44—drive side

Full size image

The hypoid factor is ZHyp = 1.0 for bevel gears without hypoid offset. In case of hypoid gear sets, the trend of the increasing hypoid factor along the path of contact, calculated according to the extended calculation method, corresponds to the results of the local calculation method. However, with increasing hypoid offset the gradient of the curve of the hypoid factor differs slightly between the extended and local calculation method. In summary, it can be stated that with increasing hypoid offset, the velocity conditions are more difficult to map using the extended approach that does not consider the microgeometry. Nevertheless, the local hypoid factor can be calculated with sufficient accuracy by use of the extended approach.

5.4 Comparison of permissible contact stress

The permissible contact stress σHP,Y is a decisive influence factor within determination of the pitting load carrying capacity. Fig. 15 shows a comparison of the permissible contact stress calculated by use of the new extended calculation method of standard category B and local calculation method of standard category A. The dashed lines represent the results of the local calculation method and the solid lines the results of the extended calculation approach. Since the pinion and the wheel show different permissible contact stresses, the calculation results regarding the pinion are shown in black and regarding the wheel in grey. As a supplement to the given calculation results the permissible contact stress according to the standard calculation method ISO 10300-2:2014 [12] is given in following figures by dotted lines. The calculated values for the wheel are plotted in grey and for the pinion in black.

Fig. 15
figure 15

Comparison of permissible contact stress according to new extended calculation approach of standard category B and local calculation method of standard category A. a G0—drive side. b G15—drive side. c G31.75—drive side. d G44—drive side

Full size image

The application of the new extended calculation approach results in slightly lower permissible contact stresses, compared to the results of the local calculation method. Furthermore, the tendency to increase the permissible contact stress along the path of contact is well reflected by the extended calculation approach, especially for hypoid gears. This behavior can be explained by the local calculation of the hypoid factor, slip factor and the speed factor. However, the presented newly developed extended calculation approach aims at determining the pitting load carrying capacity in an early design stage of the gear set without using a complex tooth contact analysis. From this point of view, the shown accuracy is sufficient for a reliable prediction of pitting of bevel gears in an early design stage and is conservative.

Due to the consideration of the bevel slip factor ZS within calculation methods of the extended approach and the loaded tooth contact analysis (LTCA) the permissible contact stresses of these calculation methods lie mostly above the calculated contact stresses according to the standard calculation method ISO 10300-2:2014 [12].

5.5 Comparison of safety factor against pitting

Finally, the results of a comparison of the safety factors against pitting determined according to the new extended calculation approach of standard category B and the local calculation method of standard category A are shown in Fig. 16. The dashed lines represent the results of the local calculation method and the solid lines the results of the extended calculation approach. The calculation results regarding the pinion are shown in black and of the wheel in grey. Again, the calculated safety factors against pitting for the standard calculation method ISO 10300-2:2014 [12] is given in following figures by dotted lines. The calculated values for the wheel are plotted in grey and for the pinion in black.

Fig. 16
figure 16

Comparison of safety factor against pitting according to new extended calculation approach of standard category B and local calculation method of standard category A. a G0—drive side. b G15—drive side. c G31.75—drive side. d G44—drive side

Full size image

It can now be seen that the quoted differences between the Hertzian contact stresses and permissible contact stresses, based on the consideration of the bevel gear factor ZK or the bevel slip factor ZS, nearly compensate each other within calculation of safety factor against pitting. The extended calculation approach of standard category B determines slightly lower safety factors against pitting compared to the results of the local calculation method of standard category A for all considered examples and is therefore on the safe side. Thus, the newly developed calculation approach has the character of a standard-capable calculation method of standard category B, which should always guarantee safer evaluation due to lack of input information compared to the local calculation method. All in all, the newly developed calculation approach is able to assess the pitting load carrying capacity of bevel and hypoid gears in an accurate way for the considered gear designs.

6 Conclusion

In this paper a new extended calculation approach is shown, which offers the possibility to determine the pitting load carrying capacity of bevel and hypoid gears along the path of contact of the corresponding virtual cylindrical gear. Thus, in an early stage of gear design more information about the pitting load carrying capacity along the midsection of bevel and hypoid gears is generated compared to the current standard, which only enables the calculation of the pitting load carrying capacity at one decisive point on the tooth flank. Additionally, a consistent calculation approach is developed with regard to ISO/TS 10300-20:2021 [9] (scuffing), ISO/DTS 10300-4:2019 [10] (tooth flank fracture) and Hombauer [5] (micropitting). The new extended calculation method was successfully validated on basis of a theoretical study using local calculation results as a reference.

Further researches regarding the phenomenon, that the gear, despite an equal safety factor against pitting as for example given in Fig. 16, does not fail as often as the corresponding pinion were done by Reimann [1] at the Gear Research Center (FZG). Initial experimental investigations see an influence of the driven and drive part of the gear set. The consideration of this investigated influence in calculation methods regarding the load carrying capacity against pitting is content of further releases of the Gear Research Center (FZG).

7 Nomenclature

7.1 Parameters

The parameters are shown in Table 2.

Table 2 Parameters
Full size table

7.2 Indices

The indices are shown in Table 3.

Table 3 Indices
Full size table