1 Introduction

Until recently, the discipline of software engineering has mainly tackled the process through which humans develop software systems. In the last few years, current breakthroughs in the fields of artificial intelligence and machine learning have opened up new possibilities that have previously been considered infeasible or just too complex to tackle with “manual” coding: Complex image recognition [40], natural language processing [15] or decision making as it is used in complex games [38, 39] are prime examples. The resulting applications are pushing toward a broad audience of users. However, as of now, they are mostly focused on non-critical areas of use, at least when implemented without human supervision [2]. Software artifacts generated via machine learning are hard to analyze, causing a lack of trustworthiness for many important application areas [26, 42].

We claim that in order to reinstate levels of trustworthiness comparable to well-known classical approaches, we need not reproduce the principles of classical software tests but need to develop a new approach toward software testing. We suggest to develop a system and its test suite in a competitive setting where each sub-system tries to outwit the other. We call this approach scenario coevolution, which we introduce formally and build the bridge to a practical application where it has already shown benefit [24]. We hope that trust in such dynamics can help to build a new process for quality assurance, even for hardly predictable systems. In this work, we want to analyze thoroughly how such an antagonist approach fits into existing formal model for adaptivity, how it instantiates current frameworks for machine learning and what impact it might have on software engineering practices. We argue that antagonist patterns such as scenario coevolution can work as a unifying concept across all these domains and eventually enable more powerful adaptive quality assurance.

In this paper, we substantially expand the work on this topic presented in [23]. Section 2 provides a short overview on related work on process models for the development of adaptive software. Following a top-down approach, we start with the description of our approach in Sect. 3 by extending a formal framework for the description of systems first introduced in [28] and augment it to also include the process of software and system development. We use said framework to first present a formal definition of an example domain used in [24] in Sect. 4. Section 5 discusses state-of-the-art algorithms to achieve adaptation and introduces the machine learning pipeline, a process model specifically designed to engineer machine learning components. From this, we derive four core concepts for the engineering of adaptive systems in Sect. 6. In order to integrate these with our formal framework, Sect. 7 introduces our notion of scenarios and their application to an incremental software testing process. In Sect. 8, we apply this new notion to our example domain, formally explaining the results of [24]. In Sect. 9, we discuss which effects scenario coevolution has on a selection of practical software engineering tasks and how it helps implement the core concepts. Finally, Sect. 10 provides a brief conclusion.

2 Related work

Many researchers and practitioners in recent years have already been concerned about the changes necessary to allow for solid and reliable software engineering processes for (self-)adaptive systems. Central challenges were collected in [36], where issues of quality assurance are already mentioned but the focus is more on bringing about complex adaptive behavior in the first place. The later research roadmap of [17] puts a strong focus on interaction patterns of already adaptive systems (both between each other and with human developers) and already dedicates a section to verification and validation issues, being close in mind to the perspective of this work. We fall in line with the roadmap further specified in [7, 12, 13].

While this work largely builds upon [28], there have been other approaches to formalize the notion of adaptivity: [34] discusses high-level architectural patterns that form multiple interconnected adaptation loops. In [4], such feedback loops are based on the MAPE-K model [29]. While these approaches largely focus on the formal construction of adaptive systems, there have also been approaches that assume a (more human-centric or at least tool-centric) software engineering perspective [3, 19, 22, 45]. We want to discuss two of those on greater detail.

In the results of the ASCENS (Autonomous Service Component ENSembles) project [46], the interplay between human developers and autonomous adaptation has been formalized in a life cycle model featuring separate states for each the development progress of each respective feedback cycle. Classical software development tasks and self-adaptation (as well as self-monitoring and self-awareness) are regarded as equally powerful contributing mechanisms for the production of software. Both can be employed in junction to steer the development process. In addition, ASCENS built upon a (in parts) similar formal notion of adaptivity [11, 32] and sketched a connection between adaptivity in complex distributed systems and multi-goal multi-agent learning [27].

ADELFE (Atelier de Développement de Logiciels à Fonctionnalité Emergente) is a toolkit designed to augment current development processes to account for complex adaptive systems [8, 9]. For this purpose, the ADELFE process is based on the Rational Unified Process (RUP) [31] and comes with tools for various tasks of software design. From a more scientific point of view, ADELFE is also based on the theory of adaptive multi-agent systems. For ADELFE, multi-agent systems are used to derive a set of stereotypes for components, which ease modeling for according types of systems. It thus imposes stronger restrictions on system design than our approach intends to.

Besides the field of software engineering, the field of artificial intelligence research is currently (re-)discovering a lot of the same issues the discipline of engineering for complex adaptive systems faced: The highly complex and opaque nature of machine learning algorithms and the resulting data structures often forces black-box testing and makes possible guarantees weak. When online learning is employed, the algorithm’s behavior is subject to great variance and testing usually needs to work online as well. The seminal paper [2] provides a good overview of the issues. When applying artificial intelligence to a large variety of products, rigorous engineering for this kind of software seems to be one of the major necessities lacking at the moment.

3 Formal framework

In this section, we introduce a formal framework as a basis for our analysis. We first build upon the framework described in [28] to define adaptive systems and then proceed to reason about the influence of their inherent structure on software architecture. In the last subsection, we introduce an example system and realize the formal definitions in its context.

3.1 Describing adaptive systems

We roughly adopt the formal definitions of our vocabulary related to the description of systems from [28]: We describe a system as an arbitrary relation over any given set of variables.

Definition 1

(System [28]) Let I be a (finite or infinite) set, and let \({\mathcal {V}} = (V_i)_{i \in I}\) be a family of sets. A system of type \({\mathcal {V}}\) is a relation S of type \({\mathcal {V}}\).

Note that from a formal point of view, this means that basically any given relation or function can be regarded as a system, so this is a rather weak definition logically and we should think of it rather as a tag attached to those entities that can be meaningfully regarded as systems rather than a formal restriction derivation of the notion. Also note that while maintaining logical consistency, we deviate a bit from the wording used in [28]: There, the same definition is used also for ensembles, a notion we forgo in favor of the word “system” and components, which in our case a defined later to be only systems which participate in composition (cf. Definition 2).

Given a system S, an element \(s \in S\) is called the state of the system. For practical purposes, we usually want to discern various parts of a system’s state space. For this reason, parts of the system relation of type \({\mathcal {V}}\) given by an index set \(J \subseteq I\), i.e., \((V_j)_{j \in J}\), may be considered inputs and other parts given by a different index set may be considered outputs [28]. Formally, this makes no difference to the system. Semantically, we usually compute the output parts of the system using the input parts.

We introduce two more designated sub-spaces of the system relation: situation and behavior. These notions correspond roughly to the intended meaning of inputs and outputs mentioned before. The situation is the part of the system state space that fully encapsulates all information the system has about its state. This may include parts that the system does have full control over. The behavior encapsulates the parts of the system that can only be computed by applying the system relation. Likewise, this does not imply that the system has full control over the values. Furthermore, a system may have an internal state, which is parts of the state space that are neither included in the situation nor in the behavior. When we are not interested in the internal space, we can regard a system as a mapping from situations to behavior, written \(S = X {\mathop {\leadsto }\limits ^{Z}} Y\) for situations X and behaviors Y, where Z is the internal state of the system S. Using these notions, we can more aptly define some properties on systems.

Further following the line of thought presented in [28], we want to build systems out of other systems. At the core of software engineering, there is the principle of reuse of components, which we want to mirror in our formalism.

Definition 2

(Composition) Let \(S_1\) and \(S_2\) be systems of types \({\mathcal {V}}_1 = (V_{1,i})_{i \in I_1}\) and \({\mathcal {V}}_2 = (V_{2,i})_{i \in I_2}\), respectively. Let \({\mathcal {R}}({\mathcal {V}})\) be the domain of all relations over \({\mathcal {V}}\). A combination operator\(\otimes \) is a function such that \(S_1 \otimes S_2 \in {\mathcal {R}}({\mathcal {V}})\) for some family of sets \({\mathcal {V}}\) with \(V_{1,1}, \ldots , V_{1,m}, V_{2,1}, \ldots , V_{2,n} \in {\mathcal {V}}\). The application of a combination operator is called composition. The arguments to a combination operator are called components.

In [28], there is a more strict definition on how the combination operator needs to handle the designated inputs and outputs of its given systems. Here, we opt for a more general definition. Note that in accordance with [28], however, our composition operator is “arbitrarily powerful” in the sense that the resulting system just needs to contain the components in some way but may add an arbitrary amount of new parts and functionality that is present in neither of the components. The reason it is still meaningful to talk about “composition” in this case is that the combination operator guarantees that we can at least project system states of the original types \({\mathcal {V}}_2\) and \({\mathcal {V}}_2\) out of it.

Composition is not only important to model software architecture within our formalism, but it also defines the formal framework for interaction: Two systems interact when they are combined using a combination operator \(\otimes \) that ensures that the behavior of (at least) one system is recognized within the situation of (at least) one other system.

Definition 3

(Interaction) Let \(S = S_1 \otimes S_2\) be a composition of type \({\mathcal {V}}\) of systems \(S_1\) and \(S_2\) of type \({\mathcal {V}}_1\) and \({\mathcal {V}}_2\), respectively, using a combination operator \(\otimes \). If there exist a \(V_1 \in {\mathcal {V}}_1\) and a \(V_2 \in {\mathcal {V}}_2\) and a relation \(R \in V_1 \times V_2\) so that for all states \(s \in S\), \((\textit{proj}(s, V_1), \textit{proj}(s, V_2)) \in R\), then the components \(S_1\) and \(S_2\) interact with respect to R.

Note that (given a state s of system S of type V and a different type \(V'\) with \(V' \subseteq V\)) we use the notation \(\textit{proj}(s, V')\) for the projection of s into the type \(V'\), i.e., we cast system state s to a system state for a system of type \(V'\) by dropping all dimensions that are not part of \(V'\).

We can model an open system S as a combination \(S = C \otimes E\) of a core system C and its environment E, both being modeled as systems again.

Hiding some of the complexity described in [28], we assume we have a logic \({\mathfrak {L}}\) in which we can express a system goal \(\gamma \). For example, if \({\mathfrak {L}}\) is zeroth-order logic, \(\gamma \) could be made up as a Boolean expression on binary system state observation, or if \({\mathfrak {L}}\) is first-order logic, \(\gamma \) could be a predicate that is given the system s as a parameter. We assume that we can always decide if \(\gamma \) holds for a given system, in which case we write \(S \models \gamma \). Based on [28], we can use this concept to define an adaptation domain:

Definition 4

(Adaptation Domain [28]) Let S be a system. Let \({\mathcal {E}}\) be a set of environments that can be combined with S using a combination operator \(\otimes \). Let \(\varGamma \) be a set of goals. An adaptation domain\({\mathcal {A}}\) is a set \({\mathcal {A}} \subseteq {\mathcal {E}} \times \varGamma \). S can adapt to \({\mathcal {A}}\), written \(S \Vdash {\mathcal {A}}\) iff for all \((E, \gamma ) \in {\mathcal {A}}\) it holds that \(S \otimes E \models \gamma \).

Definition 5

(Adaptation Space [28]) Let \({\mathcal {E}}\) be a set of environments that can be combined with S using a combination operator \(\otimes \). Let \(\varGamma \) be set of goals. An adaptation space\({\mathfrak {A}}\) is a set \({\mathfrak {A}} \subseteq {\mathfrak {P}}({\mathcal {E}}, \varGamma )\).

Note that we thus define an adaptation space to be any set of adaptation domains. We can now use the notion of an adaptation space to define a preorder on the adaptivity of any two systems.

Definition 6

(Adaptation [28]) Given two systems S and \(S'\), \(S'\) is at least as adaptive as S, written \(S \sqsubseteq S'\) iff for all adaptation spaces \({\mathcal {A}} \in {\mathfrak {A}}\) it holds that \(S \Vdash {\mathcal {A}} \Longrightarrow S' \Vdash {\mathcal {A}}\).

Both Definitions 4 and 5 can be augmented to include soft constraints or optimization goals. This means that in addition to checking against Boolean goal satisfaction, we can also assign each system S interacting with an environment E a fitness\(\phi (S \otimes E) \in F\), where F is the type of fitness values. We assume that there exists a preorder \(\preceq \) on F, which we can use to compare two fitness values. We can then generalize Definitions 4 and 5 to respect these optimization goals.

Definition 7

(Adaptation Domain for Optimization) Let S be a system. Let \({\mathcal {E}}\) be a set of environments that can be combined with S using a combination operator \(\otimes \). Let \(\varGamma \) be a set of Boolean goals. Let F be a set of fitness values and \(\preceq \) be a preorder on F. Let \(\varPhi \) be a set of fitness functions with codomain F. An adaptation domain\({\mathcal {A}}\) is a set \({\mathcal {A}} \subseteq {\mathcal {E}} \times \varGamma \times \varPhi \). S can adapt to \({\mathcal {A}}\), written \(S \Vdash {\mathcal {A}}\) iff for all \((E, \gamma , \phi ) \in {\mathcal {A}}\) it holds that \(S \otimes E \models \gamma \).

Note that in Definition 7, we only augmented the data structure for adaptation domains but did not actually alter the condition to check for the fulfillment of an adaptation domain. This means that for an adaptation domain \({\mathcal {A}}\), a system needs to fulfill all goals in \({\mathcal {A}}\) but is not actually tested on the fitness defined by \(\phi \). We could define a fitness threshold f we require a system S to surpass in order to adapt to \({\mathcal {A}}\) in the formalism. But such a check, written \(f \preceq \phi (S \otimes E)\), could already be included in the Boolean goals if we use a logic that is expressive enough.

Instead, we want to use the fitness function as soft constraints. We expect the system to perform as well as possible on this metric, but we do not (always) require a minimum level of performance. However, we can use fitness to define a fitness preorder on systems.

Definition 8

(Optimization) Given two systems S and \(S'\) as well as an adaptation space \({\mathcal {A}}\), \(S'\) is at least as optimal as S, written \(S \preceq _{\mathcal {A}} S'\), iff for all \((E, \gamma , \phi ) \in {\mathcal {A}}\) it holds that \(\phi (S \otimes E) \preceq \phi (S' \otimes E)\).

Definition 9

(Adaptation with Optimization) Given two systems S and \(S'\), \(S'\) is at least as adaptive as S with respect to optimization, written \(S \sqsubseteq ^* S'\) iff for all adaptation domains \({\mathcal {A}} \in {\mathfrak {A}}\) it holds that \(S \Vdash {\mathcal {A}} \Longrightarrow S' \Vdash {\mathcal {A}}\) and \(S \preceq _{\mathcal {A}} S'\).

In Fig. 1, we introduce a visual representation of systems and the relation of adaptivity given in Definition 9. Note that so far our notions of adaptivity and optimization are purely extensional, which originates from the black-box perspective on adaptation assumed in [28].

Fig. 1
figure 1

Illustration of adaptivity according to Definition 9. When the x-axis spans over all possible situations and the y-axis over all possible behaviors, a system like \(S_1 = X_1 \leadsto Y_1\) (orange) or \(S_2 = X_2 \leadsto Y_2\) (red) can be drawn as an area of all the behaviors of \(S_1\) or \(S_2\) so that \(S_1 \models \gamma \) or \(S_2 \models \gamma \), respectively. For each situation, we show the ideal behavior subject to the fitness \(\phi \) via the dashed black line. \(S_1\) is at least as adaptive as \(S_2\) because it covers at least as many situations as \(S_1\) and performs as least as close to the optimal fitness as \(S_2\) (colour figure online)

Full size image

3.2 Constructing adaptive systems

We now shift the focus of our analysis a bit away from the question “When is a system adaptive?” toward the question “How is a system adaptive?”. This refers to both questions of software architecture (i.e., which components should we use to build an adaptive system?) and questions of software engineering (i.e., which development processes should we use to develop an adaptive system?). We will see that with the increasing usage of methods of machine learning, design-time engineering and run-time adaptation increasingly overlap [46].

Definition 10

(Adaptation Sequence) A series of |I| systems \({\mathcal {S}} = (S_i)_{i\in I}\) with index set I with a preorder \(\le \) on the elements of I is called an adaptation sequence iff for all \(i, j \in I\) it holds that \(i \le j \Longrightarrow S_i \sqsubseteq ^* S_j\)

Note that we used adaptation with optimization in Definition 10 so that a sequence of systems \((S_i)_{i\in I}\) that each fulfill the same hard constraints (\(\gamma \) within a singleton adaptation space \({\mathfrak {A}} = \{\{(E, \gamma , \phi )\}\}\)) can form an adaptation sequence iff for all \(i, j \in I\) it holds that \(i \le j \Longrightarrow \phi (S_i \otimes E) \preceq \phi (S_j \otimes E)\). This is the purest formulation of an optimization process within our formal framework. Strictly speaking, an optimization process would further assume there exists an optimization relation o from systems to systems so that for all \(i, j \in I\) it holds that \(i \le j \Longrightarrow o(S_i, S_j)\). But for simplicity, we consider the sequence of outputs of the optimization process a sufficient representation of the whole process.

Such an adaptation sequence can be generated by continuously improving a starting system \(S_0\) and adding each improvement to the sequence. Such a task can both be performed by a team of human developers or standard optimization algorithms as they are used in artificial intelligence. Only in the latter case, we want to consider that improvement happening within our system boundaries. Unlike the previously performed black-box analysis of systems, the presence of an optimization algorithm within the system itself does have implications for the system’s internal structure. We will thus switch to a more “gray box” analysis in the spirit of [11].

Definition 11

(Self-Adaptation) A system \(S_0\) is called self-adaptive iff the sequence \((S_i)_{i \in {\mathbb {N}}, i < n}\) for some \(n \in {\mathbb {N}}\) with \(S_i = S_0 \otimes S_{i-1}\) for \(0< i < n\) and some combination operator \(\otimes \) is an adaptation sequence.

Please note that we use the term “adaptation” here to mean the improvement in adaptivity as defined in [28]. This is different from some notions of adaptation which allow for a reduction in adaptivity during adaptation as well [1, 10]. In our case of adaptation, we can imagine that the system is always able to go back to previous configuration, thus every adaptation only adds to its overall capabilities. To some extent, this already anticipates the perspective of eternal systems which is discussed later in Sect. 9.3 [33].

Note that we could define the property of self-adaptation more generally by again constructing an index set on the sequence \((S_i)\) instead of using \({\mathbb {N}}\), but chose not to do so to not further clutter the notation. For most practical purposes, adaptation is going to happen in discrete time steps anyway. It is also important to be reminded that despite its notation, the combination operator \(\otimes \) does not need to be symmetric and likely will not be in this case, because when constructing \(S_0 \otimes S_{i-1}\), we usually want to pass the previous instance \(S_{i-1}\) to the general optimization algorithm encoded in \(S_0\). Furthermore, it is important to note that the constant sequence \((S)_{i \in {\mathbb {N}}}\) is an adaptation sequence according to our previous definition and thus every system is self-adaptive with respect to a combination operator \(X \otimes Y =_\text {def} X\). However, we can construct non-trivial adaptation sequences using partial orders \(\sqsubset \) and \(\prec \) instead of \(\sqsubseteq \) and \(\preceq \). As these can easily be constructed, we do not further discuss their definitions in this paper. In [28], a corresponding definition was already introduced for \(\sqsubset \).

The formulation of the adaptation sequence used to prove self-adaptivity naturally implies some kind of temporal structure. So basing said structure around \({\mathbb {N}}\) implies a very simple, linear and discrete model of time. More complex temporal evolution of systems is also already touched upon in [28]. As noted, there may be several ways to define such a temporal structure on systems. We refer to related and future work for a more intricate discussion on this matter.

So, non-trivial self-adaptation does imply some structure for any self-adaptive system S of type \({\mathcal {V}} = (V_i)_{i \in I}\): Mainly, there needs to be a subset of the type \({\mathcal {V}}' \subseteq {\mathcal {V}}\) that is used to encode the whole relation behind S so that the already improved instances can sufficiently be passed on to the general adaptation mechanism.

For a general adaptation mechanism (which we previously assumed to be part of a system) to be able to improve a system’s adaptivity, it needs to be able to access some representation of its goals and its fitness function. This provides a gray-box view of the system. Remember that we assumed a system S could be split into situation X, internal state Z and behavior Y, written \(S = X {\mathop {\leadsto }\limits ^{Z}} Y\). If S is self-adaptive, it can form a non-trivial adaptation sequence by improving on its goals or its fitness. In the former case, we can now assume (that there exists some relation \(G \subseteq X \cup Z\) so that \(S \models \gamma \iff G \models \gamma \) for a fixed \(\gamma \) in a singleton-space adaptation sequence. In the latter case, we can assume that there exists some relation \(F \subseteq X \cup Z\) so that \(\phi (S) = \phi (F)\) for a fixed \(\phi \) in a singleton-space adaptation sequence. Effectively, if we employ a general mechanism for self-adaptation, as it is commonly done in current applications of machine learning, it is necessary that the result of the adaptation is passed back into the system.

Obviously, when we want to construct larger self-adaptive systems using self-adaptive components, the combination operator needs to be able to combine said sub-systems G and/or F as well. In the case where the components’ goals and fitnesses match completely, the combination operator can just use the same sub-system twice. However, including the global goals or fitnesses within each local component of a system does not align with common principles in software architecture (such as encapsulation) and does not seem to be practical for large or open systems (where no process may ensure such a unification). Thus, constructing a component-based self-adaptive system requires a combination operator that can handle potentially conflicting goals and fitnesses. We again define such a system for a singleton adaptation space \({\mathfrak {A}} = \{\{(E, \gamma , \phi )\}\}\) and leave the generalization to all adaptation spaces out of the scope of this paper.

Definition 12

(Multi-Agent System) Given a system \(S = S_1 \otimes \cdots \otimes S_n\) that adapts to \({\mathcal {A}} = \{(E, \gamma , \phi )\}\). Iff for each \(1 \le i \le n\) with \(i, n \in {\mathbb {N}}, n > 1\) there is an adaptation domain \({\mathcal {A}}_i = \{(E_i, \gamma _i, \phi _i)\}\) so that (1) \(E_i = E \otimes S_1 \otimes \cdots \otimes S_{i-1} \otimes S_{i+1} \otimes \cdots \otimes S_n\) and (2) \(\gamma _i \ne \gamma \) or \(\phi _i \ne \phi \) and (3) \(S_i\) adapts to \({\mathcal {A}}_i\), then S is a multi-agent system with agents \(S_1, \ldots , S_n\).

It is important to note here that the combination operator \(\otimes \) may again be arbitrarily complex and does not need to work the same way for the construction of S and the construction of \(E_i\) above. The definition of a multi-agent system only requires the decomposability of the respective systems with respect to some \(\otimes \). Obviously, the notion then varies in expressiveness and explanatory power depending on the choice of \(\otimes \).

Fig. 2
figure 2

Illustration of the emergence of an (implicit) multi-agent system in a fictitious architecture of software components. Adaptive components interact by manipulating their environment to achieve their individual goals

Full size image

For practical purposes, we usually want to use the notion of multi-agent systems in a transitive way, i.e., we can call a system a multi-agent system as soon as any part of it is a multi-agent system according to Definition 12. Formally, S is a multi-agent system if there are systems components \(S', R\) so that \(S = S' \otimes R\) and \(S'\) is a multi-agent system. We argue that this transitivity is not only justified but a crucial point for systems development of adaptive systems: Agents tend to utilize their environment to fulfill their own goals and can thus “leak” their goals into other system components (see Fig. 2). Note that Condition (2) of Definition 12 ensures that not every system constructed by composition is regarded a multi-agent system; it is necessary to feature agents with (at least slightly) differing adaptation properties.

For the remainder of this paper, we will apply Definition 12 “backwards.” Whenever we look at a self-adaptive system S, whose goals or fitnesses can be split into several sub-goals or sub-fitnesses, we can regard S as a multi-agent system. Using this knowledge, we can apply design patterns from multi-agent systems to all self-adaptive systems without loss of generality. Furthermore, we need to be aware that especially if we do not explicitly design multi-agent coordination between different sub-goals, such a coordination will be done implicitly. Essentially, there is no way around generalizing software engineering approaches for self-adaptive systems to potentially adversarial components.

4 Example domain

To illustrate the definitions of the previous section, we introduce an example system called Grid World Smart Factory, which has also been used and implemented in [24]. However, we first introduce a formal definition of a system for this domain.

4.1 Setup

An instance of the smart factory domain contains a number of items that have to be processed at workstations of different types, while avoiding collisions with dynamically placed obstacles. The system is tasked with navigating a robotic agent through the smart factory in order to eventually process all the items.

Fig. 3
figure 3

Visualization of the smart factory domain. A mobile robot can travel north, east, south and west on the grid. It needs to visit workstations in order to retrieve items and then needs to visit other workstations in order to process these items. Attempting to walk out of the grid, into a workstation or into an obstacle is penalized. Obstacle positions vary according to the setting of the scenario x

Full size image

In our example, the smart factory uses a discrete grid of size \(7 \times 8\), as shown in Fig. 3. Thus, possible positions for entities of any kind within the factory are all \(p \in P\), where \(P = \{1, \ldots , 7\} \times \{1, \ldots , 8\}\).

Five workstations \(W \subset P\) are placed at fixed positions so that \(W = \{w_1, \ldots , w_5\} = \{(1, 5),(4, 7),(5, 1),(6, 3),(6, 7)\}\). Each workstation w is assigned a fixed type \(t(w), \; t: W \rightarrow \{\textit{red}, \textit{green}, \textit{blue}\}\), so that \(t(w_1) = \textit{blue},t(w_2) = \textit{red},t(w_3) = \textit{red},t(w_4) = \textit{green},t(w_5) = \textit{green}\).

The domain is parametric on the position of four obstacles \(O = \{o_1, o_2, o_3, o_4\} \subset P\) so that \(O \cap W = \emptyset \).

A robotic agent r is given via its current position \(r \in P\). Note that the starting position of the robot always is \(r = (1,1)\). The robotic agent is able to execute four movement actions \(v \in V = \{v_\triangle , v_\rhd , v_\bigtriangledown , v_\lhd \},\;v: P \rightarrow P\), where for all \(\circ \in \{\triangle , \rhd , \bigtriangledown , \lhd \}\), we define

$$\begin{aligned} v_\circ (y, x) = {\left\{ \begin{array}{ll} v'_\circ (y, x) &{} \textit{ if } v'_\circ (y, x) \in P \setminus (W \cup O)\\ (y, x) &{}\textit{ otherwise}\end{array}\right. } \end{aligned}$$
(1)

where all \(v'_\circ \) are naturally defined as \(v'_\triangle (y, x) = (y-1, x),\;v'_\rhd (y, x) = (y, x+1),\;v'_\bigtriangledown (y, x) = (y+1, x),\;v'_\lhd (y, x) = (y, x-1)\). Note that any action that returns using the \(\textit{otherwise}\) branch in Eq. 1 is called illegal. Any action that is not illegal is called legal. It follows that when the agent position r is only altered via the application of actions, it always holds that \(\{r\}\), O, and W are fully disjunct.

Given a position \(p \in P\), we define the neighborhood of p as \(N : P \rightarrow {\mathfrak {P}}(P)\) with

$$\begin{aligned} N(y,x) = \{v_\circ (y,x) \; : \; \circ \in \{\triangle , \rhd , \bigtriangledown , \lhd \}\}.\end{aligned}$$
(2)

Since all actions are reversible, N(y, x) both contains all position that can be reached from (y, x) and all position that (y, x) can be reached from.

We call an instance of the smart factory domain valid iff the agent can reach new positions from its initial position and all workstations can be reached, i.e.,

$$\begin{aligned} \forall e \in \{r\} \cup W : N(e) \ne \emptyset .\end{aligned}$$
(3)

Note that this simple test suffices since we only have four obstacles and no two workstations are next to each other, so the only way to make any of them inaccessible is to place all four obstacles around it.

We define an item as a tuple m containing a current position and a series of workstation types, i.e., \(m = (p, \langle t_i \rangle _{i \in I})\) where \(p \in P\) and I is an index set and for all \(i \in I\) it holds that \(t_i \in \{\textit{red}, \textit{green}, \textit{blue}\}\). Semantically, an item needs to visit workstations of all the given types \(t_i\) in the given order in order to be fully processed. As long it is not fully processed, it poses a task to the system. Our system is tasked to produce five items \(M = \{m_1, \ldots , m_5\}\). When all of these are fully produced, the domain instance is finished successfully. Note that initially, items are placed at workstations. We thus define the current position of an item m as c(m) with \(c : M \rightarrow P\). Furthermore, up to one item can be carried by the mobile agent so that \(c(m) = r\). Note that it always holds for all \(m \in M\) that \(c(m) \in \{r\} \cup W\), i.e., no items can be left on the factory floor. We also define the function \(b: W \rightarrow \langle M \rangle \), which is given a workstation and returns a sequence of items so that for all workstations \(w \in W\) and all items \(m \in b(w)\) it holds that \(c(m) = w\). The first item of that sequence is the one that can be picked up next at the respective workstation.

In our setup, we use the items

$$\begin{aligned} m_1= & {} ((1, 5), \langle \textit{green}, \textit{red} \rangle ),\\ m_2= & {} ((1, 5), \langle \textit{green} \rangle ),\\ m_3= & {} ((4, 7), \langle \textit{red}, \textit{blue}, \textit{green} \rangle ),\\ m_4= & {} ((1, 5), \langle \textit{green}, \textit{blue} \rangle ),\\ m_5= & {} ((6,3), \langle \textit{red} \rangle ). \end{aligned}$$

Of course, we now need to augment our previously defined set of movement actions \(V = \{v_\triangle , v_\rhd , v_\bigtriangledown , v_\lhd \}\) to allow for interaction with items. We thus define the set of actions \(A = \{a_\triangle , a_\rhd , a_\bigtriangledown , a_\lhd , a_\boxplus , a_\boxminus \}\) so that for all \(\circ \in \{\triangle , \rhd , \bigtriangledown , \lhd , \boxplus , \boxminus \}\) and \(a_\circ : P \times {\mathfrak {P}}(P \times \langle T \rangle ) \rightarrow P \times {\mathfrak {P}}(P \times \langle T \rangle )\) it holds that

$$\begin{aligned}&a_\circ (r, M) = \nonumber \\&\quad {\left\{ \begin{array}{ll} (v'_\circ (r), M) &{} \textit{ if } \circ \in \{\triangle , \rhd , \bigtriangledown , \lhd , \}\\ &{} \textit{ and } a'_\circ (r) \in P \setminus (W \cup O)\\ (r, \{m'_\boxplus \} \cup M \setminus m) &{} \textit{ if } \circ = \boxplus \\ &{} \textit{ and } c(m) \in N(r)\\ &{} \textit{ and } \forall \hat{m} \in M : c(\hat{m}) \ne r\\ (r, \{m'_\boxminus \} \cup M \setminus m) &{} \textit{ if } \circ = \boxminus \\ &{} \textit{ and } c(m) = r\\ &{} \textit{ and }t(w) = t_1\\ (r, M) &{} \textit{ otherwise } \end{array}\right. } \end{aligned}$$
(4)

where \(m = (p, \langle t_1, \ldots , t_n \rangle )\) is any element from M, w is any element from \(W \cap N(r)\) and subsequently \(m'_\boxplus = (r, \langle t_1, \ldots , t_n \rangle )\) and \(m'_\boxminus = (w, \langle t_2, \ldots , t_n \rangle )\). We implicitly quantify existentially over all \(m \in M\). The function \(a_\circ \) still remains deterministic only because the conditions are formulated so that at most one \(m \in M\) fits them in our setup. In the more general setup, it would be valid to pick any arbitrary option. For \(w \in W \cap N(r)\), again, we implicitly quantify, although it only matters in the third case. Again, this quantification can yield at most one element as no two workstations of the same type have shared neighboring positions in our setup. For the more general case, we can simply pick a w at random should multiple assignments validate this condition here. Finally, note that when an item is fully processed, we assume \(m'_\boxminus = (w, \langle \rangle )\) for some position \(w \in P\), i.e., we keep all the processed items “lying around” with an empty task list. We could also choose to remove fully processed items entirely from the system by specifying \(a_\circ (r, M) = (r, M \setminus m)\) in that case. Since we used the power set \({\mathfrak {P}}(T \times \langle T \rangle )\) or the type of \(a_\circ \), we are flexible in that choice. For ease of definition, we will later fix the amount of items present in the adaptive system, favoring the “lying around” approach.

Again, every action that results from taking the \(\textit{otherwise}\) branch of \(a_\circ \) is called illegal. The action \(a_\boxplus \) is called pick-up and the action \(a_\boxminus \) is called drop-off.

4.2 Adaptive system

Having defined the complete setup of our smart factory domain, we can now proceed to define the adaptation domain.

We define the system \(S = X {\mathop {\leadsto }\limits ^{Z}} Y\) where X is a list of elements \(\langle x_t \rangle _{0< t < n}\) with the maximum execution length \(n \in {\mathbb {N}}\) (and likewise for Y). Note that without loss of generality, we can assume that all execution traces are of the same length n by simply setting n to the maximum length and filling up shorter paths with “nil” elements. We set

$$\begin{aligned} x = \langle r_t, M_t, O_t \rangle \end{aligned}$$
(5)

with robot position \(r_t \in P\), item list \(M_t \in (P \times \langle T \rangle )^5\) and obstacles \(O_t \in P^4\). Note that we specify a fixed amount of 5 items that may thus be present in the system. We also specify

$$\begin{aligned} y_t = \langle a_t \rangle \end{aligned}$$
(6)

with action \(a_t \in \{a_\triangle , a_\rhd , a_\bigtriangledown , a_\lhd , a_\boxplus , a_\boxminus \}\). The legal elements for X and Y are defined by the type of the system’s policy \(\varPi : (P \times (P \times \langle T \rangle )^5 \times P^4)^n \rightarrow \{a_\triangle , a_\rhd , a_\bigtriangledown , a_\lhd , a_\boxplus , a_\boxminus \}^n\) where \(n \in {\mathbb {N}}\) is the maximum execution time of the system so that

$$\begin{aligned} Y = \langle \varPi (X) \rangle .\end{aligned}$$
(7)

We omit any further specification on the policy \(\pi \) at hand (and accordingly for the internal state Z) as the policy is the core of the system’s implementation, which we discuss in more detail in Sects. 5 and 8 .

However, we can use the given definition of the system’s interface to specify its adaptation domain. We define a static environment E, which means that once a system \(S \otimes E\) is composed, the environment does not change or react to the system’s actions. In our example, the environment consists of the obstacles’ position, so

$$\begin{aligned} E = \{o_1, o_2, o_3, o_4\} \end{aligned}$$
(8)

with \(o_i \in P\) for all \(i = 1, .., 4\). Note that we could also write \(E = \emptyset \leadsto \langle \{o_1, o_2, o_3, o_4\} \rangle _{0<t<n}\) to adhere to the previously introduced notation. We then define the composed system \(S \otimes E\) to use the obstacles given by E to set all respective inputs X so that for all \(x_t\) in \(X = \langle x_t \rangle _{0< t < n}\) it holds that \(x_t = \langle r_t, M_t, \{o_1, o_2, o_3, o_4\}\rangle \) for some \(r_t, M_t\).

At this stage, we might just as well-define a dynamic environment that could change the obstacles’ positions over time by setting \(E = \emptyset \leadsto \langle \{o_{1,t}, o_{2,t}, o_{3,t}, o_{4,t}\}\rangle _{1<t<n}\) with \(o_{i,t}\) depending on the current step of system execution t. A reactive environment \(E = \langle r \rangle _{1<t<n} \leadsto \langle \{o_{1,t}, o_{2,t}, o_{3,t}, o_{4,t}\}\rangle _{1<t<n}\) might even change any obstacle’s position \(o_{i,t}\), for example with respect to the robot position r according to some environment policy \(\rho : P \times {\mathbb {N}} \rightarrow P\) so that \(o_{i,t} = \rho (r_t, i)\). However, we will omit further considerations on dynamic environments for brevity and will resort to a static environment for the running example in this paper.

However, please note that we can still generate many different static environments to be part of the adaptation domain. This will require the system to be able to handle various configurations of non-moving obstacles but not require the system to be able to handle moving obstacles.

We can now define a simple system goal such as

$$\begin{aligned} \gamma (S) \iff \exists t \; : \; \forall m \in M_t \; : \textit{finished}(m) \end{aligned}$$
(9)

where \(M_t\) is given via \(x_t = \langle r_t, M_t, O_t \rangle \) (coming from \(S = X \leadsto Y\) and \(X = \langle x_t \rangle _{0<t<n}\)) as in Eq. 5 and \(\textit{finished} : P \times \langle T \rangle \rightarrow {\mathbb {B}}\) is given via

$$\begin{aligned} \textit{finished}(\textit{pos}, \textit{tasks}) \iff \textit{tasks} = \langle \rangle . \end{aligned}$$
(10)

Semantically, \(\gamma (S)\) holds iff at some point during the execution, all items in the system have been processed. Note that we use a very raw formulation for a property that might be more fittingly expressed in some temporal logic. But using simple predicate logic is sufficient for the present running example. A different goal function might be to never execute an illegal action, which might be written as \(\gamma '(S) \iff \forall t \; : \; \lnot \textit{illegal}(a_t)\). For the running example, we will focus on the single goal function \(\gamma \), though.

The definitions made in this subsection now allow us to finally define an adaptation domain such as \({\mathcal {A}} = \{(((2,5), (4,4), (5,5), (6,5)), \gamma )\}\), which defines the environment setup shown in Fig. 3 and the goal function of Eq. 10. For our running example, we want the system to work for any arbitrary (legal) configuration of obstacle position so that we define

$$\begin{aligned} {\mathcal {A}} = \{((o_1, o_2, o_3, o_4), \gamma ) \;&: \; i = 1, \ldots , 4, \nonumber \\&\quad o_i \in P \setminus W \setminus \{(1,1)\}\}. \end{aligned}$$
(11)

We can now further augment this declaration to include an optimization target (as given in Definitions 7 and 8). Using \({\mathbb {N}}\) as the space of the fitness values and \(\ge \) as a preorder (meaning that me minimize the fitness value) we can define a fitness function

$$\begin{aligned} \phi (S \otimes E) = \min \; \{t \in {\mathbb {N}} \; | \; \; \forall m \in M_t \; : \;\textit{finished}(m)\} \end{aligned}$$
(12)

where \(M_t\) is given via \(x_t = \langle r_t, M_t, O_t \rangle \) (coming from \(S = X \leadsto Y\) and \(X = \langle x_t \rangle _{0<t<n}\)) as in Eq. 5 and \(\textit{finished} : P \times \langle T \rangle \rightarrow {\mathbb {B}}\) is given via Eq. 10. The fitness function \(\phi \) as defined in Eq. 12 then returns the amount of time steps the system took to reach the \(\textit{finished}\) predicate, i.e., the time it took to fully process all items. This would be a typical target for minimization. Note that in this case, there exists a clear correspondence between the goal function \(\gamma \) and the fitness function \(\phi \) as only systems that fulfill \(\gamma \) have a finite value for \(\phi \).

Different reasonable fitness functions exist: For example, we may want to get rid of the goal function entirely and instead formulate a fitness function that maximizes the amount of that are fully processed (instead if enforcing that all of them are eventually fully processed always). Or we may want to optimize an entirely different goal like minimizing the turns of direction the agent is taking.

In the end, setting the right \(\gamma \) and \(\phi \) for the adaptation domain is a decision to be made in system design and is crucial to fulfilling the initial requirements. In particular, the interaction between the goal and the fitness function is to be considered.

Having given an adaptation domain, we can write \(S \Vdash {\mathcal {A}}\) iff the system S can adapt to \({\mathcal {A}}\), i.e., S fulfills the goal function for all respective environments in \({\mathcal {A}}\). We can also trivially define a singleton adaptation space

$$\begin{aligned} {\mathfrak {A}} = \{{\mathcal {A}}\}, \end{aligned}$$
(13)

which shall suffice for the example given here.

5 Implementation of adaptation

So far we constructed a framework to compare the degree of adaptivity of two given systems. In this section, we discuss how to give these adaptive systems. This boils down to the problem: Given a system S, how can its adaptivity be improved, i.e., how can we generate a system \(S'\) so that \(S \sqsubseteq S'\). The art of generating (software) systems is called (software) engineering. Traditionally, we would specify higher adaptivity as a requirement and task a group of software developers to improve the system S. They would then write code to cover additional adaptation domains (within the given adaptation space) or improve the system’s performance on a given fitness function (when considering optimization) as follows from Definition 9.

5.1 Adaptation via machine learning

Newer methods in software engineering aim to automate (parts of) that process [7, 12, 46]. The most trivial means of automation is probably stochastic search. For this, we require a variation operator \(\textit{vary}: {\mathcal {R}}({\mathcal {V}}) \rightarrow {\mathcal {R}}({\mathcal {V}})\) where \({\mathcal {R}}({\mathcal {V}})\) is the domain of all relations over \({\mathcal {V}}\) and \({\mathcal {V}}\) is a type of system and \(S \in {\mathcal {R}}({\mathcal {V}})\) (see Definition 1). Note that \(\textit{vary}\) is not a function but \(\textit{vary}(S)\) returns a random variant of a given system S any time it is executed. Usually, \(\textit{vary}(S)\) will not generate new systems from scratch but reuse almost all parts of S and just implement small changes to it. We can then run a stochastic search process as shown in Algorithm 1. Note that aside from the \(\textit{vary}\) operator, we also need to provide a \(\textit{termination\_criterion}\) that allows us to stop the search once a sufficient solution has been found or we have spent too much time on searching. The operator \(\textit{chance} : [0;1] \subset {\mathbb {R}} \rightarrow {\mathbb {B}}\) can be defined generally to return \(\textit{true}\) only with the given chance and \(\textit{false}\) otherwise. Further note that computing \(S \sqsubseteq S'\) can become very expensive or even infeasible for sufficiently complex systems \(S, S'\). We later show in Sects. 7 and 8 how to construct a set of more concrete test cases against which such properties can be evaluated more efficiently, but only while losing out on the exactness of the result. In general, sampling is usually employed to approximate such properties on large domains.

figure a

What makes stochastic search of this form generally infeasible is that more adaptive systems are typically very rare among all system variants that can be generated via \(\textit{vary}\). We thus need to restrict the possible variations to somewhat meaningful systems at least. Most commonly, we do this by fixing most components of the system S and introducing a parameterization \(\theta \) of some type \(\varTheta \) describing important aspects of the system’s behavior. Stochastic search then only needs to search the much more abstract parameter space \(\varTheta \). When given a variation operation \(\textit{vary}: \varTheta \rightarrow \varTheta \) and a (usually random) initial value \(\theta _0 \in \varTheta \), we can rewrite Algorithm 1 to search for the correct parametrization as seen in Algorithm 2. In a machine learning setting, the system S could typically include a neural network whose weights are encoded in \(\theta \). This way, the weights space is relatively small compared to altering the whole system but as long as the neural network’s outputs are important to the system behavior, it can be heavily influenced by just changing the weights.

figure b

Obviously, we can still spend a lot of time sampling randomly varied settings for \(\theta \) without ending up with any good solutions. We can usually shorten the search process if we can compute a gradient for a specific point \(\theta \) in the parameter space. Note that this is generally not the case in our setting: We want to improve the system’s adaptivity by following the “at least as adaptive as” relation \(\sqsubseteq \), which is defined on subset inclusion and thus naturally discrete. Intuitively, we can recognize if system \(S'\) is at least as adaptive as S, but we have no notion of how much more adaptive it is. However, we can resort to the case of adaptation with optimization (see Definition 9): On some fitness value types F, we can define a gradient. In the case of neural networks, e.g., \(F = {\mathbb {R}}^n\) for some \(n \in {\mathbb {N}}\) and for a given fitness value \(f = \phi (S \otimes \theta )\) with fitness function \(\phi \), we can compute the gradient \(\nabla \theta = \nabla \phi (S \otimes \theta )\).

In order to find a good setting for the parameter \(\theta \), we can then use a more direct approach to search like gradient descent. As shown in Algorithm 3, when we can compute the gradient, we can use it to update the parameter \(\theta \) to the most promising direction. The update rate \(\alpha \in (0;1) \subset {\mathbb {R}}\) controls how far along the gradient we go with each iteration.

figure c

Backpropagation is a variant of gradient descent specifically fitted to update the weights of neural networks. For more details on the method, we refer to other work [20, 35, 37].

Of course, computing \(\phi (S \otimes \theta )\) tends to be non-trivial. If we have a precise model of what makes the system perform well according to \(\phi \), we can usually just build this behavior into the system and do not require elaborate and expensive search algorithms. It is important to note that, in the general case, no search algorithm can effectively beat random search. This is called the No Free Lunch Theorem [47]. However, we can always build into the search as much knowledge about the structure of the problem as we have, which then allows us to get better results for problems matching that knowledge. In the typical use case for machine learning, we do not have complete knowledge about how a good system should look like but we have single evaluation points far and between, telling us about concrete instantiations for \(\theta \) and the respective value of \(\phi (S \otimes \theta )\). Machine learning is the task of building a model from these data points.

For example, let us consider a visual system that needs to recognize if a given picture x contains a cat or not. This system might use a neural network with weights \(\theta \) and we are looking for a \(\theta \in \varTheta \) that makes the system recognize images of cats. For that search, we need a set of training data \(D = \{\langle x_1, y_1 \rangle , \ldots , \langle x_n, y_n \rangle \}\) where for all \(i \in [1;n] \subset {\mathbb {N}}\) it holds that \(x_i\) is a image from the set of all images X and \(y_i = 1\) iff \(x_i\) contains a cat, \(y_i = 0\) otherwise. We can then compute the fitness

$$\begin{aligned} \phi (S \otimes \theta ) = \sum _{i=1}^n |Y(x_i) - y_i| \end{aligned}$$
(14)

where \(Y(x_i)\) is given via \(S \otimes \theta = x_i \leadsto Y(x_i)\). When the set of training data is large and diverse enough, we assume that the parameter \(\theta \) that works best on the training data, also works best (or at least well) on new, unseen data.

figure d

Note that typically, we do not evaluate each solution candidate for \(\theta \) on the whole training set but for performance reasons opt for a more gradual process as shown in Algorithm 4, where \(\nabla \theta (x,y) = \phi (S \otimes \theta , x, y)\) and \(\phi : {\mathcal {V}} \times X \times Y \rightarrow F\) is given via

$$\begin{aligned} \phi (S \otimes \theta , x, y) = |Y(x) - y| \end{aligned}$$
(15)

where Y(x) is defined as for Eq. 14. When doing so, we usually need more iterations of the whole process (i.e., a more lenient termination_criterion) but each evaluation of \(\phi \) is much less computationally expensive. This approach represents the common ground for techniques like supervised machine learning or reinforcement learning [20, 41].

Methods as shown in Algorithms 1–4 have implications for software engineering: When applying machine learning, we are not certain of the exact system that we will end up with, which, in fact, is the whole purpose of machine learning: to not exactly figure out the full system. This buys some immense possibilities to create complex behavior and adapt to a wide range of situations. However, it also introduces new tasks into the workflow of programming systems.

5.2 Software engineering for machine learning

Fig. 4
figure 4

Machine learning pipeline. Split between classical phases of system development, we can see the central activities necessary for the successful application of machine learning

Full size image

Figure 4 shows an engineering process for machine learning. At the top blue level, we see typical phases used in process models for classical software engineering. They provide an orientation about what activities new machine learning tasks can be compared to. Note that we assume an agile development process anyway: The whole process shown in Fig. 4 is not necessarily run in sync with the development process of the rest of the system (which we still assume to be programmed in a mostly classical way). Instead, the process of engineering machine learning could be run several times (as a sprint, e.g.,) within a single activity in a surrounding development process. This is why we will put observations made during the operation of the resulting system (called “operation data” here) into the case and requirement phases of the next iteration of the machine learning pipeline (as symbolized by the large blue arrow).

At the bottom blue level, we discern show the domain within which the individual tasks take place. The first parts of the machine learning pipeline operate on a domain distribution, i.e., they are not specialized on a single instance of a use case but are designed to find models and solutions general enough to work on a range of similar tasks. Even when we only target a single domain eventually, having a decent amount of diversity during training is crucial to the success of machine learning [6, 24, 43]. During deployment, we switch from the more general distribution of possible domains to a more concrete instantiation fed with all the information we have about the deployed system and the environment it is deployed in. Again, whenever we observe our original assumptions on the distribution of domains to be flawed, we feed back gained knowledge into the next iteration of the machine learning pipeline.

This handling of domains closely mirrors the definition of the adaptation space \({\mathfrak {A}}\): Recall that in order to build a more adaptive system S, it needs to be able to adapt to larger subset of the adaptation space (or adapt to the same subset better) as stated in Definition 9. Thus, when designing the autonomous adaptation mechanisms in the first part of the machine learning pipeline, we in fact operate on the whole adaptation space \({\mathfrak {A}}\). However, when it comes to building a concrete system, we will only face a single adaptation domain \({\mathcal {A}} \in {\mathfrak {A}}\) at once, perhaps in succession.

We will now briefly discuss each task appearing in the machine learning pipeline (again cf. Fig. 4). They are depicted by the white boxes with a blue border. Some of them are grouped into logical phases using orange boxes.

Data/domain In order to even begin a case description, we need to assure that we have a sufficiently detailed description of the domain we want to use the system in (as given by the definition of environments \({\mathcal {E}}\) within the adaptation space \({\mathfrak {A}}\) as shown in Sect. 4.1). Also note that many machine learning algorithms require large amount of high-quality data, which then needs to be provided alongside or instead a full domain description.

Loss/reward This artifact is also included in the adaptation space. The definition and usage of the fitness function \(\phi \) maps exactly to the use of loss or reward functions in most machine learning approaches. It needs to be defined accurately at the beginning of the machine learning pipeline.

Objective This artifact maps to the goals \(\gamma \) within the adaptation space \({\mathfrak {A}}\). As discussed, in many cases, the fitness function will be derived from the goals or at least altered to support their fulfillment. However, there also often are additional goals which cannot be expressed in the fitness function alone, for example, because they are hard constraints on system safety that cannot be opened up to optimization. In this case, the goals \(\gamma \) need to be derived from the fitness function.

Select model/policy In this task, we need to define what parts of the system should actually be adapted using machine learning techniques. In case of supervised learning, we are usually speaking of a model representing the data; in the case of reinforcement learning, we use the word policy to refer to a way to encode behavior. Either way, the definition of the model (for example, using a policy network returning the next action of the system) is the biggest influence on the choice of the parameter space \(\varTheta \) (cf. Sect. 5.1).

Select algorithm Knowing which parameter space \(\varTheta \) is to be optimized often aids in the choice of a (possibly highly specialized) optimization algorithm. A choice of (concrete instances of) Algorithms 1–4 might be made here.

Train During the training task, the algorithm selected is applied to optimize the parameters \(\theta \in \varTheta \) for the selected model or policy. In (hopefully) all cases, this task will be performed automatically by a computer. However, it is usually very resource-intensive and thus requires a lot of manual tweaking: Setting up the right hardware/software platforms, choosing the right meta-parameters (maximum run-time, minimum success, parallelization, etc.) and so on.

Assess QoS Usually, reward yield or loss reduction are used as metrics during training automatically. However, most machine learning algorithms are highly stochastic in nature. Thus, we suggest a separate task for the assessment of the quality of service provided by the automatically trained system. At this stage, we may filter out (and/or redo) bad runs or and check if our problem formulation and selection of algorithms and data structures were sufficient to get the desired quality of a solution.

Accept model As shown in Fig. 4, the tasks involved in the selection of models/policies, training and assessing the quality of the returned solutions form a typical feedback loop. Part of the accept model task is to decide when to break this loop and what model/policy (usually represented by the parameters \(\theta \)) to return. Usually, we will return the best policy according to the quality of service assessment, but there may be cases where we want to return multiple policies (like a Pareto front, e.g.,).

Use policy Once a suitable model/policy has been found, we assume that deployment happens the same way as for classical systems. At this task, we are thus ready to execute the behavior of the system as given by the model/policy. Note that formally, executing the system S with model/policy \(\theta \) in a concrete domain \({\mathcal {A}}\) corresponds to computing \(S \otimes \theta \Vdash {\mathcal {A}}\).

Specialize model/policy As previously discussed, the training loop has not been executed on the deployed domain \({\mathcal {A}}\) but on a distribution of domains drawn from the adaptation space \({\mathfrak {A}}\). When we recognize that \({\mathcal {A}}\) is not going to be subject to substantial changes any more, it makes sense to specialize on the concrete domain instance. This can be done through classical means (adding specialized behavior, removing now inaccessible program parts) or through means of machine learning (re-running a training feedback loop but based on the experiences generated in \({\mathcal {A}}\) instead of \({\mathfrak {A}}\)). In the latter case, we could actually enter a complete other instantiation of the machine learning pipeline.

Monitor QoS Even when training and assessment have shown that our system \(S \otimes \theta \) does fulfill our quality goals, it is most important to continually monitor that property throughout operations. Mistakes in the definition of (the parts of) \({\mathfrak {A}}\) or general changes in the domain, including subtle phenomena like drift, may cause the trained system to be incapable of further operation. In order to prevent this and re-train as early as possible, we need not only to monitor the defined metrics of quality of service directly, but also keep an eye out for indicators of upcoming changes in quality, for example through means of anomaly detection [30].

It is clear that the machine learning pipeline discussed in this section has no claim of completeness. Many tasks could be changes or added to it. We introduced the pipeline to show that while some necessary changes to the software engineering process closely mirror tasks for classical systems, others introduce entirely new challenges and shift the focus where the main work of software developers should fall. We will use this analysis as a foundation to sum up the major changes into core concepts in the following section.

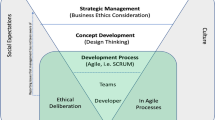
6 Core concepts of adaptive software engineering

Literature makes it clear that one of the main issues of the development of self-adapting systems lies with trustworthiness. Established models for checking systems (i.e., verification and validation) do not really fit the notion of a constantly changing system. However, these established models represent all the reason we have at the moment to trust the systems we developed. Allowing the system more degrees of freedom thus hinders the developers’ ability to estimate the degree of maturity of the system they design, which poses a severe difficulty for the engineering progress, when the desired premises or the expected effects of classical engineering tasks on the system-under-development are hard to formulate.

To aid us control the development/adaptation progress of the system, we define a set of core concepts, which are basically patterns for process models. They describe the paradigm shifts to be made in the engineering process for complex, adaptive systems in relation to more classical models for software and systems engineering.

Concept 1

(System and Test Parallelism) The system and its test suite should develop in parallel from the start with controlled moments of interchange of information. Eventually, the test system is to be deployed alongside the main system so that even during run-time, on-going online tests are possible [14]. This argument has been made for more classical systems as well and thus classical software test is, too, no longer restricted to a specific phase of software development. However, in the case of self-learning systems, it is important to focus on the evolution of test cases. The capabilities of the system might not grow as experienced test designers expect them to compare to systems entirely realized by human engineering effort. Thus, it is important to conceive and formalize how tests in various phases relate to each other.

Concept 2

(System vs. Test Antagonism) Any adaptive systems must be subject to an equally adaptive test. Overfitting is a known issue for many machine learning techniques. In software development for complex adaptive systems, it can happen on a larger scale. Any limited test suite (we expect our applications to be too complex to run a complete, exhaustive test) might induce certain unwanted biases. Ideally, once we know about the cases our system has a hard time with, we can train it specifically for these situations. For the so-hardened system, the search mechanism that gave us the hard test cases needs to come up with even harder ones to still beat the system-under-test. Employing autonomous adaptation at this stage is expected to make that arms race more immediate and faster than it is usually achieved with human developers and testers alone.

Concept 3

(Automated Realization) Since the realization of tasks concerning adaptive components usually means the application of a standard machine learning process, a lot of the development effort regarding certain tasks tends to shift to an earlier phase in the process model. The most developer time when applying machine learning techniques, e.g., tends to be spent on gathering information about the problem to solve and the right setup of parameters to use; the training of the learning agent then usually follows one of a few standard procedures and can run rather automatically. However, preparing and testing the component’s adaptive abilities might take a lot of effort, which might occur in the design and test phase instead of the deployment phase of the system life cycle.

Concept 4

(Artifact Abstraction) To provide room for and exploit the system’s ability to self-adapt, many artifacts produced by the engineering process tend to become more general in nature, i.e., they tend to feature more open parameters or degrees of freedom in their description. In effect, in the place of single artifacts in a classical development process, we tend to find families of artifacts or processes generating artifacts when developing a complex adaptive system. As we assume that the previously only static artifact is still included in the set of artifacts available in its place now, we call this shift “generalization” of artifacts. Following this change, many of the activities performed during development shift their targets from concrete implementations to more general artifact, i.e., when building a test suite no longer yields a series of runnable test cases but instead produces a test case generator. When this principle is broadly applied, the development activities shift toward “meta development.” The developers are concerned with setting up a process able to find good solutions autonomously instead of finding the good solutions directly.

7 Scenarios

We now want to include the issue of testing adaptive systems in our formal framework. To this end, we first introduce the notion of scenarios as the basis upon which we define tests for our system. We then include that notion in our description of software development. Finally, we extend our running example with software testing.

7.1 Describing scenarios

We recognize that any development process for systems following the principles described in Sect. 3 produces two central types of artifacts. The first one is a system \(S = X {\mathop {\leadsto }\limits ^{Z}} Y\) with a specific desired behavior Y so that it manages to adapt to a given adaptation space. The second is a set of situations, test cases, constraints, and checked properties that this system’s behavior has been validated against. We call artifacts of the second type by the group name of scenarios.

Definition 13

(Scenario) Let \(S = X {\mathop {\leadsto }\limits ^{Z}} Y\) be a system and \({\mathcal {A}} = \{(E, \gamma , \phi )\}\) a singleton adaptation domain. A tuple \(c = (X, Y, g, f), g \in \{\top , \bot \}, f \in \text {cod}(\phi )\) with \(g = \top \iff S \otimes E \models \gamma \) and \(f = \phi (S \otimes E)\) is called scenario.

Note that if we are only interested in the system’s performance and not how it was achieved, we can redefine a scenario to leave out Y. Semantically, scenarios represent the experience that has been gained about the system’s behavior during development, including both successful (\(S \vDash \gamma \)) and unsuccessful (\(S \nvDash \gamma \)) test runs. As stated above, since we expect to operate in test spaces we cannot cover exhaustively, the knowledge about the areas we did cover is an important asset and likewise result of the systems engineering process.

Effectively, as we construct and evolve a system S, we want to construct and augment a set of scenarios \(C = \{c_1, \ldots , c_n\}\) alongside with it. C is also called a scenario suite and can be seen as a toolbox to test S’s adaptation abilities with respect to a fixed adaptation domain \({\mathcal {A}}\).

While formally abiding to Definition 13, scenarios can be encoded in various ways in practical software development, such as:

Sets of data points of expected or observed behavior Given a system \(S' = X' \leadsto Y'\) whose behavior is desirable (for example a trained predecessor of our system or a watchdog component), we can create scenarios \((X', Y', g', f')\) with \(g' = \top \iff S' \otimes E_i \models \gamma _i\) and \(f' = \phi _i(S' \otimes E_i)\) for an arbitrary amount of elements \((E_i, \gamma _i, \phi _i)\) of an adaptation domain \({\mathcal {A}} = \{(E_1, \gamma _1, \phi _1), \ldots , (E_n, \gamma _n, \phi _n)\}\).

Test cases the system mastered In some cases, adaptive systems may produce innovative behavior before we actively seek it out. In this cases, it is helpful to formalize the produced results once they have been found so that we can ensure that the system’s gained abilities are not lost during further development or adaptation. Formally, this case matches the case for “observed behavior” described above. However, here the test case (X, Y, g, f) already existed as a scenario, so we just need to update g and f (with the new and better values) and possibly Y (if we want to fix the observed behavior).

Logical formulae and constraints Commonly, most constraints can be directly expressed in the adaptation domain. Suppose we build a system against an adaptation domain \({\mathcal {A}} = \{(E_1, \gamma _1, \phi _1), \ldots , (E_n, \gamma _n, \phi _n)\}\). We can impose a hard constraint \(\zeta \) on the system in this domain by constructing a constrained adaptation domain \(\mathcal {A'} = \{(E_1, \gamma _1 \wedge \zeta , \phi _1), \ldots , (E_n, \gamma _n \wedge \zeta , \phi _n)\}\) given that the logic of \(\gamma _1, \ldots , \gamma _n, \zeta \) meaningfully supports an operation like the logical “and” \(\wedge \). Likewise a soft constraint \(\psi \) can be imposed via \(\mathcal {A'} = \{(E_1, \gamma _1, \max (\phi _1, \psi ), ), \ldots , (E_n, \gamma _n, \max (\phi _n, \psi ))\}\) given the definition of the operator \(\max \) that trivially follows from using the relation \(\preceq \) on fitness values. Scenarios \((X', Y', g', f')\) can then be generated against the new adaptation domain \({\mathcal {A}}\) by taking preexisting scenarios (X, Y, g, f) and setting \(X' = X, Y' = Y, g = \top , f = \psi ((X \leadsto Y) \otimes E)\).

Requirements and use case descriptions (including the system’s degree of fulfilling them) If properly formalized, a requirement or use case description contains all the information necessary to construct an adaptation domain and can thus be treated as the logical formulae in the paragraph above. However, use cases are in practical development more prone to be incomplete views on the adaptation domain. We thus may want to stress the point that we do not need to update all elements of an adaptation domain when applying a constraint, i.e., when including a use case. We can also just add the additional hard constraint \(\zeta \) or soft constraint \(\psi \) to some elements of \({\mathcal {A}}\).

Predictive models of system properties For the most general case, assume that we have a prediction function p so that \(p(X) \approx Y\), i.e., the function can roughly return the behavior \(S = X \leadsto Y\) will or should show given X. We can thus construct the predicted system \(S' = X \leadsto p(X)\) and construct a scenario (X, p(X), g, f) with \(g = \top \iff S' \otimes E \models \gamma \) and \(f = \phi (S' \otimes E)\).

All of these types of artifacts will be subsumed under the notion of scenarios. We can use them to further train and improve the system and to estimate its likely behavior as well as to perform tests (and ultimately verification and validation activities).

7.2 Constructing scenarios

Scenario coevolution describes the process of developing a set of scenarios to test a system during the system-under-tests’s development. Consequently, it needs to be designed and controlled as carefully as the evolution of system behavior [5, 21].

Definition 14

(Scenario Hardening) Let \(c_1 = (X_1, Y_1, g_1, f_1)\) and \(c_2 = (X_2, Y_2,g_1, f_2)\) be scenarios for a system S and an adaptation domain \({\mathcal {A}}\). Scenario \(c_2\) is at least as hard as \(c_1\), written \(c_1 \le c_2\), iff \(g_1 = \top \implies g_2 = \top \) and \(f_1 \le f_2\).

Definition 15

(Scenario Suite Order) Let \(C = \{c_1, \ldots ,c_m\}\) and \(C' = \{c_1', \ldots , c_n'\}\) be sets of scenarios, also called scenarios suites. Scenario suite \(C'\) is at least as hard as C, written \(C \sqsubseteq C'\), iff for all scenarios \(c \in C\) there exists a scenario \(c'\in C'\) so that \(c \le c'\).

Definition 16

(Scenario Sequence) Let \({\mathcal {S}} = (S_i)_{i\in I}\), \(I = \{1, \ldots , n\}\) be an adaptation sequence for a singleton adaptation space \({\mathfrak {A}} = \{{\mathcal {A}}\}\). A series of sets \({\mathcal {C}} = (C_i)_{i \in I}\) is called a scenario sequence iff for all \(i \in I, i < n\) it holds that \(C_i\) is a scenario suite for \(S_i\) and \({\mathcal {A}}\) and \(C_i \sqsubseteq C_{i+1}\).

Note that we define the hardness of scenarios in parallel to the adaptivity of systems (cf. Definition 9). Figure 5 provides a visual representation.

Fig. 5
figure 5

Illustration of the hardness of scenarios according to Definition 14. In the same plot as in Fig. 1, scenarios from two different scenario suites \(C_1\) (green) and \(C_2\) (purple) can be depicted as points within the space of behavior where certain inputs need to be matched to certain outputs. Various scenario generators may cover different areas of the space of situations (shapes at the bottom of the plot). Although the depicted system \(S = X \leadsto Y\) fulfills both scenario suites, \(C_1\) is at least as hard as \(C_2\) because its scenarios cover the same situations and require at least as close to optimal performance (colour figure online)

Full size image

We expect each phase of development to further alter the set of scenarios just as it does alter the system behavior. The scenarios produced and used at a certain phase in development must match the current state of progress. Valid scenarios from previous phases should be kept and checked against the further specialized system. When we do not delete any scenarios entirely, the continued addition of scenarios will ideally narrow down allowed system behavior to the desired possibilities. Eventually, we expect all activities of system test to be expressible as the generation or evaluation of scenarios. New scenarios may simply be thought up by system developers or be generated automatically.

Finding the right scenarios to generate is another optimization problem to be solved during the development of any complex adaptive system. Scenario evolution represents a cross-cutting concern for all phases of system development. Treating scenarios as first-class citizen among the artifacts produced by system development thus yields changes in tasks throughout the whole process model.

8 Example application

We now return to the Grid World Smart Factory domain introduced in Sect. 4. For an instance of that domain, an instance of scenario coevolution was applied in [24]. Without human involvement, a reinforcement learning agent adapting the system’s behavior and an evolutionary algorithm adapting the scenario suite have been put together. [24] has shown that the paradigm yields better results per computation time, arguing in favor of using scenario coevolution even in this fully automated form. In this section, we provide formal definition of the involved artifacts and processes fitting into the formal framework we introduced so far. We thus abstract from the dichotomy between human developers and automated adaptation and open up the paradigm of scenario coevolution to both and (most importantly) hybrid approaches.

Recall that actions in the Grid World Smart Factory as defined in Eq. 4 can be entirely simulated (although full brute force simulations of all possible actions sequences is infeasible). However, that means we can use a simulation to generate training data. And since the simulation is complete (it can simulate any situation that we defined to be able to occur within the domain), we do not need to worry about any other source of training data. In practical real-world applications, coming up with a high-fidelity simulation is usually pretty hard or expensive. Complete simulations can often be substituted with learned simulations, with are the result of machine learning themselves.

We derived the fitness function to be used in this application in Eq. 12. It allows us to steer the system toward fully producing as many items as possible. Using this fitness function, we expect the system to learn to fulfill the overall system goal of fully producing all the requested items, as defined in Eqs. 9 and 10 .

The system’s behavior is defined by the actions it chooses for each consecutive time step. In [24], we chose to program the system to execute (when in state \(s_i\) at time step i) the action

$$\begin{aligned} a_i = \max _{a \in \{a_\triangle , a_\rhd , a_\bigtriangledown , a_\lhd , a_\boxplus , a_\boxminus \}} Q(s_i, a) \end{aligned}$$
(16)

where \(Q(s_i, a)\) is the so-called Q-value of action a in state \(s_i\). The Q-value is derived from Q-learning [41, 44] and represents the expected reward when executing an action in a given state. To estimate that value, we call a neural network with weights \(\theta \).

The network weights \(\theta \) are then optimized via reinforcement learning, variant of gradient descent as given in Algorithm 4. The training process runs for a fixed computational budget. For more details on the implementation in this case or any other part of the pipeline, please see [24]. For the quality of service of the trained system, we discern between the fitness function and the actual goal function. The network is trained to improve the average fitness, i.e., the average amount of items produced per run, but the user is only interested in the overall success rate, i.e., the amount of runs that are fully produced. The “random” (blue) plots in Figs. 6 and 7 show the difference: The score in Fig. 6, i.e., the value of the fitness function \(\phi (S \otimes \theta )\), increases slower and on a different scale than the amount of correct runs where \(S \otimes \theta \models \gamma \) shown in Fig. 7. While the network trains on the former, we assess its quality (and accept the model) using the latter.

Fig. 6
figure 6

Image taken from [24]

Scores achieved by SCoE and standard “random” reinforcement learning during training over 10,000 episodes. Scores are averages of running the current agent against 1000 randomly generated test scenarios.(colour figure online)

Full size image
Fig. 7
figure 7

Image taken from [24]

Percentage of successfully solved test scenarios by SCoE and standard “random” reinforcement learning. The values are calculated from a randomly generated set of 1000 scenarios.(colour figure online)

Full size image
Fig. 8
figure 8

Image taken from [24]

Schematic representation of the scenario coevolution process for the Grid World Smart Factory application. A population of test scenarios is first generated at random and then improved via evolution. Between evolutions, the test scenario population is fully utilized as training data for the reinforcement learning agent, which causes the agent to improve in parallel to the test scenario population.

Full size image

The learned policy is deployed on multiple independent runs. As defined in Eq. 8, these independent runs (only) differ in the position of the obstacles in the domain. For the “random” (blue) plots in Figs. 6 and 7, we generated domain instances with random obstacles. Figures 6 and 7 also show “SCoE” (orange) plots where the environments were not generated at random but by applying scenario coevolution.

For this, we need to define scenarios in the Grid World Smart Factory domain (also see Definition 13). We reduce complexity by not expecting specific outputs. We set no fixed requirement on goal fulfillment or fitness. The set of all possible scenarios \({\mathcal {C}}\) can then be given as

$$\begin{aligned} {\mathcal {C}} = \{(p, \emptyset , g, f) : p \in P^4, g \in \{\top , \bot \}, f \in \text {cod}(\phi )\}. \end{aligned}$$
(17)

To train the system, we try to choose the hardest scenarios from \({\mathcal {C}}\), i.e., we try to optimize for

$$\begin{aligned} \min _{c \in {\mathcal {C}}} \phi (S \otimes \theta , c, \emptyset ). \end{aligned}$$
(18)

It is important to note that as \(\theta \) changes, i.e., as the system learns, our notion for which scenarios are hard also changes.

To continually come up with hard scenarios, we thus need to continually optimize for them. We do so by employing an evolutionary algorithm, which is an instance of stochastic search as given in Algorithm 1. We thus form a scenario sequence where a learning system using reinforcement and a set of scenarios generated by an evolutionary algorithm coevolve. Ideally, as the scenarios get harder, the system gets better, and as the system gets better, the scenarios get harder. Figures 6 and 7 show that employing scenario coevolution in this fully automated form already yields a benefit to the results. As discussed in [24], this benefit even upholds when considering total computational effort spent. Figure 8 depicts an overview of how the various parts of the system interact.

Within the machine learning pipeline, the search for hard scenarios represents an instantiation of the task for the specialization of the model/policy by selecting specific instances in which the model/policy is to be evaluated. However, note that while a single scenario represents a concrete domain, the whole suite of generated scenarios forms a distribution of domains and is thus an ideal artifact to use for the next iteration of the machine learning pipeline, i.e., the next generation of coevolution. Scenario coevolution as a paradigm thus instantiates the whole feedback loop constituting the machine learning pipeline.

9 Patterns for scenario coevolution

Having both introduced a formal framework for adaptation and the testing of adaptive systems using scenarios, we show in this section how these frameworks can be applied to aid the trustworthiness of complex adaptive systems for practical use.

9.1 Criticality focus

It is very important to start the scenario evolution process alongside the system evolution, so that at each stage there exists a set of scenarios available to test the system’s functionality and degree of progress (see Concept 1). This approach mimics the concept of agile development where between each sprint there exists a fully functional (however incomplete) version of the system. The concept of scenario evolution integrates seamlessly with agile process models.

In the early phases of development, the common artifacts of requirements engineering, i.e., formalized requirements, serve as the basis for the scenario evolution process. As long as the adaptation space \({\mathfrak {A}}\) remains constant (and with it the system goals), system development should form an adaptation sequence. Consequently, scenario evolution should then form a scenario sequence for that adaptation sequence. This means (according to Definition 16), the scenario suite is augmented with newly generated scenarios (for new system goals or just more specialized sub-goals) or with scenarios with increased requirements on fitness. Note that every change in \({\mathfrak {A}}\) starts new sequences. Ideally, the scenario evolution process should lead the learning components on the right path toward the desired solution. The ability to re-assign fitness priorities allows for an arms race between adaptive system and scenario suite (see Concept 2).

Augmenting requirements Beyond requirements engineering, it is necessary to include knowledge that will be generated during training and learning by the adaptive components. Mainly, recognized scenarios that work well with early version of the adaptive system should be used as checks and tests when the system becomes more complex. This approach imitates the optimization technique of importance sampling on a systems engineering level. There are two central issues that need to be answered in this early phase of the development process:

  • Behavior Observation: How can system behavior be generated in a realistic manner? Are the formal specifications powerful enough? Can we employ human-labeled experience?

  • Behavior Assessment: How can the quality of observed behavior be adequately assessed? Can we define a model for the users’ intent? Can we employ human-labeled review?

Breaking down requirements A central task of successful requirements engineering is to split up the use cases in atomic units that ideally describe singular features. In the dynamic world, we want to leave more room for adaptive system behavior. Thus, the requirements we formulate tend to be more general in notion. It is thus even more important to split them up in meaningful ways in order to derive new sets of scenarios. The following design axes (without any claim to completeness) may be found useful to break down requirements of adaptive systems:

  • Scope and Locality: Can the goal be applied/checked locally or does it involve multiple components? Which components fall into the scope of the goal? Is emergent system behavior desirable or considered harmful?

  • Decomposition and Smoothness: Can internal (possibly more specific) requirements be developed? Can the overall goal be composed from a clear set of sub-goals? Can the goal function be smoothened, for example by providing intermediate goals? Can sub-goal decomposition change dynamically via adaptation or is it structurally static?

  • Uncertainty and Interaction: Are all goals given with full certainty? Is it possible to reason about the relative importance of goal fulfillment for specific goals a priori? Which dynamic goals have an interface with human users or other systems?

9.2 Adaptation cool-down

We call the problem domain available to us during system design the off-site domain. It contains all scenarios we think the system might end up in and may thus even contain contradicting scenarios, for example. In all but the rarest cases, the situations one single instance of our system will face in its operating time will be just a fraction the size of the covered areas of the off-site domain. Nonetheless, it is also common for the system’s real-world experience to include scenarios not occurring in the off-site domain at all; this mainly happens when we were wrong about some detail in the real world. Thus, the implementation of an adaptation technique faces a problem not unlike the exploration/exploitation dilemma [16], but on a larger scale: We need to decide, if we opt for a system fully adapted to the exact off-site domain or if we opt for a less specialized system that leaves more room for later adaptation at the customer’s site. The point at which we stop adaptation happening on off-site scenarios is called the off-site adaptation border and is a key artifact of the development process for adaptive systems.

In many cases, we may want the system we build to be able to evolve beyond the exact use cases we knew about during design time. The system thus needs to have components capable of run-time or online adaptation. In the wording of this work, we also talk about on-site adaptation stressing that in this case we focus on adaptation processes that take place at the customer’s location in a comparatively specific domain instead of the broader setting in a system development lab. Usually, we expect the training and optimization performed on-site (if any) to be not as drastic as training done during development. (Otherwise, we would probably have not specified our problem domain in an appropriate way.) As the system becomes more efficient in its behavior, we want to gradually reduce the amount of change we allow. In the long run, adaptation should usually work at a level that prohibits sudden, unexpected changes but still manages to handle any changes in the environment within a certain margin. The recognized need for more drastic change should usually trigger human supervision first.

Definition 17

(Adaptation Space Sequence) Let S be a system. A series of |I| adaptation spaces \({\mathbb {A}} = ({\mathfrak {A}}_i)_{i\in I}\) with index set I with a preorder \(\le \) on the elements of I is called an adaptation domain sequence iff for all \(i, j \in I, i \le j\) it holds that: S adapts to \({\mathfrak {A}}_j\) implies that S adapts to \({\mathfrak {A}}_i\).

System development constructs an adaptation space sequence (cf. Concept 4), i.e., a sequence of increasingly specific adaptation domains. Each of those can be used to run an adaptation sequence (cf. Definition 10) and a scenario sequence (cf. Definition 16, Concept 2) to test it.

For the gradual reduction of the allowed amount of adaptation for the system, we use the metaphor of a “cool-down” process. The adaptation performed on-site should allow for less change than off-site adaptation. And the adaptation allowed during run-time should be less than what we allowed during deployment. This ensures that decisions that have once been deemed right by the developers are hard to change later by accident or by the autonomous adaptation process.

9.3 Eternal deployment

For high trustworthiness, development of the test cases used for the final system test should be as decoupled from the on-going scenario evolution as possible, i.e., the data used in both processes should overlap as little as possible. Of course, following this guideline completely results in the duplication of a lot of processes and artifacts. Still, it is important to accurately keep track of the influences on the respective sets of scenarios. A clear definition of the off-site adaptation border provides a starting point for when to branch off a scenario evolution process that is independent of possible scenario-specific adaptations on the system-under-test’s side. Running multiple independent system tests (cf. ensemble methods [18, 25]) is advisable as well. However, the space of available independently generated data is usually very limited.

For the deployment phase, it is thus of key importance to carry over as much information as possible about the genesis of the system we deploy into the run-time, where it can be used to look up the traces of observed decisions. The reason to do this now is that we usually expect the responsibility for the system to change at this point. Whereas previously, any system behavior was overseen by the developers who could potentially backtrack any phenomenon to all previous steps in the system development process, now we expect on-site maintenance to be able to handle any potential problem with the system in the real world, requiring more intricate preparation for maintenance tasks (cf. Concept 3). We thus need to endow these new people with the ability to properly understand what the system does and why.

Our approach follows the vision of eternal system design [33], which is a fundamental change in the way to treat deployment: We no longer ship a single artifact as the result of a complex development process, but we ship an image of the process itself (cf. Concept 4). As a natural consequence, we can only ever add to an eternal system but hardly remove changes and any trace of them entirely. Using an adequate combination operator, this meta-design pattern is already implemented in the way we construct adaptation sequences (cf. Definition 10): For example, given a system \(S_i\) we could construct \(S_{i+1} = X {\mathop {\leadsto }\limits ^{Z}} Y\) in a way so that \(S_i\) is included in \(S_{i+1}\)’s internal state Z.

As of now, however, the design of eternal systems still raises many unanswered questions in system design. We thus resort to the notion of scenarios only as a sufficient system description to provide explanatory power at run-time and recommend to apply standard “destructive updates” to all other system artifacts.

10 Conclusion

We have introduced a new formal model for adaptation and test processes using our notion of scenarios. We connected this model to concrete challenges and arising concepts in software engineering to show that our approach of scenario coevolution is fit to tackle (a first few) of the problems when doing quality assurance for complex adaptive systems. We have put our approach into context by applying it to an example application and deriving a pipeline for the development of machine learning components from it.

As already noted throughout the text, a few challenges still persist. Perhaps most importantly, we require an adequate data structure both for the coding of systems and for the encoding of test suites and need to prove the practical feasibility of an optimization process governing the software development life cycle. For performance reasons, we expect that some restrictions on the general formal framework will be necessary. In this work, we also deliberately left out the issue of meta-processes: The software development life cycle can itself be regarded as system according to Definition 1. While this may complicate things at first, we also see potential in not only developing a process of establishing quality and trustworthiness but also a generator for such processes (akin to Concept 4).

Aside from the evolution of scenarios, we see further potential in the application of coevolution to software engineering processes. Cooperative coevolution could be used as means to break down global goals into local ones and thus coordinate various roles in a (possibly emergent) multi-agent system. Competitive coevolution as used in the scenario coevolution paradigm could also be further generalized and, for example, performed between multiple parties (instead of just two antagonists) to represent multiple different aspects of software testing (like robustness, security, data quality) by different types of scenario-like artifacts.

Systems with a high degree of adaptivity and, among those, systems employing techniques of artificial intelligence and machine learning will become ubiquitous. If we want to trust them as we trust engineered systems today, the methods of quality assurance need to rise to the challenge: Quality assurance needs to adapt to adaptive systems!