Introduction to basics of electrochemistry

A driving force is necessary for every process that takes place in our universe. In biological systems, the energy of electrons serves as the driving force for the majority of processes under physiological conditions. Electron transfer reactions play a critical role in diverse biochemical reactions, particularly in bioenergetics. Key processes such as photosynthesis and respiration rely on intricate sequences of electron/ion transfers in the complex pathway of energy conversion. These processes involve basic molecules such as carbon dioxide, water, oxygen, and glucose, as well as complex biomolecules such as enzymes, among others [1]. In a general chemical context, the exchange of electrons between two different species is known as a reduction–oxidation process or simply “redox reaction.” Redox reactions, which are essential for understanding basic biochemical processes related to the harvesting and using chemical energy via chemical bond cleavage and/or formation in living organisms, are also in the focus of electrochemistry.

Electrochemistry is an interdisciplinary science that bridges physics and chemistry, frequently referred to as a branch of physical chemistry. In experimental reality, electrochemistry is predominantly concerned with charge transfer across an interface between two different phases. The most common scenario involves the transfer of electrons across the interface created between an electronic conductor (i.e., an electrode) and an electrolyte solution (i.e., an ionic conductor). However, charge transfer is not limited to electron exchange alone. In a specific branch of electrochemistry, charge transfer is represented by ion transfer across an interface between two immiscible electrolyte solutions [2], mimicking the ion transfer across cellular membranes.

Regarding the former case of electron transfer across an electrode/electrolyte interface, it is important to note that the electrode serves only as a sink or a supply of electrons. In other words, it is a conductor of electrons only, and its chemical composition remains largely unchanged during the electrochemical experiment. However, the interfacial electron transfer causes a chemical transformation of species on the electrolyte solution side, which either gain or release electrons. This chemical transformation is a redox reaction that occurs only at the interface, thus being termed as an electrode reaction. In a broader context, electrochemistry deals with the various physical and chemical aspects and occurrences within a system that impact the transfer of electrons. For instance, it includes electric characteristics and structure of the interface (primarily the interfacial potential difference as a quantitative measure for the energy required to drive electron transfer), mass transfer phenomena of species participating in electron transfer, adsorption phenomena at the interface, consecutive chemical reactions following electron transfer, or preceding electron transfer to supply species capable of exchanging electrons with the electrode, etc. In addition to elucidating the fundamental facets of interfacial electron transfer, such as reaction mechanisms, energetics and kinetics, electrochemistry can yield valuable information regarding all electron transfer-related phenomena referenced above. Moreover, it is important to note that electrochemistry does not necessarily require an interfacial electron transfer to occur. It is simply sufficient to relate an equilibrium chemical or physical phenomenon established at the interface with its electric features. For example, an equilibrium between the two species of a single redox couple Ox and Red, established at the surface of an electrode, dictates the potential difference of the electrode/electrolyte interface, despite the fact that no net charge is exchanged across the interface. Hence, electrochemistry is an impressive interdisciplinary field that encompasses both physics and chemistry, making it one of the most versatile modern sciences.

Some basics of voltammetry

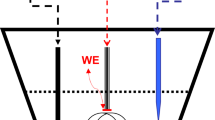
Among various electrochemical techniques, voltammetry stands out as a highly distinguished technique that offers an insight into a plethora of chemical and physical phenomena. The name “voltammetry” (abbreviation of volt-ampere-metry) actually reflects the operating mode of the technique. In voltammetry, the driving force is the potential difference (measured in volts) at the interface of the working electrode/electrolyte solution, controlled by an external power supply termed potentiostat (Fig. 1). Commonly, a working electrode is a chemically inert electronic conductor consisted of Pt, Au, or carbon, while the interfacial potential difference is controlled versus a reference electrode (an electrode designed in a way to have a constant potential in the course of the experiment) [3,4,5].

Fig. 1
figure 1

A typical instrumental setup employed in voltammetric experiments

Full size image

The measuring output in voltammetry is the magnitude of the electric current (measured in amperes) that results from an interfacial exchange of electrons between the working electrode and the species present in the electrolyte solution. The latter species are said to be electroactive, or, in terms of the analytical chemistry, are designated as an analyte. In an electric circuit comprising of a working electrode and a counter electrode, the flow of electric current occurs. The reference electrode in this set up (Fig. 1) is solely responsible for regulating the interfacial potential difference of the working electrode. Importantly, working electrode interface is significantly smaller than the interface of the large counter electrode, being a bottleneck for the overall electric current flow. Therefore, a straightforward experimental setup illustrated in Fig. 1 offers valuable information regarding the interfacial electron transfer taking place at the working electrode only. The electron transfer is accurately modulated by an external input of energy, which takes the form of an interfacial potential difference. The role of the external power supply can be alternatively understood as a controller of the electrons’ energy (activity of electrons) at the surface of the working electrode.

Nowadays, voltammetry is recognized as one of the cheapest instrumental techniques that is made even more accessible through recent advances in the design of mini-potentiostats that can be purchased for about 2000 US $ only. So far, cyclic voltammetry (CV) is the most exploited member from the family of voltametric techniques; it is widely used as an effective electrochemical technique for studying the mechanism of redox transformations of a variety of molecular and ionic species [3,4,5]. An excellent resource for students to get a basic understanding of cyclic voltammetry one finds in the report [6], which covers the fundamentals of the technique in a straightforward manner. The versatility of cyclic voltammetry not only makes it an excellent tool for basic electrochemical studies, but also for advanced scientific research [3,4,5,6].

Hints for performing simple experiment in cyclic voltammetry

Performing a conventional experiment in voltammetry is a simple task, even for those who are not highly skilled in electrochemistry. Cyclic voltammetry, like other voltammetry techniques, uses a three-electrode system (as shown in Fig. 1). To conduct a cyclic voltammetric experiment, one needs to prepare an electrochemical cell by adding a defined volume of an electrolyte solution (preferably between 10 and 50 mL, with a concentration not less than 10 mmol/L to ensure sufficient ionic conductivity) and a defined amount of the investigated analyte. The analyte is typically one of the redox forms (Red or Ox) of the studied redox couple Ox/Red, at a concentration of 1 mmol/L or less. A potentiostat is then used to sweep the applied working electrode interfacial potential difference from an initial potential up to a pre-defined final potential, and then sweeping back in the opposite direction. During this sequence, the potentiostat may repeatedly conduct potential scans back and forth and record the changing currents flowing in the system, reflecting mainly the interfacial electron transfer and redox transformation of the analyte at the surface of the working electrode. This sequence of events might generate a characteristic plot known as a cyclic voltammogram (as that shown in Fig. 2).

Fig. 2
figure 2

A cyclic voltammogram illustrating the process of electron transfer between a working electrode and a water-soluble redox analyte

Full size image

“All in” in a single cyclic voltammogram

Although performing a voltammetric experiment is not a difficult task, understanding the physical and chemical phenomena underlying a single cyclic voltammogram can be very challenging. The current–voltage curves, as that displayed in Fig. 2, may “hide” various phenomena, such as diffusion, adsorption, homogeneous chemical reactions, crystallization, and phase transformation, besides the electron transfer and resulting redox transformation as basic events [3,4,5,6]. Frequently, voltammetric curves can be rather obscure, and even a highly skilled electrochemist might have difficulty discerning the majority of physicochemical phenomena by simple examination of voltammetric features. Therefore, it is almost inevitable to compare the results of the voltammetric experiment with theoretical predictions in order to obtain a relevant set of mechanistic and quantitative information. One simulation protocol and a free Excel platform developed to simulate cyclic voltammograms are reported in [7]. However, the aim of the current work is to present a simulation protocol of a common electrochemical mechanism under conditions of square-wave voltammetry (SWV), which is recognized as one of the most sophisticated techniques in voltammetry in general [8,9,10,11].

Basics of pulse voltammetric techniques and square-wave voltammetry

The development of pulse voltammetric techniques was driven by the observation that via modulating the time-potential function in a pulsed manner during voltammetry, one can significantly reduce the so-called “non-Faradaic” (alternatively termed as “capacitive” or “charging” current) [3, 5, 8, 9]. But what does one understand by the term “charging current?” When a potential difference is applied at the working electrode interface, the desired phenomenon is the interfacial electron exchange and the consequent redox transformation of the studied electroactive species, which results in flow of so-called “Faradaic current” component [3, 5]. However, the existence of any interfacial potential difference prompts permanent formation and charging of an electrical double layer at the interface between the working electrode and the electrolyte solution [3, 5], which is a sort of a capacitor with a molecular dimensions [3]. Thus, such a phenomenon results in appearance of a capacitive (charging) current component, despite the lack of any interfacial electron transfer [3, 5]. Note that the microscopic electrical double layer is a consequence of the charge excess at the electrode surface for any given electrode potential, and the corresponding response of the mobile ionic species of the electrolyte and dipole molecules of the solvent [3, 5]. Hence, the restructuring of the electric double layer during potential variation and the corresponding charging current component are unavoidable artifacts in any voltammetric experiment.

The ratio between the Faradaic and the capacitive (charging) current is of utmost importance in voltammetry, as it determines the effectiveness of the technique in providing information on the electrode reaction and its analytical performance. In the second half of last century [8, 10], measures have been taken to reduce the impact of the charging current on the overall measured current and to maximize the Faradaic-to-charging current ratio. Pulse techniques rely on exploiting the contrasting decay rates of capacitive and Faradaic currents when subjected to potential steps. For a diffusion-affected electrode reaction, the Faradaic current component diminishes proportionally to √t, while the capacitive current declines exponentially with time (exp(t)) [3]. Therefore, by sampling the current at the end of a short potential pulse, the capacitive current component can be largely eliminated, while a significant portion of Faradaic current still remains to be detected. This current sampling procedure significantly improves analytical sensitivity in pulse voltammetry, enabling the measured current to predominantly reflect the electrode reaction of the studied electroactive species.

Figure 3 shows the potential function used in square-wave voltammetry, which is a typical pulse voltammetric technique [8, 10]. The potential function consists of symmetrical square-wave pulses with a constant height (referred to as SW amplitude, ESW) superimposed on a staircase-potential ramp. The potential is varied from a starting (Es) to a final (Ef) potential with a constant potential step increment of dE. In a typical experiment, amplitude magnitudes between 10 and 100 mV and potential step increments between 1 and 10 mV are commonly explored [8, 10]. In SWV, the current is measured at the end of each potential pulse. Pulses aligned with the direction of the staircase ramp are designated as forward, while the oppositely oriented pulses are termed reverse or backward pulses.

Fig. 3
figure 3

Scheme of the potential form in square-wave voltammetry. The inset displays a single SW cycle and the method for the current measurements in SWV

Full size image

Two adjacent, oppositely oriented pulses constitute a single potential cycle (inset of Fig. 3). The purpose of applying opposite pulses is to gain insight into the mechanism of the electrode reaction of interest by driving it consecutively in anodic (oxidation) and cathodic (reduction) directions. Another crucial parameter is the duration of a single potential step (τ), consisting of two equal-duration pulses (tp), while the inverse value of τ is referred to as the SW frequency f = 1/τ = 1/(2tp). The frequency represents the critical time of the experiment to drive the electrode reaction in both anodic and cathodic directions. The frequency typically ranges from a few to 1000 Hz, corresponding to a single pulse duration of about 0.5 to 50 ms.

The experimental data obtained from SWV is presented in the form of a square-wave voltammogram (Fig. 4). For an electrode reaction of the type Red = Ox + e, the oxidative (forward) current component (If) is composed of the currents sampled at the end of oxidative (forward) pulses, while the reduction current component (Ib) corresponds to backward pulses [8, 10, 11]. Additionally, a “net voltammetric curve” can be mathematically generated by subtracting the corresponding forward and reverse current values (ΔI ≈ Inet = If − Ib). This method actually yields a sum of the absolute current values, which has obvious advantages in an analytical context.

Fig. 4
figure 4

Square-wave voltammogram (forward, backward and net current components) portraying the electron transfer between a working electrode and a water-soluble redox analyte

Full size image

Features of a square-wave voltammogram

The square-wave voltammetric pattern shown in Fig. 4 represents the electron transfer reaction between the working electrode and an analyte that is fully soluble in the electrolyte solution [8]. It is evident from Fig. 4 that all current components, encompassing forward, backward, and net currents, exhibit a profile characterized by a peak-like shape. This feature is advantageous in analytical context since the intensity of the peak (the so-called “peak-current”) is proportional to the analyte bulk concentration, while the position on the potential axis (or the “peak-potential”) is related to the type of analyte [3, 5, 8,9,10]. By examining the profiles of the forward and backward current components and the experimental method, an analogy with cyclic voltammetry can be found, as both techniques provide insight into the mechanistic aspects of the electrode reaction. It should be noted that the intensity of the net current component is greater than that of the forward and backward components, which is a remarkable feature of SWV in analytical terms. Moreover, variation of the SW amplitude of potential pulses (i.e., the intensity of a potential pulse) is an additional valuable degree of freedom in performing the SW voltammetric experiment. Additionally, it is worth mentioning that fast scan-rates (even larger than 1 V/s) can be easily employed in SWV, making the time scale of SW voltammetric experiments significantly shorter than that of conventional cyclic voltammetry. A typical experiment that requires several minutes in cyclic voltammetry can be performed in seconds using the SWV. Furthermore, fast scan rates in SWV can be used to access rate parameters of systems undergoing rapid electrochemical/chemical transformations.

There must be a law connecting applied potential with the Faradaic current and the concentration of analyte in a single equation

Voltammetry is a dynamic experimental technique that operates outside of thermodynamic equilibrium. It involves applying a time-varying electrical potential difference, E(t), which drives the defined electrode reaction (1) in a particular direction. This process results in the flow of electric current throughout the entire experimental system.

$$Red \left(solution\right)\leftrightarrows Ox \left(solution\right)+{ne}^{-}$$
(1)

If concentrations of the redox species at the electrode surface vary during a voltammetric experiment, but still obey Nernst’s law (2) for a given applied potential throughout the experiment, then the electrode reaction is considered as electrochemically reversible, regardless of the experiment's dynamics.

$$E\left(t\right)=E^{\theta'}+(RT/nF)ln\lbrack c_{Ox}(O,t)/c_{Red}(O,t)\rbrack$$
(2)

Clearly, the term electrochemical reversibility has a different meaning than chemical reversibility, a phrase used in general chemistry, which frequently refers to the bidirectional character of a reacting system (A ⇆ B). Within the context of thermodynamics, the term “reversible” is used to describe a system that maintains a state of equilibrium and can be shifted from its initial to a final state through an infinitesimally small external force applied at an equally infinitesimal rate. In theory, this process requires an infinite amount of time to complete.

In Eq. (2) the symbol E(t) stands for the working electrode interfacial potential difference at time t of the experiment, E is the formal reduction potential of the redox couple (Ox/Red) (both potentials expressed versus particular reference electrode), R is the universal gas constant, T is thermodynamic temperature, F is Faraday constant, n is the stoichiometric number of electrons in Eq. (1), and ci(0,t) is the molar concentration at the electrode surface (i.e., at distance x = 0 measured from the electrode surface at a given time t). Another way of expressing a reversible electrode reaction is to say that at any given potential of the working electrode the redox equilibrium of reaction (1) is instantly established at the electrode surface in accordance with Nernst Eq. (2). Accordingly, changing the electrode potential E(t) affects the concentration ratio cOx(0,t)/cRed(0,t), shifting the redox equilibrium in particular direction and thus causing the current to flow in the system.

It is however important to recall again that the electrode reaction (1) takes place only at the working electrode/electrolyte interface. During the voltammetric experiment, the surface concentrations of both oxidized and reduced species (Ox and Red) deviate from their bulk concentrations. This leads to a continual occurrence of spontaneous mass transfer that happens via diffusion. For these reasons, the concentration of redox species Ox and Red is a complex function of both time and space (i.e., c(x,t)), and the evolution of this function for both redox species can be obtained only by means of a rigorous mathematical treatment and numerical simulations [3, 8, 9]. Consequently, the voltammetric outcome of a reversible electrode reaction is affected both by the Nernst law (Eq. 2) and the diffusion mass transfer, in the case of a simple electrode reaction of a dissolved redox couple. Speaking in terms of the dynamics (rate) of the two main processes, i.e., the electron transfer and the mass transfer, the latter is rate limiting one. The voltammetric features of a reversible electrode reaction are affected by both Nernst’s law, which exposes the formal redox potential E, and diffusion mass transfer, which relates the current (particularly the net peak current) to the bulk or analytical concentration of the analyte.

When the electron transfer rate is slow enough that the electrode reaction (1) is unable to attain redox equilibrium for a specific potential, it is referred to as a quasi-reversible electrode reaction. An empirically derived law relating the surface concentrations, electrode potential, kinetic parameters of the electrode reaction, and the current, is represented by the Butler-Volmer Eq. (3) [3, 5, 8,9,10,11]:

$$\frac I{FA}=k_sexp\;\left\lfloor\frac{\alpha F}{RT}\left(E-E^{\theta'}\right)\right\rfloor\left\{c_{\mathrm{Red}}(0,t)-c_{\mathrm{Ox}}(0,t)\exp\left[-\frac F{RT}\left(E-E^{\theta'}\right)\right]\right\}$$
(3)

commonly, the Butler-Volmer equation is written for a one-electron process (n = 1). Assuming a multielectron transfer electrode reaction (n ≠ 1), which indeed is a composition of sequential single-electron transfers, only one of these steps is the rate limiting. The Butler-Volmer equation is widely regarded as the fundamental equation in voltammetry [3, 5, 8, 12]. It provides a framework for understanding how the kinetics of the electrode reaction, measured through the current, depends on the electrode potential. The Eq. (3) considers two critical kinetic parameters, i.e., the standard rate constant of electron transfer ks and the electron transfer coefficient α [3, 8]. These constants are unique to each electrode reaction and depend on specific experimental conditions, such as the type of electrode, the composition of the electrolyte solution, and the temperature.

In addition to other symbols previously defined, Eq. (3) includes the electrode surface area A. Obviously, the role of the diffusion mass transfer cannot be avoided, as the actual rate of the electrode reaction depends, besides others, on the surface concentrations ci(0,t). Consequently, the voltammetric properties of a quasi-reversible electrode reaction are highly dependent upon both the kinetics of electron transfer and mass transport phenomena. However, unlike in the reversible electrode reaction, the electron transfer process is the rate-limiting step. It is finally worth to underline that Eq. (3) includes a typical thermodynamic parameter such as the formal reduction potential E. The last parameter (E) in voltammetry is related to conditions when the electrode reaction is in equilibrium at the electrode surface, while the surface concentrations of the two redox species are equal.

Simulations in voltammetry

Although voltammetry is an important electroanalytical tool, it is a very challenging technique that cannot be easily comprehended. The current–potential voltammograms portray the underlying physico-chemical processes in the system and are depicted through relatively “simple” curves. Even though experienced electroanalytical chemists may be able to intuitively perceive most of the chemistry from a single voltammogram, comparing experimental voltammetry with a corresponding theoretical prediction is necessary to obtain quantitative information. Theoretical simulations serve as valuable tools for various purposes, including the prediction and improvement of electrochemical system performance, the elucidation of electrode reaction mechanisms and the design of new experiments aimed at enhancing the accuracy and selectivity of voltammetric measurements. The entire process of theoretical modeling is quite challenging, as it requires advanced skills in mathematics to solve complex sets of differential equations. In addition, proficiency in computer programming is also necessary to represent the mathematical solutions with an algorithm that can calculate voltammetric curves. Given that simulation is almost an inevitable task for accessing the nature of the electrode mechanism and critical physical constants (such as the formal reduction potential of the redox couple, the standard rate constant, the electron transfer coefficient, the adsorption equilibrium constant, and the rate constant of a plausible chemical reaction coupled to the electrode reaction), several simulation packages have been developed. A set of simple platforms, which allow simulation of cyclic voltammograms using Excel, are already available for free [7, 13,14,15]. While not delving into solving mathematics representing a particular electrode reaction under the conditions of SWV, this article aims to introduce a simulation protocol for calculating square-wave voltammograms using the MATHCAD software.

What contains a MATHCAD working sheet for simulation of square-wave voltammograms?

Figure S1 in the Supporting Material displays a snapshot of entire working sheet of the MATHCAD file used to compute the SW voltammograms of a quasi-reversible electrode reaction of a dissolved redox couple (Eq. 1), where only the Red form of the analyte is initially present in electrolyte solution. The electrode reaction takes place at a planar macroscopic electrode, and thus, linear diffusion perpendicular to the electrode surface is considered. The algorithm is mathematically derived by applying the step-function method described in detail in [8, 16].

The MATHCAD file in Fig. S1 begins by defining the necessary constants for generating a typical potential modulation in SWV (Eqs. 1−8 in Fig. S1). To perform numerical integration, the entire duration of a single SW excitation signal is divided into a finite number of time increments (Eq. (5) in Fig. S1). The time increment, d, is related to the SW frequency via the relation d = 1/(50f). This expression indicates that each potential cycle in SWV is divided into 50 time-increments. The number of potential cycles, consisting of two oppositely oriented pulses, is determined by the ratio ∆E/dE, where ∆E is the potential interval from the starting to the final potential, and dE is the potential step increment (Eqs. 3 and 4 in Fig. S1). Therefore, the total number of time increments is (∆E/dE)·50, while the serial number of time increments ranges from 1 to (∆E/dE)·50 (Eq. (5) in Fig. S1).

Although MATHCAD has a database of various mathematical functions, none of them resembles the shape of the SW excitation signal. However, this problem can be solved by appropriately combining the mathematical “ceil” function with the logical “if” function, as reported in [17] (Eq. (8) and Graph (I) in Fig. S1). By using the potential function, one can easily define the dimensionless potential Φ used for numerical calculations (Eqs. 9–12 in Fig. S1).

The recursive formulas (18) and (19) in Fig. S1 are used to calculate the dimensionless response during the SWV experiment. The Sm factor (Eq. 17 in Fig. S1) follows from the numerical integration applied in the mathematical modeling [8, 17]. After processing the formulas (18) and (19), a new plot can be generated that displays the variation of the current with time for each SW potential pulse (Graph (II) in Fig. S1). The dimensionless function Ψ (eqs. 18, 19 in Fig. S1) incorporates critical parameters that govern the voltammetric responses, i.e., electrode potential (Eq. 8), electrode kinetics (Eqs. 14 and 15), and the mass transfer taking place via diffusion (Eq. 13 in Fig. S1).

To understand the advantages of working with dimensionless parameters, let us consider the meaning of the electrode kinetic parameter κ (Eq. (16) in Fig. S1), which determines the so called “apparent electrochemical reversibility” of the electrode reaction. In the present electrode mechanism, the latter parameter is defined as κ = ks/(Df)0.5, where ks is the standard rate constant of electron transfer, D is the common diffusion coefficient, and f is the SW frequency (eqs. 13, 14 in Fig. S1). The value of κ = 1, for example, can be obtained for the following set of parameters referring to a given electrode reaction: ks = 0.01 cm s−1, D = 0.00001 cm2 s−1, and f = 10 s−1. However, κ = 1 can also be obtained for magnitudes of ks = 0.002 cm s−1, D = 0.000004 cm2 s−1 and f = 1 s−1, referring to a different electrode reaction. Thus, the term “apparent electrochemical reversibility” may seem imprecise, but its purpose is to provide a quantitative criterion for comparing the rates of electron transfer (represented by ks) and diffusion (represented by (Df)0.5), which determine the overall voltammetric behavior. The electrode kinetic parameter κ serves as such a criterion by incorporating both effects. In previous examples, the two distinct electrode reactions are characterized with identical value of κ, (i.e., κ = 1) as the relationship between ks and (Df)0.5 is the same. Therefore, they exhibit identical apparent electrochemical reversibility, as indicated by various voltammetric characteristics, such as the net-peak potential, forward and backward components’ morphology, peak potential difference, peak-current ratio, and net half-peak width [8, 11]. Yet, the absolute value of the real current I for these two reactions differs, as it is defined as I = CΨ (see Eqs. 27–29 in Fig. S1, and the discussed below), where C is the amperometric constant, which additionally depends on D and f (Eq. 26 in Fig. S1).

Before delving into the real current calculation, it is worth noting that SWV only considers the current at the end of each potential pulse to exclude the capacitive current during the experiment and enhance the analytical sensitivity. This procedure does not include the capacitive (charging) current calculation in the current MATHCAD file. For instance, for the electrode reaction (1) in the overall oxidative direction with Red form as the initial reactant and the starting potential more negative than the formal redox potential, the forward current component (Ψf) of the SW voltammogram comprises the currents measured at the end of all forward (anodic) pulses (Eq. (22) in Fig. S1), whereas the backward component (Ψb) contains currents measured at the end of each backward (cathodic) pulse (Eq. (23) in Fig. S1). The net current component (Ψnet) is then calculated as the difference between the forward and backward currents (Eq. (24) in Fig. S1). In SWV, the current data are plotted against the potential values of the staircase ramp, which corresponds to the mid-potential of each potential cycle consisting of two adjacent oppositely oriented pulses (Eqs. 20, 21 in Fig. S1). Graph (III) in Fig. S1 depicts the dimensionless SW voltammetric response of the electrode reaction.

Finally, let us relate the real current I (which corresponds to the current measured in the experiment) to the dimensionless current Ψ (Eqs. 27–29 in Fig. S1). Specifically, the real current is a product of an amperometric constant C and the dimensionless function Ψ (Eqs. 24–31 in Fig. S1). The amperometric constant C is defined with C = FAc × (Df)1/2, and it is a collection of typical constants for a given set of experimental conditions. In the definition of C, the symbol “c*” represents the bulk molar concentration of the reactant Red, while D denotes the common diffusion coefficient of both redox species, Ox and Red (Eqs. 24–26 in Fig. S1). Additionally, f denotes the SW frequency, while the symbols F and A have already been introduced earlier. As previously noted, the product (Df)1/2 represents the rate of diffusional mass transfer, which depends on the diffusion rate constant (D) and the critical time of the experiment represented by the frequency f. In addition, Eq. (30) in Fig. S1 introduces the real formal potential of the electrode reaction, expressed versus a particular reference electrode. This allows the potential in SWV to be defined versus the given reference electrode. Finally, Graph (IV) in Fig. S1 represents a simulated SW voltammogram corresponding to a real experiment, where the current is in amperes and the potential is in volts.

How to perform simulations of square-wave voltammograms in MATHCAD?

Various voltammetric analyzes can be performed by considering the definitions of the parameters described in Fig. S1. It is important to note that during a single analysis in the MATHCAD file as that given in supplementary of this work, only one parameter can be modified while all other parameters must remain constant. For instance, the electron transfer coefficient (α) can be varied commonly within the range of 0.3 < α < 0.7 to study its role, while keeping all other parameters constant, such as temperature, starting potential, final potential, square-wave amplitude, frequency, potential step, ks, D, etc. This type of analysis allows for the comparison of the voltammetric response of electrode reactions characterized with different α values.

To extract the parameters relevant to a given electrode reaction, one approach is to construct “working curves”, as reported elsewhere [8, 9]. Working curves typically illustrate the relationships between certain measurable parameters of simulated voltammograms (peak currents, peak potentials, half-peak widths, peak-to-peak potential separation, etc.) as a function of the parameter being analyzed (e.g., frequency, SW amplitude, concentration of the analyte, kinetic parameters). From the dependencies displayed by the working curves, one can estimate the physical parameters relevant to the mechanism under consideration [3, 8, 9]. Alternatively, direct comparison between theoretical and experimental data can be done by “fitting” procedure, for the purpose of finding a set of critical parameters (e.g., the standard rate constant and the electron transfer coefficient) corresponding to the best fit.

Conclusions

This work presents readers with a fast and relatively straightforward simulation approach for computing square-wave voltammograms by using a MATHCAD platform. One major benefit of using the MATHCAD working file we offer for simulations is that no proficiency in computer programming is required. Moreover, we can provide upon request simulation-ready MATHCAD working files for numerous electrochemical mechanisms that are linked with preceding, intermediate, or follow-up chemical reactions upon request. The simulation procedure described in this work can serve as a fundamental building block for undergraduate students who wish to deepen their understanding of square-wave voltammetry. For more advanced approach involving mathematical solving of differential equations relevant for square-wave voltammetry, one can take advantage of the practical examples described in [8]. For more deeper insight into the details of the software package MATHCAD, one can use the Mathcad User’s Guide available in [18]. A 30-day MATHCAD free trial software can be downloaded at Mathcad 14.0 Download (Free trial)—mathcad.exe (informer.com).