Skip to main content

Advertisement

SpringerLink
Log in

Delegation in multiproduct downstream firms with heterogeneous channels

  • Published:
Journal of Economics Aims and scope Submit manuscript

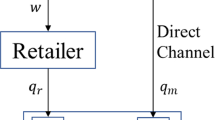
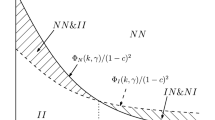
Abstract

Incorporating an exclusive dealing extension into Cournot competition, we analyze the multiproduct downstream firms’ choice of organizational form between the unitary form (U-form) for corporate incentive and the multidivisional form (M-form) for divisional incentive. The U-form in the managerial delegation for downstream firms is a dominant strategy under partial and binding exclusive dealings, while the M-form for downstream firms is a dominant strategy under non-binding exclusive dealing. If the degree of interbrand competition is sufficiently large when comparing the two forms in equilibrium, social welfare and consumer surplus within the U-form under partial exclusive dealing are greater than those within the M-form under non-binding exclusive dealing, and vice versa. When decentralized bargaining is allowed, (i) strategic delegation is redundant and (ii) regardless of the channel structure, one downstream firm chooses the M-form and the other the U-form, except for a small intermediate substitutability range.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. The pioneering works of strategic delegation are Vickers (1985), Fershtman and Judd (1987) and Sklivas (1987) among others. Later studies extend these basic models to explicitly model the endogenous choice of delegation in a duopoly (see Lambertini 2017, chapter 5) for excellent survey of divisionalization and vertical relations). Recently, Pan and D., Lee and K. Choi, (2020) demonstrated theoretical approach to clarify how firms’ delegation incentives are affected by consumers’ heterogeneity in willingness to pay.

  2. Park (2002) investigates strategic delegation among vertically related firms in where each firm produces a single homogeneous good. Consequently, the strategic value of delegation contracts disappears, and managerial downstream firms behave like owner-managed firms.

  3. For more exclusive dealing as theoretical and real-world example of contract case, see Chang (1992) and Fumagalli et al. (2018, Chapter 3).

  4. This is equivalent to the implicit assumption of the model that relates to the view of trading with a non-exclusive distribution contract.

  5. For example, the Boeing selects General Electric as the exclusive engine supplier for Boeing 777X in 1999. See “GE Unit Lands Exclusive Boeing Pact For Developing Commercial Jet Engine,” Wall Street Journal, 1999; July 8.

  6. Evidently, Boeing’s supply chain is globally spread and includes component and technology providers, which one supposes are best-in-class. Boeing moves up in the supply chain to a role as an assembler and integrator, rather than doing all work itself. Airbus has partnered with multiple companies in its tier-organized supplier base, who participate as risk-sharing partners in the program. Embraer has developed its E-jet series in close cooperation with 16 risk-sharing partners and 22 main suppliers.

  7. More specifically, “Toyota has a two supplier policy: \(\ldots\) there must always be at least two suppliers for each category of component. \(\ldots\) Guaranteeing the supplier that it will continue to make the part throughout the life of the model helps to protect any specific investment the suppliers makes (Milgrom and Roberts 1992; p. 567)”.

  8. Polasky (1992) showed that with linear demand and costless divisionalization, there is no equilibrium as firms wish continually to expand their number of divisions.

  9. See also Corchon and Gonzalez-Maestre (2000) for the case of concave demand functions.

  10. Even though we adopt \(p_i=1 - q_{ik}-\alpha q_{il} - d(q_{jk}+\alpha q_{jl})\) where \(\alpha\) measures the degree of intrabrand competition between downstream firms’ goods, we have exactly the same results. Thus, for the simplicity, we employ simple demand function with \(\alpha =1\). The detailed derivations are available from the author on request.

  11. For example, this implies that the productivity of one unit of input j, when provided by supplier A, is the same as the productivity of this input when provided by supplier B.

  12. The impact on the choice of M-form or U-form that we focus on is the symmetric one between supplier and downstream firm alluded to both sides of downward and upward exclusive dealings. See Sects. 4.3 and 6.2.

  13. This approach is similar to Moner-Colonques et al. (2004a). For the analysis of binding exclusive dealing contract, we will mention later in Sect. 4.3.

  14. Even if the supplier decides to form unitary or multidivision and other timing is still sustained, the results are not changed. That is, \(S_k^{MM}-S_k^{UM}=\frac{2d(1-c)^2 (2 + d)\Theta _2}{ (1+ d) \Psi _{MU}^2\Psi _{MM}^2}>0\) and \(S_k^{UU}-S_k^{MU}=\frac{-d(1-c)^2\Theta _3}{ 1600(1+d) \Psi _{MU}^2}<0\).

  15. When suppliers decides to form unitary or multidivision and other timing is still sustained in the case of which managers maximize profits, the results are as follows: \(\underline{S}_k^{MM}-\underline{S}_k^{UM}=\frac{2 (3 - d) d (2 + d)^2 (15 + 15 d + 4 d^2)}{(1 + d) (3 + d)^2 (3 +2 d)^2 (15 + 7 d)^2}> 0,\) \(\underline{S}_k^{UU}-\underline{S}_k^{MU}=\frac{-8 d (405+18 d -180 d^2 - 49 d^3)}{81 (1 + d) (3 + d)^2 (15 +7 d)^2}< 0\) and \(\underline{S}_k^{UU}-\underline{S}_k^{MM}=\frac{2 d^2 (63 + 63 d + 16 d^2)}{81(1 + d) (3 + d)^2 (3 + 2 d)^2}>0\).

  16. Implicit to the model is the view that, given two suppliers and two downstream firms, and all are assumed to be active, then each supplier only supplies one downstream firm and each contracting pair has information in equilibrium as analyzed by Chang (1992) and Dobson and Waterson (1996a). Even with the asymmetric exclusive dealing including upward or downward exclusive dealing, the analysis of such contracts proves to be very complex with very messy calculations compared with the relatively straightforward analysis of contracts in equilibrium (see Dobson and Waterson 1996a, footnotes 5 and 9).

  17. We obtain that \(\Pi _k^{UU*}-\Pi _k^{MM*}=\frac{2 d(1-c)^2 (80 + 71 d + 16 d^2)}{25 (1 + d)^2 (5 + 2 d)^2}>0.\)

  18. When suppliers decides to form unitary or multidivision and other timing is still sustained, the results are changed. That is, \(\hat{S}_k^{MM}-\hat{S}_k^{UM}=\frac{d(1-c)^2(12+3d-2d^2)\Theta _{10}}{2(1+d) \hat{\Psi }_{MU}^2\hat{\Psi }_{MM}^2}> 0\). However, if \(d<d^s\equiv 0.202603\) and \(d>d^p\equiv 0.761933\), we have \(\hat{S}_k^{UU}-\hat{S}_k^{MU}=\frac{-2d(1-c)^2\Theta _{11}}{(14 - 9 d)^2 (1 + d) \hat{\Psi }_{MU}^2}<0\), and vice versa if \(d\in (d^s,d^p)\).

  19. When manufactures decide to form unitary or multidivision and other timing is still sustained in the case of which managers maximize profits, the results are conversely held. That is, \(\ \tilde{S}_k^{MM}- \tilde{S}_k^{UM}=\frac{d(1-c)^2 (648 - 972 d + 1044 d^2 - 405 d^3 + 54 d^4 - 11 d^5 + 2 d^6)}{2 (6- d)^2 (3- d)^2 (2- d)^2 (1 + d) (3 + d) (3 +2 d)}> 0,\) \(\tilde{S}_k^{UU}- \tilde{S}_k^{MU}=\frac{-2 d (1-c)^2(18- 18 d+ 11 d^2- 2 d^3)}{3 (6- d)^2 (2- d)^2 (1 + d) (3 + d)}<0\) and \(\tilde{S}_k^{MM}- \tilde{S}_k^{UU}=\frac{d(1-c)^2 (36- 45 d+ 37 d^2 -10 d^3)}{6 (3- d)^2 (2-d)^2 (1 + d) (3 + 2 d)}>0\).

  20. It is easy to check that \(\overline{SW}^{UU}-\overline{SW}^{MM}=\frac{8d (1-c)^2(90 + 102 d - 54 d^2 -75 d^3 + 2 d^4 + 14 d^5 + 2 d^6)}{(5-d) (1 + d) (15+ 12 d - 6 d^2 -4 d^3)^2}>0\), \(\overline{\Pi }_k^{UU}+\overline{S}_k^{UU}-(\overline{\Pi }_k^{MM}+\overline{S}_k^{MM})=\frac{8 d(1-c)^2 (450 + 300 d - 468 d^2 - 205 d^3 + 165 d^4 + 36 d^5 - 20 d^6) }{(5- d) (1 + d) (15+ 12 d - 6 d^2-4 d^3)^2}>0\) and \(\overline{CS}^{UU}-\overline{CS}^{MM}=\frac{16d^2(1-c)^2 (2-d^2)(30 + 24 d - 14 d^2 - 8 d^3 + d^4)}{(5-d) (1 + d) (15+ 12 d - 6 d^2 -4 d^3)^2}>0\).

  21. As in previous section with linear input contract, we can obtain that \(\frac{{\partial} \overline{w}_{ik}}{{\partial} \overline{\theta }_i}>0, \frac{{\partial} \overline{w}_{ik}}{{\partial} \overline{\beta }_{ik}}>0, \frac{{\partial} \overline{f}_{ik}}{{\partial} \overline{\theta }_i}<0, \frac{{\partial} \overline{f}_{ik}}{{\partial}\overline{\beta }_{ik}}<0\).

References

Download references

Acknowledgements

We are extremely indebted to the Editor-in-Chief, Giacomo Corneo, and two anonymous referees for their extensive and useful comments, suggestions and remarks that have helped me to improve the quality and clarity of this paper.

Author information

Authors and Affiliations

  1. Graduate School of International Studies, Pusan National University, Busandaehak-ro 63 beon-gil 2, Geumjeong-gu, Busan, 46241, Republic of Korea

    Kangsik Choi

Authors
  1. Kangsik Choi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kangsik Choi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Proof of Proposition 3

Simple calculations show that in the absence of manipulating the incentives,

$$\begin{aligned}&\underline{\Pi }_k^{UU}-\underline{\Pi }_k^{MU}=\frac{-8d(1-c)^2 (405 + 18 d - 180 d^2 - 49 d^3)}{81 (1 + d) (3 + d)^2 (15 +7 d)^2}< 0,\\&\underline{\Pi }_k^{MM}-\underline{\Pi }_k^{UM}=\frac{2d(1-c)^2(3- d) (2 + d)^2 (15 + 15 d + 4 d^2)}{(1 + d) (3 + d)^2 (3 + 2 d)^2 (15 + 7 d)^2}>0. \end{aligned}$$

Proof of Proposition 4

Simple calculations yield

$$\begin{aligned}&\Pi _k^{UU*}-\Pi _k^{MM}=\frac{2 (1-c)^2\Delta _0}{25 (1 + d)\Psi _{MM}^2}>0,\ S_k^{UU*}-S_k^{MM}=\frac{2(1-c)^2 \Delta _1}{25 (1 + d) \Psi _{MM}^2}> 0.\\&SW^{UU*}-SW^{MM}=\frac{4 (1-c)^2\Delta _2}{5 (1 + d) \Psi _{MM}^2 }> 0, \ CS^{UU*}-CS^{MM}=\frac{4 (1-c)^2\Delta _3}{25 (1 + d)\Psi _{MM}^2}> 0\\&\Delta _0\equiv (14750 + 52515 d + 79124 d^2 + 65959 d^3 + 33496 d^4 + 10791 d^5 +2218 d^6 + 275 d^7 + 16 d^8)\\&\Delta _1\equiv (5450 + 19795 d + 31137 d^2 + 27792 d^3 + 15448 d^4 + 5483 d^5 +1209 d^6 + 150 d^7 + 8 d^8)\\&\Delta _2\equiv (8180 + 29170 d + 43612 d^2 + 35457 d^3 + 17013 d^4 + 4898 d^5 +824 d^6 + 75 d^7 + 3 d^8)\\&\Delta _3\equiv (90 +137 d +61 d^2+ 5 d^3 -d^4) (230 + 467 d + 331 d^2 +95 d^3 + 9 d^4). \end{aligned}$$

Proof of Proposition 10

If \(d>d^{\tau }\equiv 0.9 (d<\hat{d}^{\tau }\equiv 0.87)\), we have

$$\begin{aligned}&\overline{\Pi }_k^{UU}-\overline{\Pi }_k^{MU}=\frac{8 d^2 (1-c)^2 (135 + 108 d - 324 d^2 - 18 d^3 + 75 d^4 - 6 d^5 - 2 d^6)}{ (5- d)^2 (1 + d) (45 - 9 d - 33 d^2 + 3 d^3 + 2 d^4)^2}>0, \\&\Bigl (\overline{\Pi }_k^{UM}-\overline{\Pi }_k^{MM}=\frac{4d^2(1-c)^2 (3- d^2)^2\alpha }{ (1 + d)(15 + 12 d - 6 d^2 - 4 d^3)^2 (45 - 9 d - 33 d^2 + 3 d^3 + 2 d^4)^2}> 0\Bigr ).\\&\text{where }\quad \alpha = (405 - 81 d - 324 d^2 + 432 d^3 - 495 d^4 - 765 d^5 + 426 d^6 +378 d^7 - 64 d^8 - 40 d^9), \end{aligned}$$

and vice versa if \(d<d^{\tau } (d>\hat{d}^{\tau })\). \(\square\)

The constants \(\Theta _0\sim \Theta _{11}\) in the main text

$$\begin{aligned} \Theta _0&=351307840 + 2130082101 d + 5889454920 d^2 + 9819206943 d^3 +10993578766 d^4\\&\quad + 8703496143 d^5 + 4989679680 d^6 + 2080414670 d^7 + 620878020 d^8 + 126231603 d^9\\&\quad + 15126696 d^{10} + 396827 d^{11} -172818 d^{12}-25535 d^{13}-1200d^{14}\\ \Theta _1&=351307840 + 1006724807 d + 1225049258 d^2 + 820411609 d^3+326472460 d^4\\&\quad + 77169673 d^5 + 10028522 d^6 + 552503 d^7 \\ \Theta _2&=107074240 + 581760071 d + 1403533171 d^2 + 1956107248 d^3 + 1693631544 d^4\\&\quad + 870360524 d^5 +159942646 d^6 - 123796876 d^7 - 122041756 d^8 - 55652029 d^9\\&\quad - 16042189 d^{10} -3066604 d^{11} -379252 d^{12} - 27598 d^{13} - 900 d^{14}\\ \Theta _3&= 107074240 + 245845837 d + 229875278 d^2 + 110099219 d^3 + 27113860 d^4 \\&\quad + 2580643 d^5 - 154098 d^6 - 35427 d^7 \\ \Theta _4&=405280 + 1224023 d + 1468068 d^2 + 867342 d^3 + 242432 d^4\\&\quad +16111 d^5 - 5700 d^6 - 868 d^7\\ \Theta _5&=99680 + 208893 d + 104588 d^2 - 72678 d^3 - 101888 d^4 \\&\quad -43899 d^5 - 8300 d^6 - 588 d^7\\ \Theta _6&=23514624 + 374694336 d + 175111632 d^2 - 392065920 d^3 -169602336 d^4\\&\quad + 148324608 d^5 +45796347d^6- 28635579 d^7 - 4311900 d^8 + 2785230 d^9\\&\quad + 39987 d^{10} - 103755d^{11} + 8070 d^{12} -192 d^{13} + 64 d^{14}\\ \Theta _7&=435456 + 4478976 d - 8071056 d^2 + 1059120 d^3 + 3921696 d^4\\&\quad - 1314348 d^5 - 610143 d^6 + 269508 d^7 + 17805 d^8 - 17018 d^9\\&\quad + 1680 d^{10}\\ \Theta _8&=27216 + 113940 d - 81324 d^2 - 80667 d^3 + 47601 d^4 \\&\quad +3048 d^5 -7788 d^6 + 2816 d^7 - 384 d^8\\ \Theta _9&=18144 - 74988 d + 32400 d^2 + 119757 d^3 - 20091 d^4 \\&-43852 d^5 +7088 d^6 + 4832 d^7 - 1040 d^8\\ \Theta _{10}&=317447424 - 601302528 d - 261040320 d^2 + 2313239472 d^3 + 1351694304 d^4\\&\quad - 1579989888 d^5 - 1051400736 d^6 + 495874791 d^7 + 326904903 d^8 - 100210122 d^9\\&\quad -50117022 d^{10} + 14111847 d^{11}+ 3590055 d^{12} - 1191108 d^{13} - 61968 d^{14}\\&\quad + 42656 d^{15} - 3248d^{16}\\ \Theta _{11}&=979776 - 7222608 d + 12883104 d^2 - 4398912 d^3 -5954328 d^4\\&+ 3841569 d^5 + 505227 d^6- 638063 d^7 + 36773 d^8 + 30390 d^9 -4128 d^{10} \end{aligned}$$
Table 4 Equilibrium outcomes in each exclusive dealing under bargaining
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Choi, K. Delegation in multiproduct downstream firms with heterogeneous channels. J Econ 135, 75–102 (2022). https://doi.org/10.1007/s00712-021-00752-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00712-021-00752-w

Keywords

JEL Classification

Search

Navigation