Mathematical analysis of Holden’s polylinks

Abstract

Holden described, without mathematical analysis, a kinematical method for constructing from platonic solids polylinks with flat or solid polygonal links. No statement was made about the number of polylinks. Geometric parameters of examples shown were found by trial and error. In the present paper, it is shown that each platonic solid defines a one-parametric manifold of polylinks. The geometry of flat links and of links with circular cross section is expressed in terms of the free parameter. The solution is based on a theorem which generalizes known solutions of special cases.

1 Introduction

Polylinks in the sense of Holden [4,5,6] are kinematically constructed from platonic solids as follows. The polygonal faces of a platonic solid are interpreted as flat frames with an outer and a similar inner polygon defining the frame border width b. Each frame is individually subjected to a screw displacement consisting of a rotation $\varphi$ about and a translation $-\lambda$ along the outward face normal through the center of the solid. Under certain conditions on frame border width b, rotation $\varphi$ and translation $-\lambda$, this procedure results in a polylink having the property that each inner corner of each frame coincides, in like manner, with a point on the outer edge of an adjacent frame. The location of this contact point on the edge is another important parameter of the polylink.

The construction implies that each polylink comes in two enantiomorphic forms differing in the sign of $\varphi$. Angles made by the planes of any two frames are uneffected by the screw displacements. Following the displacements, the planes of the frames enclose a platonic solid the insphere radius of which is by $\lambda$ smaller than before the displacements. Hence, polylinks have the tetrahedral, octohedral or icosahedral rotation group of the platonic solid they are derived from. As illustrative example, see the polylink shown in Figs. 15 and 16 which is derived from a cube. There are three pairs of opposite square frames in parallel planes. The two frames of each pair are rotated relative to each other through $2\varphi$. By the six planes, a cube is enclosed the side length of which is by $2\lambda$ smaller than before the displacements.

Instead of with flat frames polylinks can be constructed with solid frames having borders of circular, square or other cross sections. The requirement that each inner corner of each flat frame coincides with a point on the outer edge of an adjacent flat frame is then replaced by the requirement that at each corner of each frame two cylinders are in tangential contact with one cylinder of an adjacent frame.

Holden showed pictures of polylinks with flat frames and with solid frames. No statement was made about the number of polylinks that can be constructed from individual platonic solids. No method was specified for calculating geometric parameters (location of points of contact, components $\varphi , \lambda$ of screw displacements, border width b of flat frames, diameter of cylindrical borders or other). For the polylinks shown, only some parameters, and these only approximately, were given. Hart [2] developed a software tool for calculating better approximations and new polylinks not known to Holden. Lang [7] claims that the total number of polylinks is fifty-four.

In the present paper, a theorem is proved which specifies for each platonic solid a one-parametric manifold of polylinks with flat or solid frame borders. In Sect. 2, geometric parameters of polylinks with flat frame borders and in Sect. 3 with frame borders of circular cross section are expressed as functions of the free parameter.

2 Flat frames

Edge-connected faces of a platonic solid are referred to as adjacent faces. Faces sharing a vertex, but not an edge, are referred to as point-connected. Only the octohedron and the icosahedron have point-connected faces. Following the screw displacements, each pair of edge-connected or point-connected faces intersects in a straight line. In polylinks constructed from the octohedron and the icosahedron, lines of intersection of point-connected faces have the effect that frame borders intersect each other in finite line segments, so that making a model by simple assembly is impossible.

The only polylinks for which an analysis is given in the literature (Ref. [1]) are the ones derived from the tetrahedron and from the octohedron in the special case when the midpoints of outer edges are the points of contact with inner corners of adjacent frames. In this case, the inner corners of a frame are located on the incircle of the outer triangle, i.e., on the circle passing through the contact points. The main contribution of the present paper is the generalization of this result.

Theorem 1

Every polylink derived from any of the five platonic solids has the property that the inner corners of a frame are located on the circle passing through the contact points on the outer edge of the frame.

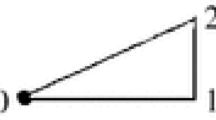
In what follows, not only a proof is given. In addition, the frame border width b, the rotation $\varphi$ and the translation $\lambda$ are expressed as functions of the parameter specifying the location of the contact points. Solid lines in Figs. 1, 2 and 3 show a single face $V_1,\dots ,V_n$ of a platonic solid of edge length 1 ($n=3:$ tetrahedron or octohedron or icosahedron in Fig. 1, $n=4:$ cube in Fig. 2, $n=5:$ dodekahedron in Fig. 3). Let $A_1, \ldots , A_n$ be the contact points. Their location is specified by the parameter $0 \le a \le 1$. The circle passing through $A_1, \ldots , A_n$ determines the inner corners $B_1,\ldots ,B_n$ of a frame (frame 0) on the face $V_1,\ldots ,V_n$ with inner side length $\ell (a)$ and border width b(a). The figures display $\varphi (a)=\angle B_3B_2A_2$.

Clockwise rotation of frame 0 about the center M through the angle $\angle B_2MA_1$ results in the frame drawn in dashed lines with vertices $V'_1,\ldots ,V'_n$. Let n frames $j=1,\ldots n$ (3, 4, 5, respectively) be superimposed on the rotated frame. Let, furthermore, frame j be connected to frame 0 only at the points $A_j$ and $B_j$. Let, finally, the frames $j=1,\ldots ,n$ be rotated, relative to frame 0, about the respective lines $A_j-B_j$ into positions in which they make with frame 0 the angle at the edge between adjacent faces of a platonic solid (tetrahedron, octohedron or icosahedron in Fig. 1, cube in Fig. 2, dodekahedron in Fig. 3). The frames thus positioned satisfy the two conditions which have to be satisfied by polylinks:

• 1. Frame j $(j=1,\ldots ,n)$ is linked with frame 0: $A_j$ is inner corner of frame j and point on the outer edge of frame 0. Reciprocally, $B_j$ is inner corner of frame 0 and point on the outer edge of frame j. From the regularity of platonic solids it follows that each frame is linked with its n adjacent frames in this pairwise reciprocal manner.

• 2. By the planes of the linked frames a platonic solid of smaller size is enclosed. Its face is the polygon $P_1,\ldots ,P_n$. This concludes the proof.

The incircle radius of the face $P_1,\ldots ,P_n$ is denoted $r_i(a)$. Let $\kappa r_i(a)$ be the insphere radius of the platonic solid. The ratio (radius of insphere)/(radius of incircle of face) is $\kappa =\sqrt{2}/2$ (tetrahedron), $\kappa =\sqrt{2}$ (octohedron), $\kappa =(\sqrt{5}+3)/2$ (icosahedron), $\kappa =1$ (cube) and $\kappa =(\sqrt{5}+1)/2$ (dodekahedron).

The angular component of the screw displacements is the angle $\varphi$ shown in the figures. The translatory component is $\lambda = \kappa [r_i(0)-r_i(a)]$. The figures determine $\ell$, b, $\varphi$ and $r_i$ as functions of a and of $\psi =\frac{1}{2} \angle V_1MV_2 =\pi /n$ $(n=3,4,5$, respectively):

(1)

Fig. 1

Frame 0 and adjacent frames $j=1,2,3$ rotated about the respective lines $A_j-B_j$ into the plane of frame 0. Parameter a, inner side length $\ell (a)$, border width b(a), rotation angle $\varphi (a)$, incircle radius $r_i(a)$

Fig. 2

Frame 0 and adjacent frames $j=1,2,3,4$

Elimination of $\ell$ and b from the first three equations results in a quadratic equation for a as function of $\varphi$. This equation has the irrelevant solution $a=(1-2\cos 2\psi )^{-1}$ independent of $\varphi$ and the relevant solution

$$\begin{aligned} a = \big (1- \cos 2 \psi +\sin 2\psi \; \text{ cotan }\,2\varphi \big )^{-1}. \end{aligned}$$

(2)

From this it follows that

$$\begin{aligned} \tan 2 \varphi =\frac{a \sin 2 \psi }{1- 2a \sin ^2 \psi }. \end{aligned}$$

(3)

Consider Figs. 1, 2, 3 again. The circle passing through $A_1,\ldots ,A_n$ intersects the outer edge of frame 0 in n more points. These are, with the same value of a, the contact points of the enantiomorphic polylink differing in the sign of $\varphi$.

Polylinks constructed from the tetrahedron, the octohedron and the icosahedron are identical in $\ell (a)$, b(a) and $\varphi (a)$ and different in $\lambda (a)$ only.

The special case $a=1/2$: $\varphi =\psi /2$; $\ell$ has its minimum $\cos \psi$ and b its maximum $\frac{1}{2}(1-\cos \psi )\text{ cotan }\,\psi$. The maximum $b_{\max }$ is $\sqrt{3}/12\approx .1443$ (triangle), $(2-\sqrt{2})/4 \approx .1464$ (square) and $(1/40)\sqrt{10(5-\sqrt{5})} \approx .1314$ (pentagon).

A parameter $a\not = 1/2$ and the parameter $a'=1-a$ determine two polylinks identical in b, but different in $\varphi$ and $\lambda$. This means: Given any polylink with parameter $a\not = 1/2$, then the frames of this polylink form a second polylink differing from the first one in $\varphi$ and $\lambda$ (see Examples 3 and 7).

Fig. 3

Frame 0 and adjacent frames $j=1,2,3,4,5$

Let ${\vec {r}}_j$ be the position vector of the vertex $V_j$ measured from the center of a platonic solid prior to screw displacements, and let ${\vec {r}}_j^{\,i}$ be the vector after the screw displacement about the unit vector ${\vec {n}}_i$. Then, (see [8], Eq. (1.38))

$$\begin{aligned} {\vec {r}}_j^{\,i}(\varphi , \lambda ) ={\vec {r}}_j \cos \varphi +\big [(1-\cos \varphi )({\vec {n}}_i\cdot {\vec {r}}_j)-\lambda \big ]{\vec {n}}_i +{\vec {n}}_i\times {\vec {r}}_j \sin \varphi . \end{aligned}$$

(4)

With $\varphi (a)$ and $\lambda (a)$, this equation determines the positions of all vertices of polylinks with flat frames as functions of a. The vertices are located on the sphere of radius

$$\begin{aligned} \vert {\vec {r}}_j^{\,i} \vert =\sqrt{ ({\vec {r}}_j)^2+\lambda ^2 -2\lambda ({\vec {n}}_i\cdot {\vec {r}}_j) }. \end{aligned}$$

(5)

A vertex of a platonic solid is shared by three faces (tetrahedron, cube, dodekahedron), by four faces (octohedron) or by five faces (icosahedron). By the screw displacements, each vertex is converted into three or four or five vertices, respectively, forming a regular polygon briefly called $\Pi$. The total number of vertices of polylinks is twelve (tetrahedron), twenty-four (cube, octohedron) or sixty (dodekahedron, icosahedron).

Examples

• 1. The parameter $a=1/3$ in Fig. 1 determines $\lambda = (\sqrt{6} -\sqrt{3}+1)/12$ (tetrahedron), $\lambda = (\sqrt{6} -\sqrt{3}+1)/6$ (octohedron), $\lambda = [ (\sqrt{6} -\sqrt{3}+1)/12][(3+\sqrt{5})/\sqrt{2}]$ (icosahedron) and in all three cases $b=(\sqrt{3}-1)/6$ and $\varphi =15^\circ$. Figure  4 shows a paper model of the polylink constructed from the tetrahedron viewed along the screw axis ${\vec {n}}_i$ of a frame $i=0,1,2,3$ arbitrary. The screw axis is orthogonally intersected by four planes, each plane spanned by an equilateral triangle of vertices centered on ${\vec {n}}_i$. On an octohedron, each face is point-connected to three faces, on an icosahedron to six faces. In as many lines, each frame of the polylink is intersected by other frames. Figure 5 shows a single frame with lines of intersection in the case of the octohedron. In Figs. 6 and 7, a paper model of this polylink is shown. $\diamond$

• 2. Subject of ref. [1] which led to Theorem 1 are the polylinks constructed from the tetrahedron and from the octohedron in the special case $a=1/2$. Both polylinks are identical. In both of them $b=\sqrt{3}/12$, $\varphi =30^\circ$ and $\lambda =\,$ radius of the insphere ($\sqrt{6}/12$ for the tetrahedron and $\sqrt{6}/6$ for the octohedron). In both of them, the centers of all frames coincide. Opposite frames of the octohedron coincide. Intersections of frames do not occur. In Figs. 8 and 9, a paper model is shown. $\diamond$

• 3. With $a=3/7$, Fig. 2 determines $b=1/7$, $\tan \varphi =1/3$, $\lambda =(1-\sqrt{10}/7)/2 \approx .2741$ of a polylink constructed from a cube. In Figs. 10 and 11, a paper model is shown. $a=4/7$ determines the polylink with the same border width $b=1/7$ and with $\tan \varphi =1/2$, $\lambda =(1-\sqrt{5}/7)/2 \approx .3403$. The polylink constructed from a cube with $a=1$ has the parameters $b=0$ (wire frames), $\varphi =45^\circ$, $\lambda =1/2$ indicating that the centers of all frames coincide and that opposite frames coincide. $\diamond$

• 4. The parameter $a=1/3$ in Fig. 3 determines $b\approx .1153$, $\varphi \approx 11.193^\circ$, $\lambda \approx .3350$ of a polylink constructed from a dodekahedron. In Figs. 12 and 13, a paper model is shown. $\diamond$

Fig. 4

Polylink constructed from tetrahedron with $a=1/3$. View normal to a frame

Fig. 5

Frame with lines of intersection in polylink constructed from octohedron with $a=1/3$

Fig. 6

Self-intersecting polylink constructed from octohedron with $a=1/3$. View normal to a pair of opposite frames

Fig. 7

Polylink of Fig. 6. View normal to a pair of opposite squares $\Pi$

Fig. 8

Polylink constructed from tetrahedron and octohedron with $a=1/2$. View normal to a frame

Fig. 9

Polylink of Fig. 8 seen along a diagonal of the octohedron (cf. [1])

Fig. 10

Polylink constructed from cube with $a=3/7$. View normal to a pair of opposite frames

Fig. 11

Polylink of Fig. 10. View normal to a pair of opposite triangles $\Pi$

Fig. 12

Polylink constructed from dodekahedron with $a=1/3$. View normal to a pair of opposite frames

Fig. 13

Polylink of Fig. 12. View normal to a pair of opposite triangles $\Pi$

3 Frame borders with circular cross section

The outer edges of flat frames are now axes of circular cylinders. The diameter 2r of two contacting cylinders with skew axes $i=1,2$ is the minimal distance between the axes. Let ${\vec {\varrho }}_i$ be an arbitrary point on axis i and let ${\vec {u}}_i$ be a vector in the direction of axis i (sense of direction and absolute value arbitrary). Then,

$$\begin{aligned} 2r= \frac{ \vert ({\vec {\varrho }}_1-\vec \varrho _2)\cdot ({\vec {u}}_1\times {\vec {u}}_2)\vert }{ \vert {\vec {u}}_1\times {\vec {u}}_2 \vert }. \end{aligned}$$

(6)

In what follows, this equation is referred to as contact condition.

Fig. 14

Axes $V_0-V_i$ of cylinders $i=1,2,3$ prior to screw displacements. Unit normal vectors ${\vec {n}}_1$, ${\vec {n}}_2$

As was said in the Introduction, two cylinders forming a corner of one frame are in contact with one cylinder of an adjacent frame. On each platonic solid contacting cylinders, vertices and unit normal vectors are labeled as follows (Fig. 14 schematically). With $V_0$ being an arbitrary vertex, $V_0-V_2$ and $V_0-V_3$ are the axes of two cylinders 2 and 3 on a frame with unit normal vector ${\vec {n}}_1$. $V_0-V_1$ is the axis of the contacting cylinder 1 on the adjacent frame with unit normal vector ${\vec {n}}_2$. With this notation, the vectors in (6) are

$$\begin{aligned} \left. \begin{aligned} {\vec {\varrho }}_1-{\vec {\varrho }}_2&={\vec {r}}_0^{\,2}-{\vec {r}}_0^{\,1 },&\\ {\vec {u}}_1&={\vec {r}}_0^{\,2}-{\vec {r}}_1^{\,2} \quad&\text{(cylinder } \text{1) }, \\ {\vec {u}}_2&={\vec {r}}_0^{\,1}-{\vec {r}}_2^{\,1}&\text{(cylinder } \text{2) }, \\ {\vec {u}}_2&={\vec {r}}_0^{\,1}-{\vec {r}}_3^{\,1}&\text{(cylinder } \text{3) }\, \end{aligned}\right\} \end{aligned}$$

(7)

and with (4)

$$\begin{aligned} \left. \begin{aligned} {\vec {\varrho }}_1-{\vec {\varrho }}_2&= [(1-\cos \varphi )({\vec {n}}_1\cdot {\vec {r}}_0)-\lambda ]({\vec {n}}_1-{\vec {n}}_2)+({\vec {n}}_1-{\vec {n}}_2)\times {\vec {r}}_0 \sin \varphi , \\ {\vec {u}}_1&=({\vec {r}}_0-{\vec {r}}_1)\cos \varphi +{\vec {n}}_2\times ({\vec {r}}_0-{\vec {r}}_1)\sin \varphi \qquad \text{(cylinder } \text{1) }, \\ {\vec {u}}_2&=({\vec {r}}_0-{\vec {r}}_2)\cos \varphi +{\vec {n}}_1\times ({\vec {r}}_0-{\vec {r}}_2)\sin \varphi \qquad \text{(cylinder } \text{2) }, \\ {\vec {u}}_2&=({\vec {r}}_0-{\vec {r}}_3)\cos \varphi +{\vec {n}}_1\times ({\vec {r}}_0-{\vec {r}}_3)\sin \varphi \qquad \text{(cylinder } \text{3) }. \end{aligned} \right\} \end{aligned}$$

(8)

Contact conditions can be obtained from coordinates of ${\vec {r}}_0$, ${\vec {r}}_1$, ${\vec {r}}_2$, ${\vec {r}}_3$. For the tetrahedron and the cube, simpler coordinate-free formulations are as follows. First, the tetrahedron. In Fig. 14, $V_0$, $V_1$, $V_2$, $V_3$ are the vertices of the tetrahedron. In accordance with this figure, face i $(i=0,1,2,3)$ with unit normal vector ${\vec {n}}_i$ is defined to be the face opposite $V_i$. Then,

$$\begin{aligned} \left. \begin{aligned} {\vec {r}}_i=-(\sqrt{6}/4){\vec {n}}_i \quad (i=0,1,2,3), \qquad {\vec {n}}_0+{\vec {n}}_1+{\vec {n}}_2+{\vec {n}}_3= {\vec {0}}, \\ {\vec {n}}_i\cdot {\vec {n}}_j = -1/3, \qquad {\vec {n}}_i\times {\vec {n}}_j = -(\sqrt{3}/3)({\vec {n}}_k-{\vec {n}}_\ell ) \quad (i\not = j). \end{aligned} \right\} \end{aligned}$$

(9)

In the last formula k and $\ell$ are functions of i and j according to Table 1. With these relationships, (8) and (6) result in the contact conditions (14).

Next, the cube. With mutually orthogonal unit normal vectors $\vec {n}_1,\,{\vec {n}}_2,\,{\vec {n}}_3$

$$\begin{aligned} {\vec {r}}_0=({\vec {n}}_1+{\vec {n}}_2+{\vec {n}}_3)/2, \qquad {\vec {r}}_0-{\vec {r}}_i={\vec {n}}_i \quad (i=1,2,3). \end{aligned}$$

(10)

This results in the contact conditions (17).

For the octohedron, the icosahedron and the dodekahedron lengthy coordinate equations are unavoidable. Cartesian coordinates of ${\vec {r}}_0$, ${\vec {r}}_1$, ${\vec {r}}_2$, ${\vec {r}}_3$ are as follows.

Table 1 Indices $k,\ell$ as functions of i, j in (9)

Octohedron:

$$\begin{aligned} {\vec {r}}_0: \frac{\sqrt{2}}{2} \left[ \begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right] , \quad {\vec {r}}_1: \frac{\sqrt{2}}{2} \left[ \begin{array}{r} 0 \\ -1 \\ 0 \end{array}\right] , \quad {\vec {r}}_2: \frac{\sqrt{2}}{2} \left[ \begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right] , \quad {\vec {r}}_3: \frac{\sqrt{2}}{2} \left[ \begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] . \end{aligned}$$

(11)

Icosahedron: With $c=(\sqrt{5}+1)/2$

$$\begin{aligned} {\vec {r}}_0: \frac{1}{2} \left[ \begin{array}{r} c \\ 0 \\ -1 \end{array}\right] , \quad {\vec {r}}_1: \frac{1}{2} \left[ \begin{array}{r} 1 \\ -c \\ 0 \end{array}\right] , \quad {\vec {r}}_2: \frac{1}{2} \left[ \begin{array}{r} 1 \\ c \\ 0 \end{array}\right] , \quad {\vec {r}}_3: \frac{1}{2} \left[ \begin{array}{c} c \\ 0 \\ 1 \end{array}\right] . \end{aligned}$$

(12)

Dodekahedron: With $c=(\sqrt{5}+1)/2$

$$\begin{aligned} {\vec {r}}_0: \frac{1}{2} \left[ \begin{array}{c} c \\ c\\ c \end{array}\right] , \quad {\vec {r}}_1: \frac{1}{2} \left[ \begin{array}{c} 1+c \\ 1 \\ 0 \end{array}\right] , \quad {\vec {r}}_2: \frac{1}{2} \left[ \begin{array}{c} 0\\ 1+c\\ 1 \end{array}\right] , \quad {\vec {r}}_3: \frac{1}{2} \left[ \begin{array}{c} 1 \\ 0 \\ 1+c \end{array}\right] . \end{aligned}$$

(13)

This leads to the contact conditions (15), (16) and (18). The complete collection of contact conditions is given below. From two contact conditions, 2r and $\lambda$ are calculated as functions of $\varphi$. The choice of signs is dictated by the condition that $\lambda$ must be positive.

Tetrahedron:

$$\begin{aligned} \left. \begin{aligned} 2r&=\frac{ 2 \left| \sqrt{6}(\sin \varphi +\sin 2\varphi ) -12\lambda \sin 2\varphi \right| }{3\sqrt{ 27+8( \cos 2\varphi -\cos 4\varphi ) } }, \\ 2r&=\frac{ 2\left| \sqrt{6}( \sin \varphi -\sqrt{3}/2 ) [1+2\sin (\varphi -30^\circ )] +12 \lambda \cos (2\varphi -30^\circ ) \right| }{ 3\sqrt{ 27-4(1+2\cos 2\varphi )[1-2\cos (2\varphi -60^\circ ) ] } }. \end{aligned} \right\} \end{aligned}$$

(14)

Octohedron:

$$\begin{aligned} \left. \begin{aligned} 2r&= \frac{\left| \sqrt{6}(\sin \varphi +\sin 2\varphi )-6\lambda \sin 2\varphi \right| }{3\sqrt{9-4\sin ^4 \varphi } }, \\ 2r&= \frac{ \sqrt{2}\left| \sqrt{6}[\sin \varphi -\sin (\varphi +60^\circ )+\sin (2\varphi +60^\circ )] -6\lambda \sin (2\varphi +60^\circ ) \right| }{3\sqrt{ 15+4\sin (2\varphi -30^\circ )+\sin (4\varphi +30^\circ ) } }. \end{aligned} \right\} \end{aligned}$$

(15)

Icosahedron: With $c=(\sqrt{5}+1)/2=2\cos 36^\circ$

$$\begin{aligned} \left. \begin{aligned} 2r&= \frac{ 2\left| \sqrt{3}(\sin \varphi +\sin 2\varphi )-6\lambda (2-c)\sin 2\varphi \right| }{3 \sqrt{ 3 (8+c)+4\cos 2 \varphi -2(5-3c) \cos 4 \varphi } }, \\ 2r&= \frac{ 2\left| \sqrt{3}[\sin (\varphi -60^\circ ) +\sin (2\varphi +60^\circ ) ]-6\lambda (2-c)\sin (2\varphi +60^\circ ) \right| }{3 \sqrt{ 3 (8+c)-4\cos (2\varphi +60^\circ ) +2(5-3c) \cos (4\varphi -60^\circ ) } }. \end{aligned} \right\} \end{aligned}$$

(16)

Cube:

$$\begin{aligned} 2r = \frac{\vert (1-2\lambda )\sin \varphi \vert }{ \sqrt{1+\sin ^2 \varphi } }, \qquad 2r = \frac{\vert \cos \varphi -\sin \varphi -(1-2\lambda ) \cos 2\varphi \vert }{ \sqrt{4- \sin ^2 2\varphi } }. \end{aligned}$$

(17)

Dodekahedron: With $S=(\sqrt{5}-1)/4=\sin 18^\circ$, $C =\sqrt{(5+\sqrt{5})/8}=\cos 18^\circ$

$$\begin{aligned} \left. \begin{aligned} 2r&=\frac{ 2 \Big \vert C[\sin \varphi -(1+2S) \sin 2 \varphi ] +2\lambda (1-S)\sin 2\varphi \Big \vert }{ 5\sqrt{1-\frac{1}{5}\Big [ (1+2S)(1-\cos 2\varphi )+S^2(3+2\cos 4\varphi ) \Big ] } }, \\ 2r&= \frac{ \Big \vert (2+3S) (\cos \varphi -\cos 2\varphi )-C[ (3+4S)\sin \varphi -\sin 2\varphi ] +4\lambda (1-S) \cos (2\varphi +18^\circ ) \Big \vert }{5 \sqrt{1-\frac{1}{10} \Big [ S(1+6S)+4S[ \sin (2\varphi +18^\circ ) +C\sin 4\varphi ] -\sin (4\varphi +18^\circ ) \Big ] } }. \end{aligned} \right\} \end{aligned}$$

(18)

Fig. 15

Polylink of Example 6. View normal to a pair of opposite frames

Fig. 16

Polylink of Example 6. View normal to a pair of opposite triangles $\Pi$

Examples

• 5. With $\varphi =30^\circ$ determined in Example 2, the contact conditions for the tetrahedron and for the octohedron yield identical polylinks with $2r=2/\sqrt{210}$, $\lambda =\,$ radius of insphere ($\sqrt{6}/12$ and $\sqrt{6}/6$, respectively). For making a model, rods of length $L =1 +2r\sqrt{3}= 1+2/\sqrt{70}$ must be cut. This yields $L /(2r)=\sqrt{3}(1+\sqrt{70}/2)\approx 8.9777$. Holden’s model in [6], Fig. 5.7, was built with $L /(2r)= 9$ found by trial and error. $\diamond$

• 6. With $\varphi =\arctan (1/3)$ determined in Example 3, Eq. (17) determine

  $$\begin{aligned} \left. \begin{aligned} 2r&= (\sqrt{10}/85) \left( 4\sqrt{11}-\sqrt{91} \right) \approx .1387 \\ \lambda&= \frac{1}{2}\left[ 1- (\sqrt{10}/85) \left( 44-\sqrt{1001} \right) \right] \approx .2701 \end{aligned} \right\} \end{aligned}$$

  (19)

  $\lambda$ is very close to $\lambda \approx .2741$ found in Example 3 for the polylink with flat frames. In Figs. 15 and 16, a model of this polylink is shown (compare with Figs. 10, 11). $\diamond$

• 7. For the pair of polylinks derived from a tetrahedron with parameters $a_1=1/3$ and $a_2=2/3$, Eq. (1) determine (see Example 1)

  $$\begin{aligned} b_1=b_2=(\sqrt{3}-1)/6\,, \quad \lambda _{1,2}=(\sqrt{6} \mp \sqrt{3} \pm 1)/12\,, \quad \varphi _1=15^\circ , \quad \varphi _2=45^\circ . \end{aligned}$$

  (20)

  With $\varphi _1$ and $\varphi _2$, Eq. (14) determine

  $$\begin{aligned} r_1=r_2= \frac{1}{ \sqrt{35}+2\sqrt{23+4\sqrt{3}} }, \quad \lambda _{1,2}= \frac{1}{12} \left[ \sqrt{6} \mp \sqrt{3} \pm \frac{3}{1+2\sqrt{(23+4\sqrt{3})/35} } \right] . \end{aligned}$$

  (21)

  Congruent polylinks with parameters $a_1\not =1/2$ and $a_2=1-a_1$ result in $r_1=r_2$.

4 Conclusion

Each platonic solid defines a one-parametric manifold of polylinks with flat or solid frame borders. The free parameter is the same for all five platonic solids. Geometric parameters of flat frame borders and of frame borders with circular cross section are expressed as functions of the free parameter. Polylinks constructed from the octohedron and the icosahedron frames intersect each other, so that simple assembly is impossible.