Skip to main content
SpringerLink
Log in

Active vibration control of the multilayered smart nanobeams: velocity feedback gain effects on the system’s behavior

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

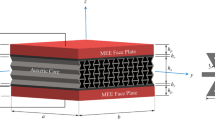
The primary focus of this study is to analyze the vibrational properties of a nanobeam with a porous structure, which is composed of a functionally graded material. Additionally, the nanobeam comprises a magnetostrictive substance known as Terfenol-D. The nanobeam is postulated to include three distinct layers, whereby the central layer is comprised of a magnetostrictive material, while the outside layers are built of functionally graded material. On the other hand, the use of higher-order parabolic shear deformation beam theory is utilized to get the kinematic relations. Moreover, Eringen’s nonlocal theory is used to include the impact of small-scale phenomena. The governing equations are derived by the application of Hamilton’s principle and then solved using analytical techniques. This study presents a thorough examination and elucidation of the influence exerted by several elements, such as aspect ratio, feedback gain, and gradient index, on the system being studied. Based on extant research, empirical evidence indicates that increasing the feedback gain results in a decrease in the natural frequencies. In order to establish the accuracy and dependability of our present study, we have undertaken a comparison examination of our results in relation to the existing body of the literature. The results of the present study have the potential to advance the understanding and progress in the field of nano-systems, namely nano-sensors and nano-actuators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Ebrahimi, F., Salari, E.: Thermal buckling and free vibration analysis of size dependent Timoshenko FG nanobeams in thermal environments. Compos. Struct. 128, 363–380 (2015)

    Google Scholar 

  2. Ebrahimi, F., Barati, M.R.: A nonlocal higher-order shear deformation beam theory for vibration analysis of size-dependent functionally graded nanobeams. Arab. J. Sci. Eng. 41(5), 1679–1690 (2016)

    MathSciNet  Google Scholar 

  3. Ebrahimi, F., Barati, M.R.: Vibration analysis of nonlocal beams made of functionally graded material in thermal environment. Europ. Phys. J. Plus 131(8), 1–22 (2016)

    Google Scholar 

  4. Tadi Beni, Y.: Size-dependent electromechanical bending, buckling, and free vibration analysis of functionally graded piezoelectric nanobeams. J. Intell. Mater. Syst. Struct. 27(16), 2199–2215 (2016)

    Google Scholar 

  5. Ebrahimi, F., Barati, M.R.: Vibration analysis of viscoelastic inhomogeneous nanobeams incorporating surface and thermal effects. Appl. Phys. A 123(1), 1–10 (2017)

    Google Scholar 

  6. Ebrahimi, F., Barati, M.R.: Hygrothermal effects on vibration characteristics of viscoelastic FG nanobeams based on nonlocal strain gradient theory. Compos. Struct. 159, 433–444 (2017)

    Google Scholar 

  7. Attia, M.A., Rahman, A.A.A.: On vibrations of functionally graded viscoelastic nanobeams with surface effects. Int. J. Eng. Sci. 127, 1–32 (2018)

    MathSciNet  Google Scholar 

  8. Eltaher, M., et al.: Modified porosity model in analysis of functionally graded porous nanobeams. J. Braz. Soc. Mech. Sci. Eng. 40(3), 1–10 (2018)

    Google Scholar 

  9. Karami, B., Janghorban, M.: A new size-dependent shear deformation theory for free vibration analysis of functionally graded/anisotropic nanobeams. Thin-Walled Struct. 143, 106227 (2019)

    Google Scholar 

  10. Kumar, Y., Gupta, A., Tounsi, A.: Size-dependent vibration response of porous graded nanostructure with FEM and nonlocal continuum model. Adv. Nano Res. 11(1), 001 (2021)

    Google Scholar 

  11. Garg, A., et al.: Predicting elemental stiffness matrix of FG nanoplates using gaussian process regression based surrogate model in framework of layerwise model. Eng. Anal. Bound. Elem. 143, 779–795 (2022)

    MathSciNet  Google Scholar 

  12. Rouabhia, A., et al.: Physical stability response of a SLGS resting on viscoelastic medium using nonlocal integral first-order theory. ICREATA’21 37, 180 (2020)

    Google Scholar 

  13. Cuong-Le, T., et al.: Nonlinear bending analysis of porous sigmoid FGM nanoplate via IGA and nonlocal strain gradient theory. Adv. Nano Res. 12(5), 441 (2022)

    Google Scholar 

  14. Bouafia, H., et al.: Natural frequencies of FGM nanoplates embedded in an elastic medium. Adv. Nano Res. 11(3), 239–249 (2021)

    Google Scholar 

  15. Van Vinh, P., Tounsi, A.: Free vibration analysis of functionally graded doubly curved nanoshells using nonlocal first-order shear deformation theory with variable nonlocal parameters. Thin-Walled Struct. 174, 109084 (2022)

    Google Scholar 

  16. Liu, G., et al.: Dynamics of imperfect inhomogeneous nanoplate with exponentially-varying properties resting on viscoelastic foundation. Europ. J. Mech. A/Solids 95, 104649 (2022)

    MathSciNet  Google Scholar 

  17. Faghidian, S.A., Tounsi, A.: Dynamic characteristics of mixture unified gradient elastic nanobeams. Facta Univ. Ser. Mech. Eng. 20(3), 539–552 (2022)

    Google Scholar 

  18. Arefi, M., et al.: Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 81, 108–117 (2018)

    Google Scholar 

  19. Zargaripoor, A., et al.: Free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory using finite element method. J. Computat. Appl. Mech. 49(1), 86–101 (2018)

    Google Scholar 

  20. Phung-Van, P., et al.: An isogeometric approach of static and free vibration analyses for porous FG nanoplates. Europ. J. Mech. A/Solids 78, 103851 (2019)

    MathSciNet  Google Scholar 

  21. Sobhy, M., Zenkour, A.M.: Porosity and inhomogeneity effects on the buckling and vibration of double-FGM nanoplates via a quasi-3D refined theory. Compos. Struct. 220, 289–303 (2019)

    Google Scholar 

  22. Hoa, L.K., et al.: Bending and free vibration analyses of functionally graded material nanoplates via a novel nonlocal single variable shear deformation plate theory. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 235(18), 3641–3653 (2021)

    Google Scholar 

  23. Singh, P.P., Azam, M.S.: Free vibration and buckling analysis of elastically supported transversely inhomogeneous functionally graded nanoplate in thermal environment using Rayleigh-Ritz method. J. Vib. Control 27(23–24), 2835–2847 (2021)

    MathSciNet  Google Scholar 

  24. Daikh, A.A., et al.: On vibration of functionally graded sandwich nanoplates in the thermal environment. J. Sandwich Struct. Mater. 23(6), 2217–2244 (2021)

    Google Scholar 

  25. Bouafia, H., et al.: Natural frequencies of FGM nanoplates embedded in an elastic medium. Adv. Nano Res. 11(3), 239–249 (2021)

    Google Scholar 

  26. Pourabdy, M., et al.: Analysis of axisymmetric vibration of functionally-graded circular nano-plate based on the integral form of the strain gradient model. J. Appl. Computat. Mech. 7(4), 2196–220 (2021)

    Google Scholar 

  27. Pham, Q.-H., et al.: A nonlocal quasi-3D theory for thermal free vibration analysis of functionally graded material nanoplates resting on elastic foundation. Case Stud. Thermal Eng. 26, 101170 (2021)

    Google Scholar 

  28. Thang, P.T., Tran, P., Nguyen-Thoi, T.: Applying nonlocal strain gradient theory to size-dependent analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Appl. Math. Model 93, 775–791 (2021)

    MathSciNet  Google Scholar 

  29. Van Vinh, P.: Nonlocal free vibration characteristics of power-law and sigmoid functionally graded nanoplates considering variable nonlocal parameter. Phys. E 135, 114951 (2022)

    Google Scholar 

  30. Tahir, S.I., et al.: Wave propagation analysis of a ceramic-metal functionally graded sandwich plate with different porosity distributions in a hygro-thermal environment. Compos. Struct. 269, 114030 (2021)

    Google Scholar 

  31. Bekkaye, T.H.L., et al.: Porosity-dependent mechanical behaviors of FG plate using refined trigonometric shear deformation theory. Comput. Concr. Int. J. 26(5), 439–450 (2020)

    Google Scholar 

  32. Zaitoun, M.W., et al.: Influence of the visco-Pasternak foundation parameters on the buckling behavior of a sandwich functional graded ceramic–metal plate in a hygrothermal environment. Thin-Walled Struct. 170, 108549 (2022)

    Google Scholar 

  33. Al-Osta, M.A., et al.: Influence of porosity on the hygro-thermo-mechanical bending response of an AFG ceramic-metal plates using an integral plate model. Smart Struct. Syst. Int. J. 28(4), 499–513 (2021)

    Google Scholar 

  34. Mudhaffar, I.M., et al.: Impact of viscoelastic foundation on bending behavior of FG plate subjected to hygro-thermo-mechanical loads. Struct. Eng. Mech. 86(2), 167–180 (2023)

    Google Scholar 

  35. Merazka, B., et al.: Hygro-thermo-mechanical bending response of FG plates resting on elastic foundations. Steel Compos. Struct. Int. J. 39(5), 631–643 (2021)

    Google Scholar 

  36. Tahir, S.I., et al.: The effect of three-variable viscoelastic foundation on the wave propagation in functionally graded sandwich plates via a simple quasi-3D HSDT. Steel Compos. Struct. 42(4), 501 (2022)

    Google Scholar 

  37. Zaitoun, M.W., et al.: An efficient computational model for vibration behavior of a functionally graded sandwich plate in a hygrothermal environment with viscoelastic foundation effects. Eng. Comput. 39(2), 1127–1141 (2023)

    Google Scholar 

  38. Sofiyev, A.: Review of research on the vibration and buckling of the FGM conical shells. Compos. Struct. 211, 301–317 (2019)

    Google Scholar 

  39. Bagheri, H., et al.: Free vibration of joined cylindrical–hemispherical FGM shells. Arch. Appl. Mech. 90, 2185–2199 (2020)

    Google Scholar 

  40. Shahmohammadi, M.A., Azhari, M., Saadatpour, M.M.: Free vibration analysis of sandwich FGM shells using isogeometric B-spline finite strip method. Steel Compos. Struct. 34(3), 361–376 (2020)

    Google Scholar 

  41. Liu, Y., Qin, Z., Chu, F.: Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate. Nonlinear Dyn. 104(2), 1007–1021 (2021)

    Google Scholar 

  42. Zghal, S., Dammak, F.: Vibration characteristics of plates and shells with functionally graded pores imperfections using an enhanced finite shell element. Comput. Math. Appl. 99, 52–72 (2021)

    MathSciNet  Google Scholar 

  43. Bennedjadi, M., et al.: Visco-elastic foundation effect on buckling response of exponentially graded sandwich plates under various boundary conditions. Geomech. Eng. 32(2), 159 (2023)

    Google Scholar 

  44. Kouider, D., et al.: An original four-variable quasi-3D shear deformation theory for the static and free vibration analysis of new type of sandwich plates with both FG face sheets and FGM hard core. Steel Compos. Struct. Int. J. 41(2), 167–191 (2021)

    Google Scholar 

  45. Tounsi, A., et al.: An integral quasi-3D computational model for the hygro-thermal wave propagation of imperfect FGM sandwich plates. Comput. Concr. 32, 61–74 (2023)

    Google Scholar 

  46. Tounsi, A., et al.: Influences of different boundary conditions and hygro-thermal environment on the free vibration responses of FGM sandwich plates resting on viscoelastic foundation. Int. J. Struct. Stab. Dyn. 23 (2023)

  47. Mudhaffar, I.M., et al.: Hygro-thermo-mechanical bending behavior of advanced functionally graded ceramic metal plate resting on a viscoelastic foundation. In: Structures, Vol. 33. Elsevier, Amsterdam, pp. 2177–2189 (2021)

    Google Scholar 

  48. Bounouara, F., et al.: The effect of visco-Pasternak foundation on the free vibration behavior of exponentially graded sandwich plates with various boundary conditions. Steel Compos. Struct. 46(3), 367–383 (2023)

    Google Scholar 

  49. Amar, L.H.H., et al.: Buckling analysis of FG plates via 2D and quasi-3D refined shear deformation theories. Struct. Eng. Mech. 85(6), 765–780 (2023)

    Google Scholar 

  50. Bouafia, K., et al.: Bending and free vibration characteristics of various compositions of FG plates on elastic foundation via quasi 3D HSDT model. Steel Compos. Struct. Int. J. 41(4), 487–503 (2021)

    Google Scholar 

  51. Hebali, H., et al.: Effect of the variable visco-Pasternak foundations on the bending and dynamic behaviors of FG plates using integral HSDT model. Arch. Appl. Mech. 83(2), 177–191 (2022)

    Google Scholar 

  52. Zenkour, A.M., El-Shahrany, H.D.: Hygrothermal effect on vibration of magnetostrictive viscoelastic sandwich plates supported by Pasternak’s foundations. Thin-Walled Struct. 157, 107007 (2020)

    Google Scholar 

  53. Zenkour, A.M., El-Shahrany, H.D.: Vibration suppression of advanced plates embedded magnetostrictive layers via various theories. J. Market. Res. 9(3), 4727–4748 (2020)

    Google Scholar 

  54. Zenkour, A.M., El-Shahrany, H.D.: Hygrothermal vibration of adaptive composite magnetostrictive laminates supported by elastic substrate medium. Europ. J. Mech. A/Solids 85, 104140 (2021)

    MathSciNet  Google Scholar 

  55. Zenkour, A.M., El-Shahrany, H.D.: Quasi-3D theory for the vibration of a magnetostrictive laminated plate on elastic medium with viscoelastic core and faces. Compos. Struct. 257, 113091 (2021)

    Google Scholar 

  56. Ebrahimi, F., Ahari, M. F.: Magnetostriction-assisted active control of the multi-layered nanoplates: effect of the porous functionally graded facesheets on the system’s behavior. Eng. Comput. 38, 1–15 (2021)

    Google Scholar 

  57. Zenkour, A.M., El-Shahrany, H.D.: Hygrothermal vibration of a cross-ply composite plate with magnetostrictive layers, viscoelastic faces, and a homogeneous core. Eng. Comput. 38(5), 4437–456 (2021)

    Google Scholar 

  58. Ebrahimi, F., Jafari, A.: A higher-order thermomechanical vibration analysis of temperature-dependent FGM beams with porosities. J. Eng. 2016, 1 (2016)

    Google Scholar 

  59. Reddy, J., Wang, C., Kitipornchai, S.: Axisymmetric bending of functionally graded circular and annular plates. Europ. J. Mech. A/Solids 18(2), 185–199 (1999)

    Google Scholar 

  60. Ebrahimi, F., Barati, M.R.: Electro-magnetic effects on nonlocal dynamic behavior of embedded piezoelectric nanoscale beams. J. Intell. Mater. Syst. Struct. 28(15), 2007–2022 (2017)

    Google Scholar 

  61. Ebrahimi, F., et al.: Vibration analysis of porous magneto-electro-elastically actuated carbon nanotube-reinforced composite sandwich plate based on a refined plate theory. Eng. Comput. 37, 921–936 (2019)

    Google Scholar 

  62. Eringen, A.C., Edelen, D.: On nonlocal elasticity. Int. J. Eng. Sci. 10(3), 233–248 (1972)

    MathSciNet  Google Scholar 

  63. Ebrahimi, F., Dabbagh, A., Rabczuk, T.: On wave dispersion characteristics of magnetostrictive sandwich nanoplates in thermal environments. Europ. J. Mech. A/Solids 85, 104130 (2021)

    MathSciNet  Google Scholar 

  64. Ghorbani, K., et al.: Investigation of surface effects on the natural frequency of a functionally graded cylindrical nanoshell based on nonlocal strain gradient theory. Europ. Phys. J. Plus 135(9), 1–23 (2020)

    Google Scholar 

  65. Ebrahimi, F., et al.: Hygro-thermal effects on wave dispersion responses of magnetostrictive sandwich nanoplates. Adv. Nano Res. 7(3), 157 (2019)

    Google Scholar 

  66. Ebrahimi, F., Ahari, M.F.: Mechanics of Magnetostrictive Materials and Structures. CRC Press, Boca Raton (2023)

    Google Scholar 

  67. Ahari, M.F., Ghadiri, M.: Resonator vibration of a magneto-electro-elastic nano-plate integrated with FGM layer subjected to the nano mass-Spring-damper system and a moving load. Waves Random Complex Media 25, 1–39 (2022)

    Google Scholar 

  68. Rao, S.S.: Vibration of Continuous Systems, vol. 464. Wiley Online Library, New York (2007)

    Google Scholar 

  69. Ebrahimi, F., Ahari M. F.: Dynamic analysis of sandwich magnetostrictive nanoplates with a mass-spring-damper stimulator. Int. J. Struct. Stab. Dyn. 23 (2023)

  70. Ebrahimi, F., Mollazeinal, A., Ahari, M. F.: Active vibration control of truncated conical porous smart composite shells. Int. J. Struct. Stab. Dyn. 23 (2023)

  71. Ebrahimi, F., Shafiee, M.-S., Ahari, M.F.: Buckling analysis of single and double-layer annular graphene sheets in thermal environment. Eng. Comput. 39, 625–639 (2022)

    Google Scholar 

  72. Ebrahimi, F., Shafiei, M.-S., Ahari, M.F.: Vibration analysis of single and multi-walled circular graphene sheets in thermal environment using GDQM. Waves Random Complex Media 30, 1–40 (2022)

    Google Scholar 

  73. Rahimi, Y., et al.: Temperature-dependent vibrational behavior of bilayer doubly curved micro-nano liposome shell: simulation of drug delivery mechanism. J. Therm. Stress. 10, 1–28 (2023)

    Google Scholar 

  74. Mizuji, Z.K., et al.: Numerical modeling of a body vessel for dynamic study of a nano cylindrical shell carrying fluid and a moving nanoparticle. Eng. Anal. Bound. Elem. 152, 362–382 (2023)

    MathSciNet  Google Scholar 

  75. Eltaher, M., Emam, S.A., Mahmoud, F.: Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 218(14), 7406–7420 (2012)

    MathSciNet  Google Scholar 

  76. Rahmani, O., Pedram, O.: Analysis and modeling the size effect on vibration of functionally graded nano-beams based on nonlocal Timoshenko beam theory. Int. J. Eng. Sci. 77, 55–70 (2014)

    Google Scholar 

Download references

Acknowledgements

The authors would like to thank the reviewers for their comments and suggestions to improve this article’s clarity.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Imam Khomeini International University, Qazvin, Iran

    Farzad Ebrahimi & Mehrdad Farajzadeh Ahari

Authors
  1. Farzad Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mehrdad Farajzadeh Ahari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest. Professor F. Ebrahimy defined the subject and guided authors regarding limitations and errors and revised the manuscript. M. F. Ahari analyzed the data and drafted the manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix 1

Appendix 1

$$\begin{gathered} K_{11} = - A_{11} \left( {o^{2} } \right) \hfill \\ K_{12} = - B_{11} \left( {o^{2} } \right) + \alpha S_{11} \left( {o^{2} } \right) \hfill \\ K_{13} = \alpha S_{11} \left( {o^{3} } \right) \hfill \\ K_{21} = - B_{11} \left( {o^{2} } \right) + \alpha S_{11} \left( {o^{2} } \right) \hfill \\ K_{22} = - D_{11} \left( {o^{2} } \right) + 2\alpha M_{11} \left( {o^{2} } \right) - \alpha^{2} L_{11} \left( {o^{2} } \right) - A_{55} + 2\beta D_{55} - \beta^{2} M_{55} \hfill \\ K_{23} = \alpha M_{11} \left( {o^{3} } \right) - \alpha^{2} L_{11} \left( {o^{3} } \right) + 2\beta D_{55} \left( o \right) - \beta^{2} M_{55} \left( o \right) - A_{55} \left( o \right) \hfill \\ K_{31} = \alpha S_{11} \left( {o^{3} } \right) \hfill \\ K_{32} = \alpha M_{11} \left( {o^{3} } \right) - \alpha^{2} L_{11} \left( {o^{3} } \right) + 2\beta D_{55} \left( o \right) - \beta^{2} M_{55} \left( o \right) - A_{55} \left( o \right) \hfill \\ K_{33} = - \alpha^{2} L_{11} \left( {o^{4} } \right) - \beta^{2} M_{55} \left( {o^{2} } \right) + 2\beta D_{55} \left( {o^{2} } \right) - A_{55} \left( {o^{2} } \right) - K_{w} \hfill \\ \quad \quad \qquad\; - K_{g} \left( {o^{2} } \right) - K_{w} \left( {\mu^{2} o^{2} } \right) - K_{g} \left( {\mu^{2} o^{4} } \right)K_{33} = - \alpha^{2} L_{11} \left( {o^{4} } \right) - \beta^{2} M_{55} \left( {o^{2} } \right) \hfill \\ \quad \qquad \quad \; + 2\beta D_{55} \left( {o^{2} } \right) - A_{55} \left( {o^{2} } \right) - K_{w} - K_{g} \left( {o^{2} } \right) - K_{w} \left( {\mu^{2} o^{2} } \right) - K_{g} \left( {\mu^{2} o^{4} } \right) \hfill \\ \end{gathered}$$
$$\begin{gathered} M_{11} = I_{0} \left( {1 + \mu^{2} o^{2} } \right) \hfill \\ M_{12} = - \left( {I_{1} - I_{3} \alpha + \mu^{2} I_{1} o^{2} + I_{3} \alpha \mu^{2} o^{2} } \right) \hfill \\ M_{13} = - \left( { - I_{3} \alpha \left( o \right) - \mu^{2} I_{3} \alpha \left( {o^{3} } \right)} \right) \hfill \\ M_{21} = - \left( {I_{1} - I_{3} \alpha + \mu^{2} I_{1} o^{2} + I_{3} \alpha \mu^{2} o^{2} } \right) \hfill \\ M_{22} = - \left( {I_{2} - 2I_{4} \alpha + I_{6} \alpha^{2} + I_{2} \mu^{2} o^{2} - 2I_{4} \alpha o^{2} + I_{6} \mu^{2} \alpha^{2} o^{2} } \right) \hfill \\ M_{23} = - \left( {I_{6} \alpha^{2} o - I_{4} \alpha \left( o \right) + I_{6} \alpha^{2} \mu^{2} o^{3} - I_{4} \alpha \mu^{2} o^{3} } \right) \hfill \\ M_{31} = - \left( { - I_{3} \alpha \left( o \right) - \mu^{2} I_{3} \alpha \left( {o^{3} } \right)} \right) \hfill \\ M_{32} = - \left( {I_{6} \alpha^{2} o - I_{4} \alpha \left( o \right) + I_{6} \alpha^{2} \mu^{2} o^{3} - I_{4} \alpha \mu^{2} o^{3} } \right) \hfill \\ M_{33} = - \left( {I_{0} + I_{6} o^{2} \alpha^{2} + I_{0} \mu^{2} o^{2} + I_{6} \mu^{2} o^{4} \alpha^{2} } \right) \hfill \\ \end{gathered}$$
$$\begin{aligned} A_{{11}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{{11}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} C_{{11}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{{11}}^{f} {\text{d}}z \\ A_{{12}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{{12}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} C_{{12}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{{12}}^{f} {\text{d}}z \\ A_{{22}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{{22}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} C_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{{22}}^{f} {\text{d}}z \\ A_{{44}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{{44}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} C_{{44}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{{44}}^{f} {\text{d}}z \\ A_{{55}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{{55}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} C_{{55}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{{55}}^{f} {\text{d}}z \\ A_{{66}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} C_{{66}}^{c} dz + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} C_{{66}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} C_{{66}}^{f} {\text{d}}z \end{aligned}$$
$$\begin{gathered} B_{{11}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{{11}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} zC_{{11}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{{11}}^{f} {\text{d}}z \hfill \\ B_{{12}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{{12}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} zC_{{12}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{{12}}^{f} {\text{d}}z \hfill \\ B_{{22}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{{22}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} zC_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{{22}}^{f} {\text{d}}z \hfill \\ B_{{44}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{{44}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} zC_{{44}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{{44}}^{f} {\text{d}}z \hfill \\ B_{{55}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{{55}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} zC_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{{55}}^{f} {\text{d}}z \hfill \\ B_{{66}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} zC_{{66}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} zC_{{66}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} zC_{{66}}^{f} {\text{d}}z \hfill \\ \end{gathered}$$
$$\begin{gathered} D_{{11}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{{11}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{2} C_{{11}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{{11}}^{f} {\text{d}}z \hfill \\ D_{{12}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{{12}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{2} C_{{12}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{{12}}^{f} {\text{d}}z \hfill \\ D_{{22}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{{22}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{2} C_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{{22}}^{f} {\text{d}}z \hfill \\ D_{{44}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{{44}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{2} C_{{44}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{{44}}^{f} {\text{d}}z \hfill \\ D_{{55}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{{55}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{2} C_{{55}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{{55}}^{f} {\text{d}}z \hfill \\ D_{{66}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{2} C_{{66}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{2} C_{{66}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{2} C_{{66}}^{f} {\text{d}}z \hfill \\ \end{gathered}$$
$$\begin{aligned} S_{{11}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{3} C_{{11}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{3} C_{{11}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{3} C_{{11}}^{f} {\text{d}}z \\ S_{{12}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{3} C_{{12}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{3} C_{{12}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{3} C_{{12}}^{f} {\text{d}}z \\ S_{{22}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{3} C_{{22}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{3} C_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{3} C_{{22}}^{f} {\text{d}}z \\ S_{{44}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{3} C_{{44}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{3} C_{{44}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{3} C_{{44}}^{f} {\text{d}}z \\ S_{{55}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{3} C_{{55}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{3} C_{{55}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{3} C_{{55}}^{f} {\text{d}}z \\ S_{{66}} &= \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{3} C_{{66}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{3} C_{{66}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{3} C_{{66}}^{f} {\text{d}}z \\ \end{aligned}$$
$$\begin{gathered} M_{{11}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{4} C_{{11}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{4} C_{{11}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{4} C_{{11}}^{f} {\text{d}}z \hfill \\ M_{{12}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{4} C_{{12}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{4} C_{{12}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{4} C_{{12}}^{f} {\text{d}}z \hfill \\ M_{{22}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{4} C_{{22}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{4} C_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{4} C_{{22}}^{f} {\text{d}}z \hfill \\ M_{{44}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{4} C_{{44}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{4} C_{{44}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{4} C_{{44}}^{f} {\text{d}}z \hfill \\ M_{{55}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{4} C_{{55}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{4} C_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{4} C_{{55}}^{f} {\text{d}}z \hfill \\ M_{{66}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{4} C_{{66}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{4} C_{{66}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{4} C_{{66}}^{f} {\text{d}}z \hfill \\ \end{gathered}$$
$$\begin{gathered} L_{{11}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{6} C_{{11}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{6} C_{{11}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{6} C_{{11}}^{f} {\text{d}}z \hfill \\ L_{{12}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{6} C_{{12}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{6} C_{{12}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{6} C_{{12}}^{f} {\text{d}}z \hfill \\ L_{{22}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{6} C_{{22}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{6} C_{{22}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{6} C_{{22}}^{f} {\text{d}}z \hfill \\ L_{{44}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{6} C_{{44}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{6} C_{{44}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{6} C_{{44}}^{f} {\text{d}}z \hfill \\ L_{{55}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{6} C_{{55}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{6} C_{{55}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{6} C_{{55}}^{f} {\text{d}}z \hfill \\ L_{{66}} = \mathop \int \nolimits_{{ - h_{c} /2}}^{{h_{c} /2}} z^{6} C_{{66}}^{c} {\text{d}}z + \mathop \int \nolimits_{{ - \frac{{\left( {hc + h_{f} } \right)}}{2}}}^{{\frac{{ - hc}}{2}}} z^{6} C_{{66}}^{f} {\text{d}}z + \mathop \int \nolimits_{{\frac{{h_{c} }}{2}}}^{{\frac{{\left( {h_{c} + h_{f} } \right)}}{2}}} z^{6} C_{{66}}^{f} {\text{d}}z \hfill \\ \end{gathered}$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, F., Ahari, M.F. Active vibration control of the multilayered smart nanobeams: velocity feedback gain effects on the system’s behavior. Acta Mech 235, 493–510 (2024). https://doi.org/10.1007/s00707-023-03769-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03769-y

Search

Navigation