Green functions for three-point boundary value problems governed by differential equation systems with applications to Timoshenko beams

Abstract

The present paper is devoted to the issue of the Green function matrices that belongs to some three-point boundary- and eigenvalue problems. A detailed definition is given for the Green function matrices provided that the considered boundary value problems are governed by a class of ordinary differential equation systems associated with homogeneous boundary and continuity conditions. The definition is a constructive one, i.e., it provides the means needed for calculating the Green function matrices. The fundamental properties of the Green function matrices—existence, symmetry properties, etc.—are also clarified. Making use of these Green functions, a class of three-point eigenvalue problems can be reduced to eigenvalue problems governed by homogeneous Fredholm integral equation systems. The applicability of the novel findings is demonstrated through a Timoshenko beam with three supports.

1 Introduction

Beams are preferred structural members because of the favorable load-carrying abilities. Research on the behavior of beams dates back to long ago and is still live and widespread [1,2,3]. The vibratory behavior is one of the topics of interest still up to date. For example, a geometrically nonlinear model is solved in [4] to find the fundamental frequencies. The related nonlinear partial differential equation is replaced with an ordinary differential equation using the Galerkin method. It is then solved in time domain using variational iteration and parametrized perturbation method. Article [5] is about the unloaded vibrations a double beam system which is connected with a Winkler elastic layer. Both rotatory inertia and shear are incorporated into the beam model presented. The governing partial differential equation system is solved with the Bernoulli–Fourier method. An analytical solution to the mode-shape equation of gravity-loaded Rayleigh–Timoshenko beams is given in [6]. The vibrations of multi-step Timoshenko beams carrying multiple concentrated elements are addressed in [7] using the continuous mass transfer matrix method. The effectiveness of the Adomian decomposition and differential transformation method is investigated through the vibrations of Timoshenko beams on viscoelastic foundation in [8]. The large amplitude vibrations of beams on variable elastic foundation are studied in [9]. The beam model is based on the Euler–Bernoulli hypothesis, and the Winkler model is used for the foundation. The Hamilton principle is used to derive the equations of motion, while the second-order homotopy perturbation method is applied to find solution to the nonlinear equation of motion.

The influence of an axial load on the natural frequencies of a uniform single-span beam is investigated in [10]. It is found that Galef’s formula is only valid for a few types of end-conditions. The effect of end-supports on the frequency is only significant for the first few modes. The vibratory behavior of clamped-free beams with an intermediate axial force is the subject of [11] using the Hamilton principle. The frequencies show an increase as the force is moved closed to the fixed end. It is studied [12] how a beam system with tendon loading vibrates. The effect of the number and location of attachment points is evaluated.

The dynamic response of beams to a moving load is sought in [13] by a linear model. The dynamic Green function is constructed in closed form for elastic end-restraints and with this; the results are found in an exact and direct method. The effect of the load speed parameter is studied on the deflections for various, limiting boundary conditions.

Apart from vibrations, it is worthy to mention some further notable results within the field of the Green function [14]. Book [15] that presents the Green theorem, introduces the concept of the Green function and applies it to electrostatic problems. Since that pioneering work, the Green function has widely been applied to various problems [16, 17]. The concept of the Green function for two-point boundary value problems governed by ordinary differential equations was first introduced in paper [18]. Furthermore, books [19, 20] extend the knowledge by defining the Green function for ordinary linear differential equations with their most important properties. Later, the Green function matrix was introduced as a generalization for a class of ordinary differential equation systems in [21]. For degenerated ordinary differential equation systems, new findings are given in [22]. The existence for some three-point boundary value problems associated with third-order nonlinear differential equations is detailed in [23] using Green functions. For a class of second-order ordinary differential equations, a method is proposed to find the corresponding Green functions for three-point boundary value problems in [24]. Similarly, article [25] is about a special class of third-order three-point boundary value problems. The author demonstrates how to find the Green function for such issues. An application is also presented. A non-local three-point boundary value problem is selected and examined in [26]. Existence and uniqueness of solutions are given, and the Green function is also constructed. A type of nonlinear third-order non-local boundary value problem is in the spotlight in [27]. The Schauder fixed point theorem is used for the solution. A third-order linear differential equation is investigated in [28]. The existence of the Green function is proven, and solution is given. Article [29] determines the Green function for compressed straight Euler–Bernoulli beams with three supports and solves the linear stability issue by a boundary element technique. The procedure is applicable when the three-point boundary value problem is governed by a single ordinary differential equation.

Based on the above, to the best knowledge of the authors, the Green function matrix has not been defined for three-point boundary value problems governed by ordinary differential equation systems. To this end, the article addresses this issue with some numerical examples as possible and effective applications. First, the related class of three-point boundary value problems is introduced. Then, a suitable definition and computation steps for the corresponding Green function matrix are given. Numerical examples related to nonhomogeneous Timoshenko beams with three supports are given as one possible demonstration of the applicability of the findings.

2 The class of three-point boundary value problems

2.1 Differential operator with boundary and continuity conditions

Consider the class of eigenvalue problems governed by the homogeneous ordinary differential equation system

$$\begin{aligned} {\textbf{K}}\left[ {\textbf{y}}\right] =\lambda \,{\textbf{M}}\left[ {\textbf{y}}\right] , \end{aligned}$$

(2.1a)

where ${\textbf{y}}(x)=[y_{1}(x)|y_{2}(x)|\ldots |y_{n}(x)],n\ge 2$ is the unknown function vector, $\lambda$ is a parameter (the eigenvalue sought), $2\kappa$ and $2\mu$ $(\kappa >\mu )$ are the order of the differential operators ${\textbf{K}}\left[ {\textbf{y}}\right]$ and ${\textbf{M}}\left[ {\textbf{y}}\right]$. Let

$$\begin{aligned} \underset{(n\times n)}{\varvec{{\mathcal {K}}}_{\nu }(x)},\quad (\nu =0,1,\ldots ,\kappa )\quad \text {and}\quad \underset{(n\times n)}{\varvec{{\mathcal {M}}}_{\nu }(x)},\quad (\nu =0,1,\ldots ,\mu ) \end{aligned}$$

be square matrices in the interval $x\in [a,c]\;(c>a)$. The differential operators ${\textbf{K}}\left[ {\textbf{y}}\right]$ and ${\textbf{M}}\left[ {\textbf{y}}\right]$ are defined by

$$\begin{aligned} \begin{aligned} {\textbf{K}}\left[ {\textbf{y}}\right]&=\sum _{\nu =0}^{\kappa }(-1)^{\nu }\left( \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{y}}^{(\nu )}(x)\right) ^{(\nu )},\qquad \frac{\textrm{d}^{n}(\ldots )}{\textrm{d}x^{n}}=(\ldots )^{(n)};\\ {\textbf{M}}\left[ {\textbf{y}}\right]&={\sum _{\nu =0}^{\mu }(-1)^{\nu }}\left( \varvec{{\mathcal {M}}}_{\nu }(x)\,{\textbf{y}}^{(\nu )}(x)\right) ^{(\nu )}. \end{aligned} \end{aligned}$$

(2.1b)

It is assumed that ($\varvec{{\mathcal {K}}}_{\nu }(x)$) [$\varvec{{\mathcal {M}}}_{\nu }(x)$] is differentiable continuously($\kappa$)[$\mu$] times and

$$\begin{aligned} \varvec{{{\mathcal {K}}}_{2\kappa }}(x)\quad \text {and}\,\quad \varvec{{{\mathcal {M}}}_{2\mu }}(x) \end{aligned}$$

have inverse if $x\in [a,c]$. It is also assumed that they are differentiable as many times as required.

Note that $2\kappa$, which is the order of the differential operator on the left side of (2.1a), is greater than $2\mu$, which is the order of the differential operator on the right side. Let $x\in [a,c]$, $c>a$, $c-a=\ell$ be the interval in which the solution of differential equation (2.1a) is sought. Further let b be an inner point in the interval $\left[ a,c\right]$: $b\in \left[ a,b\right]$, $b-a=\ell _{1}$, $c-b=\ell _{2}$, $\ell _{1}+\ell _{2}=\ell$.

Some quantities in the intervals [a, b] and [b, c] are denoted by the Latin I and II subscripts. Accordingly, $y_{I}$ and $y_{II}$ are the solutions to the differential equation (2.1) in the intervals I and II.

Differential equation system (2.1) is associated with the following boundary and continuity conditions:

$$\begin{aligned} {\textbf{U}}_{ar}[{\textbf{y}}]&=\sum _{\nu =1}^{2\kappa }\varvec{\alpha }_{\nu rI}\,{\textbf{y}}_{I}^{(\nu -1)}(a)={\textbf{0}}, \quad r =1,2,\ldots ,\kappa \end{aligned}$$

(2.2a)

$$\begin{aligned} {\textbf{U}}_{br}[{\textbf{y}}]&={\textbf{U}}_{brI}[{\textbf{y}}_{I} ]-{\textbf{U}}_{brII}[{\textbf{y}}_{II}] \nonumber \\&=\sum _{\nu =1}^{2\kappa }\left( \varvec{\beta }_{\nu rI}\,{\textbf{y}} _{I}^{(\nu -1)}(b)-\varvec{\beta }_{\nu rII}\,{\textbf{y}}_{II}^{(\nu -1)}(b)\right) ={\textbf{0}}, \quad r =1,2,\ldots ,2\kappa \end{aligned}$$

(2.2b)

$$\begin{aligned} {\textbf{U}}_{cr}[{\textbf{y}}]&=\sum _{\nu =1}^{2\kappa }\varvec{\gamma }_{\nu rII}\,{\textbf{y}}_{II}^{(\nu -1)}(c)={\textbf{0}}, \quad r =1,2,\ldots ,\kappa \end{aligned}$$

(2.2c)

where $\varvec{\alpha }_{\nu rI}$, $\varvec{\beta }_{\nu rI}$, $\varvec{\beta }_{\nu rII}$ and $\varvec{\gamma }_{\nu rII}$ are nonzero square matrices of size $n\times n$.

Differential equation (2.1) with the boundary and continuity conditions (2.2) constitute an eigenvalue problem with $\lambda$ being the eigenvalue to be found. If $\mu =0$, the right side of (2.1) changes as

$$\begin{aligned} {\textbf{M}}\left[ {\textbf{y}}\right] = \varvec{{\mathcal {M}} }_{0}(x){\textbf{y}}(x) \end{aligned}$$

(2.3)

and the eigenvalue problem is called simple. From now on, it is assumed that $\varvec{{\mathcal {M}}}_{0}(x)$ has an inverse if $x\in [a,c]$.

The eigenvalue problems that provide the eigenfrequencies for the longitudinal and torsional vibrations of rods as well as for the transverse vibrations of strings and beams are all simple ones. If $\mu >0$, the eigenvalue problem is called generalized [19].

The scalar equations that constitute the boundary- and continuity conditions should be linearly independent of each other. It is obvious that a linear combination of the boundary conditions is also a boundary condition. By selecting suitable linear combinations, derivatives with an order higher than $\kappa -1$ could be removed. If it is done in all possible ways, the total number of boundary conditions which do not involve derivatives higher than $\kappa -1$ is, say, e. These boundary conditions are called essential boundary conditions. The remaining $2k-e$ boundary conditions are the natural boundary conditions.

The column matrices ${\textbf{u}}(x)$ and ${\textbf{v}}(x)$ ($|{\textbf{u}} (x)|,|{\textbf{v}}(x)|$ are not identically equal to zero if $x\in [a,c]$) are called comparison functions if they satisfy the boundary and continuity conditions and are called eigenfunctions if they, in addition to this, satisfy differential equation (2.1).

2.2 Self-adjointness

The integrals

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{K}=\int _{a}^{c}{\textbf{u}} ^{T}(x)\,{\textbf{K}}[{\textbf{v}}(x)]\,\textrm{d}x,\qquad \quad \left( {\textbf{u}},{\textbf{v}}\right) _{M}=\int _{a}^{c}{\textbf{u}}^{T}(x)\,{\textbf{M}} [{\textbf{v}}(x)]\,\textrm{d}x \end{aligned}$$

(2.4)

taken on the set of the comparison functions ${\textbf{u}}(x)$, ${\textbf{v}}(x)$ are products defined on the operators ${\textbf{K}}$ and ${\textbf{M}}$. Let us now detail the product $\left( {\textbf{u}},{\textbf{v}}\right) _{K}$. Making use of (2.1b), one may write

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{K}= & {} \int _{a}^{b}{\textbf{u}}^{T} (x)\sum _{\nu =0}^{\kappa }(-1)^{\nu }\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu )}\textrm{d}x\nonumber \\{} & {} +\int _{b}^{c}{\textbf{u}}^{T}(x)\sum _{\nu =0}^{\kappa }(-1)^{\nu }\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu )}\textrm{d}x \end{aligned}$$

(2.5)

in which the integral

$$\begin{aligned} {\textbf{I}}_{ab}=(-1)^{\nu }\int _{a}^{b}{\textbf{u}}^{T}(x)\,\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu )}\textrm{d}x \end{aligned}$$

(2.6)

can be manipulated into a more suitable form through integrations:

$$\begin{aligned} I_{ab}= & {} (-1)^{\nu }\biggl [{\textbf{u}}^{T}(x)\left[ \varvec{{\mathcal {K}} }_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu - 1)}\biggr ]_{a} ^{b - 0}\nonumber \\{} & {} +(-1)^{\nu - 1}\int _{a}^{b}{\textbf{u}}^{T}(x)\,\left[ \varvec{{\mathcal {K}}}_{\nu }(x){\textbf{v}}^{(\nu )}(x)\right] ^{(\nu - 1)}\textrm{d}x = (-1)^{\nu }\biggl [{\textbf{u}}^{T}(x)\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu - 1)}\nonumber \\{} & {} - ({\textbf{u}}^{(1)})^{T}(x)\,\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu - 2)} + ({\textbf{u}}^{(2)} )^{T}(x)\,\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu - 3)} - \,\cdots \biggr ]_{a}^{b - 0}\nonumber \\{} & {} + \int _{a}^{b}({\textbf{u}}^{(\nu )})^{T}(x)\varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\,\textrm{d}x\nonumber \\= & {} \left[ \sum _{r=0}^{\nu -1}(-1)^{(\nu + r)}({\textbf{u}}^{(r)})^{T}(x)\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu -1-r)}\right] _{a}^{b-0}\nonumber \\{} & {} +\int _{a}^{b}\,\left( {\textbf{u}}^{(\nu )}\right) ^{T} (x)\,\varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\,\textrm{d}x. \end{aligned}$$

(2.7)

Hence,

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{K}&=\left[ \sum _{\nu =0}^{\kappa }\sum _{r=0}^{\nu -1}(-1)^{(\nu + r)}({\textbf{u}}^{(r)})^{T}(x)\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu -1-r)}\right] _{a}^{b-0}\nonumber \\&\quad +\left[ \sum _{\nu =0}^{\kappa }\sum _{r=0}^{\nu -1}(-1)^{(\nu + r)} ({\textbf{u}}^{(r)})^{T}(x)\left[ \varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu -1-r)}\right] _{b+0}^{c}\nonumber \\&\quad +\sum _{\nu =0}^{\kappa } \int _{a}^{c}\,({\textbf{u}}^{(\nu )})^{T}(x)\,\varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\,\textrm{d}x\nonumber \\&=K_{0}(u,v)+\sum _{n=0}^{\kappa }\int _{a}^{c}\,({\textbf{u}}^{(\nu )} )^{T}(x)\,\varvec{{\mathcal {K}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\,\textrm{d} x. \end{aligned}$$

(2.8a)

It follows from Eq. (2.8a) that

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{M}&=\left[ \sum _{\nu =0}^{\mu } \sum _{r=0}^{\nu -1}(-1)^{(\nu + r)}({\textbf{u}}^{(r)})^{T}(x)\left[ \varvec{{\mathcal {M}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu -1-r)}\right] _{a}^{b-0}\nonumber \\&\quad +\left[ \sum _{\nu =0}^{\mu }\sum _{r=0}^{\nu -1}(-1)^{(\nu + r)} ({\textbf{u}}^{(r)})^{T}(x)\left[ \varvec{{\mathcal {M}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\right] ^{(\nu -1-r)}\right] _{b+0}^{c}\nonumber \\&\quad +\sum _{n=0}^{\mu }\int _{a}^{c}\,({\textbf{u}}^{(\nu )})^{T}(x)\varvec{{\mathcal {M}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\,\textrm{d}x\nonumber \\&=M_{0}(u,v)+\sum _{\nu =0}^{\mu }\int _{a}^{c}\,({\textbf{u}}^{(\nu )} )^{T}(x)\varvec{{\mathcal {M}}}_{\nu }(x)\,{\textbf{v}}^{(\nu )}(x)\,\textrm{d}x. \end{aligned}$$

(2.8b)

These results are naturally valid for the products $\left( {\textbf{v}},{\textbf{u}}\right) _{K}$ and $\left( {\textbf{v}},{\textbf{u}}\right) _{M}$.

The expressions $K_{0}(u,v)$ and $M_{0}(u,v)$ defined by the right sides of Eq. (2.8) are called boundary- and continuity expressions. Eigenvalue problem (2.1), (2.2) is said to be self-adjoint if the products (2.4) are commutative, i.e., it holds that

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{K}=\left( {\textbf{v}},{\textbf{u}} \right) _{K}\qquad \text {and}\qquad \left( {\textbf{u}},{\textbf{v}}\right) _{M}=\left( {\textbf{v}},{\textbf{u}}\right) _{M}. \end{aligned}$$

(2.9)

Conditions (2.9) are called conditions of self-adjointness.

2.3 Consequences

It follows from Eqs. (2.8a) and (2.8b) that

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{K}-\left( {\textbf{v}},{\textbf{u}} \right) _{K}=K_{0}(u,v)-K_{0}(v,u)=0 \end{aligned}$$

(2.10a)

and

$$\begin{aligned} \left( {\textbf{u}},{\textbf{v}}\right) _{M}-\left( {\textbf{v}},{\textbf{u}} \right) _{M}=M_{0}(u,v)-M_{0}(v,u)=0 \end{aligned}$$

(2.10b)

if the eigenvalue problem (2.1), (2.2) is self-adjoint.

Let $\lambda _{\ell }$ be the $\ell$th eigenvalue $(\ell =1,2,3,\ldots )$. The corresponding eigenfunctions or solutions to the eigenvalue problem (2.1), (2.2) are denoted by ${\textbf{y}}_{\ell }$.

Assume that the three-point boundary value problem (2.1), (2.2) is self-adjoint. Then, the eigenfunctions are orthogonal to each other in general sense:

$$\begin{aligned} \left( {\textbf{y}}_{k},{\textbf{y}}_{\ell }\right) _{K}=\left\{ \begin{array}{ll} \lambda _{\ell }\left( {\textbf{y}}_{k},{\textbf{y}}_{\ell }\right) _{M} &{} \quad \text {if } k=\ell ,\\ 0 &{}\quad \text {if }k\ne \ell . \end{array} \right. \quad k,\ell =1,2,3\ldots \;\, \end{aligned}$$

(2.11)

In addition to this, the eigenvalues are all real numbers. These statements can be proven easily by recalling the similar proofs given for two-point boundary value problems in [30].

2.4 Sign of eigenvalues

The three-point eigenvalue problem (2.1), (2.2) is said to be positive definite if the eigenvalues are positive, positive semi-definite if one eigenvalue is zero and the other eigenvalues are all positive, negative semi-definite if one eigenvalue is zero and the other eigenvalues are all negative and finally, negative definite if the eigenvalues are negative. If $\ell =k$ in (2.11), we have

$$\begin{aligned} \left( {\textbf{y}}_{\ell },{\textbf{y}}_{\ell }\right) _{K}=\lambda _{_{\ell } }\left( {\textbf{y}}_{\ell },{\textbf{y}}_{\ell }\right) _{M}. \end{aligned}$$

(2.12)

Hence,

$$\begin{aligned} \lambda _{_{\ell }}=\frac{\left( {\textbf{y}}_{\ell },{\textbf{y}}_{\ell }\right) _{K}}{\left( {\textbf{y}}_{\ell },{\textbf{y}}_{\ell }\right) _{M}}=\frac{\displaystyle \int _{a}^{b}({\textbf{y}}_{\ell }(x))^{T}\,{\textbf{K}} [{\textbf{y}}_{\ell }(x)]\,\textrm{d}x}{\displaystyle \int _{a}^{b}({\textbf{y}} _{\ell }(x))^{T}\,{\textbf{M}}[{\textbf{y}}_{\ell }(x)]\,\textrm{d}x}. \end{aligned}$$

(2.13)

This equation shows that the sign of $\lambda _{\ell }$ is a function of the products $\left( {\textbf{y}}_{\ell },{\textbf{y}}_{\ell }\right) _{K}$ and $\left( {\textbf{y}}_{\ell },{\textbf{y}}_{\ell }\right) _{M}$. Assume that

$$\begin{aligned} \left( {\textbf{u}},{\textbf{u}}\right) _{K}>0,\quad \text {and}\quad \left( {\textbf{u}},{\textbf{u}}\right) _{M}>0 \end{aligned}$$

(2.14)

for any comparison function ${\textbf{u}}(x)$. Then, the three-point eigenvalue problem (2.1), (2.2) is positive definite.

The Rayleigh quotient is defined by the equation

$$\begin{aligned} {\mathcal {R}}[{\textbf{u}}(x)]=\frac{\left( {\textbf{u}},{\textbf{u}}\right) _{K} }{\left( {\textbf{u}},{\textbf{u}}\right) _{M}}=\frac{\displaystyle \int _{a} ^{b}{\textbf{u}}^{T}(x)\,{\textbf{K}}[{\textbf{u}}(x)]\,\textrm{d}x}{\displaystyle \int _{a}^{b}{\textbf{u}}^{T}(x)\,{\textbf{M}}[{\textbf{u}} (x)]\,\textrm{d}x} \end{aligned}$$

(2.15)

in which ${\textbf{u}}(x)$ is a comparison function. Substituting (2.8a) and (2.8b) for the numerator and denominator in (2.13) yields

$$\begin{aligned} {\mathcal {R}}[{\textbf{u}}(x)]=\frac{\left( {\textbf{u}},{\textbf{u}}\right) _{K} }{\left( {\textbf{u}},{\textbf{u}}\right) _{M}}=\frac{\displaystyle \sum _{\nu =0}^{\kappa }\int _{a}^{b}\,({\textbf{u}}^{(\nu )})^{T}(x)\varvec{{\mathcal {K}} }_{\nu }(x)(x){\textbf{u}}^{(\nu )}(x)\,\textrm{d}x+K_{0}[u(x)]}{\displaystyle \sum _{\nu =0}^{\mu }\int _{a}^{b}\,({\textbf{u}}^{(\nu )})^{T}(x)\varvec{{\mathcal {M}} }_{\nu }(x)(x){\textbf{u}}^{(\nu )}(x)\,\textrm{d}x+M_{0}[u(x)]}. \end{aligned}$$

(2.16)

If the three-point eigenvalue problem (2.1), (2.2) is self-adjoint, then

$$\begin{aligned} K_{0}[u(x)]=M_{0}[u(x)]=0. \end{aligned}$$

(2.17)

Assume that the three-point eigenvalue problem (2.1), (2.2) is self adjoint and

$$\begin{aligned} {\textbf{M}}[y]=\varvec{{\mathcal {M}}}_{0}(x){\textbf{y}}(x). \end{aligned}$$

(2.18)

Then, the considered self-adjoint three point eigenvalue problem is called simple.

2.5 Determination of the eigenvalues

Let us denote the linearly independent particular solutions of the differential equation ${\textbf{K}}\left[ {\textbf{y}}\right] =\lambda \,{\textbf{M}}\left[ {\textbf{y}}\right]$ by ${{\textbf{z}}_{\ell }}(x,\lambda )$ ($\ell =1,2,\ldots ,2\kappa \times n$). With ${\textbf{z}}_{\ell }(x,\lambda )$, the general solution is of the form

$$\begin{aligned} \begin{aligned} {{\textbf {y}}}_{I}(x)&=\sum _{\ell =1}^{2\kappa \times n}{{\textbf {z}}}_{\ell I}(x,\lambda ){\mathcal {A}}_{\ell I}\qquad \text{ if }\;\;x\in [a,b]\\ {{\textbf {y}}}_{II}(x)&=\sum _{\ell =1}^{2\kappa \times n}{{\textbf {z}}}_{\ell II}(x,\lambda ){\mathcal {A}}_{\ell II}\qquad \text{ if }\;\;x\in [b,c] \end{aligned} \end{aligned}$$

(2.19)

where ${\textbf{z}}_{\ell }(x,\lambda )={\textbf{z}}_{\ell I}(x,\lambda )={\textbf{z}}_{\ell II}(x,\lambda )$. The undetermined integration constants ${\mathcal {A}}_{\ell I}$ and ${\mathcal {A}}_{\ell II}$ can be obtained from the boundary and continuity conditions:

$$\begin{aligned}&\sum _{\ell =1}^{2\kappa \times n}{\mathcal {A}}_{\ell I}{\textbf{U}}_{ar} [{\textbf{z}}_{\ell I}] =0 \quad r =1,2,\ldots ,\kappa \end{aligned}$$

(2.20a)

$$\begin{aligned}&\sum _{\ell =1}^{2\kappa \times n}\left( {\mathcal {A}}_{\ell I}{\textbf{U}} _{brI}[{\textbf{z}}_{\ell I}]-{\mathcal {A}}_{\ell II}{\textbf{U}}_{brII} [{\textbf{z}}_{\ell II}]\right) =0 \quad r =1,2,\ldots ,2\kappa \end{aligned}$$

(2.20b)

$$\begin{aligned}&\sum _{\ell =1}^{2\kappa \times n}{\mathcal {A}}_{\ell II}{\textbf{U}}_{cr} [{\textbf{z}}_{\ell II}] =0 \quad r =1,2,\ldots ,\kappa . \end{aligned}$$

(2.20c)

Since these equations constitute a homogeneous linear equation system for the unknowns ${\mathcal {A}}_{\ell I}$ and ${\mathcal {A}}_{\ell II}$, non-trivial solutions exist if and only if the determinant of the system is zero:

$$\begin{aligned} \varDelta (\lambda )=0. \end{aligned}$$

(2.21)

This equation needs to be solved to find the eigenvalues. The determinant $\varDelta (\lambda )$ is referred to as characteristic determinant.

If $\varDelta (\lambda )$ is identically equal to zero, then each $\lambda$ is an eigenvalue. Otherwise, function $\varDelta (\lambda )$ has an infinite sequence of isolated zero points which can be ordered according to their magnitude:

$$\begin{aligned} 0\le |\lambda _{1}|\le |\lambda _{2}|\le |\lambda _{3}|\le \cdots . \end{aligned}$$

3 The Green function matrix

Consider the inhomogeneous ordinary differential equation system

$$\begin{aligned} {\textbf{L}}[{\textbf{y}}(x)]={\textbf{r}}(x) \end{aligned}$$

(3.1a)

where the differential operator of order $2\kappa$ is defined by the following equation:

$$\begin{aligned} {\textbf{L}}[{\textbf{y}}(x)]=\sum _{\nu =0}^{2\kappa }{\textbf{p}}_{\nu } (x)\,{\textbf{y}}^{(\nu )}(x). \end{aligned}$$

(3.1b)

Here, $\kappa \ge 1$ is a natural number,

$$\begin{aligned} \underset{(n\times n)}{{\textbf{p}}_{\nu }(x)},\quad (\nu =0,1,\ldots ,2\kappa ),\quad \underset{(n\times 1)}{{\textbf{y}}(x)}\;\;\text {and} \;\;\underset{(n\times 1)}{{\textbf{r}}(x)} \end{aligned}$$

are square and column matrices (vectors), ${\textbf{p}}_{\nu }(x)$ and ${\textbf{r}}(x)$ are continuous if $x\in [a,c]$ ($c>a$, $c-a=\ell$) and ${\textbf{p}}_{2\kappa }(x)$ has an inverse. Further, let b an inner point in the interval $\left[ a,c\right]$: $b\in \left[ a,b\right]$, $b-a=\ell _{1}$, $c-b=\ell _{2}$, $\ell _{1}+\ell _{2}=\ell$.

It is assumed that the inhomogeneous differential equation (3.1) is associated with the homogeneous boundary and continuity conditions given by Eq. (2.20).

Solution of the three-point boundary value problem (3.1), (2.20) is sought in the form

$$\begin{aligned} {\textbf{y}}(x)=\int _{a}^{c}{\textbf{G}}(x,\xi ){\textbf{r}}(\xi )\,\textrm{d} \xi \end{aligned}$$

(3.2)

where ${\textbf{G}}(x,\xi )$ is the Green function matrix [30] defined by the following properties:

• 1. The Green function has the following structure:

  $$\begin{aligned} {\textbf{G}}(x,\xi )= {\left\{ \begin{array}{ll} {\textbf{G}}_{1I}(x,\xi ) &{} \quad \text {if}\;\,x,\xi \in [a,b]\\ {\textbf{G}}_{2I}(x,\xi ) &{} \quad \text {if}\;\,x\in [b,c]\;\text {but}\;\xi \in [a,b]\\ {\textbf{G}}_{1II}(x,\xi ) &{} \quad \text {if}\;\,x\in [a,b]\;\text {but}\;\xi \in [b,c]\\ {\textbf{G}}_{2II}(x,\xi ) &{} \quad \text {if}\;\,x,\xi \in [b,c]. \end{array}\right. } \end{aligned}$$

  (3.3)

• 2. The function ${\textbf{G}}_{1I}(x,\xi )$ is a continuous function of x and $\xi$ in the triangular domains $a\le x\le \xi \le b$ and $a\le \xi \le x\le b$. In addition, it is $2\kappa$ times differentiable with respect to x and the derivatives

  $$\begin{aligned} \frac{\partial ^{\nu }{\textbf{G}}_{1I}(x,\xi )}{\partial x^{\nu }}={\textbf{G}} _{1I}(x,\xi )^{(\nu )}(x,\xi ),\qquad (\nu =1,2,\ldots ,2\kappa ) \end{aligned}$$

  are also continuous functions of x and $\xi$ in the triangles $a\le x\le \xi \le b$ and $a\le \xi \le x\le b$.

• 3. Let $\xi$ be fixed in [a, b]. The function ${\textbf{G}}_{1I} (x,\xi )$ and its derivatives

  $$\begin{aligned} {\textbf{G}}_{1I}^{(\nu )}(x,\xi )=\frac{\partial ^{\nu }{\textbf{G}}_{1I}(x,\xi )}{\partial x^{\nu }},\qquad (\nu =1,2,\dots ,2\kappa -2) \end{aligned}$$

  (3.4)

  should be continuous for $x=\xi$:

  $$\begin{aligned}{} & {} \lim _{\varepsilon \rightarrow 0}\left[ {\textbf{G}}_{1I}^{(\nu )} (\xi +\varepsilon ,\xi )-{\textbf{G}}_{1I}^{(\nu )}(\xi -\varepsilon ,\xi )\right] \nonumber \\{} & {} \quad =\left[ {\textbf{G}}_{1I}^{(\nu )}(\xi +0,\xi )-{\textbf{G}}_{1I}^{(\nu )}(\xi -0,\xi )\right] =0\,\quad \nu =0,1,2,\ldots 2\kappa -2. \end{aligned}$$

  (3.5a)

  The derivative ${\textbf{G}}_{1I}^{(2\kappa -1)}(x,\xi )$ should, however, have a jump

  $$\begin{aligned}{} & {} \lim _{\varepsilon \rightarrow 0}\left[ {\textbf{G}}_{1I}^{(2\kappa -1)}(\xi +\varepsilon ,\xi )-{\textbf{G}}_{1I}^{(2\kappa -1)}(\xi -\varepsilon ,\xi )\right] \nonumber \\{} & {} \quad =\left[ {\textbf{G}}_{1I}^{(2\kappa -1)}(\xi +0,\xi )-{\textbf{G}}_{1I} ^{(2\kappa -1)}(\xi -0,\xi )\right] ={\textbf{p}}_{2\kappa }^{-1}(\xi )\quad \;\mathrm{{if}}~~~x=\xi . \end{aligned}$$

  (3.5b)

  In contrast to this, ${\textbf{G}}_{2I}(x,\xi )$ and its derivatives

  $$\begin{aligned} {\textbf{G}}_{2I}^{(\nu )}(x,\xi )=\frac{\partial ^{\nu }{\textbf{G}}_{2I}(x,\xi )}{\partial x^{\nu }},\qquad (\nu =1,2,\dots ,2\kappa ) \end{aligned}$$

  (3.6)

  are all continuous functions for any x in [b, c].

• 4. Let $\xi$ be fixed in [b, c]. The function ${\textbf{G}}_{1II}(x,\xi )$ and its derivatives

  $$\begin{aligned} {\textbf{G}}_{1II}^{(\nu )}(x,\xi )=\frac{\partial ^{\nu }{\textbf{G}}_{1II}(x,\xi )}{\partial x^{\nu }},\qquad (\nu =1,2,\dots ,2\kappa ) \end{aligned}$$

  (3.7)

  are all continuous functions for any x in [a, c].

  Though the function ${\textbf{G}}_{2II}(x,\xi )$ and its derivatives

  $$\begin{aligned} {\textbf{G}}_{2II}^{(\nu )}(x,\xi )=\frac{\partial ^{\nu }{\textbf{G}}_{2II}(x,\xi )}{\partial x^{n}},\qquad (\nu =1,2,\dots ,2\kappa -2) \end{aligned}$$

  (3.8)

  are also continuous for $x=\xi$:

  $$\begin{aligned}{} & {} \lim _{\varepsilon \rightarrow 0}\left[ {\textbf{G}}_{2II}^{(\nu )} (\xi +\varepsilon ,\xi )-{\textbf{G}}_{2II}^{(\nu )}(\xi -\varepsilon ,\xi )\right] \nonumber \\{} & {} \quad =\left[ {\textbf{G}}_{2II}^{(\nu )}(\xi +0,\xi )-{\textbf{G}}_{2II}^{(\nu )} (\xi -0,\xi )\right] =0\,\quad \nu =0,1,2,\ldots 2\kappa -2 \end{aligned}$$

  (3.9a)

  the derivative ${\textbf{G}}_{2II}^{(2\kappa -1)}(x,\xi )$ should, however, have a jump

  $$\begin{aligned}{} & {} \lim _{\varepsilon \rightarrow 0}\left[ {\textbf{G}}_{2II} ^{(2\kappa -1)}(\xi +\varepsilon ,\xi )-{\textbf{G}}_{21I}^{(2\kappa -1)} (\xi -\varepsilon ,\xi )\right] \nonumber \\{} & {} \quad =\left[ {\textbf{G}}_{2II}^{(2\kappa -1)}(\xi +0,\xi )-{\textbf{G}}_{2II} ^{(2\kappa -1)}(\xi -0,\xi )\right] ={\textbf{p}}_{2\kappa }^{-1}(\xi )\quad \mathrm{{if}}\quad x=\xi . \end{aligned}$$

  (3.9b)

• 5. Let $\varvec{\alpha }^{T}=[\alpha _{1}|\alpha _{2}|\ldots |\alpha _{n}],\alpha _{\nu }\ne 0\,(\nu =1,2,\ldots ,n)$ be an arbitrary constant matrix where the elements are finite. For a fixed $\xi \in [a,c]$, the product $\hat{{\textbf{y}}}(x)={\textbf{G}}(x,\xi )\varvec{\alpha }$ as a function of x ($x\ne \xi$) should satisfy the homogeneous differential equation

  $$\begin{aligned} {\textbf{L}}\left[ {\textbf{G}}(x,\xi )\varvec{\alpha }\right] ={\textbf{L}} \left[ \hat{{\textbf{y}}}(x)\right] ={\textbf{0}}. \end{aligned}$$

• 6. The product $\hat{{{\textbf {y}}}}=G(x,\xi )\varvec{\alpha }$ as a function of x should satisfy both the boundary conditions and the continuity conditions:

  $$\begin{aligned} {\textbf{U}}_{ar}[{\textbf{y}}]&= \sum _{\nu =1}^{2\kappa }\varvec{\alpha }_{\nu rI}\,\hat{{\textbf{y}}}^{(\nu - 1)}(a)={\textbf{0}}, \quad r =1,2,\ldots ,\kappa \end{aligned}$$

  (3.10a)
  $$\begin{aligned} {\textbf{U}}_{br}[{\textbf{y}}]&= {\textbf{U}}_{brI}[\hat{{\textbf{y}} }(b-0)]-{\textbf{U}}_{brII}[\hat{{\textbf{y}}}(b+0)] \nonumber \\&=\sum _{\nu =1}^{2\kappa }\left( \varvec{\beta }_{\nu rI}\,{\hat{\textbf{y}}}^{(\nu - 1)}(b - 0) - \varvec{\beta }_{\nu rII}\,\hat{{\textbf{y}} }^{(\nu - 1)}(b + 0)\right) = {\textbf{0}}, \quad r = 1,2,\ldots ,2\kappa \end{aligned}$$

  (3.10b)
  $$\begin{aligned} {\textbf{U}}_{cr}[{\textbf{y}}]&= \sum _{\nu =1}^{2\kappa }\varvec{\gamma }_{\nu rII}\,\hat{{\textbf{y}}}^{(\nu - 1)}(c) = {\textbf{0}}, \quad r =1,2,\ldots ,\kappa . \end{aligned}$$

  (3.10c)

  These criteria should be applied to the function pairs ${\textbf{G}}_{1I} (x,\xi )$, ${\textbf{G}}_{2I}(x,\xi )$ and ${\textbf{G}}_{1II}(x,\xi )$, ${\textbf{G}}_{2II}(x,\xi )$ as well.

Remark 1

This definition is a generalization of the definition given for three-point boundary value problems governed by ordinary differential equation in [29, 31].

Remark 2

It can be proved by repeating the line of thought presented in Remark 10.4 in book [30] that vector (3.2) given in terms of the previous Green function matrix satisfies the inhomogeneous differential equation system (3.1a) and the boundary and continuity conditions (2.20).

4 Calculation of the Green function matrix

4.1 Structure of the general solution

The definition of the Green function matrix given in the previous Section is a constructive one which means that it provides the means that are needed to calculate it. The general solution of the homogeneous differential equation system

$$\begin{aligned} {\textbf{L}}\,[\,{\textbf{y}}(x)]={\textbf{0}} \end{aligned}$$

(4.1)

has the following form

$$\begin{aligned} {\textbf{y}}=\left[ \sum _{\ell =1}^{2\kappa }\underset{\left( n\times n\right) }{{\textbf{Y}}_{\,\ell }}(x)\,\underset{\left( n\times n\right) }{{\textbf{C}}_{\,\ell }}\right] \underset{(n\times 1)}{{\textbf{e}}}, \end{aligned}$$

(4.2)

where each column of the matrices ${\textbf{Y}}_{\,\ell }$ satisfies the homogeneous differential equation system (4.1), ${\textbf{C}}_{\ell }$ is a constant square matrix while ${\textbf{e}}$ is a constant column matrix (a constant vector).

Recalling the fifth property of the definition and the structure of the general solution (4.1), it follows that the elements of the Green function matrix can be given in the same form the expression in the square brackets has in (4.2) – see [30].

4.2 Calculation of the Green matrix function if $\xi \in [a,b]$

The matrix of the integration constants ${\textbf{C}}_{\,\ell }$ should be different in the two triangular domains $a\le x\le \xi \le b$ and $a\le \xi \le x\le b$. For this reason, it is assumed that

$$\begin{aligned} \begin{aligned} \underset{(n\times n)}{{\textbf{G}}_{1I}(x,\xi )}&=\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell I}(\xi )+{\textbf{B}}_{\,\ell I}(\xi )\right] ,\qquad x\le \xi ;\\ \underset{(n\times n)}{{\textbf{G}}_{1I}(x,\xi )}&=\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell I}(\xi )-{\textbf{B}}_{\,\ell I}(\xi )\right] ,\qquad x\ge \xi \end{aligned} \qquad x\in [a,b] \end{aligned}$$

(4.3)

and

$$\begin{aligned} \underset{(n\times n)}{{\textbf{G}}_{2I}(x,\xi )}=\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{C}}_{\,\ell I}(\xi ),\qquad x\in [b,c]\, \end{aligned}$$

(4.4)

where the coefficient matrices ${\textbf{A}}_{\,\ell I}(\xi )$, ${\textbf{B}}_{\,\ell I}(\xi )$ and ${\textbf{C}}_{\,\ell I}(\xi )$ are unknown function matrices.

Representation of ${\textbf{G}}_{1I}(x,\xi )$ and ${\textbf{G}}_{2I}(x,\xi )$ in the forms (4.3) and (4.4) automatically ensures the fulfillment of the first and fifth properties of the definition.

Utilizing the second and third properties of the definition, the following equations can be established for calculating the elements of the matrices ${\textbf{B}}_{\,\ell I} (\xi )$:

$$\begin{aligned} \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(\xi )\,{\textbf{B}}_{\,\ell I}(\xi )&={\textbf{0}},\quad \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }^{(1)}(\xi )\,{\textbf{B}}_{\,\ell I}(\xi ) ={\textbf{0}},\nonumber \\ \cdots&\\ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }^{(2\kappa -2)}(\xi )\,{\textbf{B}} _{\,\ell I}(\xi )&={\textbf{0}},\quad \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }^{(2\kappa -1)}(\xi )\,{\textbf{B}} _{\,\ell I}(\xi ) =-\frac{1}{2}{\textbf{p}}_{\,2\kappa }^{-1}(\xi ),\nonumber \end{aligned}$$

(4.5)

where ${\textbf{0}}$ is an $n\times n$ zero matrix. Let us denote the $\nu$th column ($\nu =1,2,\ldots ,n$) of the matrix ${\textbf{B}}_{\,\ell I}$ by $\underset{(n\times 1)}{{\textbf{B}}_{\,\ell I\,\nu }}$:

$$\begin{aligned} \underset{(n\times n)}{{\textbf{B}}_{\,\ell I}}=[\,\underset{(n\times 1)}{{\textbf{B}}_{\,\ell I\,1}}\,|\,\underset{(n\times 1)}{{\textbf{B}}_{\,\ell I\,2}}\,|\cdots \,|\,\underset{(n\times 1)}{{\textbf{B}}_{\,\ell I\,n}}\,]. \end{aligned}$$

(4.6)

The matrix

$$\begin{aligned} \underset{(1\times (2\kappa \times n))}{\varvec{{\mathcal {B}}}_{\,\nu }^{T} }=\bigl [\underset{(1\times n)}{{\textbf{B}}_{\,1I\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{B}}_{\,iI\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{B}}_{\,2\kappa I\,\nu }^{T}}\bigr ],\qquad i=2,3,\ldots ,2\kappa -1 \end{aligned}$$

(4.7)

is that of the unknowns for a given $\nu$.

Let the ith column ($i=1,2,\ldots ,n$) in the matrix ${\textbf{Y}}_{\,\ell }$ be denoted by $\varvec{\eta }_{\,\ell i}$:

$$\begin{aligned} \underset{(n\times n)}{{\textbf{Y}}_{\,\ell }}=[\,\underset{(n\times 1)}{\varvec{\eta }_{\,\ell 1}}\,|\,\underset{(n\times 1)}{\varvec{\eta }_{\,\ell 2}}\,|\cdots \,|\,\underset{(n\times 1)}{\varvec{\eta }_{\,\ell n} }\,]. \end{aligned}$$

(4.8)

Then, the matrix $\varvec{{\mathcal {B}}}_{\,\nu }$ is the solution of the linear equation system:

$$\begin{aligned} {\textbf{W}}\,\varvec{{\mathcal {B}}}_{\,\nu } =\varvec{{\mathcal {P}}}_{\,\nu }, \end{aligned}$$

(4.9a)

where

(4.9b)

while $\varvec{{\mathcal {P}}}_{\,\nu }$ is the transpose of the $\nu$th row in the matrix:

(4.9c)

Note that the coefficient matrix ${\textbf{W}}$ is the same for each $\varvec{{\mathcal {B}}}_{\,\nu }$.

Remark 3

The determinant of ${\textbf{W}}$ is the corresponding Wronskian which is different from zero [32]. This ensures that equation system (4.9a) is solvable.

After having determined the matrices ${\textbf{B}}_{\,\ell I}$, the next step is the calculation of the matrices ${\textbf{A}}_{\,\ell I}$ and ${\textbf{C}}_{\,\ell I}$ by utilizing the fourth property of the definition. Let $\varvec{\alpha }$ be the $\nu$th unit vector in the $n\times n$ space:

(4.10)

With $\varvec{\alpha }^{T}$, the sixth property of the definition yields

$$\begin{aligned}{} & {} {\textbf{U}}_{ar}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell } (x){\textbf{A}}_{\,\ell I}(\xi )\varvec{\alpha }\right] \nonumber \\{} & {} \qquad =-{\textbf{U}} _{ar}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{B}}_{\,\ell I}(\xi )\varvec{\alpha }\right] ,\quad r=1,2,\ldots ,\kappa ; \end{aligned}$$

(4.11a)

$$\begin{aligned}{} & {} {\textbf{U}}_{br}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell } (x){\textbf{A}}_{\,\ell I}(\xi )\varvec{\alpha }\right] -{\textbf{U}} _{br}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{B}}_{\,\ell I}(\xi )\varvec{\alpha }\right] \nonumber \\{} & {} \qquad ={\textbf{U}}_{br}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{C}}_{\,\ell I}(\xi )\varvec{\alpha }\right] ,\,\quad r=1,2,\ldots ,2\kappa ; \end{aligned}$$

(4.11b)

$$\begin{aligned}{} & {} {\textbf{U}}_{cr}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell } (x){\textbf{C}}_{\,\ell I}(\xi )\varvec{\alpha }\right] ={\textbf{0}}\quad r=1,2,\ldots ,\kappa . \end{aligned}$$

(4.11c)

The matrices

$$\begin{aligned} \underset{(1\times (2\kappa \times n))}{\varvec{{\mathcal {A}}}_{\,\nu }^{T} }= & {} \left[ \underset{(1\times n)}{{\textbf{A}}_{\,1I\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{A}}_{\,iI\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{A}}_{\,2\kappa I\,\nu }^{T}}\right] ,\qquad i=2,3,\ldots ,2\kappa -1 \end{aligned}$$

(4.12a)

$$\begin{aligned} \underset{(1\times (2\kappa \times n))}{\varvec{{\mathcal {C}}}_{\,\nu }^{T} }= & {} \left[ \underset{(1\times n)}{{\textbf{C}}_{\,1I\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{C}}_{\,iI\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{C}}_{\,2\kappa I\,\,\nu }^{T}}\right] ,\qquad i=2,3,\ldots ,2\kappa -1 \end{aligned}$$

(4.12b)

contain the unknowns for a fixed $\nu$ in $\varvec{\alpha }$—note that here the same notational convention is used as in Eqs. (4.6) and (4.7). Making use of Eq. (4.12) we can rewrite equation system (4.11) into the following form:

$$\begin{aligned}{} & {} {\textbf{U}}_{ar}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}} _{2\kappa \,}\right] \varvec{{\mathcal {A}}}_{\,\nu }=-{\textbf{U}}_{ar}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}}_{2\kappa \,}\right] \varvec{{\mathcal {B}}}_{\,\nu },\quad r=1,2,\ldots ,\kappa ; \end{aligned}$$

(4.13a)

$$\begin{aligned}{} & {} {\textbf{U}}_{br}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}} _{2\kappa \,}\right] \,\varvec{{\mathcal {A}}}_{\,\nu }-{\textbf{U}}_{br}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}}_{2\kappa \,}\right] \,\varvec{{\mathcal {C}}}_{\,\nu } ={\textbf{U}}_{br}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}}_{2\kappa \,}\right] \,\varvec{{\mathcal {B}}}_{\,\nu },\nonumber \\{} & {} \quad r=1,2,\ldots ,2\kappa ; \end{aligned}$$

(4.13b)

$$\begin{aligned}{} & {} {\textbf{U}}_{cr}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}} _{2\kappa \,}\right] \,\varvec{{\mathcal {C}}}_{\,\nu }={\textbf{0}}\quad r=1,2,\ldots ,\kappa , \end{aligned}$$

(4.13c)

where ${\textbf{U}}_{ar}$, ${\textbf{U}}_{br}$ and ${\textbf{U}}_{cr}$ are matrices with size $n\times (2\kappa \times n)$. The linear equation system (4.13) is solvable for $\varvec{{\mathcal {A}}}_{\,\nu }$ and $\varvec{{\mathcal {C}}}_{\,\nu }$ if its determinant is different from zero. If the boundary and continuity conditions (2.2) are linearly independent equation system (4.13) is, in general, solvable.

Remark 4

Note that the coefficient matrix in (4.13) is the same for each $\varvec{{\mathcal {A}}}_{\,\nu }$ and $\varvec{{\mathcal {C}}}_{\,\nu }$.

4.3 Calculation of the Green function if $\xi \in [b,c]$

The procedure is similar to the one described in the previous Subsection. Thus, it is assumed that

$$\begin{aligned} \begin{aligned} \underset{(n\times n)}{{\textbf{G}}_{2II}(x,\xi )}&=\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell II}(\xi )+{\textbf{B}}_{\,\ell II}(\xi )\right] ,\qquad x\le \xi ;\\ \underset{(n\times n)}{{\textbf{G}}_{2II}(x,\xi )}&=\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell II}(\xi )-{\textbf{B}}_{\,\ell II}(\xi )\right] ,\qquad x\ge \xi \end{aligned} \qquad x\in [b,c] \end{aligned}$$

(4.14)

and

$$\begin{aligned} \underset{(n\times n)}{{\textbf{G}}_{1II}(x,\xi )}=\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{C}}_{\,\ell II}(\xi ),\qquad x\in [b,c]\, \end{aligned}$$

(4.15)

where the coefficients matrices ${\textbf{A}}_{\,\ell II}(\xi )$, ${\textbf{B}} _{\,\ell II}(\xi )$ and ${\textbf{C}}_{\,\ell II}(\xi )$ are again unknown function matrices. The fourth property yields the following equations for calculating the elements of the matrices ${\textbf{B}}_{\,\ell }(\xi )$:

$$\begin{aligned}&\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(\xi )\,{\textbf{B}}_{\,\ell II}(\xi ) ={\textbf{0}},\quad \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }^{(1)}(\xi )\,{\textbf{B}}_{\,\ell II}(\xi ) ={\textbf{0}},\nonumber \\&\cdots \nonumber \\&\sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }^{(2\kappa -2)}(\xi )\,{\textbf{B}} _{\,\ell II}(\xi ) ={\textbf{0}},\quad \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }^{(2\kappa -1)}(\xi )\,{\textbf{B}} _{\,\ell II}(\xi ) =-\frac{1}{2}{\textbf{p}}_{\,2\kappa }^{-1}(\xi ). \end{aligned}$$

(4.16)

Remark 5

This equation system coincides with equation system (4.5). Hence, ${\textbf{B}}_{\ell I}={\textbf{B}}_{\ell II}$. This coincidence follows from the facts that (a) properties three and four are independent of the boundary and continuity conditions (2.2) and (b) the structure of matrices ${\textbf{G}}_{1I}$ and ${\textbf{G}}_{2II}$ is the same.

Utilizing now the boundary and continuity conditions (2.2) yields the following linear equation system for the unknown coefficients ${\textbf{A}}_{\ell II}(\xi )$ and ${\textbf{C}}_{\ell II}(\xi )$:

$$\begin{aligned}{} & {} {\textbf{U}}_{ar}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell } (x){\textbf{C}}_{\,\ell II}(\xi )\varvec{\alpha }\right] ={\textbf{0}},\quad r=1,2,\ldots ,\kappa ; \end{aligned}$$

(4.17a)

$$\begin{aligned}{} & {} {\textbf{U}}_{br}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell } (x){\textbf{C}}_{\,\ell II}(\xi )\varvec{\alpha }\right] -{\textbf{U}} _{br}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{A}}_{\,\ell II}(\xi )\varvec{\alpha }\right] \nonumber \\{} & {} \quad ={\textbf{U}}_{br}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell }(x){\textbf{B}}_{\,\ell II}(\xi )\varvec{\alpha }\right] ,\,\quad r=1,2,\ldots ,2\kappa ; \end{aligned}$$

(4.17b)

$$\begin{aligned}{} & {} {\textbf{U}}_{cr}\left[ \sum _{\ell =1}^{2\kappa }{\textbf{Y}}_{\,\ell } (x){\textbf{A}}_{\,\ell II}(\xi )\varvec{\alpha }\right] ={\textbf{0}}\quad r=1,2,\ldots ,\kappa . \end{aligned}$$

(4.17c)

By introducing the notation conventions

$$\begin{aligned} \underset{(1\times (2\kappa \times n))}{\varvec{{\mathcal {A}}}_{\,\nu }^{T} }= & {} \left[ \underset{(1\times n)}{{\textbf{A}}_{\,1II\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{A}}_{\,iII\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{A}}_{\,2\kappa II\,\nu }^{T}}\right] ,\qquad i=2,3,\ldots ,2\kappa -1 \end{aligned}$$

(4.18a)

$$\begin{aligned} \underset{(1\times (2\kappa \times n))}{\varvec{{\mathcal {C}}}_{\,\nu }^{T} }= & {} \left[ \underset{(1\times n)}{{\textbf{C}}_{\,1I\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{C}}_{\,iI\,\nu }^{T}}|\ldots |\underset{(1\times n)}{{\textbf{C}}_{\,2\kappa I\,\,\nu }^{T}}\right] ,\qquad i=2,3,\ldots ,2\kappa -1 \end{aligned}$$

(4.18b)

in the same way as for Eq. (4.12), we can manipulate equation system (4.17) into the following form:

$$\begin{aligned}{} & {} {\textbf{U}}_{ar}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}} _{2\kappa \,}\right] \,\varvec{{\mathcal {C}}}_{\,\nu }={\textbf{0}},\quad r=1,2,\ldots ,\kappa ; \end{aligned}$$

(4.19a)

$$\begin{aligned}{} & {} {\textbf{U}}_{br}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}} _{2\kappa \,}\right] \,\varvec{{\mathcal {C}}}_{\,\nu }-{\textbf{U}}_{br}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}}_{2\kappa \,}\right] \,\varvec{{\mathcal {A}}}_{\,\nu }\nonumber \\{} & {} \quad \qquad ={\textbf{U}}_{br}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}}_{2\kappa \,}\right] \,\varvec{{\mathcal {B}}}_{\,\nu },\,\quad r=1,2,\ldots ,2\kappa ; \end{aligned}$$

(4.19b)

$$\begin{aligned}{} & {} {\textbf{U}}_{cr}\left[ {\textbf{Y}}_{1\,},{\textbf{Y}}_{2\,},\ldots ,{\textbf{Y}} _{2\kappa \,}\right] \,\varvec{{\mathcal {A}}}_{\,\nu }={\textbf{0}}\quad r=1,2,\ldots ,\kappa . \end{aligned}$$

(4.19c)

If the boundary and continuity conditions (2.2) are linearly independent, the above linear equation system is also solvable for $\varvec{{\mathcal {A}}}_{\,\nu }$ and $\varvec{{\mathcal {C}}}_{\,\nu }$.

Remark 6

If equation systems (4.13) and (4.19) are solvable, then there exits the Green function matrix ${\textbf{G}}(x,\xi )$ given by Eq. (3.3).

Remark 7

If differential equation (4.1) is self-adjoint under the boundary and continuity conditions (2.2), then the Green function matrix is cross-symmetric, i.e., it holds that

$$\begin{aligned} {\textbf{G}}^{T}(x,\xi )={\textbf{G}}(x,\xi ). \end{aligned}$$

(4.20)

The proof of this statement is the same as for two-point boundary value problems. The latter is presented in Subsection 9.2.8 of [30].

5 Numerical examples

5.1 Governing equations of Timoshenko beams with cross-sectional heterogeneity

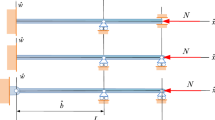
A pinned–pinned heterogeneous Timoshenko beam of length L is considered with an intermediate roller support at ${\hat{b}}$ as shown in Fig. 1. It has a uniform cross section throughout its length. The centerline of the beam coincides with the axis ${\hat{x}}$ of the coordinate system $({\hat{x}}{\hat{y}}{\hat{z}})$. Its origin is at the left end of the centerline. The coordinate plane ${\hat{x}}{\hat{z}}$ is a symmetry plane. The modulus of elasticity E, the shear modulus of elasticity G and the Poisson number satisfy the relations $E({\hat{y}},{\hat{z}})=E(-{\hat{y}},{\hat{z}})$, $G({\hat{y}},{\hat{z}})=G(-{\hat{y}},{\hat{z}})$ and $\nu ({\hat{y}},{\hat{z}})=\nu (-{\hat{y}},{\hat{z}})$ over the cross section A, which means that they are even functions of ${\hat{y}}$ and are independent of the coordinate ${\hat{x}}$. In this case, we speak about cross-sectional heterogeneity. Note that the E-weighted first moment is zero in this coordinate system:

$$\begin{aligned} Q_{ey}=\int _{A} z E({\hat{y}},{\hat{z}})\,\textrm{d}z=0. \end{aligned}$$

(5.1)

Let $A_{g}$, $I_{ey}$ be the G–weighted area and E-weighted moment of inertia:

$$\begin{aligned} A_{g}=\int _{A}G({\hat{y}},{\hat{z}})\,\textrm{d}A,\qquad I_{ey}=\int _{A}\,E({\hat{y}},{\hat{z}})z^{2}\,\textrm{d}A. \end{aligned}$$

(5.2)

The shear correction factor for Timoshenko beams with cross-sectional heterogeneity is denoted by $\kappa _{y}$, and its detailed definition is presented in “Appendix A”.

Fig. 1

A compressed beam with three supports

Equilibrium problems of Timoshenko beams with cross-sectional heterogeneity, subjected to an axial force are governed by the ordinary differential equation system [30, 33]:

$$\begin{aligned}{} & {} \frac{A_{g}\kappa _{y}}{I_{ey}}\left( \frac{\textrm{d}^{2}{\hat{w}}}{\textrm{d}{\hat{x}}^{2}}+\frac{\textrm{d}{\hat{\psi }}_{y}}{\textrm{d}{\hat{x}} }\right) +\frac{f_{z}}{I_{ey}}=0, \end{aligned}$$

(5.3a)

$$\begin{aligned}{} & {} \frac{\textrm{d}^{2}{\hat{\psi }}_{y}}{\textrm{d}{\hat{x}}^{2}}\pm \frac{N}{I_{ey} }\frac{\textrm{d}{\hat{w}}}{\textrm{d}{\hat{x}}}-\frac{A_{g}\kappa _{y}}{I_{ey} }\left( \frac{\textrm{d}{\hat{w}}}{\textrm{d}{\hat{x}}}+{\hat{\psi }}_{y}\right) +\frac{\mu _{y}}{I_{ey}}=0, \end{aligned}$$

(5.3b)

where ${\hat{w}}$ is the deflection, ${\hat{\psi }}$ is the rotation of the cross section, $f_{z}$ and $\mu _{z}$ are distributed force and moment loads, while the (plus)[minus] sign of N belongs to a (tensile) [compressive] axial force – from now on, N is regarded as if it was a positive quantity and the applied sign reflects if it is tensile or compressive. The coordinate ${\hat{\xi }}$ is measured on the axis ${\hat{x}}$ with the same origin. Let

$$\begin{aligned} x={\hat{x}}/L,~\xi ={\hat{\xi }}/L,~y_{1}=w={\hat{w}}/L,~ y_{2}=\psi ={\hat{\psi }}_{y},~ b={\hat{b}}/{\hat{\ell }},~\ell =\left. \frac{x}{L}\right| _{x=L}=1 \end{aligned}$$

(5.4)

be dimensionless quantities. Applying them to Eq. (5.3) yields

$$\begin{aligned}{} & {} \underset{\chi }{\underbrace{\frac{A_{g}\kappa _{y}L^{2}}{I_{ey}}}}\left( \frac{\textrm{d}^{2}y_{1}}{\textrm{d}x^{2}}+\frac{\textrm{d}y_{2}}{\textrm{d}x}\right) =\underset{r_{1}}{\underbrace{-\frac{f_{z}L^{3}}{I_{ey} }}},\end{aligned}$$

(5.5a)

$$\begin{aligned}{} & {} \frac{\textrm{d}^{2}y_{2}}{\textrm{d}x^{2}}\pm \underset{{\mathcal {N}} }{\underbrace{\frac{NL^{2}}{I_{ey}}}}\frac{\textrm{d}y_{1}}{\textrm{d} x}-\underset{\chi }{\underbrace{\frac{A_{g}L^{2}\kappa _{y}}{I_{ey}}}}\left( \frac{\textrm{d}y_{1}}{\textrm{d}x}+y_{2}\right) =\underset{r_{2} }{\underbrace{-\frac{\mu _{y}L^{2}}{I_{ey}}}\,}, \end{aligned}$$

(5.5b)

or in matrix form

$$\begin{aligned} \underset{\varvec{{\mathcal {K}}}_{2}}{\underbrace{\left[ \begin{array}{cc} \chi &{} 0\\ 0 &{} 1 \end{array} \right] }}\underset{{\textbf{y}}^{(2)}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}^{(2)} + \underset{\varvec{{\mathcal {K}}}_{1} }{\underbrace{\left[ \begin{array}{cc} 0 &{} \chi \\ -\chi \pm {\mathcal {N}} &{} 0 \end{array} \right] }}\underset{{\textbf{y}}^{(1)}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}^{(1)} + \underset{\varvec{{\mathcal {K}}}_{0} }{\underbrace{\left[ \begin{array}{cc} 0 &{} 0\\ 0 &{} -\chi \end{array} \right] }}\underset{{\textbf{y}}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }} = \underset{\varvec{{\mathcal {M}}}_{0}}{\underbrace{\left[ \begin{array}{cc} -1 &{} 0\\ 0 &{} -1 \end{array} \right] }}\underset{{\textbf{r}}}{\underbrace{\left[ \begin{array}{c} r_{1}\\ r_{2} \end{array} \right] }}. \end{aligned}$$

(5.6)

These equations are associated with the boundary and continuity conditions presented in Table 1.

If the beam vibrates freely, the amplitudes will be denoted in the same way as in Eq. (5.5). It can be checked with ease that the amplitude functions should satisfy the differential equations

$$\begin{aligned}{} & {} \frac{A_{g}\kappa _{y}L^{2}}{I_{ey}}\left( \frac{\textrm{d}^{2}y_{1} }{\textrm{d}x^{2}}+\frac{\textrm{d}y_{2}}{\textrm{d}x}\right) =-\underset{\lambda }{\underbrace{\frac{\rho _{a}A\omega ^{2}L^{4}}{I_{ey}}} }y_{1}, \end{aligned}$$

(5.7a)

$$\begin{aligned}{} & {} \frac{\textrm{d}^{2}y_{2}}{\textrm{d}x^{2}}\pm \frac{NL^{2}}{I_{ey}} \frac{\textrm{d}y_{1}}{\textrm{d}x}-\frac{A_{g}\kappa L^{2}}{I_{ey}}\left( \frac{\textrm{d}y_{1}}{\textrm{d}x}+y_{2}\right) =-\underset{\lambda }{\underbrace{\frac{\rho _{a}A\omega ^{2}L^{4}}{I_{ey}}}}y_{2} \,\underset{{\mathfrak {r}}^{2}}{\underbrace{\frac{I_{\rho y}}{\rho _{a}AL^{2}}}}, \end{aligned}$$

(5.7b)

where $\rho _{a}$ is the average density over the cross section and

$$\begin{aligned} I_{\rho y}=\int _{A}z^{2}\rho \,\textrm{d}A \end{aligned}$$

(5.8)

is the $\rho$ weighted moment of inertia. Equation (5.7) in matrix form are

$$\begin{aligned} \underset{\varvec{{\mathcal {K}}}_{2}}{\underbrace{\left[ \begin{array}{ll} \chi &{} \quad 0\\ 0 &{} \quad 1 \end{array} \right] }}\underset{{\textbf{y}}^{(2)}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}^{(2)} + \underset{\varvec{{\mathcal {K}}}_{1} }{\underbrace{\left[ \begin{array}{ll} 0 &{} \quad \chi \\ -\chi \pm {\mathcal {N}} &{} \quad 0 \end{array} \right] }}\underset{{\textbf{y}}^{(1)}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}^{(1)} + \underset{\varvec{{\mathcal {K}}}_{0} }{\underbrace{\left[ \begin{array}{ll} 0 &{} \quad 0\\ 0 &{} \quad -\chi \end{array} \right] }}\underset{{\textbf{y}}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }} = \underset{\varvec{{\mathcal {M}}}_{0}}{\lambda \underbrace{\left[ \begin{array}{ll} -1 &{} \quad 0\\ 0 &{} \quad -{\mathfrak {r}}^{2} \end{array} \right] }}\underset{{\textbf{r}}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}. \end{aligned}$$

(5.9)

Note that the matrices $\varvec{{\mathcal {M}}}_{0}$ in (5.6) and (5.9) are different from each other.

Table 1 Boundary- and continuity conditions for the selected beam

Consider the differential equation system

$$\begin{aligned} {\textbf{L}}[{\textbf{y}}]= & {} \varvec{{\mathcal {K}}}_{2}{\textbf{y}}^{(2)} +\varvec{{\mathcal {K}}}_{1}{\textbf{y}}^{(1)}+\varvec{{\mathcal {K}}} _{0}{\textbf{y}}\nonumber \\= & {} \left[ \begin{array}{ll} \chi &{} 0\\ 0 &{} 1 \end{array} \right] \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] ^{(2)} + \left[ \begin{array}{ll} 0 &{} \chi \\ -\chi &{} 0 \end{array} \right] \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] ^{(1)} + \left[ \begin{array}{ll} 0 &{} \chi \\ -\chi &{} 0 \end{array} \right] \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] =\left[ \begin{array}{c} -r_{1}\\ -r_{2} \end{array} \right] ={\textbf{r}} \end{aligned}$$

(5.10)

associated with the boundary and continuity conditions given in Table 1.

Remark 8

The operator ${\textbf{L}}[{\textbf{y}}]$ coincides with the left side of Eqs. (5.6) and (5.9) if the dimensionless axial force ${\mathcal {N}}$ is set to zero. Consequently, the three-point boundary value problem defined by Eq. (5.10) associated with the boundary and continuity conditions in Table 1 describes the mechanical behavior of a pinned–pinned Timoshenko beam with intermediate roller support if the beam is subjected to the dimensionless distributed load ${\textbf{r}}$.

Calculation of the Green function for the three point boundary value problem defined by Eq. (5.10) associated with the boundary and continuity conditions presented in Table 1 is detailed in “Appendix B”.

Remark 9

With the Green function matrix, the integral

$$\begin{aligned} \left[ \begin{array}{c} y_{1}(x)\\ y_{2}(x) \end{array} \right] =\int _{0}^{\ell =1}\left[ \begin{array}{ll} G_{11}(x,\xi ) &{} \quad G_{12}(x,\xi )\\ G_{21}(x,\xi ) &{} \quad G_{22}(x,\xi ) \end{array} \right] \left[ \begin{array}{c} -r_{1}(\xi )\\ -r_{2}(\xi ) \end{array} \right] \,\textrm{d}\xi \end{aligned}$$

(5.11)

is the dimensionless solution of the boundary value problem defined by differential equation system (5.10) and the boundary and continuity conditions of Table 1. Here, $-G_{11}(x,\xi )$ and $-G_{21}(x,\xi )$ are the dimensionless deflection and rotation at the point x due to a dimensionless unit force $r_{1}(\xi )=1$ exerted on the beam at the point $\xi$, while $-G_{12}(x,\xi )$ and $-G_{22}(x,\xi )$ are the dimensionless deflection and rotation at the point x due to a dimensionless unit couple $r_{2}(\xi )=1$ exerted on the beam at the point $\xi$.

Fig. 2

Element $G_{11}$ of the Green function matrix along the beam axis

Fig. 3

Element $G_{21}$ of the Green function matrix along the beam axis

Fig. 4

Element $G_{12}$ of the Green function matrix along the beam axis

Fig. 5

Element $G_{22}$ of the Green function matrix along the beam axis

Figures 2, 3, 4 and 5 represent the dimensionless displacement and angle of rotation for the cross section shown in Fig. 13 provided that the corresponding data are those we used to calculate $\chi$ by Eq. (A.6). Note that the derivative $-\textrm{d}G_{22}(x,\xi =0.75)/\textrm{d}x$ has a finite jump since the bending moment is discontinuous at this point.

5.2 Free vibration of the pinned–pinned beam with intermediate roller support

If the axial force is zero, the amplitudes of the free vibrations should satisfy the differential equitation system

$$\begin{aligned} \underset{\varvec{{\mathcal {K}}}_{2}}{\underbrace{\left[ \begin{array}{ll} \chi &{} \quad 0\\ 0 &{} \quad 1 \end{array} \right] }}\underset{{\textbf{y}}^{(2)}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}^{(2)} + \underset{\varvec{{\mathcal {K}}}_{1} }{\underbrace{\left[ \begin{array}{ll} 0 &{} \quad \chi \\ -\chi &{} \quad 0 \end{array} \right] }}\underset{{\textbf{y}}^{(1)}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}^{(1)} + \underset{\varvec{{\mathcal {K}}}_{0} }{\underbrace{\left[ \begin{array}{ll} 0 &{} \quad 0\\ 0 &{} \quad -\chi \end{array} \right] }}\underset{{\textbf{y}}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }} = \underset{\varvec{{\mathcal {M}}}_{0}}{\lambda \underbrace{\left[ \begin{array}{ll} -1 &{} \quad 0\\ 0 &{} \quad -{\mathfrak {r}}^{2} \end{array} \right] }}\underset{{\textbf{y}}}{\underbrace{\left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }} \end{aligned}$$

(5.12)

associated with the boundary and continuity conditions given in Table 1. The expression

$$\begin{aligned} \lambda \varvec{{\mathcal {M}}}_{0}{\textbf{y}}=\lambda \left[ \begin{array}{ll} -1 &{} \quad 0\\ 0 &{} \quad -{\mathfrak {r}}^{2} \end{array} \right] \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] \end{aligned}$$

on the right side of (5.9) corresponds to ${\textbf{r}}$ in solution (5.11). Hence,

$$\begin{aligned} \left[ \begin{array}{c} y_{1}\left( x\right) \\ y_{2}\left( x\right) \end{array} \right] =\lambda \int _{0}^{1}\left[ \begin{array}{ll} G_{11}\left( x,\xi \right) &{} \quad G_{12}\left( x,\xi \right) \\ G_{21}\left( x,\xi \right) &{} \quad G_{22}\left( x,\xi \right) \end{array} \right] \left[ \begin{array}{ll} -1 &{} \quad 0\\ 0 &{} \quad -{\mathfrak {r}}^{2} \end{array} \right] \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] \textrm{d}\xi . \end{aligned}$$

Introduction of the new variables $\varvec{{\mathcal {Y}}}$ and $\varvec{{\mathcal {K}}}$ as shown by the equation

$$\begin{aligned} \left[ \begin{array}{ll} 1 &{} \quad 0\\ 0 &{} \quad {\mathfrak {r}} \end{array} \right] \underset{\varvec{{\mathcal {Y}}}(x)}{\underbrace{\left[ \begin{array}{c} y_{1}\left( x\right) \\ y_{2}\left( x\right) \end{array} \right] }} =\lambda \int _{0}^{1}\underset{\varvec{{\mathcal {K}}}(x,\xi )}{\underbrace{\left[ \begin{array}{ll} 1 &{} \quad 0\\ 0 &{} \quad {\mathfrak {r}} \end{array} \right] \left[ \begin{array}{ll} -G_{11}\left( x,\xi \right) &{} \quad -G_{12}\left( x,\xi \right) \\ -G_{21}\left( x,\xi \right) &{} \quad -G_{22}\left( x,\xi \right) \end{array} \right] \left[ \begin{array}{ll} 1 &{} \quad 0\\ 0 &{} \quad {\mathfrak {r}} \end{array} \right] }}\,\underset{\varvec{{\mathcal {Y}}}(\xi )}{\underbrace{\left[ \begin{array}{ll} 1 &{} \quad 0\\ 0 &{} \quad {\mathfrak {r}} \end{array} \right] \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] }}\textrm{d}\xi \end{aligned}$$

results in an eigenvalue problem governed by the Fredholm integral equation system

$$\begin{aligned} \varvec{{\mathcal {Y}}}(x)=\lambda \int _{0}^{1}\varvec{{\mathcal {K}}} (x,\xi )\,\varvec{{\mathcal {Y}}}(\xi )\,\textrm{d}\xi . \end{aligned}$$

(5.13)

Remark 10

Integral equation system (5.13) coincides formally with integral equation system (9.151) in book [30]—the kernels are, however, different. The later was used to find the eigenvalues for four two-point eigenvalue problems established for pinned–pinned, fixed-pinned fixed-fixed and fixed-free Timoshenko beams. With the eigenvalues, the first two natural circular frequencies were also computed for these beams. The results are shown in Figures 9.3 to 9.6 in [30].

Table 2 Computational results for the first four eigenvalues

Table 3 Eigenvalues in terms of the roller position when ${\mathfrak {E}}=3.180$

Eigenvalue problem (5.13) can be reduced to an algebraic eigenvalue problem using the boundary element technique. The details are presented in Subsection 9.2.13 of [30]. A FORTRAN 90 code has been developed for solving the algebraic eigenvalue problem. The eigenvalues $\lambda$ are computed using IMSL Subroutine DGVLRG. With $\lambda _{k}$, the following equation can be utilized for calculating the corresponding circular frequency:

$$\begin{aligned} \omega _{k}=\frac{1}{L^{2}}\sqrt{\frac{\lambda _{k}I_{ey}}{\rho _{a}A}}. \end{aligned}$$

(5.14)

For the beam with cross section shown in Fig. 13 and data given by Eqs. (A.3)–(A.6)

$$\begin{aligned} {\mathfrak {E}}=3.180,\qquad {\mathfrak {r}}\simeq 0.001~443\,376,\qquad \chi =\frac{1}{{\mathfrak {E}}{\mathfrak {r}}^{2}}\simeq 150~939.0. \end{aligned}$$

(5.15)

Smaller ${\mathfrak {r}}$ means more slender beam. In this case, there cannot be significant difference between the Euler–Bernoulli and the Timoshenko beam theories. Table 2 contains the computational results for $\sqrt{\lambda _k}/\pi ^{2}$ as a function of b – for symmetry reasons $b\in [0,0.5]$. The results presented in Table 2 coincide with four to five digit accuracy with the results published in [31] for pinned–pinned beams with intermediate roller support within the framework of the Euler–Bernoulli beam theory.

The effect of ${\mathfrak {r}}$ on the first four eigenvalues is presented in Table 3 for ${\mathfrak {r}}=0.03$ and ${\mathfrak {r}}=0.05$. The results obtained for the first two eigenvalues regarding ${\mathfrak {r}}=0.001~443~3$ (Euler–Bernoulli beam theory), ${\mathfrak {r}}=0.03$, ${\mathfrak {r}}=0.05$ ${\mathfrak {r}}=0.075$, and ${\mathfrak {r}}=0.1$ as parameters are depicted in Figs. 6 and 7.

Fig. 6

The first eigenvalue for various ${\mathfrak {r}}$ parameters when ${\mathfrak {E}}=3.180$

Fig. 7

The second eigenvalue for various ${\mathfrak {r}}$ parameters when ${\mathfrak {E}}=3.180$

Table 4 Eigenvalues in terms of the roller position when ${\mathfrak {E}}=2.00$

Fig. 8

The first eigenvalue for various ${\mathfrak {r}}$ parameters when ${\mathfrak {E}}=2.00$

Fig. 9

The second eigenvalue for various ${\mathfrak {r}}$ parameters when ${\mathfrak {E}}=2.00$

The data in Table  4 reflect the effect of the parameter ${\mathfrak {E}}=2.0$ on $\sqrt{\lambda _{i}}/\pi ^{2}$, $(i=1,\ldots ,4)$ if ${\mathfrak {r}}=0.030,\; 0.050$. Figures 8 and 9 provide graphical representations for $\sqrt{\lambda _{i}}/\pi ^{2}$, $(i=1,2)$ if ${\mathfrak {r}}=0.03,\; 0.050,\;0.075,\;0.10$.

Table 5 Eigenvalues in terms of the roller position when ${\mathfrak {E}}=1.00$

Fig. 10

The first eigenvalue for various ${\mathfrak {r}}$ parameters when ${\mathfrak {E}}=1.00$

Fig. 11

The first eigenvalue for various ${\mathfrak {r}}$ parameters when ${\mathfrak {E}}=1.00$

Table  5 contains the data that reflect the effect of the parameter ${\mathfrak {E}}=1.0$ on $\sqrt{\lambda _{i}}/\pi ^{2}$, $(i=1,\ldots ,4)$ if ${\mathfrak {r}}=0.030,\; 0.050$. Figures 10 and 11 depict functions $\sqrt{\lambda _{i}}/\pi ^{2}$, $(i=1,2)$ if ${\mathfrak {r}}=0.030,\; 0.050,\;0.075,\;0.10$.

6 Conclusions

The paper is devoted to the issue of how the concept of Green function matrices can be generalized for three-point boundary value problems governed by ordinary differential equation systems. The investigations are based on the definition of the Green function matrix given for two-point boundary value problems in [30]. The definition is a constructive one since it provides the means necessary for calculating the Green function matrix. Utilizing the definition the Green function matrix is determined for pinned–pinned Timoshenko beams with an intermediate roller support (PrsP beams). After that the self-adjoint three-point eigenvalue problem that governs the free vibration of PrsP Timoshenko beams is reduced to an eigenvalue problem governed by a homogeneous Fredholm integral equation system with the Green function matrix as its kernel. This eigenvalue problem is reduced to an algebraic eigenvalue problem which is solved numerically. The solutions for the eigenvalues are presented in tabular and graphical formats.

Appendices

Shear correction factor for heterogeneous beams

Figure 12 depicts the cross section of a Timoshenko beam with cross-sectional heterogeneity.

Fig. 12

A heterogeneous cross section

The E-weighted first moment $Q_{ey}^{^{\prime }}$ of the shaded area denoted by $A^{^{\prime }}$ in Fig. 12 is defined by the integral

$$\begin{aligned} Q_{ey}^{^{\prime }}(z)=\int _{A^{\prime }}E\zeta \,\textrm{d}A. \end{aligned}$$

(A.1)

The shear correction factor is given by the equation [33]:

$$\begin{aligned} \kappa _{y}=\frac{I_{ey}^{2}}{A_{g}}\,\frac{1}{\displaystyle \int _{{A}} \frac{\,(Q_{ey}^{\prime }(z))^{2}}{G(y,z)t^{2}(z)}\,\textrm{d}A\,}. \end{aligned}$$

(A.2)

Fig. 13

A three-layered rectangular cross section

For the cross section shown in Fig. 13, it follows from Eqs. (5.2), (5.7b), (5.8) and (A.2) that

$$\begin{aligned} A_{g}= & {} \int _{A}G\,\textrm{d}A=2G_{lr}ah+G_{m}bh, \end{aligned}$$

(A.3a)

$$\begin{aligned} I_{ey}= & {} \int _{A}\,Ez^{2}\,\textrm{d}A=\frac{h^{3}}{12}\left[ 2aE_{lr} +bE_{m}\right] , \end{aligned}$$

(A.3b)

$$\begin{aligned} I_{\rho y}= & {} \int _{A}z^{2}\rho \,\textrm{d}A=\frac{h^{3}}{12}\left( 2\rho _{lr}a+\rho _{m}b\right) , \end{aligned}$$

(A.3c)

$$\begin{aligned} \rho _{a}= & {} \frac{1}{A}\int _{A}\rho \,\textrm{d}A=\frac{2\rho _{lr}a+\rho _{m} b}{2ah+bh}, \end{aligned}$$

(A.3d)

$$\begin{aligned} {\mathfrak {r}}^{2}= & {} \frac{I_{\rho y}}{\rho _{a}A\ell ^{2}}=\frac{h^{2}}{12L^{2}},\end{aligned}$$

(A.3e)

$$\begin{aligned} \kappa _{y}= & {} \frac{I_{ey}^{2}}{A_{g}}\,\frac{1}{\displaystyle \int _{{A}} \frac{\,(Q_{ey}^{\prime }(z))^{2}}{G(y,z)t^{2}(z)}\,\textrm{d}A\,}=\frac{5}{6}\frac{\left( 2aE_{lr}+bE_{m}\right) ^{2}G_{lr}G_{m}}{\left( 2aG_{lr}+bG_{m}\right) \left( 2aE_{lr}^{2}G_{m}+bE_{m}^{2}G_{lr}\right) }. \end{aligned}$$

(A.3f)

Here, (A.3f) is the shear correction factor. It also holds that

$$\begin{aligned} \chi =\frac{A_{g}\kappa _{y}L^{2}}{I_{ey}}=\frac{I_{\rho y}}{I_{ey}}\frac{A_{g} }{\rho _{a}A}\kappa _{y}\frac{1}{{\mathfrak {r}}^{2}}=\frac{1}{{\mathfrak {E}} {\mathfrak {r}}^{2}},\qquad \mathfrak {E=}\frac{\rho _{a}AI_{ey}}{A_{g}I_{\rho y} }\frac{1}{\kappa _{y}}. \end{aligned}$$

For $E_{lr}=210{,}000\,\hbox {MPa}$, $G_{lr}=80{,}000\,\hbox {MPa}$ and $E_{m}=70{,}000\,\hbox {MPa}$, $G_{m}=25{,}000\,\hbox {MPa}$:

$$\begin{aligned} \kappa _{y}=\frac{100}{3}\frac{\left( 6a+b\right) ^{2}}{\left( 32a+5b\right) \left( 45a+8b\right) }. \end{aligned}$$

(A.4)

Note that

$$\begin{aligned} \left. \kappa _{y}\right| _{a=b}=0.832\,908,\quad \text {and}\quad \left. \kappa _{y}\right| _{a=0}=\frac{5}{6}=0.833\,333. \end{aligned}$$

(A.5)

If, in addition to this, it is assumed that $L=2400$ mm,$\ a=b=4/3$ mm, $h=12$ mm, then

$$\begin{aligned} {\mathfrak {E}}=\frac{\rho _{a}AI_{ey}}{A_{g}I_{\rho y}}\frac{1}{\kappa _{y} }=3.180,\qquad {\mathfrak {r}}=\sqrt{2.\,083\,4\times 10^{-6}} \simeq 0.001443\,376,\quad \chi =\frac{1}{{\mathfrak {E}}{\mathfrak {r}}^{2}}\simeq 150939.0.\qquad \quad \end{aligned}$$

(A.6a)

Calculation of the Green function matrix for Timoshenko beams

1.1 Calculation steps if $\xi \in [0,b]$

The differential operator ${\textbf{L}}[{\textbf{y}}]={\textbf{0}}$ is given by Eq. (5.10). The general solution of the homogeneous differential equation ${\textbf{L}}[{\textbf{y}}]={\textbf{0}}$ is

$$\begin{aligned} \left[ \begin{array}{c} y_{1}\\ y_{2} \end{array} \right] =\underset{{\textbf{Y}}_{\,1}(x)}{\underbrace{\left[ \begin{array}{ll} 1 &{} \quad x\\ 0 &{} \quad -1 \end{array} \right] }}\left[ \begin{array}{c} c_{1}\\ c_{2} \end{array} \right] +\underset{{\textbf{Y}}_{\,2}(x)}{\underbrace{\left[ \begin{array}{ll} -\frac{1}{2}x^{2} &{} \quad -\frac{1}{3}x^{3}\\ x &{} \quad \frac{2}{\chi }+x^{2} \end{array} \right] }}\left[ \begin{array}{c} c_{3}\\ c_{4} \end{array} \right] . \end{aligned}$$

(B.1)

On the basis of (4.3) and (4.4), we may write

$$\begin{aligned} \begin{aligned} \underset{(2\times 2)}{{\textbf{G}}_{1I}(x,\xi )}&=\sum _{\ell =1}^{2} {\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell I}(\xi )+{\textbf{B}}_{\,\ell I}(\xi )\right] ,\qquad x\le \xi ;\\ \underset{(2\times 2)}{{\textbf{G}}_{1I}(x,\xi )}&=\sum _{\ell =1}^{2} {\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell I}(\xi )-{\textbf{B}}_{\,\ell I}(\xi )\right] ,\qquad x\ge \xi \end{aligned} \qquad x\in [0,b] \end{aligned}$$

(B.2)

and

$$\begin{aligned} \underset{(2\times 2)}{{\textbf{G}}_{2I}(x,\xi )}=\sum _{\ell =1}^{2}{\textbf{Y}} _{\,\ell }(x){\textbf{C}}_{\,\ell I}(\xi ),\qquad x\in [b,c]\, \end{aligned}$$

(B.3)

where the coefficients matrices ${\textbf{A}}_{\,\ell I}(\xi )$, ${\textbf{B}} _{\,\ell I}(\xi )$ and ${\textbf{C}}_{\,\ell I}(\xi )$ are the unknowns. For the sake of further calculations, it is worth partitioning the matrices ${\textbf{Y}}_{\,\ell }$, ${\textbf{A}}_{\,\ell I}$, ${\textbf{B}}_{\,\ell I}$ and ${\textbf{C}}_{\,\ell I}$:

$$\begin{aligned} {\textbf{Y}}_{\,\ell }= & {} \left[ \begin{array}{rr} \overset{\ell }{Y}_{11} &{} \quad \overset{\ell }{Y}_{12}\\ \overset{\ell }{Y}_{21} &{} \quad \overset{\ell }{Y}_{22} \end{array} \right] = \begin{array}{r} 1\;\{\\ 1\;\{ \end{array} \underset{(2\times 2)}{\underbrace{\left[ \begin{array}{c} {\textbf{Y}}_{\,\ell 1}\\ {\textbf{Y}}_{\,\ell 2} \end{array} \right] }}, \end{aligned}$$

(B.4a)

$$\begin{aligned} {\textbf{A}}_{\,\ell I}= & {} \left[ \begin{array}{rr} \overset{\ell }{A}_{11} &{} \quad \overset{\ell }{A}_{12}\\ \overset{\ell }{A}_{21} &{} \quad \overset{\ell }{A}_{22} \end{array} \right] =\left[ \begin{array}{cc} \underset{(2\times 1)}{{\textbf{A}}_{\,\ell 1}}&\underset{(2\times 1)}{{\textbf{A}}_{\,\ell 2}} \end{array} \right] ,\quad {\textbf{B}}_{\ell I}=\left[ \begin{array}{rr} \overset{\ell }{B}_{11} &{} \quad \overset{\ell }{B}_{12}\\ \overset{\ell }{B}_{21} &{} \quad \overset{\ell }{B}_{22} \end{array} \right] =\left[ \begin{array}{cc} \underset{(2\times 1)}{{\textbf{B}}_{\,\ell 1}}&\underset{(2\times 1)}{{\textbf{B}}_{\,\ell 2}} \end{array} \right] \end{aligned}$$

(B.4b)

$$\begin{aligned} {\textbf{C}}_{\ell I}= & {} \left[ \begin{array}{rr} \overset{\ell }{C}_{11} &{} \quad \overset{\ell }{C}_{12}\\ \overset{\ell }{C}_{21} &{} \quad \overset{\ell }{C}_{22} \end{array} \right] =\left[ \begin{array}{cc} \underset{(2\times 1)}{{\textbf{C}}_{\,\ell 1}}&\quad \underset{(2\times 1)}{{\textbf{C}}_{\,\ell 2}} \end{array} \right] . \end{aligned}$$

(B.4c)

It follows from Eq. (4.5) that the matrices ${\textbf{B}}_{\,\ell I}$ should satisfy the following equations:

$$\begin{aligned} \sum _{\ell =1}^{2}{\textbf{Y}}_{\,\ell }(\xi )\,{\textbf{B}}_{\,\ell I}(\xi )= & {} \left[ \begin{array}{cc} 1 &{} \quad \xi \\ 0 &{} \quad -1 \end{array} \right] \left[ \begin{array}{cc} \overset{1}{B}_{11} &{} \quad \overset{1}{B}_{12}\\ \overset{1}{B}_{21} &{} \quad \overset{1}{B}_{22} \end{array} \right] +\left[ \begin{array}{cc} -\frac{1}{2}\xi ^{2} &{} \quad -\frac{1}{3}\xi ^{3}\\ \xi &{} \quad \frac{2}{\chi }+\xi ^{2} \end{array} \right] \left[ \begin{array}{cc} \overset{2}{B}_{11} &{} \quad \overset{2}{B}_{12}\\ \overset{2}{B}_{21} &{} \quad \overset{2}{B}_{22} \end{array} \right] =\left[ \begin{array}{cc} 0 &{} \quad 0\\ 0 &{} \quad 0 \end{array} \right] , \nonumber \\ \end{aligned}$$

(B.5a)

$$\begin{aligned} \sum _{\ell =1}^{2}{\textbf{Y}}_{\,\ell }^{(1)}(\xi )\,{\textbf{B}}_{\,\ell I} (\xi )= & {} \left[ \begin{array}{cc} 0 &{} \quad 1\\ 0 &{} \quad 0 \end{array} \right] \left[ \begin{array}{cc} \overset{1}{B}_{11} &{} \quad \overset{1}{B}_{12}\\ \overset{1}{B}_{21} &{} \quad \overset{1}{B}_{22} \end{array} \right] +\left[ \begin{array}{cc} -\xi &{} \quad -\xi ^{2}\\ 1 &{} \quad 2\xi \end{array} \right] \left[ \begin{array}{cc} \overset{2}{B}_{11} &{} \quad \overset{2}{B}_{12}\\ \overset{2}{B}_{21} &{} \quad \overset{2}{B}_{22} \end{array} \right] =-\frac{1}{2}\left[ \begin{array}{cc} \frac{1}{\chi } &{} \quad 0\\ 0 &{} \quad 1 \end{array} \right] . \end{aligned}$$

(B.5b)

By introducing the new variables

$$\begin{aligned} a=\overset{1}{B}_{1i},\quad b=\overset{1}{B}_{2i}\quad c=\overset{2}{B} _{1i}\quad d=\overset{2}{B}_{2i} \end{aligned}$$

(B.6)

for $i=1$, equation system (B.5) assumes the form

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} \quad \xi &{} \quad -\frac{1}{2}\xi ^{2} &{} \quad -\frac{1}{3}\xi ^{3}\\ 0 &{} \quad -1 &{} \quad \xi &{} \quad \frac{2}{\chi }+\xi ^{2}\\ 0 &{} \quad 1 &{} \quad -\xi &{} \quad -\xi ^{2}\\ 0 &{} \quad 0 &{} \quad 1 &{} \quad 2\xi \end{array} \right] \left[ \begin{array}{c} a\\ b\\ c\\ d \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ -\frac{1}{2\chi }\\ 0 \end{array} \right] \end{aligned}$$

from where

$$\begin{aligned} a&=\overset{1}{B}_{11}=\frac{\xi }{2\chi }-\frac{\xi ^{3}}{12}, \quad b =\overset{1}{B}_{21}=\frac{1}{4}\xi ^{2}-\frac{1}{2\chi },\quad c =\overset{2}{B}_{11}=\frac{1}{2}\xi , \quad d =\overset{2}{B}_{21}=-\frac{1}{4}. \end{aligned}$$

(B.7a)

If $i=2$, it is found in the same way that

$$\begin{aligned} \left[ \begin{array}{cccc} 1 &{} \quad \xi &{} \quad -\frac{1}{2}\xi ^{2} &{} \quad -\frac{1}{3}\xi ^{3}\\ 0 &{} \quad -1 &{} \quad \xi &{} \quad \frac{2}{\chi }+\xi ^{2}\\ 0 &{} \quad 1 &{} \quad -\xi &{} \quad -\xi ^{2}\\ 0 &{} \quad 0 &{} \quad 1 &{} \quad 2\xi \end{array} \right] \left[ \begin{array}{c} a\\ b\\ c\\ d \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ 0\\ -\frac{1}{2} \end{array} \right] \end{aligned}$$

from where

$$\begin{aligned} a =\overset{1}{B}_{12}=\frac{1}{4}\xi ^{2}, \quad b =\overset{1}{B}_{22}=-\frac{1}{2}\xi , \quad c =\overset{2}{B}_{12}=-\frac{1}{2},\quad d =\overset{2}{B}_{22}=0. \end{aligned}$$

(B.7b)

According to Eq. (4.17a), the product ${\varvec{G}} (x,\xi )\varvec{\alpha }$ should satisfy boundary conditions at the left end of the beam. If $\varvec{\alpha }^{T}=\left[ 1|0\right] \;(i=1)$ or $\varvec{\alpha }^{T}=\left[ 0|1\right] \;(i=2)$, the boundary conditions at the left end results in the equation system

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=0} {\textbf{A}}_{\,\ell i}(\xi )&=-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=0}{\textbf{B}}_{\,\ell i}(\xi ), \end{aligned}$$

(B.8a)

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=0}{\textbf{A}}_{\,\ell i}(\xi )&=-\sum _{\ell =1}^{2}\left. {\textbf{Y}} _{\,\ell 2}^{(1)}(x)\right| _{x=0}{\textbf{B}}_{\,\ell i}(\xi ). \end{aligned}$$

(B.8b)

According to Eq. (4.17b), the product ${\varvec{G}} (x,\xi )\varvec{\alpha }$ should satisfy the continuity conditions at the intermediate roller ($x=b$). If $\varvec{\alpha }^{T}=\left[ 1|0\right] \;(i=1)$ or $\varvec{\alpha }^{T}=\left[ 0|1\right] \;(i=2)$ these continuity conditions lead to the equations

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b} {\textbf{A}}_{\,\ell i}(\xi ) =\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b}{\textbf{B}}_{\,\ell i}(\xi ), \end{aligned}$$

(B.9a)

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b} {\textbf{C}}_{\,\ell i}(\xi ) =0, \end{aligned}$$

(B.9b)

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}(x)\right| _{x=b} {\textbf{A}}_{\,\ell i}(\xi )-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}(x)\right| _{x=b}{\textbf{C}}_{\,\ell i}(\xi ) =\sum _{\ell =1} ^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b}{\textbf{B}}_{\,\ell i} (\xi ), \end{aligned}$$

(B.9c)

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=b}{\textbf{A}}_{\,\ell i}(\xi )-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=b}{\textbf{C}}_{\,\ell i}(\xi ) =\sum _{\ell =1} ^{2}\left. {\textbf{Y}}_{\,\ell 1}^{(1)}(x)\right| _{x=b}{\textbf{B}}_{\,\ell i}(\xi ). \end{aligned}$$

(B.9d)

As per Eq. (4.17a), the product ${\varvec{G}} (x,\xi )\varvec{\alpha }$ should satisfy boundary conditions at the right end of the beam. If $\varvec{\alpha }^{T}=\left[ 1|0\right] \;(i=1)$ or $\varvec{\alpha }^{T}=\left[ 0|1\right] \;(i=2)$, we get:

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=\ell }{\textbf{C}}_{\,\ell i}(\xi ) =0,\quad \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=\ell }{\textbf{C}}_{\,\ell i}(\xi ) =0. \end{aligned}$$

(B.10)

After substituting ${\textbf{Y}}_{\,\ell 1}$, ${\textbf{Y}}_{\,\ell 2}$, ${\textbf{Y}}_{\,\ell 2}^{(1)}$, ${\textbf{A}}_{\,\ell i}$, ${\textbf{B}}_{\,\ell i}$ and ${\varvec{C}}_{\,\ell i}$ into (B.8), (B.9) and (B.10), one arrives at the following equation system:

$$\begin{aligned} \left[ \begin{array}{cccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 1 &{} b &{} -\frac{1}{2}b^{2} &{} -\frac{1}{3}b^{3} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} b &{} -\frac{1}{2}b^{2} &{} -\frac{1}{3}b^{3}\\ 0 &{} -1 &{} b &{} \frac{2}{\chi }+b^{2} &{} 0 &{} 1 &{} -b &{} -\frac{2}{\chi }-b^{2}\\ 0 &{} 0 &{} 1 &{} 2b &{} 0 &{} 0 &{} -1 &{} -2b\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} \ell &{} -\frac{1}{2}\ell ^{2} &{} -\frac{1}{3}\ell ^{3}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 2\ell \end{array} \right] \left[ \begin{array}{c} \overset{1}{A}_{1i}\\ \overset{1}{A}_{2i}\\ \overset{2}{A}_{1i}\\ \overset{2}{A}_{2i}\\ \overset{1}{C}_{1i}\\ \overset{1}{C}_{2i}\\ \overset{2}{C}_{1i}\\ \overset{2}{C}_{2i} \end{array} \right] = \left[ \begin{array}{c} -\overset{1}{B}_{1i}\\ -\overset{2}{B}_{1i}\\ \overset{1}{B}_{1i}+b\overset{1}{B}_{2i}-\frac{1}{2}b^{2}\overset{2}{B} _{1i}-\frac{1}{3}b^{3}\overset{2}{B}_{2i}\\ 0\\ -\overset{1}{B}_{2i}+b\overset{2}{B}_{1i}+(\frac{2}{\chi }+b^{2})\overset{2}{B} _{2i}\\ \overset{2}{B}_{1i}+2b\overset{2}{B}_{2i}\\ 0\\ 0 \end{array} \right] \qquad \quad \quad \end{aligned}$$

(B.11)

for which

$$\begin{aligned} \overset{1}{A}_{1i}= & {} -\overset{1}{B}_{1i} \end{aligned}$$

(B.12a)

$$\begin{aligned} \overset{1}{A}_{2i}= & {} \frac{1}{6b\ell \left( b\ell \chi -b^{2}\chi +3\right) }\left( 6\overset{1}{B}_{1i}\left( 2\ell ^{2}b\chi +6\ell -b^{2}\ell \chi -b^{3}\chi \right) \right. \nonumber \\{} & {} \left. -\overset{2}{B}_{1i}b^{2}\left( 4\ell ^{2}b\chi +18\ell -6b-5b^{2} \ell \chi +b^{3}\chi \right) +6\overset{1}{B}_{2i}b\ell \left( b\chi \left( \ell -b\right) +3\right) \right) \end{aligned}$$

(B.12b)

$$\begin{aligned} \overset{2}{A}_{1i}= & {} -\overset{2}{B}_{1i} \end{aligned}$$

(B.12c)

$$\begin{aligned} \overset{2}{A}_{2i}= & {} \frac{1}{2b\ell \left( b\ell \chi -b^{2}\chi +3\right) }\left( 6\overset{1}{B}_{1i}\left( \ell -b\right) \chi +\overset{2}{B} _{1i}b\left( \ell \chi \left( 2\ell -b\right) +6-b^{2}\chi \right) \right. \nonumber \\{} & {} \left. +2\overset{2}{B}_{2i}b\left( \ell b\chi \left( \ell -b\right) +3\right) \right) \end{aligned}$$

(B.12d)

$$\begin{aligned} \overset{1}{C}_{1i}= & {} -\frac{1}{6\left( b\ell \chi -b^{2}\chi +3\right) }b\left( 2\ell -b\right) \left( 6\overset{1}{B}_{1i}\chi +\overset{2}{B}_{1i}\left( b^{2}\chi -6\right) \right) \end{aligned}$$

(B.12e)

$$\begin{aligned} \overset{1}{C}_{2i}= & {} \frac{1}{6\ell \left( b \ell \chi -b^{2}\chi +3\right) }\left( 2\ell ^{2}+2\ell b-b^{2}\right) \left( 6\overset{1}{B}_{1i} \chi +\overset{2}{B}_{1i}\left( b^{2}\chi -6\right) \right) \end{aligned}$$

(B.12f)

$$\begin{aligned} \overset{2}{C}_{1i}= & {} \frac{1}{b\ell \chi -b^{2}\chi +3}\left( 6\overset{1}{B} _{1i}\chi +\overset{2}{B}_{1i}\left( b^{2}\chi -6\right) \right) \end{aligned}$$

(B.12g)

$$\begin{aligned} \overset{2}{C}_{2i}= & {} -\frac{1}{2\ell \left( b \ell \chi -b^{2}\chi +3\right) }\left( 6\overset{1}{B}_{1i}\chi +\overset{2}{B}_{1i}\left( b^{2} \chi -6\right) \right) \end{aligned}$$

(B.12h)

are the solutions. The elements of matrices ${\textbf{A}}_{1I}$, ${\textbf{A}}_{2I}$, ${\textbf{C}}_{1I}$ and ${\textbf{C}}_{2I}$ can be given in terms of $\xi$ as well.

Matrix ${\textbf{A}}_{1I}$:

$$\begin{aligned} \overset{1}{A}_{11}= & {} -\frac{1}{2\chi }\xi +\frac{1}{12}\xi ^{3}, \quad \overset{1}{A}_{12}=\frac{1}{4}\xi ^{2}, \end{aligned}$$

(B.13a)

$$\begin{aligned} \overset{1}{A}_{21}= & {} -\frac{1}{{\mathcal {D}}_{aI}\chi }\left[ 6\ell b\left( b\chi \left( \ell -b\right) +3\right) +\xi \left( -12\ell \left( b\chi \left( \ell -2b\right) +3\right) +\chi ^{2}b^{3}\left( 4\ell -b\right) \left( \ell -b\right) \right) \right. \nonumber \\{} & {} \left. -3\ell b\xi ^{2}\chi \left( \ell b\chi -b^{2}\chi +3\right) +\chi \xi ^{3}\left( b\chi \left( 2\ell +b\right) \left( \ell -b\right) +6\ell \right) \right] ,\, \end{aligned}$$

(B.13b)

$$\begin{aligned} \overset{1}{A}_{22}= & {} \frac{1}{{\mathcal {D}}_{aI}}\left[ b^{2}\left( 4b\ell ^{2}\chi +18\ell -6b-5b^{2}\ell \chi +b^{3}\chi \right) -\right. \nonumber \\{} & {} \left. -6b\ell \xi \left( b\chi \left( \ell -b\right) +3\right) +3\xi ^{2}\left( \chi b\left( 2\ell +b\right) \left( \ell -b\right) +6\ell \right) \right] ,\, \end{aligned}$$

(B.13c)

where

$$\begin{aligned} {\mathcal {D}}_{aI}=12b\ell \left( b\chi \left( \ell -b\right) +3\right) . \end{aligned}$$

Matrix ${\textbf{A}}_{2I}$:

$$\begin{aligned} \overset{2}{A}_{11}= & {} -\frac{1}{2}\xi , \quad \overset{2}{A}_{12}=\frac{1}{2}, \end{aligned}$$

(B.14a)

$$\begin{aligned} \overset{2}{A}_{21}= & {} \frac{3}{{\mathcal {D}}_{aI}}\left( -b\left( \ell b\chi \left( \ell -b\right) +3\right) +\xi \left( 6\ell +2\ell ^{2}b\chi -\chi b^{2}\left( b+\ell \right) \right) -\chi \xi ^{3}\left( \ell -b\right) \right) , \end{aligned}$$

(B.14b)

$$\begin{aligned} \overset{2}{A}_{22}= & {} \frac{3}{{\mathcal {D}}_{aI}}\left( -b\left( \ell \chi \left( 2\ell -b\right) +6-b^{2}\chi \right) +3\chi \frac{1}{4}\xi ^{2}\left( \ell -b\right) \right) . \end{aligned}$$

(B.14c)

Matrix ${\textbf{C}}_{1I}$:

$$\begin{aligned} \overset{1}{C}_{11}= & {} -\frac{1}{{\mathcal {D}}_{cI}}\chi b\xi \left( 2\ell -b\right) \left( b^{2}-\xi ^{2}\right) ,\quad \overset{1}{C}_{12}=-\frac{1}{{\mathcal {D}}_{cI}}b\left( 2\ell -b\right) \left( 3\xi ^{2}\chi -b^{2} \chi +6\right) , \end{aligned}$$

(B.15a)

$$\begin{aligned} \overset{1}{C}_{21}= & {} \frac{\chi \xi }{\ell {\mathcal {D}}_{cI}}\left( 2\ell ^{2}+2\ell b-b^{2}\right) \left( b^{2}-\xi ^{2}\right) , \end{aligned}$$

(B.15b)

$$\begin{aligned} \overset{1}{C}_{22}= & {} \frac{1}{\ell {\mathcal {D}}_{cI}}\left( 2\ell ^{2}+2\ell b-b^{2}\right) \left( 3\xi ^{2}\chi -b^{2}\chi +6\right) ,\quad {\mathcal {D}}_{cI}=12\left( b\chi \left( \ell -b\right) +3\right) . \end{aligned}$$

(B.15c)

Matrix ${\textbf{C}}_{2I}$:

$$\begin{aligned} \overset{2}{C}_{11}= & {} \frac{6\chi \xi }{{\mathcal {D}}_{cI}}\left( b^{2}-\xi ^{2}\right) ,\qquad \overset{2}{C}_{12}=\frac{6}{{\mathcal {D}}_{cI}}\left( 3\xi ^{2}\chi -b^{2}\chi +6\right) , \end{aligned}$$

(B.16a)

$$\begin{aligned} \overset{2}{C}_{21}= & {} -\frac{3\chi \xi }{\ell {\mathcal {D}}_{cI}}\left( b^{2} -\xi ^{2}\right) ,\qquad \overset{2}{C}_{22}=-\frac{3}{\ell {\mathcal {D}}_{cI} }\left( 3\xi ^{2}\chi -b^{2}\chi +6\right) . \end{aligned}$$

(B.16b)

1.2 Calculation steps if $\xi \in [b,\ell ]$

On the basis of (4.14) and (4.15), it can be written that

$$\begin{aligned} \begin{aligned} \underset{(2\times 2)}{{\textbf{G}}_{2II}(x,\xi )}&=\sum _{\ell =1} ^{2}{\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell II}(\xi )+{\textbf{B}} _{\,\ell II}(\xi )\right] ,\qquad x\le \xi ;\\ \underset{(2\times 2)}{{\textbf{G}}_{2II}(x,\xi )}&=\sum _{\ell =1} ^{2}{\textbf{Y}}_{\,\ell }(x)\left[ {\textbf{A}}_{\,\ell II}(\xi )-{\textbf{B}} _{\,\ell II}(\xi )\right] ,\qquad x\ge \xi \end{aligned} \qquad x\in [b,\ell ] \end{aligned}$$

(B.17)

and

$$\begin{aligned} \underset{(2\times 2)}{{\textbf{G}}_{1II}(x,\xi )}=\sum _{\ell =1}^{2} {\textbf{Y}}_{\,\ell }(x){\textbf{C}}_{\,\ell II}(\xi ),\qquad x\in [b,\ell ]\, \end{aligned}$$

(B.18)

where the coefficients matrices ${\textbf{A}}_{\,\ell II}(\xi )$, ${\textbf{B}}_{\,\ell II}(\xi )$ and ${\textbf{C}}_{\,\ell II}(\xi )$ are the unknowns. Since ${\textbf{B}}_{\,\ell II}(\xi )={\textbf{B}} _{\,\ell I}(\xi )$, we turn our attention to the matrices ${\textbf{A}}_{\,\ell II}(\xi )$ and ${\textbf{C}}_{\,\ell II} (\xi )$. It is assumed that ${\textbf{A}}_{\,\ell II}(\xi )$, ${\textbf{B}}_{\,\ell II}(\xi )$ and ${\textbf{C}}_{\,\ell II}(\xi )$ are partitioned in the same manner as the matrices ${\textbf{A}}_{\,\ell I}(\xi )$, ${\textbf{B}}_{\,\ell I}(\xi )$ and ${\textbf{C}}_{\,\ell I}(\xi )$. The notation for these matrix blocks and their elements will be the same as before since this will not cause any misunderstanding.

According to Eq. (4.17a), the product ${\varvec{G}} (x,\xi )\varvec{\alpha }$ should satisfy boundary conditions at the left end of the beam. If $\varvec{\alpha }^{T}=\left[ 1|0\right] \;(i=1)$ or $\varvec{\alpha }^{T}=\left[ 0|1\right] \;(i=2)$, the boundary conditions at the left end of the beam result in the following equation system:

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=0} {\textbf{C}}_{\,\ell i}(\xi )&=0 \end{aligned}$$

(B.19a)

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=0}{\textbf{C}}_{\,\ell i}(\xi )&=0. \end{aligned}$$

(B.19b)

As per Eq. (4.17b), the product ${\varvec{G}} (x,\xi )\varvec{\alpha }$ should satisfy the continuity conditions at the intermediate roller ($x=b$). If $\varvec{\alpha }^{T}=\left[ 1|0\right] \;(i=1)$ or $\varvec{\alpha }^{T}=\left[ 0|1\right] \;(i=2)$, these continuity conditions lead to

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b} {\textbf{C}}_{\,\ell i}(\xi ) =0, \end{aligned}$$

(B.20a)

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b} {\textbf{A}}_{\,\ell i}(\xi ) =-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b}{\textbf{B}}_{\,\ell i}(\xi ), \end{aligned}$$

(B.20b)

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}(x)\right| _{x=b} {\textbf{A}}_{\,\ell i}(\xi )-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}(x)\right| _{x=b}{\textbf{C}}_{\,\ell i}(\xi ) =-\sum _{\ell =1} ^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=b}{\textbf{B}}_{\,\ell i} (\xi ), \end{aligned}$$

(B.20c)

$$\begin{aligned}&\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=b}{\textbf{A}}_{\,\ell i}(\xi )-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=b}{\textbf{C}}_{\,\ell i}(\xi ) =-\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}^{(1)}(x)\right| _{x=b}{\textbf{B}} _{\,\ell i}(\xi ). \end{aligned}$$

(B.20d)

According to Eq. (4.17a), the product ${\varvec{G}} (x,\xi )\varvec{\alpha }$ should also satisfy boundary conditions at the right end of the beam. If $\varvec{\alpha } ^{T}=\left[ 1|0\right] \;(i=1)$ or $\varvec{\alpha }^{T}=\left[ 0|1\right] \;(i=2)$, we get:

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=\ell }{\textbf{A}}_{\,\ell i}(\xi )&=\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 1}(x)\right| _{x=\ell }{\textbf{B}}_{\,\ell i}(\xi ), \end{aligned}$$

(B.21a)

$$\begin{aligned} \sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=\ell }{\textbf{A}}_{\,\ell i}(\xi )&=\sum _{\ell =1}^{2}\left. {\textbf{Y}}_{\,\ell 2}^{(1)}(x)\right| _{x=\ell }{\textbf{B}}_{\,\ell i}(\xi ). \end{aligned}$$

(B.21b)

Substituting ${\textbf{Y}}_{\,\ell 1}$, ${\textbf{Y}} _{\,\ell 2}$, ${\textbf{Y}}_{\,\ell 2}^{(1)}$, ${\textbf{A}}_{\,\ell i}$, ${\textbf{B}}_{\,\ell i}$ and ${\varvec{C}}_{\,\ell i}$ into (B.19), (B.20) and (B.10) yields

$$\begin{aligned} \left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} b &{} -\frac{1}{3}b^{3}\\ 1 &{} b &{} -\frac{1}{2}b^{2} &{} -\frac{1}{3}b^{3} &{} 0 &{} 0\\ 0 &{} -1 &{} b &{} \frac{2}{\chi }+b^{2} &{} 1 &{} -\frac{2}{\chi }-b^{2}\\ 0 &{} 0 &{} 1 &{} 2b &{} 0 &{} -2b\\ 1 &{} \ell &{} -\frac{1}{2}\ell ^{2} &{} -\frac{1}{3}\ell ^{3} &{} 0 &{} -0\\ 0 &{} 0 &{} 1 &{} 2\ell &{} 0 &{} 0 \end{array} \right] \left[ \begin{array}{c} \overset{1}{A}_{1i}\\ \overset{1}{A}_{2i}\\ \overset{2}{A}_{1i}\\ \overset{2}{A}_{2i}\\ \overset{1}{C}_{2i}\\ \overset{2}{C}_{2i} \end{array} \right] =\left[ \begin{array}{c} 0\\ -\overset{1}{B}_{1i}-b\overset{1}{B}_{2i}+\frac{1}{2}b^{2}\overset{2}{B} _{1i}+\frac{1}{3}b^{3}\overset{2}{B}_{2i}\\ \overset{1}{B}_{2i}-b\overset{2}{B}_{1i}-(\frac{2}{\chi }+b^{2})\overset{2}{B} _{2i}\\ -\overset{2}{B}_{1i}-2b\overset{2}{B}_{2i}\\ \overset{1}{B}_{1i}+\ell \overset{1}{B}_{2i}-\frac{1}{2}\ell ^{2}\overset{2}{B} _{1i}-\frac{1}{3}\ell ^{3}\overset{2}{B}_{2i}\\ \overset{2}{B}_{1i}+2\ell \overset{2}{B}_{2i} \end{array} \right] \end{aligned}$$

(B.22)

since $\overset{1}{C}_{1i}=\overset{2}{C}_{1i}=0$. The nonzero solutions are, therefore

$$\begin{aligned} \overset{1}{A}_{1i}= & {} -\frac{1}{6\left( \ell -b\right) \left( \ell b\chi -b^{2}\chi +3\right) }\left( 6\overset{1}{B}_{1i}\left( 3b-2\ell b^{2} \chi +b\chi \ell ^{2}+3\ell \right) \right. \nonumber \\{} & {} \left. +\overset{2}{B}_{1i}b\left( b^{2}+2\ell ^{2}\right) \left( b^{2} \chi -6\right) -6\overset{1}{B}_{2i}b\ell \left( b^{2}\chi -6\right) +2\overset{2}{B}_{2i}b^{3}\ell \left( b^{2}\chi -6\right) \right) , \end{aligned}$$

(B.23a)

$$\begin{aligned} \overset{1}{A}_{2i}= & {} \frac{1}{6\ell \left( \ell -b\right) \left( \ell b\chi -b^{2}\chi +3\right) }\left( -6\overset{1}{B}_{1i}\left( 4\ell b^{2}\chi -b^{3}\chi -6\ell \right) \right. \nonumber \\{} & {} +\overset{2}{B}_{1i}\left( 8\ell ^{3}b^{2}\chi -12\ell ^{3}-6b^{3}+b^{5} \chi \right) -6\overset{1}{B}_{2i}\ell \left( b\ell ^{2}\chi -3b+2\ell b^{2} \chi -3\ell \right) \nonumber \\{} & {} +\left. +2b^{3}\ell \overset{2}{B}_{2i}\left( 2\ell ^{2}\chi -6+b^{2} \chi \right) \right) , \end{aligned}$$

(B.23b)

$$\begin{aligned} \overset{2}{A}_{1i}= & {} \frac{1}{\left( \ell -b\right) \left( \ell b\chi -b^{2}\chi +3\right) }\left( -6\overset{1}{B}_{1i}b\chi +\overset{2}{B} _{1i}\left( 3b+2b^{2}\ell \chi +b\ell ^{2}\chi -3\ell \right) -6\overset{1}{B}_{2i}b\ell \chi +2\overset{2}{B}_{2i}b^{3}\ell \chi \right) , \nonumber \\ \end{aligned}$$

(B.23c)

$$\begin{aligned} \overset{2}{A}_{2i}= & {} \frac{1}{2\ell \left( \ell -b\right) \left( \ell b\chi -b^{2}\chi +3\right) }\left( 6\overset{1}{B}_{1i}b\chi -\overset{2}{B} _{1i}\left( 6b-6\ell +4\ell b^{2}\chi -b^{3}\chi \right) \right. \nonumber \\{} & {} \left. +6\overset{1}{B}_{2i}b\ell \chi +2\overset{2}{B}_{2i}\ell \left( b\ell ^{2}\chi -3b+3\ell -2b^{2}\ell \chi \right) \right) , \end{aligned}$$

(B.23d)

$$\begin{aligned} \overset{1}{C}_{2i}= & {} \frac{1}{6\ell \left( \ell b\chi -b^{2}\chi +3\right) }b^{2}\left( -6\overset{1}{B}_{1i}\chi +\overset{2}{B}_{1i}\left( 2b\ell \chi +6-b^{2}\chi +2\ell ^{2}\chi \right) \right. \nonumber \\{} & {} \left. -6\ell \overset{1}{B}_{2i}\chi +2\ell \overset{2}{B}_{2i}\left( 2b\ell \chi +6-b^{2}\chi \right) \right) , \end{aligned}$$

(B.23e)

$$\begin{aligned} \overset{2}{C}_{2i}= & {} \frac{1}{2\ell \left( \ell b\chi -b^{2}\chi +3\right) }\left( -6\overset{1}{B}_{1i}\chi +\overset{2}{B}_{1i}\left( 2b\ell \chi +6-b^{2}\chi +2\ell ^{2}\right) \right. \nonumber \\{} & {} \left. -6\overset{1}{B}_{2i}\ell \chi +2\overset{2}{B}_{2i}\ell \left( 2b\ell \chi +6-b^{2}\chi \right) \right) . \end{aligned}$$

(B.23f)

The elements of matrices ${\textbf{A}}_{1II}$, ${\textbf{A}}_{2II}$, ${\textbf{C}}_{1II}$ and ${\textbf{C}}_{2II}$ can be given in terms of $\xi$.

Matrix ${\textbf{A}}_{1II}$:

$$\begin{aligned} \overset{1}{A}_{11}= & {} \frac{1}{{\mathcal {D}}_{aII}}\left( b\ell \left( b^{2} \chi -6\right) ^{2}+6\xi \left( -3b+2b^{2}\ell \chi +b\ell ^{2}\chi -3\ell \right) -\xi b^{5}\chi ^{2}\right. \nonumber \\{} & {} \left. -2\xi \chi b^{3}\left( \ell ^{2}\chi -3\right) +3\xi ^{2}b\ell \left( b^{2}\chi -6\right) \chi +\xi ^{3}\left( 3b-2\ell b^{2}\chi +b\chi \ell ^{2} +3\ell \right) \chi \right) , \end{aligned}$$

(B.24a)

$$\begin{aligned} \overset{1}{A}_{12}= & {} -\frac{\chi }{{\mathcal {D}}_{aII}}\left( 3\xi ^{2}\left( 3b-2b^{2}\ell \chi +b\ell ^{2}\chi +3\ell \right) -b\left( b^{2}+2\ell ^{2}\right) \left( b^{2}\chi -6\right) +3\xi b\ell \left( b^{2} \chi -6\right) \right) , \nonumber \\ \end{aligned}$$

(B.24b)

$$\begin{aligned} \overset{1}{A}_{21}= & {} -\frac{1}{{\mathcal {D}}_{aII}\ell }\left[ b^{3}\ell \left( 2\ell ^{2}\chi -6+b^{2}\chi \right) \chi -6\ell \left( 2b^{2}\ell \chi +b\ell ^{2}\chi -3b-3\ell \right) \right. \nonumber \\{} & {} -\xi \left( 4\ell \left( 2b^{2}\chi -3\right) \left( \chi \ell ^{2}-3\right) +b^{5}\chi ^{2}\right) +3\xi ^{2}\chi \ell \left( 2b^{2}\ell \chi +b\ell ^{2} \chi -3b-3\ell \right) \nonumber \\{} & {} \left. -\xi ^{3}\left( 4b^{2}\ell \chi -b^{3}\chi -6\ell \right) \chi \right] , \end{aligned}$$

(B.24c)

$$\begin{aligned} \overset{1}{A}_{22}= & {} \frac{\chi }{{\mathcal {D}}_{aII}\ell }\left[ -\left( 8b^{2}\ell ^{3}\chi -12\ell ^{3}-6b^{3}+b^{5}\chi \right) \right. \nonumber \\{} & {} +6\xi \ell \left( b\ell ^{2}\chi -3b+2\ell b^{2}\chi -3\ell \right) \left. -3\xi ^{2}\left( 4b^{2}\ell \chi -b^{3}\chi -6\ell \right) \right] ,\end{aligned}$$

(B.24d)

$$\begin{aligned} {\mathcal {D}}_{aII}= & {} 12\chi \left( \ell -b\right) \left( \ell b\chi -b^{2} \chi +3\right) . \end{aligned}$$

(B.24e)

Matrix ${\textbf{A}}_{1II}$:

$$\begin{aligned} \overset{2}{A}_{11}= & {} \frac{6\chi }{{\mathcal {D}}_{aII}}\left( -b\ell \left( b^{2}\chi -6\right) +\xi \left( 2b^{2}\ell \chi +b\ell ^{2}\chi -3b-3\ell \right) -3\xi ^{2}b\ell \chi +\xi ^{3}b\chi \right) ,\end{aligned}$$

(B.25a)

$$\begin{aligned} \overset{2}{A}_{12}= & {} \frac{6\chi }{{\mathcal {D}}_{aII}}\left( \left( -2b^{2} \ell \chi -b\ell ^{2}\chi +3\ell -3b\right) +6\xi b\ell \chi -3b\xi ^{2}\chi \right) , \end{aligned}$$

(B.25b)

$$\begin{aligned} \overset{2}{A}_{21}= & {} \frac{3\chi }{{\mathcal {D}}_{aII}\ell }\left( \ell \left( 2b^{2}\ell \chi -b\ell ^{2}\chi -3b-3\ell \right) -\xi \left( 4b^{2}\ell \chi -6\ell -b^{3}\chi \right) +3\xi ^{2}b\ell \chi -\xi ^{3}\chi b\right) ,\qquad \end{aligned}$$

(B.25c)

$$\begin{aligned} \overset{2}{A}_{22}= & {} \frac{3\chi }{{\mathcal {D}}_{aII}\ell }\left( 6b-6\ell +4b^{2}\ell \chi -b^{3}\chi -3\xi b\ell \chi +3\xi ^{2}b\chi \right) . \end{aligned}$$

(B.25d)

Matrix ${\textbf{C}}_{1II}$:

$$\begin{aligned} \overset{1}{C}_{11}= & {} \overset{1}{C}_{12}=0, \end{aligned}$$

(B.26a)

$$\begin{aligned} \overset{1}{C}_{21}= & {} \frac{1}{{\mathcal {D}}_{cI}\ell }b^{2}\left[ \ell b\chi \left( b-2\ell \right) +\xi \chi \left( 2b\ell -b^{2}+2\ell ^{2}\right) -3\xi ^{2}\ell \chi +\xi ^{3}\chi \right] , \end{aligned}$$

(B.26b)

$$\begin{aligned} \overset{1}{C}_{22}= & {} \frac{1}{{\mathcal {D}}_{cI}\ell }b^{2}\left[ -\left( \chi \left( 2b\ell -b^{2}+2\ell ^{2}\right) +6\right) -3\xi ^{2}\chi +3\xi \ell \chi \right] . \end{aligned}$$

(B.26c)

Matrix ${\textbf{C}}_{2II}$:

$$\begin{aligned} \overset{2}{C}_{11}= & {} \overset{2}{C}_{12}=0, \end{aligned}$$

(B.27a)

$$\begin{aligned} \overset{2}{C}_{21}= & {} \frac{3}{{\mathcal {D}}_{cI}\ell }\left( 2b\ell ^{2}\chi +\ell b^{2}\chi -\xi \left( b^{2}\chi -2b\ell \chi -2\ell ^{2}\right) -3\ell \xi ^{2} \chi +\xi ^{3}\chi \right) , \end{aligned}$$

(B.27b)

$$\begin{aligned} \overset{2}{C}_{22}= & {} \frac{3}{{\mathcal {D}}_{cI}\ell }\left( b^{2}\chi -2b\ell \chi -2\ell ^{2}-6+6\xi \ell \chi -3\xi ^{2}\chi \right) . \end{aligned}$$

(B.27c)

Remark 11

Assume that $b=0$ and $\ell =1$. Then,

$$\begin{aligned} {\textbf{G}}_{2II}(x,\xi )= & {} \left[ \begin{array}{cc} 1 &{} x\\ 0 &{} -1 \end{array} \right] \left\{ \left[ \begin{array}{cc} -\frac{1}{2\chi }\xi +\frac{1}{12}\xi ^{3} &{} -\frac{1}{4}\xi ^{2}\\ -\frac{1}{2\chi } + \frac{\xi }{\chi } - \frac{\xi }{3} + \frac{1}{4} \xi ^{2} - \frac{1}{6}\xi ^{3} &{} \frac{1}{2}\xi ^{2} - \frac{1}{2} \xi + \frac{1}{3} \end{array} \right] \pm \left[ \begin{array}{cc} \frac{1}{2\chi }\xi -\frac{1}{12}\xi ^{3} &{} \frac{1}{4}\xi ^{2}\\ \frac{1}{4}\xi ^{2}-\frac{1}{2\chi } &{} -\frac{1}{2}\xi \end{array} \right] \right\} \nonumber \\{} & {} +\left[ \begin{array}{cc} -\frac{1}{2}x^{2} &{} -\frac{1}{3}x^{3}\\ x &{} \frac{2}{\chi }+x^{2} \end{array} \right] \left\{ \left[ \begin{array}{cc} -\frac{1}{2}\xi &{} \frac{1}{2}\\ \frac{1}{2}\xi -\frac{1}{4} &{} -\frac{1}{2} \end{array} \right] \pm \left[ \begin{array}{cc} \frac{1}{2}\xi &{} -\frac{1}{2}\\ -\frac{1}{4} &{} 0 \end{array} \right] \right\} \end{aligned}$$

(B.28)

which is the Green function matrix for pinned–pinned beams—see equation (9.101) in [30].