1 Introduction

To model torsional oscillations of a complex discrete biodynamical system, several aspects have to be considered: materials with hereditary properties [1,2,3,4,5], the application of fractional calculus in modelling such material properties [2, 6,7,8,9,10], a cantilever with constant [11] and variable [12,13,14,15] cross sections, and oscillations of cantilevers with different degrees of complexity [16, 17]. The example of rods with variable cross sections in nature are trees and their branches. In this paper, a tree stem with branches or herbaceous plant with corymb-like type of inflorescence are considered to be examples of complex discrete biodynamical systems.

Nonlinear phenomena such as energy dissipation [7, 18, 19], energy transfer and jump phenomena [16] are common for systems with nonlinear dynamics. Dynamics of hybrid fractional-type discrete continuum systems [20] and similar systems with multi-deformable bodies [21,22,23] are also of interest for modelling torsional oscillations of cantilevers with complex discrete structures.

There are theoretical [24, 25] and experimental [26] approaches to study oscillations of a tree. The mechanical properties of stems and trees are reviewed in [27, 28]. Wind effects on trees were studied in [29, 30]. Under an external force, a tree responds as a system of coupled damped oscillators [31]. Foliage plays a major role in the damping of tree motion [31, 32], but also the crown components are coupled [31] and the movements of branches relative to the trunk [33].

A simple model of a tree stem in the form of a cantilever with an apical load was given in [27, 34, 35]. To investigate the effect of structural nonlinearities for wind-induced oscillations of trees, a nonlinear model based on nonlinear partial differential equations which is discretized by using the Galerkin’s method applying the eigen-modes of a cantilevered beam is derived in [24]. This physics-based link model utilizes nonlinear, coupled differential equations to describe the motion of a trunk and its branches [25].

Results of studies of torsional oscillations of mechanical systems in engineering like those studying cantilever beams [16, 36], double torsion pendulums [37] and nonlinear dynamics of rotating flexible slender beams [17] can be of great help in modelling tree stems with branches as a complex cantilever with multiple degrees of freedom. In the classical theory of torsional oscillations of homogeneous rods and beams [38, 39], torsional oscillations of ideal elastic rods or beams with numerous segments are modelled as a discrete system with a finite number of degrees of freedom.

In the following sections, a mechanical model of a discrete biodynamical system will be presented and its dynamical behaviour regarding torsional oscillations described.

The manuscript is based on the basic principles and theorems of general mechanics. Its contributions are the use of fractional-order differential operators, the generalization of constitutive relations of visco-elastic materials, the generalization of fractional-type energy dissipation functions and the introduction of fractional-order differential equations and their approximate solutions.

2 The model and the methods

Our manuscript is dedicated to the analysis of the dynamic response to the dynamic torsional stress of a new model of a biodynamical discrete system of the fractional type exposed to a harmonic moment. We presented such a system as a dynamic model of a tree or a plant tree with a discrete leaf canopy structure. For this purpose, the previously known tree model is in the form of a simple cantilever, which derives the transverse oscillations, which we generalized, into a hybrid complex discrete model of torsional oscillations using the Kelvin–Voigt's visco-elastic model, which includes a time differential fractional-order operator.

2.1 Complex discrete biodynamical system description of the model

Torsional oscillations of a complex discrete biodynamical system will be described. The system is in the form of a cantilever, and it carries a discrete structure of material points and is made of a material with visco-elastic properties.

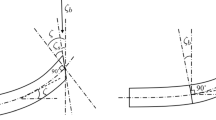
This biodynamical system consists of a visco-elastic, fractional-type cantilever (it represents a tree trunk or a plant stem) with length \(\ell\) and massless rigid rods of length \(\ell_{k}\), \(k = 1,2,3,4\) which carry mass particles at their free ends (these represent tree branches or parts of a corymb type of inflorescence) \(m_{k}\), \(k = 1,2,3,4\). Rigid massless rods have a symmetric arrangement and are rigidly connected to a visco-elastic cantilever at a suitable angle, \(\beta_{k}\), \(k = 1,2,3,4\) in sections 1, 2, 3 and 4 of the console at distances: \(\frac{\ell }{4}\), \(\frac{\ell }{2}\), \(\frac{3\ell }{4}\) and at the end of the cantilever (see Fig. 1a). In cross section 1, at distance \(\frac{\ell }{4}\) (see Fig. 1) a single-frequency momentum \(\textsf{M}{}_{z,1} = \textsf{M}{}_{z,01}\sin \left( {\Omega_{1} t + \phi_{1} } \right)\), with amplitude \(\textsf{M}{}_{z,01}\), frequency \(\Omega_{1}\) and phase \(\phi_{1}\) is applied. In cross section 1 \(m_{1} = 0\). Torsional oscillations are allowed at rigid connections of rigid massless rods with masses on their ends and visco-elastic cantilever. Figure 1. Approximations of the model: cantilever has circular cross section with diameter \(d\) which is equal along each segment along the cantilever span and is made of a creep rheological material with fractional-type properties; constitutive relation between shear stress and torsion angle is described by fractional derivatives; and the complex biodynamical system is homogeneous and has 3 (Fig. 1a) or 4 (Fig. 1b) degrees of freedom depending of the complexity of the system. The model presented in Fig. 1 resembles a corymb type of inflorescence [40].

Fig. 1
figure 1

Two models of complex discrete biodynamical system on rigid light rods with mass particles rigidly fixed on basic visco-elastic cantilever for torsional oscillations: a. with three degrees of freedom, b. with four degrees of freedom. \(\vartheta_{2u}\) and \(\vartheta_{3u}\) are upper and \(\vartheta_{2d}\) and \(\vartheta_{3d}\) are down independent generalized coordinates at cross sections 2 and 3, respectively. In cross sections  1, \(m_{1} = 0\)

Full size image

The torsional oscillations of a complex discrete biodynamical system is investigated using modifications of a previously proposed oscillatory model of a young seedling [8]. The modifications are: (1) that visco-elastic properties of the cantilever are modelled using fractional calculus and (2) that system may have multiple degrees of freedom. The novelty is also in the method for approximate analytical solutions.

2.2 Constitutive relations of the fractional-type material of the cantilever under the torsional loading and deformation

We assume that the cantilever is made of creep rheological material, properties of which are described by using the Kelvin–Voigt visco-elastic model involving the fractional-order time derivative.

Segment rigidity of a torsion cantilever is equivalent to the rigidity of a torsion spring \(c_{t}\) with fractional-order properties. \(c_{t}\) is determined by the constitutive relation between the torsion moment \({\textsf{M}}{}_{1}\) and the torsion angle.

The cantilever is of a material with dissipative fractional-type properties. The constitutive relation of each segment (there are four segments) of the cantilever material is in the form:

$${\textsf{M}}{}_{{z,k}} = - \left( {c_{{t,k}} \vartheta + c_{{t\alpha ,k}} {\textsf{D}}_{t}^{\alpha } \left[ \vartheta \right]} \right),\quad k = 1,2,3,4$$
(1)

where \(c_{t\alpha }\) is the stiffness of the fractional type of the dissipative properties of the torsion deformation of cantilever segment as a torsion spring and \({\textsf{D}}_{t}^{\alpha } \left[ \cdot \right]\) is a differential operator of the fractional order. This operator is a fractional-order differential operator of the αth derivative with respect to time in the following form (see Refs. [6, 11, 18,19,20,21]):

$${\textsf{D}}_{t}^{\alpha } \left[ {\vartheta \left( t \right)} \right] = \frac{{d^{\alpha } \vartheta \left( t \right)}}{{dt^{\alpha } }} = \vartheta ^{{\left( \alpha \right)}} \left( t \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{d}{{dt}}\int\limits_{0}^{t} {\frac{{\vartheta \left( \tau \right)}}{{\left( {t - \tau } \right)^{\alpha } }}} d\tau ,\quad \alpha \in \left( {0.1} \right),t \in \left( {0.b} \right)$$
(2)

where α is a rational number between 0 and 1, determined experimentally, and \(\Gamma \left( {1 - \alpha } \right)\) is the Gamma function. It is valid for every segment of the cantilever length \(\ell {}_{a,k} = \frac{\ell }{4}\), and we can write that: \(c_{t,k} = \frac{{{\mathbf{G}}{}_{k}{\mathbf{I}}_{0,k} }}{{\ell {}_{a,k}}} = \frac{{4{\mathbf{G}}{}_{k}{\mathbf{I}}_{0,k} }}{\ell }\) (see Refs. [38, 39]), where \(\textsf{T} = {\mathbf{GI}}_{0}\) is the torsional rigidity of the cantilever, \({\mathbf{G}}\) is the shear modulus of the cantilever’s material, \({\mathbf{I}}_{0}\) is the polar moment of inertia of the cross-sectional area of the cantilever by a pole at the centre of the cross section, while \(c_{t\alpha ,k}\) is the coefficient that defines the fractional-type properties of each segment of cantilever material in the case of torsion deformations.

A visco-elastic fractional-type cantilever that consists of material described by constitutive relations (1) and (2) is a basic element of the biodynamical system with complex discrete structure presented in Fig. 1a as well as in Fig. 1b. In general, depending on the complexity of the system, it is possible to create a generalized model with a finite number of degrees of freedom which is \(n \in N\).

2.3 The system of differential equations of fractional order for modelling torsional oscillations of a complex discrete fractional-type system

In order to construct a system of differential equations of fractional order of torsional oscillations for the system presented in Fig. 1b, we introduce four independent generalized angular coordinates, \(\vartheta_{k}\), \(k = 1,2,3,4\), corresponding to rotation angles \(a_{k}\) of cross sections 1, 2, 3 and 4, at a distance: \(\ell {}_{a,k} = \frac{\ell }{4},\,\;a_{1} = \frac{\ell }{4},\,\,\;a_{2} = a_{1} + \frac{\ell }{4},\,\,\;a_{3} = a_{2} + \frac{\ell }{4},\,\,\;a_{4} = a_{3} + \frac{\ell }{4} = \ell\) from the basic cantilever during its torsional oscillations.

For each of the pairs of masses, \(m_{k}\), on the pair of massless rods, with the length, \(\ell_{k}\), at an angle \(\beta_{k}\), the axial moments \({\mathbf{J}}_{z,k}\), of inertia of masses, for the axis of the cantilever (Fig. 1b) is:

$${\mathbf{J}}_{z,k} = 2m_{k} \left( {\ell_{k} \sin \beta_{k} } \right)^{2} ,\quad k = 1,2,3,4$$
(3)

We can now construct expressions for kinetic energy \({\mathbf{E}}_{k}\), deformation work \({\mathbf{A}}_{def}\) and the generalized function \(\Phi_{w}\) of fractional-type dissipation of total mechanical energy of the system. The kinetic energy \({\mathbf{E}}_{k}\) of the torsion oscillatory discrete structure in each of the console cross sections 1, 2, 3 and 4, which rotate around axis of the console in torsion motion, is:

$${\mathbf{E}}_{k} = \frac{1}{2}\sum\limits_{k = 1}^{k - 4} {{\mathbf{J}}_{z,k} \dot{\vartheta }_{k}^{2} } = \sum\limits_{k = 1}^{k - 4} {m_{k} \left( {\ell_{k} \sin \beta_{k} } \right)^{2} \dot{\vartheta }_{k}^{2} }$$
(4)

From expression (4), it is visible that \(m{}_{04}\) does not contribute to the kinetic energy of the torsion of the system. The reasons are the following:

  1. 1.

    material points of mass \(m_{04}\) placed on the free end of the cantilever, because its axial moment of inertia of mass \(m_{04}\) for the axis of the console, around which torsional oscillations occur, is equal to zero;

  2. 2.

    the mass of the basic console that undergoes torsional twisting during torsional oscillations. This is because its axial mass inertia moment for its own torsional axis is much smaller than axial moments of mass inertia of material particles at the tips of light rigid rods.

We assumed that the axial moment of inertia of the base of the cantilever for its own torsion axis is much smaller than axial moments of inertia of the discrete mass complex system due to the square of their divergence from the console axis, around which the whole system performs torsional oscillations. The axial moments of inertia of the cross-sectional areas of the console are adjusted when determining the torsional stiffness of the cantilever segments. This is because the torsional deformation of the cantilever and the corresponding potential energy are more significant than the kinetic torsional energy of the cantilever.

The deformation work \({\mathbf{A}}_{def}\) of the biodynamical complex system is the torsion deformation of the segments of the cantilever from section \(k\) to section \(k + 1\), and the expression can be written in the form:

$${\mathbf{A}}_{def} = {\mathbf{E}}_{p} = \frac{1}{2}c_{t,1} \vartheta_{1}^{2} + \frac{1}{2}c_{t,2} \left( {\vartheta_{2} - \vartheta_{1} } \right)^{2} + \frac{1}{2}c_{t,3} \left( {\vartheta_{3} - \vartheta_{2} } \right)^{2} + \frac{1}{2}c_{t,4} \left( {\vartheta_{4} - \vartheta_{3} } \right)^{2}$$
(5)

The generalized function \(\Phi_{w}\) of the fractional-type dissipation of the energy of the system is equal to the sum of fractional-type dissipations of energy in each of the four segments of the cantilever during torsion oscillatory deformations and can be written in the following form (see Reference [18] by Hedrih (Stevanović)):

$$\Phi _{w} = \frac{1}{2}c_{{t,\alpha ,1}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{1} } \right]} \right)^{2} + \frac{1}{2}c_{{t,\alpha ,2}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{2} - \vartheta _{1} } \right]} \right)^{2} + \frac{1}{2}c_{{t,\alpha ,3}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{3} - \vartheta _{2} } \right]} \right)^{2} + \frac{1}{4}c_{{t,\alpha ,4}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{4} - \vartheta _{3} } \right]} \right)^{2}$$
(6)

We now use generalized extended Lagrange differential equations of the second order to form a system of four differential equations of fractional order by generalized coordinates, \(\vartheta_{k}\),in the form (see References [15, 18,19,20,21, 41] by Hedrih (Stevanović) and Hedrih A. or Tenreiro Machado):

$$\frac{d}{{dt}}\frac{{\partial {\mathbf{E}}_{k} }}{{\partial \dot{\vartheta }_{k} }} - \frac{{\partial {\mathbf{E}}_{k} }}{{\partial \vartheta _{k} }} + \frac{{\partial {\mathbf{E}}_{p} }}{{\partial \vartheta _{k} }} + \frac{{\partial \Phi _{w} }}{{\partial {\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{k} } \right]}} = Q_{k}$$
(7)

Applying the previous generalized extended Lagrange differential Eqs. (7) of the second order, kinetic and potential energies (4) and the generalized function \(\Phi_{w}\) of the fractional-type dissipation of the system energy (6), we obtain the following system of fractional-order differential equations describing the torsional oscillations of the observed discrete complex structure of the biodynamical system, which is presented in Fig. 1b, in the following form:

\({\mathbf{J}}_{{z,1}} \ddot{\vartheta }_{1} + c_{{t,1}} \vartheta _{1} - c_{{t,2}} \left( {\vartheta _{2} - \vartheta _{1} } \right) + c_{{t,\alpha ,1}} {\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{1} } \right] - c_{{t,\alpha ,2}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{2} - \vartheta _{1} } \right]} \right) = {\textsf{M}}{}_{1} = {\textsf{M}}{}_{{01}}\sin \left( {\Omega _{1} t + \phi _{1} } \right)\),

(\({\mathbf{J}}_{z,1} = 0\) for model in Fig. 1a*)

$$\begin{gathered} {\mathbf{J}}_{{z,2}} \ddot{\vartheta }_{2} + c_{{t,2}} \left( {\vartheta _{2} - \vartheta _{1} } \right) - c_{{t,3}} \left( {\vartheta _{3} - \vartheta _{2} } \right) + c_{{t,\alpha ,2}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{2} - \vartheta _{1} } \right]} \right) - c_{{t,\alpha ,3}} \left( {{\text{D}}_{t}^{\alpha } \left[ {\vartheta _{3} - \vartheta _{2} } \right]} \right) = 0 \hfill \\ {\mathbf{J}}_{{z,3}} \ddot{\vartheta }_{3} + c_{{t,3}} \left( {\vartheta _{3} - \vartheta _{2} } \right) - c_{{t,4}} \left( {\vartheta _{4} - \vartheta _{3} } \right) + c_{{t,\alpha ,3}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{3} - \vartheta _{2} } \right]} \right) - c_{{t,\alpha ,4}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{4} - \vartheta _{3} } \right]} \right) = 0 \hfill \\ {\mathbf{J}}_{{z,4}} \ddot{\vartheta }_{4} + c_{{t,4}} \left( {\vartheta _{4} - \vartheta _{3} } \right) + c_{{t,\alpha ,4}} \left( {{\textsf{D}}_{t}^{\alpha } \left[ {\vartheta _{4} - \vartheta _{3} } \right]} \right) = 0 \hfill \\ \end{gathered}$$
(8)

System (8) of differential equations of the fractional order do not include the mass \(m{}_{04}\), which is attached at the end of the cantilever, because the axial moment of inertia of the mass \(m{}_{04}\) for the axis of the console is equal to zero.

This system of four fractional-order differential equations can also be written in the matrix form. We form three matrices 4 times 4: 1* the matrix \({\mathbf{A}}\) of inertial coefficients, which is diagonal, because there are no inertial constraints in the system. Only elastic constraints and dissipation properties exist in the system. Two matrices which are not diagonal are: 2* matrix \({\mathbf{C}}\) of coefficients of elasticity and 3* matrix \({\mathbf{C}}_{\alpha }\) of coefficients of the system of fractional properties. Matrices are in the following form (see Refs. [38] and [43]):

$${\mathbf{A}} = \left( {\begin{array}{*{20}c} {{\kern 1pt} \quad {\mathbf{J}}_{{z,1}} } & {} & {} & {} \\ {} & {\quad {\mathbf{J}}_{{z,2}} } & {} & {} \\ {} & {} & {\quad {\mathbf{J}}_{{z,3}} } & {} \\ {} & {} & {} & {\quad {\mathbf{J}}_{{z,4}} } \\ \end{array} } \right)$$
(9)
$${\mathbf{C}} = \left( {\begin{array}{*{20}c} {\quad c_{{t,1}} + c_{{t,2}} } & {\quad - c_{{t,2}} } & {} & {} \\ {\quad - c_{{t,2}} } & {\quad c_{{t,2}} + c_{{t,3}} } & {\quad - c_{{t,3}} } & {} \\ {} & {\quad - c_{{t,3}} } & {\quad c_{{t,3}} + c_{{t,4}} } & {\quad - c_{{t,4}} } \\ {} & {} & {\quad - c_{{t,4}} } & {\quad c_{{t,4}} } \\ \end{array} } \right)$$
(10)
$${\mathbf{C}}_{\alpha } = \left( {\begin{array}{*{20}c} {\quad c_{{t,\alpha ,1}} + c_{{t,\alpha ,2}} } & {\quad - c_{{t,\alpha ,2}} } & {} & {} \\ {\quad - c_{{t,\alpha ,2}} } & {\quad c_{{t,\alpha ,2}} + c_{{t,\alpha ,3}} } & {\quad - c_{{t,\alpha ,3}} } & {} \\ {} & {\quad - c_{{t,\alpha ,3}} } & {\quad c_{{t,\alpha ,3}} + c_{{t,\alpha ,4}} } & {\quad - c_{{t,\alpha ,4}} } \\ {} & {} & {\quad - c_{{t,\alpha ,4}} } & {\quad c_{{t,\alpha ,4}} } \\ \end{array} } \right)$$
(11)

We introduce a matrix column of independent generalized coordinates in the form:

$$\left\{ {\vartheta_{k} } \right\} = \left\{ {\begin{array}{*{20}c} {\vartheta_{1} } \\ {\vartheta_{2} } \\ {\vartheta_{3} } \\ {\vartheta_{4} } \\ \end{array} } \right\}$$
(12)

The system of the fractional-order differential equations can be written in the matrix form:

$$\textbf{A}\left\{ {\ddot{\vartheta }_{k} } \right\} + {\textbf{C}}\left\{ {\vartheta _{k} } \right\} + {\textbf{C}}_{\alpha } \left\{ {{\textsf{\bf D}}_{t}^{\alpha } \left[ {\vartheta _{k} } \right]} \right\} = 0$$
(13)

In the case where \(c_{t,\alpha ,k} = \kappa_{\alpha } c_{t,k}\), \({\mathbf{C}}_{\alpha } = \kappa_{\alpha } {\mathbf{C}}\), the system belongs to a special class of systems in which modes of fractional type are independent, and then, the formulas of transformation of the independent generalized coordinates \(\vartheta_{k}\), to the main eigen-coordinates \(\xi {}_{s}\), \(s = 1,2,3,4\) of the system can be used in the corresponding linear system (see References [19, 20]). When \(c_{t,\alpha ,k} \ne \kappa_{\alpha } c_{t,k}\), as well as \({\mathbf{C}}_{\alpha } \ne \kappa_{\alpha } {\mathbf{C}}\), then these transformation formulas can also be used to move to the principal coordinates as in the linear system, but then fractional-type modes are coupled, the system behaves as nonlinear, and there is an interaction between fractional-type modes.

2.4 The transformation of generalized coordinates to main eigen-coordinates of the system of linear differential equations of the model of torsional oscillations

Let us now consider the case when the relation \(c_{t,\alpha ,k} = \kappa_{\alpha } c_{t,k}\) is valid, that is, \({\mathbf{C}}_{\alpha } = \kappa_{\alpha } {\mathbf{C}}\). We will use the formulas for the transformation of the linear system from generalized coordinates to principal coordinates of the system. A corresponding linear system of the system of differential fractional order Eqs. (12), (13) has the following matrix form (see Refs. [38] and [43]):

$${\mathbf{A}}\left\{ {\ddot{\vartheta }_{k} } \right\} + {\mathbf{C}}\left\{ {\vartheta_{k} } \right\} = 0$$
(14)

The assumed solution of the previous linear matrix differential Eq. (14) is in the form:

$$\left\{ {\vartheta_{k} } \right\} = \left\{ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ \end{array} } \right\}\cos \left( {\omega t + \phi } \right)$$
(15)

where \(A_{k}\), \(k = 1,2,3,4\) are amplitudes of linear oscillations. Introducing them into the matrix Eq. (14), we obtain a system of homogeneous algebraic equations of the following matrix form:

$$\left( {{\mathbf{C}} - \omega^{2} {\mathbf{A}}} \right)\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ \end{array} } \right\} = 0$$
(16)

and this homogeneous algebraic equation in the matrix form has solutions, other than trivial ones, only if the determinant of that system is zero. The frequency equation is in the form:

$$\left| {{\mathbf{C}} - \omega^{2} {\mathbf{A}}} \right| = 0$$
(17)

or in the developed form:

$$\left| {\begin{array}{*{20}c} {\quad c_{{t,1}} + c_{{t,2}} - \omega ^{2} {\mathbf{J}}_{{z,1}} } & {\quad - c_{{t,2}} } & {} & {} \\ {\quad - c_{{t,2}} } & {\quad c_{{t,2}} + c_{{t,3}} - \omega ^{2} {\mathbf{J}}_{{z,2}} } & {\quad - c_{{t,3}} } & {} \\ {} & {\quad - c_{{t,3}} } & {\quad c_{{t,3}} + c_{{t,4}} - \omega ^{2} {\mathbf{J}}_{{z,2}} } & {\quad - c_{{t,4}} } \\ {} & {} & {\quad - c_{{t,4}} } & {\quad c_{{t,4}} - \omega ^{2} {\mathbf{J}}_{{z,4}} } \\ \end{array} } \right| = 0$$
(18)

Four circular eigen-frequencies, \(\omega_{s}\), \(s = 1,2,3,4\) of free oscillations of a linear system are determined from this frequency equation. We arrange the roots of the frequency equation by increasing values.

A multi-parameter analysis can be performed for the series of numerical data and parameters: the axial moment \({\mathbf{J}}_{z,k} = 2m_{k} \left( {\ell_{k} \sin \beta_{k} } \right)^{2}\), of inertia of masses, pair masses on symmetric rigid rods and the torsional stiffness of the cantilever segments.

For the homogeneous system, when \({\mathbf{J}}_{z,k} = {\mathbf{J}}_{z}\) and \(c_{t,k} = c_{t}\), the previous frequency Eq. (18) is in the form:

$$\left| {\begin{array}{*{20}c} {2 - u} & {\quad - 1} & {} & {} \\ { - 1} & {\quad 2 - u} & {\quad - 1} & {} \\ {} & {\quad - 1} & {\quad 2 - u} & {\quad - 1} \\ {} & {} & {\quad - 1} & {\quad 1 - u} \\ \end{array} } \right| = 0$$
(19)

where \(\frac{{\omega^{2} {\mathbf{J}}_{z} }}{{c_{t} }} = u\). And roots (zeros) of the previous frequency equation are: \(u_{s} = \omega_{s}^{2} \frac{{{\mathbf{J}}_{z} }}{{c_{t} }} = 4\sin^{2} \frac{2s - 1}{{18}}\pi\), \(c_{t,k} = \frac{{4{\mathbf{G}}{}_{k}{\mathbf{I}}_{0,k} }}{\ell }\), or in order \(u_{1} = \omega_{1}^{2} \frac{{{\mathbf{J}}_{z} }}{{c_{t} }} = 4\sin^{2} \frac{\pi }{18}\), \(u_{2} = \omega_{2}^{2} \frac{{{\mathbf{J}}_{z} }}{{c_{t} }} = 4\sin^{2} \frac{3\pi }{{18}}\), \(u_{3} = \omega_{3}^{2} \frac{{{\mathbf{J}}_{z} }}{{c_{t} }} = 4\sin^{2} \frac{5\pi }{{18}}\) and \(u_{4} = \omega_{4}^{2} \frac{{{\mathbf{J}}_{z} }}{{c_{t} }} = 4\sin^{2} \frac{7\pi }{{18}}\).

There are four characteristic numbers \(u_{s} = \omega_{s}^{2} \frac{{{\mathbf{J}}_{z} }}{{c_{t} }} = 4\sin^{2} \frac{2s - 1}{{18}}\pi\) (\(s = 1,2,3,4\)) as we have a system with four degrees of freedom in Fig. 1b. Circular eigen-frequencies of linear free vibrations of homogeneous system torsional oscillations are:

$$\omega {}_{1} = 2\sqrt {\frac{{c_{t} }}{{{\mathbf{J}}_{z} }}} \sin \frac{\pi }{18},\quad \omega {}_{2} = 2\sqrt {\frac{{c_{t} }}{{{\mathbf{J}}_{z} }}} \sin \frac{3\pi }{{18}},\quad \omega {}_{3} = 2\sqrt {\frac{{c_{t} }}{{{\mathbf{J}}_{z} }}} \sin \frac{5\pi }{{18}}\;{\text{and}}\;\omega {}_{4} = 2\sqrt {\frac{{c_{t} }}{{{\mathbf{J}}_{z} }}} \sin \frac{7\pi }{{18}}$$
(20)

Now, for each eigen-value, that is, for each circular eigen-frequency in the set (20) of four \(\omega_{s}\), we can determine particular solutions of the generalized coordinates \(\vartheta_{k}^{\left( s \right)}\), for the linear system in the form:

$$\left\{ {\vartheta_{k}^{\left( s \right)} } \right\} = \left\{ {\begin{array}{*{20}c} {A_{1}^{\left( s \right)} } \\ {A_{2}^{\left( s \right)} } \\ {A_{3}^{\left( s \right)} } \\ {A_{4}^{\left( s \right)} } \\ \end{array} } \right\}\cos \left( {\omega_{s} t + \phi_{s} } \right) = \left\{ {\begin{array}{*{20}c} {{\mathbf{K}}_{41}^{\left( s \right)} } \\ {{\mathbf{K}}_{42}^{\left( s \right)} } \\ {{\mathbf{K}}_{43}^{\left( s \right)} } \\ {{\mathbf{K}}_{44}^{\left( s \right)} } \\ \end{array} } \right\}C_{s} \cos \left( {\omega_{s} t + \phi_{s} } \right) = \left\{ {\begin{array}{*{20}c} {{\mathbf{K}}_{41}^{\left( s \right)} } \\ {{\mathbf{K}}_{42}^{\left( s \right)} } \\ {{\mathbf{K}}_{43}^{\left( s \right)} } \\ {{\mathbf{K}}_{44}^{\left( s \right)} } \\ \end{array} } \right\}\xi {}_{s},\quad s = 1,2,3,4$$
(21)

where the amplitudes \(A_{k}^{\left( s \right)}\) are determined from the relationship:

$$\frac{{A_{k}^{\left( s \right)} }}{{{\mathbf{K}}_{4k}^{\left( s \right)} }} = C_{s}$$
(22)

which is written based on rules for solving a system of homogeneous algebraic equations.

It follows that the amplitudes \(A_{k}^{\left( s \right)}\)\(k = 1,2,3,4\) are in the form:

$$A_{k}^{\left( s \right)} = C_{s} {\mathbf{K}}_{4k}^{\left( s \right)}$$
(23)

In the preceding expression (21) with \(\xi {}_{s} = C_{s} \cos \left( {\omega_{s} t + \phi_{s} } \right)\), we denote the main (principal) coordinates of a linear system that are one-frequency function of time, and correspond to each of their circular eigen-frequencies \(\omega_{s}\), from the set (20), while \(C_{s}\) and \(\phi_{s}\) are the set of integration constants determined from initial conditions for the linear system. In the previous particular solution (23) of amplitudes corresponding to one of four circular eigen-frequencies, \({\mathbf{K}}_{4k}^{\left( s \right)}\) denotes corresponding cofactors of elements of the fourth order and the corresponding determinant columns (frequency equations shown by determinate) (18) in the following forms for the model in Fig. 1b for four degrees of freedom of torsional oscillations.

$${\mathbf{K}}_{{41}}^{{\left( s \right)}} = - \left| {\begin{array}{*{20}c} { - c_{{t,2}} } & {} & {} \\ {c_{{t,2}} + c_{{t,3}} - \omega _{s}^{2} {\mathbf{J}}_{{z,2}} } & {\quad - c_{{t,3}} } & {} \\ { - c_{{t,3}} } & {\quad c_{{t,3}} + c_{{t,4}} - \omega _{s}^{2} {\mathbf{J}}_{{z,2}} } & {\quad - c_{{t,4}} } \\ \end{array} } \right|$$
(24)
$${\mathbf{K}}_{{42}}^{{\left( s \right)}} = + \left| {\begin{array}{*{20}c} {c_{{t,1}} + c_{{t,2}} - \omega _{s}^{2} {\mathbf{J}}_{{z,1}} } & {} & {} \\ { - c_{{t,2}} } & {\quad - c_{{t,3}} } & {} \\ {} & {\quad c_{{t,3}} + c_{{t,4}} - \omega _{s}^{2} {\mathbf{J}}_{{z,2}} } & {\quad - c_{{t,4}} } \\ \end{array} } \right|$$
(25)
$${\mathbf{K}}_{{43}}^{{\left( s \right)}} = - \left| {\begin{array}{*{20}c} {c_{{t,1}} + c_{{t,2}} - \omega _{s}^{2} {\mathbf{J}}_{{z,1}} } & {\quad - c_{{t,2}} } & {} \\ { - c_{{t,2}} } & {\quad c_{{t,2}} + c_{{t,3}} - \omega _{s}^{2} {\mathbf{J}}_{{z,2}} } & {} \\ {} & {\quad - c_{{t,3}} } & {\quad - c_{{t,4}} } \\ \end{array} } \right|$$
(26)
$${\mathbf{K}}_{{44}}^{{\left( s \right)}} = + \left| {\begin{array}{*{20}c} {c_{{t,1}} + c_{{t,2}} - \omega _{s}^{2} {\mathbf{J}}_{{z,1}} } & {\quad - c_{{t,2}} } & {} \\ { - c_{{t,2}} } & {\quad c_{{t,2}} + c_{{t,3}} - \omega _{s}^{2} {\mathbf{J}}_{{z,2}} } & {\quad - c_{{t,3}} } \\ {} & {\quad - c_{{t,3}} } & {\quad c_{{t,3}} + c_{{t,4}} - \omega _{s}^{2} {\mathbf{J}}_{{z,2}} } \\ \end{array} } \right|$$
(27)

where \(s = 1,2,3,4\). A general solution for independent generalized coordinates, \(\vartheta_{k}\), for the system of linear differential Eqs. (14), can now be written as a sum of all four particular solutions:

$$\left\{ {\vartheta_{k} } \right\} = \sum\limits_{s = 1}^{s = 4} {\left\{ {\vartheta_{k}^{\left( s \right)} } \right\}} = \sum\limits_{s = 1}^{s = 4} {\left\{ {\begin{array}{*{20}c} {A_{1}^{\left( s \right)} } \\ {A_{2}^{\left( s \right)} } \\ {A_{3}^{\left( s \right)} } \\ {A_{4}^{\left( s \right)} } \\ \end{array} } \right\}\cos \left( {\omega_{s} t + \phi_{s} } \right)} = \sum\limits_{s = 1}^{s = 4} {\left\{ {\begin{array}{*{20}c} {{\mathbf{K}}_{41}^{\left( s \right)} } \\ {{\mathbf{K}}_{42}^{\left( s \right)} } \\ {{\mathbf{K}}_{43}^{\left( s \right)} } \\ {{\mathbf{K}}_{44}^{\left( s \right)} } \\ \end{array} } \right\}C_{s} \cos \left( {\omega_{s} t + \phi_{s} } \right)} = \sum\limits_{s = 1}^{s = 4} {\left\{ {\begin{array}{*{20}c} {{\mathbf{K}}_{41}^{\left( s \right)} } \\ {{\mathbf{K}}_{42}^{\left( s \right)} } \\ {{\mathbf{K}}_{43}^{\left( s \right)} } \\ {{\mathbf{K}}_{44}^{\left( s \right)} } \\ \end{array} } \right\}\xi {}_{s}}$$
(28)

Now, with the introduction of the modal matrix \({\mathbf{K}}\) in the following form:

$${\mathbf{K}} = \left( {{\mathbf{K}}_{{4k}}^{{\left( s \right)}} } \right)\begin{array}{*{20}c} \downarrow & {k = 1,2,3,4} \\ \to & {s = 1,2,3,4} \\ \end{array} = \left( {\begin{array}{*{20}c} {{\mathbf{K}}_{{41}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{41}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{41}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{41}}^{{\left( 4 \right)}} } \\ {{\mathbf{K}}_{{42}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{42}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{42}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{42}}^{{\left( 4 \right)}} } \\ {{\mathbf{K}}_{{43}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{43}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{43}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{43}}^{{\left( 4 \right)}} } \\ {{\mathbf{K}}_{{44}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{44}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{44}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{44}}^{{\left( 4 \right)}} } \\ \end{array} } \right)$$
(29)

The formula of transformations of independent generalized coordinates \(\vartheta_{k}\), to principal main eigne-coordinates, \(\xi {}_{s} = C_{s} \cos \left( {\omega_{s} t + \phi_{s} } \right)\), of a linear system can be written in the following form:

$$\left\{ {\vartheta_{k} } \right\} = {\mathbf{K}}\left\{ {C_{s} \cos \left( {\omega_{s} t + \phi_{s} } \right)} \right\} = \left( {{\mathbf{K}}_{4k}^{\left( s \right)} } \right)\begin{array}{*{20}c} \downarrow & {k = 1,2,3,4} \\ \to & {s = 1,2,3,4} \\ \end{array} \left\{ {C_{s} \cos \left( {\omega_{s} t + \phi_{s} } \right)} \right\}$$
(30)

or in the developed forms (see Refs. [38] and [43]):

$$\left\{ {\vartheta _{k} } \right\} = {\mathbf{K}}\left\{ {\xi _{s} } \right\} = \left( {\begin{array}{*{20}c} {{\mathbf{K}}_{{41}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{41}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{41}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{41}}^{{\left( 4 \right)}} } \\ {{\mathbf{K}}_{{42}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{42}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{42}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{42}}^{{\left( 4 \right)}} } \\ {{\mathbf{K}}_{{43}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{43}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{43}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{43}}^{{\left( 4 \right)}} } \\ {{\mathbf{K}}_{{44}}^{{\left( 1 \right)}} } & {\quad {\mathbf{K}}_{{44}}^{{\left( 2 \right)}} } & {\quad {\mathbf{K}}_{{44}}^{{\left( 3 \right)}} } & {\quad {\mathbf{K}}_{{44}}^{{\left( 4 \right)}} } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\xi _{1} } \\ {\xi _{2} } \\ {\xi _{3} } \\ {\xi _{4} } \\ \end{array} } \right\}$$
(31)

2.5 The transformation of generalized coordinates to main eigen-coordinates of the system of differential equations of fractional order of the model of torsional oscillations

2.5.1 For free torsional oscillations of a complex fractional-type biodynamical system

Let us consider the special case of a system of fractional-order differential Eqs. (12), (13) in which the relation \({\textbf{C}}_{\alpha } = \kappa_{\alpha } {\textbf{C}}\) is valid. This means that stiffness matrices of the system and the coefficient matrices of the system fractional properties of the energy dissipation, \(c_{t,\alpha ,k} = \kappa_{\alpha } c_{t,k}\), are proportional to each other. The matrix form of fractional-order differential equation is:

$${\textbf{A}}\left\{ {\ddot{\vartheta }_{k} } \right\} + {\textbf{C}}\left\{ {\vartheta _{k} } \right\} + \kappa _{\alpha } {\textbf{C}}\left\{ {\textsf{\bf D}_{t}^{\alpha } \left[ {\vartheta _{k} } \right]} \right\} = 0$$
(32)

In the previous matrix differential Eq. (32) of the fractional order, we apply the formula of transformation (31) of coordinates from independent generalized \(\vartheta_{k}\), to the principal eigen-coordinates \(\xi {}_{s}\), using the transformational relations in the form \(\left\{ {\vartheta_{k} } \right\} = {\mathbf{K}}\left\{ {\xi_{s} } \right\}\), as for the corresponding linear system. Let us divide the following:

$${\mathbf{AK}}\left\{ {\ddot{\xi }_{s} } \right\} + {\mathbf{CK}}\left\{ {\xi_{s} } \right\} + \kappa_{\alpha } {\mathbf{C}}\left\{ {{\textsf{\bf D}}_{t}^{\alpha } \left[ {{\mathbf{K}}\left\{ {\xi_{s} } \right\}} \right]} \right\} = 0$$
(33)

After multiplying on the left side by \({\mathbf{K^{\prime}}}\), the transposed modal coordinate transformation matrix is:

$${\mathbf{K^{\prime}AK}}\left\{ {\ddot{\xi }_{s} } \right\} + {\mathbf{K^{\prime}CK}}\left\{ {\xi_{s} } \right\} + \kappa_{\alpha } {\mathbf{K^{\prime}C}}\left\{ {{\textsf{\bf D}}_{t}^{\alpha } \left[ {{\mathbf{K}}\left\{ {\xi_{s} } \right\}} \right]} \right\} = 0$$
(34)

Now, by analysing the orthogonality of the linear modes and the property of the modal matrix to diagonalized, the inertia coefficient matrix and the stiffness matrix of the linear system, it follows that:

$${\mathbf{K^{\prime}AK}} = {{\tilde{\mathbf{A}}}} = \left( {\begin{array}{*{20}c} {a{}_{1}} & {} & {} & {} \\ {} & {\quad a{}_{2}} & {} & {} \\ {} & {} & {\quad a{}_{3}} & {} \\ {} & {} & {} & {\quad a_{4} } \\ \end{array} } \right)$$
(35)
$${\mathbf{K^{\prime}CK}} = {\tilde{\mathbf{C}}} = \left( {\begin{array}{*{20}c} {c{}_{1}} & {} & {} & {} \\ {} & {\quad c{}_{2}} & {} & {} \\ {} & {} & {\quad c{}_{3}} & {} \\ {} & {} & {} & {\quad c_{4} } \\ \end{array} } \right)$$
(36)

The matrix differential fractional-order equation is transformed into the following form:

$${\tilde{\mathbf{A}}}\left\{ {\ddot{\xi }_{s} } \right\} + {\tilde{\mathbf{C}}}\left\{ {\xi _{s} } \right\} + \kappa _{\alpha } {\tilde{\mathbf{C}}}\left\{ {{\textsf{\bf D}}_{t}^{\alpha } \left[ {\left\{ {\xi _{s} } \right\}} \right]} \right\} = 0$$
(37)

The transformed system of differential equations of the fractional type decomposes into a system of independent differential equations of fractional order according to the main eigen-coordinates of the observed system of fractional type, and we can write:

$$a_{s} \ddot{\xi }_{s} + c_{s} \xi _{s} + \kappa _{\alpha } c_{s} {\textsf{D}}_{t}^{\alpha } \left[ {\xi _{s} } \right] = 0$$
(38)

or in the suitable form:

$$\ddot{\xi }_{s} + \omega _{s}^{2} \xi _{s} + \kappa _{\alpha } \omega _{s}^{2} {\textsf{D}}_{t}^{\alpha } \left[ {\xi _{s} } \right] = 0$$
(39)

where \(\omega_{s}^{2} = \frac{{c_{s} }}{a}\) is the square of the circular eigen-frequencies defined by expressions (20) of the principal independent eigen-mode of the fractional type and the second set of characteristic numbers \(\omega_{\alpha ,s}^{2} = \kappa_{\alpha } \frac{{c_{s} }}{a} = \frac{{c_{\alpha ,s} }}{a}\), of the principal independent eigen-modes of the fractional type of the observed biodynamical system. The approximate solutions of the differential equations of fractional order (39) are known from the literature and can be written in the following form (see References [10, 11, 19, 20, 23, 43]):

$$\begin{aligned} \xi _{{free,s}} \left( {t,\alpha ,\omega _{{0s}} ,\omega _{{\alpha ,s}} } \right) = \xi _{s} \left( 0 \right)\sum\limits_{{k = 0}}^{\infty } {\left( { - 1} \right)^{k} \omega _{{\alpha ,s}}^{{2k}} t^{{2k}} \sum\limits_{{j = 0}}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega _{{\alpha ,s}}^{{ - 2j}} t^{{ - \alpha j}} }}{{\omega _{{0s}}^{{2j}} \Gamma \left( {2k + 1 - \alpha j} \right)}}} } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + \dot{\xi }_{s} \left( 0 \right)\sum\limits_{{k = 0}}^{\infty } {\left( { - 1} \right)^{k} \omega _{{\alpha ,s}}^{{2k}} t^{{2k + 1}} \sum\limits_{{j = 0}}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega _{{\alpha ,s}}^{{ - 2j}} t^{{ - \alpha j}} }}{{\omega _{{0s}}^{{2j}} \Gamma \left( {2k + 2 - \alpha j} \right)}}} } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \alpha \in \left( {0.1} \right),\quad t \in \left( {0.b} \right),\;s = 1,2,3,4 \hfill \\ \end{aligned}$$
(40)

where \(\xi (0)\) and \(\dot{\xi }_{s} \left( 0 \right)\) denote initial conditions for \(t = 0\), \(\alpha\) is a rational number between 0 and 1. It can be assumed that in the case when a tree is ideally elastic (e.g. a young tree with a high content of water) it will take the value of 0, and in the case when the tree has viscous properties (old tree with low water content), it will take the value 1.

Theorem 1

There are corresponding \(n \in N\) main eigen-modes of fractional torsional eigen-oscillations in the dynamics of a hybrid biodynamical system of the fractional type with a complex discrete structure that consists of a visco-elastic cantilever, which carries rigid massless rods with a tip mass on each and has \(n \in N\) degrees of freedom of torsional oscillations. The torsional oscillations of such a system are described by a system of coupled ordinary fractional-order differential equations.

In the general case of such a system, dynamics of the system are nonlinear, modes depend on each other and there are interactions between modes. In the case when the model belongs to a special class of fractional systems in which the stiffness matrix of linear properties and the matrix of fractional element properties of the system are proportional, main eigen-modes of the system are independent. The independent main eigen-modes of torsional oscillations are described by a system of \(n \in N\) independent ordinary differential equations of the fractional type. Each mode is defined by one main eigen-coordinate of torsional oscillations.

Main eigen-modes of torsional free oscillators described by a system of independent ordinary fractional-order differential equations are in the form:

$$\ddot{\xi }_{s} + \omega _{s}^{2} \xi _{s} + \kappa _{\alpha } \omega _{s}^{2} {\textsf{D}}_{t}^{\alpha } \left[ {\xi _{s} } \right] = 0,\quad s = 1,2,3,4,5,...,n \in N$$
(41)

with two sets of characteristic eigen-numbers: \(\omega_{s}^{2} = \frac{{c_{s} }}{a}\) and \(\omega_{\alpha ,s}^{2} = \kappa_{\alpha } \frac{{c_{s} }}{a} = \frac{{c_{\alpha ,s} }}{a}\), and two complement main eigen-modes of free torsional oscillations: the first fractional type, main cosine-like eigen-mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega_{s} t + \alpha_{s} } \right)}}\) and the second fractional-type main sine-like eigen-mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega_{s} t + \alpha_{s} } \right)}}\) expressed by a series along time in the following analytical approximate forms:

$$\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega_{s} t + \alpha_{s} } \right)}} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \omega_{\alpha ,s}^{2k} t^{2k} \sum\limits_{j = 0}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega_{\alpha ,s}^{ - 2j} t^{ - \alpha j} }}{{\omega_{0s}^{2j} \Gamma \left( {2k + 1 - \alpha j} \right)}}} }$$
(42)
$$\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega_{s} t + \alpha_{s} } \right)}} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \omega_{\alpha ,s}^{2k} t^{2k + 1} \sum\limits_{j = 0}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega_{\alpha ,s}^{ - 2j} t^{ - \alpha j} }}{{\omega_{0s}^{2j} \Gamma \left( {2k + 2 - \alpha j} \right)}}} }$$
(43)

or as solution in the form:

$$\begin{gathered} \xi _{{free,s}} \left( {t,\alpha ,\omega _{{0s}} ,\omega _{{\alpha ,s}} } \right) = \xi _{s} \left( 0 \right)\left[ {\xi _{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega _{s} t + \alpha _{s} } \right)}} + \dot{\xi }_{s} \left( 0 \right)\left[ {\xi _{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega _{s} t + \alpha _{s} } \right)}} \hfill \\ \qquad \qquad \qquad \quad \quad \quad \quad \quad \quad \alpha \in \left( {0.1} \right),\quad t \in \left( {0.b} \right) \hfill \\ \end{gathered}$$
(44)

where \(s = 1,2,3,4,5,...,n \in N\).

Corollary 1 to Theorem 1

The formula for transformations of independent generalized coordinates to main eigen-coordinates of the fractional-type system is equal to the formula for transformations of independent generalized coordinates to the main eigen-coordinates of the corresponding system of linear differential equations for the biodynamical system with a complex discrete structure defined and considered in Theorem 1 by a system of fractional-type differential equations for free torsional fractional-type oscillations.

In the special case for the system in Theorem 1 (when the stiffness matrix of linear properties and the matrix of fractional element properties of the system are proportional), the interaction between main fractional-type modes does not exist; transfer of energy between modes does not exist eider.

Corollary 2 to Theorem 1

In the case when the biodynamical system with a complex discrete structure, which was defined and considered in Theorem 1 by a system of fractional-order differential equations belongs to a special class of the system, it is described by main fractional-type eigen-modes. Each mode has: 1) one circular frequency from the set of circular eigen-frequencies and 2) corresponding characteristic numbers that describe fractional-type properties. Each mode is described with one main eigen-coordinate.

In Fig. 2, a graphical presentation of the complement cosine-like eigen-mode of free torsion fractional-type oscillations of the described complex discrete biodynamical system is presented. In a. \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega_{s} t + \alpha_{s} } \right)}}\) fractional type cosine-like mode and in b. its first derivative (like minus sine mode) are expressed by surfaces drawn by a series along time in the analytical approximations.

Fig. 2
figure 2

A graphical presentation of the complement eigen-mode of free torsional oscillations of the models of complex discrete biodynamical system for torsional oscillations: a. fractional-order cosine-like mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega_{s} t + \alpha_{s} } \right)}}\) and b. its first derivative expressed by surfaces drown by series along time in the analytical approximations

Full size image

In Fig. 3, a graphical presentation of the complement sine-like eigen-mode of free torsion fractional-type oscillations of the described complex discrete biodynamical system is presented. In a. \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega_{s} t + \alpha_{s} } \right)}}\) fractional-type sine-like mode and in b. its first derivative (cosine-like mode) are expressed by surfaces drawn by series along time in the analytical approximations.

Fig. 3
figure 3

A graphical presentation of the complement fractional-type eigen-mode of free torsional oscillations of the models of complex discrete biodynamical system for torsional oscillations: a. fractional-type sine-like mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega_{s} t + \alpha_{s} } \right)}}\) and b. its first derivative expressed by surfaces drown by series along time in the analytical approximations

Full size image

2.5.2 For forced torsional oscillations of complex biodynamical system

If we calculate the forced torsional oscillations of the hybrid biodynamical system, then the matrix of fractional-order differential equation is in the form:

$${\mathbf{A}}\left\{ {\ddot{\vartheta }_{k} } \right\} + {\mathbf{C}}\left\{ {\vartheta _{k} } \right\} + \kappa _{\alpha } {\mathbf{C}}\left\{ {{\textsf{\bf D}}_{t}^{\alpha } \left[ {\vartheta _{k} } \right]} \right\} = {\text{M}}{}_{{01}}\sin \left( {\Omega _{1} t + \phi _{1} } \right)\left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$
(45)

After the transformation of the previous matrix differential equation of the fractional order using formula (30) of coordinates from independent generalized \(\vartheta_{k}\), \(k = 1,2,3,4\) to principal eigen-coordinates \(\xi {}_{s}\), \(s = 1,2,3,4\) using the transformational relations in the form \(\left\{ {\vartheta_{k} } \right\} = {\mathbf{K}}\left\{ {\xi_{s} } \right\}\), as for the corresponding linear system, the matrix differential fractional order Eq. (43) turns into the following transformed form along the main eigen-coordinates \(\xi {}_{s}\), \(s = 1,2,3,4\) of the fractional-type system in a special class:

$${\tilde{\mathbf{A}}}\left\{ {\ddot{\xi }_{s} } \right\} + {\tilde{\mathbf{C}}}\left\{ {\xi _{s} } \right\} + \kappa _{\alpha } {\tilde{\mathbf{C}}}\left\{ {{\textsf{\bf D}}_{t}^{\alpha } \left[ {\left\{ {\xi _{s} } \right\}} \right]} \right\} = {\textsf{\bf M}}{}_{{01}}\sin \left( {\Omega _{1} t + \phi _{1} } \right)\left\{ {\begin{array}{*{20}c} {{\mathbf{K}}_{{41}}^{{\left( 1 \right)}} } \\ {{\mathbf{K}}_{{41}}^{{\left( 2 \right)}} } \\ {{\mathbf{K}}_{{41}}^{{\left( 3 \right)}} } \\ {{\mathbf{K}}_{{41}}^{{\left( 4 \right)}} } \\ \end{array} } \right\}$$
(46)

We obtain the following system of fractional-order independent differential equations of the principal independent forced modes of the fractional type:

$$a_{s} \ddot{\xi }_{s} + c_{s} \xi _{s} + \kappa _{\alpha } c_{s} {\textsf{D}}_{t}^{\alpha } \left[ {\xi _{s} } \right] = {\mathbf{K}}_{{41}}^{{\left( s \right)}} {\textsf{M}}{}_{{01}}\sin \left( {\Omega _{1} t + \phi _{1} } \right)$$
(47)

or

$$\ddot{\xi }_{s} + \omega _{s}^{2} \xi _{s} + \kappa _{\alpha } \omega _{s}^{2} {\text{sfD}}_{t}^{\alpha } \left[ {\xi _{s} } \right] = h_{s} \sin \left( {\Omega _{1} t + \phi _{1} } \right)$$
(48)

Herein \(h_{s} = \frac{{{\textbf{K}}_{{41}}^{{\left( s \right)}} {\textsf{M}}{}_{{01}}}}{{a_{s} }}\),\(s = 1,2,3,4\). In this case too, the main forced fractional-type modes of forced torsional oscillations of a hybrid biodynamical system with discrete structure, for the model in Fig. 1b, are independent.

An approximate solution of the ordinary fractional-order differential Eqs. (48) is in the following form (for details see References [11, 19, 23]):

$$\begin{gathered} \xi _{s} \left( {t,\alpha ,\omega _{{0s}} ,\omega _{{\alpha ,s}} ,\Omega _{0} } \right) = \xi _{s} \left( 0 \right)\sum\limits_{{k = 0}}^{\infty } {\left( { - 1} \right)^{k} \omega _{{\alpha ,s}}^{{2k}} t^{{2k}} \sum\limits_{{j = 0}}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega _{{\alpha ,s}}^{{ - 2j}} t^{{ - \alpha j}} }}{{\omega _{{0s}}^{{2j}} \left( {2k + 1 - \alpha j} \right)}}} } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + \dot{\xi }\left( 0 \right)\sum\limits_{{k = 0}}^{\infty } {\left( { - 1} \right)^{k} \omega _{{\alpha ,s}}^{{2k}} t^{{2k + 1}} \sum\limits_{{j = 0}}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega _{{\alpha ,s}}^{{ - 2j}} t^{{ - \alpha j}} }}{{\omega _{{0s}}^{{2j}} \Gamma \left( {2k + 2 - \alpha j} \right)}}} } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + \int_{0}^{t} {\left\langle {h_{s} \sin \left( {\Omega _{1} \left( {t - \tau } \right) + \phi _{1} } \right)} \right\rangle \left\langle {\sum\limits_{{k = 0}}^{\infty } {\left( { - 1} \right)^{k} \omega _{{\alpha ,s}}^{{2k}} \tau ^{{2k + 1}} \sum\limits_{{m = 0}}^{k} {\left( {\begin{array}{*{20}c} k \\ m \\ \end{array} } \right)\frac{{\omega _{{\alpha ,s}}^{{ - 2m}} \tau ^{{ - \alpha m}} }}{{\omega _{{0s}}^{{2m}} \Gamma \left( {2k + 2 - \alpha m} \right)}}} } } \right\rangle } d\tau \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \alpha \in \left( {0.1} \right),\;t \in \left( {0.b} \right) \hfill \\ \end{gathered}$$
(49)

Theorem 2

If a single-frequency torsional momentum is applied to the system described in the Theorem 1, such a system oscillates with \(n \in N\) degrees of freedom of torsional oscillations and is described by the following parameters: 1) a corresponding system of \(n \in N\) coupled ordinary fractional-order differential equations, a finite number \(n \in N\) of corresponding circular frequencies of torsional eigen-oscillations, 2) characteristic numbers of fractional-order properties and 3) an additional circular frequency \(\Omega_{1}\) of forced torsional oscillations of the fractional type.

In a general case of such a system, main forced modes depend on each other, forced dynamics of the system is nonlinear and the interaction between forced modes exists. If the model belongs to a special class of fractional-type systems in which the stiffness matrix of the linear system and the matrix of fractional properties are proportional, main forced modes are independent. Main forced modes of torsional oscillations are described by a system of \(n \in N\) independent ordinary fractional-order differential equations in the form:

$$\ddot{\xi }_{s} + \omega _{s}^{2} \xi _{s} + \kappa _{\alpha } \omega _{s}^{2} {\textsf{D}}_{t}^{\alpha } \left[ {\xi _{s} } \right] = h_{s} \sin \left( {\Omega _{1} t + \phi _{1} } \right),\quad s = 1,2,3,4,5,...,n \in N$$
(50)

And for the special class with linear properties with two sets of characteristic eigen-numbers \(\omega_{s}^{2} = \frac{{c_{s} }}{a}\) and \(\omega_{\alpha ,s}^{2} = \kappa_{\alpha } \frac{{c_{s} }}{a} = \frac{{c_{\alpha ,s} }}{a}\), \(s = 1,2,3,4,5,...,n \in N\) and with one circular frequency \(\Omega_{1}\) of external torsional momentum \(h_{s} \sin \left( {\Omega_{1} t + \phi_{1} } \right)\).

Main forced modes are described by: 1) two complement main eigen-modes of free torsional oscillations: one fractional type, main cosine-like eigen-mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega_{s} t + \alpha_{s} } \right)}}\) and one fractional type, main sine-like eigen-mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega_{s} t + \alpha_{s} } \right)}}\) and 2) one forced fractional-type mode \(\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\Omega_{0} t} \right)}}\).

All main fractional-type eigen-modes expressed by a series along time are in the following analytical approximate forms:

$$\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega_{s} t + \alpha_{s} } \right)}} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \omega_{\alpha ,s}^{2k} t^{2k} \sum\limits_{j = 0}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega_{\alpha ,s}^{ - 2j} t^{ - \alpha j} }}{{\omega_{0s}^{2j} \Gamma \left( {2k + 1 - \alpha j} \right)}}} }$$
(51)
$$\left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega_{s} t + \alpha_{s} } \right)}} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \omega_{\alpha ,s}^{2k} t^{2k + 1} \sum\limits_{j = 0}^{k} {\left( {\begin{array}{*{20}c} k \\ j \\ \end{array} } \right)\frac{{\left( { \mp 1} \right)^{j} \omega_{\alpha ,s}^{ - 2j} t^{ - \alpha j} }}{{\omega_{0s}^{2j} \Gamma \left( {2k + 2 - \alpha j} \right)}}} }$$
(52)
$$\begin{gathered} \left[ {\xi_{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\Omega_{0} t} \right)}} = \int_{0}^{t} {\left\langle {h_{s} \sin \left( {\Omega_{1} \left( {t - \tau } \right) + \phi_{1} } \right)} \right\rangle \left\langle {\sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \omega_{\alpha ,s}^{2k} \tau^{2k + 1} \sum\limits_{m = 0}^{k} {\left( {\begin{array}{*{20}c} k \\ m \\ \end{array} } \right)\frac{{\omega_{\alpha ,s}^{ - 2m} \tau^{ - \alpha m} }}{{\omega_{0s}^{2m} \Gamma \left( {2k + 2 - \alpha m} \right)}}} } } \right\rangle } d\tau \hfill \\ s = 1,2,3,4,5,...,n \in N \hfill \\ \end{gathered}$$
(53)

or as a solution in the form:

$$\begin{gathered} \xi _{{free,s}} \left( {t,\alpha ,\omega _{{0s}} ,\omega _{{\alpha ,s}} } \right) = \xi _{s} \left( 0 \right)\left[ {\xi _{s} \left( t \right)} \right]_{{Like\quad \cos \left( {\omega _{s} t + \alpha _{s} } \right)}} + \dot{\xi }_{s} \left( 0 \right)\left[ {\xi _{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\omega _{s} t + \alpha _{s} } \right)}} \hfill \\ \qquad\quad \qquad \quad \quad \quad \quad \quad \quad \quad \quad + \left[ {\xi _{s} \left( t \right)} \right]_{{Like\quad \sin \left( {\Omega _{0} t} \right)}} \hfill \\ \alpha \in \left( {0.1} \right),t \in \left( {0.b} \right),\quad s = 1,2,3,4,5,...,n \in N \hfill \\ \end{gathered}$$
(54)

Corollary 1 to the Theorem 2

For the system defined in Theorem 2 by a system of coupled fractional differential equations describing the forced torsional oscillations, the formula for the transformation of independent generalized coordinates into main eigen-coordinates is equal to the formula for transformations of generalized coordinates into main eigen-coordinates of a corresponding system of linear differential equations.

In the special case of the system in Theorem 2, the interaction between main forced fractional-type modes does not exist. For defined conditions in this special case, the energy transfer between main forced fractional-type modes does not exist either.

Corollary 2 to Theorem 2

The system of fractional-order differential equations defined by the previously presented Theorem 2, which belongs to a special class of the system, is described by \(n + 1 \in N\) forced main fractional-type modes. Each mode consists of: (1) one circular frequency from the set of circular eigen-frequencies, (2) corresponding characteristic numbers that describe fractional properties and 3) one circular frequency \(\Omega_{1}\) of external torsional moment \(h_{s} \sin \left( {\Omega_{1} t + \phi_{1} } \right)\). Each mode is defined by one main coordinate of forced torsional oscillations.

2.6 The system of differential equations and solutions of fractional-order homogeneous model of torsional oscillations of a complex discrete fractional-type system

For solving a system of fractional-order differential equations, the trigonometric method can be applied in the special case when biodynamic system is a homogeneous fractional-type system. This special case is when all masses, \(m_{k}\), are equal and all angles, \(\beta_{k}\), are equal and all massless rods of the length, \(\ell_{k}\), have equal lengths, as well as all axial moments \({\mathbf{J}}_{z,k}\), \(k = 1,2,3,4\) of inertia of masses for the axis of the basic visco-elastic cantilever. Now this needs to be proved.

Let us start with a system of fractional-order differential equations in the form (12) and (13), respectively, by introducing assumptions about the homogeneity of the fractional-order matrix differential equation (see Reference [43])

$$\begin{aligned} & \left( {\begin{array}{*{20}c} {{\mathbf{J}}_{z} } & {} & {} & {} \\ {} & {{\mathbf{J}}_{z} } & {} & {} \\ {} & {} & {{\mathbf{J}}_{z} } & {} \\ {} & {} & {} & {{\mathbf{J}}_{z} } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\ddot{\vartheta }_{1} } \\ {\ddot{\vartheta }_{2} } \\ {\ddot{\vartheta }_{3} } \\ {\ddot{\vartheta }_{4} } \\ \end{array} } \right\} + \left( {\begin{array}{*{20}c} {2c} & {\quad - c} & {} & {} \\ { - c} & {\quad 2c} & {\quad - c} & {} \\ {} & {\quad - c} & {\quad 2c} & {\quad - c} \\ {} & {} & {\quad - c} & {\quad c} \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {\vartheta _{1} } \\ {\vartheta _{2} } \\ {\vartheta _{3} } \\ {\vartheta _{4} } \\ \end{array} } \right\}\\ & \quad + \kappa _{\alpha } \left( {\begin{array}{*{20}c} {2c} & {\quad - c} & {} & {} \\ { - c} & {\quad 2c} & {\quad - c} & {} \\ {} & {\quad - c} & {\quad 2c} & {\quad - c} \\ {} & {} & {\quad - c} & {\quad c} \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {D_{t}^{\alpha } \left[ {\vartheta _{1} } \right]} \\ {D_{t}^{\alpha } \left[ {\vartheta _{2} } \right]} \\ {D_{t}^{\alpha } \left[ {\vartheta _{3} } \right]} \\ {D_{t}^{\alpha } \left[ {\vartheta _{4} } \right]} \\ \end{array} } \right\} = M{}_{{01}}\sin \left( {\Omega _{1} t + \phi _{1} } \right)\left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}} \\ {} \\ {\left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}} \\ \end{array} } \right.\end{aligned}$$
(55)

Let us assume a solution in the form (15) for free torsion vibrations, and for a linear system, we obtain a system of homogeneous algebraic equations in the form (16) which for a homogeneous linear system is:

$$\left( {\begin{array}{*{20}c} {2c - \omega ^{2} {\mathbf{J}}_{z} } & {\quad - c} & {} & {} \\ { - c} & {\quad 2c - \omega ^{2} {\mathbf{J}}_{z} } & {\quad - c} & {} \\ {} & {\quad - c} & {\quad 2c - \omega ^{2} {\mathbf{J}}_{z} } & {\quad - c} \\ {} & {} & {\quad - c} & {\quad c - \omega ^{2} {\mathbf{J}}_{z} } \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$
(56)

If we now introduce the notation change, \(u = \omega^{2} \frac{{{\mathbf{J}}_{z} }}{c}\), then the system of homogeneous algebraic equations along unknown amplitudes \(A_{k}\), \(k = 2,2,3,4\), in the matrix form becomes:

$$\left( {\begin{array}{*{20}c} {2 - u} & {\quad - 1} & {} & {} \\ { - 1} & {\quad 2 - u} & {\quad - 1} & {} \\ {} & {\quad - 1} & {\quad 2 - u} & {\quad - 1} \\ {} & {} & {\quad - 1} & {\quad 1 - u} \\ \end{array} } \right)\left\{ {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {A_{3} } \\ {A_{4} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$
(57)

In its developed scalar form, this (57) matrix algebra equation of homogeneous algebraic equations by unknown amplitudes \(A_{k}\) is in the following form:

$$\begin{gathered} \left( {2 - u} \right)A_{1} - A_{2} = 0 \hfill \\ - A_{1} + \left( {2 - u} \right)A_{2} - A_{3} = 0 \hfill \\ - A_{2} + \left( {2 - u} \right)A_{3} - A_{4} = 0 \hfill \\ - A_{3} + \left( {1 - u} \right)A_{4} = 0 \hfill \\ \end{gathered}$$
(58)

Now, we applied the trigonometric method of Danilo Rašković [38], assuming that the amplitudes \(A_{k}\) of linear free oscillations are in the following form (see Refs. [38] and [43]):

$$A_{k} = C\sin k\phi ,\quad k = 1,2,3,4$$
(59)

By introducing this assumed solution (59) into a homogeneous system of algebraic Eqs. (58), we obtain the following conditions:

$$\begin{gathered} \left( {2 - u} \right)C\sin \phi - C\sin 2\phi = 0 \hfill \\ - C\sin \phi + \left( {2 - u} \right)C\sin 2\phi - C\sin 3\phi = 0 \hfill \\ - C\sin 2\phi + \left( {2 - u} \right)C\sin 3\phi - C\sin 4\phi = 0 \hfill \\ - C\sin 3\phi + \left( {1 - u} \right)C\sin 4\phi = 0 \hfill \\ \end{gathered}$$
(60)

There are boundary conditions because it is a console chain. From the first and the last equation, it follows that \(A_{0} = 0\) and \(\left( {2 - u} \right)C\sin \phi - C\sin 2\phi = 0\), and by a transformation from the first algebraic equation, \(C\sin \phi \left( {2 - u - 2\cos \phi } \right) = 0\) is obtained and finally (see Reference [38]):

$$u = 2\left( {1 - \cos \phi } \right)$$
(61)

By replacing the fourth algebra equation after the unknown parameter \(- C\sin 3\phi + \left( {1 - 2\left( {1 - \cos \phi } \right)} \right)C\sin 4\phi = 0\), we obtained:

$$\cos \frac{9}{2}\phi \sin \frac{1}{2}\phi = 0 \Rightarrow \cos \frac{9}{2}\phi = \cos \frac{2s - 1}{2}\pi = 0 \Rightarrow \phi {}_{s} = \frac{2s - 1}{9}\pi ,\quad s = 1,2,3,4$$
(62)

The relation \(u = 2\left( {1 - \cos \phi } \right)\) satisfies both the second and third algebraic Eq. (60).

And that the conditions of the console chain are satisfied; then, the set of circular eigen-frequencies is determined from the relations: \(u = \omega^{2} \frac{{{\mathbf{J}}_{z} }}{c}\) and \(u = 2\left( {1 - \cos \phi } \right)\) follows:

$$u_{s} = \omega_{s}^{2} \frac{{{\mathbf{J}}_{z} }}{c} = u = 2\left( {1 - \cos \phi_{s} } \right) = 4\sin^{2} \frac{{\phi_{s} }}{2} = 4\sin^{2} \frac{2s - 1}{{18}}\pi$$
(63)

The square of its circular eigen-frequency is: \(\omega_{s}^{2} = 4\frac{c}{{{\mathbf{J}}_{z} }}\sin^{2} \frac{2s - 1}{{18}}\pi\), \(s = 1,2,3,4\).

The set of four circular eigen-frequencies of free torsional oscillations of a homogeneous complex discrete considered biodynamical system with four degrees of freedom, described by a matrix fractional differential Eq. (55), contain four circular eigen-frequencies, four characteristic numbers expressing fractional-type properties, which are:

$$\omega_{s} = 2\sqrt {\frac{c}{{{\mathbf{J}}_{z} }}} \sin \frac{2s - 1}{{18}}\pi ,\quad s = 1,2,3,4,\quad {\mathbf{J}}_{z,k} = {\mathbf{J}}_{z} = 2m\left( {\frac{\ell }{2}\sin \beta } \right)^{2}$$
(64)
$$\omega_{\alpha ,s}^{2} = 4\kappa_{\alpha } \frac{c}{{{\mathbf{J}}_{z} }}\sin^{2} \frac{2s - 1}{{18}}\pi ,\quad s = 1,2,3,4.\quad c_{t} = \frac{{4{\mathbf{GI}}_{0} }}{\ell },\quad {\mathbf{J}}_{z,k} = {\mathbf{J}}_{z} = 2m\left( {\frac{\ell }{2}\sin \beta } \right)^{2}$$
(65)

Using obtained sets (64) and (65) of characteristic numbers of free torsional oscillations of a homogeneous complex discrete biodynamical system with four degrees of freedom and introducing them into expressions (40) and (49), an analytical approximation of the independent main fractional-type eigen-modes for free as well as for forced torsional oscillations can be composed. Results (64) and (65) can be generalized for the homogeneous visco-elastic fractional-type cantilever with \(n \in N\) degrees of freedom. In this case, the set of circular frequencies, and characteristic numbers for fractional-type properties, is defined by the following expressions:

$$\omega_{s} = 2\sqrt {\frac{c}{{{\mathbf{J}}_{z} }}} \sin \frac{2s - 1}{{2\left( {2n + 1} \right)}}\pi ,\quad {\mathbf{J}}_{z,k} = {\mathbf{J}}_{z} = 2m\left( {\frac{\ell }{4}\sin \beta } \right)^{2}$$
(66)
$$\omega_{\alpha ,s}^{2} = 4\kappa_{\alpha } \frac{c}{{{\mathbf{J}}_{z} }}\sin^{2} \frac{2s - 1}{{2\left( {2n - 1} \right)}}\pi ,\quad c_{t} = \frac{{n{\mathbf{GI}}_{0} }}{\ell },\quad {\mathbf{J}}_{z,k} = {\mathbf{J}}_{z} = 2m\left( {\frac{\ell }{4}\sin \beta } \right)^{2}$$
(67)

where \(s = 1,2,3,4,....,n \in N\).

Using obtained sets (66) and (67) of characteristic numbers of the free torsional oscillations of a homogeneous complex discrete biodynamical, fractional-type system with \(n \in N\) degrees of freedom, an analytical approximation of the \(n \in N\) independent main fractional-type eigen-modes for free, as well as for \(n \in N\) main forced eigen-modes of torsion forced fractional-type oscillations, can be composed introducing corresponding characteristic numbers (66) and (67) into expressions (40) as well as (49).

3 Discussion and concluding remarks—a fractal concept of hybrid biodynamical fractional-type system with complex discrete structure

These results present a new contribution to the knowledge of intrinsic and forced mechanical oscillations of the fractional type by introducing generalized functions of energy dissipation of the fractional type.

We introduced constitutive relations for torsion of the console material using the Kelvin–Voigt visco-elastic model involving a fractional-order time derivative. The rigidity of the cantilever material is equivalent to the rigidity of torsion springs of the fractional type.

Free and forced main eigen-modes of fractional-type torsional oscillations of a hybrid discrete biodynamical system of complex structures in the form of a cantilever with a circular cross section were analysed through the use of a system of ordinary differential fractional-order equations. The expression of the kinetic energy, deformation work and generalized function of fractional-type energy dissipation of this biodynamical system were defined. Forced torsional oscillations and the stability of 3D beams with rectangular cross sections were studied in [42], but the approach used in our model differs from that study. Our model is a planar model and the cantilever has a constant circular cross section, but torsional oscillations are in a 3D space. The same model with the same mathematical description can be extended by introducing branches with material particles outside the plane of the model, whereby only the axial moment of inertia of discrete structures for the cantilever axis changes, and all differential equations and solutions are the same.

In [42], the differential equations of motion are converted into a nonlinear algebraic form embedding the harmonic balance method. Our search of the literature yielded three different approaches to study the dynamic behaviour of a tree structure used in previous studies: mass concentrated at a discrete point, generalized displacements for uniformly distributed mass, where a trunk is treated as a beam and the finite element method [28]. Our modelling approach is close to the first method, but has the advantage of allowing the generalization to a bio system with many degrees of freedom of oscillation. The originality and advantage of our model are that the material of a tree stem is considered as a material with fractional properties and constitutive relations with the fractional differential operator. This relation enables the observation of the tree material from ideally elastic through fractional type to pure visco-elastic materials with linear dissipation. The contributions are also the obtained approximate analytical expressions of independent fractional-type main eigen-modes and eigen-value and forced fractional-type torsional oscillations.

Analysing torsion fractional-type oscillations of biodynamical fractional-type systems with complex discrete structures in the presented model shows that such systems have properties of discrete chain systems (see Ref [38]) and have independent fractional-type eigen-modes of free oscillations. In a homogeneous system of forced oscillations (when single-frequency torsional momentum in certain cross sections is applied), independent forced fractional-type modes appear. Each fractional-type mode has two characteristics numbers.

Oscillatory modes of branched structure and modes of beams are not the same.

Oscillatory behaviour of tree trunks was mainly done for bending. A method that can measure the dynamic torsional load that trees and tree branches suffer when exposed to wind has not yet been developed [28]. The presented model contributes to the study of torsional oscillations of tree trunks.

The damping effect in trees is most effective around the natural frequency region and represents a protective mechanism against large sways [28]. In our model, the damping effect will depend on α (that can be assumed to correspond to the age of a tree). Complex models of trees utilize multiple spring–mass–damper models or FEM models [25]. In the branched multi-modal method, the branches are considered as coupled masses that oscillate on the trunk, which itself is an oscillating mass [25]. In our model, the trunk is considered as an oscillating cantilever and branches as massless rigid rods with mass on their apical ends. We used Y-shaped types of branching and as a system with four degrees of freedom. In [28], damping from branches has been identified for a two-degree-of-freedom system in a T- or Y-shaped branched structure.

Based on the presented model, we introduce the concept of a fractal-type discrete chain–string structure. This type of structure consists of fractal discrete sequences on each basic overhang rigidly connected to the basic visco-elastic fractional-type cantilever. A discrete fractal sequence represents one fractal discrete chain–string from a set of numerous fractal elements of discrete structure rigidly coupled on a basic visco-elastic cantilever. Torsional oscillations of a hybrid biodynamic complex with discrete and fractal structure may take place around the axis of this cantilever.

All previously performed mathematical descriptions can be applied to models formed according to the fractal concept as shown in Fig. 4.

Fig. 4
figure 4

Fractal concept of hybrid biodynamical fractional-type system with complex discrete structure on visco-elastic fractional-type cantilever: a. basic version of the hybrid biodynamical model with discrete structure on visco-elastic fractional-type cantilever; b. hybrid model; c. details of the hybrid model; d. single discrete fractal chain–string structure

Full size image

In Fig. 4, a fractal concept of a hybrid biodynamical fractional-type system with complex discrete structure on visco-elastic fractional-type cantilever is presented: the basic model (Fig. 4a), the hybrid model (Fig. 4b), the details of the hybrid model (Fig. 4c) and one discrete fractal chain–string structure (Fig. 4d).

Our search of the literature yielded no results that refer to fractional-type biodynamical systems that torsionally oscillate with a finite number of degrees of freedom of oscillation, which we have presented here. We also pointed out that in the general case, when the special conditions of the connection between the elastic matrix elements and the matrix of coefficients of fractional properties are not met, the main free or forced, fractional-type oscillation eigen-modes are not independent. In these cases, interaction between modes and energy transfers from one mode to another appear.

The obtained results would be valuable for the inclusion in any analytical mechanics of discrete hereditary systems described by a differential fractional-order operator and we believe that this is its value.

3.1 Advantages of the presented model

  • Can be used to generate more complex structures.

  • Applicable to the analysis of complex cantilevers with different cross-sectional diameters

  • It allows the existence of independent modes of fractional type of free and forced torsional oscillations.

  • We also presented formulas for the transformation of independent generalized coordinates into the main eigen-coordinates of a biodynamic system of fractional type, in which there are no independent modes which are nonlinear and between which there is an interaction.

This approach is suitable for analysing the torsion fractional-type oscillations of trees and herbaceous plants with different types of branching and different types of inflorescences with different levels of complexity.