1 Introduction

Ferroelectric ceramics, such as lead zirconate titanate (PZT), have a broad range of technological applicability in smart devices and smart composite materials due to their multi-functional behavior. For the prediction and evaluation of the performance and reliability of components made of ferroelectric ceramics, simulations of the material behavior employing proper models are needed in addition to experiments. The ferroelectric material behavior can be characterized at different length scales, see [6, 28]. Depending on the considered length scale, different types of modeling have been established, see Fig. 1.

Fig. 1
figure 1

Modeling of ferroelectric material across length scales

Full size image

On the nanoscale, the phase field method using Ginsburg–Landau–Devonshire potentials is able to capture intrinsic electrical dipoles of atomic unit cells and to simulate ferroelectric domain reorientation. In combination with a finite element continuum approach, electromechanical boundary value problems can be solved. However, the considered length scales and the computational effort are not suited for an engineering application. Examples can be found in [1, 21, 29, 34].

On the micro-/mesoscale of single or polycrystalline ferroelectrics, micromechanical models have been elaborated, which reflect the microscopic crystal and grain structure of the ferroelectric ceramic. The basic approach goes back to the work of Huber et al. [7]. Later, the material model has been implemented by several researchers as User-defined routine in FEM codes to solve field problems for two- and three-dimensional ferroelectric structures, see, e.g., [8, 10, 17, 24, 25]. For details we refer to previous publications of our research group [19, 23, 26]. These micromechanical material models are able to simulate the ferroelectrical domain switching and consider the elastic, piezoelectric and dielectric properties for the typical tetragonal crystal anisotropy (or other phases). This is done by considering the evolution of volume fractions of the specific (six) domain variants. All physical fields are averaged by these weightings, which represents an homogenization process over a certain sub-volume of a grain. The domain switching is controlled by an energetic criterion and reproduces the evolution of remanent strains and polarization so that the irreversible ferroelectric/ferroelastic phenomena (like hystereses) can be captured. Micromechanical models are best for investigating deformation and damage behavior inside the microstructure of the polycrystalline ferroelectrics as has been done in combination with cohesive elements for grain boundary failure in [13] or for field concentrations in actuators [12].

On the other hand, there are various approaches on the macroscale using phenomenological modeling, see, e.g., [9, 15, 20, 35], which have been evaluated in [2]. Most of these models are created on continuum thermodynamic principles in analogy to plasticity. A set of fitting functions or parameters must be introduced here to fit the model to experimental results, representing the coupled electromechanical behavior. Until now, macroscale models of this type are rarely applied to analyze failure or damage in ferroelectric materials or structures. First investigations were done in [3] for the crack tip fields.

Such a macroscopic, phenomenological model for the simulation of the material behavior of polycrystalline ferroelectric ceramics under multi-axial loading was specified by Landis [15]. An essential component of the Landis model is a switching function \(\varPhi \), which describes the establishment of the irreversible processes. From this, the relations are derived, describing the evolution of the internal variables used to characterize the material state. The switching function used by Landis forces some relations [16]. For this reason, the relationships between the switching function and energetically justified requirements demand particular theoretical investigation [30]. According to the paper [30], due to the particular material behavior, convergence problems can occur in finite element analyses. This is the case irrespective of the selected material model. For the technically most important ferroelectric ceramic PZT, the required material data for the Landis model are available and approved.

During the last decades, the concept of configurational (material) forces has been established. Physically, configurational forces are interpreted as thermodynamic driving forces acting on defects during a virtual displacement. Defects may be all types of crystal defects, inclusions, interfaces, cracks, and others. After the original idea established by Eshelby [5] in 1975, various enhancements, generalizations, and a plenty of applications of the configurational force concept have been developed. Among the vast literature the review articles [11, 32] are recommended for an overview. In the context of fracture mechanics, configurational forces are closely related to the well-known J-integral, but their range of applicability goes far beyond to inelastic materials, large strain analyses, and coupled field problems. In particular for ferroelectric materials the configurational force concept has been used in combination with phase field [21, 29, 33] and micromechanical [14, 18, 23] material models. A utilization together with phenomenological macroscale models is yet not known.

The present publication is motivated by following open problems:

  • The macromechanical Landis model for ferroelectric materials has to be implemented into the commercial Abaqus environment to enable analyses of complex 2D/3D structures under arbitrary electromechanical loading conditions.

  • The performance of the Landis model has to be studied in detail for applications with field concentrations like notches or cracks. The robustness and possible problems of the numerical implementation have to be investigated.

  • The main emphasis is put on the computation of configurational forces in the context of the macroscale ferroelectric model of Landis. Therefore, a post-processing tool is developed for an Abaqus electromechanical finite element analysis. In particular, heterogeneous ferroelectric structures are considered, which contain field concentrations like holes, inclusions of dissimilar dielectric or ferroelectric materials, and interfaces between those.

2 Macromechanical switching model

Landis [15] developed a phenomenological constitutive model, which describes the macroscopic electromechanical behavior of polycrystalline ferroelectric ceramics, including nonlinear hysteresis resulting from switching processes.

Helmholtz free energy density

The Helmholtz free energy consists of the stored (reversible) \(\psi ^s\) and remanent \(\psi ^r\) parts,

$$\begin{aligned} \psi = \psi ^s(\varvec{\mathbf {\varepsilon }}, \varvec{D}, \varvec{\mathbf {\varepsilon }}^\mathrm {r}, \varvec{P}^\mathrm {r}) + \psi ^r(\varvec{\mathbf {\varepsilon }}^\mathrm {r}, \varvec{P}^\mathrm {r}). \end{aligned}$$
(1)

Internal variables are the total strains \( \varvec{\mathbf {\varepsilon }} \), the dielectric displacement vector \(\varvec{D}\), remanent polarization \(\varvec{P}^\mathrm {r}\), and remanent strain \(\varvec{\mathbf {\varepsilon }}^\mathrm {r}\). Assuming a linear piezoelectric response, \(\psi ^s\) can be written as:

$$\begin{aligned} \psi ^s = \frac{\displaystyle 1}{\displaystyle 2}(\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r}):{\mathbb {C}}:(\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r}) - (\varvec{D}-\varvec{P}^\mathrm {r})\cdot \varvec{\mathbf {d}}( \varvec{P}^\mathrm {r}):(\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r}) + \frac{\displaystyle 1}{\displaystyle 2}(\varvec{D}-\varvec{P}^\mathrm {r}) \cdot \varvec{\mathbf {\upkappa }} \cdot (\varvec{D}-\varvec{P}^\mathrm {r}) . \end{aligned}$$
(2)

Here we consider that the elastic stiffness tensor \( {\mathbb {C}} \) and the dielectric permittivity \( \varvec{\mathbf {\upkappa }} \) do not depend on internal variables, and the piezoelectric coefficients \( \varvec{\mathbf {d}}( \varvec{P}^\mathrm {r})\) depend only on remanent polarization.

The remanent part of free energy \(\psi ^r\) represents an additional contribution associated only with the internal state of the material. It is described by kinematic hardening with an exponential increase at saturation.

The stress tensor and electric field vector are derived from the Helmholtz free energy:

$$\begin{aligned} \varvec{\mathbf {\sigma }}= & {} \frac{\displaystyle \partial \psi }{\displaystyle \partial \varvec{\mathbf {\varepsilon }} } = \frac{\displaystyle \partial \psi ^s}{\displaystyle \partial \varvec{\mathbf {\varepsilon }}} = {\mathbb {C}}:(\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r}) - (\varvec{D}-\varvec{P}^\mathrm {r}) \cdot \varvec{\mathbf {d}}( \varvec{P}^\mathrm {r}), \end{aligned}$$
(3)
$$\begin{aligned} \varvec{E}= & {} \frac{\displaystyle \partial \psi }{\displaystyle \partial \varvec{D} } = \frac{\displaystyle \partial \psi ^s}{\displaystyle \partial \varvec{D} } = \varvec{\mathbf {\upkappa }} \cdot (\varvec{D}-\varvec{P}^\mathrm {r}) - \varvec{\mathbf {d}}( \varvec{P}^\mathrm {r}): (\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r}). \end{aligned}$$
(4)

The associated thermodynamic dual forces for the internal state variables \( \varvec{P}^\mathrm {r}\) and \(\varvec{\mathbf {\varepsilon }}^\mathrm {r}\) are derived as:

$$\begin{aligned} \hat{\varvec{\mathbf {\sigma }}}= & {} -\frac{\displaystyle \partial \psi }{\displaystyle \partial \varvec{\mathbf {\varepsilon }}^\mathrm {r}} =-\frac{\displaystyle \partial \psi ^s}{\displaystyle \partial \varvec{\mathbf {\varepsilon }}^\mathrm {r}} - \underbrace{ \frac{\displaystyle \partial \psi ^r}{\displaystyle \partial \varvec{\mathbf {\varepsilon }}^\mathrm {r}} }_{ = \varvec{\mathbf {\sigma _B}}} = \varvec{\mathbf {\sigma }} -\varvec{\mathbf { \sigma }}_B, \end{aligned}$$
(5)
$$\begin{aligned} \hat{\varvec{E}}= & {} - \frac{\displaystyle \partial \psi }{\displaystyle \partial \varvec{P}^\mathrm {r}} = - \frac{\displaystyle \partial \psi ^s}{\displaystyle \partial \varvec{P}^\mathrm {r}} - \underbrace{ \frac{\displaystyle \partial \psi ^r}{\displaystyle \partial \varvec{P}^\mathrm {r}} }_{ = \varvec{E}_B} = \varvec{E} + \underbrace{\bar{\varvec{E}}}_{=(\varvec{D} -\varvec{P}^\mathrm {r}) \cdot \frac{\displaystyle \partial \varvec{\mathbf {d}}}{\displaystyle \partial \varvec{P}^\mathrm {r}}:(\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r})} - \varvec{E}_B. \end{aligned}$$
(6)

Ferroelectric switching criterion and flow rule

The switching criterion is formulated as a surface in the space of electric field \( \hat{\varvec{E}} \) and deviatoric stress tensor \(\hat{\varvec{\mathbf {S}}} = \hat{\varvec{\mathbf {\sigma }}} - \frac{1}{3} {{\mathbf {t}}}{{\mathbf {r}}}(\varvec{\mathbf {\sigma }}) \varvec{\mathbf {\delta }}\):

$$\begin{aligned} \varPhi (\hat{\varvec{E}}, \hat{\varvec{\mathbf {S}}} ) = \frac{\displaystyle \hat{\varvec{E}}^2}{\displaystyle E_0^2 } +\frac{\displaystyle 3 \hat{\varvec{\mathbf {S}}}^2}{\displaystyle 2 \sigma _0^2 } + \beta \frac{\displaystyle (\hat{\varvec{E}}\varvec{P}^\mathrm {r}):\hat{\varvec{\mathbf {S}}}}{\displaystyle E_0P_0\sigma _0 } -1. \end{aligned}$$
(7)

The first part corresponds to the non-remanent straining ferroelectric behavior, the second one to the ferroelastic switching, and the third term allows for an increase in remanent strain due to the application of the electric field and for a decrease in remanent polarization due to the application of compressive stress. \(\beta \) is a positive, dimensionless scalar.

From the associated flow rule, the increments of remanent strain and polarization are found as normal to the switching surface:

$$\begin{aligned} \dot{\varvec{\mathbf {\varepsilon }}}^\mathrm {r} = \lambda \frac{\displaystyle \partial \varPhi }{\displaystyle \partial {\hat{\sigma }} } =\lambda \tilde{\varvec{\mathbf {\varepsilon }}}, \qquad \dot{\varvec{P}}_r = \lambda \frac{\displaystyle \partial \varPhi }{\displaystyle \partial \hat{\varvec{E}} } = \lambda \tilde{\varvec{P}}. \end{aligned}$$
(8)

Fully coupled ferroelectric relations

According to the original work by Landis [15], the irreversible part of the Helmholtz free energy density is divided into mechanical, electrical, and coupled parts. Thus, the switching potential has the following form:

$$\begin{aligned} \psi ^r (\varvec{\mathbf {\varepsilon }}^\mathrm {r}, \varvec{P}^\mathrm {r}) = \psi ^m (\varvec{\mathbf {\varepsilon }}^\mathrm {r}) + \psi ^e (\varvec{P}^\mathrm {r}) + \psi ^\pi (\pi _r(\varvec{\mathbf {\varepsilon }}^\mathrm {r}, \varvec{P}^\mathrm {r})) . \end{aligned}$$
(9)

The scalar function \(\pi _r\) is called difference variable and will be explained in context with \(\psi ^\pi \) in Eq. (17).

The mechanical part depends on invariants of the remanent strain tensor for which three principal remanent strains can be chosen and allows its decomposition:

$$\begin{aligned} \psi ^m (\varvec{\mathbf {\varepsilon }}^\mathrm {r})= \psi ^{mp}(\varepsilon _{r\hbox {I}}) +\psi ^{mp}(\varepsilon _{r\hbox {II}})+\psi ^{mp}(\varepsilon _{r\hbox {III}}) . \end{aligned}$$
(10)

Here \(\varepsilon _{r\hbox {I}}\), \(\varepsilon _{r\hbox {II}}\), \(\varepsilon _{r\hbox {III}}\) are the principal remanent strains.

The approach is motivated by the expected isotropy of the polycrystalline ferroelectric material concerning the remanent strain behavior. Since only the mechanical back-stresses are needed to model the material behavior, the knowledge of the derivative of \(\psi ^m\) with respect to the principal values of the remanent strains and thus of the mechanical back-stresses in the principal axis system of the remanent strains is sufficient. Thus, Landis [15] made the following specific choice for physical reasons:

$$\begin{aligned} \frac{\partial \psi ^m}{\partial \varepsilon _{rK}} = \frac{2 m^t H^\sigma _0 \varepsilon _0^{m^c+m^t} \varepsilon _{rK}}{(\varepsilon _0 + \varepsilon _{rK})^{m^c} (2 \varepsilon _0 - \varepsilon _{rK})^{m^t}}, \quad K \in \{I, II, III\}, \end{aligned}$$
(11)

with no summation over K. The quantity \(\varepsilon _0\) is the saturation strain, which results under uniaxial mechanical compressive stress. The positive values \(m^c\), \(m^t\), and \(H^\sigma _0\) are material parameters for adaptation to a particular material. The denominator’s consideration in Eq. (11) shows that the back-stress increases sharply when the principal remanent strain approaches \(-\varepsilon _0\) or \(2 \varepsilon _0\). That is why it is not possible to exceed these values, allowing the illustration of the saturation behavior of a ferroelectric ceramic under purely mechanical loading. The choice that the saturation strain under tension is twice as high as under pressure is based on micromechanical considerations of the tetragonal grain. However, it is assumed that the edge direction of the elementary cells coincides with the direction of loading. It is the case of a purely mechanically, uniaxially, and homogeneously loaded monocrystalline sample. In this case, under mechanical tensile stress, the volume fractions of the four crystal variants oriented perpendicular to the stress direction can switch toward the stress direction and produce a remanent elongation strain. In contrast, under mechanical compressive stress, only the volume fractions of the two crystal variants oriented perpendicular to the stress direction can switch to the direction perpendicular to the stress direction and cause a remanent elongation strain. Assuming that the volume fractions of all six crystal variants are identical in the initial state, the given ratio between the maximum possible remanent compression strain and elongation strain is 1:2. This assumption is only a rough approximation due to the arbitrary orientation of the grains in the polycrystal. By experiments [36] and more detailed micromechanical considerations [16], it can be determined that the amount of the remanent saturation strain under tensile stress is usually significantly less than twice the amount of the remanent saturation strain under compressive stress.

The pure electrical part \(\psi ^e\) models electrical backfields in a similar way as a mechanical part. Analogously, due to the polycrystal isotropy, it is expected that \(\psi ^e\) depends only on the remanent polarization \(\psi ^e = \psi ^e (\varvec{P}^\mathrm {r})\) as follows:

$$\begin{aligned} \psi ^e (\varvec{P}^\mathrm {r}) = \frac{\displaystyle H_0^e P_0^2}{\displaystyle (m_e-1)(m_e-2)} \bigg ( 1-\frac{\displaystyle |\varvec{P}^\mathrm {r}|}{\displaystyle P_0} \bigg )^{2-m_e} - \frac{\displaystyle H_0^e P_0}{\displaystyle m_e-1}|\varvec{P}^\mathrm {r}|. \end{aligned}$$
(12)

Here \(H_0^e\) and \(m_e\) are positive material parameters to be selected for adjustment to a particular material. The characteristics of the electrical part of the potential can be discussed based on its derivative—electrical backfield:

$$\begin{aligned} \varvec{E}_B^e = \frac{\displaystyle \partial \psi ^e}{\displaystyle \partial \varvec{P}^\mathrm {r}} = \frac{\displaystyle H_0^e P_0}{\displaystyle m_e-1} \left[ \bigg ( 1-\frac{\displaystyle |\varvec{P}^\mathrm {r}|}{\displaystyle P_0} \bigg )^{1-m_e} -1 \right] \frac{\displaystyle \varvec{P}^\mathrm {r}}{\displaystyle |\varvec{P}^\mathrm {r}|} . \end{aligned}$$
(13)

\(\varvec{E}_B^e\) corresponds to the electric backfield in the direction of the remanent polarization \(\varvec{P}^\mathrm {r}/|\varvec{P}^\mathrm {r}|\). For \(m_e > 1\), this electric backfield increases sharply when approaching the remanent saturation polarization \(P_0\) so that exceeding of the remanent saturation polarization is not possible. In this way, the saturation properties of ferroelectric ceramics are modeled with respect to the remanent polarization.

The potentials \(\psi ^m\) and \(\psi ^e\) were further modified by Landis [16] to be expressed by invariants of the strain tensor including \(J_3\)-dependency:

$$\begin{aligned} \psi ^m (\varvec{\mathbf {\varepsilon }}^\mathrm {r})= & {} \frac{\displaystyle 1}{\displaystyle 2}H_0^m\varepsilon _c\left[ \frac{\displaystyle J_2^\varepsilon }{\displaystyle \varepsilon _c}\exp \left( \frac{\displaystyle m_m}{\displaystyle 1-\frac{\displaystyle J_2^\varepsilon f(J_3^\varepsilon /J_2^\varepsilon )}{\displaystyle \varepsilon _c}}\right) \right] ^2 , \end{aligned}$$
(14)
$$\begin{aligned} \psi ^e(\varvec{P}^\mathrm {r},\pi _r)= & {} H_0^e P_\mathrm{max}\left[ \ln \left( \frac{\displaystyle 1}{\displaystyle 1 - \frac{\displaystyle |\varvec{P}^\mathrm {r}|}{\displaystyle P_{sat}(\pi _r)}} - \frac{\displaystyle |\varvec{P}^\mathrm {r}|}{\displaystyle P_{sat}(\pi _r)} \right) \right] . \end{aligned}$$
(15)

With the potentials \(\psi ^m\) and \(\psi ^e\) discussed so far, the saturation behavior of ferroelectric ceramics under purely mechanical or purely electrical loading can be mapped. Under combined electromechanical loading, however, the situation is much more complex. Due to the geometric restrictions of the domain arrangement, the achievable remanent polarization in a particular direction depends on the remanent strain state [16]. Conversely, for a particular remanent polarization state, not all remanent strain states that are possible under purely mechanical loading are accessible. To model the above-mentioned behavior, the assumed form of the potential \(\psi ^{\pi }(\pi _r)\) is introduced:

$$\begin{aligned} \psi ^{\pi }(\pi _r) = {\left\{ \begin{array}{ll} 0 &{}\quad \text {if } \pi _r \le \frac{\displaystyle 2P_0}{\displaystyle \chi } ,\\ \frac{\displaystyle 4P_0^2 H_0^{\pi }}{\displaystyle \chi ^2 (m^{\pi } +1)(m^{\pi } +2)}\bigg ( \frac{\displaystyle \chi \pi _r}{\displaystyle 2P_0} - 1 \bigg )^{m^{\pi } +2} &{}\quad \text {if } \pi _r > \frac{\displaystyle 2P_0}{\displaystyle \chi } . \end{array}\right. } \end{aligned}$$
(16)

The parameters \(H_0^\pi \), \(m^\pi \), and \(\chi \) are intended for adaptation to the actual material behavior.

The scalar difference variable \(\pi _r \) is introduced to couple the allowable states of remanent polarization and remanent strain, which are not independent from each other:

$$\begin{aligned} \pi _r(\varvec{\mathbf {\varepsilon }}^\mathrm {r},\varvec{P}^\mathrm {r}) = |\varvec{P}^\mathrm {r}| - \frac{\displaystyle P_0}{\displaystyle \chi \varepsilon _0|\varvec{P}^\mathrm {r}|^2} \varvec{\mathbf {\varepsilon }}^\mathrm {r}:(\varvec{P}^\mathrm {r}\varvec{P}^\mathrm {r}) + \frac{\displaystyle 2}{\displaystyle \chi }P_0 . \end{aligned}$$
(17)

3 Configurational forces

The idea of a configurational or material force goes back to the pioneering work of Eshelby in 1956, who investigated the thermodynamic driving forces acting on a defect in a solid. The physical meaning of the configurational force is the change in total potential energy \(\delta \varPi \) of the system of a stressed and deformed body, if the defect is virtually shifted in its material configuration by coordinates \(\delta \varvec{X}\). The associated configurational force vector \(\varvec{\varvec{G}}\) is defined by the relationship:

$$\begin{aligned} \delta \varPi = - \varvec{\varvec{G}} \cdot \delta \varvec{X} \, . \end{aligned}$$
(18)

The concept of configurational forces has been further developed in the last decades and applied to various types of defects like volume defects, dislocations, interfaces, cracks, and much more, see the overview literature in [11, 18, 32]. The vector \(\varvec{\varvec{G}}\) can be calculated from the physical field solution of the problem by means of the second-order configurational stress tensor \( \varvec{\mathbf {Q}} \), if either a volume integral is evaluated over the defect containing domain V or along its surface S:

$$\begin{aligned} {{\varvec{G}}} = \int _{V} \nabla \cdot {\mathbf {Q}} \,\mathrm {d}V = \int _S {\mathbf {Q}} \cdot {{\varvec{n}}} \, \mathrm {d}S. \end{aligned}$$
(19)

The specific expression of the tensor \( \varvec{\mathbf {Q}}\) depends on the considered field problem. For the coupled electromechanical problem at hand, it reads as:

$$\begin{aligned} \varvec{\mathbf {Q}} = h \, \varvec{\mathbf {\delta }} - \varvec{\mathbf {\sigma }} \cdot \nabla \varvec{u} -\varvec{D} \, \nabla \varvec{\phi } \, . \end{aligned}$$
(20)

Here, \( \varvec{\mathbf {\delta }} \) is the second-order unity tensor, and \(\varvec{n} \) denotes the outward normal vector on the surface S. The electric enthalpy density is expressed by the elastic strains \( \varvec{\mathbf {\varepsilon }}^\mathrm {s}=\varvec{\mathbf {\varepsilon }}-\varvec{\mathbf {\varepsilon }}^\mathrm {r}\) and the electric field \( \varvec{E} \) as follows:

$$\begin{aligned} h(\varvec{\mathbf {\varepsilon }}^\mathrm {s}, \varvec{E}, \varvec{P}^\mathrm {r}) = \frac{\displaystyle 1}{\displaystyle 2}\varvec{\mathbf {\varepsilon }}^\mathrm {s}:{\mathbb {C}}:\varvec{\mathbf {\varepsilon }}^\mathrm {s}- \varvec{E} \cdot \varvec{\mathbf {e}}: \varvec{\mathbf {\varepsilon }}^\mathrm {s}- \frac{\displaystyle 1}{\displaystyle 2}(\varvec{E} \cdot \varvec{\mathbf {\upkappa }} \cdot \varvec{E})\, - \varvec{P}^\mathrm {r}\varvec{E}. \end{aligned}$$
(21)

In analogy to the physical force equilibrium (linear momentum), one can set up a local equilibrium condition of the configurational forces in the following form (see, e.g., [11, 32]):

$$\begin{aligned} \nabla \cdot \varvec{\mathbf {Q}} + \varvec{g} = 0 \,. \end{aligned}$$
(22)

The so-called material body force vector \( \varvec{g}\) represents all possible sources for the occurrence of a configurational force, i. e. non-vanishing of Eq. (19). In case of ferrelectricity, \( \varvec{g}\) comprises all physical body forces \(\varvec{\bar{b}} \), volume charges \(\bar{w}_\mathrm {v}\), gradients of the remanent fields \( \varvec{\mathbf {\varepsilon }}^\mathrm {r}, \varvec{P}^\mathrm {r}\), and material inhomogeneities [18]:

$$\begin{aligned} \varvec{g} = - \varvec{\bar{b}} \cdot \nabla \varvec{u} + \bar{w}_\mathrm {v} \nabla \phi + \varvec{\mathbf {\sigma }} : \nabla \varvec{\mathbf {\varepsilon }}^\mathrm {r}- \nabla \phi \cdot \nabla \varvec{P}^\mathrm {r}- \frac{\partial h}{\partial \varvec{x}} \bigg |_\mathrm {expl}. \end{aligned}$$
(23)

The last term denotes an explicit dependency of the electric enthalpy h on the coordinates, which comes into effect for inhomogeneous or functionally graded materials exhibiting spatially varying properties.

The configurational forces can be computed by post-processing of the finite element solution of the considered problem. Here, we follow the approach suggested by Mueller et al. [22]. Therefore, the weak form of the balance law Eq. (22) is considered introducing a vectorial test function \(\varvec{\eta }\):

$$\begin{aligned} \int _{V} (\nabla \cdot {\mathbf {Q}} + {{\varvec{g}}} ) \cdot {\varvec{\eta }} \, \mathrm {d}V = 0 . \end{aligned}$$
(24)

Applying Gauss’ divergence theorem gives:

(25)

whereby in the case of stationary boundary conditions the test function vanishes on the boundary S and the surface integral is zero. Next, the test function \( \varvec{\eta }\) and its gradient \(\nabla \varvec{\eta }\) are approximated in every finite element by its nodal values \( \varvec{\eta }^{(l)}\) and common isoparametric shape functions \(N^{(l)}\):

$$\begin{aligned} \varvec{\eta } = \sum _{l} N^{(l)} \varvec{\eta }^{(l)}, \qquad \nabla \varvec{\eta } = \sum _{l} \nabla N^{(l)} \varvec{\eta }^{(l)} . \end{aligned}$$
(26)

Inserting into Eq. (25) and integrating over the volume \(\varOmega e\) of an element e yields:

$$\begin{aligned} \sum _{l} \left[ \int _{\varOmega e} \left( \varvec{\mathbf {Q }} \cdot \nabla N^{(l)} - N^{(l)} \varvec{g} \right) \mathrm{d}V \, \right] \cdot \varvec{\eta }^{(l)} =0 \,. \end{aligned}$$
(27)

Since this must be true for arbitrary values of the test function, the expression in brackets must be zero. Either of these two terms represents the discrete configurational force acting at the node l of an element e:

$$\begin{aligned} {{\varvec{G}}}^{e (l)} = \int _{\varOmega e} {\mathbf {Q }} \cdot \nabla N^{(l)} \mathrm {d}V = \int _{\varOmega e} N^{(l)} {{\varvec{g}}} \,\mathrm {d}V . \end{aligned}$$
(28)

The total configurational force at a global node K is assembled from the contributions \(\varvec{G}^{e(l)}\) of all elements e, where the local node number l equals the global node K:

$$\begin{aligned} \varvec{G}^{(K)} = \underset{e=1}{\overset{n_{el}}{\bigcup }} \varvec{G}^{e (l)} . \end{aligned}$$
(29)

Equation (28) offers two ways to compute the nodal configurational force: The first expression uses the tensor \(\varvec{\mathbf {Q}}\) and the derivatives of shape functions, whereas the second term is based on material body force \(\varvec{g}\), which requires to determine the gradient fields, see Eq. (23). Since the gradient of remanent fields is more difficult and less accurate to be calculated in FEM, the first way has been chosen here. The evaluation of the volume integral Eq. (28) over the HEX20 elements is performed using standard Gaussian numerical quadrature rules.

4 FEM implementation

Here, a brief outlook at the finite element (FEM) implementation as part of the commercial code Abaqus will be given. For the solution of the nonlinear coupled electromechanical boundary value problem, a library of User-defined element routines UELlib has been written at the research group. This library contains most common continuum element formulations for three-dimensions (tetra-/hexahedron) and two-dimensional plane strain state (tri-/quadrilateral) exhibiting linear or quadratic shape functions and including either full or reduced integration. The FEM formulation is based on the principle of virtual displacements and virtual potential to achieve the equilibrium conditions of forces and charges. Details may be found in [4].

A material routine for the Landis model was developed in C++ for the Ansys code by Stark [30] from the group of TU Dresden and kindly provided to us. In order to implement this routine into Abaqus and to connect it with the UELlib, an interface has been written by J.Storm, cf. Fig. 2. The right block represents the C++ routine, and the left one the UELlib in Fortran code associated with Abaqus. Additionally, an own memory management was required due to modification of the Newton–Raphson method in [31].

Fig. 2
figure 2

Interface project structure chart

Full size image

Finally, for visualization and post-processing of the solution-dependent variables (SDVs) from Abaqus UEL, the tool “Abaquser” is available [27]. Needless to say, python scripts to interact with the results stored in the Abaqus databases and extract data needed for the evaluation of the configurational forces were used.

5 Results of finite element simulations

5.1 Uniaxial electric loading of representative volume elements

To test the implementation of the macromechanical switching model, a simple set of two electromechanical 3D elements was employed. The material properties for PZT-5H used in the numerical calculations are given in Table 1.

Table 1 Material parameters for PZT-5H and PZT-PIC151 ceramics
Full size table

As initial conditions, an unpolarized PZT-5H piezoelectric ceramic was assumed. A bipolar electrical loading in the range between \(\pm \,2.0 E_{0}\) was applied to produce the full hysteresis loops, cf. Fig. 3. The calculated hysteresis loops for polarization and strain (butterfly) are plotted in Fig. 4.

Fig. 3
figure 3

Temporal course of applied electrical field \(E/E_0\)

Full size image
Fig. 4
figure 4

Polarization (left) and strain (right) hysteresis loops

Full size image
Fig. 5
figure 5

Reduction of the strain hysteresis in the RVE due to the presence of the dielectric inclusion (color figure online)

Full size image

If the material contains a periodic set of circular inclusions of a dissimilar dielectric material like phenolic resin (see data in Sect. 5.4) as depicted in Fig. 6c, an representative volume element can be defined. The macroscopic response of such a composite is simulated under the same cyclic electric loading. The obtained strain hysteresis is presented in Fig. 5 and illustrates the change of the effective mechanical properties of the composite due to the presence of the phenolic resin inclusion compared to the pure homogeneous material. For this case, the decrease in the remanent strain is roughly 25%. The main physical reason for such a substantial reduction of the hysteresis is that the dielectric inclusion was put within the non-polarized ferroelectric matrix. As the applied bipolar electrical loading exceeds the coercive field, the whole structure starts to deform due to evolved electromechanical coupling. The resin inclusion exposes restrictive action since, in contrast to the ferroelectric matrix, the dielectric material does not elongate (Fig. 6).

The distribution and localization of the electric displacement field in this RVE is similar to that shown in Fig. 18.

5.2 Poling of a plate with a hole

To present a more elaborated example for the application of the macromechanical Landis model and material configurational forces approach, a ferroelectric plate with a hole was analyzed under electric loading. The dimensions of the quadratic plate are \(20 \times 20 \times 2\) mm. A central cylindrical hole with a diameter of 6 mm is placed through the thickness direction of the plate. Due to the existing symmetries in the geometry and the boundary conditions, only one eighth of the geometry needs to be meshed for a homogeneous plate. The generated FE model is shown in Fig. 8. The meshing is performed with 960 eight-noded elements having linear shape functions and eight integration points. One element is used for discretization across the half thickness direction.

Fig. 6
figure 6

Considered structures of a plate with: a hole, b bi-material plate with hole, and c plate with an inclusion

Full size image

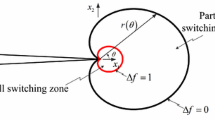
As Dirichlet boundary conditions, the mechanical displacements along the symmetry planes \(x_1 = 0\) and \(x_2 = 0\) are prevented in the direction normal to these symmetry planes. The displacements \(u_3\) in \(x_3\)-thickness direction are prohibited for all nodes. Thus, despite the use of three-dimensional elements, a plane strain state is represented. The scalar electric potential \( \phi \) is prescribed on the side surface \(x_2 = 10\) mm with alternating temporal course between maxima \(\phi = \pm \,10\) kV, cf. Fig. 7. On the opposed side of the symmetry plane \(x_2 = 0\), the electric potential is set to \(\phi = 0\). At all remaining boundary conditions, zero tractions and vanishing surface charges (impermeable case) are specified. The manufacturer’s specifications for PZT-5H as listed in Table 1 are used as the basis for determining the linear material parameters. As initial state no polarization \( \varvec{\varvec{P}^\mathrm {r}} \) is assumed. All calculations are carried out with the commercial FE software Abaqus using the electromechanical 3D User-Elements, cf. Sect. 4. The imposed electric loading is divided into as many equal increments as are needed to achieve a convergence, which is checked separately for each node of the FE model (Fig. 8).

Fig. 7
figure 7

Temporal course of applied electrical field

Full size image
Fig. 8
figure 8

Poling of a plate with hole: remanent polarization. Deformations magnified 100 times. Please refer online to media data section for video animation (color figure online)

Full size image

In the following, the results of FE calculations for an applied electric potential \(\phi = 10\) kV are presented. This magnitude of \(\phi \) would lead to a vertical electric field of \(E=\pm \) 1 kV/mm. Comparing this with the material parameters according to Table 1, the entire plate without a hole would slightly exceed the coercive field strength \(E_0\).

For the selected geometry and material parameters, a linear model behavior is observed up to \(\phi =4\) kV. Beyond this point, up to \(\phi = 10\) kV, domain switching resp. reorientation of the polarization vector is occurring during further load increment. This ascending part of loading results in a poling of the structure, mostly in the vertical direction. When the electric field is decreased and reverses its direction, the polarization field will change to a large extent. The results illustrate a concentration of the electromechanical fields near the hole, which leads to an earlier domain reorientation when the applied bipolar electrical loading is reversed, cf. Fig. 9. Here the regions of 180\(^\circ \) and 90\(^\circ \) domain switching are clearly observable. And while most material is still polarized in the vertical direction, the region at the hole is the first to undergo domain reorientation.

Fig. 9
figure 9

Reversal switching in the region with highest electric field concentration after changing the sign of the applied loading (− 80% of \(\phi _\mathrm {max}\)). Deformations magnified 100 times (color figure online)

Full size image
Fig. 10
figure 10

Vector of configurational forces near the hole by the end of poling. Deformations magnified 100 times (color figure online)

Full size image

The configurational force vectors at all nodes in the structure are calculated according to Sect. 3. The results along the boundary of the hole are presented in Fig. 10 for the magnitude \( \varvec{\varvec{G}}\) and in Fig. 11 for both components \( \varvec{G}_1, \varvec{G}_2 \) of the material forces. Due to symmetry, at the intersection of the symmetry planes (\( x_1=0, x_2=0 \)) with the hole, the depicted corresponding in-plane components of the configurational force vector are only half the actual value.

Fig. 11
figure 11

Configurational forces along the vertical and horizontal direction by the end of poling. Please refer online to media data section for video animation of the whole poling process (color figure online)

Full size image

Similar to the purely mechanical Kirsch problem, a field concentration near the hole is observed as anticipated in the coupled electromechanical case as well. This is also reflected by the distribution of the configurational forces, which represent a measure of thermodynamic driving forces on the defect, which is the hole in the present case. A component-wise distribution of the configurational forces along the circumference of the hole is plotted in Fig. 12. It can be seen that the maximum of the horizontal component (\(G_1\)) dominates over both others and is about three times larger than the maximum vertical one (\(G_2\)), moreover, \(G_1^\mathrm{max}\) and \(G_2^\mathrm{max}\) are at different locations. All components of \( \varvec{\varvec{G}} \) vanish at the upper vertex of the hole (\( \varphi =90^\circ \)) because of symmetry. The physical interpretation is that the defect (the hole\(\backslash \) void) prefers to evolve and grow in the direction of the maximum configurational forces vector, cf. Fig. 10. In contrast to the case of a sharp notch or a crack, the maximum value needs not necessarily be concentrated at one material point only. This is seen in Fig. 10 showing a certain region with high G values and is plotted in detail along the circumference of the hole in Fig. 12.

Due to the symmetry of the problem, the total sum of all configurational forces acting on the hole will be canceled out to zero, i.e., there is no effective driving energy to move the hole as a whole. Only its shape will be changed. Of course, such an evolution of the hole shape would require an appropriate physical process of material transportation as, e.g., diffusion of material by point defects or voids. Configurational forces supply merely the available driving energy.

Fig. 12
figure 12

Distribution of configurational forces along the circumference of the hole at maximum electrical loading plotted in polar coordinate angle (color figure online)

Full size image
Fig. 13
figure 13

Evolution of the configurational forces under applied electrical loading plotted for the node A (cf. Fig.10) lying at the vertex of the hole at \( \varphi =0 \) (color figure online)

Full size image

It is crucial to study the evolution of the configurational forces vector during the cyclic electrical loading. A behavior somewhat similar to the strain polarization loop (Fig. 4) is observed for each of its components, cf. Fig. 13. Here, a characteristic point A at the intersection of the hole and the horizontal symmetry plane \( \varphi =0^\circ \)) is selected, cf. Fig.10. The dominating component \( \varvec{G}_1 \) attains a maximum value at the highest applied electric field irrespective of its sign, which corresponds to maximum polarization. During the phase of the electric field reversal and induced reorientation of polarization, the configurational force reverses its sign as well. A nonzero residual value at the removed electrical loading is observed. This can be attributed to the corresponding remanent strain present in the structure after the initial poling. It is seen that the presence of the defect facilitates the initiation of the switching process starting at 0.45 kV/mm of applied loading at point A in contrast to 0.82 kV/mm seen in Fig. 4 for the homogeneous case of two finite elements (though it is only the initiation of the switching process, not yet its saturation) (Fig. 14).

5.3 Poling of a bi-material plate with a hole

To investigate the influence of the presence of another material or modified material properties at a certain part of the plate, a model with a vertical strip of dissimilar PZT-PIC151 ceramics is considered, cf. Fig. 6b. The symmetry with respect to the vertical plane is violated, so now both left and right parts have to be taken into simulations. The strip of the PZT-PIC151 ceramics of 5 mm width is located at the right part of the plane. It can be easily identified in the plot of the results, e.g., from Fig. 15. Such a strip of another piezoelectric material can resemble a composite material or a multilayer device structure. In this case, field discontinuities occur as well along the interface between the two dissimilar materials, which may affect damage or debonding. Regarding the choice of material properties, one can anticipate: A simulation with a strip of a dielectric material is straightforward and does not bring new insights. Its extra action can be imagined as that of an elastic spring attached in parallel to the plane-with-a-hole structure (Sect. 5.2). From pure mechanical analyses, it is well known that a softer strip (lower Young’s modulus) would attract the hole toward the interface, whereas a stiffer one affects repulsion. Therefore, two ferroelectric materials with somewhat different parameters have been selected, see Table 1.

In order to visualize the difference coming from the presence of another material, a polar plot of configurational force magnitude is presented in Fig. 14. Here only the circumference of the hole is addressed, although other effects within the structure are additionally present. Due to the different magnitude scales at maximum electrical loading application and complete unloading, the difference, which amounts up to 22% at the point A at zero applied electric loading, is somewhat difficult to perceive. The electrical loading used to plot this graph is specified in Fig. 14, namely, cycle time = 1 (according to Fig. 8)—“max loading”, and cycle time = 2 (according to Fig. 8)—“unloaded”. Two curves from Fig. 14 are additionally shown in Fig. 21.

Fig. 14
figure 14

Polar plot of the configurational force vector variation along the circumference of the hole. Comparison of the results for the models from Sects. 5.2 and 5.3 (color figure online)

Full size image

An interesting phenomenon to observe is the delayed ferroelectric switching in the PZT-PIC151 strip due to its higher coercive electric field (cf. Table 1). However, an even more interesting case is the delayed reverse switching in the same strip, cf. Fig. 15. One of the distinguishable differences is the presence of the strong interaction force along the boundary of the two materials, which is illustrated in Fig. 16. The effect is the strongest when the polarization of both materials is opposite, as is exemplarily shown in Fig. 15 for the time \(t = 2.90\) (according to Fig. 7). Such mismatch of the electromechanical properties can lead to high local stresses, crack initiation, and further material interface debonding even not at the maximum applied electrical loading. It should be noticed that the peak values of the configurational forces along the material boundary CD are comparable to the maximum values at the hole (point A) (Fig. 17).

Fig. 15
figure 15

Change of polarization under the reverse electrical loading. The material strip of PZT-PIC151 ceramics (right) has not undergone a reversal in polarization yet. Deformations magnified 50 times (color figure online)

Full size image
Fig. 16
figure 16

Course of configurational forces at the point B (cf. Fig. 15) at the interface between two materials (color figure online)

Full size image
Fig. 17
figure 17

Variation of configurational forces along the vertical interface CD (cf. Fig. 15) between two materials at different time points (color figure online)

Full size image

5.4 Poling of a plate with a dielectric or ferroelectric inclusion

Another important example is the case with an inclusion made of pure dielectric (phenolic resin) or ferroelectric (PZT-PIC151) materials placed in the center of the PZT-5H plate as shown in Fig. 6c. The meshing of the composite can be found in Fig. 18. PZT-PIC151 ceramics was already used as a material for the strip in Sect. 5.3. The properties of the phenolic resin are the follows: Young’s modulus 3.8 GPa, Poisson’s ratio 0.41, and dielectric constant (relative permittivity) \(\epsilon _r = 7.5\). The choice of the phenolic resin was motivated by its extensive usage in composite microelectronics components. Thus, there are three dielectric permittivity cases:

  • impermeable (hole)

  • weakly permeable (phenolic resin inclusion)

  • highly permeable (PZT-PIC151 ceramics, since it has the relative permittivity constant \(\epsilon _r = 3130\) in the poling direction).

The results for the cases considered in this and all previous Subsections are calculated and summed up here. The time point \(t=1\) is chosen, which according to Fig. 7 corresponds to the strongest applied electrical loading. The uniform response of two elements from Sect. 5.1 was used as a reference solution for a homogeneous material.

Figure 18 is an exemplary illustration of the deformation pattern and the electric displacement distribution/localization in the ferroelectric plate comprising a central dielectric inclusion.

Fig. 18
figure 18

Plate with dielectric inclusion of phenolic resin. Electric displacement distribution under the maximum electrical loading. Deformations magnified 100 times (color figure online)

Full size image

It is evident that the material properties of the inclusion are crucial for the mechanical response of the structure. Figure 19 illustrates an averaged \(\epsilon _{22}\) strain component (which directly corresponds to the deformation contour of the upper surface of the specimen), non-uniformly varying along the \(x_1\) coordinate. The hole introduces a porosity, thus softening the mechanical response the most (curves of the same color in Fig. 19). It might be expected that it is the plate with a hole where the deformation profile will experience the strongest deflection, but it is the resin inclusion that counteracts against the free expansion of the ferroelectric plate material under the applied electrical loading.

Fig. 19
figure 19

Non-uniform averaged strain distribution along the \(x_1\) axis at maximum electrical loading (color figure online)

Full size image
Fig. 20
figure 20

Electric displacement distribution at the upper surface of the plate at maximum electrical loading (color figure online)

Full size image

Figure 20 illustrates the electric displacement distribution along the upper surface of the plate. The change of the electric displacement is similar and very close whether the inclusion is a weakly permeable dielectric phenolic resin or a void (blue and black curves in Fig. 20, respectively). The electrical results for a PZT-5H plate with highly permeable PZT-PIC151 inclusion at maximum electrical loading are almost identical to those of a test case of homogeneous PZT-5H ceramics. The minor deviation is due to the difference in dielectric coefficients.

The case of a PZT-5H plate with a PZT-PIC151 strip reveals three stages (when observed from left to right in Figs. 19 and 20):

  • deformation corresponding to PZT-5H plate material

  • decrease in deformation due to the presence of the hole

  • deformation corresponding to PZT-PIC151 strip material.

As already has been mentioned in Sect. 5.3, the course of D over time shows the largest contrast within the range, where the electric coercive strengths of both materials differ. A jump is observed at the interface of two materials for the case of Sect. 5.3 (green curve in Fig. 20).

An angular distribution of the configurational force magnitude G as well as its components \(G_1\) and \(G_2\) are presented in Figs. 21 and 22, respectively. As emphasized earlier, the choice of the time snap is essential since, in the case of the bi-material, the highest configurational forces can appear during the interval of the electrical loading reverse, cf. Sect. 5.3. Here the maximum applied electric field is considered. Similar to Fig. 14, the configurational force magnitude has a maximum near point A (\(0^\circ \) or \(180^\circ \)), decreasing toward zero at the vertical symmetry plane (\(90^\circ \)). The exception is the PZT-5H plate with a PZT-PIC151 inclusion which differs substantially because both materials are ferroelectric and can undergo domain switching. In this case, the maximum is achieved near 45\(^\circ \) when the shear deformation is accumulated due to the geometry of the inclusion. The differences between other simulations in terms of configurational force distribution along the inclusion-plate interface/free surface of a hole are rather marginal, which is illustrated in Fig. 22. The component-wise distribution presented in Fig. 22 is of interest to observe the dominance of the \(G_1\) component and the different regions of the \(G_1\) and \(G_2\) maxima.

Fig. 21
figure 21

Angular distribution of the configurational force magnitude G at maximum electrical loading along the inclusion-plate interface/free surface of a hole (color figure online)

Full size image
Fig. 22
figure 22

Angular distribution of the \(G_1\) (left) and \(G_2\) (right) configurational force component at maximum electrical loading along the inclusion-plate interface/free surface of a hole (color figure online)

Full size image

6 Conclusions and discussion

The macromechanical ferroelectric model of Landis [15] is implemented as a finite element user element routine to numerically simulate domain switching in 3D ferroelectrics. It is successfully tested and applied to structures with defects, in particular, a plate with a hole, an inhomogeneity, or a bi-material strip, respectively. The simulations produce the macroscopic integral electromechanical reaction of these configurations to an applied cyclic electric field. Additionally, the local distribution of field quantities including electric potential, polarization vector and mechanical deformations, stresses, and strains are found. Peaks or jump values of the above-mentioned fields are studied and discussed, which may be responsible for damage initiation and failure. A consistent thermodynamical theory of material configurational forces and their numerical computation is presented. The results of configurational forces characterize energetic driving forces on the considered defect structures in the nonlinear ferroelectric material. They can serve for an indication to optimize the inhomogeneous design. In all examples, the large influence of the occurring non-uniform distribution of the remanent strains and polarization is revealed, which emphasizes the need for applying simulations using multi-axial ferroelectric behavior. The theory and different results presented in the current publication offer a comprehensive and effective technique to explore the impact of material inhomogeneities in ferroelectric devices and composites subjected to electromechanical loading.