Dynamic response of a gradient elastic half-space to a load moving on its surface with constant speed

Abstract

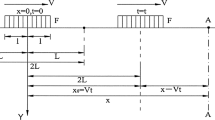
The problem of determining the dynamic response of a granular elastic half-space soil medium to a rectangular load moving on its surface is determined analytically. The granular material is modeled as a gradient elastic solid with two material constants in addition to the two classical elastic moduli. These material constants with dimensions of length are the micro-stiffness g and the micro-inertia h coefficients. The rectangular load is uniformly distributed of constant magnitude and moves with constant speed. The resulting three partial differential equations of motion are of the fourth order with respect to the horizontal x, y, and vertical z coordinates and of second order with respect to time t. These equations are solved with the aid of double complex Fourier series involving x, y, t, and the load velocity, which reduce them to a system of three ordinary differential equations of the fourth order with respect to z, which can be easily solved. Use of appropriate classical and non-classical boundary conditions can lead to the solution of the problem. The so obtained solution is used to easily assess by parametric studies the effects of the microstructural parameters g and h as well as the moving load velocity on the various response quantities.

Appendices

Appendix 1

For n = 0 and m = 0, Eqs. (27), (28), and (29) become

$$ \begin{array}{*{20}c} {U_{00}^{^{\prime\prime}} \left( z \right) - g^{2} U_{00}^{IV} \left( z \right) = 0}, \\ {V_{00}^{^{\prime\prime}} \left( z \right) - g^{2} V_{00}^{IV} \left( z \right) = 0}, \\ {W_{00}^{^{\prime\prime}} \left( z \right) - g^{2} W_{nm}^{IV} = 0}. \\ \end{array} $$

(48)

Equation (48) has the same characteristic equation

$$ \rho ^{2} \left( {1 - g^{2} \rho ^{2} } \right) = 0~~~{\text{with~roots}}~\rho _{{1,2~}} = 0,~~\rho _{{3,4}} = \pm \sqrt {\frac{1}{g}}. $$

(49)

Thus, the solutions of the above equations read

$$ \begin{array}{*{20}c} {U_{00} \left( z \right) = A_{1} e^{{\frac{1}{g}z}} + A_{2} e^{{\frac{1}{g}z}} + \left( {A_{3} z + A_{4} } \right)}, \\ {V_{00} \left( z \right) = B_{1} e^{{\frac{1}{g}z}} + B_{2} e^{{\frac{1}{g}z}} + \left( {B_{3} z + B_{4} } \right)}, \\ {W_{00} \left( z \right) = C_{1} e^{{\frac{1}{g}z}} + C_{2} e^{{\frac{1}{g}z}} + \left( {C_{3} z + C_{4} } \right)}. \\ \end{array} $$

(50)

From the classical boundary conditions of Eqs. (13) and (14), we obtain

$$ \begin{array}{*{20}l} {P_{x} |_{{z = 0}} = 0~~or~\mu U_{{00}}^{'} \left( 0 \right) - g^{2} \mu U_{{00}}^{{'''}} \left( 0 \right) = 0 \to A_{3} = 0}, \hfill \\ {P_{y} |_{{z = 0}} = 0 \to B_{3} = 0}, \hfill \\ {P_{z} |_{{z = 0}} = - F_{{00}} ~~ \to C_{3} = - \frac{{F_{{00}} }}{{\lambda + 2\mu }}}. \hfill \\ \end{array} $$

(51)

From the non-classical boundary conditions of Eq. (15), we have

$$ \begin{array}{*{20}c} {R_{x} |_{z = 0} = 0 \to U_{00}^{^{\prime\prime}} \left( 0 \right) = 0 \to A_{1} = - A_{2} }, \\ {R_{y} |_{z = 0} = 0 \to V_{00}^{^{\prime\prime}} \left( 0 \right) = 0 \to B_{1} = - B_{2} }, \\ {R_{Z} |_{ z = 0} = 0 \to W_{00}^{^{\prime\prime}} \left( 0 \right) = 0 \to C_{1} = - C_{2} }. \\ \end{array} $$

(52)

Finally, from the three displacements boundary conditions of Eqs. (16) and (17), we obtain

$$ \begin{array}{*{20}c} {u_{x} \left( {x,y,H,t} \right) = 0 \to U_{00} \left( H \right) = 0}, \\ {u_{y} \left( {x,y,H,t} \right) = 0 \to V_{00} \left( H \right) = 0}, \\ {u_{z} \left( {x,y,H,t} \right) = 0 \to W_{00} \left( H \right) = 0},\\ \end{array} $$

(53)

$$ \begin{array}{*{20}c} {\frac{{\partial u_{x} }}{\partial z}\left( {x,y,H,t} \right) = 0 \to U_{00}^{^{\prime}} \left( H \right) = 0}, \\ {\frac{{\partial u_{y} }}{\partial z}\left( {x,y,H,t} \right) = 0 \to V_{00}^{^{\prime}} \left( H \right) = 0}, \\ {\frac{{\partial u_{z} }}{\partial z}\left( {x,y,H,t} \right) = 0 \to W_{00}^{^{\prime}} \left( H \right) = 0}. \\ \end{array} $$

(54)

By substituting Eqs. (50, 51, 52) to Eqs. (53, 54), we obtain the final values of the coefficients ${A}_{i}$, ${B}_{i}$, ${C}_{i}$ ($i=1-4$) which are of the form

$$ \begin{array}{*{20}c} {A_{1} = A_{2} = A_{3} = A_{4} = B_{1} = B_{2} = B_{3} = B_{4} = 0}, \\ {C_{1} = \frac{{gF_{00} }}{{\left( {\lambda + 2\mu } \right)\left( {e^{\frac{H}{g}} + e^{{ - \frac{H}{g}}} } \right)}}}, \\ {C_{2} = - \frac{{gF_{00} }}{{\left( {\lambda + 2\mu } \right)\left( {e^{\frac{H}{g}} + e^{{ - \frac{H}{g}}} } \right)}}}, \\ {C_{3} = - \frac{{gF_{00} }}{{\left( {\lambda + 2\mu } \right)}}}, \\ {C_{4} = - \frac{{gF_{00} }}{{\left( {\lambda + 2\mu } \right)}} + \frac{{F_{00} H}}{{\left( {\lambda + 2\mu } \right)}}}. \\ \end{array} $$

(55)

From Eqs. (50) and (55), we obtain the final solutions in the form

$$ \begin{array}{*{20}c} { U_{00} \left( z \right) = 0}, \\ {V_{00} \left( z \right) = 0}, \\ {W_{00} \left( z \right) = \frac{{F_{00} }}{\lambda + 2\mu }\left( {H - z} \right) + \frac{{gF_{00} }}{\lambda + 2\mu }\left( {\frac{{e^{\frac{z}{g}} - e^{{ - \frac{z}{g}}} }}{{e^{\frac{H}{g}} - e^{{ - \frac{H}{g}}} }}} \right) - \frac{{gF_{00} }}{\lambda + 2\mu }}. \\ \end{array} $$

(56)

We can observe that for g = 0 we obtain the classical solution, which reads

$$ \begin{array}{*{20}c} {U_{00} \left( z \right) = 0}, \\ {V_{00} \left( z \right) = 0}, \\ {W_{00} \left( z \right) = \frac{{F_{00} }}{\lambda + 2\mu }\left( {H - z} \right)}. \\ \end{array} $$

(57)

The solution (57) is the same as the solution (60) given in Beskou et al. [12].

Appendix 2

For n = 0 and m > 0, Eqs. (27, 28, 29) become

$$ \alpha_{1} U_{0m} \left( z \right) + a_{2} U_{0m}^{^{\prime\prime}} \left( z \right) + \alpha_{3} U_{0m}^{IV} \left( z \right) = 0, $$

(58)

$$ b_{1} V_{{0m}} \left( z \right) + b_{2} V_{{0m}}^{{''}} \left( z \right) + b_{3} V_{{0m}}^{{IV}} \left( z \right) + b_{6} W_{{0m}}^{'} \left( z \right) + b_{7} W_{{0m}}^{{'''}} = 0, $$

(59)

$$ c_{3} V_{{0m}}^{'} \left( z \right) + c_{4} V_{{0m}}^{{'''}} \left( z \right) + c_{5} W_{{0m}} (z) + c_{6} W_{{0m}}^{{''}} \left( z \right) + c_{7} W_{{0m}}^{{IV}} = 0 $$

(60)

where

$$ \begin{array}{*{20}l} {\alpha_{1} = - \left( {\mu \mu_{m}^{2} + g^{2} \mu \mu_{m}^{4} } \right)}, \hfill \\ {a_{2} = \mu + 2g^{2} \mu \mu_{m}^{2} }, \hfill \\ {a_{3} = - g^{2} \mu }, \hfill \\ {b_{1} = - \left( {\left( {\lambda + 2\mu } \right)\mu_{m}^{2} + g^{2} \left( {\lambda + 2\mu } \right)\mu_{m}^{4} } \right)} \hfill \\ {b_{2} = \mu + g^{2} \left( {\lambda + 3\mu } \right)\mu_{m}^{2} } \hfill \\ {b_{3} = - g^{2} \mu } \hfill \\ {b_{6} = i\mu_{m} \left( {\lambda + \mu } \right)\left( {1 + g^{2} \mu_{m}^{2} } \right)} \hfill \\ {b_{7} = - ig^{2} \mu_{m} \left( {\lambda + \mu } \right)} \hfill \\ {c_{3} = i\mu_{m} \left( {\lambda + \mu } \right)\left( {1 + g^{2} \mu_{m}^{2} } \right)} \hfill \\ {c_{4} = - ig^{2} \mu_{m} \left( {\lambda + \mu } \right)} \hfill \\ {c_{5} = - \mu_{m}^{2} \mu \left( {1 + g^{2} \mu_{m}^{2} } \right)} \hfill \\ {c_{6} = \left( {\lambda + 2\mu } \right)\left( {1 + g^{2} \mu_{m}^{2} } \right) + g^{2} \mu \mu_{m}^{2} } \hfill \\ {c_{7} = - g^{2} \left( {\lambda + 2\mu } \right)}. \hfill \\ \end{array} $$

(61)

Solutions of the system of Eqs. (58), (59), and (60) are assumed to be of the form

$$ \begin{array}{*{20}c} {U_{0m} = R_{0m} e^{qz} }, \\ {V_{0m} = S_{0m} e^{qz} }, \\ {W_{0m} = T_{0m} e^{qy} }. \\ \end{array} $$

(62)

Substitution of the above solutions (62) into the system of Eqs. (58), (59), and (60) results in the equation

$$ \left\{ {\begin{array}{*{20}c} {a_{1} + \alpha_{2} q^{2} + \alpha_{3} q^{4} } & 0 & 0 \\ 0 & { b_{1} + b_{2} q^{2} + b_{3} q^{4} } & {q(b_{6} + b_{7} q^{2} )} \\ 0 & {q(c_{3} + c_{4} q^{2} )} & {c_{5} + c_{6} q^{2} + c_{7} q^{4} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {R_{0m} } \\ {S_{0m} } \\ {T_{0m} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right\}. $$

(63)

For nonzero solutions of the system of Eq. (63), the following algebraic equation should be satisfied:

$$ \left( {a_{1} + a_{2} q^{2} + a_{3} q^{4} } \right)[\left( {b_{1} + b_{2} q^{2} + b_{3} q^{4} } \right)\left( {c_{5} + c_{6} q^{2} + c_{7} q^{4} } \right) - q^{2} (c_{3} + c_{4} q^{2} )\left( {b_{6} + b_{7} q^{2} )} \right] = 0. $$

(64)

Equation (64) is solved for its 12 roots $q_{k} { }\left( {k = 1,2, \ldots 12} \right).{ }$ Thus, the solutions (62) can take the final form

$$ \begin{array}{*{20}c} {U_{0m } = R_{0m1} e^{{\lambda_{1} z}} + R_{0m2} e^{{\lambda_{2} z}} + R_{0m3} z + R_{0m4} }, \\ {V_{0m } = \mathop \sum \limits_{k = 1}^{8} S_{0mk} e^{{q_{k} z}} },\\ {W_{0m } = \mathop \sum \limits_{k = 1}^{8} T_{0mk} e^{{q_{k} z}} } \\ \end{array} $$

(65)

where $\lambda_{1}$ and $\lambda_{2}$ are the two roots of the equation $a_{3} q^{2} + a_{2} q + a_{1} = 0$, and S_0mk, T_0mk are the values of S_0m and T_0m for the q_k, respectively. By assuming S_0mk known, one obtains from (65)

$$ \begin{array}{*{20}c} {T_{0mk} = C_{k} S_{0mk} } & {for} & {k = 1,2,..8} & {\left( {k\,is \, not \, a \, summation \, index} \right)} \\ \end{array} $$

(66)

with

$$ C_{k} = \frac{{\left( {b_{1} + b_{2} q_{k}^{2} + b_{5} q_{k}^{4} } \right)}}{{q_{k} \left( {b_{6} + b_{7} q_{k}^{2} } \right)}} for \, k = 1,2,..8, $$

(67)

The displacements now take the forms

$$ \begin{array}{*{20}c} {u_{x} \left( {x,y,z,t} \right) = Re\mathop \sum \limits_{{m = 1}}^{M} \left( {R_{{0m1}} e^{{\lambda _{1} z}} + R_{{0m2}} e^{{\lambda _{2} z}} + R_{{0m3}} z + R_{{0m4}} } \right)e^{{i\mu _{m} y}} \equiv 0}, \\ {u_{y} \left( {x,y,z,t} \right) = Re\mathop \sum \limits_{{m = 1}}^{M} \left( {\mathop \sum \limits_{{k = 1}}^{8} S_{{0mk}} e^{{qz}} } \right)e^{{i\mu _{m} y}} }, \\ {u_{z} \left( {x,y,z,t} \right) = Re\mathop \sum \limits_{{m = 1}}^{M} \left( {\mathop \sum \limits_{{k = 1}}^{8} C_{k} S_{{0mk}} e^{{qz}} } \right)e^{{i\mu _{m} y}} }, \\ \end{array} $$

(68)

In the above, there are 12 constants (8 S_0mk, k = 1–8 and 4 $R_{0mi}$, i = 1–4) to be determined from the 12 boundary conditions. These boundary conditions are given by Eqs. (13), (14), (15), (16), and (17), which after the substitution of the displacements from (68) reduce to the following algebraic system of equations:

$$ \begin{array}{*{20}c} {P_{x} |_{z = 0} \, = \mu \left( {1 + 2g^{2} \mu_{m}^{2} } \right)\left( {R_{0m1} \lambda_{1} + R_{0m2} \lambda_{2} + R_{0m3} } \right) - \mu g^{2} \left( {R_{0m1} \lambda_{1}^{2} + R_{0m2} \lambda_{2}^{2} } \right) = 0}, \\ {P_{y} |_{z = 0} = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{1k} S_{0mk} = 0}, \\ {P_{z} |_{z = 0} = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{2k} S_{0mk} = - F_{0m} }, \\ \end{array} $$

(69)

$$ \begin{array}{*{20}c} {R_{x} |_{z = 0} = g^{2} \mu \left( {R_{0m1} \lambda_{1}^{2} + R_{0m2} \lambda_{2}^{2} } \right) = 0}, \\ {R_{y} |_{ z = 0} = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{3k} S_{0mk} = 0}, \\ {R_{Z} |_{ z = 0} = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{4k} S_{0mk} = 0}, \\ \end{array} $$

(70)

$$ \begin{array}{*{20}c} {U_{0m} \left( H \right) = R_{0m1} e^{{\lambda_{1} {\rm H}}} + R_{0m2} e^{{\lambda_{2} {\rm H}}} + R_{0m3} {\rm H} + R_{0m4} = 0}, \\ {V_{0m} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{5k} S_{0mk} = 0}, \\ {W_{0m} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{6k} S_{0mk} = 0}, \\ \end{array} $$

(71)

$$ \begin{array}{*{20}c} {U_{0m}^{^{\prime}} \left( H \right) = R_{0m1} \lambda_{1} e^{{\lambda_{1} {\rm H}}} + R_{0m2} \lambda_{2} e^{{\lambda_{2} {\rm H}}} + R_{0m3} = 0}, \\ {V_{0m}^{^{\prime}} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{7k} S_{0mk} = 0}, \\ {W_{0m}^{^{\prime}} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{8k} S_{0mk} = 0} \\ \end{array} $$

(72)

where ${\overline{B} }_{1k}-{\overline{B} }_{8k}$ can be obtained from Eq. (46) by setting ${\lambda }_{n}$=0 and considering that ${\overline{B} }_{1k}={B}_{2k}$, ${\overline{B} }_{2k}={B}_{3k}$, ${\overline{B} }_{3k}={B}_{5k}$, ${\overline{B} }_{4k}={B}_{6k}$, ${\overline{B} }_{5k}={B}_{8k}$, ${\overline{B} }_{6k}={B}_{9k}$, ${\overline{B} }_{7k}={B}_{11k}$, and ${\overline{B} }_{8k}={B}_{12k}$.

After solving Eqs. (69), (70), (71), and (72) for ${R}_{0mi}$ and ${S}_{0mk}$, one can compute ${U}_{0m}$, ${V}_{0m}$, and ${W}_{0m}$ from Eq. (65) and finally the displacements u_y (x, y, z, t) and u_z (x, y, z, t) from Eq. (68). For g = h = 0, we find the classical case, which is the same as that given in Appendix B in Beskou et al. [12].

Appendix 3

For n > 0 and m = 0, Eqs. (27), (28), and (29) become

$$ \alpha _{1} U_{{n0}} \left( z \right) + a_{2} U_{{n0}}^{{''}} \left( z \right) + a_{3} U_{{n0}}^{{IV}} \left( z \right) + \alpha _{6} W_{{n0}}^{'} \left( z \right) + a_{7} W_{{n0}}^{{'''}} \left( z \right) = 0, $$

(73)

$$ b_{1} V_{n0} \left( z \right) + b_{2} V_{n0}^{^{\prime\prime}} \left( z \right) + b_{3} V_{n0}^{IV} \left( z \right) = 0, $$

(74)

$$ c_{1} U_{{n0}}^{'} \left( z \right) + c_{2} U_{{n0}}^{{'''}} + c_{5} W_{{n0}} (z) + c_{6} W_{{n0}}^{{''}} \left( z \right) + c_{7} W_{{n0}}^{{IV}} \left( z \right) = 0 $$

(75)

where

$$ \begin{array}{*{20}l} {\alpha_{1} = - (\left( {\lambda + 2\mu } \right)\lambda_{n}^{2} \left( {1 + g^{2} \lambda_{n}^{2} } \right) - \rho \lambda_{n}^{2} V^{2} \left( {1 + h^{2} \lambda_{n}^{2} } \right)}, \hfill \\ {a_{2} = \mu + g^{2} \left( {\lambda + 3\mu } \right)\lambda_{n}^{2} - \rho h^{2} \lambda_{n}^{2} V^{2} }, \hfill \\ {a_{3} = - g^{2} \mu }, \hfill \\ {\alpha_{6} = i\lambda_{n} \left( {\lambda + \mu } \right)\left( {1 + g^{2} \lambda_{n}^{2} } \right)}, \hfill \\ {\alpha_{7} = - ig^{2} \lambda_{n} \left( {\lambda + \mu } \right)} \hfill \\ {b_{2} = \mu + g^{2} \mu \lambda_{n}^{2} + g^{2} \mu \lambda_{n}^{2} - \rho h^{2} \lambda_{n}^{2} V^{2} } \hfill \\ {b_{3} = - g^{2} \mu } \hfill \\ {c_{1} = i\left( {\lambda + \mu } \right)\lambda_{n} \left( {1 + g^{2} \lambda_{n}^{2} } \right)} \hfill \\ {c_{2} = - ig^{2} \left( {\lambda + \mu } \right)\lambda_{n } } \hfill \\ {c_{5} = - \lambda_{n}^{2} (\mu \left( {1 + g^{2} \lambda_{n}^{2} } \right) - \rho h^{2} \lambda_{n}^{2} V^{2} ) + \rho \lambda_{n}^{2} V^{2} } \hfill \\ {c_{6} = \left( {\lambda + 2\mu } \right)\left( {1 + g^{2} \lambda_{n}^{2} } \right) + g^{2} \mu \lambda_{n}^{2} - \rho h^{2} \lambda_{n}^{2} V^{2} ,} \hfill \\ {c_{7} = - g^{2} \left( {\lambda + 2\mu } \right)}. \hfill \\ \end{array} $$

(76)

Solutions of the system of Eqs. (73), (74), and (75) are assumed to be of the form

$$ \begin{array}{*{20}c} {U_{n0} = R_{n0} e^{qz} }, \\ {V_{n0} = S_{n0} e^{qz} }, \\ {W_{n0} = T_{n0} e^{qz} }. \\ \end{array} $$

(77)

Substitution of the above solutions (77) into the system of Eqs. (73), (74), and (75) results in the equation

$$ \left\{ {\begin{array}{*{20}c} {a_{1} + \alpha_{2} q^{2} + \alpha_{3} q^{4} } & 0 & {a_{6} q + a_{7} q^{3} } \\ 0 & { b_{1} + b_{2} q^{2} + b_{3} q^{4} } & 0 \\ {c_{1} q + c_{2} q^{3} } & 0 & {c_{5} + c_{6} q^{2} + c_{7} q^{4} } \\ \end{array} } \right\}\left\{ {\begin{array}{*{20}c} {R_{n0} } \\ {S_{n0} } \\ {T_{n0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right\}, $$

(78)

For nonzero solutions of the system of Eq. (78), the following algebraic equation should be satisfied:

$$ \left( {b_{1} + b_{2} q^{2} + b_{5} q^{4} } \right)\left[ {\left( {c_{5} + c_{6} q^{2} + c_{7} q^{4} } \right)\left( {\alpha_{1} + \alpha_{2} q^{2} + a_{3} q^{4} } \right) - q^{2} \left( {a_{6} + a_{7} q^{2} } \right)\left( {c_{1} + c_{2} q^{2} } \right)} \right] = 0. $$

(79)

Equation (79) is solved for its 12 roots $q_{k} \left( {k = 1,2, \ldots 12} \right).$ Thus, the solutions (77) can take the final form

$$ \begin{array}{*{20}c} {U_{n0 } = \mathop \sum \limits_{k = 1}^{8} R_{n0k} e^{{q_{k} z}} }, \\ {V_{n0 } = S_{n01} e^{{\lambda_{1} z}} + S_{n02} e^{{\lambda_{2} z}} + S_{n03} z + S_{n04} }, \\ {W_{n0 } = \mathop \sum \limits_{k = 1}^{8} T_{n0k} e^{{q_{k} z}} } \\ \end{array} $$

(80)

where $\lambda_{1}$ and $\lambda_{2}$ are the two roots of the equation $b_{5} q^{2} + b_{2} q + b_{1} = 0$, and $R_{n0k} , T_{n0k}$ are the values of $R_{n0}$, and $T_{n0}$ for the $q_{k}$, respectively.

By assuming R_0mk known, one obtains from (80)

$$ \begin{array}{*{20}c} {T_{n0k} = C_{k} R_{n0k} } & {for} & {k = 1,2,..8} & {\left( {k\,is \, not \, a \, summation \, index} \right)} \\ \end{array}, $$

(81)

with

$$ \begin{array}{*{20}c} {C_{k} = \frac{{\left( {a_{1} + a_{2} q_{k}^{2} + a_{3} q_{k}^{4} } \right)}}{{q_{k} \left( {a_{6} + a_{7} q_{k}^{2} } \right)}}} & {{\text{for}}} & {k = 1,2,..8,} \\ \end{array}. $$

(82)

The displacements now take the forms

$$ \begin{array}{*{20}l} \begin{gathered} u_{x} \left( {x,y,z,t} \right) = Re\sum\nolimits_{{m = 1}}^{M} {\left( {\sum\limits_{{k = 1}}^{8} {R_{{n0k}} e^{{qz}} } } \right)e^{{i\mu _{m} y}} \equiv 0}, \hfill \\ u_{y} \left( {x,y,z,t} \right) = Re\mathop \sum \limits_{{n = 1}}^{N} \left( {S_{{n01}} e^{{\lambda _{1} z}} + S_{{n02}} e^{{\lambda _{2} z}} + S_{{n03}} z + S_{{n04}} } \right), \hfill \\ \end{gathered} \hfill \\ {u_{z} \left( {x,y,z,t} \right) = Re\mathop \sum \limits_{{m = 1}}^{M} \left( {\mathop \sum \limits_{{k = 1}}^{8} C_{k} R_{{n0k}} e^{{qz}} } \right)e^{{i\mu _{m} y}} }. \hfill \\ \end{array} $$

(83)

In the above, there are 12 constants (8 ${R}_{n0k}$,  k= 1–8 and 4 ${S}_{noi}$, i = 1–4) to be determined from the 12 boundary conditions. These boundary conditions are given by Eqs. (13), (14), (15), (16), and (17), which after the substitution of the displacements from (83) reduce to the following algebraic system of equations:

$$ \begin{array}{*{20}l} {P_{x} |_{{z = 0}} = \mathop \sum \limits_{{k = 1}}^{8} \overline{{\bar{B}}} _{{1k}} R_{{n0k}} = 0}, \hfill \\ P_{y} |_{{z = 0}} = - i\rho h^{2} \lambda _{n}^{3} V^{2} \left( {S_{{n01}} + S_{{n02}} + S_{{n04}} } \right) \\ + \left[ {\mu \left( {1 + 2g^{2} \lambda _{n}^{2} } \right) - \rho h^{2} \lambda _{n}^{2} V^{2} } \right)\left( {S_{{n01}} \lambda _{1} + S_{{n02}} \lambda _{2} + S_{{n03}} } \right) \\ - g^{2} \mu \left( {S_{{n01}} \lambda _{1}^{3} + S_{{n02}} \lambda _{2}^{3} } \right), \\ {P_{z} |_{{z = 0}} = \mathop \sum \limits_{{k = 1}}^{8} \overline{{\bar{B}}} _{{2k}} R_{{n0k}} = - F_{{n0}} }, \hfill \\ \end{array} $$

(84)

$$ \begin{array}{*{20}c} {R_{x} |_{z = 0} = \mathop \sum \limits_{k = 1}^{8} \overline{{\overline{B}}}_{3k} R_{n0k} = 0}, \\ {R_{y} |_{z = 0} = g^{2} \mu \left( {S_{n01} \lambda_{1}^{2} + S_{n02} \lambda_{2}^{2} } \right)}, \\ {R_{z} |_{z = 0} = \mathop \sum \limits_{k = 1}^{8} \overline{{\overline{B}}}_{4k} R_{n0k} = 0}, \\ \end{array} $$

(85)

$$ \begin{array}{*{20}c} {U_{n0} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{5k} R_{n0k} = 0}, \\ {V_{n0} \left( H \right) = S_{n01} e^{{\lambda_{1} H}} + S_{n02} e^{{\lambda_{2} H}} + S_{n03} H + S_{n04} = 0}, \\ {W_{n0} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{{\overline{B}}}_{6k} R_{n0k} = 0}, \\ \end{array} $$

(86)

$$ \begin{array}{*{20}c} {U_{n0}^{^{\prime}} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{B}_{7k} R_{n0k} = 0}, \\ {V_{n0}^{^{\prime}} \left( H \right) = S_{n01} \lambda_{1} e^{{\lambda_{1} H}} + S_{n02} \lambda_{2} e^{{\lambda_{2} H}} + S_{n03} = 0}, \\ {W_{n0}^{^{\prime}} \left( H \right) = \mathop \sum \limits_{k = 1}^{8} \overline{{\overline{B}}}_{8k} R_{n0k} = 0} \\ \end{array} $$

(87)

where ${\stackrel{-}{\overline{B}} }_{1k}$ – ${\stackrel{-}{\overline{B}} }_{8k}$ can be obtained from Eq. (46) by setting ${\mu }_{m}$=0 and considering that ${\stackrel{-}{\overline{B}} }_{1k}={B}_{1k}$, ${\stackrel{-}{\overline{B}} }_{2k}={B}_{3k}$, ${\stackrel{-}{\overline{B}} }_{3k}={B}_{4k}$, ${\stackrel{-}{\overline{B}} }_{4k}={B}_{6k}$, ${\stackrel{-}{\overline{B}} }_{5k}={B}_{7k}$, ${\stackrel{-}{\overline{B}} }_{6k}={B}_{9k}$, ${\stackrel{-}{\overline{B}} }_{7k}={B}_{10k}$, and ${\stackrel{-}{\overline{B}} }_{8k}={B}_{12k}$.

After solving Eqs. (84), (85), (86), and (87) for ${S}_{noi}$ and ${R}_{n0k}$, one can compute ${U}_{n0}$, ${V}_{n0}$, and ${W}_{n0}$ from Eq. (80) and finally the displacements u_x (x, y, z, t) and u_z (x, y, z, t) from Eq. (83). For g = h = 0, we find the classical case, which is the same as that given in Appendix C in Beskou et al. [12].