Sequentially coupled shape and topology optimization for 2.5D and 3D beam models

Abstract

A sequentially coupled shape and topology optimization framework is presented in which the outer geometry and the internal topological layout of beam-type structures are optimized simultaneously. The outer geometry of the beam-type structures is parametrically described by non-uniform rational B-splines (NURBS), which guarantees a highly accurate description of the structural shape and enable an efficient control of the design domain with only a few control points. The computational efficiency of the coupled optimization approach is assured by applying a gradient-based optimization algorithm, for which the sensitivities are derived in closed form. The formulation of the coupled optimization approach is tailored toward 2.5D and full 3D representations of beam structures used in engineering applications. The 2.5D beam model, which has been taken from the literature, uses standard beam elements to simulate the beam response in the longitudinal direction, whereby the cross-sectional properties of the beam elements are calculated from additional 2D finite element method (FEM) analyses. A comparison study of a cantilever beam problem subjected to pure shape optimization and pure topology optimization illustrates that the 2.5D and 3D beam models lead to similar shape and topology designs, but that the 2.5D beam model has a significantly higher computational efficiency. Specifically, the computational times for the 2.5D model are about a factor 70 (shape optimization) and 1.4 (topology optimization) lower than for the 3D model, which indicates that in the coupled optimization approach the optimization of the shape provides the largest contribution to the higher computational efficiency of the 2.5D model. The coupled shape and topology optimization analysis subsequently performed on the 2.5D cantilever beam model demonstrates that the specific order at which the alternating shape and topology optimization increments are performed in the staggered update procedure turns out to have some influence on the computational speed and the value of the minimal compliance computed. Despite these differences, the final beam structures following from the different staggered update procedures illustrate how shape and topology can be efficiently optimized in an integrated, coupled fashion.

1 Introduction

Beam-type structures are widely used as load-carrying components in the fields of architectural, civil, aerospace and mechanical engineering, among others. Their structural performance can be optimized by minimizing the stresses and displacements generated under the applied loading and boundary conditions, thereby accounting for predefined design constraints on the geometry and the internal material distribution. On the one hand, this requires the application of shape optimization techniques [1, 7, 21, 26], in which the outer shape of the structure is parametrized and optimized using shape design variables, such as the spline curves applied for the geometrical description or the nodal coordinates of the underlying finite element method (FEM) model [15]. On the other hand, topology optimization may be applied to optimally place the material within a given design domain, which, for example, can be accomplished by using the so-called SIMP (Solid Isotropic Material with Penalization) approach [2, 18, 23]. In this method, the relative material density assigned to each finite element can take values between zero (a void) and unity (a solid) and is directly related to the element stiffness by means of a penalization factor. Correspondingly, the optimized material distribution can be found by minimizing the structural compliance within the design domain.

Due to the nature of the SIMP method, however, the optimization of the material distribution is bounded by the specific choice of the design domain. For obtaining more optimized solutions and to develop insight into the effect of the design domain on the topology optimization procedure, it is necessary that the design domain can vary during the process of topology optimization. This can be accomplished by a coupled shape and topology optimization approach. In addition, in the design of aeroelastic beam-type structures, such as wind turbine blades and aircraft wings, the aerodynamic performance (e.g., lift force or energy output) is usually considered to be the most important design objective [14, 17, 22]. Because the optimization of the aerodynamic performance requires a parametrization of the outer shape of the structure, a coupled shape and topology approach offers a useful tool to simultaneously optimize the aerodynamic and structural performances of aeroelastic beam-type structures. Accordingly, in the present communication, a coupled shape and topology optimization formulation is presented for 2.5D and 3D beam models, using the optimization framework recently presented in [30] as a basis. This optimization framework incorporates the shape design variables of the design domain in the SIMP topology optimization method, whereby the interactions between shape and topology variations of the design domain are taken into account through performing the corresponding optimization steps in a sequential manner using a so-called staggered update scheme. The optimization process is performed in a computationally efficient fashion by applying a gradient-based optimization algorithm.

Although shape and topology optimization of beam-type structures can be performed using 3D finite element models, for relatively slender beam-type structures, such as wind turbine blades, it is computationally more economical to use the reduced 2.5D approach proposed by [12], see also [3,4,5,6, 11]. In this approach, standard beam elements are employed to simulate the structural response in the longitudinal direction, whereby the cross-sectional properties of the beam element are calculated from additional 2D FEM analyses. The present communication investigates the applicability and performance of 2.5D beam modeling in the context of coupled shape and topology optimization, by comparing the computational results and efficiency with those obtained from 3D beam models. The geometries of the 2.5D and 3D beam models are parametrically described using non-uniform rational B-splines (NURBS) [19], which guarantees a highly accurate description of the shape boundaries by means of smooth basis functions with compact support and enables an efficient control of the design domain with only a few control points [15, 30]. In the comparison study of the 3D and 2.5D beam models, for simplicity, the loading applied in the boundary value problems considered is taken as independent of the beam outer shape. Nevertheless, it is emphasized that the presented optimization framework allows for a relatively straightforward incorporation of shape-dependent loads and constraints. For example, the proposed optimization method has been recently applied for the aerostructural design of a horizontal-axis wind turbine (HAWT) rotor blade, thereby accounting for the shape-dependent aerodynamic loads and rotor power coefficient [28].

The paper is organized as follows. Section 2 discusses the parametrization of the geometry design model by means of NURBS, thereby distinguishing between 1D curves, 2D surfaces and 3D solids. In Sect. 3, the structural analysis of 3D and 2.5D beam models is reviewed. The FEM formulations presented in this section are used as input for the derivation of the coupled shape and topology framework provided in Sects. 4 and 5, whereby Sect. 4 gives the general formulation and Sect. 5 presents the parameter sensitivities defining the gradient-based optimization algorithm. Subsequently, in Sect. 6, the optimization framework is applied in a comparison study of a cantilever beam problem modeled by 2.5D beam elements and 3D beam elements. Finally, Sect. 7 provides the main conclusions of the study.

2 Geometry design model

During the optimization procedure, an efficient control of the outer shape of the structure is enabled by using NURBS. Detailed information on the theory of NURBS can be found in [19]. In the present section, the formulation of the NURBS curves, surfaces, and solids is provided in matrix form for 1D, 2D and 3D design models, respectively, which will be subsequently used in Sect. 5 as input for the analytical derivation of the shape sensitivities.

2.1 NURBS curve

A NURBS curve is a piecewise polynomial curve composed of B-spline basis functions. The definition of such a basis function is based on a set of non-decreasing real numbers in a parametric space, defined by a so-called knot vector

$$\begin{aligned} \varvec{Z}=\left[\zeta _1, \zeta _2,...,\zeta _{l+r+1}\right]^{\text {T}} \qquad \text {with} \qquad \zeta _{k} \in {\mathbb {R}}, \end{aligned}$$

(1)

where each real number $\zeta _{k}$ reflects a knot with k being the knot index, l is the number of basis functions that comprises the B-spline, and r is the polynomial order of the B-spline. With the knot index k running from 1 to l, the B-spline basis functions $L_{k,r}$ are defined recursively for an arbitrary value of $\zeta$, i.e.,

$$\begin{aligned} \begin{array}{lcl} \vspace{1mm} \text {for} \quad r=0 : \quad L_{k,0}\left( \zeta \right) = {\left\{ \begin{array}{ll} 1&{} \text {if} \quad \zeta _k\le \zeta < \zeta _{k+1}, \\ 0&{} \text {otherwise}, \end{array}\right. } \\ \begin{aligned} \text {for} \quad r \ge 1 : \quad L_{k,r}\left( \zeta \right) = &{}\frac{\zeta -\zeta _k}{\zeta _{k+r}-\zeta _k} L_{k,r-1}\left( \zeta \right) + \frac{\zeta _{k+r+1}-\zeta }{\zeta _{k+r+1}-\zeta _{k+1}} L_{k+1,r-1} \left( \zeta \right) , \end{aligned} \end{array} \end{aligned}$$

(2)

and can be conveniently stored in a vector as

$$\begin{aligned} \mathbf{L} _{\text{b}}=\left[ L_{1,r}\left( \zeta \right) , L_{2,r}\left( \zeta \right) , \ldots , L_{l,r}\left( \zeta \right) \right] ^{\text {T}} . \end{aligned}$$

(3)

The so-called control points define the geometry of the structure, and their locations during the optimization procedure may change. Together with the corresponding weights, the control points are stored in a matrix as

$$\begin{aligned} \mathbf{P} ^{\text {1D}}_C= \left[ \begin{array}{cccc} \omega _{1} C_{1}&\omega _{2} C_{2}&\cdots&\omega _{l} C_{l} \end{array} \right] ^{\text {T}}, \end{aligned}$$

(4)

where $C_k \in \{X_{k}, Y_{k}, Z_{k} \}$, in which $X_{k}$, $Y_{k}$, $Z_{k}$ with $k=1,2,\ldots ,l$, are the x-, y- and z-coordinates of the control points and $\omega _{k}$ is the corresponding weight. Accordingly, the coordinates of an arbitrary point $\mathbf{p} =[x,y,z]^T$ of the NURBS curve are determined by

$$\begin{aligned} \mathbf{p } = \left[ \frac{\mathbf{L }_{\text{b}}^{\text {T}} \mathbf{p }^{\text {1D}}_X }{\mathbf{L }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {1D}}} , \frac{\mathbf{L }_{\text{b}}^{\text {T}} \mathbf{p }^{\text {1D}}_Y }{\mathbf{L }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {1D}}} , \frac{\mathbf{L }_{\text{b}}^{\text {T}} \mathbf{P }^{\text {1D}}_Z }{\mathbf{L }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {1D}}} \right] ^{\text {T}} , \end{aligned}$$

(5)

with the weights of the control points assembled as

$$\begin{aligned} \varvec{\varOmega }^{\text {1D}}=\left[ \omega _{1}, \omega _{2}, \ldots , \omega _{l} \right] ^{\text {T}} . \end{aligned}$$

(6)

2.2 NURBS surface

In order to construct a NURBS surface in a 2D parametric domain, the coordinates characterizing the basis functions are stored in two knot vectors, i.e.,

$$\begin{aligned} \varvec{\varXi }=[\xi _1, \xi _2,...,\xi _{n+p+1}]^{\text {T}} , \, \, \varvec{H}=[\eta _1, \eta _2,...,\eta _{m+q+1}]^{\text {T}} \, \qquad \text{ with } \qquad \xi _i, \eta _{j} \in \mathbb {R} , \end{aligned}$$

(7)

where i, j are the knot indexes, n, m are the number of basis functions and p, q are the polynomial orders. The basis functions $N_{i,p}$ and $M_{j,q}$ in the $\xi$- and $\eta$-directions can be obtained in a similar fashion as shown in Eq. (2). These basis functions are stored in the vectors $\mathbf{N} _{\text{b}}$ and $\mathbf{M} _{\text{b}}$ as

$$\begin{aligned} \mathbf{N} _{\text{b}}=\left[ N_{1,p}\left( \xi \right) , N_{2,p}\left( \xi \right) , \ldots , N_{n,p}\left( \xi \right) \right] ^{\text {T}} , \end{aligned}$$

(8)

and

$$\begin{aligned} \mathbf{M} _{\text{b}}=\left[ M_{1,q}\left( \eta \right) , M_{2,q}\left( \eta \right) , \ldots , M_{m,q}\left( \eta \right) \right] ^{\text {T}} . \end{aligned}$$

(9)

For generality, the 2D net of control points defining a NURBS surface is obtained here from the 3D grid of control points describing a NURBS solid. This is done by selecting a single layer of control points from the grid of control points describing the NURBS solid. Accordingly, by considering the directions of the knot vectors $\varvec{\varXi }$, $\varvec{H}$ and $\varvec{Z}$ in the parametric domain to correspond to the x-, y- and z-directions in the physical domain, the net of control points becomes

$$\begin{aligned} \begin{aligned} \mathbf{P} ^{\text {2D}}_{k,C}=&\left[ \begin{array}{cccc} \omega _{1,1,k} C_{1,1,k} &{}\quad \omega _{1,2,k} C_{1,2,k} &{}\quad\cdots &\quad{} \omega _{1,m,k} C_{1,m,k} \\ \omega _{2,1,k} C_{2,1,k} &\quad{} \omega _{2,2,k} C_{2,2,k} &\quad{}\cdots &\quad{} \omega _{2,m,k} C_{2,m,k}\\ \vdots &\quad{} \vdots &\quad{}\ddots &{}\quad\vdots \\ \omega _{n,1,k} C_{n,1,k} &\quad{} \omega _{n,2,k} C_{n,2,k} &\quad{}\cdots &\quad{} \omega _{n,m,k} C_{n,m,k} \end{array} \right], \end{aligned} \end{aligned}$$

(10)

with $C_{i,j,k} \in \{ X_{i,j,k},Y_{i,j,k},Z_{i,j,k} \}$, where $X_{i,j,k}$, $Y_{i,j,k}$ and $Z_{i,j,k}$ represent the x-, y- and z-coordinates of the control points, respectively. Here, the first two indices vary as $i=1,2,\ldots ,n$, $j=1,2,\ldots ,m$, while k is kept fixed as it refers to a specific layer of the 3D grid of control points. The resulting NURBS surface is defined by the tensor product of the 2D net of control points and the basis functions $\mathbf{N} _{\text{b}}$ and $\mathbf{M} _{\text{b}}$. As such, an arbitrary point $\mathbf{p}$ of the NURBS surface can be calculated as

$$\begin{aligned} \mathbf{p }=\left[ \frac{\mathbf{N }_{\text{b}}^{\text {T}} \mathbf{P }^{\text {2D}}_{k,X} \mathbf{M }_{\text{b}}}{\mathbf{N }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_k \mathbf{M }_{\text{b}}}, \frac{\mathbf{N }_{\text{b}}^{\text {T}} \mathbf{P }^{\text {2D}}_{k,Y} \mathbf{M }_{\text{b}}}{\mathbf{N }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_k \mathbf{M }_{\text{b}}}, \frac{\mathbf{N }_{\text{b}}^{\text {T}} \mathbf{P }^{\text {2D}}_{k,Z} \mathbf{M }_{\text{b}}}{\mathbf{N }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_k \mathbf{M }_{\text{b}}} \right] ^{\text {T}}, \end{aligned}$$

(11)

with the weights of the control points as

$$\begin{aligned} \varvec{\varOmega }^{\text {2D}}_k=\left[ \begin{array}{cccc} \omega _{1,1,k}&\quad{} \omega _{1,2,k} &\quad{}\cdots &\quad{}\omega _{1,m,k}\\ \omega _{2,1,k}&\quad{} \omega _{2,2,k} &\quad{}\cdots &\quad{}\omega _{2,m,k}\\ \vdots &\quad{} \vdots &\quad{}\ddots &\quad{}\vdots \\ \omega _{n,1,k}&\quad{} \omega _{n,2,k} &\quad{}\cdots &\quad{}\omega _{n,m,k} \end{array} \right] , \end{aligned}$$

(12)

where $k \in \{1,2,\ldots ,l \}$, and $\mathbf{P} ^{\text {2D}}_{k,C}$ follows from Eq. (10).

2.3 NURBS solid

Although a NURBS solid can be defined in a similar fashion as the NURBS curve and surface, it is relatively straightforward to formulate the NURBS solid by applying projections of NURBS surfaces. Using the 2D control net, Eq. (10), and the NURBS surface basis functions $\mathbf{N} _{\text{b}}$ and $\mathbf{M} _{\text{b}}$ given by Eqs. (8) and (9), a matrix $\mathbf{R} ^{\text {3D}}_C$ can be constructed as

$$\begin{aligned} \mathbf{R} ^{\text {3D}}_C= \left[ \mathbf{N} _{\text{b}}^{\text {T}} \mathbf{P} ^{\text {2D}}_{1,C} \mathbf{M} _{\text{b}}, \mathbf{N} _{\text{b}}^{\text {T}} \mathbf{P} ^{\text {2D}}_{2,C} \mathbf{M} _{\text{b}}, \ldots , \mathbf{N} _{\text{b}}^{\text {T}} \mathbf{P} ^{\text {2D}}_{l,C} \mathbf{M} _{\text{b}} \right] ^{\text {T}}, \end{aligned}$$

(13)

where $C \in \{X, Y, Z \}$ represents the x-, y- and z-coordinates of the control points. With Eq. (13), an arbitrary point $\mathbf{p}$ of the NURBS solid is described by

$$\begin{aligned} \mathbf{p} =\left[ \frac{ \mathbf{L} _{\text{b}}^{\text {T}} \mathbf{R} ^{\text {3D}}_{X} }{ \mathbf{L} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {3D}} }, \frac{ \mathbf{L} _{\text{b}}^{\text {T}} \mathbf{R} ^{\text {3D}}_{Y} }{ \mathbf{L} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {3D}} }, \frac{ \mathbf{L} _{\text{b}}^{\text {T}} \mathbf{R} ^{\text {3D}}_{Z} }{ \mathbf{L} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {3D}} } \right] ^{\text {T}}, \end{aligned}$$

(14)

with

$$\begin{aligned} \varvec{\varOmega }^{\text {3D}}= \left[ \mathbf{N} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_1 \mathbf{M} _{\text{b}}, \mathbf{N} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_2 \mathbf{M} _{\text{b}}, \ldots , \mathbf{N} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_l \mathbf{M} _{\text{b}} \right] ^{\text {T}}, \end{aligned}$$

(15)

where $\varvec{\varOmega }^{\text {2D}}_k$ (with $k=1,2,\ldots ,l$) is defined by Eq. (12), and $\mathbf{N} _{\text{b}}^{\text {T}}$, $\mathbf{M} _{\text{b}}^{\text {T}}$ and $\mathbf{L} _{\text{b}}^{\text {T}}$ are the basis functions in the three directions of the NURBS solid.

3 Structural analysis model

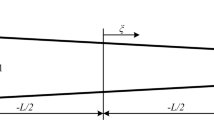
Consider the 3D beam-type structure shown in Fig. 1a, which will be used for demonstrating specific features of the shape and topology optimization procedure. The beam is modeled by means of the FEM, whereby two types of element discretization are adopted, namely (i) a discretization by 3D continuum elements, see Fig. 1b, and (ii) a discretization by 1D beam elements in the longitudinal direction of the beam, combined with additional 2D continuum elements for a detailed modeling of the cross-sectional properties of a beam element, see Fig. 1c. For brevity, in the following these two types of discretization will be denoted as the “3D beam model” and the “2.5D beam model”, respectively.

Fig. 1

A slender beam structure (a), modeled as a 3D configuration (b) and a 2.5D configuration (c)

The finite element discretizations for the 3D and 2.5D beam models are obtained by projecting a fixed, auxiliary mesh, defined in the parametric domain, onto the actual mesh in the physical domain, using Eqs. (5), (11), and (14) for 1D, 2D and 3D finite elements. This projection is schematically illustrated in Fig. 2, and enables obtaining an explicit relationship between the structural response of the beam structure and the parameters that control the geometry, i.e., the NURBS control points. Accordingly, analytical expressions can be derived for the parameter sensitivities governing the structural shape optimization, which will be presented in Sect. 5.

Fig. 2

Parameterization of the physical design domain via a coordinate projection from the parametric domain. The solid lines in the parametric domain define a fixed auxiliary mesh, which is projected by means of NURBS functions onto the actual finite element mesh that discretizes the physical design domain

3.1 3D beam model

Given the knot vectors, the control points with their weights, and a fixed auxiliary mesh in the parametric domain, the discretization of the 3D finite element model is carried out by projecting the nodal coordinates $(\xi _n,\eta _n,\zeta _n)$ of the fixed, auxiliary mesh onto the nodal coordinates $(x_n,y_n,z_n)$ of the actual mesh in the physical domain, in correspondence with Eq. (14). Hence, for each isoparametric element e, its nodal coordinates can be cast into a vector:

$$\begin{aligned} \bar{\mathbf{p }}_e=[\mathbf{p} _1^{\text {T}},\mathbf{p} _2^{\text {T}},\ldots ,\mathbf{p} _{n_e}^{\text {T}}]^{\text {T}}, \end{aligned}$$

(16)

where the coordinates $\mathbf{p} _n$ of node n, with $n=1,2,\ldots ,n_e$, are obtained from Eq. (14), with $n_e$ the total number of nodes of element e. The location of an arbitrary point $\hat{\mathbf{p }}_e=[x,y,z]^{\text {T}}$ within the finite element e can be obtained from an interpolation of the coordinates of the element nodes $\bar{\mathbf{p }}_e$ as:

$$\begin{aligned} \hat{\mathbf{p }}_e=\mathbf{N} _e \bar{\mathbf{p }}_e, \end{aligned}$$

(17)

with

$$\begin{aligned} \mathbf{N} _e=[N_1 \mathbf{I} _d \,\, N_2 \mathbf{I} _d \,\, \ldots \,\, N_{n_e} \mathbf{I} _d] , \end{aligned}$$

(18)

where $N_n$, with $n=1,2,\ldots ,n_e$, are the polynomial interpolation functions of the element, and $\mathbf{I} _d$ represents the $d \times d$ identity matrix, with d the number of degrees of freedom of the element node. By introducing the gradient operator $\varvec{\partial }=[{\partial }/{\partial \xi _e},{\partial }/ {\partial \eta _e},{\partial }/{\partial \zeta _e}]^{\text {T}}$, the Jacobian matrix of element e follows as

$$\begin{aligned} \mathbf{J} _e= \varvec{\partial } \hat{\mathbf{p }}_e^{\text {T}} . \end{aligned}$$

(19)

Inserting Eq. (17) into Eq. (19), the Jacobian matrix $\mathbf{J} _e$ can be directly expressed in terms of the nodal coordinates $\bar{\mathbf{p }}_e$, i.e.,

$$\begin{aligned} \mathbf{J} _e= \bar{\mathbf{P }}_e \left( \varvec{\partial } \mathbf{N} _e^{\text {T}} \right) , \end{aligned}$$

(20)

with

$$\begin{aligned} \bar{\mathbf{P }}_e=\left[ \begin{array}{ccc} \bar{\mathbf{p }}_e^{\text {T}} &{} \quad \mathbf{0} &{}\quad \mathbf{0} \\ \mathbf{0} &{} \quad \bar{\mathbf{p }}_e^{\text {T}} &{}\quad \mathbf{0} \\ \mathbf{0} &{} \quad \mathbf{0} &{}\quad \bar{\mathbf{p }}_e^{\text {T}} \end{array} \right] , \end{aligned}$$

(21)

where $\bar{\mathbf{p }}_e$ is given by Eq. (16). When denoting the displacement vector for an arbitrary point of the structure as $\mathbf{s} =[s_x,s_y,s_z ]^{\text {T}}$, the corresponding strain vector $\varvec{\epsilon }=[ \epsilon _{xx}, \epsilon _{yy}, 2\epsilon _{xy}, 2\epsilon _{xz}, 2\epsilon _{yz}, \epsilon _{zz} ]^{\text {T}}$ can be calculated as $\varvec{\epsilon }=\mathbf{B} \mathbf{s}$, with the matrix $\mathbf{B}$ given by:

$$\begin{aligned} \mathbf{B} = \left[ \begin{array}{cccccc} \partial / \partial x &{} 0 &{} \partial / \partial y &{} \partial / \partial z &{} 0 &{}0 \\ 0 &{} \partial / \partial y &{} \partial / \partial x &{} 0 &{} \partial / \partial z &{}0 \\ 0 &{} 0 &{}0 &{}\partial / \partial x &{} \partial / \partial y &{}\partial / \partial z \end{array} \right] ^{\text {T}} . \end{aligned}$$

(22)

At the element level, the matrix $\mathbf{B} _e$ can be expressed as [5]

$$\begin{aligned} \mathbf{B} _e=\mathbf{B} _e^1 \frac{\partial }{\partial \xi _e} + \mathbf{B} _e^2 \frac{\partial }{\partial \eta _e} + \mathbf{B} _e^3 \frac{\partial }{\partial \zeta _e} , \end{aligned}$$

(23)

with

$$\begin{aligned} \mathbf{B} _e^c=\left[ \begin{array}{ccc} (\mathbf{J} _e^{-1})_{1c} &{} 0 &{} 0\\ 0 &{} (\mathbf{J} _e^{-1})_{2c} &{} 0\\ (\mathbf{J} _e^{-1})_{2c} &{} (\mathbf{J} _e^{-1})_{1c} &{} 0\\ (\mathbf{J} _e^{-1})_{3c} &{} 0 &{} (\mathbf{J} _e^{-1})_{1c}\\ 0 &{} (\mathbf{J} _e^{-1})_{3c} &{} (\mathbf{J} _e^{-1})_{2c}\\ 0 &{} 0 &{} (\mathbf{J} _e^{-1})_{3c} \end{array} \right] \quad \text {with} \quad c \in \{ 1,2,3 \} , \end{aligned}$$

(24)

where the index c refers to the column of the inverse of the Jacobian matrix, Eq. (20). Using Eqs. (16) to (24), the stiffness matrix $\mathbf{k} _e$ of the isoparametric 3D element is computed as

$$\begin{aligned} \mathbf{k} _e= \int _{-1}^1 \int _{-1}^1 \int _{-1}^1 \left( \mathbf{B} _e \mathbf{N} _e \right) ^{\text {T}} \mathbf{Q} _e \mathbf{B} _e \mathbf{N} _e |\mathbf{J} _e| \mathrm{d}\xi _e \mathrm{d}\eta _e \mathrm{d}\zeta _e \, , \end{aligned}$$

(25)

with $|\mathbf{J} _e|$ the determinant of the Jacobian matrix $\mathbf{J} _e$. Here, the $6 \times 6$ matrix $\mathbf{Q} _e$ incorporates the constitutive properties of the element. In accordance with the SIMP approach used for topology optimization, the stiffness matrix is scaled by the relative density of the element via a power-law expression [2, 18, 23]

$$\begin{aligned} \mathbf{Q} _e=({\rho }_e)^p \mathbf{Q} , \end{aligned}$$

(26)

where $\rho _e$ is the relative density of element e, p is a penalization factor with a typical value of 3 [2] that is also adopted in the present work, and $\mathbf{Q}$ represents the constitutive behavior in a material point—taken here as linear-elastic—in accordance with $\varvec{\sigma }=\mathbf{Q} \varvec{\epsilon }$, with the stress given by $\varvec{\sigma }=[ \sigma _{xx}, \sigma _{yy}, \sigma _{xy}, \sigma _{xz}, \sigma _{yz}, \sigma _{zz} ]^{\text {T}}$. Finally, the global stiffness matrix $\mathbf{K}$ is found by assembling the element stiffness matrices:

$$\begin{aligned} \mathbf{K} =\sum _{e=1}^{N} \mathbf{k} _e , \end{aligned}$$

(27)

with N the total number of elements and the sum operator representing the assembly procedure typically used in the finite element method. The global displacement vector $\mathbf{u}$ is obtained by solving the system of equilibrium equations

$$\begin{aligned} \mathbf{K} \mathbf{u} = \mathbf{f} , \end{aligned}$$

(28)

where $\mathbf{f}$ is the global force vector.

3.2 2.5D beam model

For the 2.5D beam model, standard 1D beam elements are used to discretize the beam in the longitudinal direction, while the cross-sectional properties of the beam elements are calculated from additional 2D FEM analyses. In this section, the 2.5D FEM approach originally presented in [12] is reviewed, see also [3,4,5,6, 11] for more details; these expressions serve as input for the computation of the shape and topology sensitivities used in the gradient-based optimization algorithm, see Sect. 5.

3.2.1 Beam finite element model

In the beam FEM model, the deformations are described by translations $\varvec{\chi }=[ \chi _x, \chi _y, \chi _z ]^{\text {T}}$ and rotations $\varvec{\varphi }=[ \varphi _x, \varphi _y, \varphi _z ]^{\text {T}}$ of a cross-sectional reference point. These deformations are grouped into a single vector as $\mathbf{r} =[ \varvec{\chi }^{\text {T}}, \varvec{\varphi }^{\text {T}} ]^{\text {T}}$. In addition, the shear strains in the x- and y-directions and the normal strain in the z-direction are assembled as $\varvec{\tau }=[ \tau _x, \tau _y, \tau _z ]^{\text {T}}$, and the curvatures about the three directions are given by $\varvec{\kappa }=[ \kappa _x, \kappa _y, \kappa _z ]^{\text {T}}$. The above two deformation measures can be assembled into a single vector as $\varvec{\psi }=[ \varvec{\tau }^{\text {T}}, \varvec{\kappa }^{\text {T}} ]^{\text {T}}$. Accordingly, the strain-displacement relation becomes $\varvec{\psi }=\bar{\mathbf{B }} \mathbf{r}$, with the operator $\bar{\mathbf{B }}$ given by

$$\begin{aligned} \bar{\mathbf{B }}=\mathbf{T} _r + \mathbf{I} _6 \frac{\partial }{\partial z} , \end{aligned}$$

(29)

with

$$\begin{aligned} \begin{aligned} \mathbf{T} _{r}=&\left[ \begin{array}{cc} \mathbf{0} _3 &\quad{} \mathbf{t} _r \\ \mathbf{0} _3 &\quad{} \mathbf{0} _3 \\ \end{array} \right] \end{aligned} \begin{aligned} \quad \text {and} \quad \mathbf{t} _r=&\left[ \begin{array}{ccc} 0 &\quad{} -1 &\quad{} 0\\ 1 &\quad{} 0 &\quad{} 0\\ 0 &\quad{} 0 &\quad{} 0\\ \end{array} \right] \end{aligned} . \end{aligned}$$

(30)

Further, $\mathbf{I} _6$ is the $6\times 6$ identity matrix, $\mathbf{0} _3$ is the $3 \times 3$ matrix null matrix, and the z-direction corresponds to the longitudinal direction of the beam, see Fig. 1.

From the strains and curvatures, the normal force and shear forces $\mathbf{T} =[ T_x, T_y, T_z ]^{\text {T}}$ and bending moment and torsional moments $\mathbf{M} =[ M_x, M_y, M_z ]^{\text {T}}$ can be determined as follows:

$$\begin{aligned} \varvec{\theta }=\mathbf{K} ^{\text {s}} \varvec{\psi } , \end{aligned}$$

(31)

with $\varvec{\theta }=[ \mathbf{T} ^{\text {T}}, \mathbf{M} ^{\text {T}} ]^{\text {T}}$ and $\mathbf{K} ^{\text {s}}$ representing the stiffness matrix of the beam cross section.

Analogous to Eq.(28) for a 3D beam model, the equilibrium equations for a 2.5D beam model are defined by

$$\begin{aligned} \bar{\mathbf{K }} \bar{\mathbf{u }} = \mathbf{f}, \end{aligned}$$

(32)

with

$$\begin{aligned} \bar{\mathbf{K }} = \sum _{e=1}^{N} \mathbf{k} _e^{\text {b}}, \end{aligned}$$

(33)

where the stiffness $\mathbf{k} _e^{\text {b}},$ of the 1D beam element is computed as

$$\begin{aligned} \mathbf{k} _e^{\text {b}} = \int _{-1}^1 \left( \bar{\mathbf{B }}_e \mathbf{N} _e \right) ^{\text {T}} \mathbf{K} ^{\text {s}}_e \bar{\mathbf{B }}_e \mathbf{N} _e |\bar{\mathbf{J }}_e| \mathrm{d}\zeta _e . \end{aligned}$$

(34)

Here, $\bar{\mathbf{K }}$ is the global stiffness matrix, $\bar{\mathbf{u }}$ contains the nodal displacements and rotations of the beam, $\mathbf{N} _e$ includes the interpolation functions for the beam displacements and rotations, the operator $\mathbf{B} _e$ for each element e is given by Eq. (29), and $|\bar{\mathbf{J }}_e|$ represents the determinant of the Jacobian matrix, with $\bar{\mathbf{J }}_e$ expressed as

$$\begin{aligned} \bar{\mathbf{J }}_e= \left[ \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {\partial z }/{\partial \zeta _e} \end{array} \right] , \end{aligned}$$

(35)

where $\partial z/\partial \zeta _e$ is calculated from Eq. (17) using the beam interpolation functions. The derivation of the cross-sectional stiffness matrix $\mathbf{K} ^{\text {s}}_e$ of the beam element, which appears in Eq. (34), is discussed in Sect. 3.2.2 below.

3.2.2 Cross-sectional stiffness

The displacements $\mathbf{s}$ of an arbitrary point of the beam cross section can be expressed in terms of the rigid-body displacements and rotations $\mathbf{r}$ of the cross-sectional reference point, complemented by the in-plane and out-of-plane warping displacements $\mathbf{s} ^{\text {w}}$ associated with the deformation of the cross section, i.e.,

$$\begin{aligned} \mathbf{s} =\mathbf{Z} \mathbf{r} + \mathbf{s} ^{\text {w}} , \end{aligned}$$

(36)

with

$$\begin{aligned} \mathbf{Z} = \left[ \begin{array}{cccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad z &{}\quad -y \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad -z &{}\quad 0 &{}\quad x \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad y &{}\quad -x &{}\quad 0 \end{array} \right] , \end{aligned}$$

(37)

where x, y, and z are the coordinates of the specific location in the cross section, with x and y defined with respect to the location of the cross-sectional reference point. Using a FEM model for the cross section, the warping displacements $\mathbf{s} ^{\text {w}}$ are discretized as

$$\begin{aligned} \mathbf{s} ^{\text {w}}=\mathbf{N} \hat{\mathbf{u }} , \end{aligned}$$

(38)

where $\mathbf{N}$ contains the interpolation functions of the cross-sectional finite element and $\hat{\mathbf{u }}$ represents the vector with the nodal warping displacements of the element. As will be shown below, it is convenient to isolate the partial derivative terms $\partial / \partial z$ in the strain-displacement relation, which is done by combining $\varvec{\epsilon }=\mathbf{B} \mathbf{s}$ with Eq. (22), resulting in

$$\begin{aligned} \varvec{\epsilon }=\hat{\mathbf{B }} \mathbf{s} + \mathbf{S} \frac{\partial \mathbf{s} }{\partial z} , \end{aligned}$$

(39)

with

$$\begin{aligned} \hat{\mathbf{B }}= \left[ \begin{array}{cccccc} \partial / \partial x &{} 0 &{} \partial / \partial y &{} 0 &{} 0 &{}0 \\ 0 &{} \partial / \partial y &{} \partial / \partial x &{} 0 &{} 0 &{}0 \\ 0 &{} 0 &{}0 &{}\partial / \partial x &{} \partial / \partial y &{}0 \end{array} \right] ^{\text {T}} , \end{aligned}$$

(40)

and

$$\begin{aligned} \mathbf{S} = \left[ \begin{array}{cccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \end{array} \right] ^{\text {T}} . \end{aligned}$$

(41)

Substituting Eq. (38) into Eq. (36), and inserting the result into Eq. (39) leads to

$$\begin{aligned} \varvec{\epsilon }=\mathbf{S} \mathbf{Z} \left( \mathbf{T} _r + \mathbf{I} _6 \frac{\partial }{\partial z} \right) \mathbf{r} +\hat{\mathbf{B }} \mathbf{N} \hat{\mathbf{u }} + \mathbf{S} \mathbf{N} \frac{\partial \hat{\mathbf{u }}}{\partial z} , \end{aligned}$$

(42)

which uses the relation [5]

$$\begin{aligned} \hat{\mathbf{B }} \mathbf{Z} = \mathbf{S} \mathbf{Z} \mathbf{T} _r \, , \end{aligned}$$

(43)

with $\mathbf{T} _r$ given by Eq. (30). Invoking the kinematic relation $\varvec{\psi }=\bar{\mathbf{B }} \mathbf{r}$ with $\bar{\mathbf{B }}$ given by Eqs. (29), (42) finally turns into

$$\begin{aligned} \varvec{\epsilon }=\mathbf{S} \mathbf{Z} \varvec{\psi } + \hat{\mathbf{B }} \mathbf{N} \hat{\mathbf{u }} + \mathbf{S} \mathbf{N} \frac{\partial \hat{\mathbf{u }}}{\partial z} . \end{aligned}$$

(44)

As a next step, the equilibrium equations for the beam cross section need to be formulated. In accordance with the variational framework presented in [3,4,5,6], equilibrium is described in terms of $\hat{\mathbf{u }}$, $\varvec{\psi }$ and $\varvec{\theta }$ by the following set of partial differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \vspace{2mm} \mathbf{M} \displaystyle { \frac{\partial ^2 \hat{\mathbf{u }}}{\partial z^2} } + \left( \mathbf{C} -\mathbf{C} ^{\text {T}} \right) \displaystyle { \frac{\partial \hat{\mathbf{u }}}{\partial z} } + \mathbf{L} \displaystyle { \frac{\partial \varvec{\psi }}{\partial z} } - \mathbf{E} \hat{\mathbf{u }}-\mathbf{R} \varvec{\psi }=\mathbf{0} ,\\ \vspace{2mm} \mathbf{L} ^{\text {T}} \displaystyle { \frac{\partial \hat{\mathbf{u }}}{\partial z} } + \mathbf{R} ^{\text {T}}\hat{\mathbf{u }}+\mathbf{A} \varvec{\psi }=\varvec{\theta } ,\\ \vspace{2mm} \displaystyle { \frac{\partial \varvec{\theta }}{\partial z} } =\mathbf{T} _r^{\text {T}} \varvec{\theta } , \end{array}\right. } \end{aligned}$$

(45)

with

$$\begin{aligned} \begin{aligned}&\mathbf{A} =\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left( \mathbf{S} _e \mathbf{Z} _e \right) ^{\text {T}} \mathbf{Q} _e \mathbf{S} _e \mathbf{Z} _e |\hat{\mathbf{J }}_e| \mathrm{d}\xi _e \mathrm{d}\eta _e ,&\mathbf{R} =\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left( \hat{\mathbf{B }}_e \mathbf{N} _e\right) ^{\text {T}} \mathbf{Q} _e \mathbf{S} _e \mathbf{Z} _e |\hat{\mathbf{J }}_e| \mathrm{d}\xi _e \mathrm{d}\eta _e , \\&\mathbf{E} =\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left( \hat{\mathbf{B }}_e \mathbf{N} _e \right) ^{\text {T}} \mathbf{Q} _e \hat{\mathbf{B }}_e \mathbf{N} _e |\hat{\mathbf{J }}_e| \mathrm{d}\xi _e \mathrm{d}\eta _e ,&\mathbf{C} =\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left( \mathbf{S} _e \mathbf{N} _e\right) ^{\text {T}} \mathbf{Q} _e \hat{\mathbf{B }}_e \mathbf{N} _e |\hat{\mathbf{J }}_e| \mathrm{d}\xi _e \mathrm{d}\eta _e , \\&\mathbf{L} =\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left( \mathbf{S} _e \mathbf{N} _e\right) ^{\text {T}} \mathbf{Q} _e \mathbf{S} _e \mathbf{Z} _e |\hat{\mathbf{J }}_e| \mathrm{d}\xi _e \mathrm{d}\eta _e ,&\mathbf{M} =\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left( \mathbf{S} _e \mathbf{N} _e\right) ^{\text {T}} \mathbf{Q} _e \mathbf{S} _e \mathbf{N} _e |\hat{\mathbf{J }}_e| \mathrm{d}\xi _e \mathrm{d}\eta _e . \end{aligned} \end{aligned}$$

(46)

Note that the generalized loads $\varvec{\theta }$ given by Eq. (31) are related to the stress components by $\varvec{\theta }= \int _A \mathbf{Z} ^{\text {T}} \varvec{\sigma }_b \mathrm{d}A$, with $\mathbf{Z}$ given by Eq. (37) and the stress $\varvec{\sigma }_b$ presented by $\varvec{\sigma }_b=[\sigma _{xz},\sigma _{yz},\sigma _{zz}]^{\text {T}}$. Further, the matrices $\mathbf{A}$, $\mathbf{R}$, $\mathbf{E}$, $\mathbf{C}$, $\mathbf{L}$ and $\mathbf{M}$ presented by Eq. (46) are determined from the FEM model at cross-sectional level. In Eq. (46), the matrix $\mathbf{Z} _e$ is obtained from Eq. (37), whereby the x- and y-coordinates within a cross-sectional element are calculated from combining the element interpolation functions with the nodal coordinates of the element. The nodal coordinates of an arbitrary cross-sectional finite element e are computed via Eq. (16), where $\mathbf{p} _n$ represents the nodal coordinates determined from Eq. (11), with the z-coordinate of the control points $Z_{i,j,k}$ in Eq. (10) set to zero. Furthermore, the matrix $\mathbf{S} _e$ is computed from Eq. (41), and $\mathbf{Q} _e$ follows from Eq. (26), in which $\rho _e$ refers to the relative material density in finite element e, and $|\hat{\mathbf{J }}_e|$ is the determinant of the Jacobian matrix of the element. The Jacobian matrix has the usual form

$$\begin{aligned} \hat{\mathbf{J }}_e= \left[ \begin{array}{ccc} {\partial x}/{\partial \xi _e} &{} {\partial y}/{\partial \xi _e} &{}0 \\ {\partial x}/{\partial \eta _e} &{} {\partial y}/{\partial \eta _e} &{}0 \\ 0 &{} 0 &{}1 \end{array} \right] , \end{aligned}$$

(47)

which, by invoking Eqs. (10), (11), (16), (17), (18) and (19), can be expressed as a function of the element nodal coordinates (and thus as function of the NURBS control points):

$$\begin{aligned} \hat{\mathbf{J }}_e= \varvec{\hat{\partial }} \hat{\mathbf{p }}^{\text {T}}+\hat{\mathbf{J }}_\zeta =\bar{\mathbf{P }}_e \left( \varvec{\hat{\partial }} \mathbf{N} _e^{\text {T}} \right) +\hat{\mathbf{J }}_\zeta \quad \text {with} \quad \hat{\mathbf{J }}_\zeta =\left[ \begin{array}{ccc} 0 &{} 0 &{}0 \\ 0 &{} 0 &{}0 \\ 0 &{} 0 &{}1 \\ \end{array} \right] , \end{aligned}$$

(48)

with the derivative operator $\varvec{\hat{\partial }}= [{\partial }/{\partial \xi _e},{\partial }/{\partial \eta _e},0]^{\text {T}}$ and the matrix $\bar{\mathbf{P }}_e$ given by Eq. (21). After computing the inverse of the Jacobian matrix Eq. (48), the matrix $\hat{\mathbf{B }}_e$ appearing in Eq. (46) can be developed from Eq. (40) as

$$\begin{aligned} \hat{\mathbf{B }}_e =\hat{\mathbf{B }}^1_e \frac{\partial }{\partial \xi _e} + \hat{\mathbf{B }}^2_e \frac{\partial }{\partial \eta _e} , \end{aligned}$$

(49)

where

$$\begin{aligned} \hat{\mathbf{B }}^c_e=\left[ \begin{array}{ccc} (\hat{\mathbf{J }}^{-1}_e)_{1c} &{} 0 &{} 0\\ 0 &{} (\hat{\mathbf{J }}^{-1}_e)_{2c} &{} 0\\ (\hat{\mathbf{J }}^{-1}_e)_{2c} &{} (\hat{\mathbf{J }}^{-1}_e)_{1c} &{} 0\\ 0 &{} 0 &{} (\hat{\mathbf{J }}^{-1}_e)_{1c}\\ 0 &{} 0 &{} (\hat{\mathbf{J }}^{-1}_e)_{2c}\\ 0 &{} 0 &{} 0 \end{array} \right] \quad \text {with} \quad c \in \{ 1,2 \} . \end{aligned}$$

(50)

In order to eliminate the rigid body motions and to ensure that the cross-sectional warping displacements satisfy the orthogonality conditions formulated in Ladevèze and Simmonds [16], El Fatmi [8] and Genoese et al. [10], the following constraint equations need to be satisfied:

$$ \left[ \begin{array}{cc} {\mathbf{D}} ^{\text {T}} &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{D}} ^{\text {T} }\end{array} \right] \left[ \begin{array}{c} \hat{\mathbf{u }} \\ {\partial \hat{\mathbf{u }}}/{\partial z } \end{array} \right] = \left[ \begin{array}{c} {\mathbf{0}} \\ {\mathbf{0}} \end{array} \right] ,$$

(51)

with

$$\begin{aligned} \begin{aligned} \mathbf{D} =&\left[ \begin{array}{cccc} \mathbf{Z} _1^{\text {T}}, &{} \mathbf{Z} _2^{\text {T}}, &{} \cdots , &{} \mathbf{Z} _{n_n}^{\text {T}}\\ \end{array} \right] ^{\text {T}},\end{aligned}\end{aligned}$$

(52)

where $n_n$ is the total number of element nodes in the FEM mesh and $\mathbf{Z} _{n}$ is obtained by inserting the nodal coordinates of node n in Eq. (37). Formulating Eq. (45) in matrix-vector notation and incorporating the constraint relations, Eq. (51), results in the system of equilibrium equations [6]

$$\begin{aligned} \hat{\mathbf{K }} \mathbf{w} =\hat{\mathbf{f }} \Longleftrightarrow \begin{aligned} \left[ \begin{array}{cc} \mathbf{K} _{11} &{} \left( \mathbf{H} ^{\text {T}}-\mathbf{H} \right) \\ \mathbf{0} &{} \mathbf{K} _{11} \end{array} \right] \end{aligned} \begin{aligned} \left[ \begin{array}{c} \mathbf{w} _{1} \\ \mathbf{w} _{2} \end{array} \right] \end{aligned} = \begin{aligned} \left[ \begin{array}{c} \mathbf{f} _{1} \\ \mathbf{f} _{2} \end{array} \right] \end{aligned} , \end{aligned}$$

(53)

with

$$\begin{aligned} \begin{aligned} \mathbf{K} _{11}=&\left[ \begin{array}{ccc} \mathbf{E} &{} \mathbf{R} &{} \mathbf{D} \\ \mathbf{R} ^{\text {T}} &{} \mathbf{A} &{} \mathbf{0} \\ \mathbf{D} ^{\text {T}} &{} \mathbf{0} &{} \mathbf{0} \end{array} \right] \end{aligned} \quad \text {and} \quad \begin{aligned} \mathbf{H} =&\left[ \begin{array}{ccc} \mathbf{C} &{} \mathbf{L} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} \end{array} \right], \end{aligned} \end{aligned}$$

(54)

where $\mathbf{w} _1=[ \hat{\mathbf{u }}^{\text {T}}, \varvec{\psi }^{\text {T}}, \varvec{\lambda }_1^{\text {T}} ]^{\text {T}}$ and $\mathbf{w} _2= [ \partial \hat{\mathbf{u }}^{\text {T}} / \partial z, \partial \varvec{\psi }^{\text {T}} / \partial z, \varvec{\lambda }_2^{\text {T}} ]^{\text {T}}$, are the solution vectors, in which $\varvec{\lambda }_1$ and $\varvec{\lambda }_2$ are Langrange multipliers that relate to the constraint equations, Eq. (51). In addition, the force vectors are formulated as $\mathbf{f} _1=[ \mathbf{0} ^{\text {T}}, \varvec{\theta }^{\text {T}}, \mathbf{0} ^{\text {T}} ]^{\text {T}}$ and $\mathbf{f} _2=[ \mathbf{0} ^{\text {T}}, ( \mathbf{T} _r^{\text {T}} \varvec{\theta } )^{\text {T}}, \mathbf{0} ^{\text {T}} ]^{\text {T}}$, the matrices $\mathbf{A}$, $\mathbf{R}$, $\mathbf{E}$, $\mathbf{C}$, $\mathbf{L}$ can be calculated from Eq. (46), and the matrix $\mathbf{D}$ is presented by Eq. (52).

For computational convenience, a $6 \times 6$ matrix $\mathbf{W}$ is constructed by column-wise assembling the solutions of Eq. (53) for 6 different right-hand sides, which are distinguished by successively setting one specific entry of $\varvec{\theta }$ to unity and the remaining 5 entries to zero. Accordingly, for an arbitrary force vector $\varvec{\theta }$, with the definition of $\varvec{\theta }$ given below Eq. (31), the solution vector $\mathbf{w} =[\mathbf{w} _1, \mathbf{w} _2]^{\text {T}}$ can be straightforwardly computed as

$$\begin{aligned} \mathbf{w} =\mathbf{W} \varvec{\theta } . \end{aligned}$$

(55)

In addition, by equating the external complementary virtual work to the internal complementary virtual work, the compliance matrix $\mathbf{F} _{\text{s}}$ of the cross section follows as [6]

$$\begin{aligned} \mathbf{F} _{\text{s}}=\mathbf{W} ^{\text {T}} \begin{aligned} \left[ \begin{array}{cc} \mathbf{G} _{11} &{} \mathbf{H} ^{\text {T}}\\ \mathbf{H} &{} \mathbf{G} _{22} \end{array} \right] \end{aligned} \mathbf{W} =\mathbf{W} ^{\text {T}} \mathbf{G} \mathbf{W} , \end{aligned}$$

(56)

with

$$\begin{aligned} \begin{aligned} \mathbf{G} _{11}=&\left[ \begin{array}{ccc} \mathbf{E} &{} \mathbf{R} &{} \mathbf{0} \\ \mathbf{R} ^{\text {T}} &{} \mathbf{A} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} \end{array} \right] \end{aligned} \text {and} \quad \begin{aligned} \mathbf{G} _{22}=&\left[ \begin{array}{ccc} \mathbf{M} &{} \mathbf{0} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} \\ \mathbf{0} &{} \mathbf{0} &{} \mathbf{0} \end{array} \right], \end{aligned} \end{aligned}$$

(57)

where the matrices $\mathbf{A}$, $\mathbf{R}$, $\mathbf{E}$, $\mathbf{M}$ are provided by Eq. (46), and the matrix $\mathbf{H}$ is given by Eq. (54). Finally, the stiffness matrix of the element cross section used in Eq. (31) can be calculated via $\mathbf{K} ^{\text {s}}=\mathbf{F} _{\text{s}}^{-1}$, with $\mathbf{F} _{\text{s}}$ in accordance with Eq. (56).

4 Coupled optimization model

This section presents a coupled optimization model that is able to simultaneously optimize the outer shape and the topological layout of a beam structure. For this purpose, the formulation recently proposed in [30] is followed, which incorporates the shape-related design variables in the SIMP topology optimization method. Accordingly, the minimization of the compliance of a structure under a predefined material volume constraint is formulated as

$$\begin{aligned} \begin{aligned} \min \limits _{\varvec{\rho },\mathbf{a} }\qquad \,&c(\varvec{\rho },\mathbf{a} )= \mathbf{f }^{\text {T}} \mathbf{u} (\varvec{\rho },\mathbf{a} ) , \\ \text {subject to} \qquad&\frac{V(\varvec{\rho },\mathbf{a} )}{V_0}= f_r , \\ \text {with} \qquad&\,\, l_s\le a_s\le u_s , \qquad \qquad \,\,\,\,\,\,\, s =1,...,S , \\&\,\, 0 \le \rho _{min} \le \rho _e \le 1 , \qquad \,\,\, e =1,...,N , \end{aligned} \end{aligned}$$

(58)

in which the structural compliance c depends on both the shape design variables $\mathbf{a}$ (i.e., the spatial control points of the NURBS) and the topology design variables $\varvec{\rho }$ (i.e., the relative densities). Further, the variables $l_s$ and $u_s$ are the lower and upper bounds of the shape design variable $a_s$, S is the total number of shape design variables, $\rho _{min}$ is the minimum density, e is the element number and N is the total number of elements. The material volume V is a function of both $\mathbf{a}$ and $\varvec{\rho }$, and the parameter $V_0$ represents the initial volume of the design domain. The variable $f_r$ is the prescribed volume fraction, and $\mathbf{f}$ is the global force vector. The displacement vector $\mathbf{u}$ of the modeled system is obtained by solving the corresponding equilibrium equations, i.e., Eq. (28) for a 3D beam model and Eq. (32) for a 2.5D beam model.

Fig. 3

Flowchart of the incremental-iterative solution strategy for coupled shape and topology optimization, with iterations g and h referring to topology and shape optimization sub-loops, respectively, and iteration w referring to the outer loop

The coupled shape and topology optimization problem for the beam structure is solved in an incremental-iterative fashion using a staggered (sequential) solution strategy, which is illustrated in Fig. 3:

• 1. The geometry of the design domain is parametrically described by NURBS, as introduced in Sect. 2. Subsequently, for performing a structural analysis, the geometry data are discretized into a FEM model, as described in Sect. 3.

• 2. By keeping the shape design variables $\mathbf{a}$ momentarily fixed, the problem formulated in Eq. (58) can be regarded as a classical topology optimization problem, formulated as

  $$\begin{aligned} \begin{aligned} \min \limits _{\varvec{\rho }}\qquad \,&c(\varvec{\rho })=\mathbf{f }^{\text {T}} \mathbf{u} (\varvec{\rho }) , \\ \text {subject to}\qquad&\frac{V(\varvec{\rho })}{V_0}=f_r , \\ \text {with} \qquad&0 < \rho _{min} \le \rho _e \le 1 , \qquad e =1,...,N . \end{aligned} \end{aligned}$$

  (59)

  Accordingly, the relative densities $\varvec{\rho }$ are optimized by solving Eq. (59), which is carried out by following the typical topology optimization procedure, consisting of a structural analysis, a topology sensitivity analysis, and the update of the densities.

• 3. By momentarily freezing the updated densities $\varvec{\rho }$, Eq. (58) reduces to a shape optimization problem, formulated as

  $$\begin{aligned} \begin{aligned} \min \limits _{\mathbf{a}}\qquad \,&c(\mathbf{a} )=\mathbf{f }^{\text {T}} \mathbf{u} (\mathbf{a} ) , \\ \text {subject to}\qquad&\frac{V(\mathbf{a} )}{V_0}= f_r , \\ \text {with} \qquad&\,\, l_s\le a_s\le u_s , \qquad \, s =1,...,S . \\ \end{aligned} \end{aligned}$$

  (60)

  The shape design variables $\mathbf{a}$ are calculated by solving Eq. (60) based on the densities $\varvec{\rho }$ found in step 2. Step 3 is carried out by performing a standard gradient-based shape optimization procedure, consisting of a structural analysis, a shape sensitivity analysis, and the updating of the shape.

• 4. When the element densities $\varvec{\rho }$ obtained from step 2 are not optimal for the shape subsequently computed in step 3, in a sense that they do not lead to an immediate satisfaction of the shape convergence criteria (i.e., after the first iteration), a new topology optimization increment (step 2) is performed, based on the updated shape design variables $\mathbf{a}$. After this step has converged and the topology design variables $\varvec{\rho }$ have been updated, a new shape optimization increment (step 3) is performed, and the above check on immediate convergence is repeated. The above process is continued until the incremental-iterative solution procedure has converged. Note that updating the topology and shape configurations of the beam after convergence of the corresponding optimization increment causes the coupling effects between topology and shape to be automatically accounted for. The convergence (or stop) criteria for the individual topology and shape optimization increments and for the overall procedure are, respectively, evaluated during every iteration g, h and w, see Fig. 3, and will be specified when discussing the numerical examples in Sect. 6.

The staggered solution strategy depicted in Fig. 3 starts with an incremental topology optimization step, and, as such, is referred to as coupled topology shape optimization (CTSO). Alternatively, it can start with an incremental shape optimization step, and will then be referred to as coupled shape topology optimization (CSTO), see also [30]. In shape and topology optimization problems, the landscape of solutions is characterized by numerous local minima, whereby the convergence speed and the specific optimized solution calculated may be expected to be sensitive to the algorithmic features of the numerical update scheme applied. Despite that the main focus of the present work is on numerical discretization aspects and on comparing the outer and internal geometries of the 3D and 2.5D beam models under shape and topology optimization, possible differences in the results from the CTSO and CSTO update schemes will be also analyzed and discussed. Note that the choice of a staggered update scheme in this study is arbitrary; the coupled optimization problem, Eq. (58), could also be solved concurrently by using a monolithic scheme. A systematic comparison of the influence of staggered and monolithic update schemes on the computational efficiency and outcome of the coupled optimization approach, however, falls outside the scope of this work; for more details on this aspect, the reader is referred to [29].

5 Sensitivity analysis

For the coupled, gradient-based optimization approach, the analytical sensitivities of the structural compliance c need to be determined with respect to the shape design variables $\mathbf{a}$ and relative element densities $\varvec{\rho }$. These analytical sensitivities are elaborated below for the 2.5D and 3D beam models.

5.1 2.5D beam model

For simplicity of notation, the variable d is introduced, which represents either the shape design variable $a_s$ or the element density $\rho _e$. In correspondence with Eq. (56), the derivative of the cross-sectional compliance matrix $\mathbf{F} _{\text{s}}$ with respect to d can be expressed as

$$\begin{aligned} \frac{\partial \mathbf{F} _{\text{s}}}{\partial d}= \frac{\partial \mathbf{W} ^{\text {T}}}{\partial d} \mathbf{G} \mathbf{W} + \mathbf{W} ^{\text {T}} \frac{\partial \mathbf{G} }{\partial d} \mathbf{W} + \mathbf{W} ^{\text {T}} \mathbf{G} \frac{\partial \mathbf{W} }{\partial d} . \end{aligned}$$

(61)

Since the matrix $\mathbf{W}$ contains the solutions of the equilibrium equations given by Eq. (53), whereby in $\hat{\mathbf{f }}$ one component of $\varvec{\theta }$ equals unity and the remaining components are zero, the derivative ${\partial \mathbf{W} }/{\partial d}$ in Eq. (61) follows from Eq. (53) as

$$\begin{aligned} \frac{\partial \mathbf{W} }{\partial d}= -\hat{\mathbf{K }}^{-1} \frac{\partial \hat{\mathbf{K }}}{\partial d} \mathbf{W} . \end{aligned}$$

(62)

Inserting Eq. (62) into Eq. (61), the derivative of the cross-sectional compliance matrix becomes

$$\begin{aligned} \frac{\partial \mathbf{F} _{\text{s}}}{\partial d}=-\mathbf{W} ^{\text {T}} \frac{\partial \hat{\mathbf{K }}^{\text {T}}}{\partial d} \mathbf{V} +\mathbf{W} ^{\text {T}} \frac{\partial \mathbf{G} }{\partial d} \mathbf{W} -\mathbf{V} ^{\text {T}} \frac{\partial \hat{\mathbf{K }}}{\partial d} \mathbf{W} , \end{aligned}$$

(63)

with

$$\begin{aligned} \mathbf{V} =\hat{\mathbf{K }}^{-\text {T}} \mathbf{G} \mathbf{W} , \end{aligned}$$

(64)

where the matrix $\hat{\mathbf{K }}$ is obtained from Eqs. (53) and (54), and $\mathbf{G}$ follows from Eqs. (56) and (57). Since the stiffness matrix $\mathbf{K} ^{\text {s}}$ of the cross section is the inverse of the compliance matrix $\mathbf{F} _{\text{s}}$, the derivative of the stiffness matrix with respect to d may be expressed as

$$\begin{aligned} \frac{\partial \mathbf{K} ^{\text {s}}}{\partial d}= \frac{\partial \mathbf{F} _{\text{s}}^{-1}}{\partial d} =-\mathbf{F} _{\text{s}}^{-1} \frac{\partial \mathbf{F} _{\text{s}}}{\partial d} \mathbf{F} _{\text{s}}^{-1} =-\mathbf{K} ^{\text {s}} \frac{\partial \mathbf{F} _{\text{s}}}{\partial d} \mathbf{K} ^{\text {s}} . \end{aligned}$$

(65)

The global stiffness matrix $\bar{\mathbf{K }}$ of the beam model is based on the cross-sectional stiffness matrix $\mathbf{K} _e^{\text {s}}$ of the beam element via Eqs. (33) and (34). Accordingly, the derivative of $\bar{\mathbf{K }}$ with respect to the design variable d becomes

$$\begin{aligned} \frac{\partial \bar{\mathbf{K }}}{\partial d} = \sum _{e=1}^{N} \int _{-1}^1 \left( \bar{\mathbf{B }}_e \mathbf{N} _e \right) ^{\text {T}} \frac{\partial \mathbf{K} ^{\text {s}}_e}{\partial d} |\bar{\mathbf{J }}_e| \bar{\mathbf{B }}_e \mathbf{N} _e \mathrm{d}\zeta _e . \end{aligned}$$

(66)

Because the loads $\mathbf{f}$ are independent of the design variable d, from Eqs. (58), (32) and the symmetry relation $\bar{\mathbf{K }}=\bar{\mathbf{K }}^T$, the sensitivity of the compliance c with respect to d follows as

$$\begin{aligned} \frac{\partial c}{\partial d} = -\bar{\mathbf{u }}^{\text {T}} \frac{\partial \bar{\mathbf{K }}}{\partial d} \bar{\mathbf{u }} . \end{aligned}$$

(67)

The specific forms of the derivatives ${\partial \hat{\mathbf{K }}}/{\partial d}$ and ${\partial \mathbf{G} }/{\partial d}$ appearing in the above equations depend on the type of design variable. The derivation of these terms is presented below.

5.1.1 Shape sensitivity analysis

The shape sensitivity analysis starts with the computation of the partial derivative of the Jacobian matrix, Eq. (48), with respect to the shape design variable $a_s$, leading to

$$\begin{aligned} \partial _s (\hat{\mathbf{J }}_e)= \partial _s (\bar{\mathbf{P }}_e) (\varvec{\hat{\partial }} \mathbf{N} _e^{\text {T}}) , \end{aligned}$$

(68)

in which, for reasons of brevity, the notation $\partial _s(\cdot )=\partial (\cdot ) / \partial a_s$ has been used. The derivative $\partial _s (\bar{\mathbf{P }}_e)$ appearing in Eq. (68) is calculated by combining Eqs. (21) and (16), in which the derivative of the coordinates of an arbitrary point on the NURBS surface with respect to the shape design variable follows from Eq. (11) as

$$\begin{aligned} \partial _s (\mathbf{p} )=\left[ \frac{\mathbf{N }_{\text{b}}^{\text {T}} \partial _s(\mathbf{P }^{\text {2D}}_{k,X}) \mathbf{M }_{\text{b}}}{\mathbf{N }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_k \mathbf{M }_{\text{b}}}, \frac{\mathbf{N }_{\text{b}}^{\text {T}} \partial _s(\mathbf{P }^{\text {2D}}_{k,Y}) \mathbf{M }_{\text{b}}}{\mathbf{N }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_k \mathbf{M }_{\text{b}}}, \frac{\mathbf{N }_{\text{b}}^{\text {T}} \partial _s(\mathbf{P }^{\text {2D}}_{k,Z}) \mathbf{M }_{\text{b}}}{\mathbf{N }_{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {2D}}_k \mathbf{M }_{\text{b}}} \right] ^{\text {T}} , \end{aligned}$$

(69)

where $\partial _s(\mathbf{P} ^{\text {2D}}_{k,C})$, with $C \in \{ X,Y,Z \}$, can be easily determined from Eq. (10), in which the z-coordinate of the control points $Z_{i,j,k}$ is set to zero. Further, the matrices $\mathbf{N} _{\text{b}}$, $\mathbf{M} _{\text{b}}$ and $\varvec{\varOmega }^{\text {2D}}_k$ are obtained from Eqs. (8), (9) and (12), respectively. Eq. (68) can be used for the calculation of the derivative of the determinant of the Jacobian with respect to the shape design variable $a_s$ via

$$\begin{aligned} \partial _s(|\hat{\mathbf{J }}_e|) =( \partial _s(\hat{\mathbf{J }}_e) )_{11} (\hat{\mathbf{J }}_e)_{22} +(\hat{\mathbf{J }}_e)_{11} ( \partial _s(\hat{\mathbf{J }}_e) )_{22} -( \partial _s(\hat{\mathbf{J }}_e) )_{12} (\hat{\mathbf{J }}_e)_{21}- (\hat{\mathbf{J }}_e)_{12} ( \partial _s(\hat{\mathbf{J }}_e) )_{21} \, , \end{aligned}$$

(70)

Further, Eq. (68) can be employed in the expression for the derivative of the inverse of the Jacobian matrix with respect to the shape design variable $a_s$, which reads:

$$\begin{aligned} \partial _s(\hat{\mathbf{J }}^{-1}_e)= -\hat{\mathbf{J }}^{-1}_e \partial _s(\hat{\mathbf{J }}_e) \hat{\mathbf{J }}^{-1}_e , \end{aligned}$$

(71)

with $\hat{\mathbf{J }}_e$ provided by Eq. (48).

With the operator $\hat{\mathbf{B }}_e$ given by Eq. (49), the matrix product $\hat{\mathbf{B }}_e \mathbf{N} _e$ in Eq. (46) can be expressed as

$$\begin{aligned} \hat{\mathbf{B }}_e \mathbf{N} _e= \hat{\mathbf{B }}^1_e \frac{\partial \mathbf{N} _e}{\partial \xi _e} + \hat{\mathbf{B }}^2_e \frac{\partial \mathbf{N} _e}{\partial \eta _e} , \end{aligned}$$

(72)

where $\hat{\mathbf{B }}^c_e$, with $c \in \{ 1,2 \}$, is obtained from Eq. (50). Accordingly, the derivative of $\hat{\mathbf{B }}_e \mathbf{N} _e$ with respect to the shape design variable $a_s$ can be formulated as

$$\begin{aligned} \partial _s(\hat{\mathbf{B }}_e \mathbf{N} _e)= \partial _s(\hat{\mathbf{B }}^1_e) \frac{\partial \mathbf{N} _e}{\partial \xi _e} + \partial _s(\hat{\mathbf{B }}^2_e) \frac{\partial \mathbf{N} _e}{\partial \eta _e} , \end{aligned}$$

(73)

with

$$\begin{aligned} \partial _s(\hat{\mathbf{B }}^c_e)=\left[ \begin{array}{ccc} (\partial _s(\hat{\mathbf{J }}^{-1}_e))_{1c} &{}0 &{}0\\ 0 &{}(\partial _s(\hat{\mathbf{J }}^{-1}_e))_{2c} &{}0\\ (\partial _s(\hat{\mathbf{J }}^{-1}_e))_{2c} &{}(\partial _s(\hat{\mathbf{J }}^{-1}_e))_{1c} &{} 0\\ 0 &{} 0 &{} (\partial _s(\hat{\mathbf{J }}^{-1}_e))_{1c}\\ 0 &{} 0 &{} (\partial _s(\hat{\mathbf{J }}^{-1}_e))_{2c}\\ 0 &{} 0 &{} 0\\ \end{array} \right] , \end{aligned}$$

(74)

in which $c \in \{ 1,2 \}$, and $\partial _s(\hat{\mathbf{J }}^{-1}_e)$ is given by Eq. (71). The derivatives of the coefficient matrices $\mathbf{E}$, $\mathbf{C}$, and $\mathbf{M}$—presented in Eq. (46)—with respect to the shape design variable $a_s$ read

$$\begin{aligned} \begin{aligned}&\partial _s(\mathbf{E} )=\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left[ \begin{aligned}&\partial _s((\hat{\mathbf{B }}_e \mathbf{N} _e )^{\text {T}}) \mathbf{Q} _e \hat{\mathbf{B }}_e \mathbf{N} _e |\hat{\mathbf{J }}_e| +(\hat{\mathbf{B }}_e \mathbf{N} _e )^{\text {T}} \mathbf{Q} _e \partial _s(\hat{\mathbf{B }}_e \mathbf{N} _e) |\hat{\mathbf{J }}_e|\\&+(\hat{\mathbf{B }}_e \mathbf{N} _e )^{\text {T}} \mathbf{Q} _e \hat{\mathbf{B }}_e \mathbf{N} _e \partial _s(|\hat{\mathbf{J }}_e|) \end{aligned} \right] \mathrm{d}\xi _e \mathrm{d}\eta _e , \\&\partial _s(\mathbf{C} )=\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left[ (\mathbf{S} _e \mathbf{N} _e)^{\text {T}} \mathbf{Q} _e \partial _s(\hat{\mathbf{B }}_e \mathbf{N} _e ) |\hat{\mathbf{J }}_e| +(\mathbf{S} _e \mathbf{N} _e)^{\text {T}} \mathbf{Q} _e \hat{\mathbf{B }}_e \mathbf{N} _e \partial _s(|\hat{\mathbf{J }}_e|) \right] \mathrm{d}\xi _e \mathrm{d}\eta _e , \\&\partial _s(\mathbf{M} )=\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \left[ (\mathbf{S} _e \mathbf{N} _e)^{\text {T}} \mathbf{Q} _e \mathbf{S} _e \mathbf{N} _e \partial _s( |\hat{\mathbf{J }}_e|) \right] \mathrm{d}\xi _e \mathrm{d}\eta _e . \end{aligned} \end{aligned}$$

(75)

From the last two expressions in Eq. (75), the derivatives with respect to the shape design variable of the matrices $\mathbf{A}$, $\mathbf{R}$ and $\mathbf{L}$ in Eq. (46) are calculated as

$$\begin{aligned} \partial _s(\mathbf{A} )= \mathbf{D} ^{\text {T}} \partial _s(\mathbf{M} ) \mathbf{D} , \,\, \partial _s(\mathbf{R} )= \left( \partial _s(\mathbf{C} ) \right) ^{\text {T}} \mathbf{D} , \,\, \partial _s(\mathbf{L} )= \partial _s(\mathbf{M} ) \mathbf{D} , \end{aligned}$$

(76)

with $\mathbf{D}$ given by Eq. (52). Finally, the terms ${\partial \hat{\mathbf{K }}}/{\partial a_s}$ and ${\partial \mathbf{G} }/{\partial a_s}$ in Eq. (63) are calculated from Eqs. (53)–(57), thereby inserting the derivatives of the coefficient matrices given by Eqs. (75) and (76).

5.1.2 Topology sensitivity analysis

According to Eqs. (26) and (46), the coefficient matrices $\mathbf{A}$, $\mathbf{R}$, $\mathbf{E}$, $\mathbf{C}$, $\mathbf{L}$ and $\mathbf{M}$ of the cross section can be explicitly expressed as a function of the element density $\rho _e$. Correspondingly, by referring to an arbitrary coefficient matrix as $\mathbf{M} ^{\text {c}}$, its derivative with respect to the element density is calculated as

$$\begin{aligned} \frac{\partial \mathbf{M} ^{\text {c}} }{\partial \rho _e} = p (\rho _e)^{p-1} \mathbf{M} ^{\text {c}}_0 , \end{aligned}$$

(77)

where the variable $\mathbf{M} ^{\text {c}}_0$ refers to the corresponding coefficient matrices obtained from Eq. (46) by substituting the density-independent constitutive matrix $\mathbf{Q}$ (instead of the density-dependent constitutive matrix $\mathbf{Q} _e$, see Eq. (26)). With Eq. (77), the terms ${\partial \hat{\mathbf{K }}}/{\partial \rho _e}$ and ${\partial \mathbf{G} }/{\partial \rho _e}$ in Eq. (63) can be determined from Eqs. (53) to (57). To alleviate mesh dependency and possible checkerboard patterns in the solution computed by topology optimization, a sensitivity filter [23] is introduced that smoothens the sensitivity of the structural compliance as follows:

$$\begin{aligned} \frac{ \partial \hat{c} }{\partial \rho _e} = \frac{ 1 }{\rho _e \sum \limits _{f=1}^{N} \hat{H}_f} \sum \limits _{f=1}^{N} \hat{H}_f \rho _f \frac{\partial c }{\partial \rho _f} , \end{aligned}$$

(78)

where ${\partial c}/{\partial \rho _f}$ is calculated employing Eqs. (63)–(67). Further, $\hat{H}_f= \text {max}(0,r_{\text{min}} - \text {dist}(e,f))$, in which $\text {dist}(e,f)$ is the distance between the center of element e and the center of element f, and $r_{\text{min}}$ is the radius of the circle within which smoothing takes place.

5.2 3D beam model

5.2.1 Shape sensitivity analysis

In the three-dimensional FEM model for the beam structure, the Jacobian matrix of an element e is presented by Eq. (20). Correspondingly, its derivative with respect to the shape design variable $a_s$ follows from

$$\begin{aligned} \partial _s(\mathbf{J} _e)= \partial _s( \bar{\mathbf{P }}_e) ( \varvec{\partial } \mathbf{N} _e^{\text {T}}) . \end{aligned}$$

(79)

The term $\partial _s (\bar{\mathbf{P }}_e)$ in Eq. (79) is calculated by combining Eqs. (21) and (16) with the derivative of the nodal coordinates, Eq. (14), with respect to $a_s$:

$$\begin{aligned} \partial _s (\mathbf{p} )=\left[ \frac{ \mathbf{L} _{\text{b}}^{\text {T}} \partial _s (\mathbf{P} ^{\text {3D}}_{X}) }{ \mathbf{L} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {3D}} }, \frac{ \mathbf{L} _{\text{b}}^{\text {T}} \partial _s (\mathbf{P} ^{\text {3D}}_{Y}) }{ \mathbf{L} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {3D}} }, \frac{ \mathbf{L} _{\text{b}}^{\text {T}} \partial _s (\mathbf{P} ^{\text {3D}}_{Z}) }{ \mathbf{L} _{\text{b}}^{\text {T}} \varvec{\varOmega }^{\text {3D}} } \right] ^{\text {T}}, \end{aligned}$$

(80)

with

$$\begin{aligned} \partial _s (\mathbf{P} ^{\text {3D}}_C)= \left[ \mathbf{N} _{\text{b}}^{\text {T}} \partial _s (\mathbf{P} ^{\text {2D}}_{1,C}) \mathbf{M} _{\text{b}}, \mathbf{N} _{\text{b}}^{\text {T}} \partial _s (\mathbf{P} ^{\text {2D}}_{2,C}) \mathbf{M} _{\text{b}}, \ldots , \mathbf{N} _{\text{b}}^{\text {T}} \partial _s (\mathbf{P} ^{\text {2D}}_{l,C}) \mathbf{M} _{\text{b}} \right] ^{\text {T}},\end{aligned}$$

(81)

where $\partial _s(\mathbf{P} ^{\text {2D}}_{k,C})$, with $C \in \{ X,Y,Z \}$ and $k=1,2,\ldots ,l$, is determined based on Eq. (10), and the matrices $\mathbf{L} _{\text{b}}$, $\mathbf{N} _{\text{b}}$, $\mathbf{M} _{\text{b}}$ and $\varvec{\varOmega }^{\text {3D}}_k$ are obtained from Eqs. (3), (8), (9) and (15), respectively. From Eq. (79), the derivative of the determinant of the Jacobian matrix with respect to $a_s$ can be computed via

$$\begin{aligned} \begin{aligned} \partial _s ( |\mathbf{J} |_e) =&\,( \partial _s (\mathbf{J} _e))_{11} [( \mathbf{J} _e)_{22}(\mathbf{J} _e)_{33}-(\mathbf{J} _e)_{23}(\mathbf{J} _e)_{32})] +(\mathbf{J} _e)_{11} \left[ \begin{aligned}&( \partial _s ( \mathbf{J} _e ))_{22} (\mathbf{J} _e)_{33}+ (\mathbf{J} _e)_{22}(\partial _s(\mathbf{J} _e))_{33}\\&-( \partial _s ( \mathbf{J} _e))_{23} (\mathbf{J} _e)_{32}-(\mathbf{J} _e)_{23} (\partial _s(\mathbf{J} _e))_{32} \end{aligned} \right] \\&+(\partial _s (\mathbf{J} _e))_{21}[(\mathbf{J} _e)_{13}(\mathbf{J} _e)_{32}-(\mathbf{J} _e)_{12}(\mathbf{J} _e)_{33}] +(\mathbf{J} _e)_{21} \left[ \begin{aligned}&( \partial _s ( \mathbf{J} _e ))_{13} (\mathbf{J} _e)_{32}+(\mathbf{J} _e)_{13} (\partial _s(\mathbf{J} _e ))_{32} \\&-( \partial _s ( \mathbf{J} _e ))_{12} (\mathbf{J} _e)_{33}-(\mathbf{J} _e)_{12} (\partial _s(\mathbf{J} _e ))_{33} \end{aligned} \right] \\&+(\partial _s (\mathbf{J} _e))_{31}[(\mathbf{J} _e)_{12}(\mathbf{J} _e)_{23}-(\mathbf{J} _e)_{13}(\mathbf{J} _e)_{22}] +(\mathbf{J} _e)_{31} \left[ \begin{aligned}&( \partial _s ( \mathbf{J} _e ))_{12} (\mathbf{J} _e)_{23}+(\mathbf{J} _e)_{12} ( \partial _s ( \mathbf{J} _e ))_{23} \\&-( \partial _s ( \mathbf{J} _e ))_{13} (\mathbf{J} _e)_{22}-(\mathbf{J} _e)_{13}( \partial _s ( \mathbf{J} _e ))_{22} \end{aligned} \right] , \end{aligned} \end{aligned}$$

(82)

while the derivative of the inverse of the Jacobian matrix becomes

$$\begin{aligned} \partial _s(\mathbf{J} ^{-1}_e)= -\mathbf{J} ^{-1}_e \partial _s(\mathbf{J} _e) \mathbf{J} ^{-1}_e , \end{aligned}$$

(83)

with the Jacobian matrix $\mathbf{J} _e$ given by Eq. (20). In addition, the derivative of the matrix product $\mathbf{B} _e \mathbf{N} _e$ used in Eq. (25) is calculated with the use of Eqs. (23) and (24) as

$$\begin{aligned} \partial _s(\mathbf{B} _e \mathbf{N} _e )= \partial _s(\mathbf{B} ^1_e) \frac{\partial \mathbf{N} _e}{\partial \xi _e} + \partial _s(\mathbf{B} ^2_e) \frac{\partial \mathbf{N} _e}{\partial \eta _e}+ \partial _s(\mathbf{B} ^3_e) \frac{\partial \mathbf{N} _e}{\partial \zeta _e} , \end{aligned}$$

(84)

with

$$\begin{aligned} \partial _s(\mathbf{B} ^c_e)=\left[ \begin{array}{ccc} (\partial _s(\mathbf{J} ^{-1}_e))_{1c} &{}0 &{}0\\ 0 &{}(\partial _s(\mathbf{J} ^{-1}_e))_{2c} &{}0\\ (\partial _s(\mathbf{J} ^{-1}_e))_{2c} &{}(\partial _s(\mathbf{J} ^{-1}_e))_{1c} &{} 0\\ (\partial _s(\mathbf{J} ^{-1}_e))_{3c} &{} 0 &{} (\partial _s(\mathbf{J} ^{-1}_e))_{1c}\\ 0 &{} (\partial _s(\mathbf{J} ^{-1}_e))_{3c} &{} (\partial _s(\mathbf{J} ^{-1}_e))_{2c}\\ 0 &{} 0 &{} (\partial _s(\mathbf{J} ^{-1}_e))_{3c} \end{array} \right] , \end{aligned}$$

(85)

in which $c \in \{ 1,2,3 \}$ and $\partial _s(\mathbf{J} ^{-1}_e)$ is computed from Eq. (83). With Eq. (84) and the global stiffness matrix $\mathbf{K}$ given by Eq. (27), the derivative of the stiffness matrix with respect to the shape design variable $a_s$ can be computed as

$$\begin{aligned} \partial _s(\mathbf{K} )=\sum _{e=1}^{N} \int _{-1}^1 \int _{-1}^1 \int _{-1}^1 \left[ \begin{aligned}&\partial _s((\mathbf{B} _e \mathbf{N} _e )^{\text {T}}) \mathbf{Q} _e \mathbf{B} _e \mathbf{N} _e |\mathbf{J} _e| + (\mathbf{B} _e \mathbf{N} _e )^{\text {T}} \mathbf{Q} _e \partial _s(\mathbf{B} _e \mathbf{N} _e ) |\mathbf{J} _e| \\&+ (\mathbf{B} _e \mathbf{N} _e )^{\text {T}} \mathbf{Q} _e \mathbf{B} _e \mathbf{N} _e \partial _s(|\mathbf{J} _e|) \end{aligned} \right] \mathrm{d}\xi _e \mathrm{d}\eta _e \mathrm{d}\zeta _e . \end{aligned}$$

(86)

Following the assumption that the load vector $\mathbf{f}$ is independent of the design variables, the derivative of the structural compliance with respect to the shape design variable $a_s$ becomes

$$\begin{aligned} \partial _s(c) = -\mathbf{u} ^{\text {T}} \partial _s(\mathbf{K} ) \mathbf{u} , \end{aligned}$$

(87)

where $\partial _s(\mathbf{K} )$ is given by Eq. (86) and $\mathbf{u}$ is the global displacement vector obtained from solving the system of equilibrium equations, Eq. (28).

5.2.2 Topology sensitivity analysis

In correspondence with Eqs. (28) and (58), the derivative of the structural compliance c with respect to the relative density $\rho _e$ equals

$$\begin{aligned} \frac{\partial c }{\partial \rho _e}=- \mathbf{u} ^{\text {T}} \frac{\partial \mathbf{K} }{\partial \rho _e} \mathbf{u} . \end{aligned}$$

(88)

Since the three-dimensional element stiffness matrix is an explicit function of the element density $\rho _e$, see Eqs. (25) and (26), the derivative of the element stiffness matrix $\mathbf{k} _e$ with respect to $\rho _e$ follows as

$$\begin{aligned} \frac{\partial \mathbf{k} _e }{\partial \rho _e} = p (\rho _e)^{p-1} \mathbf{k} _0 , \end{aligned}$$

(89)

where $\mathbf{k} _0$ is obtained from Eq. (25), by substituting the density-independent constitutive matrix $\mathbf{Q}$ (instead of the density-dependent constitutive matrix $\mathbf{Q} _e$, see Eq. (26)). Correspondingly, the derivative ${\partial c }/{\partial \rho _e}$ provided by Eq. (88) is reformulated for a specific element e using Eqs. (89) and (27), i.e.,

$$\begin{aligned} \frac{\partial c }{\partial \rho _e} = -(\mathbf{u _e})^{\text {T}} \frac{\partial \mathbf{k _e}}{\partial {\rho _e}} \mathbf{u} _e =-(\mathbf{u _e})^{\text {T}} p(\rho _e)^{p-1} \mathbf{k} _0 \mathbf{u} _e . \end{aligned}$$

(90)

The filtering of Eq. (90) is performed in accordance with Eq. (78), where $r_{\text{min}}$ is the radius of a sphere (instead of a circle) within which smoothing occurs.

6 Numerical examples

6.1 Validation case studies

In order to validate the accuracy and efficiency of the coupled shape and topology optimization procedure for 2.5D beam models, an elastic cantilever beam is considered whereby the solution obtained for the 2.5D beam model is compared to that for the 3D beam model. The initial configuration of the cantilever beam is illustrated in Fig. 4, showing a slender beam with length $L_0$ and a uniform rectangular cross section with dimensions $W_0 \times H_0$. The left end of the beam is fully clamped (i.e., zero displacements and rotations in all directions), and the right end is subjected to a vertical load F. The values of the model parameters are listed in Table 1, whereby E and $\nu$ are the Young’s modulus and Poisson’s ratio of the beam material, respectively.

Fig. 4

Cantilever beam with a uniform rectangular cross section

Table 1 Parameter values of the cantilever beam problem

6.1.1 Shape optimization

As a first step, the comparison study focuses only on the optimization of the shape of the beam sketched in Fig. 4, and the topology optimization is temporarily left out of consideration. In the 3D model, the shape of the cantilever beam is parametrically described by a NURBS solid. As explained in Sect. 2.3, the NURBS solid is constructed using a one-dimensional NURBS curve in the axial direction of the beam and a two-dimensional NURBS surface for the description of the beam cross section. According to the definition of a NURBS surface introduced in Sect. 2.2, the polynomial orders in Eq. (7) are set to $p=2$ and $q=2$, and the number of basis functions in the $\xi$- and $\eta$-directions is equal to $n=3$ and $m=3$, respectively, in correspondence with the knot vectors defined as

$$\begin{aligned} \varvec{\varXi } = \left[ 0,0,0,1,1,1 \right] ^{\text {T}} , \,\, \varvec{H} = \left[ 0,0,0,1,1,1 \right] ^{\text {T}} . \end{aligned}$$

(91)

Correspondingly, the NURBS surface is characterized by a net of 9 control points, with the arrangement of the control points at the kth location along the axial (z-)direction of the beam illustrated in Fig. 5, where $\mathbf{C} _{i,j,k}=(X_{i,j,k},Y_{i,j,k},Z_{i,j,k})$, with $i=1,2,3$, $j=1,2,3$ and $k=1,2,\ldots ,l$, see also Eq. (10). The initial coordinates and weights of these control points are listed in Table 2, in which $Z_k$ with $k=1,2,\ldots ,l$ is used to replace $Z_{i,j,k}$ since all control points of a specific surface have the same z-coordinate. The value of the z-coordinate $Z_k$ of each NURBS surface is determined based on the NURBS curve, see Sect. 2.1, which describes the geometry along the beam length. The polynomial order of the NURBS curve is $r=1$, which, in correspondence with Eq. (1), represents a linear curve. In order to construct the complete beam geometry, $l=81$ NURBS surfaces are equally spaced along the beam length $L_0$. Accordingly, the knot vector $\varvec{Z}$ in Eq. (1) is defined as

$$\begin{aligned} \varvec{Z}=[0,...,(k-1)/(l-1),...,1]^{\text {T}} \qquad \text {with} \quad k=1,2,\ldots ,l , \end{aligned}$$

(92)

and the z-coordinate $Z_k$ of the control points is

$$\begin{aligned} Z_k=\frac{(k-1) L_0}{l-1} \qquad \text {with} \quad k=1,2,\ldots ,l , \end{aligned}$$

(93)

with the beam length $L_0$ given in Table 1.

Fig. 5

Control points for the NURBS surface at the kth (with $k=1,2,\ldots ,l$) location along the longitudinal direction (z-direction) of the beam

Table 2 Coordinates (in m) and corresponding weights of the control points of the kth (with $k=1,2,\ldots ,l$) NURBS surface

With the above characterization of the beam geometry, the nodal positions in parametric $\xi$-, $\eta$- and $\zeta$-coordinates are obtained after dividing the parametric domain $W_0 \times H_0 \times L_0$ into equal $6 \times 10 \times 80$ hexahedral parts. Subsequently, the nodal positions of the FEM model are found by projecting the auxiliary mesh in the parametric domain to the physical domain using Eq. (14), see also Fig. 2. These nodal positions are finally utilized to construct the 3D and 2.5D models of the cantilever beam, as illustrated in Fig. 1b and c, respectively. In accordance with the shape optimization procedure formulated in Eq. (60), the objective—the structural compliance c—and constraints—the volume V—are evaluated using the relations for the 3D FEM model introduced in Sect. 3.1. The relative element densities $\varvec{\rho }$ are uniformly kept fixed at a value of 1. In order to limit the computational demand of the 3D FEM model in the comparison study on shape optimization of 3D and 2.5D beam models, only the height H of the beam is allowed to change along the beam length, whereby the cross section is prescribed to remain rectangular. Note that this restriction in the shape design variables does not affect the nature and objectivity of the comparison study; in fact, it could have been introduced equally well as a geometrical constraint following from structural design considerations. It is further emphasized that it is straightforward to incorporate the width of beam cross sections into the set of shape design variables, as is done for the coupled shape and topology optimization analysis of the 2.5D beam model considered in Sect. 6.2. In correspondence with the above arguments, the shape design variables $\mathbf{a}$ are formulated as

$$\begin{aligned} \mathbf{a} =\left[ Y_{1,3,2} , Y_{1,3,3} , \ldots , Y_{1,3,k} \right] ^{\text {T}} \quad \text {with} \quad k=2,3,\ldots ,l , \end{aligned}$$

(94)

where $Y_{1,3,k}$ is the y-coordinate of control point $\mathbf{C} _{1,3,k}$ illustrated in Fig. 5. The upper and lower bounds of this y-coordinate are set as 0.5 m $\le Y_{1,3,k} \le$ 1.5m, which also apply to the y-coordinate of neighboring control points via the equality $Y_{1,3,k}=Y_{2,3,k}=Y_{3,3,k}$. Further, the coordinates of the control points of the first NURBS surface ($k=1$) are taken the same as those of the adjacent, second NURBS surface ($k=2$); in fact, the first cross section is only used for post-processing of the analysis results, and does not contribute to the optimization procedure, see also [6]. The values of the shape design variables $\mathbf{a}$ are efficiently updated by incorporating the analytical shape sensitivities presented in Sect. 5.2.1 in a sequential quadratic programming (SQP) procedure that was implemented in the MATLAB solver fmincon. The shape optimization is assumed to be converged when the structural compliance meets the stop criterion $\mid c^{h+1}-c^h \mid \le$1e-5, with h the iteration number, or when the shape design variables satisfy the criterion $\text {max}(\mid \mathbf{a} ^{h+1}-\mathbf{a} ^h \mid ) \le$1e-5, whereby $\mid . \mid$ refers to the absolute value of a scalar or the absolute value of each specific component of a vector.

Alternatively, the optimization procedure can be carried out by modeling the cantilever beam as a 2.5D model. The 2.5D model is composed of 80 two-node beam elements along the beam (z-)axis (shown as a dotted black line in Fig. 1c). The z-coordinate of the beam nodes is given by Eq. (93). The stiffness of each beam finite element is obtained from a 2D FEM analysis of the beam cross section (evaluated at one of the beam element nodes). The meshes of the 81 cross sections have a similar mesh density as in the 3D FEM model. In Table 2, the z-coordinate $Z_k$ (with $k=1,2,\ldots ,81$) of the control points depicted in Fig. 5 essentially is irrelevant as a result of the two-dimensional character of the NURBS surface, and therefore is arbitrarily set to zero. The shape design variables $\mathbf{a}$ relate to the height of the cross sections and are presented by Eq. (94). The shape optimization procedure is performed in accordance with Eq. (60), for which the analytical shape sensitivities are provided in Sect. 5.1.1.

The results of the shape optimization procedures with the 3D and 2.5D beam models are shown in Figs. 6 and 7. It can be observed that both models provide almost the same optimized shape, whereby the beam height near the clamped end, at which the bending moment is relatively large, is maximal and equal to 1.5m. Along the middle part of the beam the height gradually decreases, whereby it reaches the minimum value of 0.5 m close to the end at which the external load is applied. The convergence behavior of the shape optimization procedure for the two beam-type structures is illustrated in Fig. 8. The convergence rate of the structural compliance c for the 2.5D model is somewhat lower than for the 3D model, although the two models eventually provide the same minimum value of c. The computational time of the 2.5D model is about a factor of 70 lower than that of the 3D model, which illustrates that the 2.5D model is computationally much more efficient in this case.

Fig. 6

Local optimal designs by pure shape optimization using a 3D and b 2.5D beam modeling

Fig. 7

Comparison of the optimal height of the beam along the longitudinal direction, calculated by pure shape optimization for 3D (a) and 2.5D (b) beam models

Fig. 8

Convergence behavior of the compliance c for pure shape optimization of 3D (triangles) and 2.5D (circles) beam models. The iteration number h refers to the loop for shape optimization, see Fig. 3

6.1.2 Topology optimization

As a next step, the cantilever beam problem illustrated in Fig. 4 is subjected to pure topology optimization, whereby the results computed with the 2.5D and 3D beam models are mutually compared. The geometry and FEM models of the problem are in accordance with the description in Sect. 6.1.1. In the topology optimization procedure, the volume fraction $f_r$ appearing in Eq. (59) is set equal to 0.4. Further, the interior-point (IP) algorithm implemented in the MATLAB solver fmincon [20] is employed to update the element densities $\varvec{\rho }$. The sensitivities required for the gradient-based topology optimization procedure are presented in Sects. 5.1.2 and 5.2.2 for the 2.5D and 3D beam models, respectively. The topology optimization procedure is assumed to be converged when the structural compliance meets the stop criterion $\mid c^{g+1}-c^g \mid \le$1e-5, with g the iteration number, or when the topology design variables satisfy the criterion $\text {max}(\mid \varvec{\rho }^{g+1}-\varvec{\rho }^g \mid ) \le$1e-5. In order to warrant an objective comparison of the results calculated for the 2.5D and 3D beam models, the filtering of possible checkerboard patterns, which is defined by Eq. (78) and may work out differently for the 2.5D and 3D beam models, is omitted here.

Figure 9 shows the convergence behavior of the structural compliance c of the topology optimization process for the 2.5D (circles) and 3D (triangles) beam models. The overall convergence behavior and the corresponding compliance values clearly are similar for the two beam models. As a result of three-dimensional stress effects, some minor differences emerge in the relative density distributions at the clamped end and at the point of load application, see Figs. 10 and 11. The density distributions across the cross sections illustrate that most of the material is located at the top and bottom of the beam height, which is logical for a beam structure loaded in bending. The optimized configurations presented in Figs. 10 and 11 further show the presence of intermediate element densities. Note that in topology optimization analyses the appearance of intermediate densities commonly is considered as undesirable, as it fades the distinction between a solid material (material density is unity) and a void (material density is zero). An efficient way to reduce intermediate densities in topology optimization results is by increasing the penalization factor p in Eq. (26), see [25], which in the present work has been selected in accordance with the common value $p=3$ [2]. Alternative, more elaborate strategies that mitigate the appearance of intermediate densities have been presented in [13, 24, 27]. It should be further mentioned that the canonical duality method recently proposed by [9] can produce O(1) optimal density distributions without the use of a filtering step. The main purpose of Figs. 10 and 11, however, is to objectively compare the optimized configurations computed for 3D and 2.5D beam models, for which the appearance of intermediate densities is insignificant. In addition, in the analyses performed with the coupled shape and topology optimization approach as presented in Sect. 6.2, the appearance of intermediate densities turns out to be negligible.

The computational time required for solving the 3D beam model is 1.4 times larger than the time needed for solving the 2.5D beam model, indicating that the reduction in spatial dimension here only provides a relatively small gain in computational efficiency as compared to the reduction of a factor of 70 found in Sect. 6.1.1 for pure shape optimization. This can be explained by considering the computational time of the topology optimization procedure in more detail. In particular, the time required for the structural analysis of the beam for the 2.5D model is one order of magnitude smaller than for the 3D model. However, this gain in time is counterbalanced by the fact that the time required for the sensitivity analysis of the 2.5D model is one order of magnitude larger than that of the 3D model. The latter result is caused by two reasons. Firstly, in 3D topology optimization, the sensitivity of the global stiffness matrix can be efficiently obtained from the element stiffness matrices stored during the structural analysis, see Eqs. (88) and (89). In contrast, in 2.5D topology optimization, the calculation of the sensitivity of the global stiffness matrix requires the performance of a 1D FEM beam analysis, whereby the sensitivity of the stiffness matrix of each cross section needs to be determined a priori, see Eqs. (61)–(66) and (77), which obviously is computationally demanding. Secondly, the 1D beam FEM analysis must be repeated for the calculation of the sensitivity with respect to each element density. These two aspects thus make the topology sensitivity analysis for the 2.5D model computationally considerable more expensive than for the 3D model, and therefore result in only a relatively small decrease of the overall computational time by a factor of 1.4.

It should be noted that in the 2.5D beam model the number of cross sections has been chosen in accordance with the element density of the 3D beam model in longitudinal direction, in order to perform a consistent comparison of the simulation results at the cross-sectional level, see Fig. 10. From the viewpoint of computational efficiency, however, the number of cross sections in the 2.5D beam model could have been taken substantially lower without significantly compromising on the accuracy of the simulation results. It can be further noticed that the initial compliances plotted in Fig. 9 are different from those plotted in Fig. 8, although the same initial beam configuration is used in the shape and topology optimization analyses. This is, because in the shape optimization analysis the relative element densities are kept fixed at a value of 1, while the relative element densities in the topology optimization analysis are initially uniformly set equal to 0.4, in correspondence with the constraint on the volume fraction, $f_r=0.4$.

Fig. 9

Convergence behavior of the compliance c for pure topology optimization of 3D (triangles) and 2.5D (circles) beam models. The iteration number g refers to the loop for topology optimization, see Fig. 3

Fig. 10

Comparison of the optimized designs obtained by pure topology optimization of 3D (a) and 2.5D (b) beam models. The filtering of possible checkerboard patterns via Eq. (78) is omitted here in order to warrant an objective comparison of the 3D and 2.5D modeling results

Fig. 11

Cross-sectional (CS) relative densities obtained by pure topology optimization of 2.5D (top) and 3D (bottom) beam models. The number of each cross section denotes its location along the longitudinal direction of the beam, in agreement with the z-axis in Fig. 7. The filtering of possible checkerboard patterns via Eq. (78) is omitted here in order to warrant an objective comparison of the 2.5D and 3D modeling results

6.2 Coupled shape and topology optimization case studies

Now that the shape and topology implementations have been individually tested and validated, the cantilever beam problem depicted in Fig. 4 is subjected to a coupled shape and topology procedure in accordance with the sequentially-coupled computational scheme depicted in Fig. 3. The variation in shape and topology in the longitudinal beam direction is described by using 8 cross sections, which are distributed along the beam length as shown in Fig. 14a. As explained before, for post-processing of the analysis results, the first cross section at the clamped end of the cantilever beam (with index $k=1$) is taken the same as the adjacent second cross section (with index $k=2$), and thus does not contribute to the optimization procedure [6]. The locations of the control points of a cross section and the corresponding coordinates are given in Fig. 5 and Table 2. By leaving out the cross section related to the clamped end, the shape design variables $\mathbf{a}$ of the 7 remaining cross sections are assembled as

$$\begin{aligned} \mathbf{a} =\left[ (\mathbf{a} ^{\text {CS}}_2)^{\text {T}} , (\mathbf{a} ^{\text {CS}}_3)^{\text {T}} , \ldots , (\mathbf{a} ^{\text {CS}}_k)^{\text {T}} \right] ^{\text {T}} \quad \text {with} \quad k=2,3,\ldots ,8 , \end{aligned}$$

(95)

in which

$$\begin{aligned} \mathbf{a} ^{\text {CS}}_k=\left[ X_{1,1,k} , Y_{1,1,k} , Y_{2,1,k}, X_{1,2,k} \right] ^{\text {T}} , \end{aligned}$$

(96)

where $X_{1,1,k}$ and $Y_{1,1,k}$ are the x- and y-coordinates of control points $\mathbf{C} _{1,1,k}$, and $X_{1,2,k}$ and $Y_{2,1,k}$ are the x- and y-coordinates of control points $\mathbf{C} _{1,2,k}$ and $\mathbf{C} _{2,1,k}$, respectively. Note that the control points at the corners of a cross section can move in both the x- and y-directions, while the control points at the half-width and half-height of the cross section boundaries can only move in the y-direction and x-direction, respectively. The control points of a cross section are assumed to be line-symmetric with respect to the x- and y-axes, so that the locations of control points $\mathbf{C} _{3,1,k}$, $\mathbf{C} _{3,2,k}$, $\mathbf{C} _{1,3,k}$, $\mathbf{C} _{2,3,k}$ and $\mathbf{C} _{3,3,k}$ are prescribed by the corresponding control points above. The lower and upper bounds of $\mathbf{a} ^{\text {CS}}_k$ are, respectively, defined as $lb=[-1.5,-1.5,-2,-2]$ and $ub=[-0.2,-0.2,-0.2,-0.2]$. The parametric domain of the NURBS surface that defines a cross section is divided into $12 \times 20$ equally sized, rectangular parts, which define the grid for the 2D auxiliary FEM mesh. In the longitudinal direction, the model uses a discretization by 120 two-node beam elements, for which the z-coordinates are given by Eq. (93) with $l=121$. The stiffness $\mathbf{k} _e^{\text {b}}$ of each beam element e is computed from the stiffness of the corresponding cross section $\mathbf{K} _e^{\text {s}}$ via Eq. (34). Accordingly, under a stepwise change in cross-sectional properties, the optimized solution corresponds to a shape that varies linearly in the longitudinal direction. The volume fraction in Eq. (58) is defined as $f_r=0.4$. The structural compliance c and the beam volume V are calculated from the beam FEM model. The SQP and IP algorithms in the MATLAB solver fmincon are used to iteratively update the shape design variables $\mathbf{a}$ and element relative densities $\varvec{\rho }$ appearing in Eq. (58). The convergence criteria adopted for the individual shape and topology optimization steps are the same as those defined in Sect. 6.1. In addition, the outer loop of the coupled optimization procedure, which has been illustrated in the flowchart in Fig. 3, is assumed to be converged when the structural compliance meets the condition $\mid c^{w+1}-c^w \mid \le$1e−5, where w is the iteration number of the outer loop. Finally, the shape and topology sensitivities of the objective are computed with the expressions given in Sect. 5.1, whereby the 2D sensitivity filter formulated in Eq. (78) is applied in the topology optimization procedure. The filter size is set to $r_{min}=1.5\sqrt{V_e}$, where $V_e$ is the area of element e [30]. The convergence behavior for the structural compliance c is shown in Fig. 12. The CTSO solution procedure that starts with a topology optimization step takes more iterations ($w=10$) than the CSTO solution procedure that starts with a shape optimization step ($w=7$). Figure 13 shows the evolution of the first cross section at the clamped beam end during the convergence process for the CSTO and CTSO update schemes. The evolution of the cross section clearly visualizes that the CTSO and CSTO update sequences during the convergence process follow a different search path in the solution space of design variables, eventually leading to somewhat different local minima (or optimized compliances), i.e., $c=10.467$ Nm (CSTO) and $c=8.516$ Nm (CTSO).

Fig. 12

Convergence behavior for compliance c for coupled shape and topology optimization with CTSO (triangles) and CSTO (circles) update schemes. The iteration number w refers to the outer loop of the staggered update scheme, see Fig. 3

Figures 14 and 15 illustrate the optimized designs predicted by CSTO and CTSO sequences. The two solution procedures result in a comparable design concept, namely a tapered beam with a hollow cross section composed of relatively thin vertical webs and thick horizontal flanges. The cross section computed by the CSTO solution procedure has a smaller height-to-width ratio than the cross section following from the CTSO procedure. Further, the beam structure following from the CSTO update procedure contains one cross section (with index $k=4$) with an extra vertical web.

In summary, in structural optimization problems, the landscape of solutions is determined by the objective function(s), the design variables and constraints, the characteristics of the boundary value problem and the FEM discretization, which typically leads to a large number of local minima, see e.g., [25]. The above comparison of the analyses performed with the CTSO and CSTO update schemes illustrates that the convergence speed and the specific local minimum computed (i.e., the optimized compliance) are to some extent sensitive to the algorithmic features of the numerical update scheme applied, but that the final, optimized beam configurations of the two update schemes nevertheless are qualitatively similar.

Fig. 13

Evolution of the structural compliance c and the geometry of the first cross section at the clamped beam end during the convergence process for the CSTO and CTSO update schemes. The NURBS control points are indicated by the black dots, and w is the iteration of the outer loop of the update scheme, see Fig. 3

Fig. 14

Optimized control nets of 2.5D beam model. Initial design (a) and solutions obtained by coupled shape and topology optimization using CSTO (b) and CTSO (c) update schemes

Fig. 15

Optimized configurations of 2.5D beam model. Initial design (a) and solutions obtained by coupled shape and topology optimization using CSTO (b) and CTSO (c) update schemes

7 Conclusions

A coupled gradient-based optimization framework is presented that simultaneously optimizes the outer shape and the internal topology of beam-type structures by using a staggered update procedure. The objective function refers to the structural compliance, which is evaluated using 2.5D and 3D FEM models. In the 2.5D model, standard two-node beam elements are used along the longitudinal direction of the beam, whereby the cross-sectional properties of the beam elements are calculated from additional 2D FEM analyses. Conversely, in the 3D model, the beam geometry is simulated using 3D continuum elements. The shape of the beam-type structures is parameterized using NURBS, with the shape design variables being represented by the NURBS control points. The topology design variables are reflected by the relative densities assigned to each finite element. The design variables are iteratively updated by applying NURBS-based shape and density-based topology optimization techniques, which use analytic shape and topology sensitivities that ensure an accurate and computationally efficient solution procedure. A comparison study of a cantilever beam problem subjected to pure shape optimization and pure topology optimization illustrates that the 2.5D and 3D beam models lead to similar shape and topology designs, but that the 2.5D beam model has a significantly higher computational efficiency. Specifically, the computational times for the 2.5D model are about a factor 70 (shape optimization) and 1.4 (topology optimization) lower than for the 3D model, which indicates that in the coupled optimization approach the optimization of the shape provides the largest contribution to the higher computational efficiency of the 2.5D model. The coupled shape and topology optimization analysis subsequently performed on the 2.5D cantilever beam model demonstrates that the specific order at which the alternating shape and topology optimization increments are performed in the staggered update procedure turns out to have some influence on the final computational result for the boundary value problem considered. Further, the convergence speed for the optimization procedure starting with an incremental topology optimization step appears to be somewhat lower than that resulting from starting with an incremental shape optimization step, although it may be reasonably expected that this feature is problem dependent. Despite these differences, the final beam structures following from the two staggered update schemes illustrate how shape and topology can be efficiently optimized in an integrated, coupled fashion.