Self-moments stiffening effect and buckling strength of periodic Vierendeel beams

Abstract

This paper deals with the buckling phenomenon of periodic Vierendeel beams. Closed-form solutions for critical loads and deformed shapes are presented. They are built by exploiting several auxiliary solutions obtained for the discrete periodic girder and for a geometrically nonlinear micro-polar equivalent model. In particular, the girder when subjected to sinusoidal self-equilibrated systems of inner bending moments (self-moments) is analysed. The corresponding results are used for solving the large-deflection equilibrium problem of the continuous equivalent model by means of the eigenfunction expansion technique. Girder buckling conditions are then defined in terms of kinematics of the micro-polar model: more precisely, they are attained when special distributions of self-moments, able to bend the continuous system without violating compatibility of shear strains, act in the girder. It is shown that these systems, neglected in the theories presented so far, have a significant stiffening effect on the buckling girder behaviour. Moreover, they are governed by the continuity equation for micro-rotations that is solved in closed form by the Galerkin method, with the micro-polar model eigenfunctions as basis functions. The accuracy of the proposed solutions is verified by comparing them with those achieved by a series of finite element girder models.

1 Introduction

Periodic beams are very attractive design solutions from a structural point of view, since they have high strength and stiffness to density ratios. In addition, their modular character allows for both economy of manufacturing and energy and material savings; hence, they are also environmentally sustainable. In particular, the Vierendeel beam has found innumerable applications in several engineering fields like bridge and building structures, composite materials and ship constructions (i.e., [1,2,3,4,5,6,7]).

Another remarkable application of this kind of girder is the railway track. Actually, to study the conditions for the thermal buckling in the lateral plane, rails, sleepers and fasteners are treated as a Vierendeel girder constrained to the ballast by nonlinear springs whose load–deflection curve is identified by special tests [8,9,10,11,12,13,14].

The buckling properties of a Vierendeel beam under axial load may be studied by the Engesser method [15]. In [16], it is shown that this method is equivalent to modelling the discrete girder by a Timoshenko beam whose stiffness has to be evaluated by a suitable homogenization procedure (i.e. [17,18,19,20]). However, it gives unsatisfactory results when the cell size is not small compared with the girder length or non-negligible transversal shear forces and bending moments are induced in the chords [21, 22]. For these reasons, several theories have been formulated to overcome these limitations [6, 23,24,25,26,27].

An alternative approach to take into account these local effects is instead based on non-classical continuum theory. Till now, many micro-polar models have been proposed to study the behaviour of periodic beam lattices [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. Very recently, a micro-polar formulation has been adopted to analyse the buckling of web-core sandwich panels [46]. However, to the author’s best knowledge, very few publications can be found in the literature presenting continuous micro-polar models for analysing buckling properties of beam-like lattice systems.

In [17], the effective stiffness of a substitute micro-polar model was evaluated by energy equivalence concepts. The model, however, presents some doubtful stiffness couplings that make awkward the solution of its equilibrium equations. Furthermore, girder joint elasticity is not considered.

A special finite element is developed in [21] for calculating the buckling load of web-core sandwich beams. A geometrically nonlinear model is instead reported in [47] where the beam theory of [48, 49] is used. The corresponding equilibrium equations, however, cannot be solved in closed form, and the finite element method reported in [50] is adopted.

Some closed-form solutions for the buckling modes and critical loads of the Vierendeel girder are given in [51]. The continuous micro-polar model from which they are derived is based on the eigen-analysis of the unit cell transfer matrix [19, 52, 53]. The major drawback of this approach is that strains due to the longitudinal shear force are geometrically non-compatible, since they are associated to jumps in elementary cell micro-rotations. For this reason, predictions of this model are affected by large errors when the girder response is dominated by longitudinal shear strains. This occurs typically in the lateral thermal buckling of railway tracks. Actually, the present study is part of a long-term project aimed at developing a track model for designing against the thermal buckling phenomenon.

In this paper, accurate closed-form solutions for buckling loads and critical deformed shapes of the periodic girder are reported. They are obtained following a two-step methodology. First, some auxiliary solutions are built. In particular, the discrete girder response to sinusoidal self-equilibrated systems of inner bending moments (self-moments) is analysed. Next, the large-deflection equilibrium problem of the micropolar model of [51] is solved.

These results are used to study the conditions under which the girder may assume (neutral) equilibrium configurations without jumps in micro-rotations, namely it is bent without violating both equilibrium and geometrical compatibility. It is shown that the girder buckles when special distributions of self-moments act in it. These latter have been neglected in existing theories and have a significant stiffening effect on the buckling behaviour.

The remainder of this paper is organized as follows. Section 2 synthetically reviews the main aspects of the micro-polar girder model of [51]. In Sect. 3, the girder behaviour when subjected to sinusoidal self-moments is studied and the large-deflection equilibrium problem of the equivalent model under this loading condition is solved by means of the eigenfunction expansion technique. Girder critical loads and deformed shapes are obtained in Sect. 4 from the condition of continuity of the micro-rotations, using the Galerkin method. In Sects. 5 and 6, the results of a validation study carried out by the finite element method are presented and conclusions are finally drawn.

2 The micro–polar model

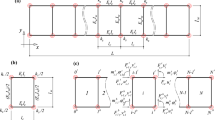
The unit cell generating the periodic beam is shown in Fig. 1. It has height $l_w$ and width $l_c$. In this scheme, web members are hinged to the chords and rotations of their end sections are restrained by torsional springs of stiffness $k_s$ fixed on the chords. These springs take into account the elasticity of the real girder joints. The chords and web rods are assumed to be Bernoulli–Euler beams made of linear elastic materials having Young’s moduli $E_c$ and $E_w$, respectively. We will denote by $A_c$ the chords cross-sectional area and by $I_c$ and $I_w$ chord and girder web second-order moments, correspondingly. Finally, web are assumed axially inextensible.

Fig. 1

Vierendeel beam unit cell

Fig. 2

Cells, sections and node labelling

Any quantity related to the girder ith nodal section will be affected in the following by the subscript i. Similarly, a quantity related to the top or bottom node of a nodal section will be denoted by the superscripts t or b, respectively. Finally, symbols $i^t$ and $i^b$ denote, respectively, top and bottom nodes of the section i (Fig. 2).

Fig. 3

Unit cell Dof’s and nodal forces

We denote by $F_{i\,x}^b$,$F_{i\,y}^b$ and $m_i^b$ and by $F_{i\,x}^t$,$F_{i\,t}^t$ and $m_{i}^t$, respectively, the horizontal and vertical force components and the moment applied on nodes $i^b$ and $i^t$ of a girder cell (Fig. 3).

Each girder node has three degrees of freedom: the horizontal and vertical displacements u and v and the rotation $\varphi$. However, in order to identify the girder’s deformed shape is more advantageous to adopt the following kinematic quantities: the mean axial displacement $u_i = 1/2 (u^t_i + u^b_i)$, the nodal section rotation $\psi _i = (u^b_i - u^t_i)/l_w$, the transverse displacement $v_i$ and, finally, the symmetric and antisymmetric parts of the section nodal rotations $\varphi _i = 1/2 (\varphi ^t_i + \varphi ^b_i)$ and ${\tilde{\varphi }}_i = 1/2 (\varphi ^t_i - \varphi ^b_i)$.

Hence, the inner static quantities performing work as results of changes of the previous kinematic variables are: the axial force ${n_i} = (F_{i\,x}^b + F_{i\,x}^t)/2,$ the bending moment ${M_i} = \left( {F_{i\,x}^b - F_{i\,x}^t} \right) {l_w}$ generated by the anti-symmetric axial forces, the shear force ${V_i} = F_{i\,y}^t + F_{i\,y}^b$, the resultant of the nodal moments ${m_i} = m_i^t + m_i^b$ and, finally, the difference between these moments ${{\tilde{m}}_i} = m_i^t - m_i^b$.

In the following, the usual convention of the beam theory is adopted for the moments $M_i$ and $m_i$ acting on a girder nodal section; namely, they will be positive if they act, respectively, counter-clockwise and clockwise on the right and left end section of a cell.

Fig. 4

Inner forces transmission modes: force sub-vector components (left column), unit cell deformed shapes (central column) and fundamental relationships (right column)

The state vector ${\mathbf {s}}$ of a girder nodal cross section consists of its displacements vector ${\mathbf {d}} = [u,\, \psi ,\, v,\, \varphi ,\, {\tilde{\varphi }} ]^\mathrm{T}$ and the vector ${\mathbf {f}}=[ n,\, M,\, V,\, m,\, {\tilde{m}}]^\mathrm{T}$ of the forces that the section transfers. Hence, the state vectors of the end sections of the cell i are ${{\mathbf {s}}_{i - 1}} = \left[ \mathbf {d}_{i - 1}^\mathrm{T}, \mathbf {f}_{i - 1}^\mathrm{T} \right] ^\mathrm{T}$ and ${{\mathbf {s}}_i} = \left[ \mathbf {d}_i^\mathrm{T}, \mathbf {f}_i^\mathrm{T}\right] ^\mathrm{T}$. They are related by the unit cell transfer matrix ${\mathbf {G}}$:

$$\begin{aligned} {\mathbf {G}}\,{{\mathbf {s}}_{i - 1}} = {{\mathbf {s}}_i}. \end{aligned}$$

The inner force transmission modes of the Vierendeel girder are sketched in Fig. 4. They are defined by the principal vectors of the matrix $\mathbf {G}$. More details on the construction of the matrix $\mathbf {G}$ and the derivation of its principal vectors may be found in [12, 19].

As shown in Fig. 4, during transmission of the bending moment, cell nodes and nodal sections to which they belong rotate by the same angle and the cell web rods remain undeformed. As a consequence of cell bending, the nodal and sectional rotations have the same change, namely $\Delta \psi = \Delta \varphi = \vartheta$ . Furthermore, the bending moment is composed of two parts: $M_h = 1/2 \beta _c \vartheta$, with $\beta _c =E_c A_c l^2_w/ l_c$, is the primary bending moment and is engendered by the couple of axial forces acting on the chords; $m_p = 2 \eta _c \vartheta$, with $\eta _c = E_c I_c/l_c$, is the secondary moment and is exclusively produced by the curvature change of the chords.

Fig. 5

Unit cell deformed shapes due to transversal (a) and longitudinal shears (b)

Fig. 6

Cross section and nodal rotations

The shear force transmission mode is instead generated by superposing the independent cell deformations shown in Figs. 5a and b. In the first one, only deformations of the chords occur. They produce the transversal shear forces V given by

$$\begin{aligned} V = \pm 24 (\eta _c / l_c) \gamma _V, \end{aligned}$$

with $\gamma _V$ being the cell shear strain highlighted in the same figure. In the second deformed shape, chords remain undeformed. Cell nodal sections rotate with respect to cell nodes by the angle $\Delta _\psi$. Consequently, the longitudinal shear forces

$$\begin{aligned}V_H = \pm 24 (\eta _w/l_w) \Delta _\psi ,\end{aligned}$$

where $\eta _w = (E_{w}\,I_{w}) / \left\{ l_{w} \left[ 1+6\,( E_{w}\,I_{w})/(k_{\theta }\,l_{w}) \right] \right\}$, and the primary bending moment change $\Delta M_h = V_H l_w$ are generated.

Finally, the axial force transmission mode causes only chords axial deformations; hence, the unit cell axial stiffness is $\beta _a = 2 E_cA_c/l_c$.

Fig. 7

Elementary cell deformed shapes due to: axial force (a), bending moment (b), transversal and longitudinal shear forces (c) and (d)

A continuous model consistent with the inner force transmission modes of Fig. 4 may be built by averaging the strain energies associated to these modes. For this aim, it is convenient to express sectional and nodal rotations in the following form:

$$\begin{aligned} \psi&= {\bar{\psi }}, \\ \varphi&= {\bar{\psi }} - \xi , \end{aligned}$$

with ${\bar{\psi }}$ being the common part of $\psi$ and $\varphi$ and $\xi$ the relative rotation of a section with respect to its nodes (Fig. 6).

Hence, the cell strain energy $E_u$ due to inner forces transmission modes can be written as [12]:

$$\begin{aligned} {{E}_{u}}=\,\,&\frac{1}{2}\left( \frac{{\beta }_{c}}{2}+2{{\eta }_{c}} \right) \Delta {{\bar{\psi _i }}^{2}}+E_s+ 12{{\eta }_{c}}{{\left( \widehat{\bar{\psi _i}}-\widehat{\xi _i} - \frac{\Delta v_i}{{{l}_{c}}} \right) }^{2}} + 12{{\eta }_{w}} \, {\widehat{{\xi _i }}^{2}} + \frac{1}{2}{{\beta }}_{a}\Delta {{u_i}^{2}}, \end{aligned}$$

(1)

where $\Delta (\,)_i$ and $\widehat{(\,)}_i$ denote, respectively, the change and the mean value of a quantity over the cell i and $E_s$ is the strain energy pertaining to the symmetric bending due to shear.

The strain energy density E of the 1-D equivalent continuum is obtained by normalizing the energy $E_u$ with respect to $l_c$ and evaluating the limit of this energy as $l_c \rightarrow 0$. Keeping in mind that $E_s$ is a higher-order infinitesimal quantity and denoting by ${\bar{\psi }} \left( x \right)$, $\xi (x)$, $u\left( x \right)$ and $v\left( x \right)$, respectively, the absolute and relative rotations and the transversal and horizontal displacements of the equivalent medium cross section, the density E may be expressed as:

$$\begin{aligned} E= \frac{1}{2} {{\Gamma }_{b}} {{\left( \frac{\mathop {}\!\mathrm {d}\bar{\psi }(x)}{\mathop {}\!\mathrm {d}x} \right) }^{2}}\!\!+\frac{1}{2}{{\kappa }_{V}}\gamma _\psi ^{2}+ \frac{1}{2}{{\kappa }_{H}}{{\xi (x) }^{2}}+ \frac{1}{2}{{\kappa }_{a}}\epsilon _a^{2}, \end{aligned}$$

where $\Gamma _b = \Gamma _h + \Gamma _p$, with $\Gamma _h = l_c \beta _c/2$ and $\Gamma _p = 2\eta _c l_c$ is the equivalent medium bending stiffness, $\kappa _a = \beta _a l_c$ the axial stiffness, $\kappa _V = 24 \eta _c / l_c$ and $\kappa _H = 24 \eta _w / l_c$, respectively, the transversal and longitudinal shear stiffness. In addition, $d {\bar{\psi }} / \mathrm{d}x$ is the bending curvature, $\gamma _\psi =\left( {{\bar{\psi }}}(x)- \xi (x) - {\mathop {}\!\mathrm {d}v(x)}/{\mathop {}\!\mathrm {d}x} \right)$ is the transverse shear strain and $\epsilon _a = \mathop {}\!\mathrm {d}u / \mathop {}\!\mathrm {d}x$ is the axial strain.

In Fig. 7 the deformed shapes of an elementary cell of the continuum medium due to the axial force, bending moment and the shear forces are shown.

Linear constitutive equations of the equivalent girder are obtained by differentiating $E_s$ with respect to these generalized strains:

$$\begin{aligned} \begin{aligned} M_b=&\, \Gamma _b \dfrac{\mathop {}\!\mathrm {d}\psi }{\mathop {}\!\mathrm {d}x}= \left( \Gamma _h + \Gamma _p \right) \dfrac{\mathop {}\!\mathrm {d}\psi }{\mathop {}\!\mathrm {d}x}, \quad \quad V = \kappa _V \gamma _\psi ,\\ T_H=&\,\kappa _H \xi , \quad \quad \quad \quad N = \kappa _a \epsilon _a. \end{aligned} \end{aligned}$$

(2)

In Eq. (2), the total bending moment is additively decomposed as $M_b = M_h + m_p$, where $M_h = \Gamma _h (d{\bar{\psi }}/\mathrm{d}x)$ and $m_p = \Gamma _p (d{\bar{\psi }}/\mathrm{d}x)$ are, respectively, the primary and secondary bending moments; moreover, V is the transversal shear force, N is the axial force, and finally $T_H$ is the primary bending moment change generated in a unit length elementary cell by the longitudinal shear force.

The importance of the micro-polar effect of the girder model may be estimated by the internal bending length $l_b$, given by the square root of the ratio between the longitudinal fibre bending modulus and its axial stiffness [54]. Assuming that couple stresses generating the micro-polar or secondary bending moment are uniformly distributed on the cross sections, the bending modulus ${\bar{\Gamma }}_p$ of the longitudinal fibres of the continuum medium may be evaluated as

$$\begin{aligned} {\bar{\Gamma }}_p =\frac{\Gamma _p}{2A_c} = \dfrac{E_c I_c}{A_c},\end{aligned}$$

while the fibres axial stiffness is equal to the chord’s Young’s modulus $E_c$. Hence, for the length $l_b$ we obtain the following very simple expression, independent of the unit cell sizes $l_c$ and $l_w$:

$$\begin{aligned} l_b = \rho _c, \end{aligned}$$

(3)

where $\rho _c$ is the central (inertial) radius of gyration of the chord cross section. Since, from results listed in Fig. 4, we easily recognize that also the ratio of the unit cell secondary bending stiffness to the cell axial stiffness is equal to $\rho _c$, we may affirm that the internal length $l_b$ given by Eq. (3) is perfectly consistent with the stiffness properties of the girder unit cell.

The equilibrium equations of the simply supported equivalent girder under the assumption of large deflections are derived by the principle of virtual work, assuming that the continuum medium is axially inextensible. The reference frame is chosen with the origin at the centre of the left end section and the x axis aligned with the girder axis. Constraints are such that the axial displacement at $x=0$ is zero, while on the right end section, at $x=L$, the axial load P is applied.

Fig. 8

Deformed shape of an equivalent girder element

Under the large deflection assumption, the axial and transversal displacements u and v of each point of the girder elastic line are not independent. Since the length $\mathrm{d}x$ of an elementary cell is unchanged during girder bending, it results (Fig. 8):

$$\begin{aligned} \mathrm{d}u = - \dfrac{1}{2} \left( \dfrac{\mathrm{d}v}{\mathrm{d}x} \right) ^2 \,\mathrm{d}x \end{aligned}$$

This corresponds in expressing the axial deformation of the 1D equivalent medium by the nonlinear Von Karman strain:

$$\begin{aligned} \epsilon _a = \dfrac{\mathrm{d}u}{\mathrm{d}x}+\dfrac{1}{2} \dfrac{\mathrm{d}v}{\mathrm{d}x}^2. \end{aligned}$$

Equilibrium conditions at inner points of the medium are:

$$\begin{aligned}&{{\Gamma }_{h}}\frac{{{d}^{2}}\bar{\psi }}{d{{x}^{2}}}={{{\kappa }_{H}}}\xi ; \end{aligned}$$

(4a)

$$\begin{aligned}&{{\Gamma }_{b}}\frac{{{d}^{2}}\bar{\psi }}{d{{x}^{2}}}={{{\kappa }_{V}}}\left( \bar{\psi }-\xi -\frac{\mathrm{d}v}{\mathrm{d}x} \right) ; \end{aligned}$$

(4b)

$$\begin{aligned}&{{{\kappa }_{V}}}\left( \frac{\mathrm{d}\bar{\psi }}{\mathrm{d}x}-\frac{\mathrm{d}\xi }{\mathrm{d}x}-\frac{{{d}^{2}}v}{d{{x}^{2}}} \right) =-P\frac{{{d}^{2}}v}{d{{x}^{2}}}. \end{aligned}$$

(4c)

Furthermore, at the end sections $x = 0$ and $x = L$ the following equalities must hold:

$$\begin{aligned}&\begin{aligned}&{{\left. {{\Gamma }_{b}}\frac{\mathrm{d}\bar{\psi }}{\mathrm{d}x} \right| }_{x=0,L }} \!\!\!\! =0,\\&\left. {{\Gamma }_{p}}\frac{\mathrm{d}\bar{\psi }}{\mathrm{d}x} \right| _{x=0,L }=0,\\ \end{aligned} \end{aligned}$$

(5)

$$\begin{aligned}&{{\left. v \right| }_{x=0,L}} = 0. \end{aligned}$$

(6)

Equation (4) are very similar to the equilibrium equations of a Timoshenko couple stress beam [48], frequently adopted as substitute continuum for Vierendeel girders [18, 20, 28], and well highlight that, to model consistently the girder shear behaviour, it is essential to consider separately the contributions to the bending moment due to the chord axial forces and bending as primary and micropolar bending moments. They reduce to the classical Timoshenko beam equilibrium equations when the relative rotations $\xi$, caused by the longitudinal shear force, are negligible that is for very stiff or rigid web rods.

Equations (5) are the boundary equilibrium conditions for the primary and micropolar bending moments. Equations (6) are instead the transversal constraint conditions for the simply supported equivalent medium.

Besides the deformations due to the inner forces, also the effects of self-equilibrated systems of bending moments have to be considered. These moments will be referred to as self-moments, for the sake of simplicity, and the same sign convention of the primary bending moment will be adopted for them. Typically, they arise each time a bending moment $M_b$, applied on an end nodal section S of the girder, is composed of primary and secondary parts $M_h'$ and $m_p'$ different from the parts $M_h =\alpha _h M_b$ and $m_p =\alpha _p m_p$ of the bending moment transferring mode, being $\alpha _h={\Gamma _h}/{\Gamma _b}$ and $\alpha _p={\Gamma _p}/{\Gamma _b}$. Since any system of primary and micro-polar bending moments $(M_h', m_p')$ may be univocally decomposed in a system that is transferred according to the cell transferring mode and in a corresponding self-moment $\mu$,

$$\begin{aligned} M'_h&= M_h+ \mu ,\\ m'_p&= m_p-\mu , \end{aligned}$$

according to the De Saint Venant principle, at a distance sufficiently large from S the self-moment $\mu$ will be negligible since it is decayed and the transmitted bending moment will be composed only of the parts $M_h$ and $m_p$.

Alternatively, two adjacent cells may interact by a self-moment to generate in the nodal section they share a jump in the nodal rotations $\varphi$. It is shown in Sect. 4 that these jumps are needed to accommodate the changes in the longitudinal shear strains.

Fig. 9

Self-moments systems decaying in positive (a), and negative verse (b), of x axis

Cell strains generated by a self-moment are given by the eigenvectors of the transfer matrix $\mathbf {G}$ associated to nonzero eigenvalues. In the case of a self-moment $\mu _{(+)}$ decaying along the positive x axis (Fig. 9a), the strains it causes are:

$$\begin{aligned}&\Delta \psi _{(+)}= 2\eta _{r}\,{\frac{\left( \lambda -1 \right) }{\lambda \Delta _{\mu }}} \, \mu _{(+)}, \end{aligned}$$

(7a)

$$\begin{aligned}&\Delta \varphi _{(+)}= -\frac{1}{2} \beta _{r} \,{\frac{ \left( \lambda -1 \right) }{\lambda \Delta _{\mu }}} \, \mu _{(+)}, \end{aligned}$$

(7b)

$$\begin{aligned}&\gamma _{\psi \, (+)} = {\hat{\psi }}_{(+)} - \dfrac{\Delta v_{(+)}}{l_c}= - \frac{1}{4} \left( 4\,\eta _{c}+\beta _{c} \right) \, {\frac{\left( \lambda +1 \right) }{\lambda \Delta _{\mu } \, }} \, \mu _{(+)}, \end{aligned}$$

(7c)

with $\Delta _\mu =\beta _{{c}} \eta _{{c}} \left( \lambda -1 \right) -6 \eta _{w} \left( \beta _{{c}}+4 \eta _{{c}} \right)$ and where $\lambda$ is the eigenvalue greater than unit of the transfer matrix, given by the following quadratic equation:

$$\begin{aligned} {\lambda }^{2}- \left( 2+12\,{\frac{\eta _{w}}{\eta _{c}}}+48\,{\frac{\eta _{w}}{\beta _{c}}} \right) \lambda +1=0 .\end{aligned}$$

In addition, it may be shown that cell deformations due to $\mu _{(+)}$ are such that the quantity $\gamma _{\varphi \, (+)}= {\hat{\varphi }}_{(+)} - \Delta v_{(+)} / l_c$ is equal to zero [12].

The cells strains due to a self-moment decaying in the negative verse may be derived by simple symmetry considerations (Fig. 9b). They are:

$$\begin{aligned}&\Delta \psi _{(-)}= 2\eta _{c}\,{\frac{\left( \lambda -1 \right) }{ \Delta _{\mu }}} \, \mu _{(-)}, \end{aligned}$$

(8a)

$$\begin{aligned}&\Delta \varphi _{(-)}= -\frac{1}{2} \beta _{c} \,{\frac{ \left( \lambda -1 \right) }{ \Delta _{\mu }}} \, \mu _{(-)}, \end{aligned}$$

(8b)

$$\begin{aligned}&\gamma _{\psi \, (-)} = \frac{1}{4} \left( 4\,\eta _{c}+\beta _{c } \right) \, {\frac{\left( \lambda +1 \right) }{ \Delta _{\mu } \, }} \, \mu _{(-)}, \end{aligned}$$

(8c)

Also in this case, the cell deforms with $\gamma _{\varphi \, (-)}= {\hat{\varphi }}_{(-)} - \Delta v_{(-)} / l_c =0$.

3 Girder analysis

We analyse the deformations occurring in a unit cell when it is subjected to a self-moment $m_r$ applied on its right-side nodal section. This particular loading condition can be built by superimposing the two systems of self-moments $\mu _{(+)}$ and $\mu _{(-)}$ decaying through the cell in the positive and negative direction, respectively. $\mu _{(+) }$ and $\mu _{(-)}$ have to satisfy the conditions

$$\begin{aligned} \begin{aligned}&\mu _{(+)} + \mu _{(-)} =0&\quad \quad \text {at the left end section,}\\&\dfrac{\mu _{(+)}}{\lambda } + \lambda \cdot \mu _{(-)} = m_r&\quad \quad \text {at the right end section}. \end{aligned} \end{aligned}$$

(9)

The solution of Eq. (9) is:

$$\begin{aligned} \mu _{(+)} =- \mu _{(-)} = \dfrac{\lambda }{1-\lambda ^2} \cdot m_r . \end{aligned}$$

(10)

Since cell strains due to $\mu _{(+)}$ and $\mu _{(-)}$ can be evaluated by Eqs. (7) and (8), those generated by $m_r$ can be written by the superposition principle as

$$\begin{aligned} \begin{aligned} \Delta \psi _r&= \Delta \psi _{(+)} \mu _{(+)} +\Delta \psi _{(-)}\mu _{(-)}=\dfrac{\lambda }{1+\lambda } \Delta \psi _{(+)} m_r = c_\psi \cdot m_r , \\ \Delta \varphi _r&= \Delta \varphi _{(+)} \mu _{(+)} +\Delta \varphi _{(-)}\mu _{(-)}=\dfrac{\lambda }{1+\lambda } \Delta \varphi _{(+)} m_r = c_\varphi \cdot m_r ,\\ \gamma _{\psi \,r}&=\Delta \gamma _{(+)} \mu _{(+)} +\Delta \gamma _{(-)}\mu _{(-)}=\dfrac{\lambda }{1-\lambda } \gamma _{(+)}, m_r = c_\gamma \cdot m_r, \end{aligned} \end{aligned}$$

(11)

where the subscript r at the RHS is adopted to indicate that these strains are due to $m_r$ and

$$\begin{aligned} \begin{aligned} c_\psi&=\dfrac{\lambda }{1+\lambda } \Delta \psi _{(+)} = \dfrac{{2{\eta _c}}}{{{\Delta _\mu }}}\dfrac{{\lambda - 1}}{{\lambda + 1}}, \\ c_\varphi&=\dfrac{\lambda }{1+\lambda } \Delta \varphi _{(+)} =- \frac{{{\beta _c}}}{{2{\Delta _\mu }}}\frac{{\lambda - 1}}{{\lambda + 1}}, \\ c_\gamma&= \dfrac{\lambda }{1-\lambda } \gamma _{(+)}= \frac{1}{2}\frac{{2{\eta _c} + {\beta _c}/2}}{{{\Delta _\mu }}}\frac{{\lambda + 1}}{{\lambda - 1}}. \end{aligned} \end{aligned}$$

(12)

The deformations due to a self-moment $m_l$ applied on the left nodal section are straightforwardly derived from those of $m_r$ by simple symmetry considerations. They are:

$$\begin{aligned} \begin{aligned} \Delta \psi _l&=c_\psi \, m_l , \\ \Delta \varphi _l&= c_\varphi \, m_l ,\\ \gamma _l&= - c_\gamma \, m_l. \end{aligned} \end{aligned}$$

(13)

Fig. 10

Girder composed of hinged cell subjected to self-moments $m_i$

We study now the behaviour of a simply supported girder composed of N cells hinged each other as shown in Fig. 10. In each nodal section i of this girder, the positive self-moment

$$\begin{aligned} m_i = m_n \sin \left( \frac{n \pi }{L} x_i \right) = m_n \sin \left( \frac{n \pi }{N} i \right) \end{aligned}$$

(14)

is applied, where $x_i = i l_c$ is the abscissa of the section i, $L=N l_c$ is the girder length, n an arbitrary integer number and $m_n$ a real parameter defining the self-moments amplitude.

The strains in the cells of this girder may be evaluated by formulae (11)–(13), by invoking the superposition principle:

$$\begin{aligned} \Delta \psi _i&= c_\psi \, \left( m_i + m_{i-1} \right) , \end{aligned}$$

(15a)

$$\begin{aligned} \Delta \varphi _i&= c_\varphi \, \left( m_i + m_{i-1} \right) , \end{aligned}$$

(15b)

$$\begin{aligned} \gamma _{\psi \, i}&= c_\gamma \, \left( m_i - m_{i-1}. \right) \end{aligned}$$

(15c)

In addition, it will result $\gamma _{\varphi \, i}= {{\hat{\varphi }}}_i - \Delta v_i/l_c=0$.

Since the cell strains are known, the deformed shape of the girder may be derived. By virtue of Eq. (15a), nodal section rotations, actually, are given by

$$\begin{aligned} \psi _j = \psi _0 + \sum _{i=1}^{j} \Delta \psi _i= \psi _0 + c_{\psi } \sum _{i=1}^j \left( m_i + m_{i-1} \right) , \end{aligned}$$

(16)

where $\psi _0$ is the rotation of the left end section, to be determined by the boundary conditions.

When Eq. (14) is substituted in Eq. (16), since $\sin \left( \dfrac{n \pi }{L} x_0 \right) = \sin \left( 0 \right) =0$, we may write the result

$$\begin{aligned} \psi _j&= \psi _0 + c_{\psi } \left[ \sum _{i=1}^j \sin \left( \dfrac{\pi n}{L} x_i \right) + \sum _{i=1}^j \sin \left( \dfrac{\pi n}{L} x_{i-1} \right) \right] = \nonumber \\&= \psi _0 + c_{\psi } \left[ \sin \left( \dfrac{\pi n}{L} x_j \right) + 2 \sum _{i=1}^{j-1} \sin \left( \dfrac{\pi n}{L} x_{i} \right) \right] . \end{aligned}$$

(17)

Furthermore, it can be shown that (Appendix A):

$$\begin{aligned} \sin \left( \dfrac{\pi n}{L} x_j \right) + 2 \sum _{i=1}^{j-1} \sin \left( \dfrac{\pi n}{L} x_{i} \right) = \left\{ \begin{aligned}&0, \quad \text {if} \quad n = h \cdot (2N), \\&\dfrac{\cos (n \pi / 2N)}{\sin (n \pi / 2N) }\left[ 1 - \cos \left( \dfrac{\pi n}{N} j \right) \right] , \quad \text {otherwise}, \end{aligned} \right. \end{aligned}$$

(18)

with $N = L/l_c$ as the number of cells composing the girder and h an integer number. Hence, when $n \ne h \cdot (2N)$, the sectional rotation $\psi _j$ may be written in the simple form

$$\begin{aligned} \psi _j = \psi _0 + c_\psi m_n \dfrac{\cos (n \pi / 2N)}{\sin (n \pi / 2N) }\left[ 1 - \cos \left( \dfrac{\pi n}{N} j \right) \right] . \end{aligned}$$

(19)

Fig. 11

Deflection change due to nodal section rotation $\psi _{i-1}$ (a), cell bending $\Delta \psi _i$ (b), and shear strain (c)

As shown by the sketch of Fig. 11, the transversal displacement change $\Delta v_i$ over the cell i is given by

$$\begin{aligned} \Delta v_i = l_c \cdot \left( \psi _{i-1} + \frac{1}{2} \Delta \psi _i - \gamma _i \right) . \end{aligned}$$

(20)

Therefore, taking into account the girder boundary conditions, the displacement $v_j$ of the nodal section j is given by:

$$\begin{aligned} v_j = \sum _{i=1}^j \Delta v_i =l_c \cdot \left( \sum _{i=1}^j \psi _{i-1} + \frac{1}{2} \sum _{i=1}^j \Delta \psi _i - \sum _{i=1}^j \gamma _i \right) . \end{aligned}$$

(21)

By virtue of Eqs. (14) and (15), the summations of the changes $\Delta \psi _i$ and shear strains $\gamma _i$ may be written as

$$\begin{aligned} \sum _{i=1}^j&\Delta \psi _i =\sum _{i=1}^j \left( \psi _j - \psi _{j-1} \right) = \psi _j - \psi _0, \nonumber \\ \sum _{i=1}^j&\gamma _i = c_\gamma \, m_n \, \sum _{i=1}^j \left\{ \sin \left[ \frac{n \pi }{N} i \right] - \sin \left[ \frac{n \pi }{N} (i-1) \right] \right\} = \nonumber \\&\quad =c_\gamma \, m_n \, \sin \left( \frac{n \pi }{N} j \right) . \end{aligned}$$

(22)

In addition, for $n \ne h (2N),$ it may be shown that (see also Appendix B):

$$\begin{aligned}&\sum _{i=1}^j \psi _{i-1} + \dfrac{1}{2} \sum _{i=1}^j \left( \psi _i - \psi _{i-1} \right) =\sum _{i=0}^{j-1} \psi _{i} + \dfrac{1}{2} \left( \psi _j - \psi _{0} \right) \end{aligned}$$

(23a)

$$\begin{aligned}&\quad = j \left( \psi _0 + c_\psi \, m_n \, \frac{\cos (n \pi / 2N)}{\sin (n \pi / 2N)} \right) - \frac{1}{2} c_\psi \, m_n \frac{\cos ^2 (n \pi / 2N)}{\sin ^2 (n \pi / 2N)} \sin \left( \frac{n \pi }{N} j \right) . \end{aligned}$$

(23b)

Substituting Eqs. (22) and (23) into Eq. (21), results in

$$\begin{aligned} v_j&= l_c \left\{ j \left( \psi _0 + c_\psi \, m_n \, \frac{\cos (n \pi / 2N)}{\sin (n \pi / 2N)} \right) - \frac{1}{2} c_\psi \, m_n \frac{\cos ^2 (n \pi / 2N)}{\sin ^2 (n \pi / 2N)} \sin \left( \frac{n \pi }{N} j \right) \right. \nonumber \\&\left. - c_\gamma \, m_n \, \sin \left( \frac{n \pi }{N} j \right) \right\} , \quad \quad \text {with} \quad n \ne h (2N). \end{aligned}$$

(24)

Since at the girder boundaries ($j=0,N$) the conditions $v_0=v_N=0$ must hold from Eq. (24), we derive the following result for $\psi _0$:

$$\begin{aligned} \psi _0 = - c_\psi \, m_n \frac{\cos (\pi n / 2 N)}{\sin (\pi N / 2 N)}, \end{aligned}$$

that, when substituted in Eqs. (19) and (24), allows to write, respectively, the sectional rotations $\psi _j$ and the transversal displacements $v_j$ as

$$\begin{aligned} \psi _j&= - m_n c_\psi \dfrac{\cos (n \pi / 2 N)}{\sin (n \pi / 2 N)} \cos \left( \dfrac{n \pi }{N} j\right) , \end{aligned}$$

(25a)

$$\begin{aligned} v_j&= - l_c \, m_n \left( c_\gamma + \dfrac{1}{2} \, c_\psi \, \dfrac{\cos ^2 (n \pi / 2N)}{\sin ^2 (n \pi / 2N)} \right) \sin \left( \dfrac{n \pi }{N} j \right) , \end{aligned}$$

(25b)

with $n \ne h (2N).$

We denote by $\varphi _i^{( - )}$ and $\varphi _i^{( + )}$ the nodal rotations that occur, respectively, at the left and right end sections of the cells i and $i+1$, sharing the nodal section i of the girder (Fig. 10).

These rotations are evaluated observing that the cells deform with $\gamma _\varphi = 0$. Hence, the following condition holds for the nodal rotations of the cell i:

$$\begin{aligned}{{\hat{\varphi }}} _{i} = \frac{1}{2}\left( {\varphi _{i - 1}^{( + )} + \varphi _i^{(-)}} \right) = \varphi _{i - 1}^{( + )} + \frac{1}{2}\Delta {\varphi _i} = \frac{\Delta {v_i}}{l_c}.\end{aligned}$$

When Eq. (20) is substituted in the previous result, we obtain

$$\begin{aligned} \varphi _{i - 1}^{( + )} = {\psi _{i - 1}} + \frac{1}{2}\Delta {\psi _i} - {\gamma _{\psi \,i}} - \frac{1}{2} {\Delta {\varphi _i}}. \end{aligned}$$

(26)

The nodal rotation $\varphi _i^{( - )}$ is then straightforwardly evaluated as

$$\begin{aligned} \varphi _i^{( - )} = \varphi _{i - 1}^{( + )} + \Delta {\varphi _i} = {\psi _{i - 1}} + \frac{1}{2}\Delta {\psi _i} - {\gamma _{\psi \,i}} + \frac{1}{2}\Delta {\varphi _i}. \end{aligned}$$

(27)

Thus, at each nodal section i of the considered girder the jump

$$\begin{aligned} \delta {\varphi _i} = \varphi _i^{( + )} - \varphi _i^{( - )} \end{aligned}$$

(28)

in the nodal rotations occurs. From Eq. (28), by means of Eqs. (26),(27), (25) and (15) and some simplifications carried out by the prosthaphaeresis formulae, the following expression of $\delta {\varphi _i}$ is derived:

$$\begin{aligned} \delta {\varphi _i}&= (\psi _i - \psi _{i-1}) + \frac{1}{2}\left[ {\left( {\Delta {\psi _{i + 1}} - \Delta {\psi _i}} \right) - \left( {\Delta {\varphi _{i + 1}} + \Delta {\varphi _i}} \right) - \left( {{\gamma _{\psi \,i + 1}} - {\gamma _{\psi \,i}}} \right) } \right] \nonumber \\&= 2\,{m_n}\left[ {\left( {{c_\psi } - {c_\varphi }} \right) {{\cos }^2}\left( {\frac{{\pi n}}{{2N}}} \right) + 2\,{c_\gamma }\, {{\sin }^2}\left( {\frac{{\pi n}}{{2N}}} \right) } \right] \sin \left( {\frac{{\pi n}}{L}x_i} \right) . \end{aligned}$$

(29)

If n is an integer multiple of the cell number N, namely $n = h N$, then $m_i = m_n \sin (\pi \, h \, i) = 0$ (with $i=0 \ldots N$), the girder will remain in the undeformed configuration and it will be trivially

$$\begin{aligned}v_i=\psi _i=\varphi _i^{(+)}=\varphi _i^{(-)}=\delta \varphi _i = 0.\end{aligned}$$

From previous results, a continuous approximation of the girder behaviour under sinusoidal distributions of inner self-moments may be straightforwardly derived. For this aim, the discrete solutions given by Eq. (25) are extended to the real range [0, L] by substituting the discrete quantity i by the ratio $x / l_c$. In the following, we will denote these continuous approximations, respectively, as $\psi _0^{(n)}(x)$, $v_0^{(n)}(x)$ where the superscript (n) is used to denote that they are obtained for a sinusoidal self-moments of wavelength L/n, with $n \ne h \, (2N)$. Obviously, the continuous approximation of the girder response when $n = h \, (2N)$ is $\psi _0^{(n)}(x) = v_0^{(n)}(x) =0$.

The nodal rotations $\varphi _0^{(n)}(x)$ of the elementary cells composing the continuum medium are instead obtained by a limiting process observing that total changes over a cell of the nodal rotations of the discrete girder may be expressed as

$$\begin{aligned} \overline{\Delta \varphi _i} = \Delta \varphi _i + \delta \varphi _i \, {\varvec{H}} (x-x_{i}), \end{aligned}$$

having denoted by ${\varvec{H}}(x)$ the Heaviside function. Hence, the nodal rotation $\varphi _j$ at section j of the discrete girder is given by

$$\begin{aligned} \varphi (x_j) = \varphi _0 + \sum _{i=1}^{j} \Delta \varphi _{i} + \sum _{i=1}^{j} \delta \varphi _i {\varvec{H}}(x_j-x_i), \end{aligned}$$

(30)

where $\varphi _0$ is the nodal rotation at section $i=0$ to be evaluated by Eq. (26) and

$$\begin{aligned} \sum _{i=1}^{j} \Delta \varphi _{i} = m_n c_{\varphi } \dfrac{\cos (n \pi / 2N)}{\sin (n \pi / 2 N)} \left[ 1 - \cos \left( \dfrac{n \pi }{L} x_j \right) \right] . \end{aligned}$$

(31)

This latter result is obtained from Eq. (15b) by the same procedure as Eq. (19).

In the limit of $l_c / L \rightarrow 0$, from Eq. (30), taking into account Eqs. (29) and (31), we obtain

$$\begin{aligned} \varphi _0^{(n)} (x)= {\bar{\varphi }}_n + \int _{0}^{x}\mathrm{d}\varphi + \int _{0}^{x} \delta \varphi , \end{aligned}$$

(32)

with ${\bar{\varphi }}_n = \varphi _0$ initial value of $\varphi _0^{(n)}$, while

$$\begin{aligned} \int _{0}^{x}\mathrm{d}\varphi = \lim _{\begin{array}{c} j\rightarrow \infty \\ j \cdot l_c = x \end{array}} \left( \sum _{i=1}^{j} \Delta \varphi _i \right) = m_n c_{\varphi } \dfrac{\cos (n \pi / 2N)}{\sin (n \pi / 2 N)} \left[ 1 - \cos \left( \dfrac{n \pi }{L} x \right) \right] \end{aligned}$$

(33)

and

$$\begin{aligned} \int _{0}^{x}\delta \varphi = \lim _{\begin{array}{c} j\rightarrow \infty \\ j \cdot l_c = x \end{array}} \left( \sum _{i=1}^{j} \delta \varphi _i {\varvec{H}}(x_j-x_i) \right) = \lim _{\begin{array}{c} j\rightarrow \infty \\ j \cdot l_c = x \end{array}} \left( \sum _{i=1}^{j} \dfrac{\delta \varphi _i}{l_c} \left( x_i - x_{i-1} \right) \right) \end{aligned}$$

(34)

are, respectively, the finite changes of the rotations $\varphi _0^{(n)}(x)$ due to the cell deformations and the micro-jumps occurring at each girder cross section. When Eq. (29) is substituted in Eq. (34) and the limit is evaluated, the following results are finally obtained for the equivalent system micro-jumps:

$$\begin{aligned} \delta \varphi _0^{(n)} (x) = {} \frac{2 \, m_n}{l_c} \, \left[ {\left( {{c_\psi } - {c_\varphi }} \right) {{\cos }^2}\left( {\frac{{\pi n}}{{2N}}} \right) + 2\,{c_\gamma }\, {{\sin }^2}\left( {\frac{{\pi n}}{{2N}}} \right) } \right] \sin \left( {\frac{{\pi n}}{N}x} \right) \mathrm{d}x. \end{aligned}$$

(35)

It is worth noting that in [6] an analysis is reported that is also based on the Heaviside function. It allows for determining the local deflections of the face plates in web-core sandwich beams. Here, instead the H() function is used for evaluating limit as $l_c / L \rightarrow 0$ of the jumps $\Delta \varphi _i$.

Fig. 12

Simply supported girder subjected to the axial load P

We study now the response of the girder when it is distorted by the self-moments of Eq. (14) and the axial load P is applied on it (Fig. 12). For this aim, we use the homogenized model of Sect. 2. Its equilibrium equations, Eq. (4), are modified by adding the term $-P\, \mathrm{d}v_0/\mathrm{d}x$ at the RHS of Eq. (4)c, to take into account the shear force generated by the axial load as consequence of the initial deflections $v_0^{(n)}$:

$$\begin{aligned} {k_V}\left( {\psi - \xi - \frac{{\mathrm{d}v}}{{\mathrm{d}x}}} \right) = - P\frac{{\mathrm{d}v}}{{\mathrm{d}x}} - P\frac{{\mathrm{d}{v_0^{(n)}}}}{{\mathrm{d}x}}, \end{aligned}$$

(36)

where by virtue of Eq. (25b)

$$\begin{aligned} \dfrac{\mathop {}\!\mathrm {d}v_0^{(n)}}{\mathop {}\!\mathrm {d}x}= \dfrac{n \pi }{L} \, V_0^{(n)} \cos \left( \dfrac{n \pi }{L} x\right) , \end{aligned}$$

(37)

with

$$\begin{aligned} V_{0}^{(n)} = \left\{ \begin{aligned}&\quad 0,\quad \quad \mathrm{{if }} \, n = h\,N ,\\&-{l_c}{m_n} \left( {{c_\gamma } + \dfrac{1}{2}{} {c_\psi } \dfrac{{{{\cos }^2}(n\pi /2N)}}{{{{\sin }^2}(n\pi /2N)}}} \right) ,\,&\mathrm{{otherwise.}} \end{aligned} \right. \end{aligned}$$

(38)

Equations (4a and b) and (36) may be solved by the Navier solution procedure. The unknown functions are expressed by the following expansion series:

$$\begin{aligned} \begin{aligned} v(x)&= \sum \limits _{k = 1}^\infty {{V_k}\sin \left( {\frac{{\pi k}}{L}x} \right) }, \\ \psi (x)&= \sum \limits _{k = 1}^\infty {{\Psi _k}\cos \left( {\frac{{\pi k}}{L}x} \right) }, \\ \xi (x )&= \sum \limits _{k = 1}^\infty {{\Xi _k}\cos \left( {\frac{{\pi k}}{L}x} \right) }, \end{aligned} \end{aligned}$$

(39)

where $V_k$, $\Psi _k$ and $\Xi _k$ are amplitudes to be determined and the basis functions are the eigenfunctions of the large deflection problem (4)–(6).

Equation (39) satisfies the boundary conditions, Eq. (5), for any value of $V_k$, $\Psi _k$ and $\Xi _k$. By substituting them in equilibrium equations (4a-b) and (36), we obtain:

$$\begin{aligned} \sum \limits _{k = 1}^{ + \infty }&{\left( {\frac{{{} {k^2}{\pi ^2}}}{{{L^2}}}{\Gamma _h}{\Psi k} + {k_H}{} {\Xi _k}} \right) \cos \left( {\frac{{k\pi {} }}{L}x} \right) } = 0 ,\\ \sum \limits _{k = 1}^{ + \infty }&{\left[ {\frac{{{k^2}{\pi ^2}}}{{{L^2}}}{\Gamma _b}{} {\Psi _k} + {k_V}{} \left( {{\Psi _k} - {\Xi _k} - \frac{{{} k\pi }}{L}{V_k}} \right) } \right] \cos \left( {\frac{{k\pi {} }}{L}x} \right) = 0}, \\ \sum \limits _{k = 1}^{ + \infty }&{\left[ {{k_V}\left( {{\Psi _k} - {\Xi _k} - \frac{{k\pi }}{L}{V_k}} \right) + P\frac{{k\pi }}{L}\left( {{V_k} + {V_{0k}}} \right) } \right] \cos \left( {\frac{{k\pi {} }}{L}x} \right) } = 0. \end{aligned}$$

When each of previous equations is multiplied by $\sin \left( m \pi x / L \right)$, with $m=1,\,2, \ldots , +\infty$, and integrated over (0, L), the following systems of algebraic equations are achieved

$$\begin{aligned} \left\{ \begin{aligned}&\dfrac{{{m^2}{\pi ^2}}}{{{L^2}}}{\Gamma _h}{\Psi _m} + {k_H}{} {\Xi _m} = 0,\\&\dfrac{{{m^2}{\pi ^2}}}{{{L^2}}}{\Gamma _b}{} {\Psi _m} + {k_V}{} \left( {{\Psi _m} - {\Xi _m} - \dfrac{{n\pi }}{L}{V_m}} \right) = 0,\\&{k_V}\left( {{\Psi _m} - {\Xi _m} - \dfrac{{n\pi }}{L}{V_m}} \right) + P\dfrac{{m\pi }}{L}\left( {{V_m} + \delta _{m\,n}{V_{0}^{(n)}}} \right) = 0, \end{aligned} \right. \end{aligned}$$

with $\delta _{mn}$ being the Kronecker symbol. Their solutions are

$$\begin{aligned} \Psi _m = V_m = \Xi _m = 0, \quad \quad \text {if} \quad m \ne n, \end{aligned}$$

(40)

and

$$\begin{aligned} \begin{aligned} {\Psi _m}&={\Psi _n} = \dfrac{{n\pi }}{L} \dfrac{P/P_{e\,n}}{1 - {P}/P_{cr\,n}} {V_{0n}}, \\ {\Xi _m}&= {\Xi _n} = - \frac{{{n^3}{\pi ^3}}}{{{L^3}}}\frac{{{\Gamma _h}}}{{{k_H}}}{V_{0n}} \dfrac{P/P_{e\,n}}{1 - {P}/P_{cr\,n}}, \\ {V_m}&={V_n} = \frac{P/{P_{cr\,n}}}{1 - {P} / P_{cr\,n}} {V_{0n}}, \end{aligned} \end{aligned}$$

(41)

if $m=n$. In Eq. (41), $P_{cr\,n}$ and $P_{e\,n}$ are given by

$$\begin{aligned} P_{cr\,n}= & {} \dfrac{P_{e \,n}}{1+P_{e\,n}\chi }, \end{aligned}$$

(42)

$$\begin{aligned} P_{e\,n}= & {} n^2 \pi ^2 \dfrac{\Gamma _b}{L^2}, \end{aligned}$$

(43)

where $\chi = 1/\kappa _V + \alpha _h/\kappa _H$ with $\alpha _h = \Gamma _h / \Gamma _b$. They are the nth critical loads, respectively, of the equivalent model of Sect. 2 and the simply supported Euler–Bernoulli beam having bending stiffness equal to $\Gamma _b$.

In conclusion, by virtue of Eqs. (39) and (41), when the axial load P is applied on the girder distorted by the self-moments of wavelength n, it causes the following rotations and transversal displacements changes:

$$\begin{aligned} \psi _P^{(n)}(x)&= \dfrac{{n\pi }}{L} \dfrac{P/P_{En}}{1 - {P}/P_{cr\,n}} {V_{0n}} \cos \left( \frac{n \pi }{L} x \right) , \end{aligned}$$

(44a)

$$\begin{aligned} \xi _P^{(n)}(x)&= - \frac{{{n^3}{\pi ^3}}}{{{L^3}}}\frac{{{\Gamma _h}}}{{{k_H}}} \dfrac{P/P_{En}}{1 - {P}/P_{cr\,n}} {V_{0n}} \cos \left( \frac{n \pi }{L} x \right) , \end{aligned}$$

(44b)

$$\begin{aligned} v_P^{(n)}(x)&= \frac{P/{P_{cr\,n}}}{1 - {P} / P_{cr\,n}} {V_{0n}} \sin \left( \frac{n \pi }{L} x\right) . \end{aligned}$$

(44c)

Obviously, the solutions given by Eqs. (44) make sense only when $P \ne P_{cr\,n}$.

4 Buckling load

In the homogenized girder the $\xi$ relative rotations are generated by the longitudinal shear is force $V_H$. From Eqs. (4a and b) and (36), it can be easily recognized that this inner force is given by

$$\begin{aligned} V_H = \alpha _h \dfrac{ V}{l_w} = - \dfrac{\alpha _h}{l_w}P \left( \frac{\mathop {}\!\mathrm {d}v_0}{\mathop {}\!\mathrm {d}x} + \frac{\mathop {}\!\mathrm {d}v}{\mathop {}\!\mathrm {d}x} \right) .\end{aligned}$$

Fig. 13

Deformations of two elementary cells due to the longitudinal shear

Since the transversal shear force is variable along the girder, the equilibrium deformed shape given by Eq. (44) is not kinematically admissible. In fact, if we consider two adjacent elementary cell located at abscissae x and $x + \mathrm{d}x$, these are subjected to the longitudinal shears $V_H$ and $V_H + d_VH$. Therefore, the relative rotations $\xi$ and $\xi + \mathrm{d}\xi$ will be produced in these cells. As is shown in Fig. 13, as a consequence of the elementary change $\mathrm{d}\xi$, in the nodal section common to the two cells the jump

$$\begin{aligned} \delta \varphi = - \mathrm{d}\xi \end{aligned}$$

in the nodal rotations will occur.

Strains due to transversal shear and bending moments, on the other hand, are always geometrically compatible, since they do not involve deformations of the transversal fibres.

The jumps in the nodal rotations of the continuous model, or equivalently the interpenetrations/gaps between the elementary cells, transversal fibres, may be eliminated if we imagine that the cells may interact also in terms of self-moments. This implies that when the equivalent medium deforms under an external action, a continuous distribution m(x) of self-moments arises. It produces relative rotations $\xi (x)$ such that the total jump $\delta \varphi (x)$ in nodal rotations is zero in each section. In other words, the continuous model is bent with the additional (inner) constraint $\delta \varphi = 0$, which is satisfied thanks to the actions of the (inner) self-moments m(x) .

By such a constrained model (subjected to self-moments m(x) ), accurate estimates of the girder critical loads and deformed shapes may be obtained. In this case, buckling conditions are attained when bent configurations satisfying Eqs. (4–6) and the continuity condition $\delta \varphi = 0$ are possible. Equivalently, the equivalent girder may buckle when special distributions of self-moments act in it. They are able to bend the system subjected to the axial load without violating equilibrium conditions and the inner compatibility of shear strains or equivalently the continuity of nodal rotations, i.e. $\delta \varphi (x) = 0,$ $\forall \, x \in [0,L]$. We assume that these distributions of self-moments may be expressed, without loss of generality, by the sine series

$$\begin{aligned} m(x)= \sum _{n=0}^{\infty } m_n \sin \left( \frac{n \pi }{L} x \right) , \end{aligned}$$

(45)

with $m_n$ the unknown self-moment amplitudes. By invoking the superposition principle, by means of results of Sects. 2 and 3 the continuity condition of nodal (micro-) rotations may be written as

$$\begin{aligned} \delta \varphi (x) = \sum _{n=0}^{\infty } \left( \delta \varphi _0^{(n)} + \delta \varphi _P^{(n)}\right) =0 , \end{aligned}$$

(46)

where $\delta \varphi _0^{(n)}(x)$ are the jumps generated in the girder free of axial load by the nth harmonic component of m(x) and are given by Eq. (35), $\delta \varphi _P^{(n)} (x)$ are instead the changes of these jumps that occur when P is applied on the girder. These latter have to be evaluated by means of Eq. (44b) and are given by

$$\begin{aligned} \delta \varphi _P^{(n)} (x) = - \dfrac{\mathop {}\!\mathrm {d}\xi _P^{(n)}(x)}{\mathop {}\!\mathrm {d}x}dx = - \frac{{{n^4}{\pi ^4}}}{{{L^4}}}\frac{{{\Gamma _h}}}{{{k_H}}} \dfrac{P/P_{e\,n}}{1 - {P}/P_{cr\,n}} {V_{0n}} \sin \left( \frac{n \pi }{L} x \right) dx . \end{aligned}$$

(47)

Equation (46) is readily solved by the Galerkin method, that is by multiplying it by each basis function $\sin (k \pi x / L)$ of series (45) and integrating over (0, L) . This corresponds to equating to zero the virtual work made by the self-moments $\sin (k \pi x / L)$ for jumps in micro-rotations due to m(x) . By this way, we obtain the set of independent algebraic equations in the unknown self-moment amplitudes $m_k$:

$$\begin{aligned} \dfrac{2 m_k}{l_c} \left\{ \left[ (c_\psi - c_\varphi ) \cos ^2 \left( \dfrac{\pi k}{2 N}\right) + 2 c_\gamma \sin ^2 \left( \dfrac{\pi k}{2 N} \right) \right] - \dfrac{k^4 \pi ^4}{L^4} \dfrac{\Gamma _h}{\kappa _H} V_{0\,k} \dfrac{P/P_{e\,k}}{1-P/P_{cr\,k}} \right\} =0 . \end{aligned}$$

(48)

The quantities in braces are dependent on the applied load P. The values $P_k$ of P for which they are zeroed are the searched critical loads of the girder. In fact, when P equals one of $P_k$, say $P_h$, the girder may bend under the action of the self-moments $m_h \sin (h \pi \, x /L)$, of undetermined amplitude $m_h$, without jumps in nodal rotations $\varphi$. Hence, from Eq. (48) we derive the following condition for the critical values of P:

$$\begin{aligned} \frac{1}{P_k} =\dfrac{1}{P_{e\,k}} + \chi - {\tilde{\chi }}_k \end{aligned}$$

(49)

with

$$\begin{aligned} {\tilde{\chi }}_k = \left( \dfrac{k \pi }{2N} \right) ^2 \dfrac{\alpha _h / \kappa _H}{\sin ^2(k \pi / 2 N)} \dfrac{2 c_\gamma \sin ^2 (k\pi /2N)+ c_\psi \cos ^2(k \pi /2N)}{2 c_\gamma \sin ^2 (k \pi / 2 N)+(c_\psi - c_\varphi )\cos ^2(k \pi / 2N)}. \end{aligned}$$

(50)

Critical transversal displacements $v_{cr}^{(k)}$ and sectional rotations $\psi _{cr}^{(k)}$ are given, up to the factor $m_k$, by adding, respectively, to $v_0^{(k)}$ and $\psi _0^{(k)}$ Eq. (44a and b) written with $P=P_k$, respectively. Regarding the corresponding nodal (micro-)rotations $\varphi _{cr}^{(k)}$, from Eq. (32), taking into account the continuity condition (47) and Eq. (44), we have

$$\begin{aligned} \varphi _{cr}^{(k)} =&\, \varphi _0^{(k)}(x) + \psi _{cr}^{(k)}(x) - \xi _P^{(k)}(x) \\ =&\, {\bar{\varphi }}_k + \int _{0}^{x} \!\! d \varphi _0^{(k)}+\int _{0}^{x} \!\! \delta \varphi _0^{(k)} + \psi _{cr}^{(k)}(x) - \xi _P^{(k)}(0) -\int _{0}^{x} \mathop {}\!\mathrm {d}\xi _P^{(k)} \\ =&\, {\bar{\varphi }}_k + \psi _{cr}^{(k)}(x) - \, \xi _P^{(k)}(0) + \int _{0}^{x} \!\! \mathop {}\!\mathrm {d}\varphi _0^{(k)}; \end{aligned}$$

here, both quantities $\xi _P^{(k)}(0)$ and $\mathrm{d}\xi _P^{(k)}$ have to be evaluated with $P=P_k$.

The girder Euler load $P_E$ is the lowest of the $P_k$ given by Eq. (49). It is obtained when $k=1$ and may be written as:

$$\begin{aligned} P_E =\dfrac{\pi \Gamma _b}{L^2}\dfrac{1}{1 + \dfrac{\pi \Gamma _b}{L^2}(\chi - {\tilde{\chi }}_1)}, \end{aligned}$$

(51)

where ${\tilde{\chi }}_1$ is obtained from Eq. (50) evaluated with $k=1$. Equation (51) has the same formal structure as the Engesser buckling load [15] and the equivalent girder Euler load derived in [51] and given by Eq. (42) evaluated with $k=1$. In the Engesser formula, in place of $\chi$ we found the shear compliance:

$$\begin{aligned} \chi _\mathrm{Eng} = \dfrac{l_c l_w}{24 E_w I_w} + \dfrac{l_c^2}{24 E_c I_c}. \end{aligned}$$

(52)

Instead, in Eq. (42) self-moment effects are neglected and in place of $\chi - {\tilde{\chi }}_1$ there is only $\chi$. In the Engesser shear compliance equation  (52), girder joint elasticity is not taken into account. Hence, in order to compare buckling load estimates of the present method with those of the Engesser formula, the following modified compliance has to be used:

$$\begin{aligned} \chi _\mathrm{Eng}=\dfrac{1}{\kappa _V}+\dfrac{1}{\kappa _H}. \end{aligned}$$

(53)

This formula is derived in Appendix C with the same basic assumptions of the Engesser method, namely that under the action of a transverse shear force, chords and web members deform with points of inflection located at their centre (Fig. 20 of Appendix B).

Since $\alpha _h <1$, we get:

$$\begin{aligned} \chi - {\tilde{\chi }}_1< \chi < \chi _\mathrm{Eng}; \end{aligned}$$

(54)

therefore, we also have that:

$$\begin{aligned} \frac{1}{P_E}< \frac{1}{P_{cr\,1}} < \frac{1}{P_\mathrm{Eng}} \end{aligned}$$

with $P_\mathrm{Eng}$ being the buckling load estimated by the Engesser formula. This result is a direct consequence of the fact that both in Eq. (42) and in Engesser theory cell interactions by means of self-moments are neglected. These latter require additional strain energy and external work and consequently the elementary cells deform with a higher stiffness.

Fig. 14

Buckling loads versus girder aspect ratio $\rho =L/l_w$

Fig. 15

Critical sectional rotations $\psi$, nodal rotations $\varphi$ and self-moments distributions of girders having $l_w=300$ mm

5 Validation study

The range of applicability of the results derived in Sect. 4 is now analysed by means of a data set obtained from a series of girder finite element models.

Both chords and web members of the unit cells composing these models were two node Euler beam rods having cubic polynomial shape functions. The girder global stiffness matrix was obtained by additive assembling of standard and geometrical stiffness matrix of single composing cells. All the phases of the FE analyses (namely, topological matrix generation, girder stiffness matrix assembling and condensation, eigenanalysis of the reduced stiffness matrix and lastly solution post-processing) were carried out in a computer algebra system by means of in-house written sub-routines.

In all the models of the validation study, both chords and webs members are assumed to have HEA100 cross section. Moreover, their Young’s moduli $E_c$ and $E_w$ were chosen as 206,000 MPa.

Fig. 16

Critical sectional rotations $\psi$, nodal rotations $\varphi$ and self-moments sm of girders having $l_w=1200$ mm

We recall that rotations and displacements of the critical deformed shapes obtained by FE and the method of Sect. 3 are defined up to an arbitrary factor. Hence, in order to compare these shapes, theoretical and numerical solutions were normalized so that the maximum transversal displacements $v_{\max }$ were equal to the unit value. However, the transversal displacements are not reported here for the sake of simplicity, since in all the examined cases those obtained by FE analysis perfectly match with the theoretical sinusoidal function (see Eq. (20a) and Eq. (44c)).

First of all, the effects the joint stiffness $k_s$ on the accuracy of theoretical buckling loads and critical deformed shapes are examined. For this aim, in Fig. 14 critical loads of girders with $l_w$ equal to 300 mm and 1200 mm and cell aspect ratio $\delta = l_w/l_c$ equal to, respectively, 1.0 and 2.0 are reported as function of the ratio $\rho =L/l_w$. The stiffness $k_s$ of these girders was chosen such that the relative compliance increment

$$\begin{aligned}z = \frac{3E I_w}{k_s l_w} \end{aligned}$$

attains the values 5, 50 and 100.

Fig. 17

Buckling loads versus girder aspect ratio $\rho$

It is noteworthy that as z increases, the longitudinal shear compliance also increases and the stiffening effect due to the self-moments becomes more important. This is evident in Fig. 14 where buckling loads of the present theory are compared with the estimates obtained by Eq. (42) with $k=1$ and the Engesser method that do not take into account the self-moments effects. It has to be noticed that the range of $\rho$ values where these latter estimates differ significantly from those of the present theory gradually extends as the z parameter is increased.

Predictions of Eq. (51) are in very good agreement with FE models results for all z values considered and in the whole range of $\rho$. In addition, as is evident in the diagrams of Figs. 15 and 16, theoretical deformed shapes and self-moments distributions match very well with FE analysis results in all the examined cases.

In the case of squat girders, both Eq. (42) and the Engesser method underestimate the girder buckling load. Instead, as the girder span increases, the shear strains have a gradually weaker influence on the buckling loads and predictions obtained from Eq. (42) and theEngesser formula tend towards results obtained from FE analysis and the theory of Sect. 4.

Fig. 18

Critical sectional rotations $\psi$, nodal rotations $\varphi$ and self-moments sm of girders having $l_w=300$ mm

When the cross sections of chords and web members are assigned, the relative importance of the transversal and longitudinal shear strains depends on the girder height $l_w$, since this parameter regulates the ratio between the bending moments $M_h$ and $M_p$ and their unit changes, respectively, given by V and $T_H$. Moreover, shear strains magnitude depends also on the cell shape ratio $\delta =l_c/l_w$, because this parameter determines the number of web rods for girder unit length. Therefore, in order to investigate the theory accuracy for girders where strains due to V and $T_H$ have different magnitude, a second series of FE analysis was carried out. The considered girders have height $l_w$ = 400, 800 and 1600 mm, z ratio equal to 150 and cell shape ratio $\delta = 0.5$, 1 and 2.

Fig. 19

Critical sectional rotations $\psi$, nodal rotations $\varphi$ and self-moments sm of girders having $l_w=1600$ mm

Numerical results are compared with theoretical predictions in diagrams of Fig. 17, where buckling load estimates obtained by Eq. (42) with $k=1$ are also reported in order to highlight the stiffening effect due to self-moments. It is evident that the theory presented is able to evaluate with good accuracy the instability loads for almost all the girder geometries examined. Large errors on buckling load estimates are noticeable only in the limit cases where $\delta =2$ and $\rho =10$, that is for girders composed only of 5 cells to which the application of any homogenization theory does not make sense.

In Figs. 18 and  19, critical sectional and nodal rotations of the girders of Fig. 17 with $l_w=$ 400 and 1600 mm are diagrammed together with the corresponding self-moment distributions. The theoretical predictions for critical values of $\psi$ are in good agreement with results obtained by FE buckling analysis in all presented cases. Nodal rotations and self-moments values are affected by significant homogenization errors only in the extreme case of very squat girders having $\rho =10$ and cell shape ratio $\delta = 2$. These errors are instead negligible for all the girder having shape ratio $\rho >$ 10.

6 Conclusions

The behaviour of a Vierendeel girder subjected to sinusoidal distributions of self-moments has been analysed. More precisely, the girders deformed shape has been obtained by composing the deformations of the unit cell given by eigenvectors of its transfer matrix associated to self-moments decaying in positive and negative verses. This result has then been extended to a micro-polar geometrically nonlinear equivalent model and the effects of the axial load on the girder initially distorted by the self-moments have been evaluated in closed form.

By means of these solutions, an alternative formulation of the buckling problem of the periodic beams is then given in terms of kinematics of the micro-polar model: buckling occurs when special distributions of self-moments are present. They are able to bend the girder without violating compatibility of the longitudinal shear strains. These systems have a significant stiffening effect on the girder buckling behaviour and are governed by the continuity equation for micro-rotations of the equivalent medium. Using the Galerkin method with the micro-polar model eigenfunctions as basis functions, closed-form solutions for critical load and deformed shape have been obtained. The validation study carried out by the results from a family FE models shows that the proposed solutions are accurate in modelling the self-moment stiffening effects influencing the beam buckling behaviour when large strains due to the longitudinal shear occur.

Appendices

Appendix A

Derivation of Eq. (18) is based on the following result [55]:

$$\begin{aligned} \sum _{i=0}^{j-1} \sin \left( \dfrac{n \pi }{N} i \right) = \left\{ \begin{aligned}&0, \quad \text {if} \quad \sin \left( \dfrac{\pi n}{2 N} \right) =0, \\&\dfrac{\sin \left( \dfrac{\pi n}{2 N} j\right) }{\sin \left( \dfrac{\pi n}{2 N} \right) }\sin \left[ \dfrac{\pi n}{2 N} (j-1) \right] , \quad \text {elsewhere}, \\ \end{aligned} \right. \end{aligned}$$

with h being an integer number. Hence, assuming $n\ne h \cdot (2N)$, we may write

$$\begin{aligned}&\sin \left( \dfrac{\pi n}{L} x_j \right) + 2 \sum _{i=1}^{j-1} \sin \left( \dfrac{\pi n}{L} x_{i} \right) = \sin \left( \dfrac{ n \pi }{N} j \right) +2 \, \dfrac{\sin \left( \dfrac{n\pi }{2N}\,j \right) \sin \left[ {\dfrac{n\pi \, }{2N}} \left( j-1 \right) \right] }{ \sin \left( {\dfrac{n\pi }{2N}} \right) }\\&\quad =\sin \left( {\dfrac{{n\pi }}{N}j} \right) - \dfrac{{\cos \left( {\dfrac{{n\pi }}{N}j - \dfrac{{n\pi }}{{2N}}} \right) - \cos \left( {\dfrac{{n\pi }}{{2N}}} \right) }}{{\sin \left( {\dfrac{{n\pi }}{{2N}}} \right) }},\end{aligned}$$

where the last equality follows from the Werner formula. Then, applying the cosine subtraction formula for the numerator of the last fraction, after some trivial simplification the RHS of Eq. (18) is obtained.

Appendix B

Equation (23) has been achieved by means of the following result [55]:

$$\begin{aligned} \sum _{i=0}^{j-1} \cos \left( \dfrac{n \pi }{N} i \right) = \left\{ \begin{aligned}&0, \quad \text {if} \quad n = h \, (2N), \\&\dfrac{\sin \left( \dfrac{\pi n}{2 N} j\right) }{\sin \left( \dfrac{\pi n}{2 N} \right) }\cos \left[ \dfrac{\pi n}{2 N} (j-1) \right] , \quad \text {elsewhere,} \\ \end{aligned} \right. \end{aligned}$$

Hence, under the assumption $n \ne h \cdot (2N)$ and taking into account Eq. (19), we may write the sum over i of sectional rotations $\psi _i$ as

$$\begin{aligned} \sum \limits _{i = 0}^{j - 1} {\psi _i}&= j{\psi _0} + {c_\psi }{m_n}\dfrac{{\cos \left( {\dfrac{{n\pi }}{{2N}}} \right) }}{{\sin \left( {\dfrac{{n\pi }}{{2N}}} \right) }}\left[ {j - \sum \limits _{i = 0}^{j - 1} {\cos \left( {\dfrac{{n\pi }}{N} i} \right) } } \right] \\&= j{\psi _0} + {c_\psi }{m_n}\frac{{\cos \left( {\dfrac{{n\pi }}{{2N}}} \right) }}{{\sin \left( {\dfrac{{n\pi }}{{2N}}} \right) }}\left[ {j - \dfrac{{\sin \left( {\dfrac{{n\pi }}{{2N}}j} \right) \cos \left[ {\dfrac{{n\pi }}{{2N}}\left( {j - 1} \right) } \right] }}{{\sin \left( {\dfrac{{n\pi }}{{2N}}} \right) }}} \right] . \end{aligned}$$

Equation (23b) is achieved by substituting previous result in to Eq. (23a) after having simplified the numerator in the bracket parenthesis by the Werner and subtraction formulae.

Appendix C

Fig. 20

Lateral deflections due to shear in a unit cell according to Engesser method

The lateral relative deflection of the unit cell obtained by sectioning the girder as shown in Fig. 20 consists of the displacements $\delta _1$ due to bending of the webs and deformation of the torsional springs, and $\delta _2$ due to bending of the chords. On each torsional spring fastened at the end of the web rod, the couple $V l_c/2$ acts and the rotation angle of the free ends of the springs is

$$\begin{aligned}\theta = \frac{V l_c}{2 \eta _w}.\end{aligned}$$

Hence, the lateral deflection due to deformations in web rod and springs is

$$\begin{aligned}\delta _1 = \theta \frac{l_c}{2} =\frac{V l_c^2}{4 \eta _w} .\end{aligned}$$

From the expression of the deflection of a cantilever beam, we obtain for the deflection $\delta _2$

$$\begin{aligned} \delta _2 = \frac{V l_c^3}{48 E_cI_c}= \frac{V}{48 \eta _c}.\end{aligned}$$

In conclusion, the shear strain of the unit cell of Fig. 20 is

$$\begin{aligned} \gamma = \frac{\delta _1 + \delta _2}{l_c/2}= \chi _\mathrm{Eng} V,\end{aligned}$$

with

$$\begin{aligned}\chi _\mathrm{Eng}= \frac{1}{\kappa _H}+\frac{1}{\kappa _V}.\end{aligned}$$