1 Introduction

Lattice beam structures are widely used in civil, mechanical, and aerospace engineering; see, e.g., [17, 32, 57]. They are formed from a periodic network of interconnected beams or rods as shown in Fig. 1 where two-dimensional (2D) and three-dimensional (3D) networks are presented. In a certain sense, these structures mimic crystalline lattices and their properties. Among very perspective properties such as a light weight, relatively high stiffness and flexibility, they have also many other useful characteristics such as an acoustic response and thermal insulation that make these materials very interesting for applications. One can meet such architectured materials for very wide ranges of scales, from nano- and microscales up to macrostructures. It is worth mentioning the famous Shuchov’s tower and other lattice structures; see, e.g., [4, 36]. Among examples of beam lattice materials, it is worth mentioning open cell foams [3, 33, 53] and aerogel [48, 72].

Fig. 1
figure 1

2D and 3D structures made of fibers

Full size image

As the basic structural element of considered structures is a beam, in Sect. 2 we briefly consider the nonlinear beam theory. Let us note that mechanics of one-dimensional structures has a long history of development after such names as Euler and Bernoulli. Mechanics of rods and beams is summarized in many books; see, for example, [1, 22, 41, 43, 51, 67, 77, 81]. Nowadays, the rod and beam structures are widely used in engineering as relatively simple robust models; see, e.g., [5, 20, 83]. Here we use the model originally introduced by the Cosserat brothers and nowadays known as a Cosserat curve. Within this direct approach, the mechanics of rods was developed in seminal papers by Ericksen and Truesdell [29], Green et al. [38, 39], DeSilva and Whitman [15], and Kafadar [44]. Let us note that despite their one-dimensional nature for the solution of the nonlinear beam equations we require a proper numerical tool; see, e.g., [10, 11, 14, 37, 54, 79, 82] and the references therein. Here we consider the Cosserat model with certain constraints. In particular, we neglect shear deformations. The equilibrium equations consist of a system of ordinary differential equations.

In Sect. 3, we consider a 2D elastic network similar to a fishnet made of orthogonal flexible fibers. The mechanics of elastic networks was studied in many works; see, e.g., the seminal works by Rivlin [66], Pipkin [61,62,63], Steigmann and Pipkin [76]. Recently, the further developments in this topic have resulted in the model of lattice shell presented in [16, 34, 70, 73,74,75]. Here we restrict ourselves to a particular class of a network assuming the orthogonality of network beams during deformations. In other words, we assume that beams are connected to each other by rigid joints. A typical example of such a structure is given in Fig. 2, where a scheme of a metal net widely used in modern civil engineering as a fence is presented. The case of an elastic network with inextensible fibers was considered in [23].

Fig. 2
figure 2

Scheme of a metal net with rigid connections

Full size image

For this net, we introduce an averaged continuum model that is a deformable material surface with particular material properties described within the framework of the six-parameter shell theory [13, 49, 50]. Within the six-parameter shell theory, the kinematics of a shell is described by three translations and three rotations as in the rigid body dynamics or in the Cosserat (micropolar) continuum [30]. So, the model is also called the micropolar shell theory [24, 26]. In the theory, only forces and moments including drilling ones are considered as stress characteristics which are also used in the static boundary conditions. Within the theory, solutions of many problems were given numerically and/or analytically; see, e.g., [8, 9, 13, 60, 85]. We briefly recall the basic equations of the micropolar shell statics paying the most attention to the constitutive relations and possible constraints for deformations. Let us note that usually shell equations are derived for a solid shell-like body; see, for example, the through-the-thickness integration technique presented in [13, 49, 50]. As here we consider deformations of completely different structures similar to a fishnet, one needs another approach; see, e.g., [45, 64, 86] for lattice shells.

Comparing discrete models for a 2D network and shell in Sect. 4, we present the constitutive equations for the shell which is equivalent in certain sense to the considered network. In fact, the homogenized constitutive equation for an elastic network has a particular form of strain energy of a six-parameter shell. The obtained results can be relatively easy generalized for networks made of extensible, shear deformable, initially curved and naturally twisted fibers. The only crucial point for the derivation is the orthogonality of fibers during deformations. This assumption results in the possibility to describe rotations of all fibers using one rotation tensor field.

Finally, in Sect. 5 we consider 3D structures made of three orthogonal families of flexible elastic fibers. In a similar way, comparing the discretization for the 3D network and a micropolar continuum we derive the continuous nonlinear micropolar model. As was mentioned in [26], homogenization is one of the main sources for derivation of the constitutive equations of micropolar solids; see, e.g., [6, 18, 19, 31, 35, 69] and the references therein.

2 Cosserat curve as a fiber model

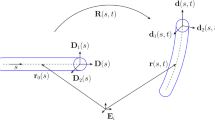
Following [1, 22, 26, 81], we briefly consider the Cosserat curve model as a model of a single fiber (beam). This approach is also known as the directed curve model. From the mathematical point of view, the model can be treated as a one-dimensional (1D) Cosserat continuum. In other words, we consider 1D medium with kinematically independent fields of translations and rotations. The deformation of the beam is described as a mapping from a reference placement into a current (deformed) one. In the reference placement, the beam occupies a volume located in the vicinity of a base curve \(\mathcal {C}_0\) which transforms after deformation into another curve \(\mathcal {C}\); see Fig. 3. For \(\mathcal {C}_0\), we use the natural parametrization given by the formula \({\mathbf {R}}={\mathbf {R}}(s),\) where s is the referential arc-length parameter. In order to describe the cross-sectional orientation of the beam, we introduce the unit orthogonal vectors \({\mathbf {D}}_k={\mathbf {D}}_k(s)\) called directors, \({\mathbf {D}}_k\cdot {\mathbf {D}}_m=\delta _{km}\), where \(\delta _{km}\) is the Kronecker symbol, the centered dot stands for the scalar product and Latin indices take values 1, 2, 3. In what follows, we use the direct tensor calculus as introduced in [25, 47, 52, 71]. Without loss of generality, we assume that \({\mathbf {D}}_1\) is tangent to \(\mathcal {C}_0\).

Fig. 3
figure 3

Deformations of a beam

Full size image

The position and orientation of the beam in the current placement are described by vectorial fields

$$\begin{aligned} {\mathbf {r}}={\mathbf {r}}(s),\quad {\mathbf {d}}_k={\mathbf {d}}_k(s), \qquad k=1,2,3, \end{aligned}$$
(1)

where \({\mathbf {r}}\) and \({\mathbf {d}}_k\) are the position vector in the current placement and the current directors, respectively. Note that here we also used s as a coordinate.

In order to introduce relative deformations, we use the displacement vector \({\mathbf {u}}\) and the proper orthogonal tensor \({\mathbf {P}}={\mathbf {d}}_k\otimes {\mathbf {D}}_k\), where \(\otimes \) denotes the dyadic product. So a deformation of a directed curve is described by the vector- and tensor-valued fields

$$\begin{aligned} {\mathbf {u}}={\mathbf {r}}(s)-{\mathbf {R}}(s),\quad {\mathbf {P}}\equiv {\mathbf {d}}_k\otimes {\mathbf {D}}_k ={\mathbf {P}}(s). \end{aligned}$$
(2)

The Lagrangian equilibrium equations take the following form [1, 22, 26, 81]:

$$\begin{aligned} {\mathbf {t}}^{\prime }(s)+{\mathbf {f}}= \mathbf {0},\quad {\mathbf {m}}^{\prime }(s)+{\mathbf {r}}^{\prime }(s)\times {\mathbf {t}}(s)+ {\mathbf {c}}= \mathbf {0} \end{aligned}$$
(3)

where \(\,{\mathbf {t}}\,\) and \(\,{\mathbf {m}}\,\) are vectors of forces and moments, \(\,{\mathbf {f}}\,\) and \(\,{\mathbf {c}}\,\) are external forces and moments given along \(\mathcal {C}_0\), \(\times \) stands for the cross product, and the prime denotes the derivative with respect to s, \((\ldots )'=\frac{\partial (\ldots )}{\partial s}\).

Considering hyperelastic materials only, we introduce the line strain energy density as follows:

$$\begin{aligned} \mathcal {U}=\mathcal {U}({\mathbf {e}},{\mathbf {k}}), \quad {\mathbf {e}}={\mathbf {P}}^\mathrm{T}\cdot {\mathbf {r}}'-{\mathbf {D}}_1,\quad {\mathbf {k}}=-\frac{1}{2}({\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}}')_\times \end{aligned}$$
(4.1-3)

where \({\mathbf {e}}\) and \({\mathbf {k}}\) are vectorial strain measures, \({\mathbf {T}}_\times \) denotes the vectorial invariant of a second-order tensor \({\mathbf {T}}\) introduced by Gibbs [84, p. 275] and defined as follows:

$$\begin{aligned} {\mathbf {T}}_\times =(T^{mn}{\mathbf {i}}_m\otimes {\mathbf {i}}_n)_\times =T^{mn}{\mathbf {i}}_m\times {\mathbf {i}}_n \end{aligned}$$

for any basis \({\mathbf {i}}_m\), \(m=1,2,3\). Vectors of internal forces and moments relate to the strain energy by the relations

$$\begin{aligned} {\mathbf {t}}=\frac{\partial \mathcal {U} }{\partial {\mathbf {e}}}\cdot {\mathbf {P}}^\mathrm{T},\quad {\mathbf {m}}=\frac{\partial \mathcal {U} }{\partial {\mathbf {k}}}\cdot {\mathbf {P}}^\mathrm{T}. \end{aligned}$$
(5)

Let us note that the line strain energy density given by (4.1-3) is the straightforward application of the material frame-indifference principle [78]. Indeed, let us consider the general form of \(\mathcal {U}\) as a function of \({\mathbf {r}}\) and \({\mathbf {P}}\) and their derivatives,

$$\begin{aligned} \mathcal {U}=\mathcal {U}({\mathbf {r}},{\mathbf {r}}^\prime ,{\mathbf {P}},{\mathbf {P}}^\prime ). \end{aligned}$$
(6)

The material frame-indifference principle says that \(\mathcal {U}\) should be invariant under transformations

$$\begin{aligned} {\mathbf {r}}\rightarrow {\mathbf {O}}\cdot {\mathbf {r}}+{\mathbf {a}},\quad {\mathbf {P}}\rightarrow {\mathbf {O}}\cdot {\mathbf {P}}\end{aligned}$$
(7)

where \({\mathbf {O}}\) and \({\mathbf {a}}\) are arbitrary constant orthogonal tensor and vector, respectively; see [26, 59] for more details in the case of micropolar solids. Considering \({\mathbf {O}}={\mathbf {I}}\), where \({\mathbf {I}}\) is the 3D unit tensor, and arbitrary \({\mathbf {a}}\), we get the following invariance property:

$$\begin{aligned} \mathcal {U}({\mathbf {r}},{\mathbf {r}}^\prime ,{\mathbf {P}},{\mathbf {P}}^\prime )=\mathcal {U}({\mathbf {r}}+{\mathbf {a}},{\mathbf {r}}^\prime ,{\mathbf {P}},{\mathbf {P}}^\prime ),\quad \forall \,\, {\mathbf {a}}. \end{aligned}$$
(8)

So \(\mathcal {U}\) does not depend on \({\mathbf {r}}\) itself. Taking \({\mathbf {O}}={\mathbf {P}}^\mathrm{T}\), we have the dependence

$$\begin{aligned} \mathcal {U}({\mathbf {r}}^\prime ,{\mathbf {P}},{\mathbf {P}}^\prime )=\mathcal {U}({\mathbf {P}}^\mathrm{T}\cdot {\mathbf {r}}^\prime ,{\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}},{\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}}^\prime ). \end{aligned}$$
(9)

Obviously, relation (9) is invariant under transformations (7), so it satisfies the material frame-indifference principle. As \({\mathbf {P}}\) is orthogonal, tensor \({\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}}^\prime \) is skew-symmetric. As any skew-symmetric tensor, it can be represented by its axial vector \({\mathbf {k}}\),

$$\begin{aligned} {\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}}^\prime ={\mathbf {k}}\times {\mathbf {I}}, \end{aligned}$$

which is given by (4.3). Finally, we take strain measures that vanish if \({\mathbf {r}}={\mathbf {R}}\) and \({\mathbf {P}}={\mathbf {I}}\) and get (4.1-3).

The system of Eqs. (3)–(5) complemented by the corresponding boundary conditions constitutes a boundary value problem, which describes finite deformations of an elastic beam taking into account its stretching/elongation, bending, torsion, and transverse shear deformations. So this model is rather general. Nevertheless, let us also note that in the case of beams we have even more complex models which take into account also warping, such as in the case of beams of thin-walled cross section [22, 41, 51] or spatial beamlike lattice structures [12, 40, 55, 56]. In what follows, we neglect transverse shear deformations. In this case, \({\mathbf {d}}_1\) will be tangent to \(\mathcal {C}\). So \({\mathbf {e}}\) takes the form \({\mathbf {e}}=\varepsilon {\mathbf {D}}_1\), and \(\mathcal {U}\) depends on scalar and vectorial strains [22, 81],

$$\begin{aligned} \mathcal {U}=\mathcal {U}(\varepsilon ,{\mathbf {k}}). \end{aligned}$$
(10)

For inextensible beams, we have that \(\varepsilon =0\) and \({\mathbf {T}}\) becomes a vectorial Lagrange multiplier related to the constraint \({\mathbf {e}}={\mathbf {0}}\). Using further simplifications, one can get even more simple beam theories. For example, the following quadratic form can be used as a strain energy density:

$$\begin{aligned} \mathcal {U}=\frac{1}{2} K_s\varepsilon ^2+\frac{1}{2} {\mathbf {k}}\cdot {\mathbf {D}}\cdot {\mathbf {k}}\end{aligned}$$
(11)

where \(K_s\) and \({\mathbf {D}}\) are stiffness moduli responsible for stretching, bending, and torsion, respectively. For the derivation of the constitutive equations for beams undergoing large deformations, we refer to the numerous works; see, e.g., [2, 7, 21, 22, 41, 81] and the references therein.

3 Discrete beam lattice

Using the above presented above beam model, we consider a structure made of two orthogonal families of beams as shown in Fig. 4 called the beam lattice. For simplicity, we assume that the beams have the same geometrical and physical properties and the cells of the lattice are squares. Here we have n horizontal and m vertical beams with distance h between intersection points. Using the orthogonality, we can chose directors \({\mathbf {D}}_1\) and \({\mathbf {D}}_2\) as tangent vectors to the first and second family of beams, respectively. In what follows, we denote the quantities related to these two families by indices 1 and 2. Introducing the Cartesian coordinates \(s_1\) and \(s_2\) and numbering nodes as in Fig. 4, we get the formulae for the position of (i, j)-node,

$$\begin{aligned} s_1^{(i)}=(i-1)h,\quad s_2^{(j)}=(j-1)h,\qquad i=1,\ldots m+1,\quad j=1,\ldots n+1. \end{aligned}$$
Fig. 4
figure 4

Rectangular beam lattice in a reference placement

Full size image

As for a single beam considered above, here for each beam we again have two kinematical descriptors \({\mathbf {r}}\) and \({\mathbf {P}}\) which are defined on the lattice lines \(s_1=s_1^{(i)}\), \(s_2= s_2^{(j)}\), \( i=1,\ldots m\), \( j=1,\ldots n\). In other words, the complete kinematics of the beam lattice is described by a set of vector- and tensor-valued functions

$$\begin{aligned} {\mathbf {r}}=&{\mathbf {r}}_1\equiv {\mathbf {r}}_1^{(j)}(s_1), \quad {\mathbf {P}}={\mathbf {P}}_1\equiv {\mathbf {P}}_1^{(j)}(s_1), \quad j=1,\ldots n,\\ {\mathbf {r}}=&{\mathbf {r}}_2\equiv {\mathbf {r}}_2^{(i)}(s_2), \quad {\mathbf {P}}={\mathbf {P}}_2\equiv {\mathbf {P}}_2^{(i)}(s_2), \quad i=1,\ldots m. \end{aligned}$$

Here \({\mathbf {P}}_1={\mathbf {d}}_k^{(1)}(s_1)\otimes {\mathbf {D}}_k\), \({\mathbf {P}}_2={\mathbf {d}}_k^{(2)}(s_2)\otimes {\mathbf {D}}_k\), where \({\mathbf {D}}_k^{(\alpha )}\) and \({\mathbf {d}}_k^{(\alpha )}\) are the referential and current directors of the \(\alpha \)-family of the beams. Note that in the nodes, i.e., in points \((s_1^{(i)},s_2^{(j)})\), we have

$$\begin{aligned} {\mathbf {d}}_k^{(1)}(s_1^{(i)})={\mathbf {d}}_k^{(2)}(s_2^{(j)}). \end{aligned}$$

As a result, we get the following geometrical constraints:

$$\begin{aligned} {\mathbf {r}}_1^{(j)}(s_1^{(i)}) ={\mathbf {r}}_2^{(i)}(s_2^{(j)}), \quad {\mathbf {P}}_1^{(j)}(s_1^{(i)}) ={\mathbf {P}}_2^{(i)}(s_2^{(j)}). \end{aligned}$$
(12)

In other words, in the nodes we can use the same values of position vectors and rotation tensors. From the physical point of view, this means that the infinite rigidity of beams connections results in consistent bending and torsion of the beams. In particular, the orthogonality condition also imposes that torsion in one of the beams is consistent with the inclination of the axis of the other one.

The Lagrangian equilibrium equations of the beam lattice consist of the system of static equations for every beam, that is,

$$\begin{aligned}&\displaystyle {\mathbf {t}}_{1,1}^{\prime }(s_1)+{\mathbf {f}}_1 = \mathbf {0}, \end{aligned}$$
(13)
$$\begin{aligned}&\displaystyle {\mathbf {m}}_{1,1}^{\prime }(s_1)+{\mathbf {r}}^{\prime }_{1,1}\times {\mathbf {t}}_1(s_1)+ {\mathbf {c}}_1 = \mathbf {0},\end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle {\mathbf {t}}_{2,2}^{\prime }(s_2)+{\mathbf {f}}_2 = \mathbf {0},\end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle {\mathbf {m}}_{2,2}^{\prime }(s_2)+{\mathbf {r}}^{\prime }_{2,2}\times {\mathbf {t}}_2(s_2)+ {\mathbf {c}}_1= \mathbf {0}. \end{aligned}$$
(16)

Here \(\,{\mathbf {t}}_\alpha \,\) and \(\,{\mathbf {m}}_\alpha \,\) are vectors of forces and couples related to the \(\alpha \)-family, \(\alpha =1,2\), \(\,{\mathbf {f}}_\alpha \) and \(\,{\mathbf {c}}_\alpha \) are external fields of forces and moments, and \((\ldots )_{,\alpha }^\prime =\frac{\partial (\ldots )}{\partial s_\alpha }\) is the differentiation with respect to \(s_\alpha \), where \(s_\alpha \) plays a role of the arc-length parameter of the \(\alpha \)-family of beams.

Numbering nodes as in Fig. 4, we write the total energy functional of the beam lattice as a sum

$$\begin{aligned} \mathcal {E}=\sum _{j=1}^n\sum _{i=1}^{m-1}\int _{s_{1}^{(i)}}^{s_{1}^{(i+1)}}\mathcal {U}(s_1)\,\mathrm{d}s_1 +\sum _{i=1}^m\sum _{j=1}^{n-1}\int _{s_{2}^{(j)}}^{s_{2}^{(j+1)}}\mathcal {U}(s_2)\,\mathrm{d}s_2 \end{aligned}$$
(17)

where m and n are numbers of beams in these families, and we introduced the line strain energy densities

$$\begin{aligned} \mathcal {U}(s_\alpha )=\mathcal {U}(\varepsilon _\alpha , {\mathbf {k}}_\alpha ), \end{aligned}$$
(18)

and the following strain measures are introduced:

$$\begin{aligned} \varepsilon _1= {\mathbf {r}}_{,1}\cdot {\mathbf {P}}\cdot {\mathbf {D}}_1-1, \quad \varepsilon _2= {\mathbf {r}}_{,2}\cdot {\mathbf {P}}\cdot {\mathbf {D}}_2-1, \quad {\mathbf {k}}_\alpha =-\frac{1}{2}({\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}}'_{,\alpha })_\times . \end{aligned}$$
(19)

In what follows, we consider finite difference approximation of (17). Using the trapezoidal rules

$$\begin{aligned} \int _{s_{1}^{(i)}}^{s_{1}^{(i+1)}}\mathcal {U}(s_1)\,\mathrm{d}s_1= & {} \frac{h}{2}\left[ \mathcal {U}(s_{1}^{(i)})+\mathcal {U}(s_{1}^{(i+1)})\right] ,\\ \int _{s_{2}^{(j)}}^{s_{2}^{(j+1)}}\mathcal {U}(s_2)\,\mathrm{d}s_1= & {} \frac{h}{2}\left[ \mathcal {U}(s_{2}^{(j)})+\mathcal {U}(s_{2}^{(j+1)})\right] , \end{aligned}$$

we transform (17) into a discrete form,

$$\begin{aligned} \mathcal {E}= & {} \frac{h}{2}\sum _{j=1}^n\left[ \mathcal {U}(s_{1}^{(1)})+\mathcal {U}(s_{1}^{(m)})+2\sum _{i=2}^{m-1} \mathcal {U}(s_{1}^{(i)})\right] \\&+\frac{h}{2}\sum _{i=1}^m\left[ \mathcal {U}(s_{2}^{(1)})+\mathcal {U}(s_{2}^{(n)})+2\sum _{j=2}^{n-1} \mathcal {U}(s_{2}^{(j)})\right] . \end{aligned}$$

Let us note that the trapezoidal rule corresponds to linear approximation of the integrands. As a result, the total energy of the lattice shell is expressed by the values of \(\mathcal {U}\) in the nodes, that is, in the points \((s_1^{(i)},s_2^{(j)})\):

$$\begin{aligned} \mathcal {E}=\sum _{i=1}^m\sum _{j=1}^nc_{ij}\left[ \mathcal {U}(s_{1}^{(i)})+\mathcal {U}(s_{2}^{(j)})\right] . \end{aligned}$$
(20)

Here \(c_{ij}\) are weight coefficients which can be obtained after summation procedure. Using (18), Eq. (20) takes the form

$$\begin{aligned} \mathcal {E}= \sum _{i=1}^m\sum _{j=1}^nc_{ij}\left[ \mathcal {U}\left( \varepsilon _1^{(ij)},{\mathbf {k}}_{1}^{(ij)}\right) +\mathcal {U}\left( \varepsilon _2^{(ij)}), {\mathbf {k}}_{2}^{(ij)}\right) \right] \end{aligned}$$
(21)

with the explicit dependence on the strain measures calculated in the nodes.

Motivating by constraints (12) instead of the functions of one variable, we introduce surface fields \({\mathbf {r}}={\mathbf {r}}(s_1, s_2)\) and \({\mathbf {P}}={\mathbf {P}}(s_1,s_2)\) such that these fields coincide with the latter when \(s_1=s_1^{(i)}\), \(s_2= s_2^{(j)}\), \( i=1,\ldots m\), \( j=1,\ldots n\), respectively,

$$\begin{aligned} {\mathbf {r}}(s_1, s_2)\big |_{s_2=s_2^{(j)}}&={\mathbf {r}}_1^{(j)}(s_1), \quad {\mathbf {P}}(s_1,s_2)\big |_{s_2=s_2^{(j)}}={\mathbf {P}}_1^{(j)}(s_1), \end{aligned}$$
(22)
$$\begin{aligned} {\mathbf {r}}(s_1, s_2)\big |_{s_1=s_1^{(i)}}&={\mathbf {r}}_2^{(i)}(s_2), \quad {\mathbf {P}}(s_1,s_2)\big |_{s_1=s_1^{(i)}}={\mathbf {P}}_2^{(i)}(s_2). \end{aligned}$$
(23)

Replacing double summation in (21) by double integration, we get the continuous analogue of the beam lattice total energy,

$$\begin{aligned} \mathcal {E}= \iint \limits _\omega \tilde{\mathcal {U} }\,d\omega ,\quad \tilde{\mathcal {U}}= \mathcal {U}(\varepsilon _1,{\mathbf {k}}_{1})+\mathcal {U}(\varepsilon _2,{\mathbf {k}}_{2}), \end{aligned}$$
(24.1,2)

where for simplicity we keep the same notations for the energy densities. One can see that the approximation of (24.1,2) up to certain accuracy leads to (21). As the discretization of total energy functionals of the discrete beam lattice (17) and its continuous analogue (24.1,2) lead to the same formulae up to a certain accuracy, we call these models equivalent. In order to characterize the equivalent continuous beam lattice shell, we consider the nonlinear resultant shell theory.

4 Continuous beam lattice shell: micropolar shell

Following [24, 26], let us briefly introduce the governing equations used within the six-parameter shell theory. Here the kinematics of a shell is described by six scalar degrees of freedom that are three translations and three rotations as in the case of the Cosserat (micropolar) continuum [26, 30]. So the model is also called the micropolar shell theory. The basic equations of the six-parameter shell theory can be derived using through-the-thickness integration of the 3D equations of motion [13, 49, 50, 58] or within the so-called direct approach [24, 26]. In a current placement, the base surface of the shell has the position vector \({\mathbf {x}}={\mathbf {x}}(q^1,q^2)\), whereas its orientation is determined by the rotation tensor \({\mathbf {Q}}(q^1,q^2)\). Here \(q^1\) and \(q^2\) are Lagrangian surface convective coordinates.

Lagrangian equilibrium equations on the base surface \(\omega \) and typical boundary conditions along its boundary \(\partial \omega =\ell _1\cup \ell _2=\ell _3\cup \ell _4\) take the form

$$\begin{aligned}&\displaystyle \nabla _s\cdot {\mathbf {T}}+ {\mathbf {f}}= {\mathbf {0}}, \quad \nabla _s\cdot {\mathbf {M}}+ \left[ {\mathbf {F}}_s^\mathrm{T} \cdot {\mathbf {T}}\right] _\times + {\mathbf {c}}= {\mathbf {0}}, \end{aligned}$$
(25)
$$\begin{aligned}&\displaystyle \ell _1: {\mathbf {x}}= {\mathbf {x}}_0(s),\end{aligned}$$
(26)
$$\begin{aligned}&\displaystyle \ell _2: \varvec{\nu }\cdot {\mathbf {T}}= {\varvec{\tau }}(s), \end{aligned}$$
(27)
$$\begin{aligned}&\displaystyle \ell _3: {\mathbf {Q}}={\mathbf {H}}(s), \end{aligned}$$
(28)
$$\begin{aligned}&\displaystyle \ell _4: \varvec{\nu }\cdot {\mathbf {M}}= \varvec{\mu }(s) \end{aligned}$$
(29)

where \({\mathbf {T}}\) and \({\mathbf {M}}\) are the stress resultant and surface couple stress tensors of the first Piola–Kirchhoff type, \({\mathbf {F}}_s=\nabla _s {\mathbf {x}}\) is the surface deformation gradient, and \({\mathbf {f}}\) and \({\mathbf {c}}\) are external surface forces and couples, respectively. Here we introduced the surface nabla and divergence operators by the formulae

$$\begin{aligned} \nabla _s(\ldots )=&{\mathbf {X}}^\alpha \otimes \frac{\partial (\ldots )}{\partial q^\alpha }, \quad \nabla _s\cdot (\ldots )= {\mathbf {X}}^\alpha \cdot \frac{\partial (\ldots )}{\partial q^\alpha },\qquad \alpha , \beta = 1, 2,\\ {\mathbf {X}}^\alpha \cdot {\mathbf {X}}_\beta =&\delta ^\alpha _\beta ,\quad {\mathbf {X}}_\beta =\frac{\partial {\mathbf {X}}}{\partial q^\beta }, \quad {\mathbf {N}}=\frac{{\mathbf {X}}_1\times {\mathbf {X}}_2}{|{\mathbf {X}}_1\times {\mathbf {X}}_2|},\quad {\mathbf {X}}^\alpha \cdot {\mathbf {N}}=0 \end{aligned}$$

where \({\mathbf {X}}={\mathbf {X}}(q^1,q^2)\) is the position vector of the shell base surface in the reference placement and \({\mathbf {N}}\) is the unit vector of the normal. In boundary conditions (2627)–(29), \({\mathbf {x}}_0(s)\), \({\mathbf {H}}(s)\), \({\varvec{\tau }}(s)\), and \(\varvec{\mu }(s)\), are given along the corresponding parts of the shell contour position vector, rotation tensor, forces and moments, respectively, and \(\varvec{\nu }\) is the vector of unit outer normal to \(\partial \omega \) such that \(\varvec{\nu }\cdot {\mathbf {N}}=0\).

For a hyperelastic shell, there exists the surface strain energy density \(\mathcal {W}\) as a function of two surface strain measures \({\mathbf {E}}\) and \({\mathbf {K}}\),

$$\begin{aligned}&\displaystyle \mathcal {W} = \mathcal {W}({\mathbf {E}}, {\mathbf {K}}), \end{aligned}$$
(30)
$$\begin{aligned}&\displaystyle {\mathbf {E}}= {\mathbf {F}}_s \cdot {\mathbf {Q}}^\mathrm{T}-{\mathbf {A}}, \quad {\mathbf {K}}= \frac{1}{2} {\mathbf {X}}^{\alpha } \otimes \left( \frac{\partial {\mathbf {Q}}}{\partial q^\alpha }\cdot {\mathbf {Q}}^\mathrm{T} \right) _\times \end{aligned}$$
(31)

where \({\mathbf {A}}= {\mathbf {I}}-{\mathbf {N}}\otimes {\mathbf {N}}\) is the surface metric tensor. For hyperelastic shells, \({\mathbf {T}}\) and \({\mathbf {M}}\) are given by

$$\begin{aligned} {\mathbf {T}}=\frac{\partial \mathcal {W} }{\partial {\mathbf {E}}}\cdot {\mathbf {Q}}^\mathrm{T},\quad {\mathbf {M}}=\frac{\partial \mathcal {W} }{\partial {\mathbf {K}}}\cdot {\mathbf {Q}}^\mathrm{T}. \end{aligned}$$
(32)

In order to compare the homogenized constitutive relation (24.2) with one for shells (30) as well as strain measures (19) and (31), we identify \(q^\alpha \) with \(s_\alpha \), \({\mathbf {r}}\) with \({\mathbf {x}}\) and \({\mathbf {P}}\) with \({\mathbf {Q}}\):

$$\begin{aligned} q^\alpha =s_\alpha ,\quad {\mathbf {r}}={\mathbf {x}},\quad {\mathbf {P}}={\mathbf {Q}}. \end{aligned}$$

So we get

$$\begin{aligned} {\mathbf {X}}^\alpha= & {} {\mathbf {X}}_\alpha ={\mathbf {D}}_\alpha ,\quad {\mathbf {A}}={\mathbf {X}}^\alpha \otimes {\mathbf {X}}_\alpha ={\mathbf {D}}_\alpha \otimes {\mathbf {D}}_\alpha ,\quad {\mathbf {F}}_s={\mathbf {D}}_\alpha \otimes {\mathbf {r}}_{,\alpha },\\ {\mathbf {E}}= & {} {\mathbf {D}}_\alpha \otimes {\mathbf {r}}_{,\alpha }\cdot {\mathbf {P}}^\mathrm{T}- {\mathbf {D}}_\alpha \otimes {\mathbf {D}}_\alpha ,\quad {\mathbf {K}}=\frac{1}{2} {\mathbf {D}}_{\alpha } \otimes \left( { {\mathbf {P}}}_{,\alpha } \cdot {\mathbf {P}}^\mathrm{T} \right) _\times ={\mathbf {D}}_\alpha \otimes {\mathbf {k}}_\alpha . \end{aligned}$$

As a result, we can conclude that

$$\begin{aligned} \varepsilon _1={\mathbf {D}}_1\cdot {\mathbf {E}}\cdot {\mathbf {D}}_1, \quad \varepsilon _2={\mathbf {D}}_2\cdot {\mathbf {E}}\cdot {\mathbf {D}}_2, \quad {\mathbf {k}}_\alpha ={\mathbf {D}}_\alpha \cdot {\mathbf {K}}. \end{aligned}$$

According to the geometrical meaning of \({\mathbf {E}}\) and \({\mathbf {K}}\) [59], \(\varepsilon _1\) and \(\varepsilon _2\) describe stretching/elongation along two orthogonal directions related to the beams axes, whereas \({\mathbf {k}}_\alpha \) describes the changes of curvature.

Finally this identification leads to the following strain energy density of a micropolar shell:

$$\begin{aligned} \mathcal {W}=\mathcal {U}({\mathbf {D}}_1\cdot {\mathbf {E}}\cdot {\mathbf {D}}_1,{\mathbf {D}}_1\cdot {\mathbf {K}})+\mathcal {U}({\mathbf {D}}_2\cdot {\mathbf {E}}\cdot {\mathbf {D}}_2,{\mathbf {D}}_2\cdot {\mathbf {K}}). \end{aligned}$$
(33)

So (24.2) is a particular case of (30). In other words, the homogenized model of a beam lattice can be modeled within the framework of six-parameter shell theory.

In [27], the detailed analysis of constitutive relations for shells was provided considering the material symmetries and the invariance properties of \(\mathcal {W}\). Here the material symmetry group contains rotations about \({\mathbf {D}}_3={\mathbf {N}}\) of angles \(\pm \frac{\pi }{2}\) and mirror reflections \({\mathbf {I}}-{\mathbf {D}}_1\otimes {\mathbf {D}}_1\) and \({\mathbf {I}}-{\mathbf {D}}_2\otimes {\mathbf {D}}_2\). So (33) belongs to the class of orthotropic shells.

Let us also note that the form of (33) is similar to one used in the nonlinear elasticity and given by

$$\begin{aligned} \mathcal {W}=f(\lambda _1)+f(\lambda _2)+f(\lambda _3) \end{aligned}$$
(34)

where \(\lambda _i\) are principal stretches and f is a given function; see Valanis and Landel [80].

5 3D elastic network and its continuous counterpart

The derivation of the constitutive relations for 3D elastic networks with rigid joints mimics the above presented above 2D case. Let us consider an elastic network with cubic cells as shown in Fig. 1. We introduce the referential directors \({\mathbf {D}}_k\), \(k=1,2,3\), as the unit tangent vectors to corresponding beam axes; see Fig. 5. The considered network occupies in the reference placement a parallelepiped given by the inequalities

$$\begin{aligned} 0\le x \le mh,\quad 0\le y \le nh,\quad 0\le z \le lh \end{aligned}$$

where x, y, and z are Lagrangian Cartesian coordinates, h is the cell size, and m, n, and l are the numbers of beams in x-, y-, and z-directions, respectively.

Fig. 5
figure 5

Cubic cell and directors

Full size image

Here we have the following kinematical descriptors:

$$\begin{aligned} {\mathbf {r}}&={\mathbf {r}}_1^{(i)}(x),\quad {\mathbf {P}}={\mathbf {P}}_1^{(i)}(x),\qquad i=1,\ldots , m, \end{aligned}$$
(35)
$$\begin{aligned} {\mathbf {r}}&={\mathbf {r}}_2^{(j)}(y),\quad {\mathbf {P}}={\mathbf {P}}_2^{(j)}(y),\qquad j=1,\ldots , n,\end{aligned}$$
(36)
$$\begin{aligned} {\mathbf {r}}&={\mathbf {r}}_3^{(k)}(z),\quad {\mathbf {P}}={\mathbf {P}}_1^{(k)}(z),\qquad k=1,\ldots , l. \end{aligned}$$
(37)

In what follows, we again assume that the beams have the same material and geometrical properties, so we can use the same strain energy function \(\mathcal {U}\) for each beam. As a result, the constitutive relations differ from each other in their arguments only,

$$\begin{aligned} \mathcal {U}=\mathcal {U}(\varepsilon _1,{\mathbf {k}}_1),\quad \mathcal {U}=\mathcal {U}(\varepsilon _2,{\mathbf {k}}_2),\quad \mathcal {U}=\mathcal {U}(\varepsilon _3,{\mathbf {k}}_3), \end{aligned}$$
(38)

where the strain measures are derived as follows:

$$\begin{aligned} \varepsilon _1&={\mathbf {D}}_1\cdot {\mathbf {r}}_{,1}\cdot {\mathbf {P}}\cdot {\mathbf {D}}_1-1,\quad \varepsilon _2={\mathbf {D}}_2\cdot {\mathbf {r}}_{,2}\cdot {\mathbf {P}}\cdot {\mathbf {D}}_2-1, \end{aligned}$$
(39)
$$\begin{aligned} \varepsilon _3&={\mathbf {D}}_3\cdot {\mathbf {r}}_{,3}\cdot {\mathbf {P}}\cdot {\mathbf {D}}_3-1,\quad {\mathbf {k}}_a=-\frac{1}{2} \left( {\mathbf {P}}^\mathrm{T}\cdot {\mathbf {P}}_{,a}\right) _\times , \qquad a=1,\ldots ,3, \end{aligned}$$
(40)

and for \(\varepsilon _a\) and \({\mathbf {k}}_a\) we use the corresponding kinematical descriptors from (35)–(37).

The total energy functional takes the following form:

$$\begin{aligned} \mathcal {E}= & {} \sum _{k=1}^l\sum _{j=1}^n\sum _{i=1}^{m-1}\int _{x^{(i)}}^{x^{(i+1)}} \mathcal {U}(x)\, \mathrm {d}x\bigg |_{y=y^{(j)}, z=z^{(k)}} \nonumber \\&+\sum _{k=1}^l\sum _{j=1}^{n-1}\sum _{i=1}^{m}\int _{y^{(j)}}^{y^{(j+1)}} \mathcal {U}(y)\, \mathrm {d}y\bigg |_{x=x^{(i)}, z=z^{(k)}}\nonumber \\&+\sum _{k=1}^{l-1}\sum _{j=1}^{n}\sum _{i=1}^{m}\int _{z^{(k)}}^{z^{(k+1)}} \mathcal {U}(z)\, \mathrm {d}z\bigg |_{x=x^{(i)}, y=y^{(j)}} \end{aligned}$$
(41)

where for cubic cells we have \(x^{(i)}=(i-1)h\), \(y^{(j)}=(j-1)h\) and \(z^{(k)}=(k-1)h\). Using the trapezoidal rule for the integrands in (41), we get an approximation

$$\begin{aligned} \mathcal {E}=\sum _{k=1}^l\sum _{j=1}^n\sum _{i=1}^{m}c_{ijk}\left[ \mathcal {U}(x^{(i)})+\mathcal {U}(y^{(j)})+\mathcal {U}(z^{(k)})\right] , \end{aligned}$$
(42)

which uses the values of \(\mathcal {U}\) in the nodes only. Here \(c_{ijk}\) are weight coefficients which can be obtained after summation. Replacing \(\mathcal {U}(x^{(i)})\), \(\mathcal {U}(y^{(j)})\), and \(\mathcal {U}(z^{(k)})\) by their expressions by the strain measures, we get

$$\begin{aligned} \mathcal {E}&=\sum _{k=1}^l\sum _{j=1}^n\sum _{i=1}^{m}c_{ijk}\left[ \mathcal {U}(\varepsilon _1^{(ijk)},{\mathbf {k}}_1^{(ijk)})\right. \nonumber \\&\quad +\mathcal {U}(\varepsilon _2^{(ijk)},{\mathbf {k}}_2^{(ijk)}) \left. +\mathcal {U}(\varepsilon _3^{(ijk)},{\mathbf {k}}_3^{(ijk)})\right] . \end{aligned}$$
(43)

In order to find the continuous counterpart of (43), we introduce fields

$$\begin{aligned} {\mathbf {r}}={\mathbf {r}}(x,y,z),\quad {\mathbf {P}}={\mathbf {P}}(x,y,z), \end{aligned}$$

in which restrictions coincide with (35)–(37). As a result, we get a continuous counterpart of (43) given by the relation

$$\begin{aligned} \mathcal {E}=\int \limits _0^{(m-1)h}\int \limits _0^{(n-1)h}\int \limits _0^{(l-1)h}\left[ \mathcal {U}(\varepsilon _1,{\mathbf {k}}_1)+\mathcal {U}(\varepsilon _2,{\mathbf {k}}_2)+\mathcal {U}(\varepsilon _3,{\mathbf {k}}_3)\right] \,\mathrm {d}x \mathrm {d}y \mathrm {d}z. \end{aligned}$$
(44)

This energy functional can be characterized within the micropolar elastic continuum model.

Following [30, 59], let us briefly recall the constitutive theory for micropolar solids. The kinematics is described by the fields

$$\begin{aligned} {\mathbf {x}}={\mathbf {x}}({\mathbf {X}}),\quad {\mathbf {Q}}={\mathbf {Q}}({\mathbf {X}}) \end{aligned}$$

where \({\mathbf {x}}\) and \({\mathbf {X}}\) are the position vectors in current and reference placements, respectively, and \({\mathbf {Q}}\) is the microrotation tensor. The strain energy density of a 3D micropolar elastic body is given by

$$\begin{aligned} \mathcal {W}=\mathcal {W}({\mathbf {E}},{\mathbf {K}}) \end{aligned}$$
(45)

where the natural strain measures \({\mathbf {E}}\) and \({\mathbf {K}}\) are defined as follows:

$$\begin{aligned} {\mathbf {E}}={\mathbf {F}}\cdot {\mathbf {Q}}^\mathrm{T}-{\mathbf {I}},\quad (\nabla {\mathbf {Q}})\cdot {\mathbf {Q}}^\mathrm{T}=-{\mathbf {K}}\times {\mathbf {I}},\qquad {\mathbf {F}}=\nabla {\mathbf {x}}\end{aligned}$$
(46)

where \({\mathbf {F}}\) is the deformation gradient and \(\nabla \) is the 3D Lagrangian nabla operator.

If we identify as previously \({\mathbf {x}}\) as \({\mathbf {r}}\) and \({\mathbf {Q}}\) as \({\mathbf {P}}\), we get relations between the couples \(\varepsilon _a\), \({\mathbf {k}}_a\) and \({\mathbf {E}}\), \({\mathbf {K}}\):

$$\begin{aligned} \varepsilon _1={\mathbf {D}}_1\cdot {\mathbf {E}}\cdot {\mathbf {D}}_1, \quad \varepsilon _2={\mathbf {D}}_2\cdot {\mathbf {E}}\cdot {\mathbf {D}}_2, \quad \varepsilon _3={\mathbf {D}}_3\cdot {\mathbf {E}}\cdot {\mathbf {D}}_3, \quad {\mathbf {k}}_a={\mathbf {D}}_a\cdot {\mathbf {K}}. \end{aligned}$$
(47)

Obviously, these relations are straightforward generalizations of the 2D case considered above.

Thus the homogenized model of 3D elastic networks with rigid joints can be characterized as a micropolar elastic solid with the strain energy density given by

$$\begin{aligned} \mathcal {W}=\mathcal {U}({\mathbf {D}}_1\cdot {\mathbf {E}}\cdot {\mathbf {D}}_1,{\mathbf {D}}_1\cdot {\mathbf {K}})+\mathcal {U}({\mathbf {D}}_2\cdot {\mathbf {E}}\cdot {\mathbf {D}}_2,{\mathbf {D}}_2\cdot {\mathbf {K}}) +\mathcal {U}({\mathbf {D}}_3\cdot {\mathbf {E}}\cdot {\mathbf {D}}_3,{\mathbf {D}}_3\cdot {\mathbf {K}}). \end{aligned}$$
(48)

This constitutive relation inherits symmetry of the beam lattice. Indeed, according to [28] this material belongs to the class of micropolar solids with cubic symmetry.

It is worth noting that (48) has the form proposed for the nonlinear elasticity by Valanis and Landel [80]. So (33) and (48) can be treated as a generalization of the Valanis–Landel hypothesis for micropolar solids.

For example, considering (11) we get the following constitutive relations:

$$\begin{aligned} \mathcal {W}&=\frac{1}{2} K_s(\varepsilon _1^2+\varepsilon _2^2+\varepsilon _3^2)+\frac{1}{2} {\mathbf {k}}_a\cdot {\mathbf {D}}\cdot {\mathbf {k}}_a\nonumber \\&=\frac{1}{2} K_s({\mathbf {D}}_a\cdot {\mathbf {E}}\cdot {\mathbf {D}}_a)^2+\frac{1}{2} ({\mathbf {D}}_a\cdot {\mathbf {K}})\cdot {\mathbf {D}}\cdot ({\mathbf {D}}_a\cdot {\mathbf {K}})\nonumber \\&=\frac{1}{2} {\mathbf {E}}:{\mathbf {C}}:{\mathbf {E}}+\frac{1}{2}{\mathbf {K}}:{\mathbf {G}}:{\mathbf {K}} \end{aligned}$$
(49)

where \({\mathbf {C}}\) and \({\mathbf {G}}\) are the fourth-order tensors of elastic moduli given by

$$\begin{aligned} {\mathbf {C}}=K_s {\mathbf {D}}_a\otimes {\mathbf {D}}_a\otimes {\mathbf {D}}_b\otimes {\mathbf {D}}_b,\quad {\mathbf {G}}=D_{pq} {\mathbf {D}}_a\otimes {\mathbf {D}}_p\otimes {\mathbf {D}}_a\otimes {\mathbf {D}}_q, \end{aligned}$$

\(D_{pq}\) are the components of \({\mathbf {D}}\) in the basis \(\{{\mathbf {D}}_k\}\), and  :  stands for the double dot product defined as follows:

$$\begin{aligned} ({\mathbf {a}}\otimes {\mathbf {b}}):({\mathbf {c}}\otimes {\mathbf {d}})=({\mathbf {a}}\cdot {\mathbf {c}})({\mathbf {b}}\cdot {\mathbf {d}}) \end{aligned}$$

for any vectors \({\mathbf {a}}\), \({\mathbf {b}}\), \({\mathbf {c}}\), and \({\mathbf {d}}\).

6 Conclusions

In the paper, we discussed the governing equations for an elastic network which consists of flexible fibers undergoing large deformations. Here we restrict ourselves to networks with orthogonal fibers with rigid connections such that the fibers keep their orthogonality during deformations. Let us note that this assumption plays a key role in the analysis, as it gives the possibility to describe the rotations of the fibers using one rotation tensor. As similar assumption was used for the derivation of the micropolar beam model considering the homogenization of beamlike lattice structures by Noor and Nemeth [55, 56]. As a result, we came to a special case of micropolar materials with the strain energy density which inherits all properties of the fibers. Let us note that in the case of micropolar materials as for any generalized medium the derivation of the constitutive equations is a rather complex quest. In addition to rather rare direct experimental data, see, e.g., [46, 68], the homogenization of highly inhomogeneous materials brings us the constitutive equations of micropolar materials; see [6, 18, 19, 31, 35, 69] and the references therein. Here we also consider a certain type of homogenization for the finite deformations as we replaced the semi-discrete network by a homogeneous medium. The presented constitutive equations can also be treated as a generalization of the Valanis–Landel hypothesis [80] for the case of micropolar shells and solids. Relaxing the assumption of orthogonality, we can obtain more general models of the equivalent medium such as strain gradient and micromorphic ones; see, e.g., [16, 42, 65].