Skip to main content
SpringerLink
Log in

Rayleigh wave at the surface of a prestressed elastic medium with arbitrary anisotropy

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

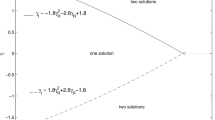
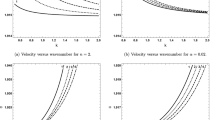
The propagation of harmonic plane waves is considered in a general anisotropic elastic medium, in the presence of prestress. A system of three homogeneous equations governs the existence of a Rayleigh wave at the stress-free plane boundary of the medium. This requires solving a complex secular equation for the implicit real phase velocity of the Rayleigh wave. For the presence of the radical, this irrational equation is never easy to solve by any standard analytical or numerical method. In this study, the system of three equations is transformed to get a real secular equation for the propagation of a Rayleigh wave, which can always be solved numerically for the real phase velocity of the Rayleigh wave. This phase velocity defines a complex slowness vector, which is used to calculate the polarisation of the Rayleigh wave at different depths in an elastic half-space. Effects of prestress and anisotropic symmetry on the phase velocity of the Rayleigh wave and associated particle motion are analysed by a numerical example.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Crampin, S.: A review of wave motion in anisotropic and cracked elastic media. Wave Motion 3, 343–391 (1981)

    Article  MATH  Google Scholar 

  2. Spencer, A.J.M.: Deformation of Fibre-Reinforced Materials. Clarendon Press, Oxford (1941)

    Google Scholar 

  3. Biot, M.A.: Influence of initial stress on elastic waves. J. Appl. Phys. 11, 522–530 (1940)

    Article  MathSciNet  MATH  Google Scholar 

  4. Biot, M.A.: Mechanics of Incremental Deformation. Wiley, New York (1965)

    Book  Google Scholar 

  5. Prikazchikov, D.A., Rogerson, G.A.: Some comments on the dynamic properties of anisotropic and strongly anisotropic prestressed elastic solids. Int. J. Eng. Sci. 41, 149–171 (2003)

    Article  MATH  Google Scholar 

  6. Sharma, M.D., Garg, N.: Wave velocities in a pre-stressed anisotropic elastic medium. J. Earth Syst. Sci. 115, 257–265 (2006)

    Article  Google Scholar 

  7. Synge, J.L.: Elastic waves in anisotropic media. Stud. Appl. Math. 35, 323–334 (1956)

    MathSciNet  MATH  Google Scholar 

  8. Stroh, A.N.: Steady state problems in anisotropic elasticity. J. Math. Phys. 41, 77–103 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  9. Currie, P.K.: Rayleigh waves on elastic crystals. Q. J. Mech. Appl. Math. 27, 489–496 (1974)

    Article  MATH  Google Scholar 

  10. Norris, A.N., Sinha, B.K.: Speed of a wave along a fluid/solid interface in the presence of anisotropy and prestress. J. Acoust. Soc. Am. 98, 1147–1154 (1995)

    Article  Google Scholar 

  11. Chai, J.-F., Wu, T.-T.: Determination of surface wave velocities in a prestressed anisotropic solid. NDT & E Int. 29, 281–292 (1996)

    Article  Google Scholar 

  12. Ting, T.C.T.: An explicit secular equation for surface waves in an elastic material of general anisotropy. Q. J. Mech. Appl. Math. 55, 297–311 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Destrade, M.: Seismic Rayleigh waves on an exponentially graded, orthotropic half-space. Proc. R. Soc. Lond. A 463, 495–502 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Vinh, P.C., Seriani, G.: Explicit secular equations of Stoneley waves in a non-homogeneous orthotropic elastic medium under the influence of gravity. Appl. Math. Comput. 215, 3515–3525 (2010)

    MathSciNet  MATH  Google Scholar 

  15. Fu, Y.B., Mielke, A.: A new identity for the surface-impedance matrix and its application to the determination of surface-wave speeds. Proc. R. Soc. Lond. A 458, 2523–2543 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kundu, S., Maity, M., Pandit, D.K., Gupta, S.: Effect of initial stress on the propagation and attenuation characteristics of Rayleigh waves. Acta Mech. (2018). https://doi.org/10.1007/s00707-018-2283-3

    MATH  Google Scholar 

  17. Chadwick, P.: The existence of pure surface modes in elastic materials with orthorhombic symmetry. J. Sound Vib. 47, 39–52 (1976)

    Article  MATH  Google Scholar 

  18. Sharma, M.D.: Rayleigh wave at the surface of a general anisotropic poroelastic medium: derivation of real secular equation. Proc. R. Soc. A 474, 20170589 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  19. Sharma, M.D.: Effect of initial stress on reflection at the free surface of anisotropic elastic medium. J. Earth Syst. Sci. 116, 537–551 (2007)

    Article  Google Scholar 

  20. Synge, J.L.: Flux of energy for elastic waves in anisotropic media. Proc. R.I.A. 58, 13–21 (1956)

    MathSciNet  MATH  Google Scholar 

  21. Fryer, G.J., Frazer, N.L.: Seismic waves in stratified anisotropic media—II. Elastodynamic eigensolutions for some anisotropic systems. Geophys. J. R. Astron. Soc. 91, 73–101 (1987)

    Article  Google Scholar 

  22. Brown, J.M., Abramson, E.H., Angel, R.J.: Triclinic elastic constants for low albite. Phys. Chem. Miner. (2006). https://doi.org/10.1007/s00269-006-0074-1

    Google Scholar 

  23. Ewing, W.M., Jardetsky, W.S., Press, F.: Elastic Waves in Layered Media. McGraw-Hill, New York (1957)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Kurukshetra University, Kurukshetra, 136 119, India

    M. D. Sharma

Authors
  1. M. D. Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. D. Sharma.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The elastic tensor \(B_{ijkl}\) represents the elastic behaviour of a general anisotropic prestressed medium. In two-suffixed notations, this fourth-order tensor is replaced by a six-order asymmetric square matrix \(\{b_{IJ}\}, I=i\delta _{ij}+(9-i-j),~ J=k\delta _{kl}+(9-k-l);~i,j,k,l=1,2,3.\) Considering the slowness vector \(\mathbf{p}=(p_1,p_2,q)\) as a row-matrix, the elements of the asymmetric square matrix \(\mathbf{Z}\) in (5) are expressed as follows:

$$\begin{aligned} Z_{11}= & {} \mathbf{p}{} \mathbf{A_{1}}{} \mathbf{p}',~~Z_{22}=\mathbf{p}{} \mathbf{A_{2}}\mathbf{p}',~~Z_{33}=\mathbf{p}{} \mathbf{A_{3}}{} \mathbf{p}',\nonumber \\ Z_{12}= & {} \mathbf{p}{} \mathbf{A_{4}}{} \mathbf{p}',~~Z_{13}=\mathbf{p}{} \mathbf{A_{5}}\mathbf{p}',~~Z_{21}=\mathbf{p}{} \mathbf{A_{6}}{} \mathbf{p}',\nonumber \\ Z_{23}= & {} \mathbf{p}{} \mathbf{A_{7}}{} \mathbf{p}',~~Z_{31}=\mathbf{p}{} \mathbf{A_{8}}\mathbf{p}',~~Z_{32}=\mathbf{p}{} \mathbf{A_{9}}{} \mathbf{p}' \end{aligned}$$
(19)

where \(\mathbf{p}'\) denotes the transpose of \(\mathbf{p}\). The \(3\times 3\) matrices \(\mathbf{A_{r}}, (\mathbf{r}=\mathbf{1},\mathbf{2}\ldots ,\mathbf{9}),\) are given by

$$\begin{aligned} \mathbf{A_{1}}= & {} \{b_{11},b_{16},b_{15};b_{61},b_{66},b_{65};b_{51},b_{56},b_{55}\}; ~~~\mathbf{A_{2}}=\{b_{66},b_{62},b_{64};b_{26},b_{22},b_{24};b_{46},b_{42},b_{44}\};\nonumber \\ \mathbf{A_{3}}= & {} \{b_{55},b_{54},b_{53};b_{45},b_{44},b_{43};b_{35},b_{34},b_{33}\}; ~~~\mathbf{A_{4}}=\{b_{16},b_{12},b_{14};b_{66},b_{62},b_{64};b_{56},b_{52},b_{54}\};\nonumber \\ \mathbf{A_{5}}= & {} \{b_{15},b_{14},b_{13};b_{65},b_{64},b_{63};b_{55},b_{54},b_{53}\}; ~~~\mathbf{A_{6}}=\{b_{61},b_{66},b_{65};b_{21},b_{26},b_{25};b_{41},b_{46},b_{45}\};\nonumber \\ \mathbf{A_{7}}= & {} \{b_{65},b_{64},b_{63};b_{25},b_{24},b_{23};b_{45},b_{44},b_{43}\}; ~~~\mathbf{A_{8}}=\{b_{51},b_{56},b_{55};b_{41},b_{46},b_{45};b_{31},b_{36},b_{35}\};\nonumber \\ ~~~\mathbf{A_{9}}= & {} \{b_{56},b_{52},b_{54};b_{46},b_{42},b_{44};b_{36},b_{32},b_{34}\}. \end{aligned}$$
(20)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, M.D. Rayleigh wave at the surface of a prestressed elastic medium with arbitrary anisotropy. Acta Mech 230, 3041–3053 (2019). https://doi.org/10.1007/s00707-019-02455-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-019-02455-2

Search

Navigation