Analysis of an orthotropic elastic plane problem of a half plane with an edge crack using a mapping function

Abstract

It is a challenging problem to derive a solution for an orthotropic elastic plane problem using a mapping function. The complex variable method is employed to introduce a mapping function. Then, comparatively arbitrary configurations can be analyzed. The boundary condition equation is represented by two complex variables. This fact makes solving the present problem difficult. This difficulty is conquered by applying Cauchy integrals. Also, mapping functions represented by an infinite terms of fractional expressions are introduced to conquer the mathematical difficulties of the Cauchy integral in the process of the derivation of the stress function. One of two stress functions is derived by analytical continuation. The final exact stress functions are represented by an irrational mapping function in a closed form. Stress components are represented by one complex variable. Therefore, the calculation of the stress components is easier than that of an isotropic problem. Half planes with a notch or a mound expressed by an irrational mapping function can be solved using their mapping functions. Such a polygonal mapping function can be derived by Schwarz–Christoffel’s transformation. As a demonstration, a half plane with a vertical edge crack subjected to uniform tension is analyzed and the stress distributions are shown for two examples of two characteristic roots of the characteristic equation for the orthotropic elastic plane.

Appendix: Rational mapping function

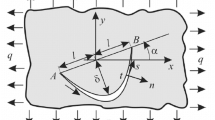
The final stress functions are expressed by an irrational mapping function (see Eq. (39)). The function (23) was used in the process to achieve the stress function $\varPhi (\zeta _1 )$. To solve the Case II problem, the rational mapping function is useful and is formed from the irrational mapping function. It is briefly described how to form a rational mapping function which maps a half plane with an oblique edge crack of the $z_1$-plane into the inside of a unit circle on the $\zeta _1$-plane (see Fig. 5a and Eq. (51)). The irrational mapping function is expressed by the following equation:

$$\begin{aligned} z_1 =\omega _1 (\zeta _1 )=l_1 \frac{(1-i)i^{-p_1 }}{2p_1^{p_1 } (1-p_1 )^{1-p_1 }}\frac{(1+i\zeta _1 )^{p_1 }(1-i\zeta _1 )^{1-p_1 }}{1-\zeta _1 }. \end{aligned}$$

(A1)

$\zeta _1 =1$ corresponds to infinity. In case of Eq. (22) (see Fig. 2a), $p_{1}=1/2$. The irrational terms $(1+i\zeta _1 )^{p_1 }$ and $(1-i\zeta _1 )^{1-p_1 }$ are transformed into the following rational mapping terms [10, 13]:

$$\begin{aligned} (1+i\zeta _1 )^{p_1 } \doteq 1+\sum _{j=1}^n {\left( {\frac{-A_{1j} }{1+i\gamma _{1j} \zeta _1 }+A_{1j} } \right) }, \nonumber \\ (1-i\zeta _1 )^{1-p_1 }\doteq 1+\sum _{j=1}^n {\left( {\frac{-B_{1j} }{1-i\delta _{1j} \zeta _1 }+B_{1j} } \right) .} \end{aligned}$$

(A2)

How to determine $A_{1j} ,\gamma _{1j}$ and $B_{1j} , \delta _{1j}$ is described in [10, 13], and $n=12\hbox { or }14$ was selected. When n is infinite, both sides are equal at the respective equations of Eq. (A2). In Eq. (A2), $\gamma _{1j}<1,\delta _{1j} <1$. Eq. (A2) is substituted into Eq. (A1), and after some manipulation, Eq. (A1) is expressed as:

$$\begin{aligned} z_1= & {} \omega _1 (\zeta _1 )=l_1 \frac{(1-i)i^{-p_1 }}{2p_1^{p_1 } (1-p_1 )^{1-p_1 }}\frac{(1+i\zeta _1 )^{p_1 }(1-i\zeta _1 )^{1-p_1 }}{1-\zeta _1 } \nonumber \\\doteq & {} l_1 \frac{(1-i)i^{-p_1 }}{2p_1^{p_1 } (1-p_1 )^{1-p_1 }}\frac{1}{1-\zeta _1 }\left\{ {1+\sum _{j=1}^n {\left( {\frac{-A_{1j} }{1+i\gamma _{1j} \zeta _1 }+A_{1j} } \right) } } \right\} \nonumber \\&\quad \left\{ {1+\sum _{j=1}^n {\left( {\frac{-B_{1j} }{1-i\delta _{1j} \zeta _1 }+B_{1j} } \right) } } \right\} \nonumber \\\equiv & {} \frac{E_{10} }{1-\zeta _1 }+\sum _{k=1}^N {\frac{E_{1k} }{\zeta _{1k} -\zeta _1 }} +E_{1c}\,\, (N=2n). \end{aligned}$$

(A3)

The constants $\left| {\zeta _{1k} } \right| >1$ and $E_{1c}$ are determined from the position of the origin of the coordinate. In this case, the origin is selected at the root of the crack (see Fig. 5). When $N=\infty$, Eq. (A3) becomes Eq. (23).