1 Introduction

A major obstacle in extreme rainfall analysis is that values are relatively coarsely represented due to the inability of measuring continuous rainfall at infinitesimal spatio-temporal scales over a long period of time (Papalexiou et al. 2016). Especially small but heavy rainfall events are difficult to capture and predict.

One common problem regarding the identification of rainfall maxima for certain time intervals (e.g., sub-hourly to annual or historical maxima) is the rainfall recording. Currently, long and reliable records are available mainly from rain gauge networks, which lack in spatial coverage. Throughout the world, there exist multiple small to large networks of rain gauge measurements with different network characteristics, data record lengths and temporal resolution. Before the advent of data-loggers, rainfall data were always characterised by coarse temporal resolution (Morbidelli et al. 2021) and until today, sub-hourly accurate measurements from rain gauges are available at certain locations only and data based on daily and hourly measurements are still widely used in analysing rainfall climatologies (Yoo et al. 2015; Dunkerley 2018; Darwish et al. 2021).

For example, daily or hourly values are often and have been for a long time measured beginning at a fixed time (e.g., every full hour or every 7:00 AM) for a given time interval. It is long known that this can result in a bias that is difficult to ignore and can underestimate extreme values significantly. Also, many times rainfall records are collected at high resolution, but aggregated before saving to decrease computing times and storage requirements (Morbidelli et al. 2018). These so-called fixed maxima (F-Maxima) can in worst case underestimate rainfall records up to 50 % compared to maxima based on moving window (M-Maxima) (Morbidelli et al. 2017; Meier et al. 2016, 2019).

F-Maxima of, for example, historical time series with lower temporal resolution can be corrected with the help of correction factors, strictly larger than 1, called, i.e., sampling adjustment factors (SAF), Hershfield factor (H) or clock hour correction factor (CHCF) (Hershfield 1961; Young and McEnroe 2003; Papalexiou et al. 2016; Ghate and Timbadiya 2022). Multiple studies in the past have analysed the differences of M-Maxima and F-Maxima based on gauge data for different temporal aggregations and time periods and derived empirical SAF values for different durations since the 1950 s [i.e.,] (Keifer and Chu 1957). Early studies compared the SAF values for calender days and 24 h (H = 1.13 (Hershfield 1961), H = 1.15 (Harihara Ayyar and Tripathi 1973), H = 1.11 (Demarée 1985). Van Montfort (1990) calculated F-maxima for 1 to 3 calender days for all months of 67 years for one station in New Zealand, and later analysed 130 stations of daily precipitation for 30 years in Eastern China (Van Montfort 1997). Other studies derived empirical correction factors for different regions, durations and temporal resolution of the original data. Some results are based on very few or short time series, such as Jakob et al. (2005), who evaluated seven Australian cities with a representative SAF = 1.15, Dwyer and Reed (1994) with SAF values of 1.167 for daily rainfall, or Fowler et al. (2005), who derived SAF values of 1.16, 1.11, 1.035, and 1.005 for 1,2,5, and 10 days between 1961 to 1990). Other studies used multiple time series or very high resolutions down to 1 min. Morbidelli et al. (2017), for example, found that the SAF factors decrease with longer aggregation windows while analysing data of 1 min resolution in Central Italy, Muñoz Proboste (2018) used 34 years of data for 52 stations in Switzerland and derived SAF factors of 1.04 to 1.22 for 20 to 120 min, Llabrés-Brustenga et al. (2020) evaluated spatial pattern of 120 weather stations, Marasini (2020) analysed 10 years of data for 809 stations in Germany with a 1 min resolution, and Hnilica et al. (2021) analysed 20 years of 1 min data for 23 gauging stations in the Prague region. Young and McEnroe (2003) focused on the ratio of the duration of interest to the sampling interval and showed a consistency across durations from 1 to 24 h.

The empirical derivations come to similar conclusions; however, there is yet no fundamental understanding of the variability and thus usefulness of these factors. There exist also some theoretical assumptions on the conversion of fixed to true interval rainfall. However, there are couple of questions involved, such as if similar correction factors can be used for different time windows or if they are dependant on weather type, regional or seasonal features. Also, the influence of rainfall characteristics is unclear. Weiss (1964) introduced some very simple statistical concept that did not consider the problems mentioned, but found similar factors as those from empirical studies. Yoo et al. (2015) updated the concept of Weiss (1964) by including different temporal rainfall distributions; however, the results do not match well with empirical observations. Finally, Papalexiou et al. (2016) proposed the SAF to be a rather random factor, using hourly 7127 stations in the USA. He further introduced a method to correct both mean and standard deviation of F-Maxima.

With ongoing technique, new possibilities arise for analysing the spatial distribution and characteristics of these correction factor. Remotely sensed rainfall, like from radar, have the advantage of a high temporal resolution and spatial coverage. Though maximum rainfall values from rain gauge measurements can usually not fully been found in remotely sensed data (Breña-Naranjo et al. 2015) and sub-pixel variability of rainfall is hard to capture (Fabry 1996; Peleg et al. 2013; Gires et al. 2014, 2014; Cristiano et al. 2017; Peleg et al. 2018), radar-based quantitative precipitation estimates (QPE) showed to be a useful tool for spatio-temporal rainfall analyses as they combine information from weather radar precipitation fields with ground-based truth from rain gauges (Panziera et al. 2018).

The aim of this study is to assess the variability of SAF for whole Germany based on radar QPE of 1 km spatial resolution and two different temporal resolution (5 min and hourly). Maximum rainfall values are derived from time series based on around 400,000 radar cells with fixed and moving window sampling for time intervals from 10 min to 3 days. F- and M-Maxima are calculated for each considered duration with focus on sub-daily and sub-hourly time intervals. F- and M-Maxima are analysed with the help of SAFs regarding their spatial variability. With this, rain gauge-based assumptions for correcting F-Maxima shall be revised.

2 Materials and methods

2.1 Quantitative precipitation estimates (QPE)

The German National Meteorological Service (DWD) is providing different rainfall products that are based on radar information from the radar network of 17 German C-band radars and radars from neighbouring countries. The so-called radar climatology project of the DWD (RADarKLIMatologie, RADKLIM, Winterrath et al. (2017)) has reanalysed the complete radar data since 2001 with a consistent method and has published the data freely available in two products (version 3 available until 2022 as of today): (1) RADKLIM-RW is an hourly precipitations product resulting from radar based precipitation estimates that are calibrated with ground stations (see Winterrath et al. 2018, and for a product evaluation Lengfeld et al. 2019); 2) RADKLIM-YW (Winterrath et al. 2018) is a 5-min product resulting from a correction/factoring of DWD’s 5-min product RADOLAN-RY with the help of RADOLAN-RH and RADKLIM-RW on a sequential hourly base (for more information on RADKLIM-YW compare) (Kreklow and Kuhnt 2019).

Both RADKLIM-YW and RADKLIM-RW versions 2017.002 were used in this study in order to account for different temporal resolution. We evaluated years 2001 to 2016 due to comparison reasons with another study at our institute. Both products come with a spatial resolution of 1 km and a total area of the product of 1100 \(\times \) 900 grid cells, where around half of the cells contain values due to the shape of Germany.

The data contains a lot of missing values (NA) (1) in the vicinity of the border in parts of Eastern, Northern and Southern Germany due to changes and ongoing extension of the radar network (some time series are for example only available from 2014 on) and (2) due to malfunctioning of the radar or general (radar) errors. Generally, missing hours of less than 10 % in most areas are still a very good coverage (Lengfeld et al. 2019).

Generally, the RADKLIM-QPE seems to underestimate values for regions with higher elevations, potentially due to radar function and sparse gauging information. We tested this for the higher elevated Ore Mountains in the South of Saxony, and the QPE showed significant lower precipitation sums than those we produced with rain gauge records. It is rather unproblematic for our analysis, since we use the same data set for the analysis and this error will not affect the comparison.

2.2 Maximum rainfall intensities

The maximum rainfall intensities for different intervals were retrieved by aggregating both data sets for each duration of interest with fixed and moving window sampling using the R package RccpRoll (Ushey 2018).

2.2.1 Overall maxima

For each time series (grid cell, denoted as cell) and each duration \(\tau \), the fixed and moving window maxima \({F}^{\tau ,cell}_{max}\) and \({M}^{\tau ,cell}_{max}\) are calculated for the whole time period of 16 years. The maxima are calculated in a first step for each grid cell. The maxima for all grid cells (N\(\sim \)400,000 cells) for each \(\tau \) are then calculated according to Eqs. 1 and 2.

$$\begin{aligned} {F}_{\text {max}}^{\tau }=\text {max} \left\{ {F}_{\text {max}}^{\tau ,1}, .., F_{\text {max}}^{\tau ,N}\right\} \end{aligned}$$
(1)
$$\begin{aligned} {M}_{\text {max}}^{\tau }=\text {max} \left\{ M_{\text {max}}^{\tau ,1}, .., M_{\text {max}} ^{\tau ,N} \right\} \end{aligned}$$
(2)

Windows from 1 h (12 \(\times \) 5 min for YW) to 3 days (864 \(\times \) 5 min for YW and 72 \(\times \) 1 h for RW) were calculated, specifically the following: 1, 2, 3, 4, 6, 8, 10, 12, 14, 16, 18, 20, 24, 36, 48 and 72 h. In order to compare the influence of the aggregation steps, additionally sub-hourly maxima for YW were calculated. Please note that the maxima for RADKLIM-YW were available from a previous study and analysed \(\tau \) differ slightly for RADKLIM-YW and RW.

2.2.2 Annual maxima

Additionally to overall maxima, for each duration \(\tau \) (\(\tau \) = 1, 2, 4, 6, 8, 12, 16, 20, 24, 30, 36, 42 and 48 h), annual fixed and moving maxima \({F}^{\tau ,cell}_{\text {max},y}\) and \({M}^{\tau ,cell}_{\text {max},y}\) (y being the individual year), respectively, were calculated based on 10,000 selected grid cells with Eqs. 3 and 4 (N \(\sim \) 10,100).

$$\begin{aligned} {F}_{\text {max},y}^{\tau }=\text {max} \left\{ {F}_{\text {max},y}^{\tau ,1}, .., F_{\text {max},y}^{\tau ,N}\right\} \end{aligned}$$
(3)
$$\begin{aligned} {M}_{\text {max},y}^{\tau }=\text {max} \left\{ M_{\text {max},y}^{\tau ,1}, .., M_{\text {max},y} ^{\tau ,N} \right\} \end{aligned}$$
(4)

We were only interested in looking at grid cells that contain time series with high precipitation maxima. This was done to later be able to analyse the “severity” of underestimating very high precipitation values better. Thus, we based the choice on RW maxima with moving window approach. The \(\sim \)400,000 grid cells were reduced by (1) calculating percentiles for each window and (2) only keeping those grid cells that exceed the 75 % percentiles for each window. This kept \(\sim \)13,000 grid cells. To reduce the grid cells to around 10,000 grid cells, additionally, the 75 % percentiles for YW maxima (moving window) for 48 and 72 h were chosen. This resulted in 10,048 grid cells for both RADKLIM products displayed in Fig. 1.

Fig. 1
figure 1

Positions of chosen grid cells (black dots) within German boundary for annual analysis of SAF and SDF and topographic map as background

Full size image

2.3 Sampling adjustment and difference factors

Based on both fixed and moving maxima, the sampling adjustment factor (SAF) is calculated as ratio of the “true” maximum \(M_{\text {max}}\) and “fixed” maximum \(F_{\text {max}}\) for each \(\tau \) (Eq. 5) as well as the average over all \({\tau }\) (Eq. 6) (Young and McEnroe (2003); Papalexiou et al. (2016); Meier et al. (2019)).

$$\begin{aligned} {SAF}_{\left( y\right) }^{\tau }=\frac{{M}_{\text {max},\left( y\right) }^{\tau }}{{F}_{\text {max},\left( y\right) }^{\tau }} \end{aligned}$$
(5)
$$\begin{aligned} {SAF}_{\left( y\right) } = \frac{E\left( {M}_{\text {max},\left( y\right) }^{\tau }\right) }{E\left( {F}_{\text {max},\left( y\right) }^{\tau }\right) } \end{aligned}$$
(6)

Note that in the classical definition, the SAF factor is not estimated as the mean value of all estimated SAF factors, i.e., \({SAF}_{\left( y\right) } = E \left( {M}_{\text {max},\left( y\right) }^{\tau }/{F}_{\text {max},\left( y\right) }^{\tau }\right) \), but equals the ratio of the moving maxima mean value to the fixed maxima mean value.

Fig. 2
figure 2

Maximum rainfall intensities for different durations (in hours), based on radar QPE from 2001 to 2016 (RADKLIM-RW and RADKLIM-YW) as well as rain gauge values from 1855 to 2014 (DWA (2015); DWD (2002, 2016))

Full size image

The factor is calculated independently of the concurrent occurrence of both F- and M-Maxima. For the annual analysis, this approach is meaningful, since using values from the same event only can lead to an underestimation of the correction factor. For the overall analysis, this approach is more critical, since it would be difficult to correct values from 2001 with values from 2016 in worst case. We consider the potential problem rather negligible since when doing a random sample analysis to check for the date of occurrence, 95% of the M-Maxima happened concurrently with the F-Maxima (overall analysis).

We additionally introduced a new measure called sampling difference factor (SDF), since the SAF does not consider the “severity” of deviation. An SAF equal to 2 would have a higher consequence if it means that instead of 100 mm 200 mm were observed for an individual time window than if instead of 10 mm 20 mm were observed. The SDF is calculated for each \(\tau \) according to Eq. 7.

$$\begin{aligned} {SDF}_{\left( y\right) }^{\tau }= {M}_{\text {max},\left( y\right) }^{\tau }-{F}_{\text {max},\left( y\right) }^{\tau } \end{aligned}$$
(7)

Both SAF and SDF were also calculated for the annual maxima (denoted as y in Eqs. 6 and 7).

Fig. 3
figure 3

Position of rainfall maxima for all considered temporal aggregation for fixed and moving window sampling as well as products RADKLIM-YW (darkgreen) and RADKLIM-RW (red). Numbers next to dots indicate the maxima’s temporal aggregation (in hours)

Full size image

3 Results and discussion

3.1 Overall rainfall maxima for whole Germany

The highest maximum rainfall values retrieved with fixed and moving window aggregation for whole Germany \({F}_{\text {max}}^{\tau }\) and \({M}_{\text {max}}^{\tau }\) are displayed in Fig. 2. Additionally, maxima from German rain gauge data for a very long period from 1855 to 2014 are shown as a reference. The rain gauge-based values follow a scaling relationship as expected from literature [e.g.,] (Jennings 1950). A detailed evaluation of the (non-)scaling behaviour of the QPE based maximum rainfall (\({M}_{\text {max}}^{\tau }\)) is carried out in Pöschmann et al. (2021).

Fig. 4
figure 4

Spatial distribution of maximum rainfall values and sampling adjustment factors (based on RADKLIM-YW): a Aggregation of 12 h, also showing underlying fixed and moving window maxima. b SAF for 6, 24 and 72 h

Full size image

For most parts, \({F}_{\text {max}}^{\tau }\) and \({M}_{\text {max}}^{\tau }\) values are lower than those taken from longer rain gauge time series, high likely due to the shorter measurement period of only 16 years for RADKLIM. Especially, \({F}_{\text {max}}^{\tau }\) are more or less consistently below the rain gauge values. Interestingly, \({M}_{\text {max}}^{\tau }\) values exceed rain gauge maxima from 24 h onwards. This indicates that a higher spatial coverage together with a moving window analysis will tremendously improve the knowledge of maximum values.

When comparing the two radar-based products, RADKLIM-YW shows lower values than the hourly product up to 16 h. Above that, RADKLIM-YW (moving window) has higher values than those of RADKLIM-RW (moving window).

As shown in Fig. 3, the maxima from Fig. 2 do not necessarily overlap in space for RADKLIM-RW and RADKLIM-YW for some durations. However, there is almost no difference when comparing locations for \({F}_{\text {max}}^{\tau }\) and \({M}_{\text {max}}^{\tau }\).

Overall, the maxima are not very scattered to different locations, but can be identified at six grid cells within Germany. When looking at sub-hourly resolution of RADKLIM-YW, there are more locations and more variations (not shown in this figure).

Fig. 5
figure 5

Empirical and fitted average SAFs (annual and overall) depending on durations from 2 to 72 h for RADKLIM products RW and YW (2001 to 2016)

Full size image

3.2 Spatial distribution of F-Maxima, M-Maxima and SAF

The difference of moving and fixed window sampling can also be seen in the spatial comparison as shown in Fig. 4 (exemplarily shown for RADKLIM-YW).

Moving window sampling gives higher maximum intensities, but is not similarly distributed. Especially for those time scales where single rainfall events occur, moving window sampling gives a significantly better spatial representation of the maximum intensities. At the example of 12 h as displayed in Fig. 4a, the differences are really strong. The figure shows around three fields of higher rainfall intensities that are potentially related to single events. From the figure, it shows that “true” patterns of rainfall can be identified better with moving window aggregation. This can be seen at the example of a large pattern in the Eastern part of Germany that evolved most likely during the desastrous August 2002 flood. When comparing moving and fixed window, it shows that the area of higher rainfall is much larger for the moving aggregation than when using fixed aggregation. Additionally, the areas of large rainfall values are connected more than for fixed window aggregation. For other time scales, this effect is especially visible in the Alpine and mountainous regions.

The different effects of different sampling methods can be further inspected with the help of the sampling adjustment factor (SAF).

Figure 4b shows the spatial variability of SAFs for the whole of Germany and for different aggregation states. Interestingly, the SAF varies a lot between the different temporal aggregation steps and spatially. This causes different spatial SAF pattern for different time scales, with no evident reason for this high variability. The figure clearly underlines the importance of investigating in the way data is collected and aggregated temporally and spatially. It seems that the SAF factors are rather randomly distributed over Germany, so a focus on regional characteristics was not further emphasised.

3.3 SAF for annual maxima

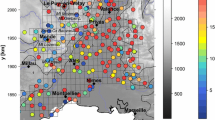
No pattern became visible from the spatial evaluation of the overall SAF; however, it looked like that the average SAF will get lower the more time steps are aggregated. This can be seen in Fig. 5 where the empirical average SAF factors are depicted for temporal aggregations between 2 and 72 (RADKLIM-RW in hours, RADKLIM-YW in 5 min steps).

Fig. 6
figure 6

Seasonal empirical and fitted average SAFs depending on durations from 2 to 72 h for RADKLIM products RW and YW (2001 to 2016)

Full size image

There is a clear difference between the hourly based RW curves and the 5-min-based YW curves. For RW, the average SAFs are higher for the annual analyses than what is found in literature. Most averages exceed values of 1.15. When comparing the different data lengths of RADKLIM-RW, there is not so much difference. For RADKLIM-YW, all curves are much lower than those of RADKLIM-RW with values similar to those found in literature around 1.14. When comparing the annual based analyses with the overall analyses, it showed that the overall SAF values are lower than the annual-based ones. This could show that when comparing higher maxima, for example, just the highest maxima of the whole time series for one grid cell instead of annual maxima, the difference between the moving and fixed values are not as significant than if including more, especially lower values. Generally, SAF based on YW data seem to stay quite stable over all aggregation steps compared to RW data.

Seasonal dependencies of the relationship are depicted in Fig. 6. Curves for RADKLIM-YW look quite similar for all seasons and show values of around 1.14 similar to those in literature. RADKLIM-RW on the other hand is more variable, even more for the seasonal analysis and goes up to SAF equal to 1.2. Also, instead of getting lower, in most cases, the average SAF increases for RADKLIM-RW, contrary to our expectations and contrary to RADKLIM-YW that shows a decline in most cases.

One possible explanation is that this study did not take into account different ways of totalizing rainfall (for fixed window sampling). Additionally, since most studies in the past base their findings on a rather low amount of rain gauges, it might also be possible that the theoretical assumption is not necessarily true and that indeed Papalexiou et al. (2016) with some thousands of rain gauges analysed is correct, who associated SAFs with a very strong random characteristic.

Table 1 Estimated parameters a, b and c for SAF distribution function from Eq. 8 based on annual SAFs
Full size table

The curves are fitted by using the simple parametric function proposed by Papalexiou et al. (2016) with parameters a, b and c retrieved for all cases.

$$\begin{aligned} {SAF\left( \tau \right) } = -a -\left( a-1\right) \text {exp}\left( -\left( \frac{\tau -1}{b}\right) ^c\right) \end{aligned}$$
(8)

The annual and seasonal relationships can be fitted quite well for most cases (parameters for the annual analyses are provided in Table 1). This is not true for overall SAFs based on YW data. For the overall relationship, no curve could be fitted with the suggested Eq. 8.

Table 2 Estimated parameters a, b and c for probabilistic distribution of SAF from Eq. 9 based on annual and overall SAFs for 2001 to 2016
Full size table

The curves are fitted by using a different simple parametric function proposed by Papalexiou et al. (2016), and parameters are provided in Table 2.

$$\begin{aligned} {Pr\left( SAF = 1\right) } = a +\left( 1-a\right) \text {exp}\left( -\left( \frac{\tau -1}{b}\right) ^c\right) \end{aligned}$$
(9)
Fig. 7
figure 7

Probability of SAF to equal 1 vs. aggregation scale (in hours for RADKLIM-RW, in 5 min steps for RADKLIM-YW) for 2001 to 2016

Full size image
Fig. 8
figure 8

Histogram of the conditional SAFs at different hourly scales, based on annual rainfall maxima (2001 to 2016)

Full size image

3.4 Probability and occurrences of SAFs

Besides average values for SAF, it is important to take a look at deviations from the mean, especially when thinking of high and very low SAFs. Figure 7 shows the probability distributions of SAF to equal 1 for annual as well as overall SAF and the different RADKLIM products between 2001 and 2016. As expected, the probability decreases quickly with higher aggregation states. The drop is quicker for RADKLIM-YW. It looks additionally like the probability increases a little bit for higher aggregation states.

Compared to the study of Papalexiou et al. (2016), SAF to equal 1 occurs more rarely in our study (annually based) and even less for the overall values. Again, the shape of the YW-curves look more alike than those of RW.

The overall distribution of SAF is displayed in Fig. 8 as conditional SAF across different time scales (in hours) for the annual analysis. It is obvious that RADKLIM-RW and -YW differ for the 2 h time scale, because YW is already aggregated 24 \(\times \) 5 min and has thus lower occurrence of SAF equal to 1. However, this difference quickly evens out, and the remaining time scales displayed show very similar distribution (just a little more SAF equal to 1 for RW). Interestingly, the higher the time scale (e.g., 12 or 24 h) higher values of SAF seem to occur a little more often.

Fig. 9
figure 9

SAF and corresponding rainfall value differences (SDF) at different hourly scales for annual values (2001 to 2016). The bigger the points, the higher the number of the SDF and SAF combination

Full size image

The distributions are very similar when looking at the overall conditional SAF distribution (Fig. 10 in Appendix), except of the different number of occurrence (not in years, but in grid cells). It shows that the overall distributions have a lower occurrence of higher SAFs. One explanation could be that if taking fixed and moving maxima out of the whole time period sample, the chances are higher to find a fixed maxima value more similar to the moving maxima value. If looking at the yearly values, it is more likely that the fixed window by chance really only captures half of the moving window maximum value, i.e., if there is only one big event within the year for example.

As mentioned before, it is of special interest what SAF equal to 1.5 or higher refer to in actual rainfall values (mm) and how often very high values occur for high SAF. Additionally, to the annual values, the overall comparison is shown in Fig. 11 of the Supplement Information. Generally, both RADKLIM products show a very similar distribution, when separately looking at overall and annual-based values.

Figure 9 compares SAFs for different hourly scales and their corresponding SDF.

For the annual analysis, SAFs equal to 2 refer to SDF values of up to 100 mm in 24 h. There is also a lower boundary for all hourly scales that shows a linear course. As expected, the differences between the 2-h and 24-h scale is rather low. Maximum SDF for SAF > 1.5 are between 40 and 80 mm, which would mean that for 12 h, it would be 3.3 to 6.6 mm/h underestimation of “true” rainfall values, but for 2 h already 20 mm/h to 40 mm/h. From the figure, we assume that for most cases, the differences between moving and fixed window maxima are based on lower aggregation states.

The relationship of SDF and SAF looks quite different for the overall values. Annual-based relationships are more scattered and have a wider range. The overall relationships are more narrow, and though the minimum SDFs show a straight course, they have a much higher slope compared to the annual ones. Another observation is that the maximum values of SDF are lower, especially for 24 h. These interesting deviation can be again explained as before: The chances are higher if only taking the whole time period that fixed and moving maxima are based on two events that are more similar; thus, lower SAF values are expected in general. However, because of the higher grid cells sample size, there are a lot of additional pairs considered than when looking at the selected grid cells for the annual analysis. That is why there are still a lot of pairs in the overall data set giving SAF of 2, but with lower SDF values.

4 Summary and conclusion

The study performed a very large analysis of two radar QPE of different temporal resolutions (1 h and 5 min) for the whole of Germany. Annual as well as overall fixed and moving interval maxima for several time scales were estimated, giving an unprecedented big data sample. The F- and M-Maxima were used to calculate the corresponding sampling adjustment factors (SAFs). Average values for each time scale as well as yearly, seasonal, regional and individual grid cells were evaluated. Our study shows a significantly high variability of the SAFs in space and time. The spatial distribution in space was much more variable the lower the aggregation step has been. This is because the underlying maxima also are not so spatially variable the longer the duration considered is.

When comparing the results with point-based studies, for RADKLIM-YW, similar SAFs equal to 1.14 can be found. This is in contrast to RADKLIM-RW, where values are in most cases higher than literature averages. Proposed equations for describing the behaviour of SAF over time scales as well as the probability of SAF equal to 1 were very suitable to fit our data to. Overall, RADKLIM-YW showed quite consistent average SAF compared to RADKLIM-RW.

Our study showed that it is important to not only consider average SAF for the individual time scales, but also take an in-depth look at the distribution of SAF when correcting fixed maxima. As expected, all values between 1 and 2 were possible for SAF, however, with a lower likelihood for higher SAFs. Nevertheless, higher SAFs are usually paired with higher “true” values of rainfall, and SAF equal to 2 can refer up to 40 mm/h for our data sample. Interestingly, the distribution of SAF as well as the “true” rainfall values do not change too much between 2 and 24 h. This indicates that higher SAFs are much more critical for lower time scales (i.e., 2 h), because it refers to much higher hourly values than for example for 24 h.

Though it is not recommended to extract single maxima per record, the findings still revealed interesting insights. We assumed that it might be possible to trade the large amount of grid cell values with annual values (thus trading space with time in a way). This however did not work out well. SAFs based on the overall analysis were generally lower than those of SAFs based on annual maxima. The reason most likely is that if taking longer time periods and neglecting the joint occurrence of fixed and moving maxima, the probability is higher that a fixed maxima in the whole data set can be found that is more comparable to the moving maxima than the “same-event” fixed maxima is. It is thus really important to consider this for further analyses.

Generally, there is a quite good consistency between RADKLIM products RW and YW. The discrepancies are explainable by the different processing as well as the fact that RADKLIM-RW already has a underlying fixed aggregation, because it is aggregated from a 5-min radar product. This means that moving window maxima for RADKLIM-RW are already a strong deviation from reality, which was not further analysed in this study. The different underlying temporal resolutions of 5 min and 1 h mainly had an effect when comparing hourly values of SAF, but not too much when comparing the different aggregation steps.

The study did not carry out a special sampling ratio analysis, did not consider different rainfall event types and also did not try different totalization types for the fixed window sampling (compare, i.e., Marasini (2020)). Still, the observations and conclusions from this study are a very good base for further analyses on the distribution of the sampling adjustment factor (SAF). It might also help to adapt current strategies to correct fixed values based on point measurements that are even interpolated in space. We suggest further developing the correction methodology proposed by Papalexiou et al. (2016) as the SAF distribution seems rather random based on our findings.

Further investigation will try to explain the different spatial pattern of SAFs in Germany as well as the scaling behaviour of rainfall maxima in space. Deeper evaluation of the radar product will help to understand the impact of data processing, especially the different temporal adjustment steps during the procedure in order to improve precipitation estimates by radar data over time scales.