Modeling end-to-end delays in TSCH wireless sensor networks using queuing theory and combinatorics

Abstract

Wireless communication offers significant advantages in terms of flexibility, coverage and maintenance compared to wired solutions and is being actively deployed in the industry. IEEE 802.15.4 standardizes the Physical and the Medium Access Control (MAC) layer for Low Power and Lossy Networks (LLNs) and features Timeslotted Channel Hopping (TSCH) for reliable, low-latency communication with scheduling capabilities. Multiple scheduling schemes were proposed to address Quality of Service (QoS) in challenging scenarios. However, most of them are evaluated through simulations and experiments, which are often time-consuming and may be difficult to reproduce. Analytical modeling of TSCH performance is lacking, as only one-hop communication with simplified traffic patterns is considered in state-of-the-art. This work proposes a new framework based on queuing theory and combinatorics to evaluate end-to-end delays in multihop TSCH networks of arbitrary topology, traffic and link conditions. The framework is validated in simulations using OMNeT++ and shows below 6% root-mean-square error (RMSE), providing quick and reliable latency estimation tool to support decision-making and enable formalized comparison of existing scheduling solutions.

1 Introduction

The role of Wireless Sensor Networks (WSNs) has been growing over the past decades as many industrial processes benefit from their extensive features, in particular wide-area coverage, low energy consumption, low cost and self-configurability [1, 36]. In the medical field, small wearables are employed to keep track of patients in- and outdoors in real time, while, e.g., for agriculture the coverage offered by WSNs is paramount for efficient crop monitoring [23]. Many scenarios require low-latency awareness of the infrastructure status combined with high data reliability [28]. To enable communication for such use cases, IEEE 802.15.4 specifies the lower two Open Systems Intercommunication (OSI) layers, see Fig. 1, while protocols such as ISA100a, WirelessHART, ZigBee and others define upper layers catered for particular scenarios.

Fig. 1

IEEE 802.15.4-based protocol stacks in relation to the OSI model

Since Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) cannot ensure strict QoS guarantees due to its probabilistic backoff mechanism (Fig. 2), Timeslotted Channel Hopping (TSCH) is considered a prominent candidate for safety-critical scenarios. The IPv6 over the TSCH mode of IEEE 802.15.4 (6TiSCH) protocol stack [32], visualized in Fig. 3, is developed by IETF to bridge WSNs with IP-based applications and enable communication scheduling through TSCH. Most of the existing research focuses on improving 6TiSCH by designing new Scheduling Functions (SFs), which are then evaluated in imulations and/or experiments. While simulations are reproducible, they often lack the credibility of a real experiment, which, on the other hand, might be time-consuming and costly. As discussed in detail in the following section, there is currently no universal approach to modeling end-to-end delays in an arbitrary TSCH network. For the decision-making process it is crucial to have a clear and reliable overview of the expected performance. To achieve such an overview with state-of-the-art research would require considerable effort of manually selecting suitable formulas depending on the use-case.

This work thus aims to simplify TSCH network planning by developing a generalized analytical framework, which captures the effect of different traffic types and variable link conditions on end-to-end delays. Our main contributions are as follows:

• Closed-form formulas are derived to calculate end-to-end delay over multiple hops for periodic and Poisson traffic.

• Intricate queuing effects of the slotted medium access are considered and the difference with traditional analytical approaches is highlighted.

• Impact of lossy links is covered by applying Markov chain-based modeling.

• Algorithms are proposed to derive precise expectations of end-to-end delays of every node in a network of arbitrary topology.

Robust validation in various scenarios with state-of-the art simulation models from OMNeT++ shows high accuracy of the presented framework and its suitability to be used in the production context.

The rest of the paper is organized as follows. Section 2 provides necessary background on the 6TiSCH stack, in particular TSCH and the SF. In Sect. 3 state of the art in terms of TSCH performance modeling is provided alongside a short summary of existing shortcomings. Section 4 outlines the analytical framework to accurately model end-to-end delays over multihop linear TSCH networks under variable traffic and link quality. Section 5 builds on top of that by extending the framework and introduces algorithms to evaluate TSCH networks with arbitrary topology. Finally, in Sect. 6, the framework is validated in simulations with OMNeT$++$ discrete event simulator combined with the INET library and the key insights are discussed, which is followed by the overall conclusion in Sect. 7.

2 Background

Among many IEEE 802.15.4-based protocols, 6TiSCH stands out as a scalable, IPv6-compatible protocol stack with the focus on communication scheduling. The flexibility granted by the SF enables 6TiSCH to be used in a wide variety of scenarios, catering to virtually any set of QoS requirements. Using SF to manage TSCH mode of IEEE 802.15.4 enables reliable, low-latency communication even under high external interference.

2.1 TSCH

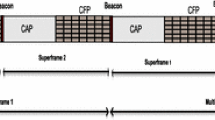
The TSCH mode is a combination of Time-Division Multiple Access (TDMA) and Frequency Division Multiple Access (FDMA), which enables scheduled communication as visualized in Fig. 2. The time is divided into slots and frequency spectrum – into channels. A tuple $( slotOffset , channelOffset )$ defines a cell, which is used for communication by a pair of nodes. The schedule is periodic and organized into slotframes, which repeat over time. Each cell is also assigned an Absolute Slot Number (ASN), which increments monotonically. The channel offset does not directly represent the channel used for communication, but is rather used as an input argument for the channel hopping procedure. According to the latter, the actual communication frequency f is determined by the following equation:

$$\begin{aligned} f = (ASN + channelOffset ) \;\textrm{mod} \; L_{hs}, \end{aligned}$$

(1)

where $L_{hs}$ is the hopping sequence length. A hopping sequence is an unordered list of channels – every transmission a new channel from the list is picked sequentially. Varying communication frequency mitigates external interference and multipath fading.

There are several cell types, depending on the communication mode. Dedicated cells are used for unicast, unidirectional communication between a pair of nodes. Shared cells can be used by multiple neighbors and employ contention mechanism similar to CSMA/CA. In this work we focus on the performance of a TSCH network with dedicated cells, as this is a typical output of most SFs.

Fig. 2

Example of a TSCH schedule

2.2 6TiSCH

Using TSCH at the MAC layer, the 6TiSCH stack brings IP-compatibility and proactive distance-vector routing to Low-Power Wide-Area Networks (LPWANs). Each node has a preferred parent, used to forward the data to Routing Protocol for Low-Power and Lossy Networks (RPL) sink. The selection of the preferred parent is governed by the Objective Function (OF) of RPL using metrics such as hop count, ETX, energy consumption, etc. The Constrained Application Protocol (CoAP) is used to enable request-response like communication between devices, following HTTP principles, but relies on User Datagram Protocol (UDP) in the transport layer and tries to minimize overhead. IPv6 over Low-Power Wireless Personal Area Networks (6LoWPAN) contains several mechanisms improving IP-compatibility of LPWANs, such as header compression, neighbor discovery optimization and others, which cater to the low-power, constrained nature of these networks.

The SF manages communication schedule in a distributed manner through transactions between nodes to add, delete or relocate cells using 6TiSCH Operation Sublayer (6top) Protocol (6P). SF plays a crucial role in ensuring that the network meets specific QoS requirements, e.g. low latency, high reliability, etc. In particular, Minimal Scheduling Function (MSF) [6] is the standardized solution proposed by IETF, which combines simplicity and robustness. MSF monitors cell utilization to add/delete cells based on predefined thresholds, thus adapting link-layer resources to the traffic load. Furthermore, cell performance is tracked in terms of the Packet Delivery Ratio (PDR), and the underperforming cells, e.g., due to external interference, are relocated using randomized slot and channel offset.

Fig. 3

IETF 6TiSCH protocol stack [32]

3 Related work

Significant portion of existing research focuses on improving 6TiSCH performance by introducing new SFs [5, 11, 14, 18, 20, 30, 31] and cross-layer optimizations [28]. Evaluation is mostly conducted by the means of simulations and experiments with limited attention paid to modeling expected improvements analytically. The latter issue is addressed to some extent in [15]. There, the impact of MSF parameters and varying traffic loads on the schedule convergence process is investigated for a linear network using a Python-based simulator. In [27] the authors model end-to-end delays in a linear TSCH network with periodic traffic using queuing theory. Limits of the minimal 6TiSCH configuration in terms of acceptable end-to-end delay and PDR are investigated experimentally in [35] for different network sizes and packet generation rates. Furthermore, the joining time in minimal 6TiSCH is evaluated through simulations with COOJA [24] in [16]. The impact of the slotframe length on end-to-end delays is investigated in [21, 22] via simulations for different number of nodes and traffic loads. Comprehensive performance evaluation is conducted for the Orchestra scheduler [11] in [25] also using simulations, where the end-to-end delay and PDR are measured for networks of variable size in a grid topology. Comparison of several autonomous scheduling functions is conducted in [26] using COOJA simulator for different network sizes and traffic rates.

Furthermore, many works on analytical [7, 10, 12, 33] as well as experimental [3] modeling of TSCH are limited to a star topology with one-hop communication. For mathematical analysis, a discrete-time Markov chain is used to derive Key Performance Indicators (KPIs) such as medium access delay, reliability and energy consumption. In [10] the capture effect is considered while [33] focuses on the impact of dedicated links and takes retransmissions into account. These works, however, feature a very limited traffic model with either a single transmission used to analyze the transmission success probability [10, 33], or periodic traffic, where the packet is discarded at the end of the slotframe [12]. Furthermore, the focus is mostly on shared CSMA/CA-based cells, which are rarely used for the transmission of application traffic in convergecast scenarios. In [29], a queueing model is also used to model end-to-end delays for heterogeneous traffic with different priorities, but only considering Poisson arrival process and one hop. Other topics related to modeling TSCH performance include evaluation of the network formation process [2, 9], energy consumption [4] and coexistence with 802.15.4 [34] or Bluetooth Low Energy (BLE) [13].

Summarizing, in state-of-the-art TSCH performance is evaluated analytically only under a one-hop communication with simplistic traffic model combined with CSMA/CA medium access. To the best of our knowledge, no holistic model exists to estimate end-to-end delays in TSCH networks with multihop communication under periodic and Poisson traffic while also considering unreliable links.

4 Analytical model

To model end-to-end delays in multihop TSCH networks, first the assumptions about the network and traffic are defined. Then, components of end-to-end delay are explained in detail. Distributions of waiting and sojourn times are derived for a single hop communication using queuing theory, stochastics and combinatorics. Finally, multihop scenarios and unreliable links are modeled.

4.1 Network model

Most TSCH networks represent a tree with the Destination-Oriented Directed Acyclic Graph (DODAG) sink collecting data from sensor nodes. To model the performance of such network, it can be broken down into linear components – end-to-end paths from each leaf node to the sink. In the following, we analyze the end-to-end delays of these linear segments under the assumptions:

• The network is operated by the 6TiSCH stack with MSF.

• Static topology with converged schedule (adapted to traffic, no cell relocations).

• Only uplink traffic using dedicated cells.

• Traffic arrivals are same for all nodes with rate $\lambda$ packets per slotframe (pkt/sf).

• Infinite queue size, no packet fragmentation.

All delays are expressed in slotframes and can be translated to ms by multiplying with $t_s S$, where S is the slotframe size in timeslots and $t_{s}$ is the timeslot duration in ms.

4.2 End-to-end delay

The end-to-end delay D is the time elapsed from the packet generation until its delivery to the destination—sink. For h hops, it is the sum of delays experienced per hop as:

$$\begin{aligned} D(h)&= \sum _{i=1}^h D_i = \sum _{i=1}^h \left( D_p + D_s + D_t + T_{i} \right) , \end{aligned}$$

(2)

where $D_i$ is the delay on i-th hop, $D_p$ is the propagation delay, $D_s$ is the processing delay, $D_t$ is the transmission delay and $T_{i}$ is the sojourn time (queuing delay). $D_s$ can be neglected considering the propagation speed of electromagnetic waves. Since a time slot contains windows to both transmit a packet and receive an acknowledgment [17], $D_t$ and $D_s$ are negligibly small as well. The last component, T, has the largest impact on the latency and can be defined as

$$\begin{aligned} T = W + Q, \end{aligned}$$

(3)

where W is the service time and Q is the queuing time. The service time refers to waiting at the head of the queue for the next available TX cell, and the queuing time denotes waiting in the queue until all preceding packets are served.

4.3 Queuing model

First, to calculate T each node can be modeled as a system with a single server, infinite buffer and a constant service rate. The latter is defined by the number of TX cells in uplink. MSF adapts the service rate $\mu$ (pkt/sf) to match the application traffic, ensuring $\mu > \lambda$. Depending on the upper cell utilization threshold $u_{high}$ configured in MSF, a cell overprovisioning is possible, which means that the service rate $\mu _i$ on a node with $i-1$ descendants is

$$\begin{aligned} \mu _{i} = \bigg \lceil \frac{\lambda _{i}}{u_{high}}\bigg \rceil = \bigg \lceil \frac{i\lambda }{u_{high}}\bigg \rceil , \end{aligned}$$

(4)

where $\lambda _i$ is the total arrival rate on a node with $i-1$ descendants. Since the number of cells and their locations in the slotframe are fixed, a deterministic departure process can be assumed. Depending on the traffic arrival process, e.g., periodic or Poisson, the queuing model on a TSCH node can be broadly classified as D/D/1 or M/D/1 in the Kendall notation, respectively. With periodic traffic, $D_{q}$ consists only of the service time W. However, both Poisson traffic and lossy links also introduce queuing time.

4.3.1 Service time

The service time W is defined by the distribution of distance between adjacent TX cells in a slotframe, see Fig. 4. Dedicated cells scheduled by MSF are uniformly distributed in a slotframe, since slot offsets are chosen randomly. Since the schedule is periodic, each of $\mu$ cells repeats with the period S, spanning a cellframe. The latter is equivalent to a slotframe shifted in time. In a cellframe, there are now $\mu -1$ TX cells with the packet arrival, $\mu$ uniformly distributed points in total. The mean service time W is then equivalent to the average distance between these $\mu$ points on a fixed interval – cellframe – and can be calculated as

$$\begin{aligned} W = \frac{1}{\mu + 1}. \end{aligned}$$

(5)

The distribution of W is that of the distance to the closest TX cell, as shown in Fig. 4. Given $\mu$ TX cells in total, the probability to be serviced within x timeslots is

$$\begin{aligned} F_W (W < x) = 1 - \left( 1 - \frac{x}{S} \right) ^\mu , \end{aligned}$$

(6)

where $F_W$ is the Cumulative Distribution Function (CDF) of the service time in timeslots.

Fig. 4

Service time x on a TSCH node with $\lambda = 1$ (periodic) and $\mu = 2$

4.4 Deterministic traffic

With a deterministic arrival process, the queuing model on each node turns into a D/D/1 system where T is largely determined by the service time (5). However, on a node i with $\lambda _i \ge 2$, randomized allocation of TX cells has an additional impact on T. If multiple RX cells are scheduled between adjacent TX cells, some packets experience queuing as visualized in Fig. 5a. The extent of this impact further depends on whether the node is a leaf or a forwarding node.

Fig. 5

Mapping arrangements of packet arrivals and TX cells in a slotframe to integer compositions, modified from [27]

The sojourn time on a forwarding node $T_d$ is given by

$$\begin{aligned} T_d = W \left( 1 + \sum _{i=2}^{{\lfloor {\lambda }\rfloor }} \left( i - 1 \right) p_{\lambda _i} \right) , \end{aligned}$$

(7)

where $p_{\lambda _i}$ is the probability of exactly i out of $\lambda$ packet arrivals falling into the same bin. To calculate $p_{\lambda _i}$, the concept of integer compositions can be utilized as described in Appendix A.

For a leaf node generating $\lambda \ge 2$ pkt/sf on its own, the queuing effect is slightly different. Instead of TX cells, periodic packet arrivals define the bins as shown in Fig. 5b. From the stability condition of a queuing system, per slotframe there should always be more TX cells than packet arrivals. Thus, having up to two TX cells in a bin does not impact the sojourn time of packets. Following the approach used for the forwarding nodes and considering now integer compositions of $\mu$ rather than $\lambda$, the sojourn time $T^*_d$ for a leaf node is

$$\begin{aligned} \begin{aligned} T^*_d&= W \left( 1 + \sum _{i=3}^\mu (i - 2) p_{\mu _i} \right) \\&= W \left( 1 + \sum _{i=3}^\mu (i - 2) \frac{1}{c_\mu } \sum _{j=1}^{{\lfloor {\mu /i}\rfloor }} \frac{ij - j - 1}{\lambda } c_{\mu _{ij}} \right) , \quad \lambda \ge 2 \end{aligned} \end{aligned}$$

(8)

where $c_{\mu _{ij}}$ is number of $\mu$-compositions where i occurs exactly j times, see (A8), and $p_{\mu _i}$ describes all possible ways $\mu _i$ TX cells can be distributed in bins between periodic packet arrivals.

For j bins with i TX cells in each, the probability of an arbitrary packet experiencing queuing is

$$\begin{aligned} \frac{i j - j - 1}{\lambda } \quad \forall i \in \{3\dots \mu \}, \; \forall j \in \{1\dots \left\lfloor \frac{\mu }{i} \right\rfloor \} , \end{aligned}$$

(9)

4.5 Poisson traffic

For packet arrivals following Poisson process, the queuing model on a leaf node can be described by an M/D/1 system with

$$\begin{aligned} T_p = W + Q_{p} = \frac{1}{\mu +1} + \frac{\rho }{2\mu (1-\rho )}, \end{aligned}$$

(10)

where $T_p$ is the sojourn time, $Q_{p}$ is the queuing time and $\rho = \lambda /\mu$ is the service utilization. For a forwarding node, the arrival process contains both Poisson arrivals from the node itself and traffic coming from the child node, thus turning the queuing system into a G/D/1. Since there is no closed-form solution for the sojourn time in such a system, we propose a heuristic method yielding accurate estimation with little computational complexity. We first differentiate between the traffic generated by the node itself and traffic forwarded from descendants. The latter is strictly bounded by the number of scheduled RX cells. Assuming each forwarded packet occupies one of $\mu _i$ TX cells,

$$\begin{aligned} \mu '_i = \mu _i - \big \lceil {\lambda _{i-1}}\big \rceil \end{aligned}$$

(11)

cells are left as the service capacity for the traffic generated by the node i. Queuing only occurs when the Poisson traffic originating from the node itself exceeds $\mu '_i$. Applying the P-K formula:

$$\begin{aligned} Q'_{pi} = \frac{\rho '_i}{2\mu '_i(1-\rho '_i)}, \end{aligned}$$

(12)

where $Q'_{pi}$ is the queuing time experienced by packets at node i with mixed Poisson and periodic traffic, $\rho '_i = \lambda _i / \mu '_i$ is the utilization of remaining service capacity by the traffic of node i. Finally, the sojourn time on a forwarding node with $i-1$ descendants (Fig. 6), each generating Poisson traffic is

$$\begin{aligned} \begin{aligned} T_{p_i} = W_i + Q'_{pi} = \frac{1}{\mu _i + 1} + \frac{\rho '_i}{2\mu '_i(1-\rho '_i)}. \end{aligned} \end{aligned}$$

(13)

Fig. 6

Cell utilization in TSCH network with Poisson traffic, $\lambda = 1$ pkt/sf per node

4.6 Impact of lossy links

Since the wireless medium is shared, collisions and packet loss stemming from interference and signal path loss must be mitigated by retransmissions at the cost of queuing delays. To assess the impact of unreliable links on end-to-end delays, we derive an analytical model under the assumption of a constant link loss probability $p_c$ for all communication links.

The sojourn time of a packet on a lossy link can be aligned into two parts: waiting for other packets in the queue, and waiting to be served at the head of the queue. The number of attempts required for a successful transmission can be represented by a geometrically distributed random variable Y with Probability Mass Function (PMF)

$$\begin{aligned} f_Y (y) = P(Y = y) = (1-p_c) p_c^{y-1}, \end{aligned}$$

(14)

and expected number of attempts until success:

$$\begin{aligned} E[Y] = \frac{1}{(1-p_c)}. \end{aligned}$$

(15)

4.6.1 Sojourn time in empty queue

First, we evaluate the sojourn time of the head-of-the-queue packet. In TSCH, if a packet transmission fails on a dedicated cell, a retransmission is only possible in the next dedicated cell. Each attempt imposes queuing time equivalent to the average distance $1/\mu$ between adjacent TX cells. Then, the expected sojourn time $T_l$ in an empty queue on a node with a lossy link is

$$\begin{aligned} T_l = \frac{1}{\mu +1} + \frac{E[Y] - 1}{\mu }, \end{aligned}$$

(16)

From the queue perspective, packets experiencing collision are returning into the queue, effectively turning the arrival rate into $\lambda E[Y]$. All equations above consider retransmission threshold $R \rightarrow \infty$. To account for a realistic R, E[Y] must be transformed into $E'[Y]$ by truncating geometric distribution at R. The corresponding success probability is then $p' = 1/E'[Y]$.

The distribution of the sojourn time for the head-of-the-queue packet on a lossy link can be expressed through multiplication of random variables W and Y:

$$\begin{aligned} \begin{aligned} F_{T_l} (z)&= P \left( WY \le z \right) = F_W \left( W < \frac{z}{k} \right) f_Y(Y=k) \\&= (1-p_c)\sum _{k=1}^R p_c^{k-1} \left( 1 - \left( 1 - \frac{z}{kS} \right) ^\mu \right) \end{aligned} \end{aligned}$$

(17)

with Probability Distribution Function (PDF):

$$\begin{aligned} f_{T_l} (z) = F^{'}_{T_l} = \frac{\mu (1-p_c)}{S}\sum _{k=1}^R \frac{p_c^{k-1}}{k} \left( 1 - \frac{z}{kS} \right) ^{\mu -1}. \end{aligned}$$

(18)

4.6.2 Sojourn time in non-empty queue

Before a packet reaches the head of the queue it waits for all preceding packets to be served. Since the time between two successful packet transmissions on a lossy link is geometrically distributed, the queuing system can be categorized as D/Geom/1. To model the queue state at packet arrival instances, an embedded discrete-time Markov chain can be used as described in Appendix B. The mean sojourn time in a non-empty queue $T'_l$ is then

$$\begin{aligned} T'_l = T_l (1 + \bar{L})(1+\rho _l), \end{aligned}$$

(19)

where $\bar{L}$ is the average queue length:

$$\begin{aligned} \bar{L} = \sum _{i=1}^{\infty } i \pi _i = \sum _{i=1}^{\infty } i (1 - z^*)(z^*)^i \end{aligned}$$

(20)

with $z^*$ being the solution of (B16) and

$$\begin{aligned} \rho _l = \frac{\lambda E[Y]}{\mu } \end{aligned}$$

(21)

is the system utilization with retransmissions.

5 Network performance evaluation

To evaluate end-to-end delays in an arbitrary network, formulas from the previous section can be applied on a hop-by-hop basis using proposed algorithms. As a result, fast and precise network performance evaluation is possible without the need to run simulations or configure experimental testbeds.

Starting with Algorithm 1, the expected end-to-end delay for each node $k \in \{1\dots n\}$ is calculated, where n is the total number of nodes in the network. Arrival and service rates at each node are aggregated based on the adjacency matrix A. In Algorithm 2, the parents of the target node k are traversed recursively to calculate expected sojourn times on each hop by aggregating arrival rates from all descendants and applying a suitable formula from the previous section. As inputs for Algorithm 1 the adjacency matrix A and the vector of traffic rates v are required. Element $a_{ij} = 1$ if node j is the parent of node i. Since links are unidirectional (only uplink traffic is considered), $a_{ij} = 1 \Rightarrow a_{ji} = 0$. To prove their applicability, proposed algorithms are validated in the next section by computing end-to-end delays for randomly generated networks.

Algorithm 1

Calculate mean end-to-end delay for packets from node k to sink s.

Algorithm 2

Calculate total arrival rate at node k

6 Validation

The analytical model proposed in Sect. 4 and the network evaluation algorithm from Sect. 5 are validated using simulations in OMNeT++ discrete event simulator together with the INET framework and our own 6TiSCH stack implementation [8]. Results are collected across multiple simulation repetitions and mean values are plotted with 95% confidence intervals. Each repetition represents a different seed for the random number generator.

6.1 Deterministic traffic

Starting with the periodic, deterministic traffic, average end-to-end delays for a single and multihop communication are visualized in Fig. 7. For the single hop case, $0.1 \le \lambda < 1$ results in a constant service rate $\mu = 1$ and corresponding end-to-end delay. The same applies for $1 \le \lambda < 2$, which requires 2 TX cells, but also results in a nearly constant end-to-end delay given by (5). However, for $\lambda \ge 2$, (5) becomes less accurate due to the added effect of the random distribution of TX cells and packet arrivals/RX cells in a slotframe. From the perspective of the node generating periodic traffic, TX cells are randomly scheduled between periodic packet arrivals. Thus, a short-term queuing is possible, as explained in Sect. 4.4. The end-to-end delay decreases with the higher traffic rate due to the service rate adaptation by MSF. Since TX cells are discrete, adding even a single one substantially decreases the service time.

For the multihop scenario with 7 nodes, the end-to-end delays are plotted in Fig. 7b as a function of distance to the sink in hops. The deviation between the simulated result and the expectation from a plain D/D/1 model (5) increases with more hops. Calculating mean waiting times using (8) for leaf nodes and (7) for forwarding nodes, a much more accurate estimation can be achieved.

Minor deviations between the expected and observed results can be explained by the fact that the model introduced in Sect. 4.4 does not account for a rare but impactful event. As visualized in Fig. 5a, only delays caused by multiple packet arrivals in a bin are considered. However, there is also the possibility of several consecutive bins with multiple packet arrivals occurring. In such a case, a packet has to wait not only for other packets from its own bin, but also for those in the following bins. As a result, the mean waiting time is marginally higher than in the assumed model.

Fig. 7

End-to-end delays in a linear network with periodic traffic, $u_{high} = 0.95$

6.2 Lossy links

The end-to-end delays for one hop lossy communication link are represented in Fig. 8a for different loss probabilities and traffic rates. As expected, there is a direct correlation between the system utilization and the end-to-end delay. The sawtooth pattern is due to the traffic adaptation by MSF – after utilization reaches the 95 % threshold, a new cell is added, which in turn lowers utilization considerably. The empirical CDF of the waiting time for the head-of-the-queue packet is plotted alongside the expected one from (17) in Fig. 8b for a fixed arrival/service rate and variable link loss probability.

Fig. 8

End-to-end delays in a one hop scenario with lossy link, variable parameters

Expectation curves in Figs. 8 and 9 mostly match simulation results, but precision degrades with higher system utilization due to the higher uncertainty of queue size estimation in (19). Nevertheless, with fixed arrival/service rates and variable link loss probability, the end-to-end delays can be still be closely predicted as shown in Fig. 9b. No substantial queuing occurs for small retransmission thresholds even under high loss probability, because packets are dropped sooner.

Fig. 9

End-to-end delays in one hop communication scenario with lossy link

Moving on to the multihop scenario, end-to-end delays for a 7-node network are visualized in Fig. 10 for different upper cell utilization thresholds. A lower threshold results in more provisioned cells, which in turn decreases the system utilization from 0.73 to 0.54 on average and enables more accurate prediction of the waiting time. The degradation in estimation accuracy for a higher utilization follows results from the one hop scenario.

Fig. 10

End-to-end delays based on the number of hops to the sink in a linear network with $p_c = 0.2$, variable traffic rates (per node) and cell utilization thresholds

6.3 Poisson traffic

The sojourn time on a TSCH node with Poisson traffic is visualized in Fig. 11a alongside the expectation curve from (10). A multihop scenario with 7 nodes and variable arrival rates is also evaluated and the end-to-end delays are plotted in Fig. 11b as a function of the distance to the sink in hops. The expectation curves reflect the waiting time formula derived in this work (13), while also a plain M/D/1 sojourn time (P-K formula) from (10) is visualized. There is a linear dependency between the end-to-end delay and the number of hops. While the simple M/D/1 model considerably overestimates the sojourn time on each hop, our proposed heuristic (13) yields much better precision, since the mixed traffic arrival process consisting of both periodic and Poisson arrivals is considered.

Fig. 11

End-to-end delays in a linear network with Poisson traffic

6.4 Random topologies

To validate algorithms from Sect. 5 simulations were carried out as follows. Experimental setup includes 20 nodes and an RPL sink, all distributed randomly uniformly in a 100 $\hbox {m}$ by 100 $\hbox {m}$ area and configured according to parameters from Table 1. During the warmup phase of 2000 $\hbox {s}$ MSF adapts local schedules to meet the traffic demand depending on the node position within the DODAG. A random topology shown in Fig. 12 is selected for the majority of evaluation, since it has no disconnected nodes and represents a typical multihop DODAG. In Fig. 13 average end-to-end delays per node are shown for the selected topology with periodic and Poisson traffic.

Table 1 Simulation parameters

For periodic traffic, expected values match simulated ones closely for all nodes, which hints at the accuracy of the proposed model. For Poisson traffic, visualized in Fig. 13b, the estimation accuracy also depends on the system utilization. For example, sojourn times on host[12] are closer to the M/D/1 model due to the relatively high utilization (0.74). Moreover, host[27] being a common parent means that the accuracy of its sojourn time estimation also affects that of all other nodes.

Fig. 12

Selected randomly generated topology (#10) with number of TX cells indicated above node icon

Fig. 13

Per-node end-to-end delays in selected generated topology

End-to-end delays calculated from assuming an M/D/1 model on each node represent an upper bound, which can be explained as follows. Since the proposed model assumes a mixed arrival process, packets experience queuing due to sporadic traffic bursts as part of the Poisson process, see (13). Considering the entire arrival process as a Poisson stream represents the worst case turning the queue at each node into an M/D/1. Thus, combining the latter with proposed heuristic yields a tight upper/lower bound pair for the end-to-end delay. Average end-to-end delays for every randomly generated topology are visualized in Fig. 14. Similar to the case with selected topology from Fig. 12, the prediction accuracy is better for periodic traffic. For Poisson traffic a combination of the proposed model with the M/D/1—based estimation defines a pair of upper/lower bounds.

Fig. 14

Average end-to-end delays per topology

Next, periodic traffic with unreliable links is evaluated. End-to-end delays per node are visualized in Fig. 15 for $p_c = 0.2$ and different upper cell utilization thresholds. Compared to scenarios with ideal links, even a moderate loss incurs considerably higher sojourn times on each node. As visible from Fig. 15b high utilization on bottleneck nodes results in lower estimation accuracy. However, with lower utilization shown in Fig. 15a, an overestimation of delays is also possible, which may be attributed to the fact that the number of TX cells scheduled on each node is not consistent across simulation runs: The period to estimate cell usage is not synchronized between nodes and cells are scheduled at random slot offsets. Between different simulation runs the utilization on some nodes fluctuates around the threshold, resulting in a slightly different number of cells scheduled on these nodes per run.

Fig. 15

Per-node end-to-end delays and utilization in randomly generated topology #10 with periodic traffic, $\lambda = 0.6$, $p_c = 0.2$ and different upper cell utilization limits

7 Conclusion

This work introduces a comprehensive approach to modeling end-to-end delays in wireless sensor networks with TSCH. The latency is crucial for safety-critical applications and was not modeled to such extent before. Using queuing theory, stochastics and combinatorics, formulas are derived for sojourn times under different traffic models while also taking into account a lossy medium. A practical, algorithmic application of these formulas is proposed to estimate end-to-end delays for arbitrary TSCH networks.

Proposed framework is validated in simulations using state-of-the-art networking models. Results show high accuracy of end-to-end delay estimations across multitude of scenarios and configurations. Thus, TSCH-based networks can be evaluated with respect to latency requirements in a fast, reliable and cost-effective manner, eliminating the necessity of simulations or testbed deployments.

For the future work, the framework accuracy under high utilization with Poisson traffic and lossy links can be improved. An experimental validation would also be beneficial for the wider adoption of the framework. The latter can be further extended to include PDR, energy consumption and other KPIs for fast and comprehensive assessment of TSCH-based WSNs during the decision-making process.

Appendices

Appendix A: Integer compositions

As mentioned in (7), on a forwarding node, $p_{\lambda _i}$ can be calculated using the concept of integer compositions. They are a subclass of integer partitions, where the order of elements matters. An integer ${\lfloor {\lambda }\rfloor }$ can be composed in different ways, reflecting the distribution of packet arrivals across bins. For example, for $\lambda = 4$, a composition $2 + 1 + 1$ implies that the first 2 packets arrive into the same bin, while the others are evenly split across remaining bins.

Given the number of packet arrivals per bin $\beta \le \lambda$, up to ${\lfloor {\lambda /\beta }\rfloor }$ occurrences of such bin per slotframe are possible. Then the probability of a packet experiencing service time iW can be computed as

$$\begin{aligned} p_{\lambda _i} = \frac{1}{c_\lambda } \sum _{j=1}^{{\lfloor {\lambda /i}\rfloor }} \frac{ij}{\lambda } c_{\lambda _{ij}}, \quad 2 < i \le \lambda \end{aligned}$$

(A1)

where i is the number of arrivals per bin, j is the number of times such bin can occur, $c_\lambda$ is the total number of compositions of $\lambda$ and $c_{\lambda _{ij}}$ is the number of compositions of $\lambda$ where element i occurs exactly j times. The total number of compositions of $\lambda$ is $c_\lambda = 2^{\lambda -1}$. Considering $c_{\lambda _{ij}}$ two cases are possible: $i > \lambda /2$ or $i \le \lambda /2$. The first one implies $j = 1$ and is much easier to calculate. The second one imposes additional constraint on element i occurring exactly j times.

Starting with $i > \lambda /2$ let us consider compositions of $r = \lambda - i$. Each r-composition with p parts can be permuted in $p+1$ ways with i. Then, the number of compositions of $\lambda$ containing i is

$$\begin{aligned} c_{\lambda _{i1}} = \sum _{p=1}^{r} (p+1) c_{r_p}, \end{aligned}$$

(A2)

where $c_{r_p}$ is the number of compositions of r with exactly p parts (p-composition of r):

$$\begin{aligned} c_{r_p} = \left( {\begin{array}{c}r-1\\ p-1\end{array}}\right) . \end{aligned}$$

(A3)

For $i \le \lambda /2$ a bin with i packet arrivals can occur multiple times $j = 1\dots {\lfloor {\lambda /i}\rfloor }$ with $r = \lambda - ij$. Unlike the first case, compositions of r may now also contain i, so the following adjustments are necessary: $c_{r_p}$ should only enumerate compositions of r without i, there are more than $p+1$ ways to permute j i-elements with each composition of $c_{r_p}$. Let us denote $c_{r_p}^{-i}$ the number of p-compositions of r without element i:

$$\begin{aligned} c_{r_p}^{-i} = c_{r_p} - c_{r_p}^{+i}, \end{aligned}$$

(A4)

where $c_{r_p}^{+i}$ is the number of compositions of r into p parts each of which contains i at least once:

$$\begin{aligned} c_{r_p}^{+i} = \sum _{k=1}^p (-1)^{k+1} \left( {\begin{array}{c}p\\ k\end{array}}\right) \left( {\begin{array}{c}r-ki-1\\ p-k-1\end{array}}\right) . \end{aligned}$$

(A5)

Then, each composition from (A4) can be permuted with other j (identical) i-elements in a number of ways (permutations with repetitions):

$$\begin{aligned} \frac{(p + j)!}{p!j!}, \end{aligned}$$

(A6)

where p is the composition size, j is the number of occurrences of i-element, which is excluded from the compositions of r. All elements in a p-composition of r are considered identical, since their rearrangement would result in a completely different composition. Combining (A4) and (A6), the number of compositions $c_{ij}$ of $\lambda$, where element $i < {\lfloor {\lambda /2}\rfloor }$ occurs exactly j times can be expressed as

$$\begin{aligned} \begin{aligned} \sum _{p=1}^r \frac{(p + j)!}{p!j!} c_{r_p}^{-i} \end{aligned} \end{aligned}$$

(A7)

where $r = \lambda - ij$ is the remainder whose compositions are counted in the outer summation while also ensuring none of them contains i. Summarizing from (A2) and (A7), the number of compositions of $\lambda$ where element i occurs exactly j times is

$$\begin{aligned} c_{\lambda _{ij}} = {\left\{ \begin{array}{ll} \sum\nolimits{_{p=1}^r} \frac{(p + j)!}{p!j!} c_{r_p}^{-i}, &{} i < {\lfloor {\lambda /2}\rfloor } \\ \sum\nolimits{_{p=1}^{r}} (p+1) c_{r_p}, &{} i \ge {\lfloor {\lambda /2}\rfloor } \end{array}\right. } \end{aligned}$$

(A8)

Substituting (A8) into (A1) and (7) yields the expression for the sojourn time $T_d$.

Appendix B: Queue state with lossy link

To represent the queue state on a node with lossy link, the Markov chain from Fig. 16 can be used with the following matrix of transition probabilities:

$$\begin{aligned} P = \begin{bmatrix} 1-b_0 &{} b_0 &{} 0 &{} 0 \\ 1 - {\textstyle \sum _{k=0}^1 b_k} &{} b_1 &{} b_0 &{} \dots \\ 1 - {\textstyle \sum _{k=0}^2 b_k} &{} b_2 &{} b_1 &{} \dots \\ \vdots &{} \vdots &{} \vdots &{} \\ 1 - {\textstyle \sum _{k=0}^M b_k} &{} b_{M-1} &{} b_{M-2} &{} \dots \\ 0 &{} 1 - {\textstyle \sum _{k=0}^M b_k} &{} b_{M-1} &{} b_{M-2} \end{bmatrix} , \end{aligned}$$

(B9)

where $b_k$ is the probability of k packets leaving the queue between subsequent arrivals and $M = \mu/\lambda$ is the average number of TX cells in the inter-arrival period. The number of "successes" (packets leaving the queue) can be calculated using binomial distribution as follows:

$$\begin{aligned} b_k = {M \atopwithdelims ()k} (1-p_c)^k p_c^{M-k}. \end{aligned}$$

(B10)

The steady-state distribution $\pi$ of the Markov chain from Fig. 16 represents the probability of i packets being in the system:

$$\begin{aligned} \pi = \pi \cdot P \quad \text {with} \quad \pi \cdot e = 1. \end{aligned}$$

(B11)

Fig. 16

Embedded, discrete-time Markov chain representing number of packets in a system with lossy link at arrival instances

Since $\pi$ is the left eigenvector of P, component-wise (B11) can be written as:

$$\begin{aligned} \pi _0 = \sum _{j=0}^{M} \pi _j \left( 1 - \sum _{k=0}^j b_k \right) \end{aligned}$$

(B12)

$$\begin{aligned} \pi _i = \sum _{k=0}^{M} \pi _{i+k-1} b_k, \quad i \ge 1 \end{aligned}$$

(B13)

Distinct to the original analysis method of G/M/1 queues [19], in this case there is an upper limit M (finite number of TX cells) to the number of possible services between two subsequent packet arrivals. Multiplying both sides of (B13) by $z^i$ and summing over all i, we achieve

$$\begin{aligned} \sum _{i=1}^{\infty } \pi _i z^i = \sum _{i=1}^{\infty } \sum _{k=0}^{M} \pi _{i+k-1} b_k z^i. \quad i \ge 1 \end{aligned}$$

(B14)

Taking into account $\pi _{i+1} = \pi _i z$, (B14) can be rewritten as

$$\begin{aligned} \sum _{i=1}^{\infty } \pi _i z^i = \sum _{i=1}^{\infty } \pi _i z^i \sum _{k=0}^{M} b_k z^{k-1}, \end{aligned}$$

(B15)

from which follows that

$$\begin{aligned} \sum _{k=0}^M b_k z^k = z \end{aligned}$$

(B16)

has a solution $z^*$ and, considering $\pi _{i+1} = \pi \cdot z$, state probabilities can be calculated recursively:

$$\begin{aligned} \pi _i = (1 - z^*) (z^*)^i. \end{aligned}$$

(B17)

Since the arrival process is deterministic, the Laplace transform of the inter-arrival times PDF, typically employed in G/M/1 analysis, is not applicable to (B16). Therefore, numerical methods are necessary to solve the polynomial equation of order M. Furthermore, to account for a limited retransmission threshold R, $b_k$ must be computed with $p'_c = 1 - p'$, where $p'$ is the success probability of a geometric distribution truncated at R. Also, E[Y] in (21) should be replaced with $E'[Y] = 1/p'$.