Abstract
Continuing previous work, this paper provides maximal characterizations of anisotropic Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{p,q}\) for the endpoint case of \(p = \infty \) and the full scale of parameters \(\alpha \in \mathbb {R}\) and \(q \in (0,\infty ]\). In particular, a Peetre-type characterization of the anisotropic Besov space \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty } = \dot{\textbf{F}}^{\alpha }_{\infty ,\infty }\) is obtained. As a consequence, it is shown that there exist dual molecular frames and Riesz sequences in \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a previous paper [20], we obtained characterizations of anisotropic Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{p,q}\), with \(\alpha \in \mathbb {R}\), \(p \in (0,\infty )\) and \(q \in (0,\infty ]\), in terms of Peetre-type maximal functions and continuous wavelet transforms. In addition, as an application of these characterizations, it was shown that these spaces admit molecular dual frames and Riesz sequences. The purpose of the present paper is to provide analogous results for the endpoint case of \(p = \infty \).
For defining the anisotropic Triebel-Lizorkin spaces, let \(A \in \textrm{GL}(d, \mathbb {R})\) be an expansive matrix, i.e., \(|\lambda |>1\) for all \(\lambda \in \sigma (A)\), and let \(\varphi \in \mathcal {S} (\mathbb {R}^d)\) be such that it has compact Fourier support
and satisfies
with \(A^*\) denoting the transpose of A. For \(j \in \mathbb {Z}\), denote its dilation by \(\varphi _j = |\det A|^j \varphi (A^j \cdot )\). The associated (homogeneous) anisotropic Triebel-Lizorkin space \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}= \dot{\textbf{F}}^{\alpha }_{\infty ,q}(A,\varphi )\), with \(\alpha \in \mathbb {R}\) and \(q \in (0, \infty ]\), is defined as the collection of all tempered distributions \(f \in \mathcal {S}'(\mathbb {R}^d)\) (modulo polynomials) that satisfy
if \(q < \infty \), and
Note that the \(\ell ^{\infty } (\mathbb {Z}_{\ge -\ell })\)-norms in Eq. (1.4) are positioned outside of the integral, whereas the \(\ell ^q(\mathbb {Z}_{\ge -\ell })\)-norms in Eq. (1.3) are part of the integrand.
In contrast to the usual quasi-norms defining (anisotropic) Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{p,q}\) for \(p < \infty \) (see, e.g., [3,4,5, 20]), the quantities (1.3) and (1.4) consider only averages over small scales. The quasi-norms (1.3) and (1.4) can therefore be considered as “localized versions”of the immediate analogue of the quasi-norms defining \(\dot{\textbf{F}}^{\alpha }_{p,q}\) for \(p< \infty \), which would lead to an unsatisfactory definition of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\), see [11, Sect. 5] and the references therein.
The above definition of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) follows Bownik [3, Sect. 3] (see also [11, Sect. 5]) for \(q < \infty \), but differs from [3, 11] for \(q=\infty \), where \(\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }\) is instead defined via the quasi-norm
with \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }\) denoting the (anisotropic) Besov space [2]. The quasi-norm (1.4) is an anisotropic version of the definition given by Bui and Taibleson [6], which (as a consequence of our main results) will be shown to be equivalent to (1.5), like for isotropic dilations [6, Theorem 3].
1.1 Maximal characterizations
As in [20], we assume additionally that the expansive matrix \(A \in \textrm{GL}(d, \mathbb {R})\) is exponential, in the sense that \(A = \exp (B)\) for some matrix \(B \in \mathbb {R}^{d \times d}\). The power of A is then defined as \(A^s := \exp (sB)\) for \(s \in \mathbb {R}\).
For \(\varphi \in \mathcal {S}(\mathbb {R}^d)\), \(s \in \mathbb {R}\) and \(\beta > 0\), the associated Peetre-type maximal function of \(f \in \mathcal {S}' (\mathbb {R}^d)\) is defined by

where \(\varphi _s := |\det A|^s \varphi (A^s \cdot )\) and where \(\rho _A : \mathbb {R}^d \rightarrow [0,\infty )\) denotes the step homogeneous quasi-norm associated with A (cf. Sect. 2.1).
The following Peetre-type maximal characterizations of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) will be proven in Sect. 3. Here, the notation  means the average integral over a measurable set \(Q \subseteq \mathbb {R}^d\) of positive measure.
means the average integral over a measurable set \(Q \subseteq \mathbb {R}^d\) of positive measure.
Theorem 1.1
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and exponential and let \(\alpha \in \mathbb {R}\). Assume that \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) has compact Fourier support satisfying the support conditions (1.1) and (1.2).
For \(q \in (0, \infty )\) and \(\beta > 1/q\), the norm equivalences

hold for all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\). For \(q = \infty \) and \(\beta >1\), the following equivalences hold

for all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\).
Theorem 1.1 provides an extension of [6, Theorem 1] to arbitrary expansive dilations, and appears to be new even for the commonly studied setting of diagonal dilation matrices \(A = {{\,\textrm{diag}\,}}( \alpha _1, ..., \alpha _d)\) with given anisotropy \( (\alpha _1, ..., \alpha _d) \in (1,\infty )^d\).
The proof method of Theorem 1.1 is modeled on the proof of the maximal characterizations of Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{p,q}\) with \(p < \infty \) given in [20]. In particular, it combines a sub-mean-value property of the Peetre-type maximal function (Proposition 3.2) with maximal inequalities. See also [22, 23, 27, 31] for similar approaches. Besides the similarities in the approach, the calculations in the proof of Theorem 1.1 differ non-trivially from these in [20, Theorem 3.5] as only averages over small scales appear in the definition of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\).
As a consequence of Theorem 1.1, we show in Sect. 4 the coincidence \(\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }= \dot{\textbf{B}}^{\alpha }_{\infty ,\infty }\) mentioned above.
1.2 Molecular decompositions
For an expansive and exponential matrix \(A \in \textrm{GL}(d, \mathbb {R})\), denote by \(G_A = \mathbb {R}^d \rtimes _A \mathbb {R}\) the associated semi-direct product group. Then \(G_A\) acts unitarily on \(L^2 (\mathbb {R}^d)\) via the quasi-regular representation \(\pi \), defined by
A vector \(\psi \in L^2 (\mathbb {R}^d)\) is called admissible if the associated wavelet transform
defines an isometry into \(L^2 (G_A)\). The existence of admissible vectors and associated Calderón-type reproducing formulae for this representation have been studied, among others, in [9, 12, 17, 21]. The assumption that A is expansive is essential for the existence of admissible vectors \(\psi \in \mathcal {S} (\mathbb {R}^d)\) satisfying \(\widehat{\psi } \in C^{\infty }_c (\mathbb {R}^d \setminus \{0\})\) (cf. Lemma 5.2), which play an important role in this paper.
A countable family \((\phi _{\gamma } )_{\gamma \in \Gamma }\) of functions \(\phi _{\gamma } \in L^2 (\mathbb {R}^d)\) parametrized by a discrete set \(\Gamma \subset G_A\) is called a molecular system if there exists a function \(\Phi \in \mathcal {W}(L^r_w)\subset L^1 (G_A)\) such that
The space \(\mathcal {W}(L^r_w)\) denotes a weighted Wiener amalgam space for \(r = \min \{1, q\}\) and the standard control weight \(w = w_{\infty , q}^{\alpha ', \beta } : G_A \rightarrow [1,\infty )\); see Sect. 6 for further details.
It should be mentioned that any family \((\pi (\gamma ) \phi )_{\gamma \in \Gamma }\) for suitable \(\phi \in L^2 (\mathbb {R}^d)\) defines a molecular system in the sense of (6.1) with \(\Phi = |W_{\psi } \phi |\), but that generally a molecular system \((\phi _{\gamma } )_{\gamma \in \Gamma }\) does not need to consist of translates and dilates of a fixed function \(\phi \). Nevertheless, general molecules \((\phi _{\gamma } )_{\gamma \in \Gamma }\) share many properties with atoms \( (\pi (\gamma ) \phi )_{\gamma \in \Gamma }\), see, e.g., [18, 32].
The following theorem provides decomposition theorems of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) in terms of molecules.
Theorem 1.2
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and exponential. For \(\alpha \in \mathbb {R}\), \(q \in (0, \infty ]\), let \(r := \min \{1, q\}\) and let \(\alpha ' = \alpha + 1/2 - 1/q\) if \(q < \infty \) and \(\alpha ' = \alpha + 1/2\), otherwise. Let \(\beta > 1/q\) if \(q < \infty \) and \(\beta > 1\) otherwise.
Suppose \(\psi \in L^2 (\mathbb {R}^d)\) is admissible satisfying \(W_{\psi } \psi \in \mathcal {W}(L^r_w)\) for the standard control weight \(w = w_{\infty , q}^{- \alpha ', \beta } : G_A \rightarrow [1,\infty )\) defined in Lemma 5.8. Additionally, suppose that \(W_{\varphi } \psi \in \mathcal {W}(L^r_w)\) for some (equivalently, all) admissible \(\varphi \in \mathcal {S}_0 (\mathbb {R}^d)\). Then there exists a compact unit neighborhood \(U \subset G_A\) with the following property: For any discrete set \(\Gamma \subset G_A\) satisfying
there exists a molecular system \((\phi _{\gamma })_{\gamma \in \Gamma }\) such that any \(f \in \dot{\textbf{F}}^{\alpha }_{\infty ,q}\) admits the expansion
where the series converges unconditionally in the weak\(^*\)-topology of \(\mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\).
Atomic decompositions of the anisotropic spaces \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) have been obtained earlier by Bownik [3]. However, Theorem 1.2 provides a frame decomposition of all elements \(f \in \dot{\textbf{F}}^{\alpha }_{\infty ,q}\) in terms of the atoms \((\pi (\gamma ) \psi )_{\gamma \in \Gamma }\) and molecules \((\phi _{\gamma })_{\gamma \in \Gamma }\), whereas the atoms in [3, Theorem 5.7] depend on the element \(f \in \dot{\textbf{F}}^{\alpha }_{\infty ,q}\) that is represented. For anisotropic Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{p,q}\) with \(p < \infty \), decompositions as in Theorem 1.2 were obtained in [19, 20], but they appear to be new for the case of \(p = \infty \). In fact, Theorem 1.2 seems even valuable for merely isotropic dilations, where the state-of-the-art [13] excludes the case \(p = \infty \).
Theorem 1.2 will be obtained from the recent results on dual molecules [26, 32] through the identification of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) with a coorbit space; see Proposition 5.10. This identification appears to be new for the full scale of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) with \(\alpha \in \mathbb {R}\) and \(q \in (0, \infty ]\), even for isotropic dilations.
In addition to the existence of dual molecular frames, we also obtain a corresponding result for Riesz sequences. Here, the space \(\dot{\textbf{p}}^{- \alpha ', \beta }_{\infty , q}\) denotes a sequence space associated to \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\); see Definition 6.3 for its precise definition.
Theorem 1.3
With assumptions and notations as in Theorem 1.2, the following holds:
There exists a compact unit neighborhood \(U \subset G_A\) with the following property: For any discrete set \(\Gamma \subset G_A\) satisfying
there exists a molecular system \((\phi _{\gamma })_{\gamma \in \Gamma }\) in \(\overline{{{\,\textrm{span}\,}}} \{ \pi (\gamma ) \psi : \gamma \in \Gamma \}\) such that the distribution \(f := \sum _{\gamma \in \Gamma } c_{\gamma } \phi _{\gamma } \in \dot{\textbf{F}}^{\alpha }_{\infty ,q}\) forms a solution to the moment problem
for any given \((c_{\gamma } )_{\gamma \in \Gamma } \in \dot{\textbf{p}}^{- \alpha ', \beta }_{\infty , q} \le \mathbb {C}^{\Gamma }\).
Riesz sequences in \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) seem not to have appeared in the literature before, which makes Theorem 1.3 new even for isotropic dilations. Similarly to Theorem 1.2, we obtain Theorem 1.3 by applying results of [26, 32] to the coorbit realization of the Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\).
1.3 Notation
We denote by \(s^+ := \max \{ 0, s \}\) and \(s^- := - \min \{ 0, s \}\) the positive and negative part of \(s \in \mathbb {R}\). If \(f_1, f_2\) are positive functions on a common base set X, the notation \(f_1 \lesssim f_2\) is used to denote the existence of a constant \(C > 0\) such that \(f_1 (x) \le C f_2 (x)\) for all \(x \in X\). The notation \(f_1 \asymp f_2\) is used whenever both \(f_1 \lesssim f_2\) and \(f_2 \lesssim f_1\). We will sometimes use \(\lesssim _\alpha \) to indicate that the implicit constant depends on a quantity \(\alpha \).
For a function \(f : \mathbb {R}^d \rightarrow \mathbb {C}\) and a matrix \(A \in \mathbb {R}^{d \times d}\), the dilation of \(f : \mathbb {R}^d \rightarrow \mathbb {C}\) is denoted by \(f_j := |\det A|^j \, f(A^j \cdot )\), where \(j \in \mathbb {Z}\). Similarly, we write \(f_s := |\det A|^s \, f(A^s \cdot )\) for \(s \in \mathbb {R}\), provided that \(A^s\) is well-defined.
The class of Schwartz functions on \(\mathbb {R}^d\) will be denoted by \(\mathcal {S} (\mathbb {R}^d)\). Its dual space is simply denoted by \(\mathcal {S}' (\mathbb {R}^d)\). Moreover, the notation \(\mathcal {P}(\mathbb {R}^d)\) will be used for the collection of polynomials on \(\mathbb {R}^d\), and we write \(\mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\) for the quotient space of tempered distributions modulo polynomials. The Fourier transform \(\mathcal {F} : \mathcal {S}(\mathbb {R}^d) \rightarrow \mathcal {S}(\mathbb {R}^d)\) is defined as \(\widehat{f} (\xi ) = \int _{\mathbb {R}^d} f(x) e^{-2\pi ix \cdot \xi } \; dx\) with inverse \(\check{f} := \mathcal {F}^{-1} f := \widehat{f}(- \, \cdot \,)\). Similar notations will be used for the extension of the Fourier transforms to \(L^2 (\mathbb {R}^d)\).
The Lebesgue measure on \(\mathbb {R}^d\) is denoted by \(\textrm{m}\). For a measurable set \(Q \subset \mathbb {R}^d\) of finite, positive measure, it will be written  for \(f : \mathbb {R}^d \rightarrow \mathbb {C}\). The closure of a set \(Q \subset \mathbb {R}^d\) is denoted by \(\overline{Q}\).
for \(f : \mathbb {R}^d \rightarrow \mathbb {C}\). The closure of a set \(Q \subset \mathbb {R}^d\) is denoted by \(\overline{Q}\).
If G is a group, then the left and right translation of a function \(F : G \rightarrow \mathbb {C}\) by \(h \in G\) will be denoted by \( L_h F = F(h^{-1} \cdot ) \) and \( R_h F = F (\cdot \, h), \) respectively. In addition, we write \(F^{\vee } (x) = F(x^{-1})\).
2 Anisotropic Triebel-Lizorkin spaces with \(p = \infty \)
This section provides preliminaries on expansive matrices and Triebel-Lizorkin spaces.
2.1 Expansive matrices
A matrix \(A \in \mathbb {R}^{d \times d}\) is said to be expansive if \(| \lambda | > 1\) for all eigenvalues \(\lambda \in \sigma (A)\), where \(\sigma (A)\) denotes the spectrum of A. Equivalently, a matrix \(A \in \mathbb {R}^{d \times d}\) is expansive if \(\Vert A^{-j} \Vert \rightarrow 0\) as \(j \rightarrow \infty \).
The following lemma collects several basic properties of expansive matrices that will be used in the sequel, see, e.g., [1, Definitions 2.3 and 2.5] and [1, Lemma 2.2]. For a more general background on spaces of homogeneous type on \(\mathbb {R}^d\), we refer to [7, 8].
Lemma 2.1
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive.
-
(i)
There exist an ellipsoid \(\Omega =\Omega _A\) (that is, \(\Omega = P (B_1 (0))\) for some \(P \in \textrm{GL}(d, \mathbb {R})\)) and \(r > 1\) such that
$$\begin{aligned} \Omega \subset r\Omega \subset A\Omega \end{aligned}$$and \(\textrm{m}(\Omega ) = 1\). The function \(\rho _A : \mathbb {R}^d \rightarrow [0,\infty )\) defined by
$$\begin{aligned} \rho _A (x) = {\left\{ \begin{array}{ll} |\det A|^j, \quad &{} \text {if} \;\; x \in A^{j+1} \Omega \setminus A^j \Omega , \\ 0, \quad &{} \text {if} \;\; x = 0, \end{array}\right. } \end{aligned}$$(2.1)is Borel measurable and forms a quasi-norm, i.e., there exists \(C \ge 1\) such that
$$\begin{aligned} \begin{aligned} \rho _A (-x)&= \rho _A(x),{} & {} \quad x \in \mathbb {R}^d ,\\ \rho _A (x)&> 0,{} & {} \quad x \in \mathbb {R}^d \setminus \{0\} , \\ \rho _A (Ax)&= |\det A| \rho _A (x),{} & {} \quad x \in \mathbb {R}^d , \\ \rho _A (x+y)&\le C \big ( \rho _A (x) + \rho _A (y) \big ),{} & {} \quad x,y \in \mathbb {R}^d. \end{aligned} \end{aligned}$$(2.2) -
(ii)
The function \(d_A : \mathbb {R}^d \times \mathbb {R}^d \rightarrow [0,\infty ), (x,y) \mapsto \rho _A(x-y)\) forms a quasi-metric. The triple \((\mathbb {R}^d, d_A, \textrm{m})\) forms a space of homogeneous type.
For an expansive matrix \(A \in \textrm{GL}(d, \mathbb {R})\), a function \(\rho _A : \mathbb {R}^d \rightarrow [0,\infty )\) defined by Eq. (2.1) will be called a step homogeneous quasi-norm associated to A. Given \(y \in \mathbb {R}^d\) and \(r>0\), its associated metric ball will be denoted by
It is readily verified that \( B_{\rho _A}(0, 1) = \Omega \). Hence, its metric balls are of the form
where \(\ell \in \mathbb {Z}\) is such that \(|\det A|^{\ell -1} < r \le |\det A|^{\ell } \).
Throughout this paper, given an expansive \(A \in \textrm{GL}(d, \mathbb {R})\), we will fix an ellipsoid \(\Omega = \Omega _A\) as appearing in Lemma 2.1 (i). This choice is not unique. Any other choice of ellipsoid will yield an equivalent quasi-norm, see, e.g., [1, Lemma 2.4].
2.2 Schwartz seminorms
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive with associated step homogeneous quasi-norm \(\rho _A\). For \(\beta > 0\), the quasi-norm properties (2.2) imply that
for \(x,y \in \mathbb {R}^d\). For ease of notation, we will often write \(\nu _{\beta } (x) = (1+\rho _A(x))^{\beta }\) for \(x \in \mathbb {R}^d\).
Let \(\lambda _{-}\) and \(\lambda _{+}\) be such that \(1< \lambda _{-}< \min _{\lambda \in \sigma (A)} |\lambda | \le \max _{\lambda \in \sigma (A)} |\lambda | < \lambda _{+}\). Put
Then [1, Lemma 3.2] (see also [20, Lemma 2.2]) implies that
Therefore, the collection
defines an equivalent family of seminorms for the Schwartz space \(\mathcal {S} (\mathbb {R}^d)\).
2.3 Analyzing vectors
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive. Choose a function \(\varphi \in \mathcal {S} (\mathbb {R}^d)\) with compact Fourier support
satisfying, in addition,
Then the function \(\psi \in \mathcal {S}(\mathbb {R}^d)\) defined by
is well-defined and satisfies
For more details and further properties, see, e.g., [5, Lemma 3.6]
2.4 Anisotropic Triebel-Lizorkin spaces
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and fix an analyzing vector \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) with compact Fourier support satisfying (2.5) and (2.6).
For \(\alpha \in \mathbb {R}\) and \(0< q < \infty \), the associated (homogeneous) anisotropic Triebel-Lizorkin space \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}= \dot{\textbf{F}}^{\alpha }_{\infty ,q}(A,\varphi )\) is defined as the collection of all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\) for which

The definition of \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}= \dot{\textbf{F}}^{\alpha }_{\infty ,q}(A, \varphi )\) is independent of the choice of analyzing vector \(\varphi \), with equivalent quasi-norms for different choices, cf. [3, Corollary 3.13]. In addition, the space \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) is continuously embedded into \(\mathcal {S}' (\mathbb {R}^d) / \mathcal {P}(\mathbb {R}^d)\), and is complete with respect to \(\Vert \cdot \Vert _{\dot{\textbf{F}}^{\alpha }_{\infty ,q}}\). See [3, Corollary 3.14] for both claims.
For the case \(q = \infty \), the space \(\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }= \dot{\textbf{F}}^{\alpha }_{\infty ,\infty }(A, \varphi )\) will be defined as the collection of all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\) satisfying

For our purposes, it will be convenient to use the metric ball \(\Omega = B_{\rho _A} (0,1)\) instead of the cube \([0,1]^d\) in defining \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\). The independence of this choice is guaranteed by the following lemma, whose simple proof follows from a standard covering argument and is hence omitted.
Lemma 2.2
Let \(F : \mathbb {R}^d \rightarrow [0, \infty )\) and \(F_j : \mathbb {R}^d \rightarrow [0, \infty )\), \(j \in \mathbb {Z}\), be measurable functions. Then

and

with implicit constants only depending on d, A.
3 Maximal function characterizations
Throughout this section, \(A \in \textrm{GL}(d, \mathbb {R})\) will denote an expansive matrix.
3.1 Peetre-type maximal function
Let \(\varphi \in \mathcal {S}(\mathbb {R}^d)\). For \(j \in \mathbb {Z}\) and \(\beta > 0\), the associated Peetre-type maximal function of \(f \in \mathcal {S}' (\mathbb {R}^d)\) is defined as

where \(\rho _A : \mathbb {R}^d \rightarrow [0,\infty )\) denotes the step homogeneous quasi-norm.
The Peetre-type maximal function has the following basic properties.
Lemma 3.1
Let \(\varphi \in \mathcal {S}(\mathbb {R}^d)\). Let \(j \in \mathbb {Z}\) and \(\beta > 0\). For any \(f \in \mathcal {S}' (\mathbb {R}^d)\), the following holds:
-
(i)
If
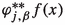 is finite for some \(x \in \mathbb {R}^d\), then it is finite for all \(x \in \mathbb {R}^d\).
is finite for some \(x \in \mathbb {R}^d\), then it is finite for all \(x \in \mathbb {R}^d\). -
(ii)
There exists an \(N = N (f , A) \in \mathbb {N}\) such that for all \(\beta \ge N\)
$$\begin{aligned} \varphi _{j,\beta }^{**}f(x) < \infty , \quad x \in \mathbb {R}^d . \end{aligned}$$
Proof
(i) Let \(x_0 \in \mathbb {R}^d\) be such that  . The symmetry of \(\rho _A\) and the inequality (2.3) for \(\nu _\beta (y) = (1 + \rho _{A}(y))^{\beta }\) yield that
. The symmetry of \(\rho _A\) and the inequality (2.3) for \(\nu _\beta (y) = (1 + \rho _{A}(y))^{\beta }\) yield that

for arbitrary \(x \in \mathbb {R}^d\).
(ii) Fix \(x, z \in \mathbb {R}^d\). Let \(\langle \cdot , \cdot \rangle _{\mathcal {S}', \mathcal {S}}\) denote the bilinear dual pairing. Since \(f \in \mathcal {S}' (\mathbb {R}^d)\) and the seminorms (2.4) are ordered, there exist \(M=M(f), N=(f,A) \in \mathbb {N}\) and a constant \(C=C(f) > 0\) such that
Consequently,
Since the constants are independent of \(z \in \mathbb {R}^d\), the claim follows easily. \(\square \)
3.2 Sub-mean-value property
The following type of result is often referred to as a “sub-mean-value property”and will play an essential role in deriving the main results. It forms an anisotropic analogue of the isotropic result [30, Theorem 5].
Proposition 3.2
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and let \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) have compact Fourier support satisfying (2.5) and (2.6). Then, for all \(q \in (0,\infty )\) and \(\beta > 0\), there exists a constant \(C= C(A,\varphi , q, \beta ) > 0\) such that

for all \(f \in \mathcal {S}'(\mathbb {R}^d)\) and all \(j \in \mathbb {Z}\).
Proof
The claim is trivial whenever  , so we assume throughout that
, so we assume throughout that  . The proof will be split into two steps dealing with \(q \in [1,\infty )\) and \(q \in (0, 1)\) separately.
. The proof will be split into two steps dealing with \(q \in [1,\infty )\) and \(q \in (0, 1)\) separately.
Step 1. (The case \(q \in [1,\infty )\)). By the compact Fourier support condition (2.5) and the identity (2.7), it follows that there exists \(N \in \mathbb {N}\) (depending on \(\varphi \) and A) such that the function \(\Phi := \sum _{k = -N}^N \varphi _{k} *\psi _{k}\) satisfies
see, e.g., the proof of [20, Theorem 3.5] for a detailed verification.
Using that \(\Phi _j = \sum _{k = -N}^N \varphi _{j + k} *\psi _{j + k}\) for \(j \in \mathbb {Z}\), the equality (3.3) gives
for all \(x, z \in \mathbb {R}^d\), \(j \in \mathbb {Z}\) and \(\beta > 0\). Combining Hölder’s inequality for \(\tfrac{1}{q}+\tfrac{1}{q'} = 1\) and the translation invariance of \(L^{q'}(\mathbb {R}^d)\) yields
If \(q \in (1,\infty )\), applying the transformation \(A^j y \mapsto \tilde{y}\) in the \(L^{q'}\)-norm above gives
Using the seminorms defined in Eq. (2.4) and the fact that \(\varphi , \psi \in \mathcal {S}(\mathbb {R}^d)\), the last integral can be estimated by a constant \(C_k = C_k(A,\varphi , q, \beta ) > 0\). Combining the above gives
with implicit constant depending on \(A, \beta , q, \varphi \). Taking the supremum over \(z \in \mathbb {R}^d\) and the q-th power yields the claim for \(q \in (1, \infty )\). The case \(q = 1\) follows by the same arguments with the usual modifications.
Step 2. (The case \(q \in (0, 1)\)). For \(f \in \mathcal {S}' (\mathbb {R}^d)\), the estimate obtained in Step 1 (for \(q=1\)) gives

By Lemma 3.1, there exists \(N' = N'(f) \in \mathbb {N}\) such that  for all \(\beta \ge N'\). Hence, if \(\beta \ge N'\), the claim follows immediately from the inequality (3.4).
for all \(\beta \ge N'\). Hence, if \(\beta \ge N'\), the claim follows immediately from the inequality (3.4).
For the case \(\beta < N'\), we use the already proven result for \(N'\) to obtain
where the second inequality used that \(\nu _{N'}(x)^{-q} \le \nu _\beta (x)^{-q}\) for \(0< \beta < N'\). Consequently,
The right-hand side being independent of \(z \in \mathbb {R}^d\), taking the supremum yields the claim for \(\beta < N'\). Overall, this completes the proof. \(\square \)
3.3 Maximal function characterizations
In this section, the matrix \(A \in \textrm{GL}(d, \mathbb {R})\) is often additionally assumed to be exponential, i.e., it is assumed that A admits the form \(A = \exp (B)\) for some \(B \in \mathbb {R}^{d\times d}\). Then the power \(A^s = \exp (s B)\) is well-defined for \(s \in \mathbb {R}\).
For \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) and \(s, \beta \in \mathbb {R}\) with \(\beta > 0\), the associated Peetre-type maximal function of \(f \in \mathcal {S}' (\mathbb {R}^d)\) is defined as in (3.1) by

whenever A is exponential.
The following theorem forms a main result of this paper. It characterizes the anisotropic Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\), with \(0 < q \le \infty \), in terms of Peetre-type maximal functions. The result forms an extension of [6, Theorem 1] to possibly anisotropic dilations.
Theorem 3.3
Suppose \(A \in \textrm{GL}(d, \mathbb {R})\) is expansive and exponential. Assume that \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) has compact Fourier support and satisfies (2.5) and (2.6).
Then, for all \(q \in (0, \infty )\), \(\alpha \in \mathbb {R}\) and \(\beta > 1/q\), the norm equivalences

hold for all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\). For \(q = \infty \), \(\alpha \in \mathbb {R}\) and \(\beta >1\), the following equivalences hold

for all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\).
(The function  is well-defined for \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\), since \(\varphi \) has infinitely many vanishing moments and hence \(P *\varphi _s = 0\) for every \(P \in \mathcal {P}(\mathbb {R}^d)\).)
is well-defined for \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\), since \(\varphi \) has infinitely many vanishing moments and hence \(P *\varphi _s = 0\) for every \(P \in \mathcal {P}(\mathbb {R}^d)\).)
Remark 3.4
The proof of Theorem 3.3 shows that the discrete characterizations

and

also hold without the assumption that \(A \in \textrm{GL}(d, \mathbb {R})\) is exponential.
Proof of Theorem 3.3
Only the cases \(q \in (0,\infty )\) will be treated; the case \(q = \infty \) follows by the arguments for \(q = 1\), with the usual modification to accommodate the supremum. The proof is split into three steps and for some parts we refer to calculations from the proof of [20, Theorem 3.5].
Throughout the proof, we will make use of the equivalent norms

and

provided by Lemma 2.2.
Step 1. In this step it will be shown that \(\Vert f \Vert _{\dot{\textbf{F}}^{\alpha }_{\infty ,q}}\) can be bounded by the middle term of (3.5). This step is modeled on Step 1 of the proof of [20, Theorem 3.5]. By the calculations constituting [20, Eqs. (3.7)–(3.11)], it follows that, for \(t \in [0,1]\), there exists \(N = N(A, \varphi ) \in \mathbb {N}\) such that

If \(q < \infty \), then raising (3.7) to the q-th power and integrating over \(t \in [0,1]\) gives

Let \(w \in \mathbb {R}^d\) be arbitrary and set \(Q_\ell = A^\ell \Omega + w\). By Lemma 2.1, it follows that \( Q_\ell \subset Q_{\ell +N}\). Therefore, averaging over \(Q_{\ell }\) gives

where \(\frac{\textrm{m}( Q_{\ell +N})}{\textrm{m}(Q_\ell )} = |\det A|^N \lesssim 1\). Consequently, taking the q-th root and the supremum over \(\ell \in \mathbb {Z}\) and \(w \in \mathbb {R}^d\) yields the desired estimate.
Step 2. In this step we estimate the middle term by the right-most term of (3.5). This requires discretizing the inner-most integral, which works analogously to Step 2 in the proof of [20, Theorem 3.5]. By [20, Eq. (3.15)], for \(t \in [0,1]\), there exists \(N = N(A, \varphi ) \in \mathbb {N}\) such that

Starting with the inner-most integral of the middle term in (3.5), we use a simple periodization argument and (3.8) to obtain

Taking the averaged integral over \(Q_\ell = A^\ell \Omega + w\) yields

where we used \(Q_\ell \subset Q_{\ell +N}\) and \(\frac{1}{\textrm{m}(Q_\ell )} = |\det A|^N \frac{1}{\textrm{m}(Q_{\ell +N})}\) in the last step. Taking the supremum over all \(\ell \in \mathbb {Z}\) and \(w \in \mathbb {R}^d\) and the q-th root yields the claim for \(q \in (0,\infty )\).
Step 3. Lastly, it will be shown that the right-most term of (3.5) can be bounded by \(\Vert f\Vert _{\dot{\textbf{F}}^{\alpha }_{\infty ,q}{}}\). We start with using Proposition 3.2 for the exponent \(0< q/r<\infty \), where \(r:=\sqrt{\beta q} >1\) by assumption. This gives for all \(x \in \mathbb {R}^d\) and \(\ell \in \mathbb {Z}\)

For fixed, but arbitrary \(x \in \mathbb {R}^d\) and \(\ell \in \mathbb {Z}\), we partition \( \mathbb {R}^d = Q_\ell (x) \cup \bigcup _{k=0}^\infty \mathring{Q}_{\ell +k+1} (x)\), where
Combining this with the simple fact that \((a+b)^r \lesssim a^r + b^r\) for \(a,b \ge 0\) yields

In the remainder, the series defining \(S_1\) and \(S_2\) will be estimated.
Step 3.1. We look at the sum \(S_1\) first. Note that since \(|\det A| > 1\), there exists \(M \in \mathbb {N}\) such that \(|\det A|^M \ge 2 C\), where \(C>0\) denotes the constant in the triangle-inequality for \(\rho _A\) (cf. Lemma 2.1). A straightforward computation shows that \(Q_\ell (x) \subset Q_{\ell +M}(w)\) for all \(w \in \mathbb {R}^d\) and \(\ell \in \mathbb {Z}\) whenever \(x \in Q_\ell (w)\). Therefore, for all \(w \in \mathbb {R}^d\), \(\ell \in \mathbb {Z}\) and \(x \in Q_\ell (w)\), it follows that
To estimate the terms \(I_1\) and \(I_2\), we will use the (anisotropic) Hardy-Littlewood maximal operator for locally integrable \(f : \mathbb {R}^d \rightarrow \mathbb {C}\) given by

where \(B = B_{\rho _A}(z, s)\) ranges over all metric balls containing x.
For estimating \(I_1\), note that \(\nu _{\beta }\big (A^j(x-y)\big )^{-q/r}=\big (1+\rho _A(A^j(x-y))\big )^{-\beta q/r} \le 1\) yields
For estimating \(I_2\), note that \(\rho _A(A^j (x-y)) = |\det A|^{m}\) for \(y \in \mathring{Q}_{m-j+1}(x)\) by definition of \(\rho _A\) (see (2.1)). This and setting \(\delta := \beta q/r - 1\) implies
where the last inequality used that \(\delta = \beta q/r - 1 >0\). Here, the implicit constant only depends on A, q and \(\beta \).
Combining (3.9) and (3.10) shows for \(x \in Q_\ell (w)\) that
Thus, averaging over \(x \in Q_\ell (w)\) and applying the maximal inequalities for \(L^r(\mathbb {R}^d)\) (see, e.g., [15, Theorem 1.2]), yield

Lastly, taking the suprema over \(w \in \mathbb {R}^d\) and \(\ell \in \mathbb {Z}\) yields

with implicit constant depending on \(A,\varphi ,q\), and \(\beta \).
Step 3.2. In this step, we deal with the sum \(S_2\). Recall again that, for \(y \in \mathring{Q}_{\ell +k+1} (x)\), \(\rho _A((A^j(x-y))) = |\det A|^{j+k+\ell }\). Hence,

where again \(\delta := \beta q / r -1 >0\). Note that \(|\det A|^{-\delta (j+\ell )} \le 1\) for \(j \ge - \ell \), which implies that

where we used Minkowski’s integral inequality (see, e.g., [29, Appendix 1]) to obtain the last line. An application of Jensen’s inequality to the integral yields

and consequently

where we used the index shift \(\ell ' = \ell + k +1\) in the penultimate estimate. Since the implicit constants are independent of \(w \in \mathbb {R}^d\) and \(\ell \in \mathbb {Z}\), it follows that

Overall, combining the estimates (3.11) and (3.13) finishes the proof. \(\square \)
4 The case \(p=q=\infty \)
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and suppose that \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) has compact Fourier support and satisfies (2.5) and (2.6). Following [2], for fixed \(\alpha \in \mathbb {R}\), the associated homogeneous anisotropic Besov space \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }= \dot{\textbf{B}}^{\alpha }_{\infty ,\infty }(A,\varphi )\) is defined as the set of all \(f \in \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\) for which
The space \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }\) is continuously embedded into \(\mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\) and complete with respect to the quasi-norm \(\Vert \cdot \Vert _{\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }}\), cf. [2, Proposition 3.3]. In addition, it is independent of the choice of defining vector \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) by [2, Corollary 3.7].
The following theorem relates the anisotropic Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\), with \(0 < q \le \infty \), to the anisotropic Besov space \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }\). In particular, it shows that \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }= \dot{\textbf{F}}^{\alpha }_{\infty ,\infty }\), providing a characterization of \(\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }\) in terms of Peetre-type maximal functions. It also shows that the definition of \(\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }\) given in Sect. 2.4 coincides with the definition in [3, Sect. 3].
Theorem 4.1
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive. Assume that \(\varphi \in \mathcal {S}(\mathbb {R}^d)\) has compact Fourier support and satisfies (2.5) and (2.6).
Then, for all \(q \in (0, \infty ]\) and \(\alpha \in \mathbb {R}\), we have the continuous embedding
In addition, \(\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }(A,\varphi ) = \dot{\textbf{B}}^{\alpha }_{\infty ,\infty }(A,\varphi )\).
Proof
The inequality \(\Vert f\Vert _{\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }} \le \Vert f\Vert _{\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }}\) is immediate. To show that \(\Vert f \Vert _{\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }} \lesssim \Vert f \Vert _{\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }}\), the norm equivalences of Theorem 3.3 will be used; see also Remark 3.4. For this, suppose \(\beta >1\). Then, for all \(\ell \in \mathbb {Z}\), \(w \in \mathbb {R}^d\), we see that

In particular, the inequality (4.1) implies that, for every \(\ell \in \mathbb {Z}\) and \(w \in \mathbb {R}^d\) there exists \(x_w \in Q_\ell (w)\) such that

If \(z \in Q_\ell (w)\), then \(\rho _A\big (A^{-\ell }(z-x_w)\big ) \lesssim \rho _A\big (A^{-\ell }(z-w)\big ) +\rho _A\big (A^{-\ell }(w-x_w)\big ) \lesssim 1\) with implicit constant depending only on A. Hence, for all \(z \in Q_\ell (w)\), it holds that

Since \(\bigcup _{w \in \mathbb {R}^d} Q_\ell (w) = \mathbb {R}^d\) for fixed, but arbitrary, \(\ell \in \mathbb {Z}\), we see by combining (4.2) and (4.3) that
for all \(z \in \mathbb {R}^d\) and \(\ell \in \mathbb {Z}\), which shows \(\dot{\textbf{F}}^{\alpha }_{\infty ,\infty }(A,\varphi ) = \dot{\textbf{B}}^{\alpha }_{\infty ,\infty }(A,\varphi )\) with equivalent norms.
An analogous argument using (3.5) gives \(\Vert f\Vert _{\dot{\textbf{B}}^{\alpha }_{\infty ,\infty }} \lesssim \Vert f\Vert _{\dot{\textbf{F}}^{\alpha }_{\infty ,q}}\), which completes the proof. \(\square \)
Theorem 4.1 is an extension of [6, Theorem 3] to the anisotropic setting.
5 Wavelet coefficient decay and Peetre-type spaces
Throughout this section, let \(A \in \textrm{GL}(d, \mathbb {R})\) be an exponential matrix. Define the associated semi-direct product \( G_A = \mathbb {R}^d \rtimes _A \mathbb {R} = \{ (x, s) : x \in \mathbb {R}^d, s \in \mathbb {R} \} \) with group operations
Left Haar measure on \(G_A\) is given by \(d \mu _{G_A} (x,s) = |\det A|^{-s} ds \, dx\) and the modular function on \(G_A\) is \(\Delta _{G_A} (x,s) = |\det A|^{-s}\). To ease notation, we will often write \(\mu := \mu _{G_A}\).
5.1 Wavelet transforms
The group \(G_A = \mathbb {R}^d \rtimes _A \mathbb {R}\) acts unitarily on \(L^2 (\mathbb {R}^d)\) by means of the quasi-regular representation \(\pi \), defined by
For a fixed vector \(\psi \in L^2 (\mathbb {R}^d) \setminus \{0\}\), the associated wavelet transform \(W_{\psi } : L^2 (\mathbb {R}^d) \rightarrow L^{\infty } (G_A)\) is defined through the coefficients
The vector \(\psi \) is called admissible if \(W_{\psi } : L^2 (\mathbb {R}^d) \rightarrow L^2 (G_A)\) is an isometry.
The following lemma is a special case of [12, Theorem 1] and [21, Theorem 1.1].
Lemma 5.1
([12, 21]) Let \(\psi \in L^2 (\mathbb {R}^d)\). Then \(\psi \) is admissible if and only if
for a.e. \(\xi \in \mathbb {R}^d\).
The significance of an admissible vector \(\psi \) is that \(W_{\psi }^* W_{\psi } = I_{L^2 (\mathbb {R}^d)}\), and hence that the weak-sense integral formula
holds for every \(f \in L^2 (\mathbb {R}^d)\). This, combined with fact that \(W_{\psi } : L^2 (\mathbb {R}^d) \rightarrow L^2 (G_A)\) intertwines the action of \(\pi \) and left translation \(L_h F = F(h^{-1} \cdot )\) on \(L^2 (G_A)\), also yields that
for all \(f, \varphi \in L^2 (\mathbb {R}^d)\). The identity (5.2) will be referred to as a reproducing formula.
Henceforth, it will always be assumed that \(A \in \textrm{GL}(d, \mathbb {R})\) is both exponential and expansive. This is essential for the existence of admissible vectors \(\psi \in \mathcal {S} (\mathbb {R}^d)\) with compact Fourier support, as the following result shows.
Lemma 5.2
([1, 9, 16, 28]) Let \(A \in \textrm{GL}(d, \mathbb {R})\) be an exponential matrix. The following assertions are equivalent:
-
(i)
The matrix A or its inverse \(A^{-1}\) is expansive.
-
(ii)
There exists an admissible \(\psi \in \mathcal {S} (\mathbb {R}^d)\) with \(\widehat{\psi } \in C_c^{\infty } (\mathbb {R}^d)\).
In addition, if A is an expansive matrix, then the admissible vector \(\psi \in L^2 (\mathbb {R}^d)\) can be chosen such that \(\widehat{\psi } \in C_c^{\infty } (\mathbb {R}^d \setminus \{0\})\) satisfies condition (2.6).
We will also need to use wavelet transforms of distributions. For this, consider the subspace of \(\mathcal {S}(\mathbb {R}^d)\) given by
and equip it with the subspace topology of \(\mathcal {S}(\mathbb {R}^d)\). Its topological dual space will be denoted by \(\mathcal {S}_0' (\mathbb {R}^d)\) and will often be identified with \(\mathcal {S}'(\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\), see, e.g., [14, Proposition 1.1.3]. The dual bracket between \(\mathcal {S}_0\) and \(\mathcal {S}_0' (\mathbb {R}^d)\) is denoted by
Note that this pairing is conjugate-linear in the second variable.
For a fixed \(\psi \in \mathcal {S}_0 (\mathbb {R}^d) \setminus \{0\}\), the extended wavelet transform of \(f \in \mathcal {S}'_0 (\mathbb {R}^d)\) is defined as
By the continuity of the map \((x,s) \mapsto \pi (x,s) \varphi \) from \(\mathbb {R}^d \times \mathbb {R}\) into \(\mathcal {S}(\mathbb {R}^d)\), the transform \(W_{\psi } : \mathcal {S}_0' (\mathbb {R}^d) \rightarrow C(G_A)\) is well-defined.
The reproducing formula (5.2) can be naturally extended to \(\mathcal {S}'_0 (\mathbb {R}^d)\). See [20, Lemma 4.7 and Lemma 4.8] for a proof of the following result.
Lemma 5.3
([20]) Let \(\psi \in \mathcal {S}_0 (\mathbb {R}^d)\) be an admissible vector. Then, for arbitrary \(f \in \mathcal {S}'_0 (\mathbb {R}^d)\) and \(\varphi \in \mathcal {S}_0 (\mathbb {R}^d)\),
In particular, the identity \(W_{\varphi } f = W_{\psi } f *W_{\varphi } \psi \) holds.
5.2 Peetre-type spaces
As in [20], we define an auxiliary class of Peetre-type spaces \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}\) on the semi-direct product \(G_A = \mathbb {R}^d \rtimes \mathbb {R}\). These spaces are an essential ingredient for identifying Triebel-Lizorkin spaces with associated coorbit spaces [10, 32].
In contrast to the spaces \(\dot{\textbf{P}}^{\alpha , \beta }_{p,q}\) defined in [20, Definition 5.1] for \(p < \infty \), the spaces \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}\) will only be defined through averages over small scales.
Definition 5.4
Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and exponential and let \(\Omega = \Omega _A\) be an associated ellipsoid as provided by Lemma 2.1. For \(\ell \in \mathbb {Z}\) and \(w \in \mathbb {R}^d\), set \(Q_{\ell } (w) := A^{\ell } \Omega + w\).
For \(\alpha \in \mathbb {R}, \beta > 0\), and \(q \in (0, \infty )\), the Peetre-type space \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}(G_A)\) is defined as the space of all (equivalence classes of a.e. equal) measurable \(F : G_A \rightarrow \mathbb {C}\) such that

For \(q = \infty \), the space \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,\infty }(G_A)\) consists of all measurable \(F : G_A \rightarrow \mathbb {C}\) satisfying

The following lemma collects some basic properties of \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}(G_A)\) and gives explicit estimates for the operator norm of left and right translation. The estimates involve the following weight function
The function v is measurable and submultiplicative by [20, Lemma 5.2].
Lemma 5.5
Let \(\alpha \in \mathbb {R}, \beta > 0\), and \(q \in (0, \infty ]\). Then the Peetre-type space \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}(G_A)\) is a solid quasi-Banach function space (Banach function space if \(q \ge 1\)). Moreover, the space \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}(G_A)\) is left- and right-translation invariant and there exists \(N = N(A, \Omega ) \in \mathbb {N}\) such that, for all \((y, t) \in G_A\), the operator norms can be bounded by
if \(q < \infty \), and
otherwise. Here, the operator norm is written \({\left| \left| \left| \cdot \right| \right| \right| } :=\Vert \cdot \Vert _{\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}\rightarrow \dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}}\).
Proof
Most of the quasi-norm properties for \(\Vert \cdot \Vert _{\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}}\) can be easily verified from the definition, while the positive definiteness follows from [20, Lemma B.1]. It is clear that \(\Vert \cdot \Vert _{\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}}\) is solid and for \(q \ge 1\) a norm. The completeness follows from \(\Vert \cdot \Vert _{\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}}\) satisfying the Fatou property (see [34, Sect. 65, Theorem 1] and [33, Lemma 2.2.15]), which is easily verified by a straightforward computation using Fatou’s lemma, see, e.g., the proof of [20, Lemma 5.3].
It remains to prove the translation invariance and associated norm estimates. We will only consider \(q \in (0, \infty )\), the arguments for \(q=\infty \) are analogous. To this end, let \(F \in \dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}(G_A)\) and \({(y,t) \in \mathbb {R}^d \times \mathbb {R}}\) be arbitrary. Then the substitutions \(\widetilde{x} = A^{-t}(x - y)\), \(\widetilde{w} = A^{-t}(w-y)\), and \(\widetilde{z} = A^{-t} z\), as well as \(\widetilde{s} = s-t\), yield

where the transformation of the domain is \(A^{-t}(Q_\ell (w)-y) = A^{-t}(A^\ell \Omega +w -y) = A^{\ell -t}\Omega + \widetilde{w}\). To estimate this further, we decompose \(t = k + t'\) with \(k \in \mathbb {Z}\) and \(t' \in [0,1)\). By [20, Lemma 2.4], there exists \(N = N(A, \Omega ) \in \mathbb {N}\) such that \(A^{-t'}\Omega \subset A^N \Omega \) for all \(t' \in [0,1)\), and hence \(Q_{\ell -t}( \widetilde{w}) \subset Q_{\ell -k+N}( \widetilde{w})\). Increasing the upper limit of the inner integral from \(\ell -t\) to \(\ell -k +N\) and substituting \(\widetilde{\ell } = \ell -k +N \in \mathbb {Z}\) gives

For the right-translation, a direct calculation using the substitutions \(\widetilde{z} = z + A^s y\) and \(\widetilde{s} = s + t\) shows that

where we used the fact that \(\bigl (1+\rho _A (A^{-\widetilde{s}} A^{t} \widetilde{z} - y)\bigr )^{-1} \le v(y,t) (1 + \rho _A (A^{-\widetilde{s}} \widetilde{z}))^{-1}\) for all \((\widetilde{z},\widetilde{s}), (y,t) \in \mathbb {R}^d \times \mathbb {R}\) by definition.
For \(t \le 0\), the claimed estimate follows immediately. For \(t > 0\), we again write \(t = k + t'\) with \(k \in \mathbb {N}_0\) and \(t' \in [0, 1)\). Then \(\ell + t \le \ell + k + 1\) and clearly \(Q_\ell (w) = A^\ell \Omega + w \subset A^{\ell +k+1} \Omega + w = Q_{\ell +k+1}(w)\) by Lemma 2.1. Hence,

and consequently
for \(t>0\), which completes the proof. \(\square \)
Lastly, we mention the following r-norm property of Peetre-type spaces.
Lemma 5.6
Let \(\alpha \in \mathbb {R}\) and \(\beta > 0\). For \(q \in (0, \infty ]\), set \(r := \min \{1, q \}\). Then \(\Vert \cdot \Vert _{\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}}\) is an r-norm, i.e.,
Proof
The claim follows immediately from the triangle inequality for \(q \in [1, \infty ]\), respectively a straightforward computation using the subadditivity of \(x \mapsto |x|^q\) for \(q \in (0, 1)\). \(\square \)
5.3 Standard envelope and control weight
We recall the definition of a standard envelope given in [20, Definition 5.5].
Definition 5.7
Let \(\sigma = (\sigma _1, \sigma _2) \in (0,\infty )^2\) and let \(L \in \mathbb {R}\). Then the standard envelope \(\Xi _{\sigma ,L} : G_A \rightarrow (0,\infty )\) is given by \(\Xi _{\sigma ,L}(x,s):= \theta _\sigma (s) \cdot \eta _L(x,s)\), where
A central notion in the theory of coorbit spaces [10, 32] is that of a so-called control weight. In the following lemma, we show the existence of such a weight for Peetre-type spaces and show that it can be estimated by standard envelopes as defined in Definition 5.7. The construction of the control weight follows [20, Lemma 5.7], but besides the slightly different parameters, the case distinction for the right translation needs to be accommodated with a few extra terms. The details are as follows.
Lemma 5.8
Let \(\alpha \in \mathbb {R}\) and \(\beta > 0\). For \(q \in (0, \infty ]\), set \(r := \min \{1, q \}\). Then there exists a continuous, submultiplicative weight \(w = w^{\alpha ,\beta }_{\infty ,q} : G_A \rightarrow [1,\infty )\) such that
with implicit constant depending on \(A,\beta \). The weight w will be referred to as the standard control weight.
Moreover, for \(q \in (0, \infty )\), set \(\sigma _1 := |\det A|^{1/r + |\alpha -1/q|}\) and \(\sigma _2 := |\det A|^{-|\alpha -1/q|}\), as well as
and
For \(q = \infty \), set \(\sigma _1 := |\det A|^{1 + |\alpha |}\) and \(\sigma _2 := |\det A|^{-|\alpha |}\), as well as
Then the standard control weight w satisfies \( w \asymp \Xi _{\sigma , 0} + \Xi _{\kappa , -\beta } . \)
Proof
By [20, Lemma 5.2], the weight \(v : G_A \rightarrow [0,\infty )\) appearing in Lemma 5.5 is submultiplicative, measurable, and locally bounded. It also satisfies \(v \ge 1\), and is therefore a weight function in the sense of [25, Definition 3.7.1]. Hence, there exists a continuous, submultiplicative function \(v_0 : G_A \rightarrow [1,\infty )\) with \(v \asymp v_0\) by the proof of [25, Theorem 3.7.5].
Let \(\tau \in \mathbb {R}\) and define \(a_{\tau }(g) = a_{\tau } (x,s) := |\det A|^{s \tau }\) for \(g = (x,s) \in G_A\). Then the weight function \(w_{\gamma , \delta , \zeta } : G_A \rightarrow [1,\infty )\) with respect to \(\gamma , \delta , \zeta \in \mathbb {R}\) is given by
Clearly \(w_{\gamma , \delta , \zeta }\) is again continuous and submultiplicative. As \(\Delta = a_{-1}\) and \(a_{\tau }^{\vee } = a_{-\tau }\), it is easily verified that
We choose the parameters \(\gamma , \delta , \zeta \) according to Lemma 5.5, i.e., \(\gamma := \alpha - 1/q\), \(\delta := \alpha - 2/q\), \(\zeta := \alpha - 1/q\) if \(q \in (0,\infty )\), and \(\gamma := \alpha \), \(\delta := \alpha - 1\), \(\zeta := \alpha \) otherwise. Set \(w= w^{\alpha , \beta }_{\infty ,q}:=w_{\gamma , \delta , \zeta }\). For \(g = (x,s) \in G_A\), an application of Lemma 5.5 implies \({\left| \left| \left| L_{g^{-1}}\right| \right| \right| } \lesssim a_{-\gamma }(g) \le w(g)\) and
It remains to show that the control weight can be estimated by standard envelopes. To this end, note that \(w \asymp w_1 + w_2\) for the weights given by \({w_1 := \max \{ a_0, a_{1/r}, a_\gamma , a_{-\gamma }, a_{1/r+\gamma }, a_{1/r-\gamma } \}}\) and \( w_2 := \max \bigl \{ a_{\delta + 1/r} \cdot (v_0^{\vee })^\beta , \,\, a_{-\delta } \cdot v_0^\beta , \,\, a_{\zeta + 1/r} \cdot (v_0^{\vee })^\beta , \,\, a_{-\zeta } \cdot v_0^\beta \bigr \} \). A straightforward computation, also done in the proof of [20, Lemma 5.7], reveals that
by the choice of \(\sigma \). For estimating \(w_2\), we use the fact that \(v_0(x,s) \asymp |\det A|^{s^-} \, \eta _{-1} (x,s)\) and \(v_0^\vee (x,s) \asymp |\det A|^{s^+} \, \eta _{-1} (x,s)\) as shown in [20, Lemma 5.7]. For \(s \ge 0\), this gives
since, in the case of \(q \in (0, \infty )\), we have
if and only if \(\alpha \ge -\frac{1/r+\beta -3/q}{2}\), with a similar case distinction for \(q = \infty \). The estimate for \(s < 0\) follows analogously. \(\square \)
5.4 Coorbit spaces
The aim of this section is to show that Triebel-Lizorkin spaces \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\) can be identified with so-called coorbit spaces [10, 32] by use of Theorem 3.3.
The definition of coorbit spaces requires the notion of a local maximal function. For a function \(F \in L^{\infty }_{{{\,\textrm{loc}\,}}} (G_A)\), its (left-sided) maximal function is defined by
where \(Q \subset G_A\) is a relatively compact unit neighborhood.
Definition 5.9
Let \(q \in (0,\infty ]\), \(\alpha \in \mathbb {R}\), and \(\beta > 0\). Let \(A \in \textrm{GL}(d, \mathbb {R})\) be expansive and exponential, and let \(Q \subset G_A\) be a relatively compact, symmetric unit neighborhood.
For admissible \(\psi \in \mathcal {S}_0(\mathbb {R}^d)\), the coorbit space \({{\,\textrm{Co}\,}}(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}) = {{\,\textrm{Co}\,}}_{\psi } (\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q})\) is the collection of all \(f \in \mathcal {S}_0'(\mathbb {R}^d)\) satisfying
The space will be equipped with the (quasi-)norm \(\Vert \, . \, \Vert _{{{\,\textrm{Co}\,}}(\dot{\textbf{P}}^{\alpha , \beta }_{p,q})}\).
The space \({{\,\textrm{Co}\,}}(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q})\) as defined in Definition 5.9 is complete with respect to the quasi-norm \(\Vert \cdot \Vert _{{{\,\textrm{Co}\,}}(\dot{\textbf{F}}^{\alpha }_{\infty ,q})}\). In addition, its definition is independent of the chosen defining vector \(\psi \) and unit neighborhood Q, with equivalent norms for different choices. These basic properties follow from the general theory [32]; see [20, Remark 5.10] for details and references.
The following is the key result of this section.
Proposition 5.10
Let \(\alpha \in \mathbb {R}\) and \(q \in (0,\infty ]\). Let \(\beta > 1/q\) if \(q \in (0, \infty )\), and \(\beta > 1\) if \(q = \infty \). Then
Proof
Throughout, let \(\psi \in \mathcal {S}(\mathbb {R}^d)\) be an admissible vector with \(\widehat{\psi } \in C^{\infty }_c (\mathbb {R}^d \setminus \{0\}\) satisfying the support condition (2.6). The existence of such vectors follows by [9, Proposition 10]; see also Lemma 5.2. Furthermore, define \(Q := [-1, 1)^d \times [-1,1)\).
We split the proof into three steps and consider only \(q \in (0, \infty )\). The case \(q = \infty \) follows with the usual adjustments. Set \(\alpha ':= \alpha + 1/2 - 1/q\). The first two steps are essentially identical to the first part of the proof of [20, Proposition 5.11], but included for completeness.
Step 1. Note that \(\psi ^{*} \in \mathcal {S}_0(\mathbb {R}^d)\) also satisfies (2.6), where \(\psi ^{*} (t) = \overline{\psi (-t)}\). A direct calculation gives
By [20, Lemma A.1], it holds for arbitrary \(\beta > 0\) and \(s \in \mathbb {R}\) that
Therefore, an application of Theorem 3.3 yields

for any \(f \in \mathcal {S}_0'(\mathbb {R}^d)\).
Step 2. The estimate \(|W_{\psi } f| \le M^L_Q W_{\psi } f\) a.e. implies that
for \(f \in \mathcal {S}_0'(\mathbb {R}^d)\).
Step 3. We prove the remaining estimate \(\Vert f \Vert _{{{\,\textrm{Co}\,}}(\dot{\textbf{P}}^{-\alpha ', \beta }_{p,q})} \lesssim \Vert f \Vert _{\dot{\textbf{F}}^{\alpha }_{p,q}}\) for \(f \in \mathcal {S}_0'(\mathbb {R}^d)\). In [20, Equation (5.12)], we already showed that
with implicit constant depending on \(A, \alpha , \beta ,q\) and N, where \(N \in \mathbb {N}\) depends on the support of \(\psi \). Combining this with Theorem 3.3 yields

where we used the fact that \( \frac{\textrm{m}(A^{\ell +N} \Omega )}{\textrm{m}(A^{\ell } \Omega )} = |\det A|^N \lesssim _N 1\) in the last step. \(\square \)
6 Molecular decompositions
In this section we use the identification of Triebel-Lizorkin spaces and associated coorbit spaces (cf. Proposition 5.10) to obtain proofs of Theorems 1.2 and 1.3.
6.1 Molecular systems
In addition to the left-sided local maximal function defined in Eq. (5.3), we will also need a two-sided version, defined by
for \(F \in L^{\infty }_{{{\,\textrm{loc}\,}}} (G_A)\), with \(Q \subset G_A\) being a fixed relatively compact unit neighborhood.
For \(r = \min \{1,q\}\) with \(q \in (0,\infty ]\) and the standard control weight \(w = w_{\infty , q}^{\alpha , \beta } : G_A \rightarrow [1,\infty )\) provided by Lemma 5.8, define the associated Wiener amalgam space \(\mathcal {W}(L^r_w)\) by
The space \(\mathcal {W}(L^r_w)\) is independent of the choice of neighborhood Q and is complete with respect to the quasi-norm \(\Vert F \Vert _{\mathcal {W}(L^r_w)} := \Vert M_Q F\Vert _{L^r_w}\); see, e.g., [24, Sect. 2] and [32, Sect. 2].
The space \(\mathcal {W}(L^r_w)\) provides the class of envelopes that will be used for defining molecules.
Definition 6.1
Let \(\psi \in L^2 (\mathbb {R}^d)\) be a non-zero vector such that \(W_{\psi } \psi \in \mathcal {W}(L^r_w)\) for the standard control weight \(w : G_A \rightarrow [1,\infty )\) defined in Lemma 5.8.
A countable family \((\phi _{\gamma })_{\gamma \in \Gamma }\) in \(L^2 (\mathbb {R}^d)\) is called an \(L^r_w\)-molecular system if there exists \(\Phi \in \mathcal {W}(L^r_w)\) such that
A function \(\Phi \in \mathcal {W}(L^r_w)\) satisfying (6.1) is called an envelope for \((\phi _{\gamma })_{\gamma \in \Gamma }\).
The following lemma provides an extended duality pairing for \(\mathcal {S}_0' (\mathbb {R}^d)\). See [20, Lemma 6.8] for its proof.
Lemma 6.2
[20] Let \(\psi \in \mathcal {S}_0 (\mathbb {R}^d)\) be an admissible vector and let \(w : G_A \rightarrow [1,\infty )\) be the standard control weight as defined in Lemma 5.8.
Suppose \(f \in \mathcal {S}_0' (\mathbb {R}^d)\) satisfies \(W_{\psi } f \in L^{\infty }_{1/w} (G_A)\) and \(\phi \in L^2 (\mathbb {R}^d)\) satisfies \(W_{\psi } \phi \in L^{1}_w (G_A)\). Then the extended pairing defined by
is well-defined and independent of the choice of admissible vector \(\psi \in \mathcal {S}_0 (\mathbb {R}^d)\).
6.2 Sequence spaces
The following definition provides a class of sequence spaces that will be used in the molecular decomposition of anisotropic Triebel-Lizorkin spaces.
Definition 6.3
Let \(U \subset G_A\) be a relatively compact unit neighborhood with non-void interior and let \(\Gamma \) be any family in \(G_A\) such that \(\sup _{g \in G_A} \# (\Gamma \cap g U ) < \infty \).
For \(\alpha \in \mathbb {R}\), \(\beta > 0\) and \(q \in (0,\infty ]\), the Peetre-type sequence space \(\dot{\textbf{p}}^{\alpha , \beta }_{\infty ,q}(\Gamma , U)\) consists of all sequences \(c \in \mathbb {C}^{\Gamma }\) satisfying
where \(\dot{\textbf{P}}^{\alpha , \beta }_{\infty ,q}(G_A)\) denotes the Peetre-type space defined in Definition 5.4.
The Peetre-type sequence space \(\dot{\textbf{p}}^{\alpha , \beta }_{\infty ,q}(\Gamma , U)\) forms a quasi-Banach space with respect to the quasi-norm \(\Vert \cdot \Vert _{\dot{\textbf{p}}^{\alpha , \beta }_{\infty ,q}}\). In addition, it is independent of the choice of the defining neighborhood U. For proofs of both facts, see, e.g., [10, 24] or [33, Lemma 2.3.16].
6.3 Proofs of Theorems 1.2 and 1.3
Theorems 1.2 and 1.3 will be obtained from corresponding results for abstract coorbit spaces [32].
Proof of Theorem 1.2
For the fact that if \(W_{\varphi } \psi \in \mathcal {W}(L^r_w)\) for some admissible \(\varphi \in \mathcal {S}_0 (\mathbb {R}^d)\), then \(W_{\phi } \psi \in \mathcal {W}(L^r_w)\) for all \(\phi \in \mathcal {S}_0 (\mathbb {R}^d)\), cf. the proof of [20, Lemma 6.9]. Throughout, we fix an admissible \(\varphi \in \mathcal {S}_0 (\mathbb {R}^d)\) with \(\widehat{\varphi } \in C^\infty _c(\mathbb {R}^d \setminus \{0\})\) satisfying condition (2.6). Such an admissible vector exists by Lemma 5.2; see [9, Proposition 10].
Step 1. Under the assumptions, it follows by an application of Proposition 5.10 that \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}= {{\,\textrm{Co}\,}}_{\varphi } (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\). For applying the relevant results of [32], it will next be shown that \({{\,\textrm{Co}\,}}_{\varphi } (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\) can be identified with the abstract coorbit spaces used in [32]. To this end, note that \(\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q}\) is a solid, translation invariant quasi-Banach space by Lemma 5.5, which satisfies the r-norm property by Lemma 5.6. The standard control weight \(w = w^{-\alpha ', \beta }_{\infty ,q}: G_A \rightarrow [1, \infty )\) of Lemma 5.8 is a strong control weight in the sense of [32, Definition 3.1], which can be dominated by a linear combination of standard envelopes.
Define the space \(\mathcal {H}^1_{w} (\psi ) := \big \{ f \in L^2 (\mathbb {R}^d) : W_{\psi } f \in L^1_{w} (G_A) \big \}\) and equip it with the norm \(\Vert f \Vert _{\mathcal {H}^1_{w} (\psi )} := \Vert W_{\psi } f \Vert _{L^1_{w}}\). Set \(\mathcal {R}_{w} (\psi ) := ( \mathcal {H}^1_{w} (\psi ) )^*\) to be its anti-dual space. Since both \(W_\psi \psi , W_\varphi \psi \in \mathcal {W}(L^r_w)\), it follows by similar arguments as proving [20, Lemma D.1] that

where \(V_{\psi } f = \langle f, \pi (\cdot ) \psi \rangle _{\mathcal {R}_w, \mathcal {H}^1_w}\) denotes the conjugate-linear pairing. In addition, for the unique extension \(\widetilde{f} \in {{\,\textrm{Co}\,}}_{\psi }^{\mathcal {H}} (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\) of \(f \in {{\,\textrm{Co}\,}}_{\psi } (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\), it holds that
where \(\langle \cdot , \cdot \rangle _{\varphi }\) denotes the extended pairing of Lemma 6.2.
Step 2. Applying [32, Theorem 6.14] yields a compact unit neighborhood \(U \subset G_A\) such that for any set \(\Gamma \subset G_A\) satisfying (1.10), there exists a family \((\phi _\gamma )_{\gamma \in \Gamma }\) of \(L^r_w\)-localized molecules in \(L^2(\mathbb {R}^d)\) such that any \(\widetilde{f} \in {{\,\textrm{Co}\,}}_{\psi }^{\mathcal {H}} (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\) can be represented as
with unconditional convergence with respect to the weak\(^*\)-topology on \(\mathcal {R}_{w}(\psi )\).
Given any \(f \in \dot{\textbf{F}}^{\alpha }_{\infty ,q}= {{\,\textrm{Co}\,}}_{\varphi } (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\), we apply (6.3) to its unique extension \(\widetilde{f} \in {{\,\textrm{Co}\,}}_{\psi }^{\mathcal {H}} (\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\). Since \(\mathcal {W}(L^r_w)\hookrightarrow L^1_{w}\) by [32, Lemma 3.3(ii)], we have that \(\psi \in \mathcal {H}^1_{w}\) and that \(\phi _\gamma \in \mathcal {H}^1_{w}\). Consequently, the dual pairings in (6.3) agree with the extended pairing of Lemma 6.2; see Eq. (6.2). Since \(\mathcal {S}_0 \hookrightarrow \mathcal {H}_{w}^1\), restricting both sides of (6.3) to \(\mathcal {S}_0\) yields the desired expansion with unconditional convergence in the weak\(^*\)-topology of \(\mathcal {S}_0' \cong \mathcal {S}' (\mathbb {R}^d) / \mathcal {P} (\mathbb {R}^d)\). \(\square \)
Proof of Theorem 1.3
As shown in Step 1 of the proof of Theorem 1.2, the map \(f \mapsto f|_{\mathcal {S}_0}\) is a well-defined bijection from \( {{\,\textrm{Co}\,}}_{\psi }^{\mathcal {H}}(\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\) into \(\dot{\textbf{F}}^{\alpha }_{\infty ,q}\), with \({{\,\textrm{Co}\,}}^{\mathcal {H}}_{\psi } ( \dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\) denoting the abstract coorbit space as defined in [32]. Therefore, applying [32, Theorem 6.15] yields a compact unit neighborhood \(U \subset G_A\) such that for any set \(\Gamma \subset G_A\) satisfying (1.11), there exists a family \((\phi _\gamma )_{\gamma \in \Gamma }\) in \( \overline{{{\,\textrm{span}\,}}} \{ \pi (\gamma ) \psi : \gamma \in \Gamma \} \subset L^2(\mathbb {R}^d)\) of \(L^r_w\)-localized molecules such that the moment problem
admits the solution \(\widetilde{f} := \sum _{\gamma \in \Gamma } c_\gamma \phi _\gamma \in {{\,\textrm{Co}\,}}_{\psi }^{\mathcal {H}}(\dot{\textbf{P}}^{-\alpha ', \beta }_{\infty ,q})\) for any sequence \((c_\gamma )_{\gamma \in \Gamma } \in \dot{\textbf{p}}^{\alpha , \beta }_{\infty ,q}[-\alpha '](\Gamma )\). Furthermore, by arguing as in the proof of Theorem 1.2, we can restrict to
to obtain the desired claim. \(\square \)
References
Bownik, M.: Anisotropic Hardy spaces and wavelets. Mem. Amer. Math. Soc. 164(781), 6–122 (2003)
Bownik, M.: Atomic and molecular decompositions of anisotropic Besov spaces. Math. Z. 250(3), 539–571 (2005)
Bownik, M.: Anisotropic Triebel-Lizorkin spaces with doubling measures. J. Geom. Anal. 17(3), 387–424 (2007)
Bownik, M.: Duality and interpolation of anisotropic Triebel-Lizorkin spaces. Math. Z. 259(1), 131–169 (2008)
Bownik, M., Ho, K.-P.: Atomic and molecular decompositions of anisotropic Triebel-Lizorkin spaces. Trans. Amer. Math. Soc. 358(4), 1469–1510 (2006)
Bui, H.-Q., Taibleson, M.H.: The characterization of the Triebel-Lizorkin spaces for \(p=\infty \). J. Fourier Anal. Appl. 6(5), 537–550 (2000)
Coifman, R.R., Weiss, G.: Analyse harmonique non-commutative sur certains espaces homogènes. Lecture Notes in Mathematics, vol. 242. Springer-Verlag, Berlin-New York (1971)
Coifman, R.R., Weiss, G.: Extensions of Hardy spaces and their use in analysis. Bull. Amer. Math. Soc. 83(4), 569–645 (1977)
Currey, B., Führ, H., Taylor, K.: Integrable wavelet transforms with abelian dilation groups. J. Lie Theory 26(2), 567–596 (2016)
Feichtinger, H.G., Gröchenig, K.H.: Banach spaces related to integrable group representations and their atomic decompositions. I. J. Funct. Anal. 86(2), 307–340 (1989)
Frazier, M., Jawerth, B.: A discrete transform and decompositions of distribution spaces. J. Funct. Anal. 93(1), 34–170 (1990)
Führ, H., Mayer, M.: Continuous wavelet transforms from semidirect products: cyclic representations and Plancherel measure. J. Fourier Anal. Appl. 8(4), 375–397 (2002)
Gilbert, J.E., Han, Y.S., Hogan, J.A., Lakey, J.D., Weiland, D., Weiss, G.: Smooth molecular decompositions of functions and singular integral operators. Mem. Amer. Math. Soc. 156(742), 8–74 (2002)
Grafakos, L.: Modern Fourier analysis. Graduate Texts in Mathematics, vol. 250. Springer, New York (2014)
Grafakos, L., Liu, L., Yang, D.: Vector-valued singular integrals and maximal functions on spaces of homogeneous type. Math. Scand. 104(2), 296–310 (2009)
Gröchenig, K.: Describing functions: atomic decompositions versus frames. Monatsh. Math. 112(1), 1–42 (1991)
Gröchenig, K., Kaniuth, E., Taylor, K.F.: Compact open sets in duals and projections in \(L^1\)-algebras of certain semi-direct product groups. Math. Proc. Cambridge Philos. Soc. 111(3), 545–556 (1992)
Gröchenig, K., Piotrowski, M.: Molecules in coorbit spaces and boundedness of operators. Stud. Math. 192(1), 61–77 (2009)
Ho, K.-P.: Frames associated with expansive matrix dilations. Collect. Math. 54(3), 217–254 (2003)
Koppensteiner,S., van Velthoven,J. T., Voigtlaender,F.: Anisotropic Triebel-Lizorkin spaces and wavelet coefficient decay over one-parameter dilation groups, I. Preprint. arXiv: 2104.14361 (2021)
Laugesen, R.S., Weaver, N., Weiss, G.L., Wilson, E.N.: A characterization of the higher dimensional groups associated with continuous wavelets. J. Geom. Anal. 12(1), 89–102 (2002)
Liang, Y., Sawano, Y., Ullrich, T., Yang, D., Yuan, W.: New characterizations of Besov-Triebel-Lizorkin-Hausdorff spaces including coorbits and wavelets. J. Fourier Anal. Appl. 18(5), 1067–1111 (2012)
Liu, J., Yang, D., Yuan, W.: Littlewood-Paley characterizations of weighted anisotropic Triebel-Lizorkin spaces via averages on balls I. Z. Anal. Anwend. 38(4), 397–418 (2019)
Rauhut, H.: Wiener amalgam spaces with respect to quasi-Banach spaces. Colloq. Math. 109(2), 345–362 (2007)
Reiter, H., Stegeman, J.D.: Classical harmonic analysis and locally compact groups. London Mathematical Society Monographs, vol. 22. The Clarendon Press, Oxford University Press, New York (2000)
Romero, J.L., van Velthoven, J.T., Voigtlaender, F.: On dual molecules and convolution-dominated operators. J. Funct. Anal. 280(10), 57 (2021)
Rychkov, V.S.: On a theorem of Bui, Paluszyński, and Taibleson. Tr. Mat. Inst. Steklova 227(18), 286–298 (1999)
Schulz,E., Taylor,K. F.: Projections in \(L^1\)-algebras and tight frames. In Banach algebras and their applications, vol. 363 of Contemp. Math., pp 313–319. Amer. Math. Soc., Providence, RI (2004)
Stein, E.M.: Singular integrals and differentiability properties of functions, vol. 30. Princeton University Press, Princeton, NJ (1970)
Strömberg, J.-O., Torchinsky, A.: Weighted Hardy spaces. Lecture Notes in Mathematics, vol. 1381. Springer-Verlag, Berlin (1989)
Ullrich, T.: Continuous characterizations of Besov-Lizorkin-Triebel spaces and new interpretations as coorbits. J. Funct. Spaces Appl. 47, 163213 (2012)
Van Velthoven,J. T., Voigtlaender,F.: Coorbit spaces and dual molecules: the quasi-Banach case. Preprint. arXiv:2203.07959 (2022)
Voigtlaender, F.: Embedding theorems for decomposition spaces with applications to wavelet coorbit spaces. RWTH Aachen University, Germany (2015)
Zaanen,A. C.: Integration. North-Holland Publishing Co., Amsterdam Interscience Publishers John Wiley & Sons, Inc., New York (1967)
Acknowledgements
S. K. was supported by project I 3403 of the Austrian Science Fund (FWF). J.v.V. gratefully acknowledges support from the Austrian Science Fund (FWF) project J-4445. F. Voigtlaender acknowledges support by the German Research Foundation (DFG) in the context of the Emmy Noether junior research group VO 2594/1–1.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Karlheinz Gröchenig.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Koppensteiner, S., van Velthoven, J.T. & Voigtlaender, F. Anisotropic Triebel-Lizorkin spaces and wavelet coefficient decay over one-parameter dilation groups, II. Monatsh Math 201, 431–464 (2023). https://doi.org/10.1007/s00605-023-01824-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-023-01824-3
Keywords
- Anisotropic Triebel-Lizorkin spaces
- Maximal functions
- Anisotropic wavelet systems
- Coorbit molecules
- Frames
- Riesz sequences
- One-parameter groups



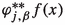 is finite for some
is finite for some