Skip to main content
SpringerLink
Log in

On curvature of surfaces immersed in normed spaces

  • Published:
Monatshefte für Mathematik Aims and scope Submit manuscript

Abstract

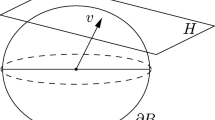
The normal map given by Birkhoff orthogonality yields extensions of principal, Gaussian and mean curvatures to surfaces immersed in three-dimensional spaces whose geometry is given by an arbitrary norm and which are also called Minkowski spaces. The relations of this setting to the field of relative differential geometry are clarified. We obtain characterizations of the Minkowski Gaussian curvature in terms of surface areas, and respective generalizations of the classical theorems of Huber, Willmore, Alexandrov, and Bertrand–Diguet–Puiseux are derived. A generalization of Weyl’s formula for the volume of tubes and some estimates for volumes and areas in terms of curvature are obtained, and in addition we discuss also two-dimensional subcases of the results in more detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alonso, J., Martini, H., Wu, S.: On Birkhoff orthogonality and isosceles orthogonality in normed linear spaces. Aequationes Math. 83, 153–189 (2012)

    Article  MathSciNet  Google Scholar 

  2. Balestro, V., Martini, H., Shonoda, E.: Concepts of curvatures in normed planes. Expos. Math. 37(4), 247–281 (2019)

    MathSciNet  MATH  Google Scholar 

  3. Balestro, V., Martini, H., Teixeira, R.: Differential geometry of immersed surfaces in three-dimensional normed spaces. Preprint, arXiv:1707.04226v2 (2017)

  4. Balestro, V., Martini, H., Teixeira, R.: Some topics in differential geometry of normed spaces, to appear in Adv. Geom.. arXiv:1709.01399 (2017)

  5. Balestro, V., Martini, H., Teixeira, R.: Surface immersions in normed spaces from the affine point of view. Geom. Dedic. 201, 21–31 (2019)

    Article  MathSciNet  Google Scholar 

  6. Barthel, W., Kern, U.: Affine und relative Differentialgeometrie. In: Giering, O., Hoschek, J. (eds.) Geometrie und ihre Anwendungen, pp. 283–317. Hanser, München (1994)

    MATH  Google Scholar 

  7. Busemann, H.: The geometry of Finsler spaces. Bull. Am. Math. Soc. 56, 5–16 (1950)

    Article  MathSciNet  Google Scholar 

  8. Duschek, A.: Über relative Flächentheorie, Sitzungsber, Akad. Wiss. Wien135, Abt. IIa, pp. 1–8 (1926)

  9. Guggenheimer, H.: Pseudo–Minkowski differential geometry. Ann. Mat. Pura Appl. 70(4), 305–370 (1965)

    Article  MathSciNet  Google Scholar 

  10. Horváth, Á.G.: Premanifolds. Note Mat. 31(2), 17–51 (2011)

    MathSciNet  MATH  Google Scholar 

  11. Horváth, Á.G.: Semi-indefinite inner product and generalized Minkowski spaces. J. Geom. Phys. 60, 1190–1208 (2010)

    Article  MathSciNet  Google Scholar 

  12. Li, P.: Geometric Analysis, Cambridge Studies in Advanced Mathematics, vol. 134. Cambridge University Press, Cambridge (2012)

    Book  Google Scholar 

  13. Martini, H., Swanepoel, K.J.: Antinorms and Radon curves. Aequ. Math. 72(1–2), 110–138 (2006)

    Article  MathSciNet  Google Scholar 

  14. Martini, H., Swanepoel, K.J.: The geometry of Minkowski spaces–a survey. Part II, Expos. Math. 22, 93–144 (2004)

    MathSciNet  MATH  Google Scholar 

  15. Martini, H., Swanepoel, K.J., Weiss, G.: The geometry of Minkowski spaces–a survey. Part I, Expos. Math. 19, 97–142 (2001)

    Article  MathSciNet  Google Scholar 

  16. Minkowski, H.: Geometrie der Zahlen. Teubner, Leipzig (1896)

    MATH  Google Scholar 

  17. Müller, E.: Relative Minimalflächen. Monatsh. Math. 31, 3–19 (1921)

    Article  MathSciNet  Google Scholar 

  18. Nomizu, K., Sasaki, T.: Affine Differential Geometry, Cambridge Tracts in Mathematics, vol. 111. Cambridge University Press, Cambridge (1995)

    Google Scholar 

  19. Rund, H.: Zur Begründung der Differentialgeometrie der Minkowskischen Räume. Arch. Math. 3, 60–69 (1952)

    Article  MathSciNet  Google Scholar 

  20. Sangwine-Yager, J. R.: Mixed volumes. In: Handbook of Convex Geometry, Vol. A, pp. 43-71, North-Holland, Amsterdam (1993)

  21. Schneider, R.: Convex Bodies: The Brunn-Minkowski Theory, Second expanded edition. Encyclopedia of Mathematics and its Applications, vol. 151, Cambridge University Press, Cambridge (2014)

  22. Schneider, R.: Differentialgeometrie im Grossen, I. Math. Z. 101, 375–406 (1967)

    Article  MathSciNet  Google Scholar 

  23. Shirokov, P.A., Shirokov, A.P.: Affine Differentialgeometrie. B. G. Teubner, Leipzig (1962)

    MATH  Google Scholar 

  24. Simon, U., Schwenk-Schellschmidt, A., Viesel, H.: Introduction to the Affine Differential Geometry of Hypersurfaces. Science University Tokyo (1991)

  25. Spivak, M.: A Comprehensive Introduction to Differential Geometry, vol. II. Publish or Perish Inc, Wilmington (1979)

    MATH  Google Scholar 

  26. Süss, W.: Zur relativen Differentialgeometrie I: Über Eilinien und Eiflächen in der elementaren und affinen Differentialgeometrie. Jap. J. Math. 4, 57–75 (1927)

    Article  Google Scholar 

  27. Süss, W.: Zur relativen Differentialgeometrie V: Über Eihyperflächen im \(R^{n+1}\). Tôhoku Math. J. 31, 202–209 (1929)

    MATH  Google Scholar 

  28. Thompson, A.C.: Minkowski Geometry, Encyclopedia of Mathematics and Its Applications, vol. 63. Cambridge University Press, Cambridge (1996)

    Google Scholar 

  29. White, B.: Complete surfaces of finite total curvature. J. Differ. Geom. 26, 315–326 (1987)

    Article  MathSciNet  Google Scholar 

  30. Witt, R.: Eine relativgeometrische Erweiterung der affinen Flächentheorie. Compos. Math. 1, 429–447 (1935)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Instituto de Matemática e Estatística, Universidade Federal Fluminense, Niterói, 24210201, Brazil

    Vitor Balestro & Ralph Teixeira

  2. Fakultät für Mathematik, Technische Universität Chemnitz, 09107, Chemnitz, Germany

    Horst Martini

Authors
  1. Vitor Balestro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Horst Martini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ralph Teixeira
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vitor Balestro.

Additional information

Communicated by Andreas Cap.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Balestro, V., Martini, H. & Teixeira, R. On curvature of surfaces immersed in normed spaces. Monatsh Math 192, 291–309 (2020). https://doi.org/10.1007/s00605-020-01394-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00605-020-01394-8

Keywords

Mathematics Subject Classification

Search

Navigation