Hydraulic Fracture Propagation in Layered Heterogeneous Rocks with Spatially Non-Gaussian Random Hydromechanical Features

Abstract

This study proposes a stochastic method to analyse the propagation of hydraulic fractures affected by layered heterogeneity in rocks in a toughness-dominated regime. The study utilises the phase-field method in the context of two-dimensional finite element analysis to model the hydraulic fracture (HF) propagation in rock materials in laboratory scale. Field data on hydrogeologic properties of some rocks reveal that material heterogeneity may appear in the form of leptokurtic marginal distributions. Generalised sub-Gaussian (GSG) model is capable of capturing physical characteristics of such rocks, and it is employed to stochastically model rocks with layered lithologic heterogeneity by generating a large number of auto- and cross-correlated random fields for hydro-geomechanical properties. To investigate the sensitivity of the cracking response to the inherent characteristics of material heterogeneity, various GSG distribution forms are considered in Monte Carlo (MC) analyses. The HF’s deviation from the theoretically predicted direction, which is perpendicular to the direction of the minimum in situ stress, is correlated with the distribution of hydro-geomechanical properties, showing a Gaussian-type distribution. This study concludes that the differential stress and the bedding orientation are the main factors affecting the HF deviation and the required breakdown pressure for initiating the HF propagation from a borehole. In the application of directional hydraulic fracturing (DHF), the effect of bedding layers becomes dominant when the bedding orientation is aligned with the direction of perforations in the boreholes.

Highlights

• The phase-field theory in the context of finite element method is employed for stochastic analysis of toughness-dominated hydraulic fracture propagation in layered heterogeneous rocks.

• Generalised sub-Gaussian random fields are generated to model the natural hydromechanical features in heterogeneous rocks.

• By order of importance, differential stress, i.e. the difference between maximum and minimum in situ stresses, and the bedding orientation are found to be the main factors in specifying the hydraulic fracture propagation path in layered heterogeneous rocks.

• Hydraulic fracture trajectories from perforated boreholes are mainly influenced by the orientation of the heterogeneous bedding layers with respect to the direction of the maximum in situ stress.

1 Introduction

Hydraulic fracturing is a well-established technique used for stimulating unconventional resources, exploitation of geothermal energy, geological carbon storage (Pan et al 2016), and cave mining (He et al 2016). However, the application of this technique includes several challenges in terms of the direction and extent of the driven hydraulic fracture (HF) into geological formations (Fisher and Warpinski 2012). This poses risks such as groundwater aquifer contamination, fault re-activation and induced seismicity, and carbon or fossil fuel leakage into shallow subsurface layers through fault zones and natural fractures. While the in situ stress field is the primary factor determining the dominant direction of HF propagation, other factors such as the presence of pre-existing faults and joints (Lecampion et al 2018) and inherent geological heterogeneity (Kissinger et al 2013) in hydromechanical characteristics of rocks can affect the cracking behaviour and the HF trajectories.

In cave mining technology, directional hydraulic fracturing (DHF) has been widely used to re-orient the propagation path of the HF for mining and cutting purposes (He et al 2016). DHF is achieved by making directional perforations in boreholes and planting fluid-pressurised boreholes to direct the HF along the desired paths (Bai et al 2020). Similarly, in the stimulation of gas resources in unconventional reservoirs, designing directional wells and inclined perforations with respect to the maximum horizontal principal stress direction while accounting for the geological structure and the inherent heterogeneity of the host rock can enhance the productivity and efficiency of operations (Bentley et al 2013). The change in perforation angle affects the required pressure for initiating the HF from the borehole (Liu et al 2020).

The extent and rate of growth of the HF are primarily influenced by mechanical properties of the host rock, the in situ stress field, and the fluid pressure inside the HF. However, the data obtained from fracture-mapping technologies in unconventional reservoirs provide evidence of the presence of lithologic heterogeneities, such as variations in hydromechanical properties of layers, can cause possible arrest or deviation of the HF (Brenner and Gudmundsson 2004; Fisher and Warpinski 2012); also, experimental observations indicate that such heterogeneity can lead to formation of more complex HF trajectories (Suarez-Rivera et al 2013). Transverse heterogeneity of the elastic properties of layers in tight gas shale formations causes a variation in the stress concentration in different layers and usually makes it more difficult for the HF to propagate perpendicular to the layers (Suarez-Rivera et al 2006). Complexities in the developed fracture network and T-shaped fractures may emerge because of the presence of bedding planes, lithologic interfaces, and mineralised fractures, which are also categorised as lithologic heterogeneities in rocks (Suarez-Rivera et al 2013).

The effective permeability of the geologic formations in unconventional reservoirs is dependent on the lithologic heterogeneity and bedding planes (Jensen et al 1987), and it is known that the permeability is an anisotropic property due to the porosity evolution and sedimentation over time, which is usually higher in the direction parallel to the layers (Zhang and Scherer 2012). This feature can affect the HF propagation by changing the effective stress field (Sesetty and Ghassemi 2016), easing the tensile failure of the porous rock in the direction parallel to the beddings. It is well known that the permeability and the elastic modulus follow opposing trends with respect to the variation of porosity in rocks (Bernabé et al 2003; Yang and Aplin 2010), so considering the correlation between hydraulic and mechanical properties would help to model the hydromechanical behaviour of heterogeneous rocks subjected to hydraulic fracturing more realistically. It can be understood from laboratorial data of Brazilian disk and semicircular bending tests on layered rock samples that material properties such as tensile strength and fracture toughness can be dependent on the bedding orientation (Nejati et al 2019; Tavallali and Vervoort 2010), and the crack-path can be diverted into the direction of bedding layers because the failure will be more favourable along the bedding layers rather than perpendicular to them (Mousavi Nezhad et al 2018a; Vervoort et al 2014). The effect of material heterogeneity on the tortuosity of HF trajectories is more profound in toughness-dominated propagation regime, compared to viscosity or leak-off-dominated regimes (Santillán et al 2017; Huang et al 2019).

In the context of numerical modelling of fracture propagation in heterogeneous rocks, the sources of heterogeneity have been considered as either (i) randomly distributed discontinuities embedded in a continuum or as (ii) spatial variation of material properties over the domain of interest. Consideration of discontinuities as joints and fissures includes modelling the interaction between a propagating HF with pre-existing joints, and the resulted trajectories contain kinking, offsetting, branching, and considerable deviation from the theoretical crack-path trajectory that is perpendicular to the direction of the least principal stress (Zhang et al 2021). The HF trajectories resulting from the first group contain the most tortuosity because no meaningful pattern can be found in the material properties. The second approach, on which the current study concentrates, models the heterogeneities by spatially distributing material properties as random fields over the computational mesh, resulting in smooth spatial distributions of material properties. Numerical studies have previously modelled material heterogeneities by distributing randomly generated properties over the elements in three general patterns depending on the nature of the rock: (i) totally random with no auto-correlation, for example (Chen et al 2018; He et al 2021; Li et al 2016a; Li et al 2021; Sarmadi and Mousavi Nezhad 2021; Lu and He 2020; Men et al 2013; Pakzad et al 2018; Santillán et al 2017; Wang et al 2009); (ii) spatially correlated (auto-correlated) as stiff bulk inclusions (Li et al 2020, 2021; Tang et al 2018; Xia et al 2017); (iii) layered lithologic settings through use of anisotropic autocorrelation (Mousavi Nezhad et al 2018a, b; Li et al 2020, 2021).

Continuum-based fracture models can be recognised as the most widely used approaches in heterogeneous materials due to their inherent versatility in numerical implementation (Li et al 2016a; Li et al 2020; Li et al 2021; Lu and He 2020; Men et al 2013; Pakzad et al 2018; Santillán et al 2017; Xia et al 2017). Consideration of rock heterogeneity has been mainly of interest in studying the vertical fracture growth height in unconventional reservoirs (Li et al 2016a, 2020; Tang et al 2018) to look for possible arrests and possible fracture containment as well as in identifying its random effects on the HF trajectory (Chen et al 2018; He et al 2021; Men et al 2013; Pakzad et al 2018; Santillán et al 2017). Increasing the degree of heterogeneity in rocks usually results in lowering the breakdown pressure to initiate the HF propagation from the point of fluid injection (Li et al 2016a, 2020; Pakzad et al 2018). Although, making general conclusions regarding the failure (Ma et al 2022a, 2022b) and fracture development (Gironacci et al 2018; Santillán et al 2017) in geomaterials requires conducting extensive Monte Carlo (MC) analyses. Studying the HF propagation under the effects of various controlling factors in rocks with such layered lithologic heterogeneity requires employing an appropriate approach capable of generating cross-correlated material properties (Tang et al 2018; Li et al 2020). Although Gaussian distributions have traditionally been used to model heterogeneity of geological formations, some studies have shown that subsurface heterogeneity is more complex than what can be captured by a simple Gaussian probability distribution function (Haslauer et al 2012; Siena et al 2020). Guadagnini et al (2018) provided evidence of hydrogeologic properties of geomaterials exhibiting slightly leptokurtic marginal distributions and introduced a generalised sub-Gaussian (GSG) model to capture the possible excess kurtosis in the distributions of heterogeneous material properties of rocks.

In this paper, a continuum finite element-based phase-field method is employed to model the HF propagation in porous rocks containing layered lithologic heterogeneity. Such rocks are modelled by generating auto- and cross-correlated random fields using Gaussian and generalised sub-Gaussian (GSG) probability distribution functions. In the context of finite element analysis, the consideration of material heterogeneity is included by assigning the random fields (hydrogeological properties) to the Gauss integration points in layered forms with no distinct boundary between the layers to replicate the natural characteristics of rocks. To understand the underlying effects of modelling heterogeneous materials using the GSG model, the results of hydraulic fracture propagation in GSG-based heterogeneous layered rocks are compared to the results taken from the models in which material heterogeneity follows the well-known Gaussian distribution. The random fields are generated for the elastic young modulus, tensile strength, critical energy release rate, porosity, and permeability. In the developed framework of this study for generating heterogeneous material properties, the layered form of heterogeneities is built based on setting different values of the correlation length in two directions (perpendicular and parallel to the layers) for defining spatial correlation between neighbouring points in the finite element mesh structure. MC analysis is conducted by generating more than one thousand realisations of cross-correlated material properties for each modelling scenario to quantify the effects of layered heterogeneity and bedding orientation. The analyses are performed for several configurations by varying the input parameters, including the in situ stresses, perforation angle, and bedding orientation to find the critical configurations where the effects due to heterogeneous layering may significantly change the circumstances for the HF propagation. Eventually, extensible conclusions are made from the results of MC simulations to provide useful information and recommendations for engineering applications of hydraulic fracturing operations in layered heterogeneous rocks.

2 Modelling Hydraulic Fractures in Heterogeneous Media

We benefit from a gradient-type continuum damage model, known as the phase-field method, to model HF propagation in heterogeneous media. This approach is implemented within a finite element framework, using a continuous mesh structure. The phase-field method enables us to accurately model the propagation of failure and fracture in heterogeneous media (Gironacci et al 2018; Mousavi Nezhad et al 2018a, b; Na et al 2017; Xia et al 2017), This is because the method allows for the spatial distribution of material heterogeneity across the Gauss integration points in the elements. In the following sections, we introduce the mathematical formulations and numerical algorithms for modelling HF propagation using this method, as well as our approach for generating hydrogeological properties in layered forms.

2.1 Phase-Field Method

According to Griffith’s theory on the development of fractures within solids, a certain amount of the strain energy stored inside the body must be consumed so that new surfaces can be created. A saturated porous medium ($\Omega$) may undergo deformations and variation of the stored fluid mass inside the pores. These hydromechanical changes will affect the energy level in $\Omega$, stored in both the solid skeleton and the pore fluid. If the stored strain energy of the solid skeleton reaches a certain level, new surfaces may develop within the volume at a certain rate of ${G}_{c}$, so-called the critical energy release rate. The creation of new fractures causes the expansion and coalescence of the pores, which will again affect the fluid movement and de-pressurisation in the pore fluid. The propagation of the HF in saturated porous media can be viewed as a coupled multi-field problem, where the energy is dissipated through an energy minimisation process. In this process, the released energy can be quantified using an integral expression as ${\Psi }_{{\text{surface}}}={\int }_{\Gamma }{G}_{c}dA$, where $\Gamma$ is the boundary domain of the new surfaces embedded in the volume. Using the phase-field method in modelling fractures, the fracture boundary ($\Gamma$) can be defined over the entire volume ($\Omega$) by defining an energy density functional and assuming the sharp fracture as a smeared damage zone (Francfort and Marigo 1998).

$${\Psi }_{{\text{surface}}}={G}_{c}{\int }_{\Omega }\gamma \left(d,\nabla d\right) dV={G}_{c}{\int }_{\Omega }\left[\frac{{l}_{0}}{2}{\left|\nabla d\right|}^{2}+\frac{1}{2{l}_{0}}{\left(1-d\right)}^{2}\right]dV,$$

(1)

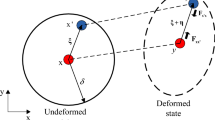
where $d$ is the phase-field (damage) scalar varying between zero (fully damaged condition) and unity (the intact condition), see Fig. 1, and $\gamma \left(d,\nabla d\right)$ is the so-called surface energy density functional. Fractures are formed throughout the body under the effect of deformations which may cause failure in the solid skeleton. Deformations cause the accumulation of the elastic strain energy in the solid skeleton which can provide the driving force for the fracture to propagate. The strain energy in the solid skeleton can be formulated based on the strains (${\varvec{\varepsilon}}$) as (Bonet and Wood 2008)

$${\Psi }_{{\text{solid}}}\left({\varvec{\varepsilon}}\right)=\frac{\lambda }{2}{\left({\text{tr}}\left[{\varvec{\varepsilon}}\right]\right)}^{2}+\mu {\text{tr}}\left[{{\varvec{\varepsilon}}}^{2}\right],$$

(2)

where ${\varvec{\varepsilon}}=1/2\left(\nabla {\varvec{u}}+{\nabla }^{{\text{T}}}{\varvec{u}}\right)$ is the strain tensor, and ${\varvec{u}}$ is the displacement field of the solid skeleton.

Fig. 1

Illustration of the diffusive damage zone and the variation of the damage parameter ($d$) from the centre line of the fracture for different values of the length-scale parameter ${l}_{0}$

2.2 Modelling Hydraulic Fracture Propagation in Porous Media

The HF propagation in saturated porous media is modelled by coupling the phase-field damage model to a hydromechanical model representing the poroelastic behaviour of the rock.

2.2.1 Governing Equations of the Hydromechanical Model

The initial mass of a unit volume element $dV$ in the body $\Omega$, which consists of solid and fluid phases ($dV=d{V}_{{\text{s}}}+d{V}_{{\text{f}}}$), is calculated as ${m}_{0}={\rho }_{{\text{s}}}{\varphi }_{0}^{{\text{s}}}+{\rho }_{{\text{f}}}{\varphi }_{0}^{{\text{f}}}$, where the porosity is ${\varphi }_{0}^{{\text{f}}}=d{V}_{{\text{f}}}/dV$. When the body undergoes hydromechanical loading, stresses will be developed in the element, and the balance of linear momentum must hold as.

$$\nabla \cdot \sigma + \left( {m_0 + m} \right)g = 0$$

(3)

where ${\varvec{\sigma}}$ is the Cauchy stress tensor, $m$ is the change in the fluid mass in the element, and ${\varvec{g}}$ is the gravity. Following Biot’s theory (Biot 1941), the Cauchy stress is defined as the summation of the effective Cauchy stress (${{\varvec{\sigma}}}{\prime}$) affecting the solid skeleton and the hydrostatic fluid pressure ($p)$ in the pores.

$$\sigma = g\left( d \right)\sigma ^{\prime} - \left( {\alpha _{\text{b}} } \right)pI.$$

(4)

The effective stress is multiplied into a degradation function $g\left(d\right)={d}^{2}+{\kappa }_{\epsilon }$ to reflect the effect of damage in the element, where ${\kappa }_{\varepsilon }\ll 1$ is the regularisation parameter (Francfort and Marigo 1998). Biot coefficient ${\alpha }_{{\text{b}}}$ is defined as $1-K/{K}_{{\text{s}}}$, where $K$ is the drained bulk modulus of the rock skeleton and ${K}_{{\text{s}}}$ is the bulk modulus of the solid constituents (Detournay and Cheng 1993).

The total mass conservation in the saturated porous body, Eq. (5), must hold in the process of deformation and the fluid flow as

$$\left( {\alpha _{\text{b}} } \right)\dot{\varepsilon }_{\text{v}} + \nabla \cdot v^{\text{r}} + \dot{p}/M_{\text{b}} = 0,$$

(5)

where ${{\varvec{v}}}^{{\text{r}}}={\varphi }^{{\text{f}}}\left({{\varvec{v}}}_{{\text{f}}}-{{\varvec{v}}}_{{\text{s}}}\right)$ is the relative superficial velocity of the fluid phase, ${{\varvec{v}}}_{{\text{f}}}$ and ${{\varvec{v}}}_{{\text{s}}}$ are the intrinsic velocities of the fluid and solid phases, respectively, and ${\dot{\varepsilon }}_{{\text{v}}}$ is the volumetric strain rate of the solid skeleton. Biot’s modulus ${M}_{{\text{b}}}$ is defined as ${M}_{{\text{b}}}={\alpha }_{{\text{b}}}^{2}\left({K}_{{\text{u}}}-K\right)$, where parameters $K$ and ${K}_{{\text{u}}}$ are experimentally measured values of the drained and undrained bulk moduli of the rock (Detournay and Cheng 1993). For modelling the fluid flow throughout the pore network, Darcy’s law is employed as

$$v^{\text{r}} = - k \cdot \left( {\nabla p - \rho _{\text{f}} g} \right),$$

(6)

where ${{\varvec{v}}}^{{\text{r}}}$ is the fluid velocity relative to the solid motion, ${\varvec{k}}=\left(\overline{k }/{\mu }_{{\text{f}}}\right){\varvec{I}}$ is the symmetric permeability tensor, ${\mu }_{{\text{f}}}$ is the dynamic viscosity of the fluid, and $\overline{k }$ is the intrinsic permeability of the porous material.

2.2.2 Weak Forms of the Hydromechanical Model

Employing a continuous Galerkin method with the weighting function ${\varvec{\eta}}$ and applying natural boundary conditions, shown in Fig. 2, the weak form of the balance of linear momentum can be obtained as

$$\int_\Omega {\nabla \eta :g(d){\mathbb{C}}:\nabla u\;dV - } \,\int_\Omega {(\alpha_b )} p(\nabla \cdot \eta )\;dV - \int_\Omega {\eta \cdot pg\;dV - \int_{\partial \Omega \sigma } {\eta \cdot T^* dA\; = \;0} }$$

(7)

Fig. 2

Dirichlet and Neumann boundary conditions for the three-field problem: displacements (${\varvec{u}}$), pore fluid pressure ($p$), and damage ($d$)

where ${{\varvec{T}}}^{*}$ is the surface stress on the Neumann boundary, ${\varvec{u}}$ is the displacement field of the solid skeleton, and ${\mathbb{C}}$ is the fourth-order elasticity tensor. Similarly, the second weak form to build the coupled ${\varvec{u}}$-$p$ formulation is derived from the total mass conservation law, choosing the weighting function $\psi$ as.

$$\int_\Omega \alpha _{\text{b}} \nabla \cdot \left( \psi \right)d{\text{V}} - {\text{ }}\int_\Omega {\nabla \psi \cdot v^r dV} + {\text{ }}\int_\Omega {\frac{{\dot{p}}}{{M_{\text{b}} }}\left( \psi \right)dV} - {\text{ }}\int_{\partial \Omega _q } {\psi qd{\text{a}} = 0}$$

(8)

where ${\varvec{q}}$ is the pre-defined flux on the Neumann boundaries. A monolithic solver based on the Newton–Raphson method is developed to satisfy Eqs. (7) and (8) and to solve for ${\varvec{u}}$ and $p$ iteratively in the finite element matrix forms of the linear system of equations.

2.2.3 Damage Evolution Model

Following the definition of the phase-field method for modelling fractures in Sect. 2.1, the development of fractures (in other words, the evolution of damage) throughout the body can be modelled by minimising the following energy functional $\Pi$ (Miehe et al 2010).

$$\Pi = \underbrace {\int_\Omega {g(d)\psi_{{\text{eff}}} (\varepsilon )} \;dV}_{{\text{degraded}}\;{\text{effective energy}}} + \;\underbrace {G_c \int_\Omega {\left[ {\frac{l_o }{2}\left| {\nabla d} \right|^2 + \frac{1}{2l_o }(1\; - \;d)^2 } \right]} \;dV}_{{\text{surface}}\;{\text{energy of the fractures}}}$$

(9)

Finding a stationary position of $\delta \Pi =0$ with respect to the arbitrary damage $\omega$ results in the weak form of the fracture evolution model as

$$\smallint _\Omega 2\frac{{\widehat{{\rm{\mathcal{H}}}}}}{{G_c }}\left( d \right)\omega dV + l_0 \smallint _\Omega \left( {\nabla \omega \cdot \nabla d} \right)dV - \smallint _\Omega \frac{{\left( {1 - d} \right)}}{{l_0 }}\omega dV = 0,$$

(10)

where $\widehat{\mathcal{H}}$ is a history field defined as the maximum strain energy developed in the solid element during the history of deformation. In the above weak form, where $\nabla d.n=0$ must hold on all the boundaries $\partial\Omega .$ The fracture driving force is identified by the scalar value $\widehat{\mathcal{H}}/{G}_{c}$. We follow the formulation presented by Miehe et al (2015) on defining the scalar history field $\widehat{\mathcal{H}}$ based on the principal effective stresses developed in the solid skeleton as

$$\widehat{{\rm{\mathcal{H}}}} = {\mathop {max}\limits_{{\rm{\mathcal{T}}} \in \left[ {0,t} \right]}} \left( {\left\langle {\sum_{i = 1}^3 {\frac{{\left\langle {\sigma ^{\prime}_i (\mathfrak{I})} \right\rangle _ + ^2 }}{{\sigma _t^2 }} - 1} } \right\rangle _ + \times \frac{{\sigma _t^2 }}{{2E^{\prime}}}} \right),$$

(11)

where $\mathcal{T}$ is the time from the start of the deformation until the current state of the body, ${\sigma }_{{\text{i}}}^{\mathrm{^{\prime}}}$ are the principal effective stresses, ${E}^{\mathrm{^{\prime}}}=\mu \left(2\mu +3 \lambda \right)/\left( \lambda +\mu \right)$ is the effective young modulus, and ${\sigma }_{{\text{t}}}$ is the tensile strength of the material (Miehe et al 2015).

2.2.4 Modelling Fluid Flow Within the Fracture

The well-known Poiseuille’s law for modelling flow between parallel surfaces is coupled with Darcy’s law, Eq. (6), by changing the permeability tensor to ${{\varvec{k}}}_{{\text{crack}}}=\left({w}^{2}/12{\mu }_{{\text{f}}}\right){\varvec{I}}$ for the cracked zone, where $w$ is the crack width and is defined as (Sarmadi and Mousavi Nezhad 2023)

$$w=\frac{\nabla d \cdot {\varvec{\varepsilon}} \cdot {\nabla }^{T}d}{{\left|\nabla d\right|}^{2}}{L}_{\perp },$$

(12)

where ${\varvec{\varepsilon}}$ is the elemental strain tensor, and ${L}_{\perp }$ is the characteristics length perpendicular to the diffusive fracture which is typically considered equal to the element size ${H}_{{\text{el}}}$ (Mauthe and Miehe 2017). Calculating the fluid flow in the manner presented requires having a sufficiently fine mesh around the diffusive fracture, so a mesh refinement algorithm is used to ensure the correct estimation of the crack width. Based on the results of mesh sensitivity analysis and the recommendations of other studies (Miehe et al. 2010; Sarmadi et al. 2023), the acceptable element size is set as ${H}_{{\text{el}}}<{l}_{0}/4$.

2.3 Modelling Rocks with Layered Lithologic Heterogeneity

The HF propagation in rocks can be significantly affected by hydrogeologic material properties, of which often limited datasets are available. Scarcity of data results in high uncertainty of the estimated hydrogeological material properties, which transfers through the HF model, resulting in high uncertainty of the model solutions. To evaluate the uncertainty in model predictions caused by random inputs, MC analyses will be conducted for multiple test cases. Traditionally, hydrogeologic properties have been modelled as Gaussian random fields; however recently, Guadagnini et al. (Guadagnini et al 2018) presented evidence of these properties having heavy-tailed distributions (i.e. positive excess kurtosis). As such, the input material properties will be modelled as the recently introduced generalised sub-Gaussian model (GSG) (Riva et al 2015). The framework we have described enables us to incorporate stochastic variability in material properties by auto-correlating these properties in space, which accounts for spatial distribution trends. Furthermore, certain properties can be cross-correlated with others to more accurately represent the complex heterogeneity of rocks. To model such heterogeneity, we generate the following material properties as random fields using probability density functions (PDF): (i) porosity ${\varphi }^{{\text{f}}}$; (ii) intrinsic permeability $\overline{k }$; (iii) elastic Young’s modulus $E$; (iv) Griffith’s fracture energy ${G}_{c}$; (v) tensile strength ${\sigma }_{{\text{t}}}$. These properties are set to be cross-correlated, according to empirical relationships and datasets, and are distributed spatially over the Gauss integration points within the finite element mesh, which will be explained in Sect. 3.

2.3.1 Autocorrelated Generalised Sub-Gaussian Random Fields

The hydrogeological properties of heterogeneous rocks are typically modelled as spatial stochastic random fields, since scarcity of data at sites of interest restrict the use of the deterministic properties. A wide range of statistical models can be used to capture the statistical behaviour of each hydrogeological property and thus specific datasets must be analysed to determine the most appropriate stochastic model. Within this research, the simulations will not be conditioned on a single dataset from a site of interest; however, it is still important to use statistical models which capture the typically observed characteristics of each property. For example, hydraulic permeability measurements of rock (e.g. sandstone and limestone) typically exhibit a log-normal distribution and are correlated with porosity (Jensen et al 1987). However, recent research works have found evidence from documented rock datasets that hydrogeological properties such as porosity (Painter 1996) and permeability (Riva et al 2013) may exhibit leptokurtic distributions and concurrently leptokurtic incremental behaviour in the distributions of the relevant measurements (Guadagnini et al 2018). Consider the distribution of the measurements of a material property $Y$; the increments, which are the variation of the material property between two points, are defined as $\Delta Y=Y\left({x}_{{\text{i}}}\right)-Y\left({x}_{{\text{i}}}+h\right)$, where ${x}_{{\text{i}}}\in\Omega$ is the spatial position vector of the i-th point in the domain ($\Omega$) and $h$ is the separation distance from the same point. According to (Riva et al 2015), incremental distributions tend to exhibit a highly leptokurtic nature at small separation distance ($h$). However, as the scale increases, the distributions tend to approach Gaussian behaviour, though they never fully conform to a pure Gaussian distribution. This implies that the statistical properties of the increment distributions change as the scale increases, highlighting the importance of choosing an appropriate model to accurately capture the spatial variability of the material properties. The GSG model concurrently captures the documented leptokurtic behaviour of both the material property distributions and their increments. The GSG model is introduced by Riva et al (2015) as

$$Y^{\prime} = U\left( {x_{\text{i}} } \right)G\left( {x_{\text{i}} } \right),$$

(13)

where $U$ is a random function in space (the so-called subordinator), which is shown in Fig. 3 and is independent of $G\left({x}_{{\text{i}}}\right)$, consisting of independent and identically distributed (iid) non-negative values at all points ${x}_{{\text{i}}}$. The function $G$ is a zero mean Gaussian random field, also shown in Fig. 3, having a designated auto-covariance function ${C}_{{\text{G}}}=\mathrm{\rm E}\left[G\left({x}_{{\text{i}}}\right)G\left({x}_{{\text{j}}}\right)\right]$, where the operator $\mathrm{\rm E}\left[X\right]$ is the expectation of random variable $X$. By definition, the mean of ${Y}{\prime}$ is zero (${\overline{\mu }}_{{Y}{\prime}}=0$); thus, to model the hydrogeological properties as random GSG fields, the mean value must be shifted via $Y\left({x}_{{\text{i}}}\right)={Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{i}}}\right)+{\overline{\mu }}_{{\text{Y}}}$, where ${\overline{\mu }}_{{\text{Y}}}$ is the target mean value of the desired hydrogeological property. Given that $U$ is independent of $G$, the auto-covariance function of the random GSG field (${Y}{\prime}$) between any two neighbouring points (${x}_{{\text{i}}},{x}_{{\text{j}}}$) is defined as

$$\mathrm{\rm E}\left[{Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{i}}}\right){Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{j}}}\right)\right]=\mathrm{\rm E}\left[\left[U\left({x}_{{\text{i}}}\right)G\left({x}_{{\text{i}}}\right)\right]\left[U\left({x}_{{\text{j}}}\right)G\left({x}_{{\text{j}}}\right)\right]\right]= \mathrm{\rm E}\left[U\left({x}_{{\text{i}}}\right)U\left({x}_{{\text{j}}}\right)\right]\mathrm{\rm E}\left[G\left({x}_{{\text{i}}}\right)G\left({x}_{{\text{j}}}\right)\right],$$

(14)

where

Fig. 3

PDFs of Gaussian random field $G\left({x}_{{\text{i}}}\right)$, log-normal subordinator $U\left({x}_{{\text{i}}}\right)$, and GSG random field ${Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{i}}}\right)$; note that ${\overline{\mu }}_{{\text{G}}}$= 0, ${\sigma }_{{\text{G}}}$=1, and the subordinator parameter is set to $\alpha$=1.5

$$\begin{array}{cc}\mathrm{\rm E}\left[{Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{i}}}\right){Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{j}}}\right)\right]=\mathrm{\rm E}\left[{U\left({x}_{{\text{i}}}\right)}^{2}\right]{C}_{{\text{G}}}\left(0\right)& {x}_{{\text{i}}}={x}_{{\text{j}}}\\ \mathrm{\rm E}\left[{Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{i}}}\right){Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{j}}}\right)\right]=\mathrm{\rm E}\left[U\left({x}_{{\text{i}}}\right)\right]\mathrm{\rm E}\left[U\left({x}_{{\text{j}}}\right)\right]{C}_{{\text{G}}}\left(\left|{x}_{{\text{j}}}-{x}_{{\text{i}}}\right|\right)& {x}_{{\text{i}}}\ne {x}_{{\text{j}}}\end{array}.$$

(15)

Observe that if$\mathrm{\rm E}\left[{U}^{2}\right]\ne \mathrm{\rm E}{\left[U\right]}^{2}$, the corresponding variogram exhibits a discontinuity at zero lag (when${x}_{{\text{i}}}={x}_{{\text{j}}}$), typically known as the so-called “nugget effect”. Following documented data evidence in Guadagnini et al (2018), in this work we assume $U\left({x}_{{\text{i}}}\right)$ to be log-normally distributed as${\text{lnN}}\left(0,{\left(2-\alpha \right)}^{2}\right)$, where $\alpha$ is the so-called “subordinator-parameter”, and the Gaussian auto-covariance function (${C}_{{\text{G}}}$) is defined as an exponential form${C}_{{\text{G}}}={\sigma }_{{\text{G}}}^{2}{e}^{-\left|{x}_{{\text{i}}}-{x}_{{\text{j}}}\right|/{l}_{{\text{G}}}^{k}}$, where ${\sigma }_{{\text{G}}}^{2}$ is the variance of the Gaussian random field ($G$), and ${l}_{{\text{G}}}^{k}$ is the autocorrelation length scale of the field $G\left({x}_{{\text{i}}}\right)$ in the $k$-direction. Using Eq. (15), the auto-covariance function of ${Y}^{\mathrm{^{\prime}}}\left({x}_{{\text{i}}}\right)$ is defined as.

$$\begin{array}{cc}{C}_{{{\text{Y}}}^{\mathrm{^{\prime}}}}({x}_{{\text{i}}}) ={e}^{{2\left(2-\alpha \right)}^{2}}{\sigma }_{{\text{G}}}^{2}& {x}_{{\text{i}}}={x}_{{\text{j}}}\\ {C}_{{{\text{Y}}}^{\mathrm{^{\prime}}}}({x}_{{\text{i}}},{x}_{{\text{j}}}) ={e}^{{\left(2-\alpha \right)}^{2}}{\sigma }_{{\text{G}}}^{2}{e}^{-\left|{x}_{{\text{i}}}-{x}_{{\text{j}}}\right|/{l}_{{\text{G}}}^{k}}& {x}_{{\text{i}}}\ne {x}_{{\text{j}}}\end{array}$$

(16)

This study aims to determine the influence of layered heterogeneity on the directional hydraulic fracturing. To generate layered heterogeneous media, the values of ${l}_{{\text{G}}}^{k}$ are set distinct values in the directions parallel and perpendicular to the bedding orientation, see Fig. 4. For instance, in two-dimensional analysis, the autocorrelation length scale in these two directions are ${l}_{{\text{G}}}^{1}$ and ${l}_{{\text{G}}}^{2},$ respectively, and a larger ratio of (${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}$) renders a sharper transition between the properties of any two adjacent layers.

Fig. 4

a, b The spatial distribution of a Gaussian distribution with mean value of zero and standard deviation of unity over a square domain for two different sets of ${l}_{{\text{G}}}^{k}$

2.3.2 Cross-Correlated Generalised Sub-Gaussian Random Fields

To implement cross-correlation between any two hydrogeological properties (${\text{m}},{\text{n}}$), e.g. porosity and permeability, an exponential cross-correlation function in the following form is used to generate multivariate normal random fields of the Gaussian random field $G\left({x}_{{\text{i}}}\right)$ in Eq. (13).

$${C}_{{G}_{{\text{m}},{\text{n}}}}\left({x}_{{\text{i}}},{x}_{{\text{j}}}\right)={\sigma }_{{{\text{G}}}_{{\text{m}}}}^{2}{\sigma }_{{{\text{G}}}_{{\text{n}}}}^{2}\left({\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}\right){e}^{-\left|{x}_{{\text{i}}}-{x}_{{\text{j}}}\right|/{l}_{{\text{G}}}^{k}.}$$

(17)

In the above equation, ${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$ is the cross-corelation coefficient between any two Gaussian random fields (${G}_{{\text{m}}}$ and ${G}_{{\text{n}}}$) at zero lag, and (${\sigma }_{{{\text{G}}}_{{\text{m}}}}^{2}$ and ${\sigma }_{{{\text{G}}}_{{\text{n}}}}^{2}$) are the values of variance for the relevant Gaussian random fields. Once the cross-correlated Gaussian fields ${G}_{{\text{m}}}\left({x}_{{\text{i}}}\right)$ are generated for each hydrogeological property, they can be implemented in Eq. (13) to subsequently generate cross-correlated GSG random fields. Note that the cross-correlation embedded in the Gaussian random fields will be dampened by multiplying the subordinator ($U$); nonetheless, a significant degree of cross-correlation will remain. As previously stated, the simulations within this investigation are not conditioned on a specific dataset at a given site of interest. However, the GSG model has been demonstrated to be sufficient in capturing the typical characteristics of hydrogeological properties (e.g. Guadagnini et al 2018 and Riva et al 2015). Within this investigation multiple test cases will be considered varying both the degree of heterogeneity, layering, as well as auto and cross-correlation to fully investigate the effects of the GSG model in HF propagation. Sections 3 and 4 document the parameter values utilised in the different test cases when generating the GSG hydrogeological property distributions for the HF simulations.

2.3.3 Numerical Algorithm

The matrix forms of the finite element weak forms presented in the previous section are implemented in a MATLAB code for the plane strain two-dimensional configuration using first-order triangular elements. The linear system of equations is solved using the built-in function “mldivide” in MATLAB. The implicit Newton–Raphson method is employed to solve for the coupled ${\varvec{u}}$-$p$ problem iteratively in discretised time steps.

In each time step (${t}_{{\text{n}}}$), the following stages are required to solve for the three-field problem (${{\varvec{u}}}_{{\text{n}}}, {p}_{{\text{n}}},{d}_{{\text{n}}}$). Notice that the global convergence of the numerical algorithm is based upon the convergence in the damage field, and $\upkappa$ refers to the iteration number in this scheme.

Applying Dirichlet and Neumann boundary conditions to form the vectors of external force and fluid mass flux.

Weak forms of the hydromechanical model, Eqs. (7) and (8), are first satisfied monolithically to solve for displacements and pore fluid pressure $\left( {{\bf{u}}_{\text{n}}^\kappa ,~\rho _{\text{n}}^\kappa } \right)$, assuming a fixed state of damage $d_{\text{n}}^{(\kappa - 1)}$. The convergence in both displacement and fluid pressure fields are checked using the relative convergence criterion between the values of two subsequent iterations. The iterative scheme solving for $\mu$ and p is separate from the global iterative scheme for the damage convergence with the iteration counter $(\kappa)$.

The history field $\widehat{{\rm{\mathcal{H}}}}$ is calculated using Eq. (11) based on the fixed state of displacement field resulted from (ii), i.e. staggered approach (Mauthe and Miehe 2017).

Damage evolution weak form, Eq. (10), is satisfied to solve for $d_{\text{n}}^\kappa$ using the constant value of $\widehat{{\rm{\mathcal{H}}}}$, which was updated in stage (iii).

The global damage convergence, which is based on the absolute convergence criterion, is checked by considering damage for two subsequent iterations $(\kappa ), (\kappa - 1)$ with an acceptable tolerance $\varepsilon _{\text{d}} \ll 1$. If $\left| {d_{\text{n}}^{(\kappa )} - d_{\text{n}}^{(\kappa - 1)} } \right| > \in _{\text{d}}$, then: $(\kappa = \kappa + 1)$ and go to (ii); otherwise, exit.

To increase the computational efficiency of the numerical code for the purpose of conducting MC simulations, a mesh refinement unit in charge of performing necessary refinements around the HF front is added to the algorithm after stage (iv). Having the mesh refinement unit ensures the independency of the ensuing results of the fracture propagation, solid deformation, and pore fluid pressure field from the computational mesh (Miehe et al 2010). The refinement algorithm is based on the h-refinement method, where nodal values of the solution in each iteration ($(u_{\text{n}}^\kappa ,\rho _{\text{n}}^\kappa ,d_{\text{n}}^\kappa )$) are interpolated over the new nodes in the refined mesh. For this purpose, a built-in MATLAB function (refinemesh) is used to split a coarse element by adding an extra node (extra degrees of freedom) to its longest boundary, see Fig. 5a. After each cycle of the mesh refinement, the stages (ii), (iii), and (iv) must be repeated to ensure the hydromechanical stability of the body (Sarmadi et al 2023). To keep the consistency of the material heterogeneity over the domain during the process of mesh refinement, material properties are assigned to the nodal points and are interpolated over the new mesh in the h-refinement process. Thereafter, the heterogeneous material properties are incorporated into the finite element weak forms by accounting for the interpolated values of material properties on the Gauss integration points using the shape functions, as depicted in Fig. 5b for first-order triangular elements.

Fig. 5

a The staged mesh refinement strategy around the HF front by adding extra nodes to the elements; b an example of considering the material heterogeneity by interpolating the nodal values of ${G}_{c}$ over the Gauss integration points. Other material properties such as Young’s modulus, porosity, permeability, and tensile strength can be interpolated over Gauss points similarly

3 Numerical Verification

The developed numerical finite element code for modelling hydraulic fracture propagation is compared to the results of experimental tests on the hydraulic fracture propagation in Sect. 3.1. In a previous study by Sarmadi et al (2024), this numerical code has been verified against the KGD model (Geertsma 1957; Geertsma and De Klerk 1969), which provides analytical solutions for the length, and internal fluid pressure of the hydraulic fracture. In Sect. 3.1 of this paper, numerical results of the fluid pressure variation inside the HF are compared to the experimental data (Cheng et al 2021). Afterwards, in Sects. 3.2, 3.3 and 3.4, the capabilities of the developed numerical code in generating heterogeneous porous rocks as well as the sensitivity of the model with respect to numerical parameters are examined.

3.1 Verification of the HF Propagation Model with Respect to the Experimental Data

Hydraulic fracturing is a multi-physics process including mechanisms such as viscous fluid flow within the fracture walls, tensile failure (cracking) in the solid, and fluid leak-off from the HF into the porous surrounding solid. There are analytical models such as the KGD and PKN models which can predict the propagation and fluid pressure evolution of a HF in semi-infinite elastic domains (Geertsma 1957; Geertsma and De Klerk 1969; Perkins and Kern 1961). Such models provide the solution for the HF’s half-length, maximum crack-width, and the internal fluid pressure as functions of time under a constant fluid injection rate. Simplifying assumptions in analytical models, e.g. having impermeable elastic medium, are not realistic and usually ignore the consideration of leak-off from the HF into the porous rock. Experimental works have tried to focus on the variation of the fluid pressure inside the HF as well as the captured HF trajectories in lab-scale specimens subjected to fluid injection and confining stresses. Cheng et al (2021) conducted several hydraulic fracturing tests on the cubic granite samples of dimensions 300 × 300 × 300 mm in a true triaxial hydraulic fracturing apparatus, and they studied the effect of fluid injection rate on the breakdown pressure (when the HF starts to propagate) by providing time histories of the fluid pressure evolution inside the fractures. In the experimental setup by Cheng et al (2021), confining stresses from three directions were applied on the cubic rock samples using hydraulic jacks. Herein, we model a two-dimensional boundary value problem based on the experimental setup of Cheng et al (2021), where the fluid injection is applied into a wellbore in the middle of a square domain, all surrounding boundaries are considered for drainage, and the maximum and minimum confining stresses are set to ${\sigma }_{{\text{H}}}$=12 MPa and ${\sigma }_{{\text{h}}}$=8 MPa, see Fig. 6a. ${\sigma }_{{\text{v}}}$ is the average stress (${\sigma }_{{\text{H}}}<{\sigma }_{{\text{v}}}<{\sigma }_{{\text{h}}}$) and is parallel to the wellbore in the true triaxial hydraulic fracturing apparatus by Cheng et al (2021). According to the fundamentals of the linear elastic fracture mechanics, the HF trajectories should align with the direction of the maximum horizontal principal stress ${\sigma }_{{\text{H}}}$. However, the observed HF trajectories in the experiments (Cheng et al 2021) contain deviations from the direction of ${\sigma }_{{\text{H}}}$ and random tortuosity due to the inherent material heterogeneity and possibly the existence of pre-existing fissures in the granite samples. Therefore, we decide to consider the material heterogeneity in our verification simulations by spatially distributing material properties as Gaussian random fields with specific values of the mean and standard deviation listed in Table 1. The mean values are chosen the same as reported by Cheng et al (2021), while the standard deviations are assumed. The critical energy release rate (${G}_{c}$) is calculated from the tensile strength and the chosen length-scale parameter using the relationship ${G}_{c}=\left(256 {\sigma }_{{\text{t}}}^{2}{l}_{0}\right)/\left(27E'\right)$, as recommended by Miehe et al (2015). As for an example of considering material heterogeneity in the domain, the distribution of ${G}_{c}$ is depicted in Fig. 6b, assuming ${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}=\pm 1$ and ${l}_{{\text{G}}}^{1}={l}_{{\text{G}}}^{2}=100$.

Fig. 6

a The experimental setup of the granite sample, the borehole location, and an observed HF path (Cheng et al 2021); b the boundary value problem used for numerical modelling and the heterogeneous state of the critical energy release rate (${G}_{{\text{c}}}$) over the domain, where dashed lines specify draining boundaries. c, d Numerical results of an HF trajectory and fluid pressure field

Table 1 Material properties taken from the experimental data in Cheng et al (2021)

An HF trajectory, taken from a realisation of the numerical simulations, is depicted in Fig. 6c, which contains tortuosity due to the modelled material heterogeneity. The HF trajectory has kept the overall direction of propagation towards the direction of ${\sigma }_{{\text{H}}}$, albeit with minor deviations, which is fairly comparable to the experimental crack pattern shown in Fig. 6a.

Our developed numerical model shows a strong capability in predicting the required breakdown pressure, and the trends in time histories of the fluid pressure evolution are similar to the experimental results, see Fig. 7. Numerous simulations are conducted by sampling from the generated Gaussian random fields of the material properties, mentioned in Table 1. Figure 7 illustrates that considering the inputs of material properties results in a range for the fluid pressure evolution inside the HF for each case of the fluid injection rate (${Q}_{{\text{inj}}}$). This approach for the verification of our model accounts for the uncertainty effects due to the inherent heterogeneity in the granite samples. To specify the HF propagation regime, dimensionless viscosity ($\mathcal{M}$) and dimensionless toughness ($\mathcal{K}$) can be calculated using the method of Santillán et al (2017).

Fig. 7

Comparing the numerical time histories of the fluid pressure variation inside the HF to the experimental results provided by Cheng et al (2021)

$${\rm{\mathcal{M}}} = \frac{{12\mu _{\text{f}} \times Q_{{\text{inj}}} }}{{E{\prime} }}\left( {\frac{{E^{\prime}}}{{K^{\prime}}}} \right)^4 ,$$

(18)

$${\rm{\mathcal{K}}} = \frac{{K^{\prime}}}{{E^{\prime}}}\left( {\frac{{E^{\prime}}}{{12\mu _{\text{f}} \times Q_{{\text{inj}}} }}} \right)^{1/4} .$$

(19)

In the above equations, ${\mu }_{{\text{f}}}$ is the dynamic viscosity of the fluid, $E^{\prime}$ is the effective Young’s modulus (introduced in Eq. 11), $K^{\prime} = 4\sqrt {{2/\pi }} K_{IC}$, and $K_{IC} = \sqrt {{G_c E^{\prime}}}$ is the fracture toughness. Using the mean values of the material parameters listed in Table 1 and different injection rates, dimensionless viscosity values were calculated and found to be in the range of $2.5\times {10}^{-5}$ and $6.5\times {10}^{-5}$, which are lower than ${\mathcal{M}}_{0}=3.4\times {10}^{-4}$, shwoing that the HF propagates in a toughness-dominated regime. Dimensionless toughness ($\mathcal{K}$) is calculated in the range of 11.2 and 14.4, which is higher than ${\mathcal{K}}_{0}=1.42$, also confirming a toughness-dominated regime for the HF propagation.

The total propagation time in depends on the HF path which may have undergone deviations from the theoretically expected propagation direction in the experiments (Cheng et al 2021). Having HF trajectories diverted from the vertical direction in the experiments can be the cause for having a longer propagation time in the experiments and a milder slope of fluid pressure drop inside the HF, see Fig. 7. In Fig. 8, a band for the possible values of the breakdown pressure with respect to each value of ${Q}_{{\text{inj}}}$ is drawn based on the ensuing numerical results. It is seen that the experimental data totally fall within the band of 95% confidence of the numerically predicted values of the breakdown pressure.

Fig. 8

A comparison between the numerical outcomes and the experimental data of Cheng et al (2021) for the required breakdown pressure for different values of ${Q}_{{\text{inj}}}$

3.2 The effects of Numerical Parameters in Generating Heterogeneous Random Fields

In the developed method for defining hydrogeological properties of rocks in Sect. 2.3, choosing different GSG statistical parameters leads to different structures in the modelled rock, which may affect the hydromechanical response of the domains subjected to hydraulic fracturing. In this section, MC simulations are run to investigate the effects of non-Gaussianity (change of the subordinator-parameter$\alpha$), cross-correlation coefficient (${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$), and autocorrelation length scale (${l}_{{\text{G}}}^{k}$) on the HF propagation in a toughness-dominated regime ($\mathcal{M}=7\times {10}^{-7}{<\mathcal{M}}_{0}$—using material properties listed in Table 2 and ${Q}_{{\text{inj}}}$ = 50 mL/min). For this purpose, numerical simulations and material properties of the sandstone are set with regards to the work of Fatahi et al (2016), where cubic samples are subjected to the injection of fluid into a borehole. It is known that the fluid pressure inside the HF increases and reaches to a peak value, known as the breakdown pressure, and is followed by a decrease as the HF propagates, reaching to a constant value that is almost equal to the minimum horizontal principal stress ${\sigma }_{{\text{h}}}$ (Fatahi et al 2016). In sandstones, the range of permeability may vary between 0.01 md and 100 md, and there can be found a correlation between the porosity ${\varphi }^{{\text{f}}}$ and${\text{ln}}\overline{k }$, according to (Jensen et al 1987). Therefore, cross-correlated GSG random fields are generated for both log-permeability and porosity, given the values of mean and standard deviation in Table 2. Other material properties ($E, {\sigma }_{{\text{t}}}, {G}_{c}$) are also given to the HF model as random fields which are correlated with the porosity following an opposing trend (Bernabé et al 2003). The cross-correlated random fields are generated with regard to the PDFs of the porosity (${\varphi }^{{\text{f}}}$) and the intrinsic permeability ($\overline{k }$) in Fig. 9. The boundary value problem is shown in Fig. 10a, where the domain is subjected to the in situ horizontal principal stresses (${\sigma }_{{\text{H}}}$=8 MPa $, {\sigma }_{{\text{h}}}$=6 MPa), and water is injected into the middle borehole with a rate of ${Q}_{{\text{inj}}}$ = 50 mL/min. The orientation of the heterogeneous bedding layers with respect to the direction of the minimum stress ${\sigma }_{{\text{h}}}$ is recognised by$\theta$, as shown in Fig. 10a.

Table 2 Material properties taken from Fatahi et al (2016), used in the phase-field model

Fig. 9

The PDFs for generating random fields for the permeability a and porosity b. The effect of parameter $\alpha$ on the shape of the GSG random fields can be seen in PDFs

Fig. 10

The boundary value problem is shown in a, where draining BCs are applied to all sides (black dashed lines), the bedding angle is specified by $\theta$, and the minimum and maximum in situ stresses are ${\sigma }_{{\text{h}}}$ and ${\sigma }_{{\text{H}}}$. The cross-correlated random fields generated for modelling layered heterogeneous media are shown in (b-d), while elastic stiffness and hydraulic permeability are correlated with porosity in opposing and direct trend

3.3 The Effect of Non-Gaussianity in the Material Distributions

To highlight the effects of long tailings, specifically positive excess kurtosis, of the considered random fields for modelling the hydrogeological heterogeneity of rocks, a series of simulations on hydraulic fracturing in heterogeneous layered sandstone are conducted assuming $\theta ={30}^{^\circ }$. In these simulations, random fields are generated using the properties listed in Table 2, having constant values for $\left|{\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}\right|=0.9$ and ${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}=100$ and different values of $\alpha$. The evolution of fluid pressure inside the HF (propagating in a toughness-dominated regime) and possible deviations of the HF trajectories from the expected theoretical direction are analysed.

To illustrate the effect of bedding orientation on the HF trajectories and the fluid pressure field, the HF model solutions from three realisations of the generated random fields are shown in Fig. 11. Theoretically expected direction of the HF trajectory is perpendicular to the direction of minimum in situ stress ${\sigma }_{{\text{h}}}$ but the bedding orientation ($\theta$) can drastically affect the propagation direction. The deviation of the HF trajectory from the theoretically expected direction is identified as the deviation angle (${\beta }_{{\text{d}}}$), shown in Fig. 11a. In fact, this deviation is the result of an unexpected effective stress field in the solid skeleton, which is caused by the anisotropic fluid pressure field developed in the samples, illustrated in Fig. 11b.

Fig. 11

The visualisation of the HF trajectory and the fluid pressure field around the HF for three realisations of the heterogeneous layering orientation, and the definition of the deviation angle ${\beta }_{{\text{d}}}$

For the case of $\theta ={30}^{^\circ }$, time histories of the fluid pressure variation inside the HF subjected to a constant injection rate, assuming two values for the subordinator parameter $\alpha$=2 and $\alpha$=1.25, are shown in Fig. 12 and are compared to the response of the homogeneous domain under the same boundary conditions. Note, when α = 2, the PDFs of the random fields become purely Gaussian, as the subordinator is equal to unity over the entire domain. In comparison, when α is much less than 2, the PDF of the generated random field is highly non-Gaussian. Thus, these two test cases correspond to a Gaussian and strong GSG conditions, respectively. For illustration purposes, the PDFs of results related to the breakdown pressure and the deviation angle are shown in Fig. 13a, c. It is evident in Fig. 13b, d that the variation of $\alpha$ does not have a significant effect on the breakdown pressure, while the variance of the resulting PDF increases as the modelled random fields get closer to a Gaussian form ($\alpha$=2). Lowering the value of $\alpha$, however, has a significant impact on both the mean value of the deviation angle and the variance of its PDF.

Fig. 12

a, b The time histories of the fluid pressure inside the HF for two cases of $\alpha =2.0$ and $\alpha =1.25$

Fig. 13

a, c The PDF for the deviation angle ${\beta }_{{\text{d}}}$ and the breakdown pressure, respectively; mean values and variance of each PDF are mentioned on the plots. The convergence of the MC simulations for the mean deviation angle and the mean breakdown pressure are depicted in b and d, respectively

Both the breakdown pressure and the deviation angle are significantly affected by changing the bedding orientation. The PDFs of breakdown pressure for three cases of bedding orientations ($\theta$ equal to ${0}^{^\circ }$, ${30}^{^\circ }$, ${60}^{^\circ }$) are compared to each other in Fig. 14a, b for two cases of $\alpha$=2 and $\alpha$=1.50. It can be understood that the required breakdown pressure to initiate the HF propagation increases when the bedding orientation gets perpendicular to the direction of ${\sigma }_{{\text{H}}}$, which is the vertical direction in our 2D simulations. Comparing Fig. 14a to b, the role of parameter $\alpha$ in changing the required breakdown pressure for the HF propagation is less significant in comparison to its role in the HF diversion (Fig. 14c and d). The sensitivity of the deviation angle with respect to the change of $\alpha$ appears to vary depending on the bedding orientation ($\theta$). The role of parameter $\alpha$ on the deviation angle becomes more important when the angular difference between the bedding orientation and the direction of ${\sigma }_{{\text{H}}}$ increases. Figure 14a clearly shows the possibility of the complete diversion of the HF into the heterogeneous layers for the case of $\theta ={0}^{^\circ }$, a visualisation of which is shown in Fig. 11. The bedding orientation becomes the dominant factor if HF gets totally diverted into the direction of layering (i.e. towards the direction of the least stresses in the case of $\theta ={0}^{^\circ }$). Therefore, the effects of layered heterogeneity can potentially change the conditions of the energetically most favourable path for the HF and should not be neglected in the simulations of hydraulic fracturing in rocks. According to Figs. 13a and 14c, d, it can be understood that using strong GSG random fields ($1<\alpha <1.75$) for hydrogeological properties of rocks generally reduces the uncertainty in predicting the HF trajectory, compared to the case of using Gaussian random fields.

Fig. 14

a, b The PDFs of the breakdown pressure in different bedding orientations and for two cases of $\alpha$=2 and $\alpha$=1.50 respectively; c, d the distribution of the HF deviation for two cases of $\alpha$ and two different bedding orientations. Mean values and variance of each PDF are mentioned on the plots

3.4 The Effects of Cross-Correlation Coefficient and Autocorrelation Length Scale

MC simulations are repeated for the case of bedding orientation $\theta ={30}^{^\circ }$ and a constant value of $\alpha$=1.50 for assigning material properties as GSG random fields throughout the domain. Setting different values for the cross-correlation coefficient (${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$) and autocorrelation length scale (${l}_{{\text{G}}}^{k}$) causes generated layered domains with different characteristics; see Fig. 4 for clarification of the effect of ${l}_{{\text{G}}}^{k}$.

In Fig. 15, the convergences of the MC simulations for the deviation angle and breakdown pressure to initiate the HF propagation from the borehole are plotted for different cases. Decreasing the cross-correlation coefficient (${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$) does not have a significant effect on the results of the deviation angle and breakdown pressure, see Fig. 15a and b, although it causes a delay in obtaining convergence, requiring more computational effort. A larger value of ${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$ guarantees a strong correlation between different properties in the layers, so a strong cross-correlation leads to a quicker convergence in the outputs. A greater ratio of (${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}$) generates layered heterogeneous media with more distinct (sharper) boundaries between adjacent layers, see Fig. 4. According to Fig. 15c, increasing ${l}_{{\text{G}}}^{1}$ resulted in a greater deviation angle, which is a natural consequence of increasing the sharpness of the layer boundaries throughout the domain. Having more distinguishable layers causes the layering effects to become dominant, i.e. more deviation from the expected theoretical direction. Increasing the ratio ${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}$ can also affect the breakdown pressure for initiating the HF from the borehole, as can be seen in Fig. 15d; however, the extent of this effect can be also dependent on the values of $\theta$ and the principal stresses. The introduced method for defining layered heterogeneous rocks is sensitive to the choice of ${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}$. Therefore, the values of autocorrelation length scale must be chosen based on the nature of the lithologic formation in terms of their bedding history and structure.

Fig. 15

a, b The convergence of the deviation angle and breakdown pressure for a constant value of ${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}$=100 and different values of ${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$. c, d The same graphs for a constant ${\rho }_{{{\text{G}}}_{{\text{m}},{\text{n}}}}$= 0.9 and different values of ${l}_{{\text{G}}}^{1}/{l}_{{\text{G}}}^{2}$

4 Stochastic Analysis of Directional Hydraulic Fracturing in Layered Heterogeneous Rock

According to the field data from hydraulic fracture operations, most of the typical sedimentary rocks in the nature are formed of thousands of horizontal layers (Fisher and Warpinski 2012). Therefore, it is of interest to evaluate the effect of layered material heterogeneity on the directional hydraulic fracturing (DHF) operations in such geologic formations. In this study, the developed stochastic FE method is employed to analyse the effects of layering on the directional HF propagation path.

4.1 Directional Hydraulic Fracturing in Horizontally Layered Rocks

Stochastic analysis on the DHF simulations in a horizontally layered heterogeneous rock is conducted for various angles of perforations ($\beta$) including ${0}^{^\circ }$, ${30}^{^\circ }$, ${60}^{^\circ }$, and ${90}^{^\circ }$, see Fig. 16a. The heterogeneous material properties are sampled from cross-correlated GSG random fields, assuming $\alpha =1.75$, based on the data provided in Table 2. Using directional perforations (having an inclined initial notch) is influential on both the required fluid pressure for initiating the HF propagation (in a toughness-dominated regime) from the notch and the propagation path. Given that input parameters are modelled stochastically, using the GSG model, MC simulations are conducted to study the typical mean behaviour and variance of both the breakdown pressure and propagation paths for a given choice of inclined notch. The maximum in situ stress (${\sigma }_{{\text{H}}}$) is in the vertical direction. Analyses were performed for two values are considered ${\sigma }_{{\text{H}}}$ equal to 8 and 10 MPa, while ${\sigma }_{{\text{h}}}$ is kept constant equal to 6 MPa. For illustrative purposes, four realisations of the HF trajectories are plotted in Fig. 16 to highlight the role of the perforation angle ($\beta$) on the HF trajectories in horizontally layered heterogeneous rocks.

Fig. 16

a The horizontally layered heterogeneous medium and the directional perforated borehole with the angle $\beta$ from the direction of the minimum in situ horizontal principal stress ${\sigma }_{{\text{h}}}$. b, c, d, e Some possible realisations of the HF trajectories taken from MC simulations for different values of the perforation angle $\beta$

For the case of perforation angle $\beta =0$, the HF is expected to propagate initially in the direction parallel to the layering orientation, before the in situ horizontal principal stresses dominate causing the HF to change direction towards ${\sigma }_{H}$. This behaviour can also be identified in the time histories of the fluid pressure inside the HF taken from MC simulations in Fig. 17a. After the HF initiation, the propagation continues, perpendicular to the direction of the maximum in situ stress, and the amount of fluid pressure inside the HF is equal to the minimum in situ stress. In Fig. 17a, it is evident that the fluid pressure of MC results is separated into two clusters concentrated around either 6 or 8 MPa confirming that the HF can propagate in two different directions. On the contrary, raising ${\sigma }_{{\text{H}}}$ to 10 MPa causes the HF to propagate towards the direction of ${\sigma }_{{\text{H}}}$ only, as it can be seen in Fig. 17b, where the fluid pressure in the propagation phase is concentrated towards 6 MPa only.

Fig. 17

a, b The time histories of the fluid pressure inside the HF for different settings of perforation angles and principal stresses in horizontally heterogeneous layered rock; c, d the convergence of the mean breakdown pressure for different values of the perforation angle and principal stresses

The breakdown pressure is dependent on the in situ stresses, the perforation angle, and the tensile strength of the rock (i.e. ${\sigma }_{{\text{t}}}$=6.8 MPa in the simulations). Comparing Fig. 17c to d, the variation of ${\sigma }_{{\text{H}}}$ does not affect the breakdown pressure for perforation angles ($\beta$) of ${60}^{^\circ }$ and ${90}^{^\circ }$ because the HF is already set to propagate towards the direction of ${\sigma }_{{\text{H}}}$ in these cases. The effect of ${\sigma }_{{\text{H}}}$ on the breakdown pressure required for initiating the HF propagation becomes important for lower perforation angles ${30}^{^\circ }$ and ${0}^{^\circ }$, according to Fig. 18a, b. This behaviour is compatible with the results of Men et al. (2013), who modelled the layered rock using parallel weak and highly permeable interfaces embedded in the rock matrix. The PDFs of the deviation angle for different cases of perforation angle and in situ stresses are shown in Fig. 18c, d. For the lower stress ratio (${\sigma }_{{\text{H}}}/{\sigma }_{{\text{h}}}$), the effect of heterogeneous layering can become dominant in diverting the HF into the layers, as there can be a significant probability for having ${\beta }_{{\text{d}}}$ equal to ${90}^{^\circ }$ for the case of perforation angle $\beta ={0}^{^\circ }$ in Fig. 18c. Increasing the stress ratio (${\sigma }_{{\text{H}}}/{\sigma }_{{\text{h}}}$) from 1.33 to 1.67 causes a significant drop in the probability of evolution of the HF along the beddings, on comparing Fig. 18d to c. Consequently, the state of in situ stresses is evaluated as the main controlling factor is specifying the propagation direction of the HF in layered heterogeneous rocks.

Fig. 18

a, b The PDFs of the required breakdown pressure for initiating HF propagation for different values of perforation angle and in situ horizontal principal stresses (${\sigma }_{{\text{H}}},{\sigma }_{{\text{h}}}$) equal to (6,8) and (6,10) MPa, respectively; similarly, c, d show the PDFs of the deviation angle (${\beta }_{{\text{d}}}$). Mean values and variance of each PDF are mentioned on the plots

4.2 Directional Hydraulic Fracturing Aligned with the Bedding Layers in Shale

To maintain the generality of the discussed effects of heterogeneous layering on the uncertainties of hydraulic fracturing operations in geologic formations, we conduct further stochastic analysis on less permeable rocks such as the shale resource plays. Although the amount of leak-off from the HF into the low-permeable shale is much lower, compared to the sandstone, the simulated propagating HF is set to remain in a toughness-dominated regime. There is a significant amount of field data available on the measured permeability and porosity of samples from oil- and gas-producing shale reservoirs; however, a great amount of uncertainty exists due to the method of measurement and the inherent heterogeneity of shale plays (Baird et al 2017). Figure 19a provides a summary of permeability and porosity values gathered from the real data in the literature (Brown 2019), which indicates that the majority of shale plays have a permeability between 0.1 nD and 1000 nD (10^–22 to 10^–18 m²). Gaussian random fields for porosity and permeability can be generated as shown in Fig. 19b and c. The hydrogeological properties of heterogeneous shale samples are chosen with regard to the data gathered from the literature on shale properties (McGinley 2015; Moghadam et al 2019; Portis et al 2013); the mean values and standard deviations are listed in Table 3. Using the material properties in Table 3 and ${Q}_{{\text{inj}}}$ = 3 mL/min, the dimensionless viscosity and toughness (from Eqs. 18 and 19) are calculated equal to $\mathcal{M}=7\times {10}^{-7}{<\mathcal{M}}_{0}$ and $\mathcal{K}=11.4>{\mathcal{K}}_{0}$, confirming the propagation in a toughness-dominated regime. It is possible to have negative values in the samples generated due to a large value for the standard deviation relative to the corresponding mean value. It is noted that if any sample includes negative value for material properties, then that sampling attempt is refused, and a new sample will be generated.

Fig. 19

a The data of permeability and porosity of shales, presented by Brown (2019), which are gathered from relevant studies. b, c The generated random field’s PDF for the porosity and permeability fields of the shale to be used in our simulations. The random field for permeability is sampled in the range specified in (a) by red dashed lines

Table 3 Hydromechanical properties of shale; the mean values were taken from Brown (2019), McGinley (2015), Moghadam et al (2019), and Portis et al (2013)

It is well known that most of the shale formations exhibit an anisotropic behaviour in terms of mechanical deformation (Jin et al 2018; Mousavi Nezhad et al 2018a, b) and hydraulic conductivity (Zhang and Scherer 2012). It is worth evaluating the effect of layering orientation ($\theta$) on the variation of the required breakdown pressure to initiate the HF propagation from a vertically perforated borehole, as shown in Fig. 20, using the developed methodology in this study. MC analysis is conducted on the HF propagation from a vertically perforated borehole in layered heterogeneous shale domains with various bedding orientations. The numerical results of the breakdown pressure taken from MC simulations are plotted for different values of $\theta$ in Fig. 20; the values of mean and variance related to each case of $\theta$ are shown. It is evident that horizontal layering ($\theta$=0) requires the maximum effort for driving the HF vertically in the direction of the maximum in situ stress (${\sigma }_{{\text{H}}}$). By increasing $\theta$, the orientation of heterogeneous layering gets aligned with the propagation direction enforced by the perforation, requiring a lower breakdown pressure to start the HF propagation process. This conclusion confirms that shales show a weaker resistance along the bedding planes, when subjected to cracking.

Fig. 20

The effect of bedding orientation ($\theta$ in degrees) on the required breakdown pressure to initiate HF propagation from a vertically perforated borehole; mean values and variance of the results are mentioned on the plot

According to the results of Sect. 4.1 on the mutual effects of bedding orientation and in situ stresses, it is best to quantify the effect of perforation angle ($\beta$) with respect to the arrangement of the heterogeneous layers and the direction of the maximum horizontal principal stress (${\sigma }_{{\text{H}}}$), concurrently. Therefore, three different positions of the perforation angle are considered in each case of modelling the layered heterogeneous rock having a specific bedding orientation ($\theta$). To clarify this matter, three different values of $\theta$ equal to ${45}^{^\circ }$, ${60}^{^\circ }$, and ${75}^{^\circ }$ are used which are highly, mildly, and slightly inclined with respect to the direction of ${\sigma }_{{\text{H}}}$. We also vary the perforation angle about the specific bedding orientation between -${15}^{^\circ }$ and +${15}^{^\circ }$ to quantify any effect of the perforation angle with respect to $\theta$. More than 1000 MC simulations are performed for each case, and the number of realisations in which the HF trajectory is parallel to the bedding orientation, albeit with a tolerance value $\pm {10}^{^\circ }$, is obtained for each case. The probability of the HF trajectory being dragged into the heterogeneous layering system is calculated as the fraction of the number of realisations in which the deviation angle is $\left[{90}^{^\circ }-\left(\theta -{10}^{^\circ }\right)\right]<{\beta }_{{\text{d}}}<\left[{90}^{^\circ }-\left(\theta +{10}^{^\circ }\right)\right]$ over the total number of simulations in the MC analysis in each case. These probabilities are plotted in Fig. 21 for different cases of $\beta$, $\theta$, and ${\sigma }_{{\text{H}}}/{\sigma }_{{\text{h}}}$. Generally, the HF is more expected to be diverted into the bedding layers for the case $\theta ={75}^{^\circ }$, which is slightly inclined with respect to the direction of ${\sigma }_{{\text{H}}}$. It can also be concluded that if the perforation angle falls between the layering orientation and the direction of ${\sigma }_{{\text{H}}}$, the chance of HF diversion along the layers would decrease significantly. In other words, the choice of $\beta -\theta ={+15}^{^\circ }$ reduces the effect of layering on the HF propagation path. Comparing Fig. 21a to b reveals that increasing the stress ratio (${\sigma }_{{\text{H}}}/{\sigma }_{{\text{h}}}$) reduces the chance of HF diversion in layered heterogeneous rocks. However, there remains a significant chance for $\theta ={75}^{^\circ }$ configuration, to drag the HF into the beddings. Our MC results indicate that the effect of bedding orientation in diverting the HF is profound if the angular difference between the bedding orientation and the maximum in situ stress (${\sigma }_{{\text{H}}}$) is less than ${20}^{^\circ }$. Increasing the fluid injection rate or using a fluid with relatively higher dynamic viscosity can change the HF propagation regime from toughness dominated to viscosity dominated, in which case the impact of material heterogeneity on deviating the HF trajectories may not be significant (Huang et al 2019). Viscosity-dominated propagation regime has not been considered in this study.

Fig. 21

The probability of the HF diversion into the bedding layers in shale with regards to the combined effects of $\beta$ and $\theta$; a and b represent the results for two configurations of in situ stresses ${\sigma }_{{\text{H}}}/{\sigma }_{{\text{h}}}$ equal to 1.33 and 1.67 respectively

5 Conclusions

A stochastic method in the context of finite element method was introduced for modelling the HF propagation in layered heterogeneous rocks. In this method, hydrogeological properties of the rock, which affect the cracking and failure behaviour significantly, are spatially distributed over a continuous finite element mesh in layered patterns using a generalised sub-Gaussian (GSG) model. This method can represent the natural characteristics of rocks having smear-type heterogeneities with no distinct boundary between adjacent layers, where the sedimentation has been the main cause of their formation. Sensitivity analyses were conducted to reveal the effects of numerical parameters in the model on the HF propagation and hydromechanical response. The main purpose of this study was to evaluate the effect of this type of heterogeneity on the propagation direction of the HF, in a toughness-dominated regime, and its deviation from the theoretically predicted direction. Based on the numerical results, the following conclusions can be made:

Changing the characteristics of the GSG random fields for defining heterogeneous material properties in the numerical models have a significant effect on the deviation of the HF from the theoretically predicted crack path. The effects of the excess kurtosis of the GSG random fields in the input material properties are reflected in the convergence of the values of breakdown pressure and deviation angle in the MC simulations. A larger difference in the chosen values of the autocorrelation length scale in two directions (parallel and perpendicular to the beddings) can significantly deviate the HF from the original direction.

The bedding orientation is found to be highly important in directional hydraulic fracturing, where inclined perforated boreholes are planted in the reservoir to drive the HF in a specific direction.

In the case of low difference between in situ stresses (low ratio of $\left( {\sigma _{\text{H}} /\sigma _{\text{h}} } \right)$, the HF may be totally diverted into the bedding layers and propagate in the direction perpendicular to the direction of maximum in situ stress $\left( {\sigma _{\text{H}} } \right)$. Increasing the ratio of $\sigma _{\text{H}} /\sigma _{\text{h}}$ helps the HF to ignore the role of heterogeneous layering in the HF deviation.

The HF is expected to initiate and propagate easier along the bedding layers, especially when the bedding orientation is parallel to the direction of $\sigma _{\text{H}}$. Higher fluid pressure is required to initiate the HF perpendicular to the layers.

The angular difference between the bedding orientation and the direction of $\sigma _{\text{H}}$ is identified as an influential factor affecting the probability of the HF deviation. As this difference increases, the maximum stress becomes more dominant. The configuration of the perforated borehole with respect to the in situ stress state and the arrangement of bedding layers is also important in deviating the HF.