1 Introduction

Rock-socketed piles (RSPs) are commonly employed for heavy structures such as towers, bridges and high-rise buildings when rock formations are present at relatively shallow depths. The presence of soft materials/infill such as rock smear and drilling mud, and roughness at the pile–rock interface (PRI) significantly influences the overall shaft resistance of RSPs (Cheng 1997; Collingwood 2000; Haberfield and Lochaden 2019). The smear, if present, reduces the effective contact area between the pile and rock and inhibits load transfer at the interface, which can significantly undermine the socket resistance (Fleming and Sliwinski 1977; Pells et al. 1980; Baker et al. 1993).

Many laboratory direct shear tests on rock–rock interface have been carried out to investigate the effect of roughness and smear on the shaft response of RSPs (Ladanyi and Archambault 1975; Johnston 1977; Lama 1978; Phien-Wej et al. 1990; De Toledo and De Freitas 1993; Papaliangas et al. 1993; Indraratna et al. 1999, 2005, 2014; Mirzaghorbanali et al. 2014; Jahanian and Sadaghiani 2015; Cheng et al. 2016; Lu et al. 2017; Shrivastava and Rao 2018). However, these research findings, while advancing the comprehension of rock–rock interfaces, are limited in accurately simulating the concrete–rock interface shear behaviour as the failure predominantly occurs in the rock asperities due to the relatively higher strength of concrete than rock. To address this limitation, mechanical models were developed to simulate pile–rock interface (PRI) behaviour, through laboratory shear testing and analytical modelling (Williams et al. 1980; Johnstone and Lam 1984; Rowe and Armitage 1987; Carter and Kulhawy 1988; Johnston and Lam 1989; Haberfield and Johnston 1994; Kodikara and Johnston 1994; Seidel and Haberfield 1995). Most of these studies illustrate the diminishing effects of interface smear on the shaft response of RSPs. For example, Hassan and O’Neill (1997) and O’Neill (2001) addressed the effects of smear in rock sockets through a finite-element study and concluded that the smeared sockets in argillaceous intermediate geomaterials may be designed as a smooth interface due to a significant reduction in shaft capacity. O’Neill and Hassan (1993) proposed a smear factor in the shaft resistance formulation based on field load tests conducted in the Eagle Ford Shale formation; however, the study approximated the effect of roughness and smear thickness without taking the asperity geometry into consideration. Based on these studies and direct shear tests on concrete–rock interfaces, Cheng (1997) and Gu (2001) postulated interface models to illustrate the relationship between the thickness of smear/infill, asperity angle and asperity height. Further advancement was made by Collingwood (2000), who proposed the construction method-based reduction factors to estimate the interface shear strength incorporating the effects of socket roughness and slurry filter cake thickness using the properties of the drilling slurry. Recent advancements in this area was made by Zhao et al. (2020), who carried out a series of direct shear tests to determine the shear behaviour of infilled joints subjected to variations in the joint roughness coefficients (JRC). It is evident that most of the previous studies determining the combined effect of infill and roughness are restricted to a particular infill material (e.g., crushed mica, kaolin, bentonite, graphite, sand and clay) or rock, and are limited in capturing the micro-mechanics at the asperity level. Moreover, the properties of the smear/infill may vary greatly within the socket due to the remoulding of rocks with different in situ materials. The rock properties also determine the basis of shearing mechanisms and significantly affect the load-transfer characteristics. In addition to this, the construction-induced smear on the socket wall differs morphologically in terms of varying thicknesses and orientations (Holden 1984; Cheng 1997), which renders it inappropriate to be classified under a single set of strength parameters. Furthermore, all the current correlations for smeared interfaces are based on 2D interface testing which renders ambiguity in the circumferential stress response at the PRI and does not consider the vertical orientation of socket wall that affects the residual shear strength from debris movement at the interface. Most importantly, to the best of the authors’ knowledge, there are no studies till date to formulate a unified interface shear model considering both the effect of socket roughness and smear fabric (thickness, placement and area fraction) for different rocks. This warrants the need for a comprehensive interface shear strength framework incorporating the predominant influential variables affecting the interface resistance.

Murali et al. (2024b) conducted three-dimensional (3D) model pile load tests using in situ micro-CT imaging to explain the effect of smear fabric on the interface shear strength. The authors subsequently carried out limited Discrete Element Method (DEM) modelling of PRI behaviour to investigate the effect of smear fabric parameters on the shaft resistance (Murali et al. 2024c). This paper proposes a unified interface shear strength framework based on 3D model pile load tests and extensive DEM modelling to capture the effect of socket roughness and smear fabric in terms of soft rocks’ properties. Three different soft rocks were adopted in the laboratory by downscaling the field rock properties to model size through material similitude analysis. These rocks were subjected to mechanical testing, which served as the basis to calibrate the Uniaxial Compressive Strength (UCS) using DEM simulations and subsequently construct the RSP-DEM model. The shear interface framework for a clean shaft was proposed in terms of the various socket roughness configurations by relating them to the different rock properties. Then, the shaft resistance decay in terms of the presence of smear at the interface (thickness and area proportion) was formulated and the difference in ultimate shaft resistances and the relevant micro-mechanisms were discussed for different smear configurations (i.e. leading-face and both-faces smeared). Finally, the effect of smear leading to the critical roughness and smear thickness parameters was incorporated into the equation of clean shaft to formulate a unified interface shear strength framework capable of predicting the lower bound value of shaft resistance for soft rocks in terms of various interface roughness configurations and smear fabrics.

2 Methodology

2.1 Sample Preparation and Rock Properties

The primary focus of this study is to develop an understanding on predicting the mechanical behaviour of model piles socketed in soft rocks for saw-toothed joints. The dimensions of the model pile have been adopted by scaling down the asperity geometries based on field-scale roughness from previous research works (Pells et al. 1980; Kodikara and Johnston 1994; Seidel and Collingwood 2001; Seol et al. 2008), as illustrated in detail in Murali et al. (2022). The results presented in the earlier studies (Murali et al. 2022, 2024b) discuss the effect of roughness and smear fabric, and their implications on the microstructural evolution of rock asperities for a single soft synthetic rock. However, to understand the effect of these parameters in much detail in relation to different rock properties, three synthetic soft rocks (SR-1, SR-2 and SR-3) were created in the laboratory to represent realistic field stiffness boundary conditions (Pells et al. 1980; Gu 2001). This was achieved by utilizing the properties of the Hawkesbury Sandstone, as reported in Pells et al. (1980) and Gu (2001), and subjecting them to material similitude analysis (Indraratna 1990). In this process, the constant normal stiffness at the PRI, Poisson’s ratio (Pells 2004), critical strain (UCS to Young’s modulus) and uniaxial strength ratio (UCS to tensile strength) between the field and the lab were maintained approximately the same (Table 1). Synthetic soft rocks were created through trial and error of various mix proportions and subjected to mechanical testing to determine the combination ratios that closely aligned with the similitude analysis. While initially designed for intact rock, the mechanical characteristics of these synthetic rocks can be extended to represent the rock mass. This is facilitated by integrating the jointing effects and other pertinent quality considerations into the material properties. The relevant properties of these synthetic rocks are summarised in Table 2.

Table 1 Similitude analysis of different synthetic soft rocks at 28 days curing
Full size table
Table 2 Properties of different synthetic soft rocks at 28 days curing
Full size table

2.2 Numerical Calibration

The results from previous research works on interface roughness (Murali et al. 2022) and smear fabric (Murali et al. 2024b) illustrate that experimental investigation yields valuable insights into the load-bearing mechanisms of piles in soft rock. However, due to the huge costs involved in fabrication, it is challenging to investigate the effect of the influential variables in detail using the same experimental procedures. Therefore, the experimental results were used to calibrate the UCS response of different soft rocks to aid in the development of an RSP-DEM model to subsequently evaluate the interface behaviour for various degrees of roughness and smear fabrics.

The existing DEM models for rocks (Potyondy and Cundall 2004; Šmilauer 2010; Scholtès and Donzé 2013; Onate et al. 2015) lack the capability to explore the combined influence of compression/tension and shear, known as mixed-mode failure. To address this limitation, this study adopts a cohesive damage plasticity model (CDPM) introduced by Nguyen et al. (2017). The CDPM is employed to assess the mechanical response of soft rocks, leveraging a damage law designed to capture the softening characteristics in both normal and shear stresses (Fig. 1).

Fig. 1
figure 1

Constitutive laws of the Cohesive Damage Plasticity Model: a Damage modes; b Yield surface [figure based on Murali et al. (2022)]

Full size image

To replicate the experimental behaviour of these synthetic soft rocks through numerical simulations, the UCS behaviour in DEM was benchmarked against the experimental results for the three rocks. Different particle sizes were adopted (0.5, 0.75 and 1.125 mm) through a particle scaling approach to increase the feasibility of the DEM simulations (Murali et al. 2022). It becomes essential to conduct distinct UCS calibrations for each particle size as the CDPM incorporates normal and shear softening micro-parameters which are dependent on particle size, necessitating similar particle sizes in the UCS calibration to maintain consistency for pile simulations, without any scaling adjustments. The micro-parameters corresponding to these UCS simulations are summarized in Table 3.

Table 3 DEM micro-parameters of the UCS simulations for the synthetic soft rocks
Full size table

Figure 2 shows the experimental UCS behaviour of all the three rocks calibrated against the DEM simulations. It further evidences the capability of CDPM to conveniently capture the behaviour of a wide range of soft rocks in reasonable agreement with the experimental results.

Fig. 2
figure 2

DEM calibration of the UCS response using experimental results for different soft rocks using varied particle sizes: a SR-1; b SR-2; c SR-3

Full size image

2.3 Basis of Calibration for the Pile Load Tests

The laboratory small-scale pile test includes a downscaled model pile, rock mould, custom-made smear moulds, a stabilizing base cover and a purpose-built pile test rig. The experimental setup and testing process of model RSPs is illustrated in Murali et al. (2024a). The compact experimental setup was supposedly scaled down to allow for an in-depth exploration of the internal interface mechanisms governing the shaft response. This was enabled through continuous and staged vertical loading of pile into the rock socket with intermittent X-ray CT imaging, which allowed for 3D visualization of the micro-mechanisms between the pile, smear and the rock. The experimental shaft resistances were determined by conducting pile-load tests on smooth piles (0° asperity roughness) and rough piles, and then subtracting the result of the smooth pile from the load–displacement behaviour of the rough piles. In this study, the load–displacement behaviour of the smooth pile did not exhibit any bond or friction characteristics at the interface, thereby providing only the base resistance (Murali et al. 2022).

This study adopts the DEM methodology of Murali et al. (2024c) for constructing the smeared RSP model. The simulations were built on the premise that the micro-parameters of different particle sizes from the UCS calibration are adopted directly into the RSP-DEM model with the micro-friction angle at the PRI being zero. This is in line with the experimental test results, indicating the negligible effect of shaft friction and bond resistance at the interface. The only calibration required for the DEM model is the smear material which was satisfied by benchmarking the experimental load–displacement behaviour with the DEM results of the various smeared pile configurations. It is worth noting that the micro-mechanics observed in the processed X-ray CT images align well with the findings from the DEM, which signifies that the RSP-DEM model is calibrated not only in terms of the load–displacement response but also in terms of the internal micro-mechanisms as well. Figure 3 shows the efficiency of calibration in terms of the pile-head resistance response with vertical loading of pile into the rock socket for different roughness configurations (Murali et al. 2022) and smear fabrics (Murali et al. 2024c), along with the cross-section of no-load stage in X-ray CT imaging and DEM modelling. This illustrates the benefit of having a comprehensive calibrated DEM model to simulate the different soft rocks in terms of different pile configurations with limited experimental test results.

Fig. 3
figure 3

Shaft resistance calibration of experimental results with DEM in terms of the load–displacement behaviour and interface micro-mechanics for SR-1: a Clean interface for different roughness configurations; b Leading-face-smeared interface for different smear area proportions

Full size image

3 Interface Shear Strength Model for Clean Sockets

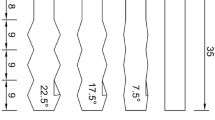
Based on the UCS calibration presented above, the DEM pile simulations were carried out to evaluate the implications of the pile loading into the various rocks (SR-1, SR-2 and SR-3) for a range of roughness configurations (0°, 7.5°, 10°, 12.5°, 15°, 17.5°, 20°, 22.5°). These values were adopted by scaling down the chord lengths and asperity heights of the roughness profiles utilized by early researchers (Williams et al. 1980; Kodikara and Johnston 1994; Seidel and Collingwood 2001), as indicated in Murali et al. (2022). The load–displacement behaviours of the individual rocks subjected to various interface roughness profiles are illustrated in Fig. 4.

Fig. 4
figure 4

Pile-load tests using DEM for different soft rocks in terms of varying roughness profiles: a SR-1; b SR-2; c SR-3

Full size image

It is evident that there is a direct correlation between the level of roughness and the corresponding increase in shaft resistance. This is due to the interactions between the pile and the rock asperities being more inclined towards shearing rather than sliding due to the shear resistance offered by a comparatively larger contact surface area between the pile and the rock. It can also be observed that the peak tends to shift towards lower displacements with an increase in the asperity angle. This is a consequence of the increase in slenderness of the asperity along with the loading area, which forces the onset of a quicker asperity failure. Furthermore, it is notable that the rate of shaft load increment beyond the peak value escalates with the increase in rock strength (SR-1 to SR-3). This phenomenon is caused due to the compression of released rock debris at the interface. The harder the rock, the higher is the resistance required at the shaft to further crush the broken wedges of rock asperities. Clearly, it can be seen that the ultimate shaft resistance is attained within a pile-head displacement of half-asperity chord length (4.5 mm), which aligns with the findings of previous research works (Kodikara and Johnston 1994; Gu 2001; Haque and Kodikara 2012). This criterion has, therefore, been adopted for evaluating the ultimate shaft resistances of the smeared interfaces in the following sections of this paper.

The ultimate shaft resistance (\({\tau }_{u}\)) for unbonded clean piles socketed in soft rock is given by

$${\tau }_{u}={\tau }_{u-{\text{rough}}}$$
(1)

\({\tau }_{u-{\text{rough}}}\) represents the shaft resistance contribution due to the socket roughness, which is expressed in terms of the roughness factor \(({\text{RF}})\) proposed by Horvath et al. (1983). This is a function of socket length \((L)\), socket radius \((r)\), mean roughness height \(\left(a\right)\) and traversed socket length \(({L}_{t})\), as shown below.

$${\text{RF}} =\frac{a{L}_{t}}{rL}$$
(2)

The relationship between the friction coefficient (\(\lambda\)) and \({\text{RF}}\) was formulated based on numerical modelling of piles with different interface roughness and rock strengths, as shown in Fig. 5. Alternatively, the socket roughness can also be expressed in terms of the Monash Roughness Model (Seidel and Collingwood 2001).

Fig. 5
figure 5

Formulation of friction coefficient \((\lambda )\) as a function of \(RF\) for different soft rocks

Full size image

In this study, the friction coefficient \((\lambda )\) was estimated by correlating the ultimate shaft resistances with the Young’s modulus (\(E\)) and UCS (\({\sigma }_{c}\)) of the rock. It is given by

$$\lambda =f({\tau }_{u-{\text{rough}}}, E, {\sigma }_{c})$$
(3)
$$\lambda = \frac{{\tau }_{u-{\text{rough}}}}{E\sqrt{\frac{{\sigma }_{c}}{{p}_{a}}}}$$
(4)

here, \({p}_{a}\) represents the atmospheric pressure (100 kPa) and is included in the equation to satisfy this relationship dimensionally.

Through the correlation presented in Fig. 5, the friction coefficient due to socket roughness can be determined as

$$\lambda =\mathrm{\eta x }RF$$
(5)

here, \(\upeta\) is the proportionality constant ranging from 0.005 (0.5 MPa < UCS < 1 MPa) to 0.007 (UCS < 0.5 MPa).

It can be observed from Fig. 5 that the proposed \(\upeta\) values tend to overestimate the \(\lambda\) parameter for lower roughness profiles (7.5° and 10°). Despite representing the sand size used in the experiment (D50 = 0.5 mm), this particle size in the DEM simulation at the PRI may not effectively capture the asperity shape for piles with lower roughness configurations. However, adopting a much smaller particle size can lead to significantly higher computational costs as the DEM model section is also larger (180°) when compared to earlier studies (30° to 90°) (McDowell et al. 2012; Falagush et al. 2015; Gutiérrez-Ch et al. 2021; Zhang and Fatahi 2021). Therefore, the DEM simulation underestimates the interface resistance due to the contact area between the pile and the rock being represented inadequately. However, this issue does not occur for the higher roughness profiles (Fig. 5) owing to the asperity shape being captured comfortably with this particle size. A similar underestimation issue was observed by Haque and Kodikara (2012) in the form of non-uniform mesh deformation for lower interface roughness while conducting FDM analyses for 2D joint profiles.

By rearranging Eq. (4), the ultimate shaft resistance for clean interfaces in terms of socket roughness can be derived as

$${\tau }_{u-{\text{rough}}} = \lambda E\sqrt{\frac{{\sigma }_{c}}{{p}_{a}}}$$
(6)

The ultimate shaft resistances from the experimental results of this study are comparable to the empirical formulations proposed by various researchers based on field-scale tests, as highlighted in Murali et al. (2022). This suggests that the influence of scale-effects on the RSP-DEM model employed in this research may be relatively minimal. It should be noted that the relationship in Eq. (6) is specifically formulated to serve as a foundation for incorporating the effect of smear fabric in the proposed shear interface framework. A field-scale validation of the same can only verify its boundaries.

4 Influence of Smear on the Interface Shear Strength

4.1 Formulation of Shear Resistance Decay

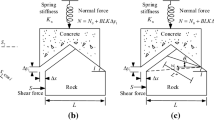
Due to the micro-mechanics of SR-1 being mapped between the experiments and DEM in detail for the leading-face-smeared interfaces (Murali et al. 2024c), this rock was utilized to investigate the preliminary aspects of the shaft resistance decay for the both-faces-smeared interfaces.

The smear area proportion and thickness contribute significantly towards the reduction in the interface shear resistance, whereas the smear placement has a negligible effect on the shaft capacity (Murali et al. 2024c). Therefore, the smear fabric effect needs to be formulated in such a manner so that the changes in ultimate shaft resistance are captured in terms of the smear area proportion (ratio of smear area to the shaft area) \({(s}_{o})\) and the ratio of smear thickness to asperity height \((t/a)\) at the interface.

The combination of these two smear variables can be defined by

$$\gamma ={s}_{o}\left(t/a\right)$$
(7)

It has been established from earlier studies (Indraratna et al. 1999) that the shaft resistance attains an almost constant value beyond a critical value of \(\left(t/a\right)\) and is represented as \(({t/a)}_{cr}\). Moreover, the maximum \({s}_{o}\) value cannot exceed the value of 1 due to it being a ratio of the shaft area and is represented as \({({s}_{o})}_{{\text{max}}}\).

Due to the presence of \({({s}_{o})}_{{\text{max}}}\) and \(({t/a)}_{cr}\), the relationship depicting the resistance reduction due to smear with respect to the clean shaft needs to be constructed as a hyperbolic relationship. For this purpose, the methodology proposed by Duncan and Chang (1970) [successful application by Indraratna et al. (1999)] was adopted in this study (Fig. 6).

Fig. 6
figure 6

Process of constructing the hyperbolic relationship: a Resistance-drop as a function of smear variable \(\gamma\); b Establishing the linear relationship to determine the resistance-drop (\(\Delta {\tau }_{p}\))

Full size image

The resistance-drop (\(\Delta {\tau }_{p}\)) in terms of the ultimate socket resistance of clean shaft (\({\tau }_{u-{\text{rough}}}\)) for the 17.5° roughness configuration was utilized to construct the hyperbolic relationship, as shown in Fig. 6a.

By plotting \(\gamma\) versus \(\gamma /\Delta {\tau }_{p}\) (Fig. 6b), a linear relationship can be established, giving the following equation:

$$\frac{\gamma }{\Delta {\tau }_{p}} ={m}_{e}\gamma +{i}_{e}$$
(8)

here, \({m}_{e}\) and \({i}_{e}\) are the slope and intercept of the linear equation representing the resistance drop. By rearranging this equation, the new resistance-drop for the hyperbolic relationship can be given by

$$\Delta {\tau }_{p}=\frac{\gamma }{{m}_{e}\gamma +{i}_{e}}$$
(9)

Based on this relationship, the strength decay of the smeared interfaces can be modelled as a combination of smear area proportion and thickness, as illustrated in Fig. 7. The cut-off for \(\gamma\) is provided at a \(t/a\) value of 1.75, which resonates with the critical value (\(({t/a)}_{cr})\), observed previously (Murali et al. 2024c).

Fig. 7
figure 7

Ultimate shaft resistances as a function of the smear variable \(\gamma\) for 17.5° roughness profile

Full size image

To provide additional support to the estimated \(({t/a)}_{cr}\) value, separate sets of simulations with the same smear configurations were carried out for different interface roughness configurations, as shown in Fig. 8. Each point in the figure represents a complete simulation of the specified roughness profile with the respective smear configuration. It is evident that the interface strength attains an almost constant value beyond a \(\gamma\) value of 1.75 in case of all the different roughness configurations, which resonates with the \(({t/a)}_{cr}\) value at the \({({s}_{o})}_{{\text{max}}}\) of 1. This is compliant with the previous studies on infilled joints whose \(({t/a)}_{cr}\) values fell in the range of 1.0 and 2.0 (Goodman 1970; Papaliangas et al. 1990; Phien-Wej et al. 1990; Jahanian and Sadaghiani 2015; Zhao et al. 2020). The empirical values of \({m}_{e}\) and \({i}_{e}\) for these different roughness configurations are evaluated in the following sections of the paper.

Fig. 8
figure 8

Shaft resistance decay with respect to the smear variable \(\gamma\) for different roughness configurations

Full size image

4.2 Effect of Smear Fabric in Terms of Leading-Faced and Both-Faced Smeared Interfaces

To understand the influence of smear in detail, separate sets of DEM results for the 17.5° pile with the same smear configurations were compared between the leading-face-smeared and both-faces-smeared interfaces. A similar process illustrated above was adopted to formulate the shear strength decay, as shown in Fig. 9.

Fig. 9
figure 9

Effects of leading-face-smeared and both-faces-smeared configurations on shaft resistance

Full size image

The values of \({m}_{e}\) and \({i}_{e}\) for the leading-face-smeared and both-faces-smeared configurations are 2.9 and 2.9, and 2.5 and 2, respectively. It is evident that the gap in the curves between these two sets of simulations widens from the top and finally leads to a 37% difference in the shaft resistance beyond the \(({t/a)}_{cr}\) value. It is caused due to the variable compressions of smear at the interface between these two sets of simulations. The smear in the leading-face-smeared configuration experiences compression from the pile upto a certain limit and is then backed up by the resistance from rock in the other half-asperity face. This support from the rock is absent in the both-faces-smeared configuration, resulting in a comparatively higher smear compression, which delays the onset of pile-rock interactions and subsequently reduces the shaft capacity. Figure 9 also indicates that at minimal smear thicknesses and area proportions, the effect of smear present on just the leading face or both faces does not differ significantly with respect to the ultimate shaft resistance. Despite the main focus in the study being on the both-faces-smeared configuration for devising the interface framework, the results reaffirm the obtained \(({t/a)}_{cr}\) value as 1.75 and provide additional validation to the proposed formulation.

4.3 Formulation of the Slope and Intercept Parameters for Smeared Interfaces

Earlier studies have formulated the shear interface model through empirical constants, which are only specific to certain roughness configurations or specific rocks (Indraratna et al. 1999; Shrivastava and Rao 2018; Zhao et al. 2020). Therefore, based on the hyperbolic relationship of the different roughness configurations presented in Fig. 8, the slope and intercept values of the interface framework in this study (\({m}_{e}\) and \({i}_{e}\)) were related back to the physical properties of the rock materials and the roughness configurations through the slope (\({\lambda }_{m}\)) and interface (\({\lambda }_{i}\)) coefficients.

The 17.5° roughness configuration was used as a base and the \({m}_{e}\) and \({i}_{e}\) values were obtained in terms of various smear configurations for SR-2 and SR-3 (Fig. 10). These values were then compared with the \({m}_{e}\) and \({i}_{e}\) values of SR-1 and cross-correlated with the values of the other roughness configurations to mitigate the extensive computational costs associated with this numerical analysis.

Fig. 10
figure 10

Shaft resistance decay of the 17.5° roughness configuration for different rocks with respect to the smear variable \(\gamma\)

Full size image

The \({\lambda }_{m}\) value was determined by correlating the \({m}_{e}\) value of each roughness configuration with the Young’s modulus (\(E\)) and UCS (\({\sigma }_{c}\)) of the different rocks, respectively. It is given by

$${\lambda }_{m}=f({m}_{e}, E, {\sigma }_{c})$$
(10)
$${\lambda }_{m}={m}_{e}{\left(\frac{E}{{\sigma }_{c}}\right)}^{2}$$
(11)

The \({\lambda }_{m}\) values were then interpreted in terms of \({\text{RF}}\) by adopting the hyperbolic decay (Fig. 11a) in a similar formulation process discussed for \(\Delta {\tau }_{p}\) and \(\gamma\). This is presented in the following equations by assuming \({C}_{p}\) = 100 as a constant.

Fig. 11
figure 11

Formulation of coefficients as a function of \(RF\): a Slope coefficient (\({\lambda }_{m}\)); b Interface coefficient (\({\lambda }_{i}\))

Full size image
$$\frac{{\lambda }_{m}}{{{C}_{p}}^{2}} ={C}_{p}-\Delta {\lambda }_{m}$$
(12)
$$\frac{{\text{RF}}}{\Delta {\lambda }_{m}} ={u}_{m}{\text{RF}}+{v}_{m}$$
(13)

Here, \({u}_{m}\) and \({v}_{m}\) represent the slope and intercept of the linear equation representing \(\Delta {\lambda }_{m}\). By combining Eqs. (12) and (13), the relationship for \({\lambda }_{m}\) can be formulated as

$${\lambda }_{m}=\left({C}_{p}-\frac{{\text{RF}}}{{u}_{m}{\text{RF}}+{v}_{m}}\right) {{C}_{p}}^{2}$$
(14)

It can be seen from Fig. 11 that the slope and the interface coefficients exhibit an exponential decay with the increase in pile roughness. Moreover, the trend tends to become residual beyond an \({\text{RF}}\) of 0.40 (17.5° roughness configuration), which indicates the almost diminished contribution of socket roughness in the load-carrying capacity of the shaft. This implies that beyond this critical \({\text{RF}}\) value (\(({{\text{RF}})}_{cr})\), smear predominantly controls the interface resistance of the RSP and the roughness of the interface does not play a major role in the interface strength. This can be explained by the basic shearing phenomenon, where for a fixed chord length, an increase in the asperity height reduces the cross-sectional area of the asperity in the loading direction. Shear plane formation through the slender asperities becomes relatively easier despite having a larger contact area as the effect of asperity slenderness ratio becomes redundant beyond a particular value. This falls in line with the observations of Seidel and Collingwood (2001).

By rearranging Eqs. (11) and (14), the slope of the linear equation representing \(\Delta {\tau }_{p}\) can be determined by

$${m}_{e}={{C}_{p}}^{2}\left({C}_{p}-\frac{{\text{RF}}}{{u}_{m}{\text{RF}}+{v}_{m}}\right){\left(\frac{{\sigma }_{c}}{E}\right)}^{2}$$
(15)

This equation limits the decay of the slope coefficient in terms of the roughness factor and conditions it such that, when \({\text{RF}}\) > \(({{\text{RF}})}_{cr}\), \({\text{RF}}\) =\(({{\text{RF}})}_{cr}\).

Similarly, with \({u}_{i}\) and \({v}_{i}\) being the slope and intercept of the linear equation representing \(\Delta {\lambda }_{i}\), the intercept of the linear equation representing \(\Delta {\tau }_{p}\) can be given as

$${i}_{e}={{C}_{p}}^{2}\left(2{C}_{p}-\frac{{\text{RF}}}{{u}_{i}{\text{RF}}+{v}_{i}}\right){\left(\frac{{\sigma }_{c}}{E}\right)}^{2}$$
(16)

The parameters \({u}_{m}\), \({v}_{m}\), \({u}_{i}\) and \({v}_{i}\) are constants for RSPs socketed in soft rocks and are presented in Table 4.

Table 4 Slope and intercept values of the \({m}_{e}\) and \({i}_{e}\) parameters for RSPs with various roughness and smear configurations socketed in different soft rocks
Full size table

5 Development of a Unified Interface Shear Strength Model

Determining the mechanical properties of smear in the field is highly challenging due to its discrete nature of formation, and unifying it under a single property may not be appropriate. Therefore, it becomes essential to characterize the smear based on its unified strength reduction capability at the PRI. In this study, the ultimate resistance deterioration at the interface for fully smeared piles is about 75% (at \({({s}_{o})}_{{\text{max}}}\) and \(({t/a)}_{cr}\))) (Fig. 9). This value can vary depending upon the properties of the smear and the stiffness of the rock mass. For example, previous studies have illustrated that in the case of bentonite smear, the peak reduction percentage is 40–50% for concrete–rock interfaces (Cheng 1997) and 70–90% for gypsum plaster interfaces (Indraratna et al. 1998). In that regard, this study proposes an interface shear strength model to determine the value of shaft resistance for the RSPs, where the presence of smear reduces the shaft resistance by at least 70% and not more than 75% for a fully smeared interface. The average undrained shear strength (\({s}_{u}\) = 4.28 kPa) of the smear material used in this study (Murali et al. 2024a) coincides with the predictions of Collingwood (2000), who estimated the filter cake shear strength in terms of gelled liquid-limit void ratios with the general predictions ranging between 0.2 and 20 kPa. However, the properties of the smear were not employed in the formulation of the shear interface model due to the smear materials exhibiting time-dependent strength gain, as illustrated in Murali et al. (2024a).

To integrate the effect of socket roughness and smear fabric into a unified shear interface model, it is essential to include the smear fabric factor (\(\kappa\)) in Eq. (17). The ultimate shaft resistance of smeared shafts is given by

$${\tau }_{u} = {\kappa \tau }_{u-{\text{rough}}}$$
(17)
$${\tau }_{u}= \kappa \lambda E\sqrt{\frac{{\sigma }_{c}}{{p}_{a}}}$$
(18)

Since the drop in shaft resistance due to smear needs to be included as a reduction factor, the hyperbolic resistance-drop is incorporated as a function of the ultimate shaft resistance of clean shafts, as given below.

$$\kappa =\frac{{\tau }_{u-{\text{rough}}}-\Delta {\tau }_{p}}{{\tau }_{u-{\text{rough}}}}$$
(19)

Finally, the combined relationship depicting the interface resistance of piles in soft rocks is given by

$${\tau }_{u}=\mathrm{\eta RF}\frac{{\tau }_{u-{\text{rough}}}-\frac{\gamma }{{m}_{e}.\gamma +{i}_{e}}}{{\tau }_{u-{\text{rough}}}}E\sqrt{\frac{{\sigma }_{c}}{{p}_{a}}}$$
(20)

The above equation is subjective to the fact that when \((t/a)\) > \(({t/a)}_{cr}\), \((t/a)\) =\(({t/a)}_{cr}\).

6 Shaft Resistance Predictions Using the Proposed Interface Model

The main output from this study is the inclusion of the smear fabric effect into the shear interface framework to capture the ultimate shaft resistance of piles socketed in soft rocks. To provide more emphasis on this parameter, various predictions for SR-2 and SR-3 based on the variability of smear distributions and smear thicknesses at the interface are presented in Figs. 12, 13, respectively.

Fig. 12
figure 12

Predictions of shaft resistance for SR-2 with changes in \(\gamma\) for different \({s}_{o}\): (a–d) and \(t/a\): (e–h)

Full size image
Fig. 13
figure 13

Predictions of shaft resistance for SR-3 with changes in \(\gamma\) for different \({s}_{o}\): (a–d) and \(t/a\): (e–h)

Full size image

It can be seen from Fig. 12 that the trend of all the curves tends to be hyperbolic but eventually reaches a residual state by approaching the critical \(({t/a)}_{cr}\) value. When the smear distribution at the interface is kept constant and the \(t/a\) value is continuously changed, the shaft resistance reduction rate tends to decrease by approaching \(({t/a)}_{cr}\). It is due to the rock in the smeared portion of the interface not being able to contribute any further towards the shaft resistance development. The same can be claimed by observing Fig. 13 as the trend exhibits a drop with respect to the clean shaft resistance for every increment of the \(t/a\) value. Subsequently, the residual interface resistance value is reached by attaining the \({({s}_{o})}_{{\text{max}}}\) value of 1.

Another interesting aspect of these predictions is the behaviour of the 22.5° (\({\text{RF}}\) = 0.51) and 17.5° (\({\text{RF}}\) = 0.40) roughness configurations. Theoretically, the interface resistance for the fully smeared case should be close for these two configurations. However, the formulation of \(({{\text{RF}})}_{cr}\) based on Fig. 11 has resulted in the shaft resistance values of the 22.5° roughness configuration to have the same \({m}_{e}\) and \({i}_{e}\) parameters as the 17.5°, but with a higher \({\tau }_{u-{\text{rough}}}\). This is the reason for the 22.5° curves to have a similar behaviour as 17.5°, but at a higher origin point in the ultimate shaft resistance axis.

It can be evidenced from these predictions that this shear strength model can be used as a framework for developing an enhanced interface model in the future to predict the shaft resistance of large-scale RSPs in terms of various rock strengths, interface roughness and smear fabrics. The input parameters for this framework can be determined in the laboratory through shear testing of concrete–rock interface to determine \({\tau }_{u-{\text{rough}}}\); and in the field through the combination of available and emerging technologies—roughness using the laser-based socket measurements (Collingwood et al. 1999), shaft area using the Shaft Area Profile Evaluator (SHAPE) (Pile Dynamics and GRL Engineers 2019), and smear thickness using the Shaft Quantitative Inspection Device (SQUID) (Pile Dynamics and GRL Engineers 2019) and Ultrasonic Borehole Imager (Schlumberger 2002). It should be noted that since there are no other experimental or field-scale studies illustrating the effect of smear fabric at the interface, it becomes challenging to compare the predictions of this interface model with the works of others.

7 Conclusions

This paper discusses the development of a unified interface shear strength framework for piles in soft rocks by conducting parametric studies through the calibrated RSP-DEM model. Three different synthetic soft rocks were created in the laboratory and subjected to calibration and validation for conducting pile-load tests in DEM. The impact of socket roughness was studied, and the effects of the various smear fabric parameters, namely the area proportion, placement and thickness, were also investigated. The main findings from this study are as follows.

  1. 1)

    The friction coefficient (adhesion factor) was determined as a function of the roughness of the interface. The socket resistance of the clean shafts was expressed in terms of the friction coefficient, Young’s modulus and UCS of the rock.

  2. 2)

    The inclusion of smear in the form of area proportion and thickness at the interface results in an exponential reduction in the shaft resistance for varied roughness configurations and rock properties. The behaviour tends to exhibit a residual response beyond a certain limit when the critical smear thickness to asperity height ratios \((({t/a)}_{cr})\) and the maximum smear area proportion at the interface \(({\left({s}_{o}\right)}_{{\text{max}}})\) have been reached. This study reaffirms the \(({t/a)}_{cr}\) value of 1.75 for different roughness configurations and varied rock properties.

  3. 3)

    The progressive decay of the slope and equation intercepts of the smeared shaft signifies a residual state beyond a critical roughness factor (\(({{\text{RF}})}_{cr})\), where the socket roughness loses its influence over the load-carrying capacity of the shaft and the smear precedes over the interface strength. This study identifies the \(({{\text{RF}})}_{cr}\) value to be 0.4.

  4. 4)

    At low smear occupancies, the effect of smear on the leading-face-smeared interface differs minimally from the both-faces-smeared interface. However, the gap in the shaft resistance starts to increase between these two configurations with the increment in smear fabric at the interface and becomes constant beyond the \(({t/a)}_{cr}\) value.

  5. 5)

    The proposed unified interface shear strength framework can capture the shaft resistance of piles in soft rocks for both the clean and smeared cases. This interface model is applicable to a RSP system where the presence of smear effectively reduces the ultimate shaft resistance by a maximum of 75% percent for a fully smeared interface. The constants employed in this interface model are generally applicable for all soft rocks and are not specific to any roughness, smear or rock properties. The main advantage of this interface framework is the inclusion of smear fabric parameter, which can help to reduce the overcompensated factors of safety in industrial design practices.